Thermoeconomic and thermoenvironomic modeling and analysis of selected gas turbine power plants in Nigeria

Abstract

This study presents comprehensive thermoeconomic and thermoenvironomic modeling and analysis of selected gas turbine power plants in Nigeria using the first and second laws of thermodynamics (exergy) concept. Exergetic analysis was conducted using operating data obtained from the power plants to determine the exergy destruction and exergy efficiency of each major component of the gas turbine in each power plant. The results of the study showed that the combustion chamber (CC) is the most exergy destructive component compared to other cycle components. The percentage of exergy destruction in CC varies between 86.05% and 94.6%. By increasing the gas turbine inlet temperature (GTIT), the exergy destruction of this component can be reduced. The total exergy improvement potential of the selected plants varies from 54.04 to 159.88 MW. The component with the highest exergy improvement potential is the CC, which has the value that varies from 30.21 to 88.86 MW. Thermoeconomic analysis showed that the cost of exergy destruction is high in the CC, and an increase in the GTIT effectively decreases this cost. The exergy costing analysis revealed that the unit cost of electricity produced in the plants ranged from cents 1.99/kWh (N3.16/kWh) to cents 5.65 /kWh (N8.98/kWh). Thermoenvironomic analysis showed that the CO₂ emissions varied between 100.18 and 408.78 kg CO₂/MWh, while cost rate of environmental impact varied from 40.18 $/h (6, 388.62 N/h) to 276.97 $/h (44, 038. 23 N/h). The results further showed that CO₂ emissions and cost of environmental impact decrease with increasing GTIT. The sustainability index increase with increasing GTIT. Finally, this study will assist efforts to understand the thermodynamic losses in the gas turbine cycle, and to improve efficiency as well as provide future recommendations for better performance, sustainability, and lessening environmental impact of power plant.

Nomenclature

c

average unit cost (fuel or product)

C. and Z.

cost rates

c_p

specific heat at constant pressure [kJ/kg]

D_p

depletion number

E.

exergy rate [kW]

E._L

exergy loss rate

E._D

exergy destruction rate

ExIP

exergetic improvement potential

eCO₂

emissions of CO₂ per unit mass of fuel

f_k

exergoeconomic factor

m.

mass flow [kg/sec]

P

power output [kW]

pe

potential energy [kJ]

PEC

purchase equipment cost

r_p

pressure compression ratio

R

gas constant [kJ/mol – K]

S.

entropy rate

T_pz

primary zone combustion temperature

TDI

thermal discharge index

y_D

exergy destruction rate ratio

N

Nigerian Currency (NGN)

γ

adiabatic index

∆p_cc

pressure drop in combustion chamber (bar)

η_c

isentropic efficiency of compressor

η_T

isentropic efficiency of turbine

η_th

thermal efficiency

ε

exergetic efficiency

∅

rational efficiency

δ

component efficiency defect

ψ

overall exergetic efficiency

ξ

exergetic performance coefficient

π

dimensionless pressure

Ψ

hydrogen–carbon ratio

Φ

fuel–air equivalent ratio

τ

residence time

ε

CO₂ emissions per unit net electricity (kg CO₂/MWh)

i

inlet

e

exit or outlet

p

pressure

a

air

pg

combustion product

f

fuel

T

turbine

cc

combustion chamber

th

thermal

sys

system

0

ambient

cv

control volume

D

destruction

gen

generation

ac

air compressor

gt

gas turbine

k

component

tot

total

PH

physical

KN

kinetic

PT

potential

CHE

chemical

T

thermal

P

mechanical

OM

operating and maintenance

CI

capital investment

Introduction

The present world energy scenario exhibits that most of the energy requirements are met by fossil fuels which cannot be newly formed at any significant rate; the present stocks are therefore finite. Also these fossil fuels are not environmental friendly and emits significant amount of pollutants causing serious environmental issues, such as global warming, ozone layer depletion, and climate change [1]. Awareness of limited hydrocarbon resources, environmental and economic concerns, and ever-increasing demand for electricity necessitates the design of optimal gas turbine (GT) power plants in terms of technical and cost aspects [2].

Thermodynamic analysis of thermal systems for design and optimization purposes is essential for effective utilization of limited available fossil fuel. In this regard, there are two essential tools available, such as energy analysis and exergy analysis [3]. The most commonly used method for analysis of the energy conversion process is the first law of thermodynamics (energy analysis). However, there is increasing interest in combined utilization of the first and second laws, using such concepts as exergy and exergy destructions in order to evaluate the efficiency with which the available energy is consumed [4]. So, by analyzing the exergy of different energy forms, we can reduce the wastage of energy and utilize it in a more efficient way thus making it available for future use [5].

Energy and exergy analyses provide insight into losses in various components of a power generating system. Unlike energy, exergy is generally not conserved but is destroyed in the system. The major causes of irreversibilities like heat transfer through a finite temperature difference, chemical reactions, friction, and mixing are accounted by exergy analysis [6]. Exergy analysis, therefore, has potential of identifying the source, magnitude, and location of exergy destruction (thermodynamic inefficiencies) in a thermal system. Based on this fact, exergy analysis usually predicts the thermodynamic performance of an energy system and the efficiency of the system components by accurately quantifying the entropy generation of the components [7].

Thus, exergy analysis plays an important role in developing strategies and in providing guidelines for more effective use of energy in the existing power plants. Another important issue for improving the existing power system is the origin of the exergy loss. Hence, a clear picture, instead of only the magnitude of exergy loss in each section, is required. Therefore, the exergy analysis has been widely used for the evaluation of the existing thermal power plants (TPPs) [3]. Increasing application and recognition of the usefulness of exergy methods in power plant design and optimization have been observed and reported in a number of articles in recent years [8-11]. Ofodu and Abam [12] applied exergy concept in analyzing the performance of Afam IV TPP. The analysis was presented in the form of Sankey and Grassman diagrams, which give energy and exergy values at prescribed points in the plant. The results showed that the greatest exergy loss occurred in the turbine and the exhaust diffuser followed by combustion chamber (CC) losses. These are traced to high temperature, incomplete combustion, and mechanical losses in the various parts of the plant. Abam and Moses [13] carried out computer simulation of the performance of a 33 MW GT power plant, using exergy analysis. The result obtained showed that the largest amount of exergy destruction occurred in the CC and the least in the GT. Ganapathy et al. [14] performed an exergy analysis on an operating 50 MWe unit of lignite fired steam power plant, aiming to find the energy efficiency and exergy efficiency of the power plant. The results revealed that maximum energy loss of 39% occurs in the condenser, whereas the maximum exergy loss of 42.73% occurs in the combustor.

Rajkumar and Ashok [15] carried out an energy and exergy study on 55 MW TPP at 40 and 55 MW output, respectively, to pinpoint the losses taking place in the plant. Over 57.822% exergy destruction took place in the boiler. The overall plant efficiency (first law) varied between 22.015% and 24.208% and the second law efficiency varied between 19.938% and 22.208%. It was concluded that exergy analysis is the realistic criteria for performance measurement of any thermal systems. Balkrishna [16] carried out study on energy and exergy analysis of an actual captive steam power plant using blast furnace gas, a by-product of pig iron production. The result showed that the energy loss as a percentage of input energy was found to be maximum in the steam condenser (64%), followed by boiler (19%). The percentage ratio of the exergy destruction to the total exergy destruction was found to be at maximum in the boiler system (75%), followed by steam turbine (11%), and then steam condenser (8%). The study concluded that the boiler was the major source of irreversibility in the power plant and the chemical reaction was the most significant source of exergy destruction in the boiler. Fagbenle et al. [17] carried out a thermodynamic first and second law analysis on a 53 MWth (net) biogas fired integrated gasification steam injected gas turbine (BIG/STIG) power plant with thermal efficiency of 41.5% (power based) and 45.0% (power and recovered heat based), respectively. The second law analysis and the energy utilization diagrams revealed that the CC has the largest irreversibility, with about 79% of the total system exergy loss. Suggestions for reduction of this large exergy loss were made. These include addition of spray water and preheating of the reactants in the CC, and the use of exergy left in the stacks from heat recovery steam generator (HRSG). Aljundi [4] presented the energy and exergy analysis of Al-Hussein power plant in Jordan. The performance of the plant was estimated by a component-wise modeling and a detailed breakup of energy and exergy losses for the plant was considered. The result of the study showed that energy losses mainly occurred in the condenser where 134 MW was lost to the environment, while only 13 MW was lost from boiler system. The percentage ratio of the exergy destruction to the total exergy destruction was found to be maximum in the boiler system (77%) followed by the turbine (13%), and then the forced draft fan condenser (9%). It was concluded that the boiler was the major source of irreversibilities in the power plant. Chemical reaction was the most significant source of exergy destruction in the boiler system which can be reduced by preheating the combustion air and reducing the air–fuel ratio. Ehsana and Yilmazoglub [18] carried out an exergy analysis on a 240 MW_el TPP to be operated with 10 different types of Turkish lignite. Exergy destruction of each component was investigated by using conservation of mass, conservation of energy, and exergy destruction in an open system at steady state. Net energy and exergy efficiencies of the plant were calculated as 37.16% and 34.84%, respectively. The analysis of the case study revealed that the boiler is the major source of exergy destruction with 299.10 MW and 83.29% of the total exergy destruction of the overall plant. Ighodaro and Aburime [19] carried out an exergetic appraisal of Delta IV Power Station, Ughelli in Nigeria. The study employed the first and second laws of thermodynamics. In the exergetic analysis, mass and energy conservation laws were applied to each component. The turbine was found to have the largest exergetic efficiency of 95.4% while that of the total plant was 45.7%. The CC had the largest exergetic destruction (56%) while that of the total plant was 58.5%. Exergy analysis of a steam cycle with double reheat and turbine extraction was presented by Rashidi et al. [20]. In this study, six heaters were used, three of them at high pressure and the other three at low pressure with deaerator. The results of the study showed that the biggest exergy loss occurred in the boiler followed by the turbine. The results also showed that the overall thermal efficiency and the second law efficiency decreased as the condenser pressure increased for any fixed outlet boiler temperature, however, these parameters increased as the boiler temperature increased for any condenser pressure.

In the assessment of existing TPPs, the exergy destruction within a component represents not only a thermodynamic inefficiency but, in general, also an opportunity to reduce the investment cost and sometimes also the environmental impact associated with the component being considered and, thus, with the overall system. Thus, assessment of economic and environmental impacts of existing thermal plants from exergy analysis point of view is worthy of consideration.

The relationship between exergy and economics, particularly the trade-offs that normally occur between efficiency and costs, has been an important concern for decades and continues to be so. Economic methods based on exergy, also known as thermoeconomics or exergoeconomics, have evolved and are applied in assessing power plants performance [21]. Also, the environmental impacts and nonsustainability of energy use have become of significant concerns recently, and exergy methods have been used as improvement efforts to (1) reduce environmental emissions and lengthening the lives of resources through increasing efficiencies and (2) assess the potential impacts of emissions [22, 23]. Thermoenvironomic or exergoenvironomic combines exergy and environment analyses to determine thermodynamic efficiency and formation of environmental impacts on plant components. The analysis reveals the interdependencies between thermodynamic behavior and environmental impacts between plant components [24].

In the literature, many studies related to the linkages between exergy, economics, and environmental impact to assess performance of TPPs are reported [25-28]. Thermoenvironmental and economic analysis of simple and regenerative GT cycles with regression modeling and optimization was performed by Memon et al. [29]. In this study, a comprehensive modeling of simple and regenerative cycle GT power plants were conducted. Result of the study showed that the power output and efficiencies increased while CO₂ emissions decreased, with decreasing compressor inlet temperature (CIT) and increasing turbine inlet temperature (TIT). With increasing pressure ratio (PR) to some initial values, power output and efficiencies increased and CO₂ emissions decreased, which vary oppositely with increasing PR further. Furthermore, five objective functions (OBFs) were optimized for maximization of net power output, energy and exergy efficiencies, and minimization of CO₂ emissions and costs of the cycles. The optimal operating parameters thus obtained exhibit a trade-off between thermoenvironmental benefits and additional costs. The study concluded that, from the thermoenvironmental point of view, TIT should be selected as high as possible, however, this leads to an increase in the capital cost and levelized cost of electricity. Seyyed et al. [30] carried out thermoenvironomic optimization of GT cycles with air preheat. In this study, the effect of air preheater (APH) on thermoeconomic and thermoenvironomic optimizations in the thermodynamic cycles was investigated. The results showed that the existence of APH increased exergetic efficiency of the cycles and environmental impacts cost flow rate, whereas it decreased the total cost flow rate. Also, in the cycles without APH, the optimum values of decision variables corresponding to thermoeconomic and thermoenvironomic OBFs do not change considerably, while in the cycles with APH, they change noticeably. Mert et al. [31] carried out exergoeconomic analysis of a cogeneration plant in an iron and steel factory, in Turkey. The result of the study showed that cost of compressed air exiting the compressor was 3696.85 $/h, while the cost of power required for the compression was 3461.38 $/h. The cost of product exiting the CC, namely combustion gas, was 8048.49 $/h. The product of the CC was also the fuel of the GT, so the cost of the fuel of the GT was also 8048.49 $/h. Power generated at GT was 6002.15 $/h, while the unit exergy cost was 17.86 $/GJ. The cost of combustion gas exiting from GT and entering HRSG as fuel was 2356.19 $/h and the cost of steam produced at HRSG was 453.21 $/h for the 14 bar steam and 1458.11 $/h for the 45 bar steam. In other words, the costs of steam were 22.66 and 26.51 $/ton, respectively. Gorji-Bandpy and Goodarzian [32] carried out exergoeconomic optimization of GT power plant operating parameters using genetic algorithms. In the study, exergoeconomic optimization and analysis were performed on a 140 MW GT power plant. The two objectives considered in the study are thermodynamic (e.g., maximum efficiency and minimum fuel consumption) and economic (e.g., minimum cost per unit of time and maximum profit per unit of production). The results of the study showed that the unit cost of product decreased from 5.25 to 4.73 $/GJ, however, with 8.77% increase in capital investment, the exergy destruction cost decreased from 2947 to 2407 $/h. Sahoo [33] studied exergoeconomic analysis and optimization of a cogeneration system using evolutionary programming. In this study, a cogeneration system that produced 50 MW of electricity and 15 kg/sec of saturated steam at 2.5 bar was optimized using exergoeconomic principles and evolutionary programming. The result showed that the product cost, cost of electricity and steam, was 9.9% lower with respect to the base case. Exergoeconomic analysis for Unit Gt14 of South Tripoli GT power plant was investigated by Fellah et al. [34]. The methodology used in the study was based on the Specific Exergy Costing approach. Results of the study showed that the average cost per unit exergy net power equal to 7.1 $/GJ at 40% design load, and equal to 5.5 $/GJ at 60% design load, and equal to 4 $/GJ at full operating load. It was found that the cost of exergy destruction in the CC presented the main contribution to the total cost of exergy loss; its value varied in the CC from 1474 $/h at 40% design load to 1123 $/h at the full operating load. The contribution and the variation of cost of exergy destruction with load are lower for the other two main components.

Most of the past studies on combined exergy, exergoeconomic, and exergoenvironomic analyses of TPPs were based on a single power unit. In the present work, economic and environmental impacts of power plants from exergy point of view are performed on 11 GT units at three different stations in Nigeria.

The prime objectives of this study are:

1. To model a GT power plant and compare the simulation code with the actual existing GT power plants in Nigeria to ensure the correctness of a simulation code.
2. To perform exergy, thermoeconomic, and thermoenvironomic analyses of selected GT power plants in Nigeria.
3. To identify the most significant source of exergy destruction in the power plants and the location(s) of occurrence and to demonstrate exergy analysis as a powerful tool to assist in the quest for sustainable development.
4. To estimate unit cost of electricity (using exergy costing) in the selected power plants.
5. To quantify the carbon dioxide (CO₂) emissions and cost of environmental impact from selected GT stations.
6. To determine the sustainability index (SI) for the system and quantify its variation with exergy destruction.

System Description

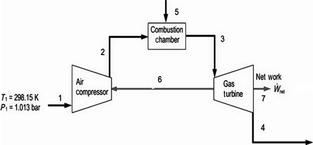
GT power plants in Nigeria operate on simple GT engine. The simple GT power plant mainly consists of a GT coupled to a rotary type air compressor and a CC which is placed between the compressor and turbine in the fuel circuit. Auxiliaries, such as cooling fan, water pumps, etc., and the generator itself are also driven by the turbine. Other auxiliaries are starting device, lubrication system, duct system, etc. For ease of analysis, the steady-state model of simple GT is presented in Figure 1.

Figure 1. A schematic diagram for a simple gas turbine cycle.

Methodology

Based on the idea that exergy represents the only rational basis for assigning both costs and environmental impacts to the energy carriers and to the inefficiencies within the system, a methodological approach called thermoeconomic (exergoeconomic) analysis is applied together with thermoenvironomic (exergoenvironomic) analysis to evaluate the performance of selected GT power plants in Nigeria.

Modeling and simulation of GT power plant

The thermodynamic performance of power plants of 11 different capacities is estimated by a component-wise modeling followed by a system simulation. A flow-sheet computer program, “MATLAB R2010a Software,” (The MathWorks, Inc., Natick, MA) is used for the study. It is designed for the steady-state thermodynamic (exergy, thermoeconomic, and thermoenvironomic) modeling and analysis of systems for the production of electricity.

The model employed in this study to simulate the performance of the simple GT system presented in Figure 1 comprises three different submodels: compressor, CC, and turbine. Under steady-state condition, application of the mass and exergy balance equations are used to determine the flow rate, exergy destruction rate, and the exergy efficiency for each component in the base case and for the whole system in the power plant.

Basic assumptions

The following basic assumptions are made to carry out thermodynamic modeling and simulation of the power plants [27, 35, 36]:

1. All the thermodynamic processes in GT cycle are considered based on the steady-state model.
2. The principle of ideal gas mixture was applied for the air and combustion products with variable specific heat.
3. The fuel injected to the CC is assumed to be natural gas.
4. The dead/reference state condition is P₀ = 1.013 bar and T₀ = 298.15 K.
5. Complete combustion of fuel occurs in CC.
6. In the CC, 2% pressure drop was assumed.
7. The exergy value of air entering the compressor was assumed zero.

The thermoeconomic (exergoeconomic) model

The thermoeconomic analysis developed in this work combines the second law of thermodynamics with the exergy concept in combination with economic engineering and the following four steps proposed by Tsatsaronis [37] were followed in this study. The first step is exergy analysis. The second step is economic analysis of each of the plant component. This step provides the monetary costs associated with investment, operation, and maintenance. The third step is the estimation of exergetic costs associated with each flow and finally, the fourth step is the exergoeconomic evaluation of each system component.

Exergy model

Exergy can be divided into four distinct components. The two important ones are the physical exergy and chemical exergy. In this study, the two other components which are kinetic exergy and potential exergy are assumed to be negligible, as the changes in them are negligible. The physical exergy is defined as the maximum theoretical useful work obtained as a system interacts with an equilibrium state. The chemical exergy is associated with the departure of the chemical composition of a system from its chemical equilibrium. The chemical exergy is an important part of exergy in combustion processes. Applying the first and the second laws of thermodynamics, the following exergy balance is obtained [27, 28, 36]:

${\dot {E}}_{x}={\sum }_{j}\left(1-{\frac {T_{0}}{T_{j}}}\right){\dot {Q}}_{j}+$${\dot {W}}_{CV}+{\sum }_{i}m_{i}e_{i}-{\sum }_{e}m_{e}e_{e}$

(1)

The subscripts i, e, j, and 0 refer to conditions at inlet and exits of control volume (CV) boundaries and reference state. Equation (1) can be written as:

$E_{i}^{\quad tot}-E_{e}^{\quad tot}-E_{D}=0$

(2)

Equation (2) implies that the exergy change of a system during a process is equal to the difference between the net exergy transfer through the system boundary and the exergy destroyed within the system boundaries as a result of irreversibilities.

The exergy balance equations and the exergy destroyed during each process and for the whole GT plant are written as follows [38]:

Air compressor

${\dot {E}}^{WAC}=\left({\dot {E}}_{1}^{\quad }T-{\dot {E}}_{2}^{\quad }T\right)+$$\left({\dot {E}}_{1}^{\quad }P-{\dot {E}}_{2}^{\quad }P\right)+$$T_{0}\left({\dot {S}}_{1}-{\dot {S}}_{2}\right)$

(3a)

${\dot {E}}_{DAC}=T_{0}({\dot {S}}_{2}-{\dot {S}}_{1})=\quad {\dot {m}}T_{0}[c_{p1-2}ln(T_{2}/T_{1})-$$Rln(P_{2}/P_{1})]$

(3b)

Combustion chamber

${\dot {E}}^{CHE}+\left({\dot {E}}_{2}^{T}+{\dot {E}}_{5}^{T}-\right.$$\left.{\dot {E}}_{3}^{T}\right)+\left({\dot {E}}_{2}^{P}+{\dot {E}}_{5}^{P}-\right.$$\left.{\dot {E}}_{3}^{P}\right)+T_{0}\left({\dot {S}}_{3}-{\dot {S}}_{2}+\right.$$\left.{\dot {S}}_{5}+{\frac {{\dot {Q}}_{CC}}{T_{0}}}\right)=$$0$

(4a)

${\begin{array}{r}{\dot {E}}_{DC}amp=T_{0}\left[{\dot {S}}_{3}-{\dot {S}}_{2}+{\dot {S}}_{5}+{\frac {{\dot {Q}}_{CC}}{T_{0}}}\right]\\amp={\dot {m}}_{T_{0}}\lbrace (c_{p2-3}ln\left(T_{3}/T_{2}\right)-Rln\left(P_{3}/P_{2}\right))+(c_{p5}ln\left(T_{5}/T_{0}\right)-Rln\left(P_{5}/P_{0}\right))+{\frac {c_{p2-3}\left(T_{3}-T_{2}\right)}{T_{inCC}}}\rbrace \end{array}}$

(4b)

Gas turbine

${\dot {E}}^{WGT}=\left({\dot {E}}_{3}^{T}-{\dot {E}}_{4}^{T}\right)+$$\left({\dot {E}}_{3}^{P}-{\dot {E}}_{4}^{P}\right)+T_{0}\left({\dot {S}}_{3}-\right.$$\left.{\dot {S}}_{4}\right)$

(5a)

${\dot {E}}_{DGT}={\dot {m}}T_{0}[c_{p3-4}ln(T_{4}/T_{3})-Rln(P_{4}/P_{3})]$

(5b)

Exergy improvement potential of GT plant

The exergy improvement potential of an energy conversion system is a measure of how much and how easily the system could be improved for optimization purposes. It is a thermodynamic approach combining exergy losses and effectiveness to have a more complete parameter of the performance of the system [39]. The exergy improvement potential makes it possible to determine the critical points of the system stating a hierarchy on its components in such a way that the measure be applied in the places where they will be most effective.

The exergetic improvement potential is obtained from the exergy losses and the efficiency of the system. It is calculated by the equation (6) [40, 41]:

${\mbox{ExIP}}=(1-\epsilon )I,$

(6)

where ExIP is the exergetic improvement potential, ε is the exergetic efficiency (%), and I is the exergy loss or irreversibility rate.

$I=\vartriangle E_{lost}=E_{in}-E_{out}>0$

(7)

For a CV at steady state, the exergetic efficiency is

$\epsilon ={\frac {{\dot {E}}_{P}}{{\dot {E}}_{F}}}=1-{\frac {{\dot {E}}_{D}+{\dot {E}}_{L}}{{\dot {E}}_{F}}}$

(8)

where the rates at which the fuel is supplied and the product is generated are denoted by E._F and E._P, respectively. E._D and E._L denote the rates of exergy destruction and exergy loss, respectively.

In any real engineering system (which is irreversible) exergy is degraded and the exergy efficiency is consequently less than unity. According to Van Gool [42], the maximum improvement in the exergy efficiency of a process or system is obviously achieved when ${\textstyle \Delta E_{lost}}$ is minimized.

The ith component efficiency defect denoted by δ_i is given by equation (9) [43]:

${\delta }_{i}={\frac {\sum \vartriangle {\dot {E}}_{Di}}{\sum \vartriangle {\dot {E}}_{xin}}}$

(9)

The overall exergetic efficiency of the entire plant is given as [43]:

${\varphi }_{i}={\frac {{\dot {W}}_{net}}{{\dot {E}}_{xfuel}}}$

(10)

The amount of exergy loss rate per unit power output as important performance criteria is given as:

$\xi ={\frac {{\dot {E}}_{D\quad Total}}{{\dot {W}}_{net}}}$

(11)

where ξ is the exergetic performance coefficient.

Exergy destruction rate and efficiency equations for the GT power plant components and for the whole cycle are summarized in Table 1.

Table 1. The exergy destruction rate and exergy efficiency equations for gas turbine

Component	Exergy destruction rate	Exergy efficiency
Compressor	${\textstyle {\dot {E}}_{DC}=\quad {\dot {E}}_{in}-\quad {\dot {E}}_{out}+}$$\quad {\dot {W}}_{C}$	${\textstyle \epsilon ={\frac {{\dot {E}}_{out}-\quad {\dot {E}}_{in}}{\dot {W}}}}$
Combustion chamber	${\textstyle {\dot {E}}_{DCC}=\quad {\dot {E}}_{in}-\quad {\dot {E}}_{out}+}$$\quad {\dot {E}}_{fuel}$	${\textstyle \epsilon ={\frac {{\dot {E}}_{out}}{{\dot {E}}_{in}-\quad {\dot {E}}_{fuel}}}}$
Gas turbine	${\textstyle {\dot {E}}_{DT}=\quad {\dot {E}}_{in}-\quad {\dot {E}}_{out}-}$$\left(\quad {\dot {W}}_{net}+\quad {\dot {W}}_{C}\right)$	${\textstyle \epsilon ={\frac {{\dot {W}}_{net}-\quad {\dot {W}}_{C}}{{\dot {E}}_{in}-\quad {\dot {E}}_{out}}}}$
Total exergy destruction rate	${\textstyle {\dot {E}}_{DTotal}=\Sigma \quad \quad {\dot {E}}_{D}=}$$\quad {\dot {E}}_{DC}+\quad {\dot {E}}_{DCC}+\quad {\dot {E}}_{DT}$

Economic model

The economic analysis, conducted as part of the exergoeconomic analysis, provides the appropriate monetary values associated with the investment, operation, maintenance, and fuel costs of the system being analyzed [44, 45]. These values are used in the cost balances [46].

The annualized (levelized) cost method of Moran [47] is used to estimate the capital cost of system component in this work.

The amortization cost for a particular component may be written as [48]:

${\mbox{PW}}={\mbox{PEC}}-\left({\mbox{SV}}\right){\mbox{PWF}}\left(i,n\right)$

(12)

where the salvage value (SV) at the end of the nth year is taken as 10% of the initial investment for component (or purchase equipment cost, PEC). The present worth (PW) of the component may be converted to the annualized cost by using the capital recovery factor, CRF (i, n) [32, 48], that is,

${\dot {C}}\left(\$,/{\mbox{year}}\right)={\mbox{PW}}\times {\mbox{CRF}}\left(i,n\right)$

(13a)

${\mbox{CRF}}\left(i,n\right)=i/1-{\left(1+i\right)}^{-n}$

(13b)

${\mbox{PWF}}={\left(1+i\right)}^{-n}$

(13c)

where i is the interest rate and it is taken to be 17% [32], n is the total operating period of the plant in years and was obtained from the selected plants. PEC is the purchased equipment cost.

Equations for calculating the PEC for the components of the GT power plant are as follows [27, 47]:

Air compressor

${\mbox{PEC}}_{ac}=\left[{\frac {71.1{\dot {m}}_{a}}{0.9-{\eta }_{sc}}}\right]\left[{\frac {P_{2}}{P_{1}}}\right]ln\left[{\frac {P_{2}}{P_{1}}}\right]$

(14)

Combustion chamber

${\mbox{PEC}}_{cc}=\left[{\frac {46.08{\dot {m}}_{a}}{0.995-P_{3}/P_{2}}}\right]\left[1+\right.$$\left.{\mbox{exp}}/!\left(0.018T_{3}-26.4\right)\right]$

(15)

Gas turbine

${\mbox{PEC}}_{gt}=\left[{\frac {479.34{\dot {m}}_{g}}{0.92-{\eta }_{st}}}\right]ln\left[{\frac {P_{3}}{P_{4}}}\right]\left[1+\right.$$\left.{\mbox{exp}}\quad \left(0.036T_{3}-54.4\right)\right]$

(16)

Dividing the levelized cost by annual operating hours, N, we obtain capital cost rate for the kth component of the plant [49]:

${\dot {Z}}_{k}={\frac {{\phi }_{k}{\quad {\dot {C}}}_{k}}{3600\times N}}$

(17)

The maintenance cost is taken into consideration through the factor φ_k = 1.06 for each plant component [27, 49].

Estimation of GT exergy costing

Exergoeconomics is based on exergy costing and is usually applied at the plant component [50].

In order to perform exergy costing calculations, GT components (Fig. 1) must be combined into suitable control volumes (CVs), on which exergetic cost balance equation was then applied, on an individual basis. The component in each CV with their input and output streams are given as follows:

• CV 1: Air compressor (AC) – Input streams: 1, 6
• Output stream: 2
• CV 2: Combustion chamber (CC) – Input streams: 2, 5
• Output stream: 3
• CV 3: Gas turbine (GT) – Input stream: 3
• Output streams: 4, 6, 7

For a component that receives heat transfer and generates power, cost balance equation may be written as follow [27, 32, 51]:

$\sum {\left(c_{e}{\quad {\dot {E}}}_{e}\right)}_{k}+c_{w,k}\quad {\dot {W}}_{k}=$$c_{q,k}{\dot {\quad E}}_{q,k}+\sum {\left(c_{i}{\dot {\quad E}}_{i}\right)}_{k}+$${\dot {Z}}_{k}$

(18)

${\dot {C}}_{j}=c_{j}{\dot {\quad E}}_{j}$

(19)

The cost–balance equations for all the components of the system construct a set of nonlinear algebraic equations, which was solved for C._j and c_j.

The formulations of cost balance for each component and the required auxiliary equations are as follows [32]:

Air compressor

${\dot {C}}_{2}={\dot {C}}_{1}+{\dot {C}}_{6}+{\dot {Z}}_{ac}$

(20)

where subscript 6 denotes the power input to the compressor.

Combustion chamber

${\dot {C}}_{3}={\dot {C}}_{2}+{\dot {C}}_{5}+{\dot {Z}}_{cc}$

(21)

Gas turbine

${\dot {C}}_{4}+{\dot {C}}_{6}+{\dot {C}}_{7}={\dot {C}}_{3}+{\dot {Z}}_{gt}$

(22)

The auxiliary equation for GT is given as:

${\frac {{\dot {C}}_{3}}{{\dot {E}}_{3}}}={\frac {{\dot {C}}_{4}}{{\dot {E}}_{4}}}$

(23)

An additional auxiliary equation is formulated assuming the same unit cost of exergy for the net power exported from the system and power input to the compressor:

${\frac {{\dot {C}}_{6}}{{\dot {W}}_{AC}}}={\frac {{\dot {C}}_{7}}{{\dot {W}}_{n}}}$

(24)

The cost rate associated with fuel (methane) is obtained from [52]:

${\dot {C}}_{f}=c_{f}\quad {\dot {m}}_{f}\times {\mbox{LHV}},$

(25)

where the fuel cost per energy unit (on an LHV basis) is c_f = 0.004$/MJ [51], ${\textstyle {\dot {m}}_{f}}$ is the mass flow rate of fuel and LHV is the lower heating value of fuel.

A zero unit cost is assumed for air entering the air compressor, that is,

${\dot {C}}_{1}=0$

(26)

In order to estimate the cost of exergy destruction in each component of the plant, the cost–balance equations were solved for each component. In application of the cost–balance equation (eq. (18)), there is usually more than one inlet and outlet streams for some components. In this case, the numbers of unknown cost parameters are higher than the number of cost–balance equations for that component. Auxiliary exergoeconomic equations (eqs. (23) and (24)) are developed to solve this problem. Implementing equation (18) for each component together with the auxiliary equations forms a system of linear equations as follows [36, 53]:

$\left[{\dot {E}}_{k}\right]\times \left[c_{k}\right]=\left[{\dot {Z}}_{k}\right]$

(27)

where [E._k], [c_k], and [Z._k] are the matrix of exergy rate which were obtained in exergy analysis, exergetic cost vector (to be evaluated), and the vector of Z._k factors (obtained in economic analysis), respectively.

The above set of equations was solved using MATLAB R2010a to obtain the cost rate of each line in Figure 1.

Exergoeconomic variables for GT components evaluation

In exergoeconomic evaluation of thermal systems, certain quantities play an important role. These are the average cost of fuel (c_F,k), average unit cost of product (c_P,k), the cost rate of exergy destruction (C._D,k), relative cost difference r_k, and exergoeconomic factor f_k.

Then the average costs per unit of fuel exergy (c_F,k) and product exergy (c_P,k) are calculated from [34]:

$c_{F,k}={\frac {{\dot {C}}_{F,k}}{{\dot {E}}_{F,k}}}$

(28)

$c_{P,k}={\frac {{\dot {C}}_{P,k}}{{\dot {E}}_{P,k}}}$

(29)

The cost rate associated with exergy destruction is estimated as:

${\dot {C}}_{D,k}=c_{F,k}\quad {\dot {E}}_{D,k}$

(30)

Relative cost difference r_k is given as [54]:

$r_{k}={\frac {c_{P,k}-c_{F,k}}{c_{F,k}}}={\frac {1-{\epsilon }_{k}}{{\epsilon }_{k}}}+$${\frac {{\dot {Z}}_{k}}{c_{F,k}{\quad {\dot {E}}}_{p,k}}}$

(31)

One indicator of exergoeconomic performance is the exergoeconomic factor, f_k. The exergoeconomic factor is defined as [32, 34]:

$f_{k}={\frac {{\dot {Z}}_{k}}{{\dot {Z}}_{k}+{\dot {C}}_{D,k}}}$

(32)

The thermoenvironomic (exergoenvironomic) model

To minimize the environmental impacts, a primary target is to increase the efficiency of energy conversion processes and, thus, decrease the amount of fuel and the related overall environmental impacts, especially the release of carbon dioxide, which is one of the main components of greenhouse gas [27].

In this study, three steps were applied to carry out the exergoenvironomic analysis of GT system. The first step is the determination of pollutant emission (CO and NOx) in grams per kilogram of fuel, the estimation of the total cost rate of product, and environmental impact and CO₂ emission calculation.

Determination of pollutant emission

In order to determine the pollutant emission in grams per kilogram of the fuel, the adiabatic flame temperature in the CC has to be computed first.

The adiabatic flame temperature in the primary zone of the CC is derived from the expression given by [55]:

$T_{PZ}=A{\sigma }^{\propto }{\mbox{exp}}\quad \left(\beta {\left(\sigma +\lambda \right)}^{2}\right){\pi }^{x}{\theta }^{y}{\psi }^{z}$

(33)

where π is a dimensionless pressure P₂/P_ref (P₂ being the combustion pressure and P_ref = 1.013 bar); θ is a dimensionless temperature T₂/T_ref (T₂ being the inlet temperature and T_ref = 298.15 K); ψ is the H/C atomic ratio (ψ = 4); σ = φ for ϕ ≤ 1 (ϕ is the fuel to air equivalent ratio), and σ = ϕ − 0.7 for ϕ ≥ 1. Moreover, x, y, and z are quadratic functions of σ based on the following equations [25, 56]:

$x=a_{1}+b_{1}\sigma +c_{1}{\sigma }^{2}$

(34)

$y=a_{2}+b_{2}\sigma +c_{2}{\sigma }^{2}$

(35)

$z=a_{3}+b_{3}\sigma +c_{3}{\sigma }^{2}$

(36)

where parameters A, α, β, λ, a_i, b_i, and c_i are constant parameters. All the parameters in equations (34)-(36) are listed in Table 2.

Table 2. Constants for equations (34)-(36)

Constants	0.3 ≤ φ ≤ 1.0		0.3 ≤ φ ≤ 1.0
	0.92 ≤ θ ≤ 2	2 ≤ θ ≤ 3.2	0.92 ≤ θ ≤ 2	2 ≤ θ ≤ 3.2
A	2361.7644	2315.752	916.8261	1246.1778
α	0.1157	−0.0493	0.2885	0.3819
β	−0.9489	−1.1141	0.1456	0.3479
λ	−1.0976	−1.1807	−3.2771	−2.0365
a1	0.0143	0.0106	0.0311	0.0361
b1	−0.0553	−0.045	−0.078	−0.085
c1	0.0526	0.0482	0.0497	0.0517
a2	0.3955	0.5688	0.0254	0.0097
b2	−0.4417	−0.55	0.2602	0.502
c2	0.141	0.1319	−0.1318	−0.2471
a3	0.0052	0.0108	0.0042	0.017
b3	−0.1289	−0.1291	−0.1781	−0.1894
c3	0.0827	0.0848	0.096	0.1037

The amount of CO and NOx produced in the CC and combustion reaction depends on the adiabatic flame temperature [25, 27, 56]. Accordingly, to determine the pollutant emission in grams per kilogram of the fuel, the equations proposed by [55] are used in this study.

${\dot {m}}_{NOx}={\frac {0.15E16{\tau }^{0.5}{\mbox{exp}}(-71100/T_{PZ})}{P_{2}^{0.05}(\Delta P_{2}/P_{2})}}$

(37)

${\dot {m}}_{CO}={\frac {0.179E9{\mbox{exp}}(7800/T_{PZ})}{P_{2}^{2}\tau (\Delta P_{2})}},$

(38)

where τ is the residence time in the combustion zone (τ is assumed constant and is equal to 0.002 sec); T_pz is the primary zone combustion temperature; P₂ is the combustor inlet pressure; ∆P₂/P₂ is the nondimensional pressure drop in the CC.

Cost of environmental impact

The cost of environmental impact expresses the environmental impact as the total pollution damage ($/s) due to CO and NOx emission by multiplying their respective flow rates by their corresponding unit damage cost (C_CO, and C_NOx are equal to 0.02086 $/kg_CO and 6.853 $/kg_NOx) [27, 45]. In the present work, the cost of pollution damage is considered to be added directly to the expenditures that must be paid.

Total cost rate:

${\dot {C}}_{Tot}={\dot {C}}_{f}+{\sum }_{k}{\dot {Z}}_{k}+{\dot {C}}_{D}+$${\dot {C}}_{env}$

(39)

where

${\dot {C}}_{env}=C_{CO}\quad {\dot {m}}_{CO}+C_{NOX}\quad {\dot {m}}_{\quad NOX}$

(40)

${\dot {C}}_{f}=c_{f}\quad {\dot {m}}_{f}\times {\mbox{LHV}}$

(41)

where ${\textstyle {\dot {Z}}_{k}}$, ${\textstyle {\dot {C}}_{f}}$, ${\textstyle {\dot {C}}_{D}}$, and ${\textstyle {\dot {C}}_{env}}$ are the purchase cost of each component, fuel cost, cost of exergy destruction, and cost of environmental impact, respectively.

CO₂ emissions calculation

Using the combustion equations, the normalized CO₂ emission of the plant is expressed as [27, 57]:

$\epsilon ={\frac {{\dot {m}}_{CO_{2}}}{{\dot {W}}_{net}}}$

(42)

where ε is the CO₂ emission per unit net electricity output (kg CO₂/MWh).

The effect of CO₂ emissions is of considerable significance, such that reduction of its harmful release is twofold. The first is obviously related to communal and environmental health. The second, as suggested in many references, is improvement in reduction of harmful emissions in the CC can lead to improvements of GT cycle efficiency.

Reduction of the harmful emissions in the CC to the environment has proven its benefits in increasing system efficiency, which in turn increases sustainability by lengthening the lives of the fuel resources. The relationships between sustainability, exergy efficiency, and environmental impact have been previously documented [22, 58]. They proposed that efficient fuel consumption could be characterized by a depletion number defined as:

$D_{p}={\frac {{\dot {E}}_{dest}}{{\dot {E}}_{xin}}}$

(43)

where E._dest is the exergy destruction and E._xin is the exergy input by fuel consumption. The relationship between the depletion number and the exergy efficiency is described by:

${\eta }_{ex}=1-D_{p}$

(44)

Furthermore, the sustainability of the fuel resource can be expressed by a sustainability index (SI) as the inverse of the depletion number [57]:

${\mbox{SI}}={\frac {1}{D_{p}}}$

(45)

Results and Discussion

The average operating data for the selected GT power plants for the period of 6 years (2005–2010) are presented in Table 3.

Table 3. Average operating data for selected gas turbine power plants

Plant/average operating data	AES station			Afam station				Delta station
	PB204(AES1)	PB209(AES2)	PB210(AES3)	GT17(AF1)	GT18(AF2)	GT19(AF3)	GT20(AF4)	GT9(DEL1)	GT10(DEL2	GT18(DEL3)	GT20(DEL4)
Ambient temperature, T1 (K)	303.63	302.31	305.28	300.34	301.48	300.38	300.9	300.55	301.41	301.15	301.79
Compressor outlet temperature, T2 (K)	622.31	627.48	636.28	593.73	595.82	610.90	618.32	613.73	619.07	634.32	630.32
Turbine inlet temperature, T3 (K)	1218.62	1256.86	1222.45	1133.4	1192.82	1200.15	1215.65	1226.15	1224.73	1233.57	1234.73
Turbine outlet temperature, T4 (K)	750.00	755.00	827.05	712.73	723.75	770.07	807.32	710.56	707.48	730.15	705.07
Temperature of exhaust gas, Texh (K)	715.40	750.52	746.48	731.45	664.65	707.23	741.48	622.65	649.90	635.65	636.73
Compressor inlet pressure, P1 (bar)	1.013	1.013	1.013	1.013	1.013	1.013	1.013	1.013	1.013	1.013	1.013
Compressor outlet pressure, P2 (bar)	9.8	9.86	9.60	9.50	9.80	9.60	9.60	11.05	10.98	10.82	10.84
Pressure ratio	9.00	9.14	9.48	9.38	9.67	9.48	9.48	10.91	10.84	10.68	10.70
Mass flow rate of fuel (kg/sec)	2.58	2.54	2.81	6.50	6.40	8.10	8.40	3.08	3.10	8.15	8.13
Inlet mass flow rate of air (kg/sec)	122.16	122.20	121.93	359.00	359.00	470	470	140	140	375	375
Power output (MW)	29.89	29.37	31.52	49.90	58.00	132	135.4	19.42	20.8	92.8	93.42
Lower heating value of fuel (kJ/kg)	47,541.57	47,541.57	47,541.57	48,948.3	48,948.3	48,948.3	48,948.3	46,778	46,778	46,778	46,778

Results of exergy analysis

The exergy flow rates at the inlet and outlet of each component of the plants were evaluated based on the values of measured properties such as pressure, temperature, and mass flow rates at various states. These quantities were used as input data to the computer program (MATLAB) written to perform the simulation of the performance of the components of the GT power plant and the overall plant.

Table 4 presents results of the net exergy flow rates crossing the boundary of each component of the plants, exergy destruction, exergy defect, exergetic performance coefficient, and exergy efficiency of each component of the plants. The two most important performance criteria, exergy efficiency and exergetic performance coefficient (ξ) vary from 15.66% to 30.72% and 1.45 to 2.44, respectively, for the considered plants. Since the condition of good performance is derived from a higher overall exergetic efficiency but lower exergetic performance coefficient for any thermal system, hence, it can be inferred that AF2, AF1, and DEL4 GT plants have good performance.

Table 4. Result of exergy performance analysis

Exergy performance indicator	PB204(AES1)	PB209(AES2)	PB210(AES3)	GT17(AF1)	GT18(AF2)	GT19(AF3)	GT20(AF4)	GT9(DEL1)	GT10(DEL2)	GT18(DEL3)	GT20(DEL4)
Installed rated power (MW)	33.5	33.5	33.5	75.0	75.0	138.0	138.0	25.0	25.0	100.0	100.0
Fuel exergy flow rate (MW)	220.53	235.23	237.68	327.96	363.28	459.15	449.06	274.85	276.78	441.20	440.24
Exergy destruction rate of AC (MW)	4.69	4.98	5.64	8.62	8.09	13.14	14.80	3.14	3.63	13.36	12.48
Exergy destruction of CC (MW)	56.55	56.58	55.35	139.42	159.84	176.78	180.83	62.52	61.76	171.84	173.33
Exergy destruction rate of turbine (MW)	0.29	0.52	0.23	5.99	1.47	9.39	14.50	0.39	0.14	0.70	1.80
Total exergy destruction rate (MW)	61.54	62.09	61.23	154.02	169.40	199.31	210.13	66.04	65.53	185.91	187.61
Exergy destruction of AC (%)	7.62	8.03	9.21	5.59	4.78	6.60	7.04	4.75	5.54	7.19	6.65
Exergy destruction of CC (%)	91.90	91.13	90.39	90.51	94.36	88.70	86.05	94.67	94.25	92.43	92.39
Exergy destruction rate of turbine (%)	0.48	0.84	0.41	3.89	0.87	4.71	6.90	0.58	0.21	0.38	0.96
Efficiency defect of AC (%)	14.01	14.83	16.83	9.15	8.43	12.46	14.03	7.79	9.05	12.52	11.69
Efficiency defect of CC (%)	66.11	66.26	64.63	58.31	58.05	58.35	56.20	73.45	72.43	56.11	56.97
Efficiency defect of turbine (%)	0.38	0.68	0.32	3.05	0.68	4.08	6.50	0.42	0.15	0.29	0.74
Total efficiency defect (%)	80.50	81.77	81.78	70.51	67.16	74.89	76.73	81.66	81.63	68.92	69.40
Exergy efficiency of AC (%)	85.99	85.17	83.17	90.85	91.57	87.54	85.97	95.21	90.95	87.48	88.31
Exergy efficiency of CC (%)	74.36	75.95	76.71	57.49	56.00	61.50	59.73	77.25	77.69	61.05	60.63
Exergy efficiency of turbine (%)	99.62	99.32	99.67	96.86	99.32	95.75	93.09	99.57	99.85	99.71	99.25
Overall exergetic efficiency (%)	19.50	18.23	18.22	29.49	32.84	25.11	23.27	18.34	18.37	31.08	30.60
Exergetic performance coefficient (ξ)	1.43	1.45	1.46	1.59	1.32	1.73	2.01	1.47	1.59	1.36	1.39
Exergy improvement potential
Air compressor (MW)	3.94	4.14	4.71	7.83	6.88	8.59	14.95	2.89	3.30	11.69	11.02
Combustion chamber (MW)	38.48	40.33	43.82	69.49	68.52	85.81	88.86	30.47	30.21	78.48	78.67
Turbine (MW)	0.015	0.023	0.13	0.19	0.22	1.05	2.50	0.15	0.17	1.00	0.38
Entire plant (MW)	119.44	147.15	159.28	98.30	89.99	124.18	59.99	54.04	56.46	159.88	143.28

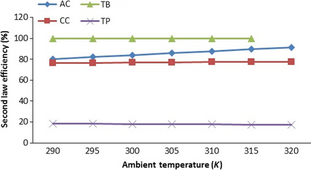
To illustrate the effect of operating parameters on the second law efficiency of the components of the GT, the AES1 (PB204) plant is considered as a typical case. The simulation of the performance of plant and components was done by varying the air inlet temperature from 290 to 320 K; and the TIT from 1000 to 1400 K, respectively. Figure 2 compares the second law efficiencies of the air compressor, CC, GT, and the overall plant when the ambient temperature increases. The exergy efficiency of the turbine component and the overall exergetic efficiency of plant decreased with increased ambient temperature, whereas the exergy efficiencies of the compressor and turbine increased with increased ambient temperature. The overall exergetic efficiency decreased from 18.53% to 17.26% for ambient temperature range of 290–320 K. It was found that a 5 K rise in ambient temperature resulted in a 1.03% decrease in the overall exergetic efficiency of the plant. The reason for the low overall exergetic efficiency is due to large exergy destruction in the CC [59].

Figure 2. Variation in second law efficiency with ambient temperature. AC, second law efficiency of compressor; CC, second law efficiency of combustion chamber; TB, second law efficiency of turbine; TP, second law efficiency of entire plant.

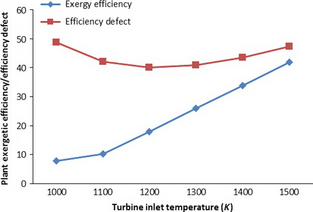
The exergetic efficiency (or second law efficiency) of the plant was also found to depend significantly on a change in TIT. Figure 3 shows that the second law efficiency of the plant increases steadily as the TIT increases. The increase in exergetic efficiency with increase in TIT is limited by turbine material temperature limit. This can be seen from the plant efficiency defect curve. As the TIT increases, the plant efficiency defect decreases to minimum value at certain TIT (1200 K), after which it increases with TIT. This shows degradation in performance of GT plant at a high TIT.

Figure 3. Variation in plant exergetic efficiency and efficiency defect with turbine inlet temperature.

Exergy improvement potential

The results of the exergy improvement potential of the selected plants are presented in Table 5. The total exergy improvement potential of the selected plants varies from 54.04 to 159.88 MW. The component with the highest exergy improvement potential is the CC, which has value varies from 30.21 to 88.86 MW. This is followed by the air compressor which has value varies from 3.30 to 14.95 MW. The high improvement potential in the CC is due to the irreversibility associated with combustion and the large temperature difference between the air entering the CC and the flame temperature. These immense losses basically mean that a large amount of energy present in the fuel, with a greater capacity to generate useful work, is being wasted. Exergy improvement potential can be afforded in the CC by preheating the reactants and by reducing the heat loss and the excess air entering the CC. The lower improvement potential in the air compressor when compared with the CC is due to an additional heat loss from the air compressor through friction as compared to large temperature difference between the air entering the CC and the flame temperature. These results have made it possible to determine the critical points of the GT system stating hierarchy on its components in such a way that the measure be applied in the places where they will be most effective.

Table 5. Exergy improvement potential

Components	AES1	AES2	AES3	AF1	AF2	AF3	AF4	DEL1	DEL2	DEL3	DEL4
Air compressor (MW)	3.94	4.14	4.71	7.83	6.88	8.59	14.95	2.89	3.30	11.69	11.02
Combustion chamber (MW)	38.48	40.33	43.82	69.49	68.52	85.81	88.86	30.47	30.21	78.48	78.67
Turbine (MW)	0.015	0.023	0.13	0.19	0.22	1.05	2.48	0.15	0.17	1.00	0.38
Entire plant (MW)	119.44	147.15	159.28	98.17	89.99	124.18	159.59	54.04	56.46	159.88	143.28

Results of thermoeconomic (exergoeconomic) analysis

The thermoeconomic performance of the selected GT plants in Nigeria was investigated considering the values of measured properties such as temperature, pressure, and mass flow rate at various points in the GT power plants. The period of operation for each plant investigated in this study are: AES station (12 years for PB204, PB209, and PB210), Afam station (30 years for GT17 and GT18; 11 years for GT19 and GT20), and Delta station (12 years for GT9, GT10, GT18, and GT20).

Solving the linear system of equations (14)-(20), the cost rates of the unknown streams of the system are obtained. For the selected GT power plants, the exergy costing method gave the unit cost of electricity produced in each plant and this varies as: from cents 3.90/kWh (N6.20/kWh) to cents 5.07/kWh (8.07/kWh) for AES station, from cents 3.30/kWh (N5.25/kWh) to cents 4.94/kWh (N7.85/kWh) for Afam station and from cents 1.88/kWh (N2.99/kWh) to cents 5.65/kWh (N8.98/kWh ) for Delta station.

The exergoeconomic parameters considered in this study include average costs per unit of fuel exergy C_F and product exergy C_P, rate of exergy destruction E._D, cost rate of exergy destruction C._D, investment and O&M costs rate Z., and exergoeconomic factor ƒ. In analytical terms, the components with the highest value of Z._k + C._Dk are considered the most significant components from an exergoeconomic perspective. This provides a means of determining the level of priority a component should be given with respect to the improving of the system.

For all the plants considered, the CC and air compressor have the highest value of the sum Z._k + C._Dk and are, therefore, the most important components from the exergoeconomic viewpoint. The low value of exergoeconomic factor, f, associated with the CC suggests that the cost rate of exergy destruction is the dominate factor influencing the component. Hence, it is implied that the component efficiency is improved by increasing the capital investment. This can be achieved by increasing gas turbine inlet temperature (GTIT). The maximum GTIT is limited by the metallurgical considerations [32, 57].

The air compressor has the highest ƒ value in most of the plants investigated except plants AES1 (PB204), AES2 (PB209), and AES3 (PB210) with ƒ value 50.44%, 45.94%, and 36.53%, respectively. The cost effectiveness of the entire system of the plants investigated can be improved if the Z. value of GT is reduced. According to equation (16) of the cost model, the capital investment and O&M costs of the GT depend on temperature T₃, PR P₃/P₄, and turbine isentropic efficiency η_st. To reduce the high Z. value associated with the GT, we need to consider a reduction in the value of at least one of the variables.

The results of the exergoeconomic analysis of the plants investigated show that the CC exhibits the greatest exergy destruction cost. The next highest source of exergy destruction cost is the air compressor. In comparing the results of exergy and exergoeconomic analyses, similar trends are revealed. Increasing GTIT effectively decreases the cost associated with exergy destruction. Further comparisons between related results are consistent with those reported previously [28], and confirm that the most significant parameter in the plant is GTIT. The finding establishes the concept that the exergy loss in the CC is associated with the large temperature difference between the flame and the working fluid. Reducing this temperature difference reduces the exergy loss. Furthermore, cooling compressor inlet air allows the compression of more air per cycle, effectively increasing the GT capacity.

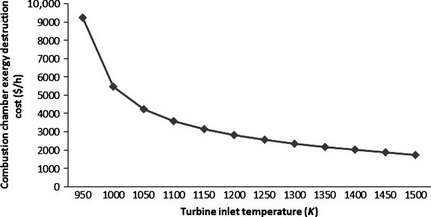
To illustrate the effect of GTIT on the exergy destruction cost of CC of the selected plants, AES1 (PB204) plant is considered as sample. The simulation was done by varying the GTIT from 950 to 1500 K. Figure 4 shows the effect of variation in GTIT on CC exergy destruction cost. This figure shows that, like the exergy analysis results, the cost of exergy destruction for the CC decreases with an increase in the GTIT. This is due to the fact that the cost of exergy destruction is proportional to the exergy destruction. Hence, an increase in the GTIT can decrease the cost of exergy destruction. Furthermore, from Figure 3, an increase in the TIT of about 200 K can lead to a reduction of about 29% in the cost of exergy destruction. Therefore, TIT is the best option to improve cycle losses.

Figure 4. Combustion chamber exergy destruction cost and turbine inlet temperature.

Result of thermoenvironomic (exergoenvironomic) analysis

Table 6 shows the results of the exergoenvironomic analysis of this work. The exergoenvironomic parameters computed are CO₂ emission in kg per MWh of electricity generated, depletion number, SI, cost flow rate of environmental impacts (C._env) in $/h, and total cost rates of products (C._Tot) in $/h. For the period considered, the CO₂ emissions for the selected plants vary from 100.18 to 408.78 kg CO₂/MWh. AF2 (GT18) has the highest value and AES3 (PB210) has the least value. This result is justified by the fact that AES GT plants are barges mounted on lagoon, whereas other GT units are mounted on land. Moreover, units AF1 and AF2 were commissioned in the year 1982. The units have been in operation for over 30 years. Hence, these units have the highest CO₂ emissions.

Table 6. Result of exergoenvironmental performance analysis

Exergoenvironmental parameters	AES1	AES2	AES3	AF1	AF2	AF3	AF4	DEL1	DEL2	DEL3	DEL4
CO2 emissions (kg CO2/MWh)	112.73	109.92	100.18	406.18	408.78	393.68	248.38	181.36	226.33	327.02	287.95
Depletion number, Dp	0.69	0.69	0.72	0.81	0.81	0.84	0.82	0.77	0.77	0.82	0.80
Sustainability index, SI	1.44	1.44	1.39	1.24	1.23	1.20	1.22	1.31	1.29	1.21	1.25
Cost flow rate of environmental impact, C.env ($/h)	51.91	51.98	46.29	257.90	243.42	276.97	209.37	61.12	76.32	252.39	247.40
Total cost rates of products, C.Tot ($/h)	2991.59	2974.18	2935.69	9473.10	9225.40	12,232.84	11,885.62	3580.25	3700.39	11,772.48	11,414.39

For comparison purpose, CO₂ emissions of selected countries are presented in Table 7. The CO₂ emission in the present study (Nigeria) is comparable with other selected countries and the Intergovernmental Panel on Climate Change CO₂ emissions factor. Thus it can be concluded that CO₂ emissions from the selected GT plants is not relatively too high.

Table 7. CO₂ emissions per MWh (kg CO₂/MWh) from electricity generation using natural gas for selected countries kg CO₂/MWh

Country	Average 2008–2010a	This study (2013)
a IEA [60]. b IPCC [61].
Canada	483
Japan	437
Spain	353
Turkey	371
United Kingdom	387
USA	405
Ukraine	379
Egypt	490
China	504
India	436
Cuba	502
IPCC emission
Factorb	225
Nigeria
AES1		112.73
AES2		109.92
AES3		100.18
AFI		406.18
AF2		408.78
AF3		393.68
AF4		248.38
DEL1		181.36
DEL2		226.33
DEL3		327.02
DEL4		287.95

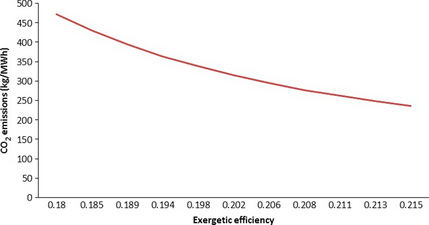
Figure 5 shows the variation of CO₂ emissions with exergetic efficiency for plant AES1 (PB204) as sample for analysis. Figure 5 illustrates that increasing exergetic efficiency results in CO₂ emission reduction. The increase of exergetic efficiency is related to reduction of ambient inlet air temperature into the compressor.

Figure 5. Variation of CO2 emissions with exergetic efficiency.

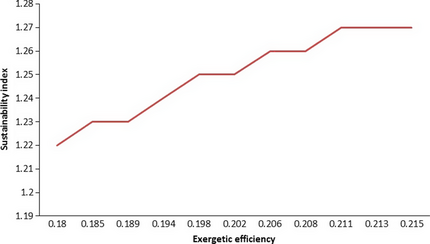
Figure 6 shows the effect of increasing exergy efficiency of GT power plant on the SI of the whole system. The efficiency of the system is directly linked to the entire system. However, it is apparent that the overall exergy destruction of the cycle decreases, while the SI increases with decreasing CIT.

Figure 6. Variation of sustainability index with exergetic efficiency.

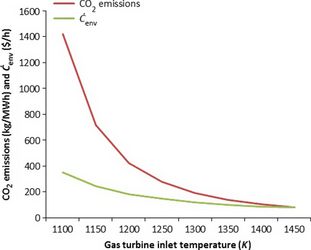
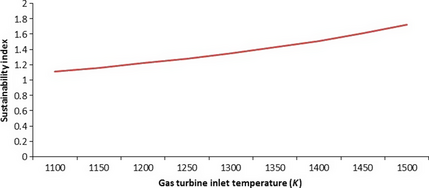
Further consideration of the results for CO₂ emissions, the effect of GTIT on cost of environmental impact and carbon dioxide emissions was investigated. The variations of both CO₂ emissions and cost of environmental impact for the gas power plant with GTIT are shown in Figure 7. CO₂ emissions and cost of environmental impact are seen to decrease with increasing GTIT. Although the mass flow rate of gases through the CC increases with GTIT, so does the net output power. The variation of GTIT with SI is shown in Figure 8. The SI is seen to increase with GTIT. Since the compressor PR is constant the exergy flow entering the CC is fixed. From the exergy balance for the CC, it is seen that increasing the GTIT increases the outlet exergy flow and exergy destruction in the CC decreases.

Figure 7. Variation of CO2 emissions and cost rate of environmental impact with gas turbine inlet temperature.

Figure 8. Variation of sustainability index with gas turbine inlet temperature.

From above discussion, exergy efficiency, exergy destruction, environmental impact, and sustainability are apparently linked in such system, and thus supporting the utility of exergoenvironomic analysis.

From this study, it is seen that improvement of power plants efficiency is twofold. By improving the most inefficient components (e.g., reducing the compressor inlet air temperature) of the system and utilizing the minimum adequate fuel flow rate ensuring maximum burn. The reduction in wasted unburned fuel and the reduction in overall system inefficiencies results in net CO₂ emissions reduction.

Validation of computer simulation code

The model developed is validated by the actual data that were taken from operational GT power plants in Nigeria. The operating parameters were taken from 2005 to 2010. Average parameters recorded within the period under review are set as baseline for comparison with the calculated results. The parameters considered in GT engine during simulation are inlet temperature of the air compressor, the mass flow rate of fuel and TIT.

The schematic flow diagram of a simple GT power plant that depicts these power plants is shown in Figure 1. The average operating data for the selected GT power plants are presented in Table 3. The results of thermodynamic properties of the cycle form the modeling part and the power plant data are illustrated in Tables 8–10.

Table 8. Results between the power plant data and simulation code (Afam power plant)

Data	Unit	AF1 (GT17)			AF3 (GT18)			AF3 (GT19)			AF4 (GT20)
		Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)
T2	K	593.73	616.79	3.88	595.82	625.13	4.92	610.90	618.88	1.31	618.32	619.95	0.26
T4	K	712.73	714.60	0.26	723.75	747.45	3.27	770.07	755.12	1.94	807.32	764.87	5.26
mf	kg/sec	__6.50	__5.95	8.46	6.4	6.56	2.5	8.1	7.46	7.90	8.4	7.6	9.52

Table 9. Results between the power plant data and simulation code (Delta power plant)

Data	Unit	DEL1 (GT9)			DEL2 (GT10)			DEL3 (GT18)			DEL4 (GT20)
		Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)
T2	K	613.73	646.80	5.38	619.07	647.38	4.57	634.32	643.89	1.51	630.32	645.63	2.43
T4	K	710.56	738.35	3.91	707.48	738.40	4.37	730.15	758.26	3.85	705.07	758.70	7.61
mf	kg/sec	3.08	2.68	12.99	3.10	2.67	13.87	8.15	7.54	7.48	8.13	7.54	7.26

Table 10. Results between the power plant data and simulation code (AES power plant)

Data	Unit	AES1 (PB204)			AES2 (PB209)			AES3 (PB210)
		Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)	Measured data	Simulation code	Difference (%)
T2	K	622.31	629.59	1.17	627.48	628.04	0.089	636.28	628.98	1.15
T4	K	750	775.02	3.34	755	776.51	2.86	827.05	816.53	1.27
mf	kg/sec	2.58	2.45	5.04	2.54	2.47	2.76	2.81	2.63	6.41

The comparison of simulation results and the actual data from the power plants shows that the average difference in the simulation results and the actual data varies from 2.32% to 7.60%. The maximum difference is about 13.87% for mass flow rate of fuel in GT unit GT10 in Delta power plant. The minimum difference is about 0.089% for compressor outlet temperature in unit PB209 in AES power plant. This validates the correct performance of the developed simulation code to model the GT power plants in Nigeria, as the results of the simulation values are close to the actual operating data of the plants considered in this study.

Conclusions and Recommendations

In the present study, exergy, thermoeconomic, and thermoenvironomic analyses were performed for 11 selected GT power plants in Nigeria.

The results from the exergy analysis show that the CC is the most significant exergy destructor in the selected power plants, which is due to the chemical reaction and the large temperature difference between the burners and working fluid. Moreover, the results show that an increase in the TIT (GTIT) leads to an increase in GT exergy efficiency due to a rise in the output power of the turbine and a decrease in the CC losses.

The results from the thermoeconomic analysis, in common with those from the exergy analysis, show that the CC has the greatest cost of exergy destruction compared to other components. In addition, the results show that by increasing the TIT (GTIT) the GT cost of exergy destruction can be decreased. The finding solidifies the concept that the exergy loss in the CC is associated with the large temperature difference between the flame and the working fluid. Reducing this temperature difference reduces the exergy loss. Furthermore, cooling compressor inlet air allows the compression of more air per cycle, effectively increasing the GT capacity. The results of this study revealed that an increase in the TIT of about 200 K can lead to a reduction of about 29% in the cost of exergy destruction. Therefore, TIT is the best option to improve cycle losses.

From exergy costing analysis, the unit cost of electricity produced in the selected power plants varies from cents 1.99/kWh (N3.16/kWh) to cents 5.65/kWh (N8.98/kWh).

The results of thermoenvironomic analysis show that CO₂ emissions in kg/MWh of electricity generated for the selected GT power plants vary from 100.18 to 408.78 kg CO₂/MWh. The cost rate of environmental impact varies from 40.18 to 276.97 $/h. The study further shows that an increase in exergetic efficiency of GT plant results in a reduction in CO₂ emissions. The increase of exergetic efficiency is related to reduction of ambient inlet air temperature into the compressor. This implies that improvement of a systems efficiency is twofold. By improving the most inefficient components (e.g., reducing the compressor inlet air temperature) of the system and utilizing the minimum adequate fuel flow rate ensuring maximum burn. The reduction in wasted unburned fuel and the reduction in overall system inefficiencies results in net CO₂ emissions reduction. Moreover, CO₂ emissions and cost of environmental impact decrease with increasing GTIT. The SI is seen to increase with GTIT.

In summary, from the study and thermodynamic analysis of selected GT power plants, it was concluded that bigger η_AC and η_GT guarantee less exergy destruction in compressor and turbine as well as less net cycle fuel consumption and operating cost. Moreover, increasing GTIT also decreases the exergy destruction in CC, saves fuel consumption, and minimizes CO₂ emissions as well.

Recommendations to improve performance of the selected power plants

The average efficiency of GT plants in the Nigerian energy utility sector over the past two decades was in the range 27–30% [43]. In order to address increasing electricity demand, cost of electricity generation, and concern for environmental safety in the selected power plants, it is imperative to install power plants based on advanced technologies which are more energy efficient, environmentally acceptable, and economically viable. Results of this research provide insight into the economic and environmental impacts from exergy analysis perspective of the selected GT power plants in Nigeria. Based on the results of this research work, the following possible economical methods and technologies to improve performance of the selected GT power plants are hereby recommended:

1. The results of this study revealed that the CC has the largest irreversibility and cost of exergy destruction. This large exergy loss can be reduced in the selected power plants by addition of spray water and preheating of the reactants in the CC.
2. Application of advanced clearance control schemes and sealing technologies. GTs are constructed with cases around the blades to contain and control the working fluid. Every molecule of working fluid that the blade does not extract work from as it passes by is called “leakage” which also reduces turbine efficiency. The problem of leakage is common in the simple GT plants in Nigeria. The possible method to control and limit the amount of leakages in turbines is through advanced clearance control schemes and sealing technologies.
3. Retrofitting with a GT air inlet cooling system (evaporative cooling, inlet fogging, or inlet chilling method) is a useful option for increasing power output of the selected power plants. This helps to increase the density of the inlet air to compressor [62].
4. The compressor airfoils of older turbines tend to be rougher than a newer model simply because of longer exposure to the environment. In addition, the compressor of older models consumes a larger fraction of the power produced by the turbine section. Therefore, improving the performance of the compressor will have a proportionately greater impact on total engine performance. Application of coatings to GT compressor blades (the “cold end” of the machine) would improve the selected GT engines performance. Compressor blade coatings provide smoother, more aerodynamic surfaces, which increase compressor efficiency. In addition, smoother surfaces tend to resist fouling because there are fewer “nooks and crannies” where dirt particles can attach. Coatings are designed to resist corrosion, which can be a significant source of performance degradation, particularly if a turbine is located near saltwater. As AES Barge GT plant is located on lagoon, compressor coating technology would improve the plant performance significantly.
5. Another option for improving the selected GT plants performance is to apply ceramic coatings to internal components. Thermal barrier coatings (TBCs) are applied to hot section parts in advanced GTs. As some of the selected GTs are over 25 years in operation, TBCs can be applied to the hot sections of the selected GTs. The TBCs provide an insulating barrier between the hot combustion gases and the metal parts. TBCs will provide longer parts life at the same firing temperature, or will allow the user to increase firing temperature while maintaining the original design life of the hot section.

Acknowledgments

The authors appreciate the Management of AES power plant, Afam power plant, and Delta power plant for providing the data used in this study.

Conflict of Interest

None declared.

References

1. Park, S. R., A. K. Pandey, V. V. Tyagi, and S. K. Tyagi. 2014. Energy and exergy analysis of typical renewable energy systems. Renew. Sustain. Energy Rev.30:105–123.
2. Mousafarash, A., and P. Ahmadi. 2014. Exergy and exergo-economic based analysis of a gas turbine power generation system. Pp. 97–108inI. Dincer, A. Midilli andH. Kucuk, eds. Progress in sustainable energy technologies vol II. Springer International Publishing, Switzerland.
3. Mitrovicć, D., D. Zivkovic, and M. S. Lakovicć. 2010. Energy and exergy analysis of a 348.5 MW steam power plant. Energy Sources Part A32:1016–1027.
4. Aljundi, I. H.2009. Energy and exergy analysis of a steam power plant in Jordan. Appl. Therm. Eng.29:324–328.
5. Silveira, J. L., C. E. Tuna, W. Q. Lamas, and I. A. Castro Villela. 2010. A contribution for thermoeconomic modelling: a methodology proposal. Appl. Therm. Eng.30:1734–1740.
6. Suresh, M. V. J. J, K. S. Reddy, and K. K. Ajit. 2006. Pp. 1–6inEnergy and exergy based thermodynamic analysis of a 62.5 MWe coal-based thermal power plant – a case study. International Conference on Energy and Environment, Malaysia.
7. Ebadi, M. J., and M. Gorji-Bandpy. 2005. Exergetic analysis of gas turbine plants. Int. J. Exergy2:31–39.
8. Edgerton, R. H.1992. P. 1992inAvailable energy and environmental economics. D.C. Heath, Toronto, Canada.
9. Dincer, I., and M. A. Rosen. 2013. Pp. 257–276inExergy, energy, environmental and sustainable development. Elsevier, Oxford, U.K.
10. Moran, M. J., and E. Sciubba. 1994. Exergy analysis: principles and practice. J. Eng. Gas Turbines Power116:285–290.
11. Rosen, M. A., I. Dincer, and M. Kanoglu. 2008. Role of exergy in increasing efficiency and sustainability and reducing environmental impact. Energy Pol.36:128–137.
12. Ofodu, J. C., and D. P. S. Abam. 2002. Exergy analysis of Afam thermal power plant. NSE Tech. Trans.37:14–28.
13. Abam, D. P. S., and N. N. Moses. 2011. Computer simulation of a gas turbine performance. Global J. Res. Eng.11:37–44.
14. Ganapathy, T. K., N. A. Murugesan, and R. P. Gakkar. 2009. Exergy analysis of operating lignite fired thermal power plants. J. Eng. Sci. Technol. Rev.2:123–130.
15. Rajkumar, S. C., and K. Ashok. 2009. Energy and exergy analysis of non-reheat thermal power plant. Proceedings of International Conference of Energy and Environmental, ISSN: 2070-3740
16. Balkrishna, M. C.2009. Energy and exergy analysis of a captive steam power plant. Proceedings of International Conference of Energy and Environmental, ISSN: 2070 – 3740
17. Fagbenle, R. L., A. B. C. Oguaka, and O. T. Olakoyejo. 2007. A thermodynamic analysis of a biogas-fired integrated gasification steam injected gas turbine (BIG/STIG) plant. Elsevier Appl. Therm. Eng.27:2220–2225.
18. Ehsana, A., and M. Z. Yilmazoglub. 2011. Design and exergy analysis of a thermal power plant using different types of Turkish lignite. Int. J. Thermodyn.14:125–133.
19. Ighodaro, O. O., and B. A. Aburime. 2011. Exergetic appraisal of Delta IV power station, Ughelli. J. Emerg. Trends Eng. Appl. Sci.2:216–218.
20. Rashidi, M. M., A. Aghagoli, and M. Ali. 2014. Thermodynamic analysis of a steam power plant with double reheat and feed water heaters. Adv. Mech. Eng.2014:1–12.
21. Dincer, I., and M. A. Rosen. 2003. Thermoeconomic analysis of power plants: an application to a coal-fired electrical generating station. Energy Convers. Manage.44:2743–2761.
22. Connelly, L., and C. P. Koshland. 1997. Two aspects of consumption: using an energy based measure of degradation to advance the theory and implementation of industrial ecology. Resour. Conserv. Recycl.19:199–217.
23. Dincer, I., and M. A. Rosen. 1999. Exergy analysis of waste emissions. Int. J. Energy Res.23:1153–1163.
24. Buchgeister, J.2010. Exergoenvironmental analysis – a new approach to support the design for environment of chemical processes?Chem. Eng. Technol.33:593–602.
25. Ahmadi, P., and I. Dincer. 2010. Exergo-environmental analysis and optimization of a cogeneration plant system using Multimodal Genetic Algorithm (MGA). Energy35:5161–5172.
26. Amrollahi, Z., I. Ertesvag, and O. Bolland. 2011. Thermodynamic analysis on post-combustion CO₂ capture of natural-gas fired power plant. Int. J. Greenhouse Gas Control5:422–426.
27. Barzegar Avval, H., P. Ahmadi, A. Ghaffarizadeh, and M. H. Saidi. 2011. ‘Thermoeconomic environmental multiobjective optimization of a gas turbine power plant with preheater using evolutionary algorithm. Int. J. Energy Res.35:389–403.
28. Ahmadi, P., M. A. Rosen, and I. Dincer. 2011. Greenhouse gas emission and exergo-environmental analyses of a trigeneration energy system. Int. J. Greenhouse Gas Control5:1540–1549.
29. Memon, A. G., K. Harijan, M. A. Uqaili, and R. A. Memon. 2013. Thermo-environmental and economic analysis of simple and regenerative gas turbine cycles with regression modeling and optimization. Energy Convers. Manage.76:852–864.
30. Seyyedi, S. M., H. Ajam, and S. Farahat. 2011. Thermoenvironomic optimization of gas turbine cycles with air preheat. Proc. Inst. Mech. Eng. Part A: J. Power and Energy225:12–23.
31. Mert, M. S., O. F. Dilmaç, S. Özkan, F. Karaca, and E. Bolat. 2012. Exergoeconomic analysis of a cogeneration plant in an iron and steel factory. Energy46:78–84.
32. Gorji-Bandpy, M., and H. Goodarzian. 2011. Exergoeconomic optimization of gas turbine power plants operating parameters using genetic algorithms: a case study. Therm. Sci.15:43–54.
33. Sahoo, P. K.2008. Exergoeconomic analysis and optimization of a cogeneration system using evolutionary programming. Appl. Therm. Eng.28:1580–1588.
34. Fellah, G. M., F. A. Mgherbi, and S. M. Aboghres. 2010. Exergoeconomic analysis for unit Gt14 of South Tripoli gas turbine power plant. Jordan J. Mech. Ind. Eng.4:507–516.
35. Regulagadda, P., I. Dincer, and G. F. Naterer. 2010. Exergy analysis of a thermal power plant with measured boiler and turbine losses. Appl. Therm. Eng.30:970–976.
36. Ahmad, P., A. H. Barzegar, A. Ghaffarizadeh, and M. H. Saidi. 2010. Thermoeconomic- environmental multi-objective optimization of a gas turbine power plant with preheater using evolutionary algorithm. Int. J. Energy Res.35:389–403.
37. Tsatsatronis, G.1993. Thermoeconomic analysis and optimization of energy systems. Prog. Energy Combust. Sci.19:227–257.
38. Abam, F. I., I. U. Ugot, and D. I. Igbong. 2012a. Effect of operating variables on exergetic efficiency of an active gas turbine power plant. J. Emerg. Trends Eng. Appl. Sci.3:131–136.
39. Rivero, R., M. Garcia, and J. Urquiza. 2004. Simulation, exergy analysis and application of diabatic distillation to a tertiary amyl methyl ether production unit of a crude oil refinery. Energy29:467–489.
40. Hammond, G. P.2004. Engineering sustainability: thermodynamics, energy systems, and the environment. Int. J. Energy Res.28:613–639.
41. Van Gool, W.1997. Energy policy fairy tales and factualities. Pp. 93–105inO. D. D. Soares, A. Martins da Cruz, G. Costa Pereira, I. M. R. T. Soares and A. J. P. S. Reis, eds. Innovation and technology-strategies and policies. Kluwer, Dordrecht.
42. Van Gool, W.1992. Exergy analysis of industrial processes. Energy17:791–803.
43. Abam, F. I., I. U. Ugot, and D. I. Igbong. 2012b. Performance analysis and components irreversiblities of a (25 MW) gas turbine power plant modeled with a spray cooler. Am. J. Eng. Appl. Sci.5:35–41.
44. Siahaya, Y.2009. Thermoeconomic analysis and optimization of gas turbine power plant.Pp. 1–10. in Proceedings of the International Conference on Fluid and Thermal Energy Conversion 2009 – FTEC 2009, Tongyeong, South Korea, 7–10 December.
45. Ahmadi, P., and I. Dincer. 2011. Thermodynamic and exergoenvironmental analyses, and multi-objective optimization of a gas turbine power plant. Appl. Therm. Eng.31:14–15.
46. Bejan, A., G. Tsatsaronis, and M. Moran. 1996. Thermal design and optimization. John Wiley & Sons Inc, New York, NY.
47. Moran, M. J.1982. Availability analysis: a guide to efficient energy use. Prentice Hall, Englewood Cliffs, NJ.
48. Kim, S., S. Oh, Y. Kwon, and H. Kwak. 1998. Exergoeconomic analysis of thermal systems. Energy2:393–406.
49. Kwon, Y., H. Kwak, and S. Oh. 2001. Exergoeconomic analysis of gas turbine cogeneration systems. Exergy Int. J.1:31–40.
50. Tsatsaronis, G., and M. Winhold. 1984. Thermoeconomic analysis of power plants, EPRI final report AP – 3651. Palo Alto, CA.
51. Ameri, M., P. Ahmadi, and A. Hamidi. 2009. Energy, exergy and exergoeconomic analysis of a steam power plant: a case study. Int. J. Energy Res.33:499–512.
52. Valero, A., M. A. Lozano, L. Serra, G. Tsatsaronis, J. Pisa, C. Frangopoulos, et al. 1994. CGAM problem: definition and conventional solution. Energy19:279–286.
53. Ameri, M., P. Ahmadi, and S. Khanmohammadi. 2007. Exergy analysis of a 420 MW combined cycle power plant. Int. J. Energy Res.32:175–183.
54. Moran, M. J., and G. Tsatsaronis. 2000. Engineering thermodynamic. Pp. 1–109inF. Kreith, ed. The CRC handbook of thermal engineering. CRC Press LLC, Boca Raton, FL.
55. Gülder, O. L.1986. Flame temperature estimation of conventional and future jet fuels. J. Eng. Gas Turbines Power108:376–380.
56. Lazzaretto, A., and A. Toffolo. 2004. Energy, economy and environment as objectives in multi – criterion optimization of thermal systems design. Energy29:1139–1157.
57. Altayib, K.2011. Energy, exergy and exergoeconomic analyses of gas-turbine based systems. M.Sc. thesis, University of Ontario Institute of Technology.
58. Chandramohan, S.2008. First and second law analysis of organic rankine cycle. Ph.D. thesis, Mississippi State University.
59. Kotas, T. J.1995. The exergy method of thermal plant analysis. Krieger Publishing Company, Malabar, FL.
60. International Energy Agency (IEA). 2012. Energy statistics and balances of non-OECD countries and energy statistics of OECD countries.
61. Inter-governmental Panel on Climate Change. 1996. IPCC second assessment climate change 1995. Volumes 1–3. Cambridge University Press, Bracknell, U.K.
62. Oyedepo, S. O., R. O. Fagbenle, S. S. Adefila, and S. A. Adavbiele. 2014. Performance evaluation and economic analysis of a gas turbine power plant in Nigeria. Energy Convers. Manage.79:431–440.