Resumen
La descripción del comportamiento mecánico de tejidos duros mediante el empleo de modelos discretos pasa por diferentes etapas de análisis, que van desde el procesamiento digital de la imagen hasta la especificación de las propiedades físicas del tejido al modelo discreto. Para lograr un buen resultado es esencial la descomposición de esos modelos en sus partes constitutivas.
En este trabajo se discute un método para la descripción geométrica de los huesos del pie a partir de una secuencia de imágenes (cortes) de tomografía computarizada (TC).
La investigación propone la combinación de la umbralización global y de la adaptativa para la determinación del dominio geométrico de los huesos en cada corte, así como el análisis de las relaciones espaciales entre contornos en planos consecutivos a fin de obtener las isosuperficies de los huesos.
Se propone un algoritmo semiautomático basado en 4 etapas: la lectura de los cortes de imágenes de TC; la determinación de los contornos que definen el tejido óseo presentes en cada corte; la formación de los volúmenes a través del agrupamiento de los contornos cuya relación espacial cumple un criterio determinado; y la eliminación de las isosuperficies no válidas.
Como resultado se obtiene la definición de la mayoría de los huesos del pie cuyo rango de valores en la escala de Hounsfield es [–1.000; 1.383].
Abstract
The description of the mechanical behavior of hard tissues by means of discrete models goes through various stages of analysis, which range from digital image processing to the specification of tissues physical properties to the discrete model. To achieve good results it is essential to decompose these models into their constituent parts.
In this paper we discuss a method for geometrical description of foot bones from a sequence of computed tomography (CT) images.
This research proposes a combination between global and adaptive thresholdings to determine the geometric domain of bones in each slice and the analysis of the spatial relationships between contours in consecutive planes in order to obtain bones’ isosurfaces.
The algorithm proposed is based on 4 stages: the reading of computed tomography (CT) images; the determination of the contours that define the bone tissue present on each slice; the grouping of contours whose relationship meet a given criteria; the elimination of non-valid volumes.
As a result, it is possible to obtain the geometrical domain of a great number of foot bones whose range in the Hounsfield is [–1000; 1383].
Palabras clave
Umbralización global ; Umbralización adaptativa ; Procesamiento de imágenes médicas ; Reconstrucción tridimensional de huesos ; Modelación geométrica ; Problema de la correspondencia
Keywords
Global threshold ; Adaptive threshold ; Medical image processing ; Bone 3D reconstruction ; Geometrical model ; Matching problem
1. Introducción
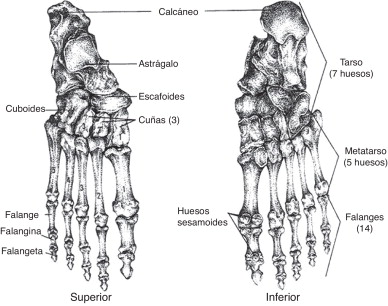
El pie humano (fig. 1 ) es la extremidad que soporta el peso del cuerpo y permite la locomoción. Contiene 26 huesos, 33 articulaciones y más de 100 músculos, ligamentos y tendones [1] .
|
|
|
Figura 1. Anatomía ósea del pie. |
Es tal su importancia que son varios los campos de investigación en los cuales se simula su comportamiento mecánico mediante la utilización de modelos discretos [2] , [3] and [4] con el objetivo de realizar estudios antropométricos y análisis cinemáticos tanto para estudiar la marcha [5] como para optimizar el diseño de prótesis y calzado [6] .
El proceso de obtención del dominio geométrico interior del pie (separación e identificación de los huesos) a partir de un conjunto de imágenes médicas es un proceso complejo porque depende de las características del tejido óseo y de la calidad de la imagen obtenida.
Los huesos del pie contienen 2 tipos de tejido óseo: tejido óseo cortical y tejido óseo esponjoso.
El tejido óseo cortical se encuentra en la superficie de los huesos, es muy denso y fuerte; como resultado, tiene mayor coeficiente de absorción electromagnética que los tejidos óseos esponjosos y cancerosos [7] .
El tejido óseo esponjoso se encuentra en el interior de los huesos e induce un determinado patrón de textura que provoca variaciones en la intensidad de la imagen en estas regiones [7] .
Dado que los coeficientes de absorción electromagnética de los tejidos cortical y esponjoso son diferentes, teóricamente se podrían definir los píxeles que representan el contorno de los huesos mediante un nivel de umbral único (en función del coeficiente de absorción electromagnética).
En la práctica no es así debido a las características del equipo de adquisición de imágenes utilizado, las determinadas patologías y los rasgos anatómicos propios del paciente.
Por tanto, en el análisis de imágenes médicas, los principales problemas sin resolver son:
- La separación de los huesos adyacentes.
- El efecto de volúmenes parciales (debido a la insuficiente resolución espacial del equipo de adquisición).
- El ruido presente en la imagen.
En el caso del pie son varias las propuestas para solucionar el problema 1:
Hirano y Hata [8] proponen la aplicación de un sistema experto basado en lógica fuzzy para la segmentación y la determinación de los huesos y de sus fragmentos en las fracturas del pie, para lo cual consideran 2 tipos de conocimiento: el de la unión y el de la distancia. Luechinger et al. [9] utilizan imágenes RM (resonancia magnética) para la obtención del dominio geométrico del pie con el objetivo de analizar las posiciones de los huesos del tarso bajo diferentes condiciones de carga. La reconstrucción se realiza utilizando AMIRA [10] . Para el análisis por elementos finitos del pie, Antunes et al. [3] utilizan el crecimiento de regiones para determinar los contornos de los huesos en el plano y la reconstrucción tridimensional mediante técnicas de interpolación 3 D. Liu et al. [11] proponen una técnica de separación interactiva de los huesos del pie (en el plano), que comienza con la selección manual de un píxel semilla en cada hueso que se va a segmentar; posteriormente, aplican la técnica de graph-cut para obtener los contornos de los huesos. Calder et al. [7] emplean conjuntos de nivel para la segmentación de imágenes del pie, de la muñeca y del tobillo.
Estos estudios demuestran la inexistencia de una estrategia única para la obtención por separado de los huesos del pie. Por tanto, es necesario obtener un procedimiento que permita extraer los volúmenes óseos del pie para realizar el estudio biomecánico, en los cuales se puedan insertar los músculos, los ligamentos, etc.
Se propone un algoritmo semiautomático para la solución del problema de la separación de los huesos adyacentes en el pie, centrado en la obtención de los huesos de las regiones del tarso y del metatarso, que son las estructuras anatómicas que se utilizan con mayor frecuencia en los estudios del comportamiento biomecánico del pie.
El mismo algoritmo ha sido desarrollado por el grupo BioMec del Instituto Superior Politécnico José Antonio Echeverría, y se basa en 4 etapas:
- Lectura de los cortes de imágenes de TC.
- Determinación de los contornos que definen el tejido óseo en cada corte.
- Formación de los volúmenes a través del agrupamiento de los contornos cuya relación espacial cumple un criterio determinado.
- Eliminación de los volúmenes no válidos.
2. Materiales y método
2.1. Imagen Digital Imaging and Communications in Medicine
El formato Digital Imaging and Communications in Medicine (DICOM) se utiliza para obtener, procesar, almacenar, enviar, consultar e imprimir imágenes médicas [12] .
Cada imagen obtenida (ecuación 1) representa un corte de la parte analizada del cuerpo y cada píxel denota el grado de atenuación del haz radiológico sobre el tejido humano.
|
|
( 1) |
donde f es la intensidad del píxel y (m, n) definen la posición de este a lo largo de un par de vértices ortogonales normalmente definidos como horizontal y vertical.
Se asume que la imagen tiene M filas y N columnas, con P niveles discretos de intensidad [13] and [14] .
En las imágenes de TC, la intensidad de la señal espacial está dada por el coeficiente de atenuación lineal μ, específico de cada materia y que expresa la atenuación sufrida por un haz de rayos X al atravesar una determinada longitud de una determinada materia.
La unidad Hounsfield (HU, por sus siglas en inglés) es una transformación lineal (ecuación 2) del coeficiente de atenuación lineal μ [15] . Se considera 0 HU la radiodensidad del agua destilada a presión y temperatura estándar (STP, por sus siglas en inglés), mientras que la radiodensidad del aire a STP es -1.000 HU.
|
|
( 2) |
De acuerdo con el estándar DICOM [12] , en imágenes de TC el valor de la intensidad de los píxeles está expresado en HU.
Varios autores [16] and [17] han realizado estudios para relacionar cada material con un valor o rango específico en la escala de Hounsfield.
Sin embargo, no han llegado a una solución consistente porque el valor de μ depende de múltiples factores, como la intensidad de las radiaciones emitidas, la resolución del equipo de adquisición [16] , [18] and [19] y la densidad mineral ósea, por lo cual no es posible asignar un valor único en HU a cada material para cualquier estudio radiológico.
Las distancias entre 2 píxeles (Dp) y entre cortes (Dc) son atributos que están presentes como un elemento de dato en los ficheros DICOM. Esto permite la realización de mediciones en distancias reales mediante la transformación de píxeles a milímetros [12] .
2.2. Formulación del problema y propuesta
Para obtener los píxeles que definen el área ocupada por cada hueso, generalmente se emplea un nivel de umbral relativamente constante (200-350 HU), incluso valores superiores para huesos duros [8] and [20] .
Sin embargo, debido a la resolución espacial limitada, a una determinada patología, implantes metálicos o a movimientos del paciente durante la adquisición de la imagen, algunos píxeles contienen una mezcla de 2 o más tipos de tejido en lugar de un único tipo.
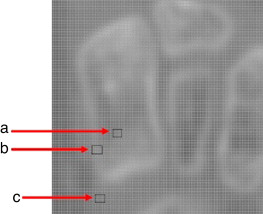
En la figura 2 se observa que el nivel de intensidad del tejido óseo cortical (fig. 2 a) no es constante alrededor de los huesos; además, el tejido óseo trabecular (fig. 2 b) tiene un nivel de intensidad similar al tejido blando (fig. 2 c).
|
|
|
Figura 2. Imagen ampliada de TC del pie. a) Región de píxeles que representan el tejido óseo cortical; b) región de píxeles que representan el tejido óseo trabecular; c) región de píxeles que representan el tejido blando. |
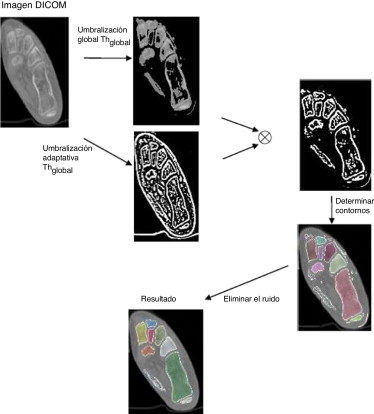
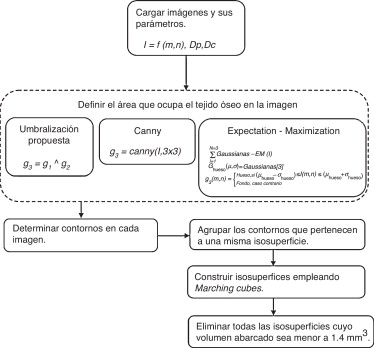
Así, no es posible especificar un valor de umbral único para determinar los huesos en la imagen, por lo que se propone la combinación de la umbralización global y de la adaptativa (fig. 3 ).
|
|
|
Figura 3. Algoritmo de segmentación propuesto. |
Las técnicas de umbralización se han utilizado en la segmentación de imágenes debido al nivel de información que pueden ofrecer, pero al mismo tiempo son subjetivas en su aplicación, no tienen en cuenta las características espaciales de la imagen, son sensibles a inhomogeneidades de la intensidad y al ruido, y se dividen en 2 clases: global y local (adaptativa).
En la umbralización global se emplea un mismo valor de umbral para toda la imagen. Los métodos de umbralización local subdividen la imagen en pequeñas áreas (subimágenes) y utilizan una función estadística para calcular el nuevo valor del píxel central de cada subimagen.
La umbralización local es computacionalmente más compleja que la umbralización global, pero muy útil para segmentar objetos en un fondo variable y en la extracción de regiones muy pequeñas y poco densas [21] .
La ventaja de combinar ambos métodos (mediante intersección de imágenes) radica en obtener, mediante la umbralización global, una imagen con los píxeles que teóricamente definen, dado un nivel de intensidad, el área del tejido óseo en tanto que la umbralización adaptativa realza los contornos en la imagen.
Si se clasifica un píxel como tejido óseo en la umbralización global pero no es parte de un contorno, este no aparecerá al aplicar la umbralización adaptativa, por lo que al multiplicar ambas imágenes ese píxel no aparece en la imagen resultante.
2.3. Imágenes empleadas
En la presente investigación se utilizaron imágenes de TC con las siguientes características:
- Pie de niño: 250 cortes de 512 × 512 píxeles, con un tamaño de vóxel de 0,4 × 0,4 × 0,5 mm. Rango de intensidad en HU: [–1.024,0; 1.383,0]. Adquiridas utilizando un escáner Siemens Sensation 64 con una energía: 120 Kvp y 131 mA.
- Pie de adulto 1: 152 cortes de 512 × 512 píxeles con un tamaño de vóxel de 0,83 × 0,83 × 1,4 mm. Rango de intensidad en HU: [–1.024,0; 1.422,0].
- Pie de adulto 2: 110 cortes de 512 × 512 píxeles con un tamaño de vóxel de 0,74 × 0,74 × 1,0 mm. Rango de intensidad en HU: [–1.024,0; 1.238,0]. Adquiridas mediante un escáner Siemens Sensation 16 con una energía: 120 Kvp y 345 mA.
- Pie de adulto 3: 160 cortes de 512 × 512 píxeles con un tamaño de vóxel de 0,84 × 0,84 × 1,4 mm. Rango de intensidad en HU: [–1.000,0; 3.138,0]. Adquiridas mediante un escáner ELSCINT CT TWIN con una energía: 120 Kvp 200 mA. Disponible gracias a la Universidad de Bruselas, Bélgica, como parte del proyecto de Animación Virtual de la Cinemática del Humano para Propósitos Educacionales y de Investigación (VAKHUM, por sus siglas en inglés).
2.4. Algoritmo propuesto
El algoritmo tiene como entrada el conjunto de imágenes DICOM (ecuación 3) que representan la región anatómica de análisis. El intervalo [A, B] es el rango del coeficiente de atenuación.
|
|
( 3) |
Para clasificar cada píxel como hueso o fondo, se filtra cada imagen mediante la umbralización global (ecuación 4), obteniéndose una nueva imagen g1 .
|
|
( 4) |
La especificación del valor de umbralización global (Thglobal ) es un aspecto importante en la detección de los contornos que representan los huesos.
Un nivel de umbral demasiado bajo provoca la unión de regiones que pertenecen a huesos distintos, pero si es demasiado alto fallará la región del hueso debido a las inhomogeneidades de la intensidad (no se obtienen contornos cerrados). Por tanto, el valor de Thglobal debe estar en función de cierto criterio volumétrico.
Para realzar los contornos presentes en la imagen I se aplica la umbralización adaptativa (ecuación 5), donde el nuevo valor de intensidad de cada píxel se calcula mediante una distribución gaussiana , con un tamaño de subimagen de 3 × 3 píxeles. Como resultado se obtiene la imagen g2 .
|
|
( 5) |
El área que ocupa el tejido óseo se determina mediante la intersección de las imágenes g1 , g2 (ecuación 6), obteniéndose la imagen binaria g3 .
|
|
( 6) |
La descripción geométrica del exterior de los huesos (contornos) se define mediante el algoritmo propuesto por Suzuki y Abe [22] . Por cada imagen segmentada se obtiene una lista de contornos (ecuación 7).
|
|
( 7) |
donde Ck es el contorno y R es el total de píxeles presentes en la imagen.
En diferentes estudios patológicos a través de imágenes se intenta diagnosticar la aparición de anomalías en momentos tempranos. En tal sentido, el área mínima de los tumores que puede ser detectada en imágenes de TC es 2-3 mm2[23] , [24] , [25] , [26] and [27] . Debido a ello, de la lista de contornos LC se eliminan aquellos cuya área sea menor de 1,5 mm2 . Cada contorno tiene una coordenada Z que se asigna en función de la distancia entre cortes (Dc) y de la posición que ocupa la imagen, a la cual pertenece, en el conjunto de imágenes de análisis.
La reconstrucción tridimensional se realiza mediante el siguiente axioma:
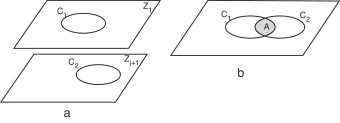
Axioma 1. Dos contornos, en planos consecutivos (fig. 4 a), pertenecen a una misma isosuperficie (estructura anatómica), si se cumple con la ecuación (8):
|
|
( 8) |
donde Ai es el valor del área de intersección entre estos (fig. 4 b), A1 , A2 son las áreas de los contornos y t es el valor permisible.
|
|
|
Figura 4. a) Contornos en planos consecutivos; b) proyección ortogonal del contorno C1,Zj en el plano Zj+1 y determinación del área de intersección con C2,Zj+1 . |
La selección del valor de t está en función de la distancia entre cortes, de la región anatómica de análisis y de la experiencia del especialista.
Se consideran 3 escenarios posibles:
- Si la relación entre las áreas es mayor o igual a t , entonces (Ck,Zj, Ck,Zj+1 ) forman parte de una misma isosuperficie.
- En caso contrario (Ck,Zj, Ck,Zj+1 ) no pertenecen a la misma isosuperficie.
- Si Ck,Zj no tiene relación con ningún contorno del plano Zj+1 entonces Ck,Zj se considera información no válida y es descartado.
Una vez finalizado este proceso, se tiene una lista en la cual cada nodo representa una isosuperficie y dentro de esta los contornos que la conforman.
La construcción tridimensional de cada isosuperficie (cerrada y definida por una malla de triángulos) se realiza empleando el algoritmo Marching Cubes[28] teniendo en cuenta, para una correcta representación espacial, los valores de la distancia entre cortes Dc y la distancia entre píxeles Dp (provistos por el formato DICOM).
A cada isosuperficie se le calcula el volumen mediante el algoritmo propuesto por [29] . Si el volumen abarcado es inferior a 1,4 mm3 se considera no válida y es descartada.
El valor mínimo de 1,4 mm3 se basa en los resultados obtenidos por Bodurka et al., quienes plantean la existencia de un volumen mínimo para el cual la contribución del ruido fisiológico es igual a la contribución de ruido del sistema de adquisición de la imagen [30] .
3. Diseño del experimento
Se desarrollaron 3 variaciones del procedimiento de umbralización (fig. 5 ), la primera basada en el algoritmo propuesto en la sección 2.4 y las restantes utilizando el algoritmo de Canny [31] y Expectation - Maximization (EM), el cual se basa en el método de segmentación del volumen parcial descrito en [32] .
|
|
|
Figura 5. Variaciones del procedimiento de umbralización para la definición del tejido óseo del pie. |
La propuesta de umbralización requiere como parámetro de entrada el valor de umbralización global (Thglobal ), sobre el cual no se ha encontrado consenso en la bibliografía consultada. Por tanto, se propone su determinación de forma experimental.
Para ello, se ejecutó el algoritmo propuesto en la sección 2.4 a las imágenes de análisis. Se varió el valor de Thglobal con un paso de 25 HU en el intervalo 50-400 HU. Se consideró como valor óptimo aquel en el cual se apreció una inflexión en el volumen de las isosuperficies obtenidas.
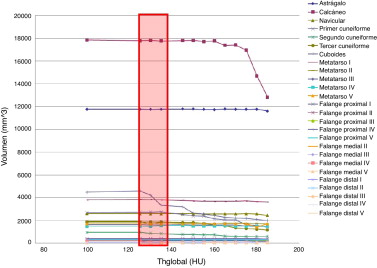
La figura 6 muestra la determinación experimental de Thglobal en un estudio del pie de un niño. En ese caso, a partir de 125 HU se observó una mayor variación volumétrica en algunas estructuras óseas. Geométricamente se observaron huecos y deformaciones en las isosuperficies, por lo cual el valor óptimo de Thglobal se consideró 125 HU.
|
|
|
Figura 6. Volúmenes de los huesos del pie con diferentes valores de Thglobal . |
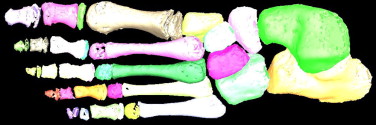
Como resultado, en la figura 7 se observa el dominio geométrico del pie del niño al aplicar el algoritmo propuesto con el valor de Thglobal definido de forma experimental. Obsérvense además los cartílagos de crecimiento.
|
|
|
Figura 7. Dominio geométrico del pie de un niño. Thglobal = 125 HU y t = 0,2. |
El algoritmo de Canny se considera uno de los mejores métodos de detección de contornos, y combina un operador diferencial con un filtro gaussiano . Una vez finalizado, se obtiene como resultado una imagen binaria en la que cada píxel se define como píxel de borde o de fondo [31] .
El algoritmo de Canny consiste en 3 grandes pasos:
- Obtención del gradiente: se calcula la magnitud y la orientación del vector gradiente en cada píxel.
- Supresión no máxima: se logra el adelgazamiento del ancho de los bordes, obtenidos con el gradiente, hasta lograr bordes de un píxel de ancho.
- Histéresis de umbral: se aplica una función de histéresis basada en 2 umbrales; con este proceso se pretende reducir la posibilidad de aparición de contornos falsos.
El algoritmo EM se clasifica como algoritmo generativo sin supervisión y se emplea en operaciones de agrupamiento (clustering) . En este, se ajustan N distribuciones gaussianas a los datos de entrada. Constituye, por tanto, una forma efectiva de representar una distribución compleja con pocos parámetros (media y varianza) [33] .
La determinación de los píxeles que definen el tejido óseo en las imágenes, mediante EM, requiere la realización de 2 pasos:
- Ajustar el histograma de la imagen a 3 distribuciones gaussianas , que identifican el fondo, el tejido blando y el tejido óseo.
- Umbralizar la imagen según los valores de la distribución gaussiana que representa el tejido óseo.
El valor de t empleado para la determinación de los contornos que pertenecen a una misma isosuperficie fue especificado manualmente, y se varió entre 0,1-0,8 hasta obtener la cantidad máxima de huesos separados correctamente.
Cada conjunto de imágenes del pie fue procesado indistintamente por las 3 variaciones y se obtuvieron los dominios geométricos correspondientes, que se compararon empleando como métricas la cantidad de huesos delimitados correctamente y el tiempo de procesamiento.
Para realizar los experimentos, se utilizó un procesador Core I7 2.67 GHz con 4 GB de RAM.
4. Resultados y discusión
Las Figura 8 , Figura 9 and Figura 10 muestran los resultados obtenidos al aplicar las variantes de umbralización propuestas a 3 estudios del pie en adultos. El nivel de descomposición del dominio geométrico alcanzado por cada una de estas se observa a través de la representación de las isosuperficies (regiones anatómicas) en diferentes colores.
|
|
|
Figura 8. Dominio geométrico del pie del adulto 1. a) Combinando la umbralización global y adaptativa con Thglobal = 180 HU; b) aplicando Canny; c) aplicando EM. Criterio de intersección de contornos t = 0,3. |
|
|
|
Figura 9. Dominio geométrico del pie del adulto 2. a) Combinando la umbralización global y adaptativa con Thglobal = 300 HU; b) aplicando Canny; c) aplicando EM. Criterio de intersección de contornos t = 0,46. |
|
|
|
Figura 10. Dominio geométrico del pie del adulto 3. a) Combinando la umbralización global y adaptativa con Thglobal = 50 (HU); b) aplicando Canny; c) aplicando EM. Criterio de intersección de contornos t = 0,3. |
En las figuras 8a, 8b y 8c , se aprecian las isosuperficies del modelo del pie adulto 1 posterior a la aplicación de los 3 algoritmos.
Mediante la combinación con la umbralización adaptativa (fig. 8 a) se obtuvieron los huesos del tarso, a excepción de los cuneiformes, que se detectaron como una sola entidad (2 de ellos unidos con el segundo y tercer metatarso). Por su parte, las umbralizaciones mediante Canny y EM no dieron buenos resultados (figs. 8b y 8c ).
En el caso del pie adulto 2, la combinación con la umbralización adaptativa (fig. 9 a) permitió la obtención de todos los huesos del tarso, excepto del segundo y del tercer cuneiforme además del segundo metatarso. De igual forma, con la umbralización mediante Canny y EM no se obtuvieron buenos resultados (figs. 9b y 9c ).
Al aplicar el algoritmo propuesto al estudio del pie de adulto 3 (fig. 10 a) se observa que los contornos que representan el calcáneo y el cuboides no se definen correctamente y aparecen fusionados. De igual forma, no se obtiene una correcta definición de las 3 cuñas. Sin embargo, los resultados obtenidos son superiores en comparación con los obtenidos mediante la umbralización por Canny (fig. 10 b) o EM (fig. 10 c).
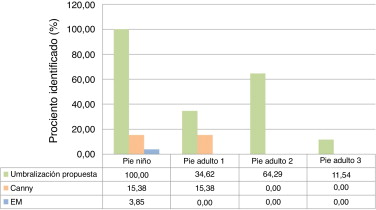
En la figura 11 se muestran los valores porcentuales de las estructuras óseas determinadas correctamente por cada una de las propuestas de umbralización en los estudios analizados. La propuesta de combinar la umbralización global y la adaptativa obtuvo mayor índice de aciertos en todos los casos.
|
|
|
Figura 11. Porcentaje de estructuras óseas identificadas correctamente por cada variante de umbralización. |
El tiempo empleado por la umbralización mediante EM (tabla 1 ) fue superior debido al procesamiento de los histogramas de las imágenes para obtener las distribuciones gaussianas .
| Estudio | Tiempo de procesamiento promedio (s) | ||
|---|---|---|---|
| Algoritmo propuesto | Canny | EM | |
| Pie niño | 81,3 | 82,4 | 187,5 |
| Pie adulto 1 | 75,6 | 77,6 | 178,2 |
| Pie adulto 2 | 57,8 | 58,9 | 93,5 |
| Pie adulto 3 | 76,8 | 75,8 | 180,4 |
Los tiempos de procesamiento mediante el algoritmo de Canny y la umbralización propuesta fueron similares, sin embargo esta última ofrece mejores resultados en cuanto a la descomposición geométrica.
4.1. Limitaciones al modelo
La principal limitación al modelo se observó en la obtención del dominio geométrico de las falanges. El algoritmo propuesto en ocasiones identifica 2 o más falanges como parte de una misma entidad geométrica.
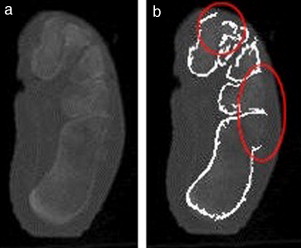
La figura 12 muestra los errores de la segmentación en un corte del pie de adulto 3. Se observa (fig. 12 b) que los contornos que representan el calcáneo y el cuboides no se definen correctamente y aparecen fusionados. De igual forma, no se obtiene una correcta definición de las 3 cuñas (fig. 12 b).
|
|
|
Figura 12. Ejemplo de fallo de la segmentación en una imagen de TC de baja resolución espacial. a) Imagen original; b) imagen con los contornos determinados. |
Esta ambigüedad en la definición de los contornos de los huesos generalmente ocurre a causa de la baja resolución espacial de las imágenes, lo cual dificulta, incluso para un experto, la segmentación de tales imágenes.
Otro elemento que se debe tener en cuenta es que como consecuencia del proceso de envejecimiento se pueden producir cambios degenerativos. Esta situación puede provocar anquilosis (fusión espontánea articular), es decir, se unen las articulaciones y en las imágenes de TC varios huesos aparecen como una sola entidad [34] . Además, esa fusión se puede realizar de forma quirúrgica (denominada artrodesis).
Como se explicó anteriormente, el tejido cortical de la superficie de los huesos debe aparecer como un borde brillante que rodea una región más oscura, correspondiente a los demás tipos de tejido óseo en imágenes de TC [7] . Esto facilitaría el desempeño del algoritmo de segmentación.
Sin embargo, factores como una determinada patología, los cambios degenerativos, la posición del paciente al tomar las imágenes y la limitada resolución espacial de la modalidad de obtención de imágenes empleada no permiten que aparezca el tejido óseo cortical de esta forma. Una posible mejora de la calidad de las imágenes sería incrementar el nivel de radiaciones emitidas, pero esto podría comprometer la salud del paciente u ocasionar problemas en el funcionamiento del equipo de adquisición [35] and [36] .
La utilización de algoritmos de filtrado en la etapa de preprocesamiento de las imágenes ayuda a proporcionar imágenes más nítidas y contrastantes [37] , [38] , [39] , [40] , [41] and [42] , procedimientos que se fundamentan en transformar y modificar la intensidad de cada píxel, pero la transformación de la intensidad podría eliminar información valiosa o relevante para diagnosticar patologías tempranas. Por tanto, los autores no incluyeron en la propuesta la utilización de ese tipo de mejoras, aunque sostienen que esto se encuentra en función del nivel de precisión requerido.
5. Conclusiones
La combinación de la umbralización global y de la adaptativa constituye un método efectivo para solventar 2 de los problemas comunes en imágenes médicas: la separación de los huesos adyacentes y el problema del volumen parcial.
La propuesta de análisis de la variación volumétrica para definir el valor de umbralización global óptimo demostró ser efectiva, si se desconoce el coeficiente de absorción electromagnética del tejido óseo para un estudio específico.
El algoritmo propuesto, bajo las mismas condiciones y en corto tiempo de procesamiento, permite la obtención del modelo geométrico del pie con resultados superiores a los obtenidos mediante la umbralización de Canny o EM.
Aunque el algoritmo generalmente falla en la detección de las falanges, permite la obtención de los huesos del tarso y del metatarso, las estructuras anatómicas que con mayor frecuencia se utilizan en los estudios cinemáticos y de carga del pie.
Los resultados obtenidos validan la efectividad del algoritmo propuesto para ser empleado como núcleo funcional en la reconstrucción tridimensional del pie y puede ser extendido a la obtención del dominio geométrico de otras estructuras anatómicas.
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Agradecimientos
Los autores agradecen la colaboración prestada durante la elaboración del presente artículo al Dr. Juan Miguel Díaz Quesada y la Lic. Yudith Díaz Gazán.
Bibliografía
- [1] A.S. Kelikian, S.K. Sarrafian; Sarrafians anatomy of foot and angle: Descriptive, topographical, functional; Lippincott Williams & Wikkins, a Wolters Kluwer business (2011)
- [2] J. Cheung, M. Zhang; Consequences of partial and total plantar fascia release - a finite element study; Foot Ankle Int, 27 (2006), pp. 125–132
- [3] P. Antunes, G.R. Dias, A.T. Coelho, F. Rebelo, T. Pereira; Non-linear finite element modelling of anatomically detailed 3 D foot model; Mimmics Inovation Awards (2007)
- [4] R.L. Actis, L.B. Ventura, K.E. Smith, P.K. Commean, D.J. Lott, T.K. Pilgram, et al.; Numerical simulation of the plantar pressure distribution in the diabetic foot during the push-off stance; Med Biol Eng Comput, 44 (8) (2006), pp. 653–663
- [5] F. Gholami, J. Kövecses, J.M. Font-Llagunes; Stuttgart, Germany, Dynamic Analysis of Foot Models for Human Locomotion in The 2nd Joint International Conference on Multibody System Dynamics (2012)
- [6] M. Davia, A. Jimeno-Morenilla, F. Salas; Footwear bio-modelling: An industrial approach; Comput. Aided Des., 45 (12) (2012), pp. 1575–1590
- [7] J. Calder, J. Tahmasebi, A. Mansouri; A variational approach to bone segmentation in CT images; Proceedings of SPIE (2011)
- [8] S. Hirano, Y. Hata; Fuzzy expert system for foot CT image segmentation; Image Vision Comput, 19 (2001)
- [9] P. Wolf, R. Luechinger, P. Boesiger, E. Stuessi, A. Stacoff; A MR imaging procedure to measure tarsal bone rotations; J Biomech Eng, 129 (6) (2007), pp. 931–936
- [10] P. Wolf, A. Stacoff, R. Luechinger; Tarsal bone positions in different foot excursions under bodyweight measured in vivo and noninvasively; Proceedings of the 2005 Int. Conference on Biomechanics of the Lower Limb in Health, Disease and Rehabilition, University of Salford (2005)
- [11] L. Liu, D. Raber, D. Nopachai, P. Commean, D. Sinacore, F. Prior, et al.; Interactive separation of segmented bones in CT volumes using graph cut; Medical Image Computing and Computer-Assisted Intervention, MICCAI 2008 (2008), pp. 296–304
- [12] NEMA, Digital Imaging and Communications in Medicine (DICOM), 2011, National Electrical Manufacturers Association, 1300 N. 17th Street. Rosslyn, Virginia 22209, USA.
- [13] I.N. Bankman; Handbook of Medical Imaging. Processing and analysis; Academic Press (2000)
- [14] A. Flores, A.A. Méndez; Detección Estable de los Bordes de la Oreja en Imágenes 2D; Comp. y Sist., 13 (2) (2009), pp. 195–208
- [15] G.N. Hounsfield; Computed Medical Imaging Nobel Lecture; J Radiol., 61 (6–7) (1980), pp. 459–468
- [16] P. Mah, T.E. Reeves, W.D. McDavid; Deriving Hounsfield units using grey levels in cone beam computed tomography; Dentomaxillofac Radiol, 39 (2010), pp. 323–335
- [17] M.O. Lagravère, Y. Fang, J. Carey, R.W. Toogood, G.V. Packota, P.W. Mayor; Density conversion factor determined using a cone-beam computed tomography unit NewTom QR-DVT 9000; Dentomaxillofac Radiol, 35 (2006), pp. 407–409
- [18] R. Molteni, From CT Numbers to Hounsfield Units in Cone Beam Volumetric Imaging: the effect off artifacts, in 62th AAOMR2011: Chicago.
- [19] D. Andisco, S. Blanco, A. Buzzi, S. Ballester; Optimización Interdisciplinaria de Protocolos en Tomografía Computada a partir de la modificación del mA y del control del ruido en la imagen; RAR, 74 (4) (2010), pp. 397–402
- [20] A. Mastmeyer, K. Engelke, C. Fuchs, W.A. Kalender; A hierarchical 3D segmentation method and the definition of vertebral body coordinate systems for QCT of the lumbar spine; Med. Image Anal., 10. (2006), pp. 560–577
- [21] J. Rogowska; Overview and Fundamentals of Medical Image Segmentation; I.N. Bankman (Ed.), Handbook of Medical Imaging. Processing and analysis, Academic Press (2000)
- [22] S. Suzuki, K. Abe; Topological structural analysis of digitized binary images by border following; Comput. Vis. Graph. Image Process., 30 (1) (1985), pp. 32–46
- [23] A.M. Aisen, W. Martel, E.M. Braunstein, K.I. McMillin, W.A. Phillips, T.F. Kling; MRI and CT Evaluation of Primary Bone and Soft-Tissue Tumors; AJR, 146 (1986), pp. 749–756
- [24] B. Fisher, J. Dignam, E. Tan-Chiu, S. Anderson, E.R. Fisher, J.L. Wittliff, et al.; Prognosis and Treatment of Patients With Breast Tumors of One Centimeter or Less and Negative Axillary Lymph Nodes; J Natl Cancer Inst, 93 (1) (2001)
- [25] A.G. Sorensen, S. Patel, C. Harmath, S. Bridges, J. Synnott, A. Sievers, et al.; Comparison of Diameter and Perimeter Methods for Tumor Volume Calculation; J Clin Oncol, 19 (2) (2001), pp. 551–557
- [26] M. Colleoni, N. Rotmensz, G. Peruzzotti, P. Maisonneuve, G. Viale, G. Renne, et al.; Minimal and small size invasive breast cancer with no axillary lymph node involvement: the need for tailored adjuvant therapies; Head Face Med., 3 (2007), p. 19
- [27] C. Rudack, S. Jörg, S. Kloska, W. Stoll, O. Thiede; Neither MRI, CT nor US is superior to diagnose tumors in the salivary glands – an extended case study; Head Face Med., 3 (2007), p. 19
- [28] W.E. Lorensen, H.E. Cline; Marching Cubes: A High Resolution 3 D Surface Construction Algorithm; Comput Graph., 21 (4) (1987), pp. 164–169
- [29] A.M. Alyassin, J.L. Lancaster, J.H. Downs 3rd , P.T. Fox ; Evaluation of new algorithms for the interactive measurement of surface area and volume; Med Phys, 21 (6) (1994)
- [30] J. Bodurka, F. Ye, N. Petridou, K. Murphy, P.A. Bandettini; Mapping the MRI Voxel Volume in Which Thermal Noise Matches Physiological Noise-Implications for fMRI; Neuroimage, 34 (2) (2007), pp. 542–549
- [31] J.F. Canny; A computational approach to edge detection; IEEE Trans Pattern Anal. Mach. Intell., 8 (6) (1986), pp. 679–698
- [32] K.V. Leemput; A Unifying Framework for Partial Volume Segmentation of Brain MR Images; IEEE Trans. Med. Imag., 22 (1) (2003), pp. 105–119
- [33] J.A. Bilmes; A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models; University of California at Berkeley, International Computer Science Institute and Computer Science Division (1998)
- [34] M.S. Casanova, F. Mesquita, A.I. Ortega, H.J. Yoo, F. Haiter-Neto; Computed tomography of the TMJ in diagnosis of ankylosis: two case reports; Med Oral Patol Oral Cir Bucal, 11 (2006), pp. E413–E416
- [35] S. Angenent, E. Pichon, A. Tannenbaum; Mathematical methods in medical image processing; Bull. Amer. Math. Soc. (2006)
- [36] R. Smith-Bindman; Is Computed Tomography Safe?; N Engl J Med, 363 (1) (2010), pp. 1–4
- [37] T.M. Nassef; New Segmentation Approach to Extract Human Mandible Bones Based on Actual Computed Tomography Data; Am. J. Biomed. Eng., 2 (5) (2012), pp. 197–201
- [38] D. Angelova, L. Mihaylova; Contour segmentation in 2 D ultrasound medical images with particle filtering; Expert Syst. Appl., 38 (7) (2011), pp. 8303–8310
- [39] T.-C. Lin; Decision-based fuzzy image restoration for noise reduction based on evidence theory; Expert Syst. Appl., 38 (7) (2011), pp. 8303–8310
- [40] H. Liu, C. Yang, N. Pan, E. Song, R. Green; Denoising 3 D MR images by the enhanced non-local means filter for Rician noise; Magn. Reson. Imaging, 28 (10) (2010), pp. 1485–1496
- [41] N. Ishak, M. Gangeh, R. Logeswaran; Comparison of denoising techniques applied on low-field MR brain images; IEEE (2008)
- [42] S. Rueda, J.A. Gil, R. Pichery, M. Alcañiz; Automatic Segmentation of Jaw Tissues in CT Using Active Appearance Models and Semi-automatic Landmarking; R. Larsen, M. Nielsen, J. Sporring (Eds.), Medical Image Computing and Computer-Assisted Intervention – MICCAI 2006, Springer Berlin /Heidelberg (2006), pp. 167–174
Document information
Published on 01/06/15
Accepted on 20/02/14
Submitted on 18/07/13
Volume 31, Issue 2, 2015
DOI: 10.1016/j.rimni.2014.02.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?