A particle finite element method for analysis of industrial forming processes

Abstract

We present a generalized Lagrangian formulation for analysis of industrial forming processes involving thermally coupled interactions between deformable continua. The governing equations for the deformable bodies are written in a unified manner that holds both for fluids and solids. The success of the formulation lays on a residual-based expression of the mass conservation equation obtained using the Finite Calculus (FIC) method that provides the necessary stability for quasi/fully incompressible situations. The governing equations are discretized with the FEM via a mixed formulation using simplicial elements with equal linear interpolation for the velocities, the pressure and the temperature. The merits of the formulation are demonstrated in the solution of 2D and 3D thermally-coupled forming processes using the Particle Finite Element Method (PFEM).

keywords: Updated Lagrangian formulation, finite element method, incompressible fluids, consistent tangent matrix, mixed formulation, stabilized method

1 INTRODUCTION

There is a large number of forming manufacturing processes in industry that involve the interaction of highly deformable continua, including viscous fluids and solids that undergo large deformations. Typically these problems also include coupled thermal effects between the interacting bodies during the forming process.

A number of numerical methods has been developed over the years for the simulation of industrial forming processes. The different methods can be classified as those based on a pure fluid mechanics formulation, i.e. the so-called flow approach developed around the 1980's [6,39,40,44,45,48] and those based on a solid mechanics formulation [11,12,19,31,47].

In this work we present a generalized continuum mechanics formulation for the analysis of industrial forming processes that involve thermally coupled interactions between deformable continua (both fluids and solids).

The motion of the deformable bodies (either a solid or a fluid) is described using a Lagrangian mixed formulation with the velocities, the pressure and the temperature as the unknown variables. Appropriate constitutive laws for the different constituent materials in the different parts of the analysis domain are used. The mixed Lagrangian formulation allows us to model the non linear interaction (including coupled thermal effects) between the different bodies involved in the forming process in a unified manner.

The continuum mechanics equations are solved with the Particle Finite Element Method (PFEM, www.cimne.com/pfem). The PFEM treats the mesh nodes in the analysis domain as virtual particles that model the behaviour of the underlying can freely move and even separate from the domain representing, for instance, the effect of water drops or cutting particles in drilling problems and machining. A mesh connects the nodes discretizing the continuum domain where the governing equations are solved using a stabilized FEM. Examples of application of PFEM to problems in fluid and solid mechanics including fluid-structure interaction (FSI) situations and coupled thermal flow problems can be found in [1,2,4,5,9,13,14,15,16,17,18,20,26,27,34,35,37,38,43]. Early attempts of the using the PFEM for solving metal forming problems were reported in [20,30].

In Lagrangian analysis procedures (such as PFEM) the motion of the virtual particles (i.e. the nodes) and of physical particles is tracked during the transient solution. Hence, the convective terms vanish in the momentum and heat transfer equations for the continuum part of the domain and no numerical stabilization is needed for treating those terms. Another source of numerical instability however remains in Lagrangian formulation, namely the treatment of incompressibility using equal order FEM interpolation for the velocities and the pressure. In this work a stabilized form of the discretized mass conservation equation is obtaining using the Finite Calculus (FIC) method proposed by Oñate et al. [21,22,23,24,25,28,29,30,36] that has excellent mass preservation features.

The generalized Lagrangian approach here described follows the ideas presented in [15] where a PFEM formulation for treating fluids and solids in a unified manner was proposed. These ideas have been extended by Franci, Oñate and Carbonell [10] using a stabilized PFEM formulation based on the FIC method.

The lay-out of the paper is the following. In the next section we present the basic equations for conservation of linear momentum, mass conservation and heat transfer for a continuum using a generalized Lagrangian framework. Next we derive the stabilized FIC form of the mass conservation equation. An incompressible continuum can be considered as the limit case of the compressible problem. Then the mixed finite element discretization using simplicial element with equal order approximation for the velocity, the pressure and the temperature is presented and the relevant matrices and vectors of the discretized problem are given. Details of the implicit solution of the Lagrangian FEM equations in time using an updated Lagrangian approach and a Newton-Raphson type iterative scheme are presented. The relevance of the bulk stiffness terms in the tangent matrix for enhancing the convergence and accuracy of the iterative solution for problems involving quasi and fully incompressible continua is discussed. The basic steps of the PFEM are described.

The efficiency and general applicability of the PFEM are verified by solving a set of thermally coupled industrial forming problems in two (2D) and three (3D) dimensions. The excellent performance of the numerical method proposed for all the problems analyzed is highlighted.

Figure 1: Initial ($t={}^{0}t$), current ($t={}^{n}t$) and updated ($t={}^{n+1}t$) configurations of a domain $V$ with Neumann ($\Gamma _{t}$) and Dirichlet ($\Gamma _{v}$) boundaries. Trajectory of a material point $i$ and velocity (${v}_{i}$) and displacement (${u}_{i}$) vectors of the point at each configuration. ${}^{n}{u}$, ${}^{n+1}{u}$ and $\Delta {u}$ denote schematically the trajectories of the overall domain between two configurations.

2 GOVERNING EQUATIONS FOR A LAGRANGIAN CONTINUUM

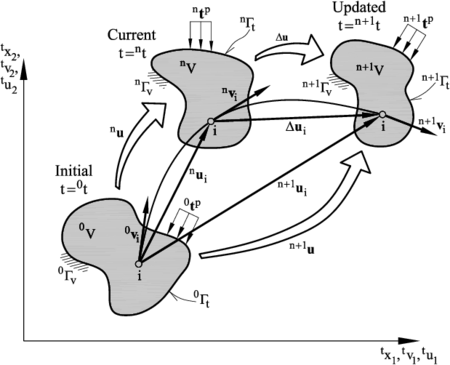
We will consider a domain containing a deformable material (either a fluid or a solid) which evolves in time due to external and internal forces and prescribed velocities and thermal conditions from an initial configuration at time ${\textstyle t={}^{0}t}$ (typically ${\textstyle {}^{0}t=0}$) to a current configuration at time ${\textstyle t={}^{n}t}$. The volume ${\textstyle V}$ and its boundary ${\textstyle \Gamma }$ at the initial and current configurations are denoted as (${\textstyle {}^{0}V,{}^{0}\Gamma }$) and (${\textstyle {}^{n}V,{}^{n}\Gamma }$), respectively. The goal is to find the domain that the material occupies, as well as the velocities, strain rates and stresses (the deviatoric stresses and the pressure) and the temperature in the so-called updated configuration at time ${\textstyle {}^{n+1}t={}^{n}t+\Delta t}$ (Figure 1). In the following a left superindex denotes the configuration where the variable is computed.

2.1 Momentum equations

The equations of conservation of linear momentum for a deformable continuum are written in the Lagrangian description as [3]

$\rho {\frac {Dv_{i}}{Dt}}-{\partial {}^{n+1}\sigma _{ij} \over \partial {}^{n+1}x_{j}}-{}^{n+1}b_{i}=0\quad ,\quad i,j=1,\cdots ,n_{s}\quad {\hbox{in }}{}^{n+1}V$

(1)

In Eq.(1), ${\textstyle {}^{n+1}V}$ is the analysis domain in the updated configuration at time ${\textstyle ^{n+1}t}$ with boundary ${\textstyle {}^{n+1}\Gamma }$, ${\textstyle v_{i}}$ and ${\textstyle b_{i}}$ are the velocity and body force components along the ${\textstyle i}$th Cartesian axis, ${\textstyle \rho }$ is the density, ${\textstyle n_{s}}$ is the number of space dimensions (i.e. ${\textstyle n_{s}=3}$ for 3D problems) and ${\textstyle {}^{n+1}\sigma _{ij}}$ are the Cauchy stresses in ${\textstyle {}^{n+1}V}$ that are split in the deviatoric (${\textstyle s_{ij}}$) and pressure (${\textstyle p}$) components as

${}^{n+1}\sigma _{ij}={}^{n+1}s_{ij}+{}^{n+1}p\delta _{ij}$

(2)

where ${\textstyle \delta _{ij}}$ is the Kronecker delta. The pressure is assumed to be positive for a tension state. Summation of terms with repeated indices is assumed in Eq.(1) and in the following.

Remark 1. The term ${\textstyle {\frac {Dv_{i}}{Dt}}}$ in Eq.(1) is the material derivative of the velocity. This term is typically computed in a Lagrangian framework as

${\frac {Dv_{i}}{Dt}}={\frac {{}^{n+1}v_{i}-{}^{n}v_{i}}{\Delta t}}$

(3)

with

${}^{n+1}v_{i}:=v_{i}({}^{n+1}{x},{}^{n+1}t)\quad ,\quad {}^{n}v_{i}:=v_{i}({}^{n}{x},{}^{n}t)$

(4)

where ${\textstyle {}^{n}v_{i}}$ is the value of the velocity at the material point that has the position ${\textstyle {}^{n}{x}}$ at time ${\textstyle t={}^{n}t}$ and ${\textstyle {x}}$ is the coordinates vector in a fixed Cartesian system [3,7,48].

Newtonian fluids

The relationship between the deviatoric Cauchy stresses ${\textstyle {}^{n+1}s_{ij}}$ and the rates of deformation ${\textstyle \varepsilon _{ij}}$ has the standard form for a Newtonian fluid,

${}^{n+1}s_{ij}=2\mu \varepsilon '_{ij}\quad {\hbox{with}}\quad \varepsilon '_{ij}=\varepsilon _{ij}-{1 \over 3}\varepsilon _{v}\delta _{ij}\quad {\hbox{and}}\quad \varepsilon _{ij}={1 \over 2}\left({\partial {}^{n+1}v_{i} \over \partial {}^{n+1}x_{j}}+{\partial {}^{n+1}v_{j} \over \partial {}^{n+1}x_{i}}\right)$

(5)

where ${\textstyle \mu }$ is the viscosity, ${\textstyle \varepsilon '_{ij}}$ are the deviatoric rates of deformation and ${\textstyle \varepsilon _{v}}$ is the volumetric strain rate defined as ${\textstyle \varepsilon _{v}=\varepsilon _{ii}}$.

The above constitutive equation can be written in matrix form as (for 2D problems)

${}^{n+1}{s}={D}{\boldsymbol {\varepsilon }}\quad {\hbox{with}}\quad {D}=2\mu \left[{\begin{array}{cccccc}2/3&-1/3&0\\-1/3&2/3&0\\0&0&1/2\\\end{array}}\right]$

(6)

In Eq.(6) ${\textstyle {s}=[s_{11},s_{22},s_{12}]^{T}}$ and ${\textstyle {\boldsymbol {\varepsilon }}=[\varepsilon _{11},\varepsilon _{22},\varepsilon _{12}]^{T}}$ are the deviatoric Cauchy stress vector and the strain rate vector, respectively.

Hypo-elastic solids

We will assume a hipo-elastic solid with a constitutive equation of the form

$\sigma _{ij}^{\nabla ^{J}}=2{\bar {\mu }}\varepsilon _{ij}+\lambda \varepsilon _{v}\delta _{ij}$

(7)

where ${\textstyle {\bar {\mu }}}$ and ${\textstyle \lambda }$ are the Lame constants and ${\textstyle \sigma _{ij}^{\nabla ^{J}}}$ is the Jaumann rate of the Cauchy stresses [3].

Tensor ${\textstyle {\boldsymbol {\sigma }}^{\nabla ^{J}}}$ is approximated in this work as

${\boldsymbol {\sigma }}^{\nabla ^{J}}\simeq {\frac {1}{J}}L({\boldsymbol {\tau }})$

(8)

where ${\textstyle J}$ is the determinant of the deformation tensor ${\textstyle {F}}$ ${\textstyle \left(F_{ij}={\partial {}^{n+1}x_{i} \over \partial ^{n}x_{j}}\right)}$, and ${\textstyle L({\boldsymbol {\tau }})}$ is the Lie derivative of the Kirchhoff stress tensor ${\textstyle \tau _{ij}}$ [3].

Combining Eqs.(7) and (8) gives the following approximation for ${\textstyle L({\boldsymbol {\tau }})}$

$L(\tau _{ij})\simeq J(2{\bar {\mu }}\varepsilon _{ij}+\lambda \varepsilon _{v}\delta _{ij})$

(9)

Remark 2. Assumption (8) is equivalent to accepting that the Truesdell and Jaumann rates of the Cauchy stresses are identical. A more accurate assumption for solving the same problem can be found in [10].

Using standard transformations of continuum mechanics gives [3]

${L}({\boldsymbol {\tau }})={F}{\dot {S}}{F}^{T}={\frac {1}{\Delta t}}{F}(\Delta {S}){F}^{T}={\frac {J}{\Delta t}}\Delta {\boldsymbol {\sigma }}$

(10)

where ${\textstyle {S}}$ are the 2nd Piola-Kirchhoff stress tensor, the upper dot denotes the time derivative and ${\textstyle \Delta {\boldsymbol {\sigma }}}$ is the increment of the Cauchy stress tensor.

Substituting Eq.(10) into (9) gives after grouping terms

${}^{n+1}\sigma _{ij}={}^{n}\sigma _{ij}+\Delta \sigma _{ij}$

(11)

where

$\Delta \sigma _{ij}=\Delta s_{ij}+\Delta p\delta _{ij}$

(12)

with

$\Delta s_{ij}=2{\bar {\mu }}\Delta t\varepsilon '_{ij}\quad {\hbox{and}}\quad \Delta p={\bar {\kappa }}\Delta t\varepsilon _{v}$

(13)

where

${\bar {\kappa }}={\frac {2}{3}}{\bar {\mu }}+\lambda$

(14)

is the bulk modulus of the solid material.

The Cauchy stresses ${\textstyle {}^{n}{\boldsymbol {\sigma }}}$ in Eq.(12) are computed on the updated configuration. These stresses can be obtained from the 2nd Piola-Kirchhoff stresses ${\textstyle {}^{n}{S}}$ on the current configuration as

${}^{n}{\boldsymbol {\sigma }}={\frac {1}{J}}{F}({}^{n}{S}){F}^{T}$

(15)

Remark 3. The relationship between the deviatoric Cauchy stress increments and the rates of deformation for a solid material can be written in the same matrix form as Eq.(6) substituting in matrix ${\textstyle D}$ the viscosity ${\textstyle \mu }$ by ${\textstyle {\bar {\mu }}\Delta t}$.

2.3 Mass conservation equation

The mass conservation equation can be written for both fluid and solids as [3,7,48]

$r_{v}=0\quad {\hbox{in }}{}^{n+1}V$

(16a)

with

$r_{v}:=-{\frac {1}{\kappa }}{\frac {Dp}{Dt}}+\varepsilon _{v}$

(16b)

For a quasi-incompressible fluid material ${\textstyle \kappa =\rho c^{2}}$ where ${\textstyle c}$ is the speed of sound in the fluid. For a solid material, ${\textstyle \kappa ={\bar {\kappa }}}$ with ${\textstyle {\bar {\kappa }}}$ given by Eq.(14). Eqs.(16) define the constitutive equation for the pressure for both solids and quasi-incompressible fluids as ${\textstyle \Delta p=\kappa \Delta t\varepsilon _{v}}$. This is consisted with the expression obtained in Eq.(13) for a hypo-elastic solid material.

For a fully incompressible material ${\textstyle \kappa =\infty }$ and Eq.(16a) simplifies to the standard form, ${\textstyle \varepsilon _{v}=0}$. In this case the pressure increment can not be obtained from Eqs.(16) and then the pressure becomes an independent variable [7,48]. In our work we will retain the quasi-incompressible form of ${\textstyle r_{v}}$ for convenience.

Remark 4. Note that for Newtonian fluids the deviatoric stresses are directly related to the rates of deformation by Eq.(5), whereas for solids the deviatoric stress increments are related to the rates of deformation by Eq.(13). On the other hand, the relationship between the pressure increment and the volumetric strain rate has the form of Eq.(13) for both fluids and solids, with the adequate definition of the bulk modulus for each case.

2.4 Thermal balance

The thermal balance equation is written in a Lagrangian framework as

$\rho c{\frac {DT}{Dt}}-{\partial \over \partial {}^{n+1}x_{i}}\left(k{\partial T \over \partial {}^{n+1}x_{i}}\right)+{}^{n+1}Q=0\quad ,\quad i,j=1,\cdots ,n_{s}\quad {\hbox{in }}{}^{n+1}V$

(17)

where ${\textstyle T}$ is the temperature, ${\textstyle c}$ is the thermal capacity, ${\textstyle k}$ is the heat conductivity and ${\textstyle Q}$ is the external heat source.

Mechanical problem

The boundary conditions at the Dirichlet (${\textstyle \Gamma _{v}}$) and Neumann (${\textstyle \Gamma _{t}}$) boundaries with ${\textstyle \Gamma =\Gamma _{v}\cup \Gamma _{t}}$ are

${}^{n+1}v_{i}-{}^{n+1}v_{i}^{p}=0\qquad {\hbox{on }}{}^{n+1}\Gamma _{v}$

(18)

${}^{n+1}\sigma _{ij}n_{j}-{}^{n+1}t_{i}^{p}=0\quad {\hbox{on }}{}^{n+1}\Gamma _{t}\quad ,\quad i,j=1,\cdots ,n_{s}$

(19)

where ${\textstyle v_{i}^{p}}$ and ${\textstyle t_{i}^{p}}$ are the prescribed velocities and prescribed tractions on the respective boundaries and ${\textstyle n_{j}}$ are the components of the unit normal vector to the boundary [3,7,48].

Thermal problem

${}^{n+1}T-{}^{n+1}T^{p}=0\quad {\hbox{on }}{}^{n+1}\Gamma _{T}$ (20) $k{\partial T \over \partial n}+{}^{n+1}q_{n}^{p}=0\quad {\hbox{on }}{}^{n+1}\Gamma _{q}$ (21)

where ${\textstyle T^{p}}$ and ${\textstyle q_{n}^{p}}$ are the prescribed temperature and the prescribed normal heat flux at the boundaries ${\textstyle \Gamma _{T}}$ and ${\textstyle \Gamma _{q}}$, respectively and ${\textstyle n}$ is the direction normal to be boundary.

3 STABILIZED MASS CONSERVATION EQUATION

In this work we will use the following stabilized form of the mass conservation equation obtained using the Finite Calculus (FIC) approach [38]

$-{\frac {1}{\kappa }}{\frac {Dp}{Dt}}+\varepsilon _{v}+\tau {\partial {}^{n+1}{\hat {r}}_{m_{i}} \over \partial {}^{n+1}x_{i}}=0\qquad {\hbox{in }}{}^{n+1}V$

(22)

The last term in Eq.(22) is the so-called stabilization term introduced by the FIC technique; in this equation ${\textstyle {\hat {r}}_{m_{i}}}$ is a static momentum term defined as

${\hat {r}}_{m_{i}}={\partial s_{ij} \over \partial x_{j}}+{\frac {\partial p}{\partial x_{i}}}+b_{i}$

(23)

and ${\textstyle \tau }$ is a stabilization parameter. Eq.(22) is a simplification of a more general FIC-based stabilized expression for quasi-incompressible fluids detailed in [38].

The stabilization parameter ${\textstyle \tau }$ is typically computed for each element as

$\tau =\left({\frac {8\mu }{(l^{e})^{2}}}+{\frac {2\rho }{\Delta t}}\right)^{-1}$

(24)

where ${\textstyle \Delta t}$ is the time step used for the transient solution and ${\textstyle l^{e}}$ is a characteristic element length computed as ${\textstyle l^{e}=2(V^{e})^{1/n_{s}}}$ where ${\textstyle V^{e}}$ is the element area (for 3-noded triangles) or volume (for 4-noded tetrahedra). For heterogeneous material the values of ${\textstyle \mu }$ and ${\textstyle \rho }$ are computed at the element center [38]. For a solid material, the viscosity ${\textstyle \mu }$ is substituted by ${\textstyle {\bar {\mu }}\Delta t}$ with ${\textstyle {\bar {\mu }}}$ defined in Eq.(7).

We note that ${\textstyle \tau =0}$ for “compressible” type problems not requiring stabilization. In these cases Eq.(22) recovers the standard form for the conservation of mass of the infinitesimal theory (see Eqs.(16)).

4 VARIATIONAL EQUATIONS

4.1 Momentum equations

Multiplying Eq.(1) by arbitrary test functions ${\textstyle w_{i}}$ with dimensions of velocity and integrating over the analysis domain ${\textstyle {}^{n+1}V}$ gives the weighted residual form of the momentum equations as [46,48]

$\int _{{}^{n+1}V}w_{i}\left(\rho {\frac {Dv_{i}}{Dt}}-{\partial {}^{n+1}\sigma _{ij} \over \partial {}^{n+1}x_{j}}-{}^{n+1}b_{i}\right)dV=0$

(25)

Integrating by parts the term involving ${\textstyle \sigma _{ij}}$ and using the Neumann boundary conditions (19) yields the weak variational form of the momentum equations as

$\int _{{}^{n+1}V}w_{i}\rho {\frac {Dv_{i}}{Dt}}dV+\int _{{}^{n+1}V}\delta \varepsilon _{ij}{}^{n+1}\sigma _{ij}dV-\int _{{}^{n+1}V}w_{i}{}^{n+1}b_{i}dV-\int _{{}^{n+1}\Gamma _{t}}w_{i}{}^{n+1}t_{i}^{p}d\Gamma =0$

(26)

where ${\textstyle \delta \varepsilon _{ij}={\partial w_{i} \over \partial {}^{n+1}x_{j}}+{\partial w_{j} \over \partial {}^{n+1}x_{i}}}$ is an arbitrary (virtual) strain rate field. Eq.(26) is the standard form of the principle of virtual power [3,7,48].

Substituting the stresses from Eq.(2) into (26) gives the following expression (in matrix form)

$\int _{{}^{n+1}V}{w}^{T}\rho {\frac {D{\hbox{v}}}{Dt}}dV+\!\int _{{}^{n+1}V}\delta {\boldsymbol {\varepsilon }}^{T}{}^{n+1}{s}dV+\!\int _{{}^{n+1}V}\delta {\boldsymbol {\varepsilon }}^{T}{m}{}^{n+1}{p}dV-$ $-\int _{{}^{n+1}V}{w}^{T}{}^{n+1}{b}dV-\!\int _{{}^{n+1}\Gamma _{t}}{\hbox{w}}^{T}{}^{n+1}{\hbox{t}}^{p}d\Gamma =0$

(27)

In Eq.(27) ${\textstyle {w},{v}}$ and ${\textstyle \delta {\boldsymbol {\varepsilon }}}$ are vectors containing the test functions, the velocities and the virtual strain rates respectively; ${\textstyle {b}}$ and ${\textstyle {\hbox{t}}^{p}}$ are the body force and surface traction vectors, respectively and ${\textstyle {m}}$ is an auxiliary vector. These vectors are defined as (for 2D problems)

${\begin{array}{l}{\hbox{w}}=[w_{1},w_{2}]^{T}\quad ,\quad {\hbox{v}}=[v_{1},v_{2}]^{T}\quad ,\quad {\hbox{b}}=[b_{1},b_{2}]^{T}\quad ,\quad {\hbox{t}}^{p}=[t_{1}^{p},t_{2}^{p}]^{T}\\[.5cm]\delta {\boldsymbol {\varepsilon }}=[\delta \varepsilon _{11},\delta \varepsilon _{22},\delta \varepsilon _{12}]^{T}\quad ,\quad {m}=[1,1,0]^{T}\end{array}}$

(28)

4.2 Mass conservation equation

We multiply Eq.(22) by arbitrary (continuous) test functions ${\textstyle q}$ (with dimensions of pressure) defined over the analysis domain. Integrating over ${\textstyle {}^{n+1}V}$ gives

$\int _{{}^{n+1}V}-{\frac {q}{\kappa }}{\frac {Dp}{Dt}}dV+\int _{{}^{n+1}V}q\varepsilon _{v}dV+\int _{{}^{n+1}V}q\tau {\partial {}^{n+1}{\hat {r}}_{m_{i}} \over \partial {}^{n+1}x_{i}}dV=0$

(29)

The third integral in Eq.(29) corresponding to the stabilization term is zero in the compressible parts of the continuum.

Integrating by parts the last integral in Eq.(29) and using (23) gives after some transformations [38]

${\begin{array}{r}\displaystyle \int _{{}^{n+1}V}{\frac {q}{\kappa }}{\frac {Dp}{Dt}}dV-\int _{{}^{n+1}V}q\varepsilon _{v}dV+\int _{{}^{n+1}V}\tau {\partial q \over \partial {}^{n+1}x_{i}}\left({\partial {}^{n+1}s_{ij} \over \partial {}^{n+1}x_{j}}+{\partial {}^{n+1}p \over \partial {}^{n+1}x_{i}}+{}^{n+1}b_{i}\right)dV\\\displaystyle -\int _{{}^{n+1}\Gamma _{t}}q\tau \left[\rho {\frac {Dv_{n}}{Dt}}-{\frac {2}{h_{n}}}\left({}^{n+1}s_{n}+{}^{n+1}p-{}^{n+1}t_{n}\right)\right]d\Gamma =0\end{array}}$

(30)

where ${\textstyle v_{n}}$ and ${\textstyle t_{n}}$ are the velocity and the traction force normal to the boundary ${\textstyle \Gamma _{t}}$, respectively and ${\textstyle s_{n}=s_{ij}n_{j}}$. The characteristic length ${\textstyle h_{n}}$ in Eq.(30) is taken as ${\textstyle h_{n}={\frac {l^{e}}{2}}}$ in practice.

4.3 Thermal balance equation

Application of the standard weighted residual method to the thermal balance equations (17), (20) and (21) leads, after standard operations, to [46,48]

$\int _{{}^{n+1}V}{\hat {w}}\rho c{\frac {DT}{Dt}}dV+\int _{{}^{n+1}V}{\partial {\hat {w}} \over \partial {}^{n+1}x_{i}}k{\partial T \over \partial {}^{n+1}x_{i}}dV-\int _{{}^{n+1}V}{\hat {w}}{}^{n+1}QdV+\int _{{}^{n+1}\Gamma _{q}}{\hat {w}}{}^{n+1}q_{n}^{p}d\Gamma =0$

(31)

where ${\textstyle {\hat {w}}}$ are the space weighting functions for the temperature.

5 FEM DISCRETIZATION

We discretize the analysis domain into finite elements with ${\textstyle n}$ nodes in the standard manner leading to a mesh with a total number of ${\textstyle N_{e}}$ elements and ${\textstyle N}$ nodes [33,46]. In our work we will choose simple 3-noded linear triangles (${\textstyle n=3}$) for 2D problems and 4-noded tetrahedra (${\textstyle n=4}$) for 3D problems with local linear shape functions ${\textstyle N_{i}^{e}}$ defined for each node ${\textstyle i}$ (${\textstyle i=1,\cdots ,n}$) of element ${\textstyle e}$ [33,47]. The velocity components, the pressure and the temperature are interpolated over the mesh in terms of their nodal values in the same manner using the global linear shape functions ${\textstyle N_{j}}$ spanning over the elements sharing node ${\textstyle j}$ (${\textstyle j=1,\cdots ,N}$) [33,46]. In matrix form we have (for 2D problems)

${v}={N}_{v}{\bar {v}}\quad ,\quad p={N}_{p}{\bar {p}}\quad ,\quad T={N}_{T}{\bar {T}}$

(32)

where

${\begin{array}{c}\displaystyle {\bar {v}}=\left\{{\begin{matrix}{\bar {v}}^{1}\\{\bar {v}}^{2}\\\vdots \\{\bar {v}}^{N}\end{matrix}}\right\}\quad {\hbox{with}}~{\bar {v}}^{i}=\left\{{\begin{matrix}{\bar {v}}_{1}^{i}\\{\bar {v}}_{2}^{i}\end{matrix}}\right\}~,~{\bar {p}}=\left\{{\begin{matrix}{\bar {p}}^{1}\\{\bar {p}}^{2}\\\vdots \\{\bar {p}}^{N}\end{matrix}}\right\}~,~{\bar {T}}=\left\{{\begin{matrix}{\bar {T}}_{1}\\{\bar {T}}_{2}\\\vdots \\{\bar {T}}^{N}\end{matrix}}\right\}\\[.5cm]\displaystyle {N}_{v}=[{N}_{1},{N}_{2},\cdots ,{N}_{N}]^{T}~,~{N}_{p}={N}_{T}=[{N}_{1},{N}_{2},\cdots ,{N}_{N}]\end{array}}$

(33)

with ${\textstyle {N}_{j}=N_{j}{I}_{2}}$ where ${\textstyle {I}_{2}}$ is the ${\textstyle 2\times 2}$ unit matrix.

In Eq.(33) vectors ${\textstyle {\bar {v}}}$, ${\textstyle {\bar {p}}}$ and ${\textstyle {\bar {T}}}$ contain the nodal velocities, the nodal pressures and the nodal temperatures for the whole mesh, respectively and the upperindex denotes the nodal value for each vector or scalar magnitude.

Substituting Eqs.(32) into Eqs.(26), (30) and (31) and choosing a Galerkin formulation with ${\textstyle w_{i}=q={\hat {w}}_{i}=N_{i}}$ leads to the following system of algebraic equations

${M}_{0}{\dot {\bar {v}}}+{g}+{Q}{}^{n+1}{\bar {p}}-{f}_{v}={0}$

(34a)

${\hbox{M}}_{1}{\dot {\bar {p}}}-{Q}^{T}{}^{n+1}{\bar {v}}+({L}+{M}_{b}){}^{n+1}{\bar {p}}-{f}_{p}={0}$

(34b)

${C}{\dot {\bar {T}}}+{\hat {L}}{}^{n+1}{\bar {T}}-{f}_{T}={0}$

(34c)

where ${\textstyle {\dot {\bar {a}}}}$ denotes the material time derivative of the components of a vector ${\textstyle {a}}$. The element form of the matrices and vectors in Eqs.(34) is given in Box 1.

Box 1. Element form of the matrices and vectors in Eqs.(34) (for 2D problems).

We note that Eqs.(34) involve the geometry at the updated configuration (${\textstyle {}^{n+1}V}$). This geometry is unknown; hence the solution of Eqs.(34) has to be found iteratively. The iterative solution scheme chosen in this work is presented in the next section.

Remark 5. The boundary terms of vector ${\textstyle {f}_{p}}$ can be incorporated into the matrices of Eq.(36). This leads to a non symmetrical set of equations. These boundary terms are computed here iteratively within the incremental solution scheme.

Remark 6. The presence of matrix ${\textstyle {M}_{b}}$ in Eq.(36) allows us to compute the pressure without the need of prescribing its value at the free surface [38].

6 TRANSIENT SOLUTION OF THE DISCRETIZED EQUATIONS

Eqs.(34) are solved in time with an implicit Newton-Raphson type iterative scheme [3,7,47]. The basic steps within a time increment ${\textstyle [n,n+1]}$ are:

• Initialize variables: ${\textstyle ({}^{n+1}{\hbox{x}}^{1},{}^{n+1}{\bar {v}}^{1},{}^{n+1}{s}^{1},{}^{n+1}{\bar {p}}^{1},{}^{n+1}{\bar {T}}^{1})\equiv \left\{{}^{n}{x},{}^{n}{\bar {v}},{}^{n}{s},{}^{n}{\bar {p}},{}^{n}{\bar {T}}\right\}}$.

  In the following ${\textstyle (\cdot )^{i}}$ denotes a value computed at the ${\textstyle i}$th iteration.

• Iteration loop: ${\textstyle i=1,\cdots ,N_{iter}}$.

  For each iteration.

Step 1. Compute the initial Cauchy stresses ${}^{n}{\boldsymbol {\sigma }}^{i}$ for solid elementsStep 1. Compute the initial Cauchy stresses n σ i {\displaystyle {}^{n}{\boldsymbol {\sigma }}^{i}} for solid elements

${}^{n}{\boldsymbol {\sigma }}^{i}={\frac {1}{J^{i}}}{F}^{i}[{}^{n}{S}]{F}^{iT}\quad {\hbox{with }}F_{kl}^{i}={\partial {}^{n+1}x_{k}^{i} \over \partial {}^{n}x_{l}}\quad {\hbox{and }}{J^{i}}=\vert {F}^{i}\vert$

(35a)

with

${}^{n}{S}={}^{n}{\boldsymbol {\sigma }}\quad {\hbox{and}}\quad {}^{n}{\sigma }_{ij}={}^{n}s_{ij}+{}^{n}p\delta _{ij}$

(35b)

Step 2. Compute the nodal velocity increments $\Delta {\bar {v}}$Step 2. Compute the nodal velocity increments Δ v ¯ {\displaystyle \Delta {\bar {v}}}

From Eq.(34a)

${H}_{v}^{i}\Delta {\bar {v}}=-{}^{n+1}{\bar {\hbox{r}}}_{m}^{i}\rightarrow \Delta {\bar {v}}$

(36a)

with the momentum residual ${\textstyle {\bar {r}}_{m}}$ and the iteration matrix ${\textstyle {H}_{v}}$ given by

${\bar {\hbox{r}}}_{m}={\hbox{M}}_{0}{\dot {\bar {v}}}+{\hbox{g}}+{\hbox{Q}}{\bar {p}}-{\hbox{f}}_{v}\quad ,\quad {\hbox{H}}_{v}={\frac {1}{\Delta t}}{\hbox{M}}_{0}+{\hbox{K}}+{\hbox{K}}_{v}$

(36b)

where ${\textstyle {\hbox{K}}_{v}}$ is the bulk tangent matrix (see Remark 9) and

${\hbox{K}}_{ij}^{e}=\int _{{}^{n}V^{e}}\left({\hbox{B}}_{i}^{eT}{\boldsymbol {\cal {C}}}_{T}{\hbox{B}}_{j}^{e}dV+{G}_{i}^{T}[{S}]{G}_{j}\Delta t\right)dV$

(36c)

where ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is the tangent constitutive matrix emanating from the linearization of Eq.(34a) (expressed in the current configuration) with respect to the nodal velocities [10,37]. The second term in matrix ${\textstyle {\hbox{K}}^{e}}$ is explained in Remark 7.

Step 3. Update the nodal velocities

${}^{n+1}{\bar {v}}^{i+1}={\bar {v}}^{i}+\Delta {\bar {v}}$

(37)

Step 4. Compute the nodal pressures

From Eq.(34b) we obtain

${\hbox{H}}_{p}^{i}{}^{n+1}{\bar {p}}^{i+1}={\frac {1}{\Delta t}}{\hbox{M}}_{1}{\bar {p}}^{i}+{Q}^{T}{\bar {v}}^{i+1}+{\bar {f}}_{p}^{i}\rightarrow {}^{n+1}{\bar {p}}^{i+1}$

(38a)

with

${\hbox{H}}_{p}={\frac {1}{\Delta t}}{\hbox{M}}_{1}+{\hbox{L}}+{\hbox{M}}_{b}$

(38b)

Step 5. Update the nodal coordinates and the deformation gradient

${}^{n+1}{x}^{i+1}={x}^{i}+{\frac {1}{2}}({\bar {v}}^{i+1}+{}^{n}{\bar {v}})\Delta t$

(39)

${}^{n+1}F_{ij}^{i+1}={\partial {}^{n+1}{x}_{i}^{i+1} \over \partial {}^{n}{x_{j}}}$

A more accurate expression for computing ${\textstyle {}^{n+1}{x}^{i+1}}$ can be used involving the nodal accelerations [37].

Step 6.Compute the deviatoric Cauchy stresses

Fluids:

${}^{n+1}{s}^{i+1}={D}_{T}{\hbox{B}}{\bar {v}}^{i+1}$

(40a)

Solids:

$\Delta {s}={D}_{T}{\hbox{B}}\Delta {\bar {v}}$

(40b)

where ${\textstyle {D}_{T}}$ is the tangent constitutive matrix for the deviatoric Cauchy stresses. For elastic solids and Newtonian fluids ${\textstyle {D}_{T}={D}}$ where ${\textstyle {D}}$ is given by Eq.(6) and ${\textstyle \mu ={\bar {\mu }}\Delta t}$ for solids.

For non-linear continua, the adequate expression for ${\textstyle {D}_{T}}$ has to be used [3,10].

Step 7.Compute the stresses

Solids:

Cauchy stresses:

${}^{n+1}\sigma _{ij}^{i+1}={}^{n}\sigma _{ij}^{i}+\Delta {s}_{ij}+\Delta {\bar {p}}\delta _{ij}$

(41a)

with

$\Delta {\bar {p}}={}^{n+1}{\bar {p}}^{i+1}-{}^{n}{\bar {p}}$

(41b)

2d Piola Kirchhoff stresses:

${}^{n+1}{S}^{i+1}=J{F}^{-1}[{}^{n+1}{\boldsymbol {\sigma }}^{i+1}]{F}^{-T}~~{\hbox{with }}~~{F}\equiv {}^{n+1}{F}^{i+1}$

(41c)

Fluids:

${}^{n+1}\sigma _{ij}^{i+1}={}^{n+1}{s}_{ij}^{i+1}+{}^{n+1}{p}^{i+1}\delta _{ij}$

(41d)

Step 8.Compute the nodal temperatures

$\left[{\frac {1}{\Delta t}}{C}+{\hat {L}}\right]\Delta {\bar {T}}=-{}^{n+1}{\bar {r}}_{T}^{i}\quad ,\quad {}^{n+1}{\bar {T}}^{i+1}={}^{n}{\bar {T}}^{i}+\Delta {\bar {T}}$

(42)

with

${\bar {r}}_{T}={C}{\dot {\bar {T}}}+{\hat {L}}{\bar {T}}-{f}_{T}$

(43)

Step 9. Check convergence

Verify the following conditions:

${\begin{array}{c}\displaystyle \Vert {}^{n+1}{\bar {v}}^{i+1}-{}^{n+1}{\bar {v}}^{i}\Vert \leq e_{v}\Vert {}^{n}{\bar {v}}\Vert \\\displaystyle \Vert {}^{n+1}{\bar {p}}^{i+1}-{}^{n+1}{\bar {p}}^{i}\Vert \leq e_{p}\Vert {}^{n}{\bar {p}}\Vert \\\displaystyle \Vert {}^{n+1}{\bar {T}}^{i+1}-{}^{n+1}{\bar {T}}^{i}\Vert \leq e_{T}\Vert {}^{n}{\bar {T}}\Vert \end{array}}$

(44)

where ${\textstyle e_{v}}$, ${\textstyle e_{p}}$ and ${\textstyle e_{T}}$ are prescribed error norms. In the examples presented in the paper we have set ${\textstyle e_{v}=e_{p}=e_{T}=10^{-3}}$.

If conditions (44) are satisfied then make ${\textstyle n\leftarrow n+1}$ and proceed to the next time step. Otherwise, make the iteration counter ${\textstyle i\leftarrow i+1}$ and repeat Steps 1–9.

The derivatives and integrals in all the matrices of the iteration matrix ${\textstyle {H}_{v}}$ are computed on the updated discretized configuration at time ${\textstyle n}$ (${\textstyle {}^{n}V}$) while the residual vectors ${\textstyle {\bar {r}}_{T}}$ and ${\textstyle {\bar {r}}_{m}}$ are computed in the current configuration. This is a particular version of the updated Lagrangian formulation [3,10,37,47,48].

Remark 7. The tangent deviatoric constitutive matrix ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ in Eq.(36c) depends on the constitutive model chosen. For Newtonian fluids ${\textstyle {\boldsymbol {\cal {C}}}_{T}={\boldsymbol {\cal {C}}}}$ where ${\textstyle {\boldsymbol {\cal {C}}}}$ is obtained by transforming the deviatoric constitutive tensor ${\textstyle {c}_{ijkl}=\mu (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})}$ from the updated to the current configuration as ${\textstyle {\cal {C}}_{ijkl}=F_{A_{i}}^{-1}F_{B_{j}}^{-1}F_{C_{k}}^{-1}F_{D_{l}}^{-1}{c}_{ABCD}}$ [3,37]. Matrix ${\textstyle {\boldsymbol {\cal {C}}}}$ is formed by applying Voigt rule to the terms of tensor ${\textstyle {\cal {C}}_{ijkl}}$. A similar expression is obtained for elastic solids changing ${\textstyle \mu }$ by ${\textstyle {\bar {\mu }}\Delta t}$ [10].

The second term in the integral of Eq.(36c) represents the initial stress contribution to matrix ${\textstyle {K}}$ [3,10,37]. Matrices ${\textstyle {G}}$ and ${\textstyle [S]}$ in Eq.(36c) are given by (for 2D problems)

${G}={\begin{bmatrix}{\bar {G}}&{\bar {0}}\\{\bar {0}}&{\bar {G}}\end{bmatrix}}~~,~~{\bar {G}}={\begin{bmatrix}{}_{n}N_{1,1}&0&|&{}_{n}N_{2,1}&0&|&\cdots &{}_{n}N_{n,1}\\{}_{n}N_{1,2}&0&|&{}_{n}N_{2,2}&0&|&\cdots &{}_{n}N_{n,1}\end{bmatrix}}~~,~~{\bar {0}}=\left\{{\begin{matrix}0\\0\end{matrix}}\right\}$

$[{S}]={\begin{bmatrix}{S}&{0}\\{0}&{S}\end{bmatrix}}~~,~~{0}={\begin{bmatrix}0&0\\0&0\end{bmatrix}}~~,~~{}_{n}N_{i,j}={\partial N_{i} \over \partial ^{n}x_{j}}$

(45)

where ${\textstyle {S}}$ is the 2d Piola-Kirchhoff stress tensor.

Remark 8. The iteration matrix ${\textstyle {\hbox{H}}_{v}}$ in Eq.(36a) is an approximation of the exact tangent matrix for the solid/fluid problem in the updated Lagrangian formulation [3,10,37]. The form of ${\textstyle {\hbox{H}}_{v}}$ used in this work has yielded good results with convergence achieved for the nodal values for the velocities, the pressure and the temperature in 3–4 iterations for all the problems analyzed.

Remark 9. Including the bulk stiffness matrix ${\textstyle {\hbox{K}}_{v}}$ in ${\textstyle {\hbox{H}}_{v}}$ is important for the fast convergence, mass preservation and overall accuracy of the iterative solution for quasi and fully incompressible materials [9,38]. The element expression of ${\textstyle {\hbox{K}}_{v}}$ can be obtained as [38]

${\hbox{K}}_{v}^{e}=\int _{{}^{n}V^{e}}{\hbox{B}}^{T}{\hbox{m}}\theta \Delta t\kappa {\hbox{m}}^{T}{\hbox{B}}dV$

(46)

where ${\textstyle \theta }$ is a positive number such that ${\textstyle 0<\theta \leq 1}$ that has the role of preventing the ill-conditioning of the iteration matrix ${\textstyle {H}_{v}}$ for highly incompressible materials. For a fully incompressible material (${\textstyle \kappa =\infty }$), a finite value of ${\textstyle \kappa }$ is used in practice within ${\textstyle {K}_{v}}$ as this helps to obtaining an accurate solution with reduced mass loss in few iterations per time step [9]. These considerations, however, do not affect the value of ${\textstyle \kappa }$ within matrix ${\textstyle {M}_{1}}$ in Eq.(34b) that vanishes for a fully incompressible material. A similar approach for improving mass conservation in incompressible fluids was proposed in [41].

Remark 10. The time step within a time interval ${\textstyle [n,n+1]}$ is chosen as ${\textstyle \Delta t=\min \left({\frac {^{n}l_{\min }^{e}}{\vert {}^{n}{v}\vert _{\max }}},\Delta t_{b}\right)}$ where ${\textstyle ^{n}l_{\min }^{e}}$ is the minimum characteristic distance of all elements in the mesh, with ${\textstyle l^{e}}$ computed as explained in Section 3, ${\textstyle \vert ^{n}{v}\vert _{\max }}$ is the maximum value of the modulus of the velocity of all nodes in the mesh and ${\textstyle \Delta t_{b}}$ is the critical time step of all nodes approaching a solid boundary defined as ${\textstyle \Delta t_{b}=\min \left({\frac {^{n}l_{b}}{\vert ^{n}{v}_{b}\vert _{\max }}}\right)}$ where ${\textstyle ^{n}l_{b}}$ is the distance from the node to the boundary and ${\textstyle ^{n}{v}_{b}}$ is the velocity of the node. This definition of ${\textstyle \Delta t}$ intends that no node crosses a solid boundary during a time step [38].

Remark 11. The material properties for the fluid and the solid may be dependent on the temperature. This effect is accounted for by updating the material properties in terms of the temperature within the iteration loop.

7 ABOUT THE PARTICLE FINITE ELEMENT METHOD (PFEM)

7.1 The basis of the PFEM

Let us consider a domain ${\textstyle V}$ containing fluid and solid subdomains. Each subdomain is characterized by a set of points, hereafter termed virtual particles. The virtual particles contain all the information for defining the geometry and the material and mechanical properties of the underlying subdomain. In the PFEM both subdomains are modelled using an updated Lagrangian formulation [3,47].

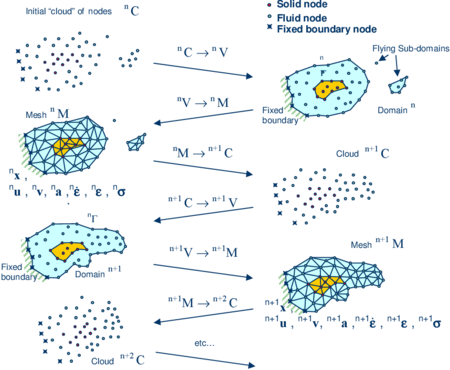
The solution steps within a time step in the PFEM are as follows:

Figure 2: Sequence of steps to update a “cloud” of virtual particles (nodes) representing a domain containing a fluid and a solid from $^{n}t$ to ${}^{n+2}t$. ${u},{v},{a},{\boldsymbol {\varepsilon }},{\dot {\boldsymbol {\varepsilon }}}$ and ${\boldsymbol {\sigma }}$ denote the displacement, the velocity, the acceleration, the strain, the strain rates and the Cauchy stresses, respectively.

1. The starting point at each time step is the cloud of points ${\textstyle C}$ in the fluid and solid domains. For instance ${\textstyle ^{n}C}$ denotes the cloud at time ${\textstyle t={}^{n}t}$ (Figure 1). The virtual particles are assumed to be coincident with the nodes in the finite element mesh generated in Step 3.
2. Identify the boundaries defining the analysis domain ${\textstyle ^{n}V}$, as well as the subdomains in the fluid and the solid. This is an essential step as some boundaries (such as the free surface in fluids) may be severely distorted during the solution, including separation and re-entering of nodes. The Alpha Shape method [8] is used for the boundary definition. Clearly, the accuracy in the reconstruction of the boundaries depends on the number of points in the vicinity of each boundary and on the Alpha Shape parameter. In the problems solved in this work the Alpha Shape method has been implementation as described in [14,26].
3. Discretize the analysis domain ${\textstyle ^{n}V}$ with a finite element mesh ${\textstyle {}^{n}M}$ using the virtual particles as the mesh nodes. We use an efficient mesh generation scheme based on an enhanced Delaunay tesselation [13,14].
4. Solve the Lagrangian equations of motion for the overall continuum using the standard FEM. Compute the state variables in the next (updated) configuration for ${\textstyle ^{n}t+\Delta t}$: velocities, pressure, strain rate and viscous stresses in the fluid and displacements, stresses and strains in the solid.
5. Move the mesh nodes to a new position ${\textstyle ^{n+1}C}$ where n+1 denotes the time ${\textstyle {}^{n}t+\Delta t}$, in terms of the time increment size.
6. Go back to step 1 and repeat the solution for the next time step to obtain ${\textstyle {}^{n+2}C}$.

Note that the key differences between the PFEM and the classical FEM are the remeshing technique and the identification of the domain boundary at each time step.

The CPU time required for meshing grows linearly with the number of nodes. As a general rule, meshing consumes for 3D problems around 15% of the total CPU time per time step, while the solution of the equations (with typically 3 iterations per time step) and the system assembly consume approximately 70% and 15% of the CPU time per time step, respectively. These figures refer to analyses in a single processor Pentium IV PC [35]. Considerable speed can be gained using parallel computing techniques.

Application of the PFEM in fluid and solid mechanics and in fluid-structure interaction problems can be found in [1,2,4,5,8,9,13,14,15,16,17,18,20,26,27,34,35,37,38,41,43] as well in www.cimne.com/pfem.

7.2 Treatment of contact conditions in the PFEM

Known velocities at boundaries in the PFEM are prescribed in strong form to the boundary nodes. These nodes might belong to fixed external boundaries or to moving boundaries linked to the interacting solids. Surface tractions are applied to the Neumann part of the boundary, as it is usual in the FEM.

Contact between fluid particles and fixed boundaries is accounted for by the incompressibility condition which naturally prevents fluid nodes to penetrate into the solid boundaries [14,26,32,35].

The contact between two solid interfaces is treated by introducing a layer of contact elements between the two interacting solid interfaces (Figure 3). This contact layer is automatically created during the mesh generation step by prescribing a minimum distance ${\textstyle \left(h_{c}\right)}$ between two solid boundaries. If the distance exceeds the minimum value ${\textstyle \left(h_{c}\right)}$ then the generated elements are treated as fluid elements. Otherwise the elements are treated as contact elements where a relationship between the tangential and normal forces and the corresponding displacement is introduced in [26,32,35].

This algorithm allows us to model complex frictional contact conditions between two or more interacting bodies moving in water in a simple manner. The algorithm has been used to model frictional contact situations between rigid or elastic solids in structural mechanics applications, such as soil/rock excavation problems [4,5]. The frictional contact algorithm described above has been extended by Oliver et al. [20] for analysis of metal cutting and machining problems.

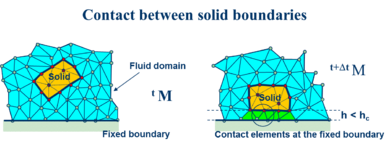
Figure 3: Layer of contact elements at a soil-solid interface modelled with the PFEM

8 EXAMPLES

8.1 Numerical examples of manufacturing problems

Some examples are presented next to show the capabilities of the method for the simulation of industrial forming processes. All the problems presented involve large strains and big changes in the geometry boundaries. The “particle” description of the continuum assumed in the PFEM introduces the capability of adapting the geometry to the computed displacement solution automatically.

The numerical solution is computed taking in account thermal and mechanical effects with the solution strategy described in Section 6.

The changes in the geometry are recognized by the PFEM features. As explained in Section 7.1, the finite element mesh is obtained by a reconnection of the particles and a remeshing of the domain. A refinement of the critical areas at each time step has been performed. The criterion to detect the critical areas for refining the mesh is based on the evaluation of the plastic energy dissipation, but other mechanical variables can be used for this purpose. Details of the application of the PFEM to solid mechanics problems can be found in [4,5].

8.2 Extrusion of a steel plate

Extrusion is one of the techniques used to reduce the section of pieces of metal and form a reduced piece of the same object. This example considers a piece of steel with the dimensions shown in Figure 4 pushed towards a rigid wall die. Two different shapes of the wall die have been analysed. Both models are depicted in Figure 4. The symmetry of the problem allows us to consider only the upper part of the piece and a 2D simulation to solve the problem. The material is modelled with a thermo-elastoplastic constitutive law with a Huber-Von Misses yield surface. The constitutive model can be found in [42]. The physical properties of the material (steel) considered in the example are shown in Box 2.

MATERIAL PROPERTIES:
Young Modulus	$206.9\times 10^{9}Pa$
Poisson Coefficient	0.29
Yield Stress	$450\times 10^{6}Pa$
Linear Hardening Modulus  ~	$129.24\times 10^{6}Pa$
Reference Hardening	$450\times 10^{6}Pa$
Saturation Hardening	$715\times 10^{6}Pa$
Hardening Exponent	16.93
Conductivity	$45N/sK$
Density	$7800kg/m^{3}$
Specific Capacity	$460m^{2}/s^{2}K$
Flow Stress Softening	$0.002K^{-1}$
Hardening Softening	$0.002K^{-1}$
Dissipation Factor	0.9
Expansion Coefficient	$10^{-5}K^{-1}$

Box 2. Material properties for the steel extrusion problem

An imposed velocity is set on the left side of the models: ${\textstyle 10mm/s}$ for the vertical die wall and ${\textstyle 2.5mm/s}$ for the inclined wall. In both models the vertical displacement is imposed to a zero value at the lower side of the steel plate. The initial temperature is ${\textstyle ^{\circ }}$T=293.15 K and the left boundary is fixed to this temperature during the analysis.

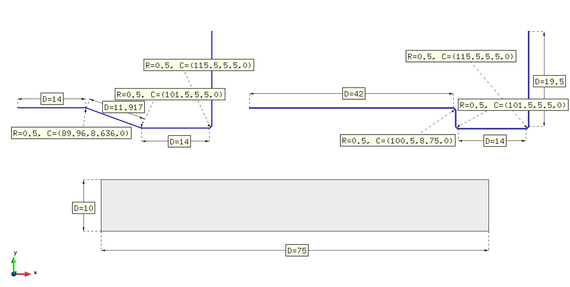
Figure 4: Extrusion of a steel plate with two wall dies. Dimensions expressed in mm.

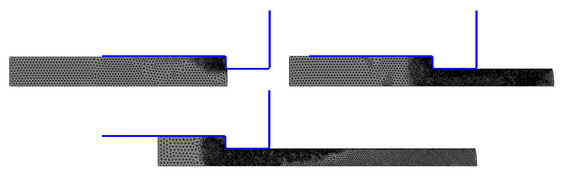
Figure 5: Extrusion of a steel plate at three time instants: t = 0.09s, t = 2.59s, t = 5.19s. Vertical die wall

The results of the extrusion analysis with the vertical step are shown in Figures 5 and 6. Different time instants are considered, from the beginning to the end of the process. The contact forces with the wall, the temperature of the model, the plastic strain and the plastic strain rate are measures that can be obtained from the numerical results. With the distribution and the values of these quantities the extrusion process can be studied and optimized.

A similar set of results for a different extrusion problems using a die wall with a progressive reduction of the section are depicted in Figures 7 and 8.

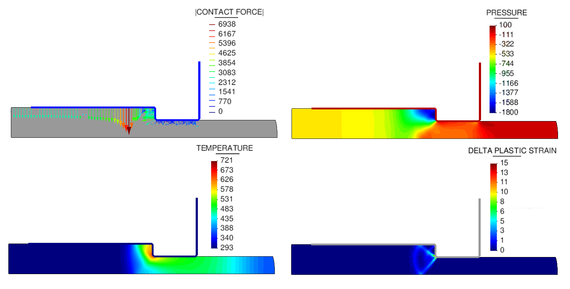
Figure 6: Results of the extrusion of a steel plate (vertical die wall) at t = 2.59s. Nodal forces in Newtons, pressure in $N/mm^{2}$, temperature in Kelvins and plastic strain rate in $1/s$.

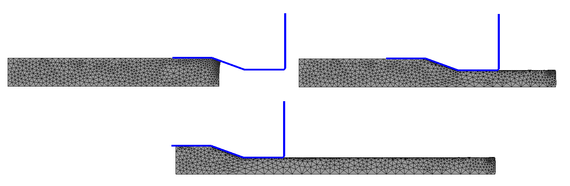
Figure 7: Extrusion of a steel plate at three time instants: t = 0.9s, t = 11.9s, t = 24.9s. Inclined die wall

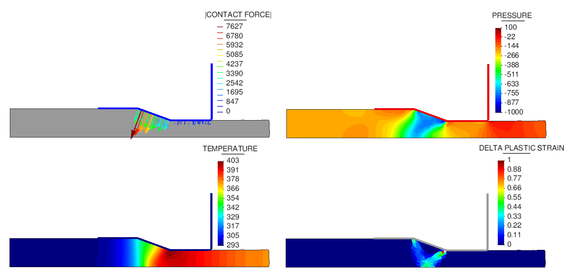
Figure 8: Results of the extrusion of a steel plate at t = 11.9s (inclined die wall). Nodal forces in Newtons, pressure in $N/mm^{2}$, temperature in Kelvins and plastic strain rate in $1/s$.

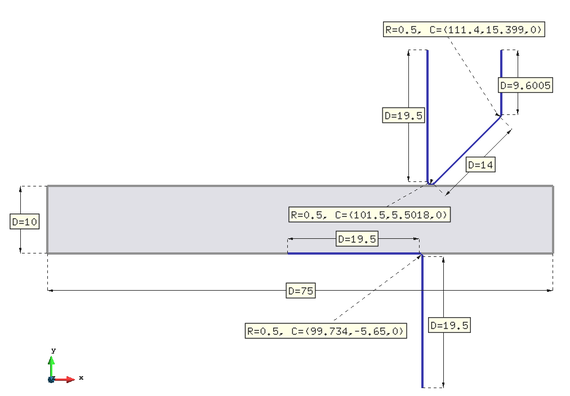
Figure 9: Cutting of a steel plate with a single cutter. Dimensions in mm.

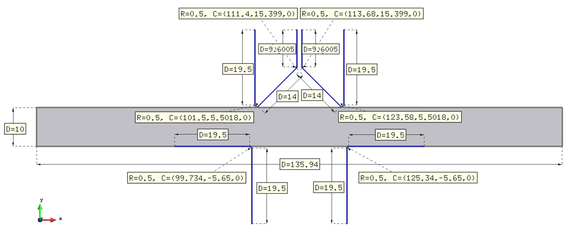
Figure 10: Cutting of a steel plate with a two symmetric cutters. Dimensions in mm.

8.3 Shear cutting

The next example shows the cutting of solid plate in 2D. It is a thermo-mechanical problem which involves large deformations and the process of cutting by means of a rigid tool. The initial conditions of the problem are depicted in Figures 9 and 10. A thermo-elastoplastic constitutive law with the same material properties as described in the previous example has been used. As previously mentioned, the PFEM combines the Lagrangian updating of the configuration with a redefinition of the domain geometry. These features allow to model naturally the cutting region by refining the solid model in the tool tip and by inserting new particles (nodes) when large flat boundaries appear at the tip contact zone.

The cutting tool moves downwards with a velocity of ${\textstyle 5mm/s}$ in the single cutter model and with a velocity of ${\textstyle 200mm/s}$ in the problem with two cutters. In both models the horizontal displacement is imposed to zero in the outer sides of the plate. The initial temperature in the domain is set to 293.15 K and is kept fixed to this value in the outer boundary sides during the analysis.

The PFEM results of the material deformation and the temperature distribution for various time instants are shown in Figures 11 and 12.

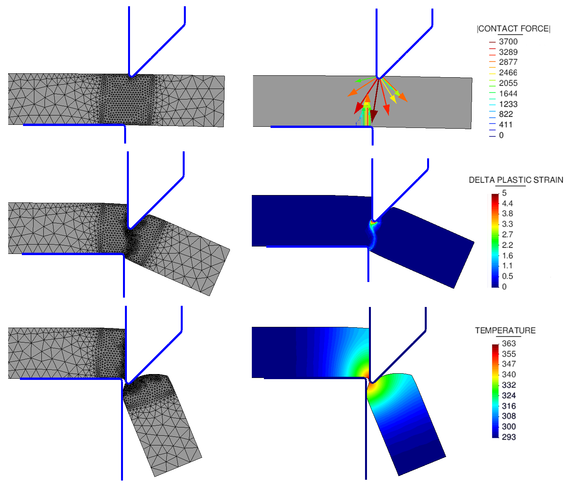
Figure 11: Cutting process. Results at the onset, the middle and the end of the process using a single cutter. Nodal forces are expressed in Newtons and the temperature in Kelvins.

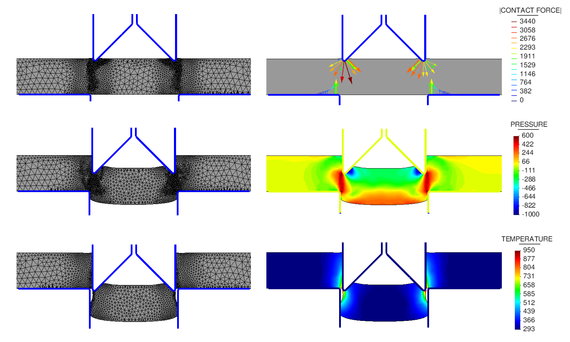
Figure 12: Results at the onset, the middle and the end of a plate cutting process with two symmetric cutters. Nodal forces are expressed in Newtons and the temperature in Kelvins.

Figure 13: Forging of a steel cylinder against to curved rigid walls. Dimensions in meters.

8.4 Forging of a cylindrical steel piece

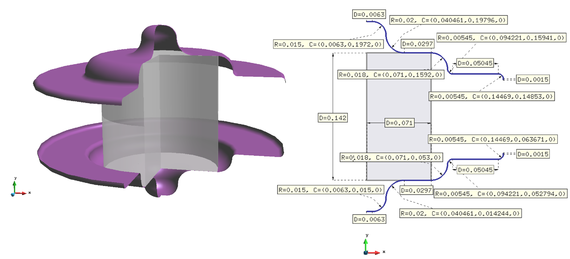
The next example considers the forging of a steel cylinder. The material properties are the same as in Box 2. The mould is defined by two rigid walls that move towards each other at the same speed, (${\textstyle 1m/s}$) and enclose the steel piece. The dimensions of the model are depicted in Figure 13. An axisymmetric solution is considered. The initial temperature of the steel material is ${\textstyle ^{\circ }}$T =293.15 K.

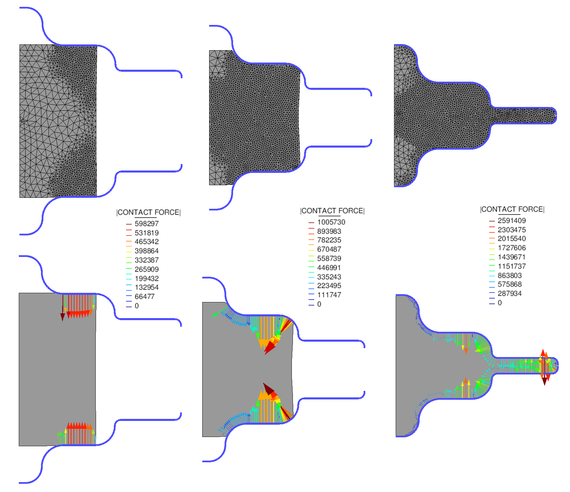
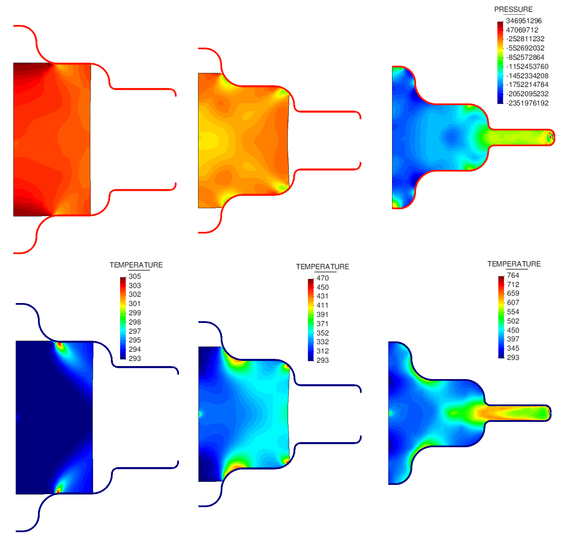
The results of the material deformation, the pressure contours and the temperature distribution for various time instants are shown in Figures 14 and 15.

Figure 14: Meshes and wall nodal forces at the beginning, the middle and the end of the forging process. Nodal forces are expressed in Newtons.

Figure 15: Pressure and temperatures at the beginning, the middle and the end of the forging process. Pressure is expressed in Pascals and the temperature in Kelvins.

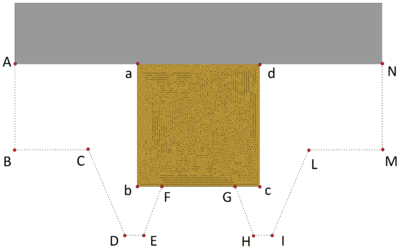
8.5 Hot forging of a metal piece

Metal hot forging consists on deforming a work piece at high temperature under compressive forces in order to obtain the desired shape of the final product. It is a largely used process in industrial metal manufacturing as it allows an improvement of the material properties of the final part via a controlled deformation process. For example, via hot forging it is possible to reduce the impurities and defects in the material, thereby avoiding stress concentrations in the final product.

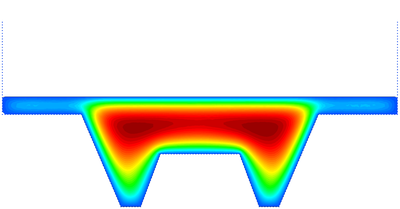
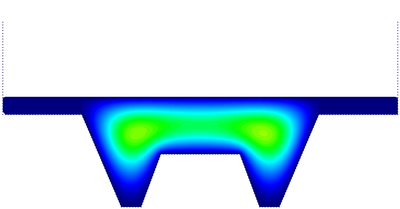
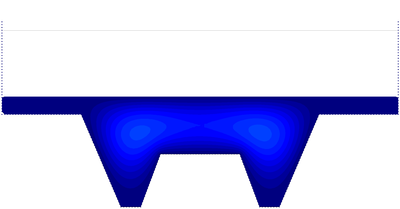
The metal forging can be performed using an open die or a closed die. In this work, the latter case is considered. The geometry and the problem data for the 2D simulation are shown in Figure 16. The forging process is performed by controlling the displacement of the upper rectangular die which is pushed downwards with a velocity v=0.01${\textstyle m/s}$ for a duration of 5.65${\textstyle s}$, while the material rigid walls are kept at the same position during the analysis. At the beginning of the process the metal piece and the lower walls have temperatures ${\textstyle ^{\circ }}$T=2000 K and ${\textstyle ^{\circ }}$T =1000 K, respectively. The forging is carried out through two steps: during the first one the piece is compressed by the descending rectangular die; then the die is stopped and from t=6.0${\textstyle s}$ to t=50.0${\textstyle s}$ the piece is cooled down. The cooling process is carried out by applying the temperature given by the following step function to both the upper rectangular die and the internal walls.

$\displaystyle {\begin{array}{l}\displaystyle T=850K6.0s<t\leq 8.5s\\\displaystyle T=600K8.5s<t\leq 10.5s\\\displaystyle T=300K10.5s<t\leq 50s\\\end{array}}$

(58)

It is assumed that the rectangular die has the same temperature of the metal piece during the compression phase. The normal heat flux through the surfaces in contact with the air has not been taken into account in the analysis.

The metal is modelled as an isotropic incompressible non-Newtonian fluid with a non-linear viscosity given by the following relation [44,45]

$\mu ={\frac {\sigma _{y}}{{\sqrt {3}}{\bar {\varepsilon }}}}$

(59)

where ${\textstyle {\sigma _{y}}}$ is the uniaxial yield stress of the material and ${\textstyle {\bar {\varepsilon }}}$ is the deviatoric strain rate invariant defined as:

${\bar {\varepsilon }}={\sqrt {{\frac {2}{3}}{\varepsilon }_{ij}{\varepsilon }_{ij}}}$

(60)

The uniaxial yield stress ${\textstyle {\sigma _{y}}}$ depends on the temperature as follows:

$\displaystyle {\begin{array}{l}\displaystyle {\sigma _{y}}=157.7T\leq 1500\\\displaystyle {\sigma _{y}}=157.7+3.6\cdot (T-1500)^{2}-3250\cdot (T-1500)1500<T\leq 1930\\\displaystyle {\sigma _{y}}=79.4T>1930\\\end{array}}$

(61)

The constitutive equation (59) is typical in the study of industrial forming processes by the plastic/viscoplastic flow approach [44,45,48].

The metal piece has been discretized using 6849 3-noded triangular finite elements. The 2D coupled thermal-mechanical simulation has been run for 50${\textstyle s}$ with ${\textstyle \Delta t}$=${\textstyle 0.0005s}$.

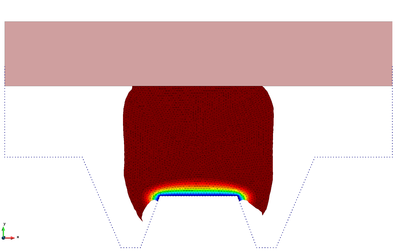
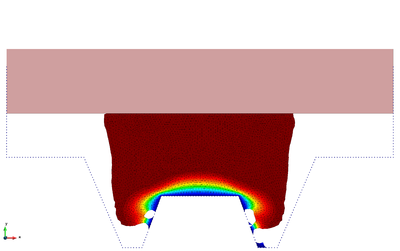
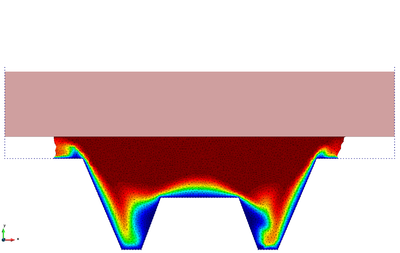
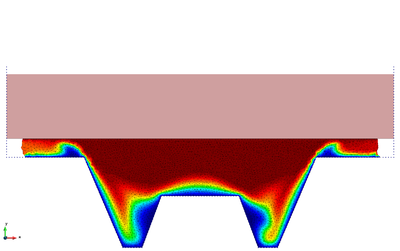
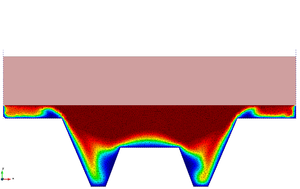
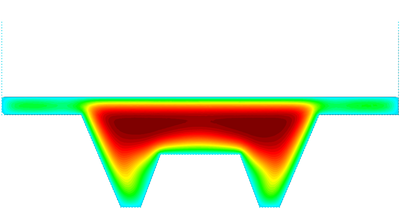
The snapshots of Figure 17 refer to the initial compression phase that has a duration of 5.65${\textstyle s}$. The upper rectangular die moves downwards forcing the metal piece to take the shape of the lower rigid walls.

Figure 18 shows four representative snapshots of the cooling period.

Figure 16: Hot forging of a metal piece. Initial geometry, coordinates of corner points and material properties.

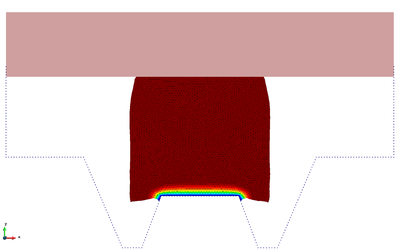
t=0.89s		t=1.50s
t=3.61s		t=5.32s
t=5.56s		t=5.65s
Figure 17: Hot forging of a metal piece. Compression phase. Snapshots of the deformation with temperature contours at different time instants.

(a) t=8.45s	(b) t=10.45s
(c) t=25.0s	(d) t=50.0s
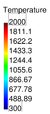
Figure 18: Hot forging of a metal piece. Cooling period. Snapshots of the temperature contours on the deformed geometry at different time steps.

Figure 19: Falling of three solid objects in a heated tank filled with a fluid. Initial geometry, thermal conditions and material properties.

8.6 Falling of three solid objects in a heated tank filled with fluid

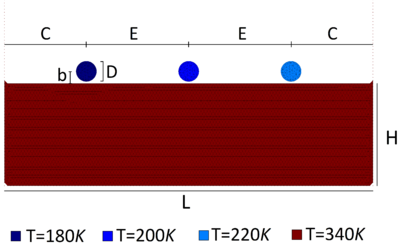
Three solid objects with the same shape fall from the same height into a tank containing a fluid at rest. The geometry, the problem data, and the initial thermal conditions are shown in Figure 19.

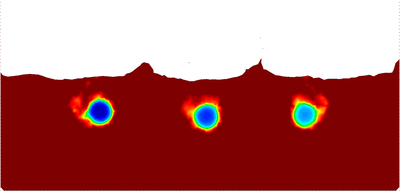
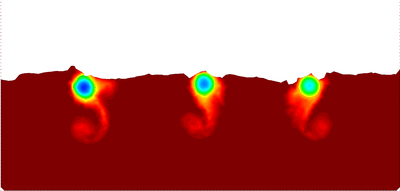
The fluid in the tank has an initial temperature of T=340${\textstyle K}$, while the solid bodies from left to right have initial temperatures of T=180 K, T=200 K, and T=220 K, respectively. The solid and the fluid domains have been discretized with a finite element mesh of 9394 3-noded triangular elements. The simulation has been run for eight seconds with ${\textstyle \Delta t}$=${\textstyle 0.0001s}$. The heat flux in the normal direction is assumed to be zero for the boundaries in contact with the air and the walls. Figure 20 shows six representative snapshots of the numerical simulation with the temperature results plotted over the fluid domain and the objects domains.

t=0.67s	t=1.82s
t=2.66s	t=4.50s
t=7.00s	t=8.00s
Figure 20: Falling of three solid objects in a heated tank filled with a fluid. Snapshots with temperature contours at different time steps.

Figure 21: Falling of three solid objects in a heated tank filled with a fluid. Evolution of the temperature at the center of the three objects.

In the graph of Figure 21 the evolution of the temperature at the central point of the three solid objects is plotted.

8.7 Melting of an ice block

A cylindrical ice block at initial temperature ${\textstyle ^{\circ }}$T=270 K is dropped into a tank containing water at rest at an initial temperature ${\textstyle ^{\circ }}$T=340 K. The initial geometry, the problem data and the initial thermal conditions for the 2D simulation are shown in Figure 22.

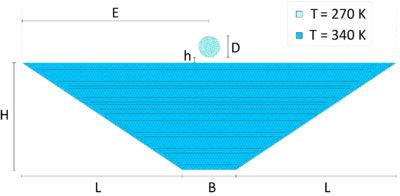
Figure 22: Melting of an ice cylinder. Geometry, material data and initial thermal conditions.

Ice is treated as a hypoelastic solid until some of its elements reach the fusion temperature (T=273.15 K ). These elements are transferred to the fluid domain and take the physical properties of the fluid. For this analysis the following assumptions were made: the mechanical and thermal properties of water and ice do not change with temperature and the heat normal flux along the boundaries in contact with the air or the walls have been considered to be zero.

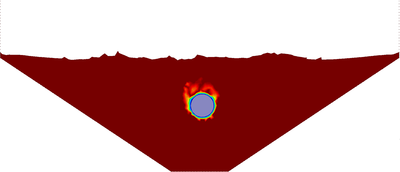
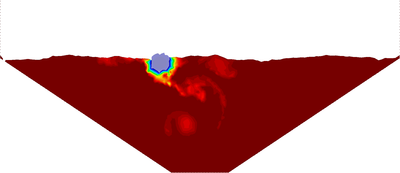
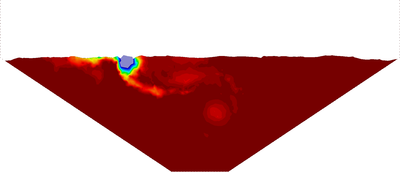
In Figure 23 snapshots of some representative instants of the analysis are shown. The temperature contours are plotted over the water domain and the ice block.

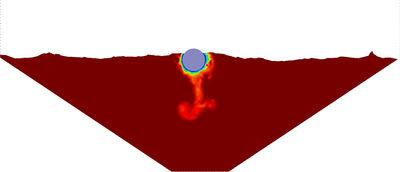
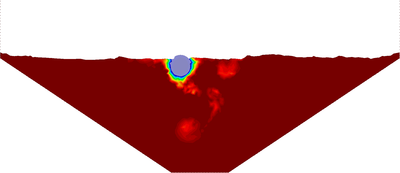
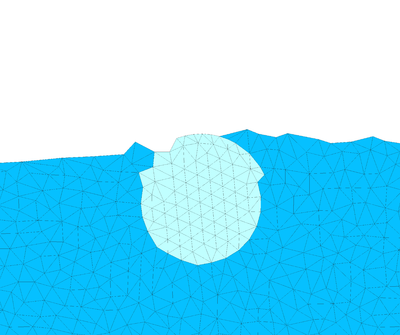
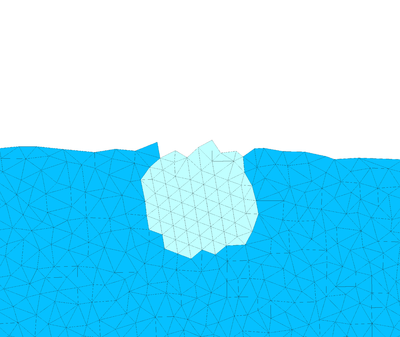
In Figure 24 the detail of the melting of the ice block is illustrated. The finite element mesh is drawn over the solid and the fluid domains.

t=0.44s	t=1.10s
t=2.63s	t=4.55s
t=10.00s	t=16.00s
Figure 23: Melting of an ice cylinder. Snapshots of the melting process with temperature contours at different time steps.

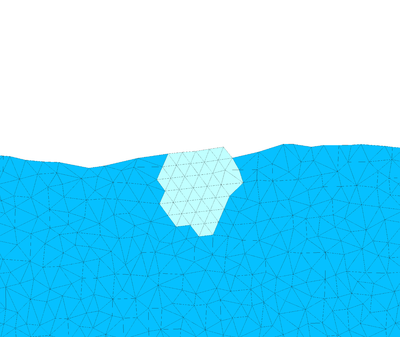
(a) t=2.81s	(b) t=4.70s	(c) t=9.77s
(d) t=12.74s	(e) t=14.69s	(f) t=15.47s
Figure 24: Melting of an ice cylinder. Zoom of the ice domain at different time instants.

8.8 Falling and warming of a solid sphere in a cilindrical tank containing hot water

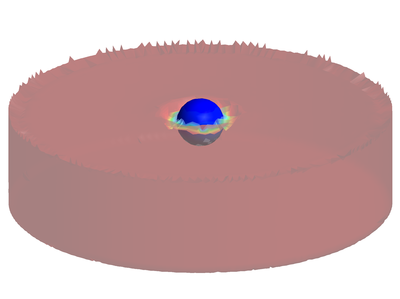
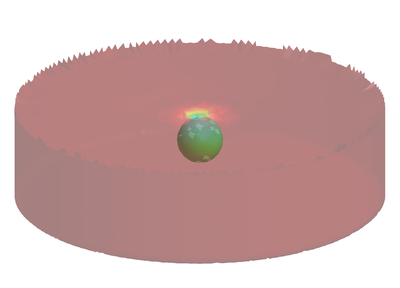
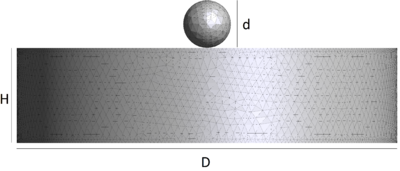
A solid sphere at ${\textstyle ^{\circ }}$T=270 K is dropped into a cilndrical tank containing still water at ${\textstyle ^{\circ }}$T=340 K. In Figure 22 the geometry and the problem data are given. The 3D simulation is run for a duration of 3${\textstyle s}$ with ${\textstyle \Delta t}$=${\textstyle 0.001s}$. A finite element mesh of 144663 4-noded tetrahedral elements has been used to discretize both the fluid domain and the sphere. Figure 26 shows six representative snapshots of the analysis. The temperature contours have been plotted over the fluid domain and the sphere.

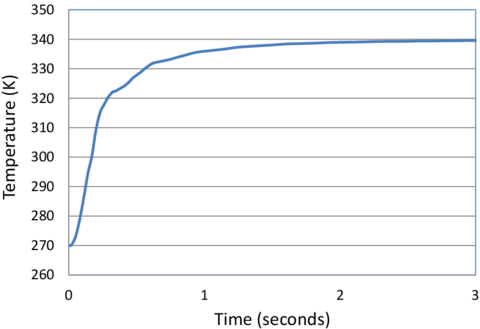
Figure 27 shows the evolution of the temperature at the center of the sphere versus time. The solid material has high conductivity and this explains its fast warming. After three seconds, it practically reaches the equilibrium temperature. We note that the normal heat flux along the boundaries in contact with the air have been considered to be zero.

Figure 25: Warming of a solid sphere with initial temperature $^{\circ }$T=270 K falling into a cylindrical tank containing a fluid at $^{\circ }$T=340 K. Initial geometry and material properties.

t=0.08s	t=0.17s
t=0.38s	t=0.53s
t=0.71s	t=3.00s
Figure 26: Warming of a solid sphere ($^{\circ }$T=270 K) falling into a cylindrical tank containing a fluid at $^{\circ }$T=340 K. Snapshots of the motion of the sphere and the temperature contours at different time steps.

Figure 27: Warming of a solid sphere ($^{\circ }$T=270 K) falling into a cylindrical tank containing a fluid at $^{\circ }$T=340 K. Evolution of the temperature at the center of the sphere.

9 CONCLUDING REMARKS

We have presented a unified Lagrangian formulation for analysis of industrial forming processes involving thermally coupled interactions between deformable continua containing fluids and solids. A residual-based expression of the mass conservation equation obtained using the FIC method provides the necessary stability for quasi/fully incompressible situations. The governing equations for the generalized continuum are discretized with the FEM using simplicial elements with equal linear interpolation for the velocities, the pressure and the temperature. The merits of the formulation in terms of its general applicability have been demonstrated in the solution of a variety of thermally-coupled industrial forming processes using the Particle Finite Element Method (PFEM).

ACKNOWLEDGEMENTS

This research was partially supported by the Advanced Grant project SAFECON of the European Research Council and the HFLUIDS project of the National Research Programme of Spain.

BIBLIOGRAPHY

[1] Aubry R, Idelsohn SR, Oñate E (2005) Particle finite element method in fluid-mechanics including thermal convection-diffusion. Computers and Structures, Vol. 83, (17-18), pp 1459–1475.

[2] Aubry R, Idelsohn SR, Oñate E (2006) Fractional step like schemes for free surface problems with thermal coupling using the Lagrangian PFEM. Computational Mechanics, Vol. 38 (4-5), pp. 294–309.

[3] Belytschko T, Liu WK, Moran B, Non linear finite element for continua and structures, 2d Edition, Wiley, 2013.

[4] Carbonell JM, Oñate E, Suárez B (2010) Modeling of ground excavation with the Particle Finite Element Method. Journal of Engineering Mechanics (ASCE) 136(4):455–463

[5] Carbonell JM, Oñate E, Suárez B (2013) Modelling of tunnelling processes and cutting tool wear with the Particle Finite Element Method (PFEM). Comput. Mech. 52(3):607–629

[6] Chenot JL, Oñate E (1988) Modelling of Metal Forming Processes, Kluwer Academic, Dordrecht.

[7] Donea J, Huerta A (2003) Finite element method for flow problems. J. Wiley

[8] Edelsbrunner H, Mucke EP (1999) Three dimensional alpha shapes. ACM Trans. Graphics 13:43–72

[9] Franci A, Oñate E, Carbonell JM (2013) On the effect of the tangent bulk stiffness matrix in the analysis of free surface Lagrangian flows using PFEM. Research Report CIMNE PI402. Submitted to Int. J. Numer. Meth. Biomed. Engng.

[10] Franci A, Oñate E, Carbonell JM (2014) Unified updated Lagrangian formulation for fluid-structure interaction problems. Publication CIMNE No. PI404.

[11] Ghosh S, Castro JC, Lee JK (2004) Material Processing and Design: Simulation and Applications. NUMIFORM 2004, American Institute of Physics.

[12] Huetnik J, Baaijens FPT (Eds) (1998) Simulation of Materials Processing: Theory, Methods and Applications, NUMIFORM 98. Enschede, Países Bajos, A.A. Balkema, Rotterdam, 22–5 Jun.

[13] Idelsohn SR, Calvo N, Oñate E (2003c) Polyhedrization of an arbitrary point set. Comput. Method Appl. Mech. Engng. 192(22-24):2649–2668

[14] Idelsohn SR, Oñate E, Del Pin F (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Numer. Meth. Biomed. Engng., 61(7):964–989

[15] Idelsohn SR, Marti J, Limache A, Oñate E (2008) Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. Comput Methods Appl Mech Engrg. 197:1762–1776

[16] Idelsohn SR, Mier-Torrecilla M, Oñate E (2009) Multi-fluid flows with the Particle Finite Element Method. Comput Methods Appl Mech Engrg. 198:2750–2767

[17] Larese A, Rossi R, Oñate E, Idelsohn SR (2008) Validation of the Particle Finite Element Method (PFEM) for simulation of free surface flows. Engineering Computations 25(4):385–425

[18] Limache A, Idelsohn, SR, Rossi R, Oñate E (2007) The violation of objectivity in Laplace formulation of the Navier-Stokes equations. Int. J. Numerical Methods in Fluids, 54:639–664.

[19] Mori K (2001) Simulation of Material Processing: Theory, Methods and Applications, A.A. Balkema, Lisse.

[20] Oliver X, Cante JC, Weyler R, González C, Hernández J (2007) Particle finite element methods in solid mechanics problems. In: Oñate E, Owen R (Eds) Computational Plasticity. Springer, Berlin, pp 87–103

[21] Oñate E (1998) Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engng. 151:233–267

[22] Oñate E, Manzan M (1999) A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. International Journal for Numerical Methods in Fluids, Vol. 31, pp. 203–221.

[23] Oñate E (2000) A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput Methods Appl Mech Engrg. 182(1–2):355–370

[24] Oñate E (2004) Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng. 60(1):255–281

[25] Oñate E, Rojek J, Taylor R, Zienkiewicz O (2004a) Finite calculus formulation for incompressible solids using linear triangles and tetrahedra. Int. J. Numer. Meth. Engng. 59(11):1473–1500

[26] Oñate E, Idelsohn SR, Del Pin F, Aubry R (2004b) The particle finite element method. An overview. Int. J. Comput. Methods 1(2):267–307

[27] Oñate E, M.A. Celigueta, Idelsohn SR (2006) Modeling bed erosion in free surface flows by the Particle Finite Element Method, Acta Geotechnia 1(4):237–252

[28] Oñate E, Valls A, García J (2006) FIC/FEM formulation with matrix stabilizing terms for incompressible flows at low and high Reynold's numbers. Computational Mechanics 38 (4-5):440–455

[29] Oñate E, García J, SR Idelsohn, Del Pin F (2006) FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches. Comput. Meth. Appl. Mech. Engng. 195(23-24):3001–3037

[30] Oñate E, Rojek J, Chiumenti M, Idelsohn SR, Del Pin F, Aubry R (2006) Advances in stabilized finite element and particle methods for bulk forming processes. Comput. Meth. Appl. Mech. Engng. 195:6750–6777

[31] Oñate E, Owen DRJ, (Eds.), Computational Plasticity, Springer 2007

[32] Oñate E, Idelsohn SR, Celigueta MA, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput. Meth. Appl. Mech. Engng. 197(19-20):1777–1800

[33] Oñate E (2009) Structural analysis with the finite element method. Linear statics. Volume 1. Basis and Solids. CIMNE-Springer

[34] Oñate E, Rossi R, Idelsohn SR, Butler K (2010) Melting and spread of polymers in fire with the particle finite element method. Int. J. Numerical Methods in Engineering, 81(8):1046–1072

[35] Oñate E, Celigueta MA, Idelsohn SR, Salazar F, Suárez B (2011) Possibilities of the particle finite element method for fluid-soil-structure interaction problems. Computational Mechanics, 48(3):307–318

[36] Oñate E, Idelsohn SR, Felippa C (2011) Consistent pressure Laplacian stabilization for incompressible continua via higher-order finite calculus. Int. J. Numer. Meth. Engng, 87 (1-5): 171–195

[37] Oñate E, Carbonell JM (2013) Updated Lagrangian finite element formulation for quasi-incompressible fluids. Research Report PI393, CIMNE. Submitted to Comput. Mechanics

[38] Oñate E, Franci A, Carbonell JM (2013) Lagrangian formulation for finite element analysis of quasi-incompressible fluids with reduced mass losses. Int. J. Num. Meth. Fluids, DOI: 10.1002/fld.3870

[39] Pietrzyk M, Kusiak J, Majta J, Hartley P, Pillinger I (2000) Metal Forming 2000. A.A. Balkema, Rotterdam

[40] Pittman JFT, Zienkiewicz OC, Wood RD, Alexander JM (Eds) (1984) Numerical Analysis of Forming Processes. Wiley, Chichester

[41] Ryzhakov P, Oñate E, Rossi R, Idelsohn SR (2012) Improving mass conservation in simulation of incompressible flows. Int. J. Numer. Meth. Engng. 90(12):1435–1451

[42] Simo JC, Miehe C (1992) Associative coupled thermoplasticity at finite strains Formulation, numerical analysis and implementation. Computer Methods in Applied Mechanics and Engineering, 98:41-104

[43] Tang B, Li JF, Wang TS (2009) Some improvements on free surface simulation by the particle finite element method. Int. J. Num. Methods in Fluids, 60 (9):1032–-1054

[44] Zienkiewicz OC, Jain PC, Oñate E (1978) Flow of solids during forming and extrusion: some aspects of numerical solutions. Int. J. Solids Struct., 14:15–38

[45] Zienkiewicz OC, Oñate E, Heinrich JC (1981) A general formulation for coupled thermal flow of metals using finite elements, Int. J. Num. Meth. Eng., 17:1497–514, 1981

[46] Zienkiewicz OC, Taylor RL, Zhu JZ (2005) The finite element method. The basis. Vol. 1, 6th Ed., Elsevier

[47] Zienkiewicz OC, Taylor RL (2005) The finite element method for solid and structural mechanics. Vol. 2, 6th Ed., Elsevier

[48] Zienkiewicz OC, Taylor RL, Nithiarasu P (2005) The finite element method for fluid dynamics. Vol. 3, 6th Ed., Elsevier