Published in Fluid Dynamics and Aeronautics New Challenges, Périaux J., Champion M., Gagnepain J.-J., Pironneau O., Stoufflet B. and Thomas Ph.(Eds.), CIMNE, Barcelona, Spain, 2003
Abstract
We present a general formulation for incompressible fluid flow analysis using the finite element method (FEM). The necessary stabilization for dealing with convective effects and the incompressibility condition are introduced via the so called finite calculus (FIC) method. The extension of the standard eulerian form of the equations to an arbitrary lagrangian-eulerian (ALE) frame adequate for treating fluid-structure interaction problems is presented. The fully lagrangian form is also discussed. Details of an effective mesh updating procedure are presented together with a method for dealing with free surface effects of importance for ship hydrodynamic analysis and many other fluid flow problems. Examples of application of the eulerian, the ALE and the fully lagrangian flow descriptions are presented.
Keywords: Stabilized formulation, incompressible fluid flow, finite calculus, finite element method, ship hydrodynamics.
1 INTRODUCTION
The development of efficient and robust numerical methods for analysis of incompressible flows has been a subject of intensive research in last decades. Much effort has been spent in developing the so called stabilized numerical methods overcoming the two main sources of instability in incompressible flow analysis, namely those originated by the high values of the convective terms and those induced by the difficulty in satisfying the incompressibility conditions.
The solution of above problems in the context of the finite element method (FEM) has been attempted in a number of ways [1]. The underdiffusive character of the Galerkin FEM for high convection flows (which incidentaly also occurs for the central finite difference (FD) and finite volume (FV) methods [2]) has been corrected by adding some kind of artificial viscosity terms to the standard Galerkin equations.
A popular way to overcome the problems with the incompressibility constraint is by introducing a pseudo-compressibility in the flow and using implicit and explicit algorithms developed for this kind of problems such as artificial compressibility schemes [4-6] and preconditioning techniques [7]. Other FEM schemes with good stabilization properties for the convective and incompressibility terms are based in Petrov-Galerkin (PG) techniques. The background of PG methods are the non-centred (upwind) schemes for computing the first derivatives of the convective operator in FD and FV methods [2,8]. More recently a general class of Galerkin FEM has been developed where the standard Galerkin variational form is extended with adequate residual-based terms in order to achieve a stabilized numerical scheme. Among the many methods of this kind in the finite element universe we can name the Streamline Upwind Petrov Galerkin (SUPG) method [1,9-18] the Galerkin Least Square (GLS) method [19,20], the Taylor-Galerkin method [21], the Characteristic Galerkin method [22-24] and its variant the Characteristic Based Split (CBS) method [25,26], pressure gradient operator methods [27] and the Subgrid Scale (SS) method [28-30]. A good review of these methods can be found in [31].
In this paper a stabilized finite element formulation for incompressible flows is derived in a different manner. The starting point are the modified governing differential equations of the fluid flow problem formulated via a finite calculus (FIC) approach [32]. The FIC method is based in invoking the balance of fluxes in a fluid domain of finite size. This introduces naturally additional terms in the classical differential equations of infinitesimal fluid mechanics which are a function of the balance domain dimensions. The new terms in the modified governing equations provide the necessary stabilization to the discrete equations obtained via the standard Galerkin finite element method [33-39].
The layout of the chapter is the following. In the next section, the main concepts of the FIC approach are introduced via a simple 1D convection-diffusion model problem. Then the basic FIC equations for incompressible flow problems are presented. The finite element discretization is introduced and the resulting matrix formulation is detailed. Both monolithic and fractional step schemes for the transient solution are presented.
The basic formulation is extended to account for free surface wave effects by using an arbitrary eulerian-lagrangian (ALE) frame and introducing the free surface boundary conditions. Here the numerical treatment of the free surface equation using the FIC method is presented. The analysis of fluid-structure interaction problems involving the movement of floating or submerged solids in a fluid is also discussed. These problems require the displacement of the mesh nodes in accordance with the motion of the structure or the free surface and here a simple and effective algorithm for updating the mesh nodes is described. In the last part of the chapter the fully lagrangian formulation for fluid flow analysis is presented as a particular case of the ALE form. The lagrangian description has many advantages for tracking the displacement of fluid particles in flows where large motions of the fluid surface occur such in the case of breaking waves, splashing of water, filling of moulds, etc. A positive feature of the lagrangian formulation is that the convective terms dissapear in the governing equations of the fluid flow; in return the updating of the mesh at almost every time step is now a necessity and efficient algorithms for mesh generation must be used.
The examples show the efficiency of the eulerian, ALE and fully lagrangian formulations to solve classical fluid flow problems, as well as fluid-structure interaction situations involving contact with moving solids, waves around ships and large motions of the free surface, among others.
2 THE FINITE CALCULUS METHOD
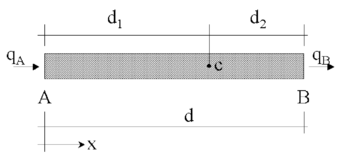
We will consider a convection-diffusion problem in a 1D domain of length . The equation of balance of fluxes in a subdomain of size belonging to (Figure 1) is written as
|
|
(1) |
|
| Figure 1: Equilibrium of fluxes in a balance domain of finite size |
where and are the incoming and outgoing fluxes at points and , respectively. The flux includes both convective and diffusive terms; i.e. , where is the transported variable, is the velocity and is the diffusitivity of the material.
Let us express now the fluxes and in terms of the flux at an arbitrary point within the balance domain (Figure 1). Expanding and in Taylor series around point up to second order terms gives
|
|
(2) |
Substituting eq.(2) into eq.(1) gives after simplification
|
|
(3) |
where and all derivatives are computed at point .
Standard calculus theory assumes that the domain is of infinitesimal size and the resulting balance equation is simply . We will relax this assumption and allow the balance domain to have a finite size. The new balance equation (3) incorporates now the underlined term which introduces the characteristic length . Obviously, accounting for higher order terms in eq.(2) would lead to new terms in eq.(3) involving higher powers of .
Distance in eq.(3) can be interpreted as a free parameter depending, of course, on the location of point (note that ). However, the fact that eq.(3) is the exact balance equation (up to second order terms) for any 1D domain of finite size and that the position of point is arbitrary, can be used to derive numerical schemes with enhanced properties simply by computing the characteristic length parameter from an adequate “optimality” rule.
Consider, for instance, the modified equation (3) applied to the convection-diffusion problem. Neglecting third order derivatives of , eq.(3) can be written in an explicit form as
|
|
(4) |
We see that the modified equation via the FIC method introduces naturally an additional diffusion term into the standard convection-diffusion equation. This is the basis of the popular “artificial diffusion” procedure [1,2,8,36]. The characteristic length is typically expressed as a function of the cell or element dimensions. The optimal or critical value of for each cell or element can be computed from numerical stability conditions such as obtaining a physically meaningful solution, or even obtaining “exact” nodal values [32-39].
Equation (3) can be extended to account for source effects. The full stabilized equation can be then written in compact form as
|
|
(5) |
with
|
|
(6) |
where is the external source. For consistency a “finite” form of the Neumann boundary condition should be used. This can be readily obtained by invoking balance of fluxes in a domain of finite size next to the boundary where the external (diffusive) flux is prescribed to a value . The modified Neumann boundary condition can be written as [32]
|
|
(7) |
The definition of the problem is completed with the standard Dirichlet condition prescribing the value of at the boundary .
The underlined terms in Eqs.(5) and (7) introduce the necessary stabilization in the discrete solution of the problem using whatever numerical scheme. For details see [32-41].
The time dimension can be introduced in the FIC method by considering the balance equation in a space-time slab domain [32,35,36]. Quite generally the FIC equation can be written for any problem in mechanics as [32].
|
|
(8) |
where is the ith standard differential equation of the infinitesimal theory, are characteristic length parameters, is a time stabilization parameter and the time; and are respectively the number of balance equations and the number of dimension of the problem along which balance of fluxes or forces is invoked (i.e., for 2D problems, etc.).
For example, in the case of the convection-diffusion problem , Eq.(8) is particularized as
|
|
(9) |
with .
The modified Neumann boundary conditions in the FIC formulation can be expressed in the general case as
|
|
(10) |
where are the generalized “fluxes” (such as the heat fluxes in a heat transfer problem or the stresses in solid or fluid mechanics), are the prescribed values of the boundary fluxes and are the components of the outward normal to the Neumann boundary . For the transient case the initial boundary condition should also be specified [32,35,36].
In Eqs.(8)-(10) we have underlined once more the terms introduced by the FIC approach which are essential for deriving stabilized numerical formulations.
The starting point in the next section are the FIC equation for a viscous incompressible fluid. A simplified version of the equation will be chosen neglecting the time stabilization term as this is not relevant for the purposes of this work.
3 GENERAL FIC EQUATIONS FOR VISCOUS INCOMPRESSIBLE FLOW
The FIC governing equations for a viscous incompressible fluid can be written as
Momentum
|
|
(11) |
Mass balance
|
|
(12) |
where
|
|
(13) |
|
|
(14) |
Above is the velocity along the ith global axis, is the (constant) density of the fluid, is the absolute pressure (defined positive in compression), are the body forces and are the viscous deviatoric stresses related to the viscosity by the standard expression
|
|
(15) |
where is the Kronecker delta and the strain rates are
|
|
(16) |
The FIC boundary conditions are
|
|
(17) |
|
|
(18) |
and the initial condition is for .
In Eqs.(17) and (18) and are surface tractions and prescribed displacements on the boundaries and , respectively, are the components of the unit normal vector to the boundary and are the total stresses given by . The sign in front the stabilization term in Eq.(17) is positive due to the definition of in Eq.(13).
The in above equations are characteristic lengths of the domain where balance of momentum and mass is enforced. In Eq.(17) these lengths define the domain where equilibrium of boundary tractions is established [32].
Eqs.(11)-(18) are the starting point for deriving stabilized finite element methods for solving the incompressible Navier-Stokes equations using equal order interpolation for the velocity and pressure variables [37-39]. Application of the FIC formulations to meshless analysis of fluid flow problems using the finite point method can be found in [40,41].
We note that the “conservative” form of the convective terms in Eq.(13) and the presence of the volumetric strain rate in the constitutive equation (15) do not take advantage of the incompressibility condition. These forms are useful for obtaining the relationship between the derivative of the volumetric strain rate and the momentum equations as shown in the next section. However, the standard form of the governing equations for incompressible flows will be used for the final derivation of the discretized FEM equations.
3.1 Stabilized integral forms
From Eq.(11) it can be obtained (taking into account Eq.(15))
|
|
(19) |
where
|
|
(20a) |
and
|
|
(20b) |
Substituting Eq.(19) into Eq.(12) and retaining the terms involving the derivatives of with respect to only, leads to the following expression for the stabilized mass balance equation
|
|
(21) |
with
|
|
(22) |
The 's in Eq.(21) are termed in the stabilization literature intrinsic time parameters. It is interesting to note that these parameters take here the values of and for the viscous limit (Stokes flow) and the inviscid limit (Euler flow), respectively. Similar values for (usually is taken) are used in other works from ad-hoc extensions of the 1D advective-diffusive problem [12-31]. It is remarkable that the intrinsic time parameters have been deduced here from the general FIC formulation and this shows the possibilities of the method.
The weighted residual form of the momentum and mass balance equations (Eqs.(11) and (21)) is written as
Momentum
|
|
(23) |
Mass balance
|
|
(24) |
where and are arbitrary weighting functions representing virtual velocity and virtual pressure fields. Integration by parts of the terms leads to
|
|
(25a) |
|
|
(25b) |
The third integral in Eq.(25a) is expressed as a sum of the element contributions to allow for discontinuities in the derivatives of along the element interfaces.
Also in Eq.(25b) we will neglect hereonwards the third integral by assuming that is negligible on the boundaries. The deviatoric stresses and the pressure terms in the first integral of Eq.(25a) are integrated by parts in the usual manner. The resulting equations are
Momentum
|
|
(26) |
Mass balance
|
|
(27) |
We note that in Eq.(26) we use now the standard form of the convective operator for incompressible flows (i.e. neglecting the contribution from the volumetric strain rate ). Also in Eq.(26)
|
|
3.2 Convective and pressure gradient projections
The computation of the residual terms can be simplified if we introduce now the convective and pressure gradient projections and , respectively defined as
|
|
(28) |
We can express in Eqs.(26) and (27) in terms of and , respectively which then become additional variables. The system of integral equations is now augmented in the necessary number of additional equations by imposing that the residual vanishes (in average sense) for both forms given by Eqs.(28). This gives the final system of governing equation as:
|
|
(29) |
|
|
(30) |
|
|
(31) |
|
|
(32) |
with . In Eqs.(31) and (32) and are appropriate weighting functions and the and weights are introduced for convenience.
4 FINITE ELEMENT DISCRETIZATION
We choose continuous linear interpolations of the velocities, the pressure, the convection projections and the pressure gradient projections over three node triangles (2D) and four node tetrahedra (3D). The linear interpolations are written as
|
|
(33) |
where (4) for triangles (tetrahedra), denotes nodal variables and are the linear shape functions 1.
Substituting the approximations (33) into Eqs.(29-32) and choosing the Galerking form with leads to following system of discretized equations
|
|
(34a) |
|
|
(34b) |
|
|
(34c) |
|
|
(34d) |
where the element contributions are given by (for 2D problems)
|
|
(35) |
with and .
In above is the standard strain rate matrix and the deviatoric constitutive matrix (assuming ). For 2D problems
|
|
(36) |
Note that the stabilization matrix adds an additional orthotropic diffusivity of value .
4.1 Quasi-implicit scheme
It can be seen that matrices and are dependent on the velocity field. The solution process can be advanced in time in a (quasi-nearly) implicit iterative manner using the following scheme.
Step 1
|
|
(37) |
Step 2
|
|
(38) |
Step 3
|
|
(39) |
Step 4
|
|
(40) |
where .
In above denote nodal values at the th time step and the ith iteration. Note that etc. Also for the computations in step 1 at the onset of the iterations.
Steps 1, 3 and 4 can be solved explicitely by choosing a lumped (diagonal) form of matrices and . In this manner the main computational cost is the solution of step 2 involving the inverse of a Laplacian matrix. This can be solved very effectively using an iterative method such as the conjugate gradient method or similar.
For the iterative proces is unavoidable. The iterations follow until convergence is reached in an adequate error norm in terms of the velocity and pressure variables, or the residuals and . Indeed some ot the 's in Eqs.(37)-(40) can be made equal to zero. Note that for the algorithm is unconditionally unstable. A particularity interesting and simple semi-implicit form is obtained by making . Now all steps can be solved explicitely with exception of Step 2 for the pressure, which still requires the solution of a simultaneous system of equations.
Convergence of this solution scheme is however difficult for some problems. An enhanced version of the algorithm can be obtained by simply adding the term where to the equation for the computation of the pressure in the second step. The new term acts as a preconditioner of the pressure equation given now by
|
|
(41) |
Note that the added term vanishes for the converged solution (i.e. when ).
An alternative to above algorithm is to use the fractional step method described in the nex section.
4.2 Fractional step method
An alternative algorithm can be obtained by splitting the pressure from the momentum equations as follow
|
|
(42a) |
|
|
(42b) |
In Eq.(42a) is a variable taking values equal to zero or one. For , and for , . Note that in both cases the sum of Eqs.(42a) and (42b) gives the time discretization of the momentum equations with the pressures computed at . The value of from Eq.(42b) is substituted now into Eq.(34b) to give
|
|
(43a) |
The product can be approximated by a laplacian matrix, i.e.
|
|
(43b) |
A semi-implicit algorithm can thus be derived as follows.
Step 1 Compute explicitely from Eq.(42a) with where subscript denotes hereonwards a diagonal matrix.
Step 2 Compute from Eq.(43a) as
|
|
(44) |
Step 3 Compute explicitely from Eq.(42b) with
Step 4 Compute explicitely from Eq.(39) with
|
|
(45) |
Step 5 Compute explicitely from Eq.(40) as
|
|
(46) |
This algorithm has an additional step than the iterative scheme of Section 4.1. The advantage is that now Steps 1 and 2 can be fully linearized by choosing . Also the equation for the pressure variables in Step 2 has improved stabilization properties due to the additional laplacian matrix .
The boundary conditions are applied as follow. No condition is applied in the computation of the fractional velocities in Eq.(44). The prescribed velocities at the boundary are applied when solving for in the step 3. The prescribed pressures at the boundary are imposed by making zero the pressure increments at the relevant boundary nodes and making equal to the prescribed pressure values.
4.3 Stokes flow
The formulation for a Stokes flow can be readily obtained simply by neglecting the convective terms in the general Navier-Stokes formulation. This also implies neglecting the convective stabilization terms in the momentum equations and, consequently, the convective projection variables are not larger necessary. Also the intrinsic time parameters take now the simpler form (see Eq.(22)):
|
|
(47) |
The resulting discretized system of equations can be written as (see Eqs.(34))
|
|
(48) |
The iterative algorithm of Section 4.1 can now be implemented. Convergence is now faster due to the absence of the non linear convective terms in the momentum equation.
The steady-state form of Eqs.(48) can be expressed in matrix form as
|
|
(49) |
The system is symmetric and always positive definite and therefore leads to a non singular solution. We note that this property holds for any interpolation function chosen for and , therefore overcoming the Babuŝka-Brezzi (BB) restrictions [1].
A reduced velocity-pressure formulation can be obtained by eliminating the pressure gradient projection variables from the last equation to give
|
|
(50) |
The reduction process is simplified by using a diagonal form of matrix . Obviously above reduction is also applicable to the transient case.
5 FLUID-STRUCTURE INTERACTION. MESH UPDATING. ALE FORMULATION
5.1 General coupled solution scheme
The two algorithms of previous section can be readily extended for fluid-structure interaction analysis. The solution process in both cases includes the two additional steps.
Step A1. Solve for the movement of the structure due to the fluid flow forces
This implies solving the dynamic equations of motion for the structure written as
|
|
(51) |
where and are respectively the displacement and acceleration vectors of the nodes discretizing the structure, and are the mass and stiffness matrices of the structure and is the vector of external nodal forces accounting for the fluid flow forces induced by the pressure and the viscous stresses. Clearly the main driving forces for the motion of the structure is the fluid pressure which acts in the form of a surface traction on the structure. Indeed Eq.(51) can be augmented with an appropriate damping term. The form of all the relevant matrices and vectors can be found in standard books on FEM for structural analysis [1].
Solution of Eq.(51) in time can be performed using implicit or fully explicit time integration algorithms. In both cases the values of the nodal displacement, velocities and accelerations at are found.
Step A2. Compute the new position of the mesh nodes
Movement of a structure in a fluid originates a distorsion in the mesh defining the control volume where the fluid equations are solved. Clearly a new mesh can be regenerated at each time step and this option is discussed in a later section dealing with lagrangian flows. A cheaper alternative is to update the position of the mesh nodes once the iterative process for the fluid and solid variables has converged. A simple algorithm for updating the mesh nodes is described in the next section.
5.2 A simple algorithm for updating the mesh nodes
Different techniques have been proposed for dealing with mesh updating in fluid-structure interaction problems. The general aim of all methods is to prevent element distortion during mesh deformation [42-44].
Chiandussi, Bugeda and Oñate [45] have proposed a simple method for the movement of mesh nodes ensuring minimum element distortion. The method is based on the iterative solution of a fictious linear elastic problem on the mesh domain. In order to minimize the mesh deformation the “elastic” properties of each mesh element are appropiately selected so that elements suffering greater movements are stiffer. The basis of the method is given below.
Let us consider an elastic domain with arbitrary homogeneous isotropic elastic properties characterized by the Young modulus and the Poisson coefficient . Once a discretized finite element problem has been solved using, for instance, standard linear triangles (in 2D) or linear tetraedra (in 3D), the principal stresses at the center of each element can be obtained. For 3D problems
|
|
(52) |
where are the principal strains. As the values of and are arbitrary it is useful to select . Eq.(32) simplifies in this case to .
Let us assume now that a uniform strain field throughout the mesh is sought. The principal stresses are then given by
|
|
(53) |
where is the unknown Young modulus for the element.
A number of criteria can be now used to find the value of . An effective approach found in [45] is to make equal the element strain energy densities in both analysis. Thus (for )
|
|
(54a) |
|
|
(54b) |
Equaling eqs.(54a) and (54b) gives the sought Young modulus as
|
|
(55) |
Note that the element Young modulus is proportional to the element deformation as desired. Also recall that both and are arbitrary constants for all elements in the mesh.
The solution process includes the following two steps.
Step 1. Consider the finite element mesh as a linear elastic solid with homogeneous material properties characterized by and arbitrary Young modulus and the Poisson ratio . Solve the corresponding elastic problem with imposed displacements at the mesh boundary.
Step 2. Compute the principal strains and the values of the new Young modulus in each element using Eq.(55) for a given value of . Repeat the finite element solution of the linear elastic problem with prescribed boundary displacements using the new values of for each element.
The movement of the mesh nodes obtained in the second step ensures a quasi uniform mesh distortion. Further details on this method including other alternatives for evaluating the Young modulus can be found in [45].
The previous algorithm for movement of mesh nodes is able to treat the movement of the mesh due to changes in position of fully submerged and semi-submerged bodies. Note however that if the floating body intersects the free surface, the changes in the analysis domain geometry can be very important. From one time step to other emersion or inmersion of significant parts of the body can occur.
A solution to this problem is to remesh the analysis domain. However, for most problems, a mapping of the moving surfaces linked to the mesh updating algorithm described above can avoid remeshing [38,46-49].
5.3 ALE formulation
The movement of the mesh defining the fluid domain requires accounting for the relative motion of the fluid particles with respect to the moving mesh. This can be dealt with by an arbitrary lagrangian-eulerian (ALE) formulation. This basically implies redefining the convective transport term in the momentum equation as
|
|
(56) |
where is the relative velocity between the moving mesh and the fluid point and is the velocity of the mesh nodes. This velocity can be simply computed dividing by the displacement vector of the nodes in the mesh obtained from the mesh updating algorithm previously described.
6 FREE SURFACE WAVE EFFECTS
Many problems of practical importance involve a free surface in the fluid. In general the position of such a free surface is unknown and has to be determined. Typical problems of this kind are water flow around ships, flow under and over water control structures, mould filling processes, etc.
On the free surface we must ensure al all times that (1) the pressure (which approximate the normal traction) equals the atmospheric pressure and the tangential tractions are zero (unless specific otherwise) and (2) that the material particles of the fluid belong to the free surface.
Condition (1) is simply fulfilled by imposing on during the solution for the nodal pressures.
The free surface condition (2) can be written in the FIC formulation (neglecting time stabilization effects) as [46-49]
|
|
(57) |
where
|
|
(58) |
where is the wave elevation (measured with respect to a reference surface of height ) and is the relative velocity defined in Eq.(56). The underlined term in Eq.(57) introduces the necessary stabilization for the solution of the highly convective (and non linear) equation defining the evolution of the wave elevation. Note that neglecting the stabilization term, the steady state form of Eq.(57) simply states that the fluid particles move in the tangential direction to the free surface (in 2D: where is the angle which the velocity vector forms with the horizontal axis).
The solution in time of Eq.(57) can be expressed in terms of the nodal velocities computed from the flow solution, as
|
|
(59) |
Eq.(59) can now be discretized in space using the standard Galerkin method and solved explicitely to give the nodal wave heights at [46-49]. This solution step should preceed the computation of the structure motion in the case of a fluid-structure interaction problem. Typically the general algorithm will be as follows:
- Solve for the nodal velocities and the pressures in the fluid domain using any of the algorithms of Section 4. When solving for the pressure variables impose at the free surface .
- Solve for the free surface elevation via Eq.(59).
- Compute the movement of the fully or semi-submerged or floating structure by solving the dynamic equations of motion of the structure (Eq.(51)).
- Compute the new position of the mesh nodes in the fluid domain at time . Alternatively, regenerate a new mesh.
The mesh updating proces can also include the free surface nodes, although this is not strictly necessary. An hydrostatic adjustement can be implemented once the new free surface elevation is computed by simple imposing the pressure at the nodes on the reference surface as
|
|
(60) |
where is the gravity constant. Eq.(60) allows to take into account the changes in the free surface without the need of updating the reference surface nodes. A higher accuracy in the solution of the flow problem can be obtained by updating the reference surface nodes after a number of time steps.
7 LAGRANGIAN FLOW FORMULATION
The Lagrangian formulation is an effective (and relatively simple) procedure for modelling the flow of fluid particles undergoing severe distorsions such as water jets, high amplitude waves, water splashing, breaking waves, filling of cavities, etc. Indeed the lagrangian formulation seems to be an excellent procedure for treating fluid-structure interaction problems where the structure has large displacements. An obvious “a priori” advantage of the lagrangian formulation is that both the structure and the fluid motions are defined in the same frame of reference.
The lagrangian fluid flow equations can be simply obtained by noting that the velocity of the mesh nodes and that of the fluid particles are the same. Hence the relative velocity is zero in Eq.(56) and the convective terms vanish in the momentum equations, while the rest of the fluid flow equations defined in Section 3 remain unchanged.
The FEM algorithms for solving the lagrangian flow equations is very similar to those for the eulerian or ALE description presented earlier and only the main differences will be given here. For preciseness we will focus in the semi-implicit fractional step algorithm of Section 4.2 (for and ) accounting also for fluid-structure interaction effects.
Step 1 Compute explicitely a predicted value of the velocities as
|
|
(61) |
Step 2 Compute from Eq.(44).
Step 3 Compute explicitely from Eq.(42b) with .
Step 4 Compute explicitely from Eq.(40).
Step 5 Solve for the motion of the structure by integrating Eq.(51).
Step 6 Update the mesh nodes in a lagrangian manner as
|
|
(62) |
Step 7 Generate a new mesh. This can be effectively performed using the extended Delaunay Tesselation described in [50]. Indeed the mesh regeneration can take place after a prescribed number of time steps or when the nodal displacements induce significant distorsions in some element shapes.
Details of the treatment of the boundary conditions in the lagrangian flow formulation can be found in [51,52].
8 TURBULENCE MODELLING
The detailed discussion on the treatment of turbulent effects in the flow equation falls outside the objective of this chapter as any of the existing turbulence model is applicable.
In the examples presented next we have chosen a turbulence model based on the Reynolds averaged Navier-Stokes equations where the deviatoric stresses are computed as sum of the standard viscous contributions and the so called Reynold stresses. Here we have chosen the Boussinesq assumption leading to a modification of the viscosity in the standard Navier-Stokes equations as sum of the “physical” viscosity and a turbulent viscosity .
One of the simplest and more effective choices for is the Smagorinski LES model giving
|
|
(63) |
where is the element size and is a constant ().
Indeed other many options are possible such as the one and two equations turbulence models (i.e. the model and the and models) and the algebraic stress models and the reader is refered to specialized books on this matter [53].
9 COMPUTATION OF THE CHARACTERISTIC LENGTHS
The evaluation of the stabilization parameters is one of the crucial issues in stabilized methods. Most of existing methods use expressions which are direct extensions of the values obtained for the simplest 1D case. It is also usual to accept the so called SUPG assumption, i.e. to admit that vector has the direction of the velocity field [32,37]. This unnecessary restriction leads to instabilities when sharp layers transversal to the velocity direction are present. This deficiency is usually corrected by adding a shock capturing or crosswind stabilization term [54,55]. Indeed, in the FIC formulation the components of introduce the necessary stabilization along both the streamline and transversal directions to the flow.
Excellent results have been obtained in all problems solved using linear tetrahedra with the same value of the characteristic length vector defined by
|
|
(64) |
where and and are the “streamline” and “cross wind” contributions given by
|
|
(65) |
|
|
(66) |
where are the vectors defining the element sides ( for tetrahedra).
As for the free surface equation the following value of the characteristic length vector has been taken
|
|
(67) |
The streamline parameter has been obtained by Eq.(65) using the value of the velocity vector over the 3 node triangles discretizing the free surface and .
The cross wind parameter has been computed by
|
|
(68) |
The cross-wind terms in eqs.(64) and (67) account for the effect of the gradient of the solution in the stabilization parameters. This is a standard assumption in most “shock-capturing” stabilization procedures [54,55].
A more consistent evaluation of based on a diminishing residual technique can be found in [37].
10 EXAMPLES
The examples chosen show the applicability of the Eulerian, ALE and lagrangian formulations presented to solve fluid flow problems. Linear tetrahedra and triangles have been used in the 3D and 2D analysis shown. The fractional step algorithm of Section 4.2 for and has been used in all cases. The first example is the standard square cavity problem solved in 3D using an Euler formulation (). The second example is the flow past a submerged NACA 0012 profile. Here the free surface equation is solved together with the flow equations.
The next four examples fall within the category of fluid-structure interaction problems. The first is the analysis of a sphere falling in a tube filled with liquid where the mesh updating procedure of Section 5.2 has been used. Then three of ship hydrodynamics problems are solved including the analysis of a Wigley hull, a scale model of a commercial ship and an American Cup racing sail boat. Numerical results are compared with experimental data in all cases.
The last series of examples show applications of the Lagrangian formulation to the simulation of the collapse of a water column, a semi-submerged rotating water mill and a solid cube falling into a water recipient.
10.1 Square cavity problem
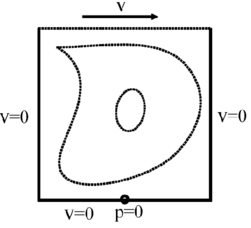
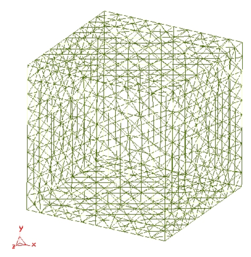
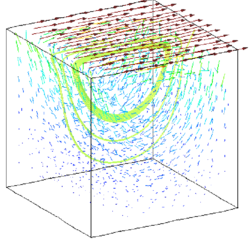
The purpose of this example is to test the stabilized formulation presented in the solution of a standard benchmark problem [17]. Figure 2 shows the definition of the problem solved with an unstructured 3D mesh of 7395 linear tetrahedra for a Reynolds number value of 1.
| |
| |
| |
| Figure 2: Square cavity problem. a) Problem definition. b) Unstructured mesh of 7395 linear tetrahedra. c) velocity field for . | |
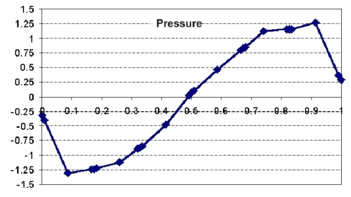
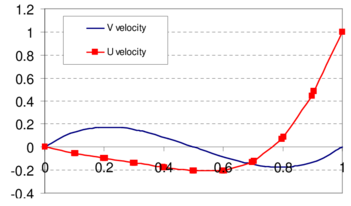
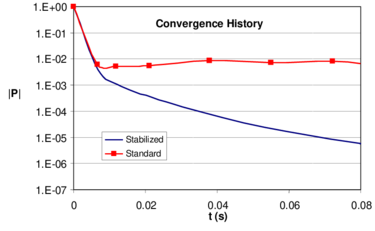
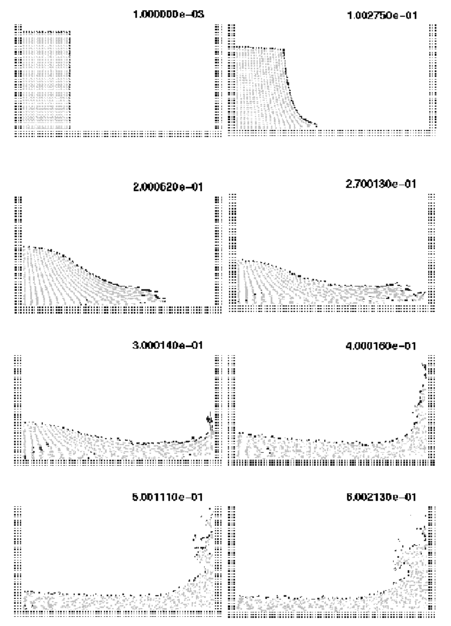
Results in Figure 3a,b are tabulated for the horizontal velocity along the vertical centerline of the mid-section and for vertical velocity and pressure along the horizontal centerline of the same section. Numerical results are fully stable and agree well with similar solutions reported [17]. The effect of the stabilization term in the pressure equation (see eq.(30)) is seen clearly in Figure 3c. The curves in this figure show the convergence towards steady state of the norm of the nodal pressures with time. The curve listed as “standard” is obtained neglecting the stabilization term, whereas the second curve shows the convergence when this term is taken into account. The difference between the two curves is noticeable as the error obtained with the fully stabilized solution is several orders of magnitude smaller than that obtained neglecting the term.
10.2 Submerged NACA 0012 profile
A 2D submerged NACA0012 profile at angle of attack is studied. This configuration was tested experimentally by Duncan [56] for high Reynolds numbers (Re=400000) and modelled numerically using the Euler equations by several authors [57-59]. The submerged depth of the airfoil is equal to the chord L. The Froude number for all the cases tested was set to where is the incoming flow velocity at infinity.
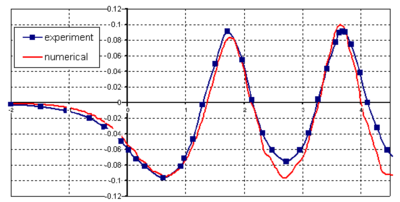
The stationary free surface and the pressure distribution are shown in Figure 4. The non-dimensional wave heights compare well with the experimental results [56].
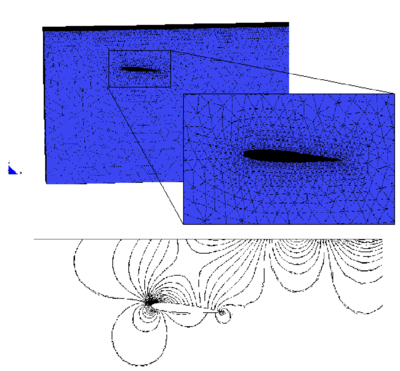
|
|
| Figure 4: Submerged NACA0012 profile. a) Detail of the mesh of 70000 linear tetrahedra chosen. b) Pressure contours. c) Stationary wave profile. |
10.3 Sphere falling in a tube filled with water
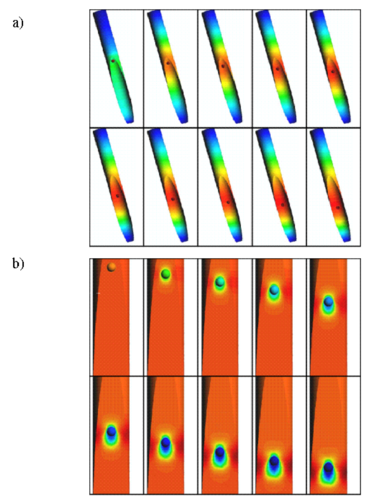
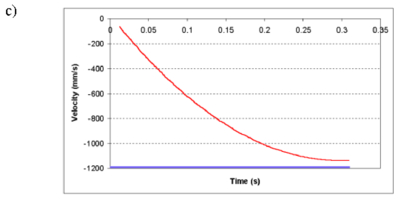
The movement of a sphere falling by gravity in a cylindrical tube filled with water is studied. The relationship between the diameters of the sphere and the tube is 1:4. The Reynolds number for the stationary speed is 100. The mesh has 85765 elements with 13946 nodes (Figure 5).
Figures 5 and 6 show the mesh deformation and contours of the mesh deformation and of the velocity in the domain for different times, respectively. The evolution of the falling speed is shown in Figure 6c. Note the good agreement with the so called Stokes velocity computed by equaling the weight of the sphere with the resistance to the movement of the sphere expressed in terms of the velocity. Obviously, this value is slightly greater than the actual one as frictional effects are neglected.
A similar problem for a greater number of spheres has been solved by Johnson and Tezduyar [60].
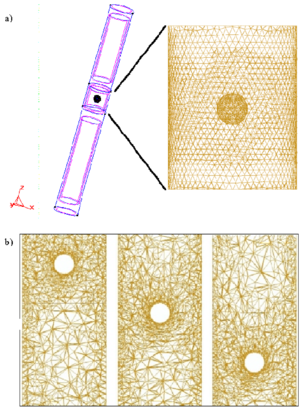
|
| Figure 5: Sphere falling in a tube filled with liquid. a) Geometry definition and detail of the mesh of 85765 linear tetrahedra chosen. b) Mesh deformation during the falling of the sphere. |
10.4 Wigley hull
The next problem case considered here is the study of the hydrodynamics of the well known Wigley Hull.
The same configuration was tested experimentally in [61] and modelled numerically by several authors [58,59,62]. We use here an unstructured 3D finite element mesh of 65434 linear tetrahedra, with a reference surface of 7800 triangles, partially represented in Figure 7.
Figure 7 also shows the results of the viscous analysis of the Wigley model in three different cases for (). In the first case the volume mesh was considered fixed, not allowing free surface nor ship movements. Secondly, the volume mesh was updated due to free surface movement, considering the model fixed. The third case corresponds to the analysis of a real free model including the mesh updating due to free surface evaluation and ship movement (sinkage and trim). A Smagorinsky turbulence model was used in the three cases.
Table 1 shows the obtained total resistance coefficient in the three cases studied compared with the experimental data.
| Experimental | Numerical | |
| Test 1 | ||
| Test 2 | ||
| Test 3 |
In the study of the free model the numerical values of sinkage and trim were -0.1% and 0.035, respectively, while experiment gave -0.15% and 0.04.
Figure 7a shows the pressure distribution obtained near the Wigley hull for the free model. A number of streamlines have also been plotted in the figure. The obtained mesh deformation in this case is also presented in Figure 7b.
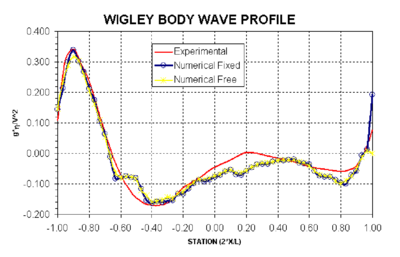
Comparisons of the obtained body wave profile with the experimental data for the free and fixed models are shown in Figure 7b. Significant differences are found close to stern in the case of the fixed model.
The free surface contours for the free ship motion are shown in Figure 7c.
10.5 KVLCC2 hull model
The example is the analysis of the KVLCC2 benchmark model. Here a partially wetted tramsom stern is expected due to the low Froude number of the test. Figure 8 shows the NURBS geometry used obtained from the Hydrodynamic Performance Research team of Korea (KRISO). The obtained results are compared with the experimental data available in the KRISO database [63].
|
| Figure 8: KVLCC2 model. Geometrical definition based on NURBS surfaces. |
The smallest element size used was 0.001 m and the largest 0.50 m. The surface mesh chosen is shown in Figure 9. A total of 550.000 tetrahedra were used in the analysis. The tramsom stern flow model presented in the previous section was used.
Test 1.- Wave pattern calculation. The main characteristics of the analysis are listed below:
- Length: , Beam (at water plane): , Draught: , Wetted Surface: .
- Velocity: , Froude Number: .
- Viscosity: , Density: , Reynolds number: .

|
| Figure 9: KVLCC2 model. Surface mesh used in the analysis. |
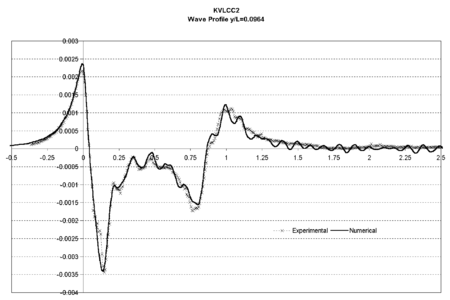
The turbulence model used in this case was the model. Figures 10 and 11 show the wave profiles on the hull and in a cut at obtained in Test 1, compared to the experimental data. The obtained results are quantitatively good close to the hull. A lost of accuracy is observed in the profiles away from the hull. This is probably due to the fact that the element sizes are not small enough in this area.
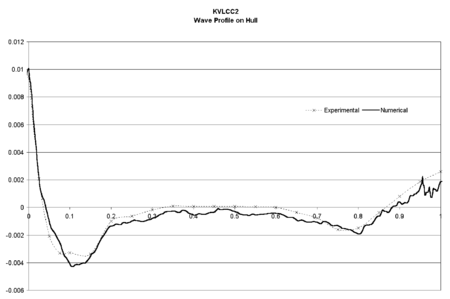
|
| Figure 10: KVLCC2 model. Wave profile on the hull compared to experimental data. Thick line shows numerical results |
|
| Figure 11 |
Test 2.- Wake analysis at different planes. Several turbulence models were used (Smagorinsky, and model) in order to verify the quality of the results. Here, only the results from the model are shown. We note that the velocity maps obtained even for the simplest model were qualitatively good, showing the accuracy of the fluid solver scheme used. The main characteristics of this analysis are listed below:
- Length: , Beam (at water plane): , Draught: , Wetted Surface: .
- Velocity: .
- Viscosity: , Density: , Reynolds number: .
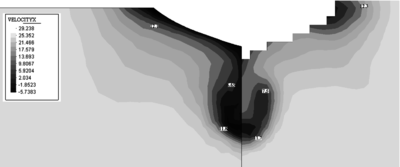
Figures 12-13 present results corresponding to the test 2. Figure 12 shows the contours of the axial (X) component of the velocity on a plane at from the orthogonal aft. Figure 13 shows the maps of the kinetic energy on this plane. Experimental results are shown for comparison in all cases. Further results for this problem can be found in [48].
|
| Figure 12: KVLCC2 model. Map of the X component of the velocity on a plane at from the orthogonal aft. Experimental results shown in the right figure. |

|
| Figure 13: KVLCC2 model. Map of the eddy kinetic energy () on a plane at from the orthogonal aft. Experimental data shown in the right figure. |
10.6 American Cup BRAVO ESPAA Model
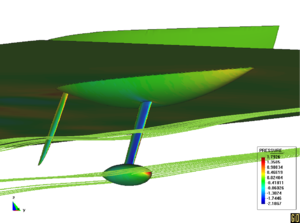
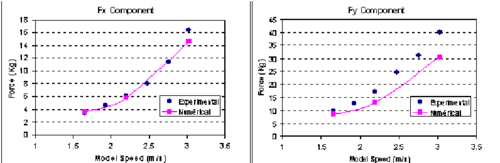
The next example is the analysis of the Spanish American Cup racing sail boat Bravo España. The finite element mesh used is shown in Figure 14. The results presented in Figures 14-17 correspond to the analysis of a non symmetrical case including appendages. Good comparison between the experimental data and the numerical results was again obtained.
Other results of the hydrodynamic analysis of American Cup racing boats carried out with the FEM formulation presented in the paper can be seen in [64].

|
| Figure 14: sail racing boat. Mesh used in the analysis. |

|
| Figure 15: . Velocity contours. |
|
| Figure 16: . Streamlines. |
|
| Figure 17: . Resistance test. Comparison of numerical results with experimental data. |
10.7 Lagrangian flow
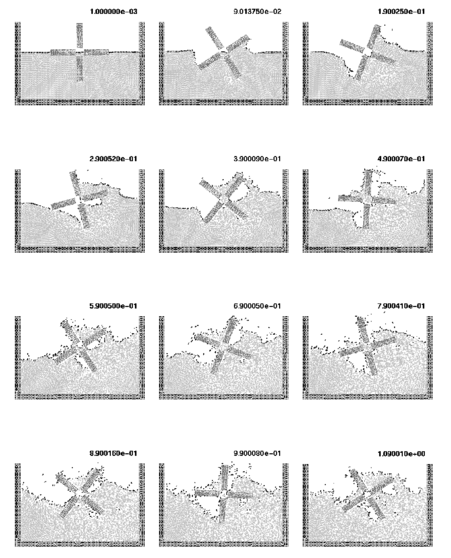
The first problem solved with the lagrangian formulation is the study of the collapse of a water column. This problem was solved by Koshizu and Oka [65] both experimentally and numerically. It has became a classical example to test the validation of the lagrangian formulation in fluid flows. The water is initially located on the left supported by a removable board. The collapse starts at time , when the removable board is removed. Viscosity and surface tension are neglected. Figure 18 shows the point positions at different time steps. The dark points represent the free-surface detected with an alpha-shape algorithm [51,52]. The internal points are gray and the fixed points are black.
The water is running on the bottom wall until, near 0.3 sec, it impinges on the right vertical wall. Breaking waves appear at 0.6 sec. Around 1 sec. the water reaches the left wall. Agreement with the experimental results of [65] both in the shape of the free surface as well as in the time evolution are excellent.
|
| Figure 18: Water column collapse at different time steps. |
|
| Figure 18: cont. |
|
| Figure 19: Rotating water mill. |
|
| Figure 20: Solid cube falling into a recipient with water. |
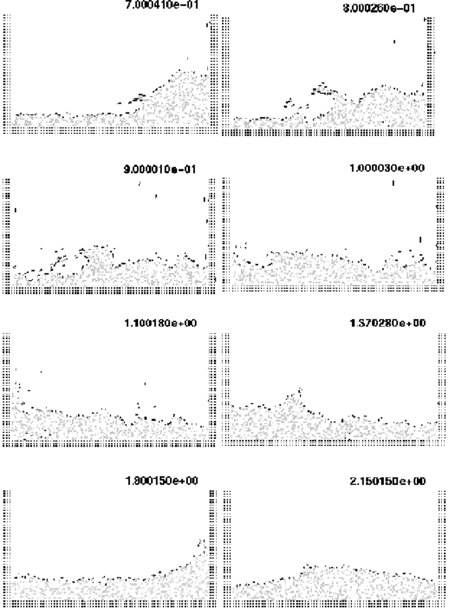
The second example is the analysis of a rotating water mill semi submerged in water. A schematic representation of a water mill is presented in Figure 19. The blades of the mill have an imposed rotating velocity, while the water is initially in a stationary and flat position. Fluid structure interactions with free-surfaces and water fragmentation are well reproduced in this example.
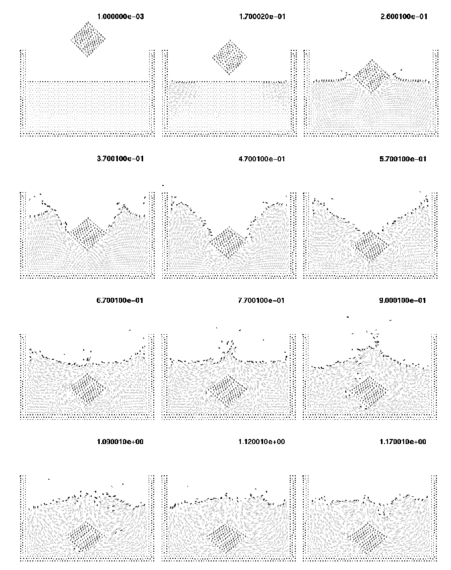
The last example represents a free cube falling down into a recipient full of water. The solid cube was modeled by introducing a high viscosity parameter in the elements in the following way: all the polyhedral elements formed by nodes contained in the cube have a high viscosity value. The other elements are inviscid. The results of Figure 20 represent correctly the contact problem when the cube hits the water and also the speed during the sinking process.
More examples showing applications of the Lagrangian formulation previously described can be found in [51,52].
11 CONCLUSIONS
The finite calculus form of the fluid mechanics equations is a good starting point for deriving stabilized finite algorithms for solving a variety of fluid flow problems using Euler, ALE and fully lagrangian descriptions. Both monolithic and fractional step algorithms with intrinsic stabilization properties can be readily derived as shown here. Free surface wave effects and fluid-structure interaction situations can be accounted for in a straight forward manner within the general flow solution schemes. The ALE formulation is particularly adequate for analysis of problems involving free surface waves of moderate amplitude typical of ship hydrodynamics situations. The lagrangian formulation allows to solve in an effective manner fluid flow problems involving large motions of the free surface and complex fluid-structure interactions.
ACKNOWLEDGEMENTS
The authors are grateful to Copa America Desafio Español SA for providing the geometry and experimental data of the racing boat analyzed.
Examples 10.1-10.7 were analyzed with the finite element code Tdyn based on the FEM formulation here presented [66].
Thanks are also given to Dr. Roberto Flores for many useful discussions.
References
[1] O.C. Zienkiewicz and R.C. Taylor,The finite element method, 5th Edition, 3 Volumes, Butterworth–Heinemann, 2000.
[2] C. Hirsch, Numerical computation of internal and external flow, J. Wiley, Vol. 1 1988, Vol. 2, 1990.
[3] A.J. Chorin, “A numerical solution for solving incompressible viscous flow problems” J. Comp. Phys., 2, 12–26, 1967.
[4] W.R. Briley, S.S. Neerarambam and D.L. Whitfield, “Multigrid algorithm for three-dimensional incompressible high-Reynolds number turbulent flows”, AIAA Journal, 33 (1), 2073–2079, 1995.
[5] J. Peraire, K. Morgan and J. Peiro, “The simulation of 3D incompressible flows using unstructured grids”, In Frontiers of Computational Fluid Dynamics, Caughey DA and Hafez MM. (eds), Chapter 16, J. Wiley, 1994.
[6] C. Sheng, L.K. Taylor and D.L. Whitfield, “Implicit lower-upper/approximate-factorization schemes for incompressible flows” Journal of Computational Physics, 128 (1), 32–42, 1996.
[7] M. Storti, N. Nigro and S.R. Idelsohn, “Steady state incompressible flows using explicit schemes with an optimal local preconditioning”, Computer Methods in Applied Mechanics and Engineering, 124, 231–252, 1995.
[8] J.C. Heinrich, P.S. Hayakorn and O.C. Zienkiewicz, “An upwind finite element scheme for two dimensional convective transport equations”, Int. J. Num. Meth. Engng., 11, 131–143, 1977.
[9] S.R. Idelsohn, M. Storti and N. Nigro, “Stability analysis of mixed finite element formulation with special mention to stabilized equal-order interpolations” Int. J. for Num. Meth. in Fluids, 20, 1003-1022, 1995.
[10] S.R. Idelsohn, N. Nigro, M. Storti and G. Buscaglia, “A Petrov-Galerkin formulation for advection-reaction-diffusion”, Comput. Meth. Appl. Mech. Engrg., 136, 27–46, 1996.
[11] A. Brooks and T.J.R. Hughes, “Streamline upwind/Petrov-Galerkin formulation for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations”, Comput. Methods Appl. Mech. Engrg, 32, 199–259, 1982.
[12] T.J.R. Hughes and M. Mallet, “A new finite element formulations for computational fluid dynamics: III. The generalized streamline operator for multidimensional advective-diffusive systems”, Comput Methods Appl. Mech. Engrg., 58, pp. 305–328, 1986.
[13] P. Hansbo and a. Szepessy, “A velocity-pressure streamline diffusion finite element method for the incompressible Navier-Stokes equations”, Comput. Methods Appl. Mech. Engrg., 84, 175–192, 1990.
[14] T.J.R. Hughes, L.P. Franca and M. Balestra, “A new finite element formulation for computational fluid dynamics. V Circumventing the Babuska-Brezzi condition: A stable Petrov-Galerkin formulation of the Stokes problem accomodating equal order interpolations”, Comput. Methods Appl. Mech. Engrg., 59, 85–89, 1986.
[15] L.P. Franca and S.L. Frey, “Stabilized finite element methods: II. The incompressible Navier-Stokes equations”, Comput. Method Appl. Mech. Engrg., Vol. 99, pp. 209–233, 1992.
[16] T.J.R. Hughes, G. Hauke and K. Jansen, “Stabilized finite element methods in fluids: Inspirations, origins, status and recent developments”, in: Recent Developments in Finite Element Analysis. A Book Dedicated to Robert L. Taylor, T.J.R. Hughes, E. Oñate and O.C. Zienkiewicz (Eds.), (International Center for Numerical Methods in Engineering, Barcelona, Spain, pp. 272–292, 1994.
[17] M.A. Cruchaga and E. Oñate, “A finite element formulation for incompressible flow problems using a generalized streamline operator”, Comput. Methods in Appl. Mech. Engrg., 143, 49–67, 1997.
[18] M.A. Cruchaga and E. Oñate, “A generalized streamline finite element approach for the analysis of incompressible flow problems including moving surfaces”, Comput. Methods in Appl. Mech. Engrg., 173, 241–255, 1999.
[19] T.J.R. Hughes, L.P. Franca and G.M. Hulbert, “A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations”, Comput. Methods Appl. Mech. Engrg., 73, pp. 173–189, 1989.
[20] T.E. Tezduyar, S. Mittal, S.E. Ray and R. Shih, “Incompressible flow computations with stabilized bilinear and linear equal order interpolation velocity–pressure elements”, Comput. Methods Appl. Mech. Engrg., 95, 221–242, 1992.
[21] J. Donea, “A Taylor-Galerkin method for convective transport problems”, Int. J. Num. Meth. Engng., 20, 101–119, 1984.
[22] J. Douglas, T.F. Russell, “Numerical methods for convection dominated diffusion problems based on combining the method of characteristics with finite element or finite difference procedures”, SIAM J. Numer. Anal., 19, 871, 1982.
[23] O. Pironneau, “On the transport-diffusion algorithm and its applications to the Navier-Stokes equations”, Numer. Math., 38, 309, 1982.
[24] R. Löhner, K. Morgan, O.C. Zienkiewicz, “The solution of non-linear hyperbolic equation systems by the finite element method”, Int. J. Num. Meth. in Fluids, 4, 1043, 1984.
[25] R. Codina, M. Vazquez and O.C. Zienkiewicz, “A general algorithm for compressible and incompressible flow - Part III. The semi-implicit form” Int. J. Num. Meth. in Fluids, 27, 13–32, 1998.
[26] R. Codina and O.C. Zienkiewicz, “CBS versus GLS stabilization of the incompressible Navier-Stokes equations and the role of the time step as stabilization parameter”, Communications in Numerical Methods in Engineering, 18 (2), 99–112, 2002.
[27] R. Codina and J. Blasco, “Stabilized finite element method for the transient Navier-Stokes equations based on a pressure gradient operator”, Comput. Methods in Appl. Mech. Engrg., 182, 277–301, 2000.
[28] T.J.R. Hughes, “Multiscale phenomena: Green functions, subgrid scale models, bubbles and the origins of stabilized methods”, Comput. Methods Appl. Mech. Engrg, Vol. 127, pp. 387–401, 1995.
[29] F. Brezzi, L.P. Franca, T.J.R. Hughes and A. Russo, ``, Comput. Methods Appl. Mech. Engrg., 145, 329–339, 1997.
[30] R. Codina, “Stabilized finite element approximation of transient incompressible flows using orthogonal subscales”, Comput. Methods Appl. Mech. Engrg., 191, 4295–4321, 2002.
[31] J. Donea and A. Huerta, “Finite element method for flow problems”, J. Wiley, 2003.
[32] E. Oñate, Derivation of stabilized equations for advective-diffusive transport and fluid flow problems, Comput. Meth. Appl. Mech. Engng., Vol. 151, pp. 233–267, (1998).
[33] E. Oñate, J. García and S. Idelsohn, Computation of the stabilization parameter for the finite element solution of advective-diffusive problems, Int. J. Num. Meth. Fluids, Vol. 25, pp. 1385–1407, (1997).
[34] E. Oñate, J. García and S. Idelsohn, An alpha-adaptive approach for stabilized finite element solution of advective-diffusive problems with sharp gradients, New Adv. in Adaptive Comp. Met. in Mech., P. Ladeveze and J.T. Oden (Eds.), Elsevier, (1998).
[35] E. Oñate and M. Manzan, A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems, Int. J. Num. Meth. Fluids, 31, 203–221, 1999.
[36] E. Oñate and M. Manzan, “Stabilization techniques for finite element analysis of convection diffusion problems”, in Computational Analysis of Heat Transfer, G. Comini and B. Sunden (Eds.), WIT Press, Southampton, 2000.
[37] E. Oñate, “A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation”, Comp. Meth. Appl. Mech. Engng., 182, 1–2, 355–370, 2000.
[38] E. Oñate and J. García, “A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation”, Comput. MethodsAppl. Mech. Engrg., 191, 635–660, (2001).
[39] E. Oñate, “Possibilities of finite calculus in computational mechanics”, Submitted to Int. J. Num. Meth. Engng., 2002.
[40] E. Oñate and S. Idelsohn, A mesh free finite point method for advective-diffusive transport and fluid flow problems,, Computational Mechanics, 21, 283–292, 1988.
[41] E. Oñate, C. Sacco and S. Idelsohn, “A finite point method for incompressible flow problems”, Computing and Visualization in Science, 2, 67–75, 2000.
[42] T.E. Tezduyar, M. Behr and J. Liou, “A new strategy for finite element computations involving moving boundaries and interfaces - the deforming-spatial-domain/space-time procedure: I. The concept and the preliminary tests”, Comput. Methods in Appl. Mech. and Engrg., 94, 339–351, 1992.
[43] S. Mittal and T.E. Tezduyar, “Parallel finite element simulation of 3D incompressible flows - fluid structure interactions”, Int. J. Num. Meth. Fluids, 21, 933–953, 1995.
[44] N. Maman and C. Farhat, “Matching fluid and structure meshes for aeroelastic computations: A parallel approach”, Computers and Structures, 54, 779–785, 1995.
[45] G. Chiandusi, G. Bugeda and E. Oñate, “A simple method for update of finite element meshes”, Commun, Numer. Meth. Engng., 16, 1–9, 2000.
[46] E. Oñate, S. Idelsohn, C. Sacco and J. García, “Stabilization of the numerical solution for the free surface wave equation in fluid dynamics”, ECCOMAS CFD98, K. Papaliou et al. (Eds.), J. Wiley, 1998.
[47] J. García, A finite element method for analysis of naval structures (in Spanish), Ph.D. Thesis, Univ. Politecnica de Catalunya, December (1999).
[48] J. García and E. Oñate, “An unstructured finite element solver for ship hydrodynamic problems”, Accepted for publication in J. Appl. Mech., 2002.
[49] E. Oñate, J. García and S.R. Idelsohn, “Ship hydrodynamics”, in Encyclopedia of Computational Mechanics, E. Stein, R. de Borst and T.J.R. Hughes (Eds), J. Wiley, 2004.
[50] S.R. Idelsohn, E. Oñate, N. Calvo and F. del Pin, “The meshless finite element method”, Accepted ofr publication in Int. J. Num. Meth. Engng., 2002.
[51] S.R. Idelsohn, E. Oñate, F. Del Pin and N. Calvo, “Lagrangian formulation: the only way to solve some free-surface fluid mechanics problems”, Fith World Congress on Computational Mechanics, Mang HA, Rammerstorfer FG and Eberhardsteiner J. (eds), July 7–12, Viena, Austria, 2002, Web...
[52] S.R. Idelsohn, E. Oñate and F. Del Pin, “A lagrangian meshless finite element method applied to fluid-structure interaction problems”, Submitted to Computer and Structures, 2002.
[53] D.C. Wilcox, Turbulence modeling for CFD, DCW Industries Inc., 1994.
[54] T.J.R. Hughes and M. Mallet, ``A new finite element formulations for computational fluid dynamics: IV. A discontinuity capturing operator for multidimensional advective-diffusive system, Comput. Methods Appl. Mech. Engrg., 58, 329–336, 1986.
[55] R. Codina, “A discontinuity-capturing crosswind dissipation for the finite element solution of the convection-diffusion equation”, Comput. Methods Appl. Mech. Engrg., 110, 325–342, 1993.
[56] J.H. Duncan, “The breaking and non-breaking wave resistance of a two-dimensional hydrofoil”, J. Fluid Mech., Vol. 126, 1983.
[57] T. Hino, L. Martinelli and A. Jameson, “A finite volument method with unstructured grid for free surface flow”, pp. 173-194 in Proc. of the 6th Int. Conf. Num. Ship Hydrodynamics, Iowa City, Iowa, 1993.
[58] S.R. Idelsohn, E. Oñate and C. Sacco, Finite element solution of free surface ship-wave problem, Int. J. Num. Meth. Engng., 45, 503–508, (1999).
[59] R. Löhner, C. Yang, E. Oñate and S. Idelsohn, An unstructured grid-based parallel free surface solver, Appl. Num. Math., 31, 271–293, (1999).
[60] A.A. Johnson and T.E. Tezduyar, “3D simulation of fluid-particle interaction with the number of particles reaching 100”, Comput. Methods Appl. Mech. Engrg., 145, 301–321, 1997.
[61] Procedings of 2nd DTNSRDC Workshop on Ship Wave Resistance Computations. David Taylor Naval Ship Research and Development Center. Noblese, F. and McCarthy J.H. (Eds.), Maryland, USA, 1983.
[62] J.R. Farmer, L. Martinelli and A. Jameson, “A fast multigrid method for solving incompressible hydrodynamic problems with free surfaces”, AIAA J., 32, 6, 1175-1182, 1993.
[63] Korea Research Institute of Ships and Ocean Engineering (KRISO).http://www.iihr.uiowa.edu/gothenburg2000/KVLCC/tanker.html.
[64] J. García, R. Luco-Salman, M. Salas, M. López-Rodríguez and E. Oñate E, ``An advanced finite element method for fluid-dynamic analysis of America's Cup boat, High Performance Yatch Design Conference, Auckland, 4–6, December, 2002.
[65] S. Koshizuka and Y. Oka, “Moving particle semi-implicit method for fragmentation of incompressible fluid”, Nuclear Engineering Science, 123, 421-434, 1996.
[66] Tdyn. A finite element code for fluid-dynamic analysis, COMPASS Ingeniería y Sistemas SA, www.compassis.com, (2002).
Document information
Published on 01/01/2003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?