Published in Trends in Computational Structural Mechanics, W. A. Wall, K.-U. Bletzinger and K. Schweizerhof (Eds.), CIMNE, Barcelona, Spain, 2001
Summary
A stabilized semi-implicit fractional step finite element method for analysis of coupled fluid interaction problems involving free surface waves has been presented. A procedure for automatic movement of mesh nodes during the coupled solution process has been developed. The method is adequate for solving large scale fluid-structure interaction situations in naval architecture and offshare engineering problems.
1 Introduction
Accurate prediction of the fluid-structure interaction effects for a totally or partially submerged body in a flowing liquid including a free surface is a problem if great relevance in offshore engineering and naval architecture among many other fields.
The difficulties in accurately solving the coupled fluid-structure interaction problem in this case are mainly due to the following reasons:
1. The difficulty of solving numerically the incompressible fluid dynamic equations which typically include intrinsic non linearities except for the simplest and limited potential flow model.
2. The obstacles in solving the constraint equation stating that at the free surface boundary the fluid particles remain on that surface which position is in turn unknown.
3. The difficulties in solving the problem of motion of the submerged body due to the interaction forces while minimizing the distorsion of the finite elements discretizing the fluid domain thus reducing the need of remeshing.
This paper presents a stabilized finite element method which allows to overcome above three obstacles. The starting point are the modified governing differential equations for the incompressible viscous flow and the free surface condition incorporating the necessary stabilization terms via a finite increment calculus (FIC) procedure developed by the authors [1–4]. The FIC approach has been successfully applied to the finite element and meshless solution of a range of advective-diffusive transport and fluid flow problems [1–5].
The modified governing equations are solved in space-time using a semi-implicit fractional step approach and the finite element method (FEM). Free surface wave effects are accounted for via the introduction of a prescribed pressure at the free surface computed from the wave height.
The movement of the submerged body within the fluid due to the interaction forces is treated by solving a structural dynamic problem using the fluid forces as input loads. A method to update the mesh for the fluid domain following the movement of the submerged body which minimizes element distorsion is presented. The mesh update procedure is based on the iterative finite element solution of a linear elastic problem on the mesh domain where fictitions elastic properties are assigned so that elements suffering higher movements are stiffer [6].
The content of the paper is structured as follows. First details of the stabilized semi-implicit fractional step approach using the FEM is described. Next the mesh updating procedure is presented. Finally some examples of a coupled fluid-interaction problem are given.
2 Stabilized finite element formulation for the fluid flow equations
We consider the motion around a body of a viscous incompressible fluid including a free surface.
The stabilized form of the governing differential equations for the three dimensional (3D) problem can be written as
Momentum
|
|
(1a) |
Mass balance
|
|
(1b) |
Free surface
|
|
(1c) |
where
|
|
(2a) |
|
|
(2b) |
|
|
(2c) |
In above is the velocity along the ith global reference axis, the (constant) density of the fluid, the pressure, the wave elevation, the body forces acting in the fluid and the viscous stresses related to the viscosity by the standard expression
|
|
(3) |
The underlined terms in eqs.(1) introduce the necessary stabilization for the approximated numerical solution.
The distances and are termed characteristic lengths and represent the dimensions of the finite domain where balance of momentum, mass and transport of fluid particles is enforced. Details of the derivation of eqs.(2) can be found in [1].
A more convenient form of equation (1b) can be written by assuming where is an intrinsic time parameter. Under this assumption and using eq.(1a) the stabilized form of the mass balance equation can be written as (neglecting high order terms) [4]
|
|
(4) |
where
|
|
(5) |
The boundary conditions for the stabilized problem are written as
|
|
(6a) |
|
|
(6b) |
where are the components of the unit normal vector to the boundary and and are prescribed tractions and displacements on the boundaries and , respectively. The underlined stabilized tersm appearing in the Neumann boundary condition (6a) are obtained via the FIC approach [1].
Eqs.(1–6) are the starting point for deriving a variety of stabilized numerical methods for solving the incompressible Navier-Stokes equations. It can be shown that a number of standard stabilized finite element methods allowing equal order interpolations for the velocity and pressure fields can be recovered from the modified form of the momentum and mass balance equations given above [4]. A semi-implicit fractional step finite element procedure for solution of eqs.(1a),(1c),(4) and (6) is presented in next section.
2.1 Stabilized fractional step method
Let us discretize in time the stabilized momentum equation (1a) as
|
|
(7) |
A fractional step method (also termed “segregation” or “splitting” procedure) can be simply derived by splitting eq.(7) as follows
|
|
(8a) |
|
|
(8b) |
Note that addition of eqs.(8) gives the original stabilized momentum equation (7).
Substitution of (8a) into eq.(4) gives after some algebra [4]
|
|
(9) |
where
|
|
(10) |
Standard fractional step procedures neglect the contribution from the terms involving in eq.(9). It can be shown that these terms have an additional stabilization effect which improves the numerical solution when the values of are small.
The free surface wave equation (1c) can be also discretized in time to give
|
|
(11) |
A typical solution in time includes the following steps.
Step 1. Solve explicitely for the so called fractional velocities using eq.(8a).
Step 2. Solve for the pressure field solving the Laplacian equation (9). The pressures at the free surface computed from step 4 below in the previous time step are used as boundary conditions for solution of eq.(9).
Step 3. Compute the movement of the submerged body by solving the dynamic equations of motion in the body subjected to the pressure field and the viscous stresses .
Step 4. Compute the new position of mesh nodes in the fluid domain by using the mesh update algorithm described in next section.
Step 5. Compute the fractional velocity and pressure fields at the new position of the nodes. This can be simply done by the following expression
|
|
(12a) |
|
|
(12b) |
In eq.(12) is the node number, are values of in the updated nodes after mesh movement whereas the r.h.s. includes values of and in the original position, and is the gradient vector.
An alternative to eq.(12b) is to compute the nodal pressures in the updated mesh configuration by solving once more eq.(9) using the values of obtained from eq.(12a). This will ensure better satisfaction of the incompressibility condition in the updated mesh.
Step 6. Compute the velocity field at the updated configuration for each mesh node
|
|
(13) |
Step 7. Solve for the updated value of the free surface elevation using eq.(11). Compute the pressure in the free surface from Benouilli equation as
|
|
(14) |
where and are reference values of the free surface elevation and the pressure respectively and is the gravity constant.
As already mentioned the effect of changes in the free surface elevation is introduced in the step 2 of the flow solution as a prescribed pressure acting on the free surface.
The accuracy of above transient solution process depends on the time step size which should satisfy stability criteria for the coupled solution. Indeed larger time steps can be used if the values at time in above equations are computed at . The solution process becomes now implicit and an iteration loop within each time step is then required.
2.2 Finite element discretization
Space discretization is carried out using the finite element method [7]. The velocity and pressure fields are interpolated within each element in the standard finite element manner as
|
|
(15) |
where and are the shape functions interpolating the velocity and pressure fields, respectively and denote nodal values.
Similarly the wave height is discretized as
|
|
(16) |
where are shape functions defined over the nodes discretizing the free surface.
It is worth noting that the stabilized formulation described allows an equal order interpolation of velocities and pressure [4]. A linear interpolation over triangles (2D) and tetrahedra (3D) for both and is chosen in the examples shown in the paper. Similarly linear elements are chosen to interpolate on the free surface mesh.
The discretized integral form is obtained by applying the standard Galerkin procedure to eqs.(8a),(8b),(9),(11),(12) and the boundary conditions (6a). The resulting expressions follow the pattern given in [4].
The computation of the stabilization parameters and can be based in the diminishing residual technique explained in [1–5]. In the example presented in Section 4 the simpler option and with where is the element volume has been taken.
3 A simple algorithm for stable updating of mesh nodes
Finite element solution of fluid-structure interaction problems usually requires the update of the analysis mesh as described in previous section. A typical example is the study of movement of an object within a flowing liquid where the fluid mesh needs to be continuously updated accordingly to the changes in position of the object due to the interaction forces.
Chiandussi, Bugeda and Oñate [6] have recently proposed a simple method for movement of mesh nodes ensuring minimum element distorsion. The method is based on the iterative solution of a fictitions linear elastic problem on the mesh domain. In order to minimize mesh deformation the “elastic” properties of each mesh element are appropiately selected so that elements suffering greater movements are stiffer. The basis of the method is given below.
Let us consider an elastic domain with homogeneous isotropic elastic properties characterized by the Young modulus and the Poisson coefficient . Once a discretized finite element problem has been solved using, for instance, standard linear triangles (in 2D) or linear tetraedra (in 3D), the principal stresses at the center of each element are obtained as
|
|
(17) |
where are the principal strains.
Let us assume now that a uniform strain field throughout the mesh is sougth. The principal stresses are then given by
|
|
(18) |
where is the unknown Young modulus for the element.
A number of criteria can be now used to find the value of . The most effective approach found in [6] is to equal the element strain energies in both analysis. Thus
|
|
(19) |
|
|
(20) |
Equaling eqs.(19) and (20) gives the sought Young modulus as
|
|
(21) |
Note that the element Young modulus is proportional to the element deformation as desired. Also recall that both and are constant for all elements in the mesh.
The solution process includes the following two steps.
Step 1. Consider the finite element mesh as a linear elastic solid with homogeneous material properties characterized by and . Solve the corresponding elastic problem with imposed displacements at the mesh boundary. These displacements can be due to a prescribed motion of a body within a fluid, to changes in the shape of the domain in an optimum design problem, etc.
Step 2. Compute the principal strains and the values of the new Young modulus in each element using eq.(21) for a given value of . Repeat the finite element solution of the linear elastic problem with prescribed boundary displacements using the new values of for each element.
The movement of the mesh nodes obtained in the second step ensures a quasi uniform mesh distorsion. Further details on this method including other alternatives for evaluating the Young modulus can be found in [6].
The previous algorithm for movement of mesh nodes is able to treat the movement of the mesh due to changes in position of fully submerged and semi-submerged bodies. Note however that if the floating body intersects the free surface, the changes in the analysis domain geometry can be very important. From one time step to other emersion or inmersion of significant parts of the body can occur.
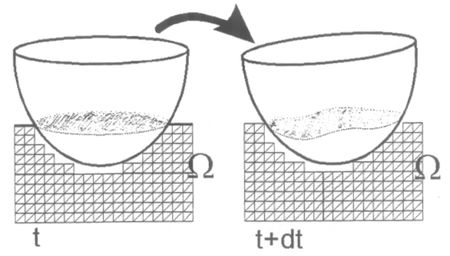
A posible solution to this problem is to remesh the analysis domain. However for m ost problems, a mapping of the moving surfaces linked to mesh updating algorithm described above can avoid remeshing (Figure 1).
The surface mapping technique used in this work is based on transforming 3D curved surfaces into reference planes. This allows to compute within each plane the local (in-plane) coordinates of the nodes for the final surface mesh accordingly to the changes in the floating line. The final step is to transform back the local coordinates of the surface mesh in the reference plane to the final curved configuration which incorporates the new floating line.
4 Example. Movement of a submerged sphere in an open channel
Figure 2 shows the geometry of the channel and the position of the sphere of 2m diameter with a weight of 1000 N and a rotational inertia of 1000 kgm. A mesh of 19870 linear tetrahedra with 4973 nodes has been used for the analysis.
The problem has been analyzed for values of Reynolds number = 200 and Froude number = 0.71 corresponding to velocity of 1m/s at the inlet.
It is assumed that the sphere can only move vertically and rotate a fluid around the global axes due to the forces induced by the fluid. The vertical displacement is constrained by a spring linking the sphere to the ground. An initial vertical velocity of 1m/s for the sphere has been taken.
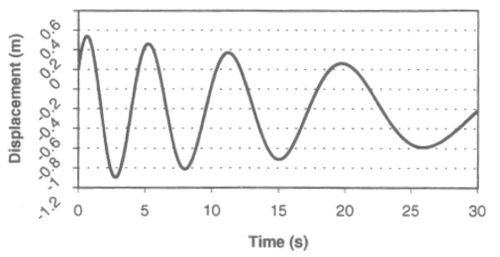
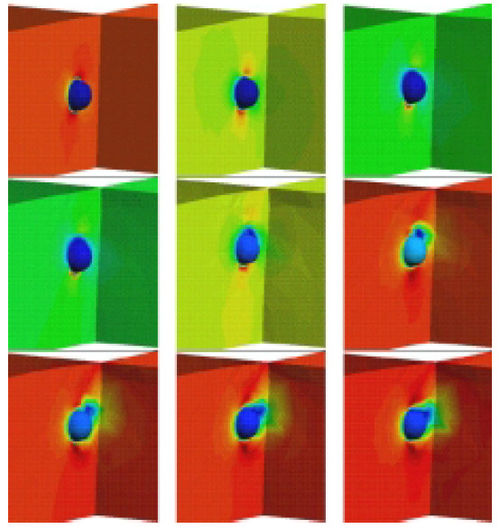
Figure 3 shows a plot of the time evolution of the vertical displacement of the sphere. The position of the sphere at different time intervals is shown in Figure 4. A plot of velocity vectors in the fluid displayed on Figure 5. Pressure contours in the fluid domain are shown in Figure 6.
The streamlines in the vecinity of the sphere at a certain time are shown in Figure 7. Figure 8 shows contours of the surface wave elevation at two particular times.
5 Conclusions
A stabilized semi-implicit fractional step finite element method for analysis of coupled fluid interaction problems involving free surface waves has been presented. A procedure for automatic movement of mesh nodes during the coupled solution process has been developed. The method is adequate for solving large scale fluid-structure interaction situations in naval architecture and offshare engineering problems.
6 Acknowledgements
This work was partially supported by Empresa Nacional BAZAN de Construcciones Navales y Militares S.A. This support is gratefully acknowledged.
7. References
1. E. Oñate - Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engng., Vol. 151, 1-2, pp. 233–267, 1998.
2. E. Oñate, J. Garcia and S. Idelsohn - Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. Int. J. Num. Meth. Fluids, Vol. 25, pp. 1385–1407, 1997.
3. E. Oñate, J. Garcia and S. Idelsohn - An alpha-adaptive approach for stabilized finite element solution of advective-diffusive problems with sharp gradients. New Adv. in Adaptive Comp. Met. in Mech., P. Ladeveze and J.T. Oden (Eds.), Elsevier, 1998.
4. E. Oñate - A finite element method for incompressible viscous flows using a finite increment calculus formulation. Research Report N. 150, CIMNE, Barcelona, January 1999.
5. E. Oñate and S. Idelsohn - A mesh free finite point method for advective-diffusive transport and fluid flow problems. Computational Mechanics, 21, 283–292, 1988.
6. Chiandusi, G., Bugeda, G. and Oñate, E. - A simple method for update of finite element meshes. Research Report 147, CIMNE, Barcelona, January 1999.
7. Zienkiewicz, O.C. and Taylor, R.C. - The finite element method, 4th Edition, Vol. 1, McGraw Hill, 1989.