Multiscale computational analysis in mechanics using finite calculus. An introduction

Published in Comput. Meth. Appl. Mech. Engng., Vol. 192 (28-30), pp. 3043-3059, 2003
doi: 10.1016/S0045-7825(03)00340-2

Abstract

The paper introduces a general procedure for computational analysis of a wide class of multiscale problems in mechanics using a finite calculus (FIC) formulation. The FIC approach is based in expressing the governing equations in mechanics accepting that the domain where the standard balance laws are established has a finite size. This introduces naturally additional terms into the classical equations of infinitesimal theory in mechanics which are useful for the numerical solution of problems involving different scales in the physical parameters. The discrete nodal values obtained with the FIC formulation and the finite element method (FEM) can be effectively used as the starting point for obtaining a more refined solution in zones where high gradients of the relevant variables occur using hierarchical or enriched FEM. Typical multiscale problems in mechanics which can be solved with the FIC method include convection-diffusion-reaction problems with high localized gradients, incompressible problems in solid and fluid mechanics, localization problems such as prediction of shear bands in solids and shock waves in compressible fluids, turbulence, etc. The paper presents an introduction of the treatment of multiscale problems using the FIC approach in conjunction with the finite element method (FEM). Examples of application of the FIC/FEM formulation to the solution of simple multiscale convection-diffusion problems are given.

1 INTRODUCTION

Multiscale problems in mechanics are characterized by the existence of numerical values of the geometrical and/or physical parameters differing in several orders of magnitude. Typical examples are convection-diffusion-absorption problems where high values of the convection or the absorption terms lead to sharp boundary and/or internal layers along which the numerical solution can change in many orders of magnitude. A similar problem is found in the analysis of thin discontinuity layers in solids, such as in the case of fracture in concrete, rock or geomaterials, or in shock waves in compressible fluids. A traditional multiscale problem is that of a turbulence fluid, where high gradients of the velocity field occur along random directions of the flow. The transition from a compressible to an incompressible solid or fluid can also be considered as a multiscale problem, in the sense that the propagation speed of sound changes from a finite value (for the compressible case) to an infinite value (in the case of incompressibility). Indeed, problems where many different scales of the material properties co-exist in a solid (such as in composites) are also classical examples of multiscale situations in solid mechanics. For the sake of conciseness, however, the case of composites will not be dealt with in the paper, although it can be also tackled with the general FIC formulation here described.

Recent attempts to develop a unified relativity theory in physics adequate for dealing with the whole spectrum of scales in the universe, from the Plank atomistic scale (${\textstyle 10^{-33}}$ cm) to the cosmological scale (${\textstyle 10^{+28}}$ cm) indicate that a suitable mathematical model should incorporate the effect of the different scales within the governing equations of the model [1]. Failing to include these scale terms may lead to unstable behaviour of the equations when solved numerically for very different values of the physical, geometrical and/or time parameters of the problem.

The Finite Calculus (FIC) method developed by Oñate and co-workers [2,3,4,5,6,7] is a consistent procedure to re-formulate the governing equation in mechanics introducing new terms involving characteristic space and time dimensions into the equations. The modified equations are derived by invoking the balance laws in mechanics in a space-time domain of finite size. The new terms introduced by the FIC approach are essential to obtain physical (stable) numerical solutions for all ranges of the parameters governing the physical problem.

This paper presents an extension of the FIC method to deal with multiscale problems in mechanics using the finite element method (FEM) [10]. The discrete (nodal) values provided by the numerical FEM solution of the FIC equations are taken as the “correct macroscale” solution for a given discretization. A more refined numerical solution in zones where high gradients of the relevant variables occur can be simply obtained by using a hierarchical FE approximations or by introducing enriched interpolation functions accounting for the “correct” shape of the solution sought. The paper describes the basic ideas of the multiscale FIC procedure proposed and two examples of application to simple 1D and 2D convection-diffusion problems showing the applicability of the method. The possibilities of the FIC method for strain localization problems are also briefly highlighted.

2 THE FINITE CALCULUS METHOD IN MECHANICS

Let us consider a 1D space-time domain ${\textstyle {\bar {\Omega }}:\Omega \times t}$, where ${\textstyle \Omega }$ is the domain length and ${\textstyle t}$ is the time.

We can now invoke any of the classical balance laws in mechanics, to be satisfied within a space-time slab of finite size ${\textstyle [x-d,x]\times [t-T,t]\subset {\bar {\Omega }}}$ where ${\textstyle d}$ is the length of the space balance domain and and ${\textstyle T}$ is a time increment defining the size of the balance domain in the time axis. Using the standard procedure of expanding in Taylor series the changes of the chosen governing variables and retaining the linear terms in ${\textstyle d}$ and ${\textstyle T}$ gives the FIC balance equations as

$r-{\frac {h}{2}}{\partial r \over \partial x}-{\frac {\delta }{2}}{\partial r \over \partial t}=0\qquad {\hbox{in }}{\bar {\Omega }}$

(1)

where ${\textstyle r}$ denotes the governing differential equations of the infinitessimal theory. In Eq.(1) ${\textstyle h}$ and ${\textstyle \delta }$ are respectively characteristic length and characteristic time parameters satisfying

${\begin{array}{c}-d\leq h\leq d\\0\leq \delta \leq T\end{array}}$

(2)

For an advection-diffusion thermal problem, Eq.(1) is the heat balance equation with

$r:=-\rho c\left(\displaystyle {\partial \phi \over \partial t}+v\displaystyle {\partial \phi \over \partial x}\right)+\displaystyle {\partial \over \partial x}\left(k\displaystyle {\partial \phi \over \partial x}\right)+Q$

(3)

where the ${\textstyle \phi }$ is the temperature, ${\textstyle \rho }$ is the density, ${\textstyle v}$ is the velocity, ${\textstyle k}$ and ${\textstyle c}$ are the thermal diffusivity and the specific heat parameters, respectively and ${\textstyle Q}$ is the heat source term.

Let us consider now a 1D solid mechanics problem. In this case Eq.(1) is the force equilibrium equation with

$r:=-\rho {\partial ^{2}u \over \partial t^{2}}+{\partial N \over \partial x}+b$

(4)

where ${\textstyle u}$ is the displacement, ${\textstyle N}$ is the axial force and ${\textstyle b}$ is the axial load.

The derivation of Eq.(1) for a simple steady state problem is given in the Appendix. Details of the derivation of the FIC equations for the transient case can be found in [6,7].

Note that as the dimensions of the balance slab tend to zero, also the values of the characteristic parameters ${\textstyle h}$ and ${\textstyle \delta }$ tend to zero. In the limit case Eq.(1) tends to

$r=0\qquad {\hbox{in }}{\bar {\Omega }}$

(5)

which is the standard form of the governing differential equations of the infinitessimal theory.

Eq.(1) can be generalized for a multidimensional problem as

$r_{i}-{\frac {h_{j}}{2}}{\partial r_{i} \over \partial x_{j}}-{\frac {\delta }{2}}{\partial r_{i} \over \partial t}=0\quad i=1,n_{b}\quad ;\quad j=1,n_{d}$

(6)

where ${\textstyle n_{b}}$ and ${\textstyle n_{d}}$ are the number of balance equations and the number of space dimensions, respectively.

A typical example of Eq.(6) are the FIC equations for an incompressible fluid written for the 3D case as

$r_{m_{i}}-{h_{j} \over 2}{\partial r_{m_{i}} \over \partial x_{j}}-{\delta \over 2}{\partial r_{m_{i}} \over \partial t}=0$ (7) $r_{d}-{h_{j} \over 2}{\partial r_{d} \over \partial x_{j}}-{\delta \over 2}{\partial r_{d} \over \partial t}=0\quad \quad i,j=1,2,3$ (8)

In above ${\textstyle r_{m_{i}}}$ and ${\textstyle r_{d}}$ are the ith momentum equation and the mass balance equation given by

$r_{m_{i}}:=-\rho \left({\partial v_{i} \over \partial t}+v_{j}{\partial v_{i} \over \partial x_{j}}\right)+{\partial \sigma _{ij} \over \partial x_{j}}+b_{i}$ (9) $r_{d}:={\partial v_{i} \over \partial x_{i}}$ (10)

where ${\textstyle v_{i}}$ are the velocities, ${\textstyle \sigma _{ij}=\tau _{ij}-p\delta _{ij}}$ are the total stresses, ${\textstyle p}$ is the pressure, ${\textstyle \tau _{ij}}$ are the viscous stresses and ${\textstyle b_{i}}$ are the body forces in the fluid [3,4].

Note that Eq.(8) is the result of applying the FIC concepts to the equations expressing the balance of mass over a space-time domain of finite size [2,4].

For a general solid mechanics problem the governing FIC equations stating the equilibrium of forces will be identical to Eq.(7) where ${\textstyle r_{m_{i}}}$ is given by Eq.(9), dropping now the convective terms [8,9].

2.1 Boundary and initial conditions

The Dirichlet and initial conditions are the same as in the standard infinitessimal theory. The Neumann boundary condition expressing balance of fluxes across the boundary ${\textstyle \Gamma _{q}}$ is however modified in the FIC formulation introducing, for consistency, the concept of balance over a domain of finite size adjacent to the Neumann boundary ${\textstyle \Gamma _{q}}$ [2]. The new boundary condition is written generally as

$q_{n_{i}}-{\bar {q}}_{n_{i}}-{1 \over 2}h_{j}n_{j}r_{i}=0\quad {\hbox{on }}\Gamma _{q}\quad i=1,n_{b}\quad ;\quad j=1,n_{d}$

(11)

where ${\textstyle q_{n_{i}}}$ is the normal “flow” across the boundary ${\textstyle \Gamma _{q}}$, ${\textstyle {\bar {q}}_{n_{i}}}$ is the prescribed flow value and ${\textstyle n_{i}}$ are the components of the unit normal to the boundary.

For example, in a 3D advection-diffusion problem, the boundary condition for the “diffusive” flux is

$n_{j}k_{j}{\partial \phi \over \partial x_{j}}+{\bar {q}}_{n}-{1 \over 2}h_{j}n_{j}r=0\quad \quad j=1,2,3$

(12)

For 3D fluid or solid mechanics problems, Eq.(11) would be

$\sigma _{ij}n_{j}-{\bar {t}}_{i}-{1 \over 2}h_{j}n_{j}r_{m_{i}}=0\quad \quad i,j=1,2,3$

(13)

where ${\textstyle {\bar {t}}_{i}}$ are the prescribed boundary tractions and ${\textstyle r_{m_{i}}}$ is given by Eq.(9).

Applications of the FIC method to problems in fluid and solid mechanics using the finite element method and the meshless finite point method can be found in [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

3 WHAT DO THE CHARACTERISTIC PARAMETERS MEAN?

The characteristic parameters in the space and time dimension (${\textstyle h_{i}}$ and ${\textstyle \delta }$) can be interpreted as free intrinsic parameters giving the “exact” expression of the balance equations (up to first order terms) in a space-time domain of finite size.

Let us consider now the discretized solution of the modified governing equations. For simplicity we will focuss here in the simplest scalar 1D problem. The variable ${\textstyle \phi }$ is approximated as ${\textstyle \phi \simeq {\hat {\phi }}}$ where ${\textstyle {\hat {\phi }}}$ denotes the approximated solution. The values of ${\textstyle {\hat {\phi }}}$ are now expressed in terms of a finite set of parameters using any discretization procedure (finite elements, finite diferences, etc.). The discretized FIC governing equation (1) would read now

${\hat {r}}-{\frac {h}{2}}{\partial {\hat {r}} \over \partial x}-{\frac {\delta }{2}}{\partial {\hat {r}} \over \partial t}=r_{\bar {\Omega }}\quad ,\qquad {\hbox{in }}{\bar {\Omega }}$

(14)

where ${\textstyle {\hat {r}}:=r({\hat {\phi }})}$ and ${\textstyle r_{\bar {\Omega }}}$ is the residual of the discretized FIC equations.

The meaning of the characteristic parameters ${\textstyle h}$ and ${\textstyle \delta }$ in the discretized equation (14) changes (although the same simbols than in Eq.(1) have been kept). The ${\textstyle h}$ and ${\textstyle \delta }$ parameters become now of the order of magnitude of the discrete domain where the balance laws are satisfied. In practice, this means that

${\begin{array}{c}-l\leq h\leq l\\0\leq \delta \leq \Delta t\end{array}}$

(15)

where ${\textstyle l}$ is the grid dimension in the space discretization (i.e. the element size in the FEM or the cell size in the FDM) and ${\textstyle \Delta t}$ is the time step used to solve the transient problem.

The values of the characteristic parameters can be found now in order to obtain an a correct numerical solution. The meaning of “correct solution” must be obviously properly defined. Ideally, this would be a solution giving “exact” values at a discrete number of points (i.e. the nodes in a FE mesh). This is infortunatelly impossible for practical problems (with the exception of very simple 1D and 2D cases) and, in practice, ${\textstyle h}$ and ${\textstyle \delta }$ are computed making use of some chosen optimality rule, such as ensuring that the error of the numerical solution diminishes for appropriate values of the characteristic parameters [2,12,13]. This suffices in practice to obtain physically sound (stable) numerical results for any range of the physical parameters of the problem, always within the limitation of the discretization method chosen.

The concept of discretization of the FIC governing equations is explained in more detail with an example in the next section.

4 FINITE ELEMENT DISCRETIZATION OF THE FIC EQUATIONS. AN EXAMPLE: THE ADVECTIVE-DIFFUSIVE PROBLEM

Let us consider the FIC governing equations for the steady-state advective-diffusive problem defined in vector form for the multidimensional case as

$r-{1 \over 2}\mathbf {h} ^{T}{\boldsymbol {\nabla }}r=0\quad {\hbox{in }}\Omega$

(16)

with

$\phi -{\bar {\phi }}=0\quad {\hbox{on }}\Gamma _{\phi }$

(17a)

$\mathbf {n} ^{T}\mathbf {D} {\boldsymbol {\nabla }}\phi +{\bar {\mathbf {q} }}-{1 \over 2}\mathbf {h} ^{T}\mathbf {n} r=0\quad {\hbox{on }}\Gamma _{q}$

(17b)

with

$r:=-\mathbf {v} ^{T}{\boldsymbol {\nabla }}\phi +{\boldsymbol {\nabla }}^{T}\mathbf {D} {\boldsymbol {\nabla }}\phi +Q$

(18)

In above equations ${\textstyle {\boldsymbol {h}}}$ is the characteristic length vector, ${\textstyle {\boldsymbol {\nabla }}}$ is the gradient vector, ${\textstyle \mathbf {D} }$ is the diffusivity matrix, ${\textstyle \mathbf {n} }$ is the normal vector and ${\textstyle \mathbf {v} }$ is the velocity vector. As usual ${\textstyle \Gamma _{\phi }}$ is the Dirichlet boundary where the unknown is prescribed to a fixed value ${\textstyle {\bar {\phi }}}$.

A finite element interpolation of the unknown ${\textstyle \phi }$ can be written as

$\phi \simeq {\hat {\phi }}=\sum N_{i}{\hat {\phi }}_{i}$

(19)

where ${\textstyle N_{i}}$ are the shape functions and ${\textstyle {\hat {\phi }}_{i}}$ are the nodal values of the approximate function ${\textstyle {\hat {\phi }}}$ [10].

Application of the Galerkin FE method to Equations (12)-(13b) gives, after integrating by parts the term ${\textstyle {\boldsymbol {\nabla }}r}$ (and neglecting the space derivatives of ${\textstyle \mathbf {h} }$) [2,10]

$\int _{\Omega }N_{i}{\hat {r}}d\Omega -\int _{\Gamma _{q}}N_{i}(\mathbf {n} ^{T}\mathbf {D} {\boldsymbol {\nabla }}{\hat {\phi }}+{\bar {q}}_{n})d\Gamma +\sum \limits _{e}{1 \over 2}\int _{\Omega ^{e}}\mathbf {h} ^{T}{\boldsymbol {\nabla }}N_{i}{\hat {r}}d\Omega =0$

(20)

The last integral in Equation (20) has been expressed as the sum of the element contributions to allow for interelement discontinuities in the term ${\textstyle {\boldsymbol {\nabla }}{\hat {r}}}$, where ${\textstyle {\hat {r}}=r({\hat {\phi }})}$ is the residual of the FE solution of the infinitesimal equations.

Note that the residual terms have disappeared from the Neumann boundary ${\textstyle \Gamma _{q}}$. This is due to the consistency of the FIC terms in Equation (17b).

Integrating by parts the diffusive terms in the first integral of (20) leads to

$\int _{\Omega }\left[N_{i}\mathbf {v} ^{T}\nabla {\hat {\phi }}+{\boldsymbol {\nabla }}^{T}N_{i}\mathbf {D} {\boldsymbol {\nabla }}{\hat {\phi }}\right]d\Omega -\sum \limits _{e}{1 \over 2}\int _{\Omega ^{e}}\mathbf {h} ^{T}{\boldsymbol {\nabla }}N_{i}{\hat {r}}d\Omega -\int _{\Omega }N_{i}Qd\Omega +\int _{\Gamma _{q}}N_{i}{\bar {q}}_{n}d\Gamma =0$

(21)

In matrix form

$\mathbf {K} \mathbf {a} =\mathbf {f}$

(22)

Matrix ${\textstyle \mathbf {K} }$ and vector ${\textstyle \mathbf {f} }$ are assembled from the element contributions given by

$K_{ij}^{e}=\int _{\Omega ^{e}}[N_{i}\mathbf {v} ^{T}{\boldsymbol {\nabla }}N_{j}+{\boldsymbol {\nabla }}^{T}N_{i}(\mathbf {D} +{1 \over 2}\mathbf {h} ^{T}\mathbf {v} ){\boldsymbol {\nabla }}N_{j}]d\Omega -{1 \over 2}\int _{\Omega ^{e}}\mathbf {h} ^{T}{\boldsymbol {\nabla }}N_{i}{\boldsymbol {\nabla }}(\mathbf {D} {\boldsymbol {\nabla }}N_{j})d\Omega$

(23)

$f_{i}^{e}=\int _{\Omega ^{e}}[N_{i}+{1 \over 2}\mathbf {h} ^{T}{\boldsymbol {\nabla }}N_{i}]Qd\Omega -\int _{\Gamma _{q}^{e}}N_{i}{\bar {q}}_{n}d\Gamma$

(24)

Note that the method introduces in ${\textstyle {\boldsymbol {K}}}$ an additional diffusivity matrix given by ${\textstyle {1 \over 2}\mathbf {h} ^{T}\mathbf {v} }$. Also the second integral of Equation (23) vanishes for linear approximations. The same happens with the second term of the first integral of Equation (24) when ${\textstyle N_{i}}$ is linear and ${\textstyle Q}$ is constant. The evaluation of these integrals is mandatory in any other case.

4.1 The discrete 1D advective-diffusive problem

The role of the stabilization parameter can be better clarified with a simple 1D steady-state advection-diffusion problem governed by the FIC equation

$r-{h \over 2}{dr \over dx}=0\quad {\hbox{in }}\quad 0\leq x\leq L$

(25)

where ${\textstyle L}$ is the length of the analysis domain and

$r=-v{d\phi \over dx}+k{d^{2}\phi \over dx^{2}}+Q$

(26)

The form of the element stiffness matrix and the element flux vector for the 1D case are obtained by simplification of Eqs.(23) and (24) as

$K_{ij}^{e}=\int _{l^{e}}\left[vN_{i}{\partial N_{j} \over \partial x}+\left(k+{vh \over 2}\right){\partial N_{i} \over \partial x}{\partial N_{j} \over \partial x}\right]dx-{1 \over 2}\int _{l^{e}}h{\partial N_{i} \over \partial x}k{\frac {\partial ^{2}N_{j}}{\partial x^{2}}}dx$

(27a)

$f_{i}^{e}=\int _{l^{e}}\left(N_{i}+{h \over 2}{\partial N_{i} \over \partial x}\right)Q\,dx-{\bar {q}}_{L}$

(27b)

For simplicity we will assume ${\textstyle Q=0}$ ${\textstyle \phi =0}$ at ${\textstyle x=0}$ and ${\textstyle \phi ={\bar {\phi }}}$ at ${\textstyle x=L}$.

We will solve the problem with the simplest mesh of two linear finite element of dimensions ${\textstyle l^{e}=L/2}$. The stencil for this problem is

${v \over 2}(\phi _{3}-\phi _{1})+\left(k+{vh \over 2}\right)\left({-\phi _{3}+2\phi _{2}-\phi _{1}) \over l^{e}}\right)=0$

(28)

The solution for the central node is obtained making ${\textstyle \phi _{1}=0}$ and ${\textstyle \phi _{3}={\bar {\phi }}}$ in Eq.(28) as

$\phi _{2}=\left[2(1+\alpha \gamma )\right]^{-1}(1-\gamma +\alpha \gamma ){\bar {\phi }}$

(29)

where ${\textstyle \gamma =\displaystyle {vl^{e} \over 2k}}$ is the element Peclet number and ${\textstyle \alpha =\displaystyle {h \over l^{e}}}$ is a dimensionless characteristic parameter.

We note that for ${\textstyle \alpha =0}$ (i.e. the discrete solution of the standard infinitessimal equations) ${\textstyle \phi _{2}={1 \over 2}(1-\gamma ){\bar {\phi }}}$ which gives non physical (unstable) negative values of ${\textstyle \phi _{2}}$ for ${\textstyle \gamma >1}$. A critical value of ${\textstyle \alpha }$ can be deduced from Eq.(29) ensuring that ${\textstyle \phi _{2}\geq 0}$ for all range of the parameters ${\textstyle u,k}$ and ${\textstyle l}$. This gives

$\alpha \geq 1-{1 \over \gamma }$

(30)

which is the well known expression of the critical stabilization parameter for this problem [10,11].

The value of ${\textstyle \alpha }$ given by Eq.(30) allow us to obtain the best possible physically meaningful solution for the problem. Indeed for this simple case we could aim to obtain the exact analytical solution at node ${\textstyle \phi _{2}}$. This is simply granted is ${\textstyle \alpha }$ is taken as ${\textstyle \alpha =\coth \gamma -1/\gamma }$ which can be again deduced from Eq.(28) [6,10]. Note that the values of this expression for ${\textstyle \alpha }$ and those of Eq.(30) are quite similar for ${\textstyle \gamma >2}$ [10].

The merit of the expression of ${\textstyle \alpha }$ of Eq.(30) is that it has been deduced with no previous knowledge of the exact solution. Indeed, the approximated solution within the element adjacent to the boundary at ${\textstyle x=L}$ will differ substantially from the exact one: the numerical solution is linear whereas the analytical solution gives a boundary layer adjacent to ${\textstyle x=L}$. The stabilized FIC numerical solution can however be taken now as the starting point to obtain a refined solution giving a more accurate description of the physical problem within the element where the boundary layer is located. This can be obtained by mesh refinement or either by enriching the approximation within that element in an adaptive manner. Here a number of possibilities can be explored using mesh refinement, hierarchical approximations, ${\textstyle p}$-refinement or enrichment techniques, etc. Some of these options are discussed in a next section.

4.2 The characteristic length vector

From the FIC expressions in Section 4 we note that in multidimensional problems the space stabilization parameters can be grouped in a vector ${\textstyle {\boldsymbol {h}}}$, where ${\textstyle {\boldsymbol {h}}}$ has the space dimensions of the problem (i.e. ${\textstyle \mathbf {h} =[h_{1},h_{2},h_{3}]^{T}}$ for 3D situations). Computation of vector ${\textstyle {\boldsymbol {h}}}$ is a crucial step as the quality of the stabilized solution depends on the choice of the module and direction of ${\textstyle {\boldsymbol {h}}}$.

We could, for instance, assume that the direction of vector ${\textstyle {\boldsymbol {h}}}$ is parallel to the velocity ${\textstyle {\boldsymbol {v}}}$, i.e. ${\textstyle \mathbf {h} =h{\mathbf {v} \over \vert \mathbf {v} \vert }}$ where ${\textstyle h}$ is a characteristic length. Under these conditions, Equation (20) reads

$\int _{\Omega }N_{i}{\hat {r}}d\Omega -\int _{\Gamma _{q}}N_{i}(\mathbf {n} ^{T}\mathbf {D} {\boldsymbol {\nabla }}{\hat {\phi }}+{\bar {q}}_{n})d\Omega {+}\sum \limits _{e}\int _{\Omega ^{e}}{h \over 2\vert \mathbf {v} \vert }\mathbf {v} ^{T}{\boldsymbol {\nabla }}N_{i}{\hat {r}}d\Omega =0$

(31)

Equation (31) coincides precisely with the so called Streamline-Upwind-Petrov-Galerkin (SUPG) method [2,10,20]. The ratio ${\textstyle \displaystyle {h \over 2\vert \mathbf {v} \vert }}$ has dimensions of time and it is termed element intrinsic time parameter ${\textstyle \tau }$.

It is important to note that the SUPG expression is a particular case of the more general FIC formulation. This explains the limitations of the SUPG method to provide stabilized numerical results in the vicinity of sharp gradients of the solution transverse to the flow direction. In general, the adequate direction of ${\textstyle \mathbf {h} }$ is not coincident with that of ${\textstyle \mathbf {v} }$ and the components of ${\textstyle \mathbf {h} }$ introduce the necessary stabilization along the streamlines and the transverse directions to the flow. In this manner, the FIC method reproduces the best-features of the so-called stabilized discontinuity-capturing schemes [5,12,13].

The computation of the characteristic vector ${\textstyle {\boldsymbol {h}}}$ is a topioc which fails outside the scope of this paper. We will just mention that in practice it is convenient to split ${\textstyle {\boldsymbol {h}}}$ as

$\mathbf {h} =\mathbf {h} _{s}+\mathbf {h} _{t}$

(32)

where ${\textstyle \mathbf {h} _{s}}$ and ${\textstyle \mathbf {h} _{t}}$ are called streamline and transverse characteristic lenght vectors. A useful option is to take

$\mathbf {h} _{s}=h_{s}{\mathbf {v} \over \vert \mathbf {v} \vert }\qquad {\hbox{and}}\quad \mathbf {h} _{t}=h_{t}{{\boldsymbol {\nabla }}\phi \over \vert {\boldsymbol {\nabla }}\phi \vert }$

(33)

The characteristic lengths ${\textstyle {h}_{s}}$ and ${\textstyle {h}_{t}}$ are computed at element level by imposing that the residual of the numerical solution diminishes over each element [2,5,12,13]. In practice, these lengths can be computed for each element as the maximum value of the scalar product between the element sides and the velocity vector (for ${\textstyle h_{s}}$) and the gradient vector (for ${\textstyle h_{t}}$) [14,15,16,17].

Note that the gradient of ${\textstyle \phi }$ in the expression of ${\textstyle \mathbf {h} _{t}}$ introduces a non linearity in the computation process which is typical of discontinuity capturing techniques. A procedure to linealize the expression of the ${\textstyle \mathbf {h} _{t}}$ in element next to boundary layers by approximating ${\textstyle {\boldsymbol {\nabla }}\phi }$ by the normal vector to the boundary is presented in [5].

5 INTERPRETATION OF THE DISCRETE SOLUTION OF THE FIC EQUATIONS

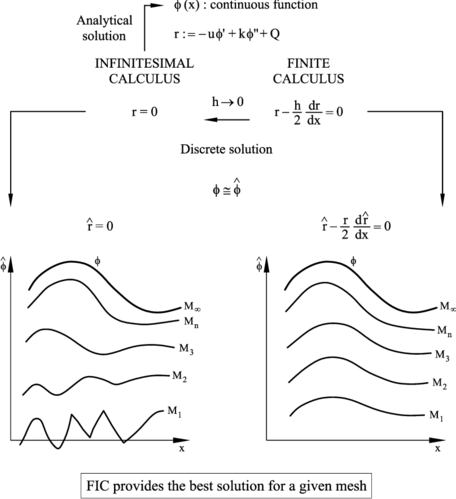
Let us consider the solution of a physical problem in a space domain ${\textstyle \Omega }$, governed by a differential equation ${\textstyle r(\phi )=0}$ in ${\textstyle \Omega }$ with the corresponding boundary conditions. The “exact” (analytical) solution of the problem will be a function giving the sought distribution of ${\textstyle \phi }$ for any value of the geometrical and physical parameters of the problem. Obviously, since the analytical solution is difficult to find (practically impossible for real situations), an approximate numerical solution is found ${\textstyle \phi \simeq {\hat {\phi }}}$ by solving the problem ${\textstyle {\hat {r}}=0}$, with ${\textstyle {\hat {r}}=r({\hat {\phi }})}$, using a particular discretization method (such as the FEM). The distribution of ${\textstyle \phi }$ in ${\textstyle \Omega }$ is now obtained for specific values of the geometrical and physical parameters. The accuracy of the numerical solution depends on the discretization parameters, such as the number of elements and the approximating functions chosen in the FEM. Figure 1 shows a schematic representation of the distribution of ${\textstyle {\hat {\phi }}}$ along a line for different discretizations ${\textstyle M_{1},M_{2},\cdots ,M_{n}}$ where ${\textstyle M_{1}}$ and ${\textstyle M_{n}}$ are the coarser and finer meshes, respectively. Obviously for ${\textstyle n}$ sufficiently large a good approximation of ${\textstyle \phi }$ will be obtained and for ${\textstyle M_{\infty }}$ the numerical solution ${\textstyle {\hat {\phi }}}$ will coincide with the “exact” (and probably unreachable) analytical solution ${\textstyle \phi }$ at all points. Indeed in some problems the ${\textstyle M_{\infty }}$ solution can be found by a “clever” choice of the discretization parameters.

An unstable solution will occur when for some (typically coarse) discretizations, the numerical solution provides non physical or very unaccurate values of ${\textstyle {\hat {\phi }}}$. A situation of this kind is represented by curves ${\textstyle M_{1}}$ and ${\textstyle M_{2}}$ of the left hand side of Figure 1. These unstabilities would disappear by an appropriate mesh refinement (curves ${\textstyle M_{3},M_{4}\cdots }$ in Figure 1) at the obvious increase of the computational cost.

In the FIC formulation the starting point are the modified differential equations of the problem and the corresponding modified boundary conditions as previously described. The modified equations are not useful to find an analytical solution, ${\textstyle \phi (x)}$, for the physical problem. However, the numerical solution of the FIC equation can be readily found. Moreover, by adequately choosing the values of the characteristic length parameter ${\textstyle h}$, the numerical solution of the FIC equations will be always stable (physically sound) for any discretization level chosen.

This process is schematically represented in Figure 1 where it is shown that the numerical oscillations for the coarser discretizations ${\textstyle M_{1}}$ and ${\textstyle M_{2}}$ dissapear when using the FIC procedure.

We can therefore conclude the FIC approach allows us to obtain a better numerical solution for a given discretization. Indeed, as in the standard infinitesimal case, the choice of ${\textstyle M_{\infty }}$ will yield the (unreachable) exact analytical solution and this ensures the consistency of the method.

Figure 1: Schematic representation of the numerical solution of a physical problem using standard infinitesimal calculus and finite calculus.

6 MULTISCALE ADAPTIVE FINITE ELEMENT ANALYSIS USING THE FIC FORMULATION

6.1 Adaptive solution by updating the stability parameters

The FIC formulation can be applied in conjunction with any numerical method (say the finite element method) in order to obtain a “correct” solution within the limit of the discretization chosen. The accuracy of the finite element solution depends greatly of the values chosen for the stabilization parameters in the FIC formulation. Indeed if these values are taken equal to zero, an unstable non physical solution is obtained in many cases. The space and time stabilization parameters ${\textstyle h_{i}}$ and ${\textstyle \delta }$ in the FIC formulation can be given adequate values such that the desired accuracy in the numerical solution is achieved. In [2,5,12,13] a procedure is presented to adaptively compute the values of the stabilization parameters so that the element error, measured in terms of the average residual of the governing equations over the element, diminishes until it reaches a prescribed value. Other procedures to compute the ${\textstyle h_{i}}$ and ${\textstyle \delta }$ parameters can be devised, all aiming to obtain the “best” possible nodal solution for a given mesh.

Once this solution has been obtained, the problem of accurately reproducing sharp gradients in selected zones remains. Some methods aiming to solve this problem are proposed next.

The nodal finite element values computed with the stabilized FIC formulation can be taken as the starting point for obtaining an enhanced solution in zones where high gradients of the sought variables occur. Three options will be considered here: mesh adaptivity, hierarchical shape functions and enriched interpolations incorporating the shape of the analytical solution.

6.2 Mesh refinement

This is the more standard procedure, although it is still unpractical for many practical 3D problems involving complex geometries. The mesh adaption process can be based on mesh regeneration or mesh enrichment procedures. The adaptivity strategy can use global or local error estimation based on adequate error norms. Details of mesh adaptivity procedures based on different error measures can be found elsewhere and will not be discussed here [10,21,22]. Given the intrinsic difficulties for modifying the meshes for 3D problems we will favour the two procedures described next versus the mesh adaptivity process.

6.3 Hierarchical interpolation

The nodal values provided by the FIC method can be considered “correct” (in the sense that they are physically sound) whithin the limitations of the mesh discretization chosen. A procedure to obtain an enhanced approximation within a particular element, or a patch of elements, is to introduce hierarchical interpolations in the selected elements. The hierarchical interpolation can be simply written for an individual element

$\phi =\sum \limits _{i=1}^{n}N_{i}\phi _{i}+\sum \limits _{j=n+1}^{m}N_{j}^{h}a_{j}^{h}$

(34)

where ${\textstyle N_{i}}$ denote the standard shape functions, ${\textstyle \phi _{i}}$ are the nodal values, ${\textstyle N_{j}^{h}}$ are the hierarchical shape functions and ${\textstyle a_{j}^{h}}$ are the hierarchical values. As usual, the functions ${\textstyle N_{j}^{h}}$ should vanish along the element edges. The simplest hierarchical interpolations (satisfying orthogonality conditions) can be based on Legendre polynomials or on standard trigonometric functions [10]. More advanced hierarchical finite element interpolations based on the concept of the partition of unity can be effectively used [23].

A good approximation of the hierarchical variables can be obtained taking the nodal values obtained with the FIC numerical solution as fixed. A simple set of equations needs to be solved at each element level only for the hierarchical variables ${\textstyle a_{j}^{h}}$. Indeed, this computation can be performed within a more general iterative procedure, where the nodal variables and the hierarchical values are updated in an staggered manner.

6.4 Enrichment interpolation using an approximation to the analytical shape of the solution

An effective procedure to obtain an enhanced solution starting with the FIC nodal values is to use a local interpolation over each element injecting into the interpolating functions a good approximation to the shape of the sought solution. This can be effectively carried out by using as the new approximation the free-space solution of the homogeneous and constant-coefficient version of the standard governing partial differential equations. A procedure of this kind has been used by Farhat et al. [24] who added the enriched field to the initial polynomial field. The resulting field is not continuous in this case and continuity is enforced by means of Lagrange multipliers.

In this work it is proposed to apply the “analytical” enrichment in order to obtain an enhanced solution within the selected elements where high gradients occur, while keeping the nodal values given by the FIC solution fixed.

Indeed the three adaptive procedures above suggested can be combined and the efficiency of the different alternatives should be investigated and tested in practice.

The concepts explained are clarified next with two simple examples of application.

7 EXAMPLES

7.1 1D advective-diffusive problem

We will consider the simplest 1D advective-diffusive problem governed by Eqs.(25) and (26) with boundary conditions ${\textstyle \phi =0}$ at ${\textstyle x=0}$, ${\textstyle \phi ={\bar {\phi }}}$ at ${\textstyle x=L}$. Again for simplicity we will consider a mesh of two linear 1D elements.

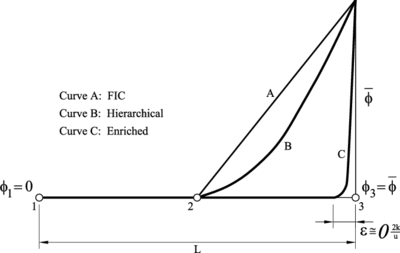
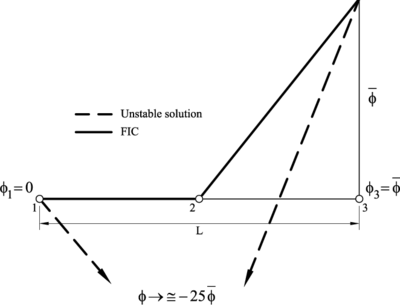
Figure 2 shows the unstable numerical solution obtained for the case of ${\textstyle \alpha =0}$ (Galerkin) and the “correct” FIC solution for a critical value of ${\textstyle \alpha =(1-{1 \over \gamma })(1+\varepsilon )}$ with ${\textstyle \varepsilon =10^{-10}}$. Note that the numerical solution, although nodally correct, is far from the “exact” analytical distribution giving a boundary layer next to the end node at ${\textstyle x=L}$.

Figure 2: 1D advection-diffusion problem solved with two linear elements ($\gamma =50$). Unstable solution (- - -) obtained for $\alpha =0$ (Galerkin). Stabilized solution (–-) obtained with the FIC method for $\alpha =(1+10^{-10})(1-{1 \over \gamma })$

We will consider next a hierarchical approximation of the solution over the element 2–3 using Eq.(34) with hierarchical interpolation functions defined as

$N_{j}^{h}=\sin j{\pi \over 2}(1+\xi )\quad {\hbox{with }}-1\leq \xi \leq 1$

(35)

Note that ${\textstyle N_{j}^{h}}$ vanishes for the element ends located at ${\textstyle \xi =\pm 1}$. Figure 3 shows the approximation of the numerical solution over the element 2–3 obtained for ${\textstyle m=3}$ keeping the nodal values given by the original FIC solution fixed. The improvement in the solution is noticeable. An almost identical solution is obtained if the value for ${\textstyle \phi _{2}}$ is recomputed until convergence is achieved. A similar improvement is obtained using Legendre polynomials up to a quartic order.

A considerable better solution over the element 2–3 can be obtained by using for approximating the unknown within this element the following interpolation

$\phi =\sum \limits _{i=1}^{2}P_{i}(\xi )\phi _{i}^{(e)}$

(36)

with ${\textstyle P_{1}=\displaystyle {e^{\gamma \xi }-e^{\gamma } \over e^{-\gamma }-e^{\gamma }}\quad ,\quad P_{2}=\displaystyle {e^{-\gamma }-e^{\gamma \xi } \over e^{-\gamma }-e^{\gamma }}}$.

The new shape functions ${\textstyle P_{1}}$ and ${\textstyle P_{2}}$ are obtained from the analytical solution of the homogeneous differential equation (${\textstyle r=0}$) for constant values of ${\textstyle u}$ and ${\textstyle k}$. Note that ${\textstyle P_{i}(\xi _{j})=1}$ for ${\textstyle i=j}$ and ${\textstyle =0}$ for ${\textstyle i\not =j}$.

Application of the approximation (36) over the element 2–3 with ${\textstyle \phi _{2}^{(e)}={\bar {\phi }}}$ and ${\textstyle \phi _{1}^{(e)}=\phi _{2}}$, where ${\textstyle \phi _{2}}$ is the nodal value at node 2 obtained with the FIC formulation, reproduces accurately the boundary layer within this element, as expected (see Figure 3). Recall that Eq.(36) has been applied “a posteriori”, once the nodal value at node 2 has been found using the original linear interpolation and the FIC method with the critical value of ${\textstyle \alpha }$ above given.

Figure 3: 1D advection-diffusion problem solved with two linear elements. Initial stabilized FIC solution (curve A). Enhanced solutions over element 2–3 using a hierarchical trigonometric interpolation (curve B) and an exponential interpolation (curve C)

This simple example shows that the nodal values provided by the FIC method are a good starting point for obtaining an enhanced numerical solution in the vecinity of sharp gradients. The results from this simple example indicate that it suffices with a straightforward “a posteriori” analysis to obtain a better solution in these regions using either a hierarchical interpolation or (ideally) an approximation enriched with the shape of the solution of the homogeneous equation for constant coefficients.

7.2 2D stationary convection-diffusion problem with diagonal velocity, zero source and uniform Dirichlet conditions

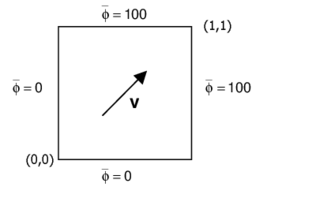
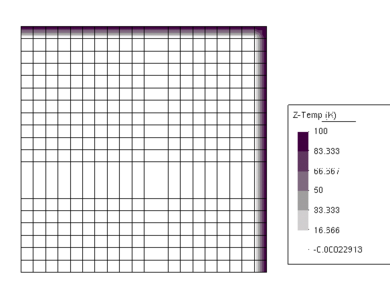
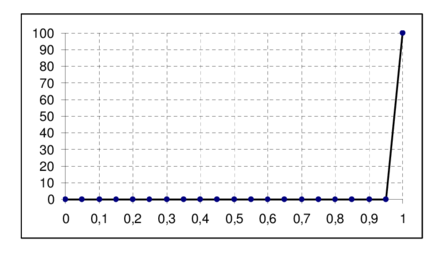
Figure 4: Convection-diffusion problem with uniform Dirichlet conditions. One step solution. Distribution of $\phi$ along the lines $AA'$ and $BB'$

The steady-state convection-diffusion equation is solved in a domain of unit size (Figure 4) with

$k_{x}=k_{y}=1\quad ,\quad \mathbf {v} =10^{10}[1,1]^{T}\quad ,\quad Q=0$

(37)

The following Dirichlet conditions are assumed

$\phi =0\quad {\hbox{on the lines }}\quad x=0\quad {\hbox{and}}\quad y=0$

$\phi =100\quad {\hbox{on the lines}}\quad x=1\quad {\hbox{and}}\quad y=1$

The expected solution is a uniform distribution of ${\textstyle \phi =0}$ over the domain except in the vecinity of the boundaries ${\textstyle x=1}$ and ${\textstyle y=1}$ where a boundary layer is formed.

The domain is discretized with a uniform mesh of 400 four node quadrilaterals (Figure 4).

The solution has been obtained in one single step using the value of ${\textstyle \mathbf {h} }$ given by Eqs.(32) and (33) approximating the gradient of ${\textstyle \phi }$ in the elements next to the outflow boundaries by the normal vector. For details see [5]. Figure 4 shows that the sharp gradients expected are perfectly captured over the boundary elements without any oscillation.

An enhanced solution over the elements adjacent to the outflow boundaries can now be obtained using hierarchical interpolations or exponential interpolations similarly as described for the 1D example in the previous section. The efficiency of these procedures is similar to that shown in Figure 4 for the 1D case giving in both cases an enhanced reproduction of the boundary layer within the elements adjacent to the lines ${\textstyle x=1}$ and ${\textstyle y=1}$.

8 POSSIBILITIES OF FINITE CALCULUS FOR STRAIN LOCALIZATION

The FIC method introduces naturally higher order derivative terms of the displacements in the equilibrium equations. These terms resemble those introduced by the Cosserat model [25] and the so called “non local” constitutive models [25,26,27,28,29]. These models are typically used in order to preserve the ellipticity of the solid mechanics equations in the presence of localized high displacement gradient zones, such as shear bands and fracture lines.

For instance, the FIC governing equations for a simple 1D bar can be written (in absence of external body forces) as [5]

${\partial N \over \partial x}-{h \over 2}{\partial ^{2}N \over \partial x^{2}}=0$

(38)

where ${\textstyle N}$ is the axial force.

The relationship between the axial force and the elongation ${\textstyle \varepsilon =\displaystyle {du \over dx}}$ in the softening branch can be written in incremental form as

$\delta N=-\vert E_{T}\vert \delta \varepsilon =-\vert E_{T}\vert {d(\delta u) \over dx}$

(39)

where ${\textstyle E_{T}}$ is the tangent modulus of the material and ${\textstyle \delta u}$ is the displacement increment.

Substituting Equation (39) into (38) gives

${d^{2}(\delta u) \over dx^{2}}-{h \over 2}{d^{3}(\delta u) \over dx^{3}}=0$

(40)

Equation (40) resembles the governing equations derived by Lasry and Belytschko [26] using localization limiters in the stress-strain relationship and by Schreier and Chen [27] using gradient-dependent plasticity constitutive models.

Many similarities can be found between the governing equations derived by the FIC method and those resulting from the non local constitutive models [30]. Although in some situations the resulting governing differential equations are the same, the basic difference between the two approaches is that non local constitutive models aim to enhance the constitutive equation by adding new terms (typically strain gradient terms), whereas the FIC method defines a new equilibrium equation applicable to all the discrete scales while preserving the features of the constitutive equation. This opens a world of possibilities for the FIC equations in solid mechanics to solve strain localization problems using standard constitutive models.

9 CONCLUSIONS

The paper has presented some basic ideas to combine the finite calculus (FIC) method with adaptive finite element strategies in order to solve problems where sharp gradients of the solution occur in localized zones. The key argument of the procedures proposed is that the discretized FE solution of the FIC equations leads to nodal values which are “as good as possible” by virtue of the adequate selection of the stabilization parameters. The FIC solution can be used as the starting point to compute an “a posteriori” enhanced solution over selected elements using hierarchical or enriched approximations. Indeed, mesh adativity can be included here as a third alternative and the combination of the different procedures opens new areas of research.

The same ideas can be used to solve a wide class of multiscale problems in mechanics where the solution changes in several orders of magnitude in specific regions.

REFERENCES

[1] Nottale, L. Relativity in all its states. (in French), Hachette, 1998.

[2] Oñate E. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Methods Appl. Mech. Engrg. 1998; 151:1-2:233–267.

[3] Oñate E, García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in Comput. Methods Appl. Mech. Engrg. 2001; 191:6-7:635-660.

[4] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Methods Appl. Mech. Engrg. 2000; 182:1–2:355–370.

[5] Oñate E. Possibilities of finite calculus in computational mechanics. To be published in Int. J. Num. Meth. Engng., 2003.

[6] Oñate E, Manzan M. Stabilization techniques for finite element analysis of convection diffusion problems. In Comput. Anal. of Heat Transfer, WIT Press, G. Comini and B. Sunden (Eds.), 2000.

[7] Oñate E, Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids 1999; 31:203–221.

[8] Oñate E, Rojek J, Taylor RL, Zienkiewicz OC. Finite calculus formulation for analysis of incompressible solids using linear triangles and tetrahedra. Submitted to Int. J. Num. Meth. Engng., May 2002.

[9] Oñate E, Rojek J, Taylor RL, Zienkiewicz OC. Linear triangles and tetrahedra for incompressible problems using a finite calculus formulation. In European Conference on Computational Mechanics (ECCM2001), Cracow, Poland, 26–29 June, 2001.

[10] Zienkiewicz OC, Taylor RL. The finite element method. 5th Edition, 3 Volumes, Butterworth–Heinemann, 2000.

[11] Hirsch C. Numerical computation of internal and external flow, J. Wiley, Vol. 1 1988, Vol. 2, 1990.

[12] Oñate E, García J, Idelsohn SR. Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. Int. J. Num. Meth. Fluids 1997;25:1385–1407.

[13] Oñate E, García J, Idelsohn SR. An alpha-adaptive approach for stabilized finite element solution of advective-diffusive problems with sharp gradients. New Advances in Adaptive Comput. Methods in Mech., Elsevier, P. Ladeveze, J.T. Oden (Eds.), 1998.

[14] García J, Oñate E. An unstructured finite element solver for ship hydrodynamics. J. Appl. Mechanics 2002.

[15] Oñate E, García J, Bugeda G, Idelsohn SR. A general stabilized formulation for incompressible fluid flow using finite calculus and the FEM. In Towards a New Fluid Dynamics with its Challenges in Aeronautics, J. Periaux, D. Champion, O. Pironneau and Ph. Thomas (Eds.), CIMNE, Barcelona, 2002.

[16] Oñate E, García J, Idelsohn SR. Ship Hydrodynamics. Encyclopedia of Computational Mechanics, T. Hughes, R. de Borst and E. Stein (Eds.), J. Wiley, 2004 (to be published).

[17] Oñate E, Taylor RL, Zienkiewicz OC, Rojek J. A residual correction method based on finite calculus. FEMClass of 42 Meeting, 30–31 May, Ibiza, 2002, www.congress.cimne.upc.es/femclass42. To be published in Engineering Computation.

[18] Oñate E, Idelsohn SR, Zienkiewicz OC, Taylor RL. A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J. Num. Meth. Engng. 1996;39:3839–3866.

[19] Oñate E, Sacco C, Idelsohn S. A finite point method for incompressible flow problems. Computing and Visualization in Science 2000; 2:67–75.

[20] Brooks A, Hughes TJR. Streamline upwind/Petrov-Galerkin formulation for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg. 1982; 32:199–259.

[21] Ladeveze P., Pelle J. La maïtrise du calcul en mecanique linearise et non lineaire. Hermes, 2001.

[22] Oñate E, Bugeda G. A study of mesh adaptivity criteria in adaptive finite element computations. Engng. Computations 1993; 10:307–321.

[23] Taylor RL, Zienkiewicz OC, Oñate E. A hierarchical finite element method based on the partition of unity. Comput. Methods Appl. Mech. Engrg. 1998; 152:73–84

[24] Farhat C, Harari I, Franca L. The discontinuous enrichment method. Comput. Methods Appl. Mech. Engrg. 2001; 190:6455–6479.

[25] de Borst R. Simulation of strain localization: A reappraisal of the Cosserat continuum. Continuum Computation 1991; 8:317–332.

[26] Larsry D, Belytschko T. Localization limiters in transient problems. Int. J. Solids and Structures 1988; 24:581–597.

[27] Schreier HL, Chen Z. One dimensional softening with localization. ASME J. Appl. Mech. 1980; 53:791–797.

[28] de Borst R. Gradient-dependent plasticity: Formulation and algorithmic aspects. Int. J. Num. Meth. Engng 1992; 35:521–539.

[29] Peric D, Yu J, Owen DRJ. On error estimates and adaptivity in elastoplastic solids: Application to the numerical simulation of strain localization in classical and Cosserat continua. Int. J. Num. Meth. Engng. 1994; 37:1351–1379.

[30] Borja R. Possibilities of the FIC method for strain localization problems. Private communication, 2001.

APPENDIX

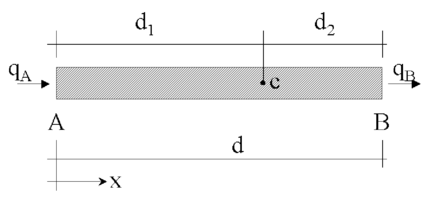
We will consider a convection-diffusion problem in a 1D domain ${\textstyle \Omega }$ of length ${\textstyle L}$. The equation of balance of fluxes in a subdomain of size ${\textstyle d}$ belonging to ${\textstyle \Omega }$ (Figure A1) is written as

$q_{A}-q_{B}=0$

(41)

where ${\textstyle q_{A}}$ and ${\textstyle q_{B}}$ are the incoming and outgoing fluxes at points ${\textstyle A}$ and ${\textstyle B}$, respectively. The flux ${\textstyle q}$ includes both convective and diffusive terms; i.e. ${\textstyle q=v\phi -k{d\phi \over dx}}$, where ${\textstyle \phi }$ is the transported variable (i.e. the temperature in a thermal problem), ${\textstyle v}$ is the velocity and ${\textstyle k}$ is the diffusitivity of the material.

Figure 5: Equilibrium of fluxes in a space balance domain of finite size

Let us express now the fluxes ${\textstyle q_{A}}$ and ${\textstyle q_{B}}$ in terms of the flux at an arbitrary point ${\textstyle C}$ within the balance domain (Figure A.1). Expanding ${\textstyle q_{A}}$ and ${\textstyle q_{B}}$ in Taylor series around point ${\textstyle C}$ up to second order terms gives

$q_{A}=q_{C}-d_{1}{\frac {dq}{dx}}\vert _{C}+{\frac {d_{1}^{2}}{2}}{\frac {d^{2}q}{dx^{2}}}\vert _{C}+O(d_{1}^{3})\quad ,\quad q_{B}=q_{C}+d_{2}{\frac {dq}{dx}}\vert _{C}+{\frac {d_{2}^{2}}{2}}{\frac {d^{2}q}{dx^{2}}}\vert _{C}+O(d_{2}^{3})$

(42)

Substituting Equation (A.2) into Equation (A.1) gives after simplification

${\frac {dq}{dx}}-{\underline {{\frac {h}{2}}{\frac {d^{2}q}{dx^{2}}}}}{\frac {h}{2}}{\frac {d^{2}q}{dx^{2}}}=0$

(43)

where ${\textstyle h=d_{1}-d_{2}}$ and all the derivatives are computed at point ${\textstyle C}$.

Standard calculus theory assumes that the domain ${\textstyle d}$ is of infinitesimal size and the resulting balance equation is simply ${\textstyle {dq \over dx}=0}$. We will relax this assumption and allow the space balance domain to have a finite size. The new balance equation (A.3) incorporates now the underlined term which introduces the characteristic length ${\textstyle h}$. Obviously, accounting for higher order terms in Equation (A2) would lead to new terms in Equation (A.3) involving higher powers of ${\textstyle h}$.

Distance ${\textstyle h}$ in Equation (A.3) can be interpreted as a free parameter depending on the location of point ${\textstyle C}$ within the balance domain. Note that ${\textstyle -d\leq h\leq d}$ and, hence, ${\textstyle h}$ can take a negative value. At the discrete solution level the domain ${\textstyle d}$ should be replaced by the balance domain around a node. This gives for an equal size discretization ${\textstyle -l^{e}\leq h\leq l^{e}}$ where ${\textstyle l^{e}}$ is the element or cell dimension. The fact that Equation (A.3) is the exact balance equation (up to second order terms) for any 1D domain of finite size and that the position of point ${\textstyle C}$ is arbitrary, can be used to derive numerical schemes with enhanced properties simply by computing the characteristic length parameter from an adequate “optimality” rule leading to an smaller error in the numerical solution.

Consider, for instance, Equation (A.3) applied to the 1D convection-diffusion problem. Neglecting third order derivatives of ${\textstyle \phi }$, Equation (A.3) can be rewritten in terms of ${\textstyle \phi }$ as

$-v{\frac {d\phi }{dx}}+\left(k+{\frac {vh}{2}}\right){\frac {d^{2}\phi }{dx^{2}}}=0$

(44)

We see clearly that the FIC method introduces naturally an additional diffusion term in the standard convection-diffusion equation. This is the basis of the popular “artificial diffusion” procedure [10,11] where the characteristic length ${\textstyle h}$ is typically expressed as a function of the cell or element dimension.

Equation (A.3) can be extended to account for source terms. The modified governing equation can then be written in compact form as

$r-{\underline {{\frac {h}{2}}{\frac {dr}{dx}}}}{\frac {h}{2}}{\frac {dr}{dx}}=0$

(45)

with

$r:=-v{\frac {d\phi }{dx}}+{\frac {d}{dx}}\left(k{\frac {d\phi }{dx}}\right)+Q$

(46)

where ${\textstyle Q}$ is the external source. For consistency a “finite” form of the Neumann boundary condition should be used. This can be readily obtained by invoking balance of fluxes in a domain of finite size next to the boundary ${\textstyle \Gamma _{q}}$ where the external flux is prescribed to a value ${\textstyle q_{p}}$. The modified Neumann boundary condition is [2]

$k{\frac {d\phi }{dx}}+q_{p}-{\underline {{\frac {h}{2}}r}}{\frac {h}{2}}r=0\quad {\hbox{at }}\Gamma _{q}$

(47)

The governing equations of the problem are completed with the standard Dirichlet condition prescribing the value of ${\textstyle \phi }$ at the boundary ${\textstyle \Gamma _{\phi }}$.

The underlined terms in Equations (A.5) and (A.7) introduce the necessary stabilization in the discrete solution using whatever numerical scheme.

The time dimension can be simply accounted for the FIC method by considering the balance equation in a space-time slab domain as described in [2,6,7].