Assessment of performance indices of selected gas turbine power plants in Nigeria

Abstract

In this study, performance assessment of selected gas turbine power plants in Nigeria was evaluated using performance indices. The results of the study showed that for the period under review (2006–2010), the percentage shortfalls from the target energy in the selected power plants range from 26.33% to 86.61% as against the acceptable value of 5–10%. The capacity factor of the selected power plants varies from 16.88% to 73.67% as against the international value of 50–80%. The plant use factor varies from 45.89% to 97.03% and the utilization factor varies from 6.31% to 93.074% as against the international best practice of over 95%. From this result, it can be concluded that the generating units were underutilized. This is due to inadequate routine maintenance and equipment fault development. The analyses of reliability indicators revealed that the mean time between failures varies from 5.42 to 378.44 h, the mean time to repair varies from 18.3 to 153.88 h and the plant availability varies from 12.86% to 91.31% as against the Institute of Electrical and Electronics Engineers recommended standard of 99.9%. Evaluation of operating figures of the selected power plants revealed that starting reliability (SR) and operating reliability vary from 71.95% to 93.9% and 5.33% to 55%, respectively. The SR of the selected power plants is low in value compared with standard value of 99.9%. The statistical analysis carried out on plant availability revealed that at 95% confidence level; there is a significant difference in availability of the selected power plants. This indicates differences in their systems installation, operation and maintenance. The performance indicator developed to evaluate the performance indices for the selected stations can also be applicable to other power stations in Nigeria and elsewhere. Measures to improve the performance indices of the plants have been suggested in this paper.

Introduction

The main objective of any power utility in the new competitive environment would be to supply customers with electrical energy as economically as possible with a higher degree of reliability and quality. The ability of the power system to provide an adequate supply of electrical energy is usually designated by the term of reliability. The concept of power-system reliability is extremely broad and covers all aspects of the ability of the system to satisfy the customer requirements [1].

The reliability of an electric power system can be increased by additional system investment. This obviously increases the cost associated with electric power. Power utilities have, therefore, to satisfy two conflicting requirements: (1) supply of electric power at an acceptable level of reliability and (2) supply of electric power at a reasonable cost. Maintaining an acceptable level of reliability at an affordable cost is, therefore, a very important aspect of modern power system management [2].

The performance of a power plant by way of its efficiency and reliability, and other operating factors has definite socioeconomic significance both on the company operating the plant as well as the nation at large. However, without adequate and reliable electricity supply, socioeconomic transformation would remain a mirage [3].

On a global scale, reliable electric power availability has been observed as effective and indispensable machinery for the rapid industrial and economic growth of any nation [4]. Therefore, by its importance in the society and its necessity for national economic growth, electrical energy supply is expected to be available 24 h a day. Based on this importance, it is expected that electric power utilities throughout the world must ensure they meet customer demands at a reasonable level of service reliability.

A modern power system is complex, highly integrated and very large. In order to meet customer demands, the system can be divided into appropriately subsystems or functional areas that can be analyzed separately [5]. These functional areas are generation, transmission and distribution. Reliability studies are carried out individually and in combinations of the three areas. This study work is limited to the evaluation of the generation reliability.

Generation system reliability focuses on the reliability of generators in the whole electric power system where electric power is produced from the conversion process of primary energy (fuel) to electricity before transmission. The generation system is an important aspect of electricity supply chain and it is crucial that enough electricity is generated at every moment to meet demand. Generating units will occasionally fail to operate and the system operator has to make sure that enough reserve is available to be operated when this situation arises [6, 7].

Generating stations form an important and integral part of the overall power system and their reliability is reflected in the reliability of the overall national supply. Reliability of a generating station is a function of the reliability of the constituent-generating units. Accurate estimates of generating unit reliability are needed for generating capacity planning and to aid improved criteria for future designs and operations. Reliability assessment of a generating system is fundamentally concerned with predicting if the system can meet its load demand adequately for the period of time intended [8].

Improving the availability of existing units is as important as improving the reliability expectation of units during the planning phase. The two are mutually supportive; design reliability impacts major changes in existing units, and information about operating availability is important to the system designers in both developing and developed countries.

Power plant availability and the causes of unavailability constitute essential performance indicator for assessing services rendered by generating power plants.

The term reliability as used in the context of a power system has a very wide range of connotations. It is therefore being discussed under two general categories namely: system adequacy and system security [9]. System adequacy relates to the existence of sufficient generators within the system to satisfy the customer load demand or system operational constraints. System adequacy is associated with static conditions of the system and do not include system disturbances [10]. System adequacy is associated with static conditions of the system and do not include system disturbances. System security, on the other hand, relates to the ability of the system to respond to disturbances arising within the system. Therefore, system security is associated with response of the system to whatever perturbation it is subjected to various factors. In this study, the reliability valuations will be focused on the generation system adequacy and will not take into consideration system security.

In a generation system study, the total system generation is examined to determine its adequacy to meet the total system load requirement. This activity is usually termed “generating system adequacy assessment”. The transmission system is ignored in generating system adequacy assessment and is treated as a load point [11]. The main reason of the generating system adequacy assessment is to estimate the generating capacity required to meet the system demand and to have excess capacity to cater for planned and forced outages events.

A failure in a generating unit results in the unit being removed from service in order to be repaired or replaced; this event is known as outage. Such outages can compromise the ability of the system to supply the required load and affect system reliability. An outage may or may not cause an interruption of service depending on the margins of generation provided. Outages also occur when the unit undergoes maintenance or other scheduled work necessary to keep it operating in good condition. A forced outage is an outage that results from emergency conditions, requiring that component is taken out of service immediately. A scheduled or planned outage is an outage that results when a component is deliberately taken out of service, usually for purpose of preventive maintenance or repair [12].

Effective quantitative assessment of power system reliability involves (1) physical appreciation of the system concerned and the modes of system success and failure, (2) suitable mathematical models for the systems under consideration, (3) fast and reliable computing capability and (4) realistic failure and repair statistics for the relevant system components [13]. The failure and repair statistics are usually obtained from past operating and outage data of comparable components and subcomponents in the system. These data must be collected by the utilities concerned for a reasonable length of time before any meaningful conclusion can be drawn from them.

Generation system reliability concentrates on the performance of the generators where fuel is converted to electricity before entering the transmission system. Generators are subjected to forced outages or reduction in available capacity, which can affect the system reliability and hence must be evaluated. System reliability is commonly interpreted as the probability of that system staying in the operating state, performing its intended purpose adequately for a period of time without failures under required conditions [14].

In recent times, generation reliability/adequacy study has received widespread interest [7-10, 14]. In generation/adequacy study, the use of deterministic reliability indices in terms of generating reserve capacity is now considered obsolete [15]. Probabilistic indices such as loss of load probability (LOLP), loss of load expectation (LOLE), frequency and duration (F and D) approach, loss of energy expectation (LOEE), availability factor (AF) and forced outage rates (FOR) (unavailability factor) etc. are used. These are the convolution of the generation (supply) model and the load (demand) model. They are the global reliability indices for generation reliability studies [16].

A general approach to an electric power-generating system reliability assessment is to determine one or a number of its reliability indices. A reliability index is defined as a quantity that measures and quantifies some aspects of system reliability performance [17]. A number of indices have been introduced in reliability studies over the past years to assist reliability evaluations and predictions. Among these are frequency and duration (F and D) approach, AF, mean time between failures (MTBF), frequency of failure/failure rate (F), repair rate (μ), operating figures, LOLP and LOLE. These are referred to as probabilistic indices. Reliability indices are extremely useful as it quantifies the reliability of the system, hence making the assessment more meaningful. They are used to assess the reliability performance of a generation system against some predetermined criteria of reliability standards. In this study, the reliability indices employed are AF, MTBF, FOR, frequency of failure/failure rate (F), operating figures, and repair rate (μ). These indices are used not only because of their easy and direct computation but also give information in detail about performance of the power-generating system.

In the past two decades, the power demand in Nigeria has been on the increase while available generating capacity remained largely static or even showing a decreasing long-term trend. The consequence of this was to load shed in order to ensure system stability (maintain equilibrium between available generation and selective demand).

Since 1999, electricity generation plants have been operating well below their capacity with available capacity barely surpassing half the installed capacity. It was observed that between 1999 and 2005, average plant availability was about 50%, significantly short of international standards of over 95%. The sector witnessed a low in 2001 when available capacity stood at 1750 MW when only 19 of the 79 installed units were functional [18, 19].

Due to the low availability of generating plants, virtually all the plants in the country operate as base-load plants. The performance of other key indicators such as the capacity factor (CF) and the load factor (LF) has also not been encouraging.

Based on the present status of gas turbine (GT) power plants in Nigeria, there is urgent need for assessment of the plants for performance improvement. The focus of this research work is to assess the performance, reliability and availability of the selected GT power plants in Nigeria. In this research work, performance assessment of the selected GT power plants in Nigeria is carried out by using failure and repair statistics (performance statistics).

The prime objectives of the study are: (1) to evaluate the performance of selected GT power plants in Nigeria over a period of 6 years (2005– 2010); (2) to establish significant difference in power availability in the selected power plants using performance statistics analysis and (3) to proffer recommendations to improve electric power generation in selected GT stations in particular, with the hope that other power stations (state owned and private-owned) would benefit from the outcome of this study.

Materials and Methods

Selected power plants for study

Most of the general data used in the work were collected from the Power Holding Company Nigeria Plc (PHCNs) and the generating stations at Afam, Ughelli, and from IPPs generating station of AES in Egbin. A total of 11 different units of GTs were selected from all the stations. That is, from AES – 3 GT units, Afam – 4 GT units, and Ughelli – 4 GT units. The three power stations are the main stations supplying over 60% of electrical energy to the national grid system.

Presentation of data

Operating data for GT units in the energy utility sector, Afam, Delta, and AES power stations were collected from the daily turbine control log sheet.

The data collected from the GT stations included such information as the following:

• Operating figures
• Number of operating hours per year
• Shutdown hours per year for compulsory or scheduled maintenance
• Unscheduled shutdown hours per year (and reasons)
• Number of starts (in a stated period, say, annually)
• Number of trips during starts (in a stated period, say, annually)
• Number of trips during operation (in a stated period, say, annually)
• Starting reliability
• Operating reliability
• Average number of operating hours between 2 trips during operation
• Average number of operating hours between 2 successful starts

Tables 1-3 show the unit energy generated and operating hours for the selected GT power plants for the period of 2005–2010. Table 4 shows the average unit operating figures for the selected GT power plants.

Table 1. Unit energy generated and operating hours for selected gas turbine power plant: Delta power plant

Year	Energy generated (MWH)				Operating hours				Expected maximum energy (MWH)a
	GT 9 (DEL1)	GT10 (DEL2)	GT18 (DEL3)	GT20 (DEL4)	GT 9 (DEL1)	GT 10 (DEL2)	GT 18 (DEL3)	GT 20 (DEL4)	GT 9 (DEL1)	GT 10 (DEL2)	GT 18 (DEL3)	GT 20 (DEL4)
a values were computed by the authors using the formula: unit installed capacity × operating hours in a year
2005	138,542.20	143,265.15	450,520.00	538,245.00	7053.30	6251.25	6236.15	6932.10	176,332.50	156,281.25	623,615.00	693,210.00
2006	141,746.70	142,365.90	559,569.00	645,377.00	7254.50	5868.70	7525.00	6830.00	181,362.50	146,717.50	752,500.00	683,000.00
2007	140,530.40	128,423.60	636,488.00	450,475.50	7141.40	6916.80	6998.70	5691.00	188,535.00	172,920.00	699,870.00	569,100.00
2008	142,372.40	95,945.50	49,667.00	417,946.00	7421.90	5039.90	552.90	5124.30	185,547.50	125,997.50	55,290.00	512,430.00
2009	70,692.20	66,765.80	465,796.60	610,015.00	4286.30	3815.00	5675.50	7073.10	107,157.50	95,375.00	567,550.00	707,310.00
2010	116,856.80	35,900.70	485,468.10	147,907.20	6211.30	2325.40	6802.75	2114.70	205,282.50	58,135.00	680,275.00	211,470.00

Table 2. Unit energy generated and operating hours for selected gas turbine power plant: Afam power plant

Year	Energy generated (MWH)				Operating hours				Expected maximum energy (MWH)a
	GT17 (AF1)	GT18 (AF2)	GT19 (AF3)	GT20 (AF4)	GT 17 (AF1)	GT 18 (AF2)	GT 19 (AF3)	GT 20 (AF4)	GT 17 (AF1)	GT 18 (AF2)	GT 19 (AF3)	GT 20 (AF4)
a values were computed by the authors using the formula: unit installed capacity × operating hours in a year
2005	176,180.73	165,755.05	390,032.61	471,391.30	4875.85	4174.21	4659.17	4770.89	365,688.75	313,065.75	642,965.46	658,382.82
2006	187,248.90	176,455.30	550,412.32	317,664.49	5440.88	4401.53	5071.52	3457.17	408,066.00	330,114.75	699,869.76	477,089.46
2007	206,843.47	197,807.87	463,223.19	443,822.83	5656.05	5187.00	5012.17	4123.91	424,203.75	389,025.00	691,679.46	569,099.58
2008	197,457.47	190,315.17	344,540.46	382,859.42	5566.43	3779.93	4001.38	3713.26	417,482.25	283,494.75	552,190.44	512,429.88
2009	143,564.00	140,588.60	347,156.96	542,039.86	3214.73	2861.25	4112.68	5125.43	241,104.75	214,593.75	567,549.84	707,309.34
2010	166,180.73	151,364.10	461,391.30	290,032.61	4258.48	3100.53	4929.53	2918.29	319,386.00	232,539.75	680,275.14	402,724.02

Table 3. Unit energy generated and operating hours for selected gas turbine power plant: AES power plant

Year	Energy generated (MWH)			Operating hours			Expected maximum energy (MWH)a
	PB204 (AES1)	PB209 (AES2)	PB210 (AES3)	PB204 (AES1)	PB209 (AES2)	PB210 (AES3)	PB204 (AES1)	PB209 (AES2)	PB210 (AES3)
a values were computed by the authors using the formula: unit installed capacity × operating hours in a year
2005	179,552.60	148,018.28	192,431.59	6818.88	5594.90	7104.38	228,432.48	187,429.15	237,996.73
2006	193,169.70	146,538.45	156,336.46	7292.93	5517.94	6151.06	244,313.16	184,850.99	206,060.51
2007	149,623.66	139,942.41	179,374.55	5602.46	4790.89	6898.72	187,682.41	160,494.82	231,107.12
2008	197,850.15	150,441.12	148,739.68	7565.46	5750.08	5719.70	253,442.91	192,627.68	191,609.95
2009	144,220.27	143,933.02	169,858.47	5223.44	5218.04	6478.25	174,985.24	174,804.34	217,021.38
2010	155,377.84	180,532.61	153,325.33	6024.40	6901.46	5832.69	201,817.40	231,198.91	195,395.12

Table 4. Average unit operating figures for selected gas turbine power plants

Plant/average unit operating figures	AES station			Afam station				Delta station
	PB204	PB209	PB210	GT17	GT18	GT19	GT20	GT9	GT10	GT18	GT20
Operating hours (on average of 6 years i.e., 2005–2010)	6421	5629	6364	4835	3917	4631	4018	6561	5036	5632	5628
Number of starts (on average of 6 years i.e., 2005–2010)	70	68	70	106	123	109	102	71	74	95	94
Shut down hours (on average of 6 years i.e., 2005–2010)	28	20	24	169	159	144	137	29	31	62	69
Number of trips during operation (on average of 6 years i.e., 2005–2010)	44	49	47	81	95	72	70	48	41	66	75
Number of trips during start (on average of 6 years i.e., 2005–2010)	10	9	10	12	12	14	13	19	16	14	12
Number of failures (on average of 6 years i.e., 2005–2010)	92	74	73	111	106	109	119	41	37	68	67

Power plant performance statistics

The GT performance statistics are considered with respect to the plant reliability indices, plant factors, and plant operating figures. These are discussed below.

Power plant reliability indices

The availability and reliability analysis of selected GT plants was based on available data over a period of 6 years (2005–2010). The records of failure frequency of installations, containing the description and analysis of the failure and other materials filed by each Power Station Efficiency Department constitute the basic source of information on the failure frequency and rate of repairs of the plant. In processing the available data, MTBF (m), mean time to repair (MTTR) (ζ), unavailability (U), and availability (Ψ) were obtained.

Mean time between failure (m)

$m={\frac {1}{\lambda }}={\frac {{\beta }_{t}}{{\varphi }_{n}}}$

(1)

where, λ is the expected failure rate, φ_n is the number of failures between maintenance, β_t is the total operating time between maintenance.

Mean time to repair (ζ)

$\zeta ={\frac {1}{\mu }}={\frac {{\Psi }_{t}}{{\varphi }_{n}}}$

(2)

where, Ψ_t is the total outage hours per year, φ_n is the number of failures per year, μ is the expected repair rate.

When these two factors are known (eqs. (1) and (2)) for any given system or component, then the availability (Ψ) and unavailability (U) can be expressed as:

Availability (Ψ)

$\Psi ={\frac {\mu }{\lambda +\mu }}={\frac {m}{m+\zeta }}$

(3)

$U={\frac {\lambda }{\lambda +\mu }}=m={\frac {\zeta }{m+\zeta }}$

(4)

The parameter U is a good approximation of a unit failure probability even when preventive maintenance is considered, provided that maintenance is scheduled during low demand periods. The unavailability is then an adequate estimator of the probability of finding a unit out of service at some point in the future. In the generating system, unit unavailability is obtained by a traditional method known as the FOR. This index is defined as the ratio of the forced outage hours (FOH) to the sum of the FOH and the in-service hours (ISH) [20].

${\mbox{FOR}}={\frac {\mbox{FOH}}{{\mbox{FOH}}\quad {\mbox{+}}\quad {\mbox{ISH}}}}$

(5)

Power plant factors

The plant factors used in evaluating a plants performance are: CF, AF, plant use factor (PUF), LF, plant reliability factor (PRF), and utilization factor (UF). Analyses of these factors are stated below.

Availability factor

The AF is the ratio of the hours the unit was available for operation to the total hours in the period under consideration. In the calculation of the “as installed” value this is irrespective of whether or not the unit was actually fit for operation but for some reasons such as planned outages it was idle. For the “as available” AF, the hours of planned outages are regarded as part of the period the unit was available.

Presented mathematically,

${\mbox{AF (As Installed)}}={\frac {{\mbox{EOH}}-({\mbox{POH}}\quad {\mbox{+}}\quad {\mbox{UOH}})}{\mbox{EOH}}}$

(6)

${\mbox{AF (As Available)}}={\frac {{\mbox{EOH}}-{\mbox{UOH}}}{\mbox{EOH}}}$

(7)

where, EOH is the expected operating hours, POH is the planned outages hours, UOH is the unplanned outages hours.

Utilization factor

This is the ratio of the maximum demand to the rated capacity of the power plant. The UF measures the use made of the total installed capacity of the plant.

${\mbox{UF}}={\frac {L_{md}}{C_{in}}}$

(8)

where, L_md is the maximum (demand) load generated in a given period, C_in is the installed (rated) capacity of the plant.

Plant use factor

This is the ratio of the actual energy generated during a given period to the product of capacity of the plant and the number of hours the plant has been in operation during the period. This is a modification of the plant CF in that only the actual number of hours that the plant was in operation is used.

${\mbox{PUF}}={\frac {E_{p}}{C_{in}\times T_{oh}}}$

(9)

where, E_p is the total energy generated (MWh) in a given period, C_in is the installed (rated) capacity of the plant, T_oh is the total number of operating hours in the given period.

Capacity factor

The extent of use of the generating plant is measured by the CF which is the ratio of the average energy output of the plant for a given period of time to the plant capacity. This is the ratio of the average load to the rated capacity of the plant.

${\mbox{CF}}={\frac {E_{p}}{C_{in}\times T_{h}}}$

(10)

where, E_p is the total energy generated (MWh) in a given period, C_in is the installed (rated) capacity of the plant, T_h is the total hours of the year.

Plant reliability factor

PRF says something about the dependability of a plant as regards unplanned events. PRF is given by:

${\mbox{PRF}}={\frac {{\mbox{EOH}}-{\mbox{UOH}}}{{\mbox{EOH}}-{\mbox{POH}}}}$

(11)

where, EOH is the expected operating hours, UOH is the unplanned outage hours, POH is the planned outage hours.

Load factor

This is the ratio of the average load to the maximum demand for a particular period of time. Since the average load is always less than the maximum demand, LF is always less than unity. The LF plays a key role in determining the overall cost per unit generated. The higher the LF of the power station, the lesser will be the cost per unit generated.

${\mbox{LF}}={\frac {L_{av}}{L_{md}}}$

(12)

where, L_av is the average (demand) load generated; L_md is the maximum (demand) load generated in a given period.

Power plant operating figures

The power plant operating figures considered in this work are.

Starting reliability

This is a parameter of dominant importance in the case of emergency reserve machines, peak regime GTs or auxiliary power sources designed for cyclic run. Starting reliability (SR) is used to assess plants and units whose life-time depends largely on the number of start-ups.

${\begin{array}{r}{\mbox{Starting reliability (SR)}}={\frac {{\mbox{No of starts (annually)}}-{\mbox{No of trips during starts (annually)}}}{\mbox{No of starts (annually)}}}\times 100\%\end{array}}$

(13)

Operating reliability

Operating reliability (OR) defines the probability that the equipment will fulfill its duty for the planned period with respect to the period of time being in operation. This qualitative parameter is a time-based measure of relevance for regularity measurements of high usage factor machines.

${\mbox{Time utilization (TU)}}={\frac {\mbox{Operating hours}}{{\mbox{No of units}}\times 8760}}\times 100\%$

(14)

Time utilization

Time utilization (TU) is a measure of a plants actual temporal deployment. It is a measure for the real utilization of a plant or plant part. It is independent of the level of the operating capacity concerned.

${\mbox{Time utilization (TU)}}={\frac {\mbox{Operating hours}}{{\mbox{No of units}}\times 8760}}\times 100\%$

(15)

Average no of operating hours between two trips during operation

This is expressed as:

(16)

Average no of operating hours between two successful starts

This operating figure is expressed as:

${\mbox{Average no of operating hrs between 2}}-{\mbox{successfulstarts}}=$${\frac {\mbox{Operating hrs}}{\mbox{No of starts‐No oftrips during starts}}}$

(17)

Statistical analysis of power plant performance indices

The statistical analysis is carried out to ascertain significant differences in performance indices of the selected power plants. The power plant performance index taken into consideration is plant availability. The analysis of variance (ANOVA) is carried out for significance levels of 0.05 and 0.01, that is, for confidence level of 95% and 99%, respectively.

In this analysis, Fishers distribution and Scheffes post hoc tests were made on the full data set on plant availability for the selected power plants.

Using one-way ANOVA, a null hypothesis of the first test is

$H_{0}:\mu ={\mu }_{0}$

(18)

That is, the means of population from which the samples are drawn are equal.

In this test, two independent estimates of the population variance are (1) within group variance estimate which deals with how different each of the values in a given sample is from other values in the same group (2) between group variance estimates which deals with how different the means of various samples (or groups) are from each other.

These are computed as follows:

The total sum of squares is

${\mbox{SS}}_{T}=\sum X_{i}^{2}-{\frac {{\left(X\right)}^{2}}{N}}$

(19)

where, the sum of squares between groups is

${\mbox{SS}}_{B}={\frac {\sum {\left(X_{1}\right)}^{2}}{N_{1}}}+$${\frac {\sum {\left(X_{2}\right)}^{2}}{N_{2}}}+\cdots \quad {\frac {\sum {\left(X_{K}\right)}^{2}}{N_{K}}}-$${\frac {\sum {\left(X\right)}^{2}}{N}}$

(20)

where k is number of groups.

The sum of squares within groups is

${\mbox{SS}}_{B}={\frac {\sum {\left(X_{1}\right)}^{2}}{N_{1}}}+$${\frac {\sum {\left(X_{2}\right)}^{2}}{N_{2}}}+\cdots \quad {\frac {\sum {\left(X_{K}\right)}^{2}}{N_{K}}}-$${\frac {\sum {\left(X\right)}^{2}}{N}}$

(21)

Computation of various degrees of freedom is as follows:

Degree of freedom between groups is

${\mbox{df}}_{B}=k-1$

(22)

Degree of freedom within group is

${\mbox{df}}_{W}=N-k$

(23)

Total degree of freedom is

${\mbox{df}}_{T}=N-1={\mbox{df}}_{B}+{\mbox{df}}_{W}$

(24)

where N is the number of observations.

Computation of mean squares between and within groups is as follows:

Mean square between the groups is

${\mbox{MSS}}_{B}={\frac {{\mbox{SS}}_{B}}{{\mbox{df}}_{B}}}$

(25)

Mean square within the groups is

${\mbox{MSS}}_{W}={\frac {{\mbox{SS}}_{W}}{{\mbox{df}}_{W}}}$

(26)

Finally, the Fishers ratio is computed as

$F={\frac {{\mbox{MSS}}_{B}}{{\mbox{MSS}}_{W}}}$

(27)

The second test, known as Scheffes post hoc test is to be carried out on the data set. This test ascertains the pair wise difference responsible for significant difference (if any) in obtained F- values in Fishers distribution test (ANOVA test). The technique behind this test is to moderate a critical value of F (usually α = 0.05) by a factor of k − 1. So, we obtain,

$S={\sqrt {\left(k-1\right)}}F_{0.05}$

(28)

where k is the sample number.

Next, we adjust the MSS_W of Fishers test by the factor k − 1 to obtain

${\mbox{SS}}_{E}={\sqrt {\left(k-1\right)}}F_{0.05}{\sqrt {{\mbox{MSS}}_{W}\left({\frac {1}{N_{1}}},+,{\frac {1}{N_{2}}},+,\cdots ,+,{\frac {1}{N_{K}}}\right)}}$

(29)

where N_K are the numbers of elements in each sample.

The two tests were made with α = 0.05, that is, the probability of making an error by saying the null hypothesis is false when it is actually true. On the other hand, (1 − α) is the probability of making the right decision when the null hypothesis is true, or the confidence level [21].

Results and Discussion

In this section, results of GT plant performance statistics are presented. The plant performance statistics discussed are percentage shortfalls from the target energy, plant factors, reliability indices, and operating figures.

Percentage shortfall from target energy

The expected full load installed capacities of the selected power plants under study vary from 25 to 100 MW (Delta power plant), 33.5 MW (AES power plant) and 25–138 MW (Afam power plant), but the generated power for the period under review ranges from around 15.44 to 94.49 MW, 25.42 to 29.21 MW and 35.47 to 108.53 MW for the Delta, AES and Afam power plant, respectively. From Tables 1-3, the stations units' targets generating/operational capacities are far from installed capacities. The average installed capacity of the plants from data obtained ranges from 46.6% to 57.1%, 51.7% to 57.4% and 25.9% to 35.3% for Delta, AES, and Afam power plant, respectively. This shows a gap between installed capacity and actual operational capacity of the selected plants which may be due to aging-generating facilities that are poorly maintained, lack of spare parts for repair of the broken down units or insufficient supply of fuel to the plants.

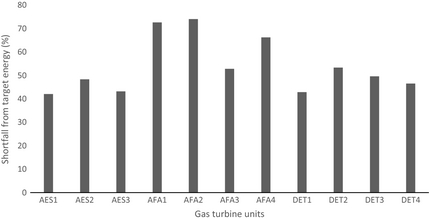
Percentage shortfalls from the target energy of selected GT units for the period under review for the selected plants are shown in Figure 1. A reduction in shortfall signifies better performance of the plant and this may be as a result of concerted efforts made by the management in carrying out preventive maintenance in the plant. For the period under review, the average shortfall ranges from 42.87% to 53.37%, 42.08% to 48.35%, and 52.83% to 74.07% for Delta, AES, and Afam power plant, respectively. GT units with least average shortfalls are AES1 (42.08%), AFA3 (52.83%), and DET1 (42.87%) in AES power plant, Afam power plant and Delta power plant, respectively. These values of percentage shortfalls in energy are far from average acceptable value of between 5% and 10% [22].

Figure 1. Shortfall from target energy for selected gas turbine units.

The percentage shortfalls in energy in the selected plants are similar to that obtained by Obodeh and Isaac [22] for Sapele thermal plant (ranged from 27.4% to 49.1%) within the period of 1997–2006. This shows the general problem of the wide gap between installed capacity and actual operational capacity of thermal power plants in Nigeria.

Power plant factors

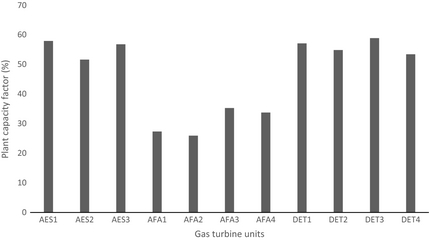
The average plants' CFs of selected GT units for the period under review are presented in Figure 2. The average CF of the plants varies from 53.46% to 58.88%, 51.65% to 57.92% and 25.94% to 35.25% for Delta, AES and, Afam power plant, respectively. GT units AFA1 and DET3 have the least and highest values, respectively, as against industry best practice of between 50% and 80% [23]. Thus, the characteristic behavior of generating plant and the extent of use of the generating plant depend substantially on the CF. High CF is desired for economic operation of the plants [24].

Figure 2. Plant capacity factor for selected gas turbine units.

In general, low CF indicates that the average energy generation is low, there is excessive plant failure which implies capacity of the plant remains underutilized for major part of the year. Hence, operational cost would be high compare to revenue. High CF is desired for economic operation of the plant [25]. If scheduled routine maintenance of the plant is significantly improved, the frequency of failure will reduce and high CF will be attained.

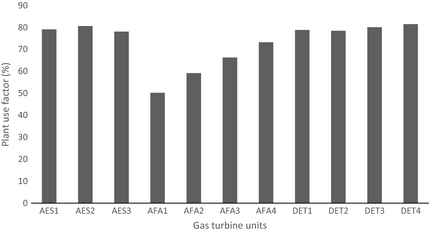
Figure 3 shows the average PUF for selected GT units. The PUF for the period under review varies from 78.82% to 81.51%, 78.11% to 80.66% and 50.28% to 73.22% for Delta, AES and, Afam power plant, respectively. GT unit AFA1 and DET4 has the least and highest PUF, respectively. High PUF indicates high ratio of actual generation to expected generation, while low PUF is an indication of low ratio of actual generation to expected generation. Low use factor also indicates excessive plant failure and hence plants generation below rated capacity. In general, selected GT units in Afam power station have low PUF when compare with GT units in other two power plants. This indicates excessive failure in the station (Afam).

Figure 3. Plant use factor for selected gas turbine units.

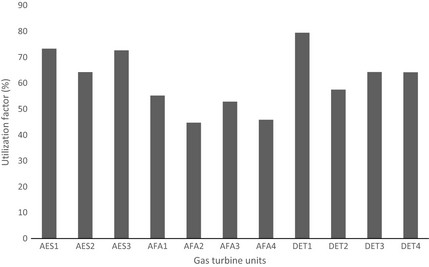
Average UF for selected GT units is presented in Figure 4. The average value of UF for the period under review ranges from 57.49% to 79.47%, 64.26% to 73.30%, and 44.72% to 55.20% for Delta, AES, and Afam power plant, respectively. GT unit DET1 has the highest UF of 79.47% while GT unit AFA2 has the least value of 44.72%. The UFs for the selected plants are far from international best practice of over 95% [22-24]. The trend of UF reflects how effectively managed the station is in terms of downtime. This result shows that the generating units were utilized less than their normal hours of utilization all year round. This is due to inadequate routine maintenance and equipment fault development.

Figure 4. Utilization factor for selected gas turbine units.

To reduce downtime occurrences and hence increase UF, planned and routine maintenance should be upheld and enhanced in the selected power plants.

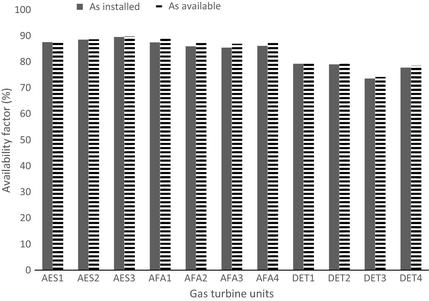
The average AFs based on “as installed” and as “as available” for the selected GT units are presented in Figure 5. The AF “as installed” varies from 73.59% to 79.24%, 87.54% to 89.52% and 85.42% to 87.43% for Delta, AES, and Afam power plant, respectively. The AF “as available” for the selected GT units varies from 74.27% to 79.58%, 87.85% to 89.80% and 87.03% to 87.78% for Delta, AES, and Afam power plant, respectively. GT units DET3 and AES3 have the least and highest values of AFs based on “as installed” and “as available”, respectively. The low value of “as installed” AF shows that so much time was lost on rehabilitation of the units. On the other hand, the low “as available” AF indicates that there were a lot of outages which kept the unit idle even when they were not generally mechanically unfit.

Figure 5. Availability factors (as installed and as available) for selected gas turbine units.

These factors also complement the notion that the selected GT units have not fared well. The situation would have been better, however, if the maintenance programme were better than what is existing in the selected stations.

Power plant reliability indices

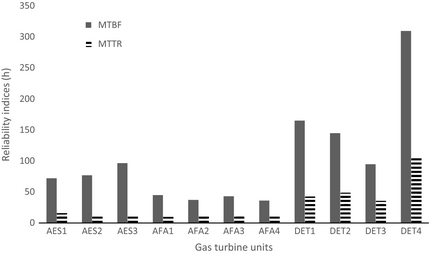
The results of reliability indices of the selected GT units over the period of 2005–2010 are presented in this section. Figures 6 shows the variation of the average MTBF and the average MTTR for the selected GT units. The MTBF of the plants varies from 94.43 to 309.36, 71.84 to 96.19, and 36.00 to 44.80 h for Delta, AES, and Afam power plants, respectively. The MTTR varies from 36.00 to 106.49, 13.23 to 15.93, and 10.01 to 12.27 h for Delta, AES and, Afam power plants, respectively. Based on the available data within the period under review, GT units AFA1 and DET4 have the least and highest value of MTTR, respectively. This shows that lot of time was spent on the unit DET4 in order to put it to operation. From this it can be concluded that there is inverse relationship between the component/equipment availability and failure rate. The operational consequences of failure can be reduced by taking steps to shorten the downtime, most often by reducing the time to procure spare parts.

Figure 6. Reliability indices for selected gas turbine units.

Result of the unit MTBF from 2005 to 2010 shows that GT units AFA4 and DET4 have the least and highest MTBF, respectively. This shows direct relation between MTBF and unit availability. As the unit with highest MTBF has high availability.

Failures in electric power stations result in downtime, production losses and economic losses as well. Obviously, to achieve the global maintenance objective of realizing high machinery availability at minimum cost, adequate cognizance must be given to the element that make up the cost, that is, the cost of machine unavailability and the cost of maintenance resources. Striking a balance between these two costs to achieve the minimum total cost creates an ideal maintenance situation. This should be the objective of a good maintenance plan [26].

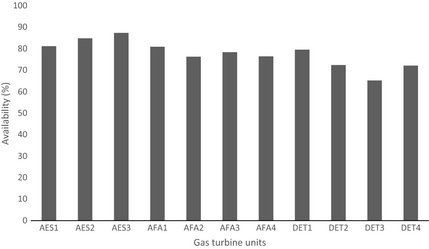
Considering the plant availability with the available data over the period 2005–2010, it was found that the average plant availability varies from 65.18% to 79.56%, 81.17% to 87.31% and 76.26% to 80.90% for Delta, AES, and Afam power plants, respectively. The results of the selected GT units' availability are presented in Figure 7. These values of availability for the selected GT units are lower than the Institute of Electrical and Electronics Engineers (IEEE) recommended standard of Average Service Availability Index (ASAI) which is 0.999 [27]. The plant availability can be improved significantly by reviewing maintenance practices by (1) giving more attention to planned or scheduled maintenance as directed by the unit manufacturers operation and maintenance manual package. In other words, routine preventive maintenance must be well planned and more regular (2) by training and retraining of technical personnel on the major equipment being used. This will improve their skill and knowledge on the current information and communication technology (ICT) as well as improve their manpower quality (3) through effective maintenance management is essential in reducing the adverse effect of equipment failure to operation (4) failure rates in the plant can be reduced if the maintenance procedure tasks involve periodic inspection and replacement of parts that were subjected to very high temperature and located in the hot gas paths (combustion chamber and turbine).

Figure 7. Availability of selected gas turbine units.

Power plant operating figures

Operating figures are very important for power plant operators. These are strategic tools to optimize the productivity of a power plant.

In this section, results of the operating figures for the selected GT plants are discussed.

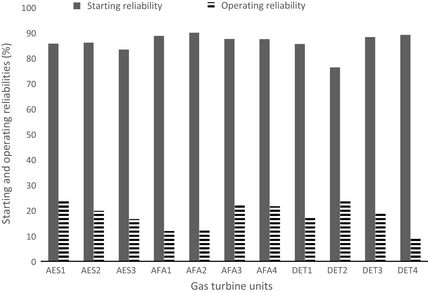
Power plant SR and OR are computed using equations (13) and (14), respectively. Figure 8 presents the results of SR and OR for the selected power plants. The average SR varies from 76.34% to 89.14%, 83.36% to 86.12% and 87.5% to 90.03% for Delta, AES, and Afam power plants, respectively. GT units DET2 and AFA2 have the least and highest values of SR, respectively. The SR of the selected plants is low compared with IEEE standard value of 99.9% [28]. The OR is defined as the probability that the equipment will fulfill its duty for the planned period with respect to the period of time being in operation. The average OR of the selected plants ranges from 9.66% to 24.10%, 16.69% to 24.26%, and 12.00% to 21.99% for Delta, AES, and Afam power plants, respectively. Low values of starting and operating reliabilities are as a result of poor maintenance strategies in the plants.

Figure 8. Starting and operating reliabilities of selected gas turbine units.

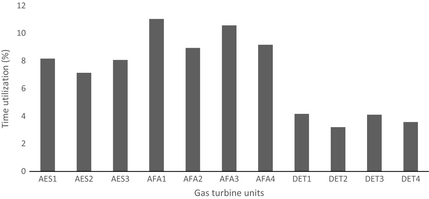
Power plant TU is a measure of a plants actual temporal deployment. TU is computed using equation (15). Figure 9 presents the results of TU of the selected power plants. Within the period under review (2005–2010), values of TU vary from 3.20% to 4.16%, 7.14% to 8.17% and 8.94% to 11.04% for Delta, AES and, Afam power plants, respectively. GT units DET3 and AFA1 have the least and highest value of TU, respectively.

Figure 9. Time utilization of selected gas turbine units.

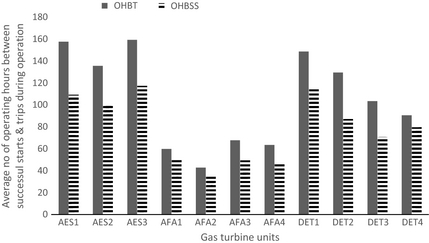
The operating figures average number of operating hours between two trips during operation (OHBT) and average number of operating hours between two successful starts (OHBSS) are computed by using equations (16) and (17), respectively. Figure 10 shows the results of the average number of OHBT and average number of OHBSS for the selected power plants. The average number of OHBT varies from 90.40 to 148.64, 135.55 to 159.28, and 42.66 to 67.67 h for Delta, AES, and Afam power plants, respectively. GT unit AFA2 has the least value while GT unit AES3 has the highest value of average OHBT. This shows that AFA2 trips off most while in operation than other units. The average number of OHBSS ranges from 70.93 to 115.59, 100.65 to 117.49, and 36.37 to 51.68 h for Delta, AES, and Afam power plants, respectively. The results show that GT unit AFA2 has the least OHBSS while GT unit AES3 has the highest value of OHBSS.

Figure 10. Plant average no. of operating hours between two successful starts and two trips during operation for selected gas turbine units. OHBT – average no of operating hours between two trips during operation. OHBSS – average no of operating hours between two successful starts.

Results of statistical analysis (ANOVA)

The results for complete data set of plant availability for the selected power plants are presented in Table 5. Relevant parameters to determine F-values in Fishers test (ANOVA test) are computed. A glance at Table 5 shows that the average availability within the period under review of the selected power plants varies from 65.18% to 87.45%. GT unit DET3 in Delta power plant has the least average availability while unit AES3 in the AES power plant has the highest average availability.

Table 5. Plant availability for selected power plants

Year/plant	Delta power plant				AES power plant			Afam power plant
	DET1 (X1)	DET2 (X2)	DET3 (X3)	DET4 (X4)	AES1 (X5)	AES2 (X6)	AES3 (X7)	AFA1 (X8)	AFA2 (X9)	AFA3 (X10)	AFA4 (X11)
2005	89.19	86.83	78.74	84.19	88.90	85.32	89.42	82.22	78.17	80.34	80.36
2006	90.73	85.66	75.61	77.93	82.60	84.56	89.21	84.33	80.23	83.25	76.89
2007	90.07	84.11	73.27	75.42	81.84	84.58	91.31	85.69	79.10	81.37	68.32
2008	88.80	74.36	12.86	66.20	89.62	86.11	81.80	82.46	65.10	76.03	79.23
2009	44.00	67.85	73.86	82.21	58.10	83.43	87.98	73.41	77.45	65.95	85.68
2010	74.56	35.37	76.75	46.47	85.92	84.86	84.95	77.37	77.45	82.24	68.05
ΣXi	497.35	432.19	391.09	432.42	486.98	508.86	524.67	485.48	457.5	469.18	458.53
${\textstyle {\overline {X}}_{i}}$	79.56	72.03	65.18	72.07	81.16	84.81	87.45	80.91	76.25	78.20	76.42
${\textstyle \Sigma X_{i}^{2}}$	39,680.03	33,337.13	28, 796.59	32,149.60	40,213.36	43,160.39	45,940.10	39,389.25	35,039.23	36,899.54	32,286.68
${\textstyle {\frac {{\left(\Sigma X_{i}\right)}^{2}}{N}}}$	41,226.17	31,131.37	25,491.90	31,164.51	39,524.92	43,156.42	45,879.77	39,281.81	34,884.38	36,688.31	35,041.63

Tables 6 and 7 show the mean number and standard deviation and ANOVA source table, respectively of plant availability for the selected power plants. From Table 6, F- value calculated is 4.03 while the tabulated values (F_0.05,10,55 and F_0.01,10,55) at 95% and 99% confidence levels are 2.00 and 2.66, respectively [21, 29]. Since the calculated F-value is greater than the tabulated, hence, there is a significant difference (P < 0.05) in availability in the selected power plants. Hence, the null hypothesis of equation (18) is rejected.

Table 6. Means and standard deviations of plants availability

	1 (n = 5)	2 (n = 5)	3 (n = 5)	4 (n = 5)	5 (n = 5)	6 (n = 5)	7 (n = 5)	8 (n = 5)	9 (n = 5)	10 (n = 5)	11 (n = 5)
Mean	79.56	72.03	65.18	72.07	81.16	84.81	87.45	80.91	76.25	78.20	76.42
Standard deviation	16.83	18.57	23.47	12.81	10.71	0.81	3.17	4.23	5.08	5.93	6.39

Table 7. ANOVA source table

Source	SS	df	MSS	${\textstyle F={\frac {{\mbox{MSS}}_{B}}{{\mbox{MSS}}_{W}}}}$	F0.05,10,55	F0.01,10,55
Between samples	2511.98	10	251.20
Within samples	3420.71	55	62.19	4.03	2.00	2.66
Within total	5932.69	65

Since the obtained F-value leads to the result being significant difference in Fishers test, we now wish to find out which pair wise means difference is responsible for the significant difference. Could it be pair wise of (μ₁ and μ₂) or (μ₁ and μ₃)? To ascertain which pair wise responsible for significant difference, a test known as Scheffes post hoc test was carried out. This test is an appropriate measure for all comparisons of mean after Fishers test (ANOVA test).

Using equation (29) and substituting the appropriate parameters we have

${\mbox{SS}}_{E}={\sqrt {\left(k-1\right)}}F_{0.05}{\sqrt {{\mbox{MSS}}_{W}\left({\frac {1}{N_{1}}},+,{\frac {1}{N_{2}}},+,\cdots ,{\frac {1}{N_{K}}}\right)}}=$$6.14$

Next, we compare this value of SS_E with difference in pairwise mean. Any pairwise mean with difference more than SS_E is responsible for the significant difference in Fishers value.

From Table 8 it is seen that there is significant difference (P < 0.05) in plant availability of the selected power plants under study. This is as a result of differences in down time hours, maintenance strategy, and number of failures and faults that occurred in the plants.

Table 8. Table of pairwise differences

Pairwise differences in Delta power plant	Pairwise differences in AES power plant	Pairwise differences in Afam power plant	Pairwise differences between two power plants
${\textstyle {\overline {X}}_{1}-{\overline {X}}_{2}=7.53}$	${\textstyle {\overline {X}}_{7}-{\overline {X}}_{5}=6.29}$	${\textstyle {\overline {X}}_{8}-{\overline {X}}_{9}=4.66}$	${\textstyle {\overline {X}}_{1}-{\overline {X}}_{9}=3.31}$
${\textstyle {\overline {X}}_{1}-{\overline {X}}_{3}=14.38}$	${\textstyle {\overline {X}}_{7}-{\overline {X}}_{6}=2.64}$	${\textstyle {\overline {X}}_{8}-{\overline {X}}_{10}=2.71}$	${\textstyle {\overline {X}}_{1}-{\overline {X}}_{10}=1.36}$
${\textstyle {\overline {X}}_{1}-{\overline {X}}_{4}=7.49}$		${\textstyle {\overline {X}}_{8}-{\overline {X}}_{11}=4.49}$	${\textstyle {\overline {X}}_{5}-{\overline {X}}_{2}=9.13}$
${\textstyle {\overline {X}}_{4}-{\overline {X}}_{3}=6.89}$		${\textstyle {\overline {X}}_{10}-{\overline {X}}_{9}=1.95}$	${\textstyle {\overline {X}}_{5}-{\overline {X}}_{3}=15.98}$
			${\textstyle {\overline {X}}_{5}-{\overline {X}}_{4}=9.09}$
			${\textstyle {\overline {X}}_{5}-{\overline {X}}_{1}=1.60}$
			${\textstyle {\overline {X}}_{6}-{\overline {X}}_{1}=5.25}$
			${\textstyle {\overline {X}}_{6}-{\overline {X}}_{2}=12.78}$
			${\textstyle {\overline {X}}_{6}-{\overline {X}}_{3}=19.63}$
			${\textstyle {\overline {X}}_{6}-{\overline {X}}_{4}=12.74}$
			${\textstyle {\overline {X}}_{7}-{\overline {X}}_{8}=6.54}$
			${\textstyle {\overline {X}}_{7}-{\overline {X}}_{11}=11.03}$
			${\textstyle {\overline {X}}_{11}-{\overline {X}}_{3}=11.24}$

Conclusions

This study has investigated the performance indices of selected GT power plants in Nigeria. Specific emphasis is on the following indicators: reliability indices (availability, failure rates and MTTR), plant factors (CF, UF, AF, PUF) and operating figures (SR, OR, TU, and operating hours). The performance indices analysed show variation in the performance indices for each GT unit considered in this study. This indicates differences in their system installation, maintenance, and operation.

Based on the available data of the installed capacities and generating capacities for the period under review, the percentage shortfalls from the target energy in the selected power plants range from 26.33% to 86.615%, 32.58% to 52.31%, and 54.47% to 78.15% for Delta, AES, and Afam power plants, respectively. These values of percentage shortfalls are far from the acceptable value of 5% and 10%.

The CF of the selected power plants varies from 16.88% to 73.67%, 49.05% to 67.02%, and 21.4% to 45.53% for Delta, AES, and Afam power plant, respectively. These values are against industry best practice of between 50% and 80%. High CF is desired for economic operation of the plants. Low CF indicates that the average energy generation is low due to excessive plant failure; hence, capacity of the plant remains unutilized or underutilized for the major part of the year.

The result of this study shows that the PUF varies from 45.89% to 97.03% and the UF varies from 6.31% to 93.074%. The UFs of the selected power plants are far from the international best practice of over 95%. From this result, it can be concluded that the generating units were underutilized all year round. This is due to inadequate routine maintenance and equipment fault development.

The reliability of power plant unit is one of the most important performance parameters which reflect the quality and standards. The great care and effort devoted to increasing the reliability and quality of electrical power is an indication of the economic implication for the power industry.

Based on a 6-year (2005–2010) data on operating hours, number of failures and total outage hours database, reliability indicators like MTBF, MTTR and availability has been estimated. The analyses revealed that the MTBF varies from 5.42 to 378.44 h and the MTTR varies from 18.3 to 153.88 h. The operational consequences of failures can be reduced by taking steps to shorten the downtime, most often by reducing the time to obtain spare parts.

The plant availability varies from 12.86% to 91.31%. These values of availability for the selected GT power plants are lower than the IEEE recommended standard of ASAI which is 99.9%. The plant availability can be improved significantly by reviewing maintenance practices in the plants.

Evaluation of operating figures of the selected power plants revealed that SR and OR vary from 71.95% to 93.9% and 5.33% to 55%, respectively. The SR of the selected power plants is low in value compared with standard value of 99.9%. TU of the plants varies from 1.34% to 12.91%.

The values of the average number of OHBT and average number of OHBSS for the selected power plants vary from 26.33 to 249.45 h and 22.19 to 170.86 h, respectively.

In each of the evaluated power plant performance parameter, the selected power plants had lower performance indices than set international standards (some considerably low and some others are close to acceptable values). A number of reasons could be adduced to be for this shortfall in performance. These include low- plant availability due to frequent or long time breakdown/failures, overdue overhaul of unit(s), obsolete technology relative to advancement in the field, load instability, aging of plant components among others.

The availability of the selected power plants can be improved significantly by reviewing maintenance practices. Planned or scheduled maintenance must be given more attention as directed by the unit manufacturers operation and maintenance manual package, if the unit has to perform properly. In other words, routine preventive maintenance must be well planned and be more regular. Measures to improve the performance indices of the plants have been suggested such as training and retraining of technical personnel on the major equipment being used, proper spare parts inventory, organizing regular management meetings, and improve general housekeeping of the plant.

The statistical analysis (ANOVA) carried out on plant availability revealed that at both 95% and 99% confidence levels; there is a significant difference in availability of the selected power plants. This indicates differences in their systems installation, operation, and maintenance.

Recommendations to improve performance of selected power plants

GT power plants operating in Nigeria are simple GTs, there is a tremendous derating factor due to higher ambient temperatures. Coupled with this, these GTs are made to operate without the application of GT inlet air cooling equipment and technology applications. The average efficiency of GT plants in the Nigerian energy utility sector over the past two decades was in the range 27–30% [30].

It is generally understood that efficiency improvement that is consistent with high plant reliability and low cost of electricity is economically beneficial. Based on the results of this research work, the following possible economical methods and technologies to improve performance of the selected GT power plants are hereby recommended:

• Retrofitting with a GT air inlet cooling system (evaporative cooling or inlet chilling method) is a useful option for increasing power output of the plant. Inlet air cooling increases output by taking advantage of the GTs characteristic of higher mass flow rate and, thus, output as the compressor inlet temperature decreases. Because the cooled air is denser, it gives the machine a higher air mass flow rate and pressure ratio, resulting in an increase in output. For example, as the AES GT plant is very close to the lagoon area, the source of cooling water can be obtained from lagoon. The inlet air cooling system is cost-effective and can be implemented in the basic system without major modification to the original system integration.
• Heat recovery from hot exhaust gases can be used to augment the performance of the GT plant. Combined cycle is a common way to recover thermal energy from the exhaust gases; it is suitable for these plants as they operate as base load plants.
• Furthermore, with the rapid increase in electricity demand in Nigeria and the expected shortages in power supply due to delays in implementation of the major power projects, retrofitting the selected power plants with inter-cooling between two compressors and regenerator cycle would be an attractive investment opportunity for the stakeholder of the plants.
• The performance of the plants (from the availability point of view) can be greatly improved and the power generation reduction can be reduced through improvement in operational and management (O & M) practices, proper spare parts inventory, improvement in general housekeeping of the plants, and regular training of O & M personnel.

Acknowledgments

The authors appreciate the Management of Afam, Delta, and AES power plants and the National Control Centre (NCC) Oshogbo for providing the data used in this study.

Conflict of Interest

None declared.

References

1. Tanrioven, M., and M. S. Alam. 2005. Reliability modeling and assessment of grid-connected PEM fuel cell power plants. J. Power Sources142:264–278.
2. Kamal, D.1988. Reliability modeling of power system components using the CEA-ERIS data base. Ph.D. thesis, University of Sakatchwan, Canada.
3. Adegboyega, G. A., and J. O. Famoriji. 2013. Determination of the central gas turbine efficiency and reliability, Edjeba, Delta State, Nigeria. Int. J. Eng. Res. Technol.2:482–490.
4. Megbowon, I. O., and T. O. Oyebisi. 2005. A reliability assessment of the south western transmission lines of the Nigerian National Grid. FUTAJEET4:17–22.
5. Gupta, S. A., and C. P. C. Tewari. 2009. Simulation modelling and analysis of a complex system of a thermal power plant. J. Ind. Eng. Manag.2:387–406.
6. Barabady, J., and U. Kumar. 2007. Availability allocation through importance measures. Int. J. Qual. Reliab. Manag.24:643–657.
7. Asis, S., K. B. Dhiren, K. Suresh, and S. Manoj. 2012. Reliability assessment of Rukhia gas turbine power plant in Tripura. Int. J. Curr. Eng. Technol.2:184–195.
8. Adamu, M. Z., B. A. Adegboye, B. G. Bajoga, J. G. Ambafi, and J. T. Omokhafe. 2012. Reliability evaluation of Kainji hydro-electric power station in Nigeria. J. Energy Technol. Policy2:15–31.
9. Popoola, J. J., A. A. Ponnle, and T. O. Ale. 2011. Reliability worth assessment of electric power utility in Nigeria: residential customer survey results. Aust. J. Technol.14:217–224.
10. Hooshmand, R. A., M. Moazzami, and A. A. Nasiri. 2009. Power system reliability enhancement by using PowerformersTM. Serb. J. Electr. Eng.6:315–331.
11. Valdma, M., M. Keel, H. Tammoja, and K. Kilk. 2007. Reliability of electric power generation in power systems with thermal and wind plants. Oil Shale24:197–208.
12. Oyedepo, S. O., and R. O. Fagbenle. 2011. A study of implementation of preventive maintenance Programme in Nigeria Power Industry—Egbin Thermal Power Plant case study. Energy Power Eng.3:207–220.
13. Olatomiwa, L. J., and M. N. Nwohu. 2011. Reliability evaluation of hydro-electric power stations in Nigeria: (A case study of Kainji units 1G7 & IG8 and Shiroro units 411G1 & 411G2). J. Asian Sci. Res.1:320–327.
14. Okonkwo, R. C.1997. Thermal power stations' reliability evaluation in a hydrothermal system. Niger. J. Technol.18:42–49.
15. Billinton, R., and R. N. Allan. 1996. Reliability evaluation of power systems. 2nd ed. Plenum Press, New York, NY.
16. Rausand, M., and A. Hoyland. 2004. System reliability theory: models statistical method and application. 2nd ed. John Wesley and Sons Inc., Canada.
17. Adegbulugbe, A. O.2007. Balancing the acts in the power sector: the unfolding story of Nigeria independent power projects, Presented at the 2007, 27th USAEE/IAEE North American Conference, at http://www.usaee.org/usaee2007/submissions/OnlineProceedings/AS%20Momodu%20Paper.doc (accessed 29 April 2009).
18. Oyedepo, S. O., R. O. Fagbenle, S. S. Adefila, and S. A. Adavbiele. 2014. Performance evaluation and economic analysis of a gas turbine power plant in Nigeria. Energy Convers. Manag.79:431–440.
19. Brown, R. E.2009. Electric power distribution reliability. 2nd ed. Taylor and Francis Group, New York, NY.
20. Adedayo, O. A.2000. Understanding statistics. JAS Publishers, Akoka, Lagos, Nigeria.
21. Kofoworola, O. F.2003. Pp. 26–28inTowards improving electricity generation in Nigeria: a conceptual approach, Proceedings of the International Conference on Mechanical Engineering (ICME 2003) December.
22. Obodeh, O., and F. O. Isaac. 2011. Performance analysis for Sapele thermal power station: case study of Nigeria. J. Emerg. Trends Eng. Appl. Sci.2:166–171.
23. Ekeh, J. C.2008. Positioning the power sector for electricity sufficiency in Nigeria to meet up with vision 2020, 20th Public Lecture Series, Covenant University, Ota, Nigeria.
24. Adegboyega, G. A., and K. O. Odeyemi. 2011. Performance evaluation of Egbin power station, Nigeria. Eur. J. Sci. Res.65:360–369.
25. Akinbulire, T. O., C. O. A. Awosope, and P. O. Oluseyi. 2007. Pp. 175–181inSolving the technical problems facing electrical energy development in Nigeria, 3rd Annual Conference Research and Fair of the University of Lagos, Nigeria, December 3.
26. Okah-Avah, B. E.1996. The science of industrial machinery and system maintenance. Spectrume Books Ltd, Lagos, Nigeria.
27. Bertling, L., and R. Eriksson. 2005. A reliability- centered asset maintenance method for assessing the impact of maintenance in power distribution systems. IEEE Trans. Power Syst.20:23–46.
28. Hale, P.2001. Survey of reliability and availability information for power distribution, power generation and HVAC components, IEEE Transactions on Industry, Vol. 37.
29. Lipson, C., and N. J. Sheth. 1973. Statistical design and analysis of engineering experiments. Mc Graw-Hill International, New York, NY.
30. Abam, F. I., I. U. Ugot, and D. I. Igbong. 2012. Performance analysis and components irreversibilities of a (25 MW) gas turbine power plant modeled with a spray cooler. Am. J. Eng. Appl. Sci.5:35–41.