Abstract
In this article, we present performance results and analysis of a novel rotary lobe expander device. This is part of a larger research effort into the analysis and design of a small-scale solar system that would compete with available distributed technologies for heat and electricity generation. To choose an appropriate working fluid and components for a distributed concentrating solar combined heat and power (DCS-CHP) system, we compared many different working fluids, collectors, and expander choices. Of the expanders analyzed, including piston expanders, radial inflow turbines, Tesla turbines, screw expanders, and scroll expanders, the rotary lobe expander shows the greatest promise in small-scale power applications due to its high efficiency in expanding fluids over large pressure ratios and its low cost to manufacture. This article focuses on testing of a prototype small-scale expander that was chosen because, to date, no suitable commercial product of less than 10 kW has been found for this application. Initial testing was completed with air to get results that should be indicative of future testing with steam. The test system consists of a compressed air expander (a prototype designed by Katrix, Inc. of Australia) connected to an induction motor driven by a variable frequency drive (VFD) that enables expander testing at varying shaft speeds. Results of the expander testing are reported isentropic efficiencies of 22–25%, thermomechanical efficiencies of 80–95%, and pressure ratios of 6–11 at the tested speeds. Despite mixed results from this particular expander, future refinements could lead to a new class of expanders with low cost and high performance for use in solar combined heat and power and waste-heat recovery.
Introduction
The purpose of this research project, of which this article is one part, was the analysis and development of a small-scale solar system that would compete with available distributed technologies for heat and electricity generation. To choose an appropriate working fluid and components for a distributed concentrating solar combined heat and power (DCS-CHP) system, we compared many different working fluids, collectors, and expander choices. Of the expander possibilities analyzed, including piston expanders, radial inflow turbines, Tesla turbines, screw expanders, and scroll expanders, the rotary lobe expander shows the greatest promise in small-scale power applications due to its high efficiency in expanding fluids over large pressure ratios and its low cost to manufacture. This article focuses on testing of a prototype small-scale expander that was chosen because, to date, no suitable commercial product of less than 10 kW has been found for this application.
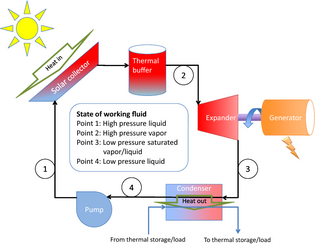
The envisioned application for which this technology was evaluated is shown in Figure 1: a solar CHP system that uses a Rankine cycle. In this cycle, water (or another working fluid) is pumped to high pressure (1000 kPa), heated in a concentrating solar collector to greater than 473 K, then expanded producing work on a shaft which is attached to a generator. The cooled fluid exits the expander and is condensed back to its original state. Ideally, the cold reservoir, to which the working fluid dumps energy, is some useful thermal load, hence completing the combined heat and power Rankine cycle.
|
|
|
Figure 1. A solar Rankine CHP system. |
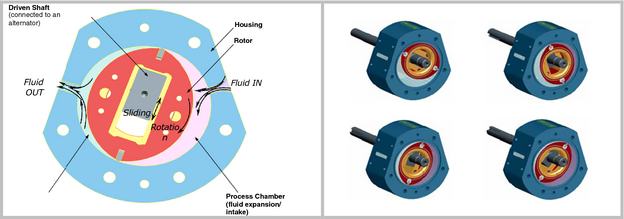
The test system consists of a compressed air expander (a prototype that was loaned to us by Katrix, Inc. of Australia) connected to an inductive motor driven by a variable frequency drive (VFD) that enables expander testing at varying shaft speeds. This expander device is in a new class of positive displacement machines that uses Limaçon motion to enable high expansion ratios, high torque, and low-speed operation in a compact package. Some of the pitfalls of other rotary lobe engines, like the Wankel, are avoided in this design by using a cylindrical chamber without the problematic apex-seals. A schematic of the stages in the Katrix expansion cycle is shown in Figure 2. Extensive evaluation and design of this concept has been performed at the University of Ballarat in Australia [1-3], and previous versions of the expander tested by CSIRO with isentropic efficiencies reported in the 40–60% range [4].
|
|
|
Figure 2. Stages in the Katrix expansion cycle. |
The reported testing is of a new prototype with modified porting to allow higher expansion ratio and higher efficiency. Results of the expander testing are reported isentropic efficiencies of 22–25%, thermomechanical efficiencies of 80–95%, and pressure ratios of 6–11 at the tested speeds. Despite mixed results from this particular expander, future refinements could lead to a new class of expanders with low cost and high performance for use in solar combined heat and power and waste-heat recovery.
Background
Because the typical heating load in many facilities is on the same order as the electrical load, increasing the fraction of electrical to heat output of a distributed generation system is desirable. Our own thermodynamic modeling has shown that an efficient large pressure ratio expansion for a Rankine cycle is crucial for getting theoretical solar-electric efficiencies as high as possible, and thereby increasing the relative fraction of electricity to heat produced by the cycle.
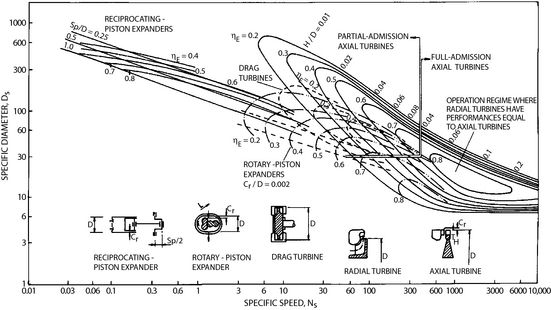
Aside from the solar collector, the enabling technology for a DCS-CHP system is an efficient small-scale expander. To date, the authors' have not found any commercial expanders suitable for this application. As Aoun and Badr conclude, volumetric expansion devices like Wankels, vane expanders, and screws/scrolls are the most promising for small-scale applications [5,[5, 6]]. Figure 3, excerpted from Badr, shows a nice summary of potential efficiencies for different expander types. The problem with small expanders in general is that the power generated is proportional to the displaced volume, however many losses are proportional to the surface area (e.g., friction on moving seals/rings in positive displacement machines), so shrinking the expander size decreases the overall efficiency because volume is a function of the cube of the characteristic dimension, whereas surface area is a function of the square of that dimension. This effect is what makes Tesla turbines so interesting in small-scale; in that they turn this relationship around as power is generated by viscous forces, dragging on the rotor, which actually increases (inversely to volumetric flow rate) as the size of the device is scaled down. Much work still needs to be done in improving Tesla and other drag turbines, however, and it remains unclear whether they will reach efficiencies in the useful realm for this application [6, [6, 7]], although some work has indicated it is possible they already have [8]. Aerodynamic turbines, even radial inflow turbines used in the smallest scale commercial applications, are also incompatible with the high pressure ratios and low power outputs needed for DCS-CHP [6,[6, 9]].
|
|
|
Figure 3. Performance map for different types of expanders (Badr et al., [6]). |
That leaves screw, scroll, piston, vane, and rotary lobe expanders (e.g., Wankel). Of those, screw and scroll expanders exhibit modest performance in small-scale (typically below 55% isentropic efficiency) [5], and pistons show good performance (typically 75–85% isentropic efficiency), but at the cost of more complex valves and more moving parts than rotary lobe expanders. Vane expanders have not been explored thoroughly in this research but may suffer from lower efficiencies than other volumetric devices at high pressure ratios, or suffer from lubrication problems with steam [5,[5, 6]]. For those reasons the rotary lobe expander appears to be a good candidate for DCS-CHP if good pressure ratios and performance can be achieved with the desired working fluid.
Keeping expanders in mind, Sunter et al. modeled a variety of working fluids in the analysis of radial inflow turbines for Solar CHP [9]. As that study concludes, the authors do not know of any suitable working fluids that would exhibit desirable properties for use in dry or wet expansion, that do not also either exhibit high global warming potential (R123, R245FA, etc.) or are highly toxic (Toluene, methanol, etc.). Aoun also came to the conclusion (in his very comprehensive dissertation devoted to residential solar CHP systems) [5] that, in terms of both heat transfer properties and maximum efficiency at higher expansion ratios, water is the preferred choice.
At temperatures above 150°C as provided by a tracking concentrating solar collector, water is a remarkable working fluid choice that is ubiquitous, safe, environmentally benign, and well-suited to CHP systems because its saturation temperature at atmospheric pressure (100°C) is good for process heat, domestic hot water, and other thermal heating and cooling demands. Considering organic working fluids (e.g., alcohols, refrigerants, pentane, etc.) we have found that the relative performance of these fluids is only better than water for Rankine cycles in lower temperature regimes, or electricity-only cycles (non-CHP). In addition, the added manufacturing, greenhouse gas and ozone depletion factors, safety concerns (flammability, toxicity, etc.), and cost make these fluids less desirable for a DCS-CHP system.
Air versus steam testing
In this research, the experimentally derived expander efficiency and pressure ratio results, using air as the working fluid, should be indicative of performance when operating with steam. This despite the fact that a dynamic similitude analysis was not done because the temperatures and pressures were not exactly the same with the air testing setup and expected steam setup, and because we did not have permission to access the internal geometry of the expander to assess Reynolds, Prandtl, Mach, or other non-dimensional parameters related to the working fluid choice. These results should therefore be used as a guide to potential ideal gas efficiency until further testing is done on the next generation Katrix expander. The use of a condensing fluid such as water is not, however, expected to negatively affect experimental efficiencies as compared to a dry fluid like air because, as has been shown with positive displacement devices, a wet fluid can actually improve sealing and lubrication and thereby increase efficiency [10]. Additionally, air at room temperature and steam at the anticipated temperatures behave as similar ideal gases as long as there is not a large fraction of condensation occurring in the expansion process, and the apparatus is well insulated to minimize heat loss. In this case, the quality of steam at the expander outlet will still be very high (above 0.9) at the designed input temperature, so results of air testing in terms of pressure ratio and efficiency should be similar to those with steam. One caveat to operation of the current expander with steam is that special lubrication (steam oil) would have been required. In the future, design changes to bearings could be explored to achieve a condensate-lubricated expander instead of the tested prototype that is oil-lubricated. An oil-free design would be valuable because it would greatly enhance the expanders utility in moderate temperature steam Rankine cycles by both eliminating a possible source of failure (i.e., oil lubrication system failure), and preventing lubricant from being mixed with the working fluid. This latter benefit of a steam-lubricated expander would enable use of a single-loop Rankine cycle, without oil separation, thereby potentially reducing cost without sacrificing system efficiency.
Test Procedure
Initially, our intent was to characterize the expander efficiency with air and steam as the working fluid, but due to time constraints, expense limitations, and problems with the current prototype, we did not complete the steam testing. This study describes results of partial completion of testing of the Katrix expander with air, at varying angular velocity.
The test system consists of the following main components:
- A compressor with inline tank and booster pump producing greater than 1000 kPa absolute pressure gas,
- the Katrix rotary lobe expander, with dimensions of 24 × 15 × 18 cm, a weight of 31 kg, and a 3.5:1 volumetric expansion ratio,
- upstream and downstream pressure and temperature probes (used to calculate enthalpy change of the working fluid),
- an in-line shaft torque measurement device,
- an upstream orifice plate flow meter with differential pressure sensor and a rotameter of known calibration (used to calculate flow rate),
- and a VFD with dynamic braking resistor pack providing load to the expander.
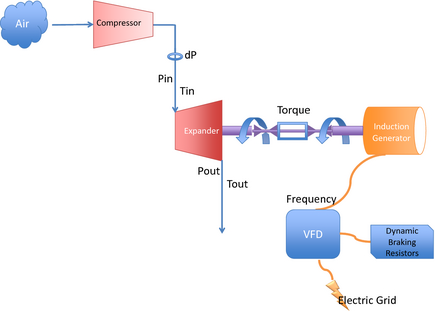
Figure 4 shows a simplified schematic of the test setup with relevant data measurement points, and Figure 5 shows actual pictures of the test equipment. It is important to note that the temperature and pressure sensors and orifice plate flow meter need to be placed in locations far enough away from bends and constrictions to ensure reasonably laminar flow. Calculations to this effect dictated sensor placement in the test apparatus. Appendix A contains a list of all equipment used in the testing, including the VFD, which is not shown in the pictures.
|
|
|
Figure 4. Simplified expander test setup schematic: collected measurements are pressure across the orifice plate (dP), pressure at inlet of expander (Pin), temperature at inlet (Tin), pressure at outlet (Pout), temperature at outlet (Tout), torque, and frequency set point of the variable frequency drive. |
|
|
|
Figure 5. Actual test setup as installed. |
Experiments follow this operating procedure:
- Turn on the VFD to the desired frequency set point (in this case 10–60 Hz AC, which corresponds to 31–188 rad/sec or 300–1800 rpm), so the electric motor spins the expander up to the desired angular velocity.
- Turn on the compressed air supply, so the expander powers the shaft to the electric motor and any excess regenerated electrical power is dissipated in a resistor bank connected to the VFD.
- After the system runs for 10–15 min to “warm up” (i.e., reach steady-state temperature at expander inlet and outlet) start data acquisition on the upstream and downstream pressure and temperature of the working fluid, torque on the shaft, and differential pressure across the orifice plate flow meter.
- After a 10–15-min data collection period, stop data acquisition and increase the VFD frequency set point by 5 Hz.
- Repeat steps 3 and 4 until the VFD frequency reaches 60 Hz (the limits of the VFD and motor) being sure to wait for steady state operation before doing data acquisition at each speed.
- Shut off the compressed air and turn off the VFD, in that order.
- Find a 300-sec period of recorded data with fairly steady characteristics of upstream pressure and temperature and calculate isentropic efficiency of the expander.
Power flow on start up is momentarily from the VFD to the expander, and once the compressed air is turned on the expander begins generating power reversing the flow (by producing negative slip in the motor) to be dissipated in the braking resistors as heat. The average power generated by the expander is only a small fraction of the rated motor power output (800 W vs. 16 kW), so the speed effect of slip is ignored.
Results of Testing
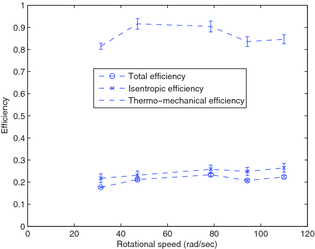
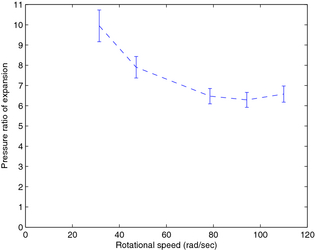
Testing on the Katrix expander using compressed air was partially completed before the failure of a bolt inside the expander halted further testing at higher speeds. The unit was shipped half way around the world to the manufacturer who repaired the failure and inspected the unit for damage (of which there was none), but at that point, there was no remaining time for continuation of testing. That being said, the Katrix expander shows a isentropic efficiency of (22–25%), and thermomechanical efficiency of (80–95%) at reasonable pressure ratios (6–11) as shown in Figures 6 and 7. The average values produced from 300 sec of steady-state operation are shown as points on the figure. Full data from the test runs are also shown in Appendix A.
|
|
|
Figure 6. Efficiencies of Katrix expander on compressed air (error bars indicate one standard deviation). |
|
|
|
Figure 7. Pressure ratio of Katrix expander on compressed air (error bars indicate combined total accuracy). |
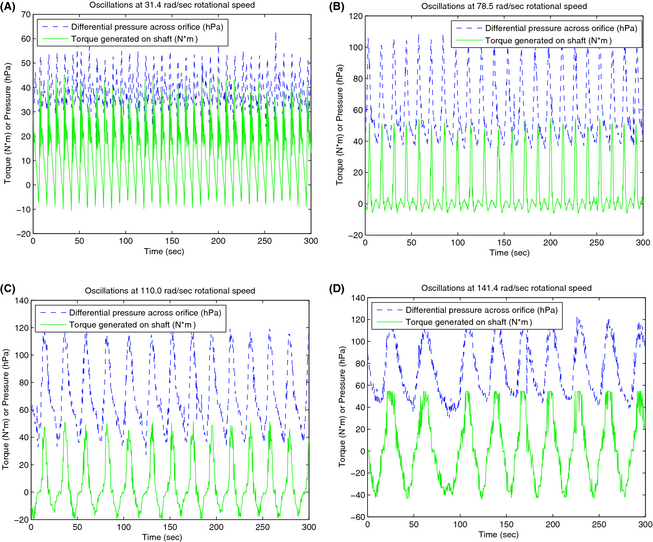
As can be seen in the figures, data were collected at VFD set points corresponding to shaft speeds between 31 and 110 rad/sec (300–1050 rpm). Results of testing at higher speeds were thrown out due to saturation of the torque sensor leading to inaccurate results as further discussed in the following sections. Testing around 60 rad/sec caused such severe resonance of the mechanical test bench that a full 15 min run could not be completed. These data were also omitted from the final results. The internal failure of the expander occurred at a VFD set point corresponding to a 141 rad/sec (1350 rpm) shaft speed, halting all further testing. The expander was disassembled by the manufacturer and the culprit for the failure was found to be a bolt that had loosened inside the expander and physically blocked the rotor from rotating, a problem we were told could be easily fixed in future designs.
Data processing
We use Matlab (The MathWorks, Inc., Natick, MA) and NIST Refprop software (Gaithersburg, MD) for post processing of the experimental data. The two independent state variables of measured temperature and pressure fully determine fluid inlet and outlet states. The specific enthalpy drop of the working fluid across the expander multiplied by the mass flow rate (from the orifice plate flow meter) is the drop in working fluid enthalpy. Work is simply torque multiplied by angular velocity of the shaft. Dividing total work output by the enthalpy drop in the working fluid yields the thermomechanical efficiency of the expander over the data collection period. Isentropic efficiency is calculated as actual enthalpy drop (h1 – h2) divided by isentropic enthalpy drop (h1 – h2s). Total efficiency is then the total work output divided by the isentropic enthalpy drop (h1 – h2s). Efficiency at each data point is calculated and then a time-average is taken to map out these device efficiencies over a range of rotational frequencies. Supplemental attachments show the full Matlab code for data processing.
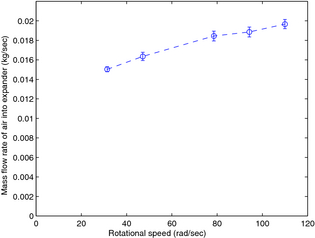
We originally intended to merely calibrate the orifice flow meter using the rotameter, but instead left the rotameter in-line during testing, therefore providing a redundant mass flow measurement. This redundancy allows for more precise reporting of the notoriously uncertain mass flow rate as shown in Figure 8. Mass flow rate is first calculated using Blevinss orifice equation for incompressible flow through a thin square-edged orifice [11]:
|
|
(1) |
where the coefficient C, the ratio of the actual flow rate to the ideal flow rate, for corner tap orifices is defined as follows:
|
|
(2) |
where the ratio of the inner diameter of the orifice to the inner diameter of the pipe on each side , and the Reynolds number:
|
|
(3) |
where U is the velocity of air through the pipe, d is the inner diameter of the orifice, D is the inner diameter of the pipe, ρ is the density of air in the pipe, ν is the kinematic viscosity, and (pu − pd ) is the differential pressure across the orifice.
|
|
|
Figure 8. Mass flow rate of air through expander (error bars indicate one standard deviation). |
The algorithm we developed solves for the mass flow rate when seeded with an air velocity estimate by first solving equation (2) for C and subsequently equation (1) for . This mass flow rate leads to a new U with which to start the next iteration using
|
|
(4) |
This procedure is repeated in code until suitable convergence on mass flow rate is reached. This calculation yields a mass flow rate that agrees well with the results of the spreadsheet provided by the orifice plate manufacturer (Dwyer Instruments, Michigan, IN).
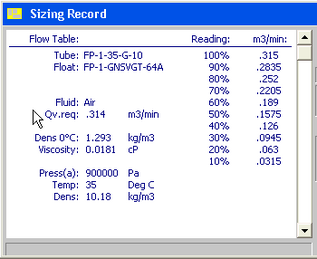
Calculating mass flow rate for the rotameter is more straightforward. During each test run, we view the rotameter float and record the percent of scale shown in steady-state. Then using the upstream pressure and temperature measurements, we calculate mass flow rate by finding the calibration of the rotameter at those conditions (with the manufacturers calibration software). See Appendix A and supplemental material for the instrument details, and Matlab code, respectively.
We use error bars in two ways in reporting the results of the expander testing. First, for quantities where there are redundant sensor measurements, or those derived from redundant sensor data (e.g., power, efficiency, mass flow rate), the error bars indicate the standard deviation s, of a data vector x, with the number of elements in the sample, n [12]:
|
|
(5) |
where
|
|
(6) |
This calculation assumes that all derived measurements are truly independent and is not strictly accurate for derived measurements such as fluid enthalpy and efficiency because, in this test setup, there are independent/redundant mass flow measurements, but some non redundant temperature and pressure measurements. As temperature and pressure measurements are comparatively more robust than mass flow rate measurement, the resulting underestimate of the standard deviation is ignored. Because the accuracy of the data acquisition hardware is so high, any data acquisition error is also omitted from the error bars. The second way in which error bars are reported here are for those sensors that have manufacturer published accuracy (e.g., pressure, temperature, rotational speed, and torque measurements). These error bars report total combined accuracy or tolerance for these types of measurements. Derived values (such as pressure ratio, torque, mechanical power) have error bars derived from the relative contribution of accuracy from each sensor. The details of these combined error calculations are available in the full Matlab code of the supplemental material.
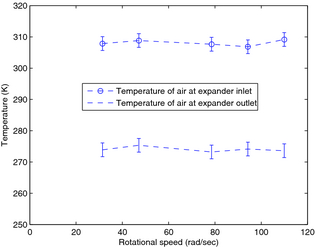
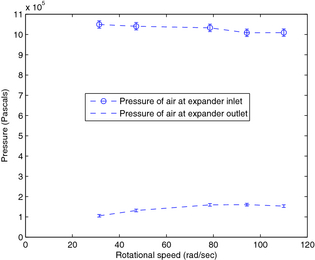
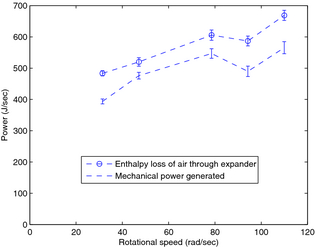
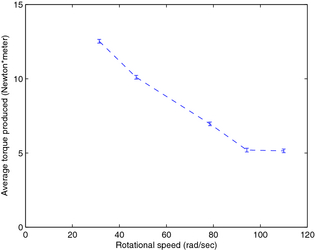
Figures 9 and 10 show air entering and exiting the expander at 310K, 10 bar, and 273K, 1 bar, respectively, with relatively small variations at different expander rotational speeds. The enthalpy change of the working fluid shown in Figure 11 is calculated from these measured temperature and pressure values using NIST reference fluid thermodynamic and transport properties database v.9.0 software [13]. Mechanical power, also shown in Figure 11, is simply calculated as rotational speed (as regulated by the VFD) multiplied by average torque, shown in Figure 12.
|
|
|
Figure 9. Temperature of air at expander inlet and outlet (error bars indicate combined total accuracy). |
|
|
|
Figure 10. Pressure of air at expander inlet and outlet (error bars indicate combined total accuracy). |
|
|
|
Figure 11. Enthalpy loss of air through expander, and mechanical power generated (error bars indicate total combined accuracy). |
|
|
|
Figure 12. Torque generated by expander (error bars indicate total combined accuracy). |
Torque oscillation and experimental error
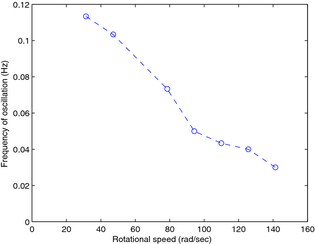
As mentioned in the last section, the torque measurement on the shaft between the expander and VFD shows large, unexplained, periodic oscillations that varied inversely with rotational speed as seen in Figure 13. Figure 14 A–D shows the 300 sec oscillating differential pressure (across the orifice plate) and torque data at several rotational speeds. Note that these speeds are set points of the VFD and all reported measurements in the derived data incorporate the potential error inherent in controlling and measuring this speed. Mass flow rate is proportional to differential pressure, therefore, the orifice plate flow meter data corroborate the oscillating torque data as a real effect. Note that the torque oscillates so greatly that the expander goes from generating power to absorbing power over the course of one period of oscillation. The full data can be found in Appendix A.
|
|
|
Figure 13. Frequency of torque oscillation on shaft. |
|
|
|
Figure 14. Torque and differential pressure oscillations at varying rotational speed set points. |
A few possibilities as to the cause of the oscillations have been hypothesized and explored limitedly:
- A Helmholtz oscillation occurs in the air intake port or supply line to the expander inlet where the opening and closing of the passageways into the expander leads to a resonance similar to that generated by blowing across the top of a bottle. Initial analysis of this phenomena indicates that the frequency of the observed torque oscillation is several orders of magnitude too low given the length of the ports internal to the expander and the air lines from the booster pump leading up to the expander.
- A beat frequency is generated by some combination of the effects of the pulsed nature of the operation and control of the induction motor by the VFD, the pulsed air intake into the expander, vibrations in the shaft couplings, etc. This option was not fully explored before the expander failed, however, given that we are using a fairly rigid coupling (Lovejoy jaw-type L coupling) between the expander shaft and the induction motor, that the air pressure remains fairly constant at the expander inlet (as shown in Appendix A), and that the VFD is operating in speed control mode, it is difficult to imagine such a large torque oscillation being the result. Additionally, a corresponding speed oscillation might be expected in such a case, and although we are not measuring rotational speed directly, the VFD would fault if speed varied by more than a couple percent. If speed did vary, we should also hear this oscillation during the operation of the expander, but we do not.
- A lubrication or other internal affect in the Katrix expander is periodically restricting flow rate into the expander. This type of problem would be a “breathing” effect as studied extensively in engine design. The result of this effect would be both an oscillating torque output and a mass flow oscillation, in agreement with measured results. Further exploration of the internal breathing of the Katrix expander and possibility of internal periodic blockage by lubricant (or something else) is recommended. All signs seem to indicate that flow is actually being restricted, unlikely to be caused by increased mechanical friction, but more likely caused by an actual periodic restriction of the intake or exhaust pathways of the air through the expander.
Whatever the cause, the oscillating torque periodically saturates the sensor at its maximum value as can be seen in Figure 14. For this reason, the last two data run at the highest rotational speeds tested, had excessive torque sensor saturation and were not reported in the efficiency analysis.
It is also worth noting that although we were careful in our data collection, there are ways in which these efficiency results could overpredict (or underpredict) actual performance. Typically, the mass flow rate measurement is the most difficult to measure, but agreement between the multiple mass flow rate sensors indicates this is not likely an issue. We also ignored environmental heat transfer into or out of the system because the temperature of the tested working fluid on average at inlet and outlet was within a couple degrees of ambient conditions. However, there were not redundant measurements for torque, temperature, angular velocity, nor downstream pressure in this test setup. If the downstream temperature or pressure measurement were too high, upstream temperature too low, or torque measured too high, these results would overpredict actual performance. Additionally, there was no downstream measurement of mass flow, so internal leakage out through the oil-sump could overpredict efficiency, although internal leakage to the outlet would not bias the results. Lastly, recording the velocity measurement as the set point of the VFD does not reflect slip due to loading of the motor, but because the rated capacity of the motor was about 20 times the output of the expander (16 kW motor vs. 800 W expander output), this slip would be inconsequential, and when combined with the inaccuracy of the VFD at maintaining set point, would still be minor (<2%) as compared with the other measurement inaccuracies in the test setup.
Given the limitations of the test setup, there are several factors that lead us to believe the measured readings were indeed accurate. For instance, the upstream piping was the right temperature to the touch, and frost formation on the expander outlet indicated the thermocouple was certainly not reading too low. Additionally, pressure gauges on the expander inlet confirmed the sensor reading, but downstream pressure was harder to verify because the expander outlet was vented to atmosphere. Furthermore, the torque sensor was calibrated by the manufacturer, and then again under static load in our laboratory.
Conclusions
The results of testing show that rotary lobe expanders exhibit promise for small-scale efficient systems. Not only are the mechanisms simple and easy to manufacture, but an expansion ratio greater than 8:1 is very good for a device this small and simple. Furthermore, positive expansion devices can expand wet fluids, opening up the possibility of using water at saturated conditions. Water is an excellent fluid to use for DCS-CHP systems because of its benign nature, ubiquity, and unsurpassed two-phase heat transfer properties. Additionally, the boiling point of water is well matched to the grades of heat used in residential and commercial establishments. Detailed analysis of DCS-CHP systems [14] shows that a combination of expander efficiency and pressure ratio enables high overall solar-electric system efficiency. Only further testing with steam will demonstrate whether the Katrix expander efficiency is good enough to justify use in solar combined heat and power systems.
In summary, the current generation Katrix expander was experimentally verified to provide an isentropic efficiency of 22–25%, thermomechanical efficiency of 80–95%, and pressure ratio of 6–11. A failure of the device, however, halted testing prematurely, and could have led to the lower measured efficiency compared to previous versions of this expander. This technology, originally developed for waste-heat applications with funding from the Australian government and private sources, will need to be optimized for use in solar Rankine cycle applications, but should, according to the manufacturer, provide greater than 20 years of reliable operation in the 10 bar and 200–250°C operating condition range needed. The next steps in development of an efficient rotary lobe expander for DCS-CHP applications will be improving reliability, design of lubricant-free bearings that work with condensing steam, and full testing with steam as the working fluid.
Acknowledgments
The authors thank the UC Berkeley Haas School of Business Sustainable Products and Solutions Program for research funding.
Conflict of Interest
None declared.
Appendix A: Katrix Testing Equipment and Data
Test equipment
This is a list of the main test equipment, including sensors' make and model used in testing the Katrix expander:
- Upstream pressure transducer: Omega PX26-250GV
- Downstream pressure transducer: Omega PX181-300G5V
- Differential (Orifice) pressure transducer: Cole Parmer EW-68071-56
- Orifice Plate Flow Meter: Dwyer TE-D-1 with Omega PS-4G series pressure snubbers on both pressure ports
- Upstream thermocouple: Omega TJ36-CAXL-18G-6
- Downstream thermocouple: Omega TJ36-CAXL-18G-6
- Torque transducer: Interface T8-50-A4A
- Variable frequency drive: Yaskawa V-1000 Series CIMR-VU2A0056FAA with Yaskawa braking resistor pack URS-000140
- Induction motor: Leeson G150006.60
- Thermocouple DAQ board: National Instruments USB-9211
- Voltage DAQ board: National Instruments USB-6210
- 12V Power supply for all sensors: Acme Electric DMP1-120125
- Computer and data logging software: Dell Dimension 4600 with LabView Signal Express
- Rotameter: Fisher & Porter (ABB) 1” tube FP-1-35-G10 with float FP-1-GNSVGT-64A
The rotameter was calibrated at the average upstream air pressure and temperature in each test run, using the ABB provided calibration software. An example of this calibration scale is shown in Figure 15.
|
|
|
Figure 15. Rotameter calibration scale for air at 9 bar absolute pressure and 35∘C. |
Katrix measured data from test runs
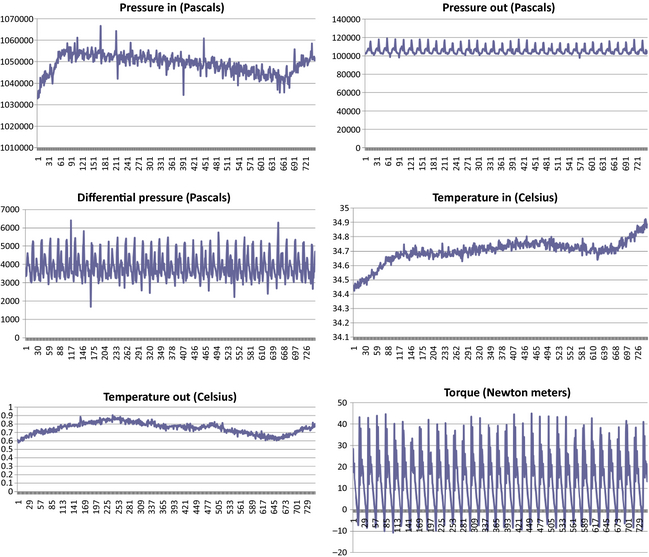
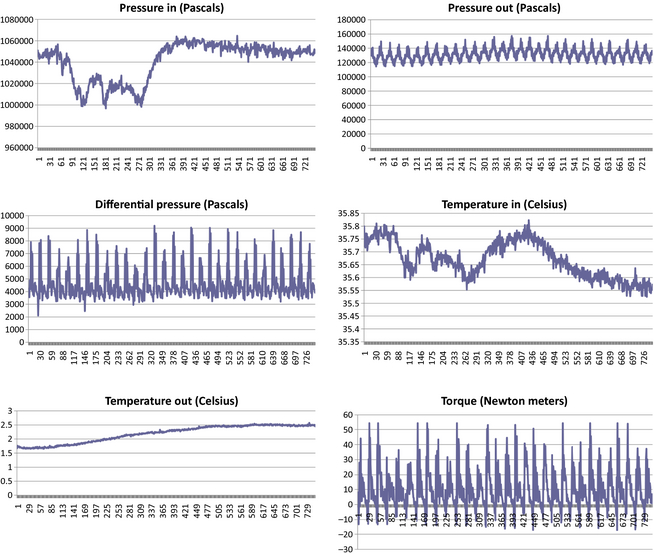
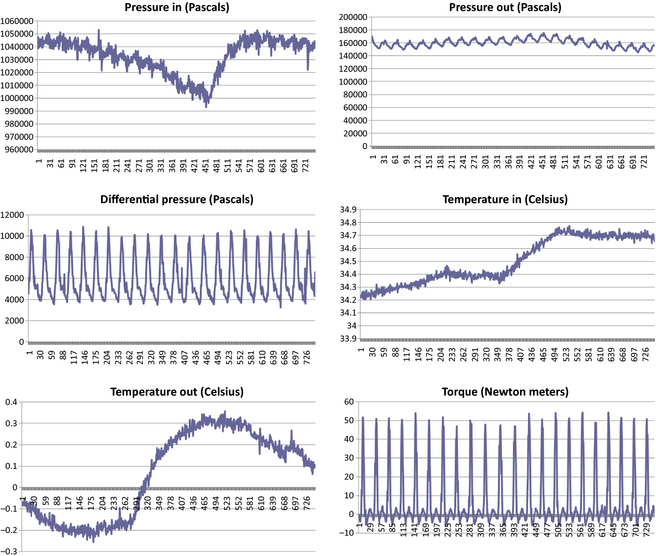
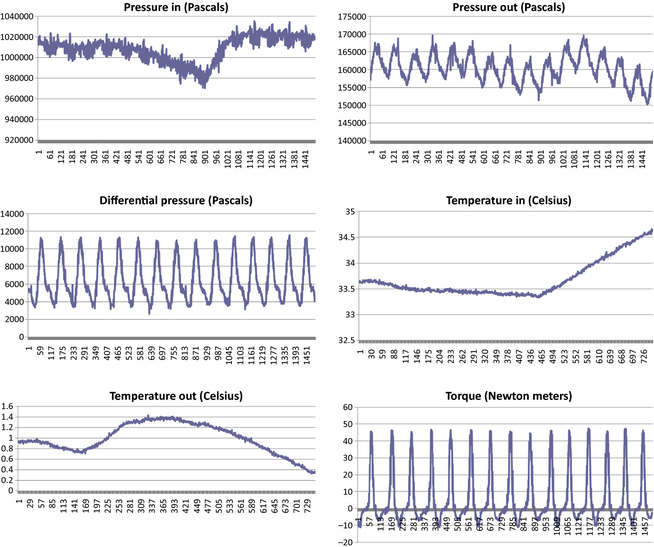
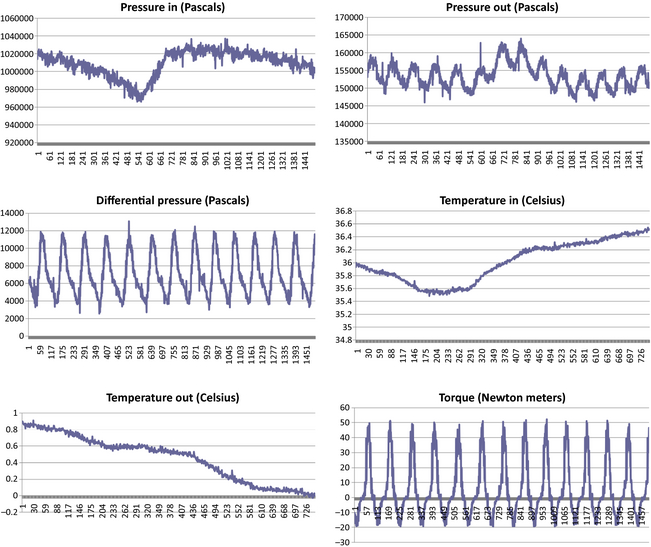
The following graphs show the raw data collected from the reported test runs (Figures 16-20).
|
|
|
Figure 16. Measured data from Katrix at 31.4 rad/sec set point, 300 sec interval. |
|
|
|
Figure 17. Measured data from Katrix at 47.1 rad/sec set point, 300 sec interval. |
|
|
|
Figure 18. Measured data from Katrix at 78.5 rad/sec set point, 300 sec interval. |
|
|
|
Figure 19. Measured data from Katrix at 94.2 rad/sec set point, 300 sec interval. |
|
|
|
Figure 20. Measured data from Katrix at 110.0 rad/sec set point, 300 sec interval. |
References
- Sultan, I. A.2005. The limacon of Pascal: mechanical generation and utilization for fluid processing. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 219:813–822.
- Sultan, I. A.2012. Optimum design of limaçon gas expanders based on thermodynamic performance. Appl. Therm. Eng.39:188–197.
- Sultan, I. A., and C. G. Schaller. 2011. Optimum positioning of ports in the limaçon gas expanders. J. Eng. Gas Turbines Power133:103002.
- Kohlenbach, P., R. McNaughton, S. Miller, and S. White. 2006. Experimental evaluation of the Katrix expander technology. Technical report, CSIRO, Collingwood, Victoria.
- Aoun, B.2009. Micro combined heat and power operating on renewable energy for residential building. Ecole Doctorale 432 Sciences des Métiers de l'Ingénieur. Paris, France.
- Badr, O., S. Naik, P. W. O'Callaghan, and S. D. Probert. 1991. Expansion machine for a low power-output steam Rankine-cycle engine. Appl. Energy39:93–116.
- Romanin, V., V. P. Carey, and Z. Norwood. 2010. Strategies for performance enhancement of Tesla turbines for combined heat and power applications. ASME Conference Proceedings2010(43956), 57–64.
- Saitoh, T., N. Yamada, and S. I. Wakashima. 2007. Solar Rankine cycle system using scroll expander. J. Environ. Eng.2: 708–719.
- Sunter, D. A., V. P. Carey, and Z. Norwood. 2010. Radial inflow turbine assessment for small-scale concentrated solar Rankine combined heat and power technology. ASME Conference Proceedings2010(43956), 45–56.
- Leibowitz, H., I. K. Smith, and N. Stosic. 2006. Cost effective small scale ORC systems for power recovery from low grade heat sources. ASME Conference Proceedings2006(47640), 521–527.
- Blevins, R. D.2003. Applied fluid dynamics, Handbook Krieger Pub. Available at http://books.google.com/books?id=WGJDPgAACAAJ.
- Mathworks. 2011. ‘No Title’. Available at http://www.mathworks.com/help/techdoc/ref/std.html.
- Lemmon, E., M. Huber, and M. McLinden. 2010. ‘NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.0’.
- Norwood, Z.2011. A better steam engine: designing a distributed concentrating solar combined heat and power system. Ph.D thesis, University of California, Berkeley. Available at http://pqdtopen.proquest.com/#abstract?dispub=3469470.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?