Hydromagnetic flow over an unsteady curved stretching surface

Abstract

In this study, the boundary layer flow of an incompressible viscous fluid over an unsteady curved stretching surface is investigated in the presence of a variable applied magnetic field. Since the geometry is curved, the basic flow equations of the present problem are modeled using curvilinear coordinates. The obtained system is then reduced into nonlinear ordinary differential equations in two dependent quantities namely the fluid pressure and velocity by introducing suitable transformations. A numerical solution for fluid pressure and velocity is obtained by using a shooting method using Runge–Kutta integration scheme. The effects of various physical parameters on the fluid velocity and pressure distribution are shown through graphs and are discussed in detail. The comparison between the present and the existing results in the literature in special case for flat unsteady stretching, i.e. (${\textstyle K\rightarrow \infty }$ ), is found in good agreement.

Keywords

Viscous fluid ; Unsteady flow ; Unsteady curved stretching sheet ; Shooting method ; Numerical solution

1. Introduction

During the past few decades, the analysis of boundary layer flows of viscous fluids due to continuously moving or stretching surface has important applications in engineering processes and polymer industry. Examples of such technological processes concerning polymers include cooling of continuous strips or filaments, glass blowing, continuous stretching of plastic films, artificial fibers, continuous casting of metals and spinning of fibers, hot rolling, wire drawing, glass fiber, paper production etc. The viscous fluid subject to a stretching surface was first analyzed by Crane [1] . He obtained an exact and closed form similarity solution. Gupta and Gupta [2] discussed the heat and mass transfer due to a porous stretching sheet. They presented the analysis for both suction and blowing cases. The existence and uniqueness of stretching flow is discussed by Macleod and Rajagopal [3] . In recent years, the Cranes problem [1] is extended to discuss the various aspects of the flow and heat transfer characteristics with linear and power-law surface velocities by many authors; for detail the readers are referred to the References [4] , [5] , [6] , [7] , [8] , [9] , [10]  and [11] and the literature therein.

In the above discussed literature the stretching velocity and flow patterns are independent of time. However, in many engineering and technological problems, the stretching may start impulsively from rest, and the transient or unsteady aspects become more interesting. Wang [12] was the first to initiate the study of boundary layer flow of a finite liquid film over an unsteady stretching surface and reduced the time dependent flow equations into nonlinear ordinary differential equations using a special type of similarity transformations. Elbashbeshy and Bazid [13] presented the similarity solution of boundary layer flow and heat transfer over an unsteady stretching sheet. Bhattacharyya et al. [14] studied the unsteady MHD boundary layer flow with diffusion and first-order chemical reaction over a permeable stretching sheet with suction or blowing. A literature survey indicates that the problem of unsteady stretching surface for various aspects have been discussed by many researchers; for the details interested readers are referred to the References [15] , [16] , [17] , [18] , [19] , [20] , [21] , [22] , [23]  and [24] and the references therein.

In all the above studies the stretching sheet is considered to be flat, and mathematical modeling is carried out using Cartesian coordinates. The mathematical modeling in the case of curved stretching sheet having a constant curvature is first provided by Sajid et al. [25] . They obtained the governing equations using a curvilinear coordinates system. Abbas et al. [26] studied the laminar flow and heat transfer analysis of an electrically conducting viscous fluid over a curved stretching surface with constant and variable surface temperature. Recently, Naveed et al. [27] analyzed the effect of radiation and magnetic field on a micropolar fluid over a curved stretching surface. Very recently, Rosca and Pop [28] have analyzed the unsteady boundary layer flow over a permeable curved stretching/shrinking surface. The present analysis aims to study the unsteady boundary layer flow of an incompressible viscous fluid over an unsteady curved stretching surface in the presence of applied magnetic field. Similarity solutions of the fluid velocity and pressure distribution are obtained, and the reduced ordinary differential equations are solved numerically using shooting method with Runge–Kutta integration scheme. Numerical results of the fluid velocity and pressure distribution as well as the local skin–friction coefficient are shown through graphs for different physical parameters.

2. Flow equations

Consider the two-dimensional, unsteady boundary layer flow of an incompressible viscous fluid over an unsteady curved stretching sheet coiled in a circle of radius ${\textstyle R}$ about the curvilinear coordinates ${\textstyle r}$ and ${\textstyle s}$ . It is further assumed that radius of curved stretching surface is a function of time and take ${\textstyle R\left(t\right)=R_{0}{\sqrt {1-\alpha t}}}$ , where ${\textstyle R_{0}}$ is a positive constant. At time ${\textstyle t=0}$ , the surface is stretched with the velocity ${\textstyle U_{w}{\mbox{ }}\left(s,{\mbox{ }}t\right)}$ along the ${\textstyle s}$ -direction. It is also assumed that the fluid is electrically conducting, and a transfer magnetic field ${\textstyle B\left(t\right)}$ is applied in the ${\textstyle r}$ -direction. The induced magnetic field is neglected due to a small magnetic Reynolds number assumption. Under these assumptions along with the boundary layer approximations, the governing equations for the flow are given as:

${\frac {\partial }{\partial r}}\left\{\left(r+R\right)v\right\}+$$R{\frac {\partial u}{\partial s}}=0,$

( 1)

${\frac {u^{2}}{r+R}}={\frac {1}{\rho }}{\frac {\partial p}{\partial r}},$

( 2)

${\frac {\partial u}{\partial t}}+v{\frac {\partial u}{\partial r}}+$${\frac {Ru}{r+R}}{\frac {\partial u}{\partial s}}+{\frac {uv}{r+R}}$ ${\mbox{ }}=-{\frac {1}{\rho }}{\frac {R}{r+R}}{\frac {\partial p}{\partial s}}+$$\nu \left({\frac {{\partial }^{2}u}{\partial r^{2}}}+{\frac {1}{r+R}}{\frac {\partial u}{\partial r}}-\right.$$\left.{\frac {u}{{\left(r+R\right)}^{2}}}\right)-{\frac {\sigma B_{0}^{2}}{\rho }}u,$

( 3)

where ${\textstyle v}$ and ${\textstyle u}$ are the velocity components in ${\textstyle r}$ - and ${\textstyle s}$ -directions, respectively, ${\textstyle \rho }$ is the fluid density, ${\textstyle p}$ is the pressure, ${\textstyle \nu }$ is the kinematics viscosity of fluid and ${\textstyle \sigma }$ is the electrical conductivity of the fluid. Here we assume that ${\textstyle B\left(t\right)}$ is of the form

$B\left(t\right)=B_{0}{\mbox{ }}{\left(1-\alpha t\right)}^{1/2}{\mbox{​}},$

where ${\textstyle B_{0}}$ is the constant magnetic field.

The appropriate boundary conditions for the velocity profile are:

${\begin{array}{llll}u={\frac {as}{\left(1-\alpha t\right)}},&v=0,&{\mbox{at}}&r=0,\\u\rightarrow 0,&{\frac {\partial u}{\partial r}}\rightarrow 0,&{\mbox{as}}&r\rightarrow \infty .\end{array}}$

( 4)

where ${\textstyle a>0}$ and ${\textstyle \alpha \geq 0}$ are constants (with ${\textstyle \alpha t<1}$ ) and have dimension of (time)⁻¹ .

We define the following similarity transformations as:

${\begin{array}{ll}u={\frac {as}{\left(1-\alpha t\right)}}f^{'}\left(\eta \right),&v={\frac {-R}{r+R}}{\sqrt {\frac {a\nu }{\left(1-\alpha t\right)}}}f\left(\eta \right),\\\eta ={\sqrt {\frac {a}{\nu \left(1-\alpha t\right)}}}r,&p={\frac {\rho a^{2}s^{2}}{{\left(1-\alpha t\right)}^{2}}}P\left(\eta \right).\end{array}}$

( 5)

Using Eq. (5) , the continuity Eq. (1) is automatically satisfied, and Eqs. (2) and (3) yield

${\frac {\partial P}{\partial \eta }}={\frac {{f^{'}}^{2}}{\eta +K}},$

( 6)

${\frac {2K}{\eta +K}}P=f^{'''}+{\frac {f^{''}}{\eta +K}}-$${\frac {f^{'}}{{\left(\eta +K\right)}^{2}}}-{\frac {K}{\eta +K}}{f^{'}}^{2}+$${\frac {K}{\eta +K}}ff^{''}$ ${\mbox{ }}+{\mbox{ }}{\frac {K}{{\left(\eta +K\right)}^{2}}}ff^{'}-$$M^{2}f^{'}-\delta \left({\frac {\eta }{2}}f^{''}+f^{'}\right),$

( 7)

subject to the boundary conditions

${\begin{array}{ll}f\left(0\right){\mbox{ }}{\mbox{ }}{\mbox{ }}=0,&f^{'}\left(0\right){\mbox{ }}{\mbox{ }}=1,\\f^{'}\left(\infty \right)=0,&f^{''}\left(\infty \right)=0.\end{array}}$

( 8)

where ${\textstyle K=R{\sqrt {a/\nu }}}$ is the dimensionless radius of curvature, ${\textstyle M^{2}=\sigma B_{0}^{2}/\rho a}$ is the dimensionless magnetic parameter or the Hartmann number, and ${\textstyle \delta =\alpha /a}$ is the unsteadiness parameter. It is worth mentioning that by taking ${\textstyle K\rightarrow \infty }$ and ${\textstyle \delta =0}$ , Eq. (7) in the absence of pressure gradient and body forces is reduced to the classical problem of flat stretching sheet discussed by Crane [1] .

$f^{'''}-{f^{'}}^{2}+ff^{''}=0.$

To eliminate the pressure from Eqs. (6) and (7) we differentiate Eq. (7) with respect to ${\textstyle \eta }$ and then putting the value of ${\textstyle \partial P/\partial \eta }$ from Eq. (6) , finally we get

$f^{iv}+{\frac {2f^{'''}}{\eta +K}}-{\frac {f^{''}}{{\left(\eta +K\right)}^{2}}}+$${\frac {f^{'}}{{\left(\eta +K\right)}^{3}}}-{\frac {K}{\eta +K}}\left(f^{'}f^{''}-\right.$$\left.ff^{'''}\right)-{\frac {K}{{\left(\eta +K\right)}^{2}}}\left(f^{{'}2}-\right.$$\left.ff^{''}\right)$ ${\mbox{ }}-{\frac {K}{{\left(\eta +K\right)}^{3}}}ff^{'}-$$M^{2}f^{''}-M^{2}{\frac {f^{'}}{\eta +K}}-{\frac {\delta }{\eta +K}}\left({\frac {\eta }{2}}f^{''}+\right.$$\left.f^{'}\right)-\delta \left({\frac {\eta f^{'''}}{2}}+\right.$$\left.{\frac {3f^{''}}{2}}\right)=0.$

( 9)

Once we obtain the fluid velocity profile${\textstyle f\left(\eta \right)}$ , the pressure can be determined from Eq. (7) of the form

$P\left(\eta \right)={\frac {\eta +K}{2K}}\left[{\begin{array}{c}f^{'''}+{\frac {f^{''}}{\eta +K}}-{\frac {f^{'}}{{\left(\eta +K\right)}^{2}}}-{\frac {K}{\eta +K}}{f^{'}}^{2}+{\frac {K}{\eta +K}}ff^{''}+\\{\frac {K}{{\left(\eta +K\right)}^{2}}}ff^{'}-M^{2}f^{'}-\delta \left({\frac {\eta }{2}}f^{''}+f^{'}\right)\end{array}}\right].$

( 10)

The physical quantity of interest is the skin–friction coefficient along the ${\textstyle s}$ -directions, which is defined as

$C_{f}={\frac {{\tau }_{rs}}{\rho u_{w}^{2}}},$

( 11)

where ${\textstyle {\tau }_{rs}}$ is the wall shear stress along the ${\textstyle s}$ -directions, which is given by

${\tau }_{rs}={\mu \left({\frac {\partial u}{\partial r}}-{\frac {u}{\left(r+R\right)}}\right)\vert }_{r=0}{\mbox{​}},$

( 12)

Using Eqs. (5) and (12) , Eq. (11) becomes

${Re}_{s}^{1/2}C_{f}=f^{''}\left(0\right)-{\frac {f^{'}\left(0\right)}{K}},$

( 13)

where ${\textstyle {Re}_{s}=as^{2}/\nu \left(1-\alpha t\right)}$ is the local Reynold number.

3. Result and discussion

We compute the velocity profile and pressure distribution by solving Eqs. (9) and (10) with the boundary conditions [Eq. (8) ] numerically using fourth order Runge–Kutta method combined with the Newton–Raphson technique. The fluid velocity ${\textstyle f^{'}\left(\eta \right)}$ and the pressure distribution ${\textstyle P\left(\eta \right)}$ are plotted in order to see the effects of the various parameters, for example, the dimensionless radius of curvature ${\textstyle K}$ , unsteadiness ${\textstyle \delta }$ and the magnetic parameter ${\textstyle M}$ in Fig. 1 , Fig. 2 , Fig. 3 , Fig. 4 , Fig. 5  and Fig. 6 . Furthermore, we calculate and show the values of the skin–friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ for several parameters both graphically and in tabular form (see Table 1  and Table 2 ).

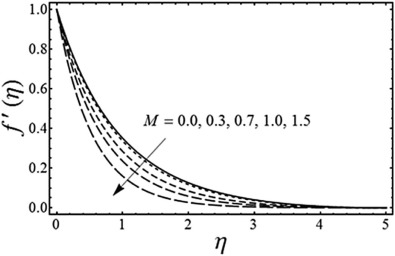
Fig. 1. Variation of the magnetic parameter ${\textstyle M}$ on the horizontal component of velocity ${\textstyle f^{'}\left(\eta \right)}$ with ${\textstyle K=10}$ and ${\textstyle \delta =0.2}$ .

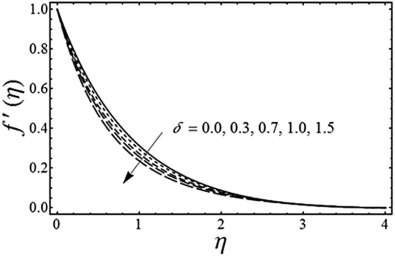
Fig. 2. Variation of the unsteady parameter ${\textstyle \delta }$ on the horizontal component of velocity ${\textstyle f^{'}\left(\eta \right)}$ with ${\textstyle M=0.5}$ and ${\textstyle K=10}$ .

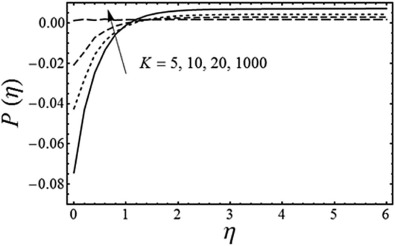
Fig. 3. Variation of the dimensionless radius of curvature ${\textstyle K}$ on the pressure distribution ${\textstyle P\left(\eta \right)}$ with ${\textstyle \delta =0.1}$ and ${\textstyle M=0.2}$ .

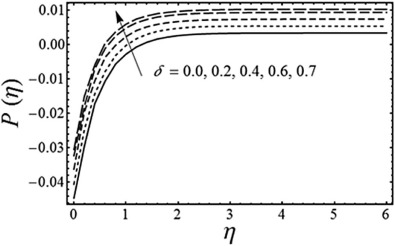
Fig. 4. Variation of the unsteadiness parameter ${\textstyle \delta }$ on the pressure distribution ${\textstyle P\left(\eta \right)}$ with ${\textstyle K=10}$ and ${\textstyle M=0.2}$ .

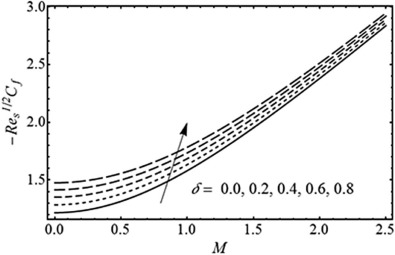
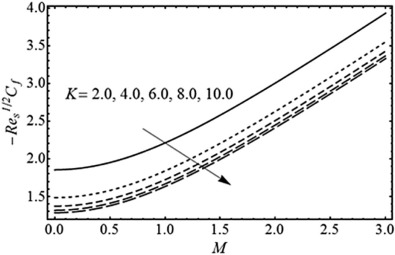
Fig. 5. Influence of unsteadiness parameter ${\textstyle \delta }$ on the skin friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ with${\textstyle M}$ and ${\textstyle K=10}$ fixed.

Fig. 6. Influence of dimensionless radius of curvature ${\textstyle K}$ on the skin friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ with ${\textstyle M}$ and ${\textstyle \delta =0.2}$ fixed.

Table 1. Numerical values of skin friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ for different values of ${\textstyle \delta }$ and ${\textstyle M}$ by keeping ${\textstyle K=1000}$ fixed.

$M$	$\delta$	Jhankal and Kumar [10]	Sharidan et al. [19]	Ibrahim and Shankar [21]	Present result
$1$		$1.531388$			$1.531386$
$3$		$2.040808$			$2.040809$
$4$		$2.262076$			$2.262075$
$1$	$1.2$			$1.7889$	$1.7889$
$3$				$2.2804$	$2.2809$
$4$				$2.4900$	$2.4904$
$0$	$0.4$			$1.1844$	$1.1845$
	$0.8$		$1.3321$	$1.3420$	$1.3421$
	$1.2$		$1.4691$	$1.4883$	$1.4883$

Table 2. Numerical values of skin friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ for different values of ${\textstyle \delta }$ , ${\textstyle M}$ and ${\textstyle K}$ .

$K$	$M$	$\delta =0$	$\delta =0.4$	$\delta =0.8$	$\delta =1.2$
5	0.2	1.36183	1.49917	1.62521	1.74143
20		1.17159	1.30220	1.42338	1.53604
100		1.12479	1.25308	1.37252	1.48388
1000		1.11452	1.24225	1.36127	1.47231
10	0	1.21635	1.35116	1.47552	1.59062
	0.5	1.31493	1.44032	1.55706	1.66599
	1.0	1.58031	1.68465	1.78378	1.87803
	2	2.37968	2.44653	2.51203	2.57619

Table 1 is made in order to validate the method in the present study and to judge the accuracy of the present results, comparisons are given with the existing results of Jhankal and Kumar [10] (in the case of steady flat stretching sheet), and with those of Sharidan et al. [19] and Ibrahim and Shankar [21] (in the case of unsteady flat stretching sheet) by taking the dimensionless radius of curvature ${\textstyle K\rightarrow \infty }$ , i.e. ${\textstyle K=1000}$ , and are found in good agreement. Table 2 is given to show the numerical values of the skin–friction coefficient for several values of ${\textstyle K}$ , ${\textstyle \delta }$ and ${\textstyle M}$ . It is found that the magnitude of ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ increased by increasing the value of ${\textstyle M}$ and ${\textstyle \delta }$ , but it has the reverse behavior for ${\textstyle K}$ as the skin–friction coefficient decreased by increasing the value of ${\textstyle K}$ .

Fig. 1 shows that the fluid velocity profile ${\textstyle f^{'}\left(\eta \right)}$ for several values of the magnetic parameter ${\textstyle M}$ with ${\textstyle K=10}$ and ${\textstyle \delta =0.2}$ is fixed. It is seen from this figure that the fluid velocity along the sheet decreases with the increase of magnetic parameter ${\textstyle M}$ . Moreover, the momentum boundary layer thickness also decreases as we increase the value of ${\textstyle M}$ . This is because for the present analysis the magnetic force acts as a resistance to the flow. Fig. 2 displays the variation of the unsteadiness parameter ${\textstyle \delta }$ on the horizontal component of velocity ${\textstyle f^{'}\left(\eta \right)}$ . It is seen from Fig. 2 that the fluid velocity decreases by increasing the value of unsteadiness parameter ${\textstyle \delta }$ . It is also evident from Fig. 2 that the thickness of the momentum boundary layer decreases with an increase in ${\textstyle \delta }$ . Fig. 3 exhibits the pressure distribution ${\textstyle P\left(\eta \right)}$ for various values of dimensionless radius of curvature ${\textstyle K}$ when ${\textstyle M=0.2}$ and ${\textstyle \delta =0.1}$ are fixed. From Fig. 3 it is found that the pressure distribution ${\textstyle P\left(\eta \right)}$ is increased inside the momentum boundary layer with an increase in the dimensionless radius of curvature. Moreover, the pressure distribution goes to zero far away from the sheet and the magnitude of the pressure distribution approaches to zero by taking the dimensionless radius of curvature ${\textstyle K\rightarrow \infty }$ (in this case the curved stretching sheet converts to the flat stretching sheet). The physical reasoning of this behavior is that as we move away from the surface the streamlines of the flow behave in the same manner as they do in the flow over a flat stretching surface. Fig. 4 elucidates the change in the pressure distribution ${\textstyle P\left(\eta \right)}$ for different values of an unsteadiness parameter ${\textstyle \delta }$ by keeping ${\textstyle M=0.2}$ and ${\textstyle K=10}$ fixed. It is seen from Fig. 4 that the absolute value of pressure distribution decrease with an increase in an unsteadiness parameter ${\textstyle \delta }$ .

Fig. 5 gives the change in the skin–friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ versus the magnetic parameter ${\textstyle M}$ for various values of unsteadiness parameter ${\textstyle \delta }$ with ${\textstyle K=10}$ fixed. From Fig. 5 it is evident that the absolute value of skin–friction coefficient is increased by increasing the magnetic parameter ${\textstyle M}$ and unsteadiness parameter ${\textstyle \delta }$ . Fig. 6 shows the change in the skin–friction coefficient versus ${\textstyle M}$ for several values of the dimensionless radius of curvature ${\textstyle K}$ with ${\textstyle \delta =0.2}$ fixed. From Fig. 6 , one can see that the absolute values of the skin–friction coefficient decrease by increasing the value of ${\textstyle K}$ ; however, it is increased with increasing of magnetic parameter ${\textstyle M}$ . The skin–friction coefficient increases with the increase of the value of ${\textstyle M}$ , and the velocity of the fluid decreases as ${\textstyle M}$ increases (see Fig. 1 ).

4. Concluding remarks

In the summary, the boundary layer flow of a viscous fluid over an unsteady curved stretching sheet with magnetic field is discussed. The resultant non-linear equations are solved numerically using a Runge–Kutta method combined with the Newton–Raphson technique. The physical interpretation of the fluid velocity, pressure distribution and the skin–friction coefficient for various values of involved parameters are given graphically and in tabular form. It is noted that the fluid velocity as well as momentum boundary layer thickness are decreased for both parameters ${\textstyle M}$ and ${\textstyle \delta }$ . Since pressure remains no more constant for curved surface as mentioned by Sajid et al. [25] the magnitude of the pressure distribution is decreased with an increase in ${\textstyle K}$ and ${\textstyle \delta }$ . The magnitude of the skin–friction coefficient ${\textstyle -{Re}_{s}^{1/2}C_{f}}$ increases with an increase in ${\textstyle \delta }$ and ${\textstyle M}$ ; however, it decreases with the increase in ${\textstyle K}$ . By taking ${\textstyle K\rightarrow \infty }$ , i.e. ${\textstyle K=1000}$ , the results of flat unsteady stretching sheet are also recovered. The present study is theoretical a study that has impact on technological application in stretch-forming machine with curving jaws.

References

1. [1] L.J. Crane; Flow past a stretching plate; Z. Angew. Math. Mech, 21 (4) (1970), pp. 645–647
2. [2] P.S. Gupta, A.S. Gupta; Heat and mass transfer on a stretching sheet with suction and blowing; Can. J. Chem. Eng, 55 (1977), pp. 744–746
3. [3] B. Macleod, K.R. Rajagopal; On the uniqueness of the flow of a Navier–Stokes fluid due to stretching boundary; Arch. Ration. Mech. Anal, 98 (4) (1987), pp. 385–393
4. [4] S.J. Liao; A new branch of solution of boundary-layer flows over a stretching flat plate; Int. J. Heat Mass Transf, 49 (2005), pp. 2529–2539
5. [5] A. Ishak, R. Nazar, I. Pop; Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet; Heat Mass Transf, 44 (2008), pp. 921–927
6. [6] S. Mukhopadhyay, G.C. Layek, S.A. Samad; Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity; Int. J. Heat Mass Transf, 48 (2005), pp. 4460–4465
7. [7] K. Vajravelu; Flow and heat transfer in a saturated porous medium over a stretching surface; J. Appl. Math. Mech, 74 (1994), pp. 605–614
8. [8] R. Cortell; Effect of viscous dissipation and radiation on the thermal boundary layer over a nonlinear stretching sheet; Phys. Lett. A, 372 (2008), pp. 631–637
9. [9] Z. Abbas, T. Hayat; Stagnation slip flow and heat transfer over a nonlinear stretching sheet; Numer. Methods Partial Differ. Equ, 27 (2011), pp. 302–314
10. [10] A.K. Jhankal, M. Kumar; MHD boundary-layer flow past a stretching plate with heat transfer; Int. J. Eng. Sci, 2 (2013), pp. 9–13
11. [11] M. Sajid, N. Ali, Z. Abbas, T. Javed; Stretching flows with general slip boundary condition; Int. J. Mod. Phys. B, 30 (2010), pp. 5939–5947
12. [12] C.Y. Wang; Liquid film on an unsteady stretching sheet; Q. Appl. Math, 48 (1990), pp. 601–610
13. [13] E.M.A. Elbashbeshy, M.A.A. Bazid; Heat transfer over an unsteady stretching surface; Heat Mass Transf, 41 (2004), pp. 1–4
14. [14] K. Bhattacharyya, S. Mukhopadhyay, G.C. Layek; Unsteady MHD boundary layer flow with diffusion and first-order chemical reaction over a permeable stretching sheet with suction or blowing; Chem. Eng. Commun, 200 (2013), pp. 379–397
15. [15] M. Abd El-Aziz; Radiation effect on the flow and heat transfer over an unsteady stretching sheet; Int. Commun. Heat Mass Transf, 36 (2009), pp. 521–524
16. [16] S. Mukhopadhyay; Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in medium; Int. J. Heat Mass Transf, 52 (2009), pp. 3261–3265
17. [17] A. Ishak, R. Nazar, I. Pop; Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature; Nonlinear Anal. Real World Appl, 10 (2009), pp. 2909–2913
18. [18] T. Hayat, M. Qasim, Z. Abbas; Radiation and mass transfer effects on the magnetohydrodynamic unsteady flow induced by a stretching sheet; Z. Naturforsch. A, 65a (2010), pp. 231–239
19. [19] S. Sharidan, T. Mahmood, I. Pop; Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet; Int. J. Appl. Mech. Eng, 11 (2006), pp. 647–654
20. [20] D. Pal; Combined effects of non-uniform heat source/sink and thermal radiation on heat transfer over an unsteady stretching permeable surface; Commun. Nonlinear Sci. Numer. Simul, 16 (2011), pp. 1890–1904
21. [21] W. Ibrahim, B. Shankar; Unsteady MHD boundary-layer flow and heat transfer due to stretching in the presence of heat source or sink; Comput. Fluids, 70 (2012), pp. 21–28
22. [22] D. Nikodijevic, Z. Stamenkovic; Generaleristics of unsteady MHD temperature boundary layer; Int. J. Non Linear Mech, 73 (2015), pp. 75–84
23. [23] A. Khalid, I. Khan, A. Khan, S. Shafie; Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium; Eng. Sci. Technol. Int. J., 18 (2015), pp. 309–317
24. [24] N. Sandeep, C. Sulochane, B.R. Kumar; Unsteady MHD radiative flow and heat transfer of a dusty nanofluid over an exponentially stretching surface; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.06.004
25. [25] M. Sajid, N. Ali, T. Javed, Z. Abbas; Stretching a curved surface in a viscous fluid; Chin. Phys. Lett, 27 (2010), p. 024703
26. [26] Z. Abbas, M. Naveed, M. Sajid; Heat transfer analysis for stretching flow over curved surface with magnetic field; J. Eng. Thermophys, 22 (04) (2013), pp. 337–345
27. [27] M. Naveed, Z. Abbas, M. Sajid; MHD flow of a micropolar fluid due to a curved stretching sheet with thermal radiation; J. Appl. Fluid Mech, 9 (1) (2016), pp. 131–138
28. [28] N.C. Rosca, I. Pop; Unsteady boundary layer flow over a permeable curved stretching/shrinking surface; Eur. J. Mech. B/Fluids, 51 (2015), pp. 61–67