Chebyshev rational functions approximation for model order reduction using harmony search

Abstract

A new method for model reduction of linear systems is presented, based on Chebyshev rational functions, using the Harmony Search (HS) algorithm. First, the full order system is expanded and then a set of parameters in a fixed structure are determined, whose values define the reduced order system. The values are obtained by minimizing the errors between the ${\textstyle l}$ first coefficients of the Chebyshev rational function expansion of full and reduced systems, using the HS algorithm. To assure stability, the Routh criterion is used as constraints in the optimization problem. To present the ability of the proposed method, three test systems are reduced. The results obtained are compared with other existing techniques. The results obtained show the accuracy and efficiency of the proposed method.

Keywords

Chebyshev rational functions ; Harmony search algorithm ; Order reduction ; Orthogonal functions ; Routh array

1. Introduction

Reduced order models are highly desirable for engineers in system analysis, synthesis and simulation of complicated high-order systems, since the analysis and design of such systems is not an easy task. Various methods for model reduction are reported in the literature in the time and frequency domains. Model reduction was started by Davison in 1966  [1] and followed by Chidambara, who suggested several modifications to Davison’s approach  [2] , [3]  and [4] . After that, different approaches were proposed using dominant eigenvalue retention  [1]  and [5] , Routh approximation  [6] , Hurwitz polynomial approximation  [7]  and [8] , the stability equation method  [9]  and [10] , moments matching [11] , [12] , [13]  and [14] , the continued fraction method  [15] , [16]  and [17] , Pade approximation  [18] and etc.

The issue of optimality in model reduction was considered by Wilson  [19]  and [20] , who suggested an optimization approach based on minimization of the integral squared impulse response error between full and reduced-order models. This attempt was continued by other researchers through other approaches  [21] , [22] , [23]  and [24] .

In 1981  [25] , the controllability and observability of the states were considered in model reduction by Moore. The suggested approach suffered from steady state errors but the stability of the reduced model was assured if the original system was also stable  [26] . Furthermore, the concept of ${\textstyle H_{\infty }}$ , ${\textstyle H_{2}}$ , ${\textstyle L_{2}}$ and ${\textstyle L_{\infty }}$ were used for model reduction in  [27] , [28] , [29]  and [30] .

In recent decades, evolutionary techniques, such as Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), have been used for order reduction of systems  [31] , [32]  and [33] . In these approaches, the reduced order model parameters are achieved by minimizing a fitness function, which is often Integral Square Error (ISE), Integral Absolute Error (IAE), ${\textstyle H_{2}}$ norm or ${\textstyle H_{\infty }}$ norm  [34] , [35]  and [36] .

This paper proposes an alternative method for order reduction based on Chebyshev rational functions, using the HS algorithm. The full order system is expanded and then the ${\textstyle l}$ first coefficients of Chebyshev rational function expansion are obtained. A desire fixed structure for the reduced order model is considered and a set of parameters are defined, whose values determine the reduced order system. These unknown parameters are determined using the harmony search algorithm by minimizing the errors between the ${\textstyle l}$ first coefficients of Chebyshev rational function expansion of full and reduced systems. To assure stability, the Routh criterion is applied, as used in  [37] , where it states optimization problems as constraints, which, subsequently, are converted to constrained optimization problems. To show the accuracy of the proposed method, three systems are reduced by the proposed method and compared with those available in the literature.

To make a proper background, Chebyshev rational functions and the harmony search are briefly explained in Sections  2  and 3 , respectively. The proposed method is explained in Section  4 . The ability of the proposed approach is shown in Section  5 , and, finally, the paper is concluded in Section  6 .

2. The Chebyshev rational functions

The Chebyshev rational functions are a sequence of functions that are both orthogonal and rational  [38] . A rational Chebyshev function of degree ${\textstyle l}$ is presented as:

$R_{l}(x)=T_{l}({\frac {x-1}{x+1}}){\mbox{,}}$

( 1)

where ${\textstyle T_{l}(x)}$ is a Chebyshev polynomial and defined by a recursive formula as:

$T_{0}(x)=1{\mbox{,}}$

( 2)

Using the orthogonality relationship, an arbitrary function, ${\textstyle f(x)}$ , can be expanded as:

$f(x)=\sum _{l=0}^{\infty }F_{l}R_{l}(x){\mbox{,}}$

( 3)

where ${\textstyle F_{l}}$ is given by the following equations:

$F_{l}={\frac {2}{c_{l}\pi }}\int _{0}^{\infty }f(x)R_{l}(x)W(x)dx{\mbox{,}}$

( 4)

in which, ${\textstyle c_{l}}$ equals 2 for ${\textstyle l=0}$ and ${\textstyle c_{l}}$ equals 1 for ${\textstyle l\geq 1}$ . Also, W is given as:

$W(x)={\frac {1}{(x+1){\sqrt {x}}}}{\mbox{.}}$

( 5)

Therefore, by considering the first ${\textstyle l}$ terms of Eq. (3) , a good approximant of ${\textstyle f(x)}$ is obtained.

3. Harmony search algorithm

The HS is based on a natural musical process, which searches for a perfect state of harmony. In general, the HS algorithm works as follows  [39]  and [40] :

Step 1. Initialization: Define the objective function and decision variables, and input the system parameters and the boundaries of the decision variables. The optimization problem can be defined as:

Minimize ${\textstyle f(x)}$ subject to ${\textstyle x_{iL}<x_{i}<x_{iU}(i=1,2,\ldots ,N)}$ where ${\textstyle x_{iL}}$ and ${\textstyle x_{iU}}$ are the lower and upper bounds for decision variables.

The HS algorithm parameters are also specified in this step. They are the Harmony Memory Size (HMS ) or the number of solution vectors in harmony memory, Harmony Memory Considering Rate (HMCR ), distance bandwidth (bw ), Pitch Adjusting Rate (PAR ), and the number of improvisations (K ), or stopping criterion. K is the same as the total number of function evaluations.

Step   2. Initialize the harmony memory (HM). The harmony memory is a memory location where all the solution vectors (sets of decision variables) are stored. The initial harmony memory is randomly generated in the region ${\textstyle [x_{iL},x_{iU}](i=1,2,\ldots ,N)}$ . This is done based on the following equation:

$x_{i}^{j}=x_{iL}+rand()\times (x_{iU}-x_{iL})\quad j=1,2,\ldots ,HMS{\mbox{,}}$

( 6)

where ${\textstyle rand()}$ is a random from a uniform distribution of ${\textstyle [0,1]}$ .

Step   3. Improvise a new harmony from the harmony memory. Generating a new harmony, ${\textstyle x_{i}^{new}}$ , is called improvisation, which is based on three rules: memory consideration, pitch adjustment and random selection. First of all, a uniform random number, r   , is generated in the range ${\textstyle [0,1]}$ . If r   is less than HMCR, the decision variable, ${\textstyle x_{i}^{new}}$ , is generated by the memory consideration; otherwise, ${\textstyle x_{i}^{new}}$ is obtained by a random selection. Then, each decision variable, ${\textstyle x_{i}^{new}}$ , will undergo a pitch adjustment with a probability of PAR if it is produced by the memory consideration. The pitch adjustment rule is given as follows:

$x_{i}^{new}=x_{i}^{new}\pm r\times bw{\mbox{.}}$

( 7)

Step   4. Update harmony memory. After generating a new harmony vector, ${\textstyle x^{new}}$ , the harmony memory will be updated. If the fitness of the improvised harmony vector, ${\textstyle x^{new}=(x_{1}^{new},x_{2}^{new},\ldots ,x_{N}^{new})}$ , is better than that of the worst harmony, the worst harmony in the HM will be replaced with ${\textstyle x^{new}}$ and become a new member of the HM.

Step 5. Repeat Steps 3–4 until the stopping criterion (maximum number of improvisations K ) is met.

4. The proposed model reduction method

Consider a stable Single-Input Single-Output (SISO) system described by the transfer function of order n as follows:

$G(s)={\frac {a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n}}{s^{n}+b_{1}s^{n-1}+b_{2}s^{n-2}+\cdots +b_{n}}}{\mbox{,}}$

( 8)

where ${\textstyle a_{i}}$ and ${\textstyle b_{i}}$ are constants.

The objective is to obtain a reduced model of order r , where r is smaller than n , such that the principal and important specifications of the full order system are retained in the reduced order model. This reduced order system is presented as follows:

$G_{r}(s)={\frac {c_{1}s^{r-1}+c_{2}s^{r-2}+\cdots +c_{r}}{s^{r}+d_{1}s^{r-1}+d_{2}s^{r-2}+\cdots +d_{r}}}{\mbox{,}}$

( 9)

where ${\textstyle c_{1},c_{2},\ldots ,c_{r}}$ and ${\textstyle d_{1},d_{2},\ldots ,d_{r}}$ are unknown constants.

To obtain the reduced model by the proposed method, firstly, the full order system is expanded based on Chebyshev rational functions. Then, the ${\textstyle l}$ first coefficients of the Chebyshev rational function expansion of the original system are obtained and shown by ${\textstyle F_{i}i=0,1,2,3,\ldots ,l}$ . Then, a desired fixed structure is considered for the reduced order model, as defined in Eq. (9) , where ${\textstyle c_{1},c_{2},\ldots ,c_{r}}$ and ${\textstyle d_{1},d_{2},\ldots ,d_{r}}$ are unknown parameters of the reduced order model that are obtained by HS. The goal of the optimization is to find the best parameters for ${\textstyle G_{r}(s)}$ . Therefore, each harmony is a ${\textstyle d}$ -dimensional vector, in which ${\textstyle d}$ is ${\textstyle c_{r}+d_{r}}$ . Each harmony is a solution to ${\textstyle G_{r}}$ and for each solution (harmony), the Chebyshev rational function expansions are obtained. Each harmony is evaluated by minimizing the following fitness function:

$J^{_{\ast }}=\sum _{i=0}^{l}(\vert F_{i}-{\overset {\mbox{ˆ}}{F}}_{i}\vert ){\mbox{,}}$

( 10)

in which ${\textstyle {\overset {\mbox{ˆ}}{F}}_{i}}$ are the coefficients of the Chebyshev rational function expansions of the reduced order system. The algorithm searches for the best harmony until the termination criteria are met. At this stage, the best parameters are given as parameters of the reduced order model.

Furthermore, the reduced model must be stable if the original system is stable. Therefore, the Routh criterion is applied to assure stability. For specifying the stability conditions, following  [41] , the denominator polynomial of the reduced order model in Eq. (9) can be shown as below:

${\begin{array}{l}\displaystyle s^{r}+h_{1}s^{r-1}+(h_{2}+h_{3}+\cdots +h_{r})s^{r-2}+h_{1}(h_{3}+h_{4}+\cdots +\\\displaystyle +h_{r})s^{r-3}+[h_{2}(h_{4}+h_{5}+\cdots +h_{r})+h_{3}(h_{5}+h_{6}+\cdots +h_{r})+\\\displaystyle +h_{4}(h_{6}+h_{7}+\cdots +h_{r})+\cdots h_{r-2}h_{r}]s^{r-4}+\cdots +\\\displaystyle +h_{1+q}h_{3+q}\cdots h_{r-2}h_{r}{\mbox{,}}\end{array}}$

( 11)

which is constructed by taking the coefficients of the first two rows of the Routh array, in which elements of its first column have the following entries:

$1,h_{1},h_{2},h_{1}h_{3},h_{2}h_{4},h_{1}h_{3}h_{5},\ldots ,h_{1+k}h_{3+k}...h_{r-2}h_{r}{\mbox{,}}$

( 12)

where k is equal to 1 for even r , and k is equal to 0 for odd r .

Comparing the entries of the array in Eq. (12) with ${\textstyle 1,d_{2},d_{4},\ldots }$ and those of the second row with ${\textstyle d_{1},d_{3},d_{5},\ldots }$ gives Eq. (13) :

${\begin{array}{c}d_{1}=h_{1}\\d_{2}=(h_{2}+h_{3}+\cdots +h_{r})\\d_{3}=h_{1}(h_{3}+h_{4}+\cdots +h_{r})\\\vdots \\d_{r}=(h_{1+k}h_{3+k}h_{r-2}h_{r}){\mbox{.}}\end{array}}$

( 13)

Substituting the above relations in the reduced order model denominators, Eq. (11) is achieved. Therefore, the necessary and sufficient condition for all roots of the reduced system to be strictly in the left-half plane is:

${\begin{array}{c}h_{1}>0\\h_{2}>0\\\vdots \\h_{r}>0{\mbox{,}}\end{array}}$

( 14)

and, subsequently:

${\begin{array}{c}d_{1}>0\\d_{2}>0\\\vdots \\d_{r}>0{\mbox{.}}\end{array}}$

( 15)

Thus, to have an optimum stable reduced system, the reduced order model’s parameters are determined by minimizing the following fitness function:

${\begin{array}{c}J=\sum _{i=0}^{l}(\vert F_{i}-{\overset {\mbox{ˆ}}{F}}_{i}\vert )\\{\mbox{subject to  }}d_{j}>0{\mbox{  for  }}j=1,\ldots ,r{\mbox{.}}\end{array}}$

( 16)

Therefore, the reduced order model is achieved, such that the ${\textstyle l}$ first coefficients of the Chebyshev rational function expansions of the full order system are equal to the ${\textstyle l}$ first coefficients of the Chebyshev rational function expansions of the reduced order model.

The proposed method can be summarized in the following steps:

Step 1: The Chebyshev rational functions of the full order system in Eq. (8) are obtained.

Step 2: A desire fixed structure is considered for the reduced order model, as defined in Eq. (9) , where ${\textstyle c_{1},c_{2}\ldots ,c_{r}}$ and ${\textstyle d_{1},d_{2},\ldots ,d_{r}}$ are unknown parameters of the reduced order model that are obtained in the next step.

Step 3: To obtain the unknown parameters, HS is applied. The goal of the optimization is to find the best parameters for ${\textstyle G_{r}(s)}$ . Therefore, each harmony is a ${\textstyle d}$ -dimensional vector, in which ${\textstyle d}$ is ${\textstyle c_{r}+d_{r}}$ . Each harmony is a solution to ${\textstyle G_{r}}$ and, for each solution (harmony), the Chebyshev rational functions are obtained. Each harmony is evaluated using the objective function defined by Eq. (16) , searching for the harmony associated with ${\textstyle J_{best}}$ until the termination criteria are met. At this stage, the best parameters are given as parameters of the reduced order model.

5. Simulation and results

To assess the efficiency of the proposed approach, it has been applied to three test systems, where a step-by-step procedure is given for the first test system.

Test system 1: The first system to be reduced is a system of order 6 given by Mukherjee in  [42] , where he uses a response matching technique to obtain the reduced system. ${\textstyle G(s)}$ is given in Box I .

${\begin{array}{l}\displaystyle G(s)=\\\displaystyle ={\frac {s^{5}+1014s^{4}+14069s^{3}+69140s^{2}+140100s+100000}{s^{6}+222s^{5}+14541s^{4}+248420s^{3}+1454100s^{2}+2220000s+1000000}}{\mbox{.}}\end{array}}$

( 17)

The reduced-order model can be obtained by the following steps:

Step 1: Based on Section  2 , the Chebyshev rational function of the full order system in Eq. (17) is obtained as:

${\begin{array}{l}\displaystyle G(s)=(0.0578)(1)+(-0.0256)({\frac {s-1}{s+1}})+\\\displaystyle +(-0.0195)({\frac {s^{2}-6s+1}{(s+1)^{2}}})+(0.0011)({\frac {s^{3}-15s^{2}+15s-1}{(s+1)^{3}}})+\\\displaystyle +(-0.0198)({\frac {s^{4}-28s^{3}+70s^{2}-28s+1}{(s+1)^{4}}})\end{array}}$

( 18)

where the fifth order (${\textstyle l=5}$ ) Chebyshev rational function of Eq. (17) is considered to present ${\textstyle G(s)}$ .

Step 2: The full order of the system represented in Eq. (17) is going to be reduced to a third-order system with the following transfer function:

$G_{r}(s)={\frac {c_{0}s^{2}+c_{1}s+c_{2}}{s^{3}+d_{0}s^{2}+d_{1}s+d_{2}}}{\mbox{,}}$

( 19)

where ${\textstyle c_{0},c_{1},c_{2}}$ and ${\textstyle d_{0},d_{1},d_{2}}$ are unknown parameters of the reduced order model.

Step 3: HS is applied to obtain the unknown parameters in Eq. (19) . Since, the goal of the optimization is to find the best parameters for ${\textstyle G_{r}(s)}$ , each harmony is a ${\textstyle d}$ -dimensional vector in which ${\textstyle d=6}$ . The HMS is selected to be 6, and the HMCR   and evaluation number are set to be 0.9 and 1000, respectively. Each harmony is a solution to ${\textstyle G_{r}}$ and, for each solution (harmony), the Chebyshev rational functions are obtained. Each harmony is evaluated using the objective function defined by Eq. (16) , searching for the best ${\textstyle J}$ , until the termination criteria are met. At this stage, the best parameters are given for the reduced order model, where the following reduced order model is obtained:

$G_{r}(s)={\frac {4.55s^{2}+27.2s+50.78}{s^{3}+54.86s^{2}+691.56s+507.67}}{\mbox{.}}$

( 20)

The Chebyshev rational functions of the obtained reduced order model are as:

${\begin{array}{l}\displaystyle G_{r}(s)=(0.0578)(1)+(-0.0256)({\frac {s-1}{s+1}})+\\\displaystyle +(-0.0195)({\frac {s^{2}-6s+1}{(s+1)^{2}}})+(0.0011)({\frac {s^{3}-15s^{2}+15s-1}{(s+1)^{3}}})+\\\displaystyle +(-0.0198)({\frac {s^{4}-28s^{3}+70s^{2}-28s+1}{(s+1)^{4}}}){\mbox{.}}\end{array}}$

( 21)

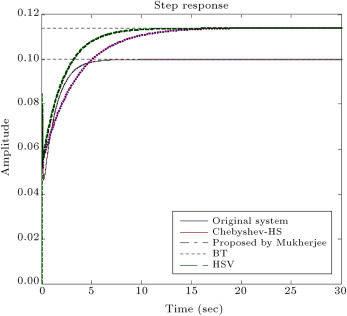
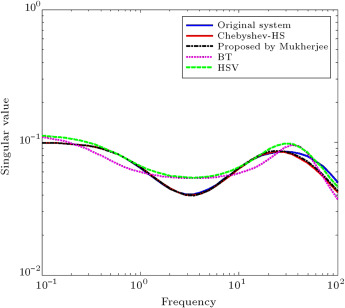
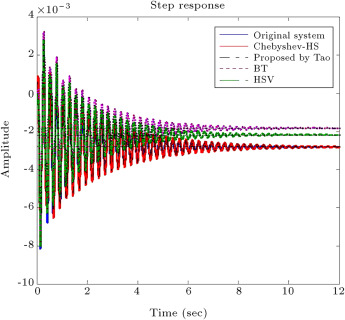
Comparing Eqs. (18)  and (21) shows that the best approximant of ${\textstyle G(s)}$ is achieved. The step response of the full order system and that of the system with a third-order reduced model is shown in Figure 1 . This figure shows that the obtained reduced order model is an adequate low-order model that retains the characteristics of a full order model. Also, to show the efficiency of the proposed method, the step and frequency responses of the obtained reduced model are compared with those available in the literature. Figure 1  and Figure 2 show a comparison of the results obtained with the proposed method by Mukherjee  [42] , Optimal Hankel norm approximation (HSV)  [43] and Balanced Truncation (BT)  [43] , respectively. It should be noted that a reduced order model is called a balanced truncation of the full order system, when a system is balanced and, then, the states corresponding to small Hankel singular values are discarded. Also, Optimal Hankel norm approximation finds a reduced order model, ${\textstyle G_{r}}$ (of degree r   ), such that the Hankel norm of the approximation error ${\textstyle (\Vert G-G_{r}\Vert _{H})}$ is minimized.

Figure 1. The step response of full order and reduced order model by the proposed method and other methods for test system 1.

Figure 2. The fequency response of full order and reduced order model by the proposed method and other methods for test system 1.

Figure 1  and Figure 2 show that the achieved results from the proposed method and the proposed method by Mukherjee are very similar to the original system, with respect to HSV and BT methods.

Furthermore, the specifications of the obtained system by the proposed method, such as steady state value, rise time, settling time and maximum overshoot, are compared with those obtained by Mukherjee  [42] , HSV and BT, shown in Table 1 . Also, Integral Square Error (ISE) and the ${\textstyle H_{\infty }}$ norm of the error between the step responses of full order and reduced order models (${\textstyle e=\vert y-y_{r}\vert }$ ) are given in Table 1 . It is clearly seen that the specifications of the reduced order model that is achieved by the proposed method and the one by Mukherjee are close to the specifications of the original system.

Table 1. Comparision of methods for test system 1.

Model	Steady state value	Over shoot (%)	Rise time (s)	Settling time (s)	ISE	Infinity-norm of error
Full order	0.1	0	2.44	4.34	–	–
Chebyshev-HS	0.1	0	2.45	4.51	1.59×10−6	0.0067
Mukherjee	0.1	0	2.45	4.5	1.34×10−6	0.0074
BT	0.114	0	5.83	11.4	0.0379	0.0141
HSV	0.114	0	3.63	7.07	0.0375	0.0139

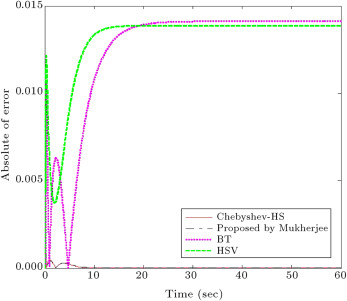
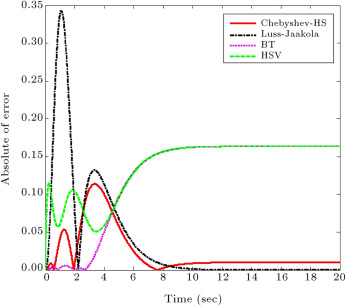
Also, the plot of ${\textstyle e=\vert y-y_{r}\vert }$ is given for the full order and reduced systems in Figure 3 . This figure illustrates that the obtained error by the proposed method in this paper and the proposed method by Mukherjee is very similar, and less than HSV and BT methods.

Figure 3. The plot of ${\textstyle e=\vert y-y_{r}\vert }$ for the full order and reduced systems by the proposed method and other methods for test system 1.

Test system 2: In  [44] , a procedure is presented to obtain a reduced order system by Routh–Pade approximation using the Luus–Jaakola algorithm. To compare the proposed method in this paper with the Luus–Jaakola algorithm, the system given in  [44] is adopted, which is a third-order system:

$G_{org}={\frac {8s^{2}+6s+2}{s^{3}+4s^{2}+5s+2}}{\mbox{.}}$

( 22)

Based on the explanations given for test system 1, the obtained reduced system by the algorithm is as follows:

$G_{Chebyshev{\mbox{-}}HS}={\frac {7.88s+4.94}{s^{2}+3.64s+4.99}}{\mbox{.}}$

( 23)

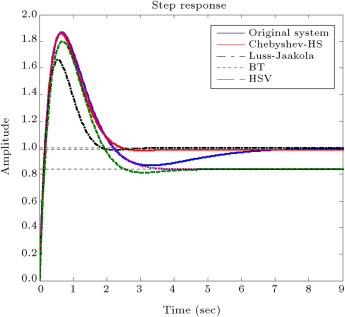
The step response of the original system and the obtained reduced model is shown in Figure 4 . In this figure, the responses of the system with second-order primary reduced models obtained by other methods are also included for comparison. Also, the plot of ${\textstyle e=\vert y-y_{r}\vert }$ is given for the full order and reduced systems in Figure 5 .

Figure 4. The step response of full order and reduced order model by the proposed method and other methods for test system 2.

Figure 5. The plot of ${\textstyle e=\vert y-y_{r}\vert }$ for the full order and reduced systems by the proposed method and other methods for test system 2.

Once again, maximum overshoot, rise time, settling time, steady state value, ISE and ${\textstyle H_{\infty }}$ norm of the error (${\textstyle e=\vert y-y_{r}\vert }$ ) are given in Table 2 . It is clearly seen that the specifications of the reduced order model achieved by the proposed method are close to the specifications of the original system, and better than other methods.

Table 2. Comparision of methods for test system 2.

	Steady state value	Overshoot (%)	Rise time (s)	Settling time (s)	ISE	Infinity-norm of error
Original model	1	86.5	0.129	6.74	–	–
Chebyshev- HS	0.99	87.9	0.127	2.35	0.0286	0.1139
Luus–Jaakola	1	66.1	0.13	1.71	0.1404	0.3425
BT	0.836	123	0.103	3.15	0.3802	0.1635
HSV	0.836	115	0.118	3.44	0.4043	0.1635

Test system 3: The third system to be reduced is a system given in  [45] by Tao, where a procedure is presented to obtain a reduced system. ${\textstyle G_{Original}}$ is given in Box II .

${\begin{array}{l}\displaystyle G_{Original}=\\\displaystyle ={\frac {0.686(s+53)(s-53)(s^{2}-152.2s+14500)(s^{2}+153.8s+14500)}{(s^{2}+s+605)(s^{2}+45.5s+2660)(s^{2}+2.51s+3900)(s^{2}+3.99s+22980)}}{\mbox{.}}\end{array}}$

( 24)

Based on the explanations given for test system 1, the obtained reduced system by the algorithm is the one which is shown in Box III .

${\begin{array}{l}\displaystyle G_{Chebyshev}=\\\displaystyle ={\frac {0.012s^{4}-0.11s^{3}+230.02s^{2}+600.15s-303893.23}{s^{5}+59.88s^{4}+4142.24s^{3}+218504.11s^{2}+2246670.14s+1.08}}{\mbox{.}}\end{array}}$

( 25)

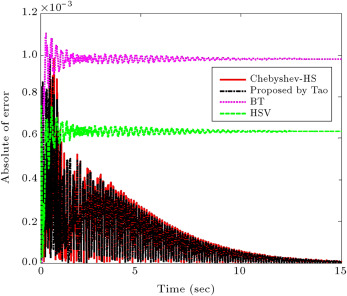
The comparison of the proposed method, the one proposed by Tao in  [45] , HSV and BT methods are shown in Figure 6  and Figure 7 and Table 3 , which illustrate that the achieved results from the proposed method and the proposed method by Tao are very similar to the original system, with respect to HSV and BT methods.

Figure 6. Step response of full order and reduced order model by the proposed method and other methods for test system 3.

Figure 7. The plot of ${\textstyle e=\vert y-y_{r}\vert }$ for the full order and reduced systems by the proposed method and other methods for test system 3.

Table 3. Comparision of methods for test system 3.

	Steady state value	Over shoot (%)	Rise time (s)	Settling time (s)	ISE	Infinity-norm of error
Original system	−0.00281	−0.00814	0.0185	7.56	–	–
Chebyshev-Hs	−0.00281	−0.0078	0.0164	9.13	5.8043×10−7	9.8248×10−4
Tao method	−0.00281	−0.00738	0.0236	9.13	5.8235×10−7	7.5718×10−4
BT	−0.00183	−0.00743	0.0146	7.31	1.4339×10−5	0.0011
HSV	−0.00218	−0.00805	0.0719	7.18	5.9557×10−6	0.0010

6. Conclusion

This paper introduces a new method for order reduction, using orthogonal polynomials, through Chebyshev rational functions and the harmony search algorithm. To get an optimum stable reduced system, Routh array is applied as constraints in the formulation. The proposed method is compared with some order reduction techniques, where the results obtained show that the proposed approach has high accuracy, and which results in an adequate low-order model that retains the characteristics of the full order model. The obtained results confirm that the proposed method can be used as an alternative method for order reduction, and the ability of other orthogonal functions can be investigated for the order reduction of the system.

References

1. [1] E.J. Davison; A method for simplifying linear dynamic systems; IEEE Trans. Automat. Control AC, 11 (1966), pp. 93–101
2. [2] M.R. Chidambara; Further comments by M.R. Chidambara; IEEE Trans. Automat. Control AC, 1 (1967), pp. 799–800
3. [3] E.J. Davison; Further reply by E.J. Davison; IEEE Trans. Automat. Control AC, 12 (1967), p. 800
4. [4] M.R. Chidambara; Two simple techniques for the simplification of large dynamic systems; JACC (1969), pp. 669–674
5. [5] Z. Elrazaz, N.K. Sinha; On the selection of dominant poles of a system to be retained in a low-order model; IEEE Trans. Automat. Control, 24 (1979), pp. 792–793
6. [6] M. Hutton, B. Friedland; Routh approximations for reducing order of linear, time-invariant systems; IEEE Trans. Automat. Control, 20 (3) (1975), pp. 329–337
7. [7] R.K. Appiah; Linear model reduction using Hurwitz polynomial approximation; Internat. J. Control, 28 (1978), pp. 477–488
8. [8] R.K. Appiah; Pade methods of Hurwitz polynomial with application to linear system reduction; Internat. J. Control, 29 (1979), pp. 39–48
9. [9] T.C. Chen, C.Y. Chang, K.W. Han; Reduction of transfer functions by the stability equation method; J. Franklin Inst., 308 (1979), pp. 389–404
10. [10] T.C. Chen, C.Y. Chang, K.W. Han; Model reduction using the stability equation method and the continued fraction method; Internat. J. Control, 21 (1980), pp. 81–94
11. [11] L.G. Gibilaro, F.P. Lees; The reduction of complex transfer function models to simple models using the method of moments; Chem. Eng. Sci., 24 (1969), pp. 85–93
12. [12] F.P. Lees; The derivation of simple transfer function models of oscillating and inverting process from the basic transformed equation using the method of moments; Chem. Eng. Sci., 26 (1971), pp. 1179–1186
13. [13] Y.P. Shih, C.S. Shieh; Model reduction of continuous and discrete multivariable systems by moments matching; Comput. Syst. Eng., 2 (1978), pp. 127–132
14. [14] V. Zakian; Simplification of linear time-variant system by moment approximation; Internat. J. Control, 18 (1973), pp. 455–460
15. [15] C.F. Chen, L.S. Shieh; A novel approach to linear model simplification; Internat. J. Control, 8 (1968), pp. 561–570
16. [16] C.F. Chen; Model reduction of multivariable control systems by means matrix continued fractions; Internat. J. Control, 20 (1974), pp. 225–238
17. [17] D.J. Wright; The continued fraction representation of transfer functions and model simplification; Internat. J. Control, 18 (1973), pp. 449–454
18. [18] Y. Shamash; Stable reduced-order models using Pade type approximation; IEEE Trans. Automat. Control, 19 (5) (1974), pp. 615–616
19. [19] D.A. Wilson; Optimal solution of model reduction problem; Proc. Inst. Electr. Eng., 117 (6) (1970), pp. 1161–1165
20. [20] D.A. Wilson; Model reduction for multivariable systems; Internat. J. Control, 20 (1974), pp. 57–64
21. [21] G. Obinata, H. Inooka; A method of modeling linear time-invariant systems by linear systems of low order; IEEE Trans. Automat. Control AC, 21 (1976), pp. 602–603
22. [22] G. Obinata, H. Inooka; Authors reply to comments on model reduction by minimizing the equation error; IEEE Trans. Automat. Control AC, 28 (1983), pp. 124–125
23. [23] E. Eitelberg; Model reduction by minimizing the weighted equation error; Internat. J. Control, 34 (6) (1981), pp. 1113–1123
24. [24] R.A. El-Attar, M. Vidyasagar; Order reduction by ${\textstyle L_{1}}$ and ${\textstyle L_{\infty }}$ Norm minimization  ; IEEE Trans. Automat. Control AC, 23 (4) (1978), pp. 731–734
25. [25] B.C. Moore; Principal component analysis in linear systems: controllability, observability and model reduction; IEEE Trans. Automat. Control AC, 26 (1981), pp. 17–32
26. [26] L. Pernebo, L.M. Silverman; Model reduction via balanced state space representation; IEEE Trans. Automat. Control AC, 27 (2) (1982), pp. 382–387
27. [27] D. Kavranoglu, M. Bettayeb; Characterization of the solution to the optimal ${\textstyle H_{\infty }}$ model reduction problem  ; Systems Control Lett., 20 (1993), pp. 99–107
28. [28] L. Zhang, J. Lam; On ${\textstyle H_{2}}$ model reduction of bilinear system  ; Automatica, 38 (2002), pp. 205–216
29. [29] W. Krajewski, A. Lepschy, G.A. Mian, U. Viaro; Optimality conditions in multivariable ${\textstyle L_{2}}$ model reduction  ; J. Franklin Inst., 330 (3) (1993), pp. 431–439
30. [30] D. Kavranoglu, M. Bettayeb; Characterization and computation of the solution to the optimal ${\textstyle L_{\infty }}$ approximation problem  ; IEEE Trans. Automat. Control, 39 (1994), pp. 1899–1904
31. [31] G. Parmar, S. Mukherjee, R. Prasad; Reduced order modeling of linear dynamic systems using particle swarm optimized eigen spectrum analysis; Int. J. Comput. Math. Sci., 1 (31) (2007), pp. 45–52
32. [32] G. Parmer, R. Prasad, S. Mukherjee; Order reduction of linear dynamic systems using stability equation method and GA; World Acad. Sci. Eng. Technol., 26 (2007), pp. 72–378
33. [33] Al-Nadi, D.A., Alsmadi, O.M. and Abo-Hammour, Z.S. “Reduced order modeling of linear MIMO systems using particle swarm optimization”, 7th Int. Conf. Autonomic and Autonomous Systems , Venice, Italy, pp. 62–66 (2011).
34. [34] S. Panda, J.S. Yadav, N.P. Padidar, C. Ardil; Evolutionary techniques for model order reduction of large scale linear systems; Int. J. Appl. Sci. Eng. Technol., 5 (2009), pp. 22–28
35. [35] Parmar, G., Pandey, M.K. and Kumar, V. “System order reduction using GA for unit impulse input and a comparative study using ISE and IRE”, 9th Int. Conf. on Advances in Computing, Communications and Control , Mumbai, India (2009).
36. [36] R. Salim, M. Bettayeb; ${\textstyle H_{2}}$ and ${\textstyle H_{\infty }}$ optimal reduction using genetic algorithm  ; J. Franklin Inst., 348 (2011), pp. 1177–1191
37. [37] S. John, R. Parthasarathy; System reduction by Routh approximation and modified Cauer continued fraction; Electron. Lett., 15 (1979), pp. 691–692
38. [38] http://en.wikipedia.org/wiki/Chebyshev_rational_functions .
39. [39] Z.W. Geem, J.H. Kim, G.V. Loganathan; A new heuristic optimization algorithm: harmony search; Trans. Soc. Model. Simul. Int., 76 (2) (2001), pp. 60–68
40. [40] Z.W. Geem; Music-Inspired Harmony Search Algorithm: Theory and Applications, Studies in Computational Intelligence; Springer, Berlin (2009)
41. [41] P.C. Parks; A new proof of the Routh–Hurwitz stability criterion using the second method of Lyapunov; Proc. Cambridge Phil. Soc., 58 (4) (1962), pp. 694–702
42. [42] S. Mukherjee, Satakhshi, R.C. Mittal; Model order reduction using response-matching technique; J. Franklin Inst., 342 (2005), pp. 503–519
43. [43] S. Skogestad, I. Postethwaite; Multivariable Feedback Control, Analysis and Design; John Wiley (1996)
44. [44] V. Singh; Obtaining Routh–Pade approximants using the Luus–Jaakola algorithm; IEE Proc. D, 152 (2) (2005), pp. 129–132
45. [45] C.S. Tao, F.B. Hsiao; Stability margin and model reduction; J. Franklin Inst., 330 (3) (1993), pp. 551–570