MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection

Abstract

In this study we analyzed the influence of thermal radiation and chemical reaction on two dimensional steady magnetohydrodynamic flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of suction/injection. We considered nanofluid volume fraction on the boundary is submissive controlled, which makes the present study entirely different from earlier studies and physically more realistic. The equations governing the flow are solved numerically. Effects of non-dimensional governing parameters on velocity, temperature and concentration profiles are discussed and presented through graphs. Also, coefficient of skin friction and local Nusselt number is investigated for stretching/shrinking and suction/injection cases separately and presented through tables. Comparisons with existed results are presented. Present results have an excellent agreement with the existed studies under some special assumptions. Results indicate that the enhancement in Brownian motion and thermophoresis parameters depreciates the nanoparticle concentration and increases the mass transfer rate. Dual solutions exist only for certain range of stretching/shrinking and suction/injection parameters.

Keywords

MHD; Nanofluid; Stretching/shrinking; Suction/injection; Radiation; Chemical reaction

1. Introduction

The development of nanotechnology is going to bring an unimaginable and multidimensional changes in our way of life, in the coming years. Recently many researchers focused on this topic due to it prominent importance in engineering and its allied areas. Choi [1] was the first person who introduced the term “nanofluid”. The detailed discussion, importance and future scope of nanofluids were pioneered by Das et al. [2]. Uddin et al. [3] proposed a mathematical model for radiative MHD flow with slip effects. Heat transfer in second order fluid over a stretching sheet with constant surface temperature was discussed by Bujurke et al. [4]. Ece [5] proposed the similarity analysis for the laminar free convection boundary layer flow in the presence of a transverse magnetic field. Mohankrishna et al. [6] and Sandeep et al. [7] discussed the heat transfer characteristics of nanofluids by immersing the high conductivity nanomaterials in base fluids and they concluded that the effective thermal conductivity of the fluid increases appreciably and consequently enhances the heat transfer characteristics by suspending the high thermal conductivity of nanomaterials into the base fluids. Zaimi et al. [8] analyzed steady two dimensional flow of a nanofluid over a stretching/shrinking sheet. Wang and Mujumdar [9] gave good literature on heat transfer characteristics of nanofluids. Rana and Bhargava [10] used finite element and finite difference methods for nonlinear stretching sheet problem. Zaimi et al. [11] extended the work of Rana and Bhargava and studied heat transfer and boundary layer flow of a nanofluid over a stretching/shrinking sheet.

Radiation effect on MHD viscous fluid over exponentially stretching sheet with porous medium was analyzed by Ahmad et al. [12]. They used homotopy analysis method to solve the boundary layer approximations. Heat and mass transfer for stagnation point flow over a stretching sheet in a porous medium by considering heat source was studied by Hamad and Ferdows [13]. The importance of heat, mass and momentum transfer over a stretching surface was explained by Atlatn et al. [14]. Ellahi et al. [15] discussed about the influence of nanoparticles shape by considering Cu–water nanofluid. Sheikholeslami et al. [16] analyzed the effect of thermal radiation on MHD nanofluid flow and heat transfer by using two phase model. Rashidi et al. [17] illustrated the stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium. Heat generation and heat flux effects on the peristaltic flow with interacting nanoparticles were presented by Akbar et al. [18]. A study of natural convection heat transfer in a nanofluid filled with elliptic inner cylinder was analyzed by Sheikholeslami et al. [19]. The influence of heat transfer on the nanofluid flow over a permeable stretching wall in a porous medium was studied by Sheikholeslami et al. [20]. Interaction of nanoparticles for the peristaltic flow in an asymmetric channel by considering the induced magnetic field was analyzed by Akbar et al. [21].

Ramesh et al. [22] explored their research on stretching sheet and they analyzed the heat transfer characteristics of a nanofluid. Many researchers like [23], [24] and [25] have studied and given valuable contribution in the field of nanofluid flows over a permeable stretching sheet. Simulation of magnetohydrodynamic CuO–water nanofluid flow and heat transfer in the presence of Lorentz forces was discussed by Sheikholeslami et al. [26]. Ellahi et al. [27] illustrated non-Newtonian nanofluids flow through a porous medium between two coaxial cylinders by considering variable viscosity. Nanofluid flow in tapering stenosed arteries with permeable walls was presented by Akbar et al. [28]. Ellahi [29] presented the analytical solution to analyze the effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe. MHD flow of water/ethylene glycol based nanofluids by considering porous medium was discussed by Zeeshan et al. [30]. Ellahi et al. [31] presented series solutions for non-Newtonian nanofluids by considering Reynolds’ and Vogel’s models by using homotopy analysis method.

All the above investigations limited their study on either stretching or shrinking case by considering suction or injection effects. In this study we are focusing on two dimensional steady magnetohydrodynamic flow of a nanofluid past a permeable stretching/shrinking sheet in a porous medium with suction/injection effects. Here we considered nanofluid volume fraction on the boundary is submissive controlled rather than active controlled [32] and [33], which makes the present study entirely different from the past studies and it is physically more realistic. The governing partial differential equations are reduced into ordinary differential equations by similarity transformation and then solved numerically by using bvp4c with MATLAB package. Effects of thermal radiation parameter, chemical reaction parameter, magnetic field parameter, Brownian motion parameter, thermophoresis parameter and porosity parameter on velocity, temperature, concentration, skin friction and local Nusselt number are thoroughly investigated for stretching/shrinking and suction/injection cases separately and presented through graphs and tables. Comparisons with existed results are presented.

2. Mathematical formulation

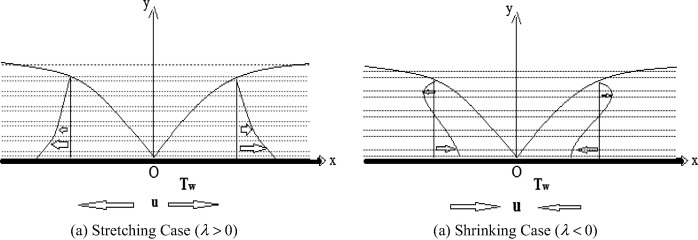
Consider a steady, incompressible, two dimensional MHD flow of a nanofluid past a permeable stretching/shrinking sheet in porous medium coinciding with the plane ${\textstyle y=0}$ and the flow is assumed to be confined to ${\textstyle y>0}$. The flow is along the x  -axis where ${\textstyle x}$ is the coordinate measured along the stretching/shrinking sheet and y  -axis is normal to the surface. A transverse magnetic field ${\textstyle B_{0}}$ is applied in the y  -direction and the stretching/shrinking sheet velocity is assumed as ${\textstyle u_{w}(x)=cx}$, where ${\textstyle c>0}$ is a constant. The uniform temperature near the sheet is assumed as ${\textstyle T_{w}}$ and the temperature, concentration far away from sheet is assumed as ${\textstyle T_{\infty }{\mbox{,}}C_{\infty }}$ respectively.

The equations that govern the present flow with above assumptions subject to the Boussinesq approximations can be expressed as

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(1)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$\nu {\frac {{\partial }^{2}u}{\partial y^{2}}}-{\frac {\sigma B_{0}^{2}}{{\rho }_{f}}}u-$${\frac {\nu }{k^{'}}}u{\mbox{,}}$

(2)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$$\alpha {\frac {{\partial }^{2}T}{\partial y^{2}}}+\tau \left[D_{B}{\frac {\partial C}{\partial y}}{\frac {\partial T}{\partial y}}+\right.$$\left.{\frac {D_{T}}{T_{\infty }}}{\left({\frac {\partial T}{\partial y}}\right)}^{2}\right]-$${\frac {1}{{\left(\rho c_{p}\right)}_{nf}}}{\frac {\partial q_{r}}{\partial y}}{\mbox{,}}$

(3)

$u{\frac {\partial C}{\partial x}}+v{\frac {\partial C}{\partial y}}=$$D_{B}{\frac {{\partial }^{2}C}{\partial y^{2}}}+{\frac {D_{T}}{T_{\infty }}}{\frac {{\partial }^{2}T}{\partial y^{2}}}-$$k_{1}(C-C_{\infty }){\mbox{,}}$

(4)

The boundary conditions of Eqs. (1), (2), (3) and (4) are

${\begin{array}{rl}&u=\lambda U_{w}{\mbox{,}}\quad v=v_{w}{\mbox{,}}\quad T=T_{w}{\mbox{,}}\quad D_{B}C^{'}+(D_{B}/T_{\infty })T^{'}=0\quad {\mbox{at}}\quad y=0{\mbox{,}}\\&u\rightarrow 0{\mbox{,}}\quad T\rightarrow T_{\infty }{\mbox{,}}\quad C\rightarrow C_{\infty }\quad {\mbox{as}}\quad y\rightarrow \infty {\mbox{,}}\end{array}}$

(5)

In Eq. (5) prime denotes differentiation with respect to ${\textstyle y}$, where ${\textstyle u}$ and ${\textstyle v}$ are the velocity components in the ${\textstyle x}$ and ${\textstyle y}$ directions respectively, ${\textstyle T}$ is the temperature, ${\textstyle C}$ is the nanoparticles volume fraction, ${\textstyle v_{w}}$ is the suction or injection velocity with ${\textstyle v_{w}<0}$ for suction and ${\textstyle v_{w}>0}$ for injection, ${\textstyle \tau ={\left(\rho c\right)}_{p}/{\left(\rho c\right)}_{f}}$, where ${\textstyle {\left(\rho c\right)}_{p}}$ is the effective heat capacity of the nanoparticles, ${\textstyle {\left(\rho c\right)}_{f}}$ is the heat capacity of the base fluid, ${\textstyle \alpha =k/{\left(\rho c\right)}_{f}}$ is the thermal diffusivity of the fluid, ${\textstyle \nu }$ is the kinematic viscosity, ${\textstyle D_{B}}$ is the Brownian diffusion coefficient, ${\textstyle D_{T}}$ is the thermophoretic diffusion coefficient, ${\textstyle {\rho }_{f}}$ is fluid density, ${\textstyle \sigma }$ is electrical conductivity, ${\textstyle k^{'}}$ is the permeability of porous medium, ${\textstyle k_{1}}$ is the chemical reaction parameter and ${\textstyle \lambda }$ is the stretching/shrinking parameter with ${\textstyle \lambda >0}$ for a stretching surface and ${\textstyle \lambda <0}$ for a shrinking surface.

By using Roseland approximation, the radiative heat flux ${\textstyle q_{r}}$ is given by

$q_{r}=-{\frac {4{\sigma }^{_{\ast }}}{3k^{_{\ast }}}}{\frac {\partial T^{4}}{\partial y}}{\mbox{,}}$

(6)

where ${\textstyle {\sigma }^{_{\ast }}}$ is the Steffen Boltzmann constant and ${\textstyle k^{_{\ast }}}$ is the mean absorption coefficient. Consider the temperature differences within the flow sufficiently small such that ${\textstyle T^{4}}$ may be expressed as the linear function of temperature. Then expanding ${\textstyle T^{4}}$ in Taylor series about ${\textstyle T_{\infty }}$ and neglecting higher-order terms takes the form

$T^{4}\cong 4T_{\infty }^{3}T-3T_{\infty }^{4}{\mbox{,}}$

(7)

In view of Eqs. (6) and (7), Eq. (3) reduces to

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$$\alpha {\frac {{\partial }^{2}T}{\partial y^{2}}}+\tau \left[D_{B}{\frac {\partial C}{\partial y}}{\frac {\partial T}{\partial y}}+\right.$$\left.{\frac {D_{T}}{T_{\infty }}}{\left({\frac {\partial T}{\partial y}}\right)}^{2}\right]+$${\frac {1}{{\left(\rho c_{p}\right)}_{nf}}}{\frac {16T_{\infty }^{3}{\sigma }^{_{\ast }}}{3k^{_{\ast }}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}{\mbox{,}}$

(8)

By introducing the following similarity transforms

${\begin{array}{rl}&\psi =c^{1/2}{\nu }^{1/2}f(\eta ){\mbox{,}}\quad \eta =c^{1/2}{\nu }^{-1/2}y{\mbox{,}}\\&\theta (\eta )=(T-T_{\infty })/(T_{w}-T_{\infty }){\mbox{,}}\quad \phi (\eta )=(C-C_{\infty })/C_{\infty }{\mbox{,}}\end{array}}$

(9)

where the stream function ${\textstyle \psi }$ is defined as ${\textstyle u=\partial \psi /\partial y\quad and\quad v=-\partial \psi /\partial x}$ which identically satisfies Eq. (1). Further ${\textstyle f(\eta ){\mbox{,}}\theta (\eta )\quad and\quad \phi (\eta )}$ are dimensionless stream, temperature and concentration functions respectively. Substituting Eq. (9) into (2), (3) and (4), we obtain

$f^{'''}+{ff}^{''}-f^{{'}2}-(M+K)f^{'}=0{\mbox{,}}$

(11)

$(1+R){\theta }^{''}+Nb{\theta }^{'}{\phi }^{'}+$$Nt{\theta }^{{'}2}+Pr\quad f{\theta }^{'}=0{\mbox{,}}$

(12)

${\phi }^{''}+{\frac {Nt}{Nb}}{\theta }^{''}+Le(f{\phi }^{'}-$$K_{l}\phi )=0{\mbox{,}}$

(13)

The boundary conditions (5) reduce to

${\begin{array}{rl}&f(0)=f_{w}{\mbox{,}}\quad f^{'}(0)=\lambda {\mbox{,}}\quad \theta (0)=1{\mbox{,}}\quad Nb{\phi }^{'}(0)+Nt{\theta }^{'}(0)=0{\mbox{,}}\\&f^{'}(\eta )\rightarrow 0{\mbox{,}}\quad \theta (\eta )\rightarrow 0{\mbox{,}}\quad \phi (\eta )\rightarrow 0\quad {\mbox{as}}\quad n\rightarrow \infty {\mbox{,}}\end{array}}$

(14)

Here prime denotes differentiation with respect to ${\textstyle \eta }$, where ${\textstyle Pr=\nu /\alpha }$ is the Prandtl number and ${\textstyle Le=\nu /D_{B}}$ is the Lewis number, ${\textstyle Nb}$ is the Brownian motion parameter, ${\textstyle Nt}$ is the Thermophoresis parameter, ${\textstyle M}$ is the magnetic field parameter, ${\textstyle K}$ is the porosity parameter, ${\textstyle K_{l}}$ is the chemical reaction parameter and ${\textstyle f_{w}}$ is the suction/injection parameter with ${\textstyle f_{w}>0}$ for suction, ${\textstyle f_{w}<0}$ for injection, which are defined as

${\begin{array}{rl}&f_{w}=v_{w}{\left(c\nu \right)}^{-1/2}{\mbox{,}}\quad Nt=\tau D_{T}(T_{w}-T_{\infty })/\alpha T_{\infty }{\mbox{,}}\quad Nb=\tau D_{B}C_{\infty }/\alpha {\mbox{,}}\\&R={\frac {16T_{\infty }^{3}{\sigma }^{_{\ast }}}{{\left(\rho c_{p}\right)}_{nf}3\alpha k^{_{\ast }}}}{\mbox{,}}\quad M={\frac {\sigma B_{0}^{2}}{c{\rho }_{f}}}{\mbox{,}}\quad K={\frac {\nu }{k^{'}c}}{\mbox{,}}\quad K_{l}={\frac {k_{1}C_{\infty }\nu }{D_{B}}}{\mbox{,}}\end{array}}$

(15)

The Coefficient of skin friction ${\textstyle C_{fx}}$ and local Nusselt Number ${\textstyle {Nu}_{x}}$ are given by

$C_{fx}={\frac {x{\mu }_{f}}{\rho u_{w}^{2}}}{\left({\frac {\partial u}{\partial y}}\right)}_{y=0}{\mbox{,}}\quad {Nu}_{x}=$$-{\frac {x}{\left(T_{w}-T_{\infty }\right)}}{\left({\frac {\partial T}{\partial y}}\right)}_{y=0}{\mbox{,}}$

(16)

Using (9) and (16), we have

${Re}_{x}^{1/2}C_{fx}=f^{''}(0){\mbox{,}}\quad {Re}_{x}^{-1/2}{Nu}_{x}=$$-{\theta }^{'}(0){\mbox{,}}$

(17)

where ${\textstyle {Re}_{x}=u_{w}x/v}$ is the local Reynolds number. It is important to mention that as per our assumed boundary condition in (5), the local Sherwood number becomes zero (see [33]).

Table 1 depicts the comparison of the present results with the published results of Chen [34] and Zaimi et al. [8]. We found good accuracy of the present results by comparing with the existed results. This shows the validity of the present results along with the accuracy of the numerical technique we used in the present study.

Table 1. Comparison of the values of ${\textstyle -{\theta }^{'}(0)}$ with published data when ${\textstyle Nt=Nb=0{\mbox{,}}M=R=K=K_{l}=f_{w}=0}$ and ${\textstyle \lambda =1}$.

Pr	0.72	1	3	7	10
Chen [34]	0.46315	0.58199	1.16523	1.89537	2.30796
Zaimi et al. [8]	0.463145	0.581977	1.165246	1.895403	2.308004
Present study	0.463146	0.581979	1.165249	1.895406	2.308008

3. Results and discussion

The system of nonlinear ordinary differential Eqs. (11), (12) and (13) with the boundary conditions (14) is solved numerically using bvp4c with MATLAB package. The results obtained show the influences of the non-dimensional governing parameters, namely thermal radiation parameter ${\textstyle R}$, chemical reaction parameter ${\textstyle K_{l}}$, magnetic field parameter ${\textstyle M}$, Brownian motion parameter ${\textstyle Nb}$, thermophoresis parameter ${\textstyle Nt}$ and porosity parameter ${\textstyle K}$ on velocity, temperature, concentration, skin friction and local Nusselt numbers are thoroughly investigated for stretching/shrinking and suction/injection cases separately and presented through graphs and tables.

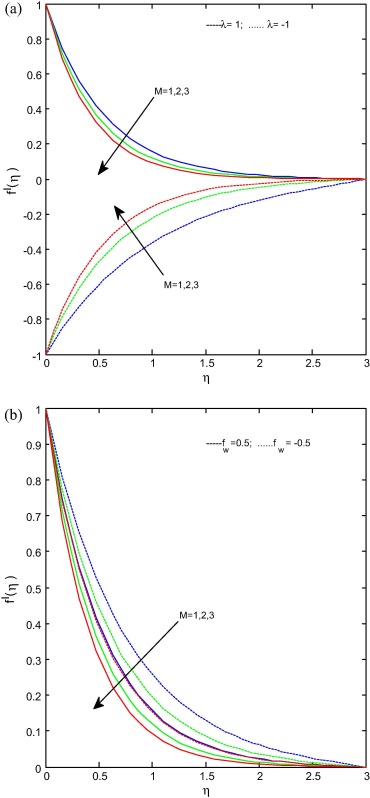
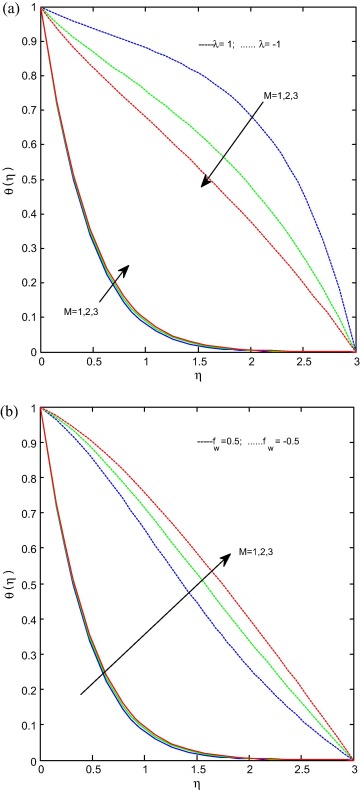
Fig. 1(a) and (b) exhibits effect of magnetic field parameter on velocity profiles for stretching/shrinking and suction/injection cases respectively. It is evident from figures that increase in magnetic field parameter decreases the velocity profiles of the fluid in stretching and suction/injection cases but it takes reverse action in shrinking case. Generally increase in magnetic field generates the opposite force to the flow, called Lorentz force. We observed that the Lorentz force helps to enhance the flow in shrinking case. It is significant to mention that magnetic field effect is comparatively less on injection case compared to suction case. This concludes that Lorentz force acts operatively on stretching and suction cases. Fig. 2(a) and (b) displays the effect of magnetic field parameter on temperature profiles for stretching/shrinking and suction/injection cases respectively. From Fig. 2(a) it is observed that increase in magnetic field parameter increases the temperature profiles in stretching case and decreases the temperature profiles in shrinking case. The reason behind this is increase in magnetic field reduces the boundary layer thickness and enhances the thermal conductivity of the fluid in the stretching surface. From Fig. 2(b) it is clear that increase in magnetic field parameter increases the temperature profiles of the fluid for both suction and injection cases and this effects high on injection compared to suction case. It is due to that fact that injection enhances the thermal conductivity of the flow. Fig. 3(a) and (b) illustrates the effect of Radiation parameter on temperature profiles for stretching/shrinking and suction/injection cases respectively. It is clear from figures that increase in radiation causes increases in fluid temperature in both cases. These show the domination of radiative heat transfer in Rosseland approximation. But radiation shows reverse action on shrinking surface. That is increase in radiation parameter causes the decrease in temperature profiles. This result can be explained by the fact that the decrease in the value of R means a decrease in the Rosseland radiation absorptivity k^∗ due to this reason we seen a fall in temperature profiles.

Figure 1. (a) and (b) Velocity profiles for various values of ${\textstyle M}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}Nt=Nb=0.5=K{\mbox{,}}K_{l}=}$$0.2$.

Figure 2. (a) and (b) Temperature profiles for various values of ${\textstyle M}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}Nt=Nb=0.5{\mbox{,}}K=0.5{\mbox{,}}K_{l}=}$$0.2$.

Figure 3. (a) and (b) Temperature profiles for various values of ${\textstyle R}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=M=1{\mbox{,}}Nt=Nb=0.5{\mbox{,}}K=0.5{\mbox{,}}K_{l}=}$$0.2$.

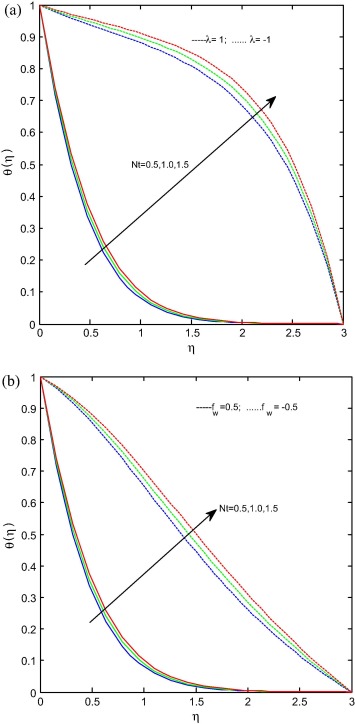
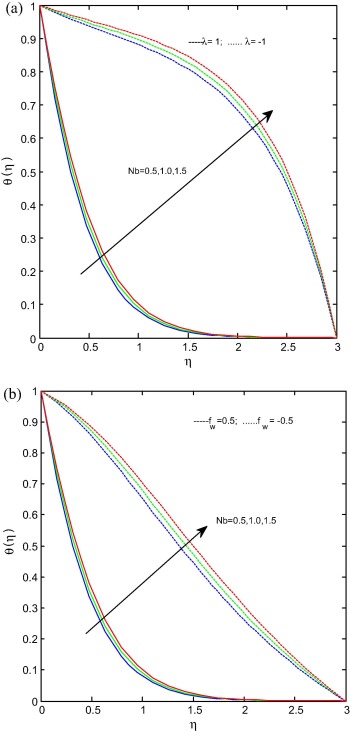
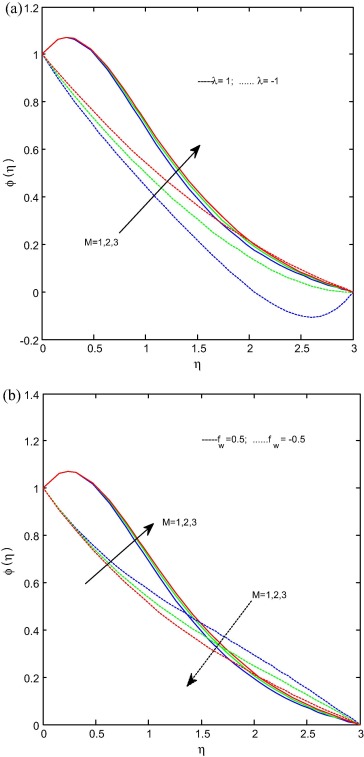
Fig. 4(a) and (b) gives the effect of the thermophoresis parameter on temperature profiles for stretching/shrinking and suction/injection cases respectively. It is noticed that the temperature profiles as well as the boundary layer thickness of the thermal field increase with increasing in Nt for both stretching/shrinking and suction/injection cases. Fig. 5(a) and (b) represents the effect of the Brownian motion parameter on temperature profiles for stretching/shrinking and suction/injection cases respectively. It is evident from figures that the Brownian motion parameter increases the temperature profiles for both cases. The reason behind this is different nanoparticles have different values of Brownian motion parameter which leads to enhance the heat transfer rate. Fig 6(a) and (b) reveals the effect of the magnetic field parameter on concentration profiles for stretching/shrinking and suction/injection cases respectively. It is noticed from figures that the increase in magnetic field parameter increases the concentration profiles for stretching/shrinking case. Suction also follows the above case but it is interesting to note that in injection case at ${\textstyle \eta =1.5}$ concentration profiles in injection case merged with suction case afterward it dominates the suction case. It may happen due to the reason that at free stream level injection helps to enhance the concentration level.

Figure 4. (a) and (b) Temperature profiles for various values of ${\textstyle Nt}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}M=1{\mbox{,}}Nb=0.5{\mbox{,}}K=}$$0.5{\mbox{,}}K_{l}=0.2$.

Figure 5. (a) and (b) Temperature profiles for various values of ${\textstyle Nb}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}M=1{\mbox{,}}Nt=0.5{\mbox{,}}K=}$$0.5{\mbox{,}}K_{l}=0.2$.

Figure 6. (a) and (b) Concentration profiles for various values of ${\textstyle M}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}Nb=Nt=0.5{\mbox{,}}K=0.5{\mbox{,}}K_{l}=}$$0.2$.

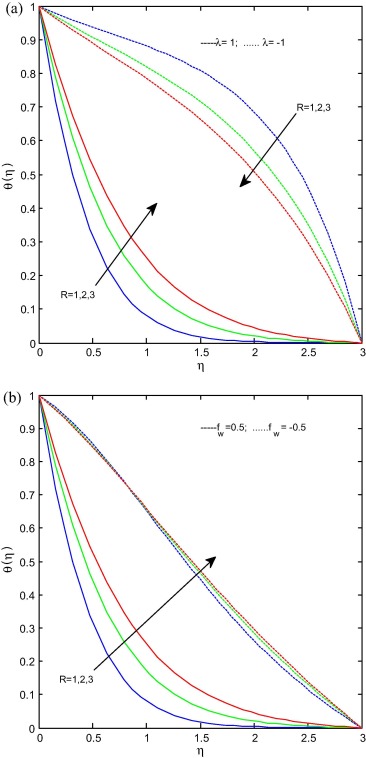
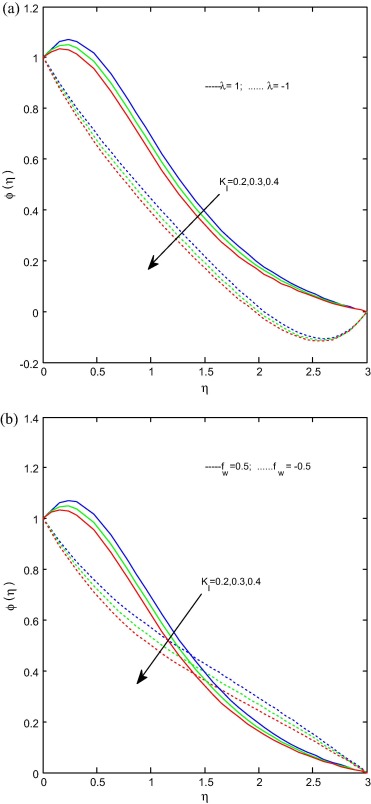
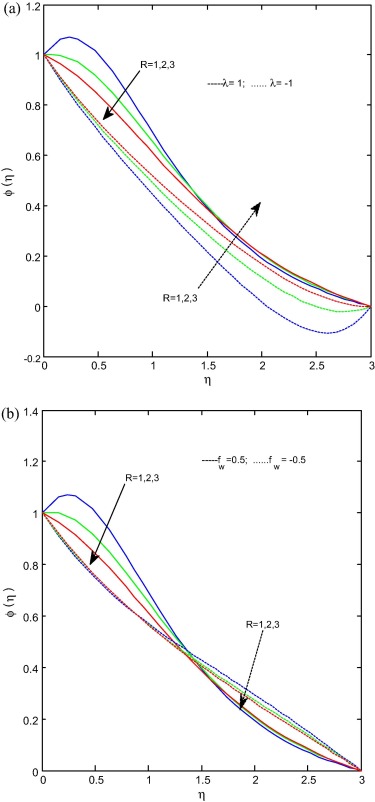
Fig. 7(a) and (b) presents the effect of the chemical reaction parameter on concentration profiles for stretching/shrinking and suction/injection cases respectively. It is clear from figures that the increase in chemical reaction parameter decreases the concentration profiles for both cases. It is prominent to mention here that at ${\textstyle \eta =1.5}$ level injection dominates the suction and developed the concentration profiles. It may happen due to the fact that chemical reaction helps to enhance the mass transfer and reduces the solutal boundary layer thickness. Fig. 8(a) and (b) illustrates the effect of the radiation parameter on concentration profiles for stretching/shrinking and suction/injection cases respectively. It is evident from figures that the increase in radiation parameter decreases the concentration profiles in stretching case and increases in shrinking case. But the concentration profiles decrease with increase in radiation profiles for suction/injection case. It is due to the fact that radiation reduces the boundary layer thickness.

Figure 7. (a) and (b) Concentration profiles for various values of ${\textstyle K_{l}}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}Nb=Nt=0.5{\mbox{,}}K=0.5{\mbox{,}}M=}$$1$.

Figure 8. (a) and (b) Concentration profiles for various values of ${\textstyle R}$. When ${\textstyle Pr=6.2{\mbox{,}}Le=R=1{\mbox{,}}Nb=Nt=0.5{\mbox{,}}K=0.5{\mbox{,}}M=}$$1$.

Table 2 shows the influence of physical parameters on the coefficient of skin friction and rate of heat transfer. From the table it is interesting to observe that an increase in magnetic field parameter reduces the skin friction as well as heat transfer rate. A raise in radiation parameter does not shown significant difference in skin friction coefficient but reduces the heat transfer rate. Enhancement in porosity parameter reduces both heat transfer rate and skin friction coefficient. An increase in chemical reaction parameter shows the similar type of results as we observed for radiation parameter. Increase in suction/injection parameter reduces the skin friction and increases the rate of heat transfer, the similar type of results we observed for stretching/shrinking parameter.

Table 2. Values of ${\textstyle f^{''}(0)\quad {\mbox{and}}\quad -{\theta }^{'}(0)}$ for different values of ${\textstyle M{\mbox{,}}R{\mbox{,}}K{\mbox{,}}K_{l}{\mbox{,}}f_{w}}$ and ${\textstyle \lambda }$ when ${\textstyle Le=1{\mbox{,}}Pr=6.2{\mbox{,}}Nt=Nb=0.5}$.

${\textstyle M}$	${\textstyle R}$	${\textstyle K}$	${\textstyle K_{l}}$	${\textstyle f_{w}}$	${\textstyle \lambda }$	${\textstyle f^{''}(0)}$	${\textstyle -{\theta }^{'}(0)}$
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
2	1	0.5	0.2	0.5	1	−2.137573	1.957554
3	1	0.5	0.2	0.5	1	−2.386029	1.932763
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
1	2	0.5	0.2	0.5	1	−1.851350	1.443626
1	3	0.5	0.2	0.5	1	−1.851350	1.155341
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
1	1	1.0	0.2	0.5	1	−2.000248	1.971734
1	1	1.5	0.2	0.5	1	−2.137573	1.957554
1	1	0.5	0.1	0.5	1	−1.851350	1.999754
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
1	1	0.5	0.3	0.5	1	−1.851350	1.976384
1	1	0.5	0.2	−0.5	1	−1.351489	0.208345
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
1	1	0.5	0.2	1.0	1	−2.158694	3.231835
1	1	0.5	0.2	0.5	−1	1.005393	0.155815
1	1	0.5	0.2	0.5	1	−1.851350	1.987456
1	1	0.5	0.2	0.5	2	−4.275473	2.405297

4. Conclusions

This paper presents numerical solution for two dimensional steady magnetohydrodynamic flow of a nanofluid past a permeable stretching/shrinking sheet in a porous medium with suction/injection effects. The findings of the results are summarized as follows:

• Magnetic field parameter has capability to reduce the flow, friction factor and heat transfer rate in stretching surface.
• Dual solutions exist only for certain range of stretching/shrinking and suction/injection parameters.
• Radiation parameter helps to enhance the temperature profiles and reduce the concentration profiles as well as heat transfer rate.
• Chemical reaction parameter does not show significant difference in friction coefficient but it reduces the heat transfer rate as well as concentration profiles.
• Suction/injection parameter and stretching/shrinking parameter help to improve the heat transfer rate.
• Raising the value of Nb and the decreasing the value of Nt produce a decrease in the nanoparticle concentration, as a result of increase in the Sherwood number.

Acknowledgments

The authors wish to express their gratitude to the very competent anonymous referees for their valuable comments and suggestions. This study is supported by research grants from University Grants Commission, India (UGC) under the UGC Dr. D. S. Kothari Post-Doctoral Fellowship Scheme (No. F.4-2/2006 (BSR)/MA/13-14/0026).

References

1. [1] S.U.S. Choi, Enhanced thermal conductivity of nanofluids with nano particles, in: Development and Applications of Newtonian flows, FED, vol. 231/MD-vol. 66, 1995, pp. 99–105.
2. [2] S.K. Das, S.U.S. Choi, W. Yu, T. Pradeep; Nanofluids Science and Technology; John Wiley & Sons (2008)
3. [3] M.J. Uddin, O.A. Beg, A.I.Md. Ismail; Mathematical modeling of radiative hyderomagnetic thermosolutal Nanofluid convection slip flow in saturated porous media; Math. Probl. Eng. (2014), pp. 1–11
4. [4] N.M. Bujurke, S.N. Biradar, P.S. Hiremath; Second-order fluid flow past a stretching sheet with heat transfer; Z. Angew. Math. Phys., 38 (1987), pp. 653–657
5. [5] M.C. Ece; Free convection flow about a cone under mixed thermal boundary conditions and a magneticfield; Appl. Math. Model., 29 (2005), pp. 1121–1134
6. [6] P. Mohankrishna, V. Sugunamma, N. Sandeep; Radiation and magneticfield effects on unsteady natural convection flow of a nanofluid past an infinite vertical plate with heat source; Chem. Process Eng. Res., 25 (2014), pp. 39–52
7. [7] N. Sandeep, V. Sugunamma, P. Mohankrishna; Effects of radiation on an unsteady natural convective flow of a EG-Nimonic 80a nanofluid past an infinite vertical plate; Adv. Phys. Theor. Appl., 23 (2013), pp. 36–43
8. [8] K. Zaimi, A. Ishak, I. Pop; Flow past a permeable stretching/shrinking sheet in a nanofluid using two phase model; PLoS ONE, 9 (11) (2014), pp. 1–6
9. [9] X.Q. Wang, A.S. Mujumdar; Heat transfer characteristics of nanofluids: a review; Int. J. Therm. Sci., 46 (2007), pp. 1–19
10. [10] P. Rana, R. Bhargava; Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: a numerical study; Commun. Nonlinear Sci. Numer. Simul., 17 (2012), pp. 212–226
11. [11] K. Zaimi, I. Ishak, I. Pop; Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid; Sci. Rep., 4 (2014), p. 4404 http://dx.doi.org/10.1038/srep04404
12. [12] I. Ahmad, M. Sajid, W. Awan, M. Rafique, W. Aziz, M. Ahmed, A. Abbasi, M. Taj; MHD flow of a viscous fluid over an exponentially stretching sheet in a porous medium; J. Appl. Math., 2014 (2014), pp. 1–7
13. [13] M.A.A. Hamad, M. Ferdows; Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with nanofluid with heat absorption/generation and suction/blowing: a lie group analysis; Commun. Nonlinear Sci. Numer. Simul., 17 (2012), pp. 132–140
14. [14] T. Atlatn, S. Oh, H. Gegel; Metal Forming Fundamentals and Applications; American Society of Metals, Metals Park, OH (1979)
15. [15] R. Ellahi, M. Hassan, A. Zeeshan; Shape effects of nano size particles in Cu–H₂0 nanofluid on entropy generation; Int. J. Heat Mass Transf., 81 (2015), pp. 449–456
16. [16] M. Sheikholeslami, D.D. Ganji, M.Y. Javed, R. Ellahi; Effect of thermal radiation on magnetohydrodynamic nanofluid flow and heat transfer by means of two phase model; J. Magn. Magn. Mater., 374 (2015), pp. 36–43
17. [17] S. Rashidi, M. Dehghan, R. Ellahi, M. Riaz, M.T. Jamal-Abad; Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium; J. Magn. Magn. Mater., 378 (2015), pp. 128–137
18. [18] N.S. Akbar, M. Raza, R. Ellahi; Influence of heat generation and heat flux in peristaltic flow with interacting nano particles; Eur. Phys. J. Plus, 129 (2014), pp. 185–192
19. [19] M. Sheikholeslami, R. Ellahi, M. Hassan, S. Soleimani; A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder; Int. J. Numer. Methods Heat Fluid Flow, 24 (8) (2014), pp. 1906–1927
20. [20] M. Sheikholeslami, R. Ellahi, H.R. Ashorynejad, G. Domairry, T. Hayat; Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium; Comput. Theor. Nanosci., 11 (2) (2014), pp. 486–496
21. [21] N.S. Akbar, M. Raza, R. Ellahi; Interaction of nano particles for the peristaltic flow in an asymmetric channel with the induced magnetic field; Eur. Phys. J. Plus, 129 (2014), pp. 155–167
22. [22] G.K. Ramesh, A.J. Chamkha, B.J. Gireesha; Magnetohydrodynamic flow of a non-Newtonian nanofluid over an impermeable surface with heat generation/absorption; J. Nanofluids, 3 (2014), pp. 78–84
23. [23] B. Rushi Kumar; MHD boundary layer flow on heat and mass transfer over a stretching sheet with slip effect; J. Naval Archit. Mar. Eng., 10 (2) (2013), pp. 16–26
24. [24] N.F.M. Noor, S. Abbasbandy, I. Hashim; Heat and mass transfer of thermoporetic MHD flow over an inclined radiate isothermal permeable surface in the presence of heat source/sink; Int. J. Heat Mass Transfer, 55 (7–8) (2012), pp. 2122–2128
25. [25] M. Subhas Abel, E. Sanjayanand, M.M. Nandeppanavar; Viscoelastic MHD flow and heat transfer over a stretching sheet with viscous and Ohmic dissipations; Commun. Nonlinear Sci. Numer. Simul., 13 (2008), pp. 1808–1821
26. [26] M. Sheikholeslami, M.G. Bandpy, R. Ellahi, A. Zeeshan; Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces; J. Magn. Magn. Mater., 369 (2014), pp. 69–80
27. [27] R. Ellahi, S. Aziz, A. Zeeshan; Non Newtonian nanofluids flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity; J. Porous Media, 16 (3) (2013), pp. 205–216
28. [28] N.S. Akbar, S.U. Rahman, R. Ellahi, S. Nadeem; Nano fluid flow in tapering stenosed arteries with permeable walls; Int. J. Therm. Sci., 85 (2014), pp. 54–61
29. [29] R. Ellahi; The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: analytical solutions; Appl. Math. Model., 37 (3) (2013), pp. 1451–1457
30. [30] A. Zeeshan, R. Ellahi, M. Hassam; Magnetohydrodynamic flow of water/ethylene glycol based nanofluids with natural convection through porous medium; Eur. Phys. J. Plus, 129 (2014), pp. 261–271
31. [31] R. Ellahi, M. Raza, K. Vafai; Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method; Math. Comput. Modell., 55 (2012), pp. 1876–1891
32. [32] S. Mansur, A. Ishak; The flow and heat transfer of a nano fluid past a stretching/shrinking sheet with convective boundary condition; Abstract Appl. Anal. (2013), Article 350647
33. [33] D.A. Nield, A.V. Kuznetsov; The one set of convection in a horizontal layer of finite depth, a revised model; Int. J. Heat Mass Transfer, 77 (2014), pp. 915–918
34. [34] C.H. Chen; Laminar mixed convection adjacent to vertical, continuously stretching sheets; Heat Mass Transfer, 33 (1998), pp. 471–476