Fast structural dynamic modeling and analysis for horizontally folding wing

Abstract

To investigate the structural dynamic characteristics of a folding wing effectively, a fast structural dynamic modeling approach is proposed. Firstly, the interface compatible relationship of the traditional fixed interface component modal synthesis method is modified, and the internal force of the interface is completely expressed in the structural dynamic equation, so that the influence of the connection stiffness on the wing structure dynamics can be considered. Then, on the basis of the fixed interface component modal synthesis method, the main mode of fixed-loaded interface is introduced to establish the mixed-loaded interface component modal synthesis method, which makes it feasible to accurately reflect the influence of elasticity and inertia of fuselage and outer wing on inner wing. The structural dynamics modeling method based on two different kinds of component modal synthesis method analyzed and deduced in detail. The application of component modal synthesis method in the fast structural dynamics modeling of folding wing is achieved. The whole program is compiled in MATLAB. At the same time, the dynamic characteristics of the folding wing with different folding angles, different connections and different connection positions is investigated. The results of the method proposed in this paper are compared with the results of the repeated finite model established in MSC.NASTRAN to verify the effectiveness from the aspects of natural frequency and vibration mode.

Keywords: Folding wing, component modal synthesis, dynamic analysis

1. Introduction

During the morphing process of morphing aircraft, the wing shape and geometric size change significantly leads to the redistribution of mass and stiffness of aircraft structure, resulting in different dynamic characteristics under different configurations [1]. The analysis of structural dynamic characteristics is the basis of flutter analysis and nonlinear aeroelastic analysis. In addition, the analysis of structural dynamic characteristics is also very important in the dynamic modeling of flexible multi-body system [2]. Therefore, it is particularly important to analyze the dynamic characteristics of the morphing aircraft, which can obtain the natural frequency and modal information of the wing structure and lay the foundation for the subsequent dynamic analysis [3].

Lee et al. [4] used Matlab to generate a high fidelity folding wing model proposed by Lockheed Martin, which is composed of rod, plate and other elements. The dynamic characteristics of the folding wing are analyzed in MSC.NASTRAN. However the effect of the fuselage on the structure is not taken into consideration in [4]. Snyder et al. [5] used MSC.PATRAN to establish the simplified structure of folding wing with different folding angles. The sensitivity of natural frequency to hinge stiffness and folding angle is analyzed in MSC.NASTRAN. The above research did not verify the correctness of the structural model. Tang et al. [6] established the theoretical model of folding wing structure using linear plate theory. Firstly, the modal analysis of each substructure is carried out by ANSYS, and then the Lagrange equation is used to synthesize to establish the dynamic model of the whole structure, and the correctness of the model is verified. At the same time, the variation rule of natural frequency with folding angle and hinge stiffness is analyzed. Andersen et al. [7] analyzed the natural frequency of the folding wing in MSC.NASTRAN and verified by the ground vibration test. Attar et al. [8] further considered the geometric nonlinearity of the structure and established the dynamic equation of the structure by using Kirchhoff plate theory and virtual work principle. Wang et al. [9] proposed a more general structural dynamic model for predicting the natural frequencies of folding wings, which is based on the beam theory. The natural frequencies of three test models in the whole folding angle range are measured. Zhao et al. [10] established the parametric structural dynamic model of the plate folding wing by the component synthesis method, and compared the results with those by MSC.NASTRAN. The correctness of the structural model is verified, and the influence factors of natural frequency are analyzed. In consideration of the nonlinear factors at the hinge of the folding wing, Hu et al. [11] established the dynamic model of the two wing segments by Lagrange equation, in which the cubic stiffness is considered. Lee et al. [12] used fictitious mass method to establish the structure with hinge free-play for the folding wing. The dynamic response characteristics are studied. Yang et al. [13] proposed a method for modeling multiple degrees of freedom in chord direction with structural nonlinearity by the fixed interface component modal synthesis method. The method introduces the angle difference between the inner and outer wing at the interface. The model synthesis of the two wing segments are achieved. Guo et al. [14-15] assumed that the wing was composed of three carbon fiber composite plates, and established the nonlinear dynamic equation by Hamilton principle and von Karman large deformation theory. The vibration modal function is solved according to the modal analysis, the results of harmonic response by ANSYS and the boundary conditions. The simulation results are compared with those by ANSYS, and the nonlinear dynamic characteristics of 1:2 resonance are further analyzed.

At present, the structural simulation method of folding wing is mainly based on finite element method, and the analytical method is used in a small number of literatures. This is because the analytical method is only suitable for simple engineering structures, while the finite element method has obvious advantages in dealing with various complex engineering problems. In most literatures, the continuous change process of folding wing of variant aircraft from unfolded state to folded state is usually decomposed into different configurations of wing, and then the repeated modeling of wing structure under different configurations is not conducive to the rapid analysis of structural dynamic characteristics of folding wing.

For the folding wing structure, the shape change exists locally, while the rest parts remain unchanged, it can be divided into different components. Only the changeable components need to be remodeled, and the whole structure model does not need to be reestablished by commercial software, so as to improve the modeling efficiency. The internal degrees of freedom of each component can be condensed, and then integrated into the overall solution equation, which greatly reduces the size of the problem and improves the computational efficiency. Component modal synthesis (CMS) is a natural choice. It enables the dynamic analysis to be performed on highly reduced matrices to save computational time. Also, it can make modifications possible to reduce the number of design iterations [16].

A fast structural dynamic modeling approach is proposed to investigate the structural dynamic characteristics of a folding wing effectively. For the folding wing with the elastic connection, the interface compatible relationship of the traditional fixed interface component modal synthesis method is modified, and the internal force of the interface is completely expressed in the structural dynamic equation, so the influence of the connection stiffness on the wing structure dynamics can be considered. For the folding wing with the rigid connection, a mixed-loaded interface component mode synthesis of a folding wing is proposed based on fixed interface and loaded interface method, which makes it feasible to accurately reflect the influence of elasticity and inertia of fuselage and outer wing on inner wing. The dynamic characteristics of the folding wing with different folding angles, different connections and different connection positions are investigated. The final dynamic equation has a highly reduced size and more concise. To verify the accuracy of this method, the results are compared with those from MSC.NASTRAN.

2. Fast structural dynamics modeling of folding wing

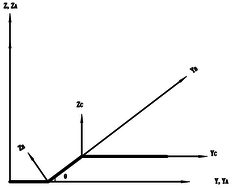
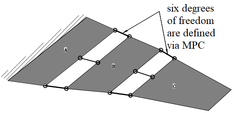
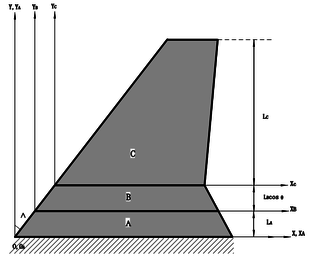
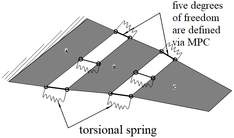
The folding wing is composed of three components, namely fuselage, inner wing and outer wing, denoted $A$, $B$ and $C$, respectively. The geometric diagram is shown in Figure 1. The coordinate system with subscript represents the local coordinate system of each component, while the coordinate system without subscript represents the global coordinate system. In order to verify the feasibility of the modeling method, the folding wing model is simplified as aluminum plate with equal thickness. All components are modeled by plates with the Yong’s modulus of $7.1\times {10}^{10}Pa$, Poisson’s coefficient of 0.33 and a density of $2.7\times {10}^{3}kg/m^{3}$, which are discretized using CQUAD4 elements with 2mm thickness in MSC.NASTRAN. Each node of this element has six degrees of freedom: three translations, namely, $u_{x},u_{y},u_{z}$ and three rotations, i.e., ${\theta }_{x},{\theta }_{y},{\theta }_{z}$. For each component, interface nodes are used at the connection positions of the folding axis to coordinate the boundary displacement. For the folding wing with rigid connection, MPC (Multi - Point Constraint) is used to couple the six degrees of freedom of interface nodes. For the folding wing with elastic connection, a set of torsion spring with a rotational degree of freedom ${\theta }_{x}$ are modeled and the other five degrees of freedom are defined via MPC. Among them, the torsional spring stiffness between components $A$ and $B$ is $K_{A}$, and that between components $B$ and $C$ is $K_{B}$. In this paper the structural dynamics model with two different connection types and different connection positions is established. The simulation method of two different connection types is shown in Figure 2.

(a) Top view	(b) Rear view
Figure 1. Geometry and coordinate system of folding wing

(a) Elastic connection	(b) Rigid connection
Figure 2. Schematic diagram of folding wing connection mode

The dynamic equations of each component with no damp in local coordinates are as follows:

${\bf {M}}_{l}^{\lambda }{\ddot {\bf {u}}}_{l}^{\lambda }+{\bf {K}}_{l}^{\lambda }{\bf {u}}_{l}^{\lambda }={\bf {f}}_{l}^{\lambda },\qquad (\lambda =A,B,C)$

(1)

where ${\boldsymbol {M}}_{l}^{\lambda }$ and ${\boldsymbol {K}}_{l}^{\lambda }$ represent mass and stiffness matrices. ${\boldsymbol {u}}_{l}^{\lambda }$ is a displacement vector, and ${\boldsymbol {f}}_{l}^{\lambda }$ is the constraints force vector.

When the local coordinate system in Figure 1 is adopted, the displacement vectors of components ${\textstyle A}$ and ${\textstyle C}$ are the same in the global coordinate system as in the local coordinate system, and no transformation is needed. For component ${\textstyle B}$, the relationship between the displacement vector in the global coordinate system and that in the local coordinate system is as follows:

${\boldsymbol {u}}_{l}^{B}={\boldsymbol {\overline {T}}}^{-1}{\boldsymbol {u}}^{B}$

(2)

where

${\boldsymbol {\overline {T}}}=blockdiag({\boldsymbol {T}},\cdots ,{\boldsymbol {T}})$, ${\boldsymbol {T}}=\left[{\begin{array}{cccccc}1&0&0&0&0&0\\0&cos\theta &-sin\theta &0&0&0\\0&sin\theta &cos\theta &0&0&0\\0&0&0&1&0&0\\0&0&0&0&cos\theta &-sin\theta \\0&0&0&0&sin\theta &cos\theta \end{array}}\right]$.

The structural dynamic equation of component ${\textstyle B}$ is transformed from the local coordinate system to the global coordinate system by pre-multiplying by ${\boldsymbol {\overline {T}}}$ on both sides of the structural dynamic equation of component ${\textstyle B}$.

In order to facilitate the application of component modal synthesis method, firstly, the displacement of each component in the global coordinate system is divided into internal node displacement and interface node displacement, and the mass matrix and stiffness matrix can be partitioned, which is similar to Ref. [10]. In this case, the structural dynamic equation of each component in the global coordinate system can be expressed as follows:

$\left[{\begin{array}{ccc}{\boldsymbol {M}}_{ii}^{A}&{\boldsymbol {M}}_{im}^{A}&{\boldsymbol {M}}_{is}^{A}\\&{\boldsymbol {M}}_{mm}^{A}&{\boldsymbol {M}}_{ms}^{A}\\sym&&{\boldsymbol {M}}_{ss}^{A}\\\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{A}\\{\boldsymbol {\ddot {u}}}_{m}^{A}\\{\boldsymbol {\ddot {u}}}_{s}^{A}\\\end{array}}\right]+\left[{\begin{array}{ccc}{\boldsymbol {K}}_{ii}^{A}&{\boldsymbol {K}}_{im}^{A}&{\boldsymbol {K}}_{is}^{A}\\&{\boldsymbol {K}}_{mm}^{A}&{\boldsymbol {K}}_{ms}^{A}\\sym&&{\boldsymbol {K}}_{ss}^{A}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{A}\\{\boldsymbol {u}}_{m}^{A}\\{\boldsymbol {u}}_{s}^{A}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{m}^{A}\\{\boldsymbol {f}}_{s}^{A}\end{array}}\right]$

(3)

$\left[{\begin{array}{ccccc}{\boldsymbol {M}}_{ii}^{B}&{\boldsymbol {M}}_{im}^{Ba}&{\boldsymbol {M}}_{is}^{Ba}&{\boldsymbol {M}}_{im}^{Bb}&{\boldsymbol {M}}_{is}^{Bb}\\&{\boldsymbol {M}}_{mm}^{Ba}&{\boldsymbol {M}}_{ms}^{Ba}&{\boldsymbol {M}}_{mm}^{Bab}&{\boldsymbol {M}}_{ms}^{Bab}\\&&{\boldsymbol {M}}_{ss}^{Ba}&{\boldsymbol {M}}_{sm}^{Bab}&{\boldsymbol {M}}_{ss}^{Bab}\\&sym&&{\boldsymbol {M}}_{mm}^{Bb}&{\boldsymbol {M}}_{ms}^{Bb}\\&&&&{\boldsymbol {M}}_{ms}^{Bb}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{B}\\{\boldsymbol {\ddot {u}}}_{m}^{Ba}\\{\boldsymbol {\ddot {u}}}_{s}^{Ba}\\{\boldsymbol {\ddot {u}}}_{m}^{Bb}\\{\boldsymbol {\ddot {u}}}_{s}^{Bb}\end{array}}\right]+\left[{\begin{array}{ccccc}{\boldsymbol {K}}_{ii}^{B}&{\boldsymbol {K}}_{im}^{Ba}&{\boldsymbol {K}}_{is}^{Ba}&{\boldsymbol {K}}_{im}^{Bb}&{\boldsymbol {K}}_{is}^{Bb}\\&{\boldsymbol {K}}_{mm}^{Ba}&{\boldsymbol {K}}_{ms}^{Ba}&{\boldsymbol {K}}_{mm}^{Bab}&{\boldsymbol {K}}_{ms}^{Bab}\\&&{\boldsymbol {K}}_{ss}^{Ba}&{\boldsymbol {K}}_{sm}^{Bab}&{\boldsymbol {K}}_{ss}^{Bab}\\&sym&&{\boldsymbol {K}}_{mm}^{Bb}&{\boldsymbol {K}}_{ms}^{Bb}\\&&&&{\boldsymbol {K}}_{ms}^{Bb}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{B}\\{\boldsymbol {u}}_{m}^{Ba}\\{\boldsymbol {u}}_{s}^{Ba}\\{\boldsymbol {u}}_{m}^{Bb}\\{\boldsymbol {u}}_{s}^{Bb}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{m}^{Ba}\\{\boldsymbol {f}}_{s}^{Ba}\\{\boldsymbol {f}}_{m}^{Bb}\\{\boldsymbol {f}}_{s}^{Bb}\end{array}}\right]$

(4)

$\left[{\begin{array}{ccc}{\boldsymbol {M}}_{ii}^{C}&{\boldsymbol {M}}_{im}^{C}&{\boldsymbol {M}}_{is}^{C}\\&{\boldsymbol {M}}_{mm}^{C}&{\boldsymbol {M}}_{ms}^{C}\\sym&&{\boldsymbol {M}}_{ss}^{C}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{C}\\{\boldsymbol {\ddot {u}}}_{m}^{C}\\{\boldsymbol {\ddot {u}}}_{s}^{C}\end{array}}\right]+\left[{\begin{array}{ccc}{\boldsymbol {K}}_{ii}^{C}&{\boldsymbol {K}}_{im}^{C}&{\boldsymbol {K}}_{is}^{C}\\&{\boldsymbol {K}}_{mm}^{C}&{\boldsymbol {K}}_{ms}^{C}\\sym&&{\boldsymbol {K}}_{ss}^{C}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{C}\\{\boldsymbol {u}}_{m}^{C}\\{\boldsymbol {u}}_{s}^{C}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{m}^{C}\\{\boldsymbol {f}}_{s}^{C}\end{array}}\right]$

(5)

where subscript i is the internal node displacement, the node displacement with MPC is denoted by subscript m, and the node displacement with torsion spring is denoted by subscript ${\textstyle s}$. the subscript a represents the interface between components ${\textstyle A}$ and ${\textstyle B}$, and ${\textstyle b}$ donates the interface between components ${\textstyle B}$ and ${\textstyle C}$.

2.1 Fixed interface component mode synthesis for folding wing with elastic connection

At present, when the fixed interface substructure modal synthesis method is applied to the modeling of complex structures, the elastic connection is rarely considered. Therefore, based on the fixed interface substructure modal synthesis method, a fast structural dynamic model of the folding wing with elastic connection is established.

For component ${\textstyle A}$, the displacements is transformed into the modal displacement by introducing the modal displacement and modal matrix:

${\boldsymbol {u}}^{A}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{A}\\{\boldsymbol {u}}_{m}^{A}\\{\boldsymbol {u}}_{s}^{A}\end{array}}\right]={\boldsymbol {\varphi }}_{CB}^{A}{\boldsymbol {p}}^{A}=$$\left[{\begin{array}{cc}{\boldsymbol {\varphi }}_{N}^{A}&{\boldsymbol {\varphi }}_{C}^{A}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {p}}_{C}^{A}\end{array}}\right]=\left[{\begin{array}{ccc}{\boldsymbol {\varphi }}_{n}^{A}&{\boldsymbol {\varphi }}_{cm}^{A}&{\boldsymbol {\varphi }}_{cs}^{A}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {u}}_{m}^{A}\\{\boldsymbol {u}}_{s}^{A}\end{array}}\right]$

(6)

where ${\boldsymbol {\varphi }}_{N}^{A}$ is the main mode, which can be obtained by solving the dynamic equation when the interface is fixed, i.e. ${\boldsymbol {K}}_{ii}^{A}{\boldsymbol {\varphi }}_{n}^{A}={\omega }_{A}^{2}{\boldsymbol {M}}_{ii}^{A}{\boldsymbol {\varphi }}_{n}^{A}$, ${\boldsymbol {\varphi }}_{C}^{A}$ is the constrained mode, i.e. ${\boldsymbol {\varphi }}_{cm}^{A}=-{\left({\boldsymbol {K}}_{ii}^{A}\right)}^{-1}{\boldsymbol {K}}_{im}^{A}$, ${\boldsymbol {\varphi }}_{cs}^{A}=-{\left({\boldsymbol {K}}_{ii}^{A}\right)}^{-1}{\boldsymbol {K}}_{is}^{A}$. Through coordinate transformation, the displacement at the interface does not change, and it is still expressed in the physical space, which is conducive to the introduction of torsional spring stiffness. If the higher order main mode is not ignored, the coordinate transformation is the complete transformation, and the accurate result can be obtained. But the order of matrix after transformation has not changed, and the purpose of reducing the degree of freedom is not achieved. Therefore, the higher-order of the main mode is usually ignored, and only the low-order mode is retained. The first coordinate transformation is introduced into the mass matrix and stiffness matrix of component ${\textstyle A}$, and the following results can be obtained:

${\boldsymbol {M}}_{CB}^{A}{\boldsymbol {\ddot {p}}}^{A}+{\boldsymbol {K}}_{CB}^{A}{\boldsymbol {p}}^{A}=$${\boldsymbol {f}}_{CB}^{A}$

(7)

where ${\boldsymbol {M}}_{CB}^{A}={\boldsymbol {\varphi }}_{CB}^{AT}{\boldsymbol {M}}^{A}{\boldsymbol {\varphi }}_{CB}^{A}$, ${\boldsymbol {K}}_{CB}^{A}={\boldsymbol {\varphi }}_{CB}^{AT}{\boldsymbol {K}}^{A}{\boldsymbol {\varphi }}_{CB}^{A}$, ${\boldsymbol {f}}_{CB}^{A}={\boldsymbol {\varphi }}_{CB}^{AT}{\boldsymbol {f}}^{A}=$${\left[{\begin{array}{ccc}{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{AT}&{\boldsymbol {f}}_{s}^{AT}\end{array}}\right]}^{T}$.

Similarly, introducing the modal coordinates ${\boldsymbol {p}}^{B}$ and modal matrices ${\boldsymbol {\varphi }}_{CB}^{B}$, the modal analysis is carried out for component ${\textstyle B}$, then:

${\boldsymbol {u}}^{B}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{B}\\{\boldsymbol {u}}_{m}^{Ba}\\{\boldsymbol {u}}_{s}^{Ba}\\{\boldsymbol {u}}_{m}^{Bb}\\{\boldsymbol {u}}_{s}^{Bb}\end{array}}\right]={\boldsymbol {\varphi }}_{CB}^{B}{\boldsymbol {p}}^{B}=$$\left[{\begin{array}{cc}{\boldsymbol {\varphi }}_{N}^{B}&{\boldsymbol {\varphi }}_{C}^{B}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{B}\\{\boldsymbol {p}}_{C}^{B}\end{array}}\right]=\left[{\begin{array}{ccccc}{\boldsymbol {\varphi }}_{n}^{B}&{\boldsymbol {\varphi }}_{cm}^{Ba}&{\boldsymbol {\varphi }}_{cs}^{Ba}&{\boldsymbol {\varphi }}_{cm}^{Bb}&{\boldsymbol {\varphi }}_{cs}^{Bb}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{i}^{B}\\{\boldsymbol {u}}_{m}^{Ba}\\{\boldsymbol {u}}_{s}^{Ba}\\{\boldsymbol {u}}_{m}^{Bb}\\{\boldsymbol {u}}_{s}^{Bb}\end{array}}\right]$

(8)

where ${\boldsymbol {K}}_{ii}^{B}{\boldsymbol {\varphi }}_{n}^{B}={\omega }_{B}^{2}{\boldsymbol {M}}_{ii}^{B}{\boldsymbol {\varphi }}_{n}^{B}$, ${\boldsymbol {\varphi }}_{cm}^{Ba}=-{\left({\boldsymbol {K}}_{ii}^{B}\right)}^{-1}{\boldsymbol {K}}_{im}^{Ba}$, ${\boldsymbol {\varphi }}_{cs}^{Ba}=-{\left({\boldsymbol {K}}_{ii}^{B}\right)}^{-1}{\boldsymbol {K}}_{is}^{Ba}$, ${\boldsymbol {\varphi }}_{cm}^{Bb}=-{\left({\boldsymbol {K}}_{ii}^{B}\right)}^{-1}{\boldsymbol {K}}_{im}^{Bb}$, ${\boldsymbol {\varphi }}_{cs}^{Bb}=-{\left({\boldsymbol {K}}_{ii}^{B}\right)}^{-1}{\boldsymbol {K}}_{is}^{Bb}$. We can obtain the first coordinate transformation of component ${\textstyle B}$:

${\boldsymbol {M}}_{CB}^{B}{\boldsymbol {\ddot {p}}}^{B}+{\boldsymbol {K}}_{CB}^{B}{\boldsymbol {p}}^{B}=$${\boldsymbol {f}}_{CB}^{B}$

(9)

where ${\boldsymbol {M}}_{CB}^{B}={\boldsymbol {\varphi }}_{CB}^{BT}{\boldsymbol {M}}^{B}{\boldsymbol {\varphi }}_{CB}^{B}$, ${\boldsymbol {K}}_{CB}^{B}={\boldsymbol {\varphi }}_{CB}^{BT}{\boldsymbol {K}}^{B}{\boldsymbol {\varphi }}_{CB}^{B}$, ${\boldsymbol {f}}_{CB}^{B}={\boldsymbol {\varphi }}_{CB}^{BT}{\boldsymbol {f}}^{B}=$${\left[{\begin{array}{ccccc}{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{BaT}&{\boldsymbol {f}}_{s}^{BaT}&{\boldsymbol {f}}_{m}^{BT}&{\boldsymbol {f}}_{s}^{BbT}\end{array}}\right]}^{T}$.

Similar expressions can be written for component ${\textstyle C}$:

${\boldsymbol {u}}^{C}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{C}\\{\boldsymbol {u}}_{m}^{C}\\{\boldsymbol {u}}_{s}^{C}\end{array}}\right]={\boldsymbol {\varphi }}_{CB}^{C}{\boldsymbol {p}}^{C}=$$\left[{\begin{array}{cc}{\boldsymbol {\varphi }}_{N}^{C}&{\boldsymbol {\varphi }}_{C}^{C}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {p}}_{C}^{A}\end{array}}\right]=\left[{\begin{array}{ccc}{\boldsymbol {\varphi }}_{n}^{C}&{\boldsymbol {\varphi }}_{cm}^{C}&{\boldsymbol {\varphi }}_{cs}^{C}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{C}\\{\boldsymbol {u}}_{m}^{C}\\{\boldsymbol {u}}_{s}^{C}\end{array}}\right]$

(10)

where ${\boldsymbol {K}}_{ii}^{C}{\boldsymbol {\varphi }}_{n}^{C}={\omega }_{C}^{2}{\boldsymbol {M}}_{ii}^{C}{\boldsymbol {\varphi }}_{n}^{C}$, ${\boldsymbol {\varphi }}_{cm}^{C}=-{\left({\boldsymbol {K}}_{ii}^{C}\right)}^{-1}{\boldsymbol {K}}_{im}^{C}$, ${\boldsymbol {\varphi }}_{cs}^{C}=-{\left({\boldsymbol {K}}_{ii}^{C}\right)}^{-1}{\boldsymbol {K}}_{is}^{C}$. The first coordinate transformation is introduced into the mass matrix and stiffness matrix of component ${\textstyle C}$, and the following results can be obtained:

${\boldsymbol {M}}_{CB}^{C}{\boldsymbol {\ddot {p}}}^{C}+{\boldsymbol {K}}_{CB}^{C}{\boldsymbol {p}}^{C}=$${\boldsymbol {f}}_{CB}^{C}$

(11)

where ${\boldsymbol {M}}_{CB}^{C}={\boldsymbol {\varphi }}_{CB}^{CT}{\boldsymbol {M}}^{C}{\boldsymbol {\varphi }}_{CB}^{C}$, ${\boldsymbol {K}}_{CB}^{C}={\boldsymbol {\varphi }}_{CB}^{CT}{\boldsymbol {K}}^{C}{\boldsymbol {\varphi }}_{CB}^{C}$, ${\boldsymbol {f}}_{CB}^{C}={\boldsymbol {\varphi }}_{CB}^{CT}{\boldsymbol {f}}^{C}=$${\left[{\begin{array}{ccc}{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{C}{}^{T}&{\boldsymbol {f}}_{s}^{C}{}^{T}\end{array}}\right]}^{T}$.

In this case, the uncoupled dynamic equation of the whole structure can be written as follows:

${\boldsymbol {M{\ddot {p}}}}+{\boldsymbol {Kp}}={\boldsymbol {f}}$

(12)

where

${\boldsymbol {M}}=diag({\boldsymbol {M}}_{CB}^{A},{\boldsymbol {M}}_{CB}^{B},{\boldsymbol {M}}_{CB}^{C})$, $\quad {\boldsymbol {K}}=diag({\boldsymbol {K}}_{CB}^{A},{\boldsymbol {K}}_{CB}^{B},{\boldsymbol {K}}_{CB}^{C})$, ${\boldsymbol {p}}={\left[{\begin{array}{ccc}{\boldsymbol {p}}^{AT}&{\boldsymbol {p}}^{BT}&{\boldsymbol {p}}^{CT}\end{array}}\right]}^{T}={\left[{\begin{array}{ccccccccccc}{\boldsymbol {p}}_{n}^{A}{}^{T}&{\boldsymbol {u}}_{m}^{A}{}^{T}&{\boldsymbol {u}}_{s}^{A}{}^{T}&{\boldsymbol {p}}_{n}^{B}{}^{T}&{\boldsymbol {u}}_{m}^{Ba}{}^{T}&{\boldsymbol {u}}_{s}^{Ba}{}^{T}&{\boldsymbol {u}}_{m}^{Bb}{}^{T}&{\boldsymbol {u}}_{s}^{Bb}{}^{T}&{\boldsymbol {p}}_{n}^{C}{}^{T}&{\boldsymbol {u}}_{m}^{C}{}^{T}&{\boldsymbol {u}}_{s}^{C}{}^{T}\end{array}}\right]}^{T}$, ${\boldsymbol {f}}={\left[{\begin{array}{ccc}{\boldsymbol {f}}_{CB}^{AT}&{\boldsymbol {f}}_{CB}^{BT}&{\boldsymbol {f}}_{CB}^{CT}\end{array}}\right]}^{T}={\left[{\begin{array}{ccccccccccc}{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{A}{}^{T}&{\boldsymbol {f}}_{s}^{A}{}^{T}&{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{Ba}{}^{T}&{\boldsymbol {f}}_{s}^{Ba}{}^{T}&{\boldsymbol {f}}_{m}^{Bb}{}^{T}&{\boldsymbol {f}}_{s}^{Bb}{}^{T}&{\boldsymbol {0}}^{T}&{\boldsymbol {f}}_{m}^{C}{}^{T}&{\boldsymbol {f}}_{s}^{C}{}^{T}\end{array}}\right]}^{T}.$

The connection relationship between the components does not expressed in Eq. (12). The components of modal coordinates ${\boldsymbol {p}}$ are not independent and cannot be directly used for the dynamic characteristics analysis of folding wing. It is necessary to eliminate the dependent modal coordinates according to the compatible conditions of the interface to obtain the whole structural dynamic model. The displacement compatible condition of the interface is as follows:

$\left\{{\begin{array}{c}{\boldsymbol {u}}_{m}^{A}={\boldsymbol {u}}_{m}^{Ba}\\{\boldsymbol {u}}_{m}^{Bb}={\boldsymbol {u}}_{m}^{C}\end{array}}\right.$

(13)

Considering the equilibrium condition of the force at the interface, the compatible condition of the force can be expressed as:

$\left\{{\begin{array}{c}{\boldsymbol {f}}_{m}^{A}+{\boldsymbol {f}}_{m}^{Ba}={\boldsymbol {0}}\\{\boldsymbol {f}}_{m}^{Bb}+{\boldsymbol {f}}_{m}^{C}={\boldsymbol {0}}\end{array}}\right.$

(14)

The torque generated by the torsion spring can be expressed as:

$\left\{{\begin{array}{c}{\begin{array}{cc}{\boldsymbol {f}}_{s}^{A}=K_{A}({\boldsymbol {u}}_{s}^{Ba}-{\boldsymbol {u}}_{s}^{A}),&{\boldsymbol {f}}_{s}^{Ba}=-K_{A}({\boldsymbol {u}}_{s}^{Ba}-{\boldsymbol {u}}_{s}^{A})\end{array}}\\{\begin{array}{cc}{\boldsymbol {f}}_{s}^{Bb}=K_{B}({\boldsymbol {u}}_{s}^{Bb}-{\boldsymbol {u}}_{s}^{C}),&{\boldsymbol {f}}_{s}^{C}=-K_{B}({\boldsymbol {u}}_{s}^{Bb}-{\boldsymbol {u}}_{s}^{C})\end{array}}\end{array}}\right.$

(15)

The independent mode coordinate transformation matrix is introduced, which can be expressed as follows:

${\boldsymbol {p}}=\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {p}}_{m}^{A}\\{\boldsymbol {p}}_{s}^{A}\\{\boldsymbol {p}}_{i}^{B}\\{\boldsymbol {p}}_{m}^{Ba}\\{\boldsymbol {p}}_{s}^{Ba}\\{\boldsymbol {p}}_{m}^{Bb}\\{\boldsymbol {p}}_{s}^{Bb}\\{\boldsymbol {p}}_{n}^{C}\\{\boldsymbol {p}}_{m}^{C}\\{\boldsymbol {p}}_{s}^{C}\end{array}}\right]={\boldsymbol {\Pi q}}=\left[{\begin{array}{ccccccccc}{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {u}}_{m}^{A}\\{\boldsymbol {u}}_{s}^{A}\\{\boldsymbol {p}}_{n}^{B}\\{\boldsymbol {u}}_{s}^{Ba}\\{\boldsymbol {u}}_{s}^{Bb}\\{\boldsymbol {p}}_{n}^{C}\\{\boldsymbol {p}}_{m}^{C}\\{\boldsymbol {u}}_{s}^{C}\end{array}}\right]$

(16)

We obtain the following expression:

${\boldsymbol {{\tilde {M}}{\ddot {q}}}}+{\boldsymbol {{\tilde {K}}q}}=$${\boldsymbol {\tilde {f}}}$

(17)

where

${\boldsymbol {\tilde {M}}}={\boldsymbol {\Pi }}^{T}{\boldsymbol {M\Pi }}$, $\quad {\boldsymbol {\tilde {K}}}={\boldsymbol {\Pi }}^{T}{\boldsymbol {K\Pi }}$, ${\boldsymbol {q}}={\left[{\begin{array}{ccccccccc}{\boldsymbol {p}}_{n}^{A}{}^{T}&{\boldsymbol {u}}_{m}^{A}{}^{T}&{\boldsymbol {u}}_{s}^{A}{}^{T}&{\boldsymbol {p}}_{n}^{B}{}^{T}&{\boldsymbol {u}}_{s}^{Ba}{}^{T}&{\boldsymbol {u}}_{s}^{Bb}{}^{T}&{\boldsymbol {p}}_{n}^{C}&{\boldsymbol {u}}_{m}^{C}&{\boldsymbol {u}}_{s}^{C}\end{array}}\right]}^{T}$, ${\boldsymbol {\tilde {f}}}={\left[{\begin{array}{ccccccccc}{\boldsymbol {0}}^{T}&{\boldsymbol {0}}^{T}&K_{A}{\left({\boldsymbol {u}}_{s}^{Ba}-{\boldsymbol {u}}_{s}^{A}\right)}^{T}&{\boldsymbol {0}}^{T}&-K_{A}{\left({\boldsymbol {u}}_{s}^{Ba}-{\boldsymbol {u}}_{s}^{A}\right)}^{T}&K_{B}{\left({\boldsymbol {u}}_{s}^{Bb}-{\boldsymbol {u}}_{s}^{C}\right)}^{T}&{\boldsymbol {0}}^{T}&{\boldsymbol {0}}^{T}&-K_{B}{\left({\boldsymbol {u}}_{s}^{Bb}-{\boldsymbol {u}}_{s}^{C}\right)}^{T}\end{array}}\right]}^{T}$.

Obviously, the right-hand term ${\boldsymbol {\tilde {f}}}$ in Eq. (17) is related to the torsional spring stiffness $K_{A}$, $K_{B}$ and the modal coordinates ${\boldsymbol {q}}$. The dynamic analysis of wing structure is usually based on free vibration. Therefore, it is necessary to take ${\boldsymbol {\tilde {f}}}$ into account in the stiffness matrix of the structure. From the previous coordinate transformation, it can be seen that the displacement at the interface is still expressed in the physical space, which is conducive to the introduction of torsional spring stiffness. Here ${\boldsymbol {\tilde {f}}}$ is written in the form of a matrix:

${\boldsymbol {\tilde {f}}}={\boldsymbol {K}}^{'}{\boldsymbol {q}}$

(18)

where

${\boldsymbol {K}}^{'}=\left[{\begin{array}{ccccccccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&-{\boldsymbol {K}}_{A}&{\boldsymbol {0}}&{\boldsymbol {K}}_{A}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {K}}_{A}&{\boldsymbol {0}}&-{\boldsymbol {K}}_{A}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {K}}_{B}&{\boldsymbol {0}}&{\boldsymbol {0}}&-{\boldsymbol {K}}_{B}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&-{\boldsymbol {K}}_{B}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {K}}_{B}\end{array}}\right]$, ${\boldsymbol {K}}_{B}=diag(K_{B},\cdots ,K_{B})$.

In the independent modal coordinates, the complete dynamic equation is as follows:

${\boldsymbol {{\tilde {M}}{\ddot {q}}}}+({\boldsymbol {\tilde {K}}}-$${\boldsymbol {K}}^{'}){\boldsymbol {q}}={\boldsymbol {0}}$

(19)

The global mass matrix is tridiagonal and the stiffness matrix is quasi diagonal. The natural frequency and modal information of the original structure can be obtained by relevant matrix characteristic analysis methods, such as Lanczos method. After two coordinate transformations, the system can return to the physical coordinates, so as to obtain the vibration mode of the whole system in the physical coordinates, namely, the reconstruction of the component.

2.2 Mixed-loaded interface component mode synthesis for folding wing with rigid connection

The advantage of the fixed interface component modal synthesis method is that the method is relatively simple, which is conducive to compile, and the calculation accuracy is generally high, but the disadvantage is that the degree of freedom of the interface is retained after the synthesis. For a complex structure, the interface degree of freedom of substructure is often very high, and the reduced degree of freedom is still high. Benfield [17] proposed fixed-loaded interface component mode synthesis. It is necessary to divide the folding wing into master-slave substructures. Although some suggestions are given for the selection of the main substructure, the specific model should be treated concretely.

Therefore, this paper assumes that the inner wing is the master component, and the fuselage and outer wing are the slave components. Here, main mode of fixed-loaded interface is adopted for the master component, and the main mode and constraint mode of fixed interface are adopted for the slave component. Finally, the mixed-loaded interface component modal synthesis for folding wing with rigid connection is established.

For the sake of simplicity, it is assumed that the fuselage and the inner wing, the inner wing and the outer wing are rigidly connected, that is, all the degrees of freedom of the interface nodes are defined by MPC. Different components have been partitioned according to internal and interface degrees of freedom. The subscripts m and s in Eqs. (3), (4) and (5) are all represented by subscript $j$, so the simpler expression is as follows:

$\left[{\begin{array}{cc}{\boldsymbol {M}}_{ii}^{A}&{\boldsymbol {M}}_{ij}^{A}\\sym&{\boldsymbol {M}}_{jj}^{A}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{A}\\{\boldsymbol {\ddot {u}}}_{j}^{A}\end{array}}\right]+\left[{\begin{array}{cc}{\boldsymbol {K}}_{ii}^{A}&{\boldsymbol {K}}_{ij}^{A}\\sym&{\boldsymbol {K}}_{jj}^{A}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{A}\\{\boldsymbol {u}}_{j}^{A}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{A}\end{array}}\right]$

(20)

$\left[{\begin{array}{ccc}{\boldsymbol {M}}_{ii}^{B}&{\boldsymbol {M}}_{ii}^{Ba}&{\boldsymbol {M}}_{ij}^{Bb}\\&{\boldsymbol {M}}_{jj}^{Ba}&{\boldsymbol {M}}_{jj}^{Bab}\\sym&&{\boldsymbol {M}}_{jj}^{Bb}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{B}\\{\boldsymbol {\ddot {u}}}_{j}^{Ba}\\{\boldsymbol {\ddot {u}}}_{j}^{Bb}\end{array}}\right]+\left[{\begin{array}{ccc}{\boldsymbol {K}}_{ii}^{B}&{\boldsymbol {K}}_{ii}^{Ba}&{\boldsymbol {K}}_{ij}^{Bb}\\&{\boldsymbol {K}}_{jj}^{Ba}&{\boldsymbol {K}}_{jj}^{Bab}\\sym&&{\boldsymbol {K}}_{jj}^{Bb}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{B}\\{\boldsymbol {u}}_{j}^{Ba}\\{\boldsymbol {u}}_{j}^{Bb}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{Ba}\\{\boldsymbol {f}}_{j}^{Bb}\end{array}}\right]$

(21)

$\left[{\begin{array}{cc}{\boldsymbol {M}}_{ii}^{C}&{\boldsymbol {M}}_{ij}^{C}\\sym&{\boldsymbol {M}}_{jj}^{C}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{C}\\{\boldsymbol {\ddot {u}}}_{j}^{C}\end{array}}\right]+\left[{\begin{array}{cc}{\boldsymbol {K}}_{ii}^{C}&{\boldsymbol {K}}_{ij}^{C}\\sym&{\boldsymbol {K}}_{jj}^{C}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{C}\\{\boldsymbol {u}}_{j}^{C}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{C}\end{array}}\right]$

(22)

For components ${\textstyle A}$ and ${\textstyle C}$, the main mode and constraint mode of fixed interface are adopted, and the expression is similar to Eqs. (6) and (10). A more concise form is given here:

${\boldsymbol {u}}^{A}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{A}\\{\boldsymbol {u}}_{j}^{A}\end{array}}\right]=\left[{\begin{array}{cc}{\boldsymbol {\varphi }}_{n}^{A}&{\boldsymbol {\varphi }}_{c}^{A}\\{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {u}}_{j}^{A}\end{array}}\right]$

(23)

${\boldsymbol {u}}^{C}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{C}\\{\boldsymbol {u}}_{j}^{C}\end{array}}\right]=\left[{\begin{array}{cc}{\boldsymbol {\varphi }}_{n}^{C}&{\boldsymbol {\varphi }}_{c}^{C}\\{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{C}\\{\boldsymbol {u}}_{j}^{C}\end{array}}\right]$

(24)

For the main mode of component ${\textstyle B}$, the influence of components ${\textstyle A}$ and ${\textstyle C}$ should also be considered. The internal degrees of freedom of components ${\textstyle A}$ and ${\textstyle C}$ can be condensed to the interface by static condensation. When the influence of inertia is not considered, the first row of Eqs.(20) and (22) can be used to calculate the static equilibrium:

${\boldsymbol {u}}^{A}=\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{c}^{A}\\{\boldsymbol {I}}\end{array}}\right]{\boldsymbol {u}}_{j}^{A}$

(25)

${\boldsymbol {u}}^{C}=\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{c}^{C}\\{\boldsymbol {I}}\end{array}}\right]{\boldsymbol {u}}_{j}^{C}$

(26)

Eqs.(25) and (26) also show that the process of static condensation is to establish the relationship between internal degrees of freedom and interface degrees of freedom by the constraint modes of the fixed interface. The displacement compatibility condition of the interface is as follows

$\left\{{\begin{array}{c}{\boldsymbol {u}}_{j}^{A}={\boldsymbol {u}}_{j}^{Ba}\\{\boldsymbol {u}}_{j}^{C}={\boldsymbol {u}}_{j}^{Bb}\end{array}}\right.$

(27)

Consequently, we obtain:

${\boldsymbol {u}}^{A}=\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{c}^{A}\\{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\end{array}}\right]\,\,{\boldsymbol {u}}^{B}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {\varphi }}_{c}^{A}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\end{array}}\right]\,\,{\boldsymbol {u}}^{B}={\boldsymbol {T}}_{1}{\boldsymbol {u}}^{B}$

(28)

${\boldsymbol {u}}^{C}=\left[{\begin{array}{c}{\boldsymbol {\varphi }}_{c}^{C}\\{\boldsymbol {I}}\end{array}}\right]\,\,\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,{\boldsymbol {u}}^{B}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {\varphi }}_{c}^{C}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {I}}\end{array}}\right]\,\,{\boldsymbol {u}}^{B}={\boldsymbol {T}}_{2}{\boldsymbol {u}}^{B}$

(29)

Eqs.(28) and (29) show that all the degrees of freedom of components ${\textstyle A}$ and ${\textstyle C}$ can be expressed by the degrees of freedom of component ${\textstyle B}$. So component ${\textstyle B}$ is the master component, and ${\textstyle A}$ and ${\textstyle C}$ are the slave components, which well reflects the connection between components. By substituting the two equations above into the dynamic equations of components ${\textstyle A}$ and ${\textstyle C}$ respectively, namely Eqs. (20) and (22), and pre-multiplying ${\boldsymbol {T}}_{1}^{T}$ and ${\boldsymbol {T}}_{2}^{T}$ on both sides, we can get the following results:

${\boldsymbol {\overline {M}}}^{A}{\boldsymbol {\ddot {u}}}^{B}+$${\boldsymbol {\overline {K}}}^{A}{\boldsymbol {u}}^{B}=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{A}\\{\boldsymbol {0}}\end{array}}\right]$, $\quad {\boldsymbol {\overline {M}}}^{C}{\boldsymbol {\ddot {u}}}^{B}+$${\boldsymbol {\overline {K}}}^{C}{\boldsymbol {u}}^{B}=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{C}\end{array}}\right]$

(30)

where

${\boldsymbol {\overline {M}}}^{A}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{A}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\end{array}}\right]$, $\quad {\boldsymbol {\overline {K}}}^{A}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{A}{}_{jj}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\end{array}}\right]$, $\quad {\boldsymbol {\overline {M}}}^{C}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{C}\end{array}}\right]$, $\quad {\boldsymbol {\overline {K}}}^{C}=\left[{\begin{array}{ccc}{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{C}\end{array}}\right]$, $\qquad$ $\quad {\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{A}={\boldsymbol {\varphi }}_{c}^{AT}{\boldsymbol {M}}_{ii}^{A}{\boldsymbol {\varphi }}_{c}^{A}+{\boldsymbol {\varphi }}_{c}^{AT}{\boldsymbol {M}}_{ij}^{A}+{\boldsymbol {M}}_{ji}^{A}{\boldsymbol {\varphi }}_{c}^{A}+{\boldsymbol {M}}_{jj}^{A}$, $\quad {\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{A}={\boldsymbol {\varphi }}_{c}^{AT}{\boldsymbol {K}}_{ii}^{A}{\boldsymbol {\varphi }}_{c}^{A}+{\boldsymbol {\varphi }}_{c}^{AT}{\boldsymbol {K}}_{ij}^{A}+{\boldsymbol {K}}_{ji}^{A}{\boldsymbol {\varphi }}_{c}^{A}+{\boldsymbol {K}}_{jj}^{A}$, $\qquad$ ${\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{C}={\boldsymbol {\varphi }}_{c}^{CT}{\boldsymbol {M}}_{ii}^{C}{\boldsymbol {\varphi }}_{c}^{C}+$${\boldsymbol {\varphi }}_{c}^{CT}{\boldsymbol {M}}_{ij}^{C}+{\boldsymbol {M}}_{ji}^{C}{\boldsymbol {\varphi }}_{c}^{C}+{\boldsymbol {M}}_{jj}^{C}$, $\quad {\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{C}={\boldsymbol {\varphi }}_{c}^{CT}{\boldsymbol {K}}_{ii}^{C}{\boldsymbol {\varphi }}_{c}^{C}+{\boldsymbol {\varphi }}_{c}^{CT}{\boldsymbol {K}}_{ij}^{C}+{\boldsymbol {K}}_{ji}^{C}{\boldsymbol {\varphi }}_{c}^{C}+{\boldsymbol {K}}_{jj}^{C}$.

Derivation of the right end term of Eq. (30) is as follows:

${\boldsymbol {T}}_{1}^{T}\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{A}\end{array}}\right]=\left[{\begin{array}{cc}{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {\varphi }}_{c}^{AT}&{\boldsymbol {I}}\\{\boldsymbol {0}}&{\boldsymbol {0}}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{A}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{A}\\{\boldsymbol {0}}\end{array}}\right]$

(31)

${\boldsymbol {T}}_{2}^{T}\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{C}\end{array}}\right]=\left[{\begin{array}{cc}{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {\varphi }}_{c}^{CT}&{\boldsymbol {I}}\end{array}}\right]\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{C}\end{array}}\right]=\left[{\begin{array}{c}{\boldsymbol {0}}\\{\boldsymbol {0}}\\{\boldsymbol {f}}_{j}^{C}\end{array}}\right]$

(32)

Through the transformation of Eqs.(31) and (32), it can be seen that the internal forces between components ${\textstyle A}$ and ${\textstyle C}$ and component ${\textstyle B}$ are respectively expressed at the interface. By adding Eqs.(30) and (21), the dynamic equation of component ${\textstyle B}$ considering the elasticity and inertia of components A and ${\textstyle C}$ at the interface can be obtained. Because the internal forces are equal in magnitude and opposite in direction, the dynamic equation of component ${\textstyle B}$ after fixed-loaded is as follows:

$({\boldsymbol {\overline {M}}}^{A}+{\boldsymbol {M}}^{B}+{\boldsymbol {\overline {M}}}^{C}){\boldsymbol {\ddot {u}}}^{B}+$$({\boldsymbol {\overline {K}}}^{A}+{\boldsymbol {K}}^{B}+{\boldsymbol {\overline {K}}}^{C}){\boldsymbol {u}}^{B}=$${\boldsymbol {0}}$

(33)

In order to better reflect the loading effect, Eq.(33) is expressed in blocks:

$\left[{\begin{array}{ccc}{\boldsymbol {M}}_{ii}^{B}&{\boldsymbol {M}}_{ii}^{Ba}&{\boldsymbol {M}}_{ij}^{Bb}\\&{\boldsymbol {M}}_{jj}^{Ba}+{\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{A}&{\boldsymbol {M}}_{jj}^{Bab}\\sym&&{\boldsymbol {M}}_{jj}^{Bb}+{\boldsymbol {\overset {\mbox{ˆ}}{M}}}_{jj}^{C}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {\ddot {u}}}_{i}^{B}\\{\boldsymbol {\ddot {u}}}_{j}^{Ba}\\{\boldsymbol {\ddot {u}}}_{j}^{Bb}\end{array}}\right]+\left[{\begin{array}{ccc}{\boldsymbol {K}}_{ii}^{B}&{\boldsymbol {K}}_{ii}^{Ba}&{\boldsymbol {K}}_{ij}^{Bb}\\&{\boldsymbol {K}}_{jj}^{Ba}+{\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{A}&{\boldsymbol {K}}_{jj}^{Bab}\\sym&&{\boldsymbol {K}}_{jj}^{Bb}+{\boldsymbol {\overset {\mbox{ˆ}}{K}}}_{jj}^{C}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{B}\\{\boldsymbol {u}}_{j}^{Ba}\\{\boldsymbol {u}}_{j}^{Bb}\end{array}}\right]={\boldsymbol {0}}$

(34)

For the above equation, the right side is zero because the equivalent force at the interface of different components is opposite. So components ${\textstyle A}$ and ${\textstyle C}$ have effect on component ${\textstyle B}$ by approximate inertial force and elastic force at the interface.

Through eigenvalue analysis of Eq.(34), the main mode ${\boldsymbol {\Phi }}_{n}^{B}$ of component ${\textstyle B}$ considering the inertia and elastic effects of adjacent components ${\textstyle A}$ and ${\textstyle C}$ is obtained

${\boldsymbol {u}}^{B}=\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{B}\\{\boldsymbol {u}}_{j}^{Ba}\\{\boldsymbol {u}}_{j}^{Bb}\end{array}}\right]={\boldsymbol {\Phi }}_{n}^{B}{\boldsymbol {p}}_{n}^{B}=\left[{\begin{array}{c}{\boldsymbol {\Phi }}_{ni}^{B}\\{\boldsymbol {\Phi }}_{nja}^{B}\\{\boldsymbol {\Phi }}_{njb}^{B}\end{array}}\right]{\boldsymbol {p}}_{n}^{B}$

(35)

By combining Eqs.(25), (26) and (35), we can obtain:

$\left[{\begin{array}{c}{\boldsymbol {u}}_{i}^{A}\\{\boldsymbol {u}}_{j}^{A}\\{\boldsymbol {u}}^{B}\\{\boldsymbol {u}}_{i}^{C}\\{\boldsymbol {u}}_{j}^{C}\end{array}}\right]={\boldsymbol {T}}_{3}\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {p}}_{n}^{B}\\{\boldsymbol {p}}_{n}^{C}\end{array}}\right]=\left[{\begin{array}{ccc}{\boldsymbol {\varphi }}_{n}^{A}&{\boldsymbol {\varphi }}_{c}^{A}{\boldsymbol {\Phi }}_{nja}^{B}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\Phi }}_{nja}^{B}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {I}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\varphi }}_{c}^{C}{\boldsymbol {\Phi }}_{njb}^{B}&{\boldsymbol {\varphi }}_{n}^{C}\\{\boldsymbol {0}}&{\boldsymbol {\Phi }}_{njb}^{B}&{\boldsymbol {0}}\end{array}}\right]\,\,\left[{\begin{array}{c}{\boldsymbol {p}}_{n}^{A}\\{\boldsymbol {p}}_{n}^{B}\\{\boldsymbol {p}}_{n}^{C}\end{array}}\right]$

(36)

The Eq.(36) is substituted into Eqs.( 21), (22) and (23).And pre-multiplying by ${\boldsymbol {T}}_{3}^{T}$ , the overall structural dynamic equation of the folding wing is obtained as follows:

${\boldsymbol {{\tilde {M}}{\ddot {q}}}}+{\boldsymbol {{\tilde {K}}q}}={\boldsymbol {0}}$

(37)

There is a certain coupling term in the mass matrix that the master-slave components are connected into one. The stiffness matrix is basically a diagonal matrix ${\boldsymbol {q}}={\left[{\begin{array}{ccc}{\boldsymbol {p}}_{n}^{AT}&{\boldsymbol {p}}_{n}^{BT}&{\boldsymbol {p}}_{n}^{CT}\end{array}}\right]}^{T}$. So far, the fast structural dynamic modeling of folding wing is completed based on the fixed interface component modal synthesis method and the mixed-loaded interface component modal synthesis method. If the structure contains multiple components and has more interfaces, the integrated modeling can be carried out according to the above steps.

3. Dynamic analysis of folding wing

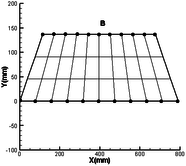
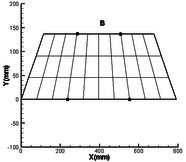
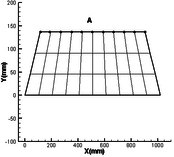
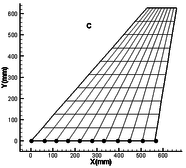
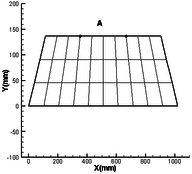
In order to verify the effectiveness of the above modeling method, this method is compared with the results of the finite element model in MSC.NASTRAN. The natural frequency and mode shape of the folding wing are verified. First, the finite element model is established in its local coordinate system in the MSC.PATRAN, and the mass matrix and stiffness matrix of the component are extracted by DMAP. Then according to the method of this paper, the fast modeling of folding wing is carried out. The whole program is compiled in MATLAB, and the dynamic analysis is completed. In this method, the folding angle, torsion spring stiffness and the connection position at the interface are changed to realize the analysis of the dynamic characteristics of the folding wing under various conditions. There is no need to repeat the modeling of the folding wing, which simplifies the modeling process. A comparative analysis of two different connection positions is made in this paper. The connection positions are shown in Figure 3.

(a) Connection position 1
(b) Connection position 2
Figure 3. Finite element model of component (each dot represents connection position)

3.1 Dynamic characteristics of folding wing with elastic connection

When the folding wings are connected by hinges, that is, elastic connection, ${\theta }_{x}$ is defined by the torsion spring and MPC are used to define the other five degrees of freedom. The fixed interface component modal synthesis method is used to quickly model and the dynamic characteristics of the folding wings with elastic connection is analyzed. The natural frequency is compared with that in MSC.NASTRAN for different connection positions in Figure 3, and $K_{A}=K_{B}=5Nm/rad$ . The compared results are as shown in Tables 1 and 2. According to the number of main modes reserved by different components, different mode combinations are formed. For example, (4,4,4) represents that components $A$, $B$ and $C$ all retain 4-order main modes, and "-" represents that the relative error is greater than 15%.

Table 1. Natural frequency of folding wing with elastic connection at connection positions 1 ($\theta =0^{\circ }$)

Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (4,4,4)		Main mode combination (5,4,5)		Main mode combination (6,8,10)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	1.73	1.61	6.9	1.61	6.9<	1.61	6.9
2	10.44	10.97	5.07	10.97	5.07	10.96	4.98
3	16.69	16.82	0.78	16.76	0.42	16.76	0.42
4	25.26	26.78	6.02	26.74	5.86	26.71	5.74
5	37.24	41.29	10.8	41.12	10.42	41.04	10.2
6	49.86	50.36	1.00	50.34	0.96	50.30	0.88
7	59.69	61.85	3.62	61.36	2.80	60.64	1.59
8	71.27	76.11	6.80	72.91	2.30	72.82	2.17
9	75.5	82.77	9.63	77.36	2.46	75.57	0.93
10	86.75	101.37	—	93.28	7.53	88.62	2.16

Table 2. Natural frequency of folding wing with elastic connection at connection positions 2 ($\theta =0^{\circ }$)

Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (4,4,4)		Main mode combination (5,4,5)		Main mode combination (6,8,10)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	0.82	0.81	1.2	0.81	1.2	0.81	1.2
2	6.88	7.55	9.7	7.54	9.59	7.54	9.59
3	10.92	11.58	6.04	11.56	5.86	11.55	5.76
4	19.77	20.81	5.26	20.79	5.15	20.72	4.8
5	25.46	26.86	5.5	26.85	5.45	26.84	5.42
6	27.34	28.84	5.48	28.84	5.48	28.78	5.26
7	38.29	42.44	10.8	41.64	8.74	40.45	5.64
8	49.46	53.69	8.5	51.98	5.09	50.03	1.15
9	54.6	61.03	11.77	59.77	9.46	56.24	3
10	63.75	91.26	—	67.81	6.36	64.66	1.43

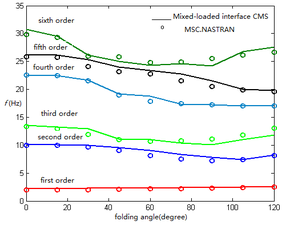
It can be seen from Tables 1 and 2 that the first six frequencies obtained by the fast structural dynamic model of folding wing with the elastic connection established based on the fixed interface component modal synthesis method with different mode combinations are compared with those obtained by MSC.NASTRAN. The relative error of each frequency is less than 10%, which is within the acceptable error range. This is mainly due to the introduction of static deformation in the fixed interface component mode synthesis method, which compensates the error caused by high-order mode truncation when obtaining the internal vibration mode and improves the accuracy of the dynamic model. For connection position 2, the first natural frequency of the folding wing is lower, which is mainly due to the lower stiffness of the torsion spring. With the increase of the number of main modes, the accuracy of higher-order frequency is improved obviously. For the main mode combination (4,4,4), which means reserved main modes of all components are four, the error of the tenth order frequency is more than 15%, which is due to the loss of modes after synthesis when there are fewer modes of components. Through frequency of multiple mode combinations, it can be found that when the number of main modes increases to a certain extent, the accuracy of the first few frequencies does not increase significantly. Therefore, in the actual calculation, the frequency truncation criterion can be used to increase the number of main modes of each component, or combined with the model reduction method in the control system to obtain better accuracy and less order mode combination, so as to facilitate the actual engineering analysis. For the folding wing with different folding angles, the main mode combination of (6,8,10) is used to calculate the natural frequency of the folding wing. Figure 4 shows the change of natural frequency with folding angle at different connection positions.

(a) Connection position 1	(b) Connection position 2
Figure 4. Variation of frequency with folding angle folding wing with elastic connection

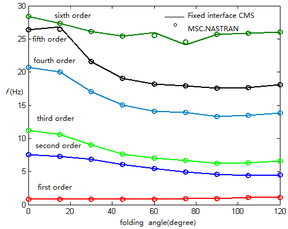
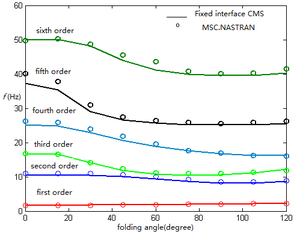
It can be seen from Figure 4 that the folding angle has a great influence on the frequency. The results are in good agreement with those by MSC.NASTRAN. The first order frequency has little change in two connection positions. When the elastic connection is adopted at the connection position 1, the second and third frequencies are close to each other at first, and then far away from each other. The fourth, fifth and sixth order frequencies have decreasing trend. The second, third and fourth order frequencies also decrease when the elastic connection is used at the connection position 2. The fifth and sixth order frequencies are coupled near the folding angle of ${15}^{\circ }$, and then separate with the increase of the folding angle. In addition, the frequencies at connection position 1 are higher than those at connection position 2. This is mainly due to the fact that the torsion spring at the interface does not increase the mass of the structure for connection position 1. When the mass of the component is the same, with the increase of torsion spring stiffness, the stiffness of the structure increases, the eigenvalue of the structure also increases, and the frequency is higher. For elastic connections, the effect of hinge stiffness on frequency is shown in Figure 5. With the mode combination of (6,8,10), the fully unfolded folded wing is analyzed, that is, $\theta =0^{\circ }$.

(a) Connection position 1	(b) Connection position 2
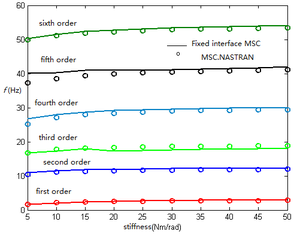
Figure 5. Variation of frequency with stiffness for folding wing with elastic connection

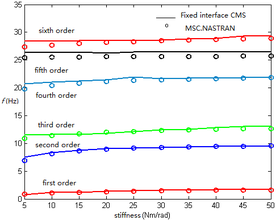
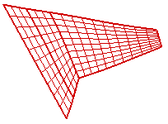
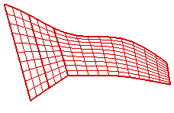
It can be seen from Figure 6 that with the increase of stiffness, the frequency basically increases. Even if the stiffness changes in a relatively large range, the fixed interface component modal synthesis can be used to well simulate the dynamic characteristics of the structure. When the connection position 1 is elastic connection, the mode shapes by the main mode combination of (6,8,10) are compared those by MSC.NASTRAN, as shown in Figure 6.

(a) Comparison of first mode shape
(b) Comparison of second mode shape
(c) Comparison of third mode shape
(d) Comparison of fourth mode shape
(e) Comparison of fifth mode shape
(f) Comparison of sixth mode shape
Figure 6. Mode shape comparison (left: fixed interface component modal synthesis method; right: MSC.NASTRAN)

It can be seen from Figure 6 that the mode shapes of the folding wing with elastic connection obtained by the fixed interface component modal synthesis method are basically consistent with those obtained by MSC.NASTRAN. The first and second order mode shape are dominated by bending mode, and the others are dominated by torsion mode. In the actual engineering analysis, the displacement response can be more accurately predicted, which lays the foundation for the further dynamic analysis of the folding wing.

3.2 Dynamic characteristics of folding wing with rigid connection

When the folding wing is rigidly connected, that is to say, the six degrees of freedom of interface nodes are defined by MPC, the mixed-loaded interface component modal synthesis method can be directly used for rapid modeling and dynamic characteristics analysis. For the two connection points in Figure 3, the results in this paper are compared with those by MSC.NASTRAN, as shown in Tables 3 and 4. According to the number of main modes reserved by different components, different mode combinations are formed. For example, (4,4,4) represents that components $A$, $B$ and $C$ retain the first four order main modes, and "-" represents that the relative error is greater than 15%.

Table 3. Natural frequency of folding wing with rigid connection at connection positions 1 ($\theta =0^{\circ }$)

Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (4,4,4)		Main mode combination (5,4,5)		Main mode combination (6,4,6)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	3.15	3.46	9.8	3.46	9.8	3.46	9.8
2	12.29	12.67	3.1	12.67	3.1	12.67	3.1
3	19.17	19.64	2.45	19.55	1.98	19.55	1.98
4	30.28	31.14	3.39	31.13	3.39	31.06	2.58
5	42.46	46.59	9.72	46.05	8.45	46.04	8.43
6	54.47	56.31	3.37	56.11	3.01	56.05	2.9
7	66.44	85..48	—	75.02	12.9	75.02	12.9
8	77.71	125.9	—	101.14	—	93.43	—
9	85.02	561.17	—	152.83	—	113.45	—
10	104.07	567.74	—	561.69	—	168.18	—
Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (6,6,6)		Main mode combination (6,7,8)		Main mode combination (6,8,10)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	3.15	3.46	9.8	3.46	9.8	3.46	9.8
2	12.29	12.67	3.1	12.67	3.1	12.67	3.1
3	19.17	19.53	1.88	19.52	1.83	19.51	1.77
4	30.28	30.92	2.11	30.91	2.08	30.87	1.95
5	42.46	46.02	8.38	45.90	8.10	45.89	8.07
6	54.47	55.64	2.15	55.55	1.98	55.44	1.78
7	66.44	67.98	2.32	67.30	1.29	67.14	1.05
8	77.71	79.38	2.16	79.20	1.92	78.98	1.63
9	85.02	88.02	3.0	87.48	2.89	87.21	2.57
10	104.07	116.13	11.58	105.51	1.38	104.88	0.78

Table 4 Natural frequency of folding wing with rigid connection at connection positions 2 ($\theta =0^{\circ }$)

Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (4,4,4)		Main mode combination (5,4,5)		Main mode combination (6,4,6)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	2.01	2.22	10.44	2.22	10.44	2.21	9.95
2	9.98	10.06	0.8	10.06	0.9	10.05	0.7
3	13.34	13.99	4.8	13.63	2.17	13.94	4.49
4	22.54	22.90	1.59	22.65	0.48	22.85	1.37
5	25.8	27.97	8.4	27.26	5.65	27.97	8.4
6	29.8	32.93	10.5	31.27	4.9	32.81	10.1
7	40.44	60.65	—	45.84	13.35	46.84	—
8	52.47	69.74	—	57.44	9.47	60.01	14.37
9	55.84	125.64	—	83.24	—	76.16	—
10	78.86	126.10	—	124.73	—	119.37	—
Mode order	Frequency by MSC.NASTRAN (Hz)	Main mode combination (6,6,6)		Main mode combination (6,7,8)		Main mode combination (6,8,10)
		Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)	Frequency (Hz)	Relative error (%)
1	2.01	2.21	9.95	2.21	9.95	2.21	9.95
2	9.98	10.05	0.7	10.05	0.7	10.05	0.7
3	13.34	13.61	2.02	13.59	1.87	13.58	1.79
4	22.54	22.53	0.04	22.53	0.04	22.53	0.04
5	25.8	27.26	5.65	27.24	5.58	27.24	5.58
6	29.8	30.81	3.38	30.80	3.35	30.78	3.28
7	40.44	43.15	6.7	43.14	6.67	42.94	6.18
8	52.47	53.36	3.49	53.07	1.14	53.05	1.11
9	55.84	60.81	8.9	59.02	5.69	58.68	5.08
10	78.86	101.51	—	81.36	3.17	79.97	1.41

It can be seen from Tables 3 and 4 that with the increase of the number of retained main modes, the accuracy of frequency is improved, especially for higher-order frequencies. For different modal combinations, the natural frequencies of the first six orders are consistent with those by MSC.NASTRAN and the relative error is within the acceptable range. For example, for the main mode combination of (4,4,4) and (6,6,6), lower order frequencies can be well obtained. This is mainly because the influence of inertia and elasticity of adjacent components is considered in the mixed-loaded interface component modal synthesis method, which improves the accuracy. With the increase of the number of main modes reserved, the accuracy of higher-order frequencies is improved. It can be seen that when the number of reserved modes of component is too small, some information of overall modes will be lost. For example, when the main mode combination is (4,4,4), the error of the first six frequencies of the two connection positions are within the acceptable range, but the error of the seventh to tenth frequencies is more than 15%. It is necessary to retain more information of the main mode to reduce the error caused by high-order mode truncation. Therefore, in order to improve the accuracy of dynamic analysis, it is very important to retain the appropriate modal information. Compared with Tables 1 and 4, it can be found that the frequency of rigid connection is higher than that of elastic connection at the same connection position, which is mainly because the rigid connection increases the overall stiffness of the wing structure. For different folding angles, the main mode combination of (6,8,10) is used to calculate the natural frequency of the folding wing. Figure 7 shows the change of the frequency with the folding angle at different connection positions.

(a) Connection position 1	(b) Connection position 2
Figure 7. Variation of frequency with stiffness for folding wing with rigid connection

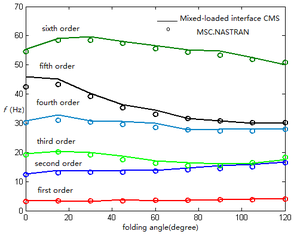
It can be seen from Figure 7 that the effect of folding angle on the frequency of folding wing is obvious, and the frequency of two different connection positions is quite different. The first frequency is not very sensitive to the folding angle when the rigid connection is used at the connection position 1. The second frequency increases with the increase of folding angle. When the folding angle is less than ${90}^{\circ }$ , the third, fourth and fifth order frequencies tend to decrease. The sixth order frequency first increases and then decreases. More importantly, the second and third frequencies, as well as the fourth and fifth frequencies, tend to couple with each other with the increase of folding angle, but there is no mode transition phenomenon. When the rigid connection is adopted at the connection position 2, the change of the first frequency is not obvious with the increase of the folding angle. The second, third and sixth order frequencies first decrease and then increase. The fourth and fifth order frequencies are basically reduced. When the rigid connection is used at connection position 2, the fifth and sixth frequencies are coupled with each other. Compared with the frequency of elastic connection, the frequency of rigid connection is higher. Compared with Figure 5, it can be seen that the frequency of rigid connection is greater than that of elastic connection. This is mainly due to the large stiffness of the structure at the interface when it is rigidly connected, which makes the folding wing structure more rigid. When the mass is constant, the eigenvalue of the structure increases, so the frequency is larger.

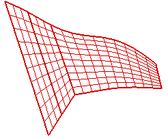
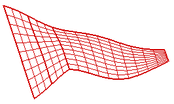
It can be seen from the comparisons that the frequency obtained by the mixed-loaded interface component modal synthesis method are consistent with those obtained by MSC.NASTRAN. The actual modal shape of the folding wing can be obtained by the eigenvectors in the eigenvalue analysis of the final folding wing dynamic equation. Taking the folding wing fully unfolded with rigid connection as an example, the main mode combination is still (6,8,10), and the actual mode comparison is shown in Figure 8.

(a) Comparison of first mode shape
(b) Comparison of second mode shape
(c) Comparison of third mode shape
(d) Comparison of fourth mode shape
(e) Comparison of fifth mode shape
(f) Comparison of sixth mode shape
Figure 8. Modal shape comparison (left: fixed interface component modal synthesis method; right: MSC.NASTRAN)

It can be seen from Figure 8 that the modal shapes by the mixed-loaded interface component modal synthesis method are consistent with those by MSC.NASTRAN. And the modal information can be obtained accurately, which is mainly due to the correct selection of the master-slave component and the correct reflection of the connection type between components. Therefore, the accurate displacements of related nodes can be obtained for further dynamic analysis.

4. Conclusions

In order to improve the analysis efficiency of structural dynamic characteristics of folding wing, a fast structural dynamic modeling of folding wing based on two different component modal synthesis methods is achieved, and the fast modeling process is deduced in detail. Firstly, the interface compatibility relation of the traditional fixed interface component modal synthesis method is modified, and the interface force is completely expressed in the equation, so that the influence of connection stiffness on wing structure dynamics can be considered; Then, on the basis of the fixed interface component mode synthesis method, the main mode of fixed-loaded interface is introduced, which can accurately reflect the influence of the elasticity and inertia of the fuselage and outer wing at the interface on the inner wing, forming a mixed-loaded interface component mode synthesis method. The structural dynamic characteristics of the folding wing with different folding angles, different connection type and different connection position are analyzed. The results of the method proposed are compared with the results of the repeated finite model established in MSC.NASTRAN. The following conclusions can be drawn：

(1) The method in this paper can accurately obtain the natural characteristics of the folded wing, i.e. frequency and modal information. Through the combination of different main modes, the final order of the folding wing dynamic model is within the acceptable range, which is conducive to the eigenvalue analysis. When a large number of main modes are reserved, the final frequency result has high accuracy. When the elastic connection is adopted, the order of the equation is the sum of the number of main modes reserved by each component and the degree of freedom of the interface. When the rigid connection is used, the order of the equation is the sum of the number of main modes reserved by each component, which is less than the order obtained by the direct finite element method.

(2) For elastic connection and rigid connection, the frequency of folding wing is sensitive to the folding angle because the folding angle has obvious influence on the structural model. With the increase of the folding angle, the frequency of the folding wing will be coupled with each other. For the elastic connection, the influence of hinge stiffness on the dynamic characteristics of the folding wing can be considered in the fast structural dynamics model. With the increase of hinge stiffness, the frequencies of each order also increase.

(3) Compared the frequencies of folding wings with different connection type and different connection positions, it can be found that the frequency of folding wings with rigid connection is higher than that with elastic connection because the rigid connection increases the stiffness of the wing structure, but the mass does not change.

Author Contributions: Y.N. (Yingge Ni) and W.Z. (Wei Zhang) conceived the whole numerical simulations; Y.N. (Yingge Ni) wrote the paper. Y. L. (Yi Lv) reviewed and edited the paper.

Conflicts of Interest: none.

References

[1] Wilson J.R. Morphing UAVs change the shape of warfare. Aerospace America, 42(2):28-29, 2004.

[2] Sofla A.Y.N., Meguid S.A., Tan K.T., Yeo W.K. Shape morphing of aircraft wing: Status and challenges. Materials and Design, 31(3):1284-1292, 2010.

[3] Ni Y.G., Zhang W., Lv Y., Zhao H. Application and modeling analysis of wing folding technology. Flight Dynamics, 38(6):1-7, 2020.

[4] Lee D.H., Weisshaar T.A. Aeroelastic studies on a folding wing configuration. 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, Texas, AIAA 2005-1996, April 2005.

[5] Snyder M.P., Sanders B. Vibration and flutter characteristics of a folding wing. Journal of Aircraft, 6(3):791-799, 2009.

[6] Tang D., Dowell E.H. Theoretical and experimental aeroelastic study for folding wing structures. Journal of Aircraft, 45(4):1136-1147, 2008.

[7] Andersen G.R., Cowan D.L. Aeroelastic modeling, analysis and testing of a morphing wing structure. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Material Conference, Honolulu, Haiwaii, AIAA 2007-1734, April 2007.

[8] Attar P.J., Tang D., Dowell E.H. Nonlinear aeroelastic study for folding wing structures．AIAA Journal, 48(10):2187-2195, 2010．

[9] Wang I., Gibbs S.C., Dowell E.H. Aeroelastic model of multi segmented folding wings: theory and experiment．Journal of Aircraft, 49(3):911-921, 2012．

[10] Zhao Y.H., Hu H.Y. Parameterized aeroelastic modeling and flutter analysis for a folding wing. Journal of Sound Vibration, 331(2):308-324, 2012.

[11] Hu W., Yang Z.C., Gu Y.S., Wang X．The nonlinear aeroelastic characteristics of a folding wing with cubic stiffness．Journal of Sound and Vibration, 400(21):22-39, 2017．

[12] Lee D.H., Chen P.C. Nonlinear aeroelastic studies on a folding wing configuration with free-play hinge nonlinearity. AIAA-2006-1734, 2006．

[13] Yang N., Wu Z.G., Yang C., Cao Q.K. Flutter analysis of a folding wing with structural nonlinearity. Engineering Mechanics, 29(2):197-196, 2012.

[14] Piao J.L., Guo X.Y., Zhang W., Zu W.Z. Nonlinear dynamics and mode analysis for a Z-type folding wings. Journal of Dynamics and Control, 15(1):29-38, 2017.

[15] Guo X.Y., Zhang Y., Zhang W. Nonlinear vibration characteristics of Z-type folding plates with internal resonance. Journal of Vibration Engineering, 31(2):183-197, 2018.

[16] Craig Jr. R.R. Coupling of substructures for dynamic analysis: an overview. 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Atlanta, 2000-1573, April 2000.

[17] Benfield W.A., Hruda R.F. Vibration analysis of structures by component substitution. AIAA Journal, 9(7):1255-1261, 1971.