Abstract
The aim of this attempt was to present an efficient algorithm for the evaluation of error bound of triangular subdivision surfaces. The error estimation technique is based on first order difference and this process is independent of parametrization. This technique can be easily generalized to higher arity triangular surfaces. The estimated error bound is expressed in-terms of initial control point sequence and constants. Here, we efficiently estimate error bound between triangular surface and its control polygon after k-fold subdivision and further extended to evaluate subdivision depth of the scheme.
Keywords
Subdivision surfaces; Control polygon; B-spline; Triangular surface; Error bound; Subdivision depth
1. Introduction
Subdivision is a simple and popular method to generate smooth limit curves and surfaces from discrete set of data points. It is an iterative algorithm, which is based on simple refinement rules to generate increasingly dense sequence of points under suitable hypothesis, converging to a continuous and smooth function. Starting from an initial control polygon, a subdivision scheme refers the computed values at the previous step according to the subdivision rules. The scheme is said to be convergent if there exists a limit curve. Efficiency of subdivision schemes is their flexibility and simplicity and they found their way into wide range of applications in computer graphics, medical imaging, industrial design and automotive design, etc. [1], [2] and [3].
Triangular surfaces [4] are one of the fundamental paradigms of Computer Aided Geometric Design (CAGD). These are defined by de Boor nets and have a regular triangular structure. This class of triangular surfaces shares the properties of univariate [5] and tensor product B-splines [6]. The procedure for subdividing triangular surfaces exactly parallels the subdivision for tensor product B-spline surfaces. Actually, these are extension of B-splines surfaces.
For many applications such as rendering, intersection testing or design, it is important to know, how well the control polygon approximate the exact curve or a surface. In the last decade several researchers attempt to answer the question and to improve the rule to estimate error bounds. The techniques presented in [7], [8], [9], [10] and [11] for computation of error bounds are based on parametrization, so they cannot be generalized to subdivision surfaces easily, methods presented in [12], [13] and [14] are based on eigen analysis. Zeng and Chen [15] introduced the concept of neighbor points and by using the first-order difference of control points of Catmull–Clark surfaces, they obtained the rate of convergence of control meshes of Catmull–Clark surface. From the result of convergence, they derived a computational formula of subdivision depth for Catmull–Clark surfaces. Cheng and Yong [16] introduced computational formula for subdivision depth, which is based on second order forward differences for extra-ordinary Catmull–Clark subdivision surface patches. Mustafa et al. [17], [18], [19], [20], [21], [22] and [23] have estimated error bound for binary, ternary, quaternary, non-stationary, n-ary curve, surface and volumetric model in-terms of maximal first order differences of the initial control point sequence and constants that depend on the subdivision mask. Huang et al. [24] derive a bound on the distance between a Catmull Clark subdivision surface patch and its limit face in terms of the maximum norm of the second order differences of the control points and a constant that depends only on the valence of the patch. Later on Mustafa et al. estimate the subdivision depth of Bajaj and subdivision schemes for both regular and irregular patches [25] and [26]. Moncayo and Amat [27] presented error bounds for a class of subdivision schemes based on the two-scale refinement equation. In recent years Hashmi et al. [28] estimated the subdivision depth for Li subdivision scheme for regular and irregular patches.
In the present literature survey, it is evident that no such attempt has been made to evaluate subdivision depth for triangular subdivision surfaces. In this paper author successfully articulates the formula for subdivision depth for triangular surfaces based on first order differences by using estimation techniques.
The rest of the paper is arranged in following fashion: Some definition and preliminary notations are given in Section 2. Section 3 is devoted for the proof of main result based on some preliminary results. Future research directions are given in Section 4. To maintain the presentation of paper as simple as possible for readers, notations and typical mathematical proof of basic results are provided in the Appendices.
2. Definition and notations
Let , , denote a sequence of points in , , where k is a non-negative integer then binary subdivision process for triangular surfaces [1, pp. 14–19] in our context can be restated as
|
|
(2.1) |
where or is greater than 2, and are defined by
|
|
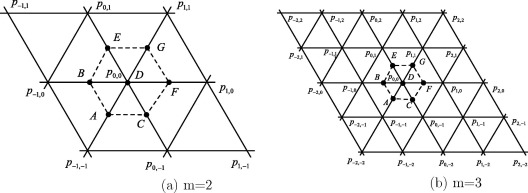
for , , , called subdivision mask. It is cautioned that (2.1) depends on labeling of the control polygon. For example for m = 2, 3, and 4, labeling of old and new points () is shown in Figs. 1(a) and (b) and 2 respectively.
|
|
|
Figure 1. (a) , , , , , , . (b) , , , , , , . |
|
|
|
Figure 2. Here m = 4, , , , , , , . |
Given initial values , , then in the limit , the process defines an infinite set of points in . A necessary condition for the convergence of the subdivision process (2.1) for arbitrary initial data is that
|
|
(2.2) |
where or .
Let us suppose
|
|
(2.3) |
where
|
|
(2.4) |
Suppose for ,
|
|
(2.5) |
where
|
|
Suppose further that
|
|
(2.6) |
where or .
Also
|
|
(2.7) |
where and .
Rest of the notations are in Appendix A.
2.1. Subdivision depth
Given control polygon of n -ary subdivision surface and an error tolerance , if we subdivide control polygon k times, so that the error between resulting polygon and subdivision surface is smaller than , then k is called subdivision depth of subdivision surface with respect to .
3. The error bounds for triangular surfaces
In this Section, the main result for error bounds is presented for triangular surfaces, which is based on some preliminary results. Finally, the section ends on subdivision depth formula.
Lemma 3.1.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)together with(2.2)then
|
|
(3.1) |
where for and are defined by(2.3) and (2.7)respectively.
Proof.
Proof is shown in . □
The proof of following Lemma is shown in .
Lemma 3.2.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)together with(2.2)then
|
|
(3.2) |
where and are defined by(2.3), (2.6), (2.7) and (A.1)respectively.
Lemma 3.3.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)together with(2.2)then
|
|
(3.3) |
where and are defined by(2.3), (2.6), (2.7) and (A.2)respectively.
Proof.
Proof is given in . □
Similarly, one can prove the following lemma.
Lemma 3.4.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)together with(2.2)then
|
|
(3.4) |
where , , , and are defined by(2.3), (2.6) and (2.7) and (A.3), (A.4), (A.5), (A.6) and (A.7)respectively. There is following correspondence between the values of v and : , , , and .
Here, we present our main result to estimate error bounds between triangular surface and its control polygon after k-fold subdivision.
Theorem 3.5.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)together with(2.2). Suppose be the piecewise linear interpolation to the values and be the limit triangular surface of the subdivision process(2.1). If then error bounds between triangular surface and its control polygon after k-fold subdivision are
|
|
(3.5) |
where and are defined by(2.7) and (A.8)respectively.
Proof.
Let denote the uniform norm. Since the maximum difference between and is attained at a point on the th control polygon (i.e. control polygon after -fold subdivision), then
|
|
(3.6) |
where is defined by (2.6).
Then from (3.2), (3.3), (3.4) and (3.6) we get
|
|
where and are defined by (2.7) and (A.8) respectively.
Using triangular inequality we get
|
|
This completes the proof. □
Remark 3.1.
It is pointed out that, most of the famous binary triangular subdivision schemes satisfies the condition . Our claim is supported by the following corollaries.
Corollary 3.6.
Given initial triangular control polygon , , let the values be defined recursively by subdivision process(2.1)for . Suppose be the piecewise linear interpolation to the values and be the limit triangular surface of the subdivision process. Then
|
|
where are defined by(2.3).
Theorem 3.7.
Let k be subdivision depth and let be the error bound between triangular subdivision surface and its k-level control polygon . For arbitrary , if
|
|
(3.7) |
then
|
|
Proof.
From (3.5), we have
|
|
This implies, for arbitrary given , when subdivision depth k satisfies the following inequality
|
|
then
|
|
This completes the proof. □
4. Future work
The technique presented in this article can be generalized to estimate error bounds between ternary and obviously to n-ary triangular surface and its control polygon after k-fold subdivision. The attempt can also be made to estimate subdivision depth for irregular triangular patches.
Appendix A. Notations
We have the following
|
|
(A.1) |
|
|
(A.2) |
|
|
(A.3) |
|
|
(A.4) |
|
|
(A.5) |
|
|
(A.6) |
|
|
(A.7) |
and
|
|
(A.8) |
Appendix B. Proof of Lemma 3.1
Proof.
|
|
where . By using similar approach of Mustafa et al. [17] (Theorem 1, p. 599 and Theorem 7, p. 609), we obtain
|
|
(B.1) |
where .
Similarly from (2.1) and (2.2) we have the following differences, for
|
|
(B.2) |
where .
Further for , we get
|
|
(B.3) |
For
|
|
(B.4) |
Using (B.1) and (B.2) recursively and utilizing (2.3) and (2.7) we get
|
|
Using (B.3) and (B.4) recursively and utilizing (2.3) and (2.7) we get
|
|
This completes the proof. □
Appendix C. Proof of Lemma 3.2
Proof.
|
|
(C.1) |
By expanding innermost summation we get
|
|
This implies
|
|
where
|
|
|
|
This implies
|
|
(C.2) |
where , , and are defined by (2.5).
Taking summation on both sides we obtain,
|
|
(C.3) |
Likewise by expanding summation appear on right hand side of above equation we get
|
|
(C.4) |
|
|
(C.5) |
where is defined by (2.5) and
|
|
(C.6) |
Substituting (C.4), (C.5) and (C.6) in (C.3) we get
|
|
where
|
|
|
|
Substituting it into (C.1) then by using (2.4) and (2.5) and taking norm we get
|
|
Using notations (2.3), (2.6) and (A.1) we get
|
|
Using (3.1) we get,
|
|
where is defined by (2.7). This completes the proof. □
Appendix D. Proof of Lemma 3.3
Proof.
|
|
(D.1) |
By expanding two summations in first term as we did in Lemma 3.2 after utilizing (2.5) we get
|
|
(D.2) |
where
|
|
|
|
Similarly by expanding two summations in second term of (D.1) and utilizing (2.5), we get
|
|
(D.3) |
|
|
Substituting (D.2) and (D.3) in (D.1) then after simplifying we have
|
|
where
|
|
Taking norm and using (2.4) and (2.5) we obtain
|
|
Using notations (2.3), (2.6) and (A.2) we get
|
|
Using (3.1), we get
|
|
where is defined by (2.7). This completes the proof. □
References
- [1] K. Rehan, M.A. Sabri; A combined ternary 4-point subdivision scheme; Appl. Math. Comput., 276 (2016), pp. 278–283
- [2] G. Mustafa, P. Ashraf, J. Deng; Generalized and unified families of interpolating subdivision schemes; Numer. Math.: Theory, Methods Appl., 7 (02) (2014), pp. 193–213
- [3] F. Khan, N. Batool, M.S. Hashmi; A new approach to approximating subdivision surface using Lagrange interpolating polynomial; Sci. Int., 26 (1) (2014), pp. 41–46
- [4] C. Loop, Smooth Subdivision Surfaces Based on Triangles, Master’s thesis, University of Utah, Department of Mathematics, 1987.
- [5] N. Dyn, A. Gregory, D. Levin; Analysis of uniform binary subdivision schemes for curve design; Const. Approx., 7 (1991), pp. 127–147
- [6] J. Hoschek, D. Lasser; Fundamentals of Computer Aided Geometric Design (Chapter 6); A K Peters, Wellesley, Massachusetts (1993)
- [7] F. Cheng; Estimating subdivision depths for rational curves and surfaces; ACM Trans. Graph., 11 (2) (1992), pp. 140–151
- [8] D. Nairn, J. Peters, D. Lutterkort; Sharp quantitative bounds on the distance between a polynomial piece and its Bézier control polygon; CAGD, 16 (1999), pp. 613–631
- [9] U. Reif; Best bounds on the approximation of polynomials and splines by their control structure; CAGD, 17 (6) (2000), pp. 579–589
- [10] D. Lutterkort, J. Peters; Tight linear envelopes for splines; Numer. Math., 89 (2001), pp. 735–748
- [11] M.I. Karavelas, P.D. Kaklis, K.V. Kostas; Bounding the distance between 2D parametric Bézier curves and their control polygon; Computing, 72 (1–2) (2004), pp. 117–128
- [12] H. Wang, Y. Guan, K. Qin; Error estimate for Doo–Sabin surfaces; Prog. Natural Sci., 12 (9) (2002), pp. 697–700
- [13] H. Wang, K. Qin; Estimating subdivision depth of Catmull–Clark surfaces; J. Comput. Sci. Tech., 19 (5) (2004), pp. 657–664
- [14] H. Wang, S. Hanqiu, K. Qin; Estimating recursion depth for Loop subdivision; Int. J. CAD/CAM, 4 (1) (2004), pp. 11–18
- [15] X.M. Zeng, X.J. Chen; Computational formula of depth for Catmull–Clark subdivion surfaces; J. Comput. Appl. Math., 195 (1–2) (2006), pp. 252–262
- [16] F. Cheng, J.H. Yong; Subdivision depth computation for Catmull–Clark subdivision surface; CAGD Appl., 3 (1–4) (2006), pp. 485–494
- [17] G. Mustafa, F. Chen, J. Deng; Estimating error bounds for binary subdivision curves/surfaces; J. Comp. Appl. Math., 193 (2006), pp. 596–613
- [18] G. Mustafa, J. Deng; Estimating error bounds for ternary subdivision curve/surfaces; J. Comput. Math., 24 (4) (2007), pp. 473–484
- [19] M.S. Hashmi, G. Mustafa; Estimating error bounds for quaternary subdivision schemes; J. Math. Anal. Appl., 358 (2009), pp. 159–167
- [20] G. Mustafa, M.S. Hashmi, F. Khan; Estimating error bounds for non-stationary binary subdivision curves/surfaces; J. Inf. Comput. Sci., 2 (3) (2007), pp. 179–190
- [21] G. Mustafa, M.S. Hashmi; Subdivision depth computation for n-ary curves/surfaces; Vis. Comput., 26 (6–8) (2010), pp. 841–851
- [22] G. Mustafa, M.S. Hashmi, N.A. Noshi; Estimating error bounds for tensor product binary subdivision volumetric model; Int. J. Comput. Math., 12 (83) (2006), pp. 879–903
- [23] G. Mustafa, M.S. Hashmi; Subdivision depth computation for n-ary volumetric models; Abstract Appl. Anal. (2011), Article 203453 http://dx.doi.org/10.1155/2011/203453
- [24] Z. Huang, J. Deng, G. Wang; A bound on the approximation of a Catmull–Clark subdivision surface by its limit mesh; CAGD, 25 (2008), pp. 457–496
- [25] G. Mustafa, M.S. Hashmi, K.P. Akhtar; Estimating error bounds of Bajaj’s solid models and their control hexahedral meshes; Lobachevskii J. Math., 26 (2007), pp. 51–61
- [26] G. Mustafa, M.S. Hashmi, F. Khan; Error bounds for subdivision surfaces; J. Univ. Sci. Tech. China, 36 (6) (2009), Article 253-2778(2009)06
- [27] M. Moncayo, S. Amat; Error bounds for a class of subdivision schemes based on the two-scale refinement equation; J. Comput. Appl. Math., 236 (2) (2011), pp. 265–278
- [28] M.S. Hashmi, G. Mustafa, F. Khan; Estimating error bounds for G. Li et al subdivision scheme; Sci. Int., 26 (1) (2014), pp. 29–34
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?