Resumo
A classe de problemas de estruturas metálicas sujeitas a carregamentos rápidos de elevada amplitude, como os que ocorrem quando são submetidas a ondas de choque produzidas por explosões, envolve grandes deformações e ação inelástica. O estado‐da‐arte em códigos explícitos para Análise por Elementos Finitos de problemas dinâmicos requerem incrementos de tempo limitados por requisitos de estabilidades e não de precisão. Para processos com altas taxas de carregamento, precisão satisfatória pode requerer incrementos de tempo muito pequenos de forma que o limite de estabilidade não seja penalizado. Precisão aceitável pode não requerer incrementos tão reduzidos se métodos implícitos forem considerados. No entanto, os métodos implícitos utilizados em análise quase‐estática requerem a solução de grandes sistemas de equações e vários desses sistemas devem ser resolvidos a cada incremento de tempo para satisfazer o equilíbrio dinâmico quando se usa iteração de Newton. Os métodos de solução direta de matrizes utilizados podem incorrer em custos computacionais que crescem a uma taxa n m2 , onde n é o número de graus de liberdade e m é a banda de largura da frente, resultando em custos proibitivos para problemas grandes, com muitos graus de liberdade. Neste trabalho, a utilização de integração implícita no tempo e livre de matrizes é explorada e verifica‐se que a eficiência computacional de códigos explícitos é combinada com a estabilidade inerente de métodos implícitos. O modelo desenvolvido é aplicado na simulação de uma estrutura complexa em um processo repetitivo, com elevado custo computacional, mostrando a sua valia.
Abstract
The class of physical problems of metal structures subject to rapid, large amplitude loads, such as occurs when they are submitted to an explosion blast, involves large deformations and inelastic action. Current state of art in explicit dynamic Finite Element Analysis codes require time steps limited by stability requirements rather than by accuracy. For very high rate processes, accuracy would require a very small time step so that the stability limit does not penalize. Acceptable accuracy may not require such small steps if implicit methods are considered. The implicit methods used in quasi‐static analysis, however, require the solution of large systems of equations, and several such systems must be solved at each time step to satisfy the dynamic equilibrium when using Newton iteration. The direct matrix solvers that are used incur in computational costs that grow as n m2, where n is number of degrees‐of‐freedom and m is the band of the front width, thus resulting in prohibitive costs for very large problems. In this work, the use of higher order, implicit time integration and matrix‐free solution of the system of equations is explored. Computational efficiency of explicit codes is combined with the inherent stability of implicit methods. The model developed is applied in the simulation of a complex structure, with elevated computational cost, showing its validity.
Palavras‐chave
Simulação ; Elementos finitos ; Carregamento impulsivo
Keywords
Simulation ; Finite elements ; Impulsive loads
1. Introdução
A maior parte dos códigos para simulação e análise do comportamento de estruturas metálicas sob carregamentos distribuídos impulsivos são baseados em métodos explícitos, sendo esperados processos com altas taxas de variação, grandes deformações e ação inelástica. A escolha típica para a formulação dessa classe de problemas é euleriana, incorrendo na necessidade do uso de incrementos de tempo muito pequenos para que a precisão obtida seja aceitável. É possível resolver esses problemas, que são esperados serem rígidos, com integração implícita (com a sua inerente estabilidade) de ordens elevadas em uma solução livre de matrizes com a eficiência computacional dos códigos explícitos [1] .
Um método desenvolvido a partir do código VODPK (Brown et al. [2] and [3] ) para a solução desses problemas foi desenvolvido, mostrando‐se um ponto de partida apropriado para o problema em questão. Nele, problemas de valor inicial são resolvidos pela combinação de regras de integração implícitas com ordem variável, precondicionamento e um solucionador de equações de Krylov livre de matrizes, adequado para a solução de grandes sistemas de equações em computadores vetoriais.
No presente trabalho, o método é introduzido através da sua aplicação na simulação da resposta dinâmica de uma viga biengastada (com não linearidade geométrica) sob um carregamento impulsivo transversal. Também é mostrado que o uso de integração de ordem elevada, implícita no tempo e livre de matrizes, pode ser utilizada para a solução do sistema de equações resultante, obtendo‐se eficiência computacional dos métodos explícitos com a estabilidade dos implícitos [1] . Subsequentemente, essa metodologia é aplicada na simulação do comportamento dinâmico de uma estrutura metálica complexa submersa em meio líquido submetida à onda de choque produzida pela explosão de uma carga submarina. Os resultados obtidos serviram de base para a otimização expedita de cargas explosivas submarinas [4] , mostrando a validade do método apresentado.
A discretização obtida pela aplicação do método dos elementos finitos em sistemas dinâmicos resulta, via de regra, em sistemas de equações diferenciais de segunda ordem no tempo que podem ser reduzidos a sistemas de primeira ordem por um artíficio simples de substituição de variáveis [1] . Seja o sistema de equações descrito pela eq. 1:
|
|
( 1) |
Fazendo‐se (3), a equação (1) pode ser reescrita como (3), ou seja, houve uma redução da ordem do sistema de equações, de segunda para primeira ordem.
A estrutura de tais sistemas de equações lhes confere uma série de propriedades e diversos estudos apresentaram propostas relacionadas à sua integração no tempo, como os métodos Newmark [5] ou HHT‐α [6] and [7] , disponíveis na literatura sobre o assunto. Tal aprofundamento, nesse e em outros tópicos que não sejam o objetivo desse trabalho, serão evitados a fim de não estender em demasia o artigo nem torná‐lo entediante, redundante com a vasta literatura disponível sobre esses assuntos.
2. Desenvolvimento
2.1. Rigidez
Um problema de valor inicial (PVI) será dito rígido se tiver um modo de vibração altamente amortecido (ou «super‐estável»), o que ocorre quando o seu jacobiano tem um autovalor com a parte real negativa. PVI podem ser descritos como [1] :
|
|
( 2) |
2.2. Precondicionamento
O sistema de equações algébricas representativo de um PVI pode ser descrito como A x''' = '''b . Entretanto, pode ser possível resolver um sistema parecido com o original que seja de solução mais fácil. A operação que produz esse novo sistema é chamada de precondicionamento. Precondicionadores são matrizes arbitrárias que são aplicadas a sistemas de equações a fim de aumentar a eficiência da solução. A seguinte transformação é utilizada no precondicionamento de uma matriz A:
|
|
( 3) |
de forma que resolve‐se o sistema A’ x''' = '''b , ao invés do sistema original. As matrizes P1 e P2 são, via de regra, diferentes e o seu produto, ('''P1) *('''P2) , deve ser uma aproximação da matriz A original. O sistema resultante deve ser mais fácil de resolver. Fazendo‐se P2 = '''I , tem‐se o chamado precondicionamento à esquerda. De forma similar, é feito precondicionamento à direita quando P1 = '''I . Devido ao fato de precondicionadores serem matrizes arbitrárias, é possível ajustar alguns de seus elementos de forma a encontrar uma forma que produza uma solução eficiente. Apenas precondicionamento à esquerda foi efetuado no presente trabalho. É importante ressaltar a existência de extensos estudos acerca de precondicionamento, como o método do gradiente conjugado [8] , novamente aqui omitidos a fim de não esteder em demasia o presente trabalho.
No presente desenvolvimento, o sistema precondicionado foi obtido como se segue [1] :
|
|
( 4) |
onde:
- I = matriz identidade
- hrl1 = um escalar relacionado ao incremento de tempo, calculado internamente pelo código
- J = a matriz jacobiana de f (y ,t)
2.3. O método
VODPK permite a solução de sistemas de equações diferenciais por uma série de métodos selecionáveis pelo usuário, com variações possíveis na escolha do método multipasso básico, ou preditor (1 , Adams implícito com coeficientes variáveis ou 2 , fórmulas com diferenciação retrógrada – Backward Differentiation Formula , com coeficientes variáveis e coeficientes precessores fixos – variable‐coefficient BDF with fixed‐leading coefficient method ) e no corretor (0 , iteração funcional básica, sem envolvimento com o jacobiano do sistema de equações, 1 , SPIGMR, uma versão incompleta do GMRES, ou 9 , uma solução utilizando uma matriz P , aproximando A , fornecida pelo usuário – sem a iteração de Krylov.
O método de escolha é selecionado pela atribuição do valor apropriado à variável MF, onde o primeiro algarismo corresponde ao método multipasso básico e, o segundo, no corretor, conforme descrito no parágrafo anterior. A combinação de interesse é o uso de BDF com o SPIGMR, ou seja, MF = 21 .
2.4. Controle de erro
O controle de erro pode ser feito por 2 parâmetros fornecidos pelo usuário: um valor absoluto (atol ), aplicado a todas as variáveis, e um valor relativo (rtol ), aplicado em adição ao valor absoluto para variáveis selecionadas. O vetor de erro, e = e (i) (i = 1, número de variáveis), é, então, calculado a cada passo pela fórmula abaixo:
|
|
( 5) |
onde:
, a Norma Quadrada de v ; e ewt = ewt (i) = rtol (i) * ABS(u (i) + atol (i)), o vetor de pesos, que precisa ser sempre positivo
Caso essas escolhas para controle de erro não sejam suficientes para o problema em questão, há outras possibilidades de controle de erro disponíveis. No presente trabalho, a tolerância adotada foi estritamente absoluta.
2.5. O elemento básico
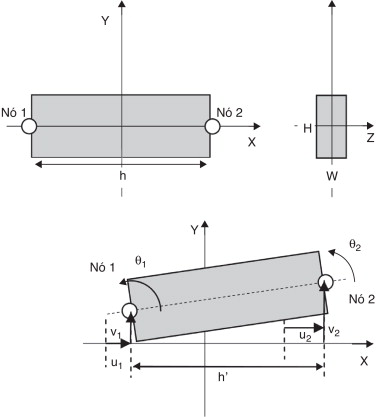
O elemento básico foi desenvolvido com base na viga biengastada com não linearidade geométrica, uma extensão da viga de Timoshenko, com 3 graus de liberdade por nó (deslocamentos vertical e horizontal e rotação). A sua seção‐reta foi mantida retangular e foi assumido estado plano de deformação. O material foi modelado como possuindo endurecimento cinemático isotrópico bilinear com comportamento visco‐plástico e não linearidade geométrica. Grandes deformações são esperadas. As deformações são dadas por ɛ = u’ –y θ + ½ (v’ )2 e γ = (v’ ‐ θ ) [1] , onde ɛ é a deformação normal, u é o deslocamento axial, y é a distância do centro da seção‐reta para qualquer ponto material, θ é a rotação, v é o deslocamento transversal e γ é a deformação angular para qualquer ponto da viga. Deformação permanente é calculada por retorno radial. Um elemento genérico é ilustrado na figura 1 .
|
|
|
Figura 1. Representações esquemáticas do elemento de viga em suas configurações original e deformada. |
A resposta dinâmica ao carregamento transversal pode ser obtida com o uso da chamada formulação de deslocamento puro (pure displacement formulation) , conhecida por produzir modelos muito rígidos para elementos finos, como no presente caso. Por causa disso, o uso de formulações mistas são preferidas, resultando no mesmo conjunto de equações, mas com uma matriz de rigidez modificada [9] . Essa variação é identificada na substituição dos termos AGh/3 e AGh/6, existentes na primeira formulação, pelo termo AGh/4, existente na segunda (onde A é a área da seção‐reta, G é o módulo de elasticidade transversal e h é a dimensão da viga no sentido transversal, ou a sua «altura»). A influência da variação entre essas formulações foi investigada [1] e foi verificado que nenhuma escolha impacta significativamente o desempenho do código. Também foi verificado que a introdução de amortecimento estrutural artificial e alterações nas características do comportamento visco‐plástico do material também não contribuíram para melhoria significativa do desempenho da solução. A formulação proposta por Bathe [9] foi adotada para o restante do desenvolvimento.
Foi escolhido e implementado um conjunto de funções de base lineares, de forma que o trabalho virtual realizado pelas forças internas pode ser escrito como:
|
|
( 6) |
onde:
- δ = incremento
- WI = trabalho virtual interno
- y = distância de um ponto material da viga à sua linha de centro
- u = deslocamento (linear) de um ponto material da viga na direção x
- v = deslocamento (linear) de um ponto material da viga na direção y
- θ = deslocamento linear de um ponto material da viga
- w = dimensão da seção reta da direção z (não representada nas figuras), ou a sua «largura»
- σ = tensão normal
- τ = tensão de cisalhamento
2.6. Quadratura e ordem da integração
Quando em regime inelástico há necessidade de se efetuarem integrações numericamente, isso pode ser feito por diversas regras de integração. Nesse desenvolvimento, foram selecionadas as quadraturas de Gauss e de Gauss‐Lobatto, com ordens de 5‐10. Comparação dos resultados obtidos mostraram que as diferenças não são significativas, tanto com a escolha da regra quanto com a da ordem de integração [1] .
2.7. Validação
A validação foi conduzida em um computador Compaq/Digital XP1000 , com CPU Alpha EV6.7 de 667 MHz, 768 MB de RAM e 4 MB de cache e os resultados foram comparados com os obtidos utilizando‐se o programa Abaqus Standard (v. 5.8, atualmente propriedade da Dassault Systems [10] ), não tendo apresentado discrepâncias e considerados aceitáveis. O tempo necessário para a simulação em questão foi de aproximadamente 10% do consumido pelo Abaqus.
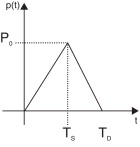
O elemento básico foi empregado na simulação de uma viga biengastada, com «comprimento» L = 1,0 m, «altura» H = 0,1 m e «largura» w = 0,01 m, submetida a um carregamento distribuído impulsivo na sua superfície «superior» (assumindo‐se a seção‐reta da dessa viga na vertical e seus lados alinhados com os eixos do sistema de referência). A viga foi dividida em 10 elementos iguais (1‐10) e 11 nós (numerados de 1‐11, sendo 6 o central), conforme esboçado na figura 2 (fora de escala).O carregamento foi modelado como um pulso triangular conforme a figura 3 :
|
|
( 7) |
|
|
|
Figura 2. Modelo da viga bi‐engastada utilizada na validação do mátodo. |
|
|
|
Figura 3. Representação esquemática do carregamento distribuído impulsivo. |
onde:
- TS = tempo de subida
- TD = tempo de descida
- P0 = valor máximo do carregamento
As propriedades do material (aço) adotado para a viga são apresentadas na tabela 1 .
| Propriedades do material (aço) | |
|---|---|
| Módulo de elasticidade, E | 207 × 109 Pa |
| Limite de elasticidade, EL | E/15 Pa |
| Módulo de endurecimento cinemático tangencial, H | E/15 Pa |
| Módulo de elasticidade transversal, G | 79,3 × 109 Pa |
| Tensão de escoamento, σy | 372,6 × 106 Pa |
| Tensão última, σu | 2,415 × 109 Pa |
| Massa específica, ρ | 76,5 × 103 N/m3 |
| Coeficiente de poisson, ν | 0,292 |
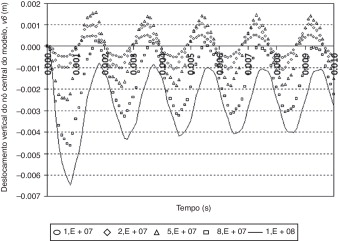
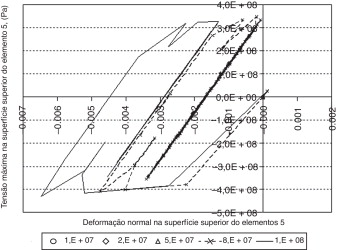
A figura 4 mostra o deslocamento vertical do nó central do modelo para carregamentos com amplitudes P0 de 1, 2, 5, 8 e 10 × 107 N/m2 . A figura 5 exibe o histórico tensão x deformação normais no ponto de integração localizado no centro da superfície superior do elemento 5.
|
|
|
Figura 4. Deslocamento vertical do nó central do modelo para várias condições de carregamento. |
|
|
|
Figura 5. Tensão x deformação normais no centro da superfície superior do elemento 5. |
A tabela 2 mostra os resultados obtidos para P0 = 108 N/m2 e ATOL = 10−5 para as diversas opções de métodos (de acordo com a variável MF, conforme descrito no item 2.3) [1] .
| MF | Tempo (s) | Número de passos |
|---|---|---|
| 10 | 0,250 | 6.533 |
| 11 | 0,533 | 5.921 |
| 19 | 0,267 | 6.059 |
| 20 | 0,300 | 8.576 |
| 21 | 0,683 | 8.091 |
| 29 | 0,317 | 8.127 |
Pode ser observado que as soluções com o método de Adams, implícito, alcançou a solução com menos passos do que o outro método básico disponível (BDF) , mas o método SPIGMR apresentou vantagens com relação às outras opções no tocante ao número de passos, mas resultados inferiores em termos de tempo de processamento.
Dessa forma, o elemento desenvolvido foi considerado válido para utilização em estudos mais complexos, apesar do uso de precondicionamento combinado com o método de Krylov considerado não ter apresentado vantagens para esse problema.
3. Aplicação em um problema complexo
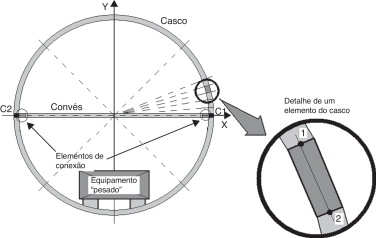
O elemento e o método descritos no item 2 foram aplicados na simulação da resposta dinâmica de uma estrutura cilíndrica submersa, representativa de um submarino, sujeita à onda de choque causada pela detonação de uma carga explosiva submarina a uma certa distância dela. Essa estrutura é um casco em aço HY‐80 com diâmetro de 6,0 m e espessura‐equivalente de 0,1 m e convés diametral com espessura‐equivalente também de 0,1 m, suportado de tal forma que não limita a deformação do casco. O seu detalhamento é apresentado esquematicamente nas Figura 6 and Figura 7 . O problema apresentado é bidimensional e é assumido estado plano de deformação. Os resultados dessa simulação proveram dados para a determinação dos valores das funções aptidão (ou funções objetivo) na otimização, por algoritmos genéticos, da carga explosiva [4] .
|
|
|
Figura 6. Representação esquemática do modelo, com a indicação de um elemento. |
|
|
|
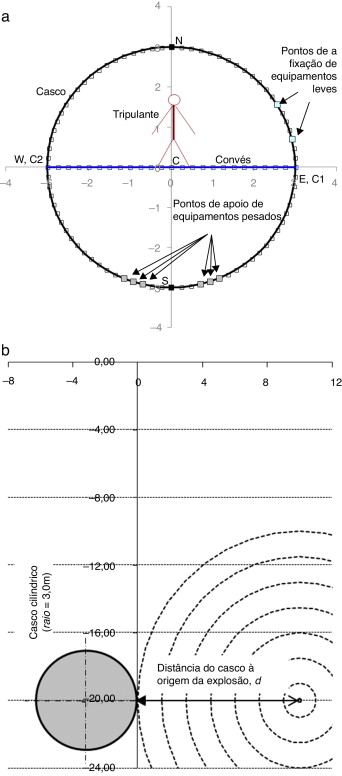
Figura 7. Discretização do modelo, com indicação de «pontos notáveis» e outros itens de interesse, bem como a configuração inicial do problema [4] . |
Foram medidas as acelerações impostas a um equipamento considerado «pesado» apoiado no fundo (como um gerador ou um banco de baterias), a um equipamento considerado «leve» instalado na antepara (como equipamentos de comunicação ou de guerra eletrônica – esses tipos de equipamentos, tipicamente, são instalados em absorvedores de choque, mas é necessário que se as acelerações máximas na base desses elementos não ultrapassem certos limites a fim de que possam filtrar corretamente os esforços a que esses sensíveis equipamentos são submetidos), acima do convés, e a um tripulante, em pé no convés e também é de interesse a tensão máxima no casco, conforme aplicado em [4] . Quanto à discretização espacial, foi verificado que a divisão do casco em menos de 80 elementos e do convés em 24 não resultam em respostas precisas, sendo esses os números mínimos de elementos aceitáveis na simulação [4] . O método de integração selecionado para os resultados aqui apresentados foi o Adams implícito com coeficientes variáveis, com iteração funcional simples, sem envolvimento com o jacobiano do sistema de equações ou precondicionamento (MF = 10), tendo em vista os resultados apresentados na tabela 2[2] .
O presente método foi implementado em um cluster de microcomputadores do Núcleo de Computação de Alto Desempenho (Nacad) da Universidade Federal do Rio de Janeiro [11] , ambiente paralelo de memória distribuída. Não serão feitas considerações sobre o ganho de desempenho obrido pela paralelização. Para a presente aplicação, o código VODPK foi substituído pelo código DVODPK [12] , a sua versão com precisão dupla.
3.1. A onda de choque
A literatura [12] , [13] , [14] and [15] mostra que ondas de choque produzidas por explosões submarinas (Underwater Explosions , UNDEX) podem ser representadas pela aproximação exponencial[4] and [13] , ou seja:
|
|
( 8) |
onde:
|
|
( 9) |
e
|
|
( 10) |
sendo:
- P(t) = amplitude da onda de choque a uma distância da explosão em um instante t após a sua ocorrência
- Pmáx = amplitude máxima ocorrida a uma distância d da explosão
- τ = constante de tempo relacionada ao decaimento exponencial
- W = massa de explosivo, em TNT‐equivalente
- d = distância à origem da explosão
- K1 , K2 , A1 , A2 = parâmetros propostos de acordo com o modelo, como os mostrados na tabela 3 .
| Parâmetro | Experimental study of underwater explosion phenomena [13] | Shin & Geers [14] | Report RE‐260‐016 [16] |
|---|---|---|---|
| K1 | 21.600 | 22.505 | 52,4 |
| A1 | 1,13 | 1,18 | 1,13 |
| K2 | 96,5 | 0,058 | 0,084 |
| A2 | –0,18 | –0,185 | 0,23 |
Caso efeitos locais, como cavitação, sejam de interesse, será necessário modelar tanto a estrutura quanto o meio líquido, com especial atenção à interação fluido‐estrutura. Nos casos em que o que se deseja é a verificação do comportamento global aproximado da estrutura, o carregamento pode ser aplicado diretamente na sua superfície, desde que sejam tomadas precauções para evitar inconsistências no tocante à existência da massa de água na sua vizinhança. Essa abordagem é conservadora, desprezando a parcela de energia consumida pela massa líquida e a sua viscosidade.
3.2. Discretização espacial e calibração do modelo
O casco foi dividido em 80 elementos e o convés, em 24. Foi verificado que o uso de menos elementos pode comprometer os resultados [4] .
Foram efetuadas 2 calibrações no presente desenvolvimento: a primeira seguiu o conceito de «massa adicionada» e levou em consideração a massa de água existente em torno do submarino; a segunda considerou o deslocamento típico do submarino [4] . Foi concluído que a calibração indicada para o problema deveria levar em conta a adição do equivalente a 75% do deslocamento submerso do submarino. Os resultados foram confrontados com os produzidos pelo Abaqus (v.6.5) e foram consideradas compatíveis em termos qualitativos. Não foram efetuadas comparações de desempenho, já que o Abaqus foi utilizado em um microcomputador e o método em desenvolvido em um ambiente paralelo de memória distribuída.
3.3. Resultados
Os resultados de maior interesse são a tensão máxima no casco a cada instante, já que tensões maiores que o valor admissível podem levá‐lo à rutura, e as acelerações nas bases dos «equipamentos» leve e pesado de interesse e no ponto relativo a um tripulante, pela sua correlação direta com possíveis danos ao material ou ao pessoal. É importante observar que os valores de interesse são os máximos ocorridos a qualquer momento, razão pela qual se considera esse valor máximo para sua utilização no cálculo da aptidão.
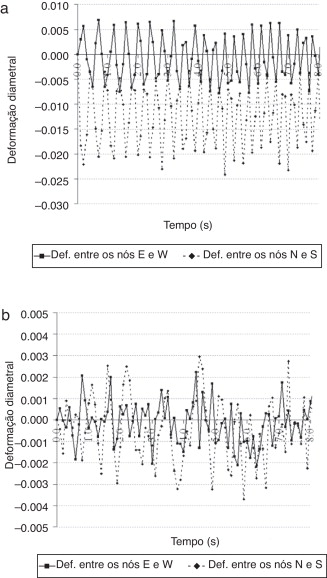
A figura 8 mostra as deformações diametrais «vertical» (entre os nós N e S , fig. 7 ) e «horizontal» (entre os nós E e W , fig. 7 ) do casco com o tempo, para 8 s de simulação, para uma carga de 300 kg de TNT detonada a 10 m de distância e outra de 80 kg, detonada a 20 m do mesmo. Esses 2 casos representam os carregamentos mais e menos intensos do modelo, respectivamente, razão pela qual são de interesse para análise individual detalhada. A configuração deformada da estrutura como um todo não é relevante para o estudo e será omitida, sendo importante ressaltar que o perfil, originalmente circular do casco, tende a se ovalizar, inicialmente pela redução da sua dimensão horizontal e aumento da vertical e, posteriormente, pelo aumento da sua dimensão horizontal e redução da vertical, e assim sucessivamente.
|
|
|
Figura 8. Deformações diametrais «vertical» e «horizontal» do casco para diferentes cargas de TNT detonadas a diferentes distâncias do mesmo: (a) carga de 300 kg de TNT detonada a 20 m de distância, (b) carga de 80 kg de TNT detonada a 10 m de distância. |
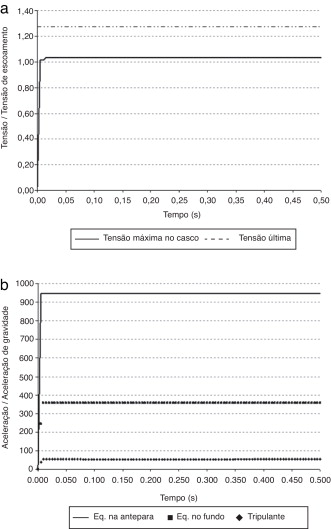
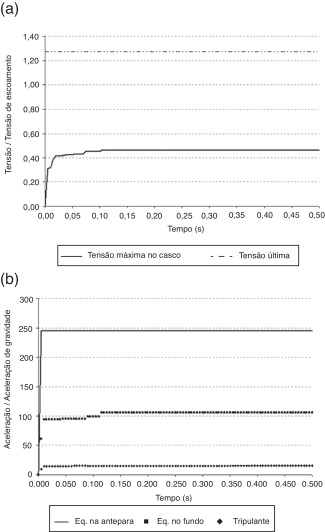
As Figura 9 and Figura 10 mostram as tensões máximas no casco e as acelerações calculadas nos pontos de interesse para a cargas e distâncias da figura 8 . É importante ressaltar que o local de ocorrência dessas tensões não é relevante, no presente caso, mas a sua intensidade, já que se trata de otimização da carga explosiva que pretende causar danos ao submarino – e no caso de ocorrência de falha do casco o relevante é se ocorrerá ou não.
|
|
|
Figura 9. Razões entre tensões e a tensão de escoamento do material e entre acelerações e a aceleração da gravidade em pontos de interesse para a explosão de 300 kg de TNT a 10,0 m de distância da estrutura com calibração com 75% do deslocamento submerso médio. |
|
|
|
Figura 10. Razões entre tensões e a tensão de escoamento do material e entre acelerações e a aceleração da gravidade em pontos de interesse para a explosão de 80 kg de TNT a 20,0 m de distância da estrutura com calibração com 75% do deslocamento submerso médio. |
4. Comentários finais
O modelo apresentado contém não linearidades físicas e geométricas típicas de aplicações importantes. O uso de uma solução livre de matrizes combinada com regras de integração implícitas, conforme implementado em VODPK, mostrou‐se eficiente, apesar da solução precondicionada não ter apresentado vantagens com relação à solução mais simples.
O método é fortemente dependente do valor da tolerância absoluta (atol – essa dependência não é monotônica) e provou ser capaz de produzir resultados adequados à otimização da carga explosiva submarina com algoritmos genéticos, com elevada eficiência computacional. A inclusão de amortecimento estrutural artificial e de comportamento visco‐plástico do material não melhoraram o desempenho e os resultados encontrados foram qualitativamente compatíveis com os esperados.
É importante ressaltar a necessidade da existência de um método eficiente, a fim de viabilizar a solução do problema em pauta – otimização da carga explosiva com algoritmos genéticos, já que o mesmo exige o cálculo de diversas configurações (no caso de 100 gerações de uma população de 100 indivíduos, 10.000 simulações são necessárias). Assim, há necessidade do desenvolvimento de um modelo simples, representativo do problema, e um método rápido de simulação, sob o risco do elevado custo inviabilizar a otimização, lacuna ocupada pelo método ora apresentado.
Conflito de interesses
Os autores declaram não haver conflito de interesses.
Bibliografia
- [1] A.A. Motta; An efficient simulation of structures under pulse pressure loading, Dissertação de Mestrado; The University of Texas at Austin (2000)
- [2] P.N. Brown, G.D. Byrne, A.C. Hindmarsh; VODE: A variable coefficient ODE solver; SIAM Journal on Scientific Computing, 10 (1989), pp. 1038–1051
- [3] G.D. Byrne; Pragmatic experiments with Krylov methods in the stiff ODE setting; J. Cash, I. Gladwell (Eds.), Computational Ordinary Differential Equations, Oxford Univ. Press, Oxford (1992), pp. 323–356
- [4] A.A. Motta; Otimização expedita de cargas explosivas submarinas com vistas aos seus efeitos terminais em estruturas de aço submersas; Tese de Doutorado, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil (2004)
- [5] N.M. Newmark; A method of computation for structural dynamics; ASCE Journal of the Engineering Mechanics Division, 85 (1959) No. EM3
- [6] H.M. Hilber, T.J.R. Hughes, R.L. Taylor; Improved numerical dissipation for time integration algorithms in structural dynamics; Earthquake Engng Struct Dyn, 5 (1977), pp. 283–292
- [7] T.J.R. Hughes; Finite element method ‐ Linear static and dynamic finite element analysis; Prentice‐Hall, Englewood Cliffs, New Jersey (1987)
- [8] M.R. Hestenes, E. Stiefel; Methods of conjugate gradient for solving linear systems; Journal of Research of the National Bureau of Standards, 49 (6) (1952), pp. 409–436
- [9] K.J. Bathe; Finite elements procedures; Prentice‐Hall, Inc, Englewood Cliffs, New Jersey (1996), pp. 274–276
- [10] Abaqus Overview ‐ Dassault Systèmes. 2013. Abaqus Overview ‐ Dassault Systèmes. [ONLINE] [consultado 2 Set 2013]. Disponível em: http://www.3ds.com/products‐services/simulia/portfolio/abaqus/overview/
- [11] Núcleo de Computação de Alto Desempenho, Universidade Federal do Rio de Janeiro [online; consultado 3 Abr 2013]. Disponível em: www.nacad.ufrj.br
- [12] P.N. Brown, G.D. Byrne, A.C. Hindmarsh; DVODPK: Variable‐coefficient ordinary differential equation solver with the preconditioned Krylov method GMRES for the solution of linear systems (2002)
- [13] R.H. Cole; Underwater explosions; Princeton University Press, Princeton, U.S.A (1948)
- [14] NDRC, Experimental study of underwater explosion phenomena, U.S.A., AD 268.905, Vol. 8.
- [15] Y.S. Shin, T.L. Geers; Response of marine structures to underwater explosions; Underwater Explosion Short Course E. U. A. (1993)
- [16] REPORT RE‐260‐016–Joint Industry Project on Platform Abandonment by in‐Situ Demolition; Surrey, Reino Unido, SLP Engineering Ltd (1997)
Document information
Published on 01/03/15
Accepted on 07/11/13
Submitted on 04/04/13
Volume 31, Issue 1, 2015
DOI: 10.1016/j.rimni.2013.11.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?