Resumen
Este artículo trata la formulación unificada de modelos lineales para la estática de piezas alargadas y, en concreto, la clase de modelos que incluyen desplazamientos generalizados adicionales a los necesarios para definir movimientos de sólido rígido de las secciones transversales. Estos modelos, denominados modelos hiperviga por los autores, se caracterizan por el acoplamiento entre variables estáticas y cinemáticas en las ecuaciones de equilibrio. En el artículo se introducen los pseudoesfuerzos , nuevas variables estáticas que representan la acción de los enlaces internos que controlan el cambio de forma de la sección transvesal. Asimismo, se desarrolla el procedimiento sistemático para evaluar la distribución de tensiones sobre las secciones transversales consistente con el modelo hiperviga, que aproxima la distribución de tensiones correspondiente a la solución elástica tridimensional. La sistemática de la formulación unificada y su potencia para la construcción de ecuaciones y para la valoración de la influencia de los distintos parámetros que intervienen en la respuesta quedan patentes mediante su aplicación a un problema que requiere la introducción de grados de libertad adicionales a los de sólido rígido: la flexión alabeada. Partiendo únicamente de la cinemática de la sección transversal expresada en función de los desplazamientos generalizados, mediante el procedimiento unificado propuesto, se obtienen las variables, los parámetros y las ecuaciones que determinan la respuesta, así como las expresiones de las tensiones en la sección consistentes con la formulación empleada.
Abstract
This paper deals with the unified formulation of linear models in rod elastostatics and, specifically, with the class of models including generalized displacements that are additional to those defining rigid body motions of the cross-sections. The main feature of these models, named hyper beam models by the authors, is the coupling between static and kinematic variables in the equilibrium equations. New static variables called pseudo forces have been introduced to represent the action of the internal constraints which control the deformation of the cross-section. Using the pseudo forces, a systematic procedure to evaluate the model-consistent stress distributions on cross-sections –which is an approximation of the 3D elastic solution– has been developed. The application of the unified formulation to a problem requiring the introduction of non rigid-body-motional degrees of freedom –warped bending– shows its ability to systematically build the equations, and to assess the influence of the intervening parameters. The response-defining variables, parameters and equations, as well as the expressions of consistent stress distributions on the sections, are obtained by means of the proposed unified procedure, parting exclusively from the cross-sectional kinematics expressed in terms of the respective generalized displacements.
Palabras clave
Modelos de vigas ; Modelo hiperviga ; Tensiones en vigas ; Esfuerzos en vigas ; Teoría de vigas de orden superior
Keywords
Beam models ; Hyperbeam model ; Stresses in beams ; Section forces in beams ; Higher order beam theory
1. Introducción
La literatura recoge ejemplos diversos de modelos que generalizan las teorías clásicas de vigas. Cabe citar los modelos basados en modos de deformación de la sección transversal propuestos por Schardt y colaboradores, aplicables a problemas lineales y no lineales [1] , [2] and [3] , o la formulación desarrollada por Carrera, basada en aproximaciones en serie de McLaurin a los desplazamientos de la sección transversal [4] and [5] . Otros planteamientos mediante aproximaciones asintóticas de la energía de deformación [6] , [7] and [8] constituyen también herramientas para la generación de modelos de piezas alargadas.
La formulación unificada de la teoría de vigas, desarrollada por el primer autor en [9] and [10] , proporciona un marco alternativo que permite expresar de modo abstracto y compacto las variables que intervienen en cualquier modelo de pieza alargada, independientemente de las restricciones cinemáticas que lo definan, y deducir sistemáticamente las correspondientes ecuaciones de campo mediante principios variacionales. Por ello, puede extenderse sin dificultad a problemas no lineales [11] y constituye el marco idóneo para desarrollar los modelos hiperviga. El concepto hiperviga fue introducido por los autores [12] and [13] para describir la clase de modelos lineales de piezas alargadas que incluyen desplazamientos generalizados adicionales a los necesarios para describir movimientos de sólido rígido (de pequeña magnitud) de las secciones transversales. Los modelos hiperviga se caracterizan por el acoplamiento entre variables estáticas y cinemáticas presente en las ecuaciones de equilibrio, aun en su formulación lineal. En otras palabras, no es posible expresar las ecuaciones de equilibrio de la estructura en función, únicamente, de los esfuerzos y las cargas exteriores; en este caso también aparecen los desplazamientos. La elección del término hiperviga se justifica precisamente por ser este acoplamiento una forma de hiperestatismo local en las ecuaciones de equilibrio.
El objetivo de este artículo es concluir el desarrollo teórico del modelo hiperviga [13] , analizando con mayor detalle la vertiente estática para obtener sistemáticamente las tensiones consistentes con la formulación empleada, así como mostrar, a través de un ejemplo completo, cómo opera la teoría en su totalidad, desde la formulación del modelo hasta la predicción de la respuesta del sólido. La potencia de la formulación para la construcción de las ecuaciones y para la valoración de la influencia de los diferentes parámetros en la respuesta de la pieza alargada queda patente en su aplicación a un problema seleccionado: el problema de flexión alabeada, que representa una formulación de la teoría de vigas capaz de proporcionar una distribución coherente de tensiones tangenciales obtenida en el marco de la propia teoría, sin necesidad de partir de razonamientos basados en condiciones de equilibrio. Se basa en relajar las exigencias de la teoría de Timoshenko, prescindiendo de la planeidad de la sección, mediante un planteamiento similar al que Reddy utiliza en el desarrollo de la teoría de placas [14] o en el desarrollo de un elemento finito de viga de orden superior [15] , que se origina en referencias previas de Levinson et al. [16] and [17] y Bickford [18] . Los resultados obtenidos para las expresiones de las tensiones incorporando la noción de hiperestatismo local y el concepto de pseudoesfuerzo proporcionan una nueva interpretación de las soluciones clásicas que permite diferenciar la fracción de las tensiones debida a los esfuerzos y la debida a los pseudoesfuerzos fruto del hiperestatismo local.
El trabajo se organiza del siguiente modo: en la sección 2 se revisa el concepto de hiperviga y su conexión directa con la idea de hiperestatismo local en el modelo unidimensional (1D); en la sección 3 se introduce la definición de pseudoesfuerzo como término presente en la ecuación de equilibrio que reproduce la acción de las coacciones internas (en el sentido variacional [19] ) asociadas a esta indeterminación local; en la sección 4, la introducción de los pseudoesfuerzos motiva la descomposición de las tensiones totales sobre los puntos de la sección en suma de tensiones primarias y tensiones complementarias; estas últimas, exclusivamente debidas al hiperestatismo local, constituyen una distribución autoequilibrada. Con el fin de mostrar cómo opera el modelo en todas sus vertientes, en la sección 5 se desarrolla la aplicación indicada incluyendo las expresiones de las variables asociadas a la formulación y las soluciones correspondientes a 3 casos con diferentes condiciones de contorno. En la sección 6 se exponen las conclusiones del artículo. Por último, en el anexo se incluye la recopilación de resultados de la formulación unificada aplicada a los modelos hiperviga para que el lector interesado pueda seguir el desarrollo del artículo sin necesidad de recurrir a las referencias citadas [9] and [13] .
2. Hiperestatismo local en los modelos hiperviga
El concepto de hiperviga fue introducido por los autores [12] and [13] al estudiar la naturaleza de las ecuaciones de equilibrio del modelo 1D y concretamente al analizar sus condiciones de desacoplamiento. La hiperviga hace referencia a la clase de modelos lineales de piezas alargadas que incluyen desplazamientos generalizados adicionales a los necesarios para describir movimientos de sólido rígido (de pequeña magnitud) de las secciones transversales. Una lectura más profunda del problema proporciona un interesante punto de vista alternativo. Para presentarlo recordamos la forma genérica que adoptan las ecuaciones de equilibrio en un modelo hiperviga (78)[13, ec. 24b] :
|
|
( 1) |
en la que f y u son los vectores que agrupan esfuerzos y desplazamientos generalizados, respectivamente; Q es el vector de fuerzas generalizadas (cargas exteriores distribuidas consistentes con los desplazamientos generalizados); H es la matriz de equilibrio local (72) ; y es la matriz que determina el acoplamiento entre las variables estáticas y cinemáticas (74) . Si la matriz de acoplamiento se anula (como sucede en el modelo de viga estándar, con 3 grados de libertad en desplazamientos y 3 en rotaciones), el equilibrio proporciona un sistema de n ecuaciones diferenciales en las n componentes de los esfuerzos generalizados que son directamente integrables:
|
|
( 2) |
En este caso, la solución general para los esfuerzos no depende de las características mecánicas del modelo –determinadas por los operadores Drs definidos mediante las ecuaciones (70) – sino tan solo de las condiciones de equilibrio interno (a través de la matriz H ). Ambas propiedades (independencia de las características mecánicas y dependencia de las condiciones de equilibrio) se asocian tradicionalmente a los problemas isostáticos, aunque es necesario incidir en que el isostatismo tiene carácter local en este contexto. Los esfuerzos adoptan, entonces, la siguiente expresión:
|
|
( 3) |
con
|
|
( 4) |
En el caso en que H sea de coeficientes constantes, la expresión se reduce a:
|
|
( 5) |
Ambas expresiones son independientes de la posible variación de sección transversal. Solo si las condiciones globales de sustentación de la viga son hiperestáticas (hiperestatismo externo), intervienen las ecuaciones constitutivas generalizadas en la determinación de las constantes de integración (vector de esfuerzos en la sección inicial de la pieza, f0 ), a través del operador D11 .
En el otro extremo tenemos el caso del equilibrio indeterminado o acoplado ( ). Este razonamiento muestra que los modelos hiperviga son localmente hiperestáticos, mientras que el modelo de viga estándar (en lo sucesivo MVE) es localmente isostático.
3. Los pseudoesfuerzos en el equilibrio local
Como acabamos de ver, en el MVE el equilibrio local es isostático en el sentido estricto (los esfuerzos son directamente integrables a partir de las ecuaciones de equilibrio). Sin embargo, en los modelos hiperviga la matriz de acoplamiento no se anula y la forma canónica de las ecuaciones del modelo 1D viene dada por (1) . En ella se puede comprobar que el sumando tiene carácter estático ya que sus dimensiones deben corresponder a las de un vector de fuerzas generalizadas. Introducimos la denominación de pseudoesfuerzos para referirnos a las componentes del vector determinado por este término, que denotaremos . Los pseudo-esfuerzos tienen, pues, las siguientes definiciones alternativas, constitutiva y estática, respectivamente:
|
|
( 6a) |
|
|
( 6b) |
Los pseudoesfuerzos son consecuencia de la introducción en la hipótesis cinemática de grados de libertad que describen cambios de forma de la sección, adicionales a los que describen movimientos de sólido rígido. La ecuación (6a) determina una relación elástica entre los pseudoesfuerzos y dichos grados de libertad adicionales, a través de la matriz de acoplamiento. Por tanto, se puede afirmar que los pseudoesfuerzos recogen la acción de los enlaces internos [19] que controlan el cambio de forma de la sección transversal. En el modelo viga estándar, como los movimientos de la sección transversal son exclusivamente de sólido rígido, todas las componentes de los pseudoesfuerzos se anulan, mientras que en los modelos hiperviga, debido al equilibrio vectorial local de la pieza, solo lo hacen las componentes de consistentes con las seis componentes del movimiento de sólido rígido de la sección transversal comunes con el MVE.
4. Evaluación de tensiones en modelos hiperviga
El vector de tensiones s* que predice el modelo 1D se deduce directamente de la matriz constitutiva C del só_lido y de las deformaciones e* que nos proporciona la formulación unificada, y puede expresarse en función de los desplazamientos generalizados y sus derivadas por medio de las matrices de deformación B0 y B1 (67):
|
|
( 7) |
Si ahora introducimos las deformaciones generalizadas e (s ) consistentes con la hipótesis cinemática (71) :
|
|
( 8) |
llegamos a una nueva fórmula que solo depende de las variables cinemáticas del modelo, u y e :
|
|
( 9) |
Teniendo en cuenta que la relación entre deformaciones generalizadas y esfuerzos es (75) , las tensiones se pueden expresar del siguiente modo:
|
|
( 10) |
A continuación vamos a demostrar que la matriz se anula en el modelo de viga estándar. Para ello analizaremos la composición de las matrices de deformación correspondientes, determinadas en la sección 5 de la referencia [13] :
|
|
( 11) |
con
|
|
( 12) |
|
|
( 13) |
En este caso particular (el modelo de viga estándar) la matriz de la hipótesis cinemática y la matriz de equilibrio tienen la composición siguiente:
|
|
( 14) |
Operando y simplificando, se comprueba que en el MVE el operador se cancela:
|
|
( 15) |
Este resultado permite confirmar que las tensiones en la viga estándar son función lineal de los esfuerzos característicos del modelo:
|
|
( 16) |
En lo sucesivo, el operador se denominará matriz de deformaciones complementarias .
Retornando a los modelos hiperviga, podemos afirmar que, con carácter general, una parte de las tensiones, que denominaremos tensiones primarias, hereda la propiedad que caracteriza el MVE ( ), mientras que la parte complementaria resulta proporcional a los desplazamientos generalizados u (s ):
|
|
( 17) |
Esta parte de las tensiones es, a su vez, proporcional a los pseudoesfuerzos . Es decir que también admite una formulación estática del tipo:
|
|
( 18) |
donde el operador se obtiene invirtiendo la relación (6a) , mediante el siguiente algoritmo:
- Se ordena agrupando en u (s ) los desplazamientos del MVE, por un lado, y los desplazamientos adicionales, característicos del modelo general, por otro.
- Se invierte el bloque de correspondiente a estos últimos (los otros 3 bloques de esta matriz son nulos debido a las propiedades del equilibrio del MVE y a su simetría intrínseca).
- Se amplía la matriz resultante, de dimensión (n − 6) × (n − 6) en el caso general, hasta n × n mediante filas y columnas de ceros en las posiciones de los seis desplazamientos generalizados de la viga estándar.
Por último, vamos a demostrar que la tensiones inducidas por el hiperestatismo local del modelo poseen una distribución autoequilibrada sobre la sección transversal de la pieza. Para ello partiremos de la definición estática de los esfuerzos generalizados (76) :
|
|
( 19) |
de acuerdo con los resultados de la teoría general. Introduciendo la descomposición del vector de tensiones resulta:
|
|
( 20) |
Recurriendo ahora a la definición del operador Ψ1(16) y teniendo en cuenta que (70) , así como la definición de S11(10) , el cofactor de los esfuerzos en el segundo miembro de la ecuación anterior resulta ser la unidad, por lo que el primer sumando del mismo ha de ser nulo. Esto demuestra el carácter autoequilibrado de :
|
|
( 21) |
Como conclusión resumimos cómo queda caracterizada la estática en los modelos hiperviga. Los esfuerzos generalizados f (s ) son las variables estáticas propias del modelo 1D, y tienen la siguiente definición constitutiva (75) y estática (76) :
|
|
( 22) |
|
|
Su equilibrio local, determinado por la ecuación (1) :
|
|
requiere la toma en consideración de unos pseudoesfuerzos definidos por:
|
|
( 23) |
|
|
Las fórmulas propuestas para la matriz de acoplamiento y para los pseudoesfuerzos, basadas ambas en el operador , son de sencilla deducción y permiten establecer un paralelismo formal directo con las definiciones de los esfuerzos del modelo. Finalmente las tensiones previstas por el modelo admiten la descomposición:
|
|
( 24) |
donde
|
|
( 25a) |
|
|
( 25b) |
proporcionan las tensiones complementarias, debidas exclusivamente al hiperestatismo local, de distribución autoequilibrada y proporcionales a los pseudoesfuerzos, y las tensiones primarias, directamente inducidas por los esfuerzos generalizados e independientes de dicho hiperestatismo.
5. Aplicación a la flexión alabeada
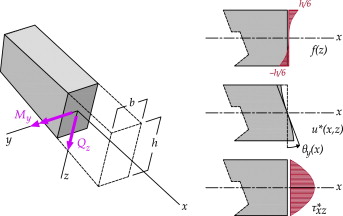
El modelo que se construye en esta sección reproduce la respuesta de flexión de la viga en un plano, asumiendo que la sección transversal, además de moverse como sólido rígido, se deforma perdiendo la planeidad según un patrón determinado por una función que denotamos f (y , z ). Con ello se pretende que la hipótesis cinemática refleje razonablemente los efectos tanto de las tensiones normales como de las tangenciales. Este modelo incluye un grado de libertad (desplazamiento generalizado) adicional a los clásicos de la flexión (traslación y giro).
5.1. Hipótesis fundamental
La hipótesis fundamental d* (x , y , z ) = h (y , z ) u (x ) se formula del siguiente modo:
|
|
( 26) |
Las variables y θy (x ) son el desplazamiento y el giro de la normal a la sección transversal por el centroide, características del problema clásico de flexión. El desplazamiento generalizado θf (x ) es la intensidad de alabeo de la sección y f (y , z ) es el patrón de alabeo o alabeo unitario de la misma. Por analogía con la estructura del desplazamiento horizontal producido por el giro de la sección, supondremos que θf (x ) es adimensional. Finalmente, la caracterización de la función que describe el alabeo unitario se trata en la sección 5.11 .
5.2. Definición estática de los esfuerzos consistentes
La definición estática (76) que proporciona la teoría unificada por medio de la matriz cinemática es:
|
|
que conduce a la definición convencional del esfuerzo cortante y el momento flector:
|
|
( 27) |
y un nuevo esfuerzo con dimensiones de momento, que denominaremos momento de alabeo :
|
|
( 28) |
5.3. Matrices de deformación
En la viga recta se pueden evaluar directamente las deformaciones del sólido, que son:
|
|
( 29a) |
|
|
( 29b) |
|
|
( 29c) |
Factorizando en los desplazamientos generalizados y sus derivadas (67) se obtienen las matrices de deformación:
|
|
( 30) |
5.4. Rigideces locales
El siguiente paso es la evaluación de las matrices de rigidez local (70) integrando las matrices de deformación:
|
|
( 31) |
En el ejemplo considerado restringimos la matriz constitutiva de modo que relaciona únicamente el alargamiento unitario y las distorsiones y con la tensión normal y la tangencial:
|
|
( 32) |
Las rigideces locales resultan:
|
|
( 33a) |
|
|
( 33b) |
|
|
( 33c) |
y quedan definidas a partir del área (A ), el momento de inercia (Iy ) y los parámetros geométricos de la sección específicos de este modelo1 , que son el área de cortante de alabeo (Sf ), el área de pseudo-cortante (Wf ), el módulo de alabeo (If ) y el producto de alabeo (Iyf ):
|
|
( 34) |
5.5. Matrices de equilibrio local y de acoplamiento
La matriz de equilibrio local (72) es:
|
|
( 35) |
Y la matriz de acoplamiento (74) :
|
|
( 36) |
|
|
( 37) |
5.6. Deformaciones generalizadas y esfuerzos
El vector e = {γ χy χf }T , que agrupa las deformaciones generalizadas, se obtiene mediante (71) :
|
|
( 38) |
y sus componentes son la distorsión γ , el cambio unitario de orientación χy y el cambio unitario de intensidad de alabeo χf , que quedan determinados por:
|
|
( 39) |
A su vez, la distorsión puede descomponerse en la asociada al modelo de Timoshenko, γz , más la asociada al alabeo de la sección, γf , definidas por:
|
|
( 40) |
El vector de esfuerzos f = {Qz My Mf }T tiene la siguiente definición constitutiva (75) :
|
|
( 41) |
que desarrollada en componentes conduce a:
|
|
( 42a) |
|
|
( 42b) |
|
|
( 42c) |
La primera ecuación muestra que el mecanismo resistente del esfuerzo cortante tiene 2 partes: el cortante de Timoshenko , que depende de la distorsión γz asociada al modelo de Timoshenko, y el cortante de alabeo −GSf θf , que depende de la intensidad de alabeo. La segunda y la tercera ecuación exhiben el acoplamiento existente entre flexión estándar y flexión alabeada.
La densidad de energía potencial expresada en función de las deformaciones generalizadas (73) es:
|
|
( 43) |
En el primer bloque se identifica la densidad de energía de deformación por cortante clásica (de Timoshenko), la debida a la distorsión por alabeo, y el término de acoplamiento entre ellas. El segundo bloque contiene la densidad de energía de deformación por flexión, la debida al cambio en la intensidad de alabeo y el término de acoplamiento correspondiente. El último bloque corresponde al potencial de las cargas exteriores, con Q = { qz my mf }T , en el que interviene la carga en la dirección z por unidad de longitud, el momento exterior de eje y por unidad de longitud, y las fuerzas generalizadas asociadas al alabeo mf , de interpretación física no tan evidente.
5.7. Ecuaciones del problema y solución general
Los términos que intervienen en el sistema de ecuaciones E ′ = WE − F que gobierna el problema —veáse (78) — son: el vector estado , el término independiente que representa las acciones exteriores F = { 0 Q }T = { 0 00 qz my mf }T y el operador W dado por:
|
|
( 44) |
Desarrollando las ecuaciones resulta:
|
|
( 45a) |
|
|
( 45b) |
|
|
( 45c) |
|
|
( 45d) |
|
|
( 45e) |
|
|
( 45f) |
|
|
En piezas de sección constante, los autovalores de W se obtienen de la ecuación característica:
|
|
( 46) |
|
|
( 47) |
Al autovalor K = 0 (de orden 4) le corresponden 4 soluciones polinómicas, y los autovalores llevan asociadas 2 soluciones trascendentes. Las soluciones linealmente independientes del problema homogéneo definen un operador fundamental Φ (x ). El operador fundamental del problema de valores iniciales G (x ) se obtiene a partir del anterior (81) :
|
|
( 48) |
Las expresiones de los operadores Φ (x ) y G (x ), en función de la coordenada adimensional ξ = x /L ∈ {0, 1} y de la esbeltez del problema de flexión alabeada λ = KL , figuran en la tabla 1 . En ella se ha introducido la siguiente constante adimensional auxiliar:
|
|
( 49) |
5.8. Pseudoesfuerzos
La definición constitutiva de los pseudoesfuerzos (6a) conduce al siguiente resultado:
|
|
( 50) |
Por otra parte, su definición estática (6b) determina:
|
|
( 51) |
Las 2 primeras componentes son nulas en virtud de las ecuaciones de equilibrio de esfuerzos cortantes y momentos flectores. Introducimos por tanto un único pseudoesfuerzo, que denominamos pseudocortante y denotamos , dado por:
|
|
( 52a) |
|
|
( 52b) |
5.9. Aplicación a la viga recta
La solución del problema de una viga recta de sección constante sometida a una carga transversal puntual se expresa mediante las fórmulas (84), teniendo en cuenta que FM = {0 0 0 F 0 0}T , del siguiente modo:
|
|
( 53a) |
|
|
( 53b) |
donde E0 = E (0), F es la magnitud de la carga puntual perpendicular a la directriz que actúa en ξ = τ , y G4 es la cuarta columna del operador G .
Para cualquier tipo de sustentación, las condiciones de contorno determinan 3 componentes del vector estado en el extremo dorsal, E0 , y 3 componentes del mismo en el extremo frontal, E (1). Sustituyéndolas en (53b) , se extrae de esta relación un sistema de 3 ecuaciones con 3 incógnitas que permite determinar los términos desconocidos de E0 .
Procediendo de este modo resolveremos a continuación el problema para 3 tipos diferentes de sustentación: viga biapoyada (A-A), ménsula (E-L) y viga biempotrada (E-E). En el primer caso el desplazamiento está coaccionado, y tanto los momentos flectores como los momentos de alabeo son nulos en las secciones extremas de la pieza. En el segundo, los desplazamientos son nulos en el origen y desconocidos en el extremo final de la ménsula, mientras los esfuerzos siguen el patrón opuesto. En la viga biempotrada los 3 desplazamientos generalizados están coaccionados y los esfuerzos son desconocidos en ambas secciones extremas. Ello determina los siguientes vectores estado en el extremo inicial de la pieza:
|
|
( 54a) |
|
|
( 54b) |
|
|
( 54c) |
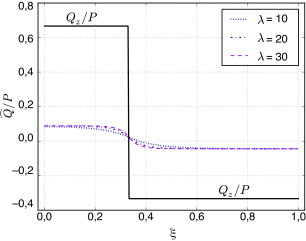
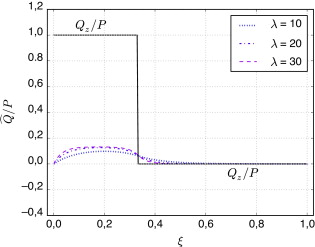
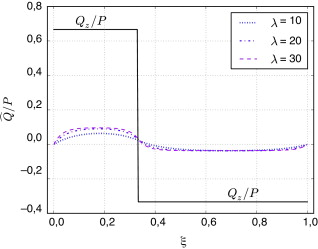
A partir de estos valores, y operando como se ha descrito arriba, se obtiene en cada caso el vector estado en el extremo inicial de la viga. Luego, mediante (53), se determina la solución del problema y, por último, sustituyendo la intensidad de alabeo en (52a) , se determina el correspondientes pseudocortante. El ejemplo se ha procesado con Mathematica® 5.0. A continuación se representan, para τ = 1/3 y sección rectangular ( y κ = 21/5), las leyes de pseudo-cortantes correspondientes a la viga biarticulada (fig. 1 ), la ménsula (fig. 2 ) y la viga biempotrada (fig. 3 ).
|
|
|
Figura 1. Pseudocortantes para , κ = 4,2 y distintos valores de la esbeltez λ . Pieza simplemente apoyada. |
|
|
|
Figura 2. Pseudocortantes para , κ = 4,2 y distintos valores de la esbeltez λ . Ménsula. |
|
|
|
Figura 3. Pseudocortantes para , κ = 4,2 y distintos valores de la esbeltez λ . Pieza biempotrada. |
5.10. Retorno al sólido tridimensional
Por lo que se refiere a la cinemática, la propia hipótesis fundamental —ecuación (26) — constituye la herramienta para estimar los movimientos espaciales u* , y de los puntos materiales de la viga. Sin embargo, tal y como se ha mostrado en la sección 4 , la estática es más compleja y requiere la evaluación de expresiones específicas.
Procediendo de acuerdo con el esquema trazado, las tensiones primarias, proporcionales a los esfuerzos f (x ), se deducen de la expresión (25b) , , con la matriz de deformaciones B1 dada por (30) y y resultan:
|
|
( 55) |
Por otro lado, las tensiones complementarias varían con los pseudoesfuerzos y se obtienen por medio de la ecuación (25a) , , como:
|
|
( 56) |
donde la matriz de deformaciones complementarias definida en (9) adopta ahora el valor:
|
|
( 57) |
y la matriz , obtenida mediante el algoritmo descrito en la sección 4 , resulta:
|
|
( 58) |
Las tensiones tangenciales complementarias, ecuación (56) , son la fracción autoequilibrada de las tensiones tangenciales.
En resumen, las tensiones totales admiten la siguiente formulación, en función de esfuerzos y pseudoesfuerzos:
|
|
( 59a) |
|
|
( 59b) |
|
|
( 59c) |
5.11. Patrón de alabeo
La determinación del alabeo unitario requiere la consideración de las condiciones de contorno estáticas en la sección transversal. Es posible adoptar el patrón de alabeo definido por la solución elástica del problema de la ménsula cargada en la punta [20, pág. 188] , [21, pág. 209] , que proporciona un resultado afinado a costa de un cálculo laborioso. Una opción más sencilla es emplear la expresión , donde ζm es la ordenada normalizada del punto medio del canto, que conduce a las distribuciones tensionales que predice la teoría de vigas en secciones simétricas sencillas.
En el caso particular de una viga de sección rectangular, podemos adoptar el siguiente patrón de alabeo:
|
|
( 60) |
donde a es una constante por determinar a partir de las condiciones de contorno exigibles a la distribución de tensiones tangenciales, .
Las constantes estáticas relevantes para la determinación de estas tensiones, expresadas en función de la constante a y del área de la sección A , resultan:
|
|
( 61) |
y llevadas a (59c) proporcionan:
|
|
( 62) |
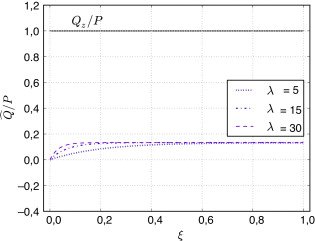
Considerando ahora una pieza en ménsula con la carga en el extremo, como es habitual en las verificaciones relativas a tensiones tangenciales en vigas, y empleando la solución hallada en la sección 5.9 (con τ = 1) se obtiene el diagrama de pseudocortantes de la figura 4 .
|
|
|
Figura 4. Pseudocortantes en una ménsula con carga en el extremo y distintos valores de la esbeltez λ |
Se observa que, para x /L > 0,1 y esbelteces λ ≥ 15 (correspondientes a una relación h /L > 1/5) se cumple . Teniendo en cuenta este dato, junto con el valor del cortante Qz /P = 1, y sustituyendo en (62) , se obtiene que , con lo que el patrón de alabeo resulta:
|
|
( 63) |
y la distribución de tensiones tiene la expresión habitual en teoría de vigas:
|
|
( 64) |
válida en este caso para x /L > 0,1. El patrón de alabeo, la cinemática de la sección y la distribución de tensiones se muestran en la figura 5 .
|
|
|
Figura 5. Patrón de alabeo, cinemática y distribución de tensiones tangenciales asociada al problema de flexión alabeada. |
6. Conclusiones
El presente trabajo supone los siguientes avances en la construcción y la comprensión de la teoría general de modelos 1D:
- El concepto de hiperestatismo local, que caracteriza los modelos hiperviga, hace referencia al acoplamiento entre esfuerzos y desplazamientos generalizados presente en las ecuaciones de equilibrio del problema, que impide la integración directa de los esfuerzos a partir de estas ecuaciones, aun en el caso de piezas externamente isostáticas.
- Esta idea ha conducido a la introducción de unas nuevas variables estáticas denominadas pseudo esfuerzos que posibilitan una nueva interpretación del acoplamiento presente en los modelos hiperviga: los pseudoesfuerzos son consecuencia de la acción de los enlaces internos que controlan el cambio de forma de la sección transversal.
- Se ha mostrado cómo, en el caso general, las tensiones que predice el modelo hiperviga se dividen en 2 partes: las tensiones primarias, directamente proporcionales a los esfuerzos generalizados, y unas tensiones complementarias exclusivamente originadas por el hiperestatismo local y proporcionales a los pseudoesfuerzos. Estas últimas poseen una distribución autoequilibrada sobre la sección transversal de la pieza.
- El modelo de viga estándar es localmente isostático ya que el problema estático está desacoplado del cinemático. En él, los pseudoesfuerzos y las tensiones complementarias son idénticamente nulos, resultando por lo tanto que estos descriptores son propios del modelo hiperviga.
- Las distribuciones de tensiones obtenidas son resultados teóricos consistentes con la hipótesis cinemática escogida. Por tanto, deben considerarse meras aproximaciones a la solución que se obtendría mediante la elasticidad tridimensional, tanto más precisas cuanto más elaborada sea la hipótesis cinemática.
- Las tensiones complementarias son función del patrón genérico de alabeo, que interviene como un dato en la formulación unificada. En general, este se obtiene mediante condiciones de carácter estático, como se ha mostrado en el caso de la flexión alabeada.
- Adicionalmente, el carácter sistemático de la formulación permite programar mediante software de cálculo simbólico las soluciones de los problemas homogéneos que determinan las funciones de forma naturales consistentes con el modelo cinemático adoptado.
Anexo. Resultados principales de la aplicación de la formulación unificada a la teoría de vigas
La formulación unificada permite la deduccón sistemática de las ecuaciones que gobiernan los problemas de vigas de directriz recta o curva (y también de los problemas de placas y láminas) partiendo únicamente de una hipótesis fundamental acerca de la cinemática que gobierna el modelo que se desea desarrollar. En este anexo incluimos las expresiones correspondientes a la viga de directriz curva contenida en un plano. Otros casos más generales pueden consultarse en [9] , [10] , [11] and [13] .
En problemas lineales, la hipótesis cinemática permite expresar los desplazamientos de los puntos materiales del sólido como producto de una matriz h cuyas componentes son funciones de las coordenadas y , z de la sección por un vector u que agrupa los desplazamientos generalizados, que son solo funciones de la posición s de la sección sobre la directriz [9, ec. 10] :
|
|
( 65) |
Las componentes físicas de la deformación del sólido pueden agruparse en un vector:
|
|
( 66) |
Introduciendo las matrices de deformación B0 y B1 , este vector puede factorizarse del siguiente modo [9, ecs. 13 y 14] :
|
|
( 67a) |
|
|
( 67b) |
|
|
( 67c) |
con:
|
|
( 68a) |
|
|
( 68b) |
donde χ es la curvatura de la directriz y μ = 1 − χ y .
La densidad lineal de energía potencial en la viga se obtiene como suma de la densidad lineal de energía de deformación más el potencial de las densidades lineales de las cargas exteriores, y admite la siguiente factorización [9, ec. 21] :
|
|
( 69) |
donde el vector Q (s ) contiene las densidades lineales de cargas consistentes con el modelo y las matrices que definen las rigideces locales Drs vienen dadas por:
|
|
( 70) |
Introduciendo el siguiente vector de deformaciones generalizadas, asociadas a la hipótesis escogida [13, ec. 18] :
|
|
( 71) |
en el que interviene la matriz H , o matriz de equilibrio local:
|
|
( 72) |
es posible factorizar la densidad lineal, que es el funcional de Lagrange del problema, como forma cuadrática de los desplazamientos y de las deformaciones generalizadas [13, ec. 17] :
|
|
( 73) |
La matriz de la forma cuadrática de los desplazamientos, o matriz de acoplamiento entre variables estáticas y cinemáticas, es:
|
|
( 74) |
Los esfuerzos correspondientes al modelo adoptado admiten una definición constitutiva [13, ec. 20] :
|
|
( 75) |
que coincide naturalmente con la definición estática [9, ec. 31] :
|
|
( 76) |
en la que es el vector que agrupa las 6 componentes físicas de la tensión en el sólido (ordenadas de forma consistente con e* ), y t* es el vector tensión que actúa sobre los puntos de la sección transversal. En el caso de la viga de directriz contenida en un plano, .
A partir del funcional de Lagrange, se deduce el siguiente funcional de Hamilton [13, ecs. 21 y 22] :
|
|
( 77) |
Empleando las ecuaciones de Hamilton se obtiene el sistema de ecuaciones diferenciales que gobierna la estática de la viga con la hipótesis cinemática escogida inicialmente [13, ecs. 23 a 25] :
|
|
( 78) |
Las variables estado u (s ) y f (s ) pueden agruparse en un único vector estado E (s ). De este modo, el sistema de ecuaciones se expresa así:
|
|
( 79) |
Las soluciones linealmente independientes del problema homogéneo definen un operador fundamental Φ (s ), cuyo producto por un vector de constantes de integración k determina la solución general del problema homogéneo. Esta también puede expresarse mediante el producto del operador fundamental del problema de valores iniciales , G (s ), por los valores de la solución homogénea en el origen [11, ec. 4.9] :
|
|
( 80) |
donde
|
|
( 81) |
La solución del problema de valores iniciales definido por la condición de contorno E (0) = E0 es suma de la solución homogénea más una solución particular del problema completo:
|
|
( 82) |
En el caso particular de piezas de sección y curvatura constante se demuestra [11, secc. 4.2.3] que G (− s ) = G−1 (s ). Por lo tanto:
|
|
( 83) |
Cuando la pieza está cargada únicamente en una sección s = sM , el término independiente es FM y en el epígrafe indicado de la referencia [11] se demuestra que la solución del problema de valores iniciales es:
|
|
( 84a) |
|
|
( 84b) |
Así pues, la teoría unificada proporciona un procedimiento sistemático de obtención de las variables (esfuerzos y deformaciones generalizadas) asociadas al modelo escogido, de las ecuaciones que rigen el problema correspondiente a dicho modelo y de las soluciones del problema de valores iniciales.
References
- [1] J.M. Davies, P. Leach; First-order generalised beam theory; J. Constr. Steel Res., 31 (2-3) (1994), pp. 187–220
- [2] J.M. Davies, P. Leach, D. Heinz; Second-order generalised beam theory; J. Constr. Steel Res., 31 (2-3) (1994), pp. 221–241
- [3] R. Schardt; Generalized beam theory – an adequate method for coupled stability problems; Thin Walled Struct., 19 (2-4) (1994), pp. 161–180
- [4] E. Carrera, C. Giunta; Refined beam theories based on a unified formulation; Int. J. Appl. Mech., 2 (1) (2010), pp. 117–143
- [5] G. Giunta, F. Biscani, S. Belouettar, E. Carrera; Analysis of thin-walled beams via a one-dimensional unified formulation through a Navier-type solution; Int. J. Appl. Mech., 3 (3) (2011), pp. 407–434
- [6] J.M. Rodríguez, J.M. Viaño; Asymptotic derivation of a general linear model for thin-walled elastic rods; Comput. Meth. Appl. Mech. Eng., 147 (3-4) (1997), pp. 287–321
- [7] L.J. Álvarez-Vázquez, J.M. Viaño; Asymptotic modelling of a nonsymmetric beam; J. Comput. Appl. Math., 126 (1-2) (2000), pp. 433–447
- [8] A. Rajagopal, D.H. Hodges, W. Yu; Asymptotic beam theory for planar deformation of initially curved isotropic strips; Thin Walled Struct., 50 (1) (2012), pp. 106–115
- [9] S. Monleón; Tópicos del análisis unidimensional de estructuras. Parte 1; Vigas y arcos. Rev. Internac. Mét. Num. Cálc. Dis. Ing., 9 (2) (1993), pp. 161–179
- [10] S. Monleón; Tópicos del análisis unidimensional de estructuras. Parte 2; Placas y láminas. Rev. Internac. Mét. Num. Cálc. Dis. Ing., 11 (1) (1995), pp. 37–59
- [11] S. Monleón; Análisis de Vigas, Arcos; Placas y Láminas: una Presentación Unificada. 2.a ed., Editorial de la Universidad Politécnica de Valencia (2001)
- [12] S. Monleón, F. Ibáñez, C. Lázaro, A. Domingo; The concept of hyper-beams in the analysis of slender members; En Proceedings of the 6th International Conference on Computation of Shell and Spatial Structures: IASS-IACM 2008 - Spanning Nano to Mega, 28-31 May 2008, Cornell University, Ithaca, New York, USA (2008)
- [13] S. Monleón, C. Lázaro; El concepto de hiperviga como generalización de los modelos unidimensionales en la estática de piezas alargadas; Rev. Internac. Mét. Num. Cálc. Dis. Ing., 27 (4) (2011), pp. 294–303
- [14] J.N. Reddy; Energy and Variational Methods in Applied Mechanics; John Wiley & Sons (1984)
- [15] P.R. Heyliger, J.N. Reddy; A higher order beam finite element for bending and vibration problems; J. Sound Vib., 126 (2) (1988), pp. 309–326
- [16] N.G. Stephen, M. Levinson; A second order beam theory; J. Sound Vib., 67 (3) (1979), pp. 293–305
- [17] M. Levinson; A new rectangular beam theory; J. Sound Vib., 74 (1) (1981), pp. 81–87
- [18] W.B. Bickford, Consistent higher order beam theory, en: Developments in Theoretical and Applied Mechanics- Proceedings of the 11th Southeast Conference on Theoretical and Applied Mechanics (SECTAM), (1982) 137–150.
- [19] C. Lanczos; The Variational Principles of Mechanics, 4th ed.; Univeristy of Toronto Press (1970)
- [20] J. Courbon; Tratado de Resistencia de Materiales. 2.a ed. ; Editorial Aguilar (1968)
- [21] I.S. Sokolnikoff; Mathematical Theory of Elasticity; McGraw-Hill Book Company (1956)
Notes
1. La comparación de las ecuaciones constitutivas del modelo con las correspondientes al MVE explica la nomenclatura adoptada.
Document information
Published on 01/06/15
Accepted on 09/01/14
Submitted on 16/10/13
Volume 31, Issue 2, 2015
DOI: 10.1016/j.rimni.2014.01.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?