Abstract
In this paper, new homotopy perturbation method (NHPM) (Biazar et al., 2007) is applied to obtain solutions of system of Burgers equations. In this method, the solution is considered as an infinite series expansion where it converges rapidly to the exact solution. In order to show the ability and reliability of the method some examples are provided. The results reveal that the method is very effective and simple. The modified method accelerates the rapid convergence of the series solution and reduces the size of work.
Keywords
System of Burger equation; New homotopy perturbation method
1. Introduction
The investigation of the numerical and exact solutions for nonlinear partial differential equations (NLPDEs) plays an important role in the study of nonlinear physical phenomena. Nonlinear wave phenomena appear in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid-state physics, chemical kinematics, chemical physics and geochemistry. The dispersion, dissipation, diffusion, reaction and convection of nonlinear wave phenomena are very important in nonlinear wave equations. In the past several decades, there have been significant improvements in the study of exact solutions. In the recent years, many authors mainly had paid attention to obtain solutions of NLPDEs by using various methods.
The purpose of this paper was to apply new homotopy perturbation method (NHPM) [10] to coupled Burgers equations.
General form of system of Burgers equations can be considered as the following forms
|
|
(1) |
with initial conditions
|
|
where are constants, and are inhomogeneous terms.
The Burgers model of turbulence is a very important fluid dynamic model and the study of this model and the theory of shock waves have been considered by many authors, both to obtain a conceptual understanding of a class of physical flows and for testing various numerical methods. The distinctive feature of Eq. (1) is that it is the simplest mathematical formulation of the competition between nonlinear advection and viscous diffusion. Homotopy perturbation method (HPM) was proposed by He [1] and [2] which is, in fact, a coupling of the traditional perturbation method and Homotopy in topology. This method has been applied to solve linear and nonlinear equations of heat transfer [3], sixth-order boundary value problems [4], quadratic Riccati differential equation of fractional order [5], conservative truly nonlinear oscillators [6], and linear and nonlinear weakly singular VIE of second kind [7], and many others [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28] and [29].
This paper is arranged as follows. In Section 2, the new modification of HPM for solving systems of Burgers equations is presented. The efficiency of this new method is verified by the numerical results for two examples in Section 3. Conclusion will appear in Section 4.
2. NHPM for coupled Burgers equations
For solving system (1) by NHPM we construct the following homotopies:
|
|
(2) |
or
|
|
(3) |
Applying the inverse operator, to both sides of Eq. (3), we obtain
|
|
(4) |
where
|
|
Let’s present the solution of the system (4) as the following
|
|
(5) |
where , are functions which should be determined.
Suppose that the initial approximation of Eq. (1) is in the following form
|
|
(6) |
where , are unknown coefficients and are specific functions.
Substituting (5) and (6) into (4) and equating the coefficients of p with the same powers lead to
|
|
(7) |
Now if we solve these equations in such a way that , then Eq. (7) results in .
Therefore the exact solution may be obtained as the following.
|
|
(8) |
It is worthwhile to mention that if , and , are analytic around , then their Taylor series can be defined as
|
|
(9) |
can be used in Eq. (7), where , are unknown coefficients which must be computed, and . are known ones.
The two most important steps in application of the new Homotopy perturbation method are to construct a suitable Homotopy equation and to choose a suitable initial guess.
To show the capability of the method, NHPM has been applied to some examples in the next section.
3. Numerical results
To demonstrate the effectiveness of the method two examples of system of Burgers equations are presented.
Example 1.
Consider the following system of Burgers equations
|
|
(10) |
with initial conditions
|
|
The exact solutions are
|
|
To solve Eq. (10), by the NHPM, we construct the following homotopies
|
|
(11) |
Applying the inverse operator, to both sides of these equations, we obtain
|
|
(12) |
Suppose the solutions of system (12) are, as assumed in (5), substituting Eq. (5) into Eq. (12), collecting the same powers of p, and equating each coefficient of p to zero, results in
|
|
Assuming
And solving the above equations for leads to the result
|
|
|
|
By vanishing coefficients are determined as
|
|
Therefore we gain the solution of Eq. (14) as
|
|
|
|
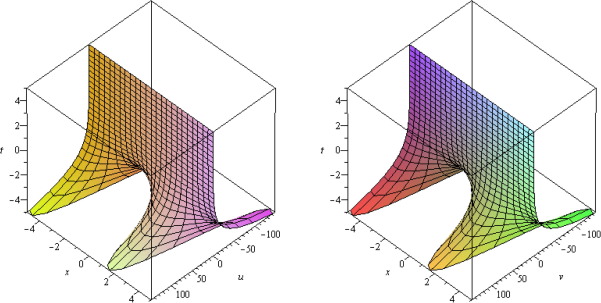
which is an exact solution (see Fig. 1).
|
|
|
Figure 1. Numerical result of Example 1. |
Example 2.
Consider the following system of coupled Burgers equations
|
|
(13) |
with initial conditions
|
|
The exact solution of Eq. (13) is
|
|
To solve Eq. (13), by the NHPM, we construct the following homotopy
|
|
(14) |
Applying the inverse operator, to the both sides of the above equations, we obtain
|
|
(15) |
Suppose the solutions of system (15) have the form (5), substituting Eq. (5) into Eq. (15), collecting the same powers of p, and equating each coefficient of p to zero, results in
|
|
By assuming and solving equations leads to the following results
|
|
|
|
Vanishing , lets the coefficients to take the following values
|
|
This implies that
|
|
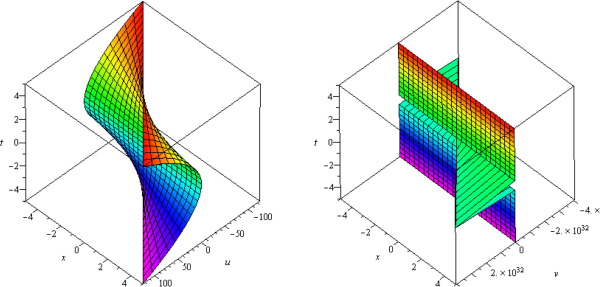
In this example we have also derived exact solutions (see Fig. 2).
|
|
|
Figure 2. Numerical result of Example 2. |
4. Conclusions
In this paper, the modified HPM is applied to approximate solutions of Burgers equations. The present method reduces the computational difficulties of the other methods and all the calculations can be made with simple manipulations. The solutions introduced in this study can be used to obtain the closed form of the solutions if they are required. Thus, it can be concluded that the MHPM is very powerful and efficient in finding analytical as well as numerical solutions for wide classes of partial differential equations. The computations associated with the examples were performed using Maple 15.
Acknowledgments
The authors would like to thank the referees for their useful comments which lead to some improvements of the current paper.
References
- [1] J.H. He; Homotopy perturbation technique; Comput. Methods Appl. Mech. Eng., 178 (1999), pp. 257–262
- [2] J.H. He; A coupling method of homotopy technique and perturbation technique for nonlinear problems; Int. J. Non-Linear Mech., 35 (1) (2000), pp. 37–43
- [3] D.D. Ganji; The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer; Phys. Lett. A, 355 (2006), pp. 337–341
- [4] Muhammad Aslam Noor, Syed Tauseef Mohyud-Din; Homotopy perturbation method for solving sixth-order boundary value problems; Comput. Math. Appl., 55 (2008), pp. 2953–2972
- [5] Z. Odibat, S. Momani; Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order; Chaos Solitons Fract., 36 (1) (2008), pp. 167–174
- [6] A. Beléndez, T. Beléndez, A. Márquez, C. Neipp; Application of He’s homotopy perturbation method to conservative truly nonlinear oscillators; Chaos Solitons Fract., 37 (3) (2008), pp. 770–780
- [7] Z. Chen, W. Jiang; Piecewise homotopy perturbation method for solving linear and nonlinear weakly singular VIE of second kind; Appl. Math. Comput., 217 (2011), pp. 7790–7798
- [8] J.H. He; Variational iteration method a kind of non-linear analytical technique: some examples; Int. J. Non-linear Mech., 34 (1999), pp. 699–708
- [9] S. Momani, S. Abuasad; Application of He’s variational iteration method to Helmholtz equation; Chaos Solitons Fract., 27 (5) (2005), pp. 1119–1123
- [10] J. Biazar, M. Eslami, H. Ghazvini; Homotopy perturbation method for systems of partial differential equations; Int. J. Nonlinear Sci. Numer. Simul., 8 (3) (2007), pp. 411–416
- [11] J. Biazar, H. Ghazvini, M. Eslami; He’s homotopy perturbation method for systems of integro-differential equations; Chaos Solitons Fract., 39 (2009), pp. 1253–1258
- [12] J. Biazar, M. Eslami; A new homotopy perturbation method for solving systems of partial differential equations; Comput. Math. Appl., 62 (2011), pp. 225–234
- [13] L. Cveticanin; Homotopy–perturbation method for pure nonlinear differential equation; Chaos Solitons Fract., 30 (2006), pp. 1221–1230
- [14] S. Abbasbandy; Numerical solutions of the integral equations: homotopy perturbation method and Adomian’s decomposition method; Appl. Math. Comput., 173 (2006), pp. 493–500
- [15] M. Dehghan, F. Shakeri; Use of He’s homotpy perturbation method for solving a partial differential equation arising in modeling of flow in porous media; J. Porous Media, 11 (2008), pp. 765–778
- [16] A. Golbabai, M. Javidi; Application of homotopy perturbation method for solving eighth-order boundary value problems; Appl. Math. Comput., 191 (1) (2007), pp. 334–346
- [17] M.A. Rana, A.M. Siddiqui, Q.K. Ghori; Application of He’s homotopy perturbation method to Sumudu transform; Int. J. Nonlinear Sci. Numer. Simul., 8 (2) (2007), pp. 185–190
- [18] T. Ozis, A. Yildirim; Traveling wave solution of Korteweg-de Vries equation using He’s homotopy perturbation method; Int. J. Nonlinear Sci. Numer. Simul., 8 (2) (2007), pp. 239–242
- [19] A. Yildirim; Application of He’s homotopy perturbation method for solving the Cauchy reaction–diffusion problem; Comput. Math. Appl., 57 (4) (2009), pp. 612–618
- [20] M.A. Jafari, A. Aminataei; Application of homotopy perturbation method in the solution of Fokker-Planck equation; Physica Scripta, 80 (5) (2009), Article 055001
- [21] M.S.H. Chowdhury, I. Hashim; Application of multistage homotopy-perturbation method for the solutions of the Chen system; Nonlinear Anal.: Real World Appl., 10 (2009), pp. 381–391
- [22] M. Matinfar, M. Eslami, M. Saeidy; An efficient method for cauchy problem of ill-posed nonlinear diffusion equation; Int. J. Numer. Methods Heat Fluid Flow, 23 (3) (2013), pp. 427–435
- [23] M. Matinfar, M. Saeidy, M. Eslami; Solving a system of linear and nonlinear fractional partial differential equations using homotopy perturbation method; Int. J. Nonlinear Sci. Numer. Simul., 14 (7–8) (2013), pp. 471–478
- [24] J. Biazar, M. Eslami; A new technique for non-linear two-dimensional wave equation; Scientia Iranica, 20 (2) (2013), pp. 359–363
- [25] M. Eslami; New homotopy perturbation method for special kind of systems of volterra integral equations in two-dimensional spaces; Comput. Math. Model., 25 (1) (2014), pp. 135–148
- [26] M. Eslami, M. Mirzazadeh; Study of convergence of Homotopy perturbation method for two dimensional linear Volterra integral equations of the first kind; Int. J. Comput. Sci. Math., 5 (1) (2014), pp. 72–80
- [27] M. Eslami, J. Biazar; Analytical solution Klein–Gordon equation by new homotopy perturbation method; Comput. Math. Model., 25 (1) (2014), pp. 124–134
- [28] Devendra Kumar, Jagdev Singh, Sunil Kumar, Sushila; Numerical computation of Klein–Gordon equations arising in quantum field theory by using homotopy analysis transform method; Alexandria Eng. J., 53 (2) (2014), pp. 469–474
- [29] Samuel O. Adesanya, J.A. Falade; Thermodynamics analysis of hydromagnetic third grade fluid flow through a channel filled with porous medium; Alexandria Eng. J., 54 (3) (2015), pp. 615–622
Document information
Published on 12/04/17
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?