Abstract
In the present study, large amplitude free vibration of beams resting on variable elastic foundation is investigated. The Euler–Bernoulli hypothesis and the Winkler model have been applied for beam and elastic foundation, respectively. The beam is axially loaded and is restrained by immovable boundary conditions, which yields stretching during vibrations. The energy method and Hamilton’s principle are used to derive equation of motion, where after decomposition an ordinary differential equation with cubic nonlinear term is obtained. The second order homotopy perturbation method is applied to solve nonlinear equation of motion. An explicit amplitude-frequency relation is achieved from solution with relative error less than 0.07% for all amplitudes. This solution is applied to study effects of variable elastic foundation, amplitude of vibration and axial load on nonlinear frequency of beams with simply supported and fully clamped boundary conditions. Proposed formulation is capable to dealing with any arbitrary distribution of elastic foundation.
Keywords
Free vibration; Large amplitude; Axial load; Variable foundation; Homotopy perturbation; Cubic nonlinear term
1. Introduction
Beams are fundamental component in engineering and have wide applications in design and fabrication of structures and machines such as tall building, huge cranes, bridges, turbine and compressor blades. They are also used as simple and accurate model for analysis of complex engineering structures. Natural frequencies and dynamic response of beam-like structure in small amplitude vibration studied by many researchers through analytical and numerical methods and different aspects have been considered. Mathematical model of small amplitude vibration is in the form of linear differential equation which is relatively simple for handling. Nowadays, the demand for light-weight structures and machines is continuously increasing. These light-weight systems are more flexible due to their high aspect ratio and external excitation such as wind load causing large amplitude vibration in them. Large amplitude vibration induced nonlinear terms in differential equation of motion. In the case of beam with immovable ends, axial stretching of the beam during vibration with large amplitude is the source of nonlinearity. The nonlinear vibration of beams due to the large amplitude of vibration has received considerable attention by many researchers. Bhashyam and Prathap [1] presented a Galerkin finite element method for studying nonlinear vibration of beams describable in terms of moderately large bending theory. Ozkaya et al. [2] study the nonlinear response of a beam-mass system with immovable ends by applying the method of multiple scales directly to partial differential equation of motion. Gayesh and Balar [3] study nonlinear parametric vibration and stability of axially moving viscoelastic Rayleigh beams, and they derived the partial-differential equation of motion for large amplitude vibration through geometrical, constitutive, and dynamical relations. Abdel-Jaber et al. [4] study nonlinear frequencies of an elastically restrained tapered beam. They used the nonlinear curvature and the axial shortening due to transverse deflection in the energy formulation of system. Merrimi et al. [5] investigate the geometrically nonlinear steady state periodic forced response of a clamped–clamped beam containing an open crack. The crack has been modeled as a linear spring in which, for a given depth, the spring constant remains the same for both directions. Sedighi et al. [6] derive an analytic solution of transversal oscillation of quintic nonlinear beam with homotopy analysis method. Baghani et al. [7] study large amplitude free vibrations and post-buckling of unsymmetrically laminated composite beams on nonlinear elastic foundation. Lai et al. [8] derive the analytical solutions for large amplitude vibration of thin functionally graded beams. Sedighi and Shirazi [9] study effect of deadzone nonlinear boundary condition on large amplitude vibration of cantilever beam. There are many other researches exist on buckling, linear and nonlinear vibrations of beams and plates [10], [11], [12], [13], [14], [15], [16], [17] and [18].
It is obvious that the accurate analysis of structures required an understanding of soil–structure interaction. The surrounding soil increases resistance of buried structures and significantly changes modal parameters of them. Many practical cases in engineering related to soil–structure interaction can be modeled by means of a beam on elastic foundation. The well-known model for elastic foundations is Winkler. The Winkler model of elastic foundation is the most preliminary in which the vertical displacement is assumed to be proportional to the contact pressure at an arbitrary point [19], in another words, the foundation modeled as a series of closely spaced and mutually independent linear elastic springs. Different problems of beams resting on elastic foundation were studied and reported in the literature [20], [21], [22], [23], [24] and [25]. Often, researcher assumed that the foundation has constant value through the length of the beam and only limited studies exist for dynamic analysis of beams on variables foundations. Eisenberger and Clastornik [26] study free vibration and buckling of the Euler–Bernoulli beams on variable Winkler foundation. Zhou [27] presents a general solution to vibration of the Euler–Bernoulli beams on variable elastic foundation. He assumed the reaction force of the foundation on the beam as the external force acting on the beam. Pradhan and Murmu [28] study thermo-mechanical vibration of sandwich beams resting on variable Winkler foundation using differential quadrature method. Kacar et al. [29] apply differential transform method to investigate free vibration of the Euler–Bernoulli beams on variable Winkler foundation.
According to literature survey, large amplitude free vibration of beam resting on variable elastic foundation has not been studied and for the first time has been studied in this paper. Equation of motion is obtained from energy method by invoking Hamilton principle, and then homotopy perturbation method [30], [31], [32] and [33] is applied to solve governing nonlinear differential equation. Comparisons are made with studies in the open literature in which special cases of the present problem have been studied and very good agreement observed. Finally, some new and more useful results are extracted from the present formulation.
2. Mathematical formulation
Consider a straight beam under axial load which resting on variable Winkler foundation as shown in Fig. 1. The beam has length L, rectangular cross section with the area of S, the cross-sectional moment of inertia of I and thickness of h. The beam was made from isotropic material with E as modulus of elasticity and as mass per unit volume. Stiffness of Winkler foundation changes along the beam length and is the function of spatial coordinate along the beam length (i.e. ). Using Euler–Bernoulli beam hypothesis, the strain energy induced by large displacement amplitude is given by the following:
|
|
(1) |
where and are axial and transverse displacements, respectively. is the mathematical expression for variable Winkler foundation. The kinetic energy is given by the following:
|
|
(2) |
|
|
|
Figure 1. Schematic of the beam under axial load and resting on variable elastic foundation. |
The external work done by axial load can be written as follows:
|
|
(3) |
Using the Lagrangian of the system and invoking Hamilton’s principle, we have the following:
|
|
(4) |
Substituting Eqs. (1), (2) and (3) into Eq. (4), performing the necessary algebra and eliminating axial displacement, the following partial differential equation is obtained for motion:
|
|
(5) |
Variable Winkler foundation can be considered as follows:
|
|
(6) |
where k is a constant and is function of the spatial coordinate along the beam length. Some dimensionless parameters are defined to better handling of equation and better representation of the numerical results, as follows:
|
|
(7) |
where is the radius of gyration of the cross section. Substituting dimensionless parameters into Eq. (5), yields the following:
|
|
(8) |
in order to solve Eq. (8), separation of variables is applied by assuming where is the first eigenmode of the beam that depends on boundary conditions of beam and for simply support and clamped boundary conditions presented in Table 1. is an unknown time-dependent function. Applying the weighted residual Bubnov–Galerkin method yields the following:
|
|
(9) |
| Boundary conditions | |
| Simply supported beam | |
| Fully clamped beam | , |
Finally, the nonlinear equation is obtained in terms of the time-dependent variable as follows:
|
|
(10) |
where and are as follows:
|
|
(11) |
It is assumed midpoint of beam subjected to an initial displacement and zero initial velocity, and accordingly, the nonlinear equation with initial conditions for large amplitude vibration of Euler–Bernoulli beam becomes the following:
|
|
(12) |
Note that is dimensionless initial displacement or dimensionless maximum amplitude of oscillation. Differential equation is obtained in Eq. (12) known as Duffing nonlinear equation.
3. Analytical solution
There are several methods developed by researchers to derive analytical solution for nonlinear differential equation such as homotopy perturbation method [30], [31], [32] and [33], energy balance method [34], [35] and [36], max–min approach [37], [38], [39] and [40], Hamiltonian approach [41], [42] and [43] and so on [44], [45], [46] and [47]. Possibility of parametric studies is most important advantage of these analytical methods rather than numerical methods. The homotopy perturbation method is utilized to derive analytical amplitude–frequency relationship for equation of motion in Eq. (12). This method does not depend upon the assumption of small parameter and is capable to solve ordinary and partial differential equations.
At first, we establish the following homotopy:
|
|
(13) |
where p is homotopy parameter. When p = 0, Eq. (13) becomes a linear ordinary differential equation and when p = 1, it becomes the original nonlinear equation. We consider T and 0 as series of p in the following form:
|
|
(14) |
|
|
(15) |
where are to be determined.
Substituting Eqs. (14) and (15) into Eq. (13) and collecting terms with identical powers of p, we can find three first linear equations with initial conditions as follows:
|
|
(16) |
|
|
(17) |
|
|
(18) |
Analytical solution of Eq. (16) is obtained as follows:
|
|
(19) |
Substituting Eq. (19) into right-hand side of Eq. (17) gives the following:
|
|
(20) |
Avoiding secular terms in T1 requires eliminating contributions proportional to on the right-hand side of Eq. (20), and therefore we have
|
|
(21) |
From Eq. (21) we obtain the following:
|
|
(22) |
First-order approximate frequency-amplitude relationship can be obtained by substituting Eq. (22) into Eq. (15) and setting p = 1 as follows:
|
|
(23) |
The solution of Eq. (17) can be obtained from Eq. (23) as follows:
|
|
(24) |
Avoiding secular terms in T2 requires the following:
|
|
(25) |
By substituting from Eqs. (19) and (24) into Eq. (25) and integrating, we obtain the following:
|
|
(26) |
Second-order approximate frequency-amplitude relationship can be obtained by substituting Eqs. (22) and (26) into Eq. (15) and setting p = 1 as follows:
|
|
(27) |
4. Numerical results
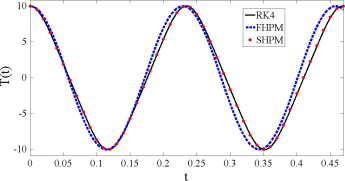
In order to analyze nonlinear frequency of beam-foundation system, it is necessary to investigate accuracy of obtained solution for nonlinear Duffing oscillator because nonlinear frequency of system is determined based on this solution. Therefore, comparison has been made between solutions obtained from first-order homotopy perturbation method (FHPM) in Eq. (23), second-order homotopy perturbation method (SHPM) in Eq. (27), exact integration method and second-order energy balance method based on Galerkin method [48] and the results are presented in Table 2. Also, the comparison between FHPM and SHPM in conjugation with fourth-order Runge–Kutta numerical solution is presented in Fig. 2. It is obvious the amplitude–frequency relation obtained from SHPM yields high accuracy and is suitable for analysis of practical problems.
| Exact | FHPM|Error%| | SHPM|Error%| | [48]|Error%| | |
|---|---|---|---|---|
| 1 | 1.3178 | 1.3228(0.379%) | 1.3178(0%) | 1.3164(0.110%) |
| 10 | 2.8666 | 2.9155(1.706%) | 2.8678(0.042%) | 2.8536(0.455%) |
| 100 | 8.5336 | 8.7178(2.158%) | 8.5391(0.064%) | 8.4843(0.579%) |
| 1000 | 26.8107 | 27.4044(2.214%) | 26.8289(0.068%) | 26.6519(0.592%) |
| 5000 | 59.9157 | 61.2454(2.219%) | 59.9566(0.068%) | 59.5599(0.594%) |
|
|
|
Figure 2. A comparison between the FHPM and SHPM in conjunction with the fourth-order Runge–Kutta method for Eq. (12) (). |
Derived formulation for nonlinear frequency yields fundamental natural or linear frequency of system by setting the initial displacement to zero. To validate accuracy of formulation, the fundamental natural frequency of beams resting on variable elastic foundation with linear and parabolic distribution studied by Kacar et al. [29] is re-examined and the results are tabulated in Table 3. The value of nonlinear to linear frequency of beam without axial load and elastic foundation is obtained from SHPM compared with other well-known studies and the results are shown in Table 4. The results of the present study show very good agreement with other studies for determination of linear and nonlinear frequencies.
| B.C. | |||||
|---|---|---|---|---|---|
| S–S | Present | 10.315 | 13.690 | 10.336 | 13.848 |
| [29] | 10.315 | 13.690 | 10.336 | 13.848 | |
| C–C | Present | 22.573 | 24.301 | 22.583 | 24.395 |
| [29] | 22.573 | 24.301 | 22.583 | 24.395 | |
| A | Simply supported beam | Fully clamped beam | ||||
|---|---|---|---|---|---|---|
| [10] | [14] | Present | [10] | [14] | Present | |
| 1 | 1.0897 | 1.0892 | 1.0892 | 1.0572 | 1.0569 | 1.0550 |
| 2 | 1.3228 | 1.3178 | 1.3178 | 1.2125 | 1.2098 | 1.2031 |
| 3 | 1.6393 | 1.6257 | 1.6258 | 1.4344 | 1.4263 | 1.4138 |
| 4 | 1.9999 | 1.9761 | 1.9764 | 1.6171 | 1.6816 | 1.6629 |
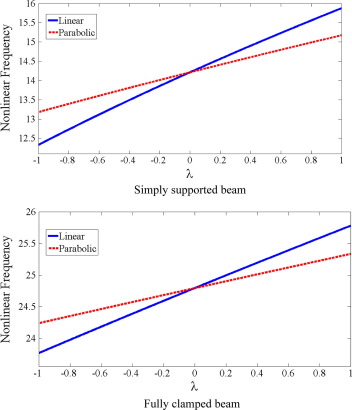
We assume foundation stiffness continuously decreases or continuously increases along beam length. One time this continuous variation has linear pattern with mathematical model as and another time this has parabolic pattern with mathematical model as . It is clear, in both cases, foundation stiffness continuously decreases from left support to right support when and continuously increases when . Fig. 3 is given to study influence of on nonlinear frequency as observed, when foundation stiffness continuously decreases from left support to right support, parabolic pattern yields higher frequency while if foundation stiffness continuously increases from left support to right support, linear pattern yields higher frequency.
|
|
|
Figure 3. Effect of linear and parabolic distribution of foundation on nonlinear frequency (). |
As mentioned in introduction, the foundation is modeled as a series of closely spaced and mutually independent linear elastic springs in the Winkler foundation theory. On this basis, we introduce total stiffness of variable Winkler foundation as follows:
|
|
(28) |
We consider three different distributions of elastic foundation along length of beam as follows:
|
|
(29) |
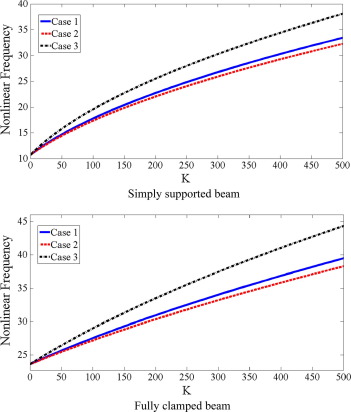
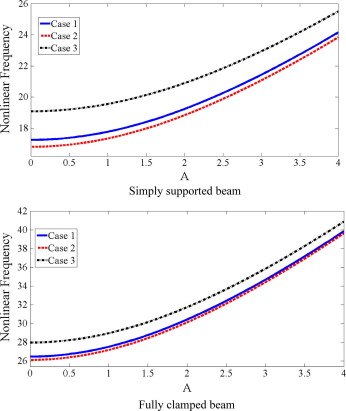
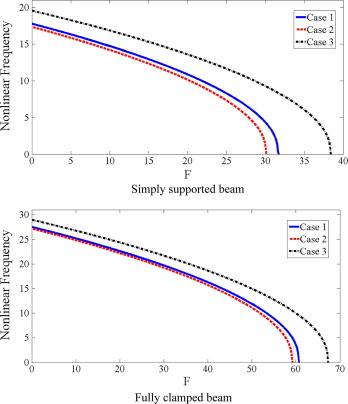
where Case 1 shows linear variation, Case 2 shows parabolic variation and Case 3 shows sinusoidal variation of elastic foundation along length of beam, respectively. Total stiffness of variable foundation is equal for these cases, when value of K be the same. Fig. 4 is given to study effect of K on nonlinear frequency. Three different distributions of Eq. (29) are considered for variable Winkler foundation. It is clear, by increasing K nonlinear frequency increased in all cases. The interesting point is that, for any value of K, sinusoidal variation yields higher frequency rather than linear and parabolic variations of elastic foundation, although the value of KTotal is equal for three cases. Fig. 5 shows the variation of nonlinear frequency versus dimensionless amplitude for different distributions according to Eq. (29). Once again, it is observed sinusoidal variation yields higher frequency although the value of KTotal is equal for three cases. Also, it is almost true, if we say beam with clamp boundary conditions is more sensitive to variation of initial amplitude rather than beam with simply boundary conditions. Effect of axial load on nonlinear frequency for different distributions according to Eq. (29) is presented in Table 5 and plotted in Fig. 6. It should be noted, in Fig. 6, anywhere nonlinear frequency becomes zero, the value of axial load is known as nonlinear post-buckling load.
|
|
|
Figure 4. Effect of on nonlinear frequency for different distributions of elastic foundation with same total stiffness (). |
|
|
|
Figure 5. Effect of dimensionless amplitude on nonlinear frequency for different distributions of elastic foundation with same total stiffness (). |
| Simply supported beam | Fully clamped beam | ||||||
|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | ||
| A = 0.1 | F = 5 | 15.75575 | 15.26582 | 17.745714 | 25.29042 | 24.923337 | 26.858019 |
| F = 10 | 14.103038 | 13.55350 | 16.29608 | 24.043613 | 23.65719 | 25.687413 | |
| F = 15 | 12.228967 | 11.59092 | 14.704228 | 22.728514 | 22.319335 | 24.46085 | |
| A = 1 | F = 5 | 16.317876 | 15.84524 | 18.246923 | 26.37416 | 26.022271 | 27.881258 |
| F = 10 | 14.727973 | 14.20247 | 16.840276 | 25.180702 | 24.811868 | 26.75518 | |
| F = 15 | 12.94396 | 12.34260 | 15.304789 | 23.927703 | 23.539214 | 25.579525 | |
| A = 5 | F = 5 | 26.312323 | 26.01669 | 27.569376 | 44.911757 | 44.70195 | 45.829805 |
| F = 10 | 25.338942 | 25.03096 | 26.644937 | 44.20747 | 43.994044 | 45.140898 | |
| F = 15 | 24.32353 | 24.00141 | 25.68505 | 43.490854 | 43.273605 | 44.440517 | |
|
|
|
Figure 6. Effect of axial load on nonlinear frequency for different distributions of elastic foundation with same total stiffness (). |
Similar to the pervious results in Figure 4 and Figure 5, it is observed in the presence of axial load sinusoidal distribution yields higher frequency and higher post-buckling load. Also, it is noticed frequency slope of variation versus axial load is the same for three cases of distribution when axial load is not near to post-buckling load.
It is seen that the sinusoidal distribution of Winkler foundation has greater effect on nonlinear frequency rather than linear and parabolic distributions while total stiffness of variable Winkler foundation is equal for three cases. It is almost true if we say this phenomenon happened because sinusoidal distribution is more close to fundamental mode shape of simply support and clamped beams. In better words, for maximizing nonlinear frequency of beam resting on variable Winkler foundation, the distribution of foundation must be close to fundamental mode shape of beam.
5. Conclusion
In this study, large amplitude free vibration of axially loaded Euler–Bernoulli beams resting on variable elastic foundation is investigated. The Winkler model is applied to elastic foundation. It is assumed beam has immovable boundary conditions which lead to mid-plane stretching during vibrations. Simply support and fully clamp boundary conditions are used as immovable ends. Energy method and Hamilton’s principle are used to derive equation of motion and partial differential equation in time and space obtained which reduced to ordinary differential equation with cubic nonlinear term after decomposition. Cubic nonlinear term is induced by mid-plane stretching. The second order homotopy perturbation method is applied to achieve explicit amplitude-frequency relation for equation of motion. Derived solution yields high level of accuracy with relative error less than 0.07% for all amplitude and is suitable for practical problems due to high accuracy and convenience for application. After definition concept of total stiffness of variable Winkler foundation, effect of distribution of elastic foundation along beam length is analyzed. Results show when distribution of elastic foundation has mathematical function near to fundamental eigenmode of beam, nonlinear frequency and post-buckling load increased. This problem handled for first time and results are new, and also, proposed formulation is capable to dealing with any arbitrary distribution of elastic foundation.
References
- [1] G.R. Bhashyam, G. Prathap; Galerkin finite element method for non-linear beam vibrations; J. Sound Vib., 72 (1980), pp. 191–203
- [2] E. Ozkaya, M. Pakdemirli, H.R. Oz; Non-linear vibrations of a beam-mass system under different boundary conditions; J. Sound Vib., 199 (1997), pp. 679–696
- [3] M.H. Gayesh, S. Balar; Non-linear parametric vibration and stability of axially moving visco-elastic Rayleigh beams; Int. J. Solids Struct., 45 (2008), pp. 6451–6467
- [4] M.S. Abdel-Jaber, A.A. Al-Qaisia, M. Abdel-Jaber, R.G. Beale; Nonlinear natural frequencies of an elastically restrained tapered beam; J. Sound Vib., 313 (2008), pp. 772–783
- [5] E. Merrimi, Kh. El bikri, R. Benamar; Geometrically non-linear steady state periodic forced response of a clamped–clamped beam with an edge open crack; Comptes Rendus Mécanique, 339 (2011), pp. 727–742
- [6] H.M. Sedighi, K.H. Shirazi, J. Zare; An analytic solution of transversal oscillation of quintic non-linear beam with homotopy analysis method; Int. J. Non-Linear Mech., 47 (2012), pp. 777–784
- [7] M. Baghani, R.A. Jafari-Talookolaei, H. Salarieh; Large amplitudes free vibrations and post-buckling analysis of unsymmetrically laminated composite beams on nonlinear elastic foundation; Appl. Math. Model., 35 (2011), pp. 130–138
- [8] S.K. Lai, J. Harrington, Y. Xiang, K.W. Chow; Accurate analytical perturbation approach for large amplitude vibration of functionally graded beams; Int. J. Non-Linear Mech., 47 (2011), pp. 473–480
- [9] H.M. Sedighi, K.H. Shirazi; A new approach to analytical solution of cantilever beam vibration with nonlinear boundary condition; J. Comput. Nonlinear Dyn., 07 (2012), p. 034502
- [10] T. Pirbodaghi, M.T. Ahmadian, M. Fesanghary; On the homotopy analysis method for non-linear vibration of beams; Mech. Res. Commun., 36 (2009), pp. 143–148
- [11] O. Civalek; Application of differential quadrature (DQ) and harmonic differential quadrature (HDQ) for buckling analysis of thin isotropic plates and elastic columns; Eng. Struct., 26 (2004), pp. 171–186
- [12] A. Barari, H.D. Kaliji, M. Ghadimi, G. Domairry; Non-linear vibration of Euler–Bernoulli beams; Lat. Am. J. Solids Struct., 8 (2011), pp. 139–148
- [13] O. Civalek; Fundamental frequency of isotropic and orthotropic rectangular plates with linearly varying thickness by discrete singular convolution method; Appl. Math. Model., 33 (2009), pp. 3825–3835
- [14] H. Rafieipour, S.M. Tabatabaei, M. Abbaspour; A novel approximate analytical method for nonlinear vibration analysis of Euler–Bernoulli and Rayleigh beams on the nonlinear elastic foundation; Arab. J. Sci. Eng., 39 (2014), pp. 3279–3287
- [15] H. Arvin, F. Bakhtiari-Nejad; Nonlinear free vibration analysis of rotating composite Timoshenko beams; Compos. Struct., 96 (2013), pp. 29–43
- [16] B. Akgoz, O. Civalek; Free vibration analysis of axially functionally graded tapered Bernoulli–Euler microbeams based on the modified couple stress theory; Compos. Struct., 98 (2013), pp. 314–322
- [17] H.M. Sedighi, K.H. Shirazi; Vibrations of micro-beams actuated by an electric field via parameter expansion method; Acta Astronaut., 85 (2013), pp. 19–24
- [18] H.M. Sedighi; Size-dependent dynamic pull-in instability of vibrating electrically actuated microbeams based on the strain gradient elasticity theory; Acta Astronaut., 95 (2014), pp. 111–123
- [19] W.Q. Chen, C.F. Lu, Z.G. Bian; A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation; Appl. Math. Model., 28 (2004), pp. 877–890
- [20] P. Malekzadeh, G. Karami; A mixed differential quadrature and finite element free vibration and buckling analysis of thick beams on two-parameter elastic foundation; Appl. Math. Model., 32 (2008), pp. 1381–1394
- [21] M. Balkaya, M.O. Kaya, A. Saglamer; Analysis of the vibration of an elastic beam supported on elastic soil using the differential transform method; Arch. Appl. Mech., 79 (2009), pp. 135–146
- [22] A. Mirzabeigy, F. Bakhtiari-Nejad; Semi-analytical approach for free vibration analysis of cracked beams resting on two-parameter elastic foundation with elastically restrained ends; Front. Mech. Eng., 9 (2014), pp. 191–202
- [23] N. Venkateshwarlu, S. Akella, T.K.K. Reddy, G.V. Rao; Applicability of simple intuitive formulation for predicting thermal post-buckling behaviour of columns resting on hardening nonlinear elastic foundation; IES J. Part A: Civ. Struct. Eng., 8 (2015), pp. 204–210
- [24] H.M. Sedighi; Nonlinear free vibrations of quintic inextensional beams lying on Winkler elastic substrate based on three-mode assumptions; Proc. IMechE Part K: J. Multi-body Dyn., 228 (2014), pp. 213–225
- [25] H.M. Sedighi, K.H. Shirazi; Accurate investigation of lateral vibrations of a quintic nonlinear beam on an elastic foundation: using an exact formulation of the beam curvature; J. Appl. Mech. Tech. Phys., 55 (2014), pp. 1066–1074
- [26] M. Eisenberger, J. Clastornik; Vibrations and buckling of a beam on a variable Winkler elastic foundation; J. Sound Vib., 115 (1987), pp. 233–241
- [27] D. Zhou; A general solution to vibrations of beams on variable Winkler elastic foundation; Comput. Struct., 47 (1993), pp. 83–90
- [28] S.C. Pradhan, T. Murmu; Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundations using differential quadrature method; J. Sound Vib., 321 (2009), pp. 342–362
- [29] A. Kacar, H.T. Tan, M.O. Kaya; Free vibration analysis of beams on variable winkler elastic foundation by using the differential transform method; Math. Comput. Appl., 16 (2011), pp. 773–783
- [30] J.H. He; Homotopy perturbation technique; Comput. Methods Appl. Mech. Eng., 178 (1999), pp. 257–262
- [31] J.H. He; Application of homotopy perturbation method to nonlinear wave equations; Chaos, Solitons Fract., 26 (2005), pp. 695–700
- [32] S. Abbasbandy; Numerical solutions of the integral equations: homotopy perturbation method and Adomian’s decomposition method; Appl. Math. Comput., 173 (2006), pp. 493–500
- [33] A. Mirzabeigy, M.K. Yazdi, A. Yildirim; Nonlinear dynamics of a particle on a rotating parabola via the analytic and semi-analytic approaches; J. Assoc. Arab. Uni. Basic Appl. Sci., 13 (2013), pp. 38–43
- [34] J.H. He; Preliminary report on the energy balance for nonlinear oscillations; Mech. Res. Commun., 29 (2002), pp. 107–111
- [35] I. Mehdipour, D.D. Ganji, M. Mozaffari; Application of the energy balance method to nonlinear vibrating equations; Curr. Appl. Phys., 10 (2010), pp. 104–112
- [36] Y. Khan, A. Mirzabeigy; Improved accuracy of He’s energy balance method for analysis of conservative nonlinear oscillator; Neural Comput. Appl., 25 (2014), pp. 889–895
- [37] J.H. He; Max-Min Approach to Nonlinear Oscillators; Int. J. Nonlinear Sci. Num. Simul., 9 (2008), pp. 207–210
- [38] S.S. Ganji, A. Barari, D.D. Ganji; Approximate analysis of two-mass–spring systems and buckling of a column; Comput. Math. Appl., 61 (2011), pp. 1088–1095
- [39] M.K. Yazdi, H. Ahmadian, A. Mirzabeigy, A. Yildirim; Dynamic analysis of vibrating systems with nonlinearities; Commun. Theor. Phys., 57 (2012), pp. 183–187
- [40] H.M. Sedighi, K.H. Shirazi, M.A. Attarzadeh; A study on the quintic nonlinear beam vibrations using asymptotic approximate approaches; Acta Astronaut., 91 (2013), pp. 245–250
- [41] J.H. He; Hamiltonian approach to nonlinear oscillators; Phys. Lett. A, 374 (2010), pp. 2312–2314
- [42] A. Yildirim, H. Askari, M.K. Yazdi, Y. Khan; A relationship between three analytical approaches to nonlinear problems; Appl. Math. Lett., 25 (2012), pp. 1729–1733
- [43] H.M. Sedighi, K.H. Shirazi, A. Noghrehabadi; Application of recent powerful analytical approaches on the non-linear vibration of cantilever beams; Int. J. Nolinear Sci. Num. Simul., 13 (2012), pp. 487–494
- [44] L. Cveticanin; Oscillators with nonlinear elastic and damping forces; Comput. Math. Appl., 62 (2011), pp. 1745–1757
- [45] Y. Khan, H. Latifizadeh, H. Rafieipour, E. Hesameddni; Analytical approximate technique for strongly nonlinear oscillators problem arising in engineering; Alex. Eng. J., 51 (2012), pp. 351–354
- [46] Md. Alal Hosen, M.S.H. Chowdhury; A new analytical technique based on harmonic balance method to determine approximate periods for Duffing-harmonic oscillator; Alex. Eng. J., 54 (2015), pp. 233–239
- [47] D. Younesian, H. Norouzi; Frequency analysis of the nonlinear viscoelastic plates subjected to subsonic flow and external loads; Thin Wall. Struct., 92 (2015), pp. 65–75
- [48] S. Durmaz, M.O. Kaya; High-order energy balance method to nonlinear oscillators; J. Appl. Math. (2012), Article Article ID. 518684.
- [49] S.S. Rao; Vibration of Continuous Systems; John Wiley & Sons, New Jersey (2007)
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?