Abstract
In this paper attempts have been done to solve nonlinear oscillator by using Akbari–Ganji’s Method (AGM). Solving nonlinear equation is difficult due to its high nonlinearity. This new approach is emerged after comparing the achieved solutions with numerical method and exact solution.
Results are presented for different values of amplitude vibration of the problem parameters which would certainly illustrate that this method (AGM) is efficient and has enough accuracy in comparison with other semi analytical and numerical methods. Moreover, results demonstrate that AGM could be applicable through other methods in nonlinear problems with high nonlinearity. Furthermore, convergence problems for solving nonlinear equations by using AGM appear small.
Keywords
Akbari–Ganji’s Method (AGM); Angular frequency; Nonlinear oscillator
Nomenclature
AGM- Akbari–Ganji’s Method
τ- torque
M- mass properties
A- vibration amplitude
ω0- angular frequency
θ(t)- angular displacement
- angular velocity
1. Introduction
Nonlinear oscillator models have been widely used in many areas of physics and engineering and are of significant importance in mechanical and structural dynamics for the comprehensive understanding and accurate prediction of motion, and in this investigation attempts have been made to solve nonlinear oscillator which has high nonlinearity.
Consider a nonlinear oscillator modeled by the following governing nonlinear differential equation [1]:
|
|
(1) |
With the following initial conditions:
|
|
(2) |
For small values of parameter θ, the governing Eq. (1) is that a Duffing-type nonlinear oscillator, i.e. , while for large values of θ the equation approximates that of a linear harmonic oscillator, i.e. . Hence, Eq. (1) is called the Duffing-harmonic oscillator [1].
Oscillators are used in different fields of engineering; therefore, using simple procedure for solving the governing nonlinear equation of them is considerable from decades and many researchers trying to reach acceptable solution for these equations due to their nonlinearity by utilizing analytical and semi-analytical methods such as: Homotopy Analysis Method [4] and [5], the He’s Amplitude Frequency Formulation (HAFF) method [6] and [7], Parameter-Expansion Method [8], Energy Balance Method [9] and [10], Differential Transformation Method (DTM) [11], Homotopy Perturbation Method [12], [13], [14] and [15], Adomian Decomposition Method [16], [17] and [18], EXP-function Method [19], [20], [21] and [22] and Variational Iteration Method [23], [24], [25] and [26].
To obtain an accurate analytical solution for frequency–amplitude relation of the Duffing-harmonic oscillator in different range of amplitude vibration due to different usage of this oscillator, this paper employs Akbari–Ganji’s Method (AGM) [2] and [3] which is a powerful and accurate method for solving nonlinear equations with respect to its simplicity through other semi analytical methods. Through these procedures with respect to the basic idea of the method a trial function would assume as solution of mentioned nonlinear problem then by set of algebraic calculation the constant parameters of trial function such as angular frequency would be obtained. Solving process of AGM for this problem has been done for different amounts of amplitude vibration with various terms for trial functions to present that AGM is applicable for solving nonlinear equations with high nonlinearity and by comparing with numerical solution it would be obvious that this method has enough efficiency and simplicity.
The main purpose of AGM is obtaining the accurate solution with simple algebraic calculation in which in comparison with other methods the process would be simpler and the obtained solution would be acceptable with minor errors in comparison with numerical method. It is necessary to mention that a summary of the excellence of this method in comparison with the other approaches can be considered as follows: initial conditions are needed in accordance with the order of differential equations in the solution procedure but when the number of initial conditions is less than the order of the differential equation, this approach can create additional new initial conditions in regard to the own differential equation and its derivatives. Therefore, it is logical to mention that AGM is operational for miscellaneous nonlinear differential equations in comparison with the other methods.
2. Mathematical formulation
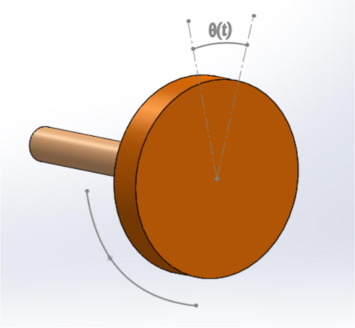
The system under consideration is shown in Fig. 1. The rigid disk is assumed to with mass M rotating at angular velocity about the inertial Z-axis. Therefore, torque τ effect on the hub causes it to rotate only. The process of formulation would be as follows:
|
|
(3) |
|
|
|
Figure 1. The geometry of the oscillator. |
By the assumption of the following values for oscillator’s equation, Eq. (1) would be obtained:
|
|
(4) |
|
|
(5) |
With the following initial conditions:
|
|
(6) |
3. Basic idea of Akbari–Ganji’s Method
In general, vibrational equations and their initial conditions are defined for different systems as follows:
|
|
(7) |
Parameter angular frequency of the harmonic force exerted on the system and (F0) the maximum amplitude its.
And initial conditions are as follows:
|
|
(8) |
3.1. Choosing the answer of the governing equation for solving differential equations by AGM
In AGM, a total answer with constant coefficients is required in order to solve differential equations in various fields of study such as vibrations, structures, fluids and heat transfer. In vibrational systems with respect to the kind of vibration, it is necessary to choose the mentioned answer in AGM. To clarify here, we divide vibrational systems into two general forms:
3.1.1. Vibrational systems without any external force
Differential equations governing on this kind of vibrational systems are introduced in the following form:
|
|
(9) |
Now, the answer of this kind of vibrational system is chosen as follows:
|
|
(10) |
According to trigonometric relationships, Eq. (10) is rewritten as follows:
|
|
(11) |
It is notable that in Eq. (7), , .
Sometimes for increasing the precision of the considered answer of Eq. (9), we are able to add another term in the form of cosine by inspiration of Fourier cosine series expansion as follows:
|
|
(12) |
In the above equation, we are able to omit the term to facilitate the computational operations in AGM if the system is considered without any damping components.
Generally speaking in AGM, Eq. (11) or Eq. (12) is assumed as the answer of the vibrational differential Eq. (9) that its constant coefficients which are (angular frequency) and φ (initial vibrational phase) can easily be obtained by applying the given initial conditions in Eq. (8). And also the above procedure will completely be explained through the presented example in the foregoing part of the paper. It is noteworthy that if there is no damping component in the vibrational system, the constant coefficient a in Eqs. (11) and (12) will automatically be computed zero in AGM solution procedure.
On the contrary, the parameter b in Eqs. (11) and (12) for the other kind of vibrational system with damping component is obtained as a nonzero parameter in AGM.
3.1.2. Vibrational systems with external force
In this step, it is assumed that the external forces exerting on the vibrational systems are defined as follows:
|
|
(13) |
As a result, the differential equation governing on the vibrational system is expressed like Eq. (7) as follows:
|
|
(14) |
The answer of the above equation is introduced as the sum of the particular solution (up) and the harmonic solution (uh) as follows:
|
|
(15) |
The result answer differential equation Eq. (14) is as follows:
|
|
(16) |
By utilizing trigonometric relationships and also by substituting the yielded equations into Eq. (16), the desired answer will be obtained in the form of
|
|
(17) |
In order to increase the precision of the achieved equation, we are able to add another term in the form of cosine by the inspiration of Fourier cosine series expansion as follows:
|
|
(18) |
And finally in accordance with the Eq. (18), the exact solution of the all vibrational differential equations can be obtained in the following equation:
|
|
(19) |
The constant coefficients of Eq. (19) which are {a1, a2, …, φ1, φ2, …, b, ω, d, ϕ} will easily be computed in AGM by applying the initial conditions of Eq. (8).
To deeply understand the above procedure, reading the following lines is recommended.
Since the constant coefficient (a) in vibrational systems without damping components is always obtained zero (a = 0) which in the case, to decrease computational operations of Eq. (18) and (or Eq. (19)) we would rewrite them in the following form:
|
|
(20) |
Based on the above explanations, by applying initial conditions on a system without damping component, the value of parameter (a) is always zero for Eqs. (17), (18) and (19). Therefore without damping component, the role of parameter (a) in both of Eqs. (17), (18) and (19) which each of them can be considered as the answer of the vibrational problems is individually considered as a catalyst for increasing the precision of the assumed answer. However according to Eqs. (17), (18) and (19) after applying initial conditions on the vibrational system in both states (with external force and without external force) by AGM, the value of parameter (a) is computed zero because the mentioned system has a free vibration without any damping component.
Again, we mention that in order to decrease computational operations for systems without damping components and since we know that (a) in the term (e−at) is zero so (e−at) can be omitted from Eqs. (17), (18) and (19). Consequently, Eq. (17) which has been considered as the answer of the systems without any damping component can be rewritten as follows:
|
|
(21) |
3.2. Application of initial conditions to compute constant coefficients and angular frequency by AGM
In AGM, the application of initial conditions of Eq. (8) is done in the two following forms:
3.2.1. Applying the initial conditions on the answer of differential equation
In regard to the kind of vibrational system (with external force and without external force) which was completely discussed in the previous part of this case study, a function is chosen as the answer of the differential equation from Eq. (11) or Eq. (12) for the systems without external forces and from Eqs. (17), (18) and (19) for the defined systems with external forces and then the initial conditions are applied on the selected function as follows:
|
|
(22) |
It is notable that IC is the abbreviation of introduced initial conditions of Eq. (8).
3.2.2. Appling the initial conditions on the main differential equation and its derivatives
After choosing a function as the answer of differential equation according to the kind of vibrational system, this is the best time to substitute the mentioned answer into the main differential equation instead of its dependent variable (u).
Assume the general equation of the vibration such as Eq. (7) with time-independent parameter (t) and dependent function (u) as follows:
|
|
(23) |
Therefore, on the basis of the kind of vibrational system, a function as the answer of the differential equation such as Eq. (11) or Eq. (10) and Eqs. (17), (18) and (19) is considered as follows:
|
|
(24) |
In this step, the aforementioned equation is substituted into Eq. (23) instead of (u) in the following form:
|
|
(25) |
Eventually, the application of initial conditions on Eq. (25) and its derivatives is expressed as follows:
|
|
(26) |
To end up, it is better to say that in AGM after applying the initial conditions on answer function Eq. (20), and also the function differential equation and on its derivatives from Eq. (26) according to the order of differential equation and utilizing the two given initial conditions of Eq. (8), a set of algebraic equations which is consisted of n equations with n unknowns is created. Therefore, the constant coefficients (a, b, c, d, angular frequency ω and initial phase φ and ϕ) at Eqs. (17) and (18) are easily achieved which this procedure will thoroughly be explained in the form of an example in the foregoing part of this paper.
It is noteworthy that in Eq. (25), we are able to use the derivatives of f(t) with higher orders until the number of yielded equations is equal to the number of the mentioned constant coefficients of the assumed answer.
4. Solving the nonlinear equation of Duffing-harmonic oscillator with AGM
First of all, we rewrite the problem Eq. (1) in the following order:
|
|
(27) |
On the basis of the given explanations in the previous section, we consider the answer of Eq. (27) as follows:
|
|
(28) |
On the basis of the given explanations, the existence of the term e−at in Eq. (28) indicates that there is a damping component in the oscillating system. Since there are not any damping components in the mentioned example, the constant a in Eq. (28) will automatically be zero after applying the initial conditions in AGM. Moreover, the constant coefficient b, the initial vibrational phase φ and finally the angular frequency ω can be computed by applying the initial conditions.
According to above theory the answer of the problem is assumed as follows:
|
|
(29) |
4.1. Applying boundary or initial conditions
In regard to the proposed physical model, there are no boundary conditions so the constant coefficients of Eq. (29) are just acquired with respect to the given initial conditions which have been presented in Eq. (2). It is notable that initial or boundary conditions are applied in two manners in the following form:
- The initial conditions are applied on Eq. (29) in the form of
|
|
(30) |
To simplify, IC is considered as the abbreviation of the initial conditions.
As a result, applying the initial conditions on Eq. (29) is done as follows:
|
|
(31) |
And
|
|
(32) |
- The application of initial or boundary conditions on the main differential equation which in this case is Eq. (27) and its derivatives is done in the following general forms:
|
|
(33) |
Therefore, according to Eq. (33), the initial conditions are applied after substituting Eq. (29) which was considered as the answer of the main differential equation into Eq. (27).
As a result, the above procedure is done on the yielded equation and its derivative as follows:
|
|
(34) |
|
|
(35) |
|
|
(36) |
By solving a set of algebraic equations which is consisted of five equations with five unknowns from
Eqs. (31) and (32) and Eqs. (34), (35) and (36), the constant coefficients b1, b2, φ1, φ2 and ω of Eq. (29) can easily be yielded as follows.
To simplify, the following new variable is introduced:
|
|
(37) |
With regard to Eq. (37), the constant coefficients of Eq. (29) can be rewritten as follows:
|
|
(38) |
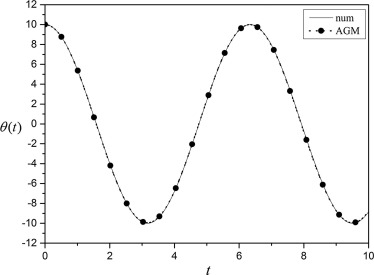
By considering the following physical quantities for Amplitude vibration (see Fig. 2),
|
|
(39) |
|
|
|
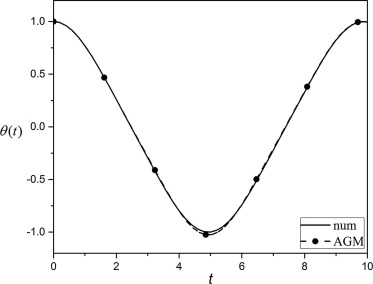
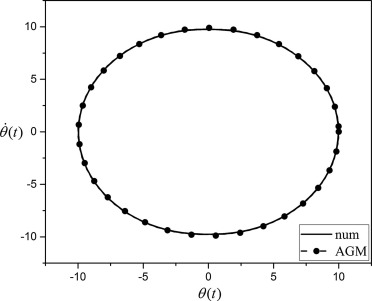
Figure 2. Comparison between obtained results of θ(x) by AGM and numerical method for A = 10. |
After substituting the mentioned physical quantities into Eqs. (37) and (38), then by substituting the final obtained values in Eq. (29) the solution of the mentioned problem will be obtained as follows:
|
|
(40) |
The above procedure can be applied to various values of A. However, for obtaining better results we continued our research for solving the mentioned problem with different values for A.
For instance in solving procedure of the problem for very small amount of A such as 0.1 and 0.01 we assumed our trial function with two terms by solving set of algebraic calculation (four equations and four unknowns) and with acceptance of real part of the obtained result as solution, the constant coefficients b1, b2, φ1, φ2 and ω of Eq. (29) can easily be yielded as follows:
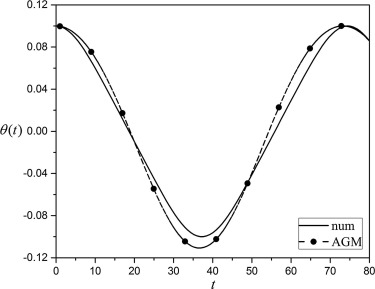
For A = 0.1 we will have (see Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7):
|
|
(41) |
|
|
|
Figure 3. Comparison between obtained results of θ(x) by AGM and numerical method for A = 0.1. |
|
|
|
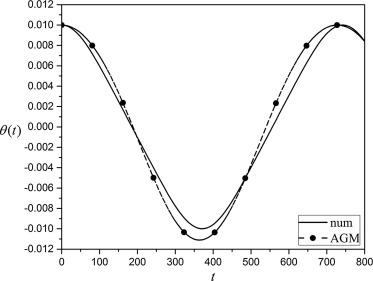
Figure 4. Comparison between obtained results of θ(x) by AGM and numerical method for A = 0.01. |
|
|
|
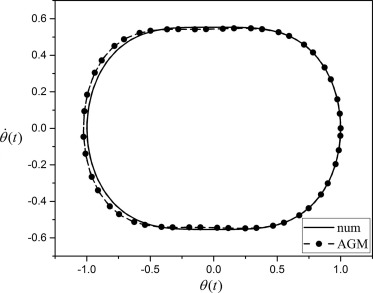
Figure 5. Comparison between obtained results of θ(x) by AGM and numerical method for A = 1. |
|
|
|
Figure 6. Comparison between the obtained θ(t) and θ′(t) by AGM and numerical method for A = 10. |
|
|
|
Figure 7. Comparison between the obtained θ(t) and θ′(t) by AGM and numerical method for A = 1. |
So the solution of the mentioned problem would have obtained as follows:
|
|
(42) |
For A = 0.01 we will have (see Fig. 4):
|
|
(43) |
So the solution of the mentioned problem would have obtained as follows:
|
|
(44) |
which are accepted results with low error in comparison with the exact answer which has been obtained by Runge–Kutta method.
Another example in this case is solving Eq. (1) with A = 1 which this process could be applied even for another values of A, so in this case we choose the procedure of solving due to our need for obtaining the answer which totally depends on our opinion or accuracy that we are looking to.
So in this case we consume the trial function up to four terms as follows:
|
|
(45) |
So by solving set of algebraic calculations (nine equations and nine unknowns) the constant coefficients b1, b2, b3, b4, φ1, φ2, φ3, φ4 and ω of Eq. (45) would be obtained as follows:
|
|
(46) |
So the solution of the mentioned problem would have obtained as follows:
|
|
(47) |
which are accepted answer with low error with the exact amount of the answer which has been obtained by Runge–Kutta method.
5. Results and discussion
The current investigation has been done to solve discussed nonlinear problem with analytical method which is called Akbari–Ganji’s Method (AGM) in order to get better solution in comparison with numerical method (Runge–Kutta, R4) and mentioned mathematical procedure has been done differently by assuming various trial function as the solution of the problem which presents the simplicity and acceptable accuracy of this method among other analytical methods. According to figures and related tables, results of excellence of this method would be obvious (see Table 1, Table 2, Table 3 and Table 4).
| t | Error (A = 10) |
|---|---|
| 0 | 0.0000000004 |
| 1 | 0.0018673829 |
| 2 | 0.0487324767 |
| 3 | 0.0379726475 |
| 4 | 0.0157708646 |
| 5 | 0.0376813682 |
| 6 | 0.0168360947 |
| 7 | 0.0313311902 |
| 8 | 0.0942359176 |
| 9 | 0.0127440686 |
| 10 | 0.0607523738 |
| t | Error (A = 0.1) |
|---|---|
| 0 | 0.0000000000 |
| 8 | 0.0079258488 |
| 16 | 0.0072122058 |
| 24 | 0.0086336631 |
| 32 | 0.0137262721 |
| 40 | 0.0091370221 |
| 48 | 0.0020672041 |
| 56 | 0.0140705200 |
| 64 | 0.0173457904 |
| 72 | 0.0024931915 |
| 80 | 0.0000038234 |
| t | Error (A = 0.01) |
|---|---|
| 0 | 0.0000000000 |
| 80 | 0.0008019579 |
| 160 | 0.0007062095 |
| 240 | 0.0009228495 |
| 320 | 0.0014249079 |
| 400 | 0.0009132327 |
| 480 | 0.0000999953 |
| 560 | 0.0015633441 |
| 640 | 0.0017874547 |
| 720 | 0.0002129877 |
| 800 | 0.0000389138 |
| t | Error (A = 1) |
|---|---|
| 0 | 0.0000000000 |
| 1 | 0.0323225843 |
| 2 | 0.0565293300 |
| 3 | 0.0694878386 |
| 4 | 0.1727424290 |
| 5 | 0.1847768542 |
| 6 | 0.0622806814 |
| 7 | 0.3681746222 |
| 8 | 0.5009673679 |
| 9 | 0.4464822849 |
| 10 | 0.1533444647 |
For obtaining better solution with more simplicity during mathematical calculation by appropriate software (such as Maple) some other assumption could be mentioned, for instance for A = 0.01, following terms in order of complex numbers could be considered:
|
|
(48) |
Then the trial function would be assumed as follows:
|
|
(49) |
The rest procedure would be applied exactly as described in previous parts. The reason of using above assumption is just for simplicity in calculation.
6. Conclusion
In this paper attempts have been done for solving nonlinear oscillator equation with Akbari–Ganji’s Method (AGM) and comparing its results with numerical method (Runge–Kutta, R4) for different values of amplitude vibration and by various processes of solution to reveal that AGM would be applied for solving nonlinear equation with high nonlinearity.
According to figures and related tables it is logical to say that AGM is a very applicable and suitable approach for solving nonlinear differential equations and has enough efficiency and acceptable accuracy. In addition to the aforementioned explanations after applying initial conditions on the considered solution, we exit from the field of differential equation into a set of algebraic equations. Then, by solving a set of algebraic equations which is a simple procedure, the constant coefficients of the trial function would be obtained.
References
- [1] R.E. Mickens; Mathematical and numerical study of the Duffing-harmonic oscillator; J. Sound Vib., 244 (2001), pp. 563–567
- [2] M.R. Akbari, D.D. Ganji, A. Majidian, A.R. Ahmadi; Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM; Front. Mech. Eng., 9 (2) (2014), pp. 177–190
- [3] S.T. Ledari, H. Mirgolbabaee, D.D. Ganji; Heat transfer analysis of a fin with temperature dependent thermal conductivity and heat transfer coefficient; New Trends Math. Sci. (2) (2015), pp. 55–69
- [4] S. Das, P. Gupta; Application of homotopy analysis method and homotopy perturbation method to fractional vibration equation; Int. J. Comput. Math., 88 (2) (2011), pp. 430–441
- [5] T. Pirbodaghi, M. Ahmadian, M. Fesanghary; On the homotopy analysis method for non-linear vibration of beams; Mech. Res. Commun., 36 (2) (2009), pp. 143–148
- [6] J.H. He; An improved amplitude–frequency formulation for nonlinear oscillators; Int. J. Nonlinear Sci. Numer. Simul., 9 (2) (2008), p. 211
- [7] S.S. Ganji, D.D. Ganji, H. Babazadeh, N. Sadoughi; Application of amplitude–frequency formulation to nonlinear oscillation system of the motion of a rigid rod rocking back; Math. Methods Appl. Sci., 33 (2) (2010), pp. 157–166
- [8] A. Kimiaeifar, A.R. Saidia, A.R. Sohouli, D.D. Ganji; Analysis of modified Van der Pol’s oscillator using He’s parameter-expanding methods; Curr. Appl. Phys., 10 (1) (2010), pp. 279–283
- [9] M.G. Sfahani, A. Barari, M. Omidvar, S.S. Ganji, G. Domairry; Dynamic response of inextensible beams by improved energy balance method; Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn., 225 (1) (2011), pp. 66–73
- [10] M. Momeni, N. Jamshidi, A. Barari, D.D. Ganji; Application of He’s energy balance method to duffing harmonic oscillators; Int. J. Comput. Math., 88 (2011), pp. 135–144
- [11] J.K. Zhou; Differential Transformation and its Applications for Electrical Circuits; Huazhong Univ. Press, Wuhan, China (1986)
- [12] D.D. Ganji, H. Mirgolbabaei, M. Miansari, M. Miansari; Application of homotopy perturbation method to solve linear and non-linear systems of ordinary differential equations and differential equation of order three; J. Appl. Sci., 8 (2008), pp. 1256–1261
- [13] H. Mirgolbabaei, D.D. Ganji; Application of homotopy perturbation method to solve combined Korteweg de Vries-Modified Korteweg de Vries equation; J. Appl. Sci., 9 (19) (2009), pp. 3587–3592
- [14] M.G. Sfahani, S.S. Ganji, A. Barari, H. Mirgolbabaei, G. Domairry; Analytical solutions to nonlinear conservative oscillator with fifth-order nonlinearity; Earthq. Eng. Eng. Vib., 9 (3) (2010), pp. 367–374
- [15] H. Mirgolbabaei, D.D. Ganji, H. Taherian; Soliton solution of the Kadomtse–Petviashvili equation by homotopy perturbation method; World J. Modell. Simul., 5 (1) (2009), pp. 38–44
- [16] S. Abbasbandy; A numerical solution of Blasius equation by Adomian’s decomposition method and comparison with homotopy perturbation method; Chaos, Solitons Fractals, 31 (2007), pp. 257–260
- [17] G. Adomian; Solving Frontier Problems of Physics. The Decomposition Method; Kluwer Academic Publishers, Boston, MA (1994)
- [18] H. Mirgolbabaei, A. Barari, L.B. ISBEN, M.G. Esfahani; Analytical solution of forced-convective boundary-layer flow over a flat plate; Arch. Civ. Mech. Eng., 10 (2) (2010), pp. 41–51
- [19] Ji-Huan He, Xu-Hong Wu; Exp-function method for nonlinear wave equations; Chaos Solitos Fractals, 30 (3) (2006), pp. 700–708
- [20] Xu-Hong WU, Ji-Huan He; Solitary solutions, periodic solutions and compacton-like solutions using the Exp-function method; Comput. Math. Appl., 54 (7–8) (2007), pp. 966–986
- [21] Selçuk Kutluay, Alaattin Esen; Exp-function method for solving the general improved KdV equation; Int. J. Nonlinear Sci. Numer. Simul., 10 (6) (2009), pp. 717–726
- [22] Jin-Rong Chang; The exp-function method and generalized solitary solutions; Comput. Math. Appl., 61 (2011), pp. 2081–2084
- [23] S. Ghafoori, M. Motevalli, M.G. Nejad, F. Shakeri, D.D. Ganji, M. Jalaal, Efficiency of differential transformation method for nonlinear oscillation: Comparison with HPM and VIM, January 2011.
- [24] A. Barari, A.T. Poor, A. Jorjani, H. Mirgolbabaei; Analysis of diffusion problems using homotopy perturbation and variational iteration methods; Int. J. Res. Rev. Appl. Sci., 14 (4) (2010), pp. 1101–1109
- [25] H. Mirgolbabaei, D.D. Ganji, M.M. Etghani, A. Sobati; Adapted variational iteration method and axisymmetric flow over a stretching sheet; World J. Modell. Simul., 5 (4) (2009), pp. 307–314
- [26] M. Miansari, A. Barari, H. Mirgolbabaei, M.J. Vahdatirad; An approximate solution for different types of wave problems; Suleyman Demirel Uni. J. Sci., 4 (2) (2009)
Document information
Published on 12/04/17
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?