Resumen
En este trabajo se plantea una solución numérica (simulación por software) del “problema de n cuerpos” que interactúan gravitacionalmente basada en la formulación de Verlet. Adicionalmente se diseña un programa que gráficamente muestra los resultados de esta solución numérica, que detalla las diferentes trayectorias, para diferentes condiciones de masa, velocidad y distancia entre los n objetos que interactúan. La interacción del usuario con la interfaz gráfica, se realiza partícula a partícula.
Palabras clave: Verlet, problema de n cuerpos, gravedad, sistema newtoniano, planetas, simulación.
Abstract
In this paper we propose a numerical solution (software simulation) of the "problem of n bodies" that interact gravitationally based on the formulation of Verlet. Additionally a program is designed that graphically shows the results of this numerical solution, which details the different trajectories, for different conditions of mass, speed and distance between the n objects that interact. The interaction of the user with the graphical interface, is performed particle by particle.
1. Introducción
El programa Planetas fue pensado para verificar gráficamente que las relaciones de la Ley de Gravitación Universal y las leyes de Kepler se cumplen utilizando las herramientas de matemáticas y cómputo además de algunos “Ansatz” aplicados durante la programación, con el objetivo de mostrar desde la idea del problema, su planteamiento matemático, refinamiento, codificación, y finalmente, utilización para sistemas inteligentes que creen la comprensión de nuevos conceptos o verifiquen los existentes como por ejemplo: Leyes de Kepler, soluciones para las trayectorias de Newton, velocidad de escape, sistemas binarios, etc.
Un problema sumamente interesante de la mecánica clásica es el llamado “Problema de n cuerpos”, cuyo tratamiento consiste en describir la trayectoria que seguirían un número arbitrario de partículas aisladas interactuando gravitacionalmente entre sí [1-5]. De forma analítica existen avances recientes en cuanto a las soluciones de sistemas de hasta 3 cuerpos, sin embargo, empleando algún método numérico eficiente, es posible generalizar la solución, estando limitado el número de cuerpos solamente por la capacidad y velocidad del equipo de cómputo.
Generalizando la segunda ley de Newton para un sistema de n cuerpos:
|
|
(1) |
y ya que la única fuerza involucrada es la fuerza gravitacional [1, 2, 9],
|
|
(2) |
se obtienen expresiones para las componentes de la aceleración de los cuerpos dadas por
|
|
(3) |
Se utilizan coordenadas bi-dimensionales (2D) debido a limitaciones técnicas en la representación en pantalla y apoyados en la idea de que muchos sistemas importantes en la naturaleza se pueden aproximar a un comportamiento 2D, como por ejemplo, el Sistema Solar.
Una vez que se cuenta con la aceleración de cada cuerpo, se podría encontrar su velocidad y posición actual por simple integración, sin embargo, como veremos más adelante, el considerar la aceleración como constante en cada punto conduce a un grave error de convergencia que se puede corregir desarrollando la función de aceleración en términos superiores de Taylor, en la llamada aprox. de Verlet [2, 3].
Para agilizar los cálculos y facilitar el manejo de las cantidades involucradas, es necesario elegir las unidades adecuadas para el problema, en este caso, se manejarán unidades astronómicas para longitud (1 ua es el radio de la órbita terrestre), años para el tiempo, y masas solares (mS) como unidad de masa [3, 4]. Ahora bien, para el cálculo de la Constante Gravitacional G en las unidades elegidas, se emplea la Tercera Ley de Kepler, la cual relaciona al periodo de un planeta con el radio de su órbita y con la masa del planeta atrayente:
|
|
(4) |
En este caso tomamos el radio de la órbita terrestre (1 ua) y el periodo de su órbita alrededor del sol (1 año), y la masa del Sol (1 mS), y despejamos G:
|
|
(5) |
el cual es un valor fácil de manejar, y dada su expresión es posible aprovechar al máximo la precisión de la máquina al realizar los cálculos. De hecho, el utilizar unidades convencionales conduciría el programa a errores de convergencia debido a la amplia variabilidad de escalas entre las cantidades empleadas.
2. Metodología
Considerar la aceleración instantánea como una constante (en cada punto), conduce a errores en la predicción de las trayectorias y produce un efecto de aparente ganancia de energía en cada rotación del sistema lo cual no tiene sentido dentro de un sistema conservativo como el que estamos estudiando. Para resolver el problema se debe considerar que cuando decidimos que la aceleración es constante, en realidad estamos expandiendo la función que representa este término a aproximación cero dentro de la serie de Taylor [6, 7].
En el caso de tratar con una derivada de segundo orden como es el caso de la aceleración, esta aproximación no es suficiente y se requiere de términos de orden cuadrático en la serie de Taylor. Así tenemos, para el tiempo n+1:
|
|
(6) |
Y para un tiempo n-1,
|
|
(7) |
Sumando (10) y (11) obtenemos
|
|
(8) |
y finalmente
|
|
(9) |
Este resultado, es la forma convencional de la aproximación de Verlet [3], para el cálculo de la posición de una partícula a un tiempo t en el método de la dinámica molecular y corrige el problema de convergencia para la aceleración .
La siguiente variante es conocida como "Algoritmo de Verlet con velocidades explícitas" [8, 10], o simplemente “Algoritmo de Verlet de la velocidad” el cual tiene la ventaja de permitir el cálculo de la posición y velocidad al tiempo t . Está dado de la siguiente forma:
|
|
(10) |
|
|
(11) |
y es totalmente equivalente a los resultados obtenidos por serie de Taylor. Los resultados (10) y (11) son los empleados en el programa “Planetas” para la actualización de las posiciones de los cuerpos.
3. Codificación del algoritmo
Aunque el programa es mucho más complejo, aquí se presenta la parte medular del algoritmo donde se resumen los resultados matemáticos descritos hasta ahora
for (a=0; a<5000; a++){
for (i=0; i<np; i++) {
aax[i]=ax[i];
aay[i]=ay[i];
ax[i]=0;
ay[i]=0;
for (j=0; j<np; j++)
if(i!=j){
xm = sx[i]-sx[j];
ym = sy[i]-sy[j];
modulo = pow(xm*xm+ym*ym, 1.5);
ax[i]-=m[j]*xm/modulo;
ay[i]-=m[j]*ym/modulo; // El menos es por atraccion
}
}
for (i=0; i<np; i++) {
sx[i]=sx[i]+dt*vx[i]+dt*dt*aax[i]; // Verlet Velocidad
vx[i]=vx[i]+0.5*dt*(aax[i]+ax[i]);
sy[i]=sy[i]+dt*vy[i]+dt*dt*aay[i];
vy[i]=vy[i]+0.5*dt*(aay[i]+ay[i]);
}
se observa que en cada iteración el programa calcula la aceleración del cuerpo i en ax y ay pero antes ha guardado el valor que tenía en el ciclo n-1 en la variable aax y aay. Esto es necesario para poder actualizar la posición sx, sy y la velocidad vx, vy de acuerdo a lo descrito en el apartado de Verlet. En el caso de una colisión todas estas fórmulas dejan de ser validas, por lo tanto se establece un criterio de salida de la simulación en caso de encontrarse este evento. En realidad, basta comparar la distancia del centro de los cuerpos con la mínima distancia permitida que sería la suma de los radios de los dos cuerpos interactuantes. Esto se realiza en la siguiente parte del código:
for (i=0; i<np; i++) { //Checa colision
for(j=i+1; j<np; j++){
xm = sx[i]-sx[j];
ym = sy[i]-sy[j];
modulo = pow(xm*xm+ym*ym, 0.5);
if (modulo<=(radio[i]+radio[j]))
bcolision = true;
}
}
3.1. La interfaz
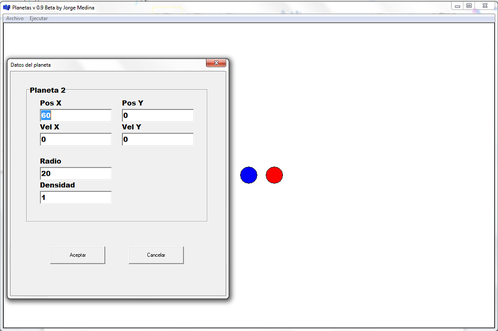
Se ha procurado que la interfaz de usuario sea tan simple como sea posible. Al iniciar el programa se observan dos círculos que representan planetas con su propia densidad, volumen, velocidad y posición inicial cada uno. A continuación se enumeran las órdenes posibles que puede realizar el programa:
- Si se desea cambiar estas propiedades para un planeta especifico basta hacer click derecho con el ratón, colocando el cursor sobre el planeta deseado y se accederá a una tarjeta como se muestra en la Figura 1.
| Figura 1. Apariencia de la interfaz para el programa de dinámica molecular clásica Planetas |
- También se puede cambiar la posición de los planetas directamente con click izquierdo sobre el planeta y click nuevamente en la posición deseada.
- Para comenzar la simulación ir al menú principal y seleccionar Ejecutar->Iniciar Simu.
- Se puede pausar y reiniciar la simulación con el comando adecuado en la sección del menú Ejecutar.
- Se puede guardar una configuración favorita desde el menú principal en Archivo-> Guardar y también se puede retomar una configuración antigua.
- Esta versión soporta un máximo de 10 planetas. Para agregar uno nuevo, hacer click derecho en cualquier parte de la interface donde no este un planeta.
4. Resultados
Se presentan los resultados de las corridas del programa para varias condiciones iniciales, los datos necesarios para generar la configuración iniciales del algunos sistemas “interesantes”, se detallan en la Tabla 1, mostrada más adelante.
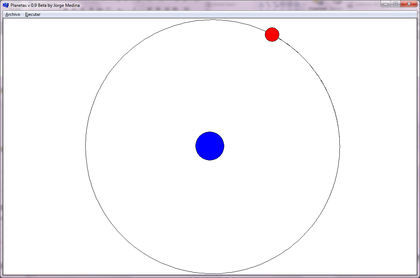
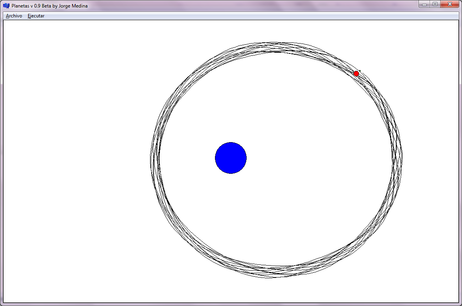
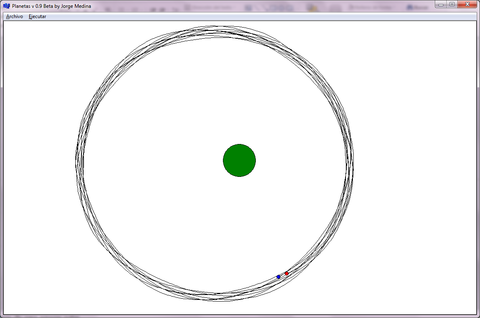
- En este primer resultado, se muestra un sistema de un planeta y su sol (masivo) alrededor del cual se mueve el planeta (Figura 2), se manejaron las masas de los objetos con sumo cuidado de tal manera que permita una órbita circular. Aún cuando en el sistema puede considerarse al sol como fijo en el espacio, dada la diferencia de masas del sistema, los tamaños de los objetos mostrados en pantalla son solo representativos y no indican la masa individual del objeto.
| Figura 2. Órbita circular: Sistema Sol-Planeta con órbita circular, datos en el inciso a) de la Tabla 1 |
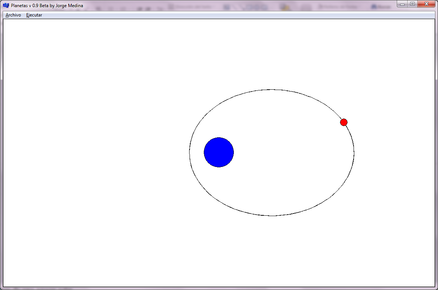
- En este segundo ejemplo, se tiene nuevamente un sistema sol-planeta (Figura 3), pero se calibraron las masas en un modo tal que permitan una órbita elíptica. Una vez más la diferencia de masas permite que el objeto que está en uno de los focos de la elipse (sol) se pueda considerar como fijo en el espacio. No se establece ninguna condición para que se fije el objeto en el espacio, solo es el resultado de la interacción gravitatoria.
| Figura 3. Órbita Elíptica: Sistema Sol-Planeta con órbita elíptica, datos en el inciso b) de la Tabla 1 |
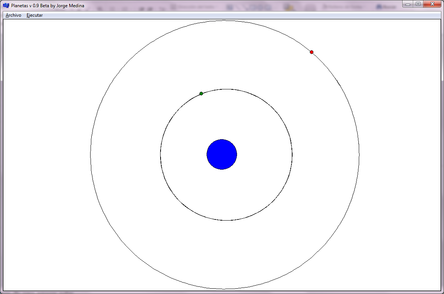
- En la tercera ejecución del programa, se muestran los resultados para un sol con dos planetas, calibrados para órbitas circulares (Figura 4). En este ejemplo se puede verificar la Tercera Ley de Kepler o ley de los períodos.
| Figura 4. Tercera Ley de Kepler: Sistema Sol con dos planetas en órbita circular, datos en el inciso c) de la Tabla 1 |
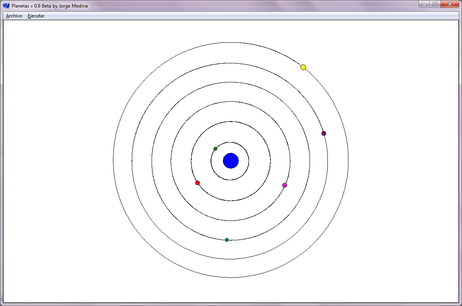
- A continuación se presenta un sistema consistente de un sol con seis planetas cuyas masas se calibran para que se generen órbitas circulares (Figura 5). Este ejemplo muestra las capacidades del programa para calcular adecuadamente la interacción de múltiples cuerpos, con un máximo de diez.
| Figura 5. Sistema Planetario: Sistema Sol con seis planetas en órbita circular, datos en el inciso d) de la Tabla 1 |
- En el siguiente resultado, se muestra una estrella con un planeta y alrededor de este un satélite, muy similar a lo que sería nuestro sistema Sol-Tierra-Luna (Figura 6). La trayectoria que se muestra es la de la luna.
| Figura 6. Sol, Tierra, Luna: Sistema Sol con planeta y satélite en órbita elíptica, datos en el inciso e) de la Tabla 1 |
- Un resultado interesante es el de un sistema binario de estrellas y un planeta girando alrededor de los mismos, como se muestra en la Figura 7. Se puede observar que el sistema se desplaza de manera estable.
| Figura 7. Sistema Binario: Sistema de soles binarios con planeta, datos en el inciso f) de la Tabla 1. |
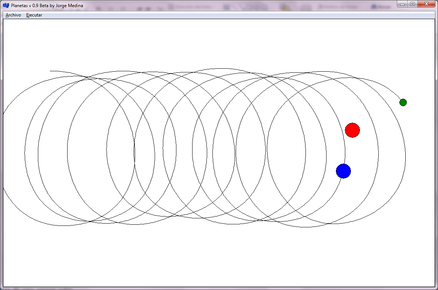
- En el siguiente sistema de tres cuerpos de masas iguales se puede observar su desplazamiento por el espacio sin colisionar entre ellos (Figura 8). Este sistema de 3 cuerpos es un buen ejemplo de sistema que sería imposible de resolver analíticamente, pero si se puede predecir su movimiento mediante simulación.
| Figura 8. Problema de 3 cuerpos: Sistema de tres objetos de masas iguales, datos en el inciso g) de la Tabla 1 |
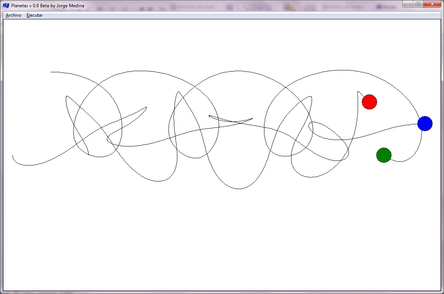
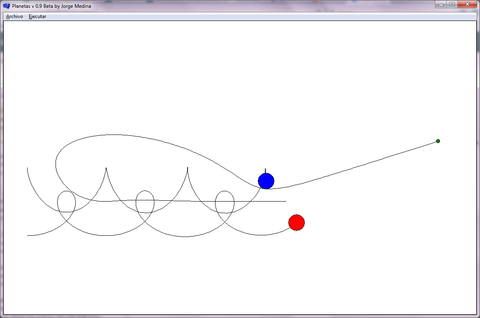
- A continuación tenemos un sistema binario interactuando con otro objeto poco masivo pero con alta velocidad que logra pasar entre estos, cambiando su trayectoria como resultado del efecto gravitacional, para posteriormente retornar y pasar nuevamente entre ellos (Figura 9).
| Figura 9. Colisión casi segura: Sistema de tres objetos de masas diferentes, datos en el inciso h) de la Tabla 1 |
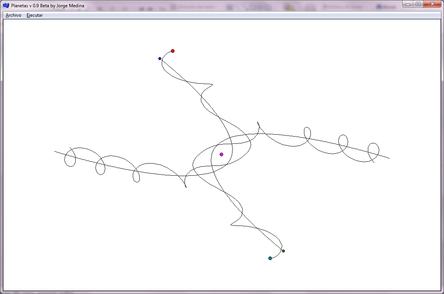
- Un resultado muy interesante que encontramos, corresponde a un sistema complejo formado por dos pares sol-planeta interactuando con otro objeto con la mitad de la masa de cualquiera de los soles, el objeto de “en medio” oscila dada la interacción con los objetos binarios (Figura 10).
| Figura 10. Sistema complejo: Sistema de dos pares de objetos binarios interactuando con otro objeto, datos en el inciso i) de la Tabla 1 |
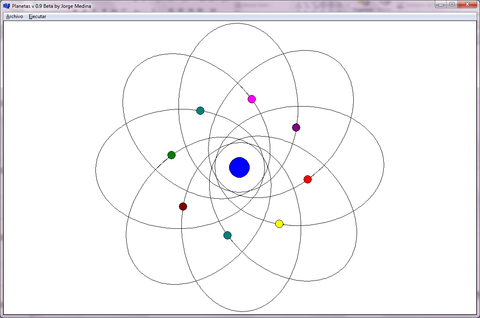
- En la Figura 11, se diseña un sistema de ocho planetas en órbitas elípticas, y se muestra que si las condiciones de simetría se presentaran en la naturaleza, el sistema podría existir, sin embargo, la menor perturbación destruye el equilibrio y los planetas terminan colisionando.
| Figura 11. Configuración atómica: Sistema de ocho objetos (planetas) interactuando con otro objeto (sol) en un símil de sistema atómico clásico, datos en el inciso j) de la Tabla 1 |
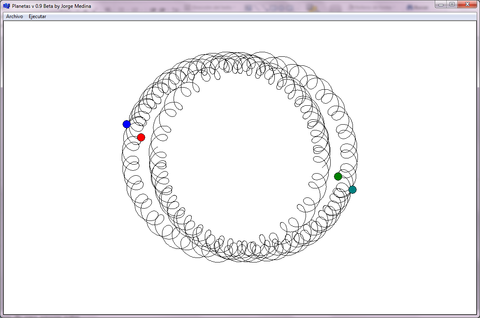
- En el ejemplo de la Figura 12, se muestran dos objetos binarios interactuando entre sí, con órbitas muy estables. Este sistema muestra que el programa puede ser utilizado para encontrar configuraciones todavía no estudiadas. Se propone el sistema como objeto de estudio de los astrónomos.
| Figura 12. Sistema binario doble: Sistema de dos pares de objetos binarios interactuando con otro objeto, datos en el inciso k) de la Tabla 1 |
- Por último, en la Figura 13 se muestra la interacción de dos objetos de masas iguales interactuando con otro muy masivo y se puede observar como las órbitas se van intercambiando pero no chocan, es decir es un sistema estable. El movimiento de los planetas recuerda al movimiento de un patinador en el hielo, de ahí el nombre que le hemos asignado al sistema.
| Figura 13. Planetas patinadores: sistema de dos objetos con masas similares interactuando con otro objeto muy masivo, datos en el inciso l) de la Tabla 1 |
| sx
(posición en x) |
sy
(posición en y) |
vx
(velocidad en x) |
vy
(velocidad en y) |
radio | densidad |
| a) Órbita Circular | |||||
| 0 | 0 | 0 | 0 | 40 | 2 |
| 360 | 0 | 0 | 33 | 5 | 0.0005 |
| b) Órbita Elíptica | |||||
| 0 | 0 | 0 | 0 | 40 | 2 |
| 360 | 0 | 0 | 20 | 5 | 0.0005 |
| c)Tercera Ley de Kepler | |||||
| 0 | 0 | 0 | 0 | 40 | 2 |
| 185 | 0 | 0 | 45 | 5 | 0.0005 |
| 360 | 0 | 0 | 33 | 5 | 0.0005 |
| d) Sistema Planetario | |||||
| 0 | 0 | 0 | 0 | 20 | 1 |
| -50 | 0 | 0 | 22 | 2 | 5x10-6 |
| 0 | 100 | 16 | 0 | 3 | 5x10-6 |
| 150 | 0 | 0 | -13 | 4 | 5x10-6 |
| 0 | -200 | -11.23 | 0 | 5 | 5x10-6 |
| -250 | 0 | 0 | 10 | 6 | 5x10-6 |
| 0 | 300 | 9.13 | 0 | 7 | 5x10-6 |
| e) Sol, Tierra, Luna | |||||
| 0 | 0 | 0 | 0 | 40 | 2 |
| 400 | 0 | 0 | 30 | 5 | 0.7 |
| 388 | 0 | 0 | 35 | 3 | 0.2 |
| f)Sistema Binario | |||||
| -550 | 0 | 0 | -5 | 20 | 1 |
| -550 | 0 | 0 | 5 | 20 | 1 |
| -450 | 218 | 15 | 0 | 10 | 1 |
| g) Problema de 3 cuerpos | |||||
| -550 | 0 | 0 | -5 | 20 | 1 |
| -350 | 0 | 0 | 5 | 20 | 1 |
| -450 | 218 | 15 | 0 | 20 | 1 |
| h)Colisión casi segura | |||||
| -517 | 0 | 0 | 0 | 20 | 1 |
| -517 | -166 | 12 | 0 | 20 | 1 |
| 112 | -82 | -5.5 | 0 | 5 | 1 |
| i) Sistema complejo | |||||
| -440 | 9 | 10 | -3 | 4 | 120 |
| -400 | 20 | 20 | -20 | 5 | 0.01 |
| 440 | -9 | -10 | 3 | 4 | 120 |
| 400 | -20 | -20 | 20 | 5 | 0.01 |
| 0 | 0 | 0 | 0 | 5 | 61.72 |
| j) Configuración atómica | |||||
| 0 | 0 | 0 | 0 | 25 | 3 |
| 200 | 0 | -20 | -20 | 10 | 1 |
| -200 | 0 | 20 | 20 | 10 | 1 |
| 0 | -200 | -20 | 20 | 10 | 1 |
| 0 | 200 | 20 | -20 | 10 | 1 |
| 141.421 | 141.421 | 0 | -28.2842 | 10 | 1 |
| 141.421 | -141.421 | -28.2842 | 0 | 10 | 1 |
| -141.421 | -141.421 | 0 | 28.2842 | 10 | 1 |
| -141.421 | 141.421 | 28.2842 | 0 | 10 | 1 |
| k) Sistema binario doble | |||||
| 200 | 50 | -5 | 3 | 10 | 1 |
| 200 | 0 | 5 | 3 | 10 | 1 |
| -200 | 50 | -5 | -3 | 10 | 1 |
| -200 | 0 | 5 | -3 | 10 | 1 |
| l) Planetas patinadores | |||||
| -400 | 0 | 0 | 20 | 5 | 0.6 |
| -380 | 0 | 0 | 25 | 5 | 0.6 |
| 0 | 0 | 0 | 0 | 40 | 1.2 |
5. Conclusiones
- Se ha creado un programa en C++ basado únicamente en las leyes de Newton y utilizando la aproximación de Verlet, el cual permite la simulación de un sistemas de n cuerpos interactuando exclusivamente a través de fuerzas gravitacionales.
- Se puede pensar en el programa como un laboratorio virtual, el cual permite confirmar leyes ya conocidas, como las de Kepler y las órbitas cónicas que caracterizan a dos cuerpos interactuando en el vacío.
- Así mismo permite el diseño y propuesta de sistemas planetarios estables, no reportados, pero que pueden existir en la naturaleza, bajo las condiciones especiales de velocidad y masa. Por ejemplo el llamado, en este trabajo, sistema binario doble o el símil de sistema atómico clásico.
- Finalmente permite la predicción cualitativa de fenómenos, que de manera analítica sería imposible predecir, como es el caso de los sistemas mostrados en las figuras 8 y 9.
- Se ha generado una carpeta en la nube de Google drive, que incluye el programa ejecutable, así como los ejemplos descritos en este trabajo para facilitar su uso. Dicha carpeta tiene la siguiente dirección electrónica:
Referencias
[1] A. Awad and A. F. Ali, Planck-scale corrections to Friedmann equation, Cent. Eur. J. Phys”, 12 (2014), 245-255.
[2] W. Dehnen and J.I. Read, N-body simulations of gravitational dynamics, Eur. Phys. J. Plus, 126, (2011) 1-28.
[3] Loup Verlet, Computer “Experiment” on Classical Fluids, I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 159, (1967), 98-103.
[4] N. A. Kaib, S. N. Raymond and M. Duncan, Planetary system disruption by Galactic perturbations to wide binary stars, Nature, 493, (2013) 381-384.
[5] R. Spurzem, M. Giersz, D. C. Heggie, and D. N. C. Lin, dynamics of planetary systems in star clusters, The Astrophysical Journal, 697 (2009) 458-482.
[6] Q. Spreiter and M. Walter, Classical Molecular Dynamics Simulation with the Velocity Verlet Algorithm at Strong External Magnetic Fields, Journal of Computational Physics , 152 (1999) 102-119.
[7] F. Renaud, P. N. Appleton, and C. K. Xu, N-body simulation of the stephan’s quintet, The Astrophysical Journal”, 724 (2010) 80-91.
[8] H. Aceves and H. Velázquez, N-body simulations of small galaxy groups, Revista Mexicana de Astronomía y Astrofísica”, 38 (2002), 199-214.
[9] R. E. Angulo and S. D. M. White, One simulation to fit them all – changing the background parameters of a cosmological N-body simulation, Mon. Not. R. Astron. Soc., 405 (2010), 143-154.
[10] V. Marry, G. Ciccotti, Trotter derived algorithms for molecular dynamics with constraints: Velocity Verlet revisited, Journal of Computational Physics, 222 (2007), 428-440.
Document information
Published on 03/01/18
Accepted on 08/05/17
Submitted on 30/03/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.6.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?