Numerical modelling of the cyclic structural behavior of slender steel members with restrained buckling

Resumen

Este trabajo presenta un modelo numérico del comportamiento estructural cíclico de barras de pandeo restringido, comúnmente utilizadas como una alternativa a las clásicas barras de arriostramiento concéntrico para protección sismorresistente de pórticos de edificios y otras estructuras. Estos dispositivos se componen normalmente de un núcleo de acero esbelto recubierto por una carcasa de mayor rigidez que tiene por objeto impedir su pandeo cuando se encuentra comprimido. La carcasa puede ser de mortero o de acero, y una interfaz de deslizamiento está interpuesta entre el núcleo y la carcasa para evitar la transferencia excesiva de tensiones tangenciales. El comportamiento del núcleo de acero se describe mediante un modelo de daño y plasticidad, el comportamiento de la carcasa de mortero se describe mediante un modelo de daño isótropo y el comportamiento de la interfaz de deslizamiento se describe mediante un modelo de penalización de contacto. Estos 3 modelos se implementan en el paquete de software Abaqus siguiendo una formulación explícita. En un artículo previo publicado en una revista de ingeniería sísmica se describió someramente el modelo, se comprobó de forma preliminar su capacidad para reproducir el comportamiento cíclico de barras de pandeo restringido y se compararon satisfactoriamente sus resultados con los de ensayos experimentales; el objetivo de este trabajo es describir el modelo en profundidad y discutir en mayor extensión las valoraciones acerca de su utilidad.

Abstract

This work presents a numerical model of the cyclic structural behavior of dissipative buckling-restrained braces, commonly used as an alternative to classical concentric braces for seismic protection of building frames and other structures. Such devices are usually composed of a slender steel core embedded in a stockiest casing that is intended to prevent its buckling when it is under compression. The casing is made either of mortar or steel, and a sliding interface is interposed between the core and the casing to prevent excessive shear stress transfer. The behavior of the steel core is described by a damage and plasticity model; the behavior of the mortar casing is described by an isotropic damage model and the sliding behavior of the interface is described by a contact penalty model. These 3 models are implemented in the Abaqus software package following an explicit formulation. In a previous article (published in an earthquake engineering journal) the model was briefly described, its ability to reproduce the cyclical behavior of buckling-restrained braces was preliminarily pointed out and their results were satisfactorily compared with those of experimental tests. The aim of this paper is to describe the model thoroughly and to present new judgments about its usefulness.

Palabras clave

Disipadores de energía ; Barras de pandeo restringido ; Control pasivo ; Simulación numérica ; Modelo de daño ; Plasticidad

Keywords

Energy dissipators ; Buckling-restrained braces ; Passive control ; Numerical simulation ; Damage model ; Plasticity

1. Introducción

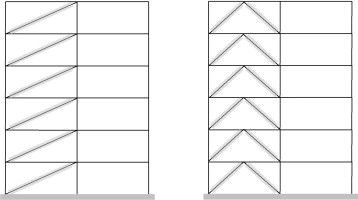
La estrategia habitual de un proyecto sismorresistente de edificios y otras construcciones consiste en dotar a sus estructuras de suficiente ductilidad como para absorber la energía aportada por el sismo de proyecto, evitando así colapsos prematuros; en otras palabras, se trata de lograr que el fallo se inicie por los elementos estructurales menos vitales (vigas y arriostramientos) y solo alcance en última instancia a las partes vitales del edificio (los pilares). Este planteamiento conduce a soluciones, en general, suficientemente seguras pero no logra evitar los daños en la estructura principal, la cual queda frecuentemente inservible; por otra parte, queda un riesgo excesivo de que sismos de intensidad superior a la prevista causen el colapso del edificio. Para superar estas limitaciones, una solución más avanzada es incorporar a la estructura elementos cuya finalidad es absorber la energía de la excitación, es decir, concentrar los daños, protegiendo así los elementos estructurales principales [1]  ;  [2] ; en otras palabras, se trata de fusibles estructurales. Los elementos incorporados se denominan disipadores de energía y son ajenos a la estructura principal; es decir, no forman parte del mecanismo resistente a acciones gravitatorias, por lo que pueden ser fácilmente sustituidos después de que movimientos sísmicos fuertes los hayan dañado. Se han propuesto distintos tipos de disipadores de energía; los basados en plastificación de metales (conocidos habitualmente como histeréticos ) son simples, económicos, robustos y suficientemente fiables. De entre los disipadores histeréticos, las barras de pandeo restringido (conocidas como “buckling restrained braces”en lengua inglesa) son unos de los tipos más utilizados, especialmente para la protección sísmica de edificios [3]  ;  [4] . Las barras de pandeo restringido son barras esbeltas de acero conectadas habitualmente a la estructura en forma de diagonales o en V invertida (fig. 1 ).

Figura 1. Barras de pandeo restringido como arriostramientos diagonales (izquierda) y en V invertida (derecha).

En la estrategia convencional de proyecto sismorresistente, las barras de arriostramiento representadas en la figura 1 se dimensionan para ser capaces de absorber las fuerzas axiales generadas en ellas por las acciones sísmicas de proyecto, habitualmente correspondientes a períodos de retorno próximos a 475 años. Esta solución, aun siendo globalmente válida, plantea diversos inconvenientes: (i) las barras de arriostramiento incrementan sensiblemente la rigidez lateral del edificio, lo cual puede generar mayores fuerzas sísmicas equivalentes por el consiguiente aumento de su período fundamental; y (ii) el nivel de amortiguamiento global del edificio no aumenta por el efecto de las barras de arriostramiento, quedando este con una ductilidad excesivamente limitada. Una alternativa más correcta consiste en dimensionar barras de arriostramiento de menor sección (o con acero de límite elástico más bajo) con la finalidad de que se plastifiquen para las acciones sísmicas de proyecto, o incluso antes. De esta manera se aporta al edificio amortiguamiento en vez de rigidez, siendo el efecto de aquel bastante más beneficioso que el de esta. En otras palabras, con movimientos sísmicos horizontales fuertes, los desplazamientos relativos entre plantas producen deformaciones axiales plásticas en estas barras, disipándose de esta forma energía.

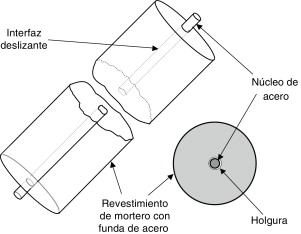
Cuando estas barras se encuentran comprimidas, su pandeo se impide rodeándolas con un revestimiento de mayor robustez, tal como se muestra en la figura 2 . Este revestimiento habitualmente es de acero [5]  ;  [6] aunque, en bastantes casos, está compuesto por elementos de acero rellenos de mortero [7] ; [8] ; [9]  ;  [10] . En dispositivos como los representados en la figura 2 , es necesario que la interfaz entre el núcleo de acero y el revestimiento de mortero permita el deslizamiento longitudinal entre ambos para impedir una transferencia excesiva de tensiones tangenciales. Por otra parte, esta interfaz debe incluir una cierta holgura para permitir la expansión transversal del núcleo durante la compresión, especialmente cuando este está plastificado.

Figura 2. Barra de pandeo restringida.

Las barras de pandeo restringido poseen ventajas relevantes en comparación con otros disipadores histeréticos. Esto ha facilitado su desarrollo: existen diversas aplicaciones [5] ; [6] ; [11]  ;  [12] y se ha desarrollado una notable actividad investigadora tanto experimental como teórica [6] ; [12] ; [13] ; [14] ; [15] ; [16] ; [17] ; [18] ; [19] ; [20] ; [21] ; [22] ; [23] ; [24] ; [25] ; [26]  ;  [27] . No obstante, algunos aspectos requieren investigación adicional. En particular, debe destacarse la ausencia de modelos numéricos precisos y fiables del comportamiento estructural de estos dispositivos. Este comportamiento es complejo ya que involucra el trabajo conjunto y no lineal de 3 materiales, existe deslizamiento parcial entre el núcleo y el revestimiento, y se producen grandes desplazamientos y deformaciones. Esta carencia obliga a que el diseño y el dimensionamiento de estos dispositivos se base en formulaciones excesivamente conservadoras y dificulta el desarrollo de soluciones innovadoras. El objetivo de este trabajo es presentar un modelo numérico del comportamiento estructural de barras de pandeo restringido. Este modelo se desarrolla en el programa de elementos finitos Abaqus siguiendo una formulación explícita [28] .

Este trabajo forma parte de un proyecto más amplio cuyo objetivo final es promover el uso masivo de barras de pandeo restringido para la protección sísmica de edificios en países en desarrollo. La investigación consta de las siguientes etapas: (i) diseñar, producir y ensayar 5 dispositivos de corta longitud (400 mm) [7]  ;  [8] ; (ii) aprovechar la experiencia adquirida para diseñar, producir y ensayar 4 dispositivos de mayor longitud (3 m) [9]  ;  [10] ; (iii) desarrollar un modelo simplificado del comportamiento a pandeo de barras de pandeo restringido [9]  ;  [10] ; (iv) desarrollar un modelo más sofisticado de este comportamiento [28]  ;  [29] ; (v) diseñar, producir y ensayar dispositivos a escala real, y (vi) llevar a cabo estudios paramétricos numéricos sobre la eficacia de estos dispositivos. Las etapas (i), (ii) y (iii) han sido completadas, la (iv) se presenta en este trabajo, y las etapas (v) y (vi) se encuentran en fase de desarrollo. La exactitud del modelo propuesto se contrastó con los resultados de la etapa (ii) y con otros resultados experimentales disponibles en la literatura técnica [29] . En este contexto, este trabajo se centra en describir con mayor detalle el modelo propuesto y en verificar exhaustivamente su capacidad para reproducir los fenómenos involucrados en el comportamiento de barras de pandeo restringido como las representadas en la figura 2 .

2. Modelización numérica de barras de pandeo restringido

El comportamiento de las barras de pandeo restringido se describe mediante un modelo numérico que representa el mortero del revestimiento, el acero del núcleo, la interfaz entre ambos y el acero de la funda exterior. El comportamiento del mortero se describe mediante un modelo isótropo de daño teniendo en cuenta que la resistencia a compresión es bastante superior a la resistencia a tracción [30] . El comportamiento del acero del núcleo se representa mediante un modelo plástico de endurecimiento cinemático e isótropo [31] ; las condiciones de agotamiento se establecen a través de un modelo de daño teniendo en cuenta que las resistencias a compresión y a tracción son iguales. El comportamiento de la interfaz entre el núcleo y el revestimiento se describe mediante un modelo de contacto de penalización [32] . El acero exterior se homogeneíza al mortero adyacente [33] . El modelo integrado resultante se implementa en el programa Abaqus [34] siguiendo una formulación explícita. El análisis considera comportamiento no lineal de los materiales; en la modelización del acero del núcleo se consideran además grandes desplazamientos y pequeñas deformaciones.

3. Modelización del mortero

Los modelos de daño describen la degradación experimentada por el material mediante una variable escalar d denominada índice de daño   y cuyos valores están entre 0 (ausencia de daño) y 1 (degradación total); este deterioro puede ser interpretado como una reducción del volumen útil del material dada por ${\textstyle {\overline {V}}=\left(1-d\right)V}$ , donde V   representa el volumen total y ${\textstyle {\overline {V}}}$ es el volumen útil, es decir, no dañado [35] ; [36] ; [37] ; [38]  ;  [39] . El coeficiente d afecta a la matriz de constantes elásticas E : ${\textstyle {\overline {\boldsymbol {\mbox{E}}}}=\left(1-d\right){\boldsymbol {E}}}$ , de tal forma que la relación constitutiva entre las tensiones σ y las deformaciones ɛ se expresa mediante la siguiente expresión tensorial:

${\boldsymbol {\sigma }}={\overline {\boldsymbol {\mbox{E}}}}:{\boldsymbol {\varepsilon }}=$$\left(1-d\right){\boldsymbol {E}}:\varepsilon =\left(1-\right.$$\left.d\right){\boldsymbol {\sigma }}_{0}$

( 1)

En esta expresión, σ₀ debe ser entendida como la tensión que correspondería a una deformación ɛ , en caso de no haber daño. La relación 1 muestra que si el modelo sin daño (σ =E :ɛ ) es isótropo, esta propiedad se mantiene en el modelo de daño.

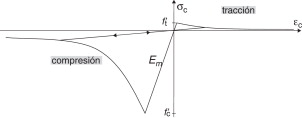
El modelo isótropo sin daño se genera a partir del comportamiento uniaxial del mortero descrito en la figura 3 .

En la figura 3 , E_m es el módulo de deformación del mortero y f  ${\textstyle {}_{c}^{'}}$ y f  ${\textstyle {}_{t}^{'}}$ son los valores característicos de sus resistencias a compresión y a tracción, respectivamente; estos valores se adoptan como resistencias en el modelo.

Figura 3. Modelo constitutivo uniaxial del mortero.

El modelo multiaxial sin daño se define a partir de la siguiente norma ψ del tensor de tensiones σ₀ :

$\psi \left({\boldsymbol {\sigma }}_{0}\right)=\left(\theta +\right.$$\left.{\frac {1-\theta }{\theta }}\right){\sqrt {{\boldsymbol {\sigma }}_{0}:{\boldsymbol {\mbox{E}}}^{-1}:{\boldsymbol {\sigma }}_{0}}}$

( 2)

En esta relación, θ es un coeficiente escalar que toma valores entre 0 en compresión triaxial y 1 en tracción triaxial:

$\theta ={\frac {{\sum }_{i=1}^{3}\left\langle {\boldsymbol {\sigma }}_{0}^{i}\right\rangle }{{\sum }_{i=1}^{3}\left|{\boldsymbol {\sigma }}_{0}^{i}\right|}}$

( 3)

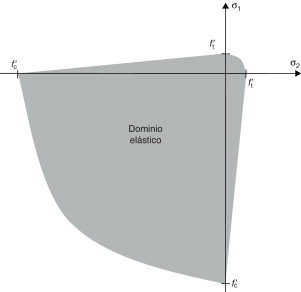
donde ${\textstyle {\boldsymbol {\sigma }}_{0}^{i}}$ es la i -ésima tensión principal considerando como positivas las tensiones de tracción [30] . La norma ψ representa, pues, una medida de la energía por unidad de volumen expresada respecto de los límites de la resistencia a tracción. La figura 4 describe, en 2 dimensiones, los límites del modelo multiaxial sin daño.

Figura 4. Modelo constitutivo biaxial del mortero.

El criterio de daño consiste en la condición F (ψ , r ) ≤ 0, donde ψ y r representan la norma y el umbral de daño en un determinado instante. Dado que la degradación del mortero es irreversible, dicho umbral debe ser igual o superior al umbral inicial de daño r₀

$F(\psi ,r)=G\left(\psi \right)-G\left(r\right)$

( 4)

En esta definición, G debe ser una función creciente que cuantifica la evolución del daño. En este trabajo se selecciona [40] :

$G\left(r\right)=1-{\frac {r}{r_{0}}}e^{A\left(1-{\frac {r}{r_{0}}}\right)}\quad \quad 0<r_{0}\leq r$

( 5)

Esta expresión muestra que ${\textstyle G\left(r_{0}\right)=0}$ y ${\textstyle {\underset {r\rightarrow \infty }{lim}}G\left(r\right)=}$$1$ . A es un parámetro adimensional que expresa la rapidez de la reducción de pendiente de las ramas de descarga de la figura 3 ; el valor de A se determina integrando en el tiempo la disipación de energía producida por el daño [41] , resultando:

$A={\left({\frac {G_{f}^{\ast }E}{l^{\ast }{f^{'}}_{t}^{2}}}-{\frac {1}{2}}\right)}^{-1}\geq 0$

( 6)

En esta expresión, ${\textstyle G_{f}^{\ast }}$ es la energía de fractura por unidad de área y l^* es una longitud característica de los elementos finitos utilizados en el análisis [42] .

La definición de la norma ψ en la ecuación ( 2 ) muestra que el umbral inicial de daño r₀ está dado por:

$r_{0}={\frac {f_{t}^{'}}{\sqrt {E}}}$

( 7)

La evolución del índice de daño d y del umbral de daño r se rige por las relaciones:

${\dot {r}}=\mu \quad \quad {\dot {d}}=\mu {\frac {\partial F}{\partial \psi }}=$$\mu {\frac {dG}{d\psi }}$

${\textstyle {\dot {\mu }}}$ es un parámetro de consistencia de daño que se utiliza para caracterizar las condiciones de carga o descarga mediante las relaciones de Kunh-Tucker:

$\mu \geq 0\quad \quad F(\psi ,r)\leq 0\quad \quad \mu F(\psi ,r)=$$0$

La integración explícita de estas relaciones proporciona los valores del índice de daño d y del umbral de daño r :

$d\left(t\right)=\int {\dot {d}}\left(t\right)dt=G\left[r\left(t\right)\right]\quad \quad r\left(t\right)=$$max\left[r_{0},r\left(s\right)\right]\quad \quad 0\leq s\leq t$

( 8)

Esta formulación se implementa en un algoritmo de cálculo iterativo paso a paso que se describe a continuación:

• Obtención de las deformaciones en el instante inicial.
• Determinación de A según la ecuación (6) .
• Inicialización r  = 0.
• Evaluación de las tensiones no dañadas σ₀  = E  : ɛ .
• Obtención de r a partir del valor máximo de la norma ψ .
• Verificar si se ha alcanzado el criterio de daño r₀  = r .
• Actualización de las variables internas ${\textstyle r=max\left[r_{0},r\left(\psi \right)\right]}$ y ${\textstyle d=G\left(r\right)}$ .
• Actualización de las tensiones ${\textstyle {\boldsymbol {\sigma }}=\left(1-d\right){\boldsymbol {\sigma }}_{0}}$ .
• Fin del cálculo.

Este algoritmo es un modelo de daño implícito que está integrado analíticamente y, por lo tanto, la solución que aquí se presenta para la evolución de la variable interna de daño contiene el criterio de convergencia fijado por el umbral de daño y las condiciones de consistencia de daño [30] .

4. Modelización del acero

4.1. Definición fenomenológica

A continuación se presenta una formulación elastoplástica con daño para representar el comportamiento del núcleo de acero de los disipadores de energía previamente descritos. La formulación está desarrollada en pequeñas deformaciones y se utiliza el contexto de una formulación en grandes desplazamientos para representar el fenómeno de inestabilidad elástica producido por la compresión que sufren estas barras. Para describir el daño se utiliza el mismo modelo que en el apartado anterior.

Hay evidencias en el comportamiento del acero que demuestran que el daño y la plasticidad actúan juntamente [31] ; sin embargo, los mecanismos de interacción entre la degradación de rigidez (daño) y las deformaciones permanentes (plasticidad) son de naturaleza muy distinta y no pueden ser simulados mediante un único modelo fenomenológico. Por esta razón se desarrolla una formulación para tratar ambos fenómenos a la vez.

Tal como se ha discutido en la descripción del modelo del mortero, el daño puede interpretarse como una reducción del área efectiva (parte no dañada del material): ${\textstyle {\overline {A}}=\left(1-d\right)A}$ representa el área útil (no dañada) y σ y ${\textstyle {\overline {\boldsymbol {\sigma }}}}$ son, respectivamente, las tensiones referidas a las áreas A   y ${\textstyle {\overline {A}}}$ ; evidentemente, ${\textstyle {\boldsymbol {\sigma }}=\left(1-d\right){\overline {\boldsymbol {\sigma }}}}$ . La reducción del área hace que el daño tienda a producir deformaciones plásticas en los metales; no obstante, no existe un “acoplamiento de estado”  sino que este se establece únicamente de forma indirecta a través de esta disminución de área.

En los metales, existe un umbral de deformación permanente (plástica) por debajo del cual no se produce daño, ya que en esta etapa la nucleación de microfisuras [31] corresponde a la acumulación de microtensiones o a dislocaciones. Por esta razón, para deformaciones inferiores a dicho umbral, se considera un modelo de plasticidad (con endurecimiento isótropo y cinemático) que comienza a actuar después de alcanzar el primer umbral de fluencia plástica definido por ${\textstyle F\left({\boldsymbol {\sigma }}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right)=}$$f\left({\boldsymbol {\sigma }}-{\boldsymbol {\eta }}\right)-$${\overline {f}}_{y}\left({\boldsymbol {\mbox{q}}}\right)\leq 0$ , donde ${\textstyle f\left({\boldsymbol {\sigma }}-{\boldsymbol {\eta }}\right)}$ es la función de tensión; η es una variable que expresa el endurecimiento plástico, es decir, la evolución de la superficie de discontinuidad plástica; ${\textstyle {\overline {f}}_{y}}$ es el límite elástico actualizado del acero; y q representa el conjunto de variables internas plásticas. El endurecimiento cinemático representa el efecto Bauschinger [43] ; este se define en forma simple en el sentido de Prager y Melan [44] como ${\textstyle {\dot {\boldsymbol {\eta }}}=c_{k}{\dot {\boldsymbol {\varepsilon }}}_{p}}$ , donde c_k es un coeficiente que cuantifica la velocidad del endurecimiento cinemático. El endurecimiento isótropo expresa la evolución de la resistencia del umbral de plasticidad a través del incremento del límite elástico del acero: ${\textstyle {\overline {f}}_{y}=f_{y}+H_{I}\left\|{\boldsymbol {\varepsilon }}_{p}\right\|}$ ; en esta expresión, H_I es el módulo de endurecimiento isótropo, f_y es el valor inicial del límite elástico del acero y ɛ_p es la deformación plástica.

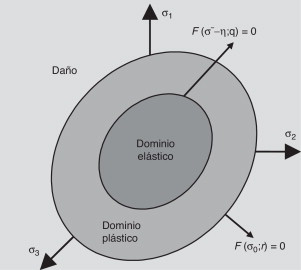
Una vez que se ha superado este primer umbral plástico, se incrementa el tamaño de la función umbral de plasticidad (manteniendo su forma) hasta alcanzar el segundo umbral establecido por el criterio ${\textstyle F(\psi ,r)=G\left(\psi \right)-G\left(r\right)\leq 0}$ (ec. 4 ). Mas allá de este umbral la plasticidad y el daño se comportan en forma acoplada; este acoplamiento se representa, a nivel constitutivo, gracias al concepto de tensión efectiva ${\textstyle {\overline {\boldsymbol {\sigma }}}}$ mencionado anteriormente. La figura 5 ilustra, en el espacio de las tensiones principales (σ₁ , σ₂ y σ₃ ), los dominios elástico, plástico y de daño del acero; estos se refieren, en el espacio de tensiones, a las regiones en que el comportamiento del material es plástico sin daño y plástico con daño, respectivamente.

Figura 5. Comportamiento de daño y plasticidad para el acero.

4.2. Modelo acoplado de daño y plasticidad

4.2.1. Introducción

Cuando se formulan modelos en los que entran en juego las leyes del daño y las leyes de endurecimiento plástico a la vez, surgen distintas posibilidades en relación con la consideración explícita del daño en la energía libre asociada al fenómeno plástico [45] ; en este trabajo se utiliza un modelo de daño y plasticidad acoplado en forma débil, en el cual la fuerza termodinámica asociada al daño es la misma que en el modelo de daño simple antes descrito, ${\textstyle f\left(\psi \right)=-{\frac {\partial \Psi }{\partial d}}}$ , y coincide con la energía libre Ψ₀ . Este enfoque consiste en considerar separadamente los dos mecanismos de daño y plasticidad y sus correspondientes funciones umbrales; se tienen entonces dos potenciales de disipación independientes y dos factores de consistencia (multiplicadores de Lagrange) independientes de plasticidad ${\textstyle {\dot {\gamma }}}$ y daño ${\textstyle {\dot {\mu }}}$ :

${\begin{array}{llll}F\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right)=f\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }}\right)-{\overline {f}}_{y}\left({\boldsymbol {\mbox{q}}}\right)\leq 0&&&{\dot {\boldsymbol {\varepsilon }}}_{p}={\dot {\gamma }}{\frac {\partial F\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right)}{\partial {\overline {\boldsymbol {\sigma }}}}}\end{array}}$

( 9)

${\begin{array}{llll}F\left({\boldsymbol {\sigma }}_{\boldsymbol {0}};r\right)=G\left[\psi \left({\boldsymbol {\sigma }}_{0}\right)\right]-G\left(r\right)\leq 0&&&{\dot {d}}={\dot {\mu }}{\frac {\partial F\left({\boldsymbol {\sigma }}_{0};r\right)}{\partial \psi }}\end{array}}$

( 10)

Este planteamiento tiene la ventaja de permitir la construcción de leyes independientes (aunque acopladas por medio del concepto de tensión efectiva) entre la plasticidad y el daño. En particular, según se regulen los umbrales de plasticidad y daño, se puede describir tanto el daño frágil (propio de materiales pétreos y cerámicos, en el que no se producen deformaciones plásticas significativas) como el daño dúctil (propio de materiales metálicos, en el que puede haber deformaciones plásticas importantes sin que se produzca daño).

4.2.2. Bases termodinámicas

El acoplamiento entre plasticidad y daño se establece definiendo la energía libre de Helmholtz mediante:

$\Psi (\epsilon ,{\sigma }_{p},{\boldsymbol {q}},d)=\left[\left(1-\right.\right.$$\left.\left.d\right){\Psi }_{0}(\epsilon )\right]-$$\left[\epsilon :{\boldsymbol {\sigma }}_{p}\right]+{\Psi }_{p}({\boldsymbol {\sigma }}_{p},{\boldsymbol {q}})$

( 11)

En esta expresión el primer sumando representa la energía del modelo con daño y los 2 sumandos siguientes corresponden a la plasticidad; Ψ_p es un potencial plástico y la energía libre sin daño Ψ₀ corresponde a:

${\Psi }_{0}({\boldsymbol {\varepsilon }})={\frac {1}{2}}{\boldsymbol {\varepsilon }}:{\boldsymbol {\mbox{E}}}:{\boldsymbol {\varepsilon }}$

( 12)

El potencial disipativo [40] se puede expresar mediante:

$\Xi ={\boldsymbol {\sigma :{\dot {\varepsilon }}-}}{\dot {\Psi }}=$${\boldsymbol {\sigma :{\dot {\varepsilon }}-}}\left(1-d\right){\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}:{\boldsymbol {{\dot {\varepsilon }}+}}{\dot {d}}{\Psi }_{0}+$${\boldsymbol {{\dot {\varepsilon }}:\sigma }}_{p}+{\boldsymbol {\varepsilon :{\dot {\sigma }}}}_{p}-$${\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\sigma }}_{\mbox{p}}}}:{\boldsymbol {{\dot {\sigma }}_{\mbox{p}}}}-$${\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\mbox{q}}}}}:{\dot {\boldsymbol {\mbox{q}}}}$ $=\left\{{\boldsymbol {\sigma -}}\left[\left(1-d\right){\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}-\right.\right.$$\left.\left.{\boldsymbol {\sigma }}_{p}\right]\right\}{\boldsymbol {:{\dot {\varepsilon }}+}}{\dot {d}}{\Psi }_{0}+$$\left[{\boldsymbol {\varepsilon -}}{\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\sigma }}_{\mbox{p}}}}\right]{\boldsymbol {:{\dot {\sigma }}}}_{p}-$${\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\mbox{q}}}}}:{\dot {\boldsymbol {\mbox{q}}}}\geq 0$

( 13)

De esta última expresión, tras aplicar las condiciones de Coleman [46] , surgen tanto las ecuaciones constitutivas secantes que describen el comportamiento del acero como las desigualdades que rigen la disipación producida por el daño y la plasticidad:

${\begin{array}{lllllll}{\boldsymbol {\sigma }}=\left(1-d\right){\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}-{\boldsymbol {\sigma }}_{p}&&{\boldsymbol {\varepsilon =}}{\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\sigma }}_{\mbox{p}}}}&&{\Xi }_{d}={\dot {d}}{\Psi }_{0}\geq 0&&{\Xi }_{p}={\frac {\partial {\Psi }_{p}}{\partial {\boldsymbol {\mbox{q}}}}}:{\dot {\boldsymbol {\mbox{q}}}}\leq 0\end{array}}$

( 14)

La variable termodinámica y conjugada de la variable de daño resulta:

$f\left(\psi \right)=-{\frac {\partial \Psi }{\partial d}}=$${\Psi }_{0}$

( 15)

4.2.3. Regla de evolución de la plasticidad

La función umbral de plasticidad en términos de las tensiones efectivas corresponde al criterio de von Mises:

$f\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }}\right)-$$f_{y}={\sqrt {{\frac {3}{2}}dev\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }}\right):dev\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }}\right)}}-$${\overline {f}}_{y}({\boldsymbol {\mbox{q}}})\leq 0$

( 16)

Utilizando la hipótesis de plasticidad asociada y la condición de consistencia plástica, se obtienen las ecuaciones que describen la evolución de la respuesta plástica en el espacio de deformaciones:

${\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\overset {\cdot }{\overline {\boldsymbol {\sigma }}}}+$${\frac {\partial f}{\partial {\boldsymbol {\eta }}}}:{\dot {\boldsymbol {\eta }}}+$${\frac {\partial f}{\partial {\boldsymbol {\mbox{q}}}}}:{\dot {\boldsymbol {\mbox{q}}}}=$$0$

( 17)

${\overset {\cdot }{\overline {\boldsymbol {\sigma }}}}={\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\varepsilon }}-$${\overset {\cdot }{\underset {p}{\overline {\boldsymbol {\sigma }}}}}=$${\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\varepsilon }}-$${\dot {\gamma }}{\frac {\partial f}{\partial {\boldsymbol {\varepsilon }}}}=$${\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\varepsilon }}-$${\dot {\gamma }}{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {\partial {\overline {\boldsymbol {\sigma }}}}{\partial {\boldsymbol {\varepsilon }}}}=$ $={\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\varepsilon }}-$${\dot {\gamma }}{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}=$${\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:\left({\dot {\varepsilon }}-\right.$$\left.{\dot {\gamma }}{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right)$

( 18)

Teniendo en cuenta la ecuación (9) , se concluye que la evolución cinemática de la superficie de discontinuidad se expresa mediante:

${\dot {\boldsymbol {\eta }}}=c_{k}{\dot {\boldsymbol {\varepsilon }}}_{p}=$${\dot {\gamma }}c_{k}{\frac {\partial F\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right)}{\partial {\overline {\boldsymbol {\sigma }}}}}=$${\dot {\gamma }}c_{k}{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}$

( 19)

En esta expresión, el coeficiente c_k se relaciona con el módulo de endurecimiento cinemático H_k mediante ${\textstyle c_{k}={\frac {2}{3}}H_{k}}$ . El vector ${\textstyle {\dot {\boldsymbol {\mbox{q}}}}}$ se relaciona con ${\textstyle {\dot {\gamma }}}$ introduciendo un vector h según:

${\dot {\boldsymbol {\mbox{q}}}}={\dot {\gamma }}{\boldsymbol {\mbox{h}}}$

( 20)

Reemplazando estos resultados de ${\textstyle {\overset {\cdot }{\overline {\boldsymbol {\sigma }}}}}$ , ${\textstyle {\dot {\boldsymbol {\eta }}}}$ y ${\textstyle {\dot {\boldsymbol {\mbox{q}}}}}$ en (17) se obtiene la derivada temporal del factor de consistencia plástica γ :

${\dot {\gamma }}={\frac {{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\boldsymbol {\varepsilon }}}}{\left({\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right)-\left(c_{k}{\frac {\partial f}{\partial {\boldsymbol {\eta }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}+{\frac {\partial f}{\partial {\boldsymbol {\mbox{q}}}}}:{\boldsymbol {\mbox{h}}}\right)}}\geq 0$

( 21)

La relación constitutiva tangente efectiva se expresa como:

${\overset {\cdot }{\overline {\boldsymbol {\sigma }}}}={\overline {\boldsymbol {\mbox{E}}}}^{T}:{\dot {\boldsymbol {\varepsilon }}}$

( 22)

El tensor constitutivo tangente resulta:

${\overline {\boldsymbol {\mbox{E}}}}^{T}={\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}-$${\frac {\left({\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right){\boldsymbol {\otimes }}\left({\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}\right)}{\left({\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right)-\left(c_{k}{\frac {\partial f}{\partial {\boldsymbol {\eta }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}+{\frac {\partial f}{\partial {\boldsymbol {\mbox{q}}}}}:{\boldsymbol {\mbox{h}}}\right)}}$

( 23)

Si se consideran modelos de plasticidad asociada este tensor es simétrico.

El límite del dominio elástico dado por la ecuación (16) , la regla de flujo dada por la ecuación (9) , la condición ${\textstyle F\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right){\dot {\gamma }}=}$$0$[46] y las relaciones ((21)  ;  (23) ) describen el comportamiento plástico del acero.

4.2.4. Tensor elastoplástico dañado tangente

El tensor constitutivo tangente obtenido en la ecuación (23) corresponde al problema elastoplástico en el espacio de tensiones efectivas; sin embargo, el acoplamiento entre daño y plasticidad exige que este tensor sea trasladado al espacio real, donde es afectado por el daño. El tensor tangente en el espacio de tensiones reales se deduce de la expresión [47] :

${\boldsymbol {\sigma }}=\left(1-d\right){\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}-$${\boldsymbol {\sigma }}_{p}=\left(1-d\right)\left({\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}-\right.$$\left.{\overline {\boldsymbol {\sigma }}}_{p}\right)=$$\left(1-d\right){\overline {\boldsymbol {\sigma }}}$

( 24)

Derivando esta relación y teniendo en cuenta la ecuación (22) se obtiene la relación constitutiva tangente

${\boldsymbol {\dot {\sigma }}}=\left(1-d\right){\overset {\cdot }{\overline {\boldsymbol {\sigma }}}}-$${\dot {d}}=\left(1-d\right){\overline {\boldsymbol {\mbox{E}}}}^{T}:{\boldsymbol {{\dot {\varepsilon }}-}}{\frac {H_{D}}{\psi }}{\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}{\dot {\boldsymbol {\varepsilon }}}:{{\overline {\boldsymbol {\sigma }}}={\boldsymbol {\mbox{E}}}}^{T}:{\dot {\boldsymbol {\varepsilon }}}$

( 25)

En esta expresión, H_D es un coeficiente que rige la evolución del daño. A partir de esta expresión se obtiene la relación entre los tensores tangentes ${\textstyle {\overline {\boldsymbol {\mbox{E}}}}^{T}}$ en el espacio de tensiones efectivas y E^T en el espacio de tensiones reales:

${\boldsymbol {\mbox{E}}}^{T}=\left(1-d\right){\overline {\boldsymbol {\mbox{E}}}}^{T}-$${\frac {H_{D}}{\psi }}\left({\overline {\boldsymbol {\sigma }}}\otimes {\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}\right)$

( 26)

En general, el tensor E^T no es simétrico, excepto en los casos de daño sin plasticidad (${\textstyle {\overline {\boldsymbol {\sigma }}}={\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}}$ , lo cual implica ${\textstyle {\overline {\boldsymbol {\sigma }}}_{p}=0}$ ) o plasticidad sin daño (plasticidad asociada y H_D  = 0).

4.2.5. Algoritmo del modelo de daño escalar acoplado con plasticidad

El procedimiento se implementa en forma desacoplada, en primer lugar el problema de daño y después el plástico, mediante un algoritmo iterativo de tipo retorno mapeado. A continuación se esquematiza este algoritmo; los índices de los procesos iterativos de daño y plástico se representan mediante n y k , respectivamente.

• Obtención del campo de deformaciones ɛⁿ .
• Predictor elástico dⁿ y umbral de daño rⁿ .
• Evaluación de la energía libre no dañada: ${\textstyle {\Psi }_{0}^{n}({\boldsymbol {\varepsilon }})={\frac {1}{2}}{\boldsymbol {\varepsilon }}^{n}:{\boldsymbol {\mbox{E}}}:{\boldsymbol {\varepsilon }}^{n}}$
• Evaluación de la norma de energía de daño: ${\textstyle {\psi }^{n}=\psi \left({\Psi }_{0}^{n}\right)}$
• Verificación del criterio de daño: si ${\textstyle F\left({\boldsymbol {\sigma }}_{\boldsymbol {0}}^{n};r^{n}\right)=}$$G\left[{\psi }^{n}\left({\boldsymbol {\sigma }}_{0}\right)\right]-$$G\left(r^{n}\right)\leq 0$ no hay evolución del daño y se continúa en la etapa 8.
• Evolución del daño. Evaluación de la variable de daño ${\textstyle d^{n}=G\left({\psi }^{n}\right)}$
• Actualización del umbral de daño: rⁿ  = ψⁿ
• Predictor elástico (k  = 0): ${\textstyle {\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{0}^{n}=}$${\overline {\boldsymbol {\sigma }}}_{p}^{n-1}$ ; ${\textstyle {\boldsymbol {\mbox{q}}}_{0}^{n}={\left({\overline {f}}_{y}\right)}_{0}^{n}=}$${\overline {f}}_{y}^{n-1}$ ; ${\textstyle {\overline {\boldsymbol {\sigma }}}_{0}^{n}={\left({\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}\right)}^{n}-}$${\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{0}^{n}$ ; ${\textstyle {\dot {\boldsymbol {\eta }}}}$${\textstyle =c_{k}{\left({\dot {\boldsymbol {\varepsilon }}}_{p}\right)}_{0}^{n}}$
• Verificación de la condición de evolución plástica: si ${\textstyle F{\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }};{\boldsymbol {\mbox{q}}}\right)}_{k}^{n}=}$$f{\left({\overline {\boldsymbol {\sigma }}}-{\boldsymbol {\eta }}\right)}_{k}^{n}-$${\left({\overline {f}}_{y}\right)}_{k}^{n}\leq 0$ no hay evolución plástica y se continúa en la etapa 14.
• Evolución del proceso plástico: k  = k  + 1, n
• Cálculo del parámetro de consistencia plástica: ${\textstyle \Delta \gamma ={\frac {{\left[{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\dot {\boldsymbol {\varepsilon }}}\right]}_{k}^{n}}{{\left[\left({\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right)-\left(c_{k}{\frac {\partial f}{\partial {\boldsymbol {\eta }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}+{\frac {\partial f}{\partial {\boldsymbol {\mbox{q}}}}}:{\boldsymbol {\mbox{h}}}\right)\right]}_{k}^{n}}}=}$${\frac {\Delta f_{k}^{n}}{{\left[\left({\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}:{\frac {{\partial }^{2}{\Psi }_{0}}{\partial {\boldsymbol {\varepsilon \otimes }}\partial {\boldsymbol {\varepsilon }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}\right)-\left(c_{k}{\frac {\partial f}{\partial {\boldsymbol {\eta }}}}:{\frac {\partial f}{\partial {\overline {\boldsymbol {\sigma }}}}}+{\frac {\partial f}{\partial {\boldsymbol {\mbox{q}}}}}:{\boldsymbol {\mbox{h}}}\right)\right]}_{k}^{n}}}$
• Actualización de las variables plásticas y de la tensión efectiva: ${\textstyle {\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{k}^{n}=}$${\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{k-1}^{n}+$$\Delta {\gamma }_{k}{\left({\frac {\partial f}{\partial {\boldsymbol {\varepsilon }}}}\right)}_{k-1}^{n}$ ; ${\textstyle {\boldsymbol {\mbox{q}}}_{k}^{n}={\boldsymbol {\mbox{q}}}_{k-1}^{n}+}$$\Delta {\gamma }_{k}\left({\boldsymbol {\mbox{h}}}\right)_{k-1}^{n}=$${\left({\overline {f}}_{y}\right)}_{k}^{n}={\overline {f}}_{y}^{0}+$$H_{p}{\boldsymbol {\overline {\varepsilon }}}_{p}$ ; ${\textstyle {\dot {\boldsymbol {\eta }}}_{k}^{n}=c_{k}{\left({\dot {\boldsymbol {\varepsilon }}}_{p}\right)}_{k}^{n}}$ ; ${\textstyle {\overline {\boldsymbol {\sigma }}}_{k}^{n}={\left({\frac {\partial {\Psi }_{0}}{\partial {\boldsymbol {\varepsilon }}}}\right)}^{n}-}$${\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{k}^{n}$
• Regresar a la etapa 9.
• Fin de la corrección plástica: ${\textstyle {\overline {\boldsymbol {\sigma }}}_{p}^{n}={\left({\overline {\boldsymbol {\sigma }}}_{p}\right)}_{k}^{n}}$ ; ${\textstyle {\boldsymbol {\mbox{q}}}^{n}={\boldsymbol {\mbox{q}}}_{k}^{n}}$ ; ${\textstyle {\overline {\boldsymbol {\sigma }}}^{n}={\overline {\boldsymbol {\sigma }}}_{k}^{n}}$ ; ${\textstyle {\boldsymbol {\sigma }}^{n}=\left(1-d\right){\overline {\boldsymbol {\sigma }}}^{n}}$
• Fin de la integración de la ecuación constitutiva.

5. Modelización de la interfaz entre el acero y el mortero

El problema de contacto entre el núcleo de acero y el mortero circundante se describe mediante un modelo de contacto de penalización [32] . La superficie de acero se considera como la penetrante, mientras que la de mortero adopta el papel de penetrada; la penetración se representa mediante una formulación de penalización interponiendo un resorte de rigidez elevada entre ambas superficies. En el correspondiente modelo de elementos finitos el contacto se establece nodo a nodo. El subsiguiente modelo de distancia mínima se resuelve minimizando la energía potencial:

$\Pi ={\frac {1}{2}}{\int }_{\Gamma }\left(k_{n}g_{n}^{2}+k_{t}g_{t}^{2}\right)dA$

( 27)

En esta ecuación, Γ es la superficie de contacto y k_n y k_t son coeficientes de penalización en dirección normal y tangencial, respectivamente. Los coeficientes escalares g_n y g_t también corresponden a dirección normal y tangencial, respectivamente, y están dados por

${\begin{array}{llll}g_{n}=\left({\boldsymbol {\mbox{x}}}_{m}-{\boldsymbol {\mbox{x}}}_{s}\right){\boldsymbol {\mbox{n}}}_{s}&&&g_{t}={\int }_{0}^{t}\left\|{\ddot {\boldsymbol {\mbox{u}}}}{\dot {\boldsymbol {\xi }}}\right\|dt\end{array}}$

( 28)

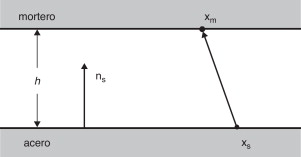
En estas expresiones, x_m y x_s son, respectivamente, las coordenadas de los puntos de mortero y de acero, n_s es el vector unitario normal a la superficie penetrante (de acero), u es el desplazamiento tangencial relativo del punto del acero y ξ es la coordenada convectiva. La figura 6 describe los significados de estas magnitudes.

Figura 6. Contacto entre mortero y acero.

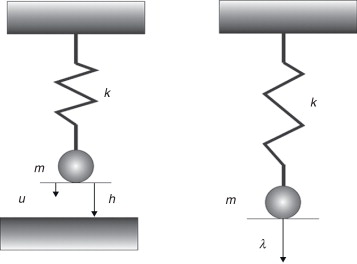
El modelo de penalización considerado se describe para una dimensión en la figura 7 .

Figura 7. Modelo unidimensional de penalización.

En la figura 7 , k es la rigidez del muelle que representa a las superficies en contacto, h es la separación entre las superficies ( fig. 6 ), u es el desplazamiento del nodo en dirección normal a la superficie y m es la masa correspondiente al nodo.

A la energía dada en la relación (27) se añade un término de penalización:

$\Pi \left(u\right)={\frac {1}{2}}ku^{2}-mgu+{\frac {1}{2}}k_{\epsilon }{\left(h-u\right)}^{2}$

( 29)

En esta expresión, g es la aceleración de la gravedad y k_ϵ es interpretado como la rigidez del muelle de la superficie de contacto (parámetro de penalización) que rige la penetración. La minimización de la energía expresada en la ecuación (29) proporciona el valor de u y, a partir de este, se determina inmediatamente la restricción h  − u :

$h-u={\frac {kh-mg}{k+k_{\epsilon }}}$

( 30)

Si h  − u  < 0 se produce penetración. La fuerza normal entre ambas superficies p_n está dada por

$p_{n}={\frac {k_{\epsilon }}{k+k_{\epsilon }}}\left(kh-\right.$$\left.mg\right)$

( 31)

El problema de contacto está gobernado por las conocidas condiciones de Herz-Signori-Moreau [33] :

${\begin{array}{lllllll}g_{n}\geq 0&&&p_{n}\leq 0&&&g_{n}p_{n}=0\end{array}}$

( 32)

En las relaciones (32) la primera desigualdad expresa la imposibilidad de penetración y la segunda indica que la fuerza normal entre ambas superficies no puede ser positiva (es decir, solo puede haber compresión) y la igualdad impone que o bien g_n  = 0 (contacto), o bien p_n  = 0 (separación).

En la formulación considerada se toman, en la expresión 27 , dos valores k_ϵT y k_ϵN que representan la penalización del contacto tangencial y normal a la superficie, respectivamente.

A continuación se describe la implementación del algoritmo resultante.

• Definición de los coeficientes k_ϵT y k_ϵN de penalización del contacto tangencial y normal.
• Determinar si hay contacto (g_n  = 0) o penetración (g_n  < 0).
• En caso de haber contacto, utilizar las condiciones de Herz-Signori-Moreau (32) para establecer si se da bloqueo o deslizamiento.
• Ensamblar la matriz tangente K_T .
• Obtener iterativamente K_T mediante el método de Newton-Raphson.
• Fin del proceso de cálculo.

6. Modelo integrado de las barras de pandeo restringido

6.1. Modelo integrado

Los modelos del mortero, del acero y del contacto descritos en los 3 apartados anteriores se implementan conjuntamente en el programa Abaqus [34] . El subsiguiente problema dinámico se resuelve numéricamente siguiendo una formulación explícita; esta se elige porque la matriz de rigidez está mal condicionada a causa del modelo de contacto de penalización. La integración de los modelos del mortero, del acero y del contacto se lleva a cabo imponiendo una condición de balance energético; para este fin el tensor de velocidades de deformación ${\textstyle {\dot {\boldsymbol {\varepsilon }}}}$ se descompone según ${\textstyle {\boldsymbol {{\dot {\varepsilon }}={\dot {\varepsilon }}}}_{e}+}$${\dot {\boldsymbol {\varepsilon }}}_{p}+{\dot {\boldsymbol {\varepsilon }}}_{d}$ , donde ɛ_d corresponde a la deformación recuperable de daño. El cumplimiento de esta condición garantiza la integración de los modelos en un modelo conjunto capaz de describir el comportamiento dinámico de barras de pandeo restringido.

6.2. Comprobación del modelo integrado de las barras de pandeo restringido

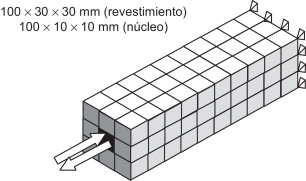
Se verifica la capacidad del modelo para reproducir el comportamiento cíclico de barras de pandeo restringido mediante el ejemplo mostrado en la figura 8 .

Figura 8. Ejemplo simplificado de barra de pandeo restringido.

La figura 8 representa una barra de pandeo restringido formada por un núcleo de acero de 100 mm de longitud y sección cuadrada de 10 mm de lado rodeada por un revestimiento de mortero de 100 mm de longitud y sección cuadrada de 30 mm de lado; las condiciones de borde indicadas (empotramiento y extremo libre) podrían corresponder a la mitad de la longitud de una barra articulada en sus extremos. Se muestra la discretización mediante elementos finitos paralelepipédicos lagrangianos de 8 nodos, cada elemento es un cubo de 10 mm de lado; para la adecuada representación del contacto entre el acero y el mortero se ha procurado que este se establezca nodo a nodo. La interfaz deslizante entre el núcleo de acero y el revestimiento de mortero consiste meramente en una holgura de 0,12 mm de espesor. El acero es S275, es decir, el tipo utilizado más comunmente en la construcción en Europa; el peso específico es 78,5 kN/m³ , el límite elástico es f_y  = 275 MPa, la resistencia última es f_u  = 410 MPa, el módulo de Young es E_s  = 210 GPa, el coeficiente de Poisson es ν  = 0,2, el módulo de endurecimiento cinemático se ha tomado como H_k  = 21 GPa y la energía de fractura por unidad de superficie se considera igual a ${\textstyle G_{f}^{\ast }=68,5}$ MPa. Para el mortero se consideran los siguientes parámetros mecánicos: peso específico 27,5 kN/m³ , resistencia a compresión ${\textstyle f_{c}^{'}=39,92}$ MPa, resistencia a tracción ${\textstyle f_{c}^{'}=3,99}$ MPa, módulo de deformación elástica E_m  = 17,52 GPa, coeficiente de Poisson ν  = 0,2 y energía de fractura por unidad de superficie ${\textstyle G_{f}^{\ast }=104}$ Pa. En el modelo de contacto el coeficiente de rozamiento es k  = 0,1, la direccionalidad es isótropa y no hay límite en la transferencia de tensiones tangenciales.

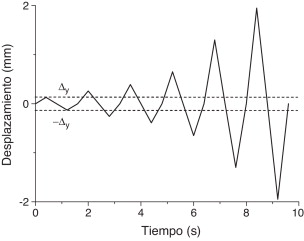
La figura 9 describe el movimiento axial impuesto al núcleo; este se somete a 6 ciclos triangulares simétricos cuyas amplitudes son, respectivamente, Δ_y , 2Δ_y , 3Δ_y , 5Δ_y , 10Δ_y y 15Δ_y ; siendo Δ_y el desplazamiento que genera plastificación del núcleo, que viene dado por ${\textstyle {\Delta }_{y}={\frac {f_{y}L}{E_{s}}}={\frac {275\times 100}{210000}}=}$$0,13$ mm. La amplitud máxima (15Δ_y ) se elige para generar los fenómenos que se desea reproducir: plastificación del acero, transferencia de tensiones tangenciales entre el núcleo y el revestimiento, daño en el mortero y daño en el núcleo.

Figura 9. Movimiento axial impuesto.

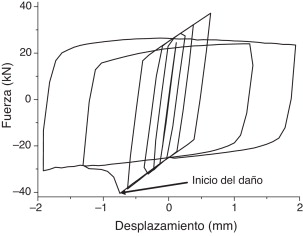
La figura 10 representa los ciclos de histéresis, es decir, diagramas de la fuerza y del desplazamiento axiales en el núcleo. Los valores positivos de fuerza y de desplazamiento corresponden a tracción y a alargamiento, respectivamente.

Figura 10. Ciclos de histéresis del modelo de la barra de pandeo restringido.

Aparte de la obvia constatación de la plastificación del acero, la figura 10 pone de manifiesto la capacidad del modelo propuesto para reproducir los fenómenos implicados en el problema considerado:

• Ya que los ciclos impuestos son simétricos (fig. 9 ), las diferencias entre las fuerzas de tracción (positivas) y de compresión (negativas) señalan la transferencia de tensiones tangenciales entre el núcleo de acero y el revestimiento de mortero generada por el bloqueo en el contacto entre ambos. Por ejemplo, en la esquina superior derecha de la rama plástica inicial el desplazamiento es 0,637 mm y la fuerza es 36,98 kN, mientras que en el punto opuesto el desplazamiento es −0,623 mm y la fuerza es −38,60 kN.
• La inclinación de las ramas plásticas de los ciclos iniciales (de pequeña amplitud) indica el endurecimiento isótropo.
• El crecimiento de las ramas plásticas de los ciclos finales (de mayor amplitud) indica el endurecimiento cinemático.
• La rama plástica decreciente (en la zona de compresiones) corresponde al daño en el acero del núcleo.

En la referencia [28] se presentan más verificaciones de la capacidad del modelo, incluyendo comparaciones con resultados experimentales.

7. Conclusiones

Este trabajo presenta un modelo numérico del comportamiento estructural cíclico de barras de pandeo restringido constituidas por un núcleo de acero esbelto recubierto por una carcasa de mortero de mayor rigidez que tiene por objeto impedir su pandeo cuando se encuentra comprimido. El comportamiento del núcleo de acero se describe mediante un modelo original que considera el acoplamiento débil entre el daño y la plasticidad, el comportamiento de la carcasa de mortero se describe mediante un modelo de daño isótropo, y el comportamiento de la interfaz de deslizamiento se describe mediante un modelo de penalización de contacto.

Se presentan resultados del modelo integrado de las barras de pandeo restringido; obviamente, ello involucra a los modelos del mortero, del acero y de la interfaz deslizante. Estos resultados ponen de manifiesto la capacidad del modelo para reproducir los fenómenos implicados en el comportamiento no lineal de barras de pandeo restringido: (i) plastificación y endurecimiento isótropo y cinemático del acero del núcleo; (ii) pandeo del núcleo expresado mediante transferencia de tensiones tangenciales entre el núcleo de acero y el revestimiento de mortero generada por el bloqueo en el contacto entre ambos, (iii) daño en el acero del núcleo. Esta constatación se completa en otro artículo (publicado en una revista de ingeniería sísmica) con la comparación satisfactoria entre los resultados experimentales y los resultados numéricos obtenidos con el modelo presentado.

Agradecimientos

Este trabajo ha sido financiado por el gobierno de España, proyectos CGL2008-00869/BTE, CGL2011-23621, BIA2008-00050 y BIA2011-26816 y por la Unión Europea (fondos Feder).

References

1. [1] G.W. Housner, L.A. Bergman, T.K. Caughey, A.G. Chassiakos, R.O. Claus, S.F. Masri, R.E. Skelton, T.T. Soong, B.F. Spencer, J.T.P. Yao; Structural control: Past, present and future; J Eng Mech-Asce, 123 (2) (1997), pp. 897–971
2. [2] T. Soong, G. Dargush; Passive energy Dissipation Systems in Structural Engineering; John Wiley, Chichester (1997)
3. [3] P. Clark, I. Aiken, K. Kasai, E. Ko, I. Kimura; Design procedures for buildings incorporating hysteretic damping devices; Proceedings of the 68th Annual Convention, Structural Engineers Association of California, Sacramento (1999), pp. 355–371
4. [4] Watanabe A, Hitomi Y, Saeki E, Wada A, Fujimoto M. Properties of Brace Encased in Buckling-Restraining Concrete and Steel Tube, Proceedings of the Ninth World Conference on Earthquake Engineering, Japan Association for Earthquake Disaster Prevention, Tokyo-Kyoto. Japan. IV. 1988 719-724.
5. [5] Iwata M.;1; (2004) Applications-design of buckling-restrained braces in Japan, 13th World Conference on Earthquake Engineering, Paper No. 3208, Vancouver Canada.
6. [6] Tsai KC, Lai JW, Hwang YC, Lin SL, Weng CH. Research and application of double-core buckling-restrained braces in Taiwan, 13th World Conference on Earthquake Engineering, Paper No. 2179 Vancouver Canada. 2004.
7. [7] G. Palazzo, F. Crisafulli, F. López Almansa, X. Cahís; Análisis numérico experimental de barras de pandeo restringido; XIX Jornadas Argentinas de Ingeniería Estructural, Mar del Plata Argentina (2006)
8. [8] G. Palazzo, F. Crisafulli; Estudio comparativo de distintos disipadores por fluencia en base a los requerimientos establecidos en distintas normas; XXXI Jornadas Sud-Americanas de Ingeniería Estructural, Mendoza, Argentina (2004)
9. [9] G. Palazzo, F. López-Almansa, X. Cahís, F. Crisafulli; A low-tech dissipative buckling-restrained brace, Design, analysis, production and testing; Eng Struct., 31 (2009), pp. 2152–2161
10. [10] G. Palazzo, F. López-Almansa, X. Cahís, F. Crisafulli; Theoretical and experimental analysis of dissipative buckling restrained braces; CIMNE Monograph Report IS-64 (2011)
11. [11] R. Tremblay, G. Degrange, J. Blouin; Seismic rehabilitation of a four-storey building with a stiffened bracing system; 8th Canadian Conference on Earthquake Engineering, Canadian Association for Earthquake Engineering Vancouver (1999), pp. 549–554
12. [12] C. Black, N. Makris, L. Aiken; Component testing, seismic evaluation and characterization of buckling-restrained braces; J Struct Eng-Asce, 130 (2004), pp. 329–337
13. [13] W.A. López, D.S. Gwie, T.W. Lauck, M. Saunders; Structural design and experimental verification of a buckling-restrained braced frame system; Eng J-Canada, 41 (4) (2004), pp. 177–186
14. [14] R. Tremblay, P. Bolduc, R. Neville, R. De Vall; Seismic testing and performance of buckling-restrained bracing systems; Can J Civil Eng, 33 (2006), pp. 183–198
15. [15] R. Tremblay, M. Lacerte, C. Christopoulos; Seismic response of multi-storey buildings with self-centering energy dissipative steel braces; J Struct Eng-Asce, 134 (2008), pp. 108–120
16. [16] Wada A, Nakashima M. From infancy to maturity of buckling-restrained braces research, 13th World Conference on Earthquake Engineering, Paper No. 1732 Vancouver Canada. 2004.
17. [17] K. Lee, M. Bruneau; Energy dissipation of compression members in concentrically braced frames: review of experimental data; J Struct Eng-Asce, 131 (2005), pp. 552–559
18. [18] M. D’Aniello, G. Della Corte, F.M. Mazzolani, R. Landolfo; Steel buckling-restrained braces; en: Seismic Upgrading of RC Buildings by Advanced Techniques - The ILVA-IDEM Research Project, Polimetrica Publisher, Italy (2006), pp. 179–223
19. [19] Kasai K, Kibayashi M. JSSI manual for building passive control technology, PART-1 Manual contents and design/analysis methods, 13th World Conference on Earthquake Engineering, Paper No. 2989, Vancouver Canada. 2004.
20. [20] Kibayashi M, Kasai K, Tsuji Y, Kikuchi M, Kimura Y, Kobayashi T, Nakamura H, Matsuba Y. JSSI manual for building passive control technology, PART-2 Criteria for implementation of energy dissipation devices, 13th World Conference on Earthquake Engineering, Paper No. 2990, Vancouver Canada. 2004.
21. [21] Sabelli R, Aiken I. US building-code provisions for buckling-restrained braced frames: basis and development, 13th World Conference on Earthquake Engineering, Paper No. 1828 Vancouver Canada. 2004.
22. [22] Sabelli R, Mahin S, Chang C.;1; (2002) Seismic demands on steel braced frame buildings with buckling-restrained braces. Earthquake Engineering Research Center. University of California [accessed Mar 2014]. Disponible en: http://nisee.berkeley.edu/library.
23. [23] R. Sabelli, S.A. Mahin, C. Chang; Seismic demands on steel braced-frame buildings with buckling-restrained braces; Eng Struct, 25 (2003), pp. 655–666
24. [24] R. Sabelli, W. Pottebaum, J.C. Brazier, W. López; Design of a buckling-restrained braced frame utilizing 2005 seismic standards. Metropolis & Beyond 2005; Proceedings of the 2005 Structures Congress and the 2005 Forensic Engineering Symposium, New York (2005)
25. [25] Fahnestock LA, Sause R, Ricles JM.;1; (2004) Seismic analysis and design of buckling-restrained braced frames. 5th International PhD Symposium in Civil Engineering, Taylor & Francis, Delft (The Netherlands).
26. [26] M. Astrella, A. Whittaker; The perfomance-based design paradigm; MCERR Report MCEER-05-0011 (2005)
27. [27] H. Choi, J. Kim; Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum; Eng Struct, 28 (2006), pp. 304–311
28. [28] JC. Castro;1; (2011) Numerical modelling of the structural behaviour of buckling-restrained braces (in Spanish), Doctoral dissertation, Technical University of Catalonia, Barcelona (Spain).
29. [29] F. López Almansa, J.C. Castro-Medina, S. Oller; A numerical model of the structural behavior of buckling-restrained braces; Eng Struct, 41 (2012), pp. 108–117
30. [30] J. Oliver, M. Cervera, S. Oller, J. Lubliner; Isotropic damage models and smeared crack analysis of concrete,; Second international conference on computer aided analysis and design of concrete structures,, 2 (1990), pp. 945–958
31. [31] F. Armero, S. Oller S, A; A general framework for continuum damage models. I. Infinitesimal plastic damage models in stress space. II. Integration algorithms, with application to the numerical simulation of porous metals; Int J Solids Struct (2000) 37:7409-7436 (I) 7437-7464 (II)
32. [32] P. Wriggers; Computational contact mechanics; Springer, Verlag (2006)
33. [33] E. Car, S. Oller, E. Oñate; A large strain plasticity model for anisotropic materials - composite material application; Int J Plasticity, 17 (2001), pp. 1437–1463
34. [34] ABAQUS analysis users manual version 6.6, Hibbitt, Karlsson & Sorensen, Inc., Pawtucket, RI, 2006.
35. [35] J. Lemaitre; A course on damage mechanics,; Springer-Verlag, Berlin, Heidelberg, Germany (1992)
36. [36] K. Runesson, P. Steinmann, R. Larsson; On localization in thermo-elastoplastic solids subjected to adiabatic conditions; Eur J Mech A-Solid, 18 (4) (1999), pp. 557–579
37. [37] Lemaitre J, Chaboche JL. Mechanics of solid materials (Trans. B. Shrivastava), Cambridge University Press, Cambridge, UK. 1990.
38. [38] J.G. Williams, H. Hadavinia; Analytical solutions for cohesive zone models; J Mech Phys Solids., 50 (2002), pp. 809–825
39. [39] B. Luccioni, S. Oller; A directional damage model, Comput. Methods. Appl; Mech. Engrg, 192 (2003), pp. 1119–1145
40. [40] J. Lubliner; Plasticity theory; McMillan, London (1990)
41. [41] J.C. Simo, J.W. Ju; Strain and stress-based continuum damage models. I. Formulation; Int J Solids Struct, 23 (7) (1987), pp. 821–840
42. [42] J. Oliver; A Consistent characteristic length for smeared cracking models; Int J Numer Meth Eng, 218 (1989), pp. 461–474
43. [43] N. Ohno, J. Wang; Kinematic hardening rules with critical state of dynamic reovery, Part I: Formulation and basic features for ratcheting behavior; Int J Plasticity, 9 (1993), pp. 375–390
44. [44] J.L. Chaboche; On the constitutive equations of materials under monotonic or cyclic loading; Rech. Aéros (1983), pp. 1983–1985
45. [45] B. Luccioni, S. Oller, R. Danesi; Coupled Plastic-Damage Model; Comput Method Appl M, 129 (1-2) (1996), pp. 81–90 ISSN: 0045-7825
46. [46] J. Lubliner, J. Oliver, S. Oller, E. Oñate; A plastic damage model for concrete,; Int J Solids Struct, 25 (3) (1989), pp. 299–326
47. [47] Oller S., Oliver J., Cervera M., Oñate E.;1; (1990) Simulación del procesos de localización en mecánica de sólidos mediante un modelo plástico. I Congreso Español de Métodos Numéricos. en: E. Oñate (Ed.), Canarias, España. Pub. CIMNE, Gran Canaria, España.1990 pp. 423-431. ISBN: 404-7042-8.