Abstract
Structural fire resistance, as integral part of structural design, is determined by testing or by calculations. This paper is focused on statically indeterminate structures where thermal expansion is restrained and significant internal forces occur in the structure leading to possible plasticization and subsequent redistribution of internal forces. In this paper different approaches of fire resistance testing are described, together with brief description of two experiments focussed on verification of behaviour of a statically indeterminate steel frame exposed to high temperature which were carried out at VŠB-TU Ostrava. The paper is complemented with calculation of steel and concrete simple frame structure exposed to elevated temperature.
Keywords
Fire resistance ; Fire loading ; Testing ; Indeterminate structure ; Plastic hinges
Introduction
Fire resistance analysis is becoming the integral part of structural design. Fire resistance is determined by testing or by calculation, using, e.g. European standards, Eurocodes. Testing and consequently calculation of the fire resistance is explored more for the statically determinate structural elements than for the complex often statically indeterminate structure as a whole. Prediction of the behaviour of indeterminate structure is complicated due to internal forces caused by restriction of thermal expansion. In general it is supposed that significant internal forces are leading to local plasticization and subsequent redistribution of internal forces.
Fire resistance testing
Testing in accredited laboratory
In Czech Republic there is one accredited laboratory for fire resistance testing and it is located in Veseli nad Luznici. Laboratory provides testing of both vertical and horizontal structures according to criteria of resistance R , entirety E , insulation I and smoke protection S . It is possible to control the growth of the temperature and to measure the temperatures on unexposed side of the structure, exceptionally also within the cross-section of the structure. Structural elements, e.g. precast panel or column, are exposed both to thermal and mechanical load. Criterion for fire resistance according to load bearing capacity is limit deflection or limit growth of deflection. However arrangement of the laboratory allows only testing of particular structural elements, Fig. 1 a. As this testing is very expensive it is common to examine a few, sometimes only two specimens, which do not allow perform statistical analysis, nevertheless measured temperatures and deformations are very valuable for fire resistance calculations ( Bradacova and Kucera, 2013 , Cajka and Mateckova, 2013 , Cajka and Mateckova, 2010 , Kralik, 2014 and Kucera et al., 2014 ). Experiments with several similar structural elements provide concept of expected behaviour of this structural element type exposed to fire and are utilized as a basis for tables which allow operative fire resistance determination on safe side.
|
|
|
Figure 1. (a) Accredited laboratory, Veseli nad Luznici, (b) fire in simple building, Veseli nad Luznici. |
Testing of simple buildings
Mechanical behaviour of structural element could vary from behaviour of the real structure that is why experiments of fire in simple building are also performed. In the literature it is possible to find the conclusions from several years testing in Cardington. Czech Technical University in Prague also organised experimental fire in buildings in 2008 in Mokrsko and 2011 in Veseli nad Luznici, Fig. 1 b. Experiments are described and analysed in series of papers, they were focused mainly on advanced analysis of steel and steel concrete structures (Pultar et al., 2010 ). As the experiments in real buildings are technically and financially demanding they are still only sporadic.
Testing at VSB – technical university
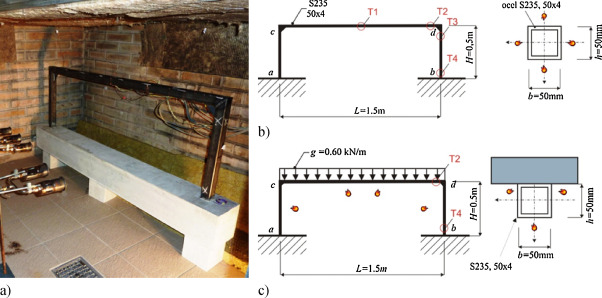
Authors are interested in statically indeterminate structures exposed to fire. It is generally assumed that significant internal forces caused by cross-section warming lead to plasticization and redistribution of internal forces. This assumption is not possible to prove with experiments in accredited laboratory and was proved only indirectly with the experiments in real buildings. The idea than was to carry out experiment with the structure which is not space demanding but which includes fixed supports. The experiment was carried out in thermal technical chamber at Faculty of Safety Engineering, Fig. 2 a. In pilot program in 2012 and 2013 there were two specimens tested (frame 1 and frame 2, Fig. 2 b and c, first exposed only to thermal load, second exposed both to thermal and mechanical load (Lausova et al., 2015 and Lausova et al., 2014 ).
|
|
|
Figure 2. (a) Testing of steel frame in 2012, (b) Static schema of tested structure, frame 1, (c) static schema, frame 2. |
Description of the experiment
Both tested models were made of the same hollow rectangular steel profile 50/4, material Fe360/S235, bottom frame girder was surrounded with concrete. The frame spans were 1.5 m, the height 0.5 m. The static schemes of both models are seen on the Fig. 2 b and c. Within the experiments temperatures and also strains were measured.
The temperatures were scanned on the selected points of the frame and in chamber space as well, using K-type sheathed thermometers with 1 mm diameter.
In the frame 1 strains were measured in points T1–T4 according to Fig. 2 b by four strain gauges 1-XC11-3/350 m intended for testing up to 350 °C. The strain gauges were placed on the internal sides of the frame. In the frame 2 the strain was scanned by four special strain gauges LZE-NC-W250G-120/2M, which are intended for measurement of strain up to 1200 °C. These strain gauges were attached to the structure at two places T2 and T4 acc. to Fig. 2 c, always in pairs in perpendicular direction on the internal sides of the frame. Mechanical load of the frame 2 was provided with concrete beam (g = 0.6 kN m−1 ) and was placed in a way to avoid the beam and frame interaction.
Evaluation of the experiment
Gas temperature and temperatures of selected places on the frame were evaluated in (Lausova et al., 2015 ). During the experiment an approximate uniform temperature distribution was obtained over the structures of the frame 1 and frame 2. There could be seen slowing the temperature rise in the steel section compared with the gas temperature. The temperature in the upper side of the frame beam was lower than in other measured places on the frame 2, which was intentionally caused by thermal loss on upper surface of the cross section into the relatively colder concrete beam.
All the obtained values of strain from the experiment were compared with the strains calculated using the finite element method in the ANSYS software environment in the thermal and structural analysis. The frame 1 was evaluated up to 300 °C, the frame 2 up to 700 °C upon physical and geometrical nonlinear solution. Complex strain evaluation exceeds the range of this paper, more details in the paper (Lausova et al., 2015 ).
Fire resistance calculation
Steel frame structure
In this part steel frame structures from testing are analysed, using the mechanical material properties and their temperature dependences on the basis of Eurocodes. The yield stress is reduced at high temperatures above 400 °C, and the internal forces decrease through reduced modulus of elasticity at elevated temperature above 200 °C. The calculation procedure of both frame 1 and frame 2 are described in detail in Lausova et al. (2015) .
Frame 1
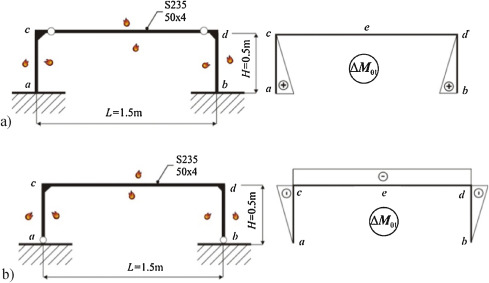
There was chosen the method of the gradual insertion of plastic hinges described in Teply and Smirak (2000) because of transient analysis variable in time. There were two possible cross sections formation of plastic hinges on the frame, inner fibres of frame corner, Fig. 3 a, option 1, and external fibres in place of restraints, Fig. 3 b, option 2.
|
|
|
Figure 3. Formation of plastic hinges – (a) option 1, (b) option 2. |
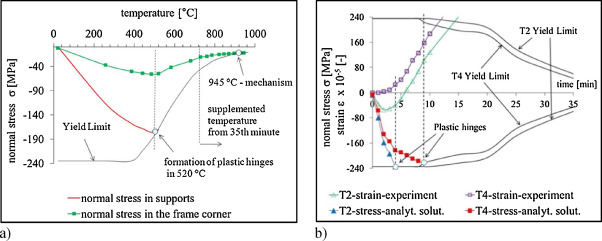
In the graph Fig. 4 a there is the curve of decreasing yield stress as a function of temperature and calculated normal stresses in frame structure caused by structural uniform temperature due to restriction of deformation. Without considering plastic behaviour of material the structure would lose its carrying capacity in supports at 520 °C, it is in the 25th minute of the experiment, 8 min according to ISO-834. Mechanism at the structure would become at 945 °C. This temperature was not reached within the experiment and it is equivalent to 53 min of fire according to ISO-834.
|
|
|
Figure 4. Generation of plastic hinges in time of the experiment: (a) frame 1, (b) frame 2. |
Frame 2
In the frame 2 except of bending moments and normal forces due to uniform temperature also bending moments arise due to non-uniform temperature on frame beam. The course is variable and depends on the temperature difference in the upper and lower fibres and also on the proportion of uniform temperature.
In the frame 2, in the beginning of the experiment, the impact of non-uniform warming in the cross-section and at the same time the relatively low overall temperature may decide on further course of deformation and consequently the stress. In the following minutes with increasing temperature the proportion of uneven temperature distribution loses its importance and also Youngs modulus decreases, and thus the normal stress decreases. Considering the influence of physical non-linearity bearing capacity of the structure would lose in the 4th minute at the frame corner, acc. Fig. 3 a, option 1. Using plastic behaviour should prolong carrying capacity to fire duration of 10 min. If, in the 4th minute, the difference in temperature of the upper and bottom fibres were lower (not much), the formation of plastic hinges at this point would not happen and the static state of the frame would follow option 2, Fig. 3 b. The results of formation plastic hinges on the frame 1 and frame 2 can be seen in the graphs Fig. 4 a and b.
Concrete frame structure
In this part the principle of plasticization and generation of plastic hinges is used for statically similar structure made of reinforced concrete. As the bottom part of the structure is not insulated it is supposed that deformation of bottom and ceiling part is similar and the additional thermal internal forces are supposed to be generated mainly from uneven warming of the cross-section.
Description
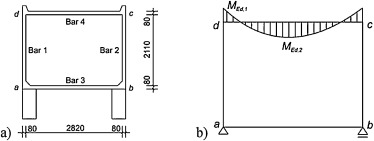
Precast reinforced concrete plate-wall structure of garage with the width 3.0 m, height 2.3 m and the length 6.0 m, Fig. 5 a, is considered as closed frame, Fig. 5 b exposed to self-weight, the car on the bottom, snow on the ceiling and wind on walls of the frame. The thickness of the slab and wall is 80 mm. Object has not been tested.
|
|
|
Figure 5. (a) Precast reinforced concrete plate-wall structure, (b) static scheme and bending moment on ceiling part. |
Permanent design situation
Extreme bending moment from action effect in the ceiling part in frame corner is MEd,1 = 2.8 kN m and in the midspan MEd,2 = 1.6 kN m. The precast structure is made of concrete C25/30, reinforced in ceiling slab on both sides with bars profile R5, distance 150 mm, concrete cover from inside 15 mm and from outside 20 mm. Ultimate negative bending moment in frame corner is MRd,1 = 3.2 kN m and positive in the midspan MRd,2 = 3.4 kN m.
Accidental design situation – fire
In the accidental design situation it is possible to take into account small probability of fire occurrence and reduce the values of action effect bending moments, which are than in frame corner MEd,1,a = 2.0 kN m and in the midspan MEd,2,a = 1.1 kN m. Significantly higher internal forces are expected due to thermal expansion restriction.
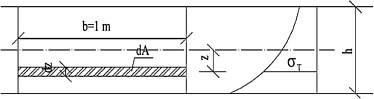
In the time t = 5 min it is expected the temperature θ = 576 °C in the fire department according to standard time/temperature curve. The temperature on the ceiling surface is 230 °C, while on the unexposed side the temperature is still 20 °C. As the temperature curve and also the thermal stress curve within the cross-section is non-linear, Fig. 6 , the bending moment was settled using numerical integration, Eq. (1) , with the value MT = −13.4 kN m (negative moment).
|
|
( 1) |
|
|
|
Figure 6. Additional bending moment. |
Expected temperature in bottom reinforcement in time 5 min does not reach 100 °C, that is why the load bearing capacity is not influenced yet.
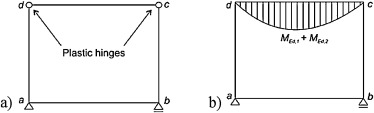
The value of the additional moment is still the object of investigation. Part of tension causes probably internal stresses due to rapid temperature gradient, the questionable is also stiffness of the cross-section after crack growth. Nevertheless expected bending moment exceeds the bearing capacity and generation of plastic hinges in frame corners and redistribution of internal forces is expected (Fig. 7 ).
|
|
|
Figure 7. Plastic hinges and internal forces redistribution. |
Providing that the plastic hinges appear, in the midspan there are added up negative and positive bending moment from action effect. The decisive factor for moment carrying capacity is the reduction of ultimate moment in the mid-span. The fire resistance is 30 min, more details also in (Cajka and Zidkova, 2005 ).
Conclusion
In the paper there are described possible approaches to fire resistance testing, from testing in accredited laboratory which allows only testing of particular structural elements to technically demanding but challenging testing of the whole structures.
Fire resistance testing provides notion about thermal and mechanical structural behaviour which is the basis for fire resistance calculation. In statically indeterminate structures the calculation is more difficult due to additional internal forces generated due to restriction of thermal deformation.
In the paper plate/wall statically indeterminate precast reinforced concrete structure was analysed. The determination of additional internal forces in reinforced concrete cross-section is questionable due to rapid temperature growth and lower stiffness after crack occurrence.
Conflict of interest
The authors declare that there is no conflict of interest.
Acknowledgement
The works were supported from sources for conceptual development of research, development and innovations for 2015 at the VŠB-Technical University of Ostrava which were granted by the Ministry of Education, Youths and Sports of the Czech Republic .
References
- Bradacova and Kucera, 2013 I. Bradacova, P. Kucera; Concrete structures restoration from the fire safety point of view; Adv. Mater. Res. (2013), pp. 113–119 http://dx.doi.org/10.4028/www.scientific.net/AMR.688.113
- Cajka and Mateckova, 2010 R. Cajka, P. Mateckova; Different types of pre-stressed hollow core panels and their fire resistance according to Eurocodes; J. Struct. Fire Eng., 1 (December (4)) (2010) http://dx.doi.org/10.1260/2040-2317.1.4.243 (Multi-Science Publishing)
- Cajka and Mateckova, 2013 R. Cajka, P. Mateckova; Fire resistance of ceiling slab concreted in trapezoidal sheet; Proceedings of Conference Concrete and Concrete Structures 2013, Terchova, Slovak Republic (2013) http://dx.doi.org/10.1016/j.proeng.2013.09.061 (Elsevier)
- Cajka and Zidkova, 2005 R. Cajka, P. Zidkova; Fire resistance of garage plate-wall prefabricated structure; COST 12 – Final Conference Proceedings, January 2005, University of Innsbruck, Austria (2005)
- Kralik, 2014 J. Kralik; A RSM approximation in probabilistic nonlinear analysis of fire, resistance of technology support structures; Adv. Mater. Res., 969 (2014) http://dx.doi.org/10.4028/www.scientific.net/AMR.969
- Kucera et al., 2014 P. Kucera, A. Lokaj, V. Vlcek; Behavior of the spruce and birch wood from the fire safety point of view; Adv. Mater. Res. (2014), pp. 725–728 http://dx.doi.org/10.4028/www.scientific.net/AMR.842.725
- Lausova et al., 2014 L. Lausova, I. Skotnicova, J. Brozovsky; Numerical analysis of effects of fire to steel frame structures; The Twelfth International Conference on Computational Structures Technology, Naples, Italy, September 2014 (2014) http://dx.doi.org/10.4203/ccp.106.20 ISSN 1759-3433, ISBN 978-1-905088-61-4
- Lausova et al., 2015 L. Lausova, V. Michalcova, I. Skotnicova, P. Konecny; Effect of non-uniform temperature distribution over the cross-section in steel frame structure; Appl. Mech. Mater., 769 (June) (2015) http://dx.doi.org/10.4028/www.scientific.net/AMM.769.65
- Pultar et al., 2010 M. Pultar, Z. Sokol, F. Wald; Temperature of external column during fire test; Structures in Fire: Proceedings of the Sixth International Conference, 978-160595027-3, DEStech Publications, Inc. (2010), p. 83
- Teply and Smirak, 2000 B. Teply, S. Smirak; Elasticity and plasticity II; VUT, Brno, Czech Republic (2000)
Document information
Published on 05/10/16
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?