Mixed optimization of power transmission structures: An application of the simulated annealing algorithm

Resumen

En el presente artículo se expone una metodología que encara una optimización general del peso de las estructuras de transporte de energía. Esta metodología se basa en la algorítmica del recocido simulado enunciada por Kirkpatrick a principios de los años ochenta, que consiste en un proceso estocástico de pruebas basado en la analogía con el recocido de los metales. El método enunciado por Kirkpatrick permite adoptar soluciones que puedan empeorar la función objetivo, con la finalidad de mejorar la exploración del entorno factible y posibilitar una mejora final de la solución obtenida. El algoritmo propuesto compatibiliza la naturaleza discreta de las secciones de las barras con la naturaleza continua de las variables que definen la geometría y la forma global de la estructura. Así se desarrolla una metodología capaz de obtener la solución a un problema de optimización mixto, evitando, a la vez, posibles explosiones combinatorias derivadas del proceso estocástico. Por otra parte, también se ha complementado el algoritmo de Kirkpatrick con un análisis de sensibilidad de primer orden que proporciona un considerable ahorro en el coste computacional del método y se implementan funciones de penalización exterior para mejorar el tratamiento de las restricciones del diseño. Con todo ello se consigue una metodología general que permite la optimización de estructuras reales de transporte de energía en tiempos de computación asumibles.

Abstract

A general methodology to optimize the weight of power transmission structures is presented in this article. This methodology is based on the simulated annealing algorithm defined by Kirkpatrick in the early ‘80s. This algorithm consists of a stochastic approach that allows to explore and analyze solutions that do not improve the objective function in order to develop a better exploration of the design region and to obtain the global optimum. The proposed algorithm allows to consider the discrete behavior of the sectional variables for each element and the continuous behavior of the general geometry variables. Thus, an optimization methodology that can deal with a mixed optimization problem and includes both continuum and discrete design variables is developed. In addition, it does not require to study all the possible design combinations defined by discrete design variables. The algorithm proposed usually requires to develop a large number of simulations (structural analysis in this case) in practical applications. Thus, the authors have developed first order Taylor expansions and the first order sensitivity analysis involved in order to reduce the CPU time required. Exterior penalty functions have been also included to deal with the design constraints. Thus, the general methodology proposed allows to optimize real power transmission structures in acceptable CPU time.

Palabras clave

Optimización mixta de estructuras ; Algoritmo de recocido simulado ; Análisis de sensibilidad ; Torres de transporte de energía

Keywords

Structural mixed optimization ; Simulated annealing algorithm ; Sensitivity analysis ; Power transmission towers

1. Antecedentes

Los inicios de la optimización de estructuras de transporte de energía tienen lugar en los años setenta, con los trabajos de Sheppard y Palmer [1] sobre la optimización de estructuras de nudos articulados mediante programación dinámica y, posteriormente, de Raj y Durrant [2] .

Más tarde, Hanssen [3] incorporó el carácter discreto del problema mediante una función objetivo implícita y discontinua dependiente de diversas variables geométricas y aplicó el método combinado aleatorio de búsqueda directa de Box [4] y el método de búsqueda directa de Powell [5] .

Posteriormente, Majid y Tang [6] analizaron la optimización de una estructura asimilable a una torre de alta tensión muy simplificada mediante métodos de programación lineal. Casi paralelamente, Saka [7] publicó su estudio de un problema con una sola cruceta mediante un criterio de optimalidad con las secciones de las barras como variables de diseño.

A finales de los ochenta, Felix y Vanderplaats [8] desarrollaron un método de optimización de estructuras articuladas considerando como variables de diseño las áreas de las barras y las coordenadas de los nodos. Del mismo modo, Martí et al. abordaron este problema y desarrollaron el software DISSENY [9]  and [10] . Ya a finales de los ochenta, plantearon la optimización conjunta de la estructura con la cimentación utilizando técnicas multiobjetivo [11] .

En los años noventa, Valera y Navarrina [12] propusieron una metodología para la minimización del peso de una estructura de transporte conforme a las especificaciones de la normativa española en vigor. La optimización se realiza mediante un algoritmo de programación lineal secuencial con búsqueda unidireccional cuadrática (SLP-QLS) [13] , utilizando un modelo tridimensional de nudos articulados. De forma paralela, la utilización de técnicas de inteligencia computacional adquirió gran auge a raíz de las publicaciones de Vieswara Rao [14] y del desarrollo de las técnicas multiobjetivo. Así, Vieswara Rao [14] estudia este problema mediante técnicas de lógica difusa.

Por otra parte, ya en el siglo xxi , Castro [15] propuso el tratamiento del problema mediante algoritmos genéticos y lo aplicó en la minimización del peso de una torre de alta tensión de simple circuito con una cruceta utilizando un modelo 2D de nudos articulados.

En la actualidad, este tipo de problemas se aborda mediante formulaciones de algoritmos genéticos pero, debido a su elevado coste computacional, entre otras limitaciones, solo se aplican en problemas simplificados. En consecuencia, no existe un consenso sólido sobre la metodología que se debe emplear para la resolución del problema de optimización de estructuras de transporte de energía.

Desde el punto de vista normativo, las estructuras metálicas de las torres de alta tensión están dentro del rango de aplicación de las normas UNE EN 50421-2005 [16] , para líneas eléctricas aéreas de entre 1 y 45 kV, y la UNE EN 50341-2001 [17] para líneas eléctricas aéreas de más de 45 kV. En el apartado estructural, los requisitos impuestos en España parten del Eurocódigo n.°3 [18] . Por otra parte, también es habitual la utilización de normativa americana específica (p. ej. ASCE 1097 [19] ). Las especificaciones relativas al régimen eléctrico se fijan en España en el Reglamento de líneas eléctricas y sus instrucciones técnicas complementarias de 2008 [20] .

2. Planteamiento del problema estructural

Las estructuras de transporte de energía se caracterizan por ser estructuras espaciales de barras en celosía con una generación modular, de forma que su geometría global se compone a partir del ensamblaje de módulos o grupos de barras con una conectividad prefijada, definidos a través de sus dimensiones generales. Estos módulos se dividen según su función y tipo en:

• Cúpulas: parte superior de la estructura.
• Crucetas: anclaje del cableado a la estructura.
• Fustes: conexión de módulos entre sí.
• Base: transmisión de cargas a la cimentación.

Por otra parte, este tipo de estructuras puede ser de diversos materiales, siendo el más común el acero laminado galvanizado. Más concretamente, los elementos que componen cada uno de los bloques se caracterizan por corresponder a perfiles angulares simétricos conectados a través de uniones atornilladas, ya que de este modo se incrementa considerablemente la facilidad constructiva.

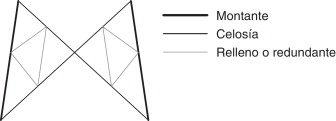
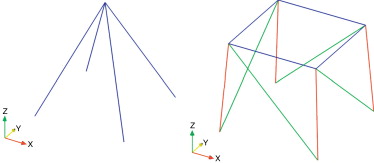
En este sentido, los elementos que configuran la geometría de este tipo de estructuras se pueden clasificar en 3 categorías diferentes (fig. 1 ):

• Montantes: asumen la carga principal de la estructura y la transmiten al terreno.
• Celosías o barras secundarias: aseguran la estaticidad de la estructura generando el sistema de arriostramiento primario.
• Rellenos o redundantes: reducen la longitud de pandeo del resto de elementos, generando el sistema de arriostramiento secundario.

Figura 1. Tipos de elementos de un bloque.

Las estructuras de transporte de energía cuentan normalmente con 4 patas de apoyo, hecho que les permite adaptarse a la geometría de los perfiles angulares y obtener una sección cuadrada que proporciona una mejor resistencia a los esfuerzos de torsión generados por el cableado, a la vez que reduce la ocupación en la base.

Desde el punto de vista del modelo estructural empleado, la normativa vigente recoge la suficiente precisión aportada por un modelo de nudos articulados, aunque también se expone que para estudios más detallados y específicos debe considerarse la naturaleza semirrígida de las uniones entre los elementos de la estructura. Por tanto, este tipo de análisis más específicos se relega a estudios muy particulares con una finalidad muy diferente a la del diseño general de las torres.

Para el análisis estructural y desde el punto de vista de las cargas actuantes en la estructura, el Reglamento de líneas de alta tensión [20] recoge la necesidad de considerar el efecto sobre la estructura de las siguientes solicitaciones:

• El peso propio de la estructura, de todos aquellos elementos auxiliares que se apoyan sobre ella y de la parte proporcional del conductor (gravivano).
• El peso del manguito de hielo sobre el conductor.
• El viento sobre el propio apoyo, los conductores (eolovano) y los elementos auxiliares.
• El tense de los conductores.

De acuerdo con el citado reglamento [20] , estas cargas se agrupan en 4 hipótesis de carga principales:

• 1.^a Hipótesis: viento.
• 2.^a Hipótesis: hielo o hielo-viento.
• 3.^a Hipótesis: desequilibrio de tracciones.
• 4.^a Hipótesis: rotura del conductor.

Las 2 primeras, llamadas hipótesis normales u operacionales, hacen referencia al comportamiento estructural del apoyo frente a situaciones climáticas adversas. Por otro lado, las segundas, llamadas anormales o accidentales, estudian la respuesta estructural frente a tareas de mantenimiento o posibles variaciones en el tense de los conductores debidas al afloje de las grapas de amarre. Del mismo modo, analizan la respuesta estructural de la torre frente a la situación accidental por excelencia para este tipo de estructuras: la rotura de uno de los conductores.

Con todo ello, en lo referente al esquema numérico empleado se ha considerado un modelo de nudos articulados con cargas concentradas aplicadas en los nodos y asumiendo un comportamiento elástico de los materiales. Por tanto, para estudiar el comportamiento estructural se ha recurrido a un modelo tridimensional de elementos finitos tipo barra.

3. Planteamiento del problema de optimización

Todo problema de optimización queda caracterizado por la función objetivo, por las variables de las que depende y por las restricciones que la condicionan. De este modo, en el caso que nos ocupa, el objetivo fundamental es desarrollar una metodología que permita la minimización del peso total de la estructura, por lo que la función objetivo se obtiene como:

$F({\boldsymbol {x}},{\boldsymbol {A}})=\rho \quad \sum _{i=1}^{n}l_{i}\quad A_{i},$

( 1)

donde l_i y A_i son la longitud y el área de cada elemento de la estructura, respectivamente, y ρ , la densidad del acero cifrada en 7.850 kg/m³ . De este modo, la función objetivo depende tanto de las coordenadas nodales de la estructura a través de la longitud de las barras como de las variables seccionales de los perfiles metálicos.

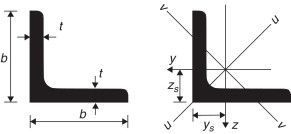
En este sentido, las variables que intervienen en el problema se caracterizan por poseer naturaleza muy diversa. Por un lado, las variables geométricas responsables de definir la forma de la estructura poseen un marcado carácter continuo únicamente delimitado por límites laterales generales que acotan sus valores por motivos de ocupación, construcción y montaje. Por otro lado, para garantizar la competitividad económica de este tipo de estructuras, las variables seccionales deben ajustarse a los valores prescritos dentro de los catálogos comerciales de perfilería metálica. Así, dado que las estructuras de transporte de energía se componen a partir de perfiles angulares simétricos, las variables seccionales que definen las características de cada barra son dos: el ancho de ala b y su espesor t ( fig. 2 ).

Figura 2. Sección transversal de un perfil angular simétrico.

No obstante, ambas variables se encuentran unívocamente relacionadas a través del perfil empleado. Este hecho les confiere un carácter marcadamente discreto en el que no solo los propios valores de ancho y espesor son discretos, sino que su propia combinación muestra la misma naturaleza. Este aspecto puede observarse en el catálogo de perfiles empleado que se adjunta en la tabla 1 .

Tabla 1. Catálogo de perfiles utilizado

Espesor t (mm)	Ancho de ala b (mm)
	25	30	35	40	45	50	60	70	75	80	90	100	110	120	150	160	180	200	230	250
3,0	X	X	X	X	X	X
4,0			X	X	X	X	X
5,0					X	X	X	X
6,0							X	X	X	X	X
7,0								X	X	X	X
8,0									X	X	X	X	X	X
9,0											X
10,0												X	X	X	X
11,0														X
12,0														X	X
13,0														X			X
14,0															X	X	X
15,0														X		X	X	X
16,0															X	X	X	X
17,0																X	X	X
18,0															X		X	X
19,0																	X	X	X
20,0																	X	X		X
21,0																		X		X
22,0																		X		X
22,2																			X
23,0																		X		X
24,0																		X		X
25,0																		X		X
25,4																			X
26,0																		X		X
27,0																				X
28,0																				X
28,6																			X
35,0																				X

Finalmente, el último de los aspectos que define el problema de optimización planteado son las restricciones que lo condicionan. Un tratamiento adecuado de las restricciones del diseño es particularmente importante, puesto que el colapso de este tipo de estructuras no solo conlleva el coste derivado de su reposición, sino que supone un elevado importe por la interrupción del servicio, pudiendo llegar a ser este último especialmente elevado y habitualmente superior al coste de la reposición en sí. En este sentido, la normativa española vigente prescribe 3 tipos de restricciones fundamentales que se deben considerar en este análisis:

• Restricciones en esbeltez seccional. Definen la capacidad resistente del perfil metálico empleado. De acuerdo con el Eurocódigo n.° 3 [18] , los perfiles angulares simétricos se inscriben dentro de la clase resistente 3. Dicha categoría se caracteriza por ser capaz de desarrollar íntegramente la rama elástica del material, a pesar de carecer de suficiente competencia para desarrollar rótulas plásticas. En la tabla 2 se recogen los límites establecidos en el Eurocódigo [18] para perfiles angulares simétricos.

Tabla 2. Límites de esbeltez seccional recogidos en el Eurocódigo 3 [18] . Unidades de f_y en MPa

b /t  ≤ 15ɛ
${\textstyle \varepsilon ={\sqrt {235/f_{y}}}}$	fy	235	275	355	420	460
	ɛ	1,00	0,85	0,66	0,56	0,51

Con todo ello, las restricciones de esbeltez seccional se implementan como:

$g_{l,i}\left(b_{i},t_{i}\right)=b_{i}-15\quad t_{i}\quad {\sqrt {235/f_{y}}}\leq 0$

( 2)

donde b_i y t_i son el ancho y el espesor del ala asociados a la barra i -ésima, f_y representa el límite elástico del material que la compone en MPa y n , el número total de barras que definen la estructura.

• Restricciones en esbeltez elemental. Dichas restricciones pretenden cuantificar la sensibilidad de la estructura frente a fenómenos de pandeo elemental, limitando la relación existente entre la longitud total y el radio de giro de la sección del elemento o barra. Estas restricciones también controlan el comportamiento de la estructura frente a estados límites de servicio como deformaciones y vibraciones.

Con todo ello, las restricciones de esbeltez elemental se plantean como:

$g_{e,i}\left(l_{i},r_{i}\right)=l_{i}-r_{i}\quad g_{0i}\leq 0$

( 3)

siendo l_i y r_i la longitud y el radio de giro de la sección asociada al elemento i y g_0i , el límite establecido por la norma para la esbeltez elemental. Dicho límite se define en función del tipo de elemento, adoptando los valores g₀  = 150 para los montantes, g₀  = 200 para las barras secundarias y g₀  = 250 para los redundantes.

• Restricciones en esfuerzo. Por último, la normativa exige la comprobación de los esfuerzos sobre la estructura. En este sentido, de acuerdo con las hipótesis asumidas dentro del modelo de cálculo empleado, existen 2 tipos de solicitaciones fundamentales: tracción y compresión. A este respecto, el Eurocódigo define que la resistencia a esfuerzo axil centrado sobre un elemento metálico con una sección clase iii corresponde a la resistencia elástica de la propia sección. No obstante, en caso de que el elemento se encuentre solicitado a compresión, dicha resistencia debe corregirse. Para ello se emplea el parámetro χ , coeficiente de pandeo en el Eurocódigo  [18] , que pretende simular el efecto que ejerce sobre la resistencia elemental la esbeltez mecánica del elemento, el tipo de estructura, las posibles imperfecciones geométricas de las secciones, la excentricidad de la carga y las tensiones residuales derivadas de la laminación de los perfiles.

De este modo, considerando un coeficiente de seguridad k , la formulación implementada para el cálculo de la restricción a esfuerzo axil de tracción queda de la siguiente manera:

$g_{s,i}\left(N_{d,i},b_{i},t_{i}\right)=k\quad N_{d,i}-$$\left(2\quad b_{i}\quad t_{i}-{t_{i}}^{2}\right)f_{y}\leq 0$

( 4)

Mientras que para el caso de los esfuerzos de compresión se establece como:

$g_{s,i}\left(N_{d,i},b_{i},t_{i}\right)=-k\quad N_{d,i}-$${\chi }_{i}\quad \left(2\quad b_{i}\quad t_{i}-{t_{i}}^{2}\right)f_{y}\leq 0$

( 5)

donde N_{d ,i} , b_i , t_i y f_y son, respectivamente, el axil de cálculo, el ancho de ala, el espesor del ala y el límite elástico del material de la barra i -ésima de la estructura. Del mismo modo, χ_i representa el valor del coeficiente de pandeo anteriormente citado.

4. Aprovechamiento estructural

Uno de los conceptos fundamentales que se desarrollan en este trabajo es el «aprovechamiento estructural». Este concepto proporciona de modo adimensional y normalizado la información relativa al grado de cumplimiento de una restricción a través de la relación entre el valor del parámetro que pretende controlar y su límite establecido por la norma. Con dicha información se puede intuir, de un modo rápido y sencillo, el nivel de ajuste de las restricciones. La adimensionalización de las restricciones, así como del problema en su conjunto, garantiza cierta generalidad en el algoritmo, evitando los posibles problemas derivados de aunar en un mismo proceso de optimización restricciones con unidades y magnitudes dispares.

En el caso que nos ocupa, las restricciones que influyen en el diseño pertenecen a 3 naturalezas muy diferenciadas. Los 2 primeros tipos de restricciones que condicionan el problema son parámetros adimensionales por naturaleza. No obstante, los valores límite que presentan los rangos de valores aceptables son muy diferentes. Por otro lado, las restricciones en esfuerzos poseen un valor fuertemente condicionado no solo por la naturaleza del esfuerzo (tracción - compresión), que modifica la expresión de cálculo, sino por la unidad de medida adoptada para el estudio. Así se observa la fuerte disparidad existente entre la naturaleza y la magnitud de las restricciones que gobiernan el problema estructural, haciendo necesario plantear su adimensionalización con el objeto de asegurar la generalidad del algoritmo.

Con todo ello, en el marco del presente estudio se ha utilizado el aprovechamiento de:

• La esbeltez seccional:

$a_{l,i}\left(b_{i},t_{i}\right)=(b_{i}/t_{i})/\left(15\quad {\sqrt {235/f_{y}}}\right)$

( 6)

• La esbeltez elemental:

$a_{e,i}\left(l_{i},r_{i}\right)=(l_{i}/r_{i})/g_{0,i}$

( 7)

• Los esfuerzos de compresión:

$a_{s,i}\left(N_{d,i},b_{i},t_{i}\right)=-k\quad N_{d,i}/({\chi }_{i}\quad A_{i}\quad f_{y})$

( 8)

• Los esfuerzos de tracción:

$a_{s,i}\left(N_{d,i},b_{i},t_{i}\right)=k\quad N_{d,i}/(A_{i}\quad f_{y})$

( 9)

A continuación se procede a enunciar detalladamente la metodología de optimización desarrollada en el presente artículo.

5. Metodología de optimización

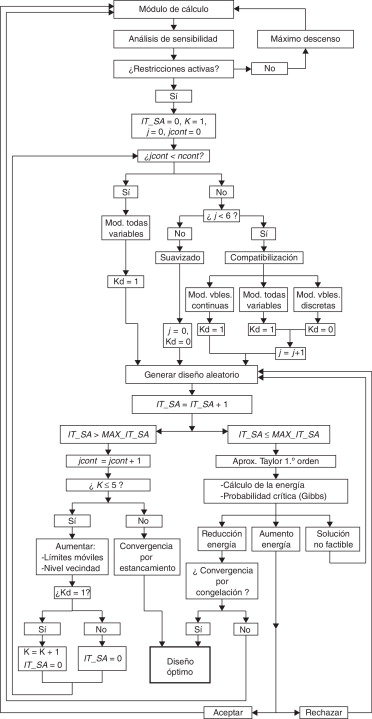
La metodología propuesta se basa en los algoritmos de optimización estocástica, que permiten incorporar de modo natural un tratamiento conjunto entre variables continuas y discretas. Este tipo de algoritmos se basa en búsquedas orientadas de configuraciones generadas aleatoriamente. La técnica de optimización implementada es la del «simulated annealing », o «recocido simulado», como se conoce en la literatura de habla hispana. Enunciada por primera vez en 1983 por Kirkpatrick  [21] , fue diseñada específicamente para el tratamiento de variables discretas, más concretamente para la resolución del «problema del viajante» [22] . Su principal inconveniente reside en el elevado número de pruebas requeridas. No obstante, en este trabajo se proponen técnicas que permiten acelerar el proceso mediante aproximaciones con desarrollos en serie de Taylor [23] . En la figura 3 se presenta un esquema de la metodología general desarrollada para la resolución del problema estudiado.

Figura 3. Esquema general de la metodología.

El algoritmo propuesto se basa en un esquema iterativo iniciado con el cálculo estructural de la torre y seguido del análisis de sensibilidad de primer orden, incorporado en la metodología propuesta para reducir el coste computacional. Una vez calculado el análisis de sensibilidad, el algoritmo entra en el módulo de decisión, en el que la metodología propuesta obtiene una nueva propuesta de diseño. Para ello se han considerado 2 alternativas diferentes: una primera basada en la dirección de máximo descenso, y una segunda basada, tal y como se expuso anteriormente, en el algoritmo del «recocido simulado». La elección de cada una de las metodologías depende de la existencia de restricciones activas, de forma que solo se empleará el primero de los métodos cuando el diseño no presente ninguna restricción activa.

El algoritmo de «recocido simulado» ejecuta una serie de pruebas para obtener una propuesta de diseño mejorado. En el caso de que el número de pruebas realizadas sea excesivo y todavía no se haya obtenido un diseño adecuado, el procedimiento desarrollado reinicia el algoritmo del «recocido» incrementando la región de exploración de las variables de diseño. De este modo, el entorno estudiado incorpora configuraciones (diseños) que suponen una mayor modificación respecto a la configuración actual.

Por otro lado, para permitir el correcto funcionamiento del método, el procedimiento propuesto incorpora módulos de compatibilización que posibilitan el tratamiento conjunto de variables continuas y discretas. De este modo, el algoritmo es capaz de asumir la diferente sensibilidad que poseen tanto la función objetivo como las restricciones respecto a las diversas variables del problema. Una vez el algoritmo obtiene un diseño aceptable, se reinicia el procedimiento con una nueva iteración.

Finalmente, el algoritmo incorpora criterios de detención basados en la temperatura de congelación y en un excesivo número de iteraciones en las que no se alcanza una mejora de la solución. De este modo, se consigue controlar la convergencia del método de manera simple y eficaz.

A lo largo del presente epígrafe se procederá a un estudio pormenorizado de todas aquellas particularidades que caracterizan el esquema general implementado, haciendo especial hincapié en los aspectos más novedosos.

5.1. Análisis de sensibilidad y entorno factible

En el algoritmo propuesto, con el objeto de reducir el coste computacional de los numerosos análisis que requiere el algoritmo del «recocido simulado» se ha implementado un análisis de sensibilidad de primer orden mediante el método de diferenciación analítica directa. De este modo, a partir del desarrollo en serie de Taylor se puede obtener una aproximación tanto de la función objetivo como de las restricciones bajo un coste computacional muy reducido. Con todo ello, se consigue una aproximación lineal de las restricciones y de la función objetivo, hecho que incrementa considerablemente la capacidad de análisis del algoritmo.

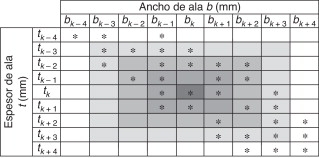
Dado que las restricciones y la propia función objetivo son funciones no lineales, la aproximación obtenida a través del desarrollo en serie de Taylor de primer orden presenta ciertas desviaciones. Este hecho motiva que los avances en las variables deban restringirse con el objeto de limitar errores en la aproximación que puedan desvirtuar el resultado. En este sentido, la evolución de las variables continuas se realiza a partir de límites móviles, cuyo rango equivale al 1% del rango total de la variable. En el caso de las variables seccionales, dado el carácter marcadamente discreto expuesto con anterioridad, se ha desarrollado específicamente una estrategia de mapeado del catálogo de perfiles que permite obtener el entorno próximo de la sección de una forma sencilla y eficaz. Para definir las parejas de ancho de ala y espesor que existen en el catálogo empleado, se adopta una función binaria que asocia la unidad a las parejas de variables existentes y valores nulos a aquellas combinaciones que no pertenezcan al dominio de estudio (fig. 4 ).

$P_{L}\left(b^{'},t^{'}\right)={\begin{array}{ll}1&si\quad \left(b^{'},t^{'}\right)\in Dom\left(P_{L}\right)\\0&si\quad \left(b^{'},t^{'}\right)\not \in Dom\left(P_{L}\right)\\&\end{array}}$

( 10)

Partiendo de esta función, se define el entorno como el conjunto de perfiles contiguos al estudiado, tanto en espesor como en ancho de ala, de forma que en función de la anchura del box , o región de estudio de la variable, se incrementa el número de perfiles considerado. En este sentido, de acuerdo con el esquema recogido en la figura 3 , el box sufre ciertas modificaciones si el algoritmo de «recocido simulado» alcanza un número de iteraciones excesivamente elevado sin haber obtenido ningún nuevo diseño adecuado. Así, el entorno de búsqueda se define como:

$E_{\left(b_{k},t_{k}\right)}=\left(b_{j},t_{l}\right)\quad tal{\mbox{ }}que{\begin{array}{l}j,l\in \mathbb {Z} \left[k-i,k+i\right]\\P_{L}\left(b_{j},t_{l}\right)=1\end{array}}$

( 11)

siendo i el cardinal que representa el contador de las iteraciones consecutivas en las que el «recocido simulado» no ha encontrado ningún diseño adecuado.

Figura 4. Determinación del entorno de estudio para las variables discretas acopladas (bk y tk ) a partir de niveles de proximidad (en escala de grises) con los valores discretos actuales. Los pares de valores discretos de las variables que corresponden a diseños reales se resaltan con un asterisco.

Con todo ello, para obtener la dirección de modificación dentro de dicho entorno, se procede a generar un número aleatorio comprendido entre −1 y 1 para cada una de las variables. En función del valor aleatorio obtenido se procede a modificar la variable estudiada asumiendo una probabilidad uniforme para todos los casos posibles. En el caso de las variables discretas (seccionales), en función del tamaño del nivel de vecindad permitido, se aplica el procedimiento 2 veces: una para obtener el ancho de ala y otra para el espesor de ala. En el caso de las variables geométricas, y debido a su carácter continuo, se multiplica directamente el tamaño del box por el valor aleatorio obtenido para cada una de ellas con el fin de obtener su modificación. De este modo, en el caso de las variables discretas se obtiene un nuevo par de valores discretos de forma directa y, en el caso de las variables continuas, se obtiene la modificación que experimentan con respecto al valor del diseño actual.

5.2. Dirección de máximo descenso

El esquema del algoritmo presentado en la figura 3 posee 2 líneas de avance en el proceso de optimización. Una línea principal que se basa en la implementación del «recocido simulado» y una segunda basada en la implementación del algoritmo de máximo descenso. Este método se activa siempre que la solución de partida no presente ninguna restricción con un aprovechamiento superior al 90% (restricciones activas) debido a su mayor velocidad de reducción de la función objetivo.

5.3. Recocido simulado

El algoritmo de «recocido simulado», o «simulated annealing » en literatura anglosajona, se basa en la analogía con el recocido de los metales, proceso que busca la configuración cristalina que proporciona una menor energía interna del sistema. Así, este procedimiento es análogo a un proceso de optimización en el que se busca la distribución de variables y que minimiza la función objetivo del problema, tal y como se puede observar en la tabla  3 .

Tabla 3. Analogía entre la termodinámica y la optimización

Termodinámica	Optimización
Configuración	Solución factible
Configuración fundamental	Solución óptima
Energía de la configuración	Función objetivo
Temperatura	Estado de la optimización

Así, el algoritmo comprueba de forma aleatoria, a partir de un estado o una configuración inicial, la modificación de la energía del sistema entre sus estados vecinos (entorno factible), de forma que, si la energía es menor, el estado se acepta y se reinicia el proceso a partir de esa nueva configuración. Por el contrario, si la energía es mayor, Kirkpatrick recurrió al algoritmo de Metropolis [24] . De este modo, Metropolis establecía que la probabilidad de transición entre configuraciones cristalinas en un sólido metálico se ajustaba a una distribución tipo Boltzmann-Gibbs.

$f\left(E,T\right)=e^{-\Delta E/k\quad T}$

( 12)

siendo ΔE la variación energética entre las configuraciones consideradas en cada iteración, T la temperatura del sistema y k la constante térmica de Boltzman.

Con todo ello, el algoritmo de Kirkpatrick genera un número aleatorio comprendido entre 0 y 1, que se compara con el valor de probabilidad proporcionado por el criterio de Gibbs, de forma que si este último es mayor, se acepta la dirección a pesar de empeorar la función de energía y, en caso contrario, se desecha y pasa a comprobarse una nueva configuración. Así, el criterio de aceptación de Gibbs proporciona 3 alternativas:

• Ascenso de colina, cuando se empeora (aumenta) levemente la energía del sistema.
• Descenso de valle, cuando se mejora (reduce) la energía del sistema.
• Dirección rechazada, cuando la variación de la energía del sistema no se ajusta al criterio de Gibbs, o bien el diseño no satisface las restricciones impuestas.

5.3.1. La función de energía

La función de energía refleja el estado del sistema en un instante determinado del proceso de optimización, aportando la información necesaria sobre la función objetivo. No obstante, la evolución del algoritmo no solo está marcada por el valor de la función objetivo, sino que las propias restricciones que condicionan el problema completan la información necesaria para establecer la convergencia. En el presente trabajo, la función de energía se establece como:

$F\left({\boldsymbol {\xi }}\right)=f\left({\boldsymbol {\xi }}\right)+$$G\left({\boldsymbol {\xi }}\right)$

( 13)

siendo ${\textstyle G\left({\boldsymbol {\xi }}\right)}$ la función que introduce la información necesaria sobre las restricciones del problema, y ${\textstyle f\left({\boldsymbol {\xi }}\right)}$ la función que incorpora la información relativa al peso total de la estructura. Para permitir que el algoritmo presente un funcionamiento independiente tanto de la configuración inicial como de las unidades consideradas se ha optado por una expresión adimensionalizada que proporcione de modo eficaz la información requerida.

De este modo, en primer lugar se incorpora la información relativa a la función objetivo a través de su cociente con el valor que toma para la configuración inicial, obteniéndose así el grado de separación respecto a la situación original que posee el estado estudiado.

En segundo lugar, la información relativa a las restricciones se incorpora a través del concepto del aprovechamiento estructural detallado anteriormente. Dado que es previsible que durante el proceso de optimización se produzcan leves transgresiones en las restricciones, debido a las aproximaciones de primer orden, se ha optado por implementar las restricciones a través de expresiones similares a las funciones de penalidad exterior. De este modo, también se indica y se tiene en cuenta el efecto de las restricciones en la función de energía, de modo que un diseño no válido tendrá mayor energía que uno válido.

Así, la expresión final de la función de energía será:

$F\left({\boldsymbol {\xi }}\right)={\frac {f_{k}\left({\boldsymbol {\xi }}\right)}{f_{0}\left({\boldsymbol {\xi }}\right)}}-$${\frac {\beta }{nrtot}}\sum _{j=1}^{nrtot}a_{j}^{\gamma }\left({\boldsymbol {\xi }}\right)$

( 14)

donde f₀ (ξ ) representa el valor de la función objetivo al inicio del proceso de optimización, f_k (ξ ) el valor de la función objetivo, a_j (ξ ) el aprovechamiento de la función, en el instante k , nrtot el número total de restricciones, y β el coeficiente de ponderación de las restricciones. En cualquier caso, dicho coeficiente se ha calibrado de forma que la información relativa a las restricciones del problema no limite en exceso la búsqueda del valor óptimo de la función objetivo. De este modo, y tras estudiar el comportamiento del algoritmo para diferentes valores de β , se considera aceptable que la incidencia de las restricciones no debe exceder el 1 % del total de la función objetivo. Por otro lado, el exponente γ del aprovechamiento debe ser positivo, proponiéndose como referencia el valor γ  = 3.

Con todo se obtiene una función totalmente adimensional, que permite corregir las perturbaciones derivadas del análisis de sensibilidad, integra la información relativa a la función objetivo y a las restricciones, y pretende independizar el problema de la solución inicial de partida.

5.3.2. La temperatura

La temperatura es el parámetro fundamental que gobierna la evolución y el comportamiento del algoritmo. En consecuencia, es necesario llevar a cabo un estudio y una caracterización detallada del proceso de enfriamiento para garantizar su correcto funcionamiento. En este sentido, la temperatura gobierna no solo el número de pruebas o la longitud del proceso evolutivo, sino que también condiciona las probabilidades de transición de un estado de energía a otro.

La temperatura en el algoritmo se caracteriza por 4 aspectos fundamentales:

• La temperatura inicial.
• La constante de optimalidad.
• El esquema de enfriamiento que proporciona y controla la velocidad de enfriamiento.
• La temperatura de parada.

En los siguientes epígrafes se estudiarán con mayor detalle los aspectos principales que caracterizan y definen el sistema de enfriamiento empleado.

5.3.2.1. La temperatura inicial

Una de las características fundamentales que debe cumplir todo algoritmo que busque la generalidad en su aplicación es que resulte independiente de la solución o del estado inicial de partida. En este sentido, y dado que el algoritmo desarrolla una cadena de Markov no estacionaria en la que las probabilidades de transición varían con la temperatura, partir de valores diferentes puede llegar a condicionar dichas probabilidades lo suficiente como para alterar el resultado final.

Tradicionalmente, este problema se soluciona utilizando valores de temperatura inicial suficientemente elevados como para conseguir que el método se estabilice antes de comenzar el descenso hacia el óptimo. Lundy y Mees [25] enunciaron que el algoritmo debería comenzar por una temperatura lo suficientemente elevada como para que la probabilidad de aceptación de ascenso de colina fuese prácticamente la unidad.

El número de movimientos debe ser lo suficientemente elevado como para permitir una cierta exploración inicial del entorno y, del mismo modo, debe ser lo suficientemente reducido como para permitir alcanzar eficazmente la temperatura de descenso.

En cualquier caso, no existe una formulación generalmente aceptada que permita predecir el valor de la temperatura inicial. De hecho, existe un cierto consenso general al respecto que indica la necesidad de calibración de dicho parámetro, poniéndose de manifiesto la variabilidad del mismo en función del problema analizado. En este sentido, los autores del presente artículo rubrican estas afirmaciones.

No obstante, el intento de adimensionalización del algoritmo basado en el empleo del concepto de aprovechamiento estructural expuesto anteriormente pretende asimilar cualquier problema que se plantee a uno estándar con un funcionamiento característico y conocido. De este modo, y desde el punto de vista teórico, este hecho permite establecer una ley que garantice la temperatura inicial independientemente del problema estudiado.

Tras estudiar el comportamiento del método en el problema que se plantea en el presente artículo, se comprueba que la rigidez del método resulta excesiva cuando la probabilidad inicial de ascenso de colina es inferior al 50,00 %. Partiendo de dicho valor, y teniendo en cuenta las condiciones iniciales del diseño, se propone una aproximación al valor de temperatura inicial que garantiza dicho comportamiento a través de la expresión que gobierna la probabilidad de transición entre estados:

$T_{0}={\frac {\left(-0,20\right)}{ln(0,50)}}\quad {\frac {nract}{nrtot}}$

( 15)

donde nract representa el número de restricciones activas del diseño inicial, y nrtot el número total de restricciones. No obstante, cabe notar que esta expresión únicamente proporciona un valor de referencia, si bien no evita la necesidad de una calibración posterior del parámetro.

5.3.2.2. La constante de optimalidad

Otro de los aspectos que influye notablemente sobre las probabilidades de transición es la constante de optimalidad. Dicha constante es fruto de la analogía con el recocido de los metales, siendo la equivalencia numérica de la constante de Boltzman. Los primeros autores restaban importancia a la influencia de dicho parámetro en el funcionamiento del algoritmo, incluso llegando a obviarlo. No obstante, algunos investigadores como Wah [32] han identificado durante los últimos años su efecto y han propuesto la necesidad de estudiar su valor empíricamente y de modo particularizado a cada problema [26] .

En cualquier caso, el objetivo estricto de la constante de optimalidad dentro del algoritmo es la de proporcionar un rescalado, ya sea de la función de energía o de la temperatura característica del sistema. Los autores del presente artículo reconocen la incidencia de dicho parámetro. No obstante, dado que desde un punto de vista conceptual carece de sentido, se propone y considera más acertado introducir dicho coeficiente dentro de la propia temperatura. De este modo, se aúnan en un solo parámetro todos los conceptos relacionados con la convergencia y la evolución del algoritmo.

5.3.2.3. El esquema de enfriamiento

Desde el nacimiento de la teoría del «recocido simulado» se han propuesto diferentes esquemas de enfriamiento que permiten evoluciones con mayor o menor velocidad hasta alcanzar la configuración elemental o de menor energía. No existe un consenso general acerca del tipo de esquema que se debe emplear. Sin embargo, sí existe una aceptación general de que este tipo de algoritmos mejora su funcionamiento cuando la velocidad de enfriamiento disminuye, como ocurre con el enfriamiento de los metales. Así, Gidas [29] y Geman [30] demuestran la convergencia asintótica del método para un patrón de enfriamiento inversamente proporcional al logaritmo de las iteraciones. Sin embargo, este criterio es exageradamente lento, y en la práctica se ha demostrado que otros criterios de mayor velocidad permiten obtener resultados igualmente válidos. En el algoritmo presentado en este artículo se ha implementado el esquema de descenso exponencial (planteado originalmente por Kirkpatrick [21] en los años ochenta) y que es actualmente el más popular entre la comunidad científica debido a su sencillez y al buen comportamiento que muestra en la resolución de problemas de optimización de muy diversa naturaleza. Así, la temperatura T_k en la iteración k se obtiene como:

$T_{k}={\alpha }^{k}\quad T_{0}$

( 16)

siendo α el factor multiplicador y T₀ el valor inicial de temperatura. Muchos autores han estudiado en profundidad el método, estableciendo el rango de valores más conveniente para el parámetro α . En este sentido, Kuik y Salomon  [27] proponen como referencia [0,80, 0,99], intervalo de valores que asegura un enfriamiento lento.

Posteriormente, Orsila et al. [31] reducen dicho rango de valores al intervalo [0,90, 0,99]. En el mismo estudio se propone como referencia general el valor de 0,95, aunque haciendo hincapié en la necesidad de particularizarlo al problema que se esté estudiando. En el caso que nos ocupa, con el objeto de garantizar una lenta velocidad de enfriamiento y mejorar así el comportamiento del algoritmo, se ha adoptado un factor multiplicador de α  = 0,99. Debido a la incorporación del análisis de sensibilidad al algoritmo y al consecuente incremento de la capacidad computacional que ello conlleva, se pueden adoptar velocidades de enfriamiento más lentas, hecho que mejora sensiblemente el comportamiento final del algoritmo.

5.3.2.4. Temperatura final

Una vez alcanzado un determinado valor de temperatura, el algoritmo pierde tal grado de flexibilidad que la probabilidad de aceptación de ascenso de colina es tan baja que el efecto de exploración de soluciones peores a la actual es prácticamente nulo. Para definir el criterio general de parada del algoritmo se establece un límite inferior de temperatura que impide en la práctica la exploración del entorno de diseño y el ascenso de colina. En 1988, Otten y Van Ginneken [28] plantearon una interpretación estadística del funcionamiento del algoritmo y propusieron un criterio de parada basado en la varianza de la energía obtenida conforme avanza el algoritmo. Dicha formulación sustituye la capacidad de mejora de la función objetivo por una estimación estadística del proceso estocástico, en el que en función de la varianza de la serie obtenida durante el desarrollo del algoritmo se decide su parada, pero en algunos casos se pueden llegar a generar situaciones de congelación indeseada. Por ello, en este artículo se propone que, a partir de la ecuación general del algoritmo y considerando una probabilidad de congelación del 0,10 %, se establezca una relación de parada. En este sentido, si se asume que la ecuación general del algoritmo se caracteriza por la función de densidad de una distribución de Boltzmann - Gibbs, que el incremento de la función objetivo tomado como referencia será de 0,10 %, y que se tiene en cuenta la configuración inicial del estudio mediante la introducción de un factor multiplicador equivalente al valor medio del aprovechamiento inicial de las restricciones, la temperatura límite se obtiene como:

$T_{lim}={\frac {-0,001\quad F_{0}}{ln\left(0,001\right)}}\quad \sum _{j=1}^{nrtot}{\frac {a_{j}\left({\boldsymbol {\xi }}\right)}{nrtot}}$

( 17)

siendo F₀ el valor inicial de la función de energía, a_j el aprovechamiento estructural de la restricción j , y nrtot el número total de restricciones.

5.4. Compatibilización de variables discretas y continuas (suavizado)

Dado que las variables concurrentes en el problema son tanto de carácter continuo como discreto, la definición del entorno de estudio condiciona en gran medida el comportamiento de la función objetivo. En este sentido, la diferente sensibilidad que poseen tanto la función objetivo como las restricciones respecto a ambos grupos de variables resulta decisiva en el comportamiento final del algoritmo.

Para que el proceso de optimización proporcione buenos resultados es necesario que las modificaciones de las variables de diseño sean comparables. Con este objetivo, se ha procedido a mitigar las diferencias de sensibilidad entre ambos tipos de variables, permitiendo al programa que estudie el comportamiento del sistema al modificar de forma independiente y aleatoria las variables geométricas, seccionales o bien ambas en conjunto. Los autores han denominado este proceso como compatibilización ( fig. 3  [23] ), y se incorpora dentro del recocido simulado entre la fase inicial, en la que se obtiene el entorno factible, y la fase de decisión, en la que se verifica que la solución escogida es viable (ascenso de colina o descenso de valle) o bien resulta rechazada (fig. 3 ). Tal y como se puede comprobar en esta misma figura 3 , para evitar que el algoritmo modifique únicamente las secciones o la geometría condicionando el resultado, el método propuesto está diseñado de forma que durante las primeras pruebas de cada iteración modifique todas las variables de forma conjunta (si jcont  ≤ ncont ). Sin embargo, si el algoritmo es incapaz de encontrar una dirección viable a lo largo de dichas pruebas, entonces el método permite la elección aleatoria del grupo de variables que modificar (compatibilización). Así, para los ejemplos de aplicación de este trabajo se propone que el algoritmo intente encontrar una solución adecuada modificando todas las variables conjuntamente hasta alcanzar 3 veces (ncont  = 3) el máximo de pruebas (MAX  _ IT  _ SA = 10.000, para estos ejemplos).

A medida que el algoritmo se aproxima al punto óptimo, y debido al carácter discreto de las secciones, existirá un elevado número de variables de este tipo que se encuentren en el valor correspondiente a la situación óptima. Debido al excesivo número de variables discretas que intervienen en el algoritmo, resulta muy poco probable que en la generación aleatoria del vector solución únicamente resulte modificada una de ellas.

Por este motivo, la metodología propuesta incluye un procedimiento complementario denominado por los autores como suavizado seccional , en el que se modifica únicamente y de forma aleatoria una de las variables seccionales del problema, siempre y cuando el algoritmo no proporcione una dirección factible tras 6 pruebas consecutivas modificando al menos las variables seccionales. De este modo, se consigue suavizar la geometría de la torre homogeneizando los incrementos de la función objetivo y permitiendo una exploración más exhaustiva del dominio de las variables geométricas, que dado su carácter continuo es teóricamente infinito. Para este fin, se utiliza una variable auxiliar (Kd en la fig. 3 ) que permite identificar las iteraciones en las que se modifican las secciones frente a las iteraciones en las que solo se modifican variables seccionales.

5.5. Implementación de los criterios de convergencia o parada

Finalmente, la detención del algoritmo se plantea a través de un doble criterio de parada. Un primer criterio, basado en la congelación del algoritmo al descender la temperatura por debajo de la temperatura límite expuesta anteriormente, y otro segundo, debido a un estancamiento del algoritmo en torno a un punto del dominio.

En el primero de los casos, la parada se realiza siempre y cuando el punto analizado del algoritmo impida un descenso de valle. Por el contrario, el segundo de los criterios de parada se origina cuando el algoritmo proporciona 5 iteraciones consecutivas superando el número máximo de iteraciones planteado. A tenor del funcionamiento del algoritmo, se ha podido comprobar que 5 iteraciones son suficientes para garantizar la detención del algoritmo. Debido a la diferente sensibilidad que tiene el problema respecto a los diversos tipos de variables, se ha optado por considerar la parada siempre y cuando esas 5 iteraciones consecutivas respondan a modificaciones de geometría. En esta situación, se considera que el algoritmo se encuentra en un punto lo suficientemente bajo como para no encontrar una nueva solución factible que mejore el diseño actual y, por tanto, se detiene.

6. Interpretación del funcionamiento del algoritmo

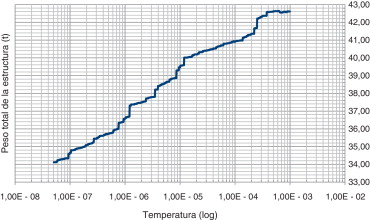
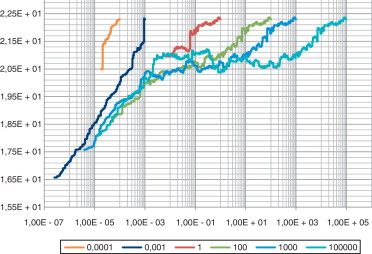
El algoritmo de Kirkpatrick se basa en una serie de pruebas aleatorias que permiten de una forma controlada la inspección del entorno del diseño actual en cada iteración. El comportamiento del algoritmo presenta normalmente 3 fases o ramas claramente diferenciadas: fase de arranque, fase de aceleración y fase de parada [21] . El algoritmo puede llegar a omitir en su desarrollo alguna de las fases, lo que normalmente indica un ajuste poco preciso de sus parámetros al problema estudiado. El arranque define el grado de exploración del entorno de la solución inicial. Su existencia es estrictamente necesaria [23] ; de lo contrario, suele indicar que la temperatura inicial es demasiado baja. Sin embargo, valores excesivamente elevados no garantizan una mejor solución, tal y como puede observarse en la figura 5 para el ejemplo de aplicación de este artículo, y requieren mayores tiempos de cálculo.

Figura 5. Evolución de la energía del algoritmo para diferentes temperaturas iniciales.

La fase de parada en un problema de optimización con variables mixtas como el que nos ocupa es difícilmente alcanzable si se entiende como una deceleración progresiva del proceso de congelación. Este hecho se debe a la menor probabilidad de aceptación de posibles ascensos de colina a bajas temperaturas y a la elevada perturbación que generan sobre la función objetivo las variaciones de las variables discretas. Así, esta rama suele generarse bruscamente para este problema.

La metodología propuesta desarrolla claramente ramas de aceleración bien definidas, mostrándose las fases de arranque y parada de un modo más tímido, lo que indica un funcionamiento correcto y ajustado en términos de coste computacional.

7. Ejemplo de aplicación

El ejemplo estudiado corresponde a una estructura de alta tensión para doble circuito de 220 kV o superior con una disposición en capa y un único cable de guarda amarrado en una cúpula simple.

La estructura estudiada corresponde a una disposición tipo amarre, capaz de soportar una desviación en ángulo de 15° con una estructura de cableado tipo dúplex. El peso total de esta tipología de torre varía sensiblemente en función de la altura nominal y de la funcionalidad del apoyo, pudiendo alcanzar valores de hasta 60 toneladas en los casos más extremos.

7.1. Geometría considerada

La estructura de transporte estudiada en este caso corresponde a una torre de alta tensión de aproximadamente 42 toneladas de peso y una altura total de 65 metros. Esta estructura permite un altura libre bajo la cruceta más baja de 43 metros, hecho que permite salvar vanos de gran longitud.

7.1.1. Geometría elemental

Tal y como se expone al comienzo del artículo, este tipo de estructuras se caracterizan por su geometría modular. Cabe notar que los módulos adoptados para el ejemplo analizado se han obtenido a través del estudio tanto de las geometrías más comunes dispuestas en torres reales como de las diversas tipologías empleadas por las empresas de montaje. En cualquier caso, la geometría de los bloques puede variar de un fabricante a otro, formando parte de la tecnología propia de cada empresa. En el ejemplo analizado se han empleado los siguientes bloques: cúpula simple (fig. 6 izquierda), súper lambda (fig. 6 derecha), cruceta corta (fig. 7 ), cruceta larga (fig. 8 ), módulo X (fig. 9 izquierda), módulo súper X (fig. 9 derecha), módulo X arriostrado (fig. 10 izquierda), módulo K (fig. 10 derecha). Los detalles específicos de cada uno de estos módulos se pueden encontrar en [23] .

Figura 6. Módulo tipo cúpula simple (izquierda) y súper lambda (derecha).

Figura 7. Módulo tipo cruceta corta.

Figura 8. Módulo tipo cruceta larga.

Figura 9. Módulo tipo X (izquierda) y súper X (derecha).

Figura 10. Módulo tipo X arriostrado (izquierda) y tipo K (derecha).

7.1.2. Geometría global

La estructura se compone mediante una secuencia modular formada por 23 bloques, con las características recogidas en la tabla 4 .

Tabla 4. Torre de 220 kV: módulos y geometría inicial

	Módulo	Altura (m)	Cota (m)	Base inf. X (m)	Base inf. Y (m)	Base sup. X (m)	Base sup. Y (m)	Long. ala (m)
1	K	7,000	7,000	10,80	10,80	9,20	9,20	—
2	X arriostrada	7,000	14,000	9,20	9,20	7,80	7,80	—
3	X arriostrada	10,000	24,000	7,80	7,80	5,80	5,80	—
4	X arriostrada	7,000	31,000	5,80	5,80	4,40	4,40	—
5	X	2,000	33,000	4,40	4,40	4,00	4,00	—
6	X	2,000	35,000	4,00	4,00	3,60	3,60	—
7	X	2,000	37,000	3,60	3,60	3,20	3,20	—
8	X	2,000	39,000	3,20	3,20	2,80	2,80	—
9	X	2,000	41,000	2,80	2,80	2,40	2,40	—
10	Súper X	2,000	43,000	2,40	2,40	2,00	2,00	—
11	Cruceta corta	1,625	44,625	2,00	2,00	2,00	2,00	5,20
12	X	1,625	46,250	2,00	2,00	2,00	2,00	—
13	X	1,625	47,875	2,00	2,00	2,00	2,00	—
14	Súper X	1,625	49,500	2,00	2,00	2,00	2,00	—
15	Cruceta larga	1,625	51,125	2,00	2,00	2,00	2,00	6,45
16	X	1,625	52,750	2,00	2,00	2,00	2,00	—
17	X	1,625	54,375	2,00	2,00	2,00	2,00	—
18	Súper X	1,625	56,000	2,00	2,00	2,00	2,00	—
19	Cruceta corta	1,625	57,625	2,00	2,00	2,00	2,00	5,20
20	Súper lambda	1,842	59,467	2,00	2,00	1,50	1,50	—
21	Súper lambda	1,842	61,309	1,50	1,50	1,00	1,00	—
22	Súper lambda	1,842	63,151	1,00	1,00	0,50	0,50	—
23	Cúpula	1,842	64,993	0,50	0,50	0,00	0,00	—

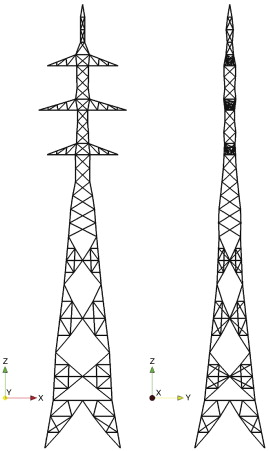
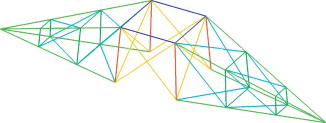
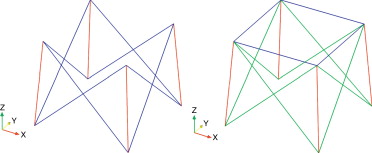
Así, se obtiene una estructura constituida por 267 nodos conectados a través de 829 elementos distribuidos en 77 secciones diferentes de acuerdo con la figura 11 . En la tabla 5 se adjuntan las características de cada uno de los materiales empleados en el diseño inicial de la estructura.

Figura 11. Torre de 220 kV: geometría inicial [23] .

Tabla 5. Torre de 220 kV: codificación de los perfiles dispuestos en la geometría [23]

Mat.	Perfil	Área (cm2 )	Inercia (cm4 )	Mat.	Perfil	Área (cm2 )	Inercia (cm4 )
1	L250.20	96,00	2304,00	40	L70.7	9,31	17,15
2	L120.10	23,00	126,74	41	L90.8	13,76	42,40
3	L120.10	23,00	126,74	42	L150.12	34,56	298,60
4	L120.10	23,00	126,74	43	L90.8	13,76	42,40
5	L100.10	19,00	71,45	44	L150.12	34,56	298,60
6	L100.10	19,00	71,45	45	L90.8	13,76	42,40
7	L120.10	23,00	126,74	46	L120.10	23,00	126,74
8	L250.20	96,00	2304,00	47	L90.8	13,76	42,40
9	L120.10	23,00	126,74	48	L90.8	13,76	42,40
10	L120.10	23,00	126,74	49	L120.10	23,00	126,74
11	L150.16	45,44	381,77	50	L90.8	13,76	42,40
12	L180.16	55,04	678,46	51	L90.8	13,76	42,40
13	L250.20	96,00	2304,00	52	L90.8	13,76	42,40
14	L120.10	23,00	126,74	53	L70.7	9,31	17,15
15	L120.10	23,00	126,74	54	L70.7	9,31	17,15
16	L120.10	23,00	126,74	55	L120.10	23,00	126,74
17	L150.16	45,44	381,77	56	L80.6	9,24	22,83
18	L200.20	76,00	1143,17	57	L120.10	23,00	126,74
19	L120.10	23,00	126,74	58	L80.6	9,24	22,83
20	L90.8	13,76	42,40	59	L120.10	23,00	126,74
21	L90.8	13,76	42,40	60	L80.6	9,24	22,83
22	L120.10	23,00	126,74	61	L90.8	13,76	42,40
23	L150.18	50,76	420,48	62	L120.10	23,00	126,74
24	L120.10	23,00	126,74	63	L70.7	9,31	17,15
25	L150.18	50,76	420,48	64	L90.8	13,76	42,40
26	L120.10	23,00	126,74	65	L70.7	9,31	17,15
27	L150.18	50,76	420,48	66	L70.7	9,31	17,15
28	L120.10	23,00	126,74	67	L60.6	6,84	9,26
29	L150.18	50,76	420,48	68	L80.6	9,24	22,83
30	L120.10	23,00	126,74	69	L70.7	9,31	17,15
31	L150.18	50,76	420,48	70	L60.6	6,84	9,26
32	L120.10	23,00	126,74	71	L80.6	9,24	22,83
33	L150.18	50,76	420,48	72	L70.7	9,31	17,15
34	L120.10	23,00	126,74	73	L60.6	6,84	9,26
35	L90.8	13,76	42,40	74	L80.6	9,24	22,83
36	L150.18	50,76	420,48	75	L70.7	9,31	17,15
37	L90.8	13,76	42,40	76	L60.6	6,84	9,26
38	L90.8	13,76	42,40	77	L80.6	9,24	22,83
39	L70.7	9,31	17,15

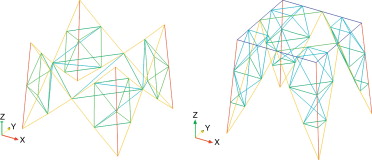
En la figura 12 se muestra la representación gráfica de la distribución de material en la estructura en su configuración inicial. En ella se puede observar una mayor concentración de material en los montantes de la estructura, así como en los perfiles principales de cada una de las alas.

Figura 12. Torre de 220 kV: distribución inicial de material en la estructura [23] .

7.2. Cargas actuantes

De acuerdo con los datos disponibles de los catálogos de empresas fabricantes, las cargas máximas admisibles para una estructura como la estudiada se recogen en la tabla 6 . Estas cargas se aplican sobre la torre de forma simétrica en los extremos de las crucetas y del bloque cúpula, salvo en el caso de la 4^a hipótesis de carga, que representa la rotura del conductor. En este caso, la 4^a hipótesis se desdobla a su vez en cuatro análisis diferentes, estudiando así el comportamiento de la estructura frente a la rotura del conductor en cada una de las crucetas con el objetivo de obtener la situación pésima.

Tabla 6. Torre de 220 kV: cargas en toneladas para las diferentes hipótesis de carga. El cable 1 corresponde al cable de guarda y los cables 2, 3 y 4 corresponden a las crucetas superior, intermedia e inferior, respectivamente

Cable	Hipótesis	Carga longitudinal (toneladas)	Carga vertical (toneladas)	Carga transversal (toneladas)
1	1a	0,000	−0,546	1,231
	2a	0,000	−1,462	1,353
	3a	1,037	−1,462	0,947
	4.1a	4,148	−1,462	1,083
	4.2a	0,000	−1,462	1,083
	4.3a	0,000	−1,462	1,083
	4.4a	0,000	−1,462	1,083
2	1a	0,000	−1,748	3,636
	2a	0,000	−4,023	3,411
	3a	2,662	−4,023	2,432
	4.1a	0,000	−4,023	2,779
	4.2a	5,323	−4,023	2,779
	4.3a	0,000	−4,023	2,779
	4.4a	0,000	−4,023	2,779
3	1a	0,000	−1,748	3,636
	2a	0,000	−4,023	3,411
	3a	2,662	−4,023	2,432
	4.1a	0,000	−4,023	2,779
	4.2a	0,000	−4,023	2,779
	4.3a	5,323	−4,023	2,779
	4.4a	0,000	−4,023	2,779
4	1a	0,000	−1,748	3,636
	2a	0,000	−4,023	3,411
	3a	2,662	−4,023	2,432
	4.1a	0,000	−4,023	2,779
	4.2a	0,000	−4,023	2,779
	4.3a	0,000	−4,023	2,779
	4.4a	5,323	−4,023	2,779

7.3. Resultados de la optimización

La aplicación del algoritmo sobre la estructura anteriormente expuesta proporciona una configuración de torre en la que el ahorro de material alcanza un 19,85%. El proceso de optimización emplea un total de 984 iteraciones con un coste computacional de 8.963,00 segundos, en un equipo de doble núcleo con 2,00 GHz y 4,00 Gb de memoria RAM. En la tabla 7 se resumen las principales características del proceso de optimización.

Tabla 7. Torre de 220 kV: resumen de las principales características y parámetros del problema

Resumen de características
de la evolución de la torre de 220 kV
Número de materiales	77
Número de elementos	829
Número total de variables	200
Número de variables discretas	154
Número de variables continuas	46
Número de restricciones	9,128
Peso inicial (t)	42,605
Peso final (t)	34,148
Porcentaje de reducción	19,848
Número de iteraciones totales	984
Tiempo de computación empleado (s)	8.963,00
Temperatura inicial	0,10e-02
Temperatura final	0,51e-07

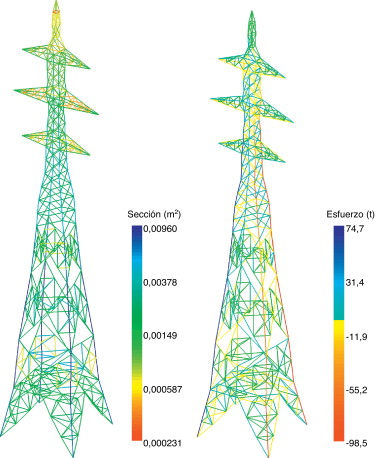
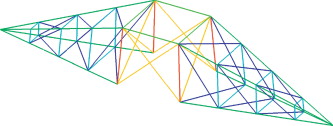
Antes de exponer en profundidad los detalles de la solución obtenida, cabe destacar el elevado número de variables discretas que intervienen en el problema. Las 77 secciones presentes en la estructura suponen un total de 154 variables discretas, número muy superior al total de variables geométricas continuas del modelo (46). La geometría obtenida como resultado del proceso de optimización se puede observar en la figura 13 y, de modo más detallado, en la tabla 8 . Por otro lado, los resultados obtenidos proporcionan un reparto de material como el que puede observarse en la figura 14 (izquierda) y en la tabla 9 .

Figura 13. Torre de 220 kV: geometría final.

Tabla 8. Torre de 220 kV: módulos y geometría final

	Módulo	Altura (m)	Base inf. X (m)	Base inf. Y (m)	Base sup. X (m)	Base sup. Y (m)	Long. ala (m)
1	K	7,000	11,01	10,25	8,59	7,38	—
2	X arriostrada	7,000	8,59	7,38	7,93	5,92	—
3	X arriostrada	10,000	7,93	5,92	5,47	3,78	—
4	X arriostrada	7,000	5,47	3,78	4,09	3,18	—
5	X	2,000	4,09	3,18	3,75	3,31	—
6	X	2,000	3,75	3,31	3,42	3,16	—
7	X	2,000	3,42	3,16	2,93	2,68	—
8	X	2,000	2,93	2,68	2,11	2,32	—
9	X	2,000	2,11	2,32	1,98	1,89	—
10	Súper X	2,000	1,98	1,89	2,09	1,65	—
11	Cruceta corta	1,625	2,09	1,65	1,82	1,59	5,20
12	X	1,625	1,82	1,59	1,62	1,74	—
13	X	1,625	1,62	1,74	1,41	1,48	—
14	Súper X	1,625	1,41	1,48	1,56	1,45	—
15	Cruceta larga	1,625	1,56	1,45	2,03	1,72	6,45
16	X	1,625	2,03	1,72	1,58	1,42	—
17	X	1,625	1,58	1,42	1,70	1,68	—
18	Súper X	1,625	1,70	1,68	1,77	1,71	—
19	Cruceta corta	1,625	1,77	1,71	1,96	1,07	5,20
20	Súper lambda	1,842	1,96	1,07	0,61	0,78	—
21	Súper lambda	1,842	0,61	0,78	0,69	0,99	—
22	Súper lambda	1,842	0,69	0,99	0,65	0,69	—
23	Cúpula	1,842	0,65	0,69	0,00	0,00	—

Figura 14. Torre de 220 kV: distribución final de material (izquierda) y envolvente de los esfuerzos obtenidos (derecha).

Tabla 9. Torre de 220 kV: codificación de los perfiles dispuestos en la geometría final

Mat.	Perfil	Área (cm2 )	Inercia (cm4 )	Mat.	Perfil	Área (cm2 )	Inercia (cm4 )
1	L200.18	68,76	1045,18	40	L60.6	6,84	9,25
2	L100.8	15,36	58,98	41	L90.8	13,76	42,40
3	L80.8	12,16	29,26	42	L150.12	34,56	298,59
4	L100.10	19,00	71,44	43	L90.7	12,11	37,75
5	L110.8	16,96	79,40	44	L150.12	34,56	298,59
6	L90.9	15,39	46,87	45	L75.8	11,36	23,86
7	L120.10	23,00	126,73	46	L120.10	23,00	126,73
8	L250.20	96,00	2304,00	47	L90.8	13,76	42,40
9	L100.8	15,36	58,98	48	L90.8	13,76	42,40
10	L70.5	6,75	12,81	49	L120.10	23,00	126,73
11	L150.16	45,44	381,77	50	L90.7	12,11	37,75
12	L180.16	55,04	678,45	51	L70.5	6,75	12,81
13	L250.20	96,00	2304,00	52	L90.8	13,76	42,40
14	L100.10	19,00	71,44	53	L50.5	4,75	4,46
15	L120.10	23,00	126,73	54	L45.5	4,25	3,19
16	L100.8	15,36	58,98	55	L110.10	21,00	96,46
17	L150.16	45,44	381,77	56	L80.6	9,24	22,82
18	L200.17	65,11	994,88	57	L110.10	21,00	96,46
19	L100.8	15,36	58,98	58	L80.6	9,24	22,82
20	L100.10	19,00	71,44	59	L100.8	15,36	58,98
21	L70.5	6,75	12,81	60	L80.6	9,24	22,82
22	L100.8	15,36	58,98	61	L90.8	13,76	42,40
23	L160.16	48,64	468,24	62	L80.6	9,24	22,82
24	L120.10	23,00	126,73	63	L70.7	9,31	17,15
25	L150.18	50,76	420,48	64	L90.7	12,11	37,75
26	L120.10	23,00	126,73	65	L50.5	4,75	4,46
27	L160.16	48,64	468,24	66	L70.7	9,31	17,15
28	L100.10	19,00	71,44	67	L50.5	4,75	4,46
29	L160.16	48,64	468,24	68	L70.5	6,75	12,81
30	L120.10	23,00	126,73	69	L70.7	9,31	17,15
31	L160.16	48,64	468,24	70	L60.6	6,84	9,25
32	L120.10	23,00	126,73	71	L70.5	6,75	12,81
33	L160.16	48,64	468,24	72	L75.6	8,64	18,66
34	L120.10	23,00	126,73	73	L70.5	6,75	12,81
35	L90.7	12,11	37,75	74	L70.5	6,75	12,81
36	L150.18	50,76	420,48	75	L60.6	6,84	9,25
37	L80.6	9,24	22,82	76	L40.3	2,31	1,42
38	L80.8	12,16	29,26	77	L70.6	8,04	15,03
39	L45.5	4,25	3,19

El resultado alcanzado de la optimización estiliza la geometría de la estructura, pudiéndose observar cómo los fustes tienden a adelgazarse de forma generalizada para incrementar su longitud en el contacto con las crucetas. Del mismo modo, en el reparto seccional se aprecia que el algoritmo redistribuye el grueso de material hacia los montantes y las barras principales, siendo las barras redundantes las que menor sección de material llevan asociadas, tal y como cabría esperar.

Cabe resaltar que las barras de mayor sección no coinciden con los montantes del módulo base, sino que corresponden con las barras de los módulos tipo X arriostrada. Este hecho se debe a que los montantes poseen una mayor longitud en dichos módulos, lo que incrementa considerablemente su esbeltez y condiciona el problema tanto desde el punto de vista de la restricción en esbeltez elemental como de la restricción en esfuerzo de compresión por los efectos del pandeo.

Este hecho indica un dimensionamiento deficiente de los bloques que componen la estructura, dado que la reorganización de tales magnitudes permitiría una mayor reducción y racionalización del peso total de la estructura.

En la figura 14 (derecha) se puede observar la envolvente de los esfuerzos obtenida del análisis estructural de la torre.

Así, la cúpula se estiliza sustancialmente debido a su escasa solicitación. Paralelamente, y para conseguir una mayor reducción de material, el algoritmo tiende a reducir la anchura de los módulos que la componen, hecho que reduce la longitud de las diagonales y barras horizontales, permitiendo secciones de menor entidad.

El proceso de optimización se detiene tras 984 iteraciones, empleando un total de 8.953,00 segundos (tabla 7 ). Si se compara el coste computacional del procedimiento cuando se implementa el análisis de sensibilidad, se observa que el ahorro en tiempo de cálculo es significativo. En ejemplos prácticos de aplicación esta reducción puede alcanzar hasta 2 órdenes de magnitud, lo que incrementa en gran medida la capacidad del algoritmo y permite encarar problemas de optimización mucho más complejos y ambiciosos.

Por otro lado, en la figura 15 se puede observar la evolución del algoritmo desde la situación inicial hasta su congelación. La geometría de la curva obtenida proporciona una leve rama casi horizontal que se extiende durante las primeras iteraciones. Posteriormente, el algoritmo desarrolla una rama de descenso claramente marcada hasta que se detiene con una temperatura de 0,51e-07. La congelación o la parada del algoritmo, en este caso, sucede de forma súbita, de modo que apenas se aprecia un cambio final de tendencia.

Figura 15. Torre de 220 kV: evolución del algoritmo durante la ejecución.

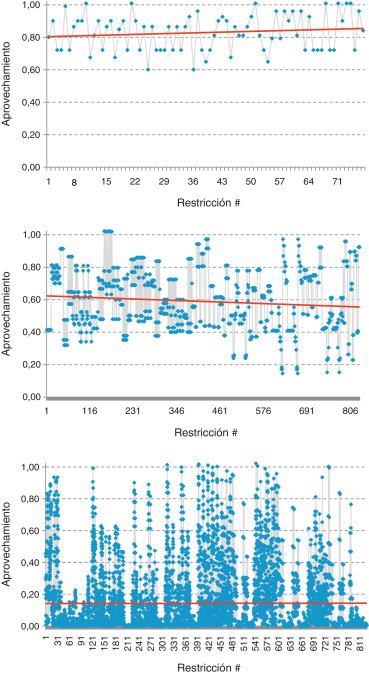
Por último, el estado de las restricciones que condicionan el problema ha experimentado un incremento generalizado. En la figura 16 se muestra el aprovechamiento estructural de las restricciones diferenciando entre las categorías expuestas anteriormente.

Figura 16. Torre de 220 kV: valor final de las restricciones de esbeltez seccional (izquierda), de esbeltez elemental (centro) y de esfuerzos (derecha).

En cualquier caso, si se analiza el número de restricciones que superan el 80% de aprovechamiento, se observa que la esbeltez elemental, y por ende la geometría de la estructura, condiciona el resultado de modo similar a como lo condiciona su estado tensional, dado el número similar de restricciones de cada tipo que superan dicho valor.

8. Conclusiones

En este trabajo se ha desarrollado una metodología de diseño óptimo de la estructura de las torres de alta tensión. La metodología desarrollada incorpora técnicas de compatibilización que permiten el tratamiento conjunto de variables de diseño continuas y discretas, necesarias para analizar correctamente y facilitar la construcción de este tipo de estructuras. El algoritmo desarrollado se ha adimensionalizado completamente con la finalidad de dotarlo de mayor generalidad y aplicabilidad práctica. Asimismo, el algoritmo también incorpora aproximaciones mediante el desarrollo en serie de Taylor (y el consecuente análisis de sensibilidad necesario) que permiten la reducción de los tiempos de cálculo hasta 2 órdenes de magnitud para ejemplos de aplicación reales. La metodología desarrollada permite alcanzar reducciones de material en torno al 20% en peso manteniendo todas las exigencias establecidas en la normativa vigente de aplicación, así como aspectos constructivos esenciales para garantizar la aplicabilidad de los diseños obtenidos.

Finalmente, es importante destacar que no se ha considerado un análisis tan completo como el presentado en el presente artículo en los estudios previos para este tipo de estructuras, en los que asumen varias simplificaciones que hacen que los resultados obtenidos se alejen de la realidad y pierdan su utilidad práctica. El resultado final obtenido con esta metodología se puede aplicar directamente a los diseños estandarizados de compañías eléctricas y permite obtener soluciones óptimas a problemas reales en tiempos de cálculo asumibles en la práctica.

Agradecimientos

Este trabajo ha sido financiado parcialmente por el MICINN (#DPI2009-14546-C02-01 y #DPI2010-16496), el MINECO (#DPI2012-33622), la CEOU de la Xunta de Galicia (#CN2011/002) y fondos FEDER.

References

1. [1] D.J. Sheppard, A.C. Palmer; Optimal design of transmission towers by dynamic programming; Computers & Structures, 1 (2) (1972), pp. 455–468
2. [2] P.P. Raj, S.O. Durrant; Optimum Structural design by dynamic programming; Journal of the Structural Division, ASCE, 102 (1976), pp. 1575–1589
3. [3] L. Hanssen; Computer program system for design of power transmission towers; 11th. ONR Naval Structural Mechanics Symposium, 12 (1981), pp. 37–45
4. [4] M.J. Box; A new method of constrained optimisation and comparison with other methods; Computer Journal, 8 (1965), pp. 42–52
5. [5] M.J.D. Powell; An efficient method for finding the minimum of a function of several variables without calculating derivatives; Computer Journal, 7 (2) (1964), pp. 155–162
6. [6] K.I. Majid, X. Tang; Optimum design of pin-jointed space structures with variable shape; Structural Engineer, 62 (1984), pp. 31–37
7. [7] M.P. Saka; Optimum design of space trusses with buckling constraints; Proceedings of the 3rd International Conference on Space Structures, Univ. of Surrey, Guildford, U.K. (1984)
8. [8] J. Felix, G.N. Vanderplaats; Configuration optimization of trusses subject to strength, displacement and frequency constraints; Revista de Obras Públicas, Trans. ASME J. Mechs., Transmiss. Automn Des., 109 (2) (1987), pp. 233–241
9. [9] P. Martí; Optimización de mallas espaciales de nudos articulados; Anales de Ingeniería Mecánica, 5-2 (1987), pp. 147–152
10. [10] Martí P., Company P.P., DISSENY 2011 v16: Manual de usuario y análisis, Universidad Politécnica de Cartagena, 2011.
11. [11] P. Martí; Optimización conjunta de torres y cimentaciones de líneas de transmisión eléctrica; I Congreso de Métodos Numéricos en Ingeniería, España (1990), pp. 725–730
12. [12] Valera A. y Navarrina F., Diseño asistido óptimo por ordenador de estructuras articuladas: Aplicación al caso de las torres de alta tensión, 1991.
13. [13] Navarrina F., Una metodología general para optimización estructural en diseño asistido por ordenador, Tesis Doctoral, Universidad Politécnica de Cataluña, Barcelona, 1987.
14. [14] G. Vieswara Rao; Optimum Design for Transmission Lina Towers; Computers & Structures, 57 (1) (1995), pp. 81–91
15. [15] Castro R., Optimizaçao de Estruturas com Multiobjetivos via Algoritmos Genéticos, PhD Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, 2001.
16. [16] Comité Técnico AEN/CTE 207 de Transporte de Energía Eléctrica, UNE EN 50421 Líneas Eléctricas Aéreas de más de 1 kV de c.a. y hasta 45 kV, 2005.
17. [17] Comité Técnico AEN/CTE 207 de Transporte de Energía Eléctrica, UNE EN 50341 Líneas Eléctricas Aéreas de más de 45 kV en Corriente Alterna, 2001.
18. [18] Comité Técnico AEN/CTN 140: 89, UNE EN 1993 Eurocódigo n.° 3: Proyecto de Estructuras de Acero, 2008.
19. [19] American Society of Civil Engineers, ASCE 1097: Design of Latticed Steel Transmission Structures, 1997.
20. [20] Ministerio de Industria, Turismo y Comercio, RD 223/2008 Reglamento sobre condiciones técnicas y garantías de seguridad en LAT y sus instrucciones técnicas complementarias ITC-LAT 01 a 09, BOE 15/02/2008, 1:16436-16554, 2008.
21. [21] S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi; Optimization by Simulated Annealing; Science, 220 (1983), pp. 671–680
22. [22] V. Cerny; Thermodynamical Approach to the Traveling Salesman Problem: An efficient Simulation Algorithm; Journal of Optimization. Theory and Applications, 45 (1985), pp. 41–45
23. [23] Martínez S., Optimización Mixta de Estructuras de Apoyo de Líneas de Transporte de Energía, Tesis Doctoral, Universidade da Coruña, La Coruña, 2012.
24. [24] N. Metropolis, A. Rosenbluth, N. Rosenbluth; Equation of State Calculations by Fast Computing Machines; Journal of Chemical Physics, 21 (1953), pp. 1081–1097
25. [25] M. Lundy, A. Mees; Convergence of an Annealing Algorithm; Mathematical Programming, 34 (1986), pp. 111–124
26. [26] S. Ledesma, G. Aviña, R. Sánchez; Practical Considerations for Simulated Annealing Implementation; Simulated Annealing, 20 (2008), pp. 401–420
27. [27] R. Kuik, M. Salomon; Multi-Level Lot Sizing Problem: Evaluation of a Simulated Annealing; European Journal of Operational Research, 45 (1) (1990), pp. 25–37
28. [28] R.H.J.M. Otten, L.P.P.P. Van Ginneken; Stop Criteria in Simulated Annealing; Proceedings of the 1988 IEEE International Conference on Computer Design, Rye Brook (NY), USA (1988), pp. 549–552
29. [29] B. Gidas; Nonstationary Markov Chains and Convergence of the Annealing Algorithm; Journal of Statistical Physics, 31 (1) (1985), pp. 73–131
30. [30] D. Geman, S. Geman; Stochastic Relaxation, Gibbs Distribution and the Bayesian Restoration of Images; IEE Transactions on Pattern Analysis and Machine Intelligence PAMI, 6 (3) (1984), pp. 721–741
31. [31] H. Orsila, E. Salminen, T.D. Hämäläinen; Best Practices for Simulated Annealing in Multiprocessor Task Distribution Problems; Simulated Annealing, 16 (2008), pp. 321–342
32. [32] B.W. Wah, Y. Chen, T. Wang; Theory and Applications of Simulated Annealing for Nonlinear Constrained Optimization; Simulated Annealing, 9 (2008), pp. 155–187