RESUMEN
Este artículo presenta un nuevo procedimiento con el que simular el fallo por delaminación en materiales compuestos. El método propuesto utiliza la teoría de mezclas serie/paralelo, desarrollada por Fernando Rastellini, para la caracterización constitutiva del material compuesto. Esta formulación obtiene el comportamiento del compuesto acoplando la respuesta constitutiva de los materiales componentes, fibra y matriz, imponiendo una relación de iso-deformación en la dirección de la fibra (dirección en paralelo) y una relación de iso-tensión en el resto de direcciones (direcciones en serie). Si bien la teoría de mezclas serie/paralelo permite simular los materiales componentes con cualquier ecuación constitutiva, el presente trabajo utiliza una formulación de daño para caracterizar la matriz y una formulación elástica para la fibra.
Se mostrará que es posible, utilizando la teoría de mezclas serie/paralelo y una formulación de daño, simular el fallo del compuesto por delaminación. Además, éste se obtiene de forma natural, sin necesidad de definir elementos especiales en los que propagar la fractura, ni ser necesario utilizar costosas técnicas numéricas como el remallado o elementos de contacto. Con el procedimiento propuesto el fallo constitutivo de la matriz conduce a una reducción de la capacidad portante del compuesto en las direcciones en serie (entre otras, la dirección de las tensiones tangenciales) sin eliminar la capacidad resistente en la dirección de la fibra. Se probará que un material compuesto con este comportamiento corresponde a un material delaminado.
La última sección de este artículo muestra la simulación del End Notch Failure Test y los resultados obtenidos son comparados con resultados experimentales. La similitud de los resultados numéricos y experimentales demuestra la validez del método propuesto para resolver problemas de delaminación en materiales compuestos.
ABSTRACT
This paper presents a new procedure to deal with the delamination problem found in laminated composites, based in a continuum mechanics formulation. The procedure proposed obtains the composite constitutive performance with the Serial/Parallel mixing theory, developed by F. Rastellini. This theory characterizes composite materials by coupling the constitutive behaviour of the composite components, imposing an iso–strain relation among the components in the fibre (or parallel) direction and an iso-stress relation in the remaining directions (serial directions). The proposed procedure uses a damage formulation to characterize the constitutive behaviour of matrix component in order to obtain the stress-strain performance of this material.
With these two formulations, the delamination phenomenon is characterized naturally by the numerical simulation, being unnecessary the definition of special elements or computationally expensive techniques like the definition of contact elements or mesh separation. Matrix failure, as a result of the stress state found in it, leads to a reduction of the stiffness and strength capacity of the composite in its serial directions, among them, the shear component. This stiffness reduction provides a composite performance equivalent to what is found in a delaminated material.
To prove the ability of the formulation proposed to solve delamination problems, the End Notch Failure test is numerically simulated and the results obtained are compared with experimental ones. The agreement found in the results with both simulations, numerical and experimental, validate the proposed methodology to solve the delamination problem.
Palabras clave
Teoria de mezclas ; Laminados ; Delaminación ; ENF test
Keywords
Mixing theory ; Laminates ; Delamination ; ENF test
1. Introducción
El uso de nuevos materiales en aplicaciones estructurales hace necesario afrontar nuevas formas de fallo y rotura, que no se dan en materiales tradicionales. En el caso de los materiales compuestos laminados, una de las formas de rotura más habituales es la delaminación. Ésta consiste en la rotura del laminado compuesto a lo largo del plano que separa las distintas capas del mismo. Esta rotura conduce a una reducción de la rigidez y capacidad resistente el compuesto que puede desembocar en el fallo del mismo.
La importancia de este tipo de fractura queda probado por la cantidad de autores que han desarrollado teorías y formulaciones para caracterizarla. Todos los autores que han estudiado el problema coinciden en la caracterización de la delaminación mediante dos fenómenos: el inicio de la rotura entre capas y la propagación de la misma a lo largo del compuesto. La iniciación de la fractura se puede obtener comparando el estado tenso-deformacional del material, en la región que delamina, con una tensión crítica [1] , [2] , [3] and [4] , o en términos de tracción versus desplazamiento relativo [5] , [6] and [7] . Por otro lado, la propagación de la delaminación se suele realizar abriendo la malla a lo largo del plano de fractura, que se suele llevar a cabo mediante dos procesos distintos: Uno de ellos es el Virtual Crack Closure Technique (VCCT)[8] , que extiende la fractura a partir de la asunción de que la energía necesaria para abrir una fractura es equivalente a la energía necesaria para cerrarla. El otro procedimiento, cada vez más utilizado, es mediante el cohesive zone model[2] . Éste consiste en añadir elementos cohesivos en la interfase que puede sufrir delaminación. La propagación de la delaminación a lo largo de estos elementos se realiza mediante formulaciones de daño o de daño plástico.
Independientemente de las diferencias existentes en los distintos modelos, definidos en la literatura para simular la delaminación, todos ellos coinciden en abrir la malla en la zona delaminada. Este proceso es numéricamente muy caro y requiere de formulaciones de contacto para evitar que un cuerpo penetre en el otro. Además, este tipo de resolución obliga a definir una formulación especial en la zona que delaminará, ya sea con elementos interfase [4] , con zonas cohesivas [5] o con nodos coincidentes tal como hace la VCCT [8] , lo que obliga a conocer el plano de delaminación antes de realizar la simulación.
La principal diferencia entre la metodología que se propone en este artículo y las distintas formulaciones existentes en la literatura es que, con el procedimiento que aquí se presenta, no es necesario hacer ninguna distinción entre los elementos que delaminarán y los que no. La metodología propuesta resuelve el problema de la delaminación mediante una formulación del continuo, capaz de simular la aparición de la rotura por delaminación, y la propagación de la misma, en cualquier elemento de la simulación. Lo que permite resolver problemas en los que no se conoce el plano de delaminación a priori .
La teoría de mezclas serie/paralelo desarrollada por Rastellini et al. [9] se utiliza para obtener el comportamiento del material compuesto y para simular el fallo del mismo por delaminación. Esta teoría se basa en la definición de ecuaciones de compatibilidad entre los estados tenso-deformacionales de los materiales componentes. En el caso de compuestos constituidos por fibras embebidas en una matriz, la teoría de mezclas serie/paralelo impone una condición de iso-deformación en la dirección de las fibras (dirección en paralelo) y una condición de iso-tensión en el resto de direcciones (direcciones en serie). En estas condiciones, si la matriz daña y, por tanto, su capacidad resistente queda anulada, la teoría de mezclas serie/paralelo anulará también la capacidad resistente de las fibras en las direcciones en serie debido a la condición de iso-tensión. Se demostrará que el comportamiento mecánico de un material, sin capacidad resistente en las direcciones en serie, equivale al comportamiento mecánico de un material delaminado.
Para obtener el comportamiento estructural descrito, la matriz del compuesto debe perder su capacidad resistente para un determinado estado tenso-deformacional. Además, para simular una fractura debida a un proceso de delaminación, esta pérdida de capacidad resistente debe ser permanente. Ésto se logra mediante una formulación de daño. La formulación de daño utilizada corresponde a la formulación de daño isótropo definida por Oller en [10] .
En la siguiente sección se describen las formulaciones que utiliza el procedimiento propuesto para simular una rotura por delaminación. Éstas son: la teoría de mezclas serie/paralelo y la formulación de daño con la que se simula el material matriz. Ninguna de las dos formulaciones se describirá en detalle, puesto que su descripción detallada, así como su implementación en un código de elementos finitos, se puede obtener de los artículos en las que se presentaron por primera vez ([9] y [11] , respectivamente). Se cree importante enfatizar esto ya que el objetivo del presente artículo no es mostrar formulaciones originales, sino probar que un uso adecuado de las mismas permite caracterizar de forma directa y precisa el fallo por delaminación de los materiales compuestos. Dicho de otro modo, el presente trabajo propone una nueva metodología con la que solucionar los problemas de delaminación, haciendo uso de la teoría de mezclas serie/paralelo.
Para probar la validez del proceso propuesto y las formulaciones utilizadas, se compararán los resultados obtenidos con una simulación numérica con resultados experimentales. Se utilizará el End Notch Flexure test (ENF), definido por la European Structural Integrity Society (ESIS). Este ensayo se usa para obtener la energía de fractura de una rotura en modo II de un compuesto, correspondiente a una fractura por delaminación. La concordancia entre los resultados experimentales y los numéricos probará la validez del procedimiento propuesto.
2. Formulación
El comportamiento mecánico o, más específicamente, el comportamiento constitutivo de los materiales compuestos laminados se obtiene haciendo uso de la teoría de mezclas serie/paralelo desarrollada por Rastellini et al. [9] , que se describe en la sección 2.1 del presente artículo. Para obtener una buena convergencia con esta formulación y, en muchos casos, para lograr convergencia de la solución, es necesario utilizar un tensor constitutivo tangente. Este tensor se puede obtener de forma analítica para algunas ecuaciones constitutivas, aunque en muchos casos su obtención es muy costosa si no imposible. Éste problema se puede solucionar calculando el tensor tangente mediante una derivación numérica. El proceso utilizado se basa en un método de perturbación y se describe en la sección 2.2 . Finalmente, la sección 2.3 describe la formulación de daño utilizada para caracterizar la matriz del compuesto.
2.1. Teoría de mezclas serie/paralelo
2.1.1. Hipótesis en las que se basa la teoría de mezclas serie/paralelo
La teoría de mezclas serie/paralelo se basa en las siguientes hipótesis para obtener el comportamiento mecánico del compuesto y sus componentes:
- El compuesto está constituido únicamente por dos materiales componentes: fibra y matriz
- Los materiales componentes tienen la misma deformación en la dirección en paralelo (dirección en que está orientada la fibra)
- Los materiales componentes tienen la misma tensión en las dirección en serie
- La respuesta del material compuesto está directamente relacionada con las fracciones volumétricas de los materiales componentes
- Los materiales componentes tienen una distribución homogénea en el material compuesto
- Se considera una unión perfecta entre los materiales componentes
2.1.2. Componentes en serie y en paralelo
Puesto que el comportamiento del compuesto es distinto en la dirección en serie y en paralelo, es necesario definir, y dividir, los componentes en serie y en paralelo de los tensores de tensión y deformación. Esta división se realiza mediante dos tensores complementarios de cuarto orden, uno correspondiente a la dirección en serie (PS ), y el otro correspondiente a la dirección en paralelo (PP ). La dirección en paralelo queda definida por la orientación de la fibra e1 . De este modo se obtiene:
|
|
( 1) |
donde,
|
|
( 2) |
Siendo la identidad. El tensor de tensiones se puede dividir de forma análoga; de modo que los componentes en serie y en paralelo del mismo se obtienen como:
|
|
( 3) |
2.1.3. Ecuaciones constitutivas de los materiales componentes
La teoría de mezclas serie/paralelo obtiene el comportamiento mecánico de los materiales constituyentes utilizando cualquier tipo de ecuación constitutiva (por ejemplo, un modelo plástico con criterio de fluencia de Mohr-Coulomb para la matriz y un modelo de daño J2 para la fibra). En el caso concreto del presente trabajo, en el que se utiliza una formulación de daño isótropo para caracterizar el material matriz y una formulación elástica para las fibras, las tensiones en los materiales componentes se pueden obtener utilizando:
|
|
( 4) |
siendo y los tensores constitutivos del material matriz y del material fibra, respectivamente.
Estas ecuaciones se pueden reescribir teniendo en cuenta la división que se hace de los tensores de tensión y deformación, en sus componentes en serie y paralelo (equaciones (1 ) y (3 )). Obteniendo:
|
|
( 5) |
donde,
|
|
( 6) |
con i = m , f , matriz y fibra respectivamente. En el caso de la fibra, como ésta se caracteriza con una formulación elástica, en la ecuación (5) ): fd =0.
2.1.4. Ecuaciones de equilibrio y compatibilidad
Las ecuaciones que definen el equilibrio tensional en el compuesto y establecen las condiciones de compatiblidad deformacional de los materiales compontentes se obtienen a partir de las hipótesis en las que se basa la formulación. A partir de éstas se puede escribir:
|
|
( 7) |
|
|
( 8) |
donde los superíndices c , m y f hacen referencia al compuesto, a la matriz y a las fibras, respectivamente; y ik corresponde a la fracción volumétrica de cada uno de los materiales constituyentes en el compuesto.
2.1.5. Algoritmo de la teoría de mezclas serie/paralelo
El algoritmo de la teoría de mezclas serie/paralelo parte de las deformaciones en el material compuesto cɛ en el instante t + Δt . A partir de estas deformaciones se deben encontrar los estados deformacionales de los componentes del compuesto, con los que calcular las tensiones en el compuesto cσ . Éstos deberán verificar las ecuaciones de equilibrio y compatibilidad, así como la correcta evolución de sus variables internas.
Lo primero que debe hacer el algoritmo es dividir el tensor de deformaciones en su componente en serie y paralelo, para poder calcular los tensores de deformación de los materiales fibra y matriz. Si bien las deformaciones en paralelo son idénticas para ambos componentes (ecuación (7) ), no ocurre lo mismo con las deformaciones en serie (ecuación (8) ), por lo que es necesario realizar una predicción de las deformaciones que se esperan en uno de los dos materiales componentes. En caso de realizar esta predicción sobre el material matriz, el incremento de las deformaciones en serie se puede obtener como:
|
|
( 9) |
donde y m ΔɛS = c [t + ΔtɛS ] − c [tɛS ]
La predicción inicial de las tensiones en serie de la matriz, propuesta por Rastellini et al. [9] y mostrada en la ecuación (9) , se obtiene a partir de una distribución de la deformación en sus componentes en serie y paralelo en función de la matriz de rigidez tangente obtenida para el compuesto en el anterior incremento de carga. Conocidas las deformaciones en la matriz, las deformaciones en la fibra se pueden obtener para la iteración n como:
|
|
( 10) |
siendo .
Una vez conocidas las componentes en serie y paralelo de las deformaciones de la fibra y la matriz, éstas se reagrupan (ecuación (3 )) para poder aplicar la ecuación constitutiva a cada uno de los materiales y obtener, de este modo, las tensiones y la evolución de las variables internas en los mismos. Con este procedimiento, tanto las tensiones en la fibra como en la matriz se pueden calcular aplicando el modelo constitutivo elegido para cada componente. Las tensiones obtenidas con sendos modelos constitutivos deberán verificar:
|
|
( 11) |
Si la tensión residual es menor que la tolerancia definida, el estado tenso-deformacional de los materiales componentes es correcto y se puede proceder a calcular el tensor de tensiones del compuesto (ecuación (3 )) para el punto de Gauss en consideración. Por otro lado, si la ecuación (11) no se cumple, la predicción inicial del tensor de deformación de la matriz no proporciona un estado tensional en equilibrio y debe ser corregido. Esta corrección se realiza mediante un procedimiento de Newton-Raphson, en el que la predicción inicial se corrige mediante el jacobiano de las fuerzas residuales. Según Rastellini et al. [12] , el jacobiano se puede obtener según la siguiente expresión:
|
|
( 12) |
y, la corrección de la componente en serie del material matriz pasa a ser:
|
|
( 13) |
Si se quiere obtener convergencia cuadrática en el algoritmo de la teoría de mezclas serie/paralelo, el jacobiano debe obtenerse mediante los tensores constitutivos tangentes de los materiales fibra y matriz. No obstante, depende de la ecuación constitutiva que se utilice para cada uno de estos materiales, la expresión del tensor constitutivo tangente no se puede calcular de forma analítica. Con el propósito de obtener un algoritmo robusto, la expresión del tensor constitutivo tangente se obtendrá mediante una derivación numérica.
2.2. Tensor constitutivo tangente algorítmico
El tensor constitutivo tangente algorítmico, , se obtiene numéricamente para cada uno de los materiales componentes del compuesto. Este cálculo se realiza mediante una estrategia de perturbación. Para ello se parte de una definición del tensor constitutivo tangente como:
|
|
( 14) |
Esta expresión se puede reescribir, en el caso de materiales isótropos y ortótropos, de forma matricial:
|
|
( 15) |
El tensor de tensiones de las ecuación (15) se puede interpretar como la suma de n tensores de tensiones, resultantes del producto de la componente j del tensor de deformaciones por la columna j del tensor constitutivo tangente. Esto es:
|
|
( 16) |
donde
|
|
( 17) |
Luego, la columna j del tensor constitutivo tangente se puede obtener a partir de la ecuación (16) como:
|
|
( 18) |
La obtención del tensor constitutivo tangente mediante un método de perturbación numérica consiste en definir n pequeñas variaciones (o perturbaciones) del tensor de deformaciones, δɛj , para obtener n tensores de tensión δjσ . El tensor constitutivo tangente se obtiene aplicando la ecuación (18) a cada uno de los tensores de tensión obtenidos y a su correspondiente perturbación.
2.2.1. Implementación numérica del cálculo del tensor constitutivo tangente algorítmico
En un código de elementos finitos, la ecuación constitutiva del material proporciona el tensor de tensiones σ y la evolución de las variables internas q , asociadas a un determinado estado deformacional ɛ . A partir del estado tenso-deformacional resultantes se aplica una pequeña perturbación al tensor de deformaciones, y se vuelven a calcular las tensiones asociadas a esta nueva deformación. Estas tensiones, junto con la perturbación aplicada, se utilizarán para calcular la matriz constitutiva tangente mediante la ecuación (18) . Es necesario aplicar n perturbaciones al tensor de deformaciones para poder calcular todas las componentes del tensor de tensiones.
Con el proceso definido, cuanto más pequeña sea la perturbación aplicada, mejor será la aproximación al tensor constitutivo tangente. Partiendo de esta consideración, el valor de la perturbación que se debe aplicar a cada componente del tensor de deformaciones se obtiene mediante el siguiente procedimiento:
|
|
( 19) |
Definiendo de este modo el tamaño de la perturbación, el incremento de deformaciones será siempre suficientemente pequeño para asegurar que la variación del vector de tensiones está cercana al valor original. El único inconveniente del proceso descrito es que puede proporcionar valores de la perturbación cercanos a cero (por ejemplo, cuando uno de las componentes del tensor de deformaciones es cercano a cero). En este caso, la ecuación (18) puede conducir a una indeterminación. Para evitar esta situación, es necesario imponer una nueva condición para asegurar que el valor de la perturbación es suficientemente grande. Esta condición es:
|
|
( 20) |
Mediante el procedimiento indicado se obtiene una buena aproximación del tensor constitutivo tangente. Además, y ésto es una de las principales ventajas del método propuesto, este cálculo es independiente de la ecuación constitutiva utilizada para caracterizar el material. La validez de este procedimento queda probada en las simulaciones realizadas por Martinez et al. en [13] .
2.3. Formulación de daño isótropo
La degradación material de un sólido debido a un proceso de fractura se puede simular mediante una formulación de daño. Esta formulación parte de considerar la reducción del area efectiva resistente del material a partir de una reducción de sus propiedades de rigidez y resistencia. Una de las principales características de una formulación de daño es que la degradación del material es permanente; esto es, una vez el material ha dañado, es imposible para éste recuperar las características originales de rigidez y resistencia. Para simular un proceso de delaminación en compuestos, la formulación que se propone utilizar para predecir el comportamiento constitutivo del material matriz es la formulación de daño isótropo definida por Oller en [10] . Esta formulación esta basada en la teoría de daño en el continuo definida originalmente por Kachanov [14] . En esta sección se describen las principales características de la formulación utilizada.
2.3.1. Modelo de daño isótropo
Un proceso de daño se puede simular, en el contexto de la mecánica de los medios contínuos, mediante la introducción de una variable interna, , que representa en nivel de daño en el material. Esta variable transforma el tensor de tensiones real, σ , en un tensor de tensiones efectivo, σ0 . Esto es:
|
|
( 21) |
En el caso de daño isótropo, todas las direcciones del tensor de tensiones sufren la misma degradación. Esta consideración permite definir la variable interna de daño mediante un escalar. De modo que la ecuación de daño se puede reescribir como:
|
|
( 22) |
La variable interna de daño toma valores comprendidos entre 0 y 1; siendo d = 0 cuando el material no está dañado y d = 1 cuando el material está completamente dañado. Las tensiones efectivas, mostradas en la ecuación (22) , corresponden a las tensiones que se obtendrían en el material si este no estuviese dañado:
|
|
( 23) |
y el tensor de tensiones real se puede obtener, a partir del estado deformacional del material, acoplando las ecuaciones (22) and (23) :
|
|
( 24) |
2.3.2. Criterio umbral de daño
El criterio umbral de daño define el estado tenso-deformacional en el que empieza la degradación del material o, lo que es lo mismo, el estado en el que se pierde el comportamiento elástico. Mediante éste es posible definir distintos comportamientos constitutivos de los materiales. Éste se suele definir a partir del tensor de tensiones y de las variables internas del material, de modo que en el punto de estudio se debe cumplir:
|
|
( 25) |
siendo c (d ) una función que define el valor límite de daño y f (σ0 ) una función que caracteriza la superficie de daño. El daño empieza la primera vez que el valor de f (σ0 ) es mayor o igual que c (d ). Normalmente, en lugar de trabajar con la ecuación (25) , el criterio de daño se convierte a un criterio equivalente mediante una función escalar G , positiva, con su derivada positiva, monótona creciente e invertible:
|
|
( 26) |
En este trabajo, el criterio umbral de daño que se utilizará está definido por la norma de las tensiones principales, distinguiendo entre la resistencia del material a tracción y compresión:
|
|
( 27) |
donde σI es el tensor de tensiones principales y ϱ una función de peso que pondera la proporción de cargas a tracción y compresión en el material. Ésta última se define como:
|
|
( 28) |
siendo , la relación entre la resistencia del material a compresión y tracción, y r0 una función escalar que define la relación a tracción y compresión en el tensor de tensiones del material, definida como:
|
|
( 29) |
con 〈x 〉 la función de McAully: 〈x 〉 = 0.5[x + | x |]
La función de peso ϱ transforma las tensiones de tracción en tensiones equivalentes de compresión, ponderándolas por la resistencia a tracción del material. Por tanto, la superficie de daño f (σ0 ) deberá compararse con un valor límite de daño c (d ) caracterizado por las tensiones de compresión.
2.3.3. Evolución del parámetro de daño. Comportamiento de ablandamiento
Los problemas de la mecánica del continuo dependientes de variables internas requieren la definición de la evolución de las mismas. En el problema de daño, la ley que define la variable de daño es [10] :
|
|
( 30) |
siendo μ un escalar no-negativo llamado parámetro de consistencia de daño. Este parámetro se utiliza para definir las condiciones de Kuhn–Tucker de carga-descarga:
|
|
( 31) |
Las condiciones de Kuhn–Tucker indican que si el criterio de daño es menor que cero, entonces y, por tanto, no hay variación en el daño del material. Por otro lado, si las tensiones se encuentran sobre la superficie de daño, y el criterio de daño es igual a cero, el parámetro de consistencia de daño es mayor que uno y, por tanto, habrá una variación del daño en el material. Haciendo uso de la condición de consistencia: , se puede probar que la expresión final del parámetro de daño es [15] :
|
|
( 32) |
De este modo, la evolución del parámetro de daño depende en la función G definida. A continuación se muestran dos posibles expresiones de la función G , que se pueden utilizar para caracterizar dos tipos de ablandamiento distintos:
- Ablandamiento lineal: La evolución del parámetro de daño, en el caso de aplicar un ablandamiento lineal, se define mediante la siguiente expresión de G :
|
|
( 33) |
- Ablandamiento exponencial: Esta expresión, propuesta por Oliver et al[11] , proporciona un ablandamiento exponencial del material. En este caso, el parámetro de daño se define como:
|
|
( 34) |
En las dos expresiones mostradas la variable de daño es función del parámetro A , que depende de la energía de fractura del material y cuya expresión se define en la siguiente sección; y del valor de τ0 , que corresponde a la tensión máxima elástica que puede aplicarse al material. En caso de utilizar la superfine de daño definida por la norma de las tensions principales, τ0 corresonde a la tensión máxima en un estado de compresión pura.
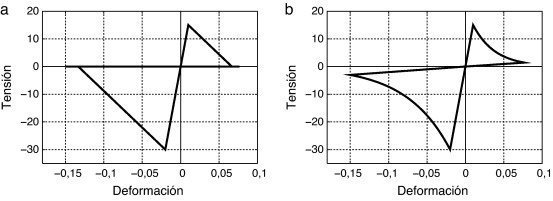
La figura 1 a muestra el comportamiento tenso-deformacional de un material con ablandamiento lineal; la figura 1 b muestra el mismo material si el ablandamiento aplicado es exponencial. En ambos casos se ha definido la relación entre la tensión límite de tracción y compresión como .
|
|
|
Fig. 1. Comportamiento tenso-deformacional de un material caracterizado con la formulación de daño propuesta. (a) Ablandamiento lineal. (b) Ablandamiento exponencial. |
2.3.4. Parámetro A
El parámetro A , que aparece en las ecuaciones (33) y (34) , se obtiene a partir de la ecuación de disipación del material, al considerar un proceso de carga uniaxial monótona creciente. La expresión de este parámetro para las dos leyes de ablandamiento consideradas es, según Oller [15] :
|
|
( 35) |
donde C0 es la rigidez inicial del material y gc corresponde a la energía máxima, por unidad de volumen, que puede disipar el material bajo cargas de compresión.
La mecánica de fractura clásica define la energía de fractura de un material como la cantidad de energía que se disipa cuando éste rompe a lo largo de una unidad de área. Esta energía se puede definir como:
|
|
( 36) |
siendo Wf la energía que disipada al final del proceso de rotura y Af el área fracturada. Al acoplar la mecánica de fractura con la mecánica del continuo, la energía disipada Wf se relaciona con la energía volumétrica de fractura gf según:
|
|
( 37) |
La energía de fractura por unidad de volumen es la característica material que necesita la mecánica del continuo. Ésta se puede obtener a partir de la energía de fractura mediante la ecuación (37) , obteniendo:
|
|
( 38) |
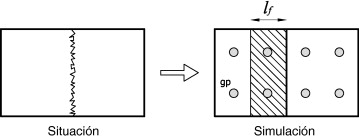
La ecuación (38 ) muestra que la energía de fractura por unidad de volumen se obtiene dividiendo la energía de fractura por la longitud de fractura. Ésta corresponde a la longitud dañada, perpendicular al plano de rotura. Esta longitud tiende a cero en la mecánica del continuo. No obstante, si esta formulación se aplica a un código de elementos finitos, en el que la formulación del continuo se transforma a una formulación discreta, la longitud de fractura pasa a ser la dimensión característica del punto de Gauss sobre el que se está calculando el estado tenso-deformacional. Asimilando la longitud de fractura a la longitud del elemento se está imponiendo que la fractura se extiende a lo largo de todo éste. La figura 2 muestra una representación de la longitud de fractura considerada.
|
|
|
Fig. 2. Fractura en un cuerpo continuo y en su homólogo discretizado. |
3. Simulación del End Notch Flexure (ENF) test
La capacidad de la formulación presentada para simular un proceso de delaminación se demuestra mediante la simulación del End Notch Flexure (ENF) test. Este ensayo está definido por la European Structural Integrity Society (ESIS) y se utiliza para obtener la tenacidad del material frente fracturas en modo II, correspondientes a rotura por cortante, en compuestos reforzados con fibras unidireccionales.
La validación de la formulación se realiza comparando los resultados numéricos con resultados experimentales. Los resultados experimentales que se utilizan corresponden a los ensayos realizados por el Centre per a la Innovació en Materials, Estructures i Processos (CIMEP) y la Universitat de Girona, para el proyecto GRINCOMP (ref. MAT2003-09768-C03) [16] .
3.1. Descripción del ensayo experimental
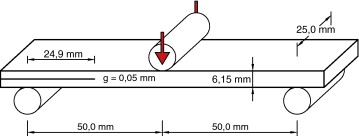
El End Notch Flexure test consiste en flexionar una viga con una fractura inicial en uno de sus extremos. Este ensayo se aplica a un compuesto de fibras de carbono embebidas en una matriz epoxídica. Las fibras en el compuesto están orientadas en la dirección longitudinal de la matriz. La fractura inicial se obtiene mediante un inserto, no adherido a las láminas colindantes, en el plano medio de la viga. El espesor del inserto debe ser menor de 50 μm. La viga tiene una luz de 100 mm y se solicita con una carga concentrada en su centro de luz, que se aplica mediante una prensa con control de desplazamiento. El CIMEP realizó ensayos sobre tres series distintas: GRIN006, GRIN015 y GRIN024, cada una consistente en 5 especímenes. La simulación numérica se ha realizado sobre el primer espécimen de la serie GRIN006 (viga 3M101, según la nomenclatura de los ensayos). Las dimensiones de este espécimen, así como las dimensiones consideradas en la simulación numérica, se muestran en la figura 3 .
|
|
|
Fig. 3. Geometría del espécimen utilizado en el ENF test. |
El ensayo consiste en aplicar un desplazamiento vertical a la viga, según se muestra en la figura 3 , hasta que la fractura inicial se empieza a propagar. El desplazamiento impuesto se aplica hasta que la progresión de la fractura para y la viga recupera su comportamiento elástico, momento en que la viga se descarga. Los principales resultados que se obtienen del ensayo experimental son el gráfico fuerza-desplazamiento de la estructura y la longitud final de la fractura. Estos dos resultados son los que se comprarán con la respuesta obtenida de la simulación numérica.
Las características del material compuesto se desconocían cuando se realizaron los ensayos experimentales, ya que no se realizaron ensayos específicos del material. No obstante, sí que se disponía de las características definidas por el fabricante, correspondientes al prepeg unidireccional de fibra de carbono HexPly 8552 de la casa Hexcel. La tabla 1 muestra las propiedades de la fibra y la matriz de este prepeg. Éstas han sido las que se han utilizado para caracterizar los materiales en la simulación numérica.
| Propiedades matriz | |
|---|---|
| Tensión de rotura | 120.66 MPa |
| Módulo elástico | 4.67 GPa |
| Módulo de Poisson | 0.30 |
| Energía de fractura (modo I) | 0.68 kJ/m2 |
| Participación volumétrica | 42.6% |
| Propiedades fibra | |
| Tensión de rotura | 4.278 MPa |
| Módulo elástico | 228 GPa |
| Módulo de Poisson | 0.0 |
| Participación volumétrica | 57.4% |
3.2. Descripción del modelo numérico
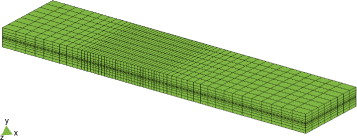
Se han desarrollado dos modelos numericos distintos para simular el End Notch Flexure test. Uno de ellos es bidimensional y utiliza una formulación de tensión plana. El segundo utiliza una formulación tridimensional. El modelo 2D contiene 627 elementos cuadriláteros lineales, mientras que el modelo 3D contiene 5.016 elementos hexaédricos lineales. La malla definida para el modelo tridimensional se muestra en la figura 4 .
|
|
|
Fig. 4. Malla utilizada en el modelo tridimensional. |
Para realizar la simulación numérica se han definido dos materiales distintos. Uno de ellos corresponde al material compuesto. El otro material definido (que denominaremos material inserto) corresponde a la lámina que se introduce en el compuesto para caracterizar la fractura inicial.
El material compuesto se define a partir de las características mecánicas de sus materiales componentes (mostradas en la tabla 1 ) y la participación volumétrica de los mismos en el compuesto. Las fibras se han definido como un material elástico y la matriz utiliza la formulación de daño definida en la sección 2.3 . El modelo de daño requiere, para poder simular correctamente la evolución del daño, conocer la relación entre las resistencias a tracción y compresión del material, así como la energía de fractura del mismo. Debido a que estos dos valores son desconocidos, en la presente simulación se ha considerado que ambas resistencias son iguales. La energía de fractura de la matriz se ha obtenido de los resultados experimentales. El valor de esta energía, para la viga 3M101, es de: GII = 1.02 kJ/m2 .
Las características mecánicas del material inserto se han definido a partir de la respuesta estructural que se espera del mismo. Éstas se muestran en la tabla 2 . El principal comportamiento que se espera de este material es que permita el deslizamiento entre las capas que separa y que no permita la inclusión de la capa superior en la inferior. Para conseguir este comportamiento se ha definido un material con una rigidez cortante cercana a cero (no se ha definido igual a cero para evitar inestabilidades numéricas); y con un modulo de elasticidad longitudinal y transversal muy alto, para evitar la inclusión de una capa dentro de la otra. Este material se ha caracterizado mediante una ley elástica.
| Propiedades inserto | |
|---|---|
| Tensión de rotura | 1.000 GPa |
| Módulo elástico | 10−9 GPa |
| Módulo de Poisson | 0.0 |
| Participación volumétrica | 100% |
3.3. Comparación de los resultados numéricos con los resultados experimentales
Los resultados numéricos y experimentales se comparan mediante el gráfico fuerza-desplazamiento que se obtiene en ambos casos. El desplazamiento representado corresponde al desplazamiento vertical en el punto en que se aplica la carga. La fuerza corresponde a la carga aplicada. Este gráfico se muestra en la figura 5 .
|
|
|
Fig. 5. Gráfico fuerza-desplazamiento del ENF test obtenido con los distintos modelos numéricos y con el ensayo experimental. |
Lo primero que se ve en la figura 5 es que aparecen dos curvas en lugar de las tres esperadas (correspondientes al ensayo experimental y al ensayo numérico 2D y 3D). Esto es porque la simulación bidimensional proporciona exactamente los mismos resultados que la simulación tridimensional. Luego, para este tipo de problemas, será preferible realizar modelos 2D debido a su bajo coste computacional. No obstante, el resultado más significativo mostrado en la figura 5 es la similitud de los resultados experimentales y numéricos. La comparación de los mismos permite concluir que:
- La rigidez inicial de la viga es prácticamente idéntica.
- La máxima carga que se puede aplicar al espécimen es la misma en ambos casos: 2.215 N en el espécimen experimental y 2.214.6 N en el modelo numérico.
- El único resultado que diverge un poco es la rigidez de la viga una vez se ha alcanzado la carga máxima, al ser el modelo numérico es un 6% más rígido que los resultados experimentales (1.146 N/mm y 1.076 N/mm, respectivamente).
El otro resultado a comparar es la longitud de la zona delaminada al final del ensayo. La longitud de fractura final para el espécimen 3M101 es de 50.34 mm y la media de las longitudes fracturadas en la serie GRIN006 (consistente en 5 especímenes) es de 49.0 mm; esto es, poco menos de la mitad de la viga.
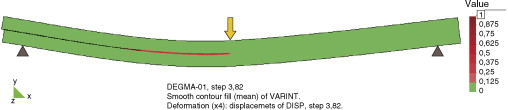
En la simulación numérica, la fractura se habrá extendido a lo largo de todos aquellos puntos en los que el parámetro de daño de la matriz sea igual a la unidad. En estos puntos la rigidez de la matriz es igual a cero, lo que implica que la rigidez en las direcciones en serie del material compuesto es también nula, debido a la condición de iso-tensión impuesta en estas direcciones por la teoría de mezclas serie-paralelo. En todos estos puntos, el compuesto no puede desarrollar esfuerzos tangenciales, lo que equivale a tener una fractura en modo II. La longitud fracturada queda definida, por tanto, por el punto más alejado del apoyo en el que el parámetro de daño de la matriz sea cercano a la unidad. La figura 6 muestra el parámetro de daño en la matriz en el instante en que la viga alcanza su máxima deflexión. En esta figura se puede ver que la longitud fracturada llega prácticamente al centro de la viga.
|
|
|
Fig. 6. Daño en el material matriz en el instante en que se alcanza la máxima deflexión en la viga. |
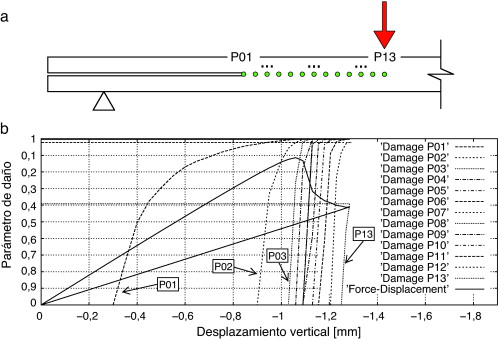
El valor exacto del parámetro de daño en la matriz se muestra, para los puntos representados en la figura 7 a, en la figura 7 b. En ésta se puede ver que en el punto 13, correspondiente al centro de luz, el parámetro de daño vale 0.6. En el punto 12, el daño vale 0.98; este valor se considera suficientemente cercano a la unidad como para considerar que la fractura ha alcanzado este punto, el cual se encuentra a 48.0 mm del apoyo. El daño en el punto situado a 49.0 mm del apoyo es de 0.89; valor que se acerca también suficientemente a la unidad como para considerar la sección dañada y concluir, por tanto, que los resultados experimentales y numéricos son coincidentes.
|
|
|
Fig. 7. Evolución del parámetro de daño en distintos puntos de la viga. |
En esta última figura se muestra también el gráfico fuerza-desplazamiento de la simulación numérica (el valor de la fuerza se ha normalizado por 2.500N para que encaje en la figura). Esta figura muestra que la fractura se propaga justo después de haber alcanzado la carga máxima en la viga. Además, la pérdida de rigidez en la viga, debido a la propagación de la fisura, se estabiliza cuando ésta alcanza el centro de luz. Ésto es debido a que en el centro de luz cambia el signo de los esfuerzos cortantes, siendo cero justo en él. De modo que la solicitación que conduce a la propagación de la delaminación es nula en el centro de luz, imposibilitando su avance.
3.4. Estudio detallado de los resultados numéricos
Según los gráficos fuerza-desplazamiento obtenidos para la viga, los resultados obtenidos mediante la simulación tridimensional son exactamente iguales que los obtenidos con la simulación bidimensional. De modo que, para simplificar la visualización de los resultados, el estudio detallado de los resultados numéricos se realizará con el modelo bidimensional.
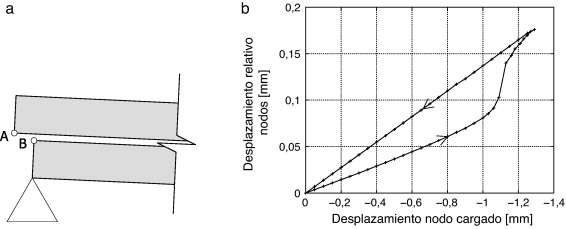
Lo primero que se debe validar de la simulación numérica es la corrección de las suposiciones hechas del material inserto. Esto es, que reduciendo la rigidez a esfuerzos tangenciales del material, se posibilita el deslizamiento entre las capas superior e inferior de la viga. Para validar este comportamiento, se ha representado el desplazamiento relativo entre los nodos sobre y bajo el inserto en el apoyo (nodos A y B representados en la figura 8 a). La figura 8 b muestra este desplazamiento. Esta figura muestra que el desplazamiento de los dos nodos es lineal para los primeros pasos de carga. Este desplazamiento prueba la validez del material definido, ya que permite el deslizamiento de una superficie sobre la otra. La separación entre A y B se mantiene constante hasta que la deflexión en la viga es algo superior a 1.0 mm, momento en que se produce la delaminación. En este instante la separación de los puntos A y B crece exponencialmente doblando su longitud. Este comportamiento exponencial se inicia cuando la fractura empieza a propagarse y finaliza cuando la fractura alcanza el centro de luz. Es interesante ver también que durante el proceso de descarga, la separación de los puntos A y B recobran su comportamiento lineal, mostrando que una vez la fractura está abierta, el compuesto delaminado se comporta como el material inserto.
|
|
|
Fig. 8. Deslizamiento relativo entre la superficie superior e inferior de la viga a lo largo del ensayo. |
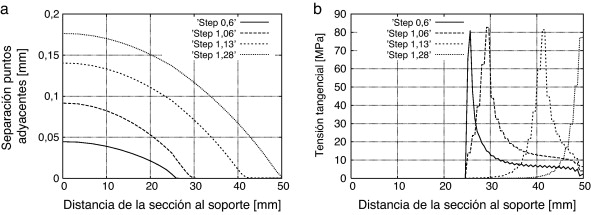
Se puede obtener una mejor compresión del comportamiento de la viga estudiando como se separan longitudinalmente puntos adyacentes, localizados sobre y bajo el plano medio de la viga. También es interesante estudiar la evolución de las tensiones tangenciales que se obtienen en el plano medio de la viga, a medida que avanza la simulación. Ambos parámetros se muestran en la figura 9 para distintos pasos de carga. Cada uno de los pasos de carga corresponde a una deflexión de la viga en el centro de luz de la misma magnitud (por ejemplo, el paso 1.06 corresponde a una deflexión de 1.06 mm). Esta figura muestra que para el paso de carga 0.60, cuando la propagación de la fractura todavía no ha empezado, el único deslizamiento se da en la sección que contiene el inserto; y, del mismo modo, todas las tensiones tangenciales se concentran en la sección adyacente al final del inserto (punto P01 en la figura 7 a). No obstante, cuando la delaminación se empieza a propagar, la zona que desliza, así como el punto con máximas tensiones tangenciales, se mueve hacia el centro de luz. Finalmente, el último paso de carga representado, 1.28, corresponde al instante en que la fractura a alcanzado el centro de luz. En este caso, las tensiones tangenciales son nulas a lo largo de toda la fractura y la sección superior de la viga desliza libremente sobre la sección inferior.
|
|
|
Fig. 9. Evolución del deslizamiento entre las capas superior e inferior (a) y evolución de las tensiones tangenciales (b) largo del plano de delaminación. |
El efecto de la propagación de la delaminación en la viga se puede ver también estudiando las tensiones longitudinales en el compuesto (fig. 10 ). En la figura 10 a se muestran las tensiones longitudinales para el paso de carga correspondiente a una deflexión de la viga de 0.6 mm, cuando la propagación de la fractura no se ha iniciado todavía. En esta figura se puede ver que la distribución de las tensiones longitudinales en las secciones afectadas por la fractura inicial corresponde a tener dos vigas a flexión, una sobre otra. Estas vigas quedan definidas por la zona comprendida entre las fibras a tracción y a compresión. Por otro lado, la sección no afectada por la fractura inicial se comporta como una única viga. A medida que se propaga la delaminación, la distribución de tensiones longitudinales equivalente a tener dos vigas se va extendiendo por la zona dañada, hasta obtener el comportamiento mostrado en la figura 10 b, cuando la fractura ha alcanzado el centro de luz.
|
|
|
Fig. 10. Tensiones longitudinales en el compuesto para dos pasos de carga distintos. |
La figura 10 muestra que, a pesar que la zona delaminada es incapaz de desarrollar tensiones tangenciales, tal como se ha mostrado en la figura 9 , esto no impide que desarrolle tensiones longitudinales. Este comportamiento se obtiene de forma natural gracias a la teoría de mezclas serie/paralelo. Cuando la matriz está completamente dañada, ésta no pude desarrollar tensiones tangenciales y, por la condición de iso-tensión, tampoco podrá desarrollar estas tensiones la fibra ni, por tanto, el compuesto. No obstante, puesto que la fibra no está dañada, ésta todavía es capaz de contribuir a la respuesta del compuesto en su dirección en paralelo. Por tanto, en este caso, la viga es capaz de seguir desarrollando tensiones longitudinales.
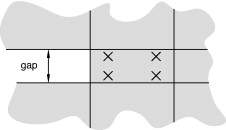
Finalmente, la última simulación numérica realizada ha sido para validar el parámetro de longitud de fractura, requerido por la formulación de daño utilizada. Según se ha explicado en la sección 2.3 , la longitud de fractura representa la distancia, perpendicular a la superficie de rotura, en la que se extiende la fractura en la simulación numérica. La malla utilizada para realizar la simulación de elementos finitos tiene un único elemento adosado a la zona en que se ha definido la fractura inicial, mediante el material inserto, tal como se muestra en la figura 11 . Esta figura también muestra los puntos de Gauss definidos en el elemento finito.
|
|
|
Fig. 11. Elementos finitos y puntos de Gauss definidos adyacentes a la fractura inicial. |
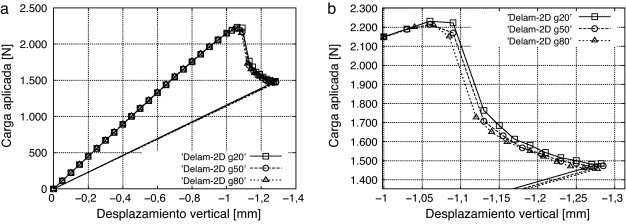
Con la distribución de puntos de Gauss mostrados en la figura 11 , la longitud de fractura que se debe definir corresponde a la mitad del espesor del inserto, ya que ésta es la longitud en la que se extenderá la fractura. Para validar este planteamiento, se han realizado tres simulaciones distintas con tres espesores distintos de la fractura inicial. El modelo Delam-2D-g20 tiene una fractura inicial con un espesor de 20 μm, por tanto, se ha definido una longitud de fractura de 10 μm; el modelo Delam-2D-g50 tiene una fractura inicial de 50 μm y una longitud de fractura de 25 μm; y, finalmente, el modelo Delam-2D-g80 tiene una fractura inicial de 80 μm y una longitud de fractura de 40 μm.
La figura 12 a muestra la respuesta en fuerza-desplazamiento de los tres modelos realizados. En 12 b se muestra un zoom del instante en que se propaga la delaminación. Tal como se puede ver en ambos gráficos, la respuesta de los tres modelos es prácticamente idéntica; observándose únicamente pequeñas variaciones en el instante en que se propaga la delaminación. La semejanza en la respuesta obtenida con los distintos modelos valida la longitud de fractura definida y permite concluir que la formulación de daño presentada es independiente del tamaño de malla.
|
|
|
Fig. 12. Gráfico fuerza-desplazamiento para los modelos realizados para validar la independencia de la solución respecto el tamaño de malla. |
4. Conclusiones
El presente artículo muestra que, si se utilizan las ecuaciones constitutivas adecuadas para caracterizar los materiales componentes, la teoría de mezclas serie/paralelo es capaz de simular el fallo por delaminación en compuestos por sí sola, sin necesidad de ninguna otra formulación específica ni elementos con propiedades específicas en la zona donde se espera que se produzca la delaminación. Esto se ha validado con la simulación del End Notch Flexure (ENF) test. Los resultados obtenidos mediante la simulación son prácticamente idénticos a los resultados experimentales.
La rotura por delaminación consiste en la pérdida de capacidad de transmisión de tensiones tangenciales entre las capas del compuesto, debido a que se produce una fractura entre las mismas. En la simulación numérica presentada, esta rotura entre capas queda caracterizada por la rotura del material matriz. La condición de iso-tensión de la teoría de mezclas serie/paralelo fuerza a que el resto de materiales tampoco puedan desarrollar tensiones en la direcciones en serie (entre ellas, la dirección correspondiente a las tensiones tangenciales), lo que se traduce en una pérdida de la rigidez transversal en el compuesto. Esta situación equivale a tener el material completamente delaminado, tal como se ha mostrado con el material inserto, el cual permite un deslizamiento perfecto entre las superficies localizadas sobre y bajo el mismo.
La gran virtud del procedimiento propuesto para simular la delaminación es que no requiere de formulaciones específicas para la simulación de la misma. De este modo se puede realizar la simulación sin hacer ninguna distinción entre los elementos que se creen que pueden delaminar y los que no. Esto permite hacer simulaciones de problemas en los que se sabe que se pueden dar roturas por delaminación, pero en los que no se sabe en que elemento, ni en que sección se puede producir la misma. Así mismo, con el prodecimiento propuesto, no es necesario remallar, ni añadir una formulación de contacto para realizar la simulación, lo que reduce significativamente los costes computacionales.
La simulación mostrada ha probado que la formulación de daño utilizada para simular el comportamiento constitutivo del material matriz es capaz de dañar el material en un proceso de delaminación. Esta formulación requiere conocer el tamaño del elemento finito, ya que la energía de fractura que se disipará depende de la longitud de fractura del mismo. Esta longitud de fractura corresponde a la longitud del elemento, perpendicular al plano de delaminación. Introduciendo esta longitud en la formulación, la simulación es independiente del tamaño de malla definido en el modelo de cálculo.
Si bien la formulación de daño utilizada ha mostrado ser adecuada, a la luz de los resultados obtenidos, se cree importante enfatizar que la teoría de mezclas serie/paralelo permite caracterizar los materiales componentes mediante cualquier modelo constitutivo. Ésto hace que sea posible, con la metodología propuesta, realizar simulaciones de procesos de delaminación en los que el material matriz tenga distintos comportamientos constitutivos (Von-Mises, Mohr-Coulomb, etc.). Así como también es posible incorporar modelos de daño que se basen en los distintos modos de fractura y combinaciones de los mismos (combinación de modo I y II, por ejemplo).
Finalmente, los resultados obtenidos han mostrado que no hay ninguna diferencia significativa, en el caso del End Notch Flexure test, entre realizar simulaciones con una formulación bidimensional o tridimensional. La formulación utilizada es capaz de iniciar y propagar la delaminación con ambas formulaciones. Este aspecto es relevante ya que el coste computacional es sustancialmente menor en el caso bidimensional. Por tanto, se cree conveniente estudiar el comportamiento estructural de los casos a resolver, optando por simulaciones bidimensionales siempre que sea posible.
Agradecimientos
Este trabajo se ha podido llevar a cabo gracias al apoyo de la CEE, en el marco del FP6 (proyecto LESSLOSS, ref. FP6-50544[GOCE]) y del Gobierno Español, a través del Ministerio de Ciencia y Tecnología (proyectos RECOMP, ref. BIA2005-06952 y DECOMAR project, ref. MAT2003-08700-C03-02) y del Ministerio de Fomento (proyecto “Reparación y refuerzo de estructuras de hormigón armado con materiales compuestos. Desarrollo numérico experimental para aplicación a uniones y propuesta de anclajes en materiales compuestos”). El autor X. Martinez realizó este trabajo estando becado por Centre Internacional de Mètodes Numèrics a l’Enginyenria (CIMNE). Los autores expresan aquí su más sincero agradecimiento a todo el apoyo recibido.
References
- [1] N. Jansson, R. Larsson; A damage model for simulation of mixed–mode delamination growth; Composite Structures, 53 (4) (2001), pp. 409–417
- [2] P. Camanho, C. Dávila, Mixed-mode decohesion finite elements for the simulation of delamination in composite materials, Technical Report TM-2002–211737, NASA, 2002.
- [3] A. Turon, P. Camanho, J. Costa, C. Dávila; A damage model for the simulation of delamination in advanced composites under variable-mode loading; Mechanics of Materials, 38 (11) (2006), pp. 1072–1089
- [4] C. Balzani, W. Wagner; An interface element for the simulation of delamination in unidirectional fiber–reinforced composite laminates; Engineering Fracture Mechanics (2007) http://dx.doi.org/10.1016/j.engfracmech.2007.03.013
- [5] R. Borg, L. Nilsson, K. Simonsson; Modeling of delamination using a discretized cohesive zone and damage formulation; Composites and Science Technology, 62 (10–11) (2002), pp. 1299–1314
- [6] R. Borg, L. Nilsson, K. Simonsson; Simulating DCB, ENF and MMB experiments using shell elements and cohesive zone model; Composites and Science Technology, 64 (2) (2004), pp. 269–278
- [7] S. Pinho, L. Iannucci, P. Robinson; Formulation and implementation of decohesion elements in an explicit finite element code; Composites Part A: Applied science and manufacturing, 37 (5) (2006), pp. 778–789
- [8] P. Krueger; Virtual crack closure technique: history, approach and applications; Applied Mechanics Reviews, 57 (2) (2004), pp. 109–143
- [9] F. Rastellini, S. Oller, O. Salomon, E. Oñate; Composite materials non-linear modelling for long fibre reinforced laminates: Continuum basis, computational aspects and validations; Computers and structures, 86 (9) (2008), pp. 879–896
- [10] S. Oller; Fractura mecánica. Un enfoque global; Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, Spain (2001)
- [11] J. Oliver, M. Cervera, S. Oller, J. Lubliner; Isotropic damage models and smeared crack analysis of concrete; H. Mang, N. Bicánić (Eds.), Second Internaltional Conference on Computer Aided Analysis and Design of Concrete Structures, Zell am See, Austria (1990), pp. 945–958
- [12] O. Salomon, F. Rastellini, S. Oller, E. Oñate, Fatigue prediction for composite materials and structures. NATO Research and technology Organisation (RTO) Eds. Air Vehicle Technology: AVT-121. Symposium on the evaluation, control and prevention of high cycle fatigue, Granada, Spain, 2005
- [13] X. Martinez, S. Oller, F. Rastellini, A. Barbat; A numerical procedure simulating RC structures reinforced with FRP using the serial/parallel mixing theory; Computers and Structures, 86 (15–16) (2008), pp. 1604–1618
- [14] L. Kachanov; Introduction to continuum damage mechanics, Mechanics of elastic stability; Martinus Nijhoff, Dordrecht, Países Bajos (1986)
- [15] S. Oller; Dinámica no–lineal; Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, Spain (2002)
- [16] B. Corbella, J. Vicens, J. Costa, Informe de los resultados de los ensayos de propagación de grieta en modo II del round robin test” del proyecto grincomp (mat2003–09768-c03). Technical Report 2004-CYT-01-IT01, CIMEP, 2004.
Document information
Published on 01/09/11
Accepted on 24/03/11
Submitted on 10/05/10
Volume 27, Issue 3, 2011
DOI: 10.1016/j.rimni.2011.07.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?