Resumen
El problema de diseño óptimo robusto de estructuras es una tarea computacionalmente costosa como consecuencia del acoplamiento de los procesos de cuantificación de incertidumbre y de optimización. Para hacer frente a este problema, en este artículo se propone una metodología, basada en modelos Kriging, para resolver de forma eficiente el problema de cuantificación de incertidumbre en el proceso de optimización. El modelo Kriging aproxima, de forma simultánea, la respuesta estructural en el dominio de diseño y en el dominio estocástico, permitiendo desacoplar los procesos de cuantificación de incertidumbre y de optimización. La metodología propuesta incluye un criterio de actualización de los modelos Kriging basado en la estimación del error en la predicción, que mejora la aproximación en las regiones cercanas al frente de Pareto. Se han resuelto 3 problemas para mostrar la aplicabilidad y la precisión de la metodología propuesta. Los resultados muestran que la metodología es adecuada para resolver el problema de diseño óptimo robusto con una precisión razonable y un número de evaluaciones del modelo de simulación muy inferior al que requieren los métodos convencionales.
Abstract
Conventional methods addressing the robust design optimization problem of structures usually require high computational requirements due to the nesting of uncertainty quantification within the optimization process. In order to address such a problem, this work proposes a methodology, based on Kriging models, to efficiently assess the uncertainty quantification in the optimization process. The Kriging model approximates the structural performance both in the design domain and in the stochastic domain, which allows to decouple the uncertainty quantification process and the optimization process. In addition, an infill criterion based on the variance of the Kriging prediction is included to update the Kriging model towards the global Pareto front. Three numerical examples show the applicability and the accuracy of the proposed methodology. The results show that the proposed method is appropriate to solve the robust design optimization problem with reasonable accuracy and a considerably lower number of function calls than required by conventional methods.
Palabras clave
Optimización estructural ; Diseño óptimo robusto ; Metamodelos ; Modelos Kriging
Keywords
Structural optimization ; Robust design optimization ; Metamodels ; Kriging models
1. Introducción
Tradicionalmente, las incertidumbres en las condiciones de carga, en las propiedades de los materiales, en la geometría o en las condiciones de contorno de las estructuras se han incluido en el proceso de diseño mediante hipótesis basadas en la experiencia o en criterios de ingeniería tales como la utilización de factores de seguridad. Utilizando dichas hipótesis se obtiene un modelo simplificado, basado en los valores nominales de las variables y de los parámetros de diseño. Sin embargo, las soluciones óptimas que se han alcanzado con este enfoque determinista tienen un comportamiento óptimo únicamente bajo condiciones cercanas a las fijadas en el proceso de optimización, pudiendo deteriorarse en gran medida cuando las condiciones se alejan de las de diseño.
La necesidad de incorporar las incertidumbres en el proceso de diseño ha estimulado el interés por la investigación de procedimientos capaces de proporcionar diseños más robustos y fiables. En la actualidad existen 2 formulaciones que consideran la respuesta probabilista de las estructuras en el proceso de diseño óptimo: el diseño óptimo basado en fiabilidad (Reliability-Based Design Optimization , RBDO [1] ) y el diseño óptimo robusto (Robust Design Optimization , RDO [2] , [3] and [4] ). La primera de ellas consiste en un problema de optimización en que se incluyen los efectos de la incertidumbre por medio de probabilidades de fallo y de valores esperados. La segunda trata de determinar un diseño menos sensible a las incertidumbres de las variables y de los parámetros que intervienen en la respuesta estructural mediante la utilización de índices de robustez.
La principal dificultad para la aplicación de los actuales métodos de diseño óptimo robusto es el elevado coste computacional, tanto para evaluar los momentos estadísticos de la respuesta estructural como para obtener las sensibilidades necesarias para el proceso de optimización. Para abordar este problema, diversos autores proponen la utilización de aproximaciones o metamodelos durante el proceso de diseño óptimo robusto [5] , [6] , [7] , [8] , [9] and [10] . Dellino et al. [9] combinaron el método Taguchi de diseño robusto con superficies de respuesta para acelerar el proceso de cuantificación de incertidumbre. Li y Kang [5] utilizaron modelos Kringing para aproximar los momentos estadísticos de la respuesta estructural y un algoritmo de recocido simulado para la búsqueda de un óptimo global. Guoqi y Daugi [10] presentaron una metodología basada en la utilización de support vector regression para la resolución del problema de diseño óptimo robusto de problemas de alta dimensionalidad. Martínez y Martí [7] propusieron un procedimiento adaptativo basado en modelos Kriging para la resolución del problema de diseño óptimo robusto multiobjetivo. Jin et al. [11] realizaron un estudio de la aplicabilidad y la precisión de diferentes técnicas de metamodelos para la resolución del problema de optimización bajo incertidumbre, en el que concluyeron que la precisión de los resultados óptimos dependía en gran medida de la capacidad del metamodelo para capturar globalmente la respuesta estructural. Beyer y Sendhoff [12] realizaron una revisión del estado de la cuestión del problema de diseño óptimo robusto, en la que pusieron de manifiesto la importancia de una mayor investigación en nuevas técnicas de metamodelos que garanticen la precisión global de la aproximación. La dificultad para obtener una aproximación global precisa ha estimulado la investigación en procedimientos adaptativos que garanticen la obtención de un diseño óptimo global. En este sentido, autores como Jurecka et al. [8] adaptaron técnicas de optimización dirigidas por metamodelos al campo del diseño óptimo robusto.
El objetivo de este artículo es proponer una metodología para la resolución del problema de diseño óptimo robusto, que utiliza modelos Kriging para resolver de forma eficiente el problema de la cuantificación de incertidumbre en el proceso de optimización. A diferencia de otros trabajos, en la metodología propuesta el modelo Kriging aproxima simultáneamente la respuesta estructural en el dominio de diseño y en el dominio estocástico. El modelo Kriging sustituye al simulador y actúa como soporte del proceso de cuantificación de incertidumbre y del proceso de optimización. Asimismo, esta metodología incluye un criterio de actualización de los modelos Kriging, basado en la estimación del error en la predicción, que mejora la aproximación en las regiones cercanas al frente de Pareto. La metodología propuesta permite: 1) evaluar la robustez del diseño utilizando un número reducido de evaluaciones en comparación con los procedimientos convencionales, tales como los métodos de simulación; 2) desacoplar los procesos de cuantificación de incertidumbre y de optimización, reduciendo el número de evaluaciones del simulador en comparación con el enfoque anidado; y 3) mejorar la precisión de la aproximación en las regiones cercanas a los óptimos de Pareto.
2. Metamodelos
Un metamodelo (model of model[13] ) se utiliza habitualmente para sustituir globalmente a un modelo de simulación que requiere un alto coste computacional para su evaluación. Esta aproximación puede utilizarse, entre otras aplicaciones, para facilitar el proceso de optimización, explorar el espacio de diseño o llevar a cabo análisis de fiabilidad. En la literatura especializada existe una gran variedad de metamodelos, tales como las superficies de respuesta [14] , los modelos Kriging [15] and [16] , las funciones de base radial [17] o las redes neuronales [15] and [18] . De entre las diferentes técnicas de metamodelos, los modelos Kriging [16] han alcanzado una gran popularidad en los últimos años gracias a su gran flexibilidad para aproximar respuestas con alto grado de no linealidad [11] y a que proporcionan información estadística del error cometido en la predicción [19] .
2.1. Modelos Kriging
Los modelos Kriging asumen que el modelo de simulación puede ser aproximado por una realización de un proceso estocástico gaussiano con una media y una covarianza , a priori desconocidas. En las expresiones anteriores, β = [β1 , …, βp ]T es un vector de parámetros desconocidos, f (x ) = [f1 (x ), …, fp (x )]T es un conjunto conocido de funciones de (funciones de regresión), α2 es la varianza de y es la función de correlación entre x y x ′. El proceso estocástico representa el conocimiento a priori de la función que aproximar, y por esta razón la selección de la función de correlación debe ser consistente con la información conocida de dicha función. El modelo de correlación más ampliamente utilizado es el modelo exponencial anisótropo generalizado:
|
|
( 1) |
Los parámetros β , α2 y ϕ son desconocidos a priori y se han de determinar a partir de las respuestas del simulador para un conjunto de diseños . Utilizando técnicas bayesianas, la distribución posterior de , condicionada a las observaciones , es gaussiana[20] con media:
|
|
( 2) |
y covarianza:
|
|
( 3) |
siendo:
|
|
( 4a) |
|
|
( 4b) |
|
|
( 4c) |
|
|
( 4d) |
|
|
( 4e) |
|
|
( 4f) |
|
|
( 4g) |
donde representa la mejor predicción del modelo de simulación en el punto x , R es la matriz de covarianza y es la varianza de la predicción, la cual proporciona intervalos de confianza sobre la predicción media .
En (2) y (3) y α2 se obtienen analíticamente y solo dependen de los parámetros de correlación ϕ . En este trabajo los parámetros de correlación se han obtenido resolviendo el problema de optimización [20] :
|
|
( 5) |
Las funciones de correlación y de regresión más adecuadas dependen de las características de la función original, a priori desconocida. En este trabajo se han considerado funciones de regresión del tipo constante, lineal, cuadrática y cúbica, en combinación con las funciones de correlación recogidas en la tabla 1 . La mejor combinación de funciones de correlación y de regresión se selecciona en base al error cuadrático medio (root mean square error , RMSE) y al coeficiente de determinación (R2 ). Estos indicadores se obtienen utilizando las respuestas del simulador y (xv ) para una muestra de validación xv :
| Nombre | R(x , x ′, ϕ ) |
|---|---|
| Exponencial | |
| Exponencial-Gaussiana | |
| Gaussiana | |
| Lineal | |
| Esférica | |
| Cúbica |
|
|
( 6) |
|
|
( 7) |
donde y yi (xv ) son la componente i-ésima del vector de respuestas obtenidas con el modelo Kriging y el simulador, respectivamente, es la media de todos los valores obtenidos con el simulador, y es el tamaño de la muestra de validación. Para no tener que utilizar muestras de validación, en este trabajo se estiman estos indicadores utilizando una medida basada en errores de validación cruzada denominada PRESS (prediction error sum of squares)[21] :
|
|
( 8) |
donde es la predicción para el punto i del modelo Kriging ajustado con la muestra inicial , y se calcula eliminando el punto de diseño i de la muestra inicial , ajustando de nuevo el modelo Kriging con los puntos restantes y obteniendo la predicción en el punto eliminado. Trabajos como los de [22] , [23] , [24] and [25] han demostrado que, cuando el número de puntos de la muestra inicial es suficiente, la estimación del error cuadrático medio (RMSE) a través del PRESS es un buen indicador para la selección de metamodelos de acuerdo con la precisión de la aproximación. En este trabajo se ha utilizado el PRESSRMSE para la selección de las funciones de correlación y de regresión que proporcionan el mejor ajuste. El PRESSRMSE resulta un buen indicador para la selección de metamodelos; sin embargo, no resulta un indicador de utilidad para determinar el grado de precisión global del metamodelo. En este trabajo se ha utilizado una estimación del R2 mediante errores de validación cruzada:
|
|
( 9) |
donde es la media de las predicciones.
2.2. Actualización de los modelos Kriging
La estimación del coeficiente de determinación se ha utilizado como indicador de la precisión global del modelo Kriging. Para valores de se actualiza el modelo Kriging con puntos situados en las zonas de peor ajuste. Los nuevos puntos se obtienen mediante la resolución del problema de optimización:
|
|
( 10a) |
|
|
( 10b) |
donde MSE(x ) es el error cuadrático medio, que en este trabajo se toma como la varianza de la predicción en el punto x definida en (3) . Para evitar problemas de condicionamiento de la matriz de covarianza R se incluyen las restricciones (10b) , que garantizan que la distancia entre los puntos candidatos para la actualización y los existentes en la muestra actual ( ) es superior a un valor predefinido ϵ .
3. Formulación del problema de diseño óptimo robusto
El problema de diseño óptimo robusto se formula como un problema de optimización multiobjetivo donde las funciones objetivo son los 2 primeros momentos estadísticos de la respuesta estructural fx ,z :
|
|
( 11a) |
|
|
( 11b) |
|
|
( 11c) |
|
|
( 11d) |
|
|
donde es un vector que contiene los valores deterministas de las variables de diseño, o las medias y las desviaciones estándar en el caso de que las variables sean aleatorias, es un vector de parámetros aleatorios, y xinf y xsup son los límites inferior y superior de las variables de diseño. Las restricciones del tipo (11b) actúan como restricciones de probabilidad bajo la hipótesis de una distribución de probabilidad normal de la función gj (x , z ). El coeficiente βj representa el índice de fiabilidad para la restricción j-ésima , que marca la probabilidad de que la restricción original sea satisfecha. Las restricciones del tipo (11c) limitan la desviación estándar de las restricciones de igualdad hk (x , z ).
En el problema de diseño óptimo robusto las 2 funciones por minimizar son habitualmente conflictivas, en el sentido de que no existe un punto de diseño que sea óptimo para ambas. En este caso, el criterio de optimalidad utilizado en la optimización mono-objetivo es sustituido por el óptimo de Pareto. Un diseño es óptimo de Pareto para el problema de diseño óptimo robusto si, y solo si, no existe ningún otro diseño factible que mejore su valor en media, sin degradar el valor de la desviación estándar o viceversa. El conjunto de óptimos de Pareto representa la solución del problema de optimización multiobjetivo y geométricamente componen el conocido como frente de Pareto.
Para la obtención del conjunto de óptimos de Pareto es práctica habitual sustituir el conjunto de funciones objetivo por una única función de escalarización. En este trabajo se ha utilizado la función de escalarización aumentada de Tchebycheff [26] , que para el problema de diseño óptimo robusto es:
|
|
( 12a) |
|
|
( 12b) |
|
|
( 12c) |
|
|
( 12d) |
|
|
( 12e) |
donde ρ es un número positivo suficientemente pequeño (en este trabajo 0,05), y son el valor de mínima media y de mínima desviación estándar y ω1 y ω2 son pesos con valores comprendidos en el intervalo [0,1] que cumplen ω1 + ω2 = 1. Minimizando la función de escalarización aumentada de Tchebycheff es posible obtener óptimos de Pareto incluso en la zona cóncava del frente, a diferencia de otras funciones de escalarización tales como la de sumas ponderadas [2] and [26] .
4. Metodología propuesta
En la metodología propuesta el modelo Kriging aproxima, de forma simultánea, la respuesta estructural en el dominio de diseño y en el dominio estocástico. Esta metodología permite: 1) evaluar la robustez del diseño utilizando un número reducido de evaluaciones en comparación con los procedimientos convencionales; 2) desacoplar los procesos de cuantificación de incertidumbre y de optimización, reduciendo el número de evaluaciones del simulador en comparación con el enfoque anidado; y 3) mejorar la precisión de la aproximación en las regiones cercanas a los óptimos de Pareto.
La metodología propuesta consta de las siguientes 5 etapas:
4.1. Aproximación global de la respuesta en el dominio de las variables de diseño y de los parámetros aleatorios, mediante
- La realización de un diseño de experimentos en el dominio de las variables de diseño y de los parámetros aleatorios ). En este trabajo se ha utilizado un hipercubo latino óptimo obtenido mediante la función lhsdesign de la toolbox de estadística de Matlab [27] con el criterio de optimalidad maximin (maximización de la mínima distancia entre puntos) [28] .
- La evaluación de la respuesta estructural, con el simulador, para cada punto de diseño: .
- El ajuste de un modelo Kriging de la respuesta estructural .
- La actualización de los modelos Kriging a través de la maximización de la varianza en la predicción (10).
4.2. Cuantificación de la incertidumbre
Los momentos estadísticos de la respuesta estructural se obtienen mediante una simulación MonteCarlo, utilizando los modelos Kriging obtenidos en la etapa 4.1 . En este trabajo el número de evaluaciones en la simulación MonteCarlo ha sido de 50.000.
4.3. Aproximación global de los momentos estadísticos de la respuesta en el dominio de las variables de diseño, mediante
- La realización de un diseño de experimentos en el dominio de las variables de diseño ). En este trabajo se ha utilizado un hipercubo latino óptimo mediante el procedimiento definido en 4.1 .
- La evaluación de la media y de la desviación estándar de las respuestas estructurales para cada punto de diseño:
|
|
- El ajuste de un modelo Kriging de los momentos estadísticos , .
- La actualización de los modelos Kriging mediante la maximización de la varianza en la predicción (10).
4.4. Optimización multiobjetivo
El problema de optimización multiobjetivo se resuelve mediante la función de escalarización aumentada de Tchebycheff (12a) , utilizando los modelos Kriging obtenidos en el apartado 4.3 . En este trabajo, el problema de optimización (12a) se ha resuelto mediante un algoritmo genético, más concretamente con la función ga de la toolbox de optimización de Matlab [27] .
4.5. Actualización de los modelos Kriging en el dominio estocástico
Los modelos Kriging obtenidos en 4.1 se actualizan en el dominio de las variables de diseño utilizando el conjunto de soluciones óptimas de Pareto x* . Para actualizar los modelos Kriging en el dominio estocástico se buscan puntos situados en zonas donde la calidad de la aproximación es pobre y que son de gran importancia para evaluar los momentos estadísticos (zonas de elevada densidad de probabilidad). Los puntos candidatos vienen dados por la resolución del problema de optimización en el dominio estocástico Ω:
|
|
( 13a) |
|
|
( 13b) |
|
|
donde MSE(x* , z ) es el error cuadrático medio, que en este trabajo se toma como la varianza de la predicción en el punto (x* , z ) definida en (3) , pZ (z ) es la densidad de probabilidad de los parámetros aleatorios, y n es el número de puntos de la muestra inicial.
Los puntos candidatos para la actualización del metamodelo (x* , z* ) se añaden a la muestra original, que se utiliza para la actualización de los modelos Kriging.
5. Aplicación numérica
5.1. Función de Branin
El objetivo de este primer ejemplo es mostrar la aplicabilidad y la precisión de la metodología propuesta mediante la resolución del problema de diseño óptimo robusto de una función analítica, la función de Branin [29] . Esta función se utiliza habitualmente como test en problemas de optimización global y se ha considerado en este trabajo por presentar mínimos locales y por ser claramente multimodal en la variable x , lo que da lugar a un amplio conjunto de soluciones para el problema de diseño óptimo robusto. La función de Branin es:
|
|
( 14) |
El espacio de diseño está limitado a −5 ≤ x ≤ 10. Se considera como fuente de incertidumbre el parámetro aleatorio z , que varía según una distribución normal con media μz = 5 y desviación estándar σz = 2. El problema de diseño óptimo robusto es:
|
|
( 15a) |
|
|
( 15b) |
El modelo Kriging inicial se ha obtenido a partir de un hipercubo latino óptimo de 40 puntos en el dominio (x , z ). La minimización de PRESSRMSE(8) da como resultado una función de correlación gaussiana y una función de regresión constante. La muestra inicial de 40 puntos se ha incrementado con 5 puntos adicionales en las zonas de mayor error (10a) . El coeficiente de determinación estimado es ,989, mientras que el obtenido a partir de una muestra de 10.000 puntos es R2 = 0,999.
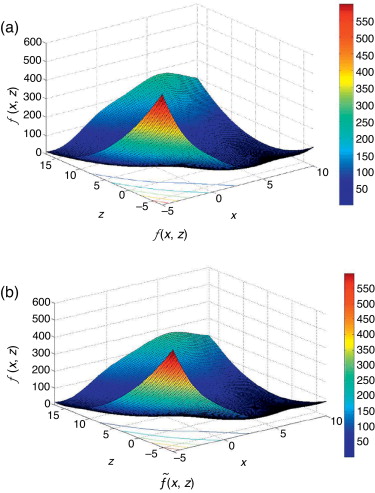
La función real y el modelo Kriging resultante se muestran en la figura 1 . Los 2 primeros momentos estadísticos de la respuesta se han aproximado en el dominio de diseño a partir de un hipercubo latino óptimo de 30 puntos, mejorado con 10 puntos adicionales en las zonas de más error (10a) .
|
|
|
Figura 1. Función de Branin. (a) función real, (b) modelo Kriging. |
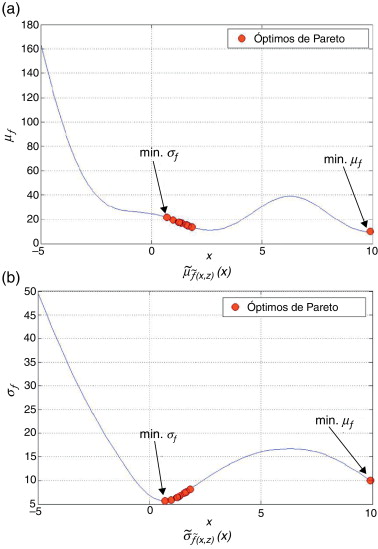
El problema de optimización multiobjetivo se ha resuelto utilizando la función de escalarización aumentada de Tchebycheff, adoptando un vector de pesos de tamaño 10, cuyos valores varían uniformemente entre 0 y 1. Los parámetros utilizados para el algoritmo genético son: número de repeticiones (8), tamaño de la población (24), probabilidad de cruce (80%), elitismo manteniendo los 2 mejores diseños y número máximo de generaciones (80). El conjunto de diseños óptimos obtenidos tras 3 actualizaciones del modelo Kriging forma el frente de Pareto de la figura 2 . Este frente permite obtener una solución de compromiso entre el diseño de mínima media (x* = 9, 915) y el diseño de mínima desviación estándar (x* = 0, 695). En este caso en la figura 2 se ha seleccionado el punto de menor distancia al origen. La figura 3 muestra los óptimos de Pareto sobre los modelos Kriging de la media y de la desviación estándar. Para comprobar el error cometido con la aproximación de los momentos estadísticos, se ha realizado una simulación de MonteCarlo con una muestra de 50.000 puntos, que se evaluaron con la función real y con el modelo Kriging. La tabla 2 muestra los resultados para los diseños de mínima media y de mínima desviación estándar. Los errores en ambos diseños son inferiores al 0,1% en media y al 0,15% en desviación estándar.
|
|
|
Figura 2. Función de Branin. Frente de Pareto, soluciones de mínima media, mínima desviación estándar y solución de compromiso seleccionada. |
|
|
|
Figura 3. Función de Branin. Óptimos de Pareto sobre los modelos Kriging de la media (a) y de la desviación estándar (b). |
| Kriging | Real | Error (%) | ||
|---|---|---|---|---|
| x* = 9.915 | μf (x ,z ) (x ) | 9.887 | 9.895 | −0,081 |
| σf (x ,z ) (x ) | 10.113 | 10.127 | −0,138 | |
| x* = 0.695 | μf (x ,z ) (x ) | 21.408 | 21.410 | −0,009 |
| σf (x ,z ) (x ) | 5.700 | 5.706 | −0,105 |
5.2. Estructura de 4 barras
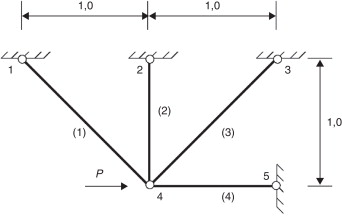
El segundo ejemplo numérico es la estructura de 4 barras [2] mostrada en la figura 4 .
|
|
|
Figura 4. Estructura de 4 barras. |
En el nudo 4 de la estructura se aplica una fuerza horizontal P . Las áreas A1 (barras 1 y 3) y A2 (barras 2 y 4) se consideran variables de diseño deterministas. Los módulos de Young E1 (barras 1 y 3) y E2 (barras 2 y 4) se consideran variables aleatorias que siguen distribuciones normales con medias y y desviaciones estándar y . La densidad del material es ρ = 1. El problema consiste en la minimización del desplazamiento horizontal (u ) del nudo 4, sujeto a una restricción de masa . La formulación del problema de diseño óptimo robusto es:
|
|
( 16a) |
|
|
( 16b) |
|
|
( 16c) |
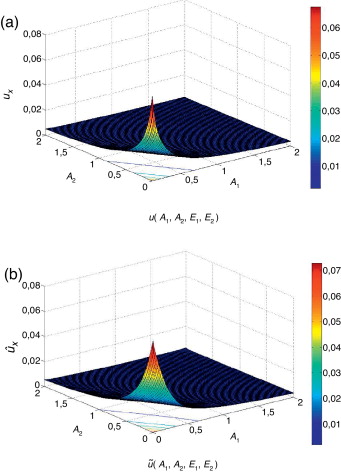
El modelo Kriging inicial se ha obtenido a partir de un hipercubo latino óptimo de 100 puntos, mejorado con 50 puntos adicionales en las regiones de mayor error. Las funciones de correlación y de regresión resultantes de la minimización del PRESSRMSE(8) son gaussiana y cuadrática, respectivamente. La respuesta real y el modelo Kriging resultante se muestran en la figura 5 . El coeficiente de determinación estimado es ,986, mientras que el obtenido a partir de una muestra de 10.000 puntos es R2 = 0,984.
|
|
|
Figura 5. Estructura de 4 barras. (a) desplazamiento real, (b) modelo Kriging. |
El problema de optimización multiobjetivo se ha resuelto utilizando la función de escalarización aumentada de Tchebycheff, adoptando un vector de pesos de tamaño 10, cuyos valores varían uniformemente entre 0 y 1. Los parámetros utilizados para el algoritmo genético son: número de repeticiones (8), tamaño de población (40), probabilidad de cruce (80%), elitismo manteniendo los 2 mejores diseños y número máximo de generaciones (100).
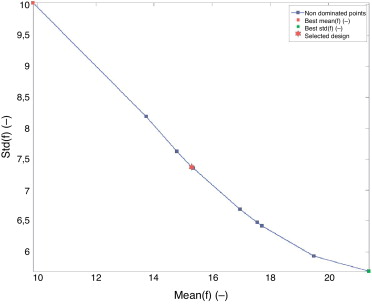
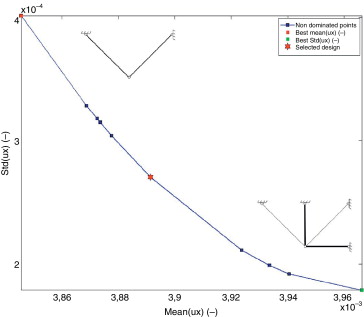
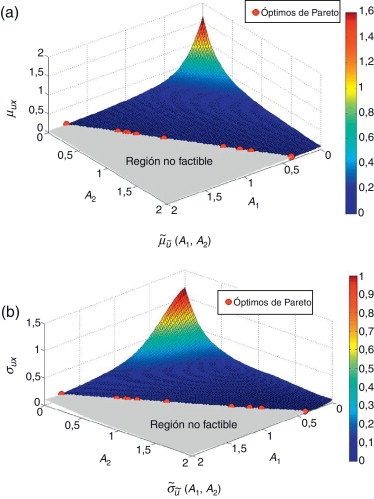
La figura 6 muestra el frente de Pareto obtenido a partir de una población inicial de 10 diseños, tras 10 actualizaciones del modelo Kringing inicial. Las figuras 7 muestran los óptimos de Pareto sobre los modelos Kriging de la media y de la desviación estándar del desplazamiento. Todos los diseños obtenidos están situados en la frontera que delimita la región factible y varían desde el diseño óptimo de mínima media (A1 =1,766, A2 =0,002) hasta el diseño óptimo de mínima desviación estándar (A1 =0,3685, A2 =1,9789).
|
|
|
Figura 6. Estructura de 4 barras. Frente de Pareto, soluciones de mínima media, mínima desviación estándar y solución de compromiso seleccionada. |
|
|
|
Figura 7. Estructura de 4 barras. Óptimos de Pareto sobre los modelos Kriging de la media (a) y de la desviación estándar (b). |
La figura 8 muestra las funciones de densidad de probabilidad y acumulada de probabilidad, reales y aproximadas, para los diseños óptimos de mínima media y de mínima desviación estándar. Los errores cometidos en la aproximación de los momentos estadísticos se muestran en la tabla 3 .
|
|
|
Figura 8. Función de densidad de probabilidad y función acumulada de probabilidad. (a) Diseño de mínima media, (b) Diseño de mínima desviación estándar. |
| Kriging | Real | Error (%) | ||
|---|---|---|---|---|
| A1 = 1, 766 | μu (A1 , A2 ) | 3.843e-3 | 3.846e-3 | 0,073 |
| A2 = 0, 002 | σu (A1 , A2 ) | 4.007e-4 | 3.961e-4 | 1,151 |
| A1 = 0, 369 | μu (A1 , A2 ) | 3.965e-3 | 3.967e-3 | 0,033 |
| A2 = 1, 979 | σu (A1 , A2 ) | 1.721e-4 | 1.786e-4 | 3,629 |
5.3. Celosía de 25 barras con incertidumbre en cargas y material
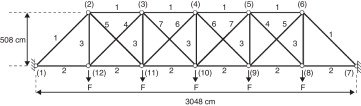
En este ejemplo se aplica la metodología propuesta a la resolución del problema de diseño robusto de la celosía de 25 barras mostrada en la figura 9 . Las variables de diseño consideradas son las dimensiones de los elementos estructurales clasificadas en 7 grupos, tal y como muestra la figura 9 . Las variables de diseño están limitadas inferiormente a un valor de 0,6452 cm2 . La estructura está sometida a unas cargas verticales en los nudos del cordón inferior cuyo valor nominal es kN. El material de las barras tiene una densidad ρ =7.833,41 kg/m3 y un módulo de Young =206.842,8 MPa. La tensión máxima admisible a tracción y compresión es σy |t ,c = 206.843 MPa. El desplazamiento de todos los nudos en las direcciones x e y está limitado a un valor máximo de 5,08 cm. El problema está parametrizado con 7 variables de diseño (áreas) y 2 variables aleatorias (ξ1 y ξ2 ) que siguen una distribución normal. está relacionada con las fuerzas aplicadas mediante la fórmula , mientras que está relacionada con el módulo de Young mediante la fórmula . Siguiendo la línea de Lagaros et al. [30] , el problema de diseño robusto consiste en la minimización del peso de la estructura y de la varianza de la respuesta estructural representada por la desviación estándar del desplazamiento vertical del nudo 10. Se analiza: 1) la precisión de los modelos Kriging de la respuesta estructural en el dominio estocástico y de diseño; 2) la precisión de la metodología propuesta para la obtención de los momentos estadísticos, 3) la precisión de los diseños óptimos obtenidos en comparación con métodos convencionales.
|
|
|
Figura 9. Celosía de 25 barras. |
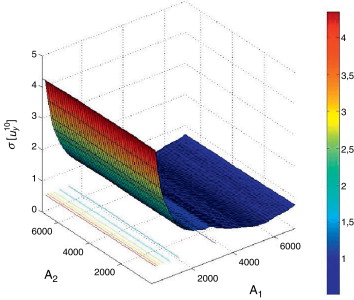
El modelo Kriging inicial se ha obtenido a partir de un hipercubo latino óptimo de 200 puntos. Las funciones de correlación y de regresión resultantes de la minimización del PRESSRMSE(8) son exponencial-gaussiana y cuadrática, respectivamente. El coeficiente de determinación estimado es =0,9973, mientras que el obtenido a partir de una muestra de 10.000 puntos es R2 = 0, 9971. La figura 10 muestra el modelo Kriging de la desviación estándar del desplazamiento vertical del nudo 10 en el espacio de diseño.
|
|
|
Figura 10. Celosía de 25 barras. Modelo Kriging de la desviación estándar de uy ,10 . |
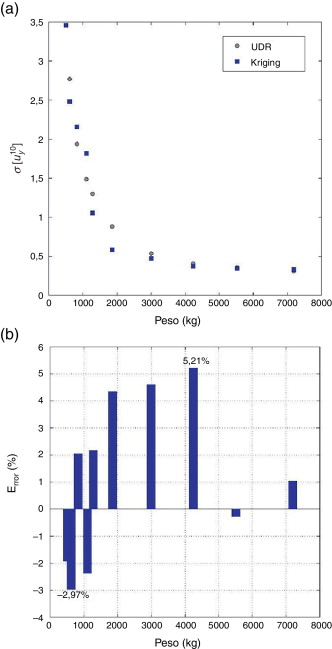
El problema de optimización multiobjetivo se ha resuelto utilizando la función de escalarización aumentada de Tchebycheff, adoptando un vector de pesos de tamaño 10. El frente de Pareto resultante tras 8 iteraciones se muestra en la figura 11 (a). El resultado obtenido se compara con el conseguido con métodos convencionales existentes en la bibliografía. En este trabajo se ha seleccionado el método Univariate Dimension Reduction (UDR) [31] and [32] por ser uno de los métodos más eficientes para la obtención de los momentos estadísticos en procesos de diseño óptimo robusto [33] . La figura 11 (a) muestra el frente de Pareto resultante estimando los momentos estadísticos mediante el método UDR. En esta figura se observa un buen acuerdo entre los frentes de Pareto obtenidos mediante el método UDR y la metodología propuesta. El número de evaluaciones del modelo de simulación necesarias utilizando el método UDR fueron 3,6e5 de acuerdo con la expresión: (4 × Nva + 1) × Nopt × Npop × Ngen . Nva es el número de variables aleatorias de problema, Nopt el tamaño de vector de pesos, Npop el tamaño de la población, y Ngen el número de generaciones. El número de evaluaciones del modelo de simulación necesarias con la metodología propuesta (280) es considerablemente inferior.
|
|
|
Figura 11. (a) Frentes de Pareto obtenidos utilizando modelos Kriging y UDR (Univariate Dimension Reduction) . (b) Errores cometidos en la aproximación de la desviación estándar mediante modelos Kriging para los óptimos de Pareto. |
La figura 11 (b) representa, para cada diseño óptimo de Pareto, el error cometido en la estimación de la desviación estándar mediante el modelo Kriging en comparación con una simulación MonteCarlo de 1e5 simulaciones. Los errores oscilan entre −3% y 5%.
6. Conclusiones
Se ha propuesto una metodología para la resolución del problema de diseño óptimo robusto que utiliza modelos Kriging para resolver, de forma eficiente, el problema de cuantificación de incertidumbre en la optimización. A diferencia de otros trabajos, en la metodología propuesta el modelo Kriging aproxima, de forma simultánea, la respuesta estructural en el dominio de diseño y en el dominio estocástico. Asimismo, la metodología incluye un criterio de actualización de los modelos Kriging, basado en la estimación del error en la predicción, que permite mejorar la calidad de la aproximación en las regiones cercanas al frente de Pareto.
La metodología propuesta permite: 1) obtener los indicadores de robustez del diseño (momentos estadísticos de la respuesta estructural) utilizando un número reducido de evaluaciones en comparación con los procedimientos convencionales; 2) desacoplar los procesos de cuantificación de incertidumbre y de optimización, resolviendo el problema con un número de evaluaciones del simulador muy inferior al enfoque anidado, y 3) mejorar la precisión de la aproximación en las regiones cercanas a los óptimos de Pareto hasta alcanzar un nivel deseado.
Para demostrar la aplicabilidad y la precisión de la metodología propuesta se han resuelto un ejemplo matemático y 2 ejemplos de diseño óptimo robusto de estructuras de nudos articulados. La metodología propuesta no está limitada a problemas de diseño óptimo robusto de estructuras de nudos articulados. Su principal campo de aplicación es el diseño óptimo robusto de problemas de ingeniería que requieren un elevado coste computacional para su resolución debido a: 1) la utilizacion de software in house o comercial, que obliga en muchos casos a utilizar estrategias de cuantificacion de incertidumbre no intrusivas (MonteCarlo), y 2) la utilización de complejos modelos de simulación de alto coste computacional.
Los resultados obtenidos muestran que los modelos Kriging son una herramienta eficaz para aproximar los momentos estadísticos de la respuesta estructural con un bajo coste computacional, y para actuar como soporte de la optimización en la búsqueda de óptimos globales. Asimismo, la reducción que se consigue en el coste computacional los hace muy adecuados para su aplicación a problemas de ingeniería que requieren modelos complejos de simulación.
Una ventaja adicional de la metodología propuesta es que las aproximaciones globales creadas durante la optimización se pueden reutilizar en nuevos procesos de optimización, en exploración de los espacios de diseño y estocástico, o en aplicaciones computacionalmente exigentes. Quedan para futuras investigaciones el estudio de nuevas técnicas de metamodelos que permitan su aplicación a problemas de alta dimensionalidad, así como su aplicación a otras formulaciones del problema de optimización bajo incertidumbre tales como el diseño óptimo basado en fiabilidad.
Agradecimientos
Este trabajo se ha desarrollado con el apoyo financiero del Ministerio Español de Economía y Competitividad, en el proyecto de investigación DPI2011-26394 «Sistema integrado de diseño óptimo robusto de topología de estructuras».
References
- [1] M. Valdebenito, G. Schuëller; A survey on approaches for reliability-based optimization; Struct. Multidiscip. Optim., 42 (2010), pp. 645–663 10.1007/s00158-010-0518-6
- [2] I. Doltsinis, Z. Kang; Robust design of structures using optimization methods; Comput. Meth. Appl. Mech. Eng., 193 (2004), pp. 2221–2237
- [3] J. Díaz, S. Hernández, L. Romera, A.N. Fontán; Diseño y análisis térmico bajo incertidumbe de estructuras aeronaúticas; Rev. Int. Métodos Numér. Cálc. Diseño ing., 17 (2011), pp. 95–104
- [4] J. Pons-Prats, G. Bugeda, F. Zárate, E. Oñate; Optimización robusta en aplicaciones aeronáuticas con la combinación de cálculo estocástico y algoritmos evolutivos; Rev. Int. Métodos Numér. Cálc. Diseño ing., 28 (2012), pp. 18–32
- [5] K. Lee, D. Kang; A robust optimization using the statistics based on Kriging metamodel; J. Mech. Sci. Technol., 20 (2006), pp. 1169–1182
- [6] J. Martínez, P. Martí, Diseño óptimo robusto de estructuras basado en modelos Kriging, en: Congress on Numerical Methods in Engineering, Coimbra, 14 to 17 June, pp. 447-448.
- [7] J. Martínez, P. Martí, Metamodel-based multi-objective robust design optimization of structures, en: Computer Aided Optimum Design in Engineering XII, New Forest, UK, 20 - 22 June, pp. 35-45.
- [8] F. Jurecka, M. Ganser, K. Bletzinger; Update scheme for sequential spatial correlation approximations in robust design optimisation; Comput. Struct., 85 (2007), pp. 606–614
- [9] G. Dellino, J. Kleijnen, C. Meloni; Robust optimization in simulation: Taguchi and Response Surface Methodology; Int. J. Prod. Econ., 125 (2010), pp. 52–59
- [10] X. Guoqi, H. Dagui; A metamodeling method based on support vector regression for robust optimization; CJME, 23 (2010)
- [11] R. Jin, X. Du, W. Chen; The use of metamodeling techniques for optimization under uncertainty; Struct. Multidiscip. Optim., 25 (2003), pp. 99–116
- [12] H. Beyer, B. Sendhoff; Robust optimization - A comprehensive survey; Comput. Meth. Appl. Mech. Eng., 196 (2007), pp. 3190–3218
- [13] J. Kleijnen; A comment on blannings metamodel for sensitivity analysis: The regression metamodel in simulation; Interfaces, 5 (1975), pp. 21–23
- [14] R. Myers, D. Montgomery; Response surface methodology; (2nd ed.)New York, Wiley-Interscience (2002)
- [15] T. Simpson, J. Poplinski, P.N. Koch, J. Allen; Metamodels for computer-based engineering design: Survey and recommendations; Eng. Comput., 17 (2001), pp. 129–150 10.1007/PL00007198
- [16] D.G. Krige; A statistical approach to some basic mine valuation problems on the Witwatersrand, Journal of the Chemical; Metallurgical and Mining Society of South Africa, 52 (1951), pp. 119–139
- [17] H. Nakayama, M. Arakawa, R. Sasaki; Simulation-based optimization using computational intelligence; Optim. Eng., 3 (2002), pp. 201–214 10.1023/A:1020971504868
- [18] M. Papadrakakis, N.D. Lagaros, Y. Tsompanakis; Structural optimization using evolution strategies and neural networks; Comput. Meth. Appl. Mech. Eng., 156 (1998), pp. 309–333
- [19] D.R. Jones; A taxonomy of global optimization methods based on response surfaces; J. Global Optim., 21 (2001), pp. 345–383
- [20] J. Sacks, W.J. Welch, T.J. Mitchell, H.P. Wynn; Design and analysis of computer experiments; Stat. Sci., 4 (1989), pp. 409–435
- [21] M. Meckesheimer, A.J. Booker, R.R. Barton, T.W. Simpson; Computationally inexpensive metamodel assessment strategies; AIAA, 40 (2002), pp. 2053–2060
- [22] F. Viana, R.T. Haftka; Cross Validation Can Estimate How Well Prediction Variance Correlates with Error; AIAA, 47 (2009), pp. 2266–2270
- [23] F. Viana, R.T. Haftka; V.S. Jr, Multiple surrogates: how cross-validation errors can help us to obtain the best predictor; Struct. Multidiscip. Optim., 39 (2009), pp. 439–457
- [24] F. Viana, R. T. Haftka, V. Steffen, S. Butkewitsch, M. F. Leal, Ensemble of Surrogates: a Framework based on Minimization of the Mean Integrated Square Error, en: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials, Schaumburg, IL, pp. 1-27.
- [25] F. Viana, V. Picheny, R.T. Haftka; Using Cross Validation to Design Conservative Surrogates; AIAA, 48 (2010), pp. 2286–2298
- [26] K. Miettinen; Nonlinear Multiobjective Optimization; Kluver Academic Publishers, Dordrecht (1999)
- [27] Matlab, The language of technical computing. (R2011a), MathWorks Inc., 2011.
- [28] M. Johnson, L. Moore, D. Ylvisaker; Minimax and maximin distance designs; J. Stat. Plann. Infer., 26 (1990), pp. 131–148
- [29] F. Branin; Widely convergent method for finding multiple solutions of simultaneous nonlinear equations; IBM J. Res. Dev., 16 (1972), pp. 504–522
- [30] N.D. Lagaros, V. Plevris, M. Papadrakakis; Reliability based robust design optimization of steel structures; Int. J. Simul. Multi. Design Optim., 1 (2007), pp. 19–29
- [31] S. Rahman, H. Xu; A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics; Probab. Eng. Mech., 19 (2004), pp. 393–408
- [32] H. Xu, S. Rahman; A generalized dimension-reduction method for multidimensional integration in stochastic mechanics; Int. J. Numer. Methods Eng., 61 (2004), pp. 1992–2019
- [33] I. Lee, K.K. Choi, L. Du, D. Gorsich; Dimension reduction method for reliability-based robust design optimization; Comput. Struct., 86 (2008), pp. 1550–1562
Document information
Published on 01/06/14
Accepted on 31/01/13
Submitted on 09/08/12
Volume 30, Issue 2, 2014
DOI: 10.1016/j.rimni.2013.01.003
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?