Uncertainty propagation using the full second-order approach for probabilistic fatigue crack growth life

Abstract

Uncertainty propagation of fatigue crack growth life commonly aims to provide the probability distribution of the lifespan needed for probabilistic damage tolerance analysis and for structural integrity assessment. This paper presents a novel methodology for efficiently estimating the parameters of the probability distribution of fatigue lifespan considering the Pearson distribution family. First, the full second-order approach for expected value and variance prediction of probabilistic fatigue crack growth life is extended to predict higher order statistical moments of the underlying distribution. That is, the expected value (first raw moment) and the variance (second central moment) equations are complemented with the probabilistic formulations for the skewness and for the kurtosis (third and fourth central standardized moments, respectively). Then, from these moments, the Pearson distribution type is automatically determined. Finally, the parameters of the particular Pearson distribution type are estimated making the statistical moments of the constructed lifespan distribution match the first four prescribed moments predicted by the probabilistic equations. The validity of the proposed method is verified by a numerical example regarding the fatigue crack growth in a railway axle under random bending loading. It is proven that the probability density function of the lifespan is properly derived by the methodology, without knowing or assuming the output probability distribution beforehand. The methodology presented enables an efficient and an accurate quantification of the lifespan uncertainties via its probabilistic distribution. This probabilistic description of fatigue crack growth life can be subsequently used in reliability studies or in damage tolerance assessment.

Keywords: Probabilistic fatigue crack growth, uncertainty propagation, lifespan probability distribution, pearson distribution family, NASGRO

Nomenclature

${\textstyle a}$: crack depth / normal semiaxis

${\textstyle {a}_{fin\,}}$: final crack depth

${\textstyle {a}_{ini\,}}$: initial crack depth

${\textstyle {{a}_{1},\,\,a}_{2}}$: real roots of the quadratic equation in the denominator of the integral of the Pearson solution

${\textstyle B}$: superscript above ${\textstyle \sigma }$ referring to the bending loading case

${\textstyle B+I}$: superscript above ${\textstyle \sigma }$ referring to the bending plus interference loading case

${\textstyle C}$: parameter of the crack growth equation in the Paris region

${\textstyle d}$: random variables number

${\textstyle da/dN\,}$: crack growth rate

${\textstyle {e}^{\mu }}$: scale parameter of the log-normal distribution

${\textstyle f}$: Newman’s crack opening function

${\textstyle f\left(x;\alpha ,\beta \right)}$: probability density function for the standardized beta distribution

${\textstyle f\left(x;\sigma \right)}$: probability density function for the standardized log-normal distribution

${\textstyle {f}_{N}}$: probability density function of the random variable fatigue life ${\textstyle N}$

${\textstyle {g}_{,j}}$: first partial derivative of ${\textstyle g}$ with respect to ${\textstyle {X}_{j}}$ ${\textstyle \left(={\frac {\partial g}{\partial {X}_{j}}}\right)}$

${\textstyle {g}_{,jk}}$: second partial derivative of ${\textstyle g}$ with respect to ${\textstyle {X}_{j}}$ and ${\textstyle {X}_{k}}$ ${\textstyle \left(={\frac {{\partial }^{2}g}{\partial {X}_{j}\partial {X}_{k}}}\right)}$

${\textstyle {g}_{\mu }}$: evaluation of ${\textstyle g\left(X\right)}$ at the mean value vector of ${\textstyle X}$ ${\textstyle \left(=\left({\mu }_{{X}_{1}},{\mu }_{{X}_{2}},\ldots ,{\mu }_{{X}_{d}}\right)\right)}$

${\textstyle i}$: step increment

${\textstyle I}$: superscript above ${\textstyle \sigma }$ referring to the interference loading case

${\textstyle j,k,l,m,r,s,t,u}$: index from 1 to ${\textstyle d}$ random variables

${\textstyle K}$: stress intensity factor (general)

${\textstyle {K}_{c}}$: critical stress intensity factor for static unstable crack growth

${\textstyle {K}_{max}}$, ${\textstyle {K}_{min}}$: maximum and minimum ${\textstyle K}$

${\textstyle M}$: bending moment

${\textstyle n}$: exponent of the crack growth equation in the Paris region

${\textstyle ns}$: steps number

${\textstyle N}$: number of applied cycles

${\textstyle p}$: parameter describing the sigmoidal shape of the crack growth equation in the threshold region

${\textstyle p(x)}$: Pearson probability density function

${\textstyle q}$: parameter describing the sigmoidal shape of the crack growth equation in the toughness region

${\textstyle R}$: stress ratio ${\textstyle \left(={\frac {{K}_{min}}{{K}_{max}}}\right)}$

${\textstyle x}$: radial coordinate direction at the axle surface

${\textstyle X}$: set of random variables ${\textstyle \left(=\left\{{X}_{1},{X}_{2},\ldots ,{X}_{d}\right\}\right)}$

${\textstyle Y}$: general multivariate function ${\textstyle \left(=g\left(X\right)\right)}$

${\textstyle \alpha ,\,\,\beta }$: shape parameters of the beta distribution

${\textstyle {\beta }_{{1}_{Y}}}$: square of skewness of ${\textstyle Y}$ ${\textstyle \left(={\left(Skew\left(Y\right)\right)}^{2}\right)}$

${\textstyle {{\beta }_{2}}_{Y}}$: kurtosis of ${\textstyle Y}$ ${\textstyle \left(=Kurt\left(Y\right)={\frac {{\mu }_{Y,4}}{{\sigma }_{Y}^{4}}}\right)}$

${\textstyle {\gamma }_{{1}_{Y}}}$: skewness of ${\textstyle Y}$ ${\textstyle \left(=Skew\left(Y\right)={\frac {{\mu }_{Y,3}}{{\sigma }_{Y}^{3}}}\right)}$

${\textstyle \Gamma \left(x\right)}$: gamma function ${\textstyle \left(=\left(x-1\right)!\right)}$

${\textstyle \Delta K}$: stress intensity factor range

${\textstyle \Delta {K}_{th}}$: threshold stress intensity factor range

${\textstyle \lambda }$: location parameter of the log-normal and the beta distributions.

${\textstyle {\mu }_{Y}}$: expected value of ${\textstyle Y}$ ${\textstyle \left(=E\left[Y\right]\right)}$ or first raw moment simply denoted ${\textstyle {\mu '}_{1}}$

${\textstyle {\mu }_{Y,3}}$: third central moment of ${\textstyle Y}$ ${\textstyle \left(=E\left[{\left(Y-E\left[Y\right]\right)}^{3}\right]\right)}$

${\textstyle {\mu }_{Y,4}}$: fourth central moment of ${\textstyle Y}$ ${\textstyle \left(=E\left[{\left(Y-E\left[Y\right]\right)}^{4}\right]\right)}$

${\textstyle \sigma }$: stress (general)

${\textstyle \sigma }$: shape parameter of the log-normal distribution

${\textstyle {\sigma }_{Y}}$: standard deviation of ${\textstyle Y}$

${\textstyle {\sigma }_{Y}^{2}}$: variance of ${\textstyle Y}$ ${\textstyle \left(=E\left[{\left(Y-E\left[Y\right]\right)}^{2}\right]\right)}$ also simply denoted ${\textstyle {\mu }_{2}}$

${\textstyle \varphi \left(x\right)}$: probability density function for the standard normal distribution

Abbreviations

FOSM: first order second moment

FEM: finite element method

SIF: stress intensity factor

MC: Monte Carlo

Pr. Eq.: probabilistic equation

PDF: probability density function

1. Introduction

The fatigue crack growth mechanism is affected by many sources of variability such as the statistical variations of the mechanical properties of solid materials [1–4], random loading conditions [5–7] and uncertainties inherent to geometrical parameters [8]. Therefore, the stochastic nature of the fatigue crack growth phenomenon requires a proper uncertainty processing for reliability assessment and durability prediction. Uncertainty propagation methods in the fatigue life prediction commonly characterize the lifespan after a certain crack growth through a probability distribution. In consequence, probabilistic fatigue crack growth analyses aim to determine the probability distribution of the random response, lifespan, as a result of the randomness of the input variables. In areas such as damage tolerance analysis in the railway sector, predicting the probability distribution of fatigue crack growth life is becoming an important aspect. However, there is still a lack of harmonization of probabilistic procedures to define in-service inspection intervals in train axles for crack detection [9,10]. This particular application still deserves some developments via the extension of the current numerical methodologies.

Probabilistic fatigue crack growth is an extensive area of research. Numerous studies develop probabilistic models based on deterministic crack growth equations such as the Paris’ law [11]. For instance, some probabilistic approaches founded on the Paris law are presented in [12–21], being the model most frequently used. Over recent years, the first advances considering the complete crack growth curve have been made because of the increasing importance of taking into account the early stages of crack growth for an adequate estimation of the lifespan. The state of the art equation in the field of the fatigue crack propagation problem is a modified version of the Paris’ law referred to as NASGRO equation [22]. The NASGRO equation is commonly applied in the evaluation of components as in the case of railway axles [18,23–25]. Additionally, the use of the first-order second-moment (FOSM) probabilistic method [26–29] has enabled some new perspectives in the fatigue crack growth analysis of components. Some examples are the fatigue life estimation according to the Paris' law [13,14], the crack nucleation stage analysis based on the Coffin-Manson model [30], the multiaxial fatigue assessment based on the virtual strain energy damage model of Liu [31,32] and especially the fatigue crack propagation based on the NASGRO equation in [25] where an extended version of the FOSM to full second-order approach is developed for predicting statistical moments of the fatigue lifetime in a railway axle under random loading.

The probabilistic fatigue crack growth strategies above provide certain statistics that describe the response distribution, for instance, mathematical moments like the expected value and the variance. Then, the problem under investigation is further analyzed according to these statistics. One such interesting analysis is to construct the whole probability density function (PDF) of fatigue crack growth life, namely, the uncertainty propagation in fatigue crack growth life. The PDF can be used to describe the relative likelihood that the value of the lifespan would be equal to a particular value. Generally, the random output variable is assumed to follow a common probability distribution, such as the normal or the log-normal distribution, and subsequently the parameters of the distribution are estimated considering the statistics of the response as constraints. An illustrative example of the previous strategy is presented in [25] where the full second-order approach provides the expected value and the variance of the random output variable lifespan and then the normal and the log-normal PDFs are constructed according to these two statistics of the lifespan. The discussion in the example mentioned above highlights some drawbacks regarding the need to assume in advance a probability distribution of two parameters, since only the expected value and the variance of the underlying lifespan probability distribution are calculated, and also that the accuracy or similarity between the constructed PDFs and the results of the Monte Carlo method (MC) can be improved. A general methodology that considers the statistics of the response and automatically provides an appropriate PDF of the response distribution will be more useful than a predefined one. It would thus be of interest to explore some alternatives to overcome the limitations aforementioned to contribute to a better knowledge of the distribution of fatigue life.

As shown in the previous literature, the scientific community has studied the uncertainty propagation in fatigue crack growth life for many years. These investigations are usually intended to provide the probability distribution of the lifespan which, as is the case of train axles, is a fundamental aspect for the maintenance planning definition to keep the probability of failure as small as possible, as far as it is economically viable. Addressing the problem in an efficient and precise manner is, therefore, a challenge. The construction of a PDF under moment constraints has historically been of great interest. In some cases, the underlying probability distribution manifests asymmetry or presents a characteristic heaviness of the tails relative to the rest of the distribution or a combination of both. Therefore the need to manage the shape of the constructed PDF arises. The shape of the constructed distribution can be handled by means of controlling its skewness and kurtosis moments. Early contributions considered this topic, devising a system of distributions, the Pearson distribution family [33], which has the appeal of encompassing several well-known distributions as members. This distribution has a rich flexibility in shape, covering a wide skewness-kurtosis region. Furthermore, the location, scale and shape parameters of a particular Pearson distribution can be estimated in terms of the first four prescribed moments, that is, the expected value, first raw moment; the variance, second central moment; the skewness, third central standardized moment, and the kurtosis, fourth central standardized moment. As a consequence, the Pearson family of distributions has been used for modelling purposes by those engaged in the probabilistic analysis of structures. However, an overall treatment of the uncertainty propagation in fatigue crack growth life based on the NASGRO equation combined with the versatile Pearson distribution family is missing. To the best of the authors’ knowledge, the work presented in this paper is the first attempt to develop an effective, efficient and practical uncertainty propagation approach that is capable of predicting the first four moments of the lifespan distribution according to the NASGRO equation and using them to construct a probability density function based on the Pearson distribution family.

The objective of this work is to providea novel uncertainty propagation methodology for efficiently estimating the parameters of the probability distribution of fatigue lifespan considering the Pearson distribution family. For this purpose, the pertinent Pearson distribution type is automatically determined depending on the stochastic moments of the underlying lifespan distribution according to the NASGRO equation. Subsequently, the parameters of the distribution are calculated making the statistical moments of the constructed lifespan distribution match the first four prescribed moments. To estimate these first four required moments in advance, the full second-order approach for expected value and variance prediction presented in [25] is extended to predict the skewness and the kurtosis of the underlying lifetime distribution. As a result, the methodology developed enables an efficient estimation of the parameters of the particular Pearson distribution type and, in the meantime, provides the first four moments of the underlying lifetime distribution. The combination of both, contributes to overcome the drawbacks previously highlighted, avoiding the need to assume a probability distribution of two parameters and also increasing the accuracy of the PDF constructed. The proposed uncertainty propagation methodology is illustrated and discussed in detail through an application example specifically oriented on the fatigue crack growth in a metallic railway axle.

The paper is organized as follows. Section 2 presents the methods used for the uncertainty propagation methodology. Firstly, the full second-order approach for the skewness and kurtosis moments of functions of random variables is described in detail. It also includes the probabilistic expressions regarding its integration with the NASGRO model. Secondly, an overview of the Pearson distribution family is given and the estimation of the distribution parameters from prescribed moments is summarized. Section 3 illustrates and discusses the proposed uncertainty propagation procedure by means of an application example in a metallic railway axle. The results of the full second-order approach are compared with those obtained by the Monte Carlo method in terms of skewness and kurtosis. Furthermore, the quality of PDF constructed with the Pearson distribution in comparison with the histogram from the Monte Carlo method is discussed. Finally, Section 6 concludes the main findings in this paper.

2. Uncertainty propagation methodology

The objective of the uncertainty propagation methodology is to efficiently estimate the parameters of the probability distribution of a random variable of interest. To establish a general methodology, a key point is to consider the Pearson distribution family because of the following two reasons combined. Firstly, it is a rich family that is able to adjust a broad range of distribution shapes and therefore it can closely represent a portion of the reality. Secondly, the Pearson distribution family is easy to use in practice because it has mathematical characteristics that make the different distribution parameters be expressed as function of the first four moments.

To obtain the first four required moments of the underlying distribution, the full second-order approach for expected value and variance prediction of probabilistic fatigue crack growth life is extended to predict higher order statistical moments of the underlying distribution. That is, the expected value (first raw moment) and the variance (second central moment) probabilistic equations (Pr. Eq.) are complemented with the Pr. Eq. for the skewness and for the kurtosis (third and fourth central standardized moments, respectively). The reasoning followed for the expected value and the variance estimation is used to derive the Pr. Eq. for the skewness and the kurtosis prediction.

2.1. Full second-order approach for skewness and kurtosis prediction of probabilistic fatigue crack growth life

The full second-order approach for the moments of functions of random variables presented in [25] enables the prediction of the expected value and the variance of the lifespan of interest. Here, the approach is extended to predict the skewness and the kurtosis of the probabilistic fatigue crack growth life. This section recalls the definition of skewness and kurtosis, then derives the full second-order approximation for the third and fourth central moments of a general function and finally provides the probabilistic formulations for propagating the third and fourth central moments through the fatigue crack growth NASGRO model.

The third central moment is a measure of the distribution symmetry or lack of symmetry. Any symmetric distribution will have a third central moment of zero. The third central moment divided by the standard deviation to the power of three is referred to as normalized or standardized third central moment and commonly known as skewness. The skewness is denoted by ${\textstyle {\gamma }_{1}}$ as it is shown in Eq. (1)

${\gamma }_{1}={\frac {{\mu }_{3}}{{\sigma }^{3}}}$

(1)

As the third central moment has units of the random variable to the power of three, after normalization, skewness is dimensionless. Usually, the square of the skewness is denoted by ${\textstyle {\beta }_{1}}$ as it is expressed in Eq. (2)

${\beta }_{1}={\gamma }_{1}^{2}$

(2)

The fourth central moment is a measure of the combined weight or heaviness of the tails relative to the rest of the distribution. As the variance, it measures the spread of the data but is more dependent on the behavior of outliers in the tails. The fourth central moment divided by the standard deviation to the power of four is known as normalized or standardized fourth central moment and generally referred to as kurtosis. The kurtosis is frequently denoted by ${\textstyle {\beta }_{2}}$ as it is presented in Eq. (3), being dimensionless for the same reason mentioned above

${\beta }_{2}={\frac {{\mu }_{4}}{{\sigma }^{4}}}$

(3)

The skewness and the kurtosis are calculated from the third and fourth central moments as indicated in the previous definitions. Following the reasoning presented in [25] to predict the expected value and the variance, the third central moment approximation is derived and as a result the skewness can be calculated. The full second-order approximation for the third central moment of a general function is given by Eq. (4)

${\mu }_{3}\left(Y,Y,Y\right)={\mu }_{Y,3}\approx {{g}_{\mu }}^{3}+\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{g}_{,j}{g}_{,k}{{g}_{,l}\mu }_{jkl}+$${\frac {1}{8}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}\sum _{s=1}^{d}{g}_{,jk}{g}_{,lm}{{g}_{,rs}\mu }_{jklmrs}+$$3{{g}_{\mu }}^{2}{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}{g}_{,jk}{\mu }_{jk}+3{g}_{\mu }\sum _{j=1}^{d}\sum _{k=1}^{d}{g}_{,j}{g}_{,k}{\mu }_{jk}+$$3{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}{g}_{,j}{g}_{,k}{g}_{,lm}{\mu }_{jklm}+$$3{g}_{\mu }{\frac {1}{4}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}{g}_{,jk}{g}_{,lm}{\mu }_{jklm}+$$3{\frac {1}{4}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}{g}_{,j}{g}_{,kl}{g}_{,mr}{\mu }_{jklmr}+$$6{g}_{\mu }{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{g}_{,j}{g}_{,kl}{\mu }_{jkl}-$$3{\mu }_{Y}{\sigma }_{Y}^{2}-{{\mu }_{Y}}^{3}$

(4)

Note that ${\textstyle {\mu }_{jk}}$ indicates second central moment ${\textstyle {\mu }_{2}\left({X}_{j},{X}_{k}\right)}$, ${\textstyle {\mu }_{jkl}}$ ${\textstyle \,}$ indicates the third central moment ${\textstyle {\mu }_{3}\left({X}_{j},{X}_{k},{X}_{l}\right)}$, ${\textstyle {\mu }_{jklm}}$ indicates the fourth central moment ${\textstyle {\mu }_{4}\left({X}_{j},{X}_{k},{X}_{l},{X}_{m}\right)}$ and so on. In other words the ${\textstyle {n}^{th}}$ central multivariate moments of continuous random variables are denoted with consecutive indexes, two for the second central moment, three indexes for the third central moment, four indexes for the fourth central moment etc.

Likewise, following the reasoning presented in [25] the fourth central moment approximation is derived and as a result the kurtosis can be calculated. The full second-order approximation for fourth central moment of a general function is given by Eq. (5)

${\mu }_{4}\left(Y,Y,Y,Y\right)={\mu }_{Y,4}\approx {{g}_{\mu }}^{4}+\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}{g}_{,j}{g}_{,k}{{g}_{,l}{g}_{,m}\mu }_{jklm}+$${\frac {1}{16}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}\sum _{s=1}^{d}\sum _{t=1}^{d}\sum _{u=1}^{d}{g}_{,jk}{g}_{,lm}{{g}_{,rs}{g}_{,tu}\mu }_{jklmrstu}+$$4{{g}_{\mu }}^{3}{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}{g}_{,jk}{\mu }_{jk}+4{g}_{\mu }\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{g}_{,j}{g}_{,k}{{g}_{,l}\mu }_{jkl}+$$4{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}{g}_{,j}{g}_{,k}{g}_{,l}{g}_{,mr}{\mu }_{jklmr}+$$4{g}_{\mu }{\frac {1}{8}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}\sum _{s=1}^{d}{g}_{,jk}{g}_{,lm}{g}_{,rs}{\mu }_{jklmrs}+$$4{\frac {1}{8}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}\sum _{s=1}^{d}\sum _{t=1}^{d}{g}_{,j}{g}_{,kl}{g}_{,mr}{g}_{,st}{\mu }_{jklmrst}+$$6{{g}_{\mu }}^{2}\sum _{j=1}^{d}\sum _{k=1}^{d}{g}_{,j}{g}_{,k}{\mu }_{jk}+6{{g}_{\mu }}^{2}{\frac {1}{4}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}{g}_{,jk}{g}_{,lm}{\mu }_{jklm}+$$6{\frac {1}{4}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}\sum _{s=1}^{d}{g}_{,j}{g}_{,k}{g}_{,lm}{g}_{,rs}{\mu }_{jklmrs}+$$12{{g}_{\mu }}^{2}{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{g}_{,j}{g}_{,kl}{\mu }_{jkl}+$$12{g}_{\mu }{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}{g}_{,j}{g}_{,k}{g}_{,lm}{\mu }_{jklm}+$$12{g}_{\mu }{\frac {1}{4}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}\sum _{m=1}^{d}\sum _{r=1}^{d}{g}_{,j}{g}_{,kl}{g}_{,mr}{\mu }_{jklmr}-$$4{\mu }_{Y}{\mu }_{Y,3}-6{{\mu }_{Y}}^{2}{\sigma }_{Y}^{2}-{{\mu }_{Y}}^{4}$

(5)

At this point, to bridge the gap between the full second-order approach presented and the fatigue crack growth life prediction, the probabilistic formulations for propagating the third and fourth central moments through the fatigue crack growth NASGRO model are deduced. To begin with, the NASGRO model described from a probabilistic point of view in [25] is adopted. This probabilistic form is adapted to obtain the distribution of the number of load cycles ${\textstyle N}$ to reach a given crack depth ${\textstyle a}$. It basically starts from the original NASGRO crack propagation rate ${\textstyle da/dN}$, isolates ${\textstyle dN}$ and using the discretised version for every ${\textstyle {i}^{th}}$ crack growth increment leads to Eq. (6)

${dN}^{i}={\frac {{da}^{i}}{C{\left({\frac {1-{f}^{i}}{1-{R}^{i}}}\,\,{\Delta K}^{i}\right)}^{n}}}\,{\frac {{\left(1-{\frac {{K}_{max}^{i}}{{K}_{c}}}\right)}^{q}}{{\left(1-{\frac {{\Delta K}_{th}^{i}}{{\Delta K}^{i}}}\right)}^{p}}}$

(6)

where, ${\textstyle R}$ is the stress ratio, ${\textstyle \Delta K}$ is the stress intensity factor (SIF) range from the ${\textstyle \,}$ maximum and minimum ${\textstyle K}$, i.e. ${\textstyle {K}_{max}}$ and ${\textstyle {K}_{min}}$, ${\textstyle f}$ is the crack opening function, ${\textstyle \Delta {K}_{th}}$ is the threshold stress intensity factor range, ${\textstyle {K}_{c}}$ is the critical stress intensity factor and ${\textstyle C}$, ${\textstyle n}$, ${\textstyle p}$, and ${\textstyle q}$ are material empirically derived constants. For a more detailed description of the previous equation refer to [22,25].

The third central moment of the fatigue life ${\textstyle {\mu }_{3}\left(N,N,N\right)}$ is obtained by applying the third central moment definition to the total number of cycles ${\textstyle N}$ which is the summation of the ${\textstyle ns}$ life increments ${\textstyle {dN}^{i}}$ up to a final crack depth ${\textstyle \,{a}_{fin}}$. Using the formula for the third central moment of the sum of random variables leads to Eq. (7)

${\mu }_{3}\left(N,N,N\right)=\,{\mu }_{3}\left(\sum _{i=1}^{ns}{dN}^{i},\sum _{i=1}^{ns}{dN}^{i},\sum _{i=1}^{ns}{dN}^{i}\right)=$$\sum _{{i}_{1}=1}^{ns}{\mu }_{3}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{1}}\right)+3\sum _{\begin{matrix}{i}_{1}\not ={i}_{2}\end{matrix}}^{ns}{\mu }_{3}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{2}}\right)+$$6\sum _{{i}_{1}\not ={i}_{2}\not ={i}_{3}}^{ns}{\mu }_{3}\left(d{N}^{{i}_{1}},d{N}^{{i}_{2}},d{N}^{{i}_{3}}\right)$

(7)

In the same manner as above, the fourth central moment of the fatigue life ${\textstyle {\mu }_{4}\left(N,N,N,N\right)}$ is obtained by using the formula for the fourth central moment of the sum of random variables giving Eq. (8)

${\mu }_{4}\left(N,N,N,N\right)=\,{\mu }_{4}\left(\sum _{i=1}^{ns}{dN}^{i},\sum _{i=1}^{ns}{dN}^{i},\sum _{i=1}^{ns}{dN}^{i},\sum _{i=1}^{ns}{dN}^{i}\right)=$$\sum _{{i}_{1}=1}^{ns}{\mu }_{4}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{1}}\right)+4\sum _{\begin{matrix}{i}_{1}\not ={i}_{2}\end{matrix}}^{ns}{\mu }_{4}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{2}}\right)+$$6\sum _{{i}_{1}\not ={i}_{2}}^{ns}{\mu }_{4}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{2}},d{N}^{{i}_{2}}\right)+$$12\sum _{{i}_{1}\not ={i}_{2}\not ={i}_{3}}^{ns}{\mu }_{4}\left(d{N}^{{i}_{1}},d{N}^{{i}_{1}},d{N}^{{i}_{2}},d{N}^{{i}_{3}}\right)+$$24\sum _{{i}_{1}\not ={i}_{2}\not ={i}_{3}\not ={i}_{4}}^{ns}{\mu }_{4}\left(d{N}^{{i}_{1}},d{N}^{{i}_{2}},d{N}^{{i}_{3}},d{N}^{{i}_{4}}\right)$

(8)

In Eqs. (7) and (8) the moments ${\textstyle {\mu }_{3}}$ and ${\textstyle {\mu }_{4}}$ of ${\textstyle {dN}^{i}}$ are obtained by applying the full second-order approximation developed to obtain the stochastic central moments of third and fourth order Eqs. (4) and (5) respectively, on the ${\textstyle {dN}^{i}}$ function Eq. (6). Eqs. (7) and (8) are referred to as the probabilistic NASGRO equations for the third and fourth central moments respectively. In summary, for each ${\textstyle {i}^{th}}$ crack growth increment the third and fourth central moments of the fatigue lifetime increment ${\textstyle {dN}^{i}}$ are calculated by applying the full second-order approximation method on the discretised version of the NASGRO equation, requiring the first to eighth order moments of the random input variables and the first and second partial derivatives of the NASGRO equation with respect to the random input variables.

2.2. Pearson distribution family and parameters estimation from prescribed moments

Many statistical analyses consider the normal distribution when there is not more information available about the underlying probability distribution, however, in some cases, this assumption does not reflect the reality. Among the different statistical distributions that can be chosen, the Pearson distribution family is considered in the methodology as it is a versatile family that covers a broad range of distribution shapes and therefore it is able to model a wide range of data accurately. Moreover, it enables the expression of the distribution parameters as a function of the first four moments of the distribution without a priori hypotheses and thus it is an efficient and objective procedure.

The Pearson distribution is a family of continuous probability distributions [33]. A Pearson probability density function ${\textstyle \,p(x)}$ is defined to be any valid solution to the first order linear differential equation presented in Eq. (9)

${\frac {p'(x)}{p(x)}}+{\frac {\left(x-\lambda \right)+a}{{b}_{0}+{b}_{1}\left(x-\lambda \right)+{b}_{2}{\left(x-\lambda \right)}^{2}}}=$$0$

(9)

with

${b}_{0}={\frac {4{\beta }_{2}-3{\beta }_{1}}{10{\beta }_{2}-12{\beta }_{1}-18}}{\mu }_{2},\,\,a\equiv {b}_{1}=$${\sqrt {{\mu }_{2}}}{\sqrt {{\beta }_{1}}}{\frac {{\beta }_{2}+3}{10{\beta }_{2}-12{\beta }_{1}-18}},\,\,{b}_{2}=$${\frac {2{\beta }_{2}-3{\beta }_{1}-6}{10{\beta }_{2}-12{\beta }_{1}-18}}$

where, ${\textstyle \lambda }$ is a location parameter, ${\textstyle {\beta }_{1}}$ is the square of the skewness, ${\textstyle {\beta }_{2}}$ is the kurtosis, and ${\textstyle {\mu }_{2}}$ is the second central moment of the distribution. The solution to the above differential equation is shown in Eq. (10)

$p\left(x\right)\propto \mathrm {exp} \,\left(-\int _{}^{}{\frac {x+a}{{b}_{2}{x}^{2}+{b}_{1}x+{b}_{0}}}dx\right)$

(10)

The variety of solutions differ in the values of the coefficients ${\textstyle a}$, ${\textstyle {b}_{0}}$, ${\textstyle {b}_{1}}$ and ${\textstyle {b}_{2}}$. These solutions are classified into different Pearson distribution types depending on the quantities ${\textstyle {\beta }_{1}}$ and ${\textstyle {\beta }_{2}}$. In other words, the type of distribution to which the data belong is entirely determined by the square of the skewness ${\textstyle {\beta }_{1}}$ presented in Eq. (2) and the kurtosis ${\textstyle {\beta }_{2}}$ expressed in Eq. (3). The Pearson distribution types correspond to common probability distributions. The following types and their common distribution associated arise: type I (beta distribution), type II (symmetrical beta distribution), type III (gamma distribution), type IV (Cauchy distribution), type V (inverse-gamma distribution), type VI (beta prime distribution), type VII (Student's tdistribution) and the limit of type I, III, IV, V (normal distribution).

Once the Pearson distribution type is determined, the two, three or four parameters of the particular distribution type can be calculated as a function of the expected value, variance, skewness and kurtosis, i.e. from the first four moments. The formulas to calculate the parameters for each type of Pearson distribution are given in [34]. As an example, the formulas for the Pearson distribution type I that corresponds to the beta distribution are included here. A random variable ${\textstyle x}$ following a beta distribution ${\textstyle Beta\left(\alpha ,\beta \right)}$ with the shape parameters ${\textstyle \alpha }$ and ${\textstyle \beta }$, can be further parametrized as ${\textstyle {\frac {x-\lambda }{{a}_{2}-{a}_{1}}}}$ with the scale parameter ${\textstyle \left({a}_{2}-\right.}$$\left.{a}_{1}\right)$ and with a location parameter ${\textstyle \lambda }$. The shape parameters ${\textstyle \alpha \,}$ and ${\textstyle \beta }$ are calculated according to the Pearson distribution family as expressed in Eq. (11)

$\alpha =-{\frac {a+{a}_{1}}{{b}_{2}\left({a}_{1}-{a}_{2}\right)}}+1\,,$ $\,\,\beta ={\frac {a+{a}_{2}}{{b}_{2}\left({a}_{1}-{a}_{2}\right)}}+1$

(11)

where ${\textstyle {a}_{1}<0<{a}_{2}}$ are the real roots of the quadratic function in the denominator of Eq. (10). Hence, they are calculated as shown in Eq. (12), and additionally they set the scale parameter ${\textstyle \left({a}_{2}-\right.}$$\left.{a}_{1}\right)$

${a}_{1}={\frac {-{b}_{1}-{\sqrt {{{b}_{1}^{2}-4b}_{2}{b}_{0}}}}{2{b}_{2}}}\,,$ $\,\,{a}_{2}={\frac {-{b}_{1}+{\sqrt {{{b}_{1}^{2}-4b}_{2}{b}_{0}}}}{2{b}_{2}}}$

(12)

Finally, the location parameter calculated according to the Pearson distribution family is shown in Eq. (13)

$\lambda ={\mu '}_{1}\,-\left({a}_{2}-{a}_{1}\right){\frac {\alpha }{\alpha +\beta }}$

(13)

where ${\textstyle {\mu '}_{1}}$ is the expected value of the distribution of the original variable ${\textstyle x}$ to model, i.e. its first raw moment.

3. Illustrative application example and discussion

The aim of this example is to illustrate the uncertainty propagation methodology described in the present paper which extends the full second-order approach for expected value and variance prediction to predict the skewness and the kurtosis of the fatigue lifetime based on NASGRO model and estimates the parameters of a particular Pearson distribution type based on the first four prescribed moments. The methodology was applied to the example 1 in [25] to verify that the proposed improvements contribute to a better knowledge of the distribution of fatigue life. Briefly, the numerical example dealt with the fatigue crack growth in the railway axle shown in Figure 1 under random bending moment. The axle was 173 mm in diameter and it was made of EA1N steel defined in the EN 13261 standard [35].

Figure 1. General axle view of a non-powered wheelset with a postulated crack in the T-transition

A semicircular initial crack ${\textstyle {a}_{ini}}$ of 2 mm was postulated at the T-transition, as indicated in the cross-section of the Figure 1. The crack grows describing the crack propagation direction defined according to the radial coordinate system ${\textstyle x}$ at the axle surface in Figure 1. The crack kept a semielliptical shape while growing up to a final crack depth ${\textstyle \,{a}_{fin}}$ of 50 mm. The fatigue crack growth material parameters used in the NASGRO model were those collected in [25].

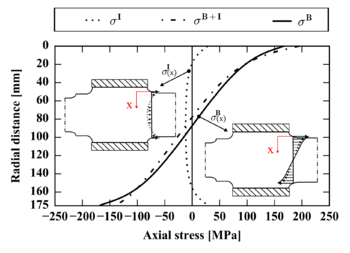
For the present study, the following two types of loads were considered: the bending moment loading mainly due to the vehicle weight and cargo and the press-fit loading produced by the wheel mounting with interference. The bending moment in the railway axle was assumed as a random input variable normally distributed with a standard deviation equal to the 5% of the mean value. The parameters of the bending moment distribution were: mean value ${\textstyle {\mu }_{M}=}$$70.32\,[MN\,mm]$ and variance ${\textstyle {\sigma }_{M}^{2}=}$$12.37\,{\left[MN\,mm\right]}^{2}$. The bending moment level selected ${\textstyle M}$ corresponded to the highest load amplitude in the spectrum of a railway axle which is caused by the weight of the wagon and cargo, 22.5 tonnes per axle, plus additional forces, generated when the train goes through curved track, over crossovers, switches, rail joints, braking efforts, etc. Additionally, the wheel was press-fitted with 0.286 mm interference in diameter. The reference bending stress amplitude for the mean value of bending moment and the interference stress normal to the crack surface needed for the stress intensity factor ${\textstyle {K}_{max}}$ and ${\textstyle {K}_{min}}$ evaluation were calculated via the finite element method (FEM). The stresses at the interference ${\textstyle {\sigma }^{I}}$, at the reference bending moment ${\textstyle {\sigma }^{B}}$ and at the combination of both ${\textstyle {\sigma }^{B+I}}$ are shown in Figure 2. In this adapted version of the original figure in [25], a schematic representation of the axial stress distributions originated at the T-transition in a solid axle under a pure press-fit with interference and under a pure bending load case is also included for clarity.

Figure 2. Schematic representation and calculated stress distributions at the T-transition in axial direction at the press-fit with interference, at the bending and at the superposition of both load cases

In the example, there was a single source of variability from the bending moment that induced variability on the bending stress and therefore there was variability in the combination of the bending with the interference stress. The stress intensity factors ${\textstyle {K}_{max}}$ and ${\textstyle {K}_{min}}$ depend on the maximum and minimum stresses and in consequence they were also stochastic. The combination of stresses was obtained considering the fact that the railway axle rotates as the train moves. Consequently, every revolution the crack goes through all possible positions with respect to the applied moment since the bending load always acts in the vertical plane and hence the resulting load type is rotary bending. The maximum and minimum stresses were related to each other as a result of the stresses symmetry. This fact together with the cyclic rotary character of the load implies that the random variables ${\textstyle {K}_{max}}$ and ${\textstyle {K}_{min}}$ were related to each other too. These two random variables used to describe the input variability were correlated variables so they were not independent. It is important to emphasize that ${\textstyle {K}_{max}}$ and ${\textstyle {K}_{min}}$ are explicitly involved in the NASGRO equation.

The full second-order approach presented was applied to calculate the third moment and the fourth central moments of ${\textstyle {dN}^{i}}$ at every crack depth, Eq. (6), with the two random input variables ${\textstyle {K}_{max}^{i}}$ and ${\textstyle {K}_{min}^{i}}$. Then, the skewness ${\textstyle {\gamma }_{{1}_{N}}}$ and the kurtosis ${\textstyle {\beta }_{{2}_{N}}}$ of the fatigue life ${\textstyle N}$ were obtained from the ${\textstyle {i}^{th}\,}$ moments, providing a continuous result along the crack depth ${\textstyle a}$. The results provided by the proposed methodology were compared with the results of 10 000 MC simulations. The skewness and kurtosis results provided by the MC were obtained by further processing the MC simulations performed in [25].

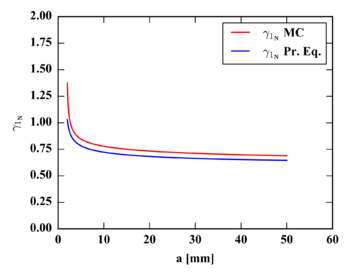
To check the accuracy of the method in terms of skewness, the ${\textstyle {\gamma }_{{1}_{N}}}$ history values provided by the MC and the Pr. Eq. are compared in Figure 3.

Figure 3. Skewness of ${\textstyle N}$ history values provided by the Monte Carlo (MC) and by the probabilistic NASGRO equation (Pr.Eq.)

The values of the skewness curves for 5-50 mm crack depths are listed in Table 1.

Table 1. Skewness of ${\textstyle N}$ provided by Monte Carlo (MC) and by the probabilistic NASGRO equation (Pr. Eq.)

	MC	Pr. Eq.	Pr. Eq.-MC
$a$	${\gamma }_{{1}_{N}}$	${\gamma }_{{1}_{N}}$	$Error$
[mm]	[dimensionless]	[dimensionless]	[%]
5	0.844	0.781	-7.52%
10	0.777	0.722	-7.14%
20	0.733	0.682	-6.91%
30	0.712	0.664	-6.70%
40	0.698	0.653	-6.47%
50	0.689	0.646	-6.24%

The skewness computed from the MC simulations distribution is considered as the framework of reference for comparison. It is observed that the skewness values are always positive, indicating that the right tail, in a sense, is longer and or heavier than the left one. Additionally, it can be seen that as the crack depth increases the skewness decreases reaching a value greater than 0.6 in both calculations. The error in the Pr. Eq. ranges from 7.5% to 6.2%, reducing as the crack depth increases. The Pr. Eq. provides a slightly lower magnitude than the MC for every crack depth. 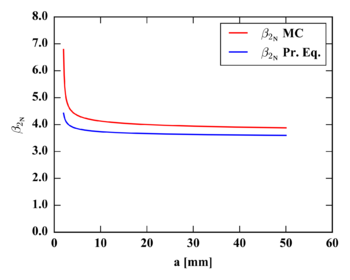To check the accuracy of the method in terms of kurtosis, the ${\textstyle {{\beta }_{2}}_{N}}$ history values provided by the MC and the Pr. Eq. are compared in Figure 4.

Figure 4. Kurtosis of ${\textstyle N}$ history values provided by the Monte Carlo (MC) and by the probabilistic NASGRO equation (Pr.Eq.)

The values of the kurtosis curves for 5-50 mm crack depths are listed in Table 2.

Table 2. Kurtosis of ${\textstyle N}$ provided by Monte Carlo (MC) and by the probabilistic NASGRO equation (Pr. Eq.)

	MC	Pr. Eq.	Pr. Eq.-MC
$a$	${{\beta }_{2}}_{N}$	${{\beta }_{2}}_{N}$	$Error$
[mm]	[dimensionless]	[dimensionless]	[%]
5	4.33	3.84	-11.33%
10	4.13	3.73	-9.53%
20	4.00	3.66	-8.38%
30	3.94	3.63	-7.83%
40	3.90	3.61	-7.47%
50	3.88	3.60	-7.22%

Once again, the kurtosis provided by the MC simulations is considered as the framework of reference. It is observed that the larger the crack the lower kurtosis and, in both calculations, a stabilization in magnitude is reached. The error in the probabilistic equation ranges from 11% to 7%, decreasing as the crack depth increases. The maximum difference of the Pr. Eq. calculates a kurtosis about 0.5 smaller.

At this point, the first part of the methodology presented in Section 2.1 is completed. As a result, the first to fourth moments of the underlying lifespan probability distribution are available after applying the full second-order approach. The expected value, first raw moment, and the variance, second central moment are taken from [25], whereas the skewness and the kurtosis, third and fourth central standardized moments, respectively, have been calculated above. Recapitulating, the moments of fatigue life ${\textstyle N}$ provided by the probabilistic NASGRO equations for a crack depth equal to 50 mm are enclosed in Table 3.

Table 3. Expected value, standard deviation, skewness and kurtosis of ${\textstyle N}$ provided by the probabilistic NASGRO equations (Pr. Eq.)

	Pr. Eq.	Pr. Eq.	Pr. Eq.	Pr. Eq.
$a$	${\mu }_{N}$	${\sigma }_{N}$	${\gamma }_{{1}_{N}}$	${{\beta }_{2}}_{N}$
[mm]	[Cycles]	[Cycles]	[dimensionless]	[dimensionless]
50	398 853	56 103	0.646	3.60

Note that the square root of the variance, i.e. the standard deviation ${\textstyle {\sigma }_{N}}$, was reported instead of the variance ${\textstyle {\sigma }_{N}^{2}}$. This is because the standard deviation is more meaningful to interpret since it is expressed in units of the original variable.

The next part of the methodology addresses the problem of constructing a PDF from prescribed moments as described in Section 2.2. In this case, it is possible to construct probability distributions with more than two parameters given that the first four moments are available. To check the benefits of the uncertainty propagation methodology presented in terms of life distributions, three scenarios were considered: (i) the lifespan was assumed to be normally distributed; (ii) the lifespan was assumed to be log-normally distributed; (iii) the Pearson distribution family was used to model the lifespan, thus avoiding the need of assuming a distribution in advance. The first two scenarios were discussed in [25], however, the latter one was not investigated as it requires the first four moments and only the expected value and the variance were calculated in the previous procedure. In the present work the third scenario considering the Pearson distribution family is also explored. The Pearson family is compared with the other two scenarios to verify that the proposed improvements contribute to a better knowledge of the distribution of fatigue life. For that purpose, the three probability density functions were constructed as described below from the moments in Table 3.

In case (i), the probability density function for the lifespan ${\textstyle N}$ is assumed to be normally distributed, and therefore it is derived from the well-known probability density function for the standard normal distribution ${\textstyle \varphi \left(x\right)}$. Specifically, the probability density function is parameterized in terms of a location parameter which is directly the expected value of the fatigue life ${\textstyle N}$, and a scale parameter which is directly the square root of the variance, i.e. the standard deviation of the random output variable fatigue life ${\textstyle N}$. As a result, the lifespan ${\textstyle N}$ distributed normally is characterised by the probability density function ${\textstyle {f}_{N}\left(N;{\mu }_{N},{\sigma }_{N}\right)}$, where ${\textstyle {\mu }_{N}}$ and ${\textstyle {\sigma }_{N}}$ are fixed parameters.

In case (ii), the probability density function for the lifespan ${\textstyle N}$ is assumed to be log-normally distributed, and therefore it is derived from the standardized form for the log-normal probability density function ${\textstyle f\left(x;\sigma \right)}$ with ${\textstyle \sigma }$ as a shape parameter. Commonly, the probability density function is further parameterized in terms of a location parameter ${\textstyle \lambda }$ and a scale parameter ${\textstyle {e}^{\mu }}$. The location parameter ${\textstyle \lambda }$ was set equal to zero, hence only two parameters remain to be estimated. The physical meaning of the location parameter is realistic since it indicates that crack growth occurs after any given cycle and so the support of the distribution is nonnegative. The shape ${\textstyle \sigma }$ and the scale ${\textstyle {e}^{\mu }}$ parameters of the log-normal are functions of the expected value and the variance of the fatigue life ${\textstyle N}$. As a consequence, the lifespan ${\textstyle N}$ distributed log-normally is described by the probability density function ${\textstyle {f}_{N}\left(N;\sigma ,\lambda ,{e}^{\mu }\right)}$ where ${\textstyle \sigma }$, ${\textstyle \lambda }$ and ${\textstyle {e}^{\mu }}$ are fixed parameters.

In case (iii), the Pearson distribution type was automatically determined based on the quantities ${\textstyle {{\beta }_{1}}_{N}=}$${{\gamma }_{1}^{2}}_{N}$ and ${\textstyle {{\beta }_{2}}_{N}}$ as it is described in Section 2.2. In this example, the procedure leads to the Pearson type I that corresponds to the beta distribution. Afterwards, the parameters of the beta distribution were estimated making the statistical moments of the constructed lifespan distribution match the first four prescribed moments predicted by the Pr. Eq. In this case, the probability density function for the lifespan ${\textstyle N}$ beta-distributed is derived from the standardized form for the beta probability density function ${\textstyle f\left(x;\alpha ,\beta \right)}$ in Eq. (14) with ${\textstyle \alpha }$, ${\textstyle \beta }$ as shape parameters and where ${\textstyle \,\Gamma }$ is the gamma function ${\textstyle \Gamma \left(x\right)=}$$\left(x-1\right)!$. Once again, the probability density function is further parameterized by introducing two parameters representing the location and the scale. The shape parameters ${\textstyle \alpha }$ and ${\textstyle \beta }$, the scale and the location parameter ${\textstyle \lambda }$ were calculated by using the closedform expressions derived in Section 2.2 that express the parameters as function of the first four moments of the fatigue life ${\textstyle N}$ distribution. Recall that in these expressions the expected value ${\textstyle {\mu }_{N}}$ or first raw moment is denoted as ${\textstyle {\mu '}_{1}}$. As a result, the lifespan ${\textstyle N}$ following a beta distribution is characterized by the probability density function ${\textstyle {f}_{N}\left(N;\alpha ,\beta ,\lambda ,{a}_{2}-\right.}$$\left.{a}_{1}\right)$ given in Eq. (15)

$f\left(x;\alpha ,\beta \right)={\frac {\Gamma \left(\alpha +\beta \right){x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}}$	(14)
${f}_{N}\left(N;\alpha ,\beta ,\lambda ,{a}_{2}-{a}_{1}\right)={\frac {f\left({\frac {N-\lambda }{{a}_{2}-{a}_{1}}};\alpha ,\beta \right)}{{a}_{2}-{a}_{1}}}$	(15)

Note that in the ${\textstyle {f}_{N}\left(N;\alpha ,\beta ,\lambda ,{a}_{2}-{a}_{1}\right)}$ probability density function the ${\textstyle \alpha }$, ${\textstyle \beta }$, ${\textstyle \lambda }$ and ${\textstyle {a}_{2}-}$${a}_{1}$ are fixed parameters.

The resulting parameters for the normal, the log-normal and the beta PDFs are collected in Table 4.

Table 4. Shape, location and scale parameters computed from the first four moments of the lifespan ${\textstyle N}$ for a crack depth equal to 50 mm

Probability Distr.	Shape	Location	Scale
Normal	-	398 853 ${\textstyle \left(={\mu }_{N}\right)}$	56 103 ${\textstyle \left({=\sigma }_{N}\right)}$
Log-normal	0.140 ${\textstyle \left(=\sigma \right)}$	0 ${\textstyle \left(=\lambda \right)}$	394 964 ${\textstyle \left(={e}^{\mu }\right)}$
Pearson type I (Beta)	8.49 ${\textstyle \left(=\alpha \right)}$,	232 076	4 825 029
	237.33 ${\textstyle \left(=\beta \right)}$	${\textstyle \left(=\lambda \right)}$	${\textstyle \left({=a}_{2}-{a}_{1}\right)}$

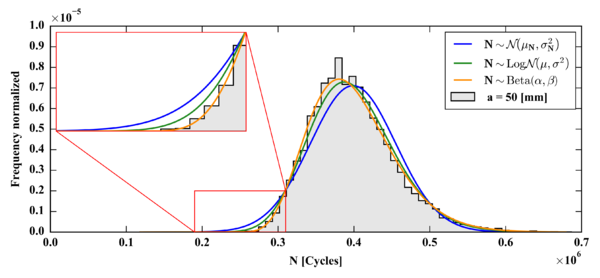
The normal distribution, the log-normal distribution, the beta distribution and the MC histogram of the fatigue life ${\textstyle N}$ for a crack depth equal to 50 mm are compared in Figure 5.

Figure 5. Histogram of fatigue life ${\textstyle N}$ provided by the Monte Carlo (MC) and PDFs of the normal, the log-normal and the beta distributions constructed from the moments provided by the probabilistic NASGRO equations (Pr.Eq.) for 50 mm crack depth

The histogram of fatigue life ${\textstyle N}$ provided by the MC simulations is taken as a benchmark for the comparison of the three PDFs constructed. The differences between the normal distribution and the MC histogram highlight the degree of nonnormality and nonsymmetry of the underlying lifespan distribution. The lognormal distribution includes a certain degree of asymmetry and therefore it is a more convenient choice over the symmetrical normal distribution. It can be observed that the lognormal is advantageous to the normal distribution in describing the lower and higher tails of the lifespan, although the degree of asymmetry in the lognormal is not directly defined. On the other hand the beta distribution was determined from the Pearson distribution family according to the quantities related to shape ${\textstyle {\beta }_{1}}$ and ${\textstyle {\beta }_{2}}$. It can be observed that the beta distribution agrees well with the MC histogram for all of the lifespan range, including the tails and also the peak. The superiority of the beta distribution over the normal and the lognormal distributions to represent the MC results is clear, especially when describing the lower tail of the distribution of lives, which is of great importance in reliability and in damage tolerance assessment. The behaviour of the normal and the lognormal distributions in the lower tail region slightly underestimate the lifespan. This aspect is clearly observed in the inset of Figure 5 which shows a zoom of the lower tail. The better tail performance of the beta distribution can be attributed to the fact that the first four moments of the lifespan ${\textstyle N}$ are matched when estimating the parameters of the Pearson distribution. That is to say that the PDF using the Pearson distribution family is sensitive to variations in skewness and kurtosis. Besides, the Pearson distribution type is selected depending on the moments that are related to the shape of the underlying distribution, and afterwards the corresponding probability distribution parameters are calculated. On the contrary, the construction of the normal and lognormal distributions do not take into account the skewness or kurtosis changes given that their third and fourth moments are not matched to the calculated lifespan ${\textstyle N}$ moments. In fact, the normal distribution has ${\textstyle 0}$ skewness and a kurtosis equal to ${\textstyle 3}$ inherently, and the skewness and the kurtosis of the lognormal distribution are determined indirectly once the distribution is defined in terms of the expected value and variance of the lifespan ${\textstyle N}$. Consequently, the quality of the normal and lognormal PDFs is influenced by the similarity between them and the actual lifespan distribution, which is not always known. In other words, the quality can only be good if the lifespan is close to the selected distribution. It must be emphasized that in some applications the normal or the log-normal assumption may be enough, however, the Pearson distribution family still offers a perceptible improvement as the goodness and quality of the PDF constructed is not compromised by an a priori selection or assumption of a probability distribution.

Additionally, a KolmogorovSmirnov test [36] was used to measure quantitatively the goodness of fit between the constructed probability distributions and the MC results. The test statistic quantifies the distance between the cumulative distribution functions of the constructed distribution and the cumulative MC histogram of reference, and therefore the lowest value indicates the best representation of the underlying distribution. The test statistics obtained were 0.052, 0.027 and 0.017 for the normal, log-normal and beta distributions, respectively. These values confirm the advantage of the beta distribution over the normal and the log-normal distributions to represent the MC results.

The following outcomes are drawn from the analysis of the results obtained by applying the uncertainty propagation methodology:

• The skewness and the kurtosis values provided by the MC and by the probabilistic NASGRO equations are really close, giving errors between them small enough to consider both probabilistic methods to be equally accurate.

• The key advantage of the full second-order approach is the lower computational time, similar to that required for a deterministic calculation. Due to the computational efficiency and the acceptable accuracy, this method outperforms the conventional MC method.

• The expected value and variance along with the skewness and kurtosis provided by the Pr. Eq. enable the construction of PDFs with more than two parameters as it is the case of the versatile Pearson distribution family.

• The automatic selection of the Pearson distribution type based on the moments of the underlying distribution makes it a more general procedure than the selection of an arbitrary probability distribution to adjust.

• The parameters of the particular Pearson distribution type are directly computed from the moments, thus avoiding the need to use minimization or maximization algorithms as in the case of optimization procedures used in other existing methods for estimating probability distribution parameters.

• The overall similarity between the Pearson type I, i.e. the beta distribution, and the MC histogram confirms that the Pearson distribution family accurately captures and provides a good description of the underlying lifespan distribution under stochastic conditions.

4. Conclusions

This paper presents a novel uncertainty propagation methodology for efficiently estimating the probability distribution of the fatigue crack growth lifetime. It implements the Pearson distribution family and takes advantage of the statistical moments of the lifetime predicted via existing and innovative approaches based on NASGRO model. In the present work the full second-order approach for expected value and variance prediction of probabilistic fatigue crack growth life presented in [25] is revisited and extended to predict higher order statistical moments of the underlying distribution. Based on that approach, the probabilistic equations for the skewness and kurtosis of the fatigue crack growth lifetime are provided. These two moments along with the expected value and variance are used to estimate the parameters of the Pearson distribution to represent the underlying lifespan distribution. The probability distribution constructed from the first four prescribed moments is helpful to describe the fatigue crack growth phenomenon under stochastic conditions such as under a random bending moment loading.

The present uncertainty propagation methodology is found to be advantageous compared to the previously applied in [25]. The main advantages that are worth mentioning include: (i) the ability to automatically determine the pertinent distribution shape using a simple and uniform criterion for choosing the corresponding Pearson distribution type and thus avoiding the need to assume a probability distribution in advance; (ii) the versatility of constructing probability distributions with more than two parameters if required given that in the current methodology the skewness and the kurtosis are calculated in addition to the expected value and variance predicted in the initial approach; (iii) the significant improvement in the accuracy of the probability density function constructed in the analysis of the fatigue crack growth in a railway axle under random bending loading, especially in the lower tail of the distribution of life which is of notable interest in reliability assessment. It demonstrates that in practical engineering it is relevant to determine the third and fourth central moments for a precise description of the probabilistic fatigue crack growth life.

In general, the uncertainty propagation methodology presented has a positive and comprehensive effect in engineering applications such as in the probabilistic life prediction. The lifespan probability distribution provided has the potential to be used in probabilistic damage tolerance design and in the integrity assessment of components and structures. Therefore, the novel uncertainty propagation methodology in this paper is expected to be an asset in a broad range of engineering problems dealing with random variables.

Acknowledgement

The authors acknowledge the Spanish Ministry of Economy, Industry and Competitive through the National Programme for Research Aimed at the Challenges of Society that financially supported the project RTC-2016-4813-4.

References

[1] Cervello S. Fatigue properties of railway axles: New results of full-scale specimens from Euraxles project. Int J Fatigue, 86:2–12, 2016. https://doi.org/10.1016/j.ijfatigue.2015.11.028.

[2] Novosad M., Fajkoš R., Řeha B., Řezníček R. Fatigue tests of railway axles. Procedia Eng, 2:2259–68, 2010. https://doi.org/10.1016/j.proeng.2010.03.242.

[3] Beretta S., Carboni M. Variable amplitude fatigue crack growth in a mild steel for railway axles: Experiments and predictive models. Eng Fract Mech, 78:848–62, 2011. https://doi.org/10.1016/j.engfracmech.2010.11.019.

[4] Mädler K., Geburtig T., Ullrich D. An experimental approach to determining the residual lifetimes of wheelset axles on a full-scale wheel-rail roller test rig. Int J Fatigue, 86:58–63, 2016. https://doi.org/10.1016/j.ijfatigue.2015.06.016.

[5] UIC B 169 RP 36:2013-12 Defect Tolerance Concept (DTC) Permitted defects and surface properties for axles under maintenance. UIC Standard, 2013.

[6] Pokorný P., Náhlík L., Hutař P. Comparison of different load spectra on residual fatigue lifetime of railway axle. Procedia Eng, 74:313–6, 2014. https://doi.org/10.1016/j.proeng.2014.06.269.

[7] Pokorný P., Hutař P., Náhlík L. Residual fatigue lifetime estimation of railway axles for various loading spectra. Theor Appl Fract Mech, 82:25–32, 2016. https://doi.org/10.1016/j.tafmec.2015.06.007.

[8] Traupe M., Landaberea A. EURAXLES - A global approach for design, production and maintenance of railway axles: WP2 - development of numerical models for the analysis of railway axles. Mater Werkst, 48:687–98, 2017. https://doi.org/10.1002/mawe.201600570.

[9] Zerbst U., Beretta S., Köhler G., Lawton A., Vormwald M., Beier H.Th., et al. Safe life and damage tolerance aspects of railway axles – A review. Eng Fract Mech, 98:214–71, 2013. https://doi.org/10.1016/j.engfracmech.2012.09.029.

[10] Zerbst U., Klinger C., Klingbeil D. Structural assessment of railway axles – A critical review. Eng Fail Anal, 35:54–65, 2013. https://doi.org/10.1016/j.engfailanal.2012.11.007.

[11] Paris P.C., Erdogan F. A critical analysis of crack propagation laws. J Basic Eng, 85:528–33, 1963. https://doi.org/10.1115/1.3656900.

[12] Akama M., Ishizuka H. Reliability analysis of Shinkhansen vehicle axle using probabilistic fracture mechanics. JSME Int J Ser Mech Mater Eng, 38(3):378–83, 1995. https://doi.org/10.1299/jsmea1993.38.3_378.

[13] Bea J.A. Simulación del crecimiento de grietas por fatiga aleatoria mediante elementos probabilistas. PhD Thesis, Universidad de Zaragoza, 1997.

[14] Bea J.A., Doblaré M., Gracia L. Evaluation of the probability distribution of crack propagation life in metal fatigue by means of probabilistic finite element method and B-models. Eng Fract Mech, 63:675–711, 1999. https://doi.org/10.1016/S0013-7944(99)00053-3.

[15] Bea J.A., Doblaré M., Gracia L. Fiabilidad de elementos metálicos en crecimiento de grieta por fatiga aleatoria mediante elementos finitos probabilistas y modelos B. Rev Int Métod Numér para Cálculo Diseño en Ing, 15(1):85–112, 1999. https://www.scipedia.com/public/Bea_et_al_1999a.

[16] Hillmansen S., Smith R.A. The management of fatigue crack growth in railway axles. Proc Inst Mech Eng Part F J Rail Rapid Transit, 218:327–336, 2004. https://doi.org/10.1243/0954409043125879.

[17] Hong Y.J., Xing J., Wang J.B. A second-order third-moment method for calculating the reliability of fatigue. Int J Press Vessels Pip, 76:567–70, 1999. https://doi.org/10.1016/S0308-0161(99)00013-7.

[18] Náhlík L., Pokorný P., Ševčík M., Fajkoš R,, Matušek P,, Hutař P. Fatigue lifetime estimation of railway axles. Eng Fail Anal, 73:139–57, 2017. https://doi.org/10.1016/j.engfailanal.2016.12.014.

[19] Wang L., Liang J., Yang Y., Zheng Y. Time-dependent reliability assessment of fatigue crack growth modeling based on perturbation series expansions and interval mathematics. Theor Appl Fract Mech, 95:104–18, 2018. https://doi.org/10.1016/j.tafmec.2018.02.010.

[20] Yasniy O., Lapusta Y., Pyndus Y., Sorochak A., Yasniy V. Assessment of lifetime of railway axle. Int J Fatigue, 50:40–6, 2013. https://doi.org/10.1016/j.ijfatigue.2012.04.008.

[21] Zhu S.-P., Liu Q., Huang H.-Z. Probabilistic modeling of damage accumulation for fatigue reliability analysis. Procedia Struct Integr, 4:3–10, 2017. https://doi.org/10.1016/j.prostr.2017.07.012.

[22] Forman R.G., Mettu S.R. Behavior of surface and corner cracks subjected to tensile and bending loads in Ti-6Al-4V alloy. ASTM STP 1131 Am Soc Test Mater Phila PA, 519–46, 1990.

[23] Beretta S., Carboni M. Experiments and stochastic model for propagation lifetime of railway axles. Eng Fract Mech, 73:2627–2641, 2006. https://doi.org/10.1016/j.engfracmech.2006.04.024.

[24] Beretta S., Villa A. A RV approach for the analysis of fatigue crack growth with NASGRO equation. Proceedings of the 4th International ASRANet Colloquium, 1–7, 2008.

[25] Mallor C., Calvo S., Núñez J.L., Rodríguez-Barrachina R., Landaberea A. Full second-order approach for expected value and variance prediction of probabilistic fatigue crack growth life. Int J Fatigue, 133:105454, 2020. https://doi.org/10.1016/j.ijfatigue.2019.105454.

[26] Mayer M. Die Sicherheit der Bauwerke und ihre Berechnung nach Grenzkräften anstatt nach zulässigen Spannungen. Berlin, Springer Verlag, 1926.

[27] Mayer M. La seguridad en las construcciones y su cálculo aplicando los esfuerzos límite en lugar de las tensiones admisibles = Safety in constructional works and its design according to limit states instead of permissible stresses. Madrid, INTEMAC, 1975.

[28] Cornell C.A. A Probability-based structural code. ACI J Proc, 66:974–85, 1969. https://doi.org/10.14359/7446.

[29] Cornell C.A. Structural safety specifications based on second-moment reliability analysis. IABSE Symposium on Concepts of Safety of Structures and Methods of Design, 1969. https://doi.org/10.5169/seals-5948.

[30] Núñez J.L. Análisis del fenómeno de la fatiga en metales en etapa de nucleación mediante la utilización de modelos estadísticos de daño acumulado y elementos finitos probabilistas. PhD Thesis, Universidad de Zaragoza, 2003.

[31] Calvo S. Determinación de la probabilidad de fallo en componentes métalicos sometidos a estados multiaxiales de tensión mediante la utilización de elementos finitos probabilistas y modelos estadísticos de daño acumulado. PhD Thesis, Universidad de Zaragoza, 2008.

[32] Calvo S., Canales M., Gómez C., Valdés J.R., Núñez J.L. Probabilistic formulation of the multiaxial fatigue damage of Liu. Int J Fatigue, 33:460–5, 2011. https://doi.org/10.1016/j.ijfatigue.2010.10.003.

[33] Pearson K. X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material. Philos Trans R Soc Lond A, 186:343–414, 1895. https://doi.org/10.1098/rsta.1895.0010.

[34] Johnson N.L., Kotz S., Balakrishnan N. Continuous univariate distributions. Wiley-Interscience, Vol. 1, 2nd edition, 784 pages, 1994.

[35] EN 13261:2009+A1:2010: Railway applications – Wheelsets and bogies – Axles – Product requirements. European Committee for Standardization, 2010.

[36] Haldar A., Mahadevan S. Probability, reliability, and statistical methods in engineering design. John Wiley, 320 pages, 1999.