Subdomain method in time with waveform relaxation in space applied to the wave equation combined with the multigrid method

Abstract

This work aims to evaluate a parallelizable approximate solution model for the wave equation. For that, we used the temporal sweep known as the Waveform Relaxation method to guarantee the parallelization in space. However, this technique has limitations for this class of problems. Therefore, we proposed the combination of the Subdomain method in a non-conventional way in time with the Multigrid method, intending to reduce computational time and improve the convergence factors. In this work, we presented the mathematical analysis of the stability of the discretization model, which uses the Central Finite Difference method with weighting at each time step. As an application of the proposed method, in addition to a problem with a known analytical solution, we solved a wave propagation problem with reflection and phase inversion.

Keywords: Finite difference method, convergence factor, von Neumann criterion

1. Introduction

In this work, we intended to present an efficient and parallelizable method for solving sparse and large systems of equations that result from the discretization of the wave equation, which is a transient Partial Differential Equation (PDE) that models many problems found in several areas of applications. Among these problems are the vibration of strings and membranes, sound waves in gases or liquids, electromagnetic waves, transverse waves in solids, surface ocean waves, among others.

Explicit schemes for obtaining a solution of the wave equation are common in the literature, as in [1,2,3]. In general, such techniques are conditionally stable, which can be a disadvantage when performing refinements in time or space, as some criteria must be accepted for convergence. Another possibility is to use implicit methods, which are commonly unconditionally stable, thus assuring the reliability of the approximate solutions obtained [4].

The wave propagation problem can be studied in two manners, with the Helmholtz equation in the stationary form [5,6,7], or by directly solving the wave equation in the transient form [8,9,10,11]. In this context, we discretized the transient wave equation with the Finite Difference Method (FDM) weighted with a parameter ${\textstyle \eta }$ at different time steps [12,13], thus generating an implicit method, which results in a linear system at each time step, which can be solved by using a solver such as Gauss-Seidel, with lexicographical or red-black order.

One way to Speed-up the process of obtaining the system solution resulting from the discretization is to apply the Multigrid method, which significantly improves the convergence factors in the process of solving systems of equations [14,15]. According to Umetani et al. [5] and Franco et al. [16], the anisotropy related to physical and numerical factors generated with large values of ${\textstyle \alpha }$ (${\textstyle \alpha }$ being associated with wave propagation velocity) may be a challenge in solving the wave equation.

According to Brandt and Livshits [7], there are limitations when attempting to solve the wave equation, even in its stationary form (Helmholtz Equation), because the solver loses efficiency when used in the standard Multigrid method. Therefore, the authors proposed modifications in the numerical experiments so that they would present better convergence rates.

Solutions with high-order compact methods for the wave equation were analyzed by Britt et al. [17], who studied the stability of explicit and implicit methods as well as the effectiveness of the Multigrid and Conjugate Gradients methods. The authors' analysis confirms the Multigrid effectiveness in solving problems with many degrees of freedom.

With the emergence of new technologies and high-performance computing, it became of paramount importance to develop algorithms that can use a large number of cores for data processing, as this greatly increases the efficiency in solving some problems involving PDEs [18].

In that context, a new method was developed: Waveform Relaxation (WR), which is an iterative method proposed to solve large systems of Ordinary Differential Equations (ODEs), but which can be adapted to time-dependent PDEs. In WR, the spatial domain is decomposed by a set of points and for each of these points, a system of ODEs is solved in all time steps [19,20,21,22]. A WR method was developed to solve the poroelasticity problem [23], which is modeled by a system of parabolic PDEs. Other works that apply parallelization are presented in Bellen and Zennaro [24] and Chartier and Philippe [25] for initial value problems and in Keller [26] for boundary value problems.

To non-steady state problems, the WR algorithms differ from the standard time sweep methods (Time-Stepping) in the fact that their iterates are functions in time [21,27]. The Partial Differential Equations is transformed into a large set of Ordinary Differential Equations, and an iterative algorithm can be used to solve this system. This numerical solution needs a high computational effort due to the necessity of solving systems of large dimension at each step point. WR iterations are designed in order to decouple the original large system in smaller subsystems: in this way, the iteration process can be implemented in a parallel computational environment, since each subsystem can be treated by a single processor [28].

In Ruprecht [29], the dispersion relation that occurred in the approximate solution was analyzed by using Parallel-in-Time, which is a time parallelization method used for solving hyperbolic equations. The author investigated propagation and stability characteristics and observed that instability in convergence is mainly caused by adopting medium and high wavenumbers.

Efficient solutions to the one-dimensional wave equation are already found in the literature, as in Baccouch and Temimi [30] for high-order methods and in Erbay et al. [31] for the non-linear cases. However, there are still challenges to be overcome when employing the Multigrid method, especially when combining with schemes that allow parallelization [11]. In this sense, the novelty of this work is the use of the Subdomains in Time method, combined with the Waveform Relaxation strategy and the Multigrid method, in order to reduce the large initial perturbations existing in Gander et al. [11]. Differently from Ong and Mandal [32], we work with a reduced number of subdomains in time, with the aim of reducing the CPU time and at the same time increase the degree of parallelization of the codes used.

The present work is organized as follows: In Section 2, we present the mathematical and numerical models adopted for the implicit discretization of the wave equation, as well as the stability of the numerical model and a foundation for the Multigrid method. In Section 3, we cover the details of the WR and Subdomain methods. In Section 4, we expose the results of simulations and comparisons between conventional WR and the method proposed in this paper. In Section 5, we present an application to the wave propagation problem with reflection, and finally, in Section 6, we present the conclusions.

2. Mathematical and numerical models

2.1 One-dimensional wave equation

Given a positive scalar ${\textstyle \alpha }$, such that ${\textstyle \alpha ^{2}={\dfrac {1}{V^{2}}}}$, where ${\textstyle V}$ is related to the linear density and the stress in a string (wave propagation velocity), we present the one-dimensional wave equation [33], as

${\dfrac {\partial ^{2}u}{\partial t^{2}}}={\alpha ^{2}}{\dfrac {\partial ^{2}u}{\partial x^{2}}},$

(1)

$u(x,0)=f(x),0\leq x\leq l,$

(2)

$u_{t}(x,0)=g(x),0\leq x\leq l,$

(3)

$u(0,t)=u(l,t)=0,t>0,$

(4)

where ${\textstyle u(x,t)}$ is the displacement at position ${\textstyle x}$ and time ${\textstyle t}$, ${\textstyle f(x)}$ is the initial configuration, ${\textstyle g(x)}$ is the initial velocity, ${\textstyle l}$ is the string length, and finally, ${\textstyle u(0,t)}$ and ${\textstyle u(l,t)}$ are the boundary conditions. This set of equations models a problem of vibration of a string fixed at the ends, in which the general solution is built with the fundamental frequencies of vibration, which are given by

$u(x,t)=\sum \limits _{n=1}^{\infty }(c_{n}w_{n}(x,t)+d_{n}z_{n}(x,t)),$

(5)

where,

$w_{n}(x,t)=\cos \left({\dfrac {n\pi \alpha t}{l}}\right)\sin \left({\dfrac {n\pi x}{l}}\right),$

(6)

$z_{n}(x,t)=\sin \left({\dfrac {n\pi \alpha t}{l}}\right)\sin \left({\dfrac {n\pi x}{l}}\right),$

(7)

$c_{n}={\dfrac {2}{l}}\int _{0}^{l}f(x)\sin \left({\dfrac {n\pi x}{l}}\right)dx,$

(8)

$d_{n}={\dfrac {2}{n\pi \alpha }}\int _{0}^{l}g(x)\sin \left({\dfrac {n\pi x}{l}}\right)dx.$

(9)

2.2 Discretization

Spatial and temporal discretizations are performed by using the Finite Difference Method (FDM), where the approximation process starts with the representation of the continuous domain ${\textstyle \Omega }$ by a discrete domain, which consists of an ordered set of points that form the grid [4]. In this way, it is possible to use a Taylor series expansion to represent an analytic function ${\textstyle \Phi (x)}$ in the neighborhood of ${\textstyle x_{i}}$ and thus obtain an approximation for the second derivative of ${\textstyle \Phi (x_{i})}$ given by

${\dfrac {d^{2}\Phi (x_{i-1})}{dx^{2}}}\approx {\dfrac {\Phi (x_{i-1})-2\Phi (x_{i})+\Phi (x_{i+1})}{h^{2}}},$

(10)

with a truncation error

$\varepsilon \left({\dfrac {d^{2}\Phi (x_{i})}{dx^{2}}}\right)=-{\dfrac {h^{2}}{12}}{\dfrac {d^{4}\Phi (x_{i})}{dx^{4}}}-{\dfrac {h^{4}}{360}}{\dfrac {d^{6}\Phi (x_{i})}{dx^{6}}}-{\dfrac {h^{6}}{20160}}{\dfrac {d^{8}\Phi (x_{i})}{dx^{8}}}-...$

(11)

Assuming the problem defined by Eqs. (1) to (4), we define the size of the spatial interval ${\textstyle h={\dfrac {l}{N_{x}-1}}}$ and the increment in time ${\textstyle \tau ={\dfrac {t_{f}}{N_{t}-1}}}$, with the number of spatial points ${\textstyle N_{x}>0}$ and temporal points ${\textstyle N_{t}>0}$, for the final time ${\textstyle t_{f}>0}$. Assuming ${\textstyle v_{i}^{k}}$ as an approximation for the solution ${\textstyle u}$ at coordinate point ${\textstyle x_{i}}$ and time step ${\textstyle k}$, we can write Eq. (1) in the discretized form, applying weighting in the spaces [12], given by

${\dfrac {v_{i}^{k-1}-2v_{i}^{k}+v_{i}^{k+1}}{\tau ^{2}}}-{\dfrac {\tau ^{2}}{12}}{\dfrac {\partial ^{4}v_{i}}{\partial t^{4}}}-{\dfrac {\tau ^{4}}{360}}{\dfrac {\partial ^{6}v_{i}}{\partial t^{6}}}-{\dfrac {\tau ^{6}}{20160}}{\dfrac {\partial ^{8}v_{i}}{\partial t^{8}}}-...=$ $\alpha ^{2}\eta \left({\dfrac {v_{i-1}^{k+1}-2v_{i}^{k+1}+v_{i+1}^{k+1}}{h^{2}}}-{\dfrac {h^{2}}{12}}{\dfrac {\partial ^{4}v_{i}^{k+1}}{\partial x^{4}}}-{\dfrac {h^{4}}{360}}{\dfrac {\partial ^{6}v_{i}^{k+1}}{\partial x^{6}}}-{\dfrac {h^{6}}{20160}}{\dfrac {\partial ^{8}v_{i}^{k+1}}{\partial x^{8}}}-...\right)$ $+\alpha ^{2}(1-2\eta )\left({\dfrac {v_{i-1}^{k}-2v_{i}^{k}+v_{i+1}^{k}}{h^{2}}}-{\dfrac {h^{2}}{12}}{\dfrac {\partial ^{4}v_{i}^{k}}{\partial x^{4}}}-{\dfrac {h^{4}}{360}}{\dfrac {\partial ^{6}v_{i}^{k}}{\partial x^{6}}}-{\dfrac {h^{6}}{20160}}{\dfrac {\partial ^{8}v_{i}^{k}}{\partial x^{8}}}-...\right)$ $+\alpha ^{2}\eta \left({\dfrac {v_{i-1}^{k-1}-2v_{i}^{k-1}+v_{i+1}^{k-1}}{h^{2}}}-{\dfrac {h^{2}}{12}}{\dfrac {\partial ^{4}v_{i}^{k-1}}{\partial x^{4}}}-{\dfrac {h^{4}}{360}}{\dfrac {\partial ^{6}v_{i}^{k-1}}{\partial x^{6}}}-{\dfrac {h^{6}}{20160}}{\dfrac {\partial ^{8}v_{i}^{k-1}}{\partial x^{8}}}-...\right),$

(12)

where ${\textstyle \eta }$ is a weighting parameter. The Figure 1 illustrates the points used to calculate ${\textstyle v_{i}^{k}}$, with spatial coordinate ${\textstyle i}$, at a certain time step ${\textstyle k}$.

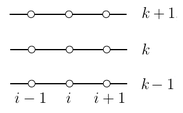
Figure 1. Space-time discretization scheme for the 1D grid

By reordering the terms of Eq. (12), we obtain

${v_{i}^{k-1}-2v_{i}^{k}+v_{i}^{k+1}}={\dfrac {\alpha ^{2}\tau ^{2}}{h^{2}}}{\bigg [}\eta ({v_{i-1}^{k+1}-2v_{i}^{k+1}+v_{i+1}^{k+1}})+(1-2\eta )({v_{i-1}^{k}-2v_{i}^{k}+v_{i+1}^{k}})+$ $\eta ({v_{i-1}^{k-1}-2v_{i}^{k-1}+v_{i+1}^{k-1}}){\bigg ]}$ (13)

with a truncation error of the order ${\textstyle O(h^{2}\tau ^{2},\tau ^{4})}$, given by

$\varepsilon _{1D}={\dfrac {\tau ^{4}}{12}}{\dfrac {\partial ^{4}v_{i}}{\partial t^{4}}}+...$ $-{\dfrac {\alpha ^{2}\tau ^{2}h^{2}\eta }{12}}{\dfrac {\partial ^{4}v_{i}^{k+1}}{\partial x^{4}}}-...-{\dfrac {\alpha ^{2}\tau ^{2}h^{2}}{12}}(1-2\eta ){\dfrac {\partial ^{4}v_{i}^{k}}{\partial x^{4}}}-...$$-{\dfrac {\alpha ^{2}\tau ^{2}h^{2}\eta }{12}}{\dfrac {\partial ^{4}v_{i}^{k-1}}{\partial x^{4}}}-...$

(14)

Assuming that ${\textstyle \lambda ={\dfrac {\alpha ^{2}\tau ^{2}}{h^{2}}}}$ (herein called anisotropy factor), we have the following system of equations

$a_{p}v_{i}^{k+1}=a_{w}v_{i-1}^{k+1}+a_{e}v_{i+1}^{k+1}+b_{p},$

(15)

where,

$a_{p}=1+2\eta \lambda ,$

(16)

$a_{w}=a_{e}=\eta \lambda ,$

(17)

$b_{p}=(-1-2\eta \lambda )v_{i}^{k-1}+(2+(-2+4\eta )\lambda )v_{i}^{k}+(1-2\eta )\lambda (v_{i-1}^{k}$$+v_{i+1}^{k})+\eta \lambda (v_{i-1}^{k-1}+v_{i+1}^{k-1}).$

(18)

To perform the first iteration, it is necessary to know the solution in two previous time steps ${\textstyle v_{i}^{0}}$ and ${\textstyle v_{i}^{1}}$. To start the process, ${\textstyle v_{i}^{0}}$ is given by the initial setup while ${\textstyle v_{i}^{1}}$ is given in Burden and Faires [4], by

$v_{i}^{1}=(1-\lambda )f(x_{i})+{\dfrac {\lambda }{2}}f(x_{i+1})+{\dfrac {\lambda }{2}}f(x_{i-1})+\tau g(x_{i})+O(h^{2}\tau ^{2}).$

(19)

2.3 Stability

Next, we will use the Von Neumann criterion [34] to determine the stability of the discretization method described in section 2.2. For that, let us assume that the global error is given by a Fourier series of local errors, also called harmonics. So, the error in the first time step can be expressed as:

$E_{i}=\sum _{n=0}^{N_{x}}a_{n}e^{\left(\iota {\dfrac {n\pi }{l}}ih\right)},$

(20)

with ${\textstyle \iota ={\sqrt {-1}}}$. Note that we have a system with ${\textstyle N_{x}+1}$ equations and ${\textstyle N_{x}+1}$ unknowns, where the coefficient matrix is non-singular [12]. Now let us assume that a generic harmonic can be written in the form

$U_{i}^{k}=e^{\gamma k}e^{\iota \beta i},$

(21)

where ${\textstyle \beta \in \Re }$ and ${\textstyle \gamma \in \mathbb {C} }$, both being arbitrary. Consequently, to analyze the stability of the discretization method, it is enough to verify the propagation of this harmonic as ${\textstyle k}$ increases. By substituting Eq. (21) into Eq. (13), with ${\textstyle \eta =1/2}$ [12,13], we have

$e^{\gamma (k+1)}e^{\iota \beta i}-2e^{\gamma k}e^{\iota \beta i}+e^{\gamma (k-1)}e^{\iota \beta i}=$${\dfrac {\lambda }{2}}[e^{\gamma (k+1)}e^{\iota \beta (i+1)}-2e^{\gamma (k+1)}e^{\iota \beta i}$$+e^{\gamma (k+1)}e^{\iota \beta (i-1)}+e^{\gamma (k-1)}e^{\iota \beta (i+1)}$ ${\textstyle -2e^{\gamma (k-1)}e^{\iota \beta i}+e^{\gamma (k-1)}e^{\iota \beta (i-1)}],}$

(22)

or yet,

$e^{\gamma }e^{\gamma k}e^{\iota \beta i}-2e^{\gamma k}e^{\iota \beta i}+e^{-\gamma }e^{\gamma k}e^{\iota \beta i}=$${\dfrac {\lambda }{2}}[e^{\gamma }e^{\gamma k}e^{\iota \beta i}e^{\iota \beta }-2e^{\gamma }e^{\gamma k}e^{\iota \beta i}$$+e^{\gamma }e^{\gamma k}e^{\iota \beta i}e^{-I\beta }+e^{-\gamma }e^{\gamma k}e^{\iota \beta i}e^{\iota \beta }$ $-2e^{-\gamma }e^{\gamma k}e^{\iota \beta i}+e^{-\gamma }e^{\gamma k}e^{\iota \beta i}e^{-\iota \beta }].$

(23)

By dividing both sides of Eq. (23) by ${\textstyle e^{\gamma k}e^{\iota \beta i}}$ and rearranging the terms, we have

$e^{\gamma }-2+e^{-\gamma }={\dfrac {\lambda }{2}}[e^{\gamma }(e^{\iota \beta }-2+e^{-\iota \beta })+e^{-\gamma }(e^{\iota \beta }-2+e^{-\iota \beta })].$

(24)

Using Euler's formula, ${\textstyle e^{\iota \beta }=\cos(\beta )+\iota \sin(\beta )}$, we can rewrite Eq. (24) as

$e^{\gamma }-2+e^{-\gamma }={\dfrac {\lambda }{2}}[(e^{\gamma }+e^{-\gamma })(2\cos(\beta )-2)],$

(25)

or yet,

$(e^{\gamma }+e^{-\gamma })(1+\lambda (1-\cos(\beta )))=2.$

(26)

Using the trigonometric identities ${\textstyle (1-\cos(\beta ))=2\sin ^{2}\left({\dfrac {\beta }{2}}\right)}$ and ${\textstyle \cosh(\gamma )={\dfrac {e^{\gamma }+e^{-\gamma }}{2}}}$, Eq. (26) can be rewritten as

$\cosh(\gamma )={\dfrac {1}{1+2\lambda \sin ^{2}\left({\dfrac {\beta }{2}}\right)}},$

(27)

or yet,

$\gamma =\arccos h\left({\dfrac {1}{1+2\lambda \sin ^{2}\left({\dfrac {\beta }{2}}\right)}}\right).$

(28)

From Eq. (21) we have that ${\textstyle U_{i}^{k+1}=e^{\gamma }U_{i}^{k}}$, that is, ${\textstyle e^{\gamma }}$ is the amplification factor. Let us look at what happens to the generic harmonic ${\textstyle U_{i}^{k+1}}$ as ${\textstyle k}$ increases. From Eq. (28) we know that ${\textstyle \beta \in \Re }$, ${\textstyle \lambda \geq 0}$ and ${\textstyle 0~\leq ~\sin ^{2}\left({\dfrac {\beta }{2}}\right)~\leq 1}$, so it is enough to analyze the following cases:

1) ${\textstyle \sin ^{2}\left({\dfrac {\beta }{2}}\right)\rightarrow 1^{-}}$, which implies that ${\textstyle \gamma \rightarrow ~\arccos h\left({\dfrac {1}{1+2~\lambda }}\right)}$. In this case, the anisotropy factor ${\textstyle \lambda }$ must be analyzed in the following situations:

1.1) ${\textstyle \lambda \rightarrow +\infty }$, which implies ${\textstyle \gamma \rightarrow {\dfrac {\pi \iota }{2}}}$. Note that in this case the harmonic tends to stay the same as ${\textstyle k}$ increases, but it will not be amplified.

1.2) ${\textstyle \lambda \rightarrow 0^{+}}$, which implies ${\textstyle \gamma \rightarrow 0^{+}}$. Note that in this case ${\textstyle e^{\gamma }}$ has a decreasing amplitude.

2) ${\textstyle \sin ^{2}\left({\dfrac {\beta }{2}}\right)\rightarrow 0^{+}}$, regardless of the value of ${\textstyle \lambda }$, we will have ${\textstyle \gamma \rightarrow 0^{+}}$, which also produces a decreasing amplitude for ${\textstyle e^{\gamma }}$.

Given the above, the harmonics will not be amplified, since ${\textstyle 0<e^{\gamma }<1}$. Therefore, the discretization method used in Eq. (13) with ${\textstyle \eta =1/2}$ is unconditionally stable.

2.4 Multigrid method

In some cases, when discretizing PDEs that model physical problems, we can obtain sparse and large linear systems, as described by Eq. (15), which can be rewritten as

$Au=b.$

(29)

These systems can be solved by using direct or iterative methods (herein called solvers). Due to the characteristics of these systems, the direct methods become unfeasible due to the high computational cost [4]. In this case, we opt for iterative methods. However, these methods generally have good smoothing properties only at the beginning of the iterative process.

After a few iterations, the approximation error becomes smooth, but not necessarily small. This problem is due to the characteristic of classical iterative methods in quickly smoothing out high-frequency errors (oscillatory modes), leaving only low-frequency errors (smooth modes) [35].

In this context, the Multigrid method [36] can be applied. It is used for accelerating the convergence in obtaining the solution of this type of system, since when using a set of grids, it is possible to smooth both the oscillatory and smooth modes, as the smooth modes in fine grids become more oscillatory in coarser grids [14,37]. This approach allows the iterative process of the Multigrid method to act on all error components [38,39,40,41].

The way it runs through the different grid levels is called a cycle [42]. In this work, we used the V-cycle, shown below in Figure 2, where there is an example of a V-cycle for 5 levels of coarsening; from fine grid ${\textstyle \Omega ^{h}}$ to the desired or coarsest grid ${\textstyle \Omega ^{16h}}$. Note that we use the coarsening ratio ${\textstyle q=2}$, with ${\textstyle h}$ being the spacing in the fine grid and ${\textstyle 2h}$ the spacing in the immediately coarser grid.

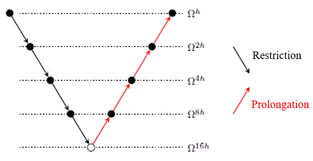
Figure 2. Multigrid V-cycle

In this cycle, the system of equations is smoothed ${\textstyle \nu _{1}}$ times (pre-smoothing) in the fine grid, and then we restrict its residue to the immediately coarser grid with the restriction operators (${\textstyle I_{h}^{2h}}$). In this work, we used the full weighting operator, given by

$r_{2h}(x_{i})=I_{h}^{2h}r_{h}(x_{i})={\dfrac {1}{4}},$

(30)

where ${\textstyle r_{h}}$ and ${\textstyle r_{2h}}$ are, respectively, the residue in the fine and coarse grid. This process is repeated until the coarsest grid is reached and only then the problem is solved

Next, the prolongation of corrections is performed by using the linear interpolation operator (${\textstyle I_{2h}^{h}}$), given by

$v_{h}(x_{i})=I_{2h}^{h}v_{h}(x_{i})=\left\lbrace {\begin{array}{l}{\dfrac {1}{2}}[v_{2h}(x_{i-1})+v_{2h}(x_{i+1})],\quad {\mbox{for}}\,\neq i,\\\\v_{2h}(x_{i}),\quad {\mbox{for}}\,=i.\end{array}}\right.$

(31)

where the first equation is for even ${\textstyle i}$ and the other is for odd ${\textstyle i}$, in the ${\textstyle \Omega ^{h}}$. The solution is then corrected and the system of equations is smoothed ${\textstyle \nu _{2}}$ times (post-smoothing), and the process is repeated until the finer grid ${\textstyle \Omega ^{h}}$ is reached, where the solution is smoothed ${\textstyle \nu _{2}}$ times [39]. The V-cycle is repeated until the stopping criterion is met. This approach allows the iterative process of the Multigrid method to smooth all the components [43].

3. Waveform relaxation and the subdomain methods

Waveform Relaxation (WR) is an iterative method that was initially proposed to solve large systems of Ordinary Differential Equations (ODEs) [19], but it can also be applied in time-dependent PDEs, where the spatial domain is decomposed by a set of points, and for each of them a system of ODEs is solved in all time steps [22,23,44,45]. This method allows the parallelization of algorithms for transient PDEs to be performed. According to [46], the feature of the WR method that transforms PDEs into an ODE system presents the form

${\dfrac {d^{2}v_{i}}{dt^{2}}}=G_{i}(v_{i},t),$

(32)

where ${\textstyle G_{i}}$ are vectors or functions that contain temporal information for each spatial coordinate ${\textstyle i}$, and which is calculated with the values of ${\textstyle v_{i}=(v_{1},v_{2},v_{3},...v_{d})}$. Thus, for each node ${\textstyle x_{i}}$ of the spatial discretization, a temporal ODE is solved to the final time independently. Each component of the system given in Eq. (32) can be written as an ODE, as follows

$\left\lbrace {\begin{array}{l}{\dfrac {d^{2}v_{1}}{dt^{2}}}=G_{1}(v_{1},v_{2},v_{3},...,v_{d},t),\quad {\mbox{with}}\quad v_{1}(0)=v_{1}^{0}\quad {\mbox{and}}\quad {\dfrac {dv_{1}}{dt}}=g_{1}^{0},\\\\{\dfrac {d^{2}v_{2}}{dt^{2}}}=G_{2}(v_{1},v_{2},v_{3},...,v_{d},t),\quad {\mbox{with}}\quad v_{2}(0)=v_{2}^{0}\quad {\mbox{and}}\quad {\dfrac {dv_{2}}{dt}}=g_{2}^{0},\\\vdots \\{\dfrac {d^{2}v_{d}}{dt^{2}}}=G_{d}(v_{1},v_{2},v_{3},...,v_{d},t),\quad {\mbox{with}}\quad v_{d}(0)=v_{d}^{0}\quad {\mbox{and}}\quad {\dfrac {dv_{d}}{dt}}=g_{d}^{0}.\end{array}}\right.$

(33)

where ${\textstyle d}$ is the dimension of the system and the notations ${\textstyle v_{i}(0)=v_{i}^{0}}$ and ${\textstyle {\dfrac {dv_{i}}{dt}}=g_{i}^{0}}$ with ${\textstyle 1\leq i\leq d,}$ indicate respectively, the initial configurations and velocities, for each point of the spatial discretization. Each line of the system of Eqs. (33) can be solved separately using a core for each line, as illustrated in Figure 3 for ${\textstyle N_{x}=12}$.

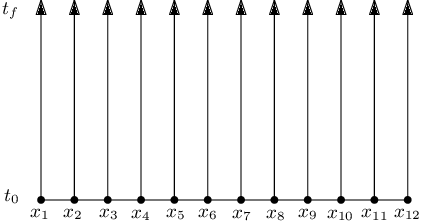
Figure 3. Waveform Relaxation method

Each temporal ODE can be solved in all spatial nodes separately, where the update of unknowns can be performed at the end of a WR cycle. Thus, we have an iterative method of repeating the procedure until a stopping criterion is reached [47]. We can obtain a fully parallelizable method in space by using a colored ordering scheme in the solver, such as Gauss-Seidel Red-Black (GSRB) [45].

It is possible to combine Waveform Relaxation and the Multigrid method when performing coarsening only in the spatial direction because WR is continuous in time. This way, the number of temporal discretization points is kept constant [45]. For example, for a fine grid ${\textstyle \Omega ^{h}}$ with ${\textstyle N_{x}\times N_{t}=33\times 33}$ points, the coarser grids, with a coarsening ratio ${\textstyle q=2}$, are ${\textstyle \Omega ^{2h}}$, ${\textstyle \Omega ^{4h}}$, ${\textstyle \Omega ^{8h}}$ and ${\textstyle \Omega ^{16h}}$, which respectively have ${\textstyle 17\times 33}$, ${\textstyle 9\times 33}$, ${\textstyle 5\times 33}$ and ${\textstyle 3\times 33}$ points. Then, a Multigrid cycle is performed at all spatial points for all time steps. In Algorithm 1, the structure of the Waveform Relaxation and Multigrid is presented for the solution of system ${\textstyle A_{h}(t)v_{h}(t)=f_{h}(t)}$, adapted from [23].}

Algorithm 1. Waveform Relaxation with Multigrid (WRMG): $v_{h}^{k}(t)\rightarrow v_{h}^{k+1}(t)$

if we are on the coarsest grid-level (with spatial grid-size given by $h_{0}$) then

${\textstyle A_{h_{0}}(t)v_{h_{0}}^{k+1}(t)=f_{h_{0}}(t)}$ Solve with a direct or fast solver.

else

${\textstyle {\bar {v}}_{h}^{k}(t)=S_{h}^{\nu _{1}}(u_{h}^{k}(t))}$ Pre-smoothing: $\nu _{1}$ steps of the GSRB Waveform Relaxation.

${\textstyle {\bar {r}}_{h}^{k}(t)=f_{h}(t)-A_{h}(t){\bar {v}}_{h}^{k}(t)}$ Compute the defect.

${\textstyle {\bar {r}}_{2h}^{k}(t)=I_{h}^{2h}{\bar {r}}_{h}^{k}(t)}$ Restrict the defect.

${\textstyle A_{2h}(t){\widehat {e}}_{2h}^{k}(t)={\bar {r}}_{2h}^{k}(t),{\widehat {e}}_{2h}^{k}(0)=0}$ Solve the defect equation $G_{2h}$ by performingone V-cycle of WRMG.

${\textstyle {\widehat {e}}_{h}^{k}(t)=I_{2h}^{h}{\widehat {e}}_{2h}^{k}(t)}$ Interpolate the correction.

${\textstyle {\bar {v}}_{h}^{k+1}(t)={\bar {v}}_{h}^{k}(t)+{\widehat {e}}_{h}^{k}(t)}$ Compute a new approximation.

${\textstyle {\bar {v}}_{h}^{k}(t)=S_{h}^{\nu _{2}}(u_{h}^{k+1}(t))}$ Post-smoothing: $\nu _{2}$ steps of the GSRB Waveform Relaxation.

end if

In Gander et al. [11] there is a variation of the Waveform Relaxation method, which can be applied to PDEs, where the domain ${\textstyle \Omega }$ is divided into ${\textstyle K}$ spatial subdomains. Remember that each point is solved independently and continuously until the final time, which generates a parallelizable strategy. See Figure 4 for ${\textstyle K=3}$.

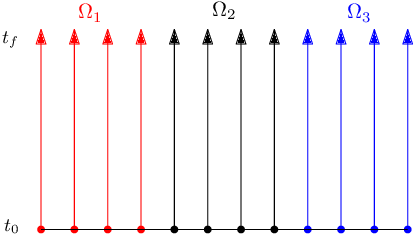
Figure 4. Division of the domain $\Omega$ into $K=3$ spatial subdomains

We can notice that in the case where the subdomains are the smallest possible, the subdomains ${\textstyle \Omega _{1},\Omega _{2},...,\Omega _{K}}$ are respectively equal to the points ${\textstyle x_{1},x_{2},...,x_{N_{x}}}$. That is, we will have the standard Waveform Relaxation method. Note that parallelization can be performed by using a processing core for each spatial subdomain.

In Gander et al. [11] and Gong et al. [48] a study is carried out to assess the stability of using this approach for heat and Helmholtz equations, as well as the ways of exchanging information between the subdomains. The authors also mention that at the beginning of the iterative process, the convergence is negatively affected, and perturbations may occur in the approximate solution, but as the iterative process advances, the solution converges to the desired values. See Figure 5, taken from Gander et al. [11].

Figure 5. Error for the heat equation with Waveform Relaxation by spatial subdomains [11]

In this case, Gander et al. [11] shows the convergence for the one-dimensional heat transfer problem with the method called Dirichlet-Neumann Waveform Relaxation. In the left figure, the author presents the theoretical error (error) and the numerical error (bound) obtained with five fixed spatial subdomains and different final times (${\textstyle T}$, as used in the figure). In the right figure, the number of subdomains varies, and the final time is fixed at ${\textstyle T=2}$s. We can notice that the initial oscillations are higher when the final time is higher and/or there are more subdomains in space. Here we have a great challenge: the higher the number of subdomains, the higher the degree of parallelization; however, the oscillations at the beginning of the iterative process will be also higher.

Another approach is proposed in Ong and Mandal [32], where, besides the division in ${\textstyle K}$ spatial subdomains, there is also a division in ${\textstyle J}$ temporal subdomains, thus generating an approach that is highly parallelizable (see Figure 6 for ${\textstyle K=3}$ and ${\textstyle J=2}$).

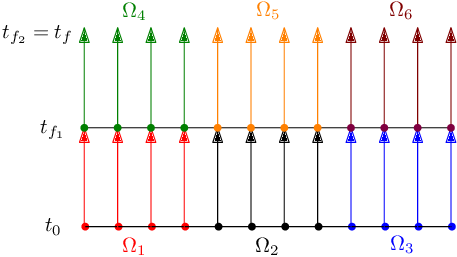
Figure 6. Waveform Relaxation method by $K=3$ spatial and $J=2$ temporal subdomains

Notice that the approach proposed in Gander et al. [11] is a specific case of the approach presented in Ong and Mandal [32], which adopts ${\textstyle J=1}$. In this work, we propose a thorough analysis of the second methodology, which adopts the minimum number of spatial subdomains (${\textstyle K=1}$) and a reduced number of temporal subdomains, to solve the wave equation with the WR method, aiming to reduce the oscillations at the beginning of the iterative process. For this, we analyze the effect of parameters such as time and space interval, physical properties of the wave, number of temporal subdomains, among others. This method is applied using recursively the Algorithm 1 according to Figure 7.

Efficient solutions to the one-dimensional wave equation are already found in the literature, such as in Baccouch and Temimi [30] for high-order methods and in [31] for nonlinear cases. However, there are still challenges to solve when using the Multigrid method, especially when combined with schemes that allow parallelization, as in Gander et al. [11]. In this sense, one of the novelties of this work focuses on the use of the Subdomains in Time method, combined with the Waveform Relaxation strategy and the Multigrid method, in order to reduce the existing large initial oscillations. Unlike the Ong and Mandal [32], here we work with a reduced number of subdomains in time, in order to reduce CPU time while increasing the degree of parallelization of the codes used.

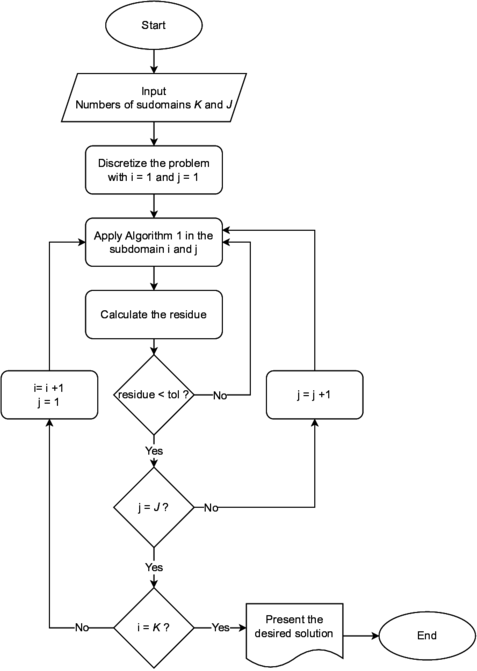
Figure 7. Waveform relaxation with subdomain method

4 Results

In this section, we present the main results of this work, where we solve a one-dimensional problem with Dirichlet boundary conditions, Eqs. (1) to (4), which serves to validate the proposed methodology. We approach techniques of code verification based on the errors of the numerical simulations and on a posteriori analyses of the results found with the Multigrid (with V-cicle(2,2)) and Singlegrid formulations. In our analyses, we use the Gauss-Seidel solver with Red-Black ordering. Then, we discuss the characteristics of the application of the standard Waveform Relaxation method in the one-dimensional wave equation and some problems regarding the use of this formulation. To deal with these problems, we apply the Subdomain Method proposed by Ong and Mandal [32]. We innovate by assuming a fixed parameter ${\textstyle K=1}$ with variation only in ${\textstyle J}$. Finally, we analyze the convergence factors, complexity order (with a non-linear adjustment), CPU time, and Speed-ups.

The one-dimensional wave propagation problem modeled by Eqs. (1) to (4) is solved by admitting ${\textstyle \alpha =2}$, with initial condition ${\textstyle f(x)=\sin(\pi x)}$ and initial velocity ${\textstyle g(x)=0}$. We adopt the same number of points in the spatial and time discretization ${\textstyle N_{x}=N_{t}}$ (denoted by ${\textstyle N}$), weighting parameter ${\textstyle \eta =0.5}$, final time ${\textstyle t_{f}=1.0s}$ and ${\textstyle x\in (0,1)}$. Tests were performed in a computer with Intel Corei3 1.5 GHz processor, 4 GB RAM, and 64-bits Windows 10 operational system with double precision.

4.1 Discretization error

The discretization error is related to the truncation in the Taylor series [4] and consequently, to the size of the grid elements. For the sake of assessing the behavior of this type of error, we disregard iteration and round-off errors. For this, each problem was solved until the round-off error was reached. Next, we present in Figure 8 the infinity norm of the error in the solution approximated with the Waveform Relaxation (WR), combined with the Multigrid (MG) and Singlegrid (SG) for values of ${\textstyle N}$.

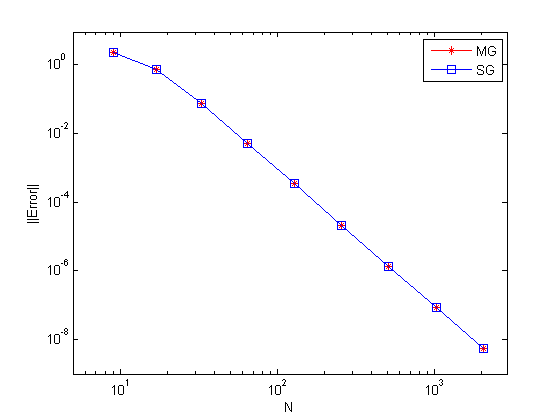
Figure 8. Infinity norm of the discretization error for different grid sizes with the Waveform Relaxation method

We noticed that the discretization error decreases as the grid is refined. The errors presented in Figure 8 are the same found in Malacarne et al. [13] using the Time-Stepping method, which generates a 4th-order method, which can be easily verified using the methodology present in da Silva et al. [49]. This test serves to verify the code used here, which utilizes time sweeping given by WR.

4.2 Oscillations in the approximate solution

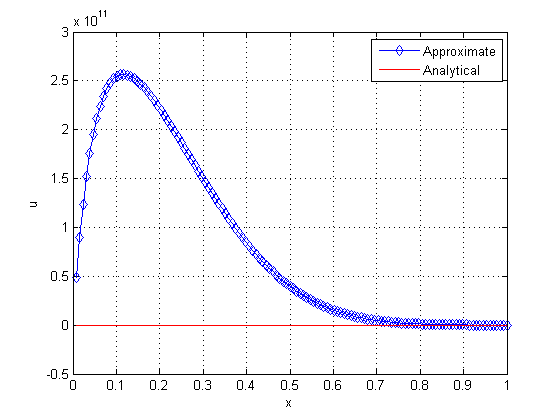
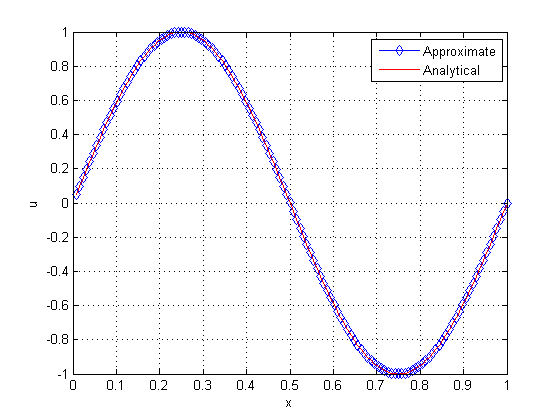
Next, we show the oscillatory behavior of the solution during the iteration process, when using the Waveform Relaxation method. For such, we solve a one-dimensional problem modeled by Eqs. (1) to (4), using Singlegrid (SG) and Gauss-Seidel with Red-Black ordering as the solver, in a grid with ${\textstyle N=129}$ points. Figure 9 presents the solutions for ${\textstyle 2}$ and ${\textstyle 50}$ iterations, and Figure 10 shows the solutions for ${\textstyle 200}$ and ${\textstyle 1000}$ iteration, both using final time ${\textstyle t_{f}=1.0s}$.

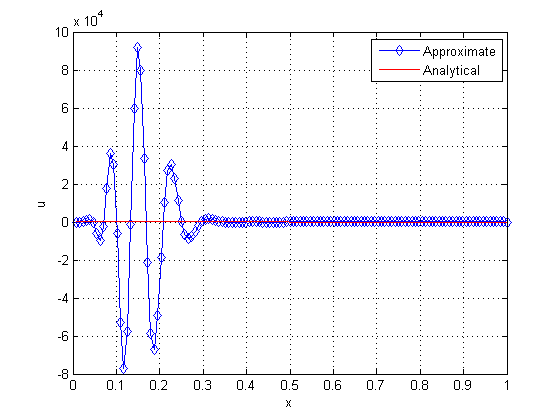
Figure 9. Solution with 2 (left) and 50 iterations (right)

Figure 10. Solution with 200 (left) and 1000 iterations (right)

We verified significant initial oscillations when applying the standard WR method, even when using coarser grids (with fewer points). Despite the strong oscillation at the beginning of the process, the numerical solution converges to the desired values as a large number of iterations are performed.

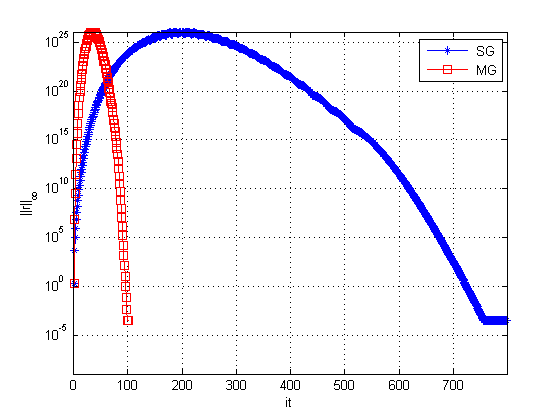
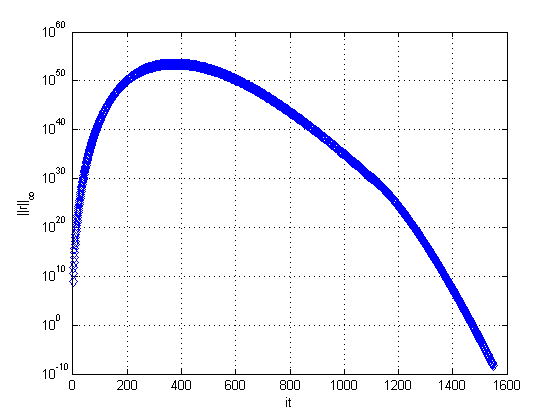
In Figure 11 it is possible to observe the behavior of the infinity norm of the residue as the iterations are performed, for Singlegrid and Multigrid.

Figure 11. Residue versus iterations for singlegrid and multigrid

Even though MG performs fewer cycles than SG, the order of perturbation of the residue of both is the same. This initial perturbation is not a desirable characteristic in the approximation process and despite being well-known in the literature, its causes remain an unknown [11] and negatively interfere in the convergence factors and in the CPU time.

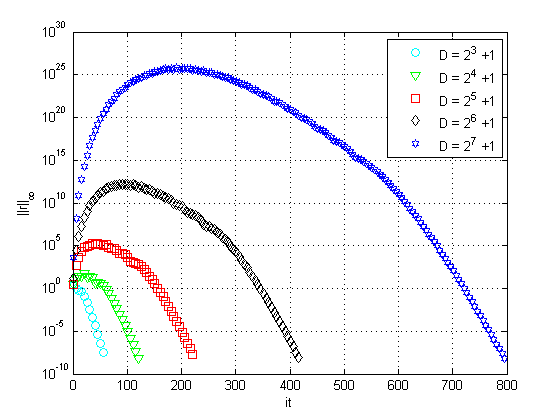
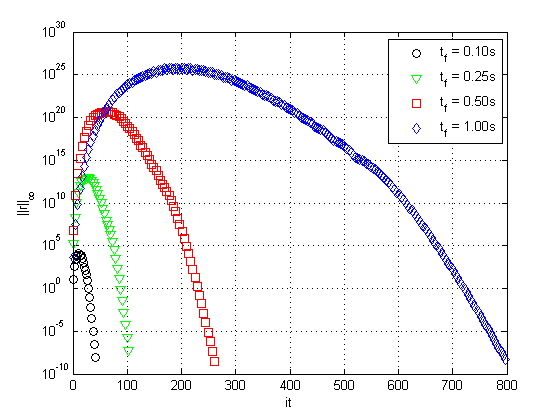
In Figure 12, we present the infinity norms of the residues for different numbers of points, with final time fixed at ${\textstyle t_{f}=1.0s}$ (left), and then varying the final time ${\textstyle t_{f}}$, with ${\textstyle N=2^{7}+1}$ (right), using SG and standard WR.

Figure 12. Residue versus iterations varying $N$, with $t_{f}=1.0s$ (left), and varying $t_{f}$, with $N=2^{7}+1$ (right)

Notice that with the increase in the final time, the maximum residue increases considerably, at the order of ${\textstyle 10^{25}}$, similarly to what happens when the number of points in the grid increases. This implies a loss of efficiency when solving problems with WR and Singlegrid with many degrees of freedom and/or a final time relatively large. Very similar residues are found when applying the Multigrid method for these cases, as seen in Figure 11.

4.3 Average convergence factor - Standard waveform relaxation

Here we apply the standard Waveform Relaxation method for the problem described in the previous section, but with varying final time. For this, let the convergence factor be ${\textstyle \rho =||r^{it}||_{\infty }/||r^{it-1}||_{\infty }}$, with ${\textstyle r^{it}}$ being the residue generated in the iteration ${\textstyle it}$. We know that ${\textstyle \rho \approx 0}$ results in more efficient methods, while ${\textstyle \rho \approx 1}$ means the opposite [50]. We also define the average convergence factor ${\textstyle \rho _{m}}$ [39], by

$\rho _{m}={\sqrt[{it}]{\frac {||r^{it}||_{\infty }}{||r^{0}||_{\infty }}}}$

(34)

According to Thole and Trottenberg [51] and Horton and Vandewalle [52] ${\textstyle \lambda =\alpha ^{2}\tau ^{2}/h^{2}}$ can be considered as a measure of the anisotropy level in the discretized operator in a given grid, and such anisotropy can affect the performance of the solver. As ${\textstyle \lambda }$ depends on the temporal and spatial increments adopted in the discretization and on the velocity of the propagation of the wave, ${\textstyle \lambda }$ thus represents a measure of physical and geometrical anisotropy of the wave equation.

We can write the final time depending directly on ${\textstyle \lambda }$ and ${\textstyle \alpha }$, with the expression ${\textstyle t_{f}={\sqrt {\lambda }}/\alpha }$. Then, we present the test results, where we vary the value of the parameter ${\textstyle \lambda }$ and calculate ${\textstyle \rho _{m}}$ for a wide range of problems, which covers the vast majority of real cases of wave propagation. In order to verify the behavior of the standard Waveform Relaxation method, using the Singlegrid and Multigrid Methods (Figure 13).

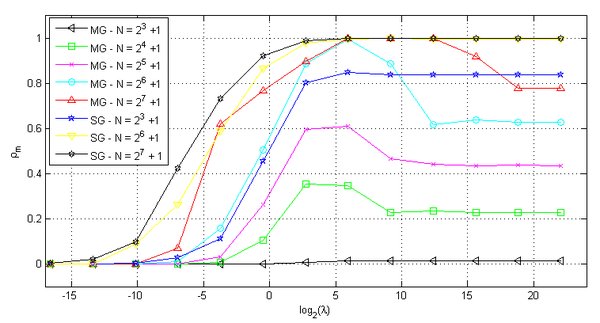
Figure 13. $\rho _{m}$ versus $\lambda$ with standard Waveform Relaxation using Multigrid and Singlegrid

We can observe in Figure 13, that as ${\textstyle \lambda }$ increases, the average convergence factors of the Multigrid and Singlegrid Methods also increase, becoming ${\textstyle \rho _{m}\approx 1.0}$, which is not good. With this, we can conclude that the solution model is neither efficient nor robust for intermediate or large ${\textstyle \lambda }$ values (in this cases we have many unkwows and longer final times). This result supports the hypothesis that it is inefficient to apply the standard Waveform Relaxation method to solve the wave equation, whether with the Multigrid or Singlegrid methods.

The hyperbolic transient wave computational simulation problem can be solved in different ways, but most of them have limitations, especially for relatively large end times. For these cases, explicit schemes exhibit instabilities that compromise the reliability of the approximate solution [53]. As we have seen, even implicit methods present difficulties to solve these cases, because at the beginning of the iterative process, the approximate solutions present strong oscillations, which are smoothed out as the number of iterations increases (Figures 9 and 10), but this seriously compromises the efficiency of such methods. Therefore, we seek to improve the applicability of parallelizable methods, such as the Waveform Relaxation Method. For this, we combine the methodology developed so far with the Subdomains in Time method.

4.4 Applying the subdomain method

From this section on, we present the results of the Waveform Relaxation Method combined with the Subdomain in Time method. For this, we will always adopt ${\textstyle K=1}$ for the number of spatial subdomains. For the number ${\textstyle J}$ of subdomains in time, we will always adopt the smallest possible value, but one that is able to provide good average convergence factors (${\textstyle \rho _{m}}$). Next in Table 1 are the values used for ${\textstyle J}$, which may vary depending on the values of ${\textstyle N^{2}=N_{x}N_{t}}$ and ${\textstyle \lambda }$. The choice of ${\textstyle J}$ was based on empirical analysis of this data so that ${\textstyle \rho _{m}\approx 0.4}$, ie, so that the implicit numerical model can be considered acceptable [39].

Table 1. Number $J$ of subdomain in time according to the ranging of $N$ and $\lambda$

$N^{2}$ - $\lambda$	$10^{-2}$	$10^{-1}$	$10^{0}$	$10^{+1}$	$10^{+2}$	$10^{+3}$	$10^{+4}$	$10^{+5}$	$10^{+6}$	$10^{+7}$
${\textstyle 9^{2}}$	1	1	1	1	1	1	1	1	1	1
$17^{2}$	1	1	1	1	2	2	2	2	2	2
$33^{2}$	1	1	1	2	2	2	2	2	2	2
$65^{2}$	1	1	2	4	4	4	4	4	4	4
$129^{2}$	1	1	2	4	8	8	8	8	8	8
$257^{2}$	1	2	8	16	16	16	16	16	16	16

We should also note that, for large ${\textstyle J}$, the number of spatial meshes within each temporal subdomain will be small, which may reduce the level of parallelization of the method. Thus, it is always interesting to have the smallest possible value for ${\textstyle J}$, but in the case of ${\textstyle J=1}$, we have the standard Waveform Relaxation method, which we already know is not efficient. We point out that all the following tests were performed using the number of subdomains in time that are present in the Table 1.

It is also possible to notice that for domains with small ${\textstyle N}$, the largest number of subdomains in time is ${\textstyle J=2}$, regardless of the value of ${\textstyle \lambda }$. But for problems with large ${\textstyle N}$, depending on the value of ${\textstyle \lambda }$, we cannot work with a very small number for ${\textstyle J}$, because the instabilities of the standard Waveform Relaxation will negatively affect the values of ${\textstyle \rho _{m}}$.

To solve the problem of higher residues during the initial iterations, we analyzed the method parameters as proposed by Ong and Mandal [32], with the goal to improve the average convergence factors. We kept the number of spatial subdomains fixed at ${\textstyle K=1}$ and analyzed the number of temporal subdomains ${\textstyle J}$. This way, we obtained a highly parallelizable strategy when using the Waveform Relaxation method. Figure 14 shows the behavior of the residue, using SG and WR for ${\textstyle N=2^{8}+1}$ that is, a total of ${\textstyle 66049}$ points, with ${\textstyle t_{f}=1.0s}$.

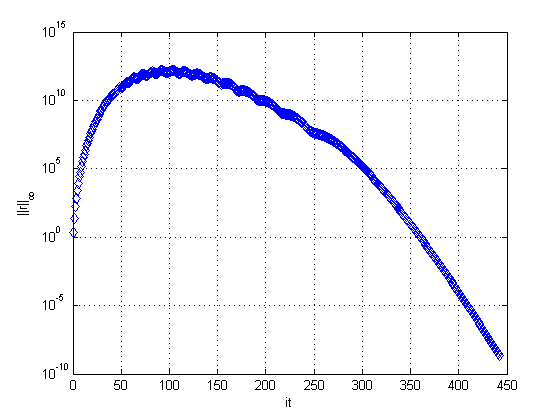
Figure 14. Residues versus iterations for $t_{f}=1.0s$, $N=2^{8}+1$ and $K=1$, with $J=1$ (left) and $J=4$ (right)

By solving the wave equation with SG and WR using only one temporal subdomain (${\textstyle J=1}$), we have the ${\textstyle t_{CPU}~=~14.15s}$, with a maximum residue of the order of ${\textstyle 10^{53}}$. However, by using four temporal subdomains (${\textstyle J=4}$), where the subdomain values vary from ${\textstyle 0.0s}$ to ${\textstyle 0.25s}$, from ${\textstyle 0.25s}$ to ${\textstyle 0.50s}$, from ${\textstyle 0.50s}$ to ${\textstyle 0.75s}$, and from ${\textstyle 0.75s}$ to ${\textstyle 1.0s}$, we have the maximum residue of the order of ${\textstyle 10^{12}}$ and the processing time is reduced to ${\textstyle t_{CPU}=4.01s}$.

In Figure 15 we can observe the behavior of the order of the maximum residue concerning the number of temporal subdomains ${\textstyle J}$, as well as the values of ${\textstyle N}$, considering ${\textstyle K=1}$.

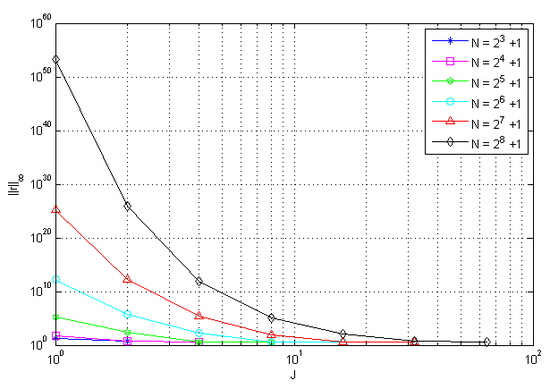
Figure 15. Residue versus $J$, for $t_{f}=1.0s$ and $K=1$, varying $N$, with SG and WR

We verified that the largest reductions in the residue are found in the first subdivisions of the domain. For instance, for ${\textstyle N=2^{8}+1}$ and ${\textstyle J=1}$, the maximum residue has an order of ${\textstyle 10^{53}}$ and ${\textstyle t_{CPU}=14.15s}$, however, when using Subdomain Method, this residue decreases to an order of ${\textstyle 10^{5}}$ and ${\textstyle t_{CPU}=2.35s}$. We further highlight the considerable improvement in the order of residue and computational time.

4.5 Average convergence factor - Waveform relaxation with subdomain in time

Next, Figure 16 presents the average convergence factors ${\textstyle \rho _{m}}$ for the Multigrid and Singlegrid methods with different values of ${\textstyle \lambda }$ for different values of ${\textstyle N}$, combined with the Waveform Relaxation method, where the choice of the appropriate number of subdomains was made based on Table 1.

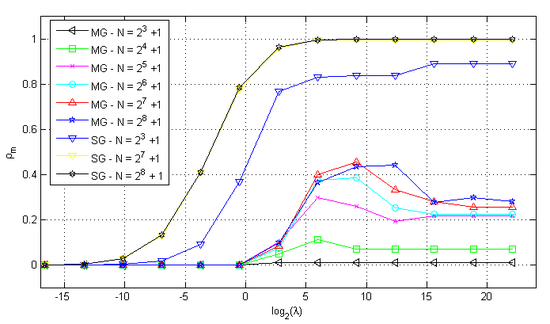
Figure 16. $\rho _{m}$ for the Multigrid and Singlegrid methods, combined with Waveform Relaxation Relaxation, $K=1$ and suitable $J$

In this case, we used the same number of subdomains for the MG and SG. We found out that both methods present ${\textstyle \rho _{m}\approx 0}$, for values of ${\textstyle log_{2}(\lambda )<0}$, which implies high efficiency. But, as ${\textstyle log_{2}(\lambda )}$ increases, the SG shows values of ${\textstyle \rho _{m}\approx 1}$ with the refinement of the grid, that is, the method is inefficient in this region. In the same region, the MG shows values of ${\textstyle \rho _{m}\approx 0.45}$ with the refinement of the grid. In the worst case, in the region near ${\textstyle \lambda =10^{2}}$, the MG presents ${\textstyle \rho _{m}\approx 0.6}$, though it still shows lower convergence factors than those presented by the SG method.

Therefore, the MG method proposed for the wave equation is much more efficient for these values of ${\textstyle \lambda }$. Besides, we notice that the values of ${\textstyle \rho _{m}}$ tend to not depend on the value of ${\textstyle \lambda }$ for finer grids, which evidences the robustness of the method. In this work, high values of ${\textstyle \lambda }$ can mean higher final times or wavenumbers ${\textstyle \alpha }$, or even, highly refined spatial grids.

An example can be given for the case ${\textstyle \lambda =10^{4}}$ , with ${\textstyle N=2^{8}+1}$, ${\textstyle 16}$ temporal subdomains and ${\textstyle 1}$ spatial subdomain. For the SG method, we have ${\textstyle t_{CPU}=1320.62s}$, with ${\textstyle \rho _{m}\approx 0.9999}$ and a total of ${\textstyle 120000}$ iterations. For the MG method, we have ${\textstyle t_{CPU}=4.67s}$, ${\textstyle \rho _{m}\approx 0.4301}$, and a total of 23 V-cycles${\textstyle (2,2)}$, which confirms the advantage of employing the MG combined with the Subdomain technique for the WR proposed in this work, that is, temporal subdomains ${\textstyle J}$ and spatial subdomain ${\textstyle K=1}$. A possible explanation for this advantage can be found in the reduction of the average convergence factor of the MG method with the increase in the number of temporal subdomains (${\textstyle J}$), as seen in Figure 17.

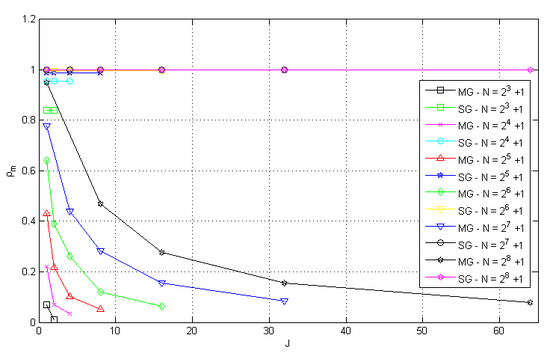
Figure 17. $\rho _{m}$ for the MG and SG methods with Waveform Relaxation and different numbers of temporal subdomains $J$ and $N$, with $\lambda =10^{5}$

4.6 Order of complexity

We made a geometrical adjustment [4] to verify the complexity of the algorithm that uses WR combined with subdomains and compared the results for Single and Multigrid. For this, we used the following expression

$t_{CPU}=c.\mathbf {N} ^{p},$

(35)

where ${\textstyle c}$ is the coefficient of the method, ${\textstyle p}$ represents the order of complexity of the solver related to the slope of the adjustment curve and ${\textstyle \mathbf {N} }$ is the total number of variables of the problem, which in our case will be ${\textstyle ~\mathbf {N} ~=~(N_{x}~-~2)~.~(N_{t}~-2~)~}$. Theoretically, ${\textstyle p}$ must be near ${\textstyle 1}$ for the Multigrid method [14]. Table 2 shows the results for these parameters, with different values of ${\textstyle \lambda }$. To find the values of ${\textstyle \lambda }$, we kept ${\textstyle \mathbf {N} }$ fixed and varied the final time.

Table 2. Geometrical adjustment parameters for the 1D wave equation

${\textstyle \lambda }$	$c_{SG}$	$p_{SG}$	$c_{MG}$	$p_{MG}$
${\textstyle 10^{0}}$	3.00E-04	0.6997	2.00E-04	0.7101
$10^{1}$	2.00E-04	0.8943	4.00E-04	0.7822
$10^{2}$	9.00E-05	1.2051	1.00E-04	1.0319
$10^{3}$	6.00E-05	1.6515	8.00E-05	1.0833
$10^{4}$	2.00E-06	1.8277	3.00E-04	0.8955
$10^{5}$	2.00E-06	1.8188	1.00E-04	0.9898

As the values of ${\textstyle \lambda }$ increase, the ${\textstyle p_{MG}}$ tends to values near ${\textstyle 1}$ and the ${\textstyle p_{SG}}$ near ${\textstyle 2}$. This trend confirms the linear behavior of the Multigrid method and highlights the disadvantage of using the Singlegrid method for large values of ${\textstyle \lambda }$, which corroborates the results depicted in Figures 16 and 17.

4.7 Speed-up

In this section, we analyze the Speed-up, which is given by the ratio between the computational time of the SG and the MG. Figure 18 shows the Speed-up results for increasing number of points of the problem (${\textstyle N^{2}}$), for different values of ${\textstyle \lambda }$, considering ${\textstyle K=1}$ and ${\textstyle J=8}$.

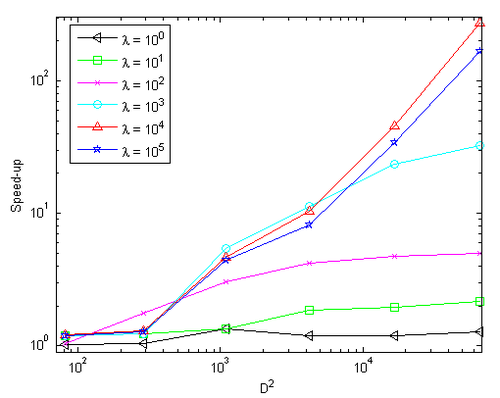
Figure 18. Speed-up versus $N^{2}$ for different values of $\lambda$, $K=1$ and $J=8$

Notice that the Speed-up increases along with the increase in the number of points (desirable property) and also for higher values of ${\textstyle \lambda }$. For example, when ${\textstyle \lambda =10^{5}}$, with ${\textstyle N=2^{8}~+1}$ and temporal subdomain ${\textstyle J=8}$, the MG method has a ${\textstyle t_{cpu}=8.13s}$ and the SG a ${\textstyle t_{cpu}=1477.82s}$. That is, the MG method solves the problem roughly ${\textstyle 182}$ times faster than the SG method.

5. Application: Wave propagation problem with reflection

Here we approach a more realistic problem that is solved by approximation. We admit ${\textstyle \Omega =[0,1]}$, ${\textstyle \alpha =2}$, ${\textstyle t_{f}=1.0s}$, initial configuration and velocity ${\textstyle f(x)=g(x)=0}$, ${\textstyle u(0,0)=u(1,t)=0}$, that is, we have a straight string in rest position in the initial time, fixed at both ends. Time can be divided in the intervals ${\textstyle t_{1},t_{2},t_{3},...,t_{p-1},t_{p},t_{p+1},...,2t_{p},...,t_{f}}$, where the ${\textstyle t_{p}}$ is the time in which the oscillation reaches the maximum displacement. Then, we apply a pulse in the extremity ${\textstyle x=0}$, between the interval ${\textstyle (t_{3};2t_{p})}$. This pulse can be inserted into the problem, given by the following boundary conditions

$u(0,t)=\left\lbrace {\begin{array}{lll}0,&{\mbox{for}}&t\in [t_{1},t_{2}],\\\\\sin(\pi t),&{\mbox{for}}&t\in [t_{3},t_{p}],\\\\\sin(\pi (2t_{p}-t)),&{\mbox{for}}&t\in (t_{p},2t_{p}],\\\\0,&{\mbox{for}}&t>2t_{p}.\end{array}}\right.$

(36)

In this work, we adopt ${\textstyle t_{p}=0.109s}$, ${\textstyle 2t_{p}=0.218s}$, ${\textstyle t_{f}=1.000s}$, ${\textstyle \lambda =10^{0}}$ and ${\textstyle N=2^{6}+1}$. One can verify the propagation of the pulse as time varies on Figure 19.

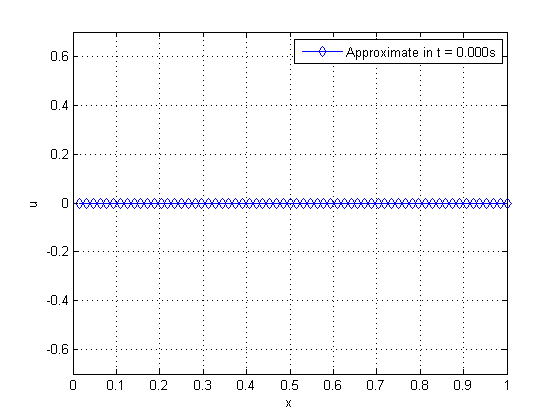
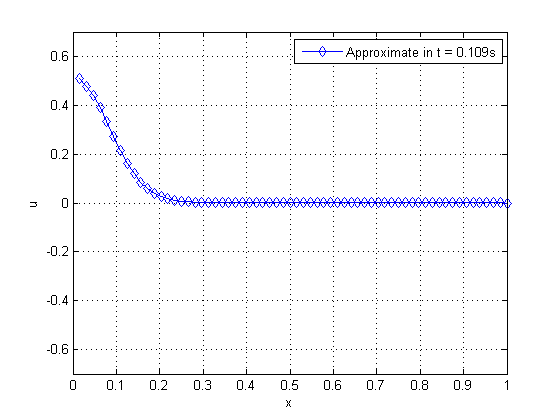
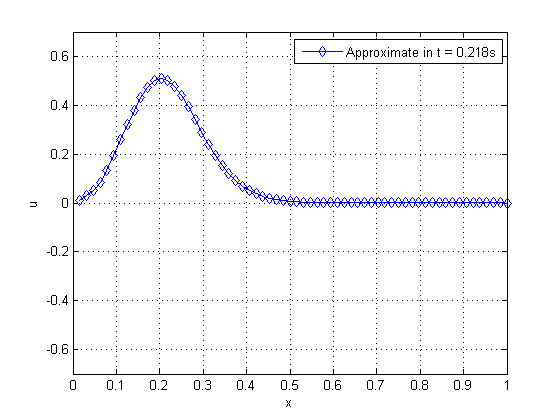
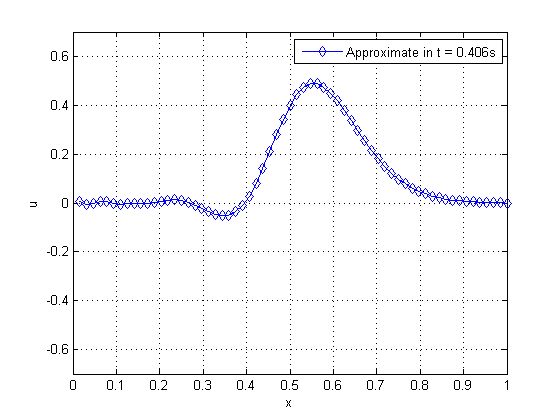
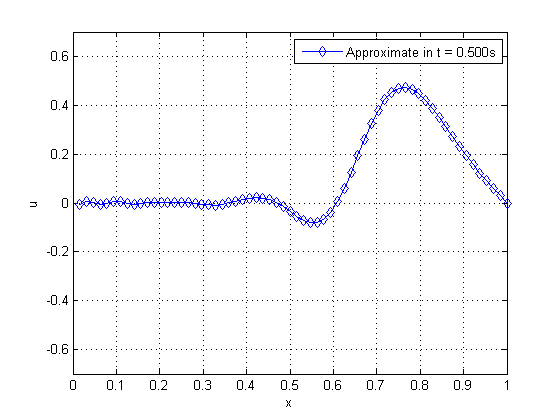
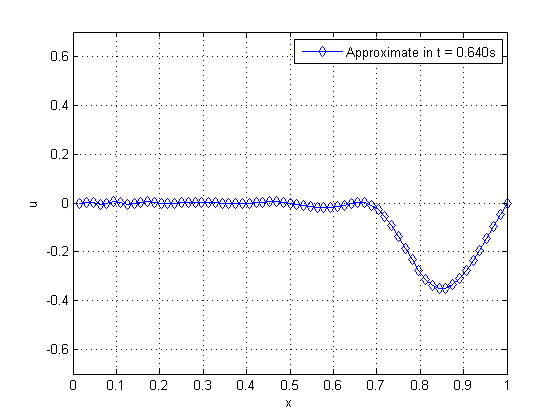
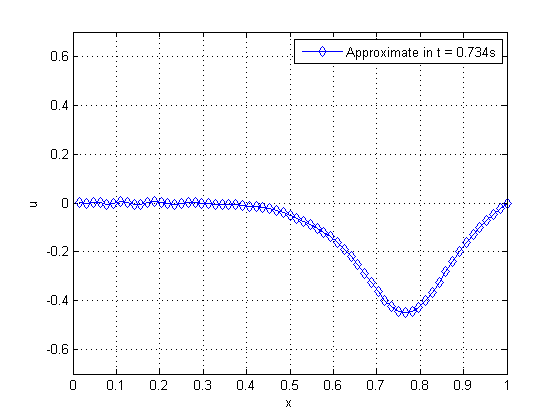
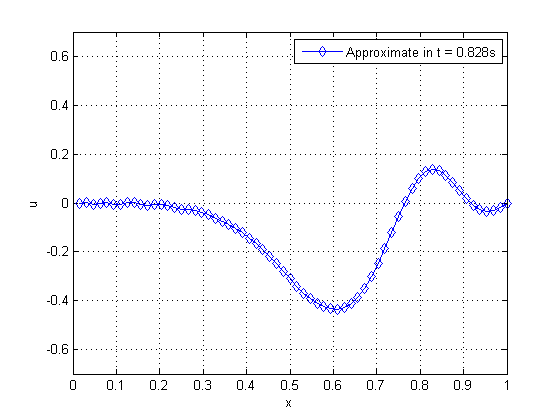
Figure 19. Propagation of pulse on a string as time advances

By observing Figure 19, from left to right and from top to bottom, we can verify the phenomenon of wave propagation on a string, where there is an inversion of the phase in which the pulse was applied. We solve this problem by applying the WR method with ${\textstyle J=1}$ (standard) and WR with temporal subdomains ${\textstyle J=4}$ , combined with the SG and MG for both cases. Table 3 shows some of the parameters assessed.

Table 3. Parameters of the solution with standard WR ($J=1$) and with WR with temporal subdomains $J=4$,
for wave propagation with reflection and phase inversion

	$WR_{SG}$	$WR_{MG}$	$WR_{SG-SUB}$	$WR_{MG-SUB}$
${\textstyle t_{CPU}}$	2.94E-01	1.67E-01	1.23E-01	6.59E-02
$\rho _{m}$	9.51E-01	7.38E-01	8.72E-01	2.35E-02
$||r||_{\infty }$	1.03E+12	1.03E+12	5.67E+01	5.67E+01

By using ${\textstyle J=4}$, the analyzed parameters improve significantly, especially the average convergence factor ${\textstyle \rho _{m}}$ combined with MG, thus proving the efficiency of this applied method for the wave equation.

6. Comments

The methodology presented here, can be extended also to more realistic problems, by considering the external forces operating on the problem, by inserting ${\textstyle F(x,t)}$ in the right hand side of Eq. (1), because according to Trottenberg et al. [14] causes changes only source term of the system of equations, not changing the performance of the method. Another possibility is to check the applicability of the Waveform Relaxation method with Subdomains in Time to two-dimensional and three-dimensional problems. As well as the application of the Multigrid method, which as seen in this article, can signifcantly decrease the average convergence factors, making it possible to obtain powerful parallelizable methods.

7. Conclusions

In this work, we presented a scheme of parallelizable solutions for the one-dimensional wave propagation problem that uses discretization combined with the Finite Difference Method, weighted by a parameter ${\textstyle \eta }$ in different stages of time. The innovation can be seen in the application of the Waveform Relaxation method with temporal subdomains ${\textstyle J}$ and only one spatial subdomain, in which we were able to significantly reduce the order of the maximum residue. We also innovated when applying the Multigrid method for this class of problems and we showed a considerable improvement in the processing time and convergence factors, in codes that allow parallelization, mainly when working with large values of ${\textstyle \lambda }$. Moreover, we applied this technique to analyze the solution of a problem of pulse propagation on a string, thus proving the efficiency of the proposed method.

We also point out that the main challenge of using the Waveform Relaxation method for the wave equation is in the initial increase of the residual, since this negatively alters all the parameters analyzed, and that it was already known in the literature [11]. We emphasize that this problem was solved satisfactorily with the methodology presented in this work.

Disclosure statement: No potential conflict of interest was reported by the authors.

Funding: This study was financed in part by the Coordenco de Aperfeicoamento de Pessoal de Nível Superior (CAPES), Finance Code 88882.381810/2019-01.

References

[1] Weber I., Kreiss G., Nazarov M. Stability analysis of high order methods for the wave equation, Journal of Computational and Applied Mathematics, 404:113900, 2022.

[2] Gander M.J., Halpern L., Nataf F. Optimal Schwarz waveform relaxation for the one dimensional wave equation. SIAM Journal on Numerical Analysis, 41(5):1643&-1681, 2003.

[3] Bamberger A., Glowinski R., Tran Q.H. A domain decomposition method for the acoustic wave equation with discontinuous coefficients and grid change. SIAM Journal on Numerical Analysis, 34(2):603-639, 1997.

[4] Burden R., Faires J.D. Numerical analysis. Brooks/Cole Cengage Learning, pp. 882, 2016.

[5] Umetani N., MacLachlan S.P., Oosterlee C.W. A multigrid-based shifted Laplacian preconditioner for a fourth-order Helmholtz discretization. Numerical Linear Algebra with Applications, 16(8):603–626, 2009.

[6] Ernst O.G., Gander M.J. Multigrid methods for Helmholtz problems: a convergent scheme in 1D using standard components. Direct and Inverse Problems in Wave Propagation and Applications, De Gruyer (Ed.), 135-186, 2013.

[7] Brandt A., Livshits I. Wave-ray multigrid method for standing wave equations. Electronic Transactions on Numerical Analysis, 6:162-181, Kent State Univesity, 1997.

[8] Dehghan M., Mohebbi A. The combination of collocation, finite difference, and multigrid methods for solution of the two-dimensional wave equation. Numerical Methods for Partial Differential Equations: An International Journal, 24(3):897–910, 2008.

[9] Malacarne M.F., Pinto M.A.V., Franco S.R. Computational simulation of one-dimensional waves with the Multigrid Method. Brazilian Journal of Development, 7(8):83763–83775, 2021.

[10] Gander M.J., Halpern L., Rannou J., Ryan J. A direct time parallel solver by diagonalization for the wave equation. SIAM Journal on Scientific Computing, 41(1):A220–A245, 2019.

[11] Gander M.J., Kwok F., Mandal B.C. Dirichlet–Neumann waveform relaxation methods for parabolic and hyperbolic problems in multiple subdomains. BIT Numerical Mathematics, 173–207, Springer, 2021.

[12] Cuminato J.A., Meneguette M. Discretization of partial differential equations: finite difference techniques (in Portuguese). Brazilian Mathematical Society, 2013.

[13] Malacarne M.F., Pinto M.A.V., Franco S.R. Performance of the multigrid method with time-stepping to solve 1D and 2D wave equations. International Journal for Computational Methods in Engineering Science and Mechanics, 23(1):45–56, Taylor & Francis, 2022.

[14] Trottenberg U., Oosterlee C.W., Schuller A. Multigrid. Elsevier, pp. 631, 2000.

[15] Wienands R., Oosterlee C.W. On three-grid Fourier analysis for multigrid. SIAM Journal on Scientific Computing, 23(2):651–671, 2001.

[16] Franco S.R., Gaspar F.J., Pinto M.A.V., Rodrigo C. Multigrid method based on a space-time approach with standard coarsening for parabolic problems. Applied Mathematics and Computation, 317:25–34, 2018.

[17] Britt S., Turkel E., Tsynkov S. A high order compact time/space finite difference scheme for the wave equation with variable speed of sound. Journal of Scientific Computing, 76(2):777–811, 2018.

[18] Gander M.J., Neumuller M. Analysis of a new space-time parallel multigrid algorithm for parabolic problems. SIAM Journal on Scientific Computing, 38(4):A2173–A2208, 2016.

[19] Lelarasmee E., Ruehli A.E., Vincentelli S.A.L. The waveform relaxation method for time domain analysis of large scale integrated circuits theory and apllications. IEEE Trans. Comput. Aided Design Integr. Circ. Systems, 1(3):131-145, 1982.

[20] Lubich Ch., Ostermann A. Multi-grid dynamic iteration for parabolic equations. BIT Numerical Mathematics, 27(2):216–234, 1987.

[21] Vandewalle S., Horton G. Multicomputer-multigrid solution of parabolic partial differential equations. Multigrid Methods IV: Proceedings of the Fourth European Multigrid Conference, Springer Basel AG, Vol. 116, pp. 97-109, 1993.

[22] Gander M.J. Overlapping Schwarz for linear and nonlinear parabolic problems. 9th International Conference on Domain Decomposition Methods, pp. 97–104, 1996.

[23] Franco S.R., Rodrigo C., Gaspar F.J., Pinto M.A.V. A multigrid waveform relaxation method for solving the poroelasticity equations. Computational and Applied Mathematics, 37(4):4805–4820, 2018.

[24] Bellen A., Zennaro M. Parallel algorithms for initial-value problems for difference and differential equations. Journal of Computational and applied mathematics, 25(3):341–350, 1989.

[25] Chartier P., Philippe B. A parallel shooting technique for solving dissipative ODE's. Computing, 51(3-4):209–236, 1993.

[26] Keller H.B. Numerical methods for two-point boundary-value problems. Courier Dover Publications, pp. 397, 1992.

[27] Gander M.J. 50 years of time parallel time integration. Springer International Publishing, 69-113, 2015.

[28] Conte D., D'Ambrosio R., Paternoster B. GPU-acceleration of waveform relaxation methods for large differential systems. Numerical Algorithms, 71(2):293–310, 2016.

[29] Ruprecht D. Wave propagation characteristics of Parareal. Computing and Visualization in Science, 19(1-2):1–17, 2018.

[30] Baccouch M., Temimi H. A high-order space–time ultra-weak discontinuous Galerkin method for the second-order wave equation in one space dimension. Journal of Computational and Applied Mathematics, 389:113331, 2021.

[31] Erbay H.A., Erbay S., Erkip A. A semi-discrete numerical method for convolution-type unidirectional wave equations. Journal of Computational and Applied Mathematics, 387:112496, 2021.

[32] Ong B.W, Mandal B.C. Pipeline implementations of Neumann–Neumann and Dirichlet–Neumann waveform relaxation methods. Springer. Numerical Algorithms, 78(1):1–20, 2018.

[33] Olver P.J. Introduction to partial differential equations. Undergraduate Texts in Mathematics, Springer, pp. 651, 2014.

[34] Thomas J.W. Numerical partial differential equations: finite difference methods. Texts in Applied Mathematics, Vol. 22, Springer Science & Business Media, 2013.

[35] Wesseling P. Introduction to multigrid methods. NASA ICASE, Final Report, 1995.

[36] Brandt A., Livshits I. Multi-level adaptive solutions to boundary-value problems. Mathematics of Computation, 31(138):333-390, 1977.

[37] Brandt A., Livne O.E. Multigrid techniques: 1984 guide with applications to fluid dynamics. SIAM, Classics in Applied Mathematics, Series Number 67, pp. 230, 2011.

[38] Elman H.C., Ernst O.G., O'leary D.P. A multigrid method enhanced by Krylov subspace iteration for discrete Helmholtz equations. SIAM Journal on Scientific Computing, 23(4):1291–1315, 2001.

[39] Trottenberg U., Clees T. Multigrid software for industrial applications-from MG00 to SAMG. 100 Volumes of ‘Notes on Numerical Fluid Mechanics’, Springer, pp. 423–436, 2009.

[40] Rutz G.V., Pinto M.A.V., Gonçalves S.F.T. On the robustness of the multigrid method combining ILU and Partial Weight applied in an orthotropic diffusion problem. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 35(1), 23, 2019.

[41] Anunciação M.A.M., Pinto M.A.V., Neundorf R.L.A. Solution of the Navier-Stokes equations using projection method and preconditioned conjugated gradient with multigrid and ilu solver. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 36(1), 17, 2020.

[42] Laís de Oliveira M., Pinto M.A.V., Gonçalves S.F.T., Rutz G.V. On the robustness of the xy-zebra-gauss-seidel smoother on an anisotropic diffusion problem. Tech Science Press. Computer Modeling in Engineering & Sciences, 117(2):251–270, 2018.

[43] Falgout R.D., Friedhoff S., Kolev T.V., MacLachlan S.P., Schroder J.B., Vandewalle S. Multigrid methods with space–time concurrency. Computing and Visualization in Science, 18(4-5):123–143, 2017.

[44] Liu J., Jiang Y.-J. Waveform relaxation for reaction–diffusion equations. Journal of Computational and Applied Mathematics, 235(17):5040-5055, 2011.

[45] Vandewalle S. Parallel multigrid waveform relaxation for parabolic problems. Teubner Skripten zur Numerik, Springer-Verlag, pp. 247, 2013.

[46] Vandewalle S., Horton G. Fourier mode analysis of the multigrid waveform relaxation and time-parallel multigrid methods. Computing, 54:317-330, 1995.

[47] Crow M.L., Ilic M. The parallel implementation of the waveform relaxation method for transient stability simulations. IEEE Transactions on Power Systems, 5(3):922–932, 1990.

[48] Gong S., Gander M.J., Graham I.G., Lafontaine D., Spence E.A. Convergence of parallel overlapping domain decomposition methods for the Helmholtz equation. Numerical Mathematics, 152:259–306, 2022.

[49] da Silva L.P., Rutyna B.B., Righi A.R.S., Pinto M.A.V. High order of accuracy for Poisson equation obtained by grouping of repeated Richardson extrapolation with fourth order schemes. Computer Modeling in Eengineering & Sciences, 128(2):699–715, 2021.

[50] Briggs W.L., Henson V.E., McCormick S.F. A multigrid tutorial. SIAM, Other Titles in Applied Mathematics, 2nd Edition, pp. 193, 2000.

[51] Thole C.-A., Trottenberg U. Basic smoothing procedures for the multigrid treatment of elliptic 3D operators. Applied Mathematics and Computation, 19(1-4):333–345, 1986.

[52] Horton Gr., Vandewalle S. A space-time multigrid method for parabolic partial differential equations. SIAM Journal on Scientific Computing, 16(4):848–864, 1995.

[53] Bailly C., Juve . Numerical solution of acoustic propagation problems using linearized Euler equations. AIAA Journal, 38(1):22–29, 2000.