Abstract
Removal of the cationic dyes rhodamine B (RhB) and methylene blue (MB) by waste seeds Aleurites moluccana (WAM) was studied in a batch system. The adsorbent was characterized by Fourier transform infrared spectroscopy (FTIR), thermogravimetric analysis (TGA), point of zero charge measurement, and the Boehm titration method. The effects of contact time and pH were investigated for the removal of cationic dyes. An increase in pH from 3 to 9 was accompanied by an approximately three-fold increase in the amount of dye adsorbed. The adsorptions equilibrium values were obtained and analyzed using the Langmuir, Freundlich, Sips, and Redlich–Peterson equations, the Sips isotherm being the one that showed the best correlation with the experimental values. The maximum adsorption capacities of the dyes were 178 mg/g for the MB and 117 mg/g for the RhB. The kinetic sorption was evaluated by the pseudo-first-order, pseudo-second-order, and intraparticle diffusion models, where it was observed that sorption follows the pseudo-second-order kinetic model. The study of thermodynamics showed that the adsorption is a spontaneous and endothermic process. The results indicate that waste seeds of A. moluccana could be used as a low cost material for the removal of cationic dyes from wastewater.
Keywords
Aleurites moluccana; Low cost adsorbent; Cationic dye; Adsorption
1. Introduction
Dyes are organic compounds that represent an important group of pollutants. They are used in various areas, such as the textile, plastics, rubber, leather, cosmetics and paper industries, with highly toxic components and serious environmental impacts. It is believed that the dyeing industry is responsible for releasing 100 tons of dyes per year into the environment, contaminating rivers and springs [1] and [2]. Of these dyestuffs, 5–10% is lost in industrial effluents, and consequently, wastewater treatment is one of the biggest problems we face today [3].
Once the dyes are exposed to water, they are difficult to remove, as they are of synthetic origin and have a very complex molecular structure, with stability designed to withstand degradation by light, chemical, biological and other factors. This makes them very difficult to degrade [4].
There is no universal method capable of removing dye effluents. The best choice depends on the types of dyes to be removed, their composition, concentrations and production flow into the wastewater. Different physical, chemical, and biological methods for the removal of dyes from aqueous solutions have been investigated [3].
Of the removal methods, adsorption is one that is gaining increasing attention due to its potential efficiency, low energy consumption, high selectivity at molecular level, easy operation, and ability to separate various chemical compounds [5] and [6]. Adsorption is a physical–chemical treatment of wastewater in which the dissolved molecule is attached to an adsorbent surface by means of physical and chemical properties. Depending on the nature of the adsorbent and the origin of the dyes, different interactions may be performed, such as electrostatic interaction and Van der Waals forces [3].
In order to meet the growing demand for clean and renewable sources of energy, the production of biodiesel from vegetable oils is growing at a remarkable pace, generating a considerable amount of residual cake composed mainly of cellulose, hemicellulose and lignin. It is estimated that for each ton of seed, about half a ton of cellulose cake is generated. Biodiesel production is increasing every year, the volume of waste generated is becoming a major environmental issue, and the best form of disposal of this byproduct (agro-industrial waste) requires study [7], [8] and [9]. Therefore, one of the main problems to be solved by the biodiesel industry is the adequate disposal of these wastes [10], [11], [12], [13], [14] and [15].
One of the alternative materials for removing effluent waste is seeds of Aleurites moluccana, which have features that enable them to be used as adsorbent. The plant has the advantage of large-scale production of seeds all year round, low cost, and easy access. Thus, the aim of this study was to evaluate the potential application of waste from the seeds of A. moluccana for the removal of methylene blue dye (MB) and Rhodamine B (RhB) from aqueous solution.
The effects were investigated of various parameters on pH, dye concentration and temperature. The kinetics of adsorption and maximum adsorption capacity were also studied, through the application of mathematical models of adsorption.
2. Material and methods
2.1. Adsorbent material
The exocarp of chestnuts and almonds was removed, and ground. The ground material was dried at 80 °C for 2 h. To a round-bottomed flask equipped with heating mantle and reflux condenser, 350 g of previously ground seed and 500 mL of hexane were added. The system was heated under reflux for 24 h to remove the oil. After cooling, the mixture was filtered and washed with hexane and hot water. The residue was dried, crushed and sieved through a 35 mesh sieve.
2.2. Characterization of the adsorbent
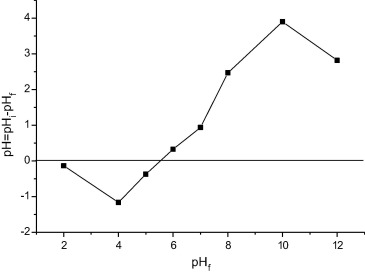
The pHzpc of the waste seeds A. moluccana (WAM) was determined by the method described by Ponnusami et al. [16]: 0.05 g of waste seeds of A. moluccana was added to 20 mL of 0.1 M NaCl. The pH values were adjusted to between 2 and 12, using either 1.0 M HCl or 1.0 M NaOH. The solutions with the WAM were stirred for 24 h. The pH was then recorded. The ΔpH value was calculated by the difference between the initial and final pH values (ΔpH = pHi − pHf) and a plot of ΔpH vs pHf was prepared. The pH zero point charge (pHzpc) was defined as a pH value ΔpH of zero.
The surface chemistry of waste seeds of A. moluccana was characterized by Boehm method, as follows: 0.5 g WAS were dispersed in 50 mL of 0.05 M NaHCO3, 0.025 M Na2CO3, 0.05 M NaOH, 0.05 M HCl, contained in conical flasks of 250 mL capacity and stirred for 24 h. After 24 h, the samples were filtered through filter paper and titrated in triplicate with 0.1 M NaOH or 0.1 M HCl depending on the starting solution used. The number of groups on the surface of WAM was analyzed as follows: NaHCO3 (carboxylic groups), Na2CO3 (carboxylic groups and lactones), NaOH (carboxylic groups, lactones and phenolic groups) and HCl (basic sites) [17].
The method used for determining specific surface area (SSA) of WAM was performed as follows [18]: 0.05 g of WAM was mixed with 20 mL of deionized water. The MB solution (100 mg/L) was then added to the WAM suspension with 0.5 mL increments. The suspension was mixed continually for about 2 h with a shaker. 2 mL of the solution was then removed, and centrifuged. The remnant concentration of MB in the solution was determined.
The value of SSA was derived from the point of complete cation replacement determined on the titration curve. When the curve deviates from the 45° line, this means that the MB added cannot be completely adsorbed by WAM. In other words, all the exchange sites of the adsorbent were covered by the MB molecules. At this optimum point, the SSA is computed from the amount of adsorbed MB, by the following equation:
|
|
(1) |
where mMB = mass of the adsorbed MB (mg/g) at the point of complete adsorption, Av = the Avogadro’s number (6.02 × 1023 mol−1), AMB = area covered by one MB molecule (assumed to be 130 A2), and ms = mass of JB (mg).
The Fourier transform infrared spectra (FTIR) of adsorbents (in the form of KBr pellets) were measured using a IRPrestige-21 Shimadzu, in the range of 700–2000 cm−1.
The TGA analyses were performed on equipment model Netzsch STA 449 F3 Jupiter at a temperature range of 30–500 °C and a heating rate of 10 °C/min, using about 10.0 mg sample in cell alumina with nitrogen gas flow of 50 mL/min.
2.3. Batch adsorption experiment
2.3.1. Influence of pH
The pH effect on dyes adsorption was studied in the range 2–10. Dyes solutions were prepared using buffers tris hydroxymethyl aminomethane (TRIS buffer) (pH 9.0), monochloroacetic acid (pH 3.0) and not buffered (pH 6.0). Amounts of 50 mg of adsorbent were contacted with 20 mL of 300 mg/L congo red (CR) rhodamine B (RhB) and methylene Blue (MB) solutions, respectively, a shaker agitation under constant speed of 250 rpm for 60 min to ensure equilibrium. Afterward, all samples were centrifuged for 10 min at 3500 rpm and the concentration of each dye was calculated from the measured absorbance in the supernatant at their corresponding maximum absorption wavelength (554 nm for RhB, 540 nm for CR and 668 nm for MB). The adsorption capacity (qe) was calculated according to Eq. (2):
|
|
(2) |
where C0 and Ce (mg/L) are the initial and equilibrium dye concentrations in the liquid phase, respectively, v (L) is the volume of solution and m (g) is the amount of adsorbent.
2.3.2. Adsorption isotherm study
Equilibrium adsorption isotherms were obtained by contacting 50 mg of adsorbent with 20 mL of MB or RhB solutions of different initial concentrations (50–300 mg/L), agitation time of 60 min, temperature of 25, 35, 45, 55 °C and pH of 3.0, 6.0 and 9.0. The concentration of the dye in the solution and the adsorption capacity were determined as described above.
2.3.3. Adsorption kinetics
Kinetic experiments were performed by agitating 50 mg of adsorbent with 20 mL of 100 mg/L MB and RhB solutions, individually, at the same constant speed (250 rpm) and at the temperature 55 °C, and pH 9.0 (the pH of the solution was selected as the optimum from the pH effect experiments). Samples were withdrawn at appropriate time intervals (15, 30, 60, 90, 120 and 160 min), and absorbance in the supernatant was measured. The concentration of the dye in the solution and adsorption capacity were determined as described above.
2.4. Error analysis
To assess the adequacy of the equations applied on the experimental data, we used the statistical parameters sum of squared residuals (SSR), Eq. (3):
|
|
(3) |
where, qe,cal and qe,meas are the values of adsorption capacity (mg/g) obtained by applying the model and the experimental values, respectively. The lower the value the better the SSR curve fits the experimental values.
Chi-square (χ2) was also used, to analyze the model, Eq. (2):
|
|
(4) |
where, qe,cal and qe,meas are the values of adsorption capacity (mg/g) obtained by applying the model and the experimental value, respectively. If the data from the model are similar to the experimental data, χ2 will be a small number; if they are different, χ2 will be a large number.
3. Results and discussion
3.1. Characterization of the adsorbent
The pHzpc of solid surface is the pH values at which the amount of acidic and basic functional groups is equal. Fig. 1 shows the plot of ΔpH vs pHf. The pHZPC of the WAM was found to be 5.84, indicating that acidic groups are predominant on the surface of the adsorbents, and below these pH is most suitable for the adsorption of anionic dye. The pHPCZ is slightly below that found in shells of Jatobá, which was pH 6.25 [19] and well below that of waste processing mustard oil, which was pH 9.0 [20], but well above that of waste radish, which was pH 3.4 [14] and Jatropha oil cake which was 5.0 [12]. The specific surface area (SSA) of WAM was found to be 54.56 m2/g. This specific surface area is large when compared with residue of Madhuca indica seeds (28.24 m2/g) [16], powdered activated mustard cake (26 m2/g) [21], pongamia oil cake (0.6 m2/g) [22], and rapeseed oil cake (11.98 m2/g) [23]. However, the SSA is lower when compared with other adsorbents obtained from plants, such as Opuntia ficus-indica fruit waste 348 m2/g [24], waste tea leaves 480.16 m2/g [25], and Moringa oleifera 787.34 m2/g [26].
|
|
|
Figure 1. Determining the point of zero charge. |
The functional groups present on the surface chemistry of WAM were characterized through the Boehm, showing a prevalence of acidic sites, particularly phenol (46.06 mg/g), lactones (1.8 mg/g), and carboxylic acid (9 mg/g) compared with the basic functional group (5.6 mg/g). The higher amount of acid sites shows that the surface is rich in OH groups, which results in greater ability to adsorption cationic dyes [27].
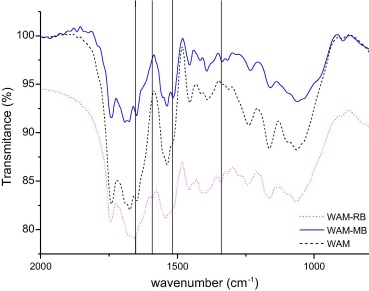
The infrared spectrum of the WAM waste was performed before and after the adsorption process, Fig. 2. The presence of peaks at 1743 cm−1 represented the carbonyl (—C═O) stretching vibration present in WAM. The peaks observed at 1675 cm−1 are of strong stretching vibrations of (—C═O). The bands at 1035 cm−1 (C—O) can be assigned to esters. These peaks are attributed to the carbonyl of the long-chain acids and esters that still remained in the residue after the extraction of oil. A peak at 1450 cm−1 indicates the presence of a (—CH) group. A peak at 1240 cm−1 was assigned to CH═CH stretching, and small peaks ranging from 1100 to 1000 cm−1 were assigned to C(—O stretching [28].
|
|
|
Figure 2. FTIR in the region 2000 cm−1 and 700 cm−1 for waste of seed A. moluccana before and after adsorptions to the dye methylene blue (MB) and rhodamine B (RhB). |
Fig. 2 also shows the FTIR spectra of WAM after RhB or MB adsorption. The spectra show new peaks, which are absent from the spectrum of the WAM Peaks at 1647 cm−1 and 1655 cm−1 corresponding to the stretching vibration of (C═C) bonds, and the peaks found at 1537 cm−1 and 1542 cm−1 confirm the presence of aromatic bonds of (C═C) in both dyes. However, in the spectra after adsorption of both dyes, the peaks of the WAM were predominant, due to the small amount of dye adsorbed.
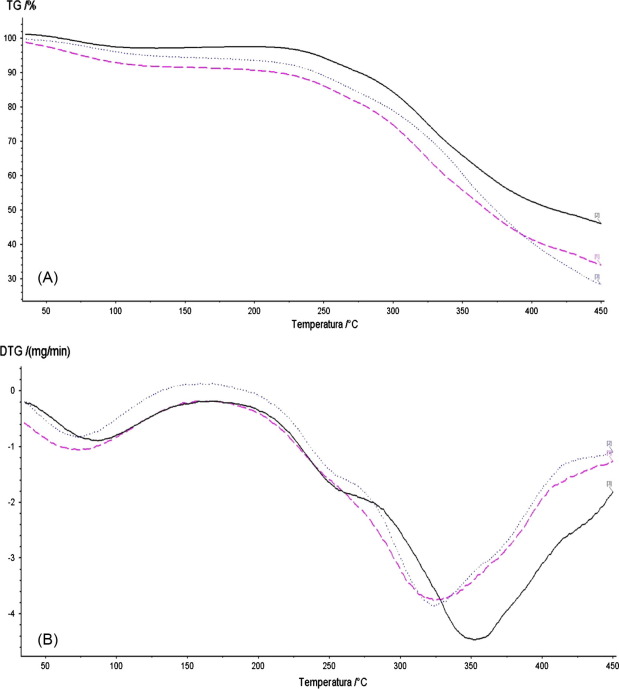
Thermogravimetric analysis (TGA) of the WAM was performed before and after the adsorption process, in order to investigate the thermal characteristics of the adsorbent, and TGA is shown in Fig. 3(A), which shows that at approximately 150 °C, there was a small loss of weight due to elimination of moisture retained in the material. Another mass loss starts at approximately 250 °C, caused by the thermal degradation of cellulose and hemicellulose. At 400 °C it is observed that the WAN before the adsorption process had greater weight loss than compared with the material after the adsorption process, which can be attributed to decomposition of the dye. The final weight loss occurs at about 450 °C, and may be attributed to the degradation of lignin, which has a much higher thermal stability than either cellulose or hemicellulose polymers.
|
|
|
Figure 3. TGA (A) and DTA (B) curves of WAM (___), WAM–RhB (- - -) and WAM–MB (.....) in nitrogen atmosphere, heating rate: 10 °C/min. |
Fig. 3(B) further displays DTG profiles of WAM and dye adsorbed on WAM samples. For WAM combustion presents two peaks centered at 100 °C and 350 °C. For both dyes WAM–RhB and WAM–MB combustion was occurring at lower temperatures with the TG peak centered at 330 °C. Therefore, adsorption of the dyes on WAM introduced functional groups, resulting in reduced stability of WAM.
3.2. Effect of pH
The initial pH is an important factor affecting adsorption. The influence of pH on the adsorption of the dyes MB, RhB was investigated by varying the initial pH of the solutions (3.0, 6.0 and 9.0). Table 1 shows the effect of pH on the adsorption of the dyes.
| pH | 25 °C | 55 °C | |||
|---|---|---|---|---|---|
| CR | MB | RhB | MB | RhB | |
| 3 | 16 | –⁎ | 40 | – | 20 |
| 6 | 12 | 60 | 40 | 47 | 42 |
| 9 | – | 105 | 41 | 106 | 22 |
⁎. (–) The amount of dye adsorbed, for these conditions, was not significant.
The values in Table 1 show an increase in adsorption capacity with increasing pH for the dye MB, while for RhB, this trend was not observed. This behavior could be explained by pHpzc of the material, as well as the molecular nature of the dyes. At pH 3.0 the adsorbed amount of MB was very low (near zero) and may result in decreased negative charge on adsorbent [2]. Thus, when the solution pH was less than the pHpzc of WAM (pH below 5.84), the sorbent surface was likely to have a net positive charge, and therefore cationic dye adsorption was low because of the repulsive forces between the positive surface of the adsorbent and the cationic molecules.
On the other hand, when the solution pH was higher than 5.84, the adsorbent surface was likely to have a net negative charge that favored cationic dye adsorption. This behavior can be observed for the results of the adsorption capacity of anionic dye CR, Table 1, which is well below those for cationic dyes.
The adsorption of cationic dyes is favored when the pH is higher than pHPCZ, due to the presence of functional groups such as —NH2—+ and S+ in the different classes of dyes. The reduction of MB adsorption capacity with decreasing pH was also reported by Vieira et al. [2], employing the residue as adsorbent and Macauba due to the decreased amount of negative charge on the adsorbent.
The results indicate that the main mechanism of adsorption is the electrostatic interaction between the surface of the adsorbent negative and the positive parts of the dye molecule.
Due to the low adsorption capacity of CR, it was not used further in the studies.
3.3. Adsorption isotherm
The adsorption isotherm is the relationship between the amount of dye adsorbed and its concentrations in the equilibrium solution at constant temperature. This experiment enables the maximum adsorption capacity of a given adsorbent to be calculated, depending on the mathematical model applied. We tested four different models, in order to find the most appropriate one: Langmuir, Freundlich, Sips, and Redlich–Peterson.
The experimental isotherms were used as the non-linear Langmuir Eq. (5), valid for monolayer adsorption [29]. This model contains a limited number of sites and provides a homogeneous distribution of adsorption energies.
|
|
(5) |
where qe is the amount of dye adsorbed at equilibrium (mg/g), Ce the dye concentration at equilibrium (mg/L), KL the Langmuir adsorption constant (L/mg), related to adsorption energy, and qm is the maximum adsorption capacity (mg/g).
The Freundlich Eq. (6) can be applied to describe heterogeneous systems, as well as multilayer adsorption [30].
|
|
(6) |
where KF is the Freundlich adsorption constant (L/mg) related to adsorption capacity, and n is the heterogeneity factor that indicates whether the type of isotherm is irreversible (n = 0), favorable (0 < n < 1) or unfavorable (n > 1).
The combination of the Freundlich and Langmuir gave the Sips model Eq. (7)[31].
|
|
(7) |
where KLF is the adsorption constant of Sips (L/mg). At low dye concentrations, this model reduces to the Freundlich isotherm; while at high concentrations, it characterizes a Langmuir type isotherm. When the heterogeneity factor is 1, the model assumes the Langmuir model, and when n > 1, positive cooperativity is assumed, while when 0 < n < 1, negative adsorption cooperativity is expected.
The Redlich–Peterson isotherm Eq. (8) is another mathematical model used to describe adsorption processes [32].
|
|
(8) |
where KRP is the Redlich–Peterson adsorption constant (L/mg) and αRP is the affinity coefficient (L/mg). If the value of n is equal to 1, the Redlich–Peterson isotherm is reduced to the Langmuir and αRPCen where the term is much greater than 1; the model approximates the Freundlich equation.
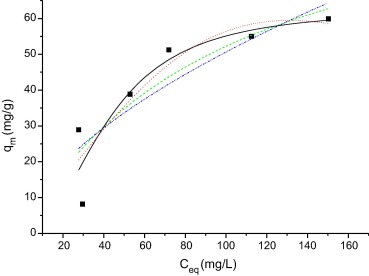
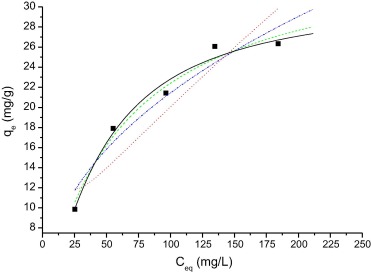
Figure 4 and Figure 5 show the application of different mathematical models for the dyes MB and RB. The parameters obtained for the different mathematical models, different pH and temperature conditions are shown in Table 2, Table 3, Table 4 and Table 5.
|
|
|
Figure 4. Isotherm of adsorption of the MB on WAM. Temperature 25 °C, agitation time 60 min, pH 6.0 and quantity of adsorbent 0.05 g. The lines represent the result of the application of mathematical models: Langmuir (___), Freundlich (.-..-..-), Sips (- - - -), and Redlich–Peterson (……..). |
|
|
|
Figure 5. Isotherm of adsorption of the RhB on WAM. Temperature 25 °C, agitation time 60 min, pH 6.0, quantity of adsorbent 0.05 g. The lines represent the result of the application of mathematical models: Langmuir (___), Freundlich (.-..-..-), Sips (- - - -), and Redlich–Peterson (....). |
| Langmuir | Freundlich | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | KL (mg L−1) | qm (mg g−1) | r2 | SSR | χ2 | KF (mg L−1) | n | r2 | SSR | χ2 |
| pH 9 | ||||||||||
| 25 | 3.8 × 10−3 | 101 | 0.996 | 5 | 3 | 2.8 | 0.4 | 0.962 | 11 | 4 |
| 35 | 3.3 × 10−3 | 94 | 0.971 | 94 | 23 | 0.5 | 0.8 | 0.963 | 23 | 110 |
| 45 | 5.3 × 10−3 | 76 | 0.991 | 11 | 3 | 1.2 | 0.7 | 0.991 | 3 | 12 |
| 55 | 7.3 × 10−3 | 50 | 0.969 | 16 | 5 | 1.2 | 0.6 | 0.963 | 19 | 6 |
| pH 6 | ||||||||||
| 25 | 4.1 × 10−3 | 81 | 0.993 | 8 | 2 | 0.9 | 0.7 | 0.991 | 11 | 3 |
| 35 | 3.1 × 10−3 | 85 | 0.984 | 50 | 10 | 1.0 | 0.7 | 0.967 | 29 | 12 |
| 45 | 5.1 × 10−3 | 99 | 0.974 | 54 | 13 | 1.3 | 0.7 | 0.957 | 89 | 22 |
| 55 | 2.9 × 10−3 | 119 | 0.996 | 6 | 2 | 0.8 | 0.8 | 0.994 | 9 | 2 |
| pH 3 | ||||||||||
| 25 | 5.8 × 10−3 | 57 | 0.932 | 45 | 15 | 0.9 | 0.7 | 0.905 | 61 | 20 |
| 35 | 3.3 × 10−3 | 94 | 0.971 | 14 | 7 | 0.5 | 0.8 | 0.963 | 9 | 9 |
| 45 | 1.7 × 10−2 | 30 | 0.944 | 15 | 7 | 2.8 | 0.4 | 0.901 | 26 | 13 |
| 55 | 1.9 × 10−3 | 64 | 0.993 | 3 | 1 | 0.2 | 0.8 | 0.987 | 0 | 1 |
| Sips | Redlich–Peterson | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | KL (mg L−1) | qm (mg g−1) | n | r2 | SSR | χ2 | KRP (mg L1) | aRP (mg L−1) | n | r2 | SSR | χ2 |
| pH 9 | ||||||||||||
| 25 | 7.4 × 10−4 | 31 | 1.3 | 0.992 | 3 | 1 | 3.0 × 10−2 | −1.2 | −0.1 | 0.903 | 34 | 17 |
| 35 | 1.8 × 10−4 | 58 | 2.1 | 0.989 | 74 | 25 | 1.9 × 10−2 | −1.1 | 0.1 | 0.977 | 16 | 8 |
| 45 | 6.3 × 10−3 | 101 | 0.9 | 0.992 | 11 | 4 | 2.1 × 10−2 | −1.0 | 0.1 | 0.986 | 18 | 10 |
| 55 | 3.1 × 10−3 | 23 | 3.9 | 0.972 | 7 | 4 | 1.8 × 10−2 | −1.1 | 0.1 | 0.954 | 23 | 12 |
| pH 6 | ||||||||||||
| 25 | 4.2 × 10−3 | 82 | 0.9 | 0.993 | 8 | 3 | 1.4 × 10−2 | −1.0 | 7.8 | 0.988 | 14 | 5 |
| 35 | 1.8 × 10−3 | 95 | 1.1 | 0.997 | 6 | 5 | 1.2 × 10−3 | −1.0 | 6.4 | 0.975 | 16 | 6 |
| 45 | 2.0 × 10−4 | 105 | 1.7 | 0.993 | 76 | 25 | 2.8 × 10−1 | −1.1 | 3.7 | 0.995 | 11 | 4 |
| 55 | 2.8 × 10−3 | 145 | 1.0 | 0.996 | 6 | 2 | 8.6 × 10−3 | −1.0 | 5.8 | 0.993 | 10 | 4 |
| pH 3 | ||||||||||||
| 25 | 2.8 × 10−6 | 28 | 3.1 | 0.995 | 10.4 | 3.5 | 2.3 × 10−1 | −1.1 | 5.5 | 0.984 | 10.9 | 5.5 |
| 35 | 1.8 × 10−4 | 34 | 2.1 | 0.989 | 5.4 | 5.4 | 2.1 × 10−3 | −0.9 | 4.2 | 0.962 | 18.7 | 18.7 |
| 45 | 5.2 × 10−4 | 23 | 2.1 | 0.973 | 7.3 | 7.3 | 2.4 × 10−2 | −1.2 | 3.5 | 0.801 | 48.6 | 48.6 |
| 55 | 2.9 × 10−4 | 27 | 1.7 | 0.999 | 0.07 | 0.02 | 1.0 × 10−1 | −1.0 | 3.2 | 0.997 | 1.2 | 0.4 |
| Langmuir | Freundlich | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | KL (mg L−1) | qm (mg g−1) | r2 | SSR | χ2 | KF (mg L−1) | n | r2 | SSR | χ2 |
| pH 9 | ||||||||||
| 25 | 1.2 × 10−3 | 61 | 0.912 | 250 | 72 | 8.5 × 10−2 | 2.6 | 0.937 | 814 | 203 |
| 35 | 4.6 × 10−3 | 42 | 0.965 | 48 | 42 | 1.4 × 10−2 | 2.5 | 0.926 | 881 | 220 |
| 45 | 3.9 × 10−3 | 89 | 0.954 | 96 | 51 | 9.1 × 10−8 | 5.4 | 0.912 | 1022 | 255 |
| 55 | 2.8 × 10−3 | 43 | 0.962 | 101 | 25 | 2.9 × 10−3 | 2.9 | 0.947 | 650 | 162 |
| pH 6 | ||||||||||
| 25 | 9.9 × 10−3 | 105 | 0.900 | 357 | 89 | 3.3 | 0.6 | 0.879 | 428 | 107 |
| 35 | 6.8 × 10−3 | 142 | 0.930 | 196 | 65 | 1.9 | 0.7 | 0.912 | 245 | 82 |
| 45 | 6.9 × 10−3 | 90 | 0.919 | 196 | 49 | 1.9 | 0.6 | 0.885 | 274 | 68 |
| 55 | 2.1 × 10−3 | 178 | 0.953 | 61 | 20 | 0.67 | 0.8 | 0.946 | 69 | 23 |
Table 5.
Isotherm parameters of Sips and Redlich–Peterson for MB adsorption by WAM. Solution volume 20 mL; adsorbent mass 0.05 g, agitation time 60 min.
| Sips | Redlich–Peterson | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | KL-F (mg L−1) | qm (mg g−1) | n | r2 | SSR | χ2 | KRP | aRP | n | r2 | SSR | χ2 |
| pH 9 | ||||||||||||
| 25 | 8.9 × 10−23 | 266 | 13.9 | 0.883 | 787 | 262 | 2.9 | 1.9 × 1045 | −29 | 0.961 | 85 | 256 |
| 35 | 4.6 × 10−14 | 103 | 9.0 | 0.895 | 220 | 241 | 2.7 | 8.9 × 1026 | −18 | 0.991 | 18 | 55 |
| 45 | 2.5 × 10−6 | 153 | 7.8 | 0.951 | 103 | 310 | 3.8 | 2.7 × 1012 | −8.6 | 0.950 | 106 | 319 |
| 55 | 1.7 × 10−15 | 112 | 10.0 | 0.999 | 2 | 5 | 4.2 | 1.0 × 1012 | −1.9 | 0.897 | 649 | 162 |
| 25 | 2.2 × 10−4 | 63 | 2.3 | 0.926 | 267 | 90 | 0.7492 | 2.8 × 10−6 | 2.5 | 0.919 | 290 | 98 |
| 35 | 2.6 × 10−4 | 57 | 3.6 | 0.997 | 9 | 5 | 1.792 | 3.7 × 10−1 | 0.9 | 0.841 | 182 | 546 |
| 45 | 2.2 × 10−4 | 64 | 7.5 | 0.958 | 46 | 139 | 0.4279 | 9.8 × 10−12 | 4.8 | 0.980 | 49 | 16 |
| 55 | 1.1 × 10−7 | 48 | 3.7 | 0.994 | 7 | 4 | 0.3164 | 4.5 × 10−14 | 5.6 | 0.967 | 42 | 21 |
As can be seen, the model that applies to the adsorption of the dyes in the adsorbent MB and RhB is the Sips model, since the values of r2 are close to 1 and for c > 1, indicating a high factor of heterogeneity. The molecular structure of the dyes plays a very important role in their adsorption with WAM. The molecular structure of MB (thiazine) and RhB (xanthene) is flatter, so the adsorption capacity is higher [19].
Nonlinear regression was used to determine the best-fitted model, and two error functions were evaluated: SSR and χ2. The results of its application to the experimental data of adsorption isotherms are presented in Table 2, Table 3, Table 4 and Table 5. By comparing the results of the values of SSR and χ2 for Langmuir, Sips isotherms are smaller than other isotherms for all conditions.
The WAM used in this study had maximum adsorption capacity for the MB 178 mg/g. This value, for example, is above those reported for palm Macauba (57.5 mg/g), a by-product of biodiesel production reported in the literature, in same working conditions and using the same mathematical model of Sips [2]. This value is also higher compared with the adsorption of MB by residues of wild radish, another waste from the process of obtaining biodiesel, where the maximum adsorption capacity is only 19.8 mg/g [33]. The WAM presents adsorption capacity approximately 10 times higher than the cake of sunflower oil (15.80 mg/g), a by-product from the production of sunflower oil [34]. The adsorption capacity of MB by WAM is about five times higher than for solid waste of Madhuca indica oil cake (31.4 mg/g) [26]. Higher adsorption capacities for MB are reported in the literature, for example, Dragon fruit skin (640 mg/g) [35], Breadnut core (369 mg/g) [36], and Breadnut peel (409 mg/g) [37]; but it is important to emphasize that these are not a by-product of biodiesel production like WAM.
The maximum adsorption capacity of RhB by WAM is 105 mg/g almost 70 times higher than that of mustard seed residue 1.52 mg/g using the same conditions and Langmuir model [38]. Meanwhile, Jatoba bark showed adsorption capacity of 54.8 mg/g under the same conditions and mathematical models [19].
Therefore it is possible to confirm the advantage of using WAS when compared with other by-products of obtaining biodiesel.
3.4. Adsorption kinetics
The contact time between the adsorbent and the dye is of significant importance in the treatment of waste water by adsorption. The adsorption kinetics can be studied by adsorption on the basis of constant speed. This adsorption constant is an important factor in the choice of material to be used for adsorption.
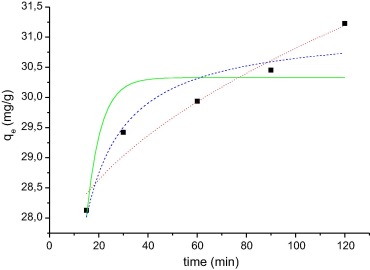
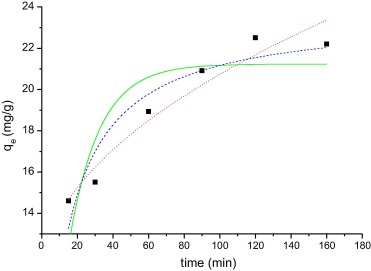
Figure 6 and Figure 7 show the adsorption of RhB and MB on WAM from aqueous solution as a function of contact time. It can be noted from Figure 6 and Figure 7 that the adsorption of both dyes increased as contact time increased. The maximum adsorption of RhB and MB was achieved almost within 120 and 160 min respectively.
|
|
|
Figure 6. Kinetics of adsorption of the RhB at WAM. RB concentration of 100 mg/L, 0.05 g adsorbent mass, temperature 55 °C, and pH 9.0. The lines show the result of mathematical models: pseudo-first order (___), pseudo-second order (- - - -), and intraparticle (…). |
|
|
|
Figure 7. Kinetics curve adsorption of the MB on WAM. MB concentration of 50 mg/L, 0.05 g adsorbent mass, temperature 55 °C, pH 9.0. The lines show the result of application mathematical models: pseudo-first order (__), pseudo second-order (- - -), and intraparticle (…). |
In order to establish an equilibrium time for maximum adsorption, different mathematical models have been used to explain the adsorption kinetics of dyes. In a review of the literature, it was identified that two kinetic models have been widely used to describe the adsorption models, with the model of pseudo first order and pseudo second order obtained under conditions far from equilibrium.
The model of pseudo-first order, also known as Lagergren equation is represented in Eq. (9)[39]:
|
|
(9) |
where qt is the amount of dye adsorbed on the time (t), qe (mg/g) is the value in the state of equilibrium and K1 (min−1) is the adsorption constant of the pseudo-first order.
The model of the pseudo-second order, developed by Ho and McKay, is represented by Eq. (10):
|
|
(10) |
where K2 is the rate constant of pseudo-second order adsorption (mg/g min) [40].
Another model uses intraparticle diffusion, represented in Eq. (11), to identify a possible mechanism of intraparticle diffusion as a limiting step:
|
|
(11) |
where Ki is the intraparticle diffusion constant (mg/g min0.5) and Ci is a constant related to the extent of the boundary layer effect. In this equation it is assumed that the intraparticle diffusion is the rate limiting step in the overall adsorption, and has been used to describe the values obtained on this occasion [41].
The results of the adsorption kinetics were obtained for MB and RhB. The parameters obtained are shown in Table 6. The adsorption kinetic curves are shown in Figure 6 and Figure 7. Usually the best fit can be selected based on the value of the correlation coefficient (r2).
| Pseudo first order | MB | RhB |
|---|---|---|
| qe (mg g−1) | 30.3 | 21.23 |
| K1 (1/min | 0.17 | 0.06 |
| r2 | 0.847 | 0. 866 |
| SSR | 1.5 | 14.4 |
| χ2 | 0.51 | 3.61 |
| Pseudo second order | ||
| qe (mg g−1) | 31.2 | 23.65 |
| K2 (mg g−1 min) | 0.019 | 0.004 |
| r2 | 0.959 | 0.949 |
| SSR | 0.42 | 5.7 |
| χ2 | 0.14 | 1.41 |
| Intraparticle | ||
| C (mg g−1) | 26.9 | 10.81 |
| Ki (mg/g min0.5) | 0.394 | 0.308 |
| r2 | 0.977 | 0.972 |
| SSR | 0.25 | 3.2 |
| χ2 | 0.08 | 0.81 |
Based on the results it can be seen that the adsorption kinetics of RhB and MB can be well explained by the pseudo-second order adsorption model with high r2 (0.949 and 0.959 respectively). Error analysis reveals that the SSR and χ2 are very low for this mathematical model. The intraparticle model also shows a high r2 value and χ2 value and very low SSR, and this model has a high Ci value, which is not considered good for this model, since it should be close to zero. For MB the qe, experimental (31.2 mg/g) is equal to qe calculated (Table 4) for the pseudo-second order model. For RhB, the qe, experimental (22.3 mg/g) and the qe, calculated values (23.68 mg/g) are very close to one another for the pseudo-second order model compared with the value of the pseudo-first order. The r2 are also closer to unity for pseudo-second order kinetics than that for the pseudo-first order kinetics. Usually the model pseudo-second order is the model that best represents the adsorption of cationic dyes. The same behavior was reported for the adsorption of MB by Jatoba bark [19], Mhaduca indica oil cake [28], waste of palm Macauba [2] and in the adsorption of RhB using termite feces [42].
The value of K2 found in this work is close to that reported for adsorption of MB by the waste palm Macaúba 0.055 mg/g min [2]. However, the value found is lower than that observed for the adsorption of MB in Mhaduca indica oil cake (0.760 mg/g min) [28].
3.5. Thermodynamic parameters
The thermodynamic parameters of adsorption, shown in Table 7, including Gibbs free energy (ΔG0), enthalpy (ΔH0) and entropy (ΔS0), were calculated by the following equations [43]:
|
|
(12) |
|
|
(13) |
|
|
(14) |
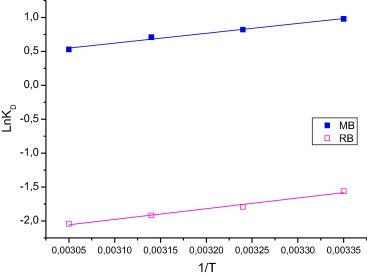
where KD is the equilibrium constant, Cs is the amount of dye adsorbent (mg/g), Ce is the equilibrium concentration of dye in the solution (mg/L), R is the gas constant (8.314 mol/K) and T is the absolute solution temperature (K). The plot of ln KD vs 1/T is linear ( Fig. 8). Values of ΔH0 and ΔS0 were calculated from the slope and intercept respectively (Table 7).
| ΔH0 (kJ mol−1) | ΔS0 (J mol−1) | ΔG0 (kJ mol−1) (T K) | r | |
|---|---|---|---|---|
| RhB | −12.97 | −57.12 | 5.05 (298) | 0.9927 |
| 4.92 (308) | ||||
| 4.73 (318) | ||||
| 4.25 (328) | ||||
| MB | −12.09 | −32.26 | −1.36 (298) | 0.9913 |
| −1.74 (308) | ||||
| −2.17 (318) | ||||
| −2.67 (328) | ||||
|
|
|
Figure 8. Plot of ln KD vs 1/T. |
The negative value of ΔG0 indicates that the MB dye adsorption process is spontaneous and favorable, and that the more negative the value of ΔG0 is, the more energetically favorable the process is. Positive values of ΔG0 for the dye RhB represent an increase in randomness of the system during the adsorption process. The values of ΔH0 were negative for both dyes, indicating that the process is exothermic in nature. The negative values of ΔS0 show the decreased affinity of WAM toward the dyes. In general, adsorption can be ascribed to physical or chemical adsorption. ΔH0 for physical adsorption ranges from −4 to −40 kJ mol−1, compared to that of chemical adsorption ranging from −40 to −800 kJ/mol. The values in Table 7 suggest that dye adsorption on WAM may be due to physical binding.
4. Conclusions
The results obtained show that the seed residue of A. moluccana can be used as a low cost adsorbent for removal of dye methylene blue and rhodamine B. The pH at the point of zero charge, indicating that it was 5.84 in the adsorbent, has the property of adsorption of cationic dyes such as methylene blue and rhodamine B. The adsorption of dyes follows the Sips isotherm model and pseudo second-order kinetics. Based on the results of adsorption capacity, it is concluded that the waste of the WAM may be used as adsorbent, as it showed higher adsorption capacity when compared to other by-products derived from the process for obtaining biodiesel.
Acknowledgments
This work was supported by grants from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) (Project 46-2009, 551107/2010-3).
References
- [1] B. Ramaraju, P.M.K. Reddy, C. Subrahmanyam; Low cost absorbent from agricultural waste for removal of dyes; Environ. Prog. Sustain. Energy, 33 (2014), pp. 38–46
- [2] S.S. Vieira, Z.M. Magriotis, N.A.V. Santos, M.G. Cardoso, A.A. Saczk; Macauba palm (Acrocomia aculeata) cake from biodiesel processing: an efficient and low cost substrate for the adsorption of dye; Chem. Eng. J., 183 (2012), pp. 152–161
- [3] A. Ebrahimi, M. Arami, H. Bahrami, E. Pajootan; Fish Bone as a low-cost adsorbent for dye removal from wastewater: response surface methodology and classical method; Environ. Model. Assess., 18 (2013), pp. 1–10
- [4] M.F. Attallah, I.M. Ahmed, M.M. Hamed; Treatment of industrial wastewater containing congo red and naphthol green B using low-cost adsorbent; Environ. Sci. Pollut. Res., 20 (2013), pp. 1106–1116
- [5] K.G. Akpomie, F.A. Dawodu, K.O. Adebowale; Mechanism on the sorption of heavy metals from binary solution by a low cost montmorillonite and its desorption potential; Alex. Eng. J., 54 (2015), pp. 757–767
- [6] M.T. Yagub, T.K.S. Sen, S. Afroze, H.M. Ang; Dye and its removal from aqueous solution by adsorption: a review; Adv. Colloid Interface Sci., 209 (2014), pp. 172–184
- [7] M.K. Dahri, M.R.R. Kooh, L.B.L. Lim; Application of Casuarina equisetifolia needle for the removal of methylene blue and malachite green dyes from aqueous solution; Alex. Eng. J., 54 (4) (2015), pp. 1253–1263
- [8] S. Saroj, S.V. Singh, D. Mohan; Removal of colour (Direct Blue 199) from carpet industry wastewater using different biosorbents (Maize Cob, Citrus Peel and Rice Husk); Arab. J. Sci. Eng., 40 (2015), pp. 1553–1564
- [9] R. Lafi, A. ben Fradj, A. Hafiane, B.H. Hameed; Coffee waste as potential adsorbent for the removal of basic dyes from aqueous solution; Korean J. Chem. Eng., 31 (2014), pp. 2198–2206
- [10] A.M. Rizzuti, D.J. Lancaster; Utilizing soybean hulls and rice hulls to remove textile dyes from contaminated water; Waste Biomass Valor., 4 (2013), pp. 647–653
- [11] M. Shanmugaprakash, V. Sivakumar, M. Manimaran, J. Aravind; Batch and dynamics modeling of the biosorption of Cr(VI) from aqueous solutions by solid biomass waste from the biodiesel production; Environ. Prog. Sustain. Energy, 33 (2013), pp. 342–351
- [12] M. Shanmugaprakash, V. Sivakumar, M.K.J. Prasana, R. Nandusha; Biosorption of Cr(VI) and Zn(II) ions from aqueous solution onto the solid biodiesel waste residue: mechanistic, kinetic and thermodynamic studies; Environ. Sci. Pollut. Res., 21 (2014), pp. 593–608
- [13] Z.M. Magriotis, M.Z. Carvalho, P.F. de Sales, F.C. Alves, R.F. Resende, A.A. Saczk; Castor bean (Ricinus communis L.) presscake from biodiesel production: An efficient low cost adsorbent for removal of textile dyes; J. Environ. Chem. Eng., 2 (2014), pp. 1731–1740
- [14] Z.M. Magriotis, S.S. Vieira, A.A. Saczk, N.A.V. Santos, N.R. Stradiotto; Removal of dyes by lignocellulose adsorbents originating from biodiesel production; J. Environ. Chem. Eng., 2 (2014), pp. 2199–2210
- [15] S. Muthusamy, S. Venkatachalam, P.M.K. Jeevamani, N. Rajarathinam; Biosorption of Cr(VI) and Zn(II) ions from aqueous solution onto the solid biodiesel waste residue: mechanistic, kinetic and thermodynamic studies; Environ. Sci. Pollut. Res., 21 (2014), pp. 593–608
- [16] V. Ponnusami, V. Gunasekar, S.N. Srivastava; Kinetics of methylene blue removal from aqueous solution using gulmohar (Delonix regia) plant leaf powder: multivariate regression analysis; J. Hazard. Mat., 169 (2009), pp. 119–127
- [17] G.M.S. El Shafei, I.M.A. ElSherbiny, A.S. Darwish, C.A. Philip; Silkworms feces-based activated carbons as cheap adsorbents for removal of cadmium and methylene blue from aqueous solution; Chem. Eng. Res. Design., 30 (2013), pp. 1–10
- [18] Y. Yukselen, A. Kaya; Suitability of the methylene blue test for surface area, cation exchange capacity and swell potential determination of clayey soils; Eng. Geol., 102 (2008), pp. 38–45
- [19] C.A. Demarchi, A. Debrassi, C.A. Rodrigues; The use of Jatobá bark for removal of cationic dyes; Color. Technol., 128 (2012), pp. 1–10
- [20] R.F.L. Ribeiro, V.C. Soares, L. Costa, C.C. Nascentes; Efficient removal of Cd2+ from aqueous solutions using by-product of biodiesel production; J. Hazard. Mat., 237 (2012), pp. 170–179
- [21] K. Singh, R. Bharose, S.K. Verma, V.K. Singh; Potential of powdered activated mustard cake for decolorizing raw sugar; J. Sci. Food Agr., 93 (2013), pp. 157–165
- [22] M. Shanmugaprakash, V. Sivakumar; Batch and fixed-bed column studies for biosorption of Zn(II) ions onto pongamia oil cake (Pongamia pinnata) from biodiesel oil extraction; J. Environ. Manage., 164 (2015), pp. 161–170
- [23] S. Ucar, M. Erdem, T. Tay, S. Karagoz; Removal of lead (II) and nickel (II) ions from aqueous solution using activated carbon prepared from rapeseed oil cake by Na2CO3 activation; Clean Technol. Environ. Policy, 17 (2015), pp. 747–756
- [24] A.A. Peláez-Cid, I. Velázquez-Ugalde, A.M. Herrera-González, J. García-Serrano; Textile dyes removal from aqueous solution using Opuntia ficus-indica fruit waste as adsorbent and its characterization; J. Environ. Manage., 130 (2013), pp. 90–97
- [25] M.K. Mondal; Removal of Pb(II) ions from aqueous solution using activated tea waste: adsorption on a fixed-bed column; J. Environ. Manage., 90 (2009), pp. 3266–3271
- [26] M.H. Kalavathy, R.M. Lima; Moringa oleifera – a solid phase extractant for the removal of copper, nickel and zinc from aqueous solutions; Chem. Eng. J., 158 (2010), pp. 188–199
- [27] M. Farahani, S.R.S. Abdullah, S. Hosseini, S. Shojaeipour, M. Kashisaz; Adsorption-based cationic dye using the carbon active sugarcane bagasse; Procedia Environ. Sci., 10 (2011), pp. 203–208
- [28] R. Gottipati, S. Mishra; Application of biowaste (waste generated in biodiesel plant) as an adsorbent for the removal of hazardous dye methylene blue from aqueous phase; Braz. J. Chem. Eng., 27 (2010), pp. 357–367
- [29] I. Langmuir; The adsorption of gases on plane surfaces of glass, mica and platinum; J. Am. Chem. Soc., 40 (1918), pp. 1361–1403
- [30] H.M.F. Freundlich; Over the adsorption in solution; J. Phys. Chem., 57 (1906), pp. 385–471
- [31] R. Sips; On the structure of a catalyst surface II; J. Chem. Phys., 18 (1950), pp. 1024–1027
- [32] O. Redlich, D.L. Peterson; A useful adsorption isotherm; J. Phys. Chem., 63 (1959), p. 1024
- [33] D.A. Lazaro, C.L. Caldeira, M.S.S. Dantas, M.B. Mansur, L.S. Oliveira, A.S. Franca; Adsorption of methylene blue onto carbons made of residues from the biodiesel industry; Int. J. Sust. Dev. Plan., 7 (2012), pp. 446–456
- [34] S. Karagöz, T. Tay, S. Ucar, M. Erdem; Activated carbons from waste biomass by sulfuric acid activation and their use on methylene blue adsorption; Bioresour. Technol., 99 (2008), pp. 6214–6222
- [35] N. Priyantha, L.B.L. Lim, M.K. Dahri; Dragon fruit skin as potential biosorbent for the removal of methylene blue dye from aqueous solution; Int. Food Res. J., 22 (2015), pp. 2141–2148
- [36] L.B.L. Lim, N. Priyantha, H.I. Chieng, M.K. Khairud Dahri; Artocarpus camansi Blanco (Breadnut) core as low-cost adsorbent for the removal of methylene blue: equilibrium, thermodynamics and kinetics studies; Desalin. Water Treat., 57 (2016), pp. 5673–5685
- [37] L.B.L. Lim, N. Priyantha, D.T.B. Tennakoon, H.I. Chieng, M.K. Dahri, M. Suklueng; Breadnut peel as a highly effective low-cost biosorbent for methylene blue: equilibrium, thermodynamic and kinetic studies; Arab. J. Chem. (2013) http://dx.doi.org/10.1016/j.arabjc.2013.12.018)
- [38] V. Gupta, R. Jain, M.N. Siddiqui, T.A. Saleh, S. Agarwal, S. Malati, D. Pathak; Equilibrium and thermodynamic studies on the adsorption of the dye rhodamine-B onto mustard cake and activated carbon; J. Chem. Eng. Data, 55 (2010), pp. 5225–5229
- [39] Y. Liu, Y.J. Liu; Biosorption isotherms, kinetics and thermodynamics; Sep. Pur. Technol., 61 (2008), pp. 229–242
- [40] Y.S. Ho, G. Mckay; Pseudo-second order model for sorption processes; Process Biochem., 34 (1999), pp. 451–465
- [41] W.J. Weber, J.C. Morris; Kinetics of adsorption on carbon from solution; J. Sanit. Eng. Div., 89 (1963), pp. 31–60
- [42] A. Debrassi, C.A. Rodrigues; Adsorption of cationic dyes from aqueous solution by termite feces, a non-conventional adsorbent; Clean-Soil Air Water, 39 (2011), pp. 549–556
- [43] K.M. Doke, E.M. Khan; Adsorption thermodynamics to clean up wastewater; critical review; Rev. Environ. Sci. Biotechnol., 12 (2012), pp. 1–20
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?