Numerical solution of the equations of motion of multi-story buildings with severe nonlinearities

Resumen

Este artículo presenta un algoritmo para resolver las ecuaciones del movimiento de edificios de varias plantas que incorporan disipadores de energía friccionales como protección sismorresistente. El comportamiento de los disipadores se representa mediante modelos de Coulomb de rozamiento seco; estos introducen no linealidades severas en el comportamiento dinámico de la estructura cada vez que cambian las condiciones de contacto (bloqueo o deslizamiento) en los disipadores. Estas no linealidades complican la resolución de las ecuaciones del movimiento, ya que habitualmente este se describe mediante modelos planos de masas concentradas cuyos grados de libertad son los desplazamientos de las plantas y, al variar las condiciones de bloqueo o de deslizamiento, los grados de libertad deben ser modificados: para condiciones de bloqueo estos son solamente los desplazamientos de las plantas, mientras que para condiciones de deslizamiento han de considerarse, además, los desplazamientos de los disipadores. En artículos previos se ha verificado la exactitud del algoritmo comparándolo satisfactoriamente con resultados experimentales; asimismo, se ha constatado la eficacia computacional del algoritmo comparando ventajosamente los recursos requeridos (en términos de tiempo de cálculo o de asignación de memoria) con los de otros algoritmos. Los objetivos de este artículo son, por un lado, describir en detalle la resolución numérica de las ecuaciones del movimiento y, por otro, presentar ejemplos representativos que confirmen la capacidad del algoritmo para reproducir el comportamiento dinámico de edificios con disipadores y que ilustren de forma preliminar la utilidad de dichos dispositivos para reducir las oscilaciones de la estructura que proteger.

Abstract

This paper presents a new algorithm for solving the equations of motion of multi-storey buildings that incorporate frictional energy dissipators as seismic protection. The behavior of the dissipators is represented by Coulomb dry friction models; they introduce severe nonlinearities in the dynamic behavior of the structure every time that the contact conditions (stick or slip) change in the dissipators. These nonlinearities complicate the resolution of the equations of motion as it usually is described by lumped masses models whose degrees of freedom are the displacements of the floors and, as the stick or slip conditions change, the degrees of freedom must be modified: for blocking conditions they are only the displacements of the storeys while under sliding conditions the displacements of the dissipators have to be also considered. In previous articles the accuracy of the proposed algorithm has been verified by comparison with experimental results; as well, the computational efficiency of the algorithm has been confirmed by comparing the required resources (in terms of computation time and of memory allocation) with those of other algorithms. The objectives of this paper are to describe in detail the numerical solution of the equations of motion and present representative examples confirming the ability of the algorithm to reproduce the dynamic behavior of buildings with friction dissipators and reporting preliminarily about the usefulness of such devices to reduce the oscillations of the structure to be protected.

Palabras clave

Disipadores de energía friccionales ; Estructuras de edificación ; Dinámica de estructuras ; Resolución de las ecuaciones del movimiento ; Sistemas de varios grados de libertad ; Procedimientos paso a paso ; No linealidades severas ; Análisis no lineal

Keywords

Frictional energy dissipators ; Building structures ; Dynamics of structures ; Solution of the equations of motion ; Multi Degree-Of-Freedom systems ; Step-by-step procedures ; Severe nolinealities ; Nonlinear analysis

1. Introducción

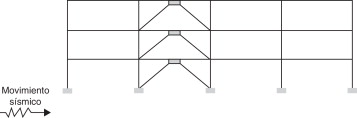
El objetivo básico del proyecto sismorresistente de edificios sometidos a acciones sísmicas intensas es reducir sus oscilaciones horizontales, tanto en términos de desplazamientos relativos (entre plantas o respecto al terreno) como de aceleraciones absolutas; el primer objetivo limita los daños estructurales; el segundo persigue minimizar los daños no estructurales. La estrategia tradicional consiste en dotar a las estructuras de los edificios de la rigidez y resistencia necesarias para que sus movimientos laterales sean suficientemente pequeños. No obstante, esta estrategia no es útil para evitar los daños, ya que la energía aportada por el movimiento del terreno posee un elevado poder destructivo, y lograr que se disipe sin causar daños constituye un objetivo prácticamente inalcanzable por razones económicas; por ello, las normas permiten reducir la resistencia a cambio de que se proporcione capacidad para disipar energía de forma estable mediante deformaciones plásticas, es decir, daño. Una vez constatada la inevitabilidad del daño, el proyecto sismorresistente de edificios se orientó a forzar que este se concentrase en los elementos estructurales menos vitales (en general, las vigas) y así proteger los elementos más importantes (en general, los pilares). Por otra parte, también se procuró que el daño total para acciones sísmicas de gran severidad no generara el colapso del edificio. Esta estrategia es la que proponen la práctica totalidad de normativas sismorresistentes vigentes; no obstante, una actitud más racional sería que, en vez de concentrar el daño en las vigas, se procurase que este se produjese en elementos ajenos a la estructura y dispuestos expresamente para este fin [1]  and [2] . Estos elementos poseen elevada capacidad de disipación de energía y, por no formar parte del mecanismo resistente a acciones gravitatorias, es factible instalarlos de manera que puedan ser fácilmente reemplazados después de ser dañados por movimientos sísmicos fuertes. En otras palabras, los disipadores de energía actúan como fusibles estructurales que protegen la estructura principal logrando que esta permanezca en el dominio elástico (sin daño, pues) y absorbiendo la práctica totalidad de la energía aportada por el sismo. La figura 1 muestra un pórtico de nudos rígidos perteneciente a un edificio de 3 plantas que incorpora disipadores de energía.

Figura 1. Estructura de edificación protegida con disipadores de energía.

El sistema descrito en la figura 1 está concebido para reducir los daños estructurales producidos por las componentes horizontales del movimiento sísmico, es decir, para reducir los desplazamientos relativos entre plantas. Los disipadores están conectados a la estructura principal de forma que cuando en esta se produzcan desplazamientos excesivos entre plantas, se generen en estos deformaciones importantes, disipándose de esta manera energía. En la figura 1 , en cada planta los disipadores están conectados a un sistema rígido de arriostramiento y a la viga de techo de dicha planta; en dicha figura el arriostramiento está formado por barras con configuración en V invertida, pero también podría estar constituido por otros sistemas análogos como muros de hormigón o de obra de fábrica. Ya que una de las recomendaciones más habituales en el proyecto sismorresistente de estructuras es la uniformidad en altura, en la figura 1 los disipadores se sitúan en todas las plantas. Cabe destacar que, en general, se procura que los disipadores de energía aporten amortiguamiento (es decir, capacidad de disipación de energía) al edificio pero, si el período fundamental del edificio se sitúa en la rama descendente del espectro de proyecto, no conviene que incrementen en demasía su rigidez lateral para evitar que las fuerzas sísmicas equivalentes crezcan excesivamente a causa de la reducción de dicho período.

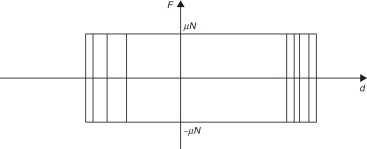
Se han propuesto distintos tipos de disipadores de energía, principalmente los basados en plastificación de metales, en deslizamiento entre superficies rugosas o en el uso de materiales viscosos o viscoelásticos [1] . Este trabajo se centra en el segundo tipo de disipadores, conocidos como friccionales. Se han propuess distintos disipadores de este tipo [1] , [3] , [4] , [5] , [6] , [7]  and [8] , y se diferencian por su complejidad mecánica o por las superficies deslizantes consideradas, pero en prácticamente todos los casos, prescindiendo de la dependencia del coeficiente de rozamiento de la velocidad, el comportamiento histerético se puede representar por modelos de rozamiento seco (de Coulomb) como el representado en la figura 2 .

Figura 2. Lazos de histéresis friccionales.

En la figura 2 , F es la fuerza de rozamiento, d es el deslizamiento en la superficie de fricción, μ es el coeficiente de rozamiento y N es la fuerza transversal que comprime entre sí ambas superficies deslizantes. La figura 1 muestra que el deslizamiento d está vinculado con el desplazamiento entre plantas mediante relaciones cinemáticas directas.

Los disipadores friccionales poseen distintas ventajas significativas:

• Alta capacidad de disipación de energía, tanto por ciclo (para un valor determinado del deslizamiento máximo) como total, estando esta última limitada únicamente por la abrasión de las superficies deslizantes.
• Fuerza de rozamiento fácilmente controlable a través de la presión N entre las superficies deslizantes.
• Ciclos de histéresis estables.

Sin embargo, los disipadores friccionales también presentan algunos puntos oscuros que pueden poner en tela de juicio su utilidad:

• La energía disipada por ciclo (igual al área comprendida en los rectángulos representados en la figura 2 ) es proporcional al deslizamiento d y no a su cuadrado, tal como sucede en los disipadores basados en materiales viscosos o viscoelásticos. Esta circunstancia limita la utilidad de los disipadores friccionales frente a acciones impulsivas y frente a excitaciones cuya frecuencia predominante esté próxima a la fundamental de la estructura, ya que la capacidad de los disipadores friccionales para amortiguar respuestas en resonancia es escasa [9] .
• Debido a los frecuentes cambios bruscos en las condiciones de deslizamiento o de bloqueo en las superficies en contacto, se pueden generar componentes de alta frecuencia en la respuesta. Esto podría ser relevante en la aparición de importantes aceleraciones absolutas de respuesta.
• La durabilidad de los disipadores friccionales es un tema controvertido, debido a la elevada sensibilidad del coeficiente de rozamiento respecto a las condiciones de las superficies deslizantes.

El uso de modelos generales de análisis no lineal de estructuras no resulta aconsejable para describir el comportamiento de edificios con disipadores, ya que la complejidad inherente a estos no está suficientemente aprovechada, al comportarse los disipadores de manera no lineal para proteger la estructura principal (es decir, casi todo el volumen por analizar), que se mantiene en el rango lineal. Por otra parte, se podrían producir errores numéricos relevantes, ya que la matriz de rigidez está mal condicionada por incluir elementos con rigideces muy diferentes, dado que los disipadores coexisten con las barras de la estructura principal, cuyas rigideces son muy superiores. Por otro lado, la figura 2 muestra que el comportamiento dinámico de los disipadores friccionales es altamente no lineal, puesto que cada vez que se invierte el sentido del movimiento la fuerza de rozamiento cambia bruscamente desde μ  N a −μ  N ; en consecuencia, la resolución numérica de las ecuaciones del movimiento es una operación complicada. Se han propuesto modelos ad hoc, como el considerado en el programa ADINA [10] . En este programa las ecuaciones del movimiento se resuelven mediante métodos de penalización, y en otros programas se utilizan multiplicadores de Lagrange; en cualquier caso estos métodos, aun siendo bastante precisos, son costosos en tiempo de cálculo por requerir un número excesivo de grados de libertad. Otros programas describen el rozamiento mediante modelos histeréticos bilineales equivalentes (propios de disipadores histeréticos); de hecho, esta formulación fue utilizada previamente por uno de los autores [11] . De esta manera se pueden obtener resultados básicamente correctos, pero existen importantes discrepancias derivadas de las diferencias entre los correspondientes lazos de histéresis; estos aspectos se describen en mayor profundidad en las referencias [12]  and [13] , donde se concluye que los resultados obtenidos a partir de modelos bilineales [14] son básicamente correctos en términos de desplazamientos y aceleraciones, pero no tanto en términos de energía disipada.

Esta relativa carencia de modelos numéricos capaces de reproducir con suficiente fiabilidad el comportamiento estructural de edificios con disipadores friccionales hace que queden aún demasiados interrogantes acerca de la utilidad de estos dispositivos para reducir la respuesta sísmica de edificios; entre los temas controvertidos puede citarse la introducción de altas frecuencias en la respuesta [7] y el comportamiento para movimientos sísmicos impulsivos (generados por mecanismos de proximidad de falla) [8] .

El objetivo de este trabajo es presentar un nuevo algoritmo para resolver las ecuaciones del movimiento de edificios con disipadores de energía friccionales, como los casos descritos en la figura 1 . El modelo propuesto también es capaz de reproducir el comportamiento dinámico de edificios con aisladores de base friccionales (por ejemplo, Friction Pendulum System [FPS] [15] ) u otras situaciones similares.

Este trabajo forma parte de un proyecto de mayor envergadura orientado a investigar la eficiencia de disipadores friccionales para reducir la respuesta sísmica de edificios; este proyecto incluye ensayos, simulación numérica y estudios paramétricos. En las referencias [13] , [16]  and [17] se ha verificado la exactitud del algoritmo propuesto comparando los resultados proporcionados por este con resultados experimentales obtenidos por los autores o disponibles en la literatura técnica. Asimismo, se ha constatado la eficacia computacional del algoritmo comparando ventajosamente los recursos requeridos (en términos de tiempo de cálculo o de asignación de memoria) con los de otros algoritmos. En la referencia [17] se describen los ensayos efectuados por 2 de los autores de este trabajo.

2. Ecuaciones del movimiento

En este apartado se formulan las ecuaciones del movimiento horizontal de un pórtico plano correspondiente a un edificio de varias plantas con disipadores friccionales en cada planta, como los representados en la figura 1 . El número de plantas del edificio se representa mediante N . El comportamiento estructural del pórtico se representa mediante un modelo discreto de masas concentradas en el que la masa se concentra a la altura de cada planta. En ausencia de disipadores se considera un grado de libertad por planta (N ); en presencia de los disipadores friccionales es necesario considerar 2 grados de libertad por planta: uno de ellos es el desplazamiento relativo x_i de cada planta i   respecto a la base, y el otro es el desplazamiento relativo ${\textstyle x_{i}^{'}}$ entre el disipador de la planta i (es decir, el que conecta a las planta i e i  − 1) y la base. En los instantes en que en un disipador no existe deslizamiento (bloqueo), los movimientos de la planta y del disipador son solidarios y se verifica la relación cinemática ${\textstyle {\dot {x}}_{i}^{'}={\dot {x}}_{i}}$ ; en caso contrario (deslizamiento) ambas velocidades son distintas. En consecuencia, el número de grados de libertad cambia continuamente, tomando todos los valores posibles entre N (cuando no existe deslizamiento en ningún disipador) y 2N (cuando existe deslizamiento en todos los disipadores).

A continuación se describe la deducción de las ecuaciones del movimiento del edificio con los disipadores, suponiendo que el comportamiento lateral del pórtico se asimila al de una estructura cuyo comportamiento corresponde a la deformación generada por la fuerza cortante, es decir, considerando que las rigideces a flexión de las vigas son infinitamente superiores a las de los pilares. En dicho caso, las 2N ecuaciones del movimiento (cuando se produce deslizamiento en todos los disipadores) son:

$m_{1}\quad ({\ddot {x}}_{1}+{\ddot {x}}_{g})+c_{1}\quad {\dot {x}}_{1}+$$k_{1}\quad x_{1}-c_{2}\left({\dot {x}}_{2}-\quad {\dot {x}}_{1}\right)-$$k_{2}\left(\quad x_{2}-\quad x_{1}\right)-$ $c_{2}^{'}\left({\dot {x}}_{2}^{'}-\quad {\dot {x}}_{1}\right)-$$k_{2}^{'}\left(x_{2}^{'}-\quad x_{1}\right)=-F_{1}$

( 1)

$m_{1}^{'}\left({\ddot {x}}_{1}^{'}+{\ddot {x}}_{g}\right)+$$c_{1}^{'}\quad {\dot {x}}_{1}^{'}+k_{1}^{'}\quad x_{1}^{'}=$$F_{1}$

( 2)

$m_{2}\left({\ddot {x}}_{2}+{\ddot {x}}_{g}\right)+c_{2}\quad \left({\dot {x}}_{2}-\right.$$\left.\quad {\dot {x}}_{1}\right)+k_{2}\left(x_{2}-\quad x_{1}\right)-$$c_{3}\left({\dot {x}}_{3}-\quad {\dot {x}}_{2}\right)-k_{3}\left(x_{3}-\right.$$\left.\quad x_{2}\right)-$ $c_{3}^{'}\left({\dot {x}}_{3}^{'}-\quad {\dot {x}}_{2}\right)-$$k_{3}^{'}\left(x_{3}^{'}-\quad x_{2}\right)=-F_{2}$

( 3)

$m_{2}^{'}\left({\ddot {x}}_{2}^{'}+{\ddot {x}}_{g}\right)+$$c_{2}^{'}\quad \left({\dot {x}}_{2}^{'}-\quad {\dot {x}}_{1}\right)+$$k_{2}^{'}\left(x_{2}^{'}-\quad x_{1}\right)=F_{2}$

( 4)

$...$

$m_{i}\left({\ddot {x}}_{i}+{\ddot {x}}_{g}\right)+c_{i}\quad \left({\dot {x}}_{i}-\right.$$\left.\quad {\dot {x}}_{i-1}\right)+k_{i}\left(x_{i}-\quad x_{i-1}\right)-$$c_{i+1}\left({\dot {x}}_{i+1}-\quad {\dot {x}}_{i}\right)-$$k_{i+1}\left(x_{i+1}-\quad x_{i}\right)-$ $c_{i+1}^{'}\left({\dot {x}}_{i+1}^{'}-\quad {\dot {x}}_{i}\right)-$$k_{i+1}^{'}\left(x_{i+1}^{'}-\quad x_{i}\right)=$$-F_{i}$

( 5)

$m_{i}^{'}\left({\ddot {x}}_{i}^{'}+{\ddot {x}}_{g}\right)+$$c_{i}^{'}\quad \left({\dot {x}}_{i}^{'}-\quad {\dot {x}}_{i-1}\right)+$$k_{i}^{'}\left(x_{i}^{'}-\quad x_{i-1}\right)=F_{i}$

( 6)

$...$

$m_{N}\quad \left({\ddot {x}}_{N}+{\ddot {x}}_{g}\right)+c_{N}\quad \left({\dot {x}}_{N}-\right.$$\left.\quad {\dot {x}}_{N-1}\right)+k_{N}\quad \left(x_{N}-\right.$$\left.\quad x_{N-1}\right)=-F_{N}$

( 7)

$m_{N}^{'}\quad \left({\ddot {x}}_{N}^{'}+{\ddot {x}}_{g}\right)+$$c_{N}^{'}\quad \left({\dot {x}}_{N}^{'}-\quad {\dot {x}}_{N-1}\right)+$$k_{N}^{'}\quad \left(x_{N}^{'}-\quad x_{N-1}\right)=$$F_{N}$

( 8)

En las relaciones anteriores, ${\textstyle {\ddot {x}}_{g}}$ es la aceleración del terreno (excitación sísmica); m_i , c_i y k_i son, respectivamente, la masa, el amortiguamiento y la rigidez de la planta i   ; y ${\textstyle m_{i}^{'}}$ , ${\textstyle c_{i}^{'}}$ y ${\textstyle k_{i}^{'}}$ son los correspondientes valores para los elementos de arriostramiento a los que se conecta el disipador de la planta i . F_i es la fuerza de interacción (de rozamiento) entre el disipador y la estructura.

Los valores de F_i están limitados por las relaciones que caracterizan el modelo de Coulomb de los disipadores friccionales:

$\left|F_{i}\right|\leq {\mu }_{i}\quad N_{i}$

( 9)

En esta relación, μ_i es el coeficiente de rozamiento del disipador ubicado en la planta i y N_i es la presión entre las correspondientes superficies deslizantes.

Las 2 N ecuaciones del movimiento se pueden descomponer en 2 grupos de N ecuaciones que se refieren a la estructura principal y a los disipadores, respectivamente:

$\left({\begin{array}{cccc}m_{1}&0&&\\0&m_{2}&&\\&&\ddots &\\&&&m_{N}\end{array}}\right)\left({\begin{array}{c}{\ddot {x}}_{1}\\{\ddot {x}}_{2}\\\vdots \\{\ddot {x}}_{N}\end{array}}\right)+\left({\begin{array}{cccc}c_{1}+c_{2}+c_{2}^{'}&-c_{2}&&\\-c_{2}&c_{2}+c_{3}+c_{3}^{'}&\ddots &\\&&\ddots &-c_{N}\\&&-c_{N}&c_{N}\end{array}}\right)\left({\begin{array}{c}{\dot {x}}_{1}\\{\dot {x}}_{2}\\\vdots \\{\dot {x}}_{N}\end{array}}\right)+$ $+\left({\begin{array}{cccc}0&-c_{2}^{'}&&\\0&0&\ddots &\\&&\ddots &-c_{N}^{'}\\&&0&0\end{array}}\right)\left({\begin{array}{c}{\dot {x}}_{1}^{'}\\{\dot {x}}_{2}^{'}\\\vdots \\{\dot {x}}_{N}^{'}\end{array}}\right)+\left({\begin{array}{cccc}k_{1}+k_{2}+k_{2}^{'}&-k_{2}&&\\-k_{2}&k_{2}+k_{3}+k_{3}^{'}&&\\&&\ddots &-k_{N}\\&&-k_{N}&k_{N}\end{array}}\right)\left({\begin{array}{c}x_{1}\\x_{2}\\\vdots \\x_{N}\end{array}}\right)+$ $+\left({\begin{array}{cccc}0&-k_{2}^{'}&&\\0&0&\ddots &\\&&\ddots &-k_{N}^{'}\\&&0&0\end{array}}\right)\left({\begin{array}{c}x_{1}^{'}\\x_{2}^{'}\\\vdots \\x_{N}^{'}\end{array}}\right)=-\left({\begin{array}{cccc}m_{1}&0&&\\0&m_{2}&&\\&&\ddots &\\&&&m_{N}\end{array}}\right)\left({\begin{array}{c}1\\1\\\vdots \\1\end{array}}\right){\ddot {x}}_{g}-\left({\begin{array}{c}F_{1}\\F_{2}\\\vdots \\F_{N}\end{array}}\right)$

( 10)

$\left({\begin{array}{cccc}m_{1}^{'}&0&&\\0&m_{2}^{'}&&\\&&\ddots &\\&&&m_{N}^{'}\end{array}}\right)\left({\begin{array}{c}{\ddot {x}}_{1}^{'}\\{\ddot {x}}_{2}^{'}\\\vdots \\{\ddot {x}}_{N}^{'}\end{array}}\right)+\left({\begin{array}{cccc}0&0&&\\-c_{2}^{'}&0&&\\&\ddots &\ddots &0\\&&-c_{N}^{'}&0\end{array}}\right)\left({\begin{array}{c}{\dot {x}}_{1}\\{\dot {x}}_{2}\\\vdots \\{\dot {x}}_{N}\end{array}}\right)+$ $+\left({\begin{array}{cccc}c_{1}^{'}&0&&\\0&c_{2}^{'}&&\\&&\ddots &\\&&&c_{N}^{'}\end{array}}\right)\left({\begin{array}{c}{\dot {x}}_{1}^{'}\\{\dot {x}}_{2}^{'}\\\vdots \\{\dot {x}}_{N}^{'}\end{array}}\right)+\left({\begin{array}{cccc}0&0&&\\-k_{2}^{'}&0&&\\&\ddots &\ddots &0\\&&-k_{N}^{'}&0\end{array}}\right)\left({\begin{array}{c}x_{1}\\x_{2}\\\vdots \\x_{N}\end{array}}\right)+$ $+\left({\begin{array}{cccc}k_{1}^{'}&0&&\\0&k_{2}^{'}&&\\&&\ddots &\\&&&k_{N}^{'}\end{array}}\right)\left({\begin{array}{c}x_{1}^{'}\\x_{2}^{'}\\\vdots \\x_{N}^{'}\end{array}}\right)=-\left({\begin{array}{cccc}m_{1}^{'}&0&&\\0&m_{2}^{'}&&\\&&\ddots &\\&&&m_{N}^{'}\end{array}}\right)\left({\begin{array}{c}1\\1\\\vdots \\1\end{array}}\right){\ddot {x}}_{g}+\left({\begin{array}{c}F_{1}\\F_{2}\\\vdots \\F_{N}\end{array}}\right)$

( 11)

Los 2 subconjuntos de ecuaciones anteriores se pueden expresar en formato matricial como:

${\boldsymbol {\mbox{M}}}^{ss}\quad {\ddot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{ss}\quad {\dot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{sd}\quad {\dot {\boldsymbol {\mbox{x}}}}^{d}+$${\boldsymbol {\mbox{K}}}^{ss}\quad {\boldsymbol {\mbox{x}}}^{s}+$${\boldsymbol {\mbox{K}}}^{sd}\quad {\boldsymbol {\mbox{x}}}^{d}=$$-{\boldsymbol {\mbox{M}}}^{ss}{\boldsymbol {\quad {\boldsymbol {\mbox{r}}}\quad }}{\ddot {x}}_{g}-$${\boldsymbol {\mbox{F}}}$

( 12)

${\boldsymbol {\mbox{M}}}^{dd}\quad {\ddot {\boldsymbol {\mbox{x}}}}^{d}+$${\left({\boldsymbol {\mbox{C}}}^{sd}\right)}^{T}\quad {\dot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{dd}\quad {\dot {\boldsymbol {\mbox{x}}}}^{d}+$${\left({\boldsymbol {\mbox{K}}}^{sd}\right)}^{T}\quad {\boldsymbol {\mbox{x}}}^{s}+$${\boldsymbol {\mbox{K}}}^{dd}\quad {\boldsymbol {\mbox{x}}}^{d}=$$-{\boldsymbol {\mbox{M}}}^{dd}{\boldsymbol {\quad {\boldsymbol {\mbox{r}}}\quad }}{\ddot {x}}_{g}+$${\boldsymbol {\mbox{F}}}$

( 13)

El vector F contiene las fuerzas de rozamiento y r  = (1, ⋯ , 1)^T es el vector de localización. Los superíndices s y d   se refieren a la estructura y a los disipadores, respectivamente: ${\textstyle {\boldsymbol {\mbox{x}}}^{s}={\left(x_{1},\ldots ,x_{i},\ldots ,x_{N}\right)}^{T}}$ y ${\textstyle {\boldsymbol {\mbox{x}}}^{d}={\left(x_{1}^{'},\ldots ,x_{i}^{'},\ldots ,x_{N}^{'}\right)}^{T}}$ . El segundo grupo de ecuaciones (13) se descompone en 2 subgrupos que se representan con los subíndices sl (deslizamiento) y st (bloqueo); los grados de libertad que corresponden a cada uno de dichos subgrupos varía continuamente según lo hagan las condiciones de deslizamiento o de bloqueo en cada disipador.

En el caso de que no pueda suponerse que las rigideces a flexión de las vigas sean infinitamente superiores a las de los pilares, las matrices de rigidez y de amortiguamiento ya no responderán exactamente al mismo formato que en las relaciones escalares anteriores, pero las ecuaciones del movimiento continuarán pudiendo expresarse como en (12) y (13) .

Las relaciones (12) y (13) describen el movimiento de un edificio con disipadores friccionales sometido a una excitación sísmica, es decir, transmitida por su base; si la excitación procede de fuerzas que actúan sobre cada planta (en caso de ráfagas de viento, por ejemplo) el movimiento se describe mediante:

${\boldsymbol {\mbox{M}}}^{ss}\quad {\ddot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{ss}\quad {\dot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{sd}\quad {\dot {\boldsymbol {\mbox{x}}}}^{d}+$${\boldsymbol {\mbox{K}}}^{ss}\quad {\boldsymbol {\mbox{x}}}^{s}+$${\boldsymbol {\mbox{K}}}^{sd}\quad {\boldsymbol {\mbox{x}}}^{d}=$${\boldsymbol {\mbox{P}}}-{\boldsymbol {\mbox{F}}}$

( 14)

${\boldsymbol {\mbox{M}}}^{dd}\quad {\ddot {\boldsymbol {\mbox{x}}}}^{d}+$${\left({\boldsymbol {\mbox{C}}}^{sd}\right)}^{T}\quad {\dot {\boldsymbol {\mbox{x}}}}^{s}+$${\boldsymbol {\mbox{C}}}^{dd}\quad {\dot {\boldsymbol {\mbox{x}}}}^{d}+$${\left({\boldsymbol {\mbox{K}}}^{sd}\right)}^{T}\quad {\boldsymbol {\mbox{x}}}^{s}+$${\boldsymbol {\mbox{K}}}^{dd}\quad {\boldsymbol {\mbox{x}}}^{d}=$${\boldsymbol {\mbox{F}}}$

( 15)

P es un vector que contiene las N fuerzas que actúan sobre cada planta.

3. Resolución numérica de las ecuaciones del movimiento

3.1. Edificios de una planta

En este subapartado se describe el procedimiento propuesto para resolver las ecuaciones del movimiento de la estructura (12) y de los disipadores (13) para un edificio de una planta, es decir, N  = 1; evidentemente, en este caso solo puede existir un disipador. El algoritmo se aplica a las relaciones (12) y (13) pero puede ser modificado fácilmente para (14) y (15) . El sistema que hay que resolver consta de 2 ecuaciones acopladas y la mayor dificultad radica en que las condiciones de bloqueo o de deslizamiento en el disipador pueden variar continuamente y, por tanto, deben ser verificadas en cada instante de cálculo.

El método propuesto consiste básicamente en un procedimiento paso a paso que puede ser considerado como una modificación del método de la aceleración lineal. En cada instante k  + 1 se obtiene la respuesta a partir de la correspondiente al instante anterior k utilizando un algoritmo iterativo. Este se describe a continuación empezando por el instante inicial y analizando después un instante genérico.

Instante inicial. En el instante inicial los desplazamientos x₀ y ${\textstyle x_{0}^{'}}$ y las velocidades ${\textstyle {\dot {x}}_{0}}$ y ${\textstyle {\dot {x}}_{0}^{'}}$ de la estructura y del disipador se suponen conocidos. Hay 2 posibilidades:

• Si ${\textstyle {\dot {x}}_{0}={\dot {x}}_{0}^{'}}$ existe bloqueo, en consecuencia las relaciones (12) y (13) para N  = 1 pueden ser sumadas, obteniéndose la ecuación del movimiento del conjunto estructura-disipador:

$\left(m+m^{'}\right){\ddot {x}}_{0}+(c+c^{'})\quad {\dot {x}}_{0}+$$k\quad x_{0}+k^{'}x_{0}^{'}=-(m+m^{'})\quad {\ddot {x}}_{g}(0)$

( 16)

La aceleración ${\textstyle {\ddot {x}}_{0}={\ddot {x}}_{0}^{'}}$ se obtiene de esta relación y la fuerza de rozamiento F₀ se determina a partir de (12) o (13) . Si ${\textstyle \left|F_{0}\right|\geq \mu N}$ , F₀ se iguala a μN si F₀ ≥ μN o a −μN si F₀ ≤ −μN . Para el instante siguiente debe considerarse condición de deslizamiento.

• Si ${\textstyle {\dot {x}}_{0}\not ={\dot {x}}_{0}^{'}}$ hay deslizamiento, por tanto la fuerza de rozamiento F₀ en el instante inicial viene dada por:

$F_{0}=sgn\left[{\dot {x}}_{0}-{\dot {x}}_{0}^{'}\right]\mu \quad N$

( 17)

Las aceleraciones de la estructura ${\textstyle {\ddot {x}}_{0}}$ y del disipador ${\textstyle {\ddot {x}}_{0}^{'}}$ se obtienen a partir de las correspondientes ecuaciones del movimiento:

$m{\ddot {x}}_{0}+c{\dot {x}}_{0}+kx_{0}=-m{\ddot {x}}_{g}(0)-$$sgn\left[{\dot {x}}_{0}-{\dot {x}}_{0}^{'}\right]\mu N$

( 18)

$m^{'}{\ddot {x}}_{0}^{'}+c^{'}{\dot {x}}_{0}^{'}+$$k^{'}x_{0}^{'}=-m^{'}{\ddot {x}}_{g}(0)+sgn\left[{\dot {x}}_{0}-\right.$$\left.{\dot {x}}_{0}^{'}\right]\mu N$

( 19)

Instante genérico. En un instante genérico k  + 1 las ecuaciones del movimiento (12) y (13) para N  = 1 se expresan como:

$m{\ddot {x}}_{k+1}+c{\dot {x}}_{k+1}+kx_{k+1}=-m{\ddot {x}}_{g}(k+$$1)-F_{k+1}$

( 20)

$m^{'}{\ddot {x}}_{k+1}^{'}+c^{'}{\dot {x}}_{k+1}^{'}+$$k^{'}x_{k+1}^{'}=-m^{'}{\ddot {x}}_{g}(k+1)+F_{k+1}$

( 21)

• Si en el instante previo k se daban condiciones de bloqueo, se mantienen inicialmente dichas condiciones para el instante actual k  + 1, por tanto ${\textstyle {\dot {x}}_{k+1}={\dot {x}}_{k+1}^{'}}$ , ${\textstyle {\ddot {x}}_{k+1}={\ddot {x}}_{k+1}^{'}}$ , ${\textstyle x_{k+1}-x_{k+1}^{'}=x_{k}-x_{k}^{'}}$ , y el movimiento solidario de la estructura y del disipador puede ser descrito mediante un solo grado de libertad y se rige por la ecuación (16) aplicada al instante actual:

$\left(m+m^{'}\right){\ddot {x}}_{k+1}+(c+c^{'}){\dot {x}}_{k+1}+$$kx_{k+1}+k^{'}x_{k+1}^{'}=-(m+m^{'}){\ddot {x}}_{g}(t_{k+1})$

( 22)

El desplazamiento x_{k +1} y la velocidad ${\textstyle {\dot {x}}_{k+1}}$ se obtienen de la relación (22) utilizando el método de Newmark [18]  and [19] . La fuerza de rozamiento F_{k +1} se calcula a partir de las ecuaciones (20) o (21) . Si ${\textstyle \left|F_{k+1}\right|<\mu N}$ , la condición de bloqueo se mantiene para el instante siguiente k  + 2; si ${\textstyle \left|F_{k+1}\right|\geq \mu N}$ , dicha condición se invierte. En dicho caso, se impone que ${\textstyle \left|F_{k+1}\right|=\mu N}$ y se repite el cálculo.

• Si en el instante previo k se daban condiciones de deslizamiento, se mantiene inicialmente la misma condición para el instante actual k  + 1, es decir, F_{k +1}  = F_k  =sgn${\textstyle \left({\dot {x}}_{k}-{\dot {x}}_{k}^{'}\right)\mu N}$ . En este caso el movimiento de la estructura y de los disipadores se describe mediante las 2 siguientes ecuaciones escalares desacopladas (20) y (21) ; estas se resuelven utilizando el método de Newmark [18]  and [19] . En el caso en que se verifique la desigualdad ${\textstyle \left({\dot {x}}_{k}-{\dot {x}}_{k}^{'}\right)\left({\dot {x}}_{k+1}-\right.}$$\left.{\dot {x}}_{k+1}^{'}\right)>0$ el sentido del deslizamiento relativo entre la estructura y el disipador no cambia y se considera que se mantienen las condiciones de deslizamiento para el instante siguiente k  + 2; en caso contrario, se considera que estas se convierten en condiciones de bloqueo.

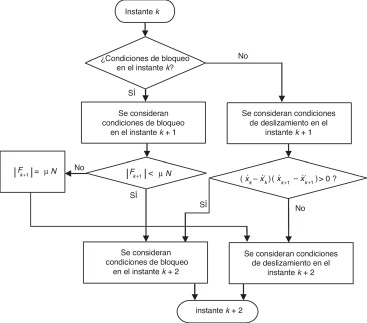
La figura 3 ilustra el diagrama de flujo de la obtención de la respuesta en el instante k  + 1 a partir de la respuesta en el instante k .

Figura 3. Diagrama de flujo del algoritmo propuesto para N  = 1.

3.2. Edificios de varias plantas

Este subapartado describe la principal contribución de este artículo, es decir, la resolución numérica de las ecuaciones (12) y (13) para N  > 1. Las mayores dificultades radican en el acoplamiento entre ambas ecuaciones a través de las matrices C^sd (y ${\textstyle {\left({\boldsymbol {\mbox{C}}}^{sd}\right)}^{T}{\boldsymbol {\quad }}}$ ) y K^sd (y ${\textstyle {\left({\boldsymbol {\mbox{K}}}^{sd}\right)}^{T}{\boldsymbol {\quad }}}$ ) y, sobre todo, en el hecho de que los grados de libertad correspondientes a condiciones de bloqueo y de deslizamiento cambien continuamente. Al igual que en el procedimiento descrito en el subapartado anterior para N  = 1, el algoritmo se aplica a las relaciones (12) y (13) pero puede ser modificado fácilmente para (14) y (15) .

El método propuesto consiste básicamente en una generalización del algoritmo para N  = 1 descrito en el subapartado anterior; en consecuencia, se trata de un procedimiento paso a paso que puede ser considerado como una modificación del método de la aceleración lineal. En cada instante k  + 1 se obtiene la respuesta a partir de la correspondiente al instante anterior k   , utilizando 3 bucles anidados que involucran a las magnitudes que establecen el acoplamiento entre las ecuaciones de la estructura principal y de los disipadores (es decir, ${\textstyle {\dot {\boldsymbol {\mbox{x}}}}^{d}}$ , x^d , ${\textstyle {\dot {\boldsymbol {\mbox{x}}}}^{s}}$ , x^s y F ) y a los valores estimados de las aceleraciones en el instante k  + 1 (${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }}$ y ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }}$ ); la convergencia de los 3 bucles anidados garantiza el cumplimiento de las ecuaciones del movimiento (12) y (13) y de las relaciones constitutivas de los disipadores (9) . En cada instante de cálculo se verifican las condiciones de bloqueo o de deslizamiento en cada planta; en consecuencia, el número de grados de libertad oscila continuamente entre N , cuando todos los disipadores están bloqueados, y 2N , cuando todos los disipadores están deslizando.

Al igual que en algoritmo para N  = 1, en cada instante k  + 1 el proceso iterativo se inicia suponiendo que se mantienen las mismas condiciones de bloqueo o de deslizamiento en cada planta que en el instante anterior k   . Se adoptan inicialmente unos valores supuestos de las aceleraciones en la estructura (${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }}$ para ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ ) y en los disipadores (${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }}$ para ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ y ${\textstyle {}_{st}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }}$ para _stF_{k +1} , donde los subíndices sl y st   se refieren a los disipadores en condiciones de deslizamiento o de bloqueo, respectivamente) y de las fuerzas de interacción en los disipadores que se encuentran en condiciones de deslizamiento (${\textstyle {}_{sl}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }}$ para _slF_{k +1} ). Habitualmente, se parte de los valores para el instante anterior de las aceleraciones en la estructura y de las aceleraciones y las fuerzas en los disipadores que deslizan: ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }=}$${\ddot {\boldsymbol {\mbox{x}}}}_{k}^{s}$ , ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }=}$$_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k}^{d}$ y ${\textstyle {}_{sl}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }=}$$_{sl}{\boldsymbol {\mbox{F}}}_{k}$ ; las aceleraciones en los disipadores bloqueados son obviamente iguales a las de las correspondientes plantas de la estructura, y las fuerzas _stF_i son iguales a sgn${\textstyle \left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)\quad {\mu }_{i}\quad N_{i}}$ . Tal como se indica en el párrafo anterior, el algoritmo propuesto consiste en 3 bucles anidados; en cada uno de ellos se itera con respecto a ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ , _stF_{k +1} y ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ , respectivamente. El criterio de interpolación del método de la aceleración lineal [18] y [19] proporciona los siguientes resultados:

${\boldsymbol {\mbox{x}}}_{k+1}^{s}={\boldsymbol {\mbox{x}}}_{k}^{s}+$$\Delta t\quad {\dot {\boldsymbol {\mbox{x}}}}_{k}^{s}+{\frac {{\left(\Delta t\right)}^{2}}{6}}\left(2\quad {\ddot {\boldsymbol {\mbox{x}}}}_{k}^{s}+\right.$$\left.{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }\right)$

( 23)

${\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}={\dot {\boldsymbol {\mbox{x}}}}_{k}^{s}+$${\frac {\Delta t}{2}}\left({\ddot {\boldsymbol {\mbox{x}}}}_{k}^{s}+\right.$$\left.{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }\right)$

( 24)

${\boldsymbol {\mbox{x}}}_{k+1}^{d}=\quad {\boldsymbol {\mbox{x}}}_{k}^{d}+$$\Delta t\quad {\dot {\boldsymbol {\mbox{x}}}}_{k}^{d}+{\frac {{\left(\Delta t\right)}^{2}}{6}}\left(2\quad {\ddot {\boldsymbol {\mbox{x}}}}_{k}^{d}+\right.$$\left.\quad {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }\right)$

( 25)

${\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}=\quad {\dot {\boldsymbol {\mbox{x}}}}_{k}^{d}+$${\frac {\Delta t}{2}}\left({\ddot {\boldsymbol {\mbox{x}}}}_{k}^{d}+\right.$$\left.\quad {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }\right)$

( 26)

Se describe a continuación la verificación de la condición bloqueo-deslizamiento para el instante k  + 1 en un disipador genérico que ocupe la i -ésima posición (9) . Tal como se ha indicado previamente, como en el algoritmo para N  = 1 se supone inicialmente que se mantiene la misma condición que en el instante anterior k ; en función de cuál fuera dicha condición se sigue una de las 2 estrategias siguientes:

• Si en el instante k   se daban condiciones de bloqueo, el valor calculado ${\textstyle {\left|F_{i}\right|}_{k+1}}$ se compara con μ_i  N_i . Si ${\textstyle {\left|F_{i}\right|}_{k+1}\geq {\mu }_{i}\quad N_{i}}$ , hay deslizamiento y por tanto se impone que ${\textstyle {\left(F_{i}\right)}_{k+1}=}$ sgn${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}\quad {\mu }_{i}\quad N_{i}}$ y se repite el cálculo; por el contrario, si ${\textstyle {\left|F_{i}\right|}_{k+1}<{\mu }_{i}\quad N_{i}}$ hay bloqueo y se tiene que ${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}=}$$0$ .
• Si en el instante k   se daban condiciones de deslizamiento, se calcula la velocidad relativa ${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}}$ entre la planta y el disipador. Si ${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k}\quad {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}>0}$ , se mantienen las mismas condiciones de deslizamiento, ya que esta desigualdad indica que no se ha invertido el sentido del movimiento relativo entre la planta y el disipador; por el contrario, si ${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k}\quad {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}\leq 0}$ se ha invertido el sentido del movimiento relativo y se supone que este se bloquea, con lo que se impone que la velocidad relativa sea nula, es decir, ${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}=}$$0$ . De hecho, en este último caso también podría suceder que el movimiento se hubiese invertido y continuase en dirección contraria; aunque la estrategia considerada no es capaz de detectar esta circunstancia, esto sería percibido en el instante siguiente k  + 2.

Las ecuaciones del movimiento (12) y (13) (para los instantes k y k  + 1), los criterios de interpolación (23) , (24) , (25) y (26) y las condiciones de bloqueo o deslizamiento (9) rigen el movimiento del edificio equipado con los disipadores friccionales. Tal como se ha anunciado previamente, el algoritmo propuesto consiste esencialmente en ejecutar en cada instante 3 cálculos iterativos anidados, es decir, en alcanzar la convergencia de un bucle que se encuentra en el interior de otro y este a su vez está dentro de un tercero. La convergencia de estos 3 procesos garantiza el cumplimiento para el instante k  + 1 de las ecuaciones anteriores, las cuales rigen el problema que se está estudiando; de una forma más precisa, la convergencia del bucle interior garantiza el cumplimiento de las ecuaciones de movimiento de la estructura (12) , la convergencia del bucle intermedio garantiza además el cumplimiento de las ecuaciones de movimiento (13) de los disipadores que se encuentran en condiciones de bloqueo, y la convergencia del bucle exterior asegura el cumplimiento de las ecuaciones de movimiento (13) de los disipadores que se encuentran en condiciones de deslizamiento. Cada uno de estos bucles consiste en obtener magnitudes de la respuesta para el instante k  + 1 a partir de los valores para el instante k ; a continuación se describen las operaciones efectuadas en cada uno de los 3 bucles.

Primer bucle.   Es el bucle interior. Los desplazamientos ${\textstyle {\boldsymbol {\mbox{x}}}_{k+1}^{s}}$ y las velocidades ${\textstyle {\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ de la estructura se obtienen a partir de los criterios de interpolación (23) y (24) suponiendo que ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }=}$${\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}$ (inicialmente ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ se toma igual a ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k}^{s}}$ ). En los disipadores en que no hay deslizamiento, los desplazamientos ${\textstyle {}_{st}{\boldsymbol {\mbox{x}}}_{k+1}^{d}}$ y las velocidades ${\textstyle {}_{st}{\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ son iguales a ${\textstyle {\boldsymbol {\mbox{X}}}kdst+\left({\boldsymbol {\mbox{X}}}k+1sst-\right.}$$\left.{\boldsymbol {\mbox{X}}}ksst\right)$ y a ${\textstyle {}_{st}{\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ , respectivamente. En los disipadores en que hay deslizamiento, los desplazamientos ${\textstyle {}_{sl}{\boldsymbol {\mbox{x}}}_{k+1}^{d}}$ y las velocidades ${\textstyle {}_{sl}{\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ se obtienen de (25) y (26) , respectivamente, tomando ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }=}$$_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k}^{d}$ . A continuación se calcula ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ a partir de (12) (para el instante k  + 1). Si ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}\not =}$${\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }$ (con una determinada tolerancia ɛ_a ) se repite esta operación tomando ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }=}$${\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}$ sin efectuar ningún cambio en las condiciones de bloqueo o de deslizamiento de los disipadores. Una vez se alcanza la convergencia (es decir, ${\textstyle \left\|{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}-\right.}$$\left.{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }\right\|\leq {\varepsilon }_{a}$ ), se interrumpen las iteraciones y se puede garantizar para el instante k  + 1 el cumplimiento de la ecuación (12) que rige el movimiento de la estructura principal.

Segundo bucle. Es el bucle intermedio. En los disipadores que se encuentran en condiciones de deslizamiento las fuerzas de interacción _slF_{k +1} en el instante k  + 1 son conocidas: ${\textstyle {\left(F_{i}\right)}_{k+1}=}$ sgn${\textstyle {\left({\dot {x}}_{i}-{\dot {x}}_{i}^{'}\right)}_{k+1}\quad {\mu }_{i}\quad N_{i}}$ . En los disipadores que se encuentran presumiblemente en condiciones de bloqueo, las fuerzas de interacción _stF_{k +1} en el instante k  + 1 se obtienen a partir de las correspondientes ecuaciones en (13) ; las fuerzas F_i , cuyos valores absolutos exceden a los correspondientes umbrales de deslizamiento μ_i  N_i , son igualadas a dichos umbrales. Todas las fuerzas de interacción de los disipadores en condiciones de bloqueo _stF_{k +1} se comparan con los valores supuestos inicialmente ${\textstyle {}_{st}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }}$ ; si son distintas (con una determinada tolerancia ɛ_f ), los nuevos valores de ${\textstyle {}_{st}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }}$ se igualan a las fuerzas calculadas _stF_{k +1} . A continuación se obtienen nuevos valores de las aceleraciones de la estructura principal ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ a partir de las ecuaciones del movimiento (12) y estas aceleraciones se sustituyen en los criterios de interpolación (23) y (24) para obtener valores actualizados de los desplazamientos ${\textstyle {\boldsymbol {\mbox{x}}}_{k+1}^{s}}$ y de las velocidades ${\textstyle {\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ . Debe recordarse que, ya que los bucles están anidados, es necesario retornar al primer bucle. Este procedimiento se repite hasta que las fuerzas en los disipadores bloqueados sean iguales a los valores supuestos _stF_{k +1}  = ${\textstyle {}_{st}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }}$ (con la tolerancia supuesta, es decir, ${\textstyle \left\|{}_{st}{\boldsymbol {\mbox{F}}}_{k+1}{-}_{st}{\boldsymbol {\mbox{F}}}_{k+1}^{\ast }\right\|\leq {\varepsilon }_{f}}$ ). Una vez se haya alcanzado esta convergencia, se garantiza el cumplimiento de las ecuaciones del movimiento de la estructura (12) y de las ecuaciones del movimiento de los disipadores (13) que se encuentren en condiciones de bloqueo.

Tercer bucle. Es el bucle exterior. Una vez alcanzada en el bucle anterior la convergencia en las fuerzas de interacción en los disipadores en condiciones de bloqueo _stF_{k +1} , las aceleraciones ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ en los disipadores en condiciones de deslizamiento se calculan a partir de las correspondientes ecuaciones del movimiento en (13) . Si ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}{\not =}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }}$ (con una determinada tolerancia ɛ_a ) los valores actuales de ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }}$ se igualan a ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ . A continuación se determinan nuevos valores de los desplazamientos ${\textstyle {}_{sl}{\boldsymbol {\mbox{x}}}_{k+1}^{d}}$ y de las velocidades ${\textstyle {}_{sl}{\dot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}}$ de los disipadores en condiciones de deslizamiento a partir de los criterios de interpolación (23) y (24) , respectivamente; también se obtienen nuevos valores de las aceleraciones de la estructura ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s}}$ a partir de las ecuaciones del movimiento (12) . Estos valores se utilizan como nuevas aproximaciones de las aceleraciones ${\textstyle {\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{s\ast }}$ y en este momento el proceso iterativo debe volver al primer bucle. Este proceso se culmina cuando las aceleraciones de los disipadores en condiciones de deslizamiento convergen: ${\textstyle {}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}=}$$_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }$ (de hecho, ${\textstyle \left\|{}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d}{-}_{sl}{\ddot {\boldsymbol {\mbox{x}}}}_{k+1}^{d\ast }\right\|\leq {\varepsilon }_{a}}$ ). Una vez se logra esta convergencia, se puede garantizar el cumplimiento de las ecuaciones del movimiento de la estructura (12) y de los disipadores (13) , tanto los que se encuentran en condiciones de deslizamiento como de bloqueo. En consecuencia, se satisfacen todas las condiciones requeridas para el instante k  + 1.

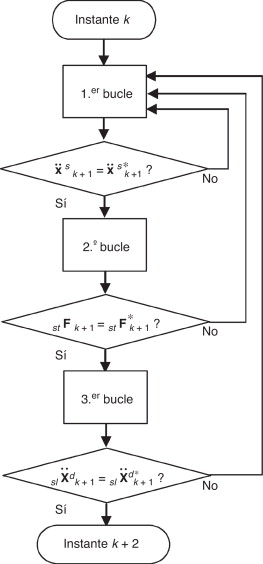
La figura 4 ilustra el diagrama de flujo de los 3 bucles anidados utilizados para la obtención de la respuesta en el instante k  + 1 a partir de la respuesta en el instante k .

Figura 4. Diagrama de flujo del algoritmo propuesto para N  > 1.

En cualquier algoritmo no lineal la estabilidad no puede ser demostrada de forma teórica; por otra parte, la estabilidad en el rango linealizado no garantiza la estabilidad en el rango completo. En consecuencia, el valor del incremento de tiempo Δt (período de discretización temporal) se establece a partir de un proceso de prueba-error buscando la precisión deseada e intentando evitar inestabilidades numéricas. Las tolerancias ɛ_a y ɛ_f se seleccionan para obtener el grado buscado de exactitud con un número razonable de iteraciones. En la mayor parte de los casos se adoptó Δt  = T_F /200, ${\textstyle {\varepsilon }_{a}={\left|{\ddot {x}}_{g}\right|}_{max}\quad /\quad {10}^{5}}$ y ɛ_f  = μN /10⁵ , donde T_F es el período fundamental del pórtico desnudo, es decir, en ausencia de disipadores. La elección de un incremento de tiempo tan limitado reduce la necesidad de verificar las condiciones de bloqueo y de deslizamiento en el interior de dicho intervalo. Al final del siguiente apartado se muestra, en un ejemplo de un edificio de varias plantas, la eficacia computacional de este algoritmo en comparación con otros propuestos previamente.

4. Ejemplos

4.1. Ejemplos en un edificio de una planta

Este subapartado presenta algunos resultados del algoritmo propuesto para N  = 1.

Se considera un edificio de una planta en que el disipador se sitúa como en los casos representados en la figura 1 . Los parámetros de masa, amortiguamiento y rigidez de la estructura principal son m  = 5.740, 39 kg, c  = 13.121, 77 N ·s / m y k  = 2.999, 47 kN / m, respectivamente; la frecuencia natural del pórtico desnudo es ω₀  = 22, 86 rad/s y el factor de amortiguamiento modal es ζ  = 0, 05. Los correspondientes parámetros del sistema de arriostramiento son m ′ = 19, 61 kg, c ′ = 0 (ζ ′ = 0) y k ′ = 2.597, 01 kN / m. El umbral de deslizamiento es μ  N  = 39.325 kN. En los análisis, el período de discretización temporal adoptado es Δt  = 0, 00115 s.

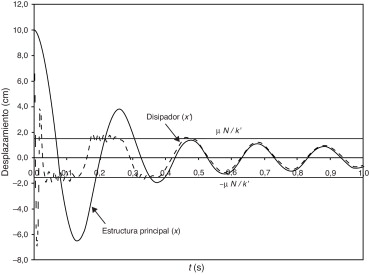
La figura 5 muestra la respuesta de la estructura (x , trazo grueso) y del disipador (x   ′, trazo fino) a un desplazamiento inicial impuesto a ambos: ${\textstyle x_{0}=x_{0}^{'}=10}$  cm. En la figura 5 las 2 líneas horizontales corresponden a los umbrales del desplazamiento x ′ del disipador μ  N /k ′ y −μ  N /k ′, respectivamente; las oscilaciones en torno a estas líneas se deben a que cada vez que x ′ intenta excederlas se produce deslizamiento y se generan vibraciones debidas a las fuerzas de inercia asociadas a la masa m ′. La figura 5 muestra que inicialmente la respuesta de la estructura principal se amortigua con bastante rapidez debido al efecto del disipador, pero una vez cesa el deslizamiento (al cabo de t  = 0,48 s, aproximadamente) este efecto desaparece y los movimientos del disipador y de la estructura se convierten en solidarios (${\textstyle {\dot {x}}={\dot {x}}^{'}}$ ).

Figura 5. Respuesta de un edificio de una planta a un desplazamiento inicial impuesto.

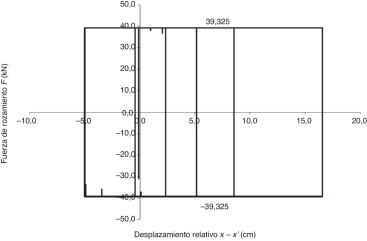
La figura 6 representa el comportamiento histerético del disipador para las oscilaciones libres consideradas en la figura 5 .

Figura 6. Lazos de histéresis del disipador del edificio de una planta para un desplazamiento impuesto.

En términos globales, las figuras 5 y 6 confirman la capacidad del algoritmo para reproducir el comportamiento dinámico libre, es decir, en ausencia de excitación, de un edificio de una planta con un disipador friccional; por otra parte, tal como se ha comentado previamente, en la figura 5 se aprecia que el disipador genera inicialmente un importante incremento del amortiguamiento, pero una vez cesa el deslizamiento este aumenta meramente la rigidez de la estructura.

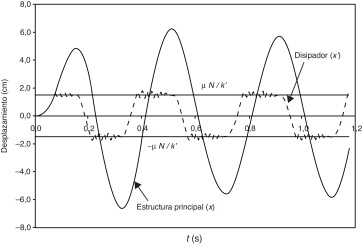
La figura 7 representa la respuesta de la estructura principal y del disipador a una fuerza armónica de excitación P   que actúa sobre el pórtico: ${\textstyle P\left(t\right)=P_{0}sin\Omega t}$ ; la amplitud P₀ de esta excitación es 127, 491 kN y su frecuencia Ω es 15, 98 rad/s. De forma análoga a la figura 5 las 2 líneas horizontales corresponden a los umbrales μ  N /k ′ y −μ  N /k ′ de x ′; las oscilaciones en torno a estas líneas deben interpretarse como en dicha figura. Los tramos en que el desplazamiento del disipador (x   ′) oscila en torno a los umbrales corresponden a condiciones de deslizamiento; en el resto de los instantes se dan condiciones de bloqueo y los movimientos de la estructura y del disipador son paralelos, es decir, ${\textstyle {\dot {x}}={\dot {x}}^{'}}$ .

Figura 7. Respuesta de un edificio de una planta a una fuerza de excitación armónica.

La figura 7 confirma la capacidad del modelo propuesto para reproducir el comportamiento dinámico forzado, es decir, en presencia de una excitación continuada.

La amplitud de la respuesta permanente de la estructura sin disipador a la excitación armónica considerada sería

$x={\frac {P_{0}}{k}}{\frac {1}{\sqrt {{\left(1-{\left({\frac {\Omega }{{\omega }_{0}}}\right)}^{2}\right)}^{2}+{\left(2\quad \zeta \quad {\frac {\Omega }{{\omega }_{0}}}\right)}^{2}}}}=$${\frac {127491}{2999470}}{\frac {1}{\sqrt {{\left(1-{\left({\frac {15,98}{22,86}}\right)}^{2}\right)}^{2}+{\left(2\times 0,05\quad {\frac {15,98}{22,86}}\right)}^{2}}}}=$$8,24\quad cm$

La comparación entre esta amplitud y la mostrada en la figura 7 señala la capacidad del disipador para reducir la respuesta dinámica de la estructura a una excitación continuada.

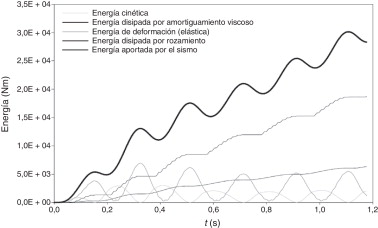
La figura 8 representa la evolución temporal del balance de energía de la estructura sometida a la excitación armónica. La energía aportada por la excitación se descompone en energía cinética y elástica (ambos términos tienden a desaparecer una vez concluida la excitación), en energía disipada por el amortiguamiento ordinario de la estructura y en energía absorbida por los disipadores friccionales. La figura 8 muestra que la mayor parte de la energía se absorbe en los disipadores; no obstante, la relativamente modesta reducción de la amplitud máxima (8, 24 cm frente a 6, 30 cm, fig. 7 ) señala la limitada utilidad de los mecanismos de fricción, debida probablemente a que el área abarcada por los lazos de histéresis crece de forma solo lineal con la amplitud (fig. 2 ), tal como se discute con mayor extensión en la referencia [17] .

Figura 8. Disipación de energía en un edificio de una planta sometido a una fuerza de excitación armónica.

La figura 9 muestra la respuesta dinámica del edificio de una planta considerado a la componente 90^o del registro de Santa Mónica del terremoto de Northridge (17 de enero de 1994) cuyas ordenadas han sido escaladas mediante un factor igual a 5 [13] ; las 2 curvas representadas corresponden a las respuestas en ausencia y en presencia de disipadores, respectivamente. En este caso el umbral de deslizamiento es μN  = 78, 456 kN y en los análisis numéricos el período de discretización temporal considerado es Δt  = 0, 00125 s. La figura 9 confirma la capacidad del modelo para reproducir el comportamiento dinámico de edificios de una planta con disipadores friccionales y la utilidad de estos para reducir la respuesta del edificio frente a acciones sísmicas.

Figura 9. Respuesta, en presencia y en ausencia de disipadores, de un edificio de una planta sometido a una acción sísmica.

4.2. Ejemplos en un edificio de varias plantas

Este subapartado presenta algunos resultados del algoritmo propuesto para N  > 1.

Se considera un edificio de 3 plantas en el que los disipadores se sitúan como en el caso representado en la figura 1 . Esta estructura ha sido propuesta [20] para constituir una referencia comparativa (benchmark) para cualquier sistema de reducción de vibraciones de estructuras de edificación. Los umbrales de deslizamiento para los 3 disipadores son, respectivamente, μ₁N₁  = 834,10 kN, μ₂N₂  = 740, 83 kN y μ₃N₃  = 43, 51 kN; el resto de las características de la estructura está descrito en la referencia [13] . El incremento de tiempo considerado es Δt  = 0, 00125 s, el tiempo de cálculo es 10 s y las tolerancias son ɛ_a  = 0, 01 cm/s² y ɛ_f  = 1 N.

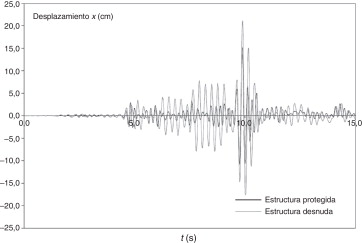
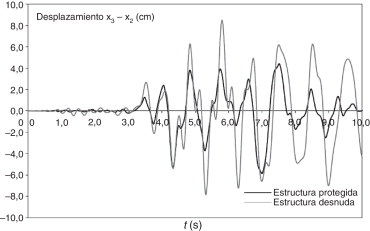
La figura 10 representa las respuestas del edificio, en términos del desplazamiento entre la tercera y la segunda planta, en presencia y en ausencia de disipadores, respectivamente. La excitación es la componente 90° del registro de Santa Mónica del terremoto de Northridge (17 de enero de 1994). La respuesta con disipadores es significativamente inferior a la de la estructura sin este tipo de protección. No obstante, en torno al instante t  = 7 s, se observa que la reducción de la respuesta es escasa; este fenómeno parece deberse a la presencia de un fuerte impulso en la excitación para el que la eficacia del amortiguamiento es limitada.

Figura 10. Desplazamiento entre las plantas tercera y segunda del edificio de referencia.

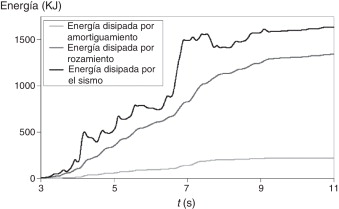
La figura 11 muestra la historia temporal de la energía aportada por la acción sísmica y las energías disipadas por el amortiguamiento de la estructura y por los deslizamientos en los disipadores; se aprecia que la mayor parte de la energía se absorbe mediante los disipadores.

Figura 11. Balance de energía para el edificio de referencia.

Las figuras 10 y 11 confirman tanto la capacidad del algoritmo propuesto para reproducir la respuesta sísmica de edificios de varias plantas que incorporan disipadores de energía friccionales como la utilidad de estos dispositivos para reducir dicha respuesta.

Para este ejemplo, se ha llevado a cabo una comparación entre el coste computacional del algoritmo propuesto y del programa comercial ADINA [10] . En casi todos los casos se han encontrado diferencias significativas mostrando que ALMA es más rápido y requiere menos asignación de memoria. Las principales características del ordenador utilizado en esta prueba son: procesador Pentium II a 233 MHz y 96 MB de RAM; con el fin de obtener resultados comparables se procuró que ningún otro programa se ejecutase al mismo tiempo. Para ambos programas, los períodos de discretización se han elegido como los menores que son capaces de proporcionar estabilidad y precisión. Para ADINA el tiempo de CPU fue de 15 minutos y se requirieron 500 MB de memoria, mientras que para ALMA el tiempo de CPU fue de 3 minutos 20 segundos y no hubo necesidad de asignación significativa de memoria.

5. Conclusiones e investigaciones futuras

Este trabajo presenta un modelo numérico del comportamiento dinámico horizontal de pórticos planos de varias plantas que incorporan disipadores friccionales como sistema de protección sismorresistente. Con pequeñas modificaciones el modelo propuesto puede describir también edificios sometidos a ráfagas de viento o apoyados sobre aisladores friccionales. El algoritmo es un método de integración paso a paso de las ecuaciones del movimiento y consiste básicamente en una modificación del método de aceleración lineal; la principal aportación radica en la comprobación en cada instante discreto de cálculo de las condiciones de deslizamiento o de bloqueo en los disipadores de fricción. De esta manera el número de grados de libertad oscila continuamente entre uno por planta cuando se dan condiciones de bloqueo en todos los disipadores, o 2 por planta cuando se dan condiciones de deslizamiento en todos los disipadores. En trabajos previos se constató la exactitud, la fiabilidad y la economía del algoritmo propuesto mediante simulación numérica y comparación con resultados experimentales; los objetivos de este artículo son describir en mayor profundidad la estrategia numérica propuesta, confirmar su capacidad para simular el comportamiento dinámico de edificios con disipadores y verificar, de forma preliminar, que los disipadores friccionales reducen las oscilaciones de la estructura por proteger. En la actualidad se está llevando a cabo un estudio sistemático y general de esta utilidad.

Agradecimientos

Este trabajo ha sido financiado por el gobierno de España, proyectos CGL2008-00869/BTE, CGL2011-23621, BIA2008-00050 y BIA2011-26816, y por la Unión Europea (fondos Feder).

References

1. [1] T.T. Soong, G.F. Dargush; Passive Energy Dissipation Systems in Structural Engineering; John Wiley & Sons (1997)
2. [2] R. Hanson, I. Aiken, D. Nims, P. Richter, R. Bachman; State of the Art of the Practice in Seismic Energy Dissipation; Proc. ATC 17-1 on Seismic Isolation, Energy Dissipation, and Active Control (1993) 2:449-471
3. [3] S. Vezina, P. Proulx, R. Pall, A. Pall; Friction-Dampers for Aseismic Design of Canadian Space Agency; 10th World Conference on Earthquake Engineering, Madrid (1992), pp. 4123–4128
4. [4] S. Cherry, A. Filiatrault; Seismic response Control of Buildings Using Friction Dampers; Earthquake Spectra, 9 (3) (1993), pp. 447–466
5. [5] D.K. Nims, P.J. Richter, R.E. Bachman; The Use of the Energy Dissipating Restraint for Seismic Hazard Mitigation; Earthquake Spectra, 9 (3) (1993), pp. 467–490
6. [6] C.E. Grigorian, T.S. Yang, E.P. Popov; Slotted Bolted Connection Energy Dissipators; Earthquake Spectra, 9 (3) (1993), pp. 491–504
7. [7] G.W. Housner, L.A. Bergman, T.K. Caughey, A.G. Chassiakos, R.O. Claus, S.F. Masri, et al.; Structural Control: Past, Present and Future. Journal of Engineering Mechanics; ASCE, 123 (2) (1997), pp. 897–971
8. [8] P.J. Richter, D.K. Nims, J.M. Kelly, R.M. Kallembach; The EDR.- Energy Dissipating Restraint. A New Device for Mitigation of Seismic Effects; Proceedings of the 1990 SEAOC Convention (1990) 1:377-L 40
9. [9] J.M. Kelly; Earthquake-Resistant Design with Rubber; Springer-Verlag (1993)
10. [10] K.J. Bathe; Finite Element Procedures in Engineering Analysis; Prentice-Hall (1982)
11. [11] D. Foti, L.M. Bozzo, F. López Almansa; Numerical Efficiency Assessment of Energy Dissipators for Seismic Protection of Buildings; Earthquake Engineering & Structural Dynamics, 27 (1998), pp. 543–556
12. [12] S.T. De la Cruz, F. López Almansa, L.M. Bozzo, L.G. Pujades; Dynamic equivalence between a SDOF bi-linear structure and a SDOF structure equipped with an energy dissipation device of friction.; Third World Conference on Structural Control, Como (Italy) (2002)
13. [13] De la Cruz ST. Contribution to the Assessment of the Efficiency of Friction Dissipators for Seismic Protection of Buildings. PhD Thesis. Technical University of Catalonia, Barcelona, 2003.
14. [14] Charney FA. Nonlinear Dynamic Time History Analysis of Single Degree of Freedom Systems (NONLIN). Federal Emergency Management Agency (FEMA) [consultado Oct 2013]. Disponible en: https://nees.org/resources/nonlin , 1996.
15. [15] A. Mokha, M.C. Constantinou, A.M. Reinhorn, V. Zayas; Experimental study of friction-pendulum isolation system; Journal of Structural Engineering, 117 (4) (1991), pp. 1201–1217
16. [16] S.T. De la Cruz, F. López Almansa, S. Oller; Numerical Simulation of the Dynamic Behavior of Building Structures Equipped with Friction Energy Dissipators; Computers & Structures Journal, 85 (1-2) (2007), pp. 30–42
17. [17] F. López Almansa, S.T. de la Cruz, C. Taylor; Tests about Friction Energy Dissipators for Seismic Protection of Building Structures; Earthquake Engineering and Engineering Vibration, 10 (3) (2011), pp. 1–12
18. [18] G. Berg; Elements of Structural Dynamics; Prentice-Hall (1989)
19. [19] R. Clough, J. Penzien; Dynamics of Structures; McGraw-Hill (1992)
20. [20] Ohtori Y, Christenson R, Spencer B, Dyke S. Benchmark Control Problems for Seismically Excited Nonlinear Buildings. Journal of Engineering Mechanics 130, Special issue: benchmark structural control problem, 366-385 2004.