Dynamic modeling of a small open Joule cycle reciprocating Ericsson engine: simulation results

Abstract

Externally heated Joule cycle reciprocating engines, also known as Ericsson engines, are particularly suitable for small-scale solar energy conversion and microcogeneration using biomass or gas effluents at high temperatures. These types of engine have been developed in the context of the current issue of climate change, combined with a progressive depletion of fossil fuels. A dynamic model of a 1.67 kW small open Joule cycle engine has been developed in order to study operational stability and behavioral control, especially during transient phases. Models are implemented on a Matlab/Simulink platform where simulations of the dynamics of engine start-up and steady conditions are carried out. The optimal settings of valves and the key engine parameters have also been determined. Simulation results reveal a rapid transient phase. Hot starting is achieved in about 5.3 sec and the system is stabilized, with a thermal efficiency of approximately 29%. The system responds well when subjected to selected perturbations.

Introduction

In the context of the progressive depletion of fossil energy resources development of the reciprocating Joule cycle heat engine has regained renewed interest, particularly in the field of microcogeneration. The Ericsson engine seems to have notable assets compared to the internal combustion engine.[1] It is compatible with any type of energy source and fulfills the environmental requirements which constitute one of the major challenges in energy generation with thermal energy conversion systems. These advantages provide an alternative to existing systems, within a range of applications such as micro-combined heat and power (CHP) in residential areas; valorization of biomass in remote sites for electricity generation; or thermodynamic valorization of solar energy.

For CHP purposes, gas turbines generally produce electricity ranging from 1 to 30 MW; microturbines on the other hand produce power levels up to 30 kW. A study [2] of the impact of size on performance of a microturbine with heat supply suggests that the efficiency of this kind of machine is markedly reduced at low power: it is estimated at 22.5% for a 5 kW installation, whereas it is about 27% for a typical 30 kW machine. The development of such microturbines (1–5 kW) capable of meeting the needs of domestic CHP, for example, seems to be difficult (for example, with issues such as leakage, low efficiencies, cost.). In this power range, the reciprocating internal combustion engine operation is expensive (especially maintenance) and noisy. The Joule cycle reciprocating Ericsson engine seems to be more suitable for thermal energy conversion in lower power ranges [3].

In the existing literature, studies have reported theoretical developments of the reciprocating Joule cycle engines on aspects such as thermodynamic optimization, design, and performance, in view of their implementation in the cogeneration sector. Bell and Partridge [4] conducted a study on an open Joule cycle reciprocating engine with regeneration, implemented in a CHP system and decentralized power generation. Despite the performance recorded and some similarities with the Ericsson engine, it should be noted that the machine described, however, differs from the latter by its combustion chamber. In a study conducted by Moss et al. [5] on a Joule cycle reciprocating engine similar to that described above and intended for household micro-CHP, the problem of dimensioning was examined. The study predicts a thermal efficiency of 35% and an overall electrical efficiency of 33.2%. However, this level of performance is explained by the relatively high values of the pressure ratio (equivalent to 7.5) and the engine rotation speed (1000 rpm). Wojewoda and Kazimierski [6] performed a dynamic model to describe operating conditions of an externally heated reciprocating valve engine, based on the closed Joule cycle with highly pressurized air of 25 kW, which could reach a thermal efficiency of up to 25%. However, in order to achieve this level of performance, the system requires a high rotational speed (3000 rpm) and a relatively high compression ratio (compressed air from 15 to 95 bar). It is noted that the heat transfer takes place at over 1160 K in the heater, making it difficult to achieve such an air heat exchanger for this engine. However, in this paper, the transient problems related to start-up and driving of this type of engine were not examined.

As for all energy systems understanding and controlling the dynamic behavior of Joule cycle reciprocating Ericsson engines is an important aspect of the development of this type of machine [7]. In fact, it is necessary to be able to manage the transient phases (start-up, part load, etc.), and to guarantee the stability of operation around the nominal operating point. The objective of this work is to develop a tool for modeling and the dynamic simulation of reciprocating Joule cycle engines, which makes it possible to anticipate the possible problems of operation stability that could occur, in order to set up devices and strategies of control for such systems. But it should be noted that at this stage of the engine modeling, the thermal inertia of cylinder metallic parts is not taken into account, therefore the developed model simulates engine functioning only from a hot start-up, when wall temperature of the main components are considered as constant.

The engine configuration considered in this study will be presented, and its dynamic model developed. This will be followed by an analysis of the engine simulation results including the start-up transient phase and transient issues in the system after the engine operation is stabilized.

The Ericsson Engine

Principle and reference cycle

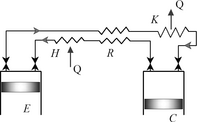
A classification of heat engines has been proposed in a previous study [8], which identified a family of specific machines: reciprocating engines with external heat supply, with separate compression and expansion cylinders, with or without a regenerator, with a gaseous working fluid. This family of engines includes two subfamilies; the Stirling engines, working without any kind of valves and the Ericsson engines (Fig. 1) using valves at the inlet and outlet of the cylinders.

Figure 1. Typical Ericsson engine.

From a thermodynamic point of view, the Ericsson engine is similar to a gas turbine where the turbo compressor has been replaced by a reciprocating compressor, and the turbine by a piston/cylinder machine. The theoretical cycle of Ericsson (2 isotherms and 2 isobars) is not adapted to describe an ideal Ericsson engine [9]. In an ideal Ericsson engine, heat transfers should take place at constant pressure while compression and expansion are supposed to be isentropic, corresponding to the Joule cycle, often used to describe the gas turbine principle.

Description of the studied open Joule cycle Ericsson engine

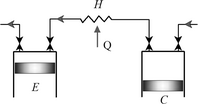
The Ericsson engine simulation can be carried out either in a closed cycle (Fig. 1) with a cooler (in this case the system can run at high pressure and allows the use of working fluids such as helium or hydrogen), or by an open cycle with or without regeneration (in this case, the working fluid is air that can be expanded down to the atmospheric pressure). For this study, an open Joule cycle without heat recovery is assumed (Fig. 2). The open cycle was identified to correspond to present needs in the field of domestic micro-CHP, as well as for solar or wood energy conversion of energy into electricity [3, 10]. In these machines, the compressor and the expansion cylinder run at low rotational speed, in order to limit the pressure losses due to the valves and also to reduce the mechanical losses. This solution ensures the best performance. The atmospheric air is compressed by the compressor C. It receives heat from the hot source through the heater H. The pressurized hot air produces work by expansion in the expansion cylinder E.

Figure 2. Open cycle Ericsson engine without heat recovery.

System Modeling

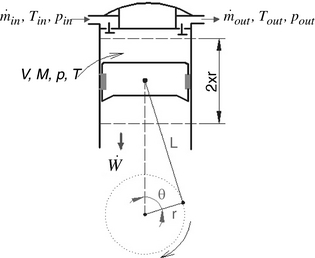
The engine model is developed on the basis of the mass and energy balance equations applied to control volumes of its three main components. This model takes into account the evolution over time of mass, pressure, and temperature of the working fluid in the control volumes and interfaces, as well as heat transfer in the heater and dynamic of the valves in the working cylinders. The model considers only losses associated with the gas flowing in and out of the valves. Further investigations have to be performed to include the other aspects of losses, such as the pressure drop in the heat exchanger, the frictional effects and also accounting for the effect of the so-called gas springs associated with the heat transfer which occurs during the compression and expansion strokes when the valves of this kind of reciprocating engine are closed. The air used as the working fluid is considered as an ideal gas. Moreover, all its thermophysical properties are considered to be constant. The mass, the temperature and the pressure in the three compartments C, H, and E of the engine are assumed to be uniform and determined by integration of equations (1), (2), and (3) as follows:

${\frac {dM}{dt}}={\overset {\cdot }{m}}_{in}-{\overset {\cdot }{m}}_{out}$

(1)

${\overset {\cdot }{Q}}-{\overset {\cdot }{W}}=c_{v}T{\frac {dM}{\mbox{dt}}}+$$c_{v}M{\frac {dT}{\mbox{dt}}}+c_{p}({\overset {\cdot }{m}}_{out}T_{out}-$${\overset {\cdot }{m}}_{in}T_{in})$

(2)

${\frac {dp}{dt}}=p\left({\frac {1}{M}}{\frac {dM}{dt}}+{\frac {1}{T}}{\frac {dT}{dt}}-\right.$$\left.{\frac {1}{V}}{\frac {dV}{dt}}\right).$

(3)

The compression and the expansion work are given by the expression:

${\overset {\cdot }{W}}=p{\frac {dV}{dt}}.$

(4)

For both the compressor (cold cylinder) and expander (hot cylinder), the amount of gas in the cylinder is determined according to the crank-rod kinematic given by:

$V_{j}={\frac {Vs_{j}}{2}}\left(1+{\lambda }_{j}-cos\theta -\right.$$\left.{\sqrt {{\lambda }_{j}^{2}-{sin}^{2}\theta }}\right)+$$Vc_{j},$

(5)

where, θ = 2πNt. Usual reciprocating valves are considered for both compressor and expander. The expansion piston is assembled on the same rod as the compressor piston but it moves in phase reversal compared to that of the compressor. The modeling of these valves is similar to that used for internal combustion engines [11]. The air flow rate through the inlet and the exhaust valves is given by the expression:

${\overset {\cdot }{m}}_{j}=A_{j}{Cd}_{j}p_{high}{\left({\frac {2\gamma }{(\gamma -1)rT_{high}}}\left({R_{j}}^{{}^{\frac {2}{\gamma }}}-{R_{j}}^{{}^{\frac {\gamma +1}{\gamma }}}\right)\right)}^{\frac {1}{2}},$

(6)

where A_j  = πLv_jDv_j is the so-called curtain area [11] and R_j  = p_low,j /p_high,j . The discharge coefficient Cd_j is considered equal to 0.85 as found in the literature for similar design [6]. In the case where the flow velocity reaches that of the sound, the critical ratio is then evaluated as follows:

$R_{j}={\left({\frac {2}{\lambda +1}}\right)}^{\frac {\lambda }{\lambda -1}}.$

(7)

The inlet and the exhaust valve lifts of the compressor are modeled by sinusoids, and given, respectively, by:

$Lv_{in,c}={\frac {Lv_{maxc}}{2}}\left[1-cos2\pi \left({\frac {\theta -{\mbox{IVO}}}{\pi -{\mbox{IVO}}}}\right)\right]$

(8)

$Lv_{ex,c}={\frac {Lv_{maxc}}{2}}\left[1-cos2\pi \left({\frac {\theta -{\mbox{EVO}}-\pi }{\pi -{\mbox{EVO}}}}\right)\right]$

(9)

where IVO ≤ θ ≤ πand(π + EVO) ≤ θ ≤ 2π

Closing of the inlet and exhaust valves of the compressor takes place at the bottom-dead-center and top-dead-center, respectively, while their opening is delayed to angles equal, respectively, to IVO and EVO.

The inlet and the exhaust valve lifts of the hot cylinder are also modeled by sinusoids as follows:

$Lv_{in,e}={\frac {Lv_{maxe}}{2}}\left[1-cos2\pi \left({\frac {\theta }{\pi -{\mbox{IVC}}}}\right)\right]$

(10)

$Lv_{ex,e}={\frac {Lv_{maxe}}{2}}\left[1-cos2\pi \left({\frac {\theta -\pi }{\pi -{\mbox{EVC}}}}\right)\right]$

(11)

where 0 ≤ θ ≤ (π − IVC)andπ ≤ θ ≤ (2π − EVC)

The opening of inlet and exhaust valves of the expander occur at the top-dead-center and bottom-dead-center, respectively, while their closing are advanced by angles, respectively, equal to IVC and EVC.

These inlet and exhaust valve opening and closing angles of both cylinders are set in order to correspond to and optimal engine operation with a pressure of 4 bar under stable operating conditions. The other parameters are listed in the Table 1 below.

Table 1. Engine specifications

Component	Parameters
Compressor	Swept volume: 22.6 × 10−4 m3
	Clearance volume: 11% swept volume
	Bore: 0.12 m
	Connecting rod length: 0.10 m
	Ratio of connecting rod to crank radius: 3
	Opening of the inlet valve delay: 40° Opening of the exhaust valve delay: 120°
Heater	Volume: 0.18 m3
	Temperature of wall: 873 K
	Heat exchange area: 8 m2
Expander	Swept volume: 42.5 × 10−4 m3
	Clearance volume: 8% swept volume
	Bore: 0.16 m
	Connecting rod length: 0.104 m
	Rod to crank radius ratio: 3
	Closing of the inlet valve advance: 112° Closing of the exhaust valve advance: 25°
Rotational speed: 480 rpm

Compression and expansion are assumed adiabatic in the two working cylinders, and gas leakages through the segmentation are considered to be null. Heat exchange between these components and the surrounding is thus neglected. The following equations are based upon these assumptions.

${\overset {\cdot }{Q}}_{c}={\overset {\cdot }{Q}}_{e}=0.$

(12)

In this engine, as in any other hot air engine, heat is transferred from the heat source to the working fluid through a heat exchanger, whatever the origin of this heat [12]. The heater considered in this study is a shell-and-tube heat exchanger in which the working fluid flows inside the tubes. This heat exchanger technology was chosen for its simplicity in terms of construction, durability, and comparatively low cost, under very severe working conditions due to the high temperature and pressure differences between the two fluids. The heat exchanger processes are modeled assuming that the spatial variations of the gas parameters along the heater are not taken into account. This leads us to consider only the time-dependent relations. Heat transfer between the working fluid and the hot internal walls of the heater is assumed to be at a constant temperature (considering the hot start-up assumptions) and is thus modeled as follows:

${\overset {\cdot }{Q}}_{h}=h_{h}S_{h}(T_{wh}-T_{h}).$

(13)

In turbulent flow (Re > 2300), the Nusselt number is calculated by the following correlation [13]:

${\mbox{Nu}}={\frac {d_{t}.h_{h}}{k}}=0.021{\mbox{Re}}^{0.8}{\mbox{Pr}}^{0.6}.$

(14)

In case of laminar flow (Re < 2300), the correlation of Kays is used [14]:

${\mbox{Nu}}=3.66+{\frac {0.104({\mbox{Re}}{\mbox{Pr}}dt/Lt)}{1+0.016({\mbox{Re}}{\mbox{Pr}}dt/Lt)^{0.8}}}.$

(15)

The thermal efficiency of the engine is calculated as follows:

$\eta =100\times {\frac {{\overset {\cdot }{W}}_{e}+{\overset {\cdot }{W}}_{c}}{{\overset {\cdot }{Q}}_{h}}}.$

(16)

All the variables-per-cycle that are used below in the simulation model results are calculated using the following formula:

${\overline {X}}={\frac {{\int }_{\tau }^{\tau +T}Xd\tau }{T}}.$

(17)

Simulation Results

The models were simulated in the Matlab/Simulink environment. The Solver ode23 based on an explicit Runge–Kutta (2, 3) was used with a maximum step size of 2 × 10⁻³ sec. It was, therefore, necessary to first conduct several simulations to determine the optimum valve settings. Indeed, this adjustment must permit the stabilized functioning of the engine to the pressure of 4 bar with the settings indicated in Table 1.

Start-up transient and stability of the system

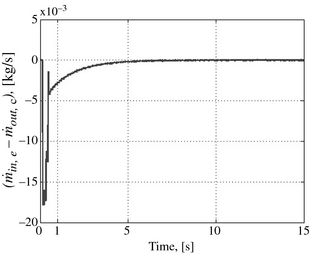
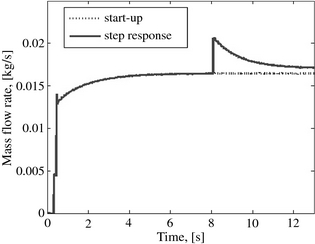
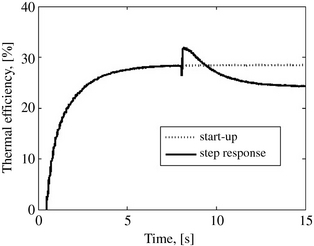
At the beginning of the simulation, pressure in the two cylinders and the heater is equal to atmospheric pressure and temperature equals 300 K. The start-up of the engine begins with the assumption that the temperature of the internal walls of the heaters tubes is constant and equals the fixed value of 873 K. This then implies a hot start, as indicated earlier in the introduction. Figures 3 and 4 presents the three-phase dynamic of the engines start-up, illustrated by the aid of the evolution as a function of time of the difference between the hot gas flow admitted into the expansion cylinder ${\textstyle {\overset {\cdot }{m}}_{in,e}}$ and that discharged by the compressor into the heater ${\textstyle {\overset {\cdot }{m}}_{out,c}}$ . The first phase corresponds to the pressurization of the engine (at the expense of some mechanical external energy source). During this phase, the expansion cylinder is isolated from the heater, the inlet valve is closed, and the exhaust valve is open. Figure 4 shows that the part of the curve corresponding to the pressurization of the engine is negative, and presents the oscillations that translate the increase in pulsating flow rate of the gas discharged from the compressor to the heater. When the pressure reaches the adopted level for starting the expander (set at 3 bar), the second start-up phase begins with the release of the expander valves. The corresponding part of the curve grows with a positive slope. This means that the flow rate of the working fluid admitted into the expansion cylinder increases progressively and produces work. Following that, there is equality between the flow rate discharged from the compressor and that admitted into the expander. This equilibrium corresponds to the engines third operational phase where the functioning parameters are stabilized after 50 rotation cycles. In this stationary state, the mass flow rate of the working fluid through the system is such that the flow remains laminar in the tubes of the heater, due to the engines low speed as adopted for this study. Under these stable operating conditions, the engine develops an output of 1.67 kW and a thermal efficiency of about 29.3%.

Figure 3. Working cylinder.

Figure 4. Dynamic of the mass flow rate difference between the expander and the compressor.

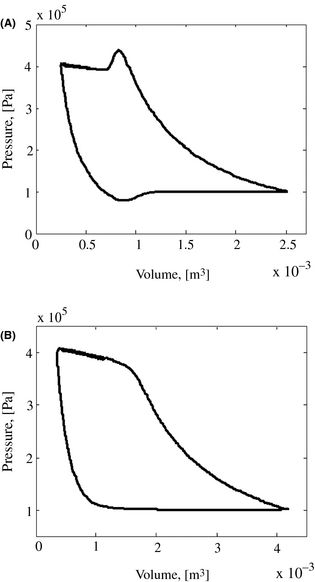
Figure 5A and B illustrate the evolution of the pressure, respectively, in the compression cylinder and the expansion cylinder (under stable operational conditions). The first diagram shows that the pressure inside the compressor increases during the discharge, while the second diagram shows that the pressure inside the expansion cylinder drops during the hot gas inlet process. These two trends, whose evolution negatively impacts the engines performance, are due to the fact that the volume of the heater is not sufficiently large enough and moreover, the expansion piston is assembled on the same rod as the compressor piston, but it moves in phase reversal compared to that of the compressor. To eliminate this phenomenon without modifying the initial configuration of the pistons of the two cylinders, it is enough either to increase the volume of the heater in order to raise the V_h/VE ratio, or to consider a buffer volume upstream of the heater. This solution allows adjustment of the observed parts of the curves, however, the modified installation becomes less compact and the duration of the required start-up transient phase will increase.

Figure 5. pV plot of (A) compressor and (B) expander.

Comparing the engines thermal efficiency with that of Joules ideal cycle

The expression (16) of the thermal efficiency makes it possible to appreciate the thermodynamic performances of the developed model of the Ericsson engine based on the open Joule cycle without heat recovery. Under similar operating conditions, the thermal efficiency of corresponding Joules ideal cycle is known to be calculated only as function of the engine pressure ratio and the kind of the working fluid [15]:

${\eta }_{th}=100.\left[1-{\left({\frac {1}{r}}\right)}^{\frac {\gamma -1}{\gamma }}\right].$

(18)

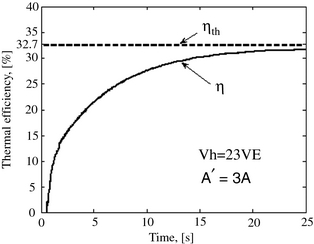
In this study, the comparison between the two efficiencies will be valid only under the stable operating conditions of the engine, following the start-up transient phase. The curve of the thermal efficiency corresponding to the simulated model is plotted under the conditions where the flow area of the valves is increased by three and the size of the heater is sufficiently increased as indicated on Figure 6. These two considerations make it possible to on the one hand, to significantly reduce pressure drops in the valves, and on the other hand, to eliminate the phenomenon of variation of the instantaneous pressure in the heater throughout every rotation cycle. However, as it was mentioned above these aspects largely lengthen the heaters pressurization time and, consequently, the duration of the simulation. The curves on Figure 6 show that when the engine tends to be stabilized, the modeled thermal efficiency tends to be toward a value closer to that of the theoretical open Joule cycle efficiency. It should be noted that the exact value can be reached only under the theoretical conditions when the valve flow areas are infinite (no pressure drop) and the heater of infinite volume.

Figure 6. Comparison of the thermal efficiencies.

The systems response to perturbations

Two types of perturbance have been modeled and simulated in order to study the dynamic behavior of the transient phases resulting from them, how they influence the systems stability, and how they impact the engines performances.

Expansion cylinder inlet valve closing angle delayed by 11.2°

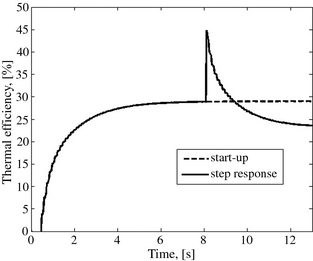
It should be noted that the operation angles of the reciprocating valves of this type of engine determine the compression pressure (the expansion, respectively) and, consequently, the efficiency of the compression process (the expansion, respectively), as well as the work which results from it. When the system is stabilized, this first perturbation consists of delaying the closing angle of the hot cylinders inlet valve by 11.2° crankshaft and then, to analyze the dynamic behavior of the engine.

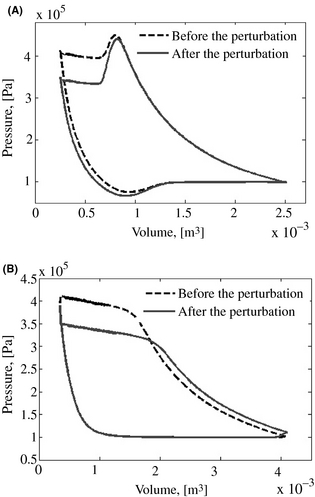
The simulation results are presented in Figures 7, 8, and 9 where it is noted that as a result of this sudden action, the system goes through a transient phase before being stabilized at a lower pressure after about 4.3 sec. The indicated diagrams of the compression and expansion cylinders are significantly modified. The expanders inlet time grows; this leads to a significant reduction of the pressure inside the heater and, consequently, a 3.5% increase of the mass flow rate of the working fluid in the engine. This increase is shown in Figure 8. From the point when the closing of the inlet valve of the hot cylinder is delayed, this valve remains open longer than before, which leads to an increase of the filling time of the expansion cylinder, which involves a reduction in the expansion time. The effect of this is the underexpansion observed in Figure 7B. The pressure drop, in addition to the reduction of the expansion time, accounts for the drop in the performances of the engine. The thermal efficiency whose trend is depicted in Figure 9 decreases during this transient phase from 29% to 23%. The peak, which is observed on the curve of the thermal efficiency of the machine at the moment when the disturbance is provoked, follows the spike experienced by the air mass flow rate as result of the instantaneous transient effect of the sudden action. Therefore, the interpretation of this peak value proves to be numerical rather than physical with regard to the meaning.

Figure 7. Model response to an expander inlet valve perturbation. (A) pV plot of the compressor (B) pV plot of the expander.

Figure 8. Dynamic of the mass flow rate.

Figure 9. Dynamic of the engine thermal efficiency.

Sudden pressure drop at the compressor inlet

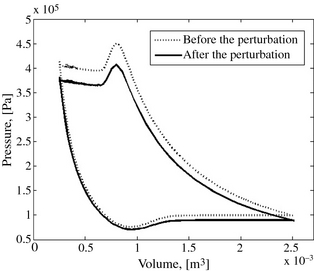
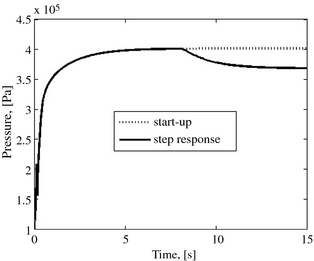
This second perturbation has to do with simulating a sudden drop of the compressor inlet pressure of 10 kPa after the engine starts and stable operation been established. Such a drop is practically possible and could for instance be the result of the plugging of the atmospheric air filter in the suction line. This phenomenon is simulated on 120 engine rotation cycles and the results are displayed in Figures 10, 11, and 12. The two curves in Figure 10 show that at the end of the perturbation the compressor indicator diagram moves downwards, after having crossed a transient phase as depicted in the other figures. This evolution of the engine pressure is illustrated in Figure 11. The pressure drop resulting from the disturbance involves a decrease of the mass flow rate of the working fluid throughout the system in accordance with relation (6). This implies a decrease in the resulting power output and the performance of the engine when the engine operation is stabilized. In fact, Figure 12 shows that the decrease of the system pressure in addition to a decrease in the mass flow rate throughout the engine involves a decrease in the thermal efficiency. This performance parameter will be stabilized after 36 rotation cycles due to the response of the system to the disturbance.

Figure 10. pV plot of the compressor before and after the perturbation.

Figure 11. Dynamic of the engine pressure.

Figure 12. Dynamic of the engine thermal efficiency.

Conclusion

The dynamic model of the open cycle Ericsson engine presented in this paper predicts a stable operation of the engine. Simulations showed a rapid hot start-up and the performances achieved when the engine reaches the steady state are globally satisfactory with regard to its configuration without heat recovery. Subjected to some selected perturbations (delay of closing of the expansion cylinder inlet valve, inlet pressure drop), the engine operation is stabilized after a rapid transient phase but undergoes, logically, a drop of power output and efficiency. In our further investigations, a more realistic dynamic model of the engine will be set up, taking into account the heat transfer and the thermal inertia of metallic parts of the main components of the engine and the integration of other factors of losses, such as the pressure drop in the heat exchanger, the frictional effects, and a focus on the gas springs heat transfer.

Conflict of Interest

None declared.

References

1. Stouffs, P.2002. Le moteur Ericsson, un moyen de valorisation de l'énergie thermique à réhabiliter?Entropie241:26–32.
2. Kaikko, J., and J. Backman. 2007. Technical and economic performance analysis for a microturbine in combined heat and power generation. Energy22:378–387.
3. Bonnet, S., M. T. Alaphilippe, and P. Stouffs. 2005. Energy, exergy and cost analysis of a micro-cogeneration based on an Ericsson engine. Int. J. Therm. Sci.44:1161–1168.
4. Bell, M. A., and T. Partridge. 2003. Thermodynamic design of a reciprocating Joule cycle engine. Proc. Inst. Mech. Eng. A: J. Power Energy217:239–249.
5. Moss, R. W., A. P. Roskilly, and S. K. Nanda. 2005. Reciprocating Joule-Cycle engine for domestic CHP systems. Appl. Energy80:169–185.
6. Wojewoda, J., and Z. Kazimierski. 2010. Numerical model and investigations of the externally heated Joule engine. Energy35:2099–2108.
7. Flax, P.-H., and C.-W. Hong. 2006. On the start-up transient simulation of a turbo fuel cell system. J. Power Sources160:1230–1241.
8. Stouffs, P. 2002. Does the ericsson engine deserve more consideration than the stirling engine? Int: Proceedings of the European Stirling Forum. ECOS GmbH, Osnabruck, Germany.
9. Bonnet, S., M. Alaphilippe, and P. Stouffs. 2004. Etude énergétique d'un moteur à apport de chaleur externe de type ERICSSON pour des applications de micro-cogénération. Pp. 933-938 in Actes du Congrès SFT 2004, Presqu'île de Giens, 25–28 mai 2004.
10. Alaphilippe, M., S. Bonnet, and P. Stouffs. 2007. Low power thermodynamic solar energy conversion: coupling of a parabolic trough concentrator and an Ericsson engine. Int. J. Thermodynamics.10:37–45.
11. Heywood, J. 1988. Internal combustion engine fundamentals. Mc Graw-Hill, New York.
12. Finkelstein, T., and A. J. Organ. 2001. Air engines. Professional Engineering Publishing, U.K.
13. Padet, J. 2006. Convection thermique et massique. Techniques de l'Ingénieur, BE 8206.
14. Sacadura, J. F. 2000. Initiation aux transferts thermiques. Editions TEC and Doc, Paris.
15. Müller, I., and W. H. Müller. 2009. Fundamentals of thermodynamics and applications. Springer, Berlin Heidelberg.