An A-CAES pilot installation in the distribution system: A technical study for RES integration

Abstract

In the last decade in Europe, the power generated by Renewable Energy Sources (RES) has significantly increased. For the electric power system, the integration of a high amount of power generated by RES represents a big challenge. Energy Storage Systems (ESS) may help to solve problems related to the grid integration of RES. In this study, an analysis of the benefits that a planned and dedicated Adiabatic Compressed Air Energy Storage (A-CAES) system may provide to a distribution network with a high penetration of RES will be carried out. The A-CAES system, taken into account in this investigation, is based on the proposed German study so-called “ADELE project”. The technical benefits as well as the corresponding costs that A-CAES brings to the system which were analyzed using the load and RES generation time series for 2010 and 2020, and were based on technical data from a selected part of a German distribution power network, were evaluated and results of those broad investigations are presented in this study. The result of the investigations shows that the direct technical benefits are quite limited for the A-CAES technology as it exists today.

Introduction

The European Union aims to cover 20% of its primary energy demand by using Renewable Energy Sources (RES) by 2020. Consequently, in the last decade the installed generation capacity of power plants based on RES, mainly wind and solar, has highly increased. By 2020 it is expected that 220 GW of wind plants and 390 GW of Photovoltaic plants (PV) will be installed in Europe [[[#ese338-bib-0001|[1]]], [2]]. However, these power plants are not able to always generate power when it is demanded, but instead they generate it according to meteorological conditions. This explains how difficult it is, and how increasingly difficult it will be in the future, for the system operators to cope with the power generated by RES and fed into the electric grid. An energy storage system, although still expensive, is one of possible solutions for technical integration of power generated by RES into the network [[[#ese338-bib-0003|[3]]], [4], [5], [6]]. Accordingly, many power utilities worldwide are investing in different projects regarding the application of Energy Storage Systems (ESS) [7]. Such projects are mostly pilot projects as there are still four challenges that slow down the development of ESS, namely, investment costs, reliability, reasonable environmental and social acceptance.

Energy Storage in the Power System. Aim of this Study

In this study, the results of initial investigations (preliminary study) in the scope of the project ADELE [8], which is related to the planed usage of an adiabatic compressed air storage system in the region of Saxony-Anhalt in Germany, are described. The study aims to evaluate the technical benefits and the overall costs that the application of an Adiabatic Compressed Air Storage (A-CAES) system may evoke within the electric power system. Additionally, through a sensitivity analysis regarding the cost–benefit issue, the minimal required storage capacity is found.

A two-criterion method is generally used to classify the ESS: the system power rating and the discharge time at rated power. Furthermore, the ESS' applications can be classified in three categories: ESS for power quality applications, ESS for bridging power applications, and ESS for energy management applications [9]. Related to the energy management applications, the ESS are characterized as being able to store a high amount of power (up to some GW) for a long time (in the range of many hours or days). Pumped hydro, Compressed Air Storage Systems (CAES), hydrogen–methane, and some types of batteries are the most suitable technologies for this task [4]. However, the usage of pumped hydro systems as well as CAES systems is geographically limited. In fact, to build a pumped hydro system water sources as well as a particular ground local ability are needed, as pumped hydro storage needs differences in altitude, while the CAES systems need caverns in which the compressed air can be stored. With regard to the hydrogen–methane method, new concepts are being developed. One of these, the so-called “power to gas concept” [[[#ese338-bib-0010|[10]]], [11]], has as a main idea the ability to feed the hydrogen produced through electrolysis into the natural gas network. Alternatively, the hydrogen can be methanized by adding carbon dioxide and subsequently fed into the natural gas network or inside caverns to be stored for later use.

Nowadays, the pumped hydro technology is the mostly used energy storage system worldwide. Related to the CAES, there are only two plants in operation [12], both of which use the conventional concept, diabatic CAES technology.

Among the battery technologies, Sodium–Sulfur high-temperature batteries (NaS) have experienced a significant popularity recently due to their extremely flexible range of applications [13] and to their expected long life time (15 years [14]).

For power quality applications the ESS have to be able to discharge power in a very short time. Batteries, flywheels, Superconducting Magnetic Energy Storage (SMES), and Suparcaps are the storage technologies suitable for this purpose. For these technologies the charge/discharge power ranges from few kW to few MW, while the charge/discharge time ranges from seconds up to some hours.

The energy storage costs depend mostly on the storage technology and their application. Table 1 shows the energy storage costs of three technologies for energy management. In both applications the storage costs for pumped hydro are cheaper than the CAES and the hydrogen options. However, the hydrogen, for seasonal storage application (long term), may be more competitive than the pumped hydro and the CAES system.

Table 1. Energy storage costs related to the storage application [15].

Application	Technology	Storage costs (c/kWh)
Load leveling	CAES	4–7
	Pumped hydro	3–6
	Hydrogen	12–25
Long term	CAES	23–40
	Pumped hydro	3–12
	Hydrogen	12–27

Compressed Air Energy Storage Systems

A CAES system may store the electricity either as only mechanical energy (for the diabatic system) or as mechanical and thermal energy (for the adiabatic system). In both of the options, the electricity is used to drive a compressor train which compresses the air. The compressed air is stored inside an underground space (unlined cavern and porous structures or lined cavern and salt formation [16]). In the discharge phase, the compressed air is heated before the expansion in the turbine. The heating of the compressed air may occur inside combustion chambers (for the diabatic CAES) or by a thermal exchanger system (for the adiabatic CAES) which reuses the thermal energy recovered and stored during the compression process. From a thermodynamic point of view, the most efficient CAES should continuously subtract heat during the compression and continuously add heat during the expansion, keeping the air temperature at its ambient value (isothermal process). However, in practice, such isothermal processes are not easy to achieve, even if some proposals using hydraulic air or water injection have been made [[[#ese338-bib-0017|[17]]], [18], [19]]. In reality, most compressors and turbines do exchange a limited amount of heat with the ambient; therefore their processes may be considered as adiabatic [20]. Thus, in reality, the isothermal compression is substituted by sequences of adiabatic compressions with intermediate cooling, while the isothermal expansion is substituted by adiabatic expansions with intermediate heating.

Generally, a diabatic CAES system can be considered a hybrid unit made up of an energy storage and a gas turbine plant. Different from a conventional gas turbine, the CAES precompresses the air in appropriate underground spaces during the charging process and successively utilizes it, burning it in a combustion chamber together with some gas fuel (i.e., natural gas) during the discharging process. The overall efficiency of a diabatic CAES is generally evaluated according to the equation (1), in which η depicts the efficiency of the system, E_out the electricity discharged/generated, and E_in the sum between the amount of the stored electricity and the amount of the energy included in the burned fuel amount.

$\eta ={\frac {E_{out}}{E_{in}}}$

(1)

In order to increase the overall efficiency, a recuperator may be used to preheat the compressed air before being applied to the combustion chamber. The recuperator recovers part of the energy of the exhaust gases thereby decreasing the need for combusting fuel. Depending on their configuration (with or without recuperator) the overall efficiency of realized diabatic CAES plants ranges between 54% and 42%, respectively [21].

In an adiabatic CAES system (A-CAES), the heat generated during the compression of air is stored in a Thermal Energy Storage (TES). With reference to the ADELE project [[[#ese338-bib-0008|[8]]], [22]], the compressor train compresses the air up to 70 bar. This compressed hot air, with temperatures reaching over 650°C, flows through the TES, which is a 40-m-long container with beds of stones or ceramic molded bricks. The heat storage material inside the TES is then heated up, while the temperature of compressed air decreases on output significantly. The cooled compressed air is then guided into an underground cavern. In the discharge phase, the compressed air passes along the heated material of the TES again, thus its temperature is increased. Related to the round trip efficiency, for the ADELE project it is expected that it will reach a value of about 70% [22] (a similar relatively high efficiency value has also been assumed by [18]).

The application field of an adiabatic CAES can range from the energy management tasks up to the supporting of the power network operation. In the last case, apart from local system services such as short circuit power and reactive power provision, A-CAES systems principally can deliver primary, secondary, and tertiary (minute reserve) controls. However, for the primary and secondary control, A-CAES systems can only supply these services under certain constructional and operational conditions, as is typical for any kind of thermal power plant due to material-related thermal stress restrictions of turbo machinery.

Study Case: A-CAES System in a Distribution Network with a High Penetration of RES

Aims of the study case, assumption, and investigation approach

In Germany, a consortium of enterprises is planning to build an A-CAES system in the region of Saxony-Anhalt [23]. For several years this region has been known as the “green energy export region” mainly because of a high overproduction of electric power generated by wind farms and photovoltaic. Therefore, this part of the German power network was considered as a study case in this study. The purpose of this study is not to model and validate in detail each individual technology considered in the study, but rather to evaluate whether the entire surplus of electric power generated by wind and sun plants could be better integrated (reused) within the region Saxony-Anhalt by the means of the A-CAES application. Furthermore, the different technical and economic benefits, which a storage system can bring to the analyzed network, should be focused on. Additionally, this study aims to identify potential problems with the A-CAES itself concerning the aforementioned application fields and give first estimation of a useful storage capacity at which the benefits outweigh the costs.

For the analysis two assumptions were made:

1. the balance between the electric power generation and consumption within the studied power network should be first satisfied with minimal consideration of the influences that the neighboring networks can have on the regional energy balancing zone requirements,
2. the primary A-CAES modus operandi will not be based on the market price signals (as is generally common for the ESS). It will rather focus on the technical issues, which take into account provision of the support for RES integration into the considered distribution grid.

The adopted investigation approach is composed of four steps. In the first step the electric network is modeled, in the second one the characteristic of the RES generation and of the load in the investigated area are identified. The third step deals with the simulation and analysis of the electric system without the use of the A-CAES system, while in the last step the simulation and the analysis of the system with the A-CAES were done. The benefits analyses are based on a comparison of the results of the two last steps.

Electric networks modeling approach

The study case considered the high voltage network (110 kV) of the region Saxony-Anhalt and two different chronological scenarios: the year 2010 and 2020.

The investigation approach and the modeling of the electric network consist of five points:

1. analysis (for the scenario 2010) and estimation (for the scenario 2020) of the installed RES power and of the electric power demand;
2. estimation of the generation profiles for the wind farms and the PV plants as well as electric load profiles in the form of time series with 1-h resolution for a time period of 1 year;
3. modeling of the physical parameters of the electric network;
4. modeling of the physical and economic parameters of the largest conventional power plants installed in the analyzed network;
5. specification of the physical and economical parameters of the A-CAES system.

Analysis and estimation of the installed RES power and of the demanded electric load

The proposed scenarios (2010 and 2020) have been selected by the project consortium and should present the general tendencies regarding the changes in the optimal operation within the analyzed region. In order to depict both of the scenarios, statistical and forecasting data from the region have been used [[[#ese338-bib-0023|[23]]], [24]]. Table 2 shows, for scenarios, the peak electric load demand and the installed power for the wind and PV generation. Due to the analyzed time period a decrease in electrical power demand is forecasted, which mainly depends on the forecasted decrease in population as well as on the efficiency increase in electrical devices. Thus, the peak load demand in the year 2020 is 4.91% lower than in the year 2010. The installed capacity of RES for the year 2020 has been estimated according to the German energy policy targets [25], which were linearly scaled up for the region Saxony-Anhalt. Moreover, it was assumed that the wind farms as well as the PV plants in the year 2020 were located in the same nodes as the units in 2010, as the density of RES in the considered region was already very high in 2010 and there are not so many new areas available. The increase will be achieved generally using repowering for wind or extending the array fields for PV.

Table 2. Peak demanded and installed RES power in the network of Saxony-Anhalt.

Scenario	Peak load (MW)	Wind power (MW)	Photovoltaic (MW)
2010	2856.6	3240	480
2020	2716.2	4210	1350

Evaluation profiles for the RES-based plants and for the electric loads

The weather database REMO [26] was used to simulate the electricity generation profiles for the wind parks and the PV. REMO is a special prognostic system designed by the Max Planck Institute for Weather Forecasting, based on advance statistical analyses, and provides information about the wind speed at an altitude of 10 m aboveground and about solar irradiation. This information is given for each middle point in the defined geographic raster for Germany, Austria, and Switzerland. Furthermore, the REMO database can deliver both historical data and future forecasted meteorological data (from the year 1950 to the year 2100), which can be used for the generation of stochastic independent synthetic profiles. For this study, weather data with 1-h time resolutions were considered.

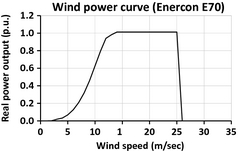
Regarding the evaluation of the wind power generation, all the wind parks installed in Saxony-Anhalt by the year 2010 as well as the estimates for 2020 were analyzed in the first step. Then, based on this analysis, the average installed power per wind turbine was evaluated and estimated (for the case 2020). Using these values and considering the technical characteristics of four different wind turbine types (see Table 3), an equivalent hub height and an equivalent characteristic curve were selected. As the second step, the generation profile for the wind turbines was elaborated. In order to do this, an application was developed, which allows to extract the required input data (the wind speed information) from the REMO database for each year and geographic location, then using equation (2) [27] to estimate the wind speed at the hub height of the wind turbines, and finally, by considering the power characteristic curve (see Fig. 1) to elaborate the power generation profile.

$v\left(h\right)=v\left(h_{10}\right).{\left({\frac {h}{h_{10}}}\right)}^{\alpha },$

(2)

Table 3. Wind turbine characteristics for four different types.

	Enercon E66	Enercon E70	Enercon E82	Repower MM82
Nominal power (kW)	2000	2000	2000	2000
Height (m)	67–98	57–113	78–138	59–100
	Av. 90	Av. 105	Av. 120	Av. 85

Figure 1. Characteristic curve of wind power plant [30].

where:

• v(h) is the wind speed at the particular height h,
• v(h₁₀) is wind speed at the reference height h₁₀ (10 m),
• α is the roughness coefficient (for countryside α is 0.16 [28]).

It is important to note that the wind speed could be also estimated according to a logarithmic law. However, even if in some conditions the logarithmic law can better estimate the resulting wind speed, in a comparison in which different assumptions were taken, such as that all the wind farms are installed in countryside areas or to not consider the seasonal effects on the terrain characteristic, the use of a more precise and complicate equation had not brought significant advantages [29]. Therefore, a simplified power law equation was chosen.

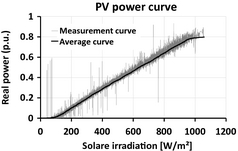
Regarding the evaluation of power generation by PV plants, the developed program reads the information about the solar irradiation from the REMO database, and then it elaborates the generation profiles by considering the photovoltaic plants efficiency and the inverter efficiency characteristic. In order to do this, a PV power curve function was modeled (see Fig. 2). This function is based on the test 2.5 kW PV plants located in the analyzed area. The maximal value of the real power that the PV can feed into the grid is 80% of the nominal value for the scenario 2010 and 85% for the scenario 2020. These values are similar to those suggested by the local distributed system operators and reflect the pollution and other regional-based reduction factors.

Figure 2. Measured characteristic of photovoltaic unit.

Related to the electric load profiles, in this study a mix of four standard profiles typical for the German consumers were considered. They depict the load demand of four different consumer categories: residential, agricultural, commercial, and industrial. In addition, statistic information related to the demographic and economic factors was considered for the all the macroareas of the region Saxony-Anhalt.

Model of the electric network

The electric network was modeled using the commercial power system simulator PSS^®NETOMAC (Siemens AG, Erlangen, Germany). In order to model the structure of the grid, information (voltage level and transfer power capacity for each line) from the ENTSO-E and the TSO (50 Hertz) was used. Moreover, the components within the grid model were parameterized using data from [27] and [31] as well as from the TSO. The geographic locations of network nodes (25 nodes in total), substations, and corresponding line lengths were obtained using the software GoogleEarth^® [32], while for the geographic locations of the wind farms and PV as well as the conventional power plants, the database of the TSO was adopted. For the sake of simplicity, the RES plants were aggregated according to their geographic positions and coupled with their nearest node of the network. Moreover, to each node an electric load was coupled, which represents one of the four different kinds of consumption profiles as mentioned above (residential, agricultural, commercial, and industrial).

Model of the conventional power plants

In the region of Saxony-Anhalt, three large natural gas fired power plants and a large coal power plant are in operation (data related to the year 2010) [33]. By considering the age of each power plant and their standard life time, it was assumed that the same power plants will still be in operation in the year 2020.

The natural gas fired power plants are all Combined Cycle Gas Turbines (CCGT) with installed power ranges from 114 MW to 140 MW, while the coal power plant has an installed power of 980 MW. For modeling the technical behavior of the CCGT, it was considered that their minimal operating power can reach 20% of the nominal value, while for the coal power plant the minimal operating power can reach 50% of the nominal value. Besides this, quadratic input–output characteristics were used to evaluate the power generation costs of all this power plants. Moreover, in order to evaluate the power generation costs, the fuel price for the year 2010 and those estimated for the year 2020 were considered. Table 4 shows the assumed fuel prices and the input–output functions.

Table 4. Fuel prices and input–output function.

Power plant type	Fuel price (€/GJ) [34]	Input–output function [35]
a For scenario 2010. b For scenario 2020.
Coal power Plant	2.4a	IO(P) = 0.00078P2 + 7.72P + 1200
	3.8b
CCGT	8a	IO(P) = 0.00067P2 + 7.47P + 1130
	10.8b

Specification of the physical and economic parameters of the A-CAES system

As aforementioned, the A-CAES system aims to support the integration of the power generated by RES into the local electric network. In order to achieve this target, an A-CAES with a maximal charging–discharging power of 90 MW, a storage capacity of 360 MWh, and a Depth of Discharge (DOD) of 100% was considered. Depending on the storage operation mode and definition of capacity this DOD is realistic. All these data are based on some of the expected technical characteristics of the ADELE Project and will be verified when the more exact data are available in the future.

Related to the economic parameters of the A-CAES, it was assumed that for each installed kW an investment of 1000 € will be necessary. As there have not been any A-CAES installed yet, this assumption could either overestimate or underestimate the real costs of an A-CAES. However, by considering some values found in literature, the taken investment costs seem to overestimate them by about 25% [21] and by about 40% if the costs of a conventional CAES were benchmarked [36]. Besides the investment costs related to the purchase of the machinery, the costs for preparation of the underground reservoir were assumed at 3 € per kWh of storage capacity [37]. Finally, in the economic analysis of the A-CAES, a lifetime of 20 years and a discount factor of 5% were considered.

Analysis of the RES generation and load profile without A-CAES support

The second step of the analysis process consists of inspecting the RES generation and the load profiles for the case in which the electric system is not supported by the A-CAES (benchmark case). Two main outputs are obtained from this investigation:

1. The evaluation of the RES gradients;
2. The evaluation of the Residual Load (RL) and its ramping values.

Both these parameters are quite new, if computing power system with high RES generation. Especially, the high RES gradients can be critical from the power system stability point of view, if there are other generation units in the considered region based on the power plant types with low or slow regulation capability. This is often the case with the high in-feed of RES.

Analysis of RES power gradients

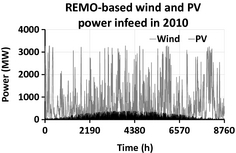
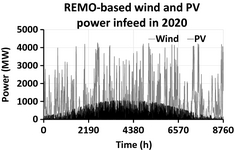
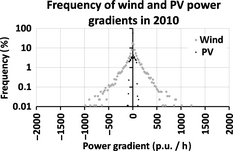
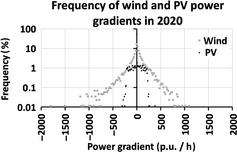
The RES power gradient was computed through the analysis of their generation profiles, which are depicted in Figures 3, 4. The variation in the RES power gradient is a good indicator of the challenges that the system operators have to face for integrating a high amount of power generated by RES. For example, the installed PV power in Germany amounted to 32.6 GW [39] at the end of 2012. To balance a power gradient of 0.2 p.u. per hour, it means that circa 6 GW per hour of electric power have to increase or decrease. Figures 5, 6 show the frequency of the relative power gradient for wind- and solar-based generators both for the year 2010 and for the year 2020. Related to the power gradient of wind farms, the gradient estimated by the weather model REMO shows a similar distribution profile when compared with that based on the measured data (see [38]). By analyzing the gradients (see Table 5) it can be pointed out that for the scenario 2010 their maximal value ranges between −1053 MW/h and +1202 MW/h; however, the vast majority (about 70%) of the RES gradient is within −100 MW/h and +100 MW/h. By separating the contribution of the RES gradient, it can be seen that the wind power has the highest impact. Its gradient is between −980 MW/h and +1202 MW/h, while the contribution of the PV is about a tenth of that generated by wind. When considering the scenario 2020, the RES gradient ranges between −1899 MW/h and +1252 MW/h. Different from the scenario 2010, in scenario 2020 about 78% of the gradient ranges between −200 MW/h and +200 MW/h. Also in this scenario the wind power has the largest contribution. It should be noted that for the year 2020 the maximum value of the wind generation power gradient is lower than that for the year 2010 (see Table 5), even though the installed power is higher than in 2010. This unexpected result could be justified by the probabilistic characteristic of the applied synthetic weather data from REMO. Some windy years tend to be followed by less windy years, and this is the case in 2020. Indeed, when comparing the wind gradient of year 2019 and 2021 with that of year 2010 such unexpected results as in 2020 were not observed; the gradients for 2019 and 2021 are higher than 2010.

Table 5. Results of gradient analysis.

RES	Scenario 2010 (MW/h)	Scenario 2020 (MW/h)
PV	−112	−305
	+115	+370
Wind	−980	−1817
	+1202	+1092
Total	−1053	−1899
	+1202	+1252

Figure 3. RES power generation for the scenario 2010.

Figure 4. RES power generation for the scenario 2020.

Figure 5. Frequency of RES power gradients for the scenario 2010.

Figure 6. Frequency of RES power gradients for the scenario 2020.

Evaluation of Residual Load and its ramping value

The Residual Load (RL), which was evaluated according to equation (3), is defined as the difference between the electric power demand (Load) and the RES power generation (RES) at each hour (t).

$RL(t)=load(t)-RES(t)$

(3)

When the RL is positive, it represents the net load that the conventional power plants and the A-CAES plant have to cover, while a negative RL represents the power surplus that the A-CAES has to store. The amount of energy that the A-CAES can store depends on its storage capacity.

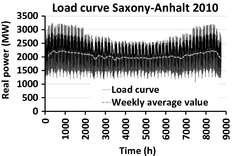
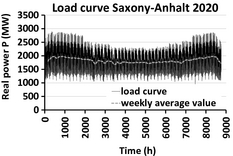
In order to evaluate the RL, the electric load should be analyzed first. With reference to the scenario 2010, the minimum and maximum demanded load ranges, respectively, from 1.07 GW to 2.85 GW (see Fig. 7), while the energy demanded is about 17.96 TWh. In the same year scenario, the RES power ranges from 0 to 3.53 GW, generating 6.70 TWh of electricity. In comparison with the scenario 2010, the energy demand in the year 2020 is about 11% lower (see Fig. 8), while the share of the RES increases from 37.3%, in 2010, to 64.1% in 2020. Table 6 summarizes the most relevant values of the demand and RES generation.

Table 6. Characteristics of the load and RES generation for selected scenarios.

	2010		2020
	Load	RES generation	Load	RES generation
Pmin (GW)	1.07	0.0	0.96	0.0
Pmax (GW)	2.85	3.53	2.71	5.19
Paverage (GW)	2.05	0.77	1.83	1.17
Load factor	0.632	0.217	0.632	0.226
Full load hours (h)	5539	1899	5539	1975
Energy (TWh)	17.96	6.70	16.0	10.25

Figure 7. Hourly electric power demand profile for the scenario 2010.

Figure 8. Hourly electric power demand profile for the scenario 2020.

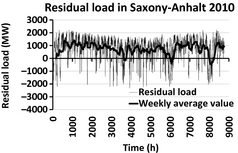
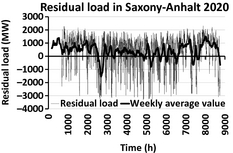
The hourly profiles of the RL are depicted in Figures 9, 10 for 2010 and 2020, respectively. For the scenario 2010 the maximal value of the negative RL was evaluated as 2.2 GW. This value significantly increases up to 3.3 GW for the scenario 2020. The maximum value of the positive RL does not vary so much from scenario 2010 to scenario 2020: In both scenarios a RL of 2.3 GW was estimated.

Figure 9. Residual load for the year 2010.

Figure 10. Residual load for the year 2020.

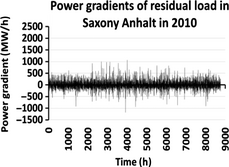
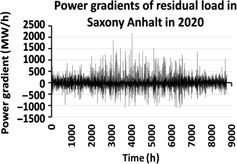
By analyzing the Residual Load Gradient (RLG) for both scenarios it can be seen that these profiles have a more uniform characteristic. In fact, the extreme values for the scenario 2010 are +1.05 GW/h and −1.17 GW/h (see Fig. 11), while for scenario 2020 they are +2.17 GW/h and −1.11GW/h (see Fig. 12).

Figure 11. Residual load gradient for the scenario 2010.

Figure 12. Residual load gradient for the scenario 2020.

Analysis of the Residual Load profile with an A-CAES system

The storage located in the power system can also support the network by balancing the RL. This function can save the investment in the reinforcement of power lines for local peak RL and, in this case, to help in the higher but also more efficient integration of renewables. The investigation uses as input the evaluated RL, which has to be balanced through the conventional power plants, the storage, and in the RES-based plants. In case of negative RL, it is balanced firstly by activating the A-CAES (charging phase), secondly by decreasing the generated power of the conventional plants (according to their generation costs and their technical parameters), and finally (if necessary) by “switching off” the power plants based on RES. In the case of positive RL, it is firstly balanced by discharging the power from the A-CAES, then by increasing the power from conventional power plants (according to their generation costs and technical parameters), and finally (if necessary) by importing power from an external source.

Residual Load Gradient

In order to estimate RLG, the load flow in the analyzed network was computed and the value of the RLG was found. By comparing the analyzed network with the case in which the storage was not used (benchmark case), in the scenario 2010, the maximal absolute value of the RLG was reduced by 8.6% (from 1052 MW/h to 962 MW/h), while the minimal absolute value was reduced by 7.7% (from −1172 MW/h to −1082 MW/h). Moreover, the A-CAES storage is operated 442 full cycles each year which corresponds, on average, to 1.21 full charges and discharges per day. These values are quite similar to those simulated for the scenario 2020, where the usage of the A-CAES increases by about 8% (480 full charging/discharging cycles per year) compared to the scenario 2010. The main results of the analysis are summarized in Table 7.

Table 7. Residual load gradient reduction using the A-CAES.

	RLG without A-CAES (MW/h)	RLG with A-CAES (MW/h)	Var. (%)	Full charging/discharging cycles
Scen., Scenario; RLG, Residual Load Gradient; Var., Variation; Av., Average; abs., absolute.
Scen. 2010
Max	1052	962	−8.6	442
Min	−1172	−1082	−7.7
Av. of abs. value	130	98	−24.5
Scen. 2020
Max	2172	2082	−4.1	480
Min	−1114	−1024	−8.1
Av. of abs. value	170	135	−20.3

Residual Load balancing costs analysis

The costs for balancing the RL were estimated as:

• redispatching costs for the four conventional power plants;
• costs for switching off the plants based on RES (only the wind turbines were considered);
• costs to import electricity;
• investment costs of the A-CAES system (levelized costs).

The redispatching costs were evaluated considering an optimal scheduling of the plants which aimed to minimize the fuel costs in each time step i (hour) (see eq. (4)). Two categories j of power plants were considered: the CCGT and the coal power plants. The optimal scheduling was subjected to the following constrains:

1. (a)Power balance, see equation (4);
2. (b)Maximal and minimal power capacity of each power plant category, see equations (6) and (7);
3. (c)State Of Charge (SOC) of the energy storage system, see equation (8);
4. (d)Maximal power flow on the transmission lines, see equation (9).

A linear programming algorithm based on Matlab^® (Natick, MA, United States) was used as an optimization tool. As the optimization considers hourly time steps, and as the ramp rate for the coal power plant and the CCGT are, respectively, in the order of 3% and 5% per minute [38], no ramp-up and ramp-down limitations were considered.

$min\lbrace fuel\quad costs(i)\rbrace ;$

(4)

${\begin{array}{cl}&\sum _{j=1}^{2}P_{j}\left(i\right)=P_{RL}\left(i\right)\mp \\&P_{A-CAES}\left(i\right)+P_{loss}\left(i\right)\end{array}};$

(5)

$P_{1,min}\leq P_{1}\left(i\right)\leq P_{1,max};$

(6)

$P_{1,min}\leq P_{2}\left(i\right)\leq P_{1,max};$

(7)

${SOC}_{min}\leq SOC\left(i\right)\leq {SOC}_{max};$

(8)

$\vert P_{zy}\vert \leq P_{zy,max}.$

(9)

Concerning the evaluation of the costs caused by switching off the plants based on RES, it was assumed that only the wind turbines could be switched off. To estimate these costs, the German law, which supports the generation from RES, was considered [40]. Taking into consideration this law, the operators of plants based on RES may receive remuneration not only if their plants are producing electric power but also if the power they might produce could not be fed into the grid. In this study it was considered that the operators of wind turbines receive 66.2 € for each MWh of electricity. The import costs were estimated for the cases when the positive RL cannot be satisfied by the existing conventional power plants and by the A-CAES. In this case, the system operator has to buy the power from other networks at the corresponding market price. Due to the lack of hourly information on the spot market prices, an average value of the European Power Exchange (EPEX) spot daily index for the year 2009 was considered, which was 42.84 € per MWh.

The yearly investment costs for the A-CAES system were evaluated according to the Levelized Unit Energy Costs Method and with the assumptions listed in section: “Specification of physical and economic parameters of the A-CAES System”.

Cost–Benefits Analysis: Results and Sensitivity Analysis

Cost – benefit analysis

The use of an A-CAES system represents a cost (mainly an investment cost) for the network operator. On the other hand, by using it the redispatching costs, the costs for reducing or disconnecting the wind turbines, as well as the costs to import electricity from other networks may be reduced. In fact, by comparing the benchmark scenario (without the A-CAES) with the scenarios with the A-CAES, the benefits that the A-CAES brings to the system are evident: the power generation from wind sources increases by 30.19 GWh (for the scenario 2010) and by 35.45 GWh (for the scenario 2020). At the same time, the imported energy decreases by 22.74 GWh for the scenario 2010 and by 27.16 GWh for the scenario 2020. In comparison with the scenario 2010, in the scenario 2020 the amount of wind energy fed into the electric network decreases by 0.5 TWh. This is mainly due to two factors: the overall reduction in energy demanded and the increase in installed PV power. Table 8 summarizes the main benefits obtained by the A-CAES.

Table 8. Benefits obtained by the usage of the A-CAES system.

Scenario	2010	2020
Electricity producible by wind turbines (TWh/year)	6.19	7.68
Electricity produced by wind turbines (TWh/year)	4.00	3.50
Wind energy not fed into the grid (GWh)	2.19	4.18
Increase in wind generation in comparison with the scenario without A-CAES (GWh/year)	30.19	35.45
Max imported power (MW)	861.2	934.1
Yearly imported energy (GWh)	432.53	297.86
Reduction in imported energy in comparison with the scenario without A-CAES (GWh/year)	−22.74	−27.16

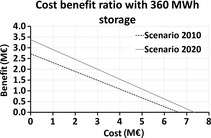
However, although the A-CAES is beneficial to the network operator, the costs that the network operator has to face to build it are still higher than the benefits it provides, and an investment in it could not be justified for the assumed boundary conditions (see Fig. 13). This result does not only depend on the assumed investment costs of the A-CAES but also on its storage capacity and on its modus operandi. It is presumable that if the A-CAES worked as “market-price driven”, then the economic benefits it could bring to the network could be higher. However, the question in this study is as follows: with the assumed modus operandi, how much should the A-CAES cost and how much storage capacity should it have in order to have higher benefits than costs?

Figure 13. Cost–benefit ratio for the scenario 2010 (black line) and the scenario 2020 (gray line).

Sensitivity analysis

The aim of the sensitivity analysis is as follows:

• (a)to find the relation that the A-CAES investment costs, its storage capacity, and the electricity market price have on the costs and benefits;
• (b)to identify the limit values, referring to the A-CAES investment costs and its storage capacity, by which the benefits associated with the use of the A-CAES are higher than their costs.

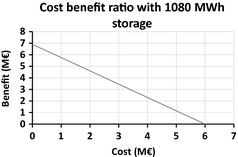
Therefore, with a varying electricity market price of ±20%, the minimal A-CAES investment cost and its minimal storage capacity were found. By analyzing all the possible combinations, the sensitivity analysis shows that if the A-CAES investment costs were lower than 800 € per kW and if the storage capacity was at least 1080 MWh, then the use of the A-CAES could be justified as the benefits would be higher than the costs (see Fig. 14).

Figure 14. Cost–benefit ratio with a storage capacity of 1080 MWh and with an investment cost of 800 €/kW.

Conclusions

In this study, part of the German electric power network, which is characterized by a very high penetration level of RES generation, with a planned storage system in form of A-CAES was modeled and analyzed.

The technical investigation of the storage use was done under consideration of time series for generation, load, and storage with a 1-h resolution for two different years – 2010 and 2020. Generally, the investigation was focused on the short-term balancing of RES fluctuation and the target was to maximize the RES integration while keeping costs at a minimum. Additionally, the variation in the RES power gradients and the RLGs for both years was pointed out. To balance the RLG, an A-CAES system, whose technical data are based on the ADELE project, with a storage power of 90 MW and a storage capacity of 360 MWh, was modeled and the related benefits as well as the related costs were estimated. In the evaluation of the cost–benefit, it was assumed that the A-CAES did not operate as market driven. It can be summarized that the benefits of an enhanced integration of RES into the grid alone do not yet justify the energy storage investment costs under current market boundary conditions. The analysis shows that in order to gain economic benefits from the ESS, the investment costs should be lower than 800 € per kW and the storage capacity should be higher than 1080 MWh for the assumed energy prices. Hence, to estimate the entire value of such a tool in the electricity supply system, other benefits related to the implementation of storage need to be considered, such as “optimization of the conventional back-up power plant fleet” (i.e., avoidance of partial load and shut downs), black start capability, or ancillary grid services.

Conflict of Interest

None declared.

References

1. EWEA. 2011. Wind energy and EU climate policy, achieving 30% lower emission by 2020. European Wind Energy Association (EWEA), Brussels, BE, October 2011. Available at http://www.ewea.org/fileadmin/files/library/publications/reports/20110909_ClimateReport.pdf (accessed January 1, 2014).
2. EPIA. 2012. Connecting the sun, solar photovoltaic on the road to large scale grid integration. European Photovoltaic Industry Association (EPIA), Brussels, BE, September 2012. Available at http://www.epia.org/fileadmin/user_upload/Publications/Connecting_the_Sun_Full_Report_converted.pdf (accessed January 1, 2014).
3. Pickard, W. F., A. Q. Shen, and N. J. Hansing. 2009. Parking the power: strategies and physical limitations for bulk energy storage in supply-demand matching on a grid whose input power is provided by intermittent sources. Renewable Sustainable Energy Rev.13:1934–1945.
4. Styczynski, Z. A., P. Lombardi, R. Seethapathy, M. Piekutowski, M. Ohler, B. Roberts, et al. 2009. Electric energy storage and its tasks in the integration of wide-scale renewable resources. ”; CIGRE- PES Symposium, Calgary, Canada.
5. Crotogino, F. 2010. Compressed Air Energy Storage caverns to integrate fluctuating wind energy within transmission grids in Germany. Underground Storage of CO2 and Energy - Proceedings of the Sino-German Conference, and the Sino-German Workshop – Eor and New Drilling Technology.
6. Lerch, E. 2007. Energy storage to balance wind power fluctuations. Proceedings of the 3rd IASTED Asian Conference on Power and Energy Systems, AsiaPES.
7. US Department of Energy. 2013. Grid energy storage. Available at http://energy.gov/sites/prod/files/2013/12/f5/Grid%20Energy%20Storage%20December%202013.pdf (accessed January 1, 2014).
8. RWE. 2010. ADELE-adiabatic compressed air energy storage for energy supply. Essen, Germany, January 2010. Available at http://www.rwe.com/web/cms/mediablob/en/391748/data/364260/1/rwe-power-ag/innovations/adele/Brochure-ADELE.pdf (accessed January 1, 2014).
9. Armaroli, N., and V. Balzani. 2011. Towards an electricity-powered world. Energy Environ. Sci.4:3193.
10. Otti. 2012. Power to Gas. Regensburg, Germany. ISBN 978-3-941785-98-4.
11. Henel, M. 2012. Ergebnisse aus der Innovations offensive p2 g Projekt (Konzepte, Fallstudien, Einspeisung in das Gasnetz, etc) Power To Gas Forum, October 2012. Regensburg, Germany. ISBN 978-3-941785-98-4.
12. Pickard, W. F., N. J. Hansing, and A. Q. Shen. 2009. Can large-scale advanced-adiabatic compressed air energy storage be justified economically in an age of sustainable energy?J. Reneable Sustainable Energy1:033102. doi: 10.1063/1.3139449
13. Norris, B. L., J. Newmiller, and G. Peek. 2007. NAS^® Battery Demonstration at American Electric Power A Study for the DOE Energy Storage Program. Sandia National Laboratories, Albuquerque, New Mexico and Livermore, California.
14. EPRI-DOE. 2003. Handbook of energy storage for transmission and distribution applications. Washington, DC.
15. VDE-Study. Energy storage in power supply systems with a high share of renewable energy sources. 2008.
16. Yun, T. S., J. Lee, S. Lee, A. J. Kim, and H. Yoon. 2011. Geothecnical Issues related to renewable energy. Journal of Civil Engineering15:635–642.
17. Bidini, G., C. V. Grimaldi, and I. Postrioti. 1999. Performance analysis of a hydraulic air compressor. I. Mech. E. Proc. Inst. Mech. Eng.213 pt. A:191–203.
18. Kim, Y., J. Lee, S. Kim, and D. Favrat. 2012. Potential and evolution of compressed air energy storage: energy and exergy analyses. Entropy14:1501–1521.
19. Coney, M. W., P. Stephenson, A. Malmgren, and C. Linnemann. 2002. Development of a reciprocating compressor using water injection to achieve quasi-isotheral compression. ”, 16th Int Compressor Eng. Conf, West Lafayett, IN, July, Pp. 16–19.
20. Grazzini, G., and A. Milazzo. 2012. A thermodynamic analysis of multistage adiabatic CAES. Proceeding of the IEEE, Vol 100, No 2, February 2012.
21. Nyserda. 2009. Compressed energy storage engineering and economic study. New York, NY.
22. General Electric. Adele′s receipt for energy storage, Energy 2.0, pp. 29–31, May 2012. Available at http://www.ge.com/europe/downloads/Adeles_recipe_for_energy_storage_26_06_12.pdf (accessed January 1, 2014).
23. Pressemitteilungen 2009 des statistischen Landesamtes Sachsen-Anhalt. Available at http://www.stala.sachsen-Anhalt.de/Internet/Home/Veroeffentlichungen/Pressemitteilungen/2009/12/153.html. (accessed January 1, 2014).
24. Ministerium für Landesentwicklung und Verkehr des Landes Sachsen-Anhalt, Stabstelle Demografische Entwicklung und Prognosen. Bevölkerungsprognose für Sachsen-Anhalt bis 2025, Sachsen-Anhalt BevProg_2025_Analyse.pdf.
25. Bundesministerium für Umwelt, Naturschutz und Reaktorsicherheit. Leitstudie 2010 Langfristszenarien und Strategien für den Ausbau der erneuerbaren Energien in Deutschland bei Berücksichtigung der Entwicklung in Europa und global. December 2010 Available at http://www.erneuerbare-energien.de/fileadmin/ee-import/files/pdfs/allgemein/application/pdf/leitstudie2011_bf.pdf (accessed January 1, 2014).
26. Regionales Klimamodell REMO. Available at http://www.remo-rcm.de/REMO-UBA.1189.0.html (accessed January 1, 2014).
27. Happold, H., and D. Oeding. Elektrische Kraftwerke und Netze 5. Auflage, ISBN 3-540-08305-7, Springer 1.
28. Kaltschmitt, M., W. Streicher, and A. Wiese. 2007. Renewable energy: technology, economics, and environment. Springer, Berlin, ISBN 3540709479, 9783540709473.
29. Ray, M. L., A. L. Rogers, and J. G. McGowan. 2006. Analysis of wind share models and trends in different terrains. Conference Proceeding: American Wind Energy Association Windpower, Anaheim, 22–25 May 2006.
30. Enercon EN_Produktuebersicht_0710 Erzeugungkennlinie einer Windkraftanlage mit Sturmregelung.
31. Heuck, K., and K. D. Dettmann. 1995. Elektrische Energieversorgung. 3, Auflage, ISBN 3-528-28547-8, Vieweg-Verlag 1995.
32. GoogleEarth. Available at: http://www.google.com/earth/index.html (accessed January 1, 2014).
33. Ministerium für Wissenschaft und Wirtschaft Sachsen-Anhalt. Energiebericht des Landes Sachsen-Anhalt 2008. Juli 2011.
34. Zero Emission Platforms. The costs to capture CO₂, transport and storage. Available at www.zeroemissionsplatform.eu/library/ publication/165-zep-cost-report-summary.html (accessed January 1, 2014).
35. Hawary, M., and G. Christensen. 1979. Optimal economic operation of electric power systems. Richard Bellman, University of Southern California. ISBN: 0122368509.
36. Cavallo, A. 2007. Controllable and affordable utility-scale electricity from intermittent wind resources and compressed air energy storage (CAES). Energy32 pt:120–127.
37. Styczynski, Z. A., P. Lombardi, R. Seethapathy, M. Piekutowski, C. Ohler, B. Roberts et al. Electric energy storage systems. Electra 255, April 2011, CIGRE Paris. ISBN: 978- 2- 85873- 147-3.
38. Holttinen, H., A. Orths, et al. 2009. Design and operation of power systems with large amounts of wind power – Final report pase one 2206-2008. IEA WIND Task 25, Helsinki.
39. Bundesministerium für Umwelt und Reaktorsicherheit. Zeitreihen zur Entwicklung der erneuerbaren Energien in Deutschland. Availble at http://www.erneuerbare-energien.de/die-themen/datenservice/zeitreihen-entwicklung-ab-1990/, December 2013, (accessed 22 March 2014).
40. Bundesministerium für Umwelt. Naturschutz und Reaktorsicherheit. Available at http://www.bmu.de/erneuerbare_energien/downloads/doc/40508.php (accessed January 10, 2010).