Resumo
O presente trabalho tem como finalidade implementar e avaliar uma estratégia generalizada baseada no método da compatibilidade de deformações (MCD) para a obtenção das curvas de resistência e de início de plastificação de estruturas mistas de aço e concreto. Devido à anisotropia do concreto, a definição da resistência de seções transversais que possuem tal material em sua composição não é tão simples como nas estruturas metálicas. Recorre‐se ao método da rótula plástica refinado (MRPR) para realizar, via método dos elementos finitos (MEF), análises avançadas, ou seja, considerando conjuntamente os efeitos não lineares geométricos e físicos. Desse modo, a perda gradual da rigidez no MRPR é determinada através da combinação de esforço normal e momento fletor na seção transversal. Para a solução das equações não lineares global e local (a nível da seção transversal) utiliza‐se o método iterativo de Newton‐Rahpson acoplado a estratégias para passar por pontos críticos. Apresentam‐se análises numéricas avançadas de sistemas estruturais mistos de aço e concreto através da formulação implementada. Os resultados obtidos são comparados com respostas numéricas e experimentais presentes na literatura.
Abstract
This work presents the computational implementation and evaluation of a generalized strategy based on Strain Compatibility Method to obtain the initial and full yield curves of steel‐concrete composite structures. Due to anisotropy of concrete the evaluation of the full yield capacity of cross sections that have this material in its compostion is not so simple as for steel structures. Use is made of the Refined Plastic Hinge Method (RPHM) to perform, via Finite Element Method (FEM), the advanced analysis considering simultaneously second order and inelasticity effects. Thus, the gradual decrease of the stiffness in RPHM is determined by a section combination of axial force and bending moment. The Newton‐Raphson method with path‐following strategies is adopted for solving the nonlinear global and local (in cross section level) equations. Advanced numerical analysis of composite steel‐concrete structural systems are performed through the presented numerical formulation and the results obtained here are compared with experimental and numerical data given in the literature.
Palavras‐chave
Análise não linear ; Estruturas mistas ; Método dos elementos finitos ; Método da compatibilidade de deformações ; Método da rótula plástica refinado ; Curvas de resistência
Keywords
Nonlinear Analysis ; Composite Structures ; FEM ; Strain Compatibility Method ; Refined Plastic‐Hinge Method ; Yield Curves
1. Introdução
Na concepção dos projetos estruturais na engenharia civil, os projetistas iniciam os cálculos baseados em 3 premissas: segurança, tempo (elaboração dos projetos e execução da obra) e economia. Para se atingir o equilíbrio entre essas variáveis há uma gama de materiais e métodos disponíveis. De forma isolada, o aço e o concreto são os materiais mais utilizados na construção civil.
A associação do aço e do concreto visa, fundamentalmente, o melhor aproveitamento físico e mecânico desses materiais [1] . Dessa forma, as estruturas mistas de aço e concreto apresentam vantagens no que diz respeito à resistência, rigidez, proteção dos elementos metálicos (incêndio e corrosão), custo‐benefício, etc. As estruturas mistas também possuem vantagens durante a execução. Durante a cura do concreto, esse pode ser suportado por perfis metálicos e fôrmas, reduzindo gastos com escoramentos e aumentando o espaço livre de circulação na obra.
Apesar do uso generalizado de sistemas mistos de aço e concreto, procedimentos numéricos precisos para a sua análise e concepção não evoluíram da mesma forma como para estruturas de aço. Como consequência, as referências normativas possuem falhas quando aplicadas ao projeto seguro e econômico de estruturas mistas [2] . Landesmann [3] cita que, nas análises de estruturas com alta deslocabilidade, normas de projeto [4] ; [5] ; [6] não são capazes de descrever o comportamento real da estrutura. Além disso, Weng e Yen [7] demonstram experimentalmente que as diferentes formas como as normas de projeto abordam as estruturas mistas também podem aproximar ou distanciar‐se do comportamento estrutural real.
Fong [8] destaca que muitas normas tendem a recomendar o uso de uma análise de segunda ordem e um método de projeto como forma de se obter resultados mais precisos e de maneira eficiente. Alguns trabalhos recentes tiveram como objetivo o propósito de obter formulações numéricas para análise avançada de estruturas mistas de aço e concreto, com base no método da rótula plástica refinado (MRPR) [3] ; [8] . Por sua vez, o MRPR [9] é descrito como método de análise de plasticidade concentrada, já que a consideração da plastificação do material é avaliada nos pontos nodais de cada elemento finito.
Para a avaliação da resistência de elementos mistos de aço e concreto através do método da compatibilidade de deformações (MCD), 2 estratégias de solução se destacam. Abordado no presente trabalho, em um raro acoplamento ao MRPR, o método de Newton‐Raphson [10] ; [11] usa como variáveis de ajuste a deformação axial no centroide plástico (CP) da seção e a curvatura em um dos eixos principais (problema 2 D). Determina‐se então a deformação axial em cada ponto discreto da seção e utilizam‐se as respectivas relações constitutivas para o somatório de tensões. O procedimento consiste na construção da relação momento‐curvatura (problema não linear), onde, para um dado esforço axial, o ponto limite de momento fletor encontrado reflete a combinação Normal‐Momento responsável pela plastificação da seção. Tal metodologia é abordada na Seção 2 deste trabalho. Adeptos dos métodos quasi‐Newton, alguns autores [12] ; [13] utilizam esse procedimento de solução para problemas não lineares acoplado ao método da falsa posição. O processo consiste na determinação da posição da linha neutra e sua orientação, no caso de problemas tridimensionais, que são os parâmetros ajustados no ciclo iterativo. Com isso, podem‐se obter os esforços internos resistentes.
Tem‐se como objetivo neste trabalho acoplar o MCD ao MRPR e, juntamente com o conceito de rigidez homogeneizada [14] , proporcionar à plataforma Computational System of Advanced Structural Analysis[15] – CS‐ASA – a possibilidade de realizar análises avançadas de estruturas mistas. Além disso, para ampliar a gama de possibilidades de análise, prescrições normativas [5] ; [16] para obtenção da capacidade resistente dos elementos foram também implementadas. Torna‐se assim possível avaliar o comportamento estrutural de elementos mistos em relação às considerações normativas, comparando‐o com resultados obtidos através da formulação generalizada, proposta através do acoplamento MRPR/MCD.
O problema estrutural não linear global, no contexto do método dos elementos finitos (MEF) e MRPR/MCD, é resolvido por meio da seguinte equação:
|
|
( 1) |
sendo Fi o vetor de forças internas, que é escrito em função do vetor de deslocamentos nodais U , esforços internos nos membros, P , e do parâmetro de avaliação da degradação da rigidez à flexão da seção, Sh . O vetor de forças externas é definido pelo produto entre o parâmetro de carga, λ, e Fr , que é o vetor de forças externas de referência.
Para cada passo de carga, a primeira etapa na solução de (1) envolve a avaliação da chamada solução incremental predita (Δλ0 e ΔU0 ). Para isso, o incremento inicial do parâmetro de carga, Δλ0 , é determinado através de alguma estratégia, que neste trabalho é feita através da técnica do deslocamento generalizado [17] . Em seguida, pode‐se determinar o incremento inicial dos deslocamentos nodais, ΔU0 , através de uma analogia ao sistema KU = F . Porém, em um problema estrutural não linear, dificilmente a solução predita define uma configuração de equilíbrio do sistema. Dessa forma, numa segunda etapa, são necessárias correções nessa solução predita, que neste trabalho é feita através do método de Newton‐Raphson e técnicas de continuidade para obtenção do traçado completo da trajetória de equilíbrio. A correção do parâmetro de carga ao longo do processo iterativo é feita aqui através da norma mínima dos deslocamentos residuais [18] acoplada ao método de Newton‐Raphson.
O presente artigo está organizado em mais 4 seções. Na Seção 2 é apresentado o MCD, juntamente com as relações constitutivas utilizadas e o modelo de discretização da seção transversal. Mais adiante, na Seção 3, a formulação numérica baseada no MRPR [9] é detalhada, incluindo o conceito de rigidez homogeneizada, na montagem da matriz de rigidez do elemento. São simulados alguns problemas na Seção 4 para validação da metodologia proposta, que vão desde a obtenção da capacidade resistente de seções transversais isoladas até ao comportamento de sistemas estruturais bidimensionais. A formulação utilizada permite fazer comparações com prescrições normativas tais como o AISC [16] e o Eurocode 4 [5] . Por fim, alguns aspectos importantes observados nos exemplos estudados são levantados na Seção 5.
2. Método da compatibilidade de deformações
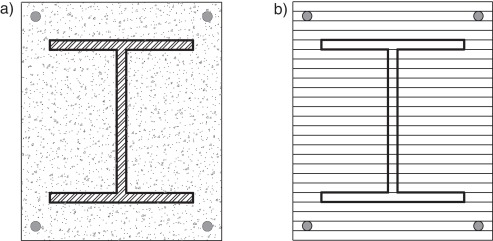
Esse método busca acoplar a configuração deformada da seção às relações constitutivas dos materiais que a compõem. Deve‐se definir então uma forma de discretização para que as deformações da seção sejam capturadas da forma mais eficiente possível. A divisão da área em fatias (problema bidimensional), como ilustrado na figura 1 , fornece bons resultados [13] ; [14] , mas é sensível ao grau de refinamento imposto pelo analista.
|
|
|
Figura 1. Discretização da seção transversal em fatias: (a) seção transversal, (b) discretização em fatias. |
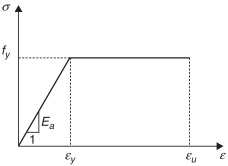
Neste trabalho, optou‐se por utilizar o método iterativo de Newton‐Raphson com uma estratégia de incrementos constantes para a obtenção da relação momento‐curvatura. Sendo assim, as relações tensão‐deformação dos materiais foram utilizadas. Para o aço, foi adotada uma relação constitutiva elastoplástica perfeita, ilustrada na figura 2 , em que:
|
|
( 2) |
sendo fy a resistência de escoamento, Ea o módulo de elasticidade do aço, ɛy e ɛu as deformações de escoamento e última, respectivamente.
|
|
|
Figura 2. Relação constitutiva do aço. |
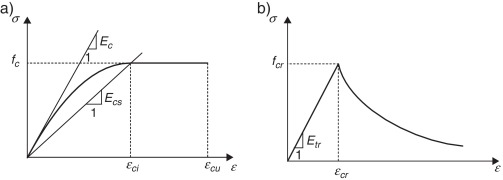
Para o concreto, a relação constitutiva é definida através de 2 trechos. Quando comprimido, o diagrama parábola retângulo é adotado (fig. 3 a), limitado pela deformação última do concreto à compressão, ɛcu . Há ainda a possibilidade da consideração, ou não, da resistência à tração dada por trecho linear até que a deformação de início de fissuração, ɛtr , seja atingida, juntamente com a máxima resistência à tração, fcr (fig. 3 b). Dessa forma, tem‐se:
|
|
( 3) |
em que fc e fcr são as resistência máxima à compressão e à tração do concreto, respectivamente. Vale ressaltar que fcr é dada como uma função de fc , sendo obtida por 1,4(fc /10)2/3 . Ec , Ecs e Etr são, respectivamente, os módulos de elasticidade tangente inicial, secante e à tração do concreto, ɛci é a deformação limite do regime parabólico do concreto à compressão, α1 é o fator que considera a interação das barras longitudinais com o concreto, e α2 é o fator que considera os efeitos de duração da carga e cargas cíclicas. Os parâmetros α1 e α2 são obtidos de forma experimental, porém Chiorean [11] utiliza valores fixos em suas análises (α1 = 1 e α2 = 0,75). Dessa forma esses mesmos valores serão adotados neste trabalho.
|
|
|
Figura 3. Relação constitutiva do concreto: (a) compressão, (b) tração. |
2.1. Relação momento‐curvatura
Uma vez discretizada a seção transversal, 2 variáveis são relevantes para se empregar o MCD acoplado ao método de Newton‐Raphson: a área das fatias e sua respectiva posição. Essa segunda é referenciada ao CP, já que alguns pesquisadores [10] ; [12] ; [19] apontam que dessa forma os problemas de convergência são minimizados.
A posição do CP da seção é obtida através da seguinte expressão [20] :
|
|
( 4) |
com Ac , Aa e Ab sendo as áreas de concreto, do perfil metálico e da armadura longitudinal; γ é um coeficiente que indica se o concreto está confinado (γ = 1,0) ou não (γ = 0,85); yc , ya e yb são as coordenadas do centroide, das respectivas áreas no eixo das ordenadas, em relação a um sistema de referência; e fcd , fyd e fybd são a resistência de cálculo do concreto, as resistências de escoamento de cálculo do perfil e das armaduras, respectivamente.
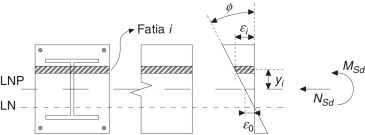
A figura 4 ilustra a distribuição de deformações na seção mista para uma combinação de esforços axial e de momento fletor. Note que a deformação axial na i ‐ésima fatia, ɛi , é dada por uma função linear já que foi adotado que os elementos apresentarão interação total. Escreve‐se assim:
|
|
( 5) |
em que yi é a distância entre os CP da fatia analisada e da seção transversal, ɛ0 é a deformação axial no CP da seção e ϕ , a respectiva curvatura.
|
|
|
Figura 4. Campo de deformações bidimensional. |
Para a notação matricial adotada a seguir, as variáveis ɛ0 e ϕ serão posições do vetor de deformações X = [ɛ0ϕ ]T . Chiorean [11] ressalta que adotando X = 0 na primeira iteração, a convergência é atingida mais rapidamente. Numericamente, pode‐se dizer que o equilíbrio da seção é obtido quando a seguinte equação é satisfeita:
|
|
( 6) |
em que o vetor de forças externas fext é dado pelo esforço axial, N , e pelo momento fletor, M , ou seja:
|
|
( 7) |
Já o vetor de forças internas é dado por expressões integrais clássicas para o esforço axial, Nint , e momento fletor, Mint . Uma vez conhecidas as áreas, Ai , e posições, yi , de cada fatia, a integral passa a ser o somatório descrito como:
|
|
( 8) |
Embora seja eficiente iniciar o processo com X = 0 , a convergência só é atingida na primeira iteração se as forças externas forem nulas. Assim, para a iteração seguinte, k + 1, o vetor de deformações é dado por:
|
|
( 9) |
na qual F’ é a matriz de rigidez tangente da seção transversal ou matriz Jacobiana do problema não linear expresso na Equação (6), isto é:
|
|
( 10) |
em que ET,i são os módulos de elasticidade tangentes dos materiais presentes em cada fatia.
O critério de convergência adotado neste trabalho [11] é baseado na razão das normas Euclidianas do vetor de forças desequilibradas, F , e do vetor de forças externas, fext . Assim, escreve‐se:
|
|
( 11) |
com Tol sendo a tolerância, assumida igual a 10−5 , como proposto por Chiorean [11] .
Na tabela 1 é detalhado, na forma de algoritmo, o processo de obtenção da relação momento‐curvatura.
| 1. | Leitura dos dados da seção transversal e dos materiais |
|---|---|
| 2. | Discretização da seção em fatias |
| 3. | Obtenção do centroide plástico CP (Equação 4) |
| 4. | Translação do sistema de referência para o CP |
| 5. | Inicialização: X = 0 |
| 6. | para cada incremento de momento fletor faça |
| 7. | Monta‐se fext |
| 8. | para k = 1, nmax faça |
| 9. | Determina‐se ɛ (Equação 5) |
| 10. | Monta‐se fint (Equação 8) |
| 11. | Calcula‐se F (X ) (Equação 6) |
| 12. | se ||F ||/||fext || = Tol → Pare o processo iterativo e siga para linha 16 |
| 13. | Monta‐se a matriz de rigidez tangente da seção F’ (Equação 10) |
| 14. | Verificação da singularidade de F’ |
| 15. | se F’ é singular → Momento último resistente encontrado–parar processo |
| 16. | Correção do vetor de deformações X (Equação 9) |
| 17. | fim para |
| 18. | fim para |
2.2. Curvas de resistência
Quando, para um dado esforço axial, é atingido o momento máximo da relação momento‐curvatura, tem‐se a plastificação total da seção. Define‐se então, que esse par de esforços é um ponto da curva de resistência.
A curva de início de plastificação também é obtida da relação momento‐curvatura. Quando a primeira fatia da seção apresenta deformação axial, ɛ , maior que a deformação de início de escoamento do aço (do perfil e das barras longitudinais) e/ou a deformação de início de plastificação do concreto, a fatia inicia o processo de degradação e consequentemente a seção perde rigidez. O momento responsável por esse fato é tido como momento de início de plastificação.
2.3. Curva de início de plastificação simplificada
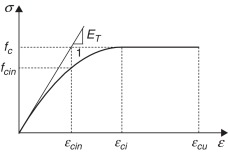
Para viabilizar o uso do MRPR com algumas metodologias de normas de projeto foi necessário introduzir um limite para o regime elástico, combinando esforço normal e momento fletor. Fong e Chan [21] propuseram que uma deformação de início de degradação para o concreto poderia ser determinada relacionando a lei de Hooke com a relação constitutiva do concreto sob compressão, como ilustrada na figura 5 .
|
|
|
Figura 5. Relação constitutiva do concreto à compressão com deformação de início de plastificação alterada. |
Com a análise do trecho parabólico definido na Equação (3), define‐se que a deformação ɛcin é igual à metade de ɛci , e consequentemente fcin é dado por 0,75fc . Dessa forma, os esforços isolados, axiais e momentos fletores, que correspondem ao início de degradação da rigidez à flexão da seção são determinados através da soma de tensões elásticas limites desprezando a resistência à tração do concreto.
3. Modelagem numérica via método da rótula plástica refinado
A definição da capacidade resistente dos elementos estruturais descrita na seção anterior foi introduzida à plataforma computacional CS‐ASA [15] . Esse programa, que vem sendo desenvolvido ao longo dos anos, já é consolidado para análises não lineares de estruturas de aço, utilizando metodologias para análise da plasticidade concentrada, nos pontos nodais, tal como o MRPR [9] . As considerações feitas na Seção 2, juntamente com o conceito de rigidez homogeneizada, viabilizam a análise não linear de estruturas mistas de aço e concreto.
As hipóteses descritas a seguir são consideradas na modelagem das estruturas a serem analisadas:
- interação total entre os materiais presentes na seção transversal;
- todos os elementos são inicialmente retos e prismáticos, e o empenamento é desconsiderado;
- considera‐se que o sistema estrutural é perfeitamente travado no eixo ortogonal ao plano da estrutura, caracterizando um problema bidimensional;
- efeitos de instabilidade localizados são desprezados;
- grandes deslocamentos e rotações de corpo rígido são permitidos;
- os efeitos de deformações causadas pelo cisalhamento serão desprezados.
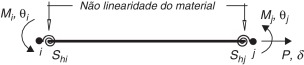
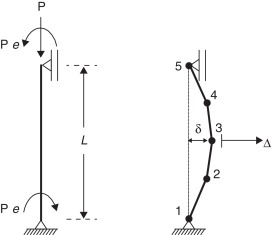
Na modelagem do sistema estrutural via MEF utiliza‐se o elemento finito de pórtico plano delimitado pelos pontos nodais i e j , como mostrado na figura 6 . Também são ilustrados os esforços internos, Mi , Mj e P , e os respectivos graus de liberdade θi , θj e δ , referentes ao sistema corrotacional. São inseridas molas fictícias, de comprimento nulo, nas extremidades do elemento para simular a degradação da rigidez à flexão através do parâmetro Sh .
|
|
|
Figura 6. Elemento finito de viga‐coluna com molas fictícias referenciado ao sistema corrotacional. |
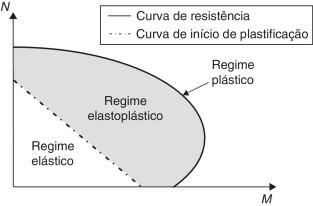
O parâmetro Sh , que é dado por unidade de rigidez à flexão por radianos, é definido dentro de 3 domínios, como ilustrado na figura 7 . Quando em regime elástico, Sh é tido como infinito, em termos numéricos adota‐se 1016 . Tal regime é limitado pela curva de início de plastificação. Uma vez atingido o regime plástico (situação onde as forças internas atingem a curva de resistência), tem‐se a degradação completa da rigidez à flexão. Nesse caso, Sh é tomado, numericamente, como 10−10 .
|
|
|
Figura 7. Diagrama de interação esforço normal momento fletor: definição da rigidez à flexão das molas fictícias. |
Entre as curvas, de início de plastificação e de resistência, considera‐se que a perda de rigidez ocorre de forma gradativa através da seguinte equação:
|
|
( 12) |
em que L é o comprimento do elemento finito; Mpr e Mer são, respectivamente, os momentos resistente último e de início de plastificação, definidos na Seção 2; e (EI )comp é a rigidez à flexão da seção mista homogeneizada, que para seções duplamente simétricas é dada por:
|
|
( 13) |
em que os subscritos a , b e c referem‐se, respectivamente, ao perfil de aço, às armaduras e ao concreto; μ o fator de redução da rigidez flexional de concreto devido à fissuração; e η um coeficiente de redução da rigidez global. Esses últimos são tidos como dados de entrada, já que há uma gama de possibilidades de valores disponíveis na literatura [5] ; [8] ; [16] . No caso de lajes apoiadas sobre perfis I , usa‐se a seguinte expressão [22] :
|
|
( 14) |
sendo Icomp e I’comp os momentos de inércia da seção mista em regiões de momento positivo e de momento negativo, respectivamente, e Ea é módulo de elasticidade do aço do perfil.
Para o elemento ilustrado na figura 6 , a relação força‐deslocamento é expressa por [8] ; [9] ; [13] ; [14] ; [15] :
|
|
( 15) |
em que β = (Shi + kii )(Shj + kjj ) − kjikij . Os subscritos i e j indicam as extremidades do elemento e o subscrito c o sistema de coordenadas utilizado (corrotacional); (EA )comp é a rigidez axial da seção transversal mista homogeneizada; ΔP e ΔM são, respectivamente, o esforço normal e o momento fletor incrementais; Δδ e Δθ são os incrementos de deformação axial e rotação nodais.
Os termos kii , kij , kji e kjj são responsáveis por simular os efeitos de segunda ordem que, neste trabalho, são definidos como [17] :
|
|
( 16) |
sendo Acomp e Icomp propriedades geométricas da seção mista homogeneizada.
Uma vez formadas rótulas plásticas na estrutura, um incremento de carga faz com que as forças internas tendem a violar o domínio resistente naquele ponto. Faz‐se necessária então uma estratégia para que isso não ocorra. Assim, o esforço axial é mantido constante e o momento fletor é reduzido de forma a não violar a curva de resistência. Essa estratégia é denominada return mapping[15] . Uma vez definida a relação força‐deslocamento no sistema corrotacional, deve‐se levá‐la ao sistema global. Maiores detalhes sobre a transformação de sistemas e o return mapping podem ser vistos em Silva [15] .
4. Exemplos numéricos
Nesta seção, as estratégias numéricas apresentadas são utilizadas visando o estudo de sistemas estruturais mistos de aço e concreto. Os exemplos avaliados são divididos em 4 grupos: relação momento‐curvatura, curvas de resistência, coluna isolada e pórtico simples. Ressalta‐se que os resultados encontrados são comparados com os apresentados na literatura, obtidos de forma numérica e/ou experimental. Além disso, é feito um estudo comparativo entre a metodologia generalizada de obtenção da resistência (MCD) e as descritas em normas de projetos.
4.1. Relação momento‐curvatura
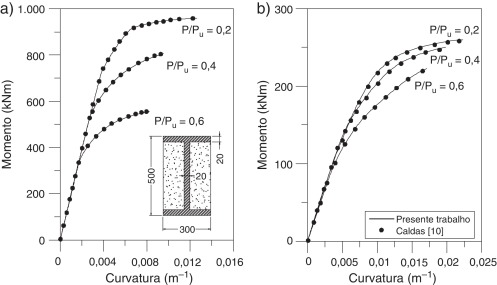
O objetivo deste primeiro exemplo é a construção da relação momento‐curvatura de uma seção mista parcialmente revestida, ilustrada na figura 8 a, que foi inicialmente analisada por Caldas [10] . O aço do perfil I possui módulo de elasticidade de 205.000 MPa e resistência de escoamento de 250 MPa. O concreto utilizado foi confeccionado para atingir uma resistência de compressão característica, fck , de 20 MPa quando o mesmo apresentar deformação entre ‐ 0,0035 e ‐ 0,002. Os coeficientes de minoração da resistência do aço e do concreto são tomados, respectivamente, como 1,10 e 1,40.
|
|
|
Figura 8. Relações momento‐curvatura da seção mista parcialmente revestida: (a) maior inércia, (b) menor inércia. |
As cargas axiais fixas aplicadas na seção para a construção de cada uma das relações momento‐curvatura são frações da carga axial última resistente denominada Pu , tais como 20, 40 e 60%. Considerando um campo de deformações uniforme igual a ‐ 0,002 em todas as 15 fatias da seção discretizada, tem‐se Pu = −6.382,177 kN.
Ressalta‐se que a tração no concreto foi desprezada e foi adotada uma relação constitutiva elástica‐perfeitamente plástica, com ɛu tomado igual a 0,01, para descrever o comportamento do aço.
Os resultados obtidos são ilustrados nas figura 8 a e b para os eixos de maior e menor inércia, respectivamente.
Pode‐se observar na figura 8 uma boa convergência entre os resultados obtidos pelo presente trabalho e por Caldas [10] . Esse autor utiliza para essa mesma análise a curvatura como variável incremental e, além disso, o critério de parada do processo incremental e iterativo é definido pelos domínios de deformação do concreto. Destaca‐se que a estratégia de verificação da singularidade da matriz de rigidez da seção para finalizar o processo realizado nesta pesquisa é eficiente.
4.2. Capacidade resistente de uma seção de concreto armado
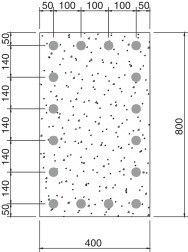
Liu et al. [13] estudaram, por meio de métodos quasi ‐Newton, a capacidade resistente da seção de concreto armado ilustrada na figura 9 . As propriedades dos materiais que compõem a seção são apresentadas na tabela 2 . A tração no concreto é desprezada na análise denominada concreto sem tração (CST) e considerada na análise concreto com tração (CCT), e o aço tem seu comportamento descrito por meio de uma relação tensão‐deformação elástica perfeitamente plástica, com ɛu = 0,01.
|
|
|
Figura 9. Seção de concreto armado (dados em mm). |
| Concreto | fck | 40 MPa |
|---|---|---|
| Ec | 35 GPa | |
| γc | 1,5 | |
| Barras de aço | fys | 355 MPa |
| Eb | 205 GPa | |
| γs | 1,15 | |
| ϕ | 20 mm |
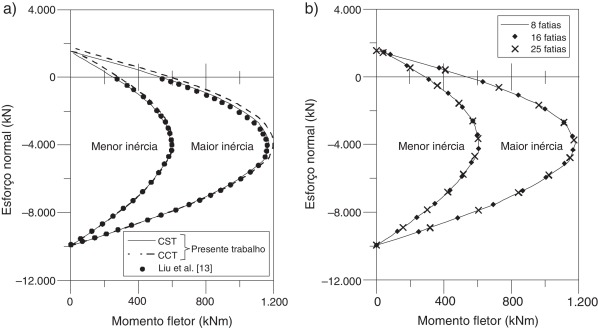
O objetivo deste exemplo é avaliar a capacidade resistente da seção de concreto armado no estado limite último (ELU), para a combinação de esforços normal e momento fletor, tanto no eixo de maior quanto no de menor inércia. Verifica‐se na figura 10 a uma boa convergência nos resultados encontrados no presente trabalho e os apresentados por Liu et al. [13] por meio da metodologia denominada bloco de tensão equivalente, sendo a resistência à tração do concreto desprezada. Nota‐se que a consideração da tração na relação constitutiva do concreto amplifica a resistência da seção em aproximadamente 2% na região acima do esforço normal de compressão igual a 5.000 kN. Isso se deve ao fato de que nesse trecho da curva de resistência algumas fatias da seção passam a apresentar deformações de tração.
|
|
|
Figura 10. Capacidade resistente da seção de concreto armado: (a) comparação com a literatura, (b) Influência da discretização. |
Além da comparação com o resultado presente na literatura, fez‐se um estudo da sensibilidade à discretização da seção transversal. O objetivo desse estudo é avaliar o número mínimo de fatias para que a resposta seja aceitável e, assim, reduzir o número de loops necessários para a montagem da matriz de rigidez e do vetor de forças internas da seção. Essa avaliação se torna importante na simulação de sistemas estruturais com grande número de graus de liberdade, uma vez que é necessária a obtenção das curvas de resistência em cada ponto nodal da estrutura.
Foram testadas 3 discretizações para esse estudo: 8, 16 e 25 fatias. Como ilustrado na figura 10 b, pode‐se concluir que a capacidade resistente obtida com o menor índice de refinamento já é suficiente. Outra conclusão que deve ser ressaltada é que índices de refinamento menores que 8 fatias não satisfazem o critério de parada proposto. Isso ocorre pois as fatias intermediárias não atingem valores de deformação suficientes para a singularização da matriz de rigidez. Pode‐se afirmar que para um número de fatias inferior a 8 a curva de resistência seria determinada quando uma fatia apresentar deformação superior à deformação última de um dos materiais componentes da seção. Em outras palavras, parte da seção ainda estaria em regime elástico.
4.3. Capacidade resistente de uma seção mista de aço e concreto
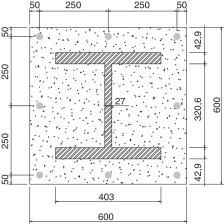
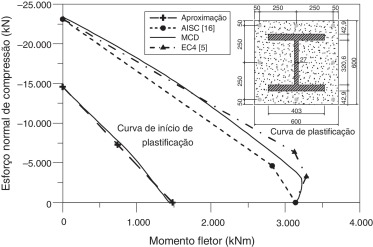
Neste exemplo, uma seção mista totalmente revestida com concreto é estudada (fig. 11 ). As propriedades dos materiais componentes da seção são dadas na tabela 3 e os resultados obtidos aqui são confrontados com os fornecidos em Liu et al. [13] . Além disso, são feitas comparações com as metodologias apresentadas em normas de projeto [5] ; [16] e a metodologia simplificada para a curva de início de plastificação apresentada no item 2.3.
|
|
|
Figura 11. Seção mista (dados em mm). |
| Concreto | fck | 35 MPa |
|---|---|---|
| Ec | 34 GPa | |
| γc | 1,5 | |
| Barras de aço | fys | 460 MPa |
| Eb | 205 GPa | |
| γs | 1,15 | |
| ϕ | 32 mm | |
| Perfil | fy | 355 MPa |
| Ea | 200 GPa | |
| γs | 1,05 |
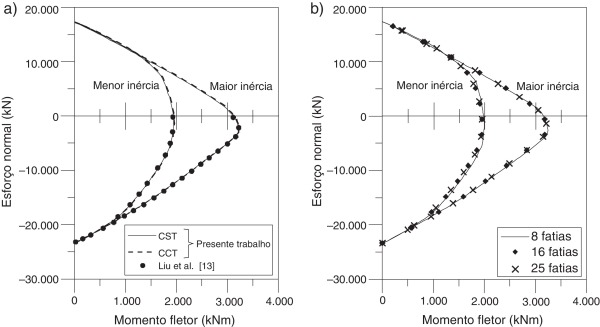
Assim como no exemplo anterior, o MCD acoplado ao método de Newton‐Raphson feito no presente trabalho é satisfatório se comparado com o resultado de Liu et al. [13] , como visto na figura 12 . Na literatura, a curva de resistência é apresentada apenas no trecho referente à combinação do esforço axial de compressão e de momentos positivos. É importante salientar que a consideração da resistência à tração no concreto não é significativa, pois a análise dos pontos das curvas indica um acréscimo médio de 0,5% na resistência nos trechos em que parte da seção encontra‐se tracionada.
|
|
|
Figura 12. Capacidade resistente da seção mista de aço e concreto: (a) comparação com a literatura, (b) influência da discretização. |
Foram realizadas novamente simulações para diferentes discretizações da seção, como visto na figura 12 b. Diferentemente da seção em concreto armado, uma pequena divergência ocorre nos trechos próximos à carga axial nula. Quanto menor o refinamento, nota‐se que a capacidade resistente é levemente superestimada, como mostrado na tabela 4 .
| Eixo | MRd,8 /MRd,16 | MRd,8 /MRd,25 | MRd,16 /MRd,25 |
|---|---|---|---|
| Maior inércia | 1,003 | 1,005 | 1,002 |
| Menor inércia | 1,017 | 1,017 | 1,0 |
Na figura 13 são ilustradas as curvas de resistência obtidas com o MCD, pelo EUROCODE 4 [5] e pelo AISC [16] , além da curva de início de plastificação aproximada. Vale ressaltar que ao mesmo tempo que o AISC [16] é conservador, o EUROCODE 4 [5] apresenta pontos com resistência superior ao MCD. Na mesma figura é mostrada a boa convergência entre a curva de início de plastificação por aproximação linear e a obtida pelo MCD. Assim, pode‐se acoplá‐la aos métodos normativos viabilizando as análises via MRPR.
|
|
|
Figura 13. Curvas de resistência: MCD x prescrições normativas. |
4.4. Colunas mistas isoladas
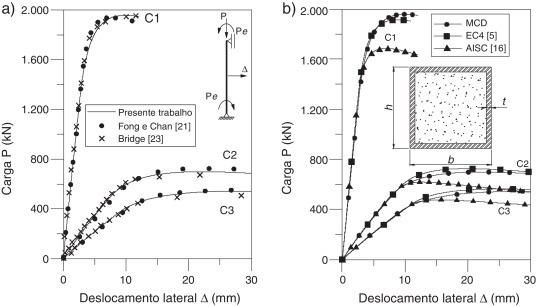
Bridge [23] realizou testes experimentais em pilares tubulares retangulares e seus resultados têm sido estudados por vários pesquisadores [21] ; [24] ; [25] . No presente trabalho, 3 pilares com excentricidade em apenas um dos eixos são simulados, como ilustrado na figura 14 . Os protótipos se diferenciam basicamente pela sua geometria, excentricidade da carga e propriedades dos materiais constituintes. A coluna denominada C1 apresenta menor comprimento, maior seção transversal e materiais mais resistentes do que as demais. Já as colunas C2 e C3 são semelhantes, apresentando diferença apenas na excentricidade da carga vertical aplicada. Esses dados são apresentados na tabela 5 . Foi adotado o módulo de elasticidade do aço igual a 205.000 MPa. Para o concreto, o módulo de elasticidade secante é facilmente obtido pela relação entre a resistência máxima de compressão e a deformação ɛci .
|
|
|
Figura 14. Modelo idealizado para análise de pilares isolados com excentricidade. |
| Espécime | L (mm) | e (mm) | b (mm) | h (mm) | t (mm) | fy (kN/mm2 ) | fc (kN/mm2 ) |
|---|---|---|---|---|---|---|---|
| C1 | 2.130 | 38 | 203,7 | 203,9 | 9,96 | 0,291 | 0,0302 |
| C2 | 3.050 | 38 | 152,5 | 152,3 | 6,48 | 0,254 | 0,035 |
| C3 | 3.050 | 64 | 152,5 | 152,3 | 6,48 | 0,254 | 0,035 |
As trajetórias de equilíbrio obtidas com o CS‐ASA são ilustradas, juntamente com os resultados da literatura, na figura 15 a. As curvas de resistência são determinadas por meio do MCD e de normas [5] ; [16] . Também são apresentadas as cargas últimas atingidas pelas colunas C1, C2 e C3, experimentalmente [23] (PTest ), por Fong e Chan [21] (PFC ) e pelo CS‐ASA (PMCD ), na tabela 6 . Pode‐se verificar a boa concordância entre os resultados obtidos no presente trabalho e os apresentados na literatura.
|
|
|
Figura 15. Trajetórias de equilíbrio: pilares C1, C2 e C3 (a) comparação com a literatura, (b) comparação MCD x normas de projeto. |
| Espécime | PTest | PFC | PMCD | PMCD /PTest | PMCD /PFC |
|---|---|---|---|---|---|
| C1 | 1.956 | 1.938,7 | 1.956,32 | 1,000 | 1,009 |
| C2 | 680 | 723,5 | 699,18 | 1,028 | 0,966 |
| C3 | 513 | 548,6 | 544,16 | 1,060 | 0,992 |
| Média | 1,029 | 0,989 | |||
| Desvio padrão | 0,030 | 0,022 | |||
As trajetórias de equilíbrio ilustram que o comportamento do elemento estrutural ao longo do histórico de carregamento, obtido de forma numérica, retrata o comportamento real obtido em laboratório por Bridge [23] . Em termos estatísticos, verifica‐se uma diferença média entre os resultados numéricos (CS‐ASA) e experimentais de apenas 3%. Destaca‐se também a pequena dispersão dos resultados através do desvio padrão, tabela 6 .
Em relação aos resultados de Fong e Chan [21] , que também utilizaram o MRPR, vale destacar que esses autores empregaram diferentes: formulação geométrica não linear e avaliação da capacidade resistente da seção transversal.
As análises utilizando as recomendações do AISC [16] são conservadoras para estruturas mistas. Como consequência, as cargas máximas encontradas por simulações usando a norma americana, PAISC , são menores do que as das análises considerando o EUROCODE 4 [5] e o MCD. Já a norma europeia, em média, superestima a carga última do elemento estrutural, PEC4 . Porém, em termos estatísticos, apresenta resultados mais próximos ao MCD, como mostrado nas Tabela 7 ; Tabela 8 .
| Espécime | PEC4 | PEC4 /PTest | PEC4 /PFC | PEC4 /PMCD |
|---|---|---|---|---|
| C1 | 1.912,56 | 0,978 | 0,987 | 0,978 |
| C2 | 725,18 | 1,067 | 1,002 | 1,037 |
| C3 | 563,33 | 1,098 | 1,027 | 1,035 |
| Média | 1,048 | 1,005 | 1,017 | |
| Desvio padrão | 0,062 | 0,020 | 0,034 | |
| Espécime | PAISC | PAISC /PTest | PAISC /PFC | PAISC /PMCD |
|---|---|---|---|---|
| C1 | 1.685,70 | 0,862 | 0,870 | 0,862 |
| C2 | 618,39 | 0,909 | 0,855 | 0,884 |
| C3 | 476,12 | 0,928 | 0,868 | 0,875 |
| Média | 0,900 | 0,864 | 0,874 | |
| Desvio padrão | 0,034 | 0,008 | 0,011 | |
Na figura 15 b são apresentadas as trajetórias de equilíbrio obtidas com as curvas de resistência de normas [5] ; [16] .
4.5. Pórtico com pilares metálicos e viga mista
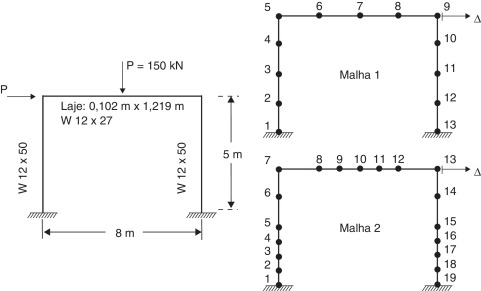
Huu e Kim [26] analisaram o pórtico simples biengastado apresentado na figura 16 . O vão livre entre os pilares metálicos com seção W12 × 50 é de 8 m e a viga possui uma laje apoiada, com espessura de 0,102 m e largura 1,219 m, sobre um perfil W12 × 27. Eles ainda consideraram a interação total entre a laje e o perfil. O sistema estrutural é modelado com concreto de resistência máxima de compressão fc igual a 16 MPa e o aço com resistência de escoamento fy e módulo de elasticidade iguais a 252,4 MPa e 200.000 MPa, respectivamente. Para esse exemplo, as curvas de resistência são definidas através do MCD. A tração no concreto é desprezada e sua deformação de início de plastificação na compressão é tomada igual a ‐ 0,002. Cargas concentradas de igual intensidade, 150 kN, são aplicadas de forma proporcional e simultaneamente no centro do vão livre da viga e no topo do pilar posicionado à esquerda. Duas discretizações foram testadas: a malha um apresenta uma divisão regular dos membros; já a malha 2 apresenta um refinamento maior, com pontos nodais concentrados em regiões de momentos fletores máximos.
|
|
|
Figura 16. Pórtico com viga mista: geometria, carregamento e discretização. |
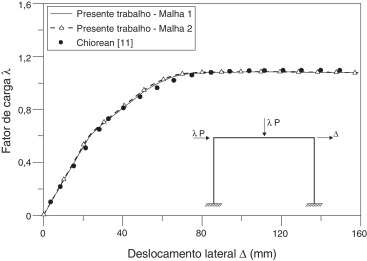
Na figura 17 , o fator de carga, λ, e o deslocamento lateral no topo do pilar direito são comparados com dados apresentados por Chiorean [11] . Conclui‐se que as simulações pelo MRPR, utilizando as curvas de resistência obtidas através do MCD, estão condizentes, mais uma vez, com a resposta presente da literatura [11] . Observa‐se uma perda de rigidez brusca próximo ao fator de carga igual a 0,6. O motivo para tal observação se deve às relações constitutivas adotadas, que implicam uma proximidade das curvas de início de plastificação e de resistência. Nesse ponto, a avaliação indica a formação de uma rótula plástica na extremidade direita da viga (região de momento negativo), local onde o perfil metálico trabalha praticamente isolado. Vale ressaltar que o aumento do refinamento da malha, concentrando pontos nodais em locais estratégicos, não influenciou significativamente na resposta obtida.
|
|
|
Figura 17. Trajetória de equilíbrio do pórtico analisado. |
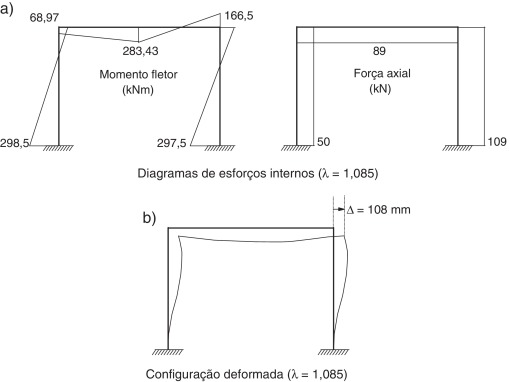
As figuras 18 a e 18b mostram, respectivamente, os diagramas de esforços internos solicitantes e a deformada do pórtico, referentes à carga máxima atingida na análise, λ = 1,085. Pode‐se observar o momento fletor de 166,5 kNm atuando no nó 9, onde ocorre a formação da rótula plástica. Dessa forma, um incremento das forças externas faz com que os esforços solicitantes superem a capacidade resistente do elemento. Para que essa violação não comprometa a análise, foi necessário, portanto, retornar a combinação de esforços (M,N) para o limite resistente da seção através do return mapping[15] .
|
|
|
Figura 18. Diagrama de esforços e configuração deformada do pórtico simples quando se atinge a carga máxima. (a) Diagramas de esforços internos (λ = 1,085), (b) configuração deformada (λ = 1,085). |
5. Considerações finais
No presente trabalho foi apresentada uma metodologia generalizada para a obtenção da capacidade resistente de elementos mistos de aço e concreto. A formulação é baseada no MCD e utiliza o método de Newton‐Raphson para a determinação da relação momento‐curvatura. Sua generalidade permite, que através das relações constitutivas apresentadas, seções puramente de aço ou de concreto armado submetidas à combinação de esforço axial e de momento fletor sejam também modeladas.
Na análise de estruturas mistas, os métodos normativos podem tanto superestimar quanto subestimar a capacidade resistente da seção, uma vez que o MCD é tido como mais próximo à realidade. Observa‐se claramente o conservadorismo do AISC [16] ante uma avaliação mais realista proporcionada pelo MCD. Essa característica é oposta à observada na curva de resistência do EUROCODE 4 [5] .
O uso do MRPR acoplado a curvas de resistência propostas por normas de projeto foi testado. Fez‐se necessária a introdução de uma curva simplificada para indicar o início da degradação da rigidez à flexão da seção. Além disso, as rigidezes axial e flexional foram determinadas através do conceito de homogeneização da seção transversal. A comparação com resultados experimentais [23] e numéricos [21] presentes na literatura validam a metodologia proposta, uma vez que os resultados via MCD foram mais próximos aos obtidos em laboratório, quando comparados com curvas de normas de projeto [5] ; [16] .
Como etapas futuras desta pesquisa, pretende‐se estudar o comportamento de elementos mistos com interação parcial e pórticos mistos com ligações semirrígidas. Além disso, pretende‐se estender as formulações e simulações ao contexto da análise dinâmica não linear de estruturas mistas.
Agradecimentos
Os autores agradecem ao CNPq, CAPES, FAPEMIG e PROPEC/PROPP/UFOP o apoio recebido para a realização deste trabalho.
Referências
- [1] M.D. Denavit, Characterization of behavior of steel‐concrete composite members and frames with applications for design. Doctoral thesis, Graduate College of the University of Illinois Urbana‐Champaign, Illinois, United States of America, 2012.
- [2] C.K. Iu, M.A. Bradford, W.F. Chen; Second‐order inelastic analysis of composite framed structures based on the refined plastic hinge method; Eng Struct, 31 (2009), pp. 799–813
- [3] A. Landesmann; Plastic‐hinge approach for inelastic analysis of steel‐concrete framed structures; J Constr Steel Res, 66 (2010), pp. 323–334
- [4] AISC; Specification for Structural Steel Buildings; Chicago (2005)
- [5] Eurocode 4, Design of composite steel and concrete structures Part 1: General rules an rules for buildings. Comite Europeen de Normalisation (CEN), Brussels, Belgium, 2004.
- [6] NBR 8800, Projeto de Estruturas de Aço e de Estruturas Mistas de Aço e Concreto de Edifícios. Associação Brasileira de Normas Técnicas (ABNT), Rio de Janeiro, Brasil, 2008.
- [7] C.C. Weng, S.L. Yen; Comparisons of concrete‐encased composite column strength provision of ACI code and AISC specifications; Eng Struct, 24 (2002), pp. 59–72 Elsevier
- [8] M. Fong, Second‐order analysis of imperfect light weight and composite structures. Doctoral thesis, Department of Civil and Structural Engineering, Hong Kong Polytechnic University, Hong Kong, China, 2012.
- [9] S.L. Chan, P. Chui; Non‐linear static and cyclic analysis of steel frames with semi‐rigid connections; Elsevier, Oxford (2000)
- [10] R.B. Caldas, Análise numérica de pilares mistos aço‐concreto, Dissertação de Mestrado, Programa de Pós‐Graduação em Engenharia Civil, Deciv/EM/UFOP, Ouro Preto, MG, Brasil, 2004.
- [11] C.G. Chiorean; A computer method for nonlinear inelastic analysis of 3 D composite steel‐concrete frame structures; Eng Struct, 57 (2013), pp. 125–152
- [12] S. Chen, J.G. Teng, S.L. Chan; Design of biaxially loaded short composite columns of arbitrary section; J Struct Eng, 127 (6) (2001), pp. 678–685
- [13] S.W. Liu, Y.P. Liu, S.L. Chan; Advanced analysis of hybrid steel and concrete frames part 1: Cross‐section analysis technique and second order analysis; J Constr Steel Res, 70 (2012), pp. 326–336
- [14] S.L. Chan, S.W., Liu, Y.P. Liu, Advanced analysis of hybrid frames structures by refined plastic hinge approach, In: Uy, B.; Tao,Z.; Mashiri, F.; Zhu, X.; Mirza, O.; Tan, E. L. (Ed.). Steel and Composite Structures–Proceedings of 4 th International Conference. 2010.
- [15] A.R.D. Silva, Sistema Computacional para a Análise Avançada Estática e Dinâmica de Estruturas Metálicas, Tese de Doutorado, Programa de Pós‐Graduação em Engenharia Civil, Deciv/EM/UFOP, Ouro Preto, MG, Brasil, 2009.
- [16] A.I.S.C.; Specification for Structural Steel Buildings; Chicago (2010)
- [17] Y.B. Yang, S.B. Kuo; Theory & Analysis of Nonlinear Framed Structures; Prentice Hall (1994)
- [18] S.L. Chan; Geometric and material nonlinear analysis of beam‐columns and frames using the minimum residual displacement method; Int J Numer Meth Eng, 26 (1988), pp. 2657–2669
- [19] M.G. Sfakianakis; Biaxial bending with axial force or reinforced, composite and repaired concrete section of arbitrary shape by fiber model and computer graphics; Adv Eng Softw, 33 (2002), pp. 227–242
- [20] K. Roik, R. Bergmann; Design method for composite columns with unsymmetrical croos‐sections; J Contr Steel Res, 15 (1990), pp. 153–168
- [21] M. Fong, S.L. Chan, Advanced analysis of steel concrete composite beam‐columns by refined plastic hinge method, International Journal of Structural Stability and Dynamics, 12 (2012).
- [22] J. Liew, H. Chen, N. Shanmugam; Inelastic analysis of steel frames with composite beams; J Struct Eng, 127 (2001), pp. 194–202
- [23] R. Bridge; Concrete filled steel tubular columns; Civil Eng Transact, 18 (1976), pp. 127–133
- [24] S.W. Liu, Y.P. Liu, S.L. Chan; Advanced analysis of hybrid steel and concrete frames part 2: Refined plastic hinge and advanced analysis; J Constr Steel Res, 70 (2012), pp. 337–349
- [25] R. Gonçalves, J. Carvalho; An efficient geometrically exact beam element for composite columns and its application to concrete encased steel I sections; Eng Struct, 75 (2014), pp. 213–224
- [26] C.N. Huu, S.E. Kim; Pratical nonlinear analysis of steel‐concrete composite frames using fiber‐hinge method; J Constr Steel Res, 74 (2012), pp. 90–97
Document information
Published on 01/03/17
Accepted on 15/10/15
Submitted on 07/05/15
Volume 33, Issue 1, 2017
DOI: 10.1016/j.rimni.2015.10.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?