Plataforma computacional para el análisis y simulación de sistemas rotor-cojinete de múltiples grados de libertad

Resumen

En este artículo, se presenta el desarrollo de una plataforma computacional para el análisis y simulación de sistemas rotor-cojinete de múltiples grados de libertad. La plataforma computacional se programó utilizando el software comercial Matlab, y está soportada por la formulación matemática basada en el método del elemento finito para el modelado de sistemas rotodinámicos. Para lo anterior, se consideró un elemento finito tipo viga con cuatro grados de libertad por nodo, efectos de inercia rotacional, momentos giroscópicos, deformaciones por cortante y amortiguamiento externo. El objetivo de la plataforma computacional es resolver la ecuación general de movimiento del sistema rotor-cojinete mediante los métodos de solución: directo y Newmark. La solución mediante el método directo permite conocer información del sistema tal como: frecuencias naturales, diagrama de Campbell, formas modales y la respuesta de vibración del sistema en estado estable. Por otro lado, la respuesta vibratoria en función del tiempo se obtiene de forma numérica mediante el método de Newmark. La validación de la plataforma computacional se realizó comparando los resultados obtenidos con resultados reportados en la literatura, así como con datos experimentales.

Palabras Clave: Programación numérica, método del elemento finito, rotodinámica, respuesta en frecuencia, método de Newmark, diagramas de Campbell

Abstract

In this paper, we present the development of a computational platform for the analysis and simulation of rotor-bearing systems of multiple degrees of freedom. The computational platform was programmed using the Matlab commercial software, and is supported by the mathematical formulation based on the finite element method for the modeling of rotodynamic systems. For the above, a beam type finite element was considered with four degrees of freedom per node, rotational inertia effects, gyroscopic moments, shear deformations and external damping. The purpose of the computational platform is to solve the general equation of motion of the rotor-bearing system using the solution methods: direct and Newmark. The solution through the direct method allows to know information of the system such as: natural frequencies, Campbell diagram, modal shapes and the vibration response of the system in steady state. On the other hand, the vibrational response as a function of time is obtained numerically using the Newmark method. The validation of the computational platform was done by comparing the results obtained with results reported in the literature, as well as with experimental data.

Keywords: Numerical programing, finite element method, rotordynamic, frequency response, Newmark method, Campbell diagrams

Nomenclatura

$a$: Efecto cortante en la viga $c$: Coeficiente de amortiguamiento viscoso $D$: Disco ${e}_{D}$: Espesor del disco $E$: Módulo de elasticidad ${f}_{n}$: Frecuencia natural del sistema $F{q}_{i}$: Fuerzas generalizadas ${F}_{1}$: Fuerza constante ${F}_{2}$: Componente de fuerza centrífuga en la dirección ${\textstyle x}$ debido al desbalance ${F}_{3}$: Componente de fuerza centrífuga en la dirección ${\textstyle z}$ debido al desbalance $I$: Momento de inercia de la sección transversal de la viga $k$: Coeficiente de rigidez de los soportes $L$: Longitud de la viga ${m}_{u}$: Masa de desbalance ${m}_{u}d$: Parámetro de desbalance del sistema $N(y)$: Función de forma o de interpolación ${q}_{i}$: Coordenada generalizada ${r}_{e}$: Radio de la sección transversal del eje ${r}_{eD}$: Radio externo del disco ${r}_{iD}$: Radio interno del disco $S$: Área de la sección transversal de la viga $t$: Tiempo $T$: Energía cinética ${T}_{e}$: Energía cinética del elemento viga $u$: Desplazamiento en la dirección ${\textstyle x}$ $U$: Energía de deformación ${U}_{e}$: Energía de deformación del elemento viga $VC$: Velocidad crítica $w$: Desplazamiento en la dirección ${\textstyle z}$ $\left[{C}_{1}\right]$: Matriz de amortiguamiento atribuible a los soportes ${\overset {\cdot }{\phi }}\left[{C}_{2}\right]$ : Matriz de efectos giroscópicos del sistema $\left[C\left({\overset {\cdot }{\phi }}\right)\right]$: Matriz de amortiguamiento global del sistema $\left[{K}_{1}\right]$: Matriz de rigidez atribuible a los soportes $\left[{K}_{2}\right]$: Matriz de rigidez del rotor ${\ddot {\phi }}\left[{K}_{3}\right]$: Matriz de rigidez derivada de la aceleración angular del sistema $\left[K\left({\ddot {\phi }}\right)\right]$: Matriz de rigidez global del sistema $\left[{M}_{T}\right]$: Matriz de masa traslacional $\left[{M}_{R}\right]$: Matriz de masa rotacional $\left[M\right]$: Matriz de masa global del sistema $\alpha$: Posición angular de la masa de desbalance $\delta$: Vector de desplazamiento nodal $\Delta t$: Incremento de tiempo $\theta$: Pendiente de la viga en el plano ${\textstyle yz}$ $\nu$: Relación de Poisson $\rho$: Densidad $\phi$: Desplazamiento angular del rotor ${\overset {\cdot }{\phi }}$: Velocidad angular del rotor ${\ddot {\phi }}$: Aceleración angular del rotor $\psi$: Pendiente de la viga en el plano ${\textstyle xy}$ $\Omega$: Velocidad angular contante del rotor

1. Introducción

Las plataformas de simulación computacional constituyen una herramienta importante para el análisis y predicción del comportamiento dinámico de un sistema real. Estas se basan en modelos matemáticos que rigen su comportamiento, por tanto, la validez de la simulación dependerá de la cercanía entre los modelos matemático y real. En ese sentido, un modelo matemático más completo supondrá una mejor aproximación del sistema real.

En el pasado, se desarrollaron con éxito varias aproximaciones numéricas para el análisis del comportamiento dinámico de sistemas rotodinámicos. De tales aproximaciones numéricas, tal vez el enfoque más popular por su alta eficiencia y conveniencia del modelado, es el método del elemento finito [1]. De acuerdo con Chandrupatla y Belegundu [2] en este método de análisis, una región compleja que define un sistema continuo se discretiza en formas geométricas simples llamadas elementos finitos. Las propiedades del material y las relaciones gobernantes son consideradas sobre esos elementos y se expresan en términos de valores desconocidos en los bordes del elemento. Un proceso de ensamble, cuando se consideran debidamente las cargas y restricciones, da lugar a un conjunto de ecuaciones. La solución de esas ecuaciones proporciona el comportamiento aproximado del sistema continuo. Una breve historia acerca de los orígenes de la invención del método del elemento finito se encuentra en Gupta y Meek [3].

En los primeros años de la década de 1960, los ingenieros usaron el método del elemento finito para obtener soluciones aproximadas en problemas de análisis de esfuerzos, flujo de fluidos, transferencia de calor y otras áreas [2]. No obstante, la aplicación de esta metodología a la rotodinámica, se llevó a cabo aproximadamente una década más tarde. Ruhl y Booker [4] publicaron el primer artículo en el que se presenta la aplicación del método del elemento finito al análisis de sistemas rotodinámicos. Sin embargo, para el elemento finito utilizado solo se consideró la energía de flexión elástica y energía cinética de traslación, mientras que los efectos de la inercia rotatoria, los momentos giroscópicos, carga axial, torque axial, la deformación por cortante y el amortiguamiento interno, no se consideraron en el modelado. Por su parte Nelson y McVaugh [5] generalizaron el trabajo de Ruhl y Booker [4] al proponer una formulación de elemento finito donde se incluyen los efectos de la inercia rotatoria, momentos giroscópicos y el efecto de una carga axial. Posteriormente, Zorzi y Nelson [6] incorporaron los efectos del amortiguamiento interno en el modelo de elemento finito, y Nelson [7] introdujo el efecto de la deformación por cortante utilizando la teoría de vigas de Timoshenko, con lo que fue posible simular un sistema de un rotor flexible soportado por cojinetes de rigidez lineal y amortiguamiento viscoso.

Actualmente, existen programas comerciales enfocados al análisis y simulación de sistemas rotodinámicos tales como: Ansys Rotordynamics, COMSOL Rotordynamics module y Rotorinsa, por mencionar algunos. Sin embargo, además de los costos elevados las plataformas anteriores no pueden ser modificadas por el usuario. En contraste, la plataforma computacional que se presenta en este trabajo tiene la posibilidad de adaptarse de acuerdo a las necesidades del usuario, debido a que el código fuente se puede modificar o incrementar.

2. Modelado matemático del sistema rotor-cojinete de múltiples grados de libertad

Los elementos básicos de un sistema rotor-cojinete son: el disco, el eje, los cojinetes y los sellos [8,9] y de forma adicional las fuerzas generadas a causa de las masas de desbalance. Para caracterizar los diferentes elementos del rotor como el disco y la masa de desbalance, es necesario determinar las expresiones para la energía cinética ${\textstyle T}$. En lo que respecta al eje, además de la energía cinética se requiere el conocimiento de la energía de deformación ${\textstyle U}$. Por otro lado, las fuerzas derivadas de los cojinetes y/o sellos se obtienen a partir del principio de los trabajos virtuales. Después de determinar las expresiones de energía se aplica la ecuación de Lagrange (1), para obtener las ecuaciones que rigen el comportamiento de cada elemento del sistema. Posteriormente, el ensamblaje de las ecuaciones individuales genera la ecuación general de movimiento del sistema rotor-cojinete de múltiples grados de libertad

${\frac {d}{dt}}\left({\frac {\partial T}{\partial {\overset {\cdot }{q}}_{i}}}\right)-$${\frac {\partial T}{\partial {q}_{i}}}+{\frac {\partial U}{\partial {q}_{i}}}=F{q}_{i}$

(1)

donde ${\textstyle i}$ es el número de grados de libertad del sistema, ${\textstyle {q}_{i}}$ son las coordenadas generalizadas, ${\textstyle F{q}_{i}}$ son las fuerzas generalizadas y ${\textstyle {\overset {\cdot }{q}}_{i}}$ indica diferenciación con respecto al tiempo ${\textstyle t}$.

El modelo matemático para el sistema rotor-cojinete de múltiples grados de libertad se obtiene mediante el método del elemento finito. El eje se modela utilizando un elemento finito tipo viga, y se considera que posee una sección transversal circular que permanece constante a lo largo de su longitud. El elemento finito seleccionado tiene dos nodos, donde cada nodo tiene cuatro grados de libertad: dos desplazamientos laterales y dos ángulos (flexiones de la viga), tal y como se muestra en la Figura 1.

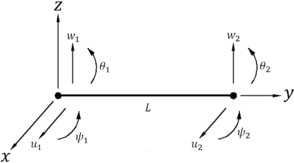
Figura 1. Elemento finito tipo viga para el modelado del eje

La relación entre desplazamientos y ángulos están dadas por:

$\theta ={\frac {\partial w}{\partial y}}$

(2)

$\psi =-{\frac {\partial u}{\partial y}}$

(3)

De acuerdo con la Figura 1, el vector de desplazamiento nodal se define como:

$\left\{\delta \right\}={\left\{{u}_{1},{w}_{1},{{\psi }_{1},\theta }_{1},{u}_{2},{w}_{2}{,{\psi }_{2},\theta }_{2}\right\}}^{T}$

(4)

donde el superíndice $T$ denota transpuesta. El vector (4) incluye los desplazamientos correspondientes a los movimientos en las direcciones ${\textstyle x}$ y ${\textstyle z}$, los cuales se definen como:

$\left\{{\delta }_{u}\right\}={\left\{{u}_{1},{\psi }_{1},{u}_{2},{\psi }_{2}\right\}}^{T}$ $\left\{{\delta }_{w}\right\}={\left\{{w}_{1},{\theta }_{1},{w}_{2},{\theta }_{2}\right\}}^{T}$

(5)

Al derivar la ec. (5) con respecto al tiempo, se obtienen los vectores de velocidad ${\textstyle \left\{{\overset {\cdot }{\delta }}\right\}}$ y aceleración ${\textstyle \left\{{\ddot {\delta }}\right\}}$, respectivamente.

Por otra parte, el elemento finito se construye a partir de las siguientes relaciones:

$u={N}_{1}\left(y\right){\delta }_{u}$ $w={N}_{2}\left(y\right){\delta }_{w}$

(6)

donde ${\textstyle {N}_{1}\left(y\right)}$ y ${\textstyle {N}_{2}\left(y\right)}$ son las funciones de desplazamiento (funciones de forma o de interpolación) típicas de una viga en flexión (Apéndice A).

De acuerdo con Lalanne y Ferraris [9], la ecuación general de la energía cinética de un eje de longitud ${\textstyle L}$ y sección transversal constante se expresa como:

${T}_{e}={\frac {\rho S}{2}}\int _{0}^{L}\left({\overset {\cdot }{u}}^{2}+{\overset {\cdot }{w}}^{2}\right)dy+$${\frac {\rho I}{2}}\int _{0}^{L}\left({\overset {\cdot }{\psi }}^{2}+{\overset {\cdot }{\theta }}^{2}\right)dy+$$\rho I\int _{0}^{L}{\overset {\cdot }{\phi }}^{2}dy+2\rho I\int _{0}^{L}{\overset {\cdot }{\phi }}{\overset {\cdot }{\psi }}\theta dy$

(7)

donde ${\textstyle \rho }$ es la densidad, ${\textstyle S}$ es el área de la sección transversal de la viga, ${\textstyle I}$ es el momento de inercia de área de la sección transversal del eje a lo largo del eje neutro. Asimismo, en (7) la primera integral es la expresión clásica de la energía cinética de un eje en flexión; la segunda integral, es el efecto secundario de la inercia rotacional (de acuerdo a la viga de Timoshenko); y la última integral representa el efecto giroscópico del eje.

Al sustituir la ec. (6) en la ec. (7), además de las funciones de desplazamiento y sus derivadas y realizando las integraciones correspondientes, la ecuación para la energía cinética del eje se convierte en:

${T}_{e}={\frac {1}{2}}{\delta {\overset {\cdot }{u}}}^{T}{M}_{1}\delta {\overset {\cdot }{u}}+$${\frac {1}{2}}{\delta {\overset {\cdot }{w}}}^{T}{M}_{2}\delta {\overset {\cdot }{w}}+{\frac {1}{2}}{\delta {\overset {\cdot }{u}}}^{T}{M}_{3}\delta {\overset {\cdot }{u}}+$${\frac {1}{2}}{\delta {\overset {\cdot }{w}}}^{T}{M}_{4}\delta {\overset {\cdot }{w}}+{\overset {\cdot }{\phi }}{\delta {\overset {\cdot }{u}}}^{T}{M}_{5}\delta w\,+$$\rho IL{\overset {\cdot }{\phi }}^{2}$

(8)

con

${M}_{1}=\rho S\int _{0}^{L}{N}_{1}^{T}\left(y\right){N}_{1}\left(y\right)dy$$\quad \quad \quad \quad \quad \quad \,\,{M}_{2}=\rho S\int _{0}^{L}{N}_{2}^{T}\left(y\right){N}_{2}\left(y\right)dy$ ${M}_{3}=\rho I\int _{0}^{L}{\frac {{dN}_{1}^{T}\left(y\right)}{dy}}{\frac {{dN}_{1}\left(y\right)}{dy}}dy$ $\quad \quad \quad \quad \,\,{M}_{4}=\rho I\int _{0}^{L}{\frac {d{N}_{2}^{T}\left(y\right)}{dy}}{\frac {{dN}_{2}\left(y\right)}{dy}}dy$ ${M}_{5}=2\rho I\int _{0}^{L}{\frac {{dN}_{1}^{T}\left(y\right)}{dy}}{\frac {{dN}_{2}\left(y\right)}{dy}}dy\quad \quad \quad \quad \quad \quad$

donde las matrices ${\textstyle {M}_{1}}$ y ${\textstyle {M}_{2}}$ son las matrices de masa, ${\textstyle {M}_{3}}$ y ${\textstyle {M}_{4}}$ representan la influencia del efecto secundario de la inercia rotatoria y ${\textstyle {M}_{5}}$ proporciona los efectos giroscópicos. Después de aplicar la ec. (1) a la ec. (8) se obtiene:

$\left[{M}_{T}+{M}_{R}\right]\left\{{\ddot {\delta }}\right\}+{\overset {\cdot }{\phi }}\left[{C}_{2}\right]\left\{{\overset {\cdot }{\delta }}\right\}+$${\ddot {\phi }}\left[{K}_{3}\right]\left\{\delta \right\}$

(9)

En la ecuación (9), ${\textstyle \left[{M}_{T}\right]}$ y ${\textstyle \left[{M}_{R}\right]}$ se obtienen de las matrices ${\textstyle \left[{M}_{1}\right]}$, ${\textstyle \left[{M}_{2}\right]}$ y ${\textstyle \left[{M}_{3}\right]}$, ${\textstyle \left[{M}_{4}\right]}$ respectivamente, la matriz ${\textstyle \left[{C}_{2}\right]}$ de ${\textstyle \left[{M}_{5}\right]}$ y ${\textstyle \left[{K}_{3}\right]}$ es una matriz de rigidez que está multiplicada por la aceleración angular del rotor. Las expresiones para las matrices en (9) se encuentran en el apéndice A.

Por otra parte, la energía de deformación ${\textstyle {U}_{e}}$ de un eje de longitud ${\textstyle L}$ y sección transversal simétrica se puede definir como [9]:

${U}_{e}={\frac {EI}{2}}\int _{0}^{L}\left[{\left({\frac {{\partial }^{2}u}{\partial {y}^{2}}}\right)}^{2}+{\left({\frac {{\partial }^{2}w}{\partial {y}^{2}}}\right)}^{2}\right]dy$

(10)

donde ${\textstyle E}$ es el módulo de elasticidad.

Al sustituir la ec. (6) en la ec. (10), además de las funciones de desplazamiento y sus derivadas y realizando las integraciones correspondientes, la ecuación para la energía de deformación del eje se convierte en:

${U}_{e}={\frac {1}{2}}{\delta u}^{T}{K}_{01}\delta u+{\frac {1}{2}}{\delta w}^{T}{K}_{02}\delta w$

(11)

con

${K}_{01}=EI\int _{0}^{L}{\frac {{{d}^{2}N}_{1}^{T}\left(y\right)}{d{y}^{2}}}{\frac {{{d}^{2}N}_{1}\left(y\right)}{d{y}^{2}}}dy$ ${K}_{02}=EI\int _{0}^{L}{\frac {{{d}^{2}N}_{2}^{T}\left(y\right)}{d{y}^{2}}}{\frac {{{d}^{2}N}_{2}\left(y\right)}{d{y}^{2}}}dy$

donde ${\textstyle {K}_{01}}$ y ${\textstyle {K}_{02}}$ son las matrices clásicas de rigidez. Aplicando la ec. (1) a la ec. (11) se obtiene:

${U}_{e}=\left[{K}_{2}\right]\,\left\{\delta \right\}$

(12)

donde ${\textstyle \left[{K}_{2}\right]}$ se forma a partir de la suma de ${\textstyle \left[{K}_{01}\right]}$ y ${\textstyle \left[{K}_{02}\right]}$ y de la consideración del efecto cortante en el elemento tipo viga. La matriz correspondiente a ${\textstyle \left[{K}_{2}\right]}$ se muestra en el Apéndice A.

Siguiendo la metodología propuesta por Nelson y McVaugh [5] y Lalanne y Ferraris [9] para el modelado de los discos, cojinetes y desbalance y después de aplicar la ec. (1), se tiene que el modelo matemático para el sistema rotor-cojinete de múltiples grados de libertad esta dado como:

$\left[M\right]\left\{{\ddot {\delta }}\right\}+\left[C\left({\overset {\cdot }{\phi }}\right)\right]\left\{{\overset {\cdot }{\delta }}\right\}+$$\left[K\left({\ddot {\phi }}\right)\right]\left\{\delta \right\}=\left\{{F}_{1}\right\}+$${\overset {\cdot }{\phi }}^{2}\left\{{F}_{2}\left(\phi \right)\right\}+{\ddot {\phi }}\left\{{F}_{3}\left(\phi \right)\right\}$

(13)

con

$\left[C\left({\overset {\cdot }{\phi }}\right)\right]=\left[{C}_{1}\right]+{\overset {\cdot }{\phi }}\left[{C}_{2}\right]$

$\left[K\left({\ddot {\phi }}\right)\right]=\left[{K}_{1}\right]+\left[{K}_{2}\right]+$${\ddot {\phi }}\left[{K}_{3}\right]$

$\left\{{F}_{2}\left(\phi \right)\right\}=\left\{{m}_{u}d\left(\mathrm {sin} \,\left(\phi +\alpha \right)+\right.\right.$$\left.\left.\mathrm {cos} \,\left(\phi +\alpha \right)\right)\right\}$

$\left\{{F}_{3}\left(\phi \right)\right\}=\left\{{m}_{u}d\left(\mathrm {sin} \,\left(\phi +\alpha \right)-\right.\right.$$\left.\left.\mathrm {cos} \,\left(\phi +\alpha \right)\right)\right\}$

donde ${\textstyle {m}_{u}d}$ es el desbalance presente en el sistema y ${\textstyle \left\{\delta \right\}}$ representa su posición angular. Asimismo, ${\textstyle \left\{\delta \right\}}$ es el vector que contiene todos los desplazamientos nodales; ${\textstyle \left[M\right]}$ es la matriz de masa global del sistema y está formada por ${\textstyle \left[{M}_{T}\right]+}$$\left[{M}_{R}\right]$. ${\textstyle \left[C\left({\overset {\cdot }{\phi }}\right)\right]}$, es la matriz de amortiguamiento global, que incluye los efectos giroscópicos en función de la velocidad de rotación ${\textstyle \left({\overset {\cdot }{\phi }}\left[{C}_{2}\right]\right)}$, y ${\textstyle \left[{C}_{1}\right]}$ que contiene el amortiguamiento atribuible a los soportes. ${\textstyle \left[K\left({\ddot {\phi }}\right)\right]}$ es la matriz de rigidez global, y está formada por: ${\textstyle \left[{K}_{1}\right]}$ que incluye la rigidez de los soportes, ${\textstyle \left[{K}_{2}\right]}$ que representa la rigidez del rotor y ${\textstyle \left({\ddot {\phi }}\left[{K}_{3}\right]\right)}$ que es un término de rigidez que está en función de la aceleración angular del rotor. Asimismo, ${\textstyle \left\{{F}_{1}\right\}}$ representa un vector de fuerza constante, como el peso debido a la influencia de la gravedad, ${\textstyle \left\{{F}_{2}\left(\phi \right)\right\}}$ y ${\textstyle \left\{{F}_{3}\left(\phi \right)\right\}}$ son los vectores de fuerza generados por el desbalance ${\textstyle {m}_{u}d}$. Finalmente, los términos ${\textstyle \phi }$, ${\textstyle {\overset {\cdot }{\phi }}}$ y ${\textstyle {\ddot {\phi }}}$ representan el desplazamiento, la velocidad y la aceleración angular del rotor en función del tiempo, respectivamente.

3. Solución de la ecuación general de movimiento del sistema rotor-cojinete

La ecuación general de movimiento del sistema rotor-cojinete se resuelve para las condiciones del sistema: en estado estable y en estado transitorio. La solución en estado estable se lleva a cabo utilizando el llamado método directo, mientras que para el estado transitorio se usa el método de Newmark [10].

3.1 Método directo

La aplicación de este método consiste en resolver la ec. (13) en estado estable, al considerar incrementos constantes en la velocidad de rotación del rotor, la cual se considera constante (es decir, ${\textstyle {\overset {\cdot }{\phi }}\Omega }$ = constante). Por lo tanto, la ec. (13) toma la siguiente forma:

$\left[M\right]\left\{{\ddot {\delta }}\right\}+\left[C\left(\Omega \right)\right]\left\{{\overset {\cdot }{\delta }}\right\}+$$\left[K\right]\left\{\delta \right\}=\left\{{F}_{1}\right\}+\left\{{F}_{2}\right\}\mathrm {sin} \,\left(\Omega t\right)+$$\left\{{F}_{3}\right\}\mathrm {cos} \,\left(\Omega t\right)$

(14)

con

$\left[C\left(\Omega \right)\right]=\left[{C}_{1}\right]+\Omega \left[{C}_{2}\right]$

$\left[K\right]=\left[{K}_{1}\right]+\left[{K}_{2}\right]$

$\left\{{F}_{2}\right\}={m}_{u}d{\Omega }^{2}\left\{{\begin{matrix}\mathrm {cos} \,\left(\alpha \right)\\-\mathrm {sin} \,\left(\alpha \right)\end{matrix}}\right\}$

$\left\{{F}_{3}\right\}={m}_{u}d{\Omega }^{2}\left\{{\begin{matrix}\mathrm {sin} \,\left(\alpha \right)\\\mathrm {cos} \,\left(\alpha \right)\end{matrix}}\right\}$

Para la obtención de los eigenvectores y eigenvalores, así como el diagrama de Campbell característico del sistema rotodinámico, la ec. (14) se considera en su forma homogénea, por tanto:

$\left[M\right]\left\{{\ddot {\delta }}\right\}+\left[C\left(\Omega \right)\right]\left\{{\overset {\cdot }{\delta }}\right\}+$$\left[K\right]\left\{\delta \right\}=0$

(15)

Para la solución de la ec. (15), se propone una solución del tipo exponencial de la forma:

$\delta =\Delta {e}^{rt}$

(16)

Al sustituir la ec. (16) y sus derivadas correspondientes en la ec. (15) y considerando la igualdad ${\textstyle \left[M\right]\Delta \,=[M]\Delta }$, se encuentra la siguiente relación matemática:

$\left[A\right]\left\{X\right\}=\lambda \left[B\right]\left\{X\right\}$

(17)

donde

$A=\left[{\begin{matrix}\left[0\right]\\\left[M\right]\end{matrix}}\,\,{\begin{matrix}\left[M\right]\\\left[C(\Omega )\right]\end{matrix}}\right]$

$B=\left[{\begin{matrix}\left[M\right]\\\left[0\right]\end{matrix}}\,\,{\begin{matrix}\left[0\right]\\-\left[K\right]\end{matrix}}\right]$

$\lambda =1/r$

$\left\{X\right\}=\left\{{\begin{matrix}r\Delta \\\Delta \end{matrix}}\,\,\right\}$

Como se puede observar, la ec. (17) adopta la forma del clásico problema de eigenvalores generalizados [11]. De la solución de la ec. (17) se obtienen los eigenvalores y eigenvectores del sistema rotodinámico, los cuales presentan la estructura de un número complejo conjugado.

Por otra parte, la respuesta vibratoria en estado estable del sistema rotor-cojinete que considera una masa de desbalance como fuente de excitación se determina al resolver la ec. (14), para la cual se propone una respuesta de la forma:

$\left\{\delta \right\}=\left\{{p}_{2}\right\}\sin \,\left(\Omega t\right)+\left\{{p}_{3}\right\}\cos \,\left(\Omega t\right)$

(18)

Ahora se sustituye la ec. (18) y sus derivadas correspondientes en la ec. (14) y, posteriormente, se agrupan los términos afectados por las funciones $\sin(\Omega t)$ y $\cos \Omega t)$, con lo que se obtiene:

$\left[{\begin{matrix}\left[K\right]-\left[M\right]{\Omega }^{2}\\\Omega \left[C(\Omega )\right]\end{matrix}}\,\,{\begin{matrix}-\Omega \left[C(\Omega )\right]\\\left[K\right]-\left[M\right]{\Omega }^{2}\end{matrix}}\right]\left\{{\begin{matrix}{p}_{2}\\{p}_{3}\end{matrix}}\right\}=$$\left\{{\begin{matrix}{F}_{2}\\{F}_{3}\end{matrix}}\right\}$

(19)

La ec. (19) se soluciona para diferentes valores de la velocidad de rotación del sistema ($\Omega$), calculando los vectores {$p_{2}$} y {$p_{3}$} que representan los desplazamientos del sistema rotodinámico, tal y como se aprecia en la ec. (18).

3.2 Método de Newmark

Este método consiste en integrar la ecuación general de movimiento del sistema rotor-cojinete (13) mediante un procedimiento numérico paso a paso. Asimismo, se basa en la suposición de que la aceleración del sistema varía linealmente entre dos instantes de tiempo. En este método, se utilizan los parámetros ${\textstyle \beta }$ y ${\textstyle \gamma }$, cuyos valores pueden cambiar para adaptarse a un problema en particular. Para este método, las expresiones para la velocidad y el desplazamiento están determinadas por [12]:

${\overset {\cdot }{\delta }}\left(t+\Delta t\right)={\overset {\cdot }{\delta }}\left(t\right)+\left[\left(1-\beta \right){\ddot {\delta }}\left(t\right)+\beta {\ddot {\delta }}\left(t+\Delta t\right)\right]\Delta t$

(20)

$\delta \left(t+\Delta t\right)=\delta \left(t\right)+{\overset {\cdot }{\delta }}\left(t\right)\Delta t+\left[\left({\frac {1}{2}}-\gamma \right){\ddot {\delta }}\left(t\right)+\gamma {\ddot {\delta }}\left(t+\Delta t\right)\right]{\Delta t}^{2}$

(21)

Para la solución de un sistema rotodinámico, los valores de los parámetros ${\textstyle \beta }$ y ${\textstyle \gamma }$ se deben tomar como 1/2 y 1/4, respectivamente. Lo cual corresponde a la suposición de que la aceleración se mantiene constante en un valor promedio de ${\textstyle \left[{\ddot {\delta }}\left(t\right)+\right.}$$\left.{\ddot {\delta }}\left(t+\Delta t\right)\right]/2$.

Para la solución de la ecuación de movimiento del sistema rotor-cojinete mediante el método de Newmark, se supone que se conoce el comportamiento del sistema (13), es decir, ${\textstyle \delta \left(t\right)}$, ${\textstyle {\overset {\cdot }{\delta }}\left(t\right)}$ y ${\textstyle {\ddot {\delta }}\left(t\right)}$ se conocen en el instante ${\textstyle t}$. Entonces, el equilibrio del sistema en el instante ${\textstyle t+}$$\Delta t$, utilizando (13), (20) y (21), se escribe como:

$\left\{{a}_{0}M+\left[C\left({\overset {\cdot }{\phi }}\left(t+\Delta t\right)\right)\right]{a}_{1}+\right.$$\left.\left[K\left({\ddot {\phi }}\left(t+\Delta t\right)\right)\right]\right\}\delta \left(t+\right.$$\left.\Delta t\right)$ $-M\left[{a}_{0}\delta \left(t\right)+{a}_{2}{\overset {\cdot }{\delta }}\left(t\right)+\right.$$\left.{a}_{3}{\ddot {\delta }}\left(t\right)\right]$ $-\left[C\left({\overset {\cdot }{\phi }}\left(t+\Delta t\right)\right)\right]\left[{a}_{1}\delta \left(t\right)+\right.$$\left.{a}_{4}{\overset {\cdot }{\delta }}\left(t\right)+{a}_{5}{\ddot {\delta }}\left(t\right)\right]$ $={\overset {\cdot }{\phi }}^{2}\left(t+\Delta t\right){F}_{2}\left[\phi \left(t+\right.\right.$$\left.\left.\Delta t\right)\right]+{\ddot {\phi }}\left(t+\Delta t\right){F}_{3}\left[\phi \left(t+\right.\right.$$\left.\left.\Delta t\right)\right]$

(22)

A partir de la solución de la ec. (22), se obtiene el vector de desplazamientos ${\textstyle \delta \left(t+\right.}$$\left.\Delta t\right)$ y, a continuación, las ecs. (20) y (21) proporcionan, respectivamente, ${\textstyle {\overset {\cdot }{\delta }}\left(t+\right.}$$\left.\Delta t\right)$ y ${\textstyle {\ddot {\delta }}\left(t+\right.}$$\left.\Delta t\right)$. El proceso del cálculo numérico se comienza en ${\textstyle {t}_{0}=}$$0$, con las condiciones iniciales ${\textstyle \delta \left(0\right)}$ y ${\textstyle {\overset {\cdot }{\delta }}\left(0\right)}$. El vector de aceleración ${\textstyle {\ddot {\delta }}\left(0\right)}$ se obtiene a partir de la ec. (13) debido a que, en el instante ${\textstyle {t}_{0}=}$$0$, los vectores ${\textstyle \delta \left(0\right)}$, ${\textstyle {\overset {\cdot }{\delta }}\left(0\right)}$ y ${\textstyle {\ddot {\delta }}\left(0\right)}$ satisfacen dicha ecuación. Por lo tanto, para el primer paso de tiempo ${\textstyle \Delta t}$, la ec. (22) se convierte en:

$\left\{{a}_{0}M+\left[C\left({\overset {\cdot }{\phi }}\left(\Delta t\right)\right)\right]{a}_{1}+\right.$$\left.\left[K\left({\ddot {\phi }}\left(\Delta t\right)\right)\right]\right\}\delta \left(\Delta t\right)$ $-M\left[{a}_{0}\delta \left(0\right)+{a}_{2}{\overset {\cdot }{\delta }}\left(0\right)+\right.$$\left.{a}_{3}{\ddot {\delta }}\left(0\right)\right]$ $-\left[C\left({\overset {\cdot }{\phi }}\left(\Delta t\right)\right)\right]\left[{a}_{1}\delta \left(0\right)+\right.$$\left.{a}_{4}{\overset {\cdot }{\delta }}\left(0\right)+{a}_{5}{\ddot {\delta }}\left(0\right)\right]$ $={\overset {\cdot }{\phi }}^{2}\left(\Delta t\right){F}_{2}\left[\phi \left(\Delta t\right)\right]+$${\ddot {\phi }}\left(\Delta t\right){F}_{3}\left[\phi \left(\Delta t\right)\right]$

(23)

donde

${\textstyle {a}_{0}=}$${\frac {1}{\gamma {(\Delta t)}^{2}}}$; ${\textstyle {a}_{1}=}$${\frac {\beta }{\gamma \Delta t}}$; ${\textstyle {a}_{2}=}$${\frac {1}{\gamma \Delta t}}$; ${\textstyle {a}_{3}=}$${\frac {1}{2\gamma }}-1$

${\textstyle {a}_{4}=}$${\frac {\beta }{\gamma }}-1$ y ${\textstyle {a}_{5}=}$${\frac {\Delta t}{2}}\left({\frac {\beta }{\gamma }}-2\right)$

De esta forma, se obtiene ${\textstyle \delta \left(\Delta t\right)}$ y, posteriormente, ${\textstyle {\overset {\cdot }{\delta }}\left(\Delta t\right)}$ y ${\textstyle {\ddot {\delta }}\left(\Delta t\right)}$. Ahora, la ec. (22) se tiene que resolver para cada incremento de tiempo.

4. Implementación de la plataforma computacional

La plataforma computacional se desarrolló utilizando el software comercial Matlab, la cual resuelve la ec. (13) mediante los métodos directo y Newmark. El proceso de análisis de la plataforma computacional se muestra en la Figura 2. Para la validación de la programación numérica, se compararon los resultados de un sistema rotor-cojinete reportado en la literatura con los resultados obtenidos con la plataforma desarrollada. La Figura 3 muestra el esquema del sistema analizado, así como, su discretización [9].

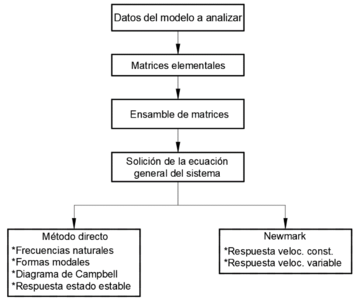
Figura 2. Diagrama de la plataforma computacional

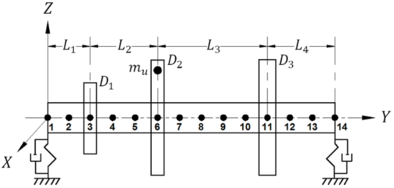
Figura 3. Modelo del sistema rotor-cojinete

Para la solución del sistema por el método del elemento finito, se realizó una discretización del rotor mostrado en la Figura 3 en 13 elementos finitos tipo viga de igual longitud. El rotor contiene tres discos inerciales cuya posición coincide con los nodos 3, 6 y 11, respectivamente, mientras que los soportes del rotor se ubican en los nodos 1 y 14. La ubicación nodal de los elementos del sistema es importante, ya que asegura que la simulación corresponda con las condiciones reales del sistema.

Las Tablas 1 y 2 muestran las propiedades mecánicas y geométricas del eje y los discos, respectivamente.

Tabla 1. Propiedades mecánicas y geométricas del eje [9]

Propiedades mecánicas	Geometría
$E=2\times 10^{11}$ N/m$^{2}$	$r_{e}=0.05$m
$\rho =7800$ kg/ m$^{3}$	$L_{1}=0.2$m	$L_{2}=0.3$m
${\textstyle \nu =0.3}$	$L_{3}=0.5m$	$L_{4}=0.3$m

Tabla 2. Propiedades mecánicas y geométricas de los discos [9]

Propiedades mecánicas
$E=2\times 10^{11}$ N/m$^{2}$	Disco	$D_{1}$	$D_{2}$	$D_{3}$
$\rho =7800$ kg/ m$^{3}$	$e_{D}$ (m)	0.05	0.05	0.06
${\textstyle \nu =0.3}$	$r_{iD}$ (m)	0.05	0.05	0.05
	$r_{eD}$ (m)	0.12	0.20	0.20

La Tabla 3 muestra las características de rigidez y amortiguamiento viscoso de los soportes.

Tabla 3. Propiedades de rigidez y amortiguamiento de los soportes [9]

Rigidez	Coeficiente de amortiguamiento
$k_{xx}=5\times 10^{7}$ N/m	$c_{xx}=5\times 10^{2}$ N·s/m
$k_{zz}=7\times 10^{7}$ N/m	$c_{zz}=7\times 10^{2}$ N·s/m
$k_{xz}=k_{zx}=0$	$c_{xz}=c_{zx}=0$

4.1 Diagrama de Campbell

El diagrama de Campbell es una de las herramientas más importantes para conocer el comportamiento dinámico de un sistema rotor-cojinete. En la Figura 4, se muestra el diagrama de Campbell para el rotor de la Figura 3. Este diagrama se obtiene al graficar las frecuencias naturales del rotor en función de la velocidad de rotación. Para lo anterior, se consideró un rango de velocidad de rotación de 0 a 30,000 revoluciones por minuto (rpm). En la Figura 4, se presentan las diez primeras frecuencias naturales del rotor obtenidas mediante el método directo.

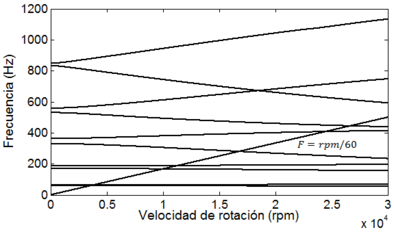
Figura 4. Diagrama de Campbell del sistema

En la Tabla 4 se presentan las frecuencias naturales obtenidas de la simulación y su comparación con las frecuencias naturales reportadas en la literatura [9], se puede observar que la diferencia porcentual máxima entre los valores es menor al 2%. Por lo que se concluye que la plataforma desarrollada proporciona resultados confiables. Cabe señalar que estos valores corresponden a las frecuencias naturales que se excitan debido a masas de desbalance presentes en el sistema.

Tabla 4. Comparación de las frecuencias naturales

Frecuencia natural (Hz)	Plataforma Comput.	Lalanne y Ferraris, [9]	Desviación (%)
$f_{n1}$	60.2	60.3	0.17
$f_{n2}$	63.1	63.3	0.32
$f_{n3}$	166.7	170.0	1.94
$f_{n4}$	189.1	188.0	0.59
$f_{n5}$	278.1	279.8	0.61
$f_{n6}$	405.2	407.0	0.44
$f_{n7}$	441.5	443.5	0.45

4.2 Formas modales

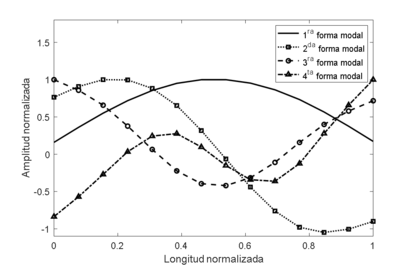
Para cada frecuencia natural, el rotor adopta una forma específica de vibración la cual se conoce como forma modal. En la Figura 5, se presentan las formas modales del sistema rotodinámico mostrado en la Figura 3.

Figura 5. Formas modales del sistema para el plano ${\textstyle yz}$

Para una mejor visualización, en la Figura 5, sólo se muestran las primeras cuatro formas modales del rotor. Por otro lado, determinar las formas modales es un paso necesario para la comprensión del comportamiento dinámico del sistema.

4.3 Respuesta de vibración

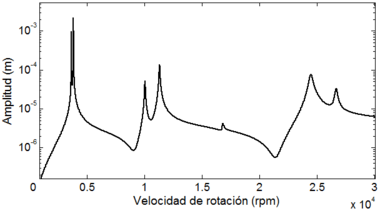
En la Figura 6, se muestra la respuesta de vibración en estado estable del sistema de la Figura 3, al considerar un desbalance con magnitud $m_{u}d=2\times 10^{-4}$ kg·m en una posición angular de 0° ubicado en el disco inercial $D_{2}$ nodo 6, tal y como se muestra en la Figura 3. Asimismo, en la Tabla 5 se presentan las amplitudes de vibración lateral del sistema para cada velocidad crítica.

Figura 6. Señal de vibración en estado estable en el nodo 6

Tabla 5. Velocidades críticas y amplitud de vibración del sistema

Velocidad crítica	Valor (rpm)	Amplitud (m)
${VC}_{1}$	3,622	9.792$\times 10^{-4}$
${VC}_{2}$	3,800	2.203$\times 10^{-3}$
${VC}_{3}$	10,030	5.218$\times 10^{-5}$
${VC}_{4}$	11,300	1.398$\times 10^{-4}$
${VC}_{5}$	16,800	4.244$\times 10^{-6}$
${VC}_{6}$	24,460	7.741$\times 10^{-5}$
${VC}_{7}$	26,670	3.358$\times 10^{-5}$

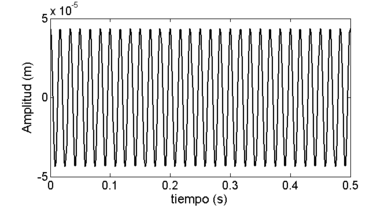
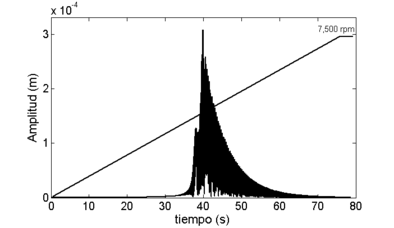
Por otra parte, la respuesta vibratoria del sistema rotor-cojinete en estado transitorio, se obtiene de la solución de la ec. (13) mediante el método de integración numérica de Newmark. La solución del sistema se llevó a cabo al considerar los esquemas de velocidad constante y con rampa de excitación de tipo lineal [13] para la operación del rotor. Cabe mencionar que el periodo de tiempo de muestreo utilizado fue de 1 ms, periodo de tiempo en el que se observó la convergencia del método de Newmark para la solución de la ec. (13). La Figura 7 muestra la señal de vibración del sistema para el nodo 6 al considerar una velocidad de rotación del rotor de ${\textstyle {\overset {\cdot }{\phi }}}$= 3,600 rpm, mientras que en la Figura 8 se muestra la respuesta vibratoria del sistema considerando una rampa de excitación de tipo lineal con ${\textstyle {\ddot {\phi }}=10}$rad/s$^{2}$.

Figura 7. Señal de vibración en el nodo 6

Figura 8. Respuesta de vibración del sistema en el nodo 6

Como era de esperar, la señal de vibración de la Figura 7 tiene un comportamiento sinusoidal, debido a que la velocidad de simulación se mantuvo constante en un valor de 3,600 rpm. Por otro lado, en la Figura 8 solo se muestra la señal de vibración del sistema para el rango de velocidad de 0 a 7,500 rpm. Cabe mencionar que, para este caso, la velocidad de rotación del rotor se fue incrementando a razón de 10 rad/s cada segundo.

4.4 Tamaño del elemento finito y su influencia en los resultados

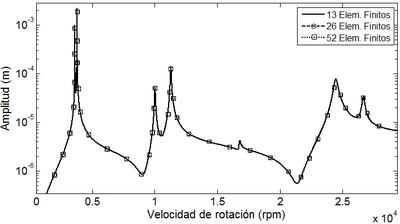
En la Tabla 6, se presenta una comparación de las primeras siete frecuencias naturales para el rotor de la Figura 3, considerando discretizaciones del rotor con diferente número de elementos finitos. Asimismo, en la Figura 9 se muestra el diagrama de Bode de la respuesta de vibración correspondiente al nodo 6, posición del disco inercial 2, para tres diferentes discretizaciones del rotor 13, 26 y 52 elementos finitos

Tabla 6. Comparación de frecuencias naturales

Frecuencia Natural (Hz)	Modelo del Rotor
	13 Elementos Finitos	26 Elementos Finitos	52 Elementos Finitos	Desviación (%)
$f_{n1}$	60.15	60.36	60.36	0.35
$f_{n2}$	63.10	63.33	63.33	0.36
$f_{n3}$	166.70	167.10	167.10	0.24
$f_{n4}$	189.10	188.20	188.20	0.48
$f_{n5}$	278.10	279.60	279.60	0.54
$f_{n6}$	405.20	407.50	407.50	0.57
$f_{n7}$	441.50	444.40	444.40	0.65

Figura 9. Respuesta de vibración del sistema en el nodo 6

De acuerdo con los resultados mostrados en la Tabla 6, los valores de las frecuencias naturales obtenidas por los modelos de 26 y 52 elementos finitos son similares, y la desviación porcentual entre estos datos y los correspondientes para el modelo de 13 elementos finitos son menores al 1%, lo que justifica el uso de unos pocos elementos finitos para las simulaciones presentadas en este trabajo. De igual forma, la Figura 9 muestra que para los diferentes esquemas de discretización del sistema rotor-cojinete a partir de 13 elementos finitos, no influye en la respuesta del rotor.

5. Pruebas experimentales

Se determinaron las frecuencias naturales y las formas modales de un sistema rotor-cojinete experimental y se compararon los resultados con los arrojados por la plataforma computacional desarrollada. En la Figura 10, se muestra el rotor experimental utilizado, marca Bently Nevada modelo RK4. El sistema rotodinámico experimental se compone de un eje sólido circular de 10 mm de diámetro, dos masas inerciales con un peso de 800 gramos cada una, de diámetro exterior de 73 mm y 25 mm de espesor, así como dos soportes colocados a los extremos.

Figura 10. Sistema rotor-cojinete experimental RK4 de Bently Nevada

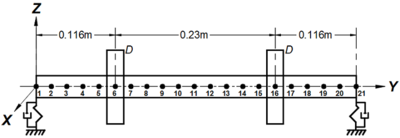
En la Figura 11, se muestra un esquema del arreglo experimental, así como la discretización del rotor. En la figura se puede apreciar que el sistema se discretizó en 20 elementos finitos tipo viga, obteniendo un total de 21 nodos. Nótese que los soportes se encuentran ubicados en los nodos 1 y 21, mientras que los discos inerciales en los nodos 6 y 16.

Figura 11. Modelo y discretización del sistema rotor-cojinete experimental

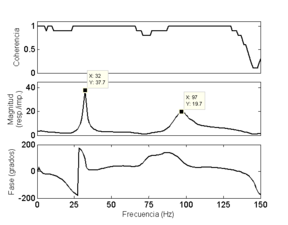
Las frecuencias naturales y formas modales del sistema experimental se determinaron utilizando un martillo de impacto marca Kistler modelo 9722A 2000 y un acelerómetro Kistler tipo 8632C50 con rango de medición de 50 g y sensibilidad de 99.8 mV/g. Para la adquisición y el análisis de las señales experimentales, se utilizó la aplicación de Impact Test del software LabVIEW, con una tarjeta National Instruments Ni usb-6251. Cabe señalar que para las pruebas se eligió el nodo 3 (Figura 11) como punto de golpeo, mientras que el acelerómetro se fue colocando en una posición nodal diferente para cada prueba, desde el nodo 2 hasta el nodo 20. En la Figura 12, se muestran los resultados del análisis de la prueba de impacto para el nodo 5.

Figura 12. FRF para el nodo 5

En la Figura 12, se observan las dos primeras frecuencias naturales del sistema rotor-cojinete experimental, cuyos valores son $f_{n1}=32$ Hz y $f_{n2}=97$. En la Tabla 7, se muestra la comparación entre los valores de las frecuencias naturales del sistema determinadas experimentalmente, contra los valores obtenidos de la simulación del sistema experimental utilizando la plataforma computacional desarrollada.

Tabla 7. Comparación de las frecuencias naturales del rotor experimental

Frecuencia natural (Hz)	Experimental	Plataforma Computacional	Desviación (%)
$f_{n1}$	32	32.08	0.25
$f_{n2}$	97	96.3	0.72

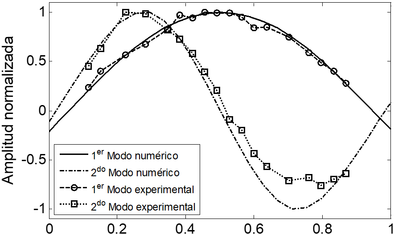
En la Tabla 7, se puede observar que la desviación entre los valores numéricos y experimentales para las dos primeras frecuencias naturales del sistema es menor al 1%, lo cual implica que los resultados arrojados por la plataforma computacional son confiables, y el modelo numérico si reproduce el comportamiento de un sistema real. Esto también se puede observar en la Figura 13, en la cual se comparan las formas modales del rotor numéricas y experimentales.

Figure 13. Comparación numérico experimental de las formas modales

6. Conclusión

En este trabajo se desarrolló una plataforma computacional que sirve como herramienta para el análisis y simulación de sistemas rotor-cojinete de múltiples grados de libertad. Para la formulación matemática se tomó como base el método del elemento finito para el modelado de sistemas rotodinámicos. La plataforma computacional se validó tanto numérica como experimentalmente, y se concluye que los resultados que proporciona son confiables. Asimismo, la plataforma computacional desarrollada presenta las siguientes características:

• Los elementos del sistema rotor-cojinete se incluyen en el modelado a partir de sus coordenadas nodales.

• Fácil para su uso y rápida configuración de nuevos análisis.

• En teoría se pueden utilizar cualquier cantidad de elementos finitos para la discretización del eje, sin embargo, incrementar el número de elementos finitos en la simulación también incrementa el costo computacional.

• Modelado de rotores de sección transversal circular: sólidos y huecos.

• Modelado de rotores con cambio de sección transversal en su dirección axial.

• Modelado de múltiples soportes, discos inerciales y masas de desbalance en el sistema.

• Se puede obtener la respuesta del sistema en estado estable o transitorio.

• Es interactiva, se pueden incluir códigos para el modelado de fenómenos adicionales en los sistemas rotor-cojinete como, por ejemplo: diferentes fuentes de excitación, modelado de eje asimétrico o fractura por mencionar algunos. Esto es posible debido a que se tiene el conocimiento y el control de cada parte del código fuente, lo cual no sería posible para un usuario que utilice un programa comercial ya que no se tiene el acceso a su código.Por otro lado, la facilidad o dificultad para agregar nuevo código a la plataforma computacional dependerá del tipo de fenómeno que se quiera incorporar.

Las características anteriores han hecho de la plataforma computacional una herramienta básica que actualmente se está utilizando en investigaciones por parte de algunos de los autores, además constituye una herramienta fundamental para el desarrollo de algunas tesis de posgrado.

Agradecimientos

Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (CONACYT) el apoyo brindado.

Referencias

[1] Fei Z., Tong S., Wei C. Investigation of the dynamic characteristics of a dual rotor system and its start-up simulation based on finite element method. Journal of Zhejiang University-SCIENCE A., 14(4):268-280, 2013.

[2] Chandrupatla T.R., Belegundu A.D. Introducción al estudio del elemento finito en ingeniería. Pearson Prentice Hall, 2a edición, 1999.

[3] Gupta K.K., Meek J.L. A brief history of the beginning of the finite element method. International Journal for Numerical Methods in Engineering, 39:3761-3774, 1996.

[4] Ruhl R.L., Booker J.F. A finite element model for distributed parameter turborotor systems. ASME, Journal of Engineering for Industry, 94(1):126-132, 1972.

[5] Nelson H.D., McVaugh J.M. The dynamics of rotor-bearing systems using finite elements. ASME, Journal of Engineering for Industry, 98(2):593-600, 1976.

[6] Zorzi E.S., Nelson H.D. Finite element simulation of rotor-bearing systems with internal damping. ASME, Journal of Engineering for Power, 99(1):71-76, 1977.

[7] Nelson H.D. A finite rotating shaft element using Timoshenko beam theory. ASME, Journal of Mechanical Design, 102(4):793-803, 1980.

[8] Lalanne M., Berthier P., Der Hagopian J. Mechanical vibrations for engineers. John Wiley & Sons, 1983.

[9] Lalanne M., Ferraris G. Rotordynamics prediction in engineering. John Wiley & Sons, 2 Edition, 1998.

[10] Newmark N.M. A method of computation for structural dynamics. Journal of the Engineering Mechanics Division, 85(3):67-94, 1959.

[11] Borri M., Mantegazza M. Efficient solution of quadratic eigenproblem arising in dynamic analysis of structures. Comp. Met. Appl. Mech. Eng., 12(1):19-31, 1977.

[12] Dukkipati R.V. MATLAB an introduction with applications. New Age International Publishers, 2010.

[13] Mendoza Larios J.G., Colín Ocampo J., Blanco Ortega A., Abúndez Pliego A., Gutiérrez Wing E.S. Balanceo automático de un sistema rotor-cojinete: identificador algebraico en línea del desbalance para un sistema rotodinámico. Revista Iberoamericana de Automática e Informática Industrial RIAI, 13(3):281-292, 2016.

Apéndice A

Funciones de forma para el elemento finito tipo viga

${N}_{1}\left(y\right)=\left[1-{\frac {3{y}^{2}}{{L}^{2}}}+{\frac {2{y}^{3}}{{L}^{3}}}\,;\,-\right.$$\left.y+{\frac {2{y}^{2}}{L}}-{\frac {{y}^{3}}{{L}^{2}}}\,;\,{\frac {3{y}^{2}}{{L}^{2}}}-\right.$$\left.{\frac {2{y}^{3}}{{L}^{3}}}\,;\,{\frac {{y}^{2}}{L}}-{\frac {{y}^{3}}{{L}^{2}}}\right]$

${N}_{2}\left(y\right)=\left[1-{\frac {3{y}^{2}}{{L}^{2}}}+{\frac {2{y}^{3}}{{L}^{3}}}\,;\,y-\right.$$\left.{\frac {2{y}^{2}}{L}}+{\frac {{y}^{3}}{{L}^{2}}}\,;\,{\frac {3{y}^{2}}{{L}^{2}}}-\right.$$\left.{\frac {2{y}^{3}}{{L}^{3}}}\,;-\,{\frac {{y}^{2}}{L}}+{\frac {{y}^{3}}{{L}^{2}}}\right]$

Las expresiones para las matrices en (13) son:

$\left[{M}_{T}\right]={\frac {\rho SL}{420}}\left[{\begin{matrix}156\\0\\0\\-22L\\54\\0\\0\\13L\end{matrix}}\,{\begin{matrix}0\\156\\22L\\0\\0\\54\\-13L\\0\end{matrix}}\,{\begin{matrix}0\\22L\\4{L}^{2}\\0\\0\\13L\\-3{L}^{2}\\0\end{matrix}}\,{\begin{matrix}-22L\\0\\0\\4{L}^{2}\\-13L\\0\\0\\-3{L}^{2}\end{matrix}}{\begin{matrix}54\\0\\0\\-13L\\156\\0\\0\\22L\end{matrix}}\,{\begin{matrix}0\\54\\13L\\0\\0\\156\\-22L\\0\end{matrix}}\,{\begin{matrix}0\\-13L\\-3{L}^{2}\\0\\0\\-22L\\4{L}^{2}\\0\end{matrix}}\,{\begin{matrix}13L\\0\\0\\-3{L}^{2}\\22L\\0\\0\\4{L}^{2}\end{matrix}}\right]$

$\left[{M}_{R}\right]={\frac {\rho I}{30L}}\left[{\begin{matrix}36\\0\\0\\-3L\\-36\\0\\0\\-3L\end{matrix}}\quad {\begin{matrix}0\\36\\3L\\0\\0\\-36\\-3L\\0\end{matrix}}\quad {\begin{matrix}0\\3L\\4{L}^{2}\\0\\0\\3L\\-{L}^{2}\\0\end{matrix}}\quad {\begin{matrix}-3L\\0\\0\\4{L}^{2}\\3L\\0\\0\\-{L}^{2}\end{matrix}}\,\,{\begin{matrix}-36\\0\\0\\3L\\36\\0\\0\\3L\end{matrix}}\,\,{\begin{matrix}0\\-36\\3L\\0\\0\\36\\-3L\\0\end{matrix}}\quad {\begin{matrix}0\\3L\\-{L}^{2}\\0\\0\\-3L\\4{L}^{2}\\0\end{matrix}}\quad {\begin{matrix}3L\\0\\0\\-{L}^{2}\\3L\\0\\0\\4{L}^{2}\end{matrix}}\right]$

${\textstyle \left[{C}_{1}\right]=\left[{\begin{matrix}{c}_{xx}&{c}_{xz}&0&0\\{c}_{zx}&{c}_{zz}&0&0\\0&0&0&0\\0&0&0&0\end{matrix}}\right]}$ ${\textstyle \left[{K}_{1}\right]=}$$\left[{\begin{matrix}{k}_{xx}&{k}_{xz}&0&0\\{k}_{zx}&{k}_{zz}&0&0\\0&0&0&0\\0&0&0&0\end{matrix}}\right]$

$\left[{C}_{2}\right]={\frac {\rho I}{15L}}\left[{\begin{matrix}0\\36\\3L\\0\\0\\-36\\3L\\0\end{matrix}}\quad {\begin{matrix}-36\\0\\0\\3L\\36\\0\\0\\3L\end{matrix}}\quad {\begin{matrix}-3L\\0\\0\\4{L}^{2}\\3L\\0\\0\\-{L}^{2}\end{matrix}}\quad {\begin{matrix}0\\-3L\\-4{L}^{2}\\0\\0\\3L\\{L}^{2}\\0\end{matrix}}\,\,{\begin{matrix}0\\-36\\-3L\\0\\0\\36\\-3L\\0\end{matrix}}\,\,{\begin{matrix}36\\0\\0\\-3L\\-36\\0\\0\\-3L\end{matrix}}\quad {\begin{matrix}-3L\\0\\0\\-{L}^{2}\\3L\\0\\0\\4{L}^{2}\end{matrix}}\quad {\begin{matrix}0\\-3L\\{L}^{2}\\0\\0\\3L\\4{L}^{2}\\0\end{matrix}}\right]$

$\left[K\right]={A}_{0}\left[{\begin{matrix}12\\0\\0\\-6L\\-12\\0\\0\\-6L\end{matrix}}\,{\begin{matrix}0\\12\\6L\\0\\0\\-12\\6L\\0\end{matrix}}\,{\begin{matrix}0\\6L\\\left(4+a\right){L}^{2}\\0\\0\\-6L\\\left(2-a\right){L}^{2}\\0\end{matrix}}\,{\begin{matrix}-6L\\0\\0\\(4+a){L}^{2}\\6L\\0\\0\\\left(2-a\right){L}^{2}\end{matrix}}{\begin{matrix}-12\\0\\0\\6L\\12\\0\\0\\6L\end{matrix}}\,{\begin{matrix}0\\-12\\-6L\\0\\0\\12\\-6L\\0\end{matrix}}\,{\begin{matrix}0\\6L\\\left(2-a\right){L}^{2}\\0\\0\\-6L\\(4+a){L}^{2}\\0\end{matrix}}\,{\begin{matrix}-6L\\0\\0\\\left(2-a\right){L}^{2}\\6L\\0\\0\\\left(4+a\right){L}^{2}\end{matrix}}\right]$

con

${A}_{0}={\frac {EI}{\left(1+a\right){L}^{3}}}$ y $a={\frac {12EI}{GS{L}^{2}}}$

donde ${\textstyle a\,}$ es el efecto cortante y ${\textstyle G}$ es el módulo a cortante del material.

$\left[{K}_{3}\right]={\frac {\rho I}{15L}}\left[{\begin{matrix}0\\0\\0\\0\\0\\0\\0\\0\end{matrix}}\quad {\begin{matrix}-36\\0\\0\\3L\\36\\0\\0\\3L\end{matrix}}\quad {\begin{matrix}-3L\\0\\0\\4{L}^{2}\\3L\\0\\0\\-{L}^{2}\end{matrix}}\quad {\begin{matrix}0\\0\\0\\0\\0\\0\\0\\0\end{matrix}}\,\,{\begin{matrix}0\\0\\0\\0\\0\\0\\0\\0\end{matrix}}\,\,{\begin{matrix}36\\0\\0\\-3L\\-36\\0\\0\\-3L\end{matrix}}\quad {\begin{matrix}-3L\\0\\0\\-{L}^{2}\\3L\\0\\0\\4{L}^{2}\end{matrix}}\quad {\begin{matrix}0\\0\\0\\0\\0\\0\\0\\0\end{matrix}}\right]$