Abstract
An experimental apparatus has been developed to evaluate the drying process of green tea leaves. Tea drying is an energy-intensive process which results in the removal of leaf moisture; it is essential to the quality of the final product. In order to more efficiently use process energy, a prototype drying system has been built and tested. The prototype incorporates a rotating perforated drum which helps speed the drying process. Experiments were carried out with multiple temperatures, airflow rates, and drum rotation rates; a subset of those results is shown here. In particular, the impact of airflow rate on the process was studied. It was found that as the airflow increased, the drying rate increased, as expected. However, the efficiency of energy use, which was quantified by the Specific Energy Consumption rate, varied considerably with flow. While higher flows led to faster drying, it resulted in a lower energy efficiency. Also, a two parameter predictive model was developed that was able to accurately match the moisture removal rates for a very wide range of flows. This predictive model, which is based on thermal-fluid fundamentals, can be used to extrapolate the presented results to cases which were not considered.
Introduction
Tea is the most commonly consumed nonwater beverage in the world. It is consumed throughout virtually in all regions and has experienced recent significant growth rates in its consumption [1]. Approximately two-third of the worlds tea is categorized as black tea with the remainder mainly comprising green teas with small amounts of others such as oolong, jasmine, and Pu-erh teas constituting the balance.
The volumes of tea produced in various parts of the world are large. For instance, worldwide ~4.1 million metric tons (4.1 × 109 kg) are produced with nearly 650,000 tons (6.5 × 108 kg) produced in the continent of Africa. With respect to green teas, the corresponding numbers are ~1 million metric tons (1 × 109 kg) globally.
The production of tea involves multiple energy-intensive processes. The large volumes of material and significant energy costs motivate studies into the improvements of the processing and the present study. The processing of green tea, in particular, requires four stages: 1, steaming; 2, shaping; 3, drying; and 4, postprocessing. Briefly, the steaming process is employed to prevent aeration and to halt oxidation. The duration of the steaming process impacts the quality of the resulting product. While steaming processes vary, they often last for 30–150 sec.
Next, shaping of the leaves is carried out through various machine-driven processes or by human labor. The rolling output dictates the shape of the tea leaves and impacts the release of flavors during steeping.
Third, tea leaves are dried to reduce the moisture content within the cellular structure. A variety of drying methodologies are available including spray drying, rotary drying, fluid-bed drying, infrared heating, microwave heating and others. The most common approach uses fluidized bed systems, which leads to a uniform drying of leaves to a low moisture content. Fluidized bed drying (FBD) is characterized by a high rate of moisture and heat transfer with a high degree of control. Despite these characteristics, FBD can lead to poor quality products if defluidization of the tea leaves occurs, an issue that is particularly prevalent with high moisture-content teas such as green tea [2]. In order to alleviate this problem, some researchers have experimented with agitation of the leave bed during the processing [3].
Despite the general widespread use of FBD, in many regions, particularly in developing regions, it has not yet been successfully employed. Consequently, there is a need for improvement to the FBD method with a focus on improving the quality of the product and reducing energy utilization during the processing.
In particular, the goal is to design an improved drying system which is agitated (rather than static). It is hoped that a bed, agitated through rotary motion, will speed the rate of drying, reduce fluidization velocities, without sacrificing efficiency. In particular, measurements of the efficiency will be given based on a thermodynamic analysis of the heat transferred during the drying process per unit of mass transfer. More details will be given later.
Another motivation for the device which is presented here is that the drying method will preserve the tea aroma compared to conventional drying methods.
The goal of this study is the implementation of FBD for green tea drying specifically and the quantification of energy use during the drying stage. Furthermore, a quantitative model will be developed that allows the prediction of the performance for other situations not studied in this project.
For further background, interested readers are directed to [4-11]. That collection of papers deals with some of the fundamental heat transfer and fluid flow concepts which govern cases such as this.
FBD Experiments
Great care was taken to ensure that the results from the FBD experiments were of the highest quality. First, tea leaves were collected from plants in a consistent manner. Six high-yielding tea clones were identified and at least 1 kg of fresh leaves was collected daily from each clone. Two leaves and a bud were removed from each plant, the standard harvesting method [12]. Harvesting was performed in the morning and evening hours to reduce moisture loss from the leaves.
The leaves were spread on perforated trays that promoted air circulation. In [3], three drying methods were then employed in replicate (three times). Those methods were microwave drying, conventional FBD, and drying with a newly invented prototype FBD technique. Only results for the prototype will be conveyed in this manuscript. The prototype FBD incorporated a rotating perforated drum to hold the leaves and promote a more uniform drying. The rotary method also was found to reduce energy utilization [2].
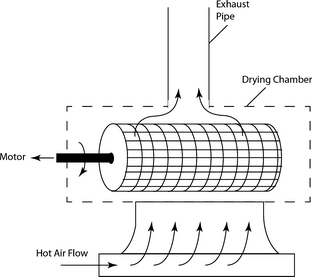
A simple schematic has been prepared in Figure 1 to show the essential components of the system. In the figure, a shaft is shown which connects the circular drum to a driving motor. Hot air enters the system from an upstream heating section. The drum diameter and length are 279 and 660 mm, respectively. The hole size for the mesh which contains the tea leaves was 1 mm. This size was large enough to permit airflow, yet small enough to avoid spillage of tea-leaf components.
|
|
|
Figure 1. Schematic diagram showing rotating tea drying perforated drum and airflow patterns. |
The drying drum was conditioned by six 1 kW heating elements which were collectively enclosed in a cylindrical casing. One effect of the casing was that the air temperature emerged at a uniform, well-mixed temperature. The heating system was surrounded by an asbestos-cement material whose thermal conductivity was 2.07 W/m°C. A final enclosing layer of concrete was used to contain the asbestos. Air motion was caused by 1 kW centrifugal forward-curved fans which were able to deliver up to 10 m3/sec of airflow.
Moisture content measurements were taken with a Mettler-Toledo-HR83 device with a resolution of 0.01%. Air speed was measured in the ducting system at locations away from bends and obstructions. Measurements made at multiple locations in the cross section displayed a high degree of velocity uniformity. The measurements were taken with a digital hot-wire anemometer. With the motor control of the rotating drum, it was possible to control the rotational speed of the prototype dryer. Results for various rotating speeds will be presented.
For all experiments, the local humidity of the inlet air was very low compared to that of the air exiting the drying chamber. The initial leaf moisture content varied among the individual experiments but it was ~80% by mass for all cases. The electrical power provided to the heaters were set to result in air temperatures of 80°C. Ten different flowrates were examined that varied from 41 to 167 L/sec. Leaf moisture content was measured at 600, 1200, 1800, and 2400 sec. Results from the experiments are compared with a mathematical model that will be presented in the next section. The rotation was achieved through the use of induction motors. The speed of the motor was controlled by power input through an inverter and was varied from 0 to 21.3 rad/sec (0–203 rpm). It was found that 12.56 rad/sec (120 rpm) was required for proper agitation of the leaves and maximal drying rate. All of the results which are presented here correspond to 120 rpm.
Predictive Model
It is useful to develop a model that is capable of predicting the time-wise reduction of leaf moisture. To develop this model, it is necessary to describe the fundamental heat and mass transfer processes. During drying processes, there are typically three stages of transfer. Initially, the material to be dried (tea leaves) are heated from a starting temperature to an elevated value. During this phase, mass transfer occurs but it increases as the heating process proceeds. When a more or less constant temperature is reached, the mass transfer occurs at a relatively steady rate. The actual rate of transport is dictated by processes at the interface between the fluid and the solid object. During this phase, resistance to mass transport within the material (diffusion) is significantly lower than surface transport resistances. As the amount of water within the object further decreases, the internal resistance grows and can exceed surface transport resistances. The focus here is on the second phase which is characterized by constant drying. This phase is the longest duration and most moisture transport occurs here.
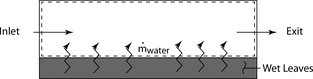
The first law of thermodynamics requires that energy transfer from the leaves is matched by energy loss from the preheated air. A control volume, defined so that it encompasses the airstream but not the leaves will incorporate heat transfer processes between the air stream and leaves as a boundary condition. A simple schematic of the control volume is shown in Figure 2. There, a dashed line signifies the control–volume boundary. Flows across the boundary occur at the inlet, exit, and the leaf–volume interface.
|
|
|
Figure 2. Simplified diagram showing the thermodynamic control volume. |
With the control volume identified, it is possible to express the first law of thermodynamics as
|
|
(1) |
Here, the symbol q represents the rate of heat transfer across the boundary (excluding latent energy transfer). The symbols represent mass flowrates and the h terms are specific enthalpies. While there will be some heat loss to the environment and also some heat transfer between the leaves and the airstream, both of these constituents are expected to be small. Heat loss to the environment would be that heat which travels through the insulation wall by conduction. A simple one-dimensional heat conduction analysis shows that this term is orders of magnitude below the rates of heat exchange between the fluid and the leaves. Consequently, it was neglected. With these assumptions, equation (1) can be rewritten as
|
|
(2) |
Equation (2) can further be reduced by recognizing that the mass flowrates are a combination of the air and water vapor components in the two airstreams, so that
|
|
(3) |
where the subscripts a and v represent dry air and vapor. Combination of equations (2) and (3), along with cancellation gives
|
|
(4) |
The symbols ω are the specific humidity levels at the respective locations. In equation (4), all terms aside from hexit and ωexit were known prior to the experiments.
Proper formulation of the energy balance is essential for the energy optimization of the system. A primary goal of the device was to maximize the rate of moisture removal for a quantity of input energy. To create a performance metric, the specific energy consumption rate (SEC) was introduced [13] which is the rate of heat transfer to the air prior to its introduction into the dryer for each unit mass of moisture loss. This metric can be expressed mathematically as
|
|
(5) |
It certainly is true that other performance measures can be utilized to quantify the efficiency of a tea-leaf drying system. The SEC was chosen as the most appropriate measure for the present study.
The movement of moisture from a solid object to a fluid stream is governed by internal diffusive processes and by external convective processes. At different times during the drying, one or the other of these two processes dominates. When drying is convective limited, it means that there are more or less constant surface moisture levels. On the other hand, when moisture transport is diffusively dominated, significant moisture gradients are developed within the object and the surface becomes drier than the interior. In the first of these situations, the rate of mass transfer is approximately constant. In the second of these, the rate of mass transfer decreases with time.
Consequently, during the drying process, there are three primary stages, each governed by different phenomena. The first stage is typically a short initial transient wherein the temperature of the drying object is increased by the warm drying fluid. Next, there is a constant drying rate period where the moisture transfer is dominated by convection. Finally, the last stage where the drying rate decreases until it ultimately becomes zero. These stages and their behaviors have been described in prior literature [14]. Often, the largest loss of mass occurs in the second (constant-rate) stage. This observation has been reported in the literature and in experiments carried out in support of this research project.
One of the goals of the present manuscript is to provide the ability to simply model the moisture content of tea leaves during the constant rate drying stage. During this portion of the drying process, the rate of moisture transfer was steady and the expression in equation (5) can be rewritten as
|
|
(6) |
where Mwater is the total water transfer across the control volume boundary in some duration t.
While the aforementioned expressions allow a comparison of performance, they do not provide a predictive means of estimating the moisture content in the leaves for various flowrates. In order to create a predictive method, it is necessary to express the water mass transfer as a constitutive equation. That results in
|
|
(7) |
Here, ΔωB.L. represents the difference in specific humidity across the mass-transfer boundary layer separating the tea leaves from the air stream. The term Asurf is the surface area of the leaves and hmass is the mass transfer coefficient. From equation (7), the requirements for a steady rate of moisture loss is evident. The mass transfer coefficient (hmass), the surface area of the leves (Asurf) and the difference in specific humidity between the surfaces of the leaves and the airstream ΔωB.L. must all be constant in time. Inasmuch as hmass depended on the specifics of the fluid flow (similar to the convective coefficient between a surface and a fluid), it is common to relate the transfer coefficient to the flowrate [15] such as
|
|
(8) |
Here Sh, Re, and Sc are the Sherwood, Reynolds, and Schmidt numbers, respectively. The symbols C and n are experimentally determined constants from external convective experiments carried over the past nine decades [15]. Since by definition, the Sherwood number is related to the mass transfer coefficient through
|
|
(9) |
where Lc and D are a characteristic length of the leaf and the mass diffusivity of water vapor in air. The length was measured with a 300-mm ruler; it was taken to be the distance from the bud to the leaf tip. When it is recognized that the Reynolds number scales with flowrate, equations (7)-(9) can be combined and simplified to
|
|
(10) |
for the portion of the drying process where the rate of drying is constant. To test the validity of the model, ten separate experiments were performed for flowrates that varied from 41 to 167 L/sec and with drum rotation rates of 120 rpm. In equation (10), a number of constant multipliers have been combined into a new symbol C′. The symbol n is identical to that of equation (8). Values of C′ = 0.0016 and n = 0.8 are used to provide the fit to that data. It should be noted that the value of n used here is in good agreement with the values reported in [15] for other external-flow convective situations. This agreement lends credibility to the present results.
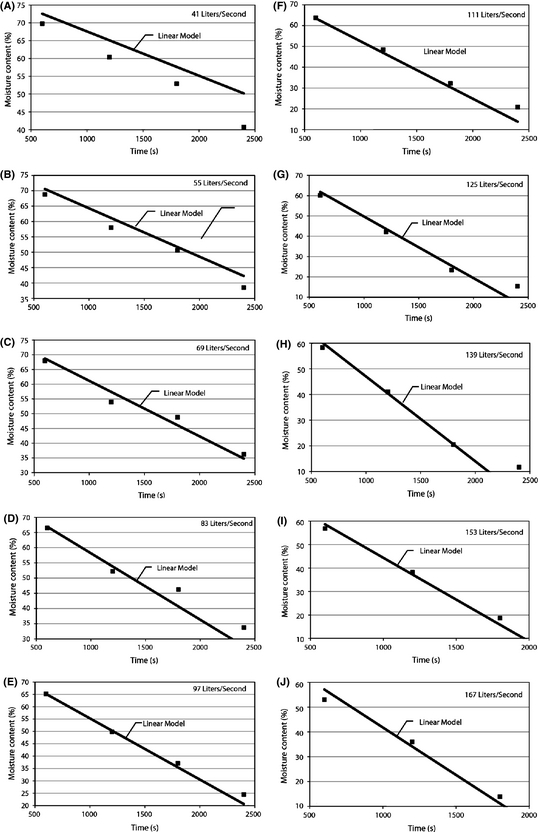
Here, moisture content is a mass fraction of liquid in the leaves (measured on a wet-basis), Q is volumetric flowrate in m3/sec, and time is in seconds. With only these two parameters, the results in Figure 3A–J were obtained. The specific flowrates for each comparison are listed in the image. For the results shown in the image, initial moisture contents were 80%. Also, in the experiments, the inlet air temperature was set to 80°C for all cases.
|
|
|
Figure 3. Comparisons of linear two-parameter model with experiments for ten different flowrates. Each flowrate are listed as annotations within the images. |
It is seen that there is very good agreement between this simple model and the experimental results. This finding suggests that the dependency of the mass transfer on flowrate is adequately found through the power relationship. Close inspection of the images reveals that for higher flowrates, there was a slowing of the evaporation process when the moisture content drops to values below the 10–15% range. This finding is expected as the constant drying regime gives way to a diffusion limited drying process. In recognition of this, the linear model should not be used to predict moisture contents below 10–15%. At those levels, internal diffusion dominates the process and the rate of mass transfer decreases. Since final green tea moisture levels are often below 10–15%, it is necessary for practitioners to make an account for this. Nevertheless, the methodology employed here is useful for rotating drum drying systems and can be extended to other systems as well.
Comparison of Energy Efficiency
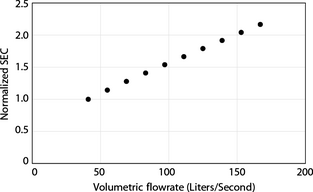
Next, a comparison of the energy efficiency for the above reported cases will be made. In particular, the SEC expressions from equation (6) will be found for each of the ten cases in Figure 3. The results are then normalized to the energy use for the lowest flowrate. So, the definition of the normalized SEC is
|
|
(11) |
The results are shown in Figure 4. There it is seen that flowrate significantly impacts energy use. All of the results of Figure 4 correspond to inlet air temperatures of 80°C and 2400 sec of drying. However, the results are representative of other inlet temperatures and other durations. It is clearly seen that if the desire is to dry with minimal energy requirements, lower flowrates should be employed. On the other hand, if the goal is to obtain very low moisture rates for a specified drying duration, higher flowrates should be used. To quantify the results, flowrates of 170 L/sec will more than double the energy requirement for each evaporated unit of moisture.
|
|
|
Figure 4. Impact of flowrate on energy usage. |
Comparison of the new rotating dryer to a conventional drying system
In order to justify the effort of the new system, it must provide superior performance compared to the simpler alternative (a static system). The comparison will be made using a number of metrics: drying time, evaporation rate, and SEC. Experiments were carried out at multiple air temperature settings to elucidate sensitivity of the results to those parameters. The following results were obtained. The experiments were carried out so that similar overall mass transfer was achieved with the two drying methods. It is seen that in all cases, the rotating system outperforms the static device. The rotating drying time is 2.5 times less than for the static system. The evaporation rate of the static system is ~55% of that for the rotating system. Finally, in all cases, the use of energy was lower for the rotating system (Tables 1-3).
| Dryer type | Drying time (sec) | Evap. rate (g/m2 per sec) | SEC (kJ/kg) | Ratio of drying time | Ratio of evap. rate | Ratio of SEC |
|---|---|---|---|---|---|---|
| Static | 2280 | 0.41 | 2760 | 2.5 | 0.54 | 1.92 |
| Rotating | 900 | 0.76 | 1440 |
| Dryer type | Drying time (sec) | Evap. rate (g/m2 per sec) | SEC (kJ/kg) | Ratio of drying time | Ratio of evap. rate | Ratio of SEC |
|---|---|---|---|---|---|---|
| Static | 1800 | 0.52 | 2970 | 2.5 | 0.55 | 2.33 |
| Rotating | 720 | 0.95 | 1270 |
| Dryer type | Drying time (sec) | Evap. rate (g/m2 per sec) | SEC (kJ/kg) | Ratio of drying time | Ratio of evap. rate | Ratio of SEC |
|---|---|---|---|---|---|---|
| Static | 1200 | 0.78 | 1650 | 2.5 | 0.55 | 1.43 |
| Rotating | 480 | 1.4 | 1150 |
Experimental Reproducibility
To provide some assessment of the quality for the experiments and the reproducibility of the results set forth in Figure 3, values of the standard deviation from various cases have been obtained. The results, shown in Table 4, reveal that the standard deviation for the moisture content is very small compared to the magnitude of the measurements. The quantification of the uncertainty lends credibility to the conclusions which are derived from the experiments.
| Airflow (L/sec) | Standard deviation of moisture content | |||
|---|---|---|---|---|
| 600 sec | 1200 sec | 1800 sec | 2400 sec | |
| 41 | 1.084 | 0.665 | 0.451 | 0.501 |
| 55 | 1.178 | 0.266 | 0.465 | 1.135 |
| 69 | 0.445 | 0.148 | 0.769 | 0.582 |
| 83 | 0.827 | 0.580 | 0.873 | 1.122 |
| 97 | 1.555 | 0.235 | 0.251 | 0.290 |
| 111 | 1.490 | 0.274 | 0.665 | 0.601 |
| 125 | 1.717 | 4.289 | 0.484 | 0.684 |
| 139 | 0.421 | 0.238 | 0.467 | 0.499 |
| 153 | 0.948 | 0.548 | 2.113 | 1.406 |
| 167 | 0.841 | 0.750 | 0.636 | 0.393 |
Concluding Remarks
Here, a set of experiments have been performed to assess the performance of a prototype rotating tea drying system. The system allows variation of the rotating rate of the drum which holds the tea, incoming air temperature, and air flowrate. It was found that for the system under consideration, 120 rpm was required to properly agitate the tea leaves. Experiments focused on elucidating the impact of airflow on drying performance were completed.
It was found that higher airflow rates led to faster drying of the tea leaves. While this result was expected, it was also found that higher airflows led to significantly more energy use (lower energy efficiency) than lower airflows. In fact, the thermal performance varied linearly with airflow. A secondary benefit which is expected but was not quantified as part of this research is that the rotating drying method will better preserve the aroma of green tea compared to static drying beds.
The experiments spanned the three main drying regimes (initial drying where tea leaves are brought to an elevated and steady temperature, main drying during which surface mass transfer is the main resistance, and mass loss in steady rate over time, and final drying where tea-leaf moisture decreases substantially so that internal diffusion resistances are dominate). The most important stage is the main drying phase. A simple two-parameter model was developed to model moisture loss in this region. Despite the wide range of air flowrates, the two-parameter model was sufficient for meaningful predictions. In fact, it can be used to predict moisture loss for air flowrates that were not considered here. While the two parameters are expected to be dictated by the specific operation of the dryer, it is believed that other drying systems can similarly develop two-parameter models that can be used for similar purpose.
Conflict of Interest
None declared.
References
- International Tea Limited, 2008. Tea trade statistics and research, 1 Carlton House Terrace, London.
- Langat, N. 2014. Development of an improved fluid bed dryer system for green tea drying in the industry, PhD Thesis, Kenyatta University.
- Sadeghi, M., and M. H. Khoshtaghaza. 2012. Vibration effect on particle bed aerodynamic behavior and thermal performance of black tea in fluidized bed dryers. J. Agric. Sci. Technol.14:781–788.
- Udell, K. S.1985. Heat transfer in porous media considering phase change and capillarity – the heat pipe effect. Int. J. Heat Mass Transf.28:485–495.
- Vafai, K.1984. Convective flow and heat transfer in variable-porosity media. J. Fluid Mech.147:233–259.
- Alazmi, B., and K. Vafai. 1999. Analysis of variants within the porous media transport models. J. Heat Transfer122:303–326.
- Vafai, K., R. L. Alkire, and C. L. Tien. 1985. An experimental investigation of heat transfer variable in porous media. J. Heat Transfer107:642–647.
- Mickley, H. S., and C. A. Trilling. 1949. Heat transfer characteristics of fluidized beds. Ind. Eng. Chem.41:1135–1147.
- Vafai, K., and R. Thiyagaraja. 1987. Analysis of flow and heat transfer at the interface region of a porous medium. Int. J. Heat Mass Transf.30:1391–1405.
- Amiri, A., and K. Vafai. 1998. Transient analysis of incompressible flow through a packed bed. Int. J. Heat Mass Transf.41:4259–4279.
- Minkowycz, W. J., A. Haji-Sheikh, and K. Vafai. 1999. On departure from local thermal equilibrium in porous media due to a rapidly changing heat source: the Sparrow number. Int. J. Heat Mass Transf.42:3373–3385.
- Harold, N., and P. D. Graham. 1992. Green tea composition, consumption, and polyphenol chemistry. J. Prev. Med. Hyg.3:334–350.
- Strumillo, C., and T. Kudra. 1986. Drying: principles, applications, and design. Gordon and Breach Scientific Publishers, New York, NY.
- Kawai, S.1993. Granulation and drying of powdery or liquid materials by fluidized-bed technology. Drying Technol.11:719–731.
- Sparrow, E. M., J. P. Abraham, and J. C. K. Tong. 2004. Archival correlations for average heat transfer coefficients for non-circular and circular cylinders and for spheres in cross flow. Int. J. Heat Mass Transf.47:5285–5296.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?