Stabilized mixed explicit finite element formulation for compressible and nearly-incompressible solids

Resumen

El presente estudio presenta una formulación mixta de elementos finitos capaz de abordar problemas quasi-incompresibles en forma explícita. Esta formulación se aplica a elementos con interpolaciones independientes e iguales de desplazamientos y deformaciones, estabilizadas mediante subescalas variacionales (VMS). Como continuación del estudio presentado en la referencia [23] , en la que se introdujo la sub-escala de las deformaciones, en este trabajo se incluyen los efectos de la sub-escala de los desplazamientos, con el fin de estabilizar el campo de las presiones. La formulación evita la condición de Ladyzhenskaya-Babuska-Brezzi (LBB) y sólo requiere la resolución de un sistema diagonal de ecuaciones. En este artículo se tratan también los principales aspectos de implementación. Finalmente, ejemplos de validación numérica muestran el comportamiento de estos elementos en comparación con la formulación irreducible.

Abstract

This study presents a mixed finite element formulation able to address nearly-incompressible problems explicitly. This formulation is applied to elements with independent and equal interpolation of displacements and strains, stabilized by variational subscales (VMS). As a continuation of the study presented in reference [23] , in which the strains sub-scale was introduced, in this work the effects of sub-scale displacements are included, in order to stabilize the pressure field. The formulation avoids the Ladyzhenskaya-Babuska-Brezzi (LBB) condition and only requires the solution of a diagonal system of equations. The main aspects of implementation are also discussed. Finally, numerical examples validate the behaviour of these elements compared with the irreductible formulation.

Palabras clave

Estabilización ; Formulación irreducible ; Formulación mixta explícita

Keywords

Stabilization ; Irreductible formulation ; Explicit mixed formulation

1. Introducción

En mecánica computacional de sólidos y estructuras es habitual elegir los desplazamientos como incógnitas y calcular las deformaciones por diferenciación del campo de los desplazamientos. Dado que no es posible realizar una reducción adicional en la elección del campo incógnita, los enfoques basados en la formulación estándar de desplazamientos se conocen como formulaciones irreducibles . Estas formulaciones son muy efectivas en el tratamiento de una amplia gama de problemas prácticos; sin embargo, en ciertos casos, conducen a un comportamiento rígido o dependiente de la malla. Por ejemplo, el rendimiento de los elementos estándares de bajo orden es pobre en condiciones de elasticidad y plasticidad quasi-incompresibles, mostrando un bloqueo volumétrico que se manifiesta como un comportamiento exageradamente rígido. Existe una vasta literatura proponiendo soluciones para este tipo de problemas, con las primeras propuestas basadas en técnicas de integración reducida o en el uso de deformaciones asumidas, véase, por ejemplo, el método B-bar [18]  ;  [19] .

A partir los años 90 se emplearon enfoques mixtos basados en desplazamiento-presión (u , p ) para la solución de problemas incompresibles [6] ; [17] ; [24] ; [26] ; [28]  ;  [29] . Tales técnicas demostraron también ser aplicables en problemas compresibles (véase, por ejemplo [27] ). La razón para utilizar formulaciones mixtas es, fundamentalmente, obtener un mejor orden de convergencia en las variables de interés y, especialmente, en las tensiones.

En este trabajo se emplea una formulación mixta dentro de un esquema explícito de integración temporal y estabilizada mediante el Método de Multi-Escala Variacional (VMS) [9] ; [20] ; [21] ; [22]  ;  [25] , a fin de abordar satisfactoriamente problemas de mecánica de sólidos compresibles y quasi-incompresibles, tanto en análisis quasi-estáticos como dinámicos. Aunque no es posible resolver el límite incompresible mediante el empleo de un esquema puramente explícito, en este trabajo se incluyen las subescalas de los desplazamientos a fin de estabilizar el campo de las presiones y proporcionar una solución quasi-incompresible.

La organización del presente artículo es la siguiente. En la sección 2 se presentan el planteamiento mixto estándar, su correspondiente planteamiento en multi-escalas, los métodos de estabilización y los aspectos relevantes de la implementación numérica de la formulación propuesta. En la sección 3 se comprueba el buen comportamiento de los elementos mixtos explícitos mediante diversas verificaciones numéricas y se compara con los resultados de formulación estándar.

2. Formulación

2.1. Formulación mixta

En la mecánica de sólidos deformables, las deformaciones ɛ pueden ser consideradas como variables independientes, adicional al campo de los desplazamientos u . Los grados de libertad para un problema tridimensional se incrementan de 3, u  = {u_x , u_y , u_z }, a 9, incluyendo los componentes del tensor simétrico de las deformaciones, ɛ  = {ɛ_xx , ɛ_yy , ɛ_zz , ɛ_xy , ɛ_yz , ɛ_xz }.

En tal caso, la formulación fuerte del problema puede escribirse como: hallar el campo de los desplazamientos u , sus respectivas derivadas temporales (velocidad ${\textstyle {\dot {\boldsymbol {u}}}}$ y aceleración ${\textstyle {\ddot {\boldsymbol {u}}}}$ ) y el campo de deformaciones ɛ , dadas unas fuerzas másicas b , tales que:

$\nabla \cdot {\boldsymbol {\sigma }}+{\boldsymbol {b}}=\rho {\ddot {\boldsymbol {u}}}\quad en\quad \Omega$

( 1)

${\boldsymbol {\varepsilon }}-{\nabla }^{s}{\boldsymbol {\mbox{u}}}=$${\boldsymbol {0}}\quad en\quad \Omega$

( 2)

donde ${\textstyle \Omega \subset {\mathbb {R} }^{n_{dim}}}$ es el volumen ocupado por el sólido en un espacio de n_dim dimensiones; ρ denota la densidad del material y σ es el tensor de tensiones de Cauchy, expresado como:

${\boldsymbol {\sigma }}={\boldsymbol {C}}({\boldsymbol {\varepsilon }}):{\boldsymbol {\varepsilon }}$

( 3)

donde C representa el tensor constitutivo secante. Además de las ecuaciones (1) y (2) , que se deben satisfacer para cualquier tiempo ${\textstyle t\in I}$ del intervalo de tiempo de interés ${\textstyle I=(0,T)}$ , el problema está sujeto a unas apropiadas condiciones de contorno, conocidas como condición de Dirichlet y condición de Von Neumann especificadas en el contorno del dominio ∂Ω = ∂Ω_u  ∪ ∂Ω_σ y ∂Ω_u ∩ ∂Ω_σ  = ∅. Las variables del problema ɛ , u y sus derivadas, ${\textstyle {\dot {\boldsymbol {u}}}}$ están sujetas a unas condiciones iniciales en t  = t₀ , es decir; ${\textstyle {\boldsymbol {\varepsilon }}\vert _{t=t_{0}}={\boldsymbol {\varepsilon }}_{0}=}$${\nabla }^{s}{\boldsymbol {u}}_{0}$ , ${\textstyle {\boldsymbol {u}}\vert _{t=t_{0}}={\boldsymbol {u}}_{0}}$ y ${\textstyle {\dot {\boldsymbol {u}}}\vert _{t=t_{0}}={\boldsymbol {v}}_{0}}$ .

Después de multiplicar las ecuaciones (1) y (2) por sus respectivas funciones de peso e integrando por partes la ecuación (1) , la formulación variacional del problema es:

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}:{\boldsymbol {\sigma }}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}\cdot \rho {\ddot {\boldsymbol {u}}}\quad d\Omega =$${\int }_{\partial \Omega }{\boldsymbol {\omega }}\cdot {\overline {\boldsymbol {t}}}\quad d\Gamma +$${\int }_{\Omega }{\boldsymbol {\omega }}\cdot {\boldsymbol {b}}\quad d\Omega \quad \quad \quad \forall {\boldsymbol {\omega }}$

( 4)

${\int }_{\Omega }{\boldsymbol {\gamma }}\cdot {\boldsymbol {\varepsilon }}\quad d\Omega =$${\int }_{\Omega }{\boldsymbol {\gamma }}\cdot {\nabla }^{s}{\boldsymbol {\mbox{u}}}\quad d\Omega \quad \quad \forall {\boldsymbol {\gamma }}$

( 5)

donde ${\textstyle {\boldsymbol {\omega }}\in V}$ y ${\textstyle {\boldsymbol {\gamma }}\in T}$ son las funciones de prueba para el campo de los desplazamientos y el campo de las deformaciones, respectivamente; ${\textstyle V}$ y ${\textstyle T}$ son los espacios de los desplazamientos y deformaciones admisibles y ${\textstyle {\overline {\boldsymbol {t}}}={\boldsymbol {\sigma }}{\boldsymbol {n}}}$ son las tracciones en la dirección normal saliente n en ∂Ω_σ .

2.2. Discretización espacial y temporal

Para definir la forma discreta del problema, se considera un campo de desplazamientos discretos u  = u_h , sus derivadas temporales discretas (${\textstyle {\dot {\boldsymbol {u}}}={\dot {\boldsymbol {u}}}_{h}}$ y ${\textstyle {\ddot {\boldsymbol {u}}}={\ddot {\boldsymbol {u}}}_{h}}$ ) y un campo de deformaciones discretas ɛ  = ɛ_h . La forma discreta de (4) y (5) es:

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {\sigma }}_{h}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\boldsymbol {u}}}_{h}\quad d\Omega =$${\int }_{\partial \Omega }{\boldsymbol {\omega }}_{h}\cdot {\overline {\boldsymbol {t}}}\quad d\Gamma +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot {\boldsymbol {b}}\quad d\Omega \quad \quad \quad \forall {\boldsymbol {\omega }}_{h}$

( 6)

${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\boldsymbol {\varepsilon }}_{h}\quad d\Omega =$${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}\quad d\Omega \quad \quad \forall {\boldsymbol {\gamma }}_{h}$

( 7)

donde ahora ${\textstyle {\boldsymbol {\omega }}_{h}\in V_{h}}$ y ${\textstyle {\boldsymbol {\gamma }}_{h}\in T_{h}}$ son las funciones de prueba definidas sobre el espacio de los elementos finitos ${\textstyle V_{h}}$ y ${\textstyle T_{h}}$ , respectivamente. La condición de Ladyzhenskaya-Babuska-Brezzi (condición inf-sup LBB) impone restricciones en las funciones de interpolación para garantizar estabilidad y unicidad de la solución [1]  ;  [15] . De ahí que los espacios de solución para los desplazamientos y las deformaciones no puedan ser escogidos libremente. Lamentablemente, muchos elementos de bajo orden, incluyendo el elemento con igual orden lineal de interpolación para los desplazamientos y las deformaciones, de interés en este trabajo, no cumplen la condición LBB, por lo que no son estables y presentan oscilaciones en el campo de los desplazamientos que contaminan la solución. Afortunadamente, las restricciones de la condición LBB pueden ser evitadas mediante la utilización de apropiadas técnicas de estabilización numérica que pueden proveer la estabilidad necesaria para la convergencia. Los métodos de elementos finitos estabilizados consisten en añadir a la forma discreta términos que son función de los residuos de las ecuaciones (6) y (7) evaluados dentro de los elementos y que disminuyen con el refinamiento de la malla.

Además, como las ecuaciones (6) y (7) son discretas en el espacio pero continuas en el tiempo, se requiere un algoritmo de discretización temporal. En este trabajo se usa el esquema explícito de diferencias centradas.

2.3. Método de los elementos finitos estabilizados

2.3.1. Multi-escalas variacionales de resolución

El método de estabilización empleado en este trabajo se basa en el concepto de Sub-escalas o Multi-Escalas Variacionales (VMS) [21] . La idea fundamental es que al definir una malla de elementos finitos quedan establecidas dos escalas o niveles de resolución , una que corresponde a la malla y será captado mediante la aproximación de los elementos finitos (escala gruesa) y otra más fina, que corresponde a la parte que la malla no logra captar y que denominaremos simplemente sub-escala. La solución del problema continuo contiene componentes de ambas escalas. De acuerdo con este concepto, se deben aproximar de alguna manera los efectos de la sub-escala con el objetivo de mejorar las propiedades de estabilidad de la formulación. En base a este concepto, el campo de los desplazamientos y deformaciones se aproximan como:

${\boldsymbol {u}}\approx {\boldsymbol {u}}_{h}+{\tilde {\boldsymbol {u}}}$

( 8)

${\boldsymbol {\varepsilon }}\approx {\boldsymbol {\varepsilon }}_{h}+$${\tilde {\boldsymbol {\varepsilon }}}$

( 9)

Las velocidades ${\textstyle {\dot {\boldsymbol {u}}}}$ y las aceleraciones ${\textstyle {\ddot {\boldsymbol {u}}}}$ se obtienen por diferenciación temporal de los desplazamientos, o sea:

${\dot {\boldsymbol {u}}}={\dot {\boldsymbol {u}}}_{h}+{\dot {\tilde {\boldsymbol {u}}}}$

( 10)

${\ddot {\boldsymbol {u}}}={\ddot {\boldsymbol {u}}}_{h}+{\ddot {\tilde {\boldsymbol {u}}}}$

( 11)

donde ${\textstyle {\boldsymbol {\boldsymbol {\varepsilon }}}_{h}\in T_{h}}$ y ${\textstyle ({\boldsymbol {u}}_{h},{\dot {\boldsymbol {u}}}_{h},{\ddot {\boldsymbol {u}}}_{h})\in V_{h}}$ son las deformaciones, desplazamientos, velocidades y aceleraciones en la escala gruesa mientras que ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}\in {\tilde {T}}}$ y ${\textstyle ({\tilde {\boldsymbol {u}}},{\dot {\tilde {\boldsymbol {u}}}},{\ddot {\tilde {\boldsymbol {u}}}})\in {\tilde {V}}}$ son las deformaciones y desplazamientos (con sus derivadas temporales) de la sub-escala.

Al considerar las correspondientes funciones de prueba en la sub-escala ${\textstyle {\tilde {\boldsymbol {\omega }}}\in {\tilde {V}}}$ y ${\textstyle {\tilde {\boldsymbol {\gamma }}}\in {\tilde {T}}}$ , nótese que la aproximación de la solución en el campo de deformaciones y desplazamientos se extiende ahora a ${\textstyle T\simeq T_{h}\oplus {\tilde {T}}}$ y ${\textstyle V\simeq V_{h}\oplus {\tilde {V}}}$ respectivamente. Cada método particular de elementos finitos estabilizados se define de acuerdo a cómo se escogen los espacios ${\textstyle {\tilde {V}}}$ y ${\textstyle {\tilde {T}}}$ . El método clásico de Galerkin de obtiene cuando ${\textstyle {\tilde {V}}={\tilde {T}}=\lbrace 0\rbrace }$ .

Por otra parte, el tensor de tensiones en la ecuación (3) toma la forma:

${\boldsymbol {\sigma }}({\boldsymbol {\varepsilon }})\approx {\boldsymbol {\sigma }}_{h}+$${\tilde {\boldsymbol {\sigma }}}$

( 12)

en el cual σ_h  = C (ɛ_h ) : ɛ_h y ${\textstyle {\tilde {\boldsymbol {\sigma }}}={\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}):{\tilde {\boldsymbol {\varepsilon }}}}$ son respectivamente las tensiones continuas y las tensiones de la escala fina. Obsérvese que se ha empleado la aproximación C (ɛ ) ≈ C (ɛ_h ). Esta aproximación y la correspondiente descomposición aditiva del tensor de tensiones en la ecuación (12) están justificados en [3]  ;  [4] .

Introduciendo las ecuaciones (8) , (9) , (11) y (12) en (4) y (5) , el problema se lee ahora como:

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {\sigma }}_{h}\quad d\Omega +$${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\tilde {\boldsymbol {\sigma }}}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho \left({\ddot {\boldsymbol {u}}}_{h}+\right.$$\left.{\ddot {\tilde {\boldsymbol {u}}}}\right)\quad d\Omega =$${\boldsymbol {F}}_{ext}({\boldsymbol {\omega }}_{h})\quad \forall {\boldsymbol {\omega }}_{h}$

( 13)

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\tilde {\omega }}}:{\boldsymbol {\sigma }}_{h}\quad d\Omega +$${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\tilde {\omega }}}:{\tilde {\boldsymbol {\sigma }}}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\tilde {\omega }}}\cdot \rho \left({\ddot {\boldsymbol {u}}}_{h}+\right.$$\left.{\ddot {\tilde {\boldsymbol {u}}}}\right)\quad d\Omega =$${\boldsymbol {F}}_{ext}({\boldsymbol {\tilde {\omega }}})\quad \forall {\boldsymbol {\tilde {\omega }}}$

( 14)

${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\boldsymbol {\varepsilon }}_{h}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\tilde {\boldsymbol {\varepsilon }}}\quad d\Omega =$${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}\quad d\Omega -$${\int }_{\Omega }\left(\nabla \cdot {\boldsymbol {\gamma }}_{h}\right)\cdot {\tilde {\boldsymbol {\mbox{u}}}}\quad d\Omega \quad \forall {\boldsymbol {\gamma }}_{h}$

( 15)

${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\boldsymbol {\varepsilon }}_{h}\quad d\Omega +$${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\tilde {\boldsymbol {\varepsilon }}}\quad d\Omega =$${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}\quad d\Omega +$${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\nabla }^{s}{\tilde {\boldsymbol {\mbox{u}}}}\quad d\Omega \quad \forall {\tilde {\boldsymbol {\gamma }}}$

( 16)

donde en la ecuación (15) se ha empleado la integración por partes y se ha despreciado la integral sobre contorno [3]  ;  [9] . Las fuerzas externas F_ext (ω_h ) se escriben de la forma:

${\boldsymbol {F}}_{ext}({\boldsymbol {\omega }}_{h})={\int }_{\partial \Omega }{\boldsymbol {\omega }}_{h}\cdot {\overline {\boldsymbol {t}}}\quad d\Gamma +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot {\boldsymbol {b}}\quad d\Omega$

( 17)

Debido a la aproximación empleada en (8) y (9) , la ecuación (1) se desdobla en las dos ecuaciones (13) y (14) , cada una de ellas relacionadas con la escala correspondiente. Asimismo, la ecuación (2) se desdobla en las ecuaciones (15) y (16) .

Dado que las ecuaciones (14) y (16) no se resuelven dentro del espacio de los elementos finitos, se requiere una aproximación de las mismas. Obsérvese que no son necesarios los valores punto a punto, sino sólo el valor de la integral correspondiente al término de estabilización en (13) y (15)[3] . El objetivo de estas aproximaciones es obtener una estimación variacional de los efectos de las sub-escalas ${\textstyle {\tilde {\boldsymbol {u}}}}$ y ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}}$ en las ecuaciones de balance.

Los residuos correspondientes a las ecuaciones en la sub-escala de los elementos finitos son:

${\boldsymbol {r}}_{\varepsilon ,h}={\nabla }^{s}{\boldsymbol {u}}_{h}-$${\boldsymbol {\varepsilon }}_{h}$

( 18)

${\boldsymbol {r}}_{u,h}=\rho {\ddot {\boldsymbol {u}}}_{h}-$$\nabla \cdot {\boldsymbol {\sigma }}_{h}-{\boldsymbol {b}}$

( 19)

Esto permite escribir las ecuaciones (14) y (16) como:

${\int }_{\Omega }{\tilde {\boldsymbol {\omega }}}\cdot \left(\nabla \cdot \left({\boldsymbol {C}}:{\tilde {\boldsymbol {\varepsilon }}}\right)\right)\quad d\Omega -$${\int }_{\Omega }\rho {\tilde {\boldsymbol {\omega }}}\cdot {\ddot {\tilde {\boldsymbol {u}}}}\quad d\Omega =$${\int }_{\Omega }{\tilde {\boldsymbol {\omega }}}\cdot {\boldsymbol {r}}_{u,h}\quad d\Omega$

( 20)

${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\tilde {\boldsymbol {\varepsilon }}}\quad d\Omega -$${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\nabla }^{s}{\tilde {\boldsymbol {u}}}\quad d\Omega =$${\int }_{\Omega }{\tilde {\boldsymbol {\gamma }}}\cdot {\boldsymbol {r}}_{\varepsilon ,h}\quad d\Omega$

( 21)

Los términos de la derecha en las ecuaciones (20) y (21) son las proyecciones ${\textstyle P(\bullet )}$ de los residuos sobre el espacio de las sub-escalas. Por tanto, las ecuaciones (20) y (21) relacionan las sub-escalas ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}}$ y ${\textstyle {\tilde {\boldsymbol {u}}}}$ con los residuos de la escala de elementos finitos, representados por r_{ɛ ,h} y r_{u ,h} , respectivamente.

Existen diversas posibilidades para definir la aproximación a las sub-escalas. En principio el espacio de la escala fina podría ser cualquier espacio complementario al espacio de elementos finitos. Tómese en cuenta que en la ecuación (20) aparece la segunda derivada temporal de la sub-escala ${\textstyle {\tilde {\boldsymbol {u}}}}$ , por lo que ésta necesita discretizarse en el tiempo [12] . Es necesario, en primer lugar, seguir la evolución en el tiempo de la sub-escala y, en segundo lugar, el método de integración temporal de la sub-escalas tiene que ser compatible con el esquema explícito empleado en el espacio de los elementos finitos, por lo que también se requiere resolver en forma explícita la sub-escala de los desplazamientos ${\textstyle {\tilde {\boldsymbol {u}}}}$ . La subescala de las deformaciones ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}}$ puede ser tratada implícitamente (véase [9] ).

Considérese una partición uniforme en el tiempo [0, T ] de tamaño Δt , tal que el tiempo tⁿ  = n Δt . Por simplicidad, se supone Δt constante. Empleando el método de diferencias centrales en la ecuación (20) , las aceleraciones en la sub-escala se escriben:

${\ddot {\tilde {\boldsymbol {u}}}}^{n}={\frac {1}{\Delta t^{2}}}({\tilde {\boldsymbol {u}}}^{n+1}-$$2{\tilde {\boldsymbol {u}}}^{n}+{\tilde {\boldsymbol {u}}}^{n-1})$

( 22)

Sustituyendo (22) en (20) y siendo ${\textstyle P_{\boldsymbol {\varepsilon }}}$ y ${\textstyle P_{\boldsymbol {u}}}$ las proyecciones sobre ${\textstyle {\tilde {T}}}$ y ${\textstyle {\tilde {V}}}$ , respectivamente, el problema (20) y (21) se lee ahora como: dados ${\textstyle {\tilde {\boldsymbol {u}}}^{n}}$ y ${\textstyle {\tilde {\boldsymbol {u}}}^{n-1}}$ , hallar ${\textstyle {\tilde {\boldsymbol {u}}}^{n+1}}$ y ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}^{n+1}}$ tal que [9]  ;  [12] :

$P_{u}\left(\nabla \cdot {\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}):{\tilde {\boldsymbol {\varepsilon }}}^{n+1}-\right.$$\left.{\frac {\rho }{\Delta t^{2}}}{\tilde {\boldsymbol {u}}}^{n+1}\right)=$$P_{u}\left({\frac {\rho }{\Delta t^{2}}}(2{\tilde {\boldsymbol {u}}}^{n}-\right.$$\left.{\tilde {\boldsymbol {u}}}^{n-1})+{\boldsymbol {r}}_{u,h}^{n}\right)$

( 23)

$P_{\boldsymbol {\varepsilon }}\left({\tilde {\boldsymbol {\varepsilon }}}^{n+1}-\right.$$\left.{\nabla }^{s}{\tilde {\boldsymbol {u}}}^{n+1}\right)=$$P_{\boldsymbol {\varepsilon }}\left({\boldsymbol {r}}_{\varepsilon ,h}^{n+1}\right)$

( 24)

Se requiere resolver de forma aproximada las ecuaciones (23) y (24) para obtener los valores de ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}^{n+1}}$${\textstyle {\tilde {\boldsymbol {u}}}^{n+1}}$ . Aplicando el mismo procedimiento que en [11] , se pueden aproximar las sub-escalas mediante un análisis de Fourier del problema. Así, ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}^{n+1}}$ y ${\textstyle {\tilde {\boldsymbol {u}}}^{n+1}}$ pueden aproximarse dentro de cada elemento Ω_e como:

${\boldsymbol {\tilde {\boldsymbol {u}}}}^{n+1}\approx {\tau }_{u_{t}}{\frac {\rho }{\Delta t^{2}}}\left(2{\tilde {\boldsymbol {u}}}^{n}-\right.$$\left.{\tilde {\boldsymbol {u}}}^{n-1}\right)+{\tau }_{u_{t}}P_{u}\left(-\right.$$\left.{\boldsymbol {r}}_{u,h}^{n}\right)$

( 25)

${\tilde {\boldsymbol {\varepsilon }}}^{n+1}\approx {\tau }_{\varepsilon }P_{\varepsilon }\left({\boldsymbol {r}}_{\varepsilon ,h}^{n+1}\right)$

( 26)

donde ${\textstyle {\tau }_{u_{t}}}$ y τ_ɛ son los parámetros de estabilización dados por:

${\tau }_{u_{t}}={\left({\frac {\rho }{\Delta t^{2}}}+{\frac {1}{{\tau }_{u_{s}}}}\right)}^{-1}\quad y\quad {\tau }_{\varepsilon }=$$c_{\varepsilon }{\frac {h}{L_{0}}}$

( 27)

donde ${\textstyle {\tau }_{u_{s}}=c_{u}{hL}_{0}/\mu }$ es el parámetro de estabilización estático, c_u  > 0 y c_ɛ  > 0 son constantes algorítmicas adimensionales, L₀ es la longitud característica del problema el cual se toma como el diámetro del dominio computacional Ω y μ  > 0 es el módulo de rigidez secante al corte. La experiencia numérica en análisis estáticos muestra que los valores de c_ɛ y c_u se pueden escoger en el rango de [0.01, 1.0].

Para definir completamente el método y calcular las sub-escalas, se requiere seleccionar adecuadamente las proyecciones ${\textstyle P_{\boldsymbol {u}}}$ y ${\textstyle P_{\boldsymbol {\varepsilon }}}$ . La elección más simple para las proyecciones es tomar las mismas como la identidad ${\textstyle I}$ . Este procedimiento se conoce como Método de las Sub-Escalas Algebraicas (Algebraic Sub-Scales (ASGS)) [8] . Codina propuso para el espacio de las sub-escalas ${\textstyle {\tilde {V}}}$ y ${\textstyle {\tilde {T}}}$ el espacio ortogonal al espacio de los elementos finitos ${\textstyle V_{h}}$ y ${\textstyle T_{h}}$ . Esta definición da origen a una formulación denominada Método de las Sub-escalas Ortogonales (Orthogonal Sub-Scales (OSS)) [8] ; [9]  ;  [10] . De acuerdo con este planteamiento, el espacio de las deformaciones y desplazamientos se aproxima como ${\textstyle T\simeq T_{h}\oplus T_{h}^{\perp }}$ y ${\textstyle V\simeq V_{h}\oplus V_{h}^{\perp }}$ respectivamente. En este trabajo se ha optado por este método. Por practicidad se introduce el operador de proyección ortogonal ${\textstyle P_{h}^{\perp }(\bullet )=(\bullet )-P_{h}(\bullet )}$ . Además se supone que el campo de las fuerzas másicas b puede ser descrito completamente en el espacio de ${\textstyle V_{h}}$ , se tiene que ${\textstyle P_{h}^{\perp }({\boldsymbol {b}})=0}$[2] ; [5]  ;  [30] . Por consiguiente, se pueden tomar ${\textstyle {\tilde {\boldsymbol {u}}}}$ y ${\textstyle {\tilde {\boldsymbol {\varepsilon }}}}$ como:

${\tilde {\boldsymbol {u}}}^{n+1}\simeq {\tau }_{u_{t}}{\frac {\rho }{\Delta t^{2}}}\left(2{\tilde {\boldsymbol {u}}}^{n}-\right.$$\left.{\tilde {\boldsymbol {u}}}^{n-1}\right)+{\tau }_{u_{t}}\left(\nabla \cdot {\boldsymbol {\sigma }}_{h}^{n}-\right.$$\left.P_{h}\left(\nabla \cdot {\boldsymbol {\sigma }}_{h}^{n}\right)\right)$

( 28)

${\tilde {\boldsymbol {\varepsilon }}}^{n+1}\simeq {\tau }_{\varepsilon }\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}-\right.$$\left.P_{h}\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}\right)\right)=$${\tau }_{\varepsilon }\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}-\right.$$\left.{\breve {\boldsymbol {\varepsilon }}}_{h}^{n+1}\right)$

( 29)

siendo ${\textstyle {\breve {\boldsymbol {\varepsilon }}}_{h}^{n+1}=P_{h}\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}\right)}$ .

El residuo en la ecuación (19) puede escribirse en función de la parte volumétrica y desviadora del tensor de tensiones, es decir, ∇ · σ_h  = ∇ · S_h  + ∇ p_h , siendo S el tensor desviador. En problemas quasi-incompresibles o incompresibles, sólo el gradiente de la presión ∇p_h necesita incluirse en el residuo para asegurar la estabilidad en el campo de las presiones. Esto permite estabilizar la presión minimizando la magnitud del término de estabilización. El hecho de no considerar una parte del residuo introduce un cierto error de consistencia, pero en el método de OSS este error es de orden óptimo y no altera la velocidad de convergencia del esquema.

Por otra parte, se puede introducir un efecto simple de amortiguamiento numérico a fin de considerar un esquema disipativo y eliminar las frecuencias espurias en la sub-escala de los desplazamientos, que pueden afectar la estabilidad del sistema. En tal sentido, despreciando el término desviador en la ecuación (28) e introduciendo un coeficiente de disipación ${\textstyle {\tilde {\xi }}\in [0,1]}$ , se obtiene una versión modificada de OSS [2] . En consecuencia, ${\textstyle {\tilde {\boldsymbol {u}}}}$ estará ahora dado por:

${\tilde {\boldsymbol {u}}}^{n+1}\simeq {\tau }_{u_{t}}{\frac {\rho }{\Delta t^{2}}}\left((2-\right.$$\left.{\tilde {\xi }}){\tilde {\boldsymbol {u}}}^{n}-(1-\right.$$\left.{\tilde {\xi }}){\tilde {\boldsymbol {u}}}^{n-1}\right)+$${\tau }_{u_{t}}\left(\nabla p_{h}^{n}-P_{h}\left(\nabla p_{h}^{n}\right)\right)$

( 30)

2.4. Ecuación discreta y estabilizada de la ecuación de movimiento. Formulación mixta estabilizada explícita

Para definir la ecuación discreta y estabilizada de la ecuación de movimiento (13) , ésta tiene que ser discretizada en el tiempo. En la referencia [23] se discuten las ventajas de la formulación mixta explícita en conjunto con un estudio numérico de estabilidad y convergencia. Naturalmente, este método mixto-explícito es condicionalmente estable, pero su precisión es superior a su contraparte irreducible. Al igual que la formulación irreducible, los desplazamientos u y deformaciones ɛ en el tiempo t^{n +1} se computan a partir de la ecuación de equilibrio dinámico evaluada en el tiempo tⁿ . En consecuencia, la ecuación (13) se expresa en el tiempo tⁿ como:

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {\sigma }}_{h}^{n}\quad d\Omega +$${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\tilde {\boldsymbol {\sigma }}}^{n}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho \left({\ddot {\boldsymbol {u}}}_{h}^{n}+\right.$$\left.{\ddot {\tilde {\boldsymbol {u}}}}^{n}\right)\quad d\Omega =$${\boldsymbol {F}}_{ext}^{n}({\boldsymbol {\omega }}_{h})\quad \forall {\boldsymbol {\omega }}_{h}$

( 31)

Al emplear el método de estabilización OSS, el término ${\textstyle {\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\tilde {\boldsymbol {u}}}}^{n}\quad d\Omega =}$${\boldsymbol {0}}$ por la condición de ortogonalidad. Sustituyendo la ecuación (29) en (31) , la ecuación discreta y estabilizada de equilibrio dinámico en t  = tⁿ se escribe finalmente como:

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {C}}({\boldsymbol {\boldsymbol {\varepsilon }}}_{h}^{n}):{\boldsymbol {\varepsilon }}_{h}^{n}\quad d\Omega +$${\tau }_{\varepsilon }{\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}^{n}):\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n}-\right.$$\left.{\breve {\boldsymbol {\varepsilon }}}_{h}^{n}\right)\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\boldsymbol {u}}}_{h}^{n}\quad d\Omega =$${\boldsymbol {F}}_{ext}^{n}({\boldsymbol {\omega }}_{h})\quad \quad \quad \forall {\boldsymbol {\omega }}_{h}$

( 32)

Por otra parte, sustituyendo la ecuación (29) en la ecuación (15) evaluada en t^{n +1} se obtiene:

${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\boldsymbol {\varepsilon }}_{h}^{n+1}\quad d\Omega +$${\tau }_{\boldsymbol {\varepsilon }}{\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot \left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}-\right.$$\left.{\breve {\boldsymbol {\varepsilon }}}_{h}^{n+1}\right)\quad d\Omega =$${\int }_{\Omega }{\boldsymbol {\gamma }}_{h}\cdot {\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n+1}\quad d\Omega -$${\int }_{\Omega }\left(\nabla \cdot {\boldsymbol {\gamma }}_{h}\right)\cdot {\tilde {\boldsymbol {u}}}^{n+1}\quad d\Omega$

( 33)

Por la propiedad de idempotencia del operador de proyección, es decir, ${\textstyle P_{h}(P_{h}(\bullet ))=P_{h}({\left(\bullet \right)}_{h})=}$${\left(\bullet \right)}_{h}$ , y teniendo en cuenta que las sub-escalas de los desplazamientos en t^{n +1} están dados por la ecuación (28) o (30) , las deformaciones continuas ${\textstyle {\boldsymbol {\varepsilon }}_{h}^{n+1}}$ se expresan finalmente:

${\boldsymbol {\varepsilon }}_{h}^{n+1}={\breve {\boldsymbol {\varepsilon }}}_{h}^{n+1}-$$P_{h}\left(\left(\nabla \cdot {\boldsymbol {\gamma }}_{h}\right)\cdot {\tilde {\boldsymbol {u}}}^{n+1}\right)$

( 34)

Si no se considera la sub-escala de los desplazamientos, el segundo término del lado derecho de la ecuación (34) es nulo, obteniéndose la misma expresión que en [23] . Por otro lado, dado que el segundo término del lado derecho de la ecuación (34) es pequeño frente a ${\textstyle {\breve {\boldsymbol {\varepsilon }}}_{h}^{n+1}}$ , se puede tomar ${\textstyle {\breve {\boldsymbol {\varepsilon }}}_{h}\approx {\boldsymbol {\varepsilon }}_{h}}$ . En tal caso, la ecuación de movimiento estabilizada de equilibrio dinámico en (33) se reescribe como:

$(1-{\tau }_{\varepsilon }){\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}^{n}):{\boldsymbol {\varepsilon }}_{h}^{n}\quad d\Omega +$${\tau }_{\varepsilon }{\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}^{n}):\left({\nabla }^{s}{\boldsymbol {\mbox{u}}}_{h}^{n}\right)\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\boldsymbol {u}}}_{h}^{n}\quad d\Omega =$${\boldsymbol {F}}_{ext}^{n}({\boldsymbol {\omega }}_{h})\quad \quad \quad \forall {\boldsymbol {\omega }}_{h}$

( 35)

Reagrupando los términos, se obtiene la expresión:

${\boldsymbol {\varepsilon }}_{h}^{stab,n}=(1-{\tau }_{\varepsilon }){\boldsymbol {\varepsilon }}_{h}^{n}-$${\tau }_{\varepsilon }{\nabla }^{s}{\boldsymbol {u}}_{h}^{n}$

( 36)

${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {C}}({\boldsymbol {\varepsilon }}_{h}^{n}):{\boldsymbol {\varepsilon }}_{h}^{stab,n}\quad d\Omega +$${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\boldsymbol {u}}}_{h}^{n}\quad d\Omega =$${\boldsymbol {F}}_{ext}^{n}({\boldsymbol {\omega }}_{h})$

( 37)

donde ɛ^stab son las deformaciones estabilizadas . El primer término del lado izquierdo de la la ecuación (37) es el vector de fuerzas internas estabilizadas:

${\boldsymbol {F}}_{int}^{stab,n}({\boldsymbol {\omega }}_{h})=$${\int }_{\Omega }{\nabla }^{s}{\boldsymbol {\omega }}_{h}:{\boldsymbol {\sigma }}^{stab,n}\quad d\Omega$

( 38)

siendo σ^stab  = C  : ɛ^stab las tensiones estabilizadas . Esto permite reescribir la ecuación (37) como:

${\int }_{\Omega }{\boldsymbol {\omega }}_{h}\cdot \rho {\ddot {\boldsymbol {u}}}_{h}^{n}\quad d\Omega =$${\boldsymbol {F}}_{ext}^{n}({\boldsymbol {\omega }}_{h})-{\boldsymbol {F}}_{int}^{stab,n}({\boldsymbol {\omega }}_{h})$

( 39)

Si se considera las fuerzas viscosas, la ecuación (39) toma el formato matricial de equilibrio dinámico:

${\boldsymbol {M}}{\ddot {\boldsymbol {u}}}_{h}^{n}+{\boldsymbol {D}}{\dot {\boldsymbol {u}}}_{h}^{n}=$${\boldsymbol {F}}_{ext}^{n}-{\boldsymbol {F}}_{int}^{stab,n}$

( 40)

donde M es la matriz de masa y D la matriz de amortiguamiento. El proceso de integración temporal de la ecuación de movimiento en un esquema mixto explícito es idéntico al procedimiento realizado en un esquema irreducible, salvo que se requieren fundamentalmente dos pasos adicionales (3 y 4), los cuales se describen a continuación:

• 1. Cómputo de las fuerzas internas estabilizadas ${\textstyle {\boldsymbol {F}}_{int}^{stab,n}}$ .
• 2. Cómputo de los desplazamientos en t  = t^{n +1}  :

${\boldsymbol {\mbox{u}}}^{n+1}={\left[2{\boldsymbol {M}}+\Delta t{\boldsymbol {D}}\right]}^{-1}[(4{\boldsymbol {M}}{\boldsymbol {\mbox{u}}}^{n}-$$[2{\boldsymbol {M}}-\Delta t{\boldsymbol {D}}]{\boldsymbol {\mbox{u}}}^{n-1}+$$2\Delta t^{2}({\boldsymbol {F}}_{ext}^{n}-{\boldsymbol {F}}_{int}^{stab,n})]$

• 3. Evaluación de las sub-escalas de los desplazamientos ${\textstyle {\tilde {\boldsymbol {u}}}^{n+1}}$ empleando (28) o (30) .
• 4. Actualización de las deformaciones ${\textstyle {\boldsymbol {\varepsilon }}_{h}^{n+1}}$ con (34) .
• 5. Ir a siguiente paso.

La formulación propuesta puede ser incorporada con facilidad en cualquier código de elementos finitos explícitos agregando simplemente los pasos 3 y 4, que pueden ejecutarse en única rutina de cálculo. Además, en los pasos 3 y 4 pueden aplicarse técnicas de paralización computacional ya que las operaciones involucradas se realizan a nivel de elementos y nodos de la malla.

Nótese que los desplazamientos ${\textstyle {\boldsymbol {u}}_{h}^{n+1}}$ se obtienen a partir de los valores del paso tⁿ y más específicamente de ${\textstyle {\boldsymbol {\varepsilon }}_{h}^{stab,n}}$ , por lo que la ecuación (34) es compatible con un esquema explícito. Una vez calculadas los valores de los desplazamientos ${\textstyle {\boldsymbol {u}}_{h}^{n+1}}$ , se calculan los valores de los desplazamientos de la sub-escala ${\textstyle {\tilde {\boldsymbol {u}}}^{n+1}}$ y por último los valores de las deformaciones nodales ${\textstyle {\boldsymbol {\varepsilon }}_{h}^{n+1}}$ con la ecuación (34) . Este esquema sólo requiere la resolución de un sistema diagonal de ecuaciones, frente a las formulaciones mixtas implícitas, que requieren la resolución de mayores sistemas de ecuaciones. A partir de ahora, a esta formulación propuesta la denominaremos Método de Elementos Finitos Mixtos Explícitos (Mixed Explicit Finite Element Method) o simplemente MEX-FEM, por sus siglas en inglés.

2.5. Aspectos de implementación computacional

La integración temporal explícita es efectiva si las matrices de masa M y de amortiguamiento D en (40) son diagonales [7] . Considérese un elemento tetraedro de cuatros nodos empleando las mismas funciones lineales de interpolación para los desplazamientos y deformaciones. En la formulación mixta, las deformaciones no son constantes dentro del elemento, sino que varían linealmente. En este trabajo se usa una cuadratura cerrada Gauss-Lobatto, en la cual los puntos de integración se sitúan sobre los nodos de los elementos finitos, a fin de evaluar correctamente las integrales sobre el dominio de los elementos finitos Ω_e .

Nótese que que al emplear el método de Galerkin, las funciones de prueba ω_h para el espacio de los desplazamientos y γ_h para el espacio de las deformaciones son las funciones de interpolación, convencionalmente escritas en notación matricial como ${\textstyle {\boldsymbol {N}}_{\alpha }=[{\boldsymbol {N}}_{\alpha }^{1}{\boldsymbol {N}}_{\alpha }^{2}{\boldsymbol {N}}_{\alpha }^{3}{\boldsymbol {N}}_{\alpha }^{4}]}$ ∀α  ∈ {u , ɛ }. Los desplazamientos y las deformaciones nodales dentro del elemento se interpolan como:

${\boldsymbol {u}}_{h}=\sum _{i=1}^{4}{\boldsymbol {N}}_{u}^{i}{\boldsymbol {u}}_{h}^{i}\quad y\quad {\boldsymbol {\varepsilon }}_{h}=$$\sum _{i=1}^{4}{\boldsymbol {N}}_{\boldsymbol {\varepsilon }}^{i}{\boldsymbol {\varepsilon }}_{h}^{i}$

( 41)

siendo ${\textstyle {\boldsymbol {N}}_{u}^{i}}$ la submatriz diagonal de 3 × 3 ${\textstyle ({\boldsymbol {N}}_{u}^{i}=diag\lbrace N_{i},N_{i},N_{i}\rbrace )}$ de las funciones de interpolación del campo de los desplazamientos en el nodo i  ${\textstyle ({\boldsymbol {u}}_{h}^{i}=\lbrace u_{x,h}^{i},u_{y,h}^{i},u_{z,h}^{i}\rbrace )}$ y ${\textstyle {\boldsymbol {N}}_{\boldsymbol {\varepsilon }}^{i}}$ la submatriz diagonal de 6 × 6 ${\textstyle ({\boldsymbol {N}}_{\boldsymbol {\varepsilon }}^{i}=diag\lbrace N_{i},N_{i},N_{i},N_{i},N_{i},N_{i}\rbrace )}$ de las funciones de interpolación del campo de las deformaciones en el nodo i  ${\textstyle ({\boldsymbol {\varepsilon }}_{h}^{i}=\lbrace {\boldsymbol {\varepsilon }}_{xx,h}^{i},{\boldsymbol {\varepsilon }}_{yy,h}^{i},{\boldsymbol {\varepsilon }}_{zz,h}^{i},{\boldsymbol {\varepsilon }}_{xy,h}^{i},{\boldsymbol {\varepsilon }}_{yz,h}^{i},{\boldsymbol {\varepsilon }}_{xz,h}^{i}\rbrace )}$ . Por otra parte, en la ecuación (38) , ${\textstyle {\nabla }^{s}{\boldsymbol {\omega }}_{h}={\boldsymbol {B}}_{u}^{T}}$ es el clásico operador matricial de gradiente simétrico discreto, en el cual B_u  = [B₁B₂B₃B₄ ], donde cada sub-matriz B_i se escribe como:

${\boldsymbol {B}}_{i}={\left({\begin{array}{cccccc}{\frac {\partial N_{i}}{\partial X}}&0&0&{\frac {\partial N_{i}}{\partial Y}}&0&{\frac {\partial N_{i}}{\partial Z}}\\0&{\frac {\partial N_{i}}{\partial Y}}&0&{\frac {\partial N_{i}}{\partial X}}&{\frac {\partial N_{i}}{\partial Z}}&0\\0&0&{\frac {\partial N_{i}}{\partial Z}}&0&{\frac {\partial N_{i}}{\partial Y}}&{\frac {\partial N_{i}}{\partial X}}\\&&&&&\end{array}}\right)}^{T}$

( 42)

De igual manera, el operador de divergencia ∇ · γ_h en (34) toma la forma de ${\textstyle {\boldsymbol {B}}_{\varepsilon }=[{\boldsymbol {B}}_{1}^{T}{\boldsymbol {B}}_{2}^{T}{\boldsymbol {B}}_{3}^{T}{\boldsymbol {B}}_{4}^{T}]}$ .

3. Verificación. Simulaciones numéricas

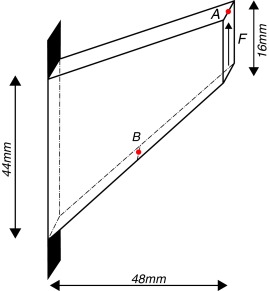
La eficacia de la formulación MEX-FEM se muestra a continuación en una serie de tests numéricos realizados sobre la Membrana de Cook, mostrado en la figura 1 . Se consideran casos de elasticidad compresible y quasi-incompresible, con las constantes elásticas: Módulo de Young E  = 200 Mpa y coeficiente de Poisson ν  = 0.30 y ν  = 0.499. La densidad del material se toma 10 kg/m³ . El problema se analiza realizando análisis quasi-estático y dinámico bajo la hipótesis de deformación plana (con espesor unitario) y haciendo un análisis completamente tridimensional (espesor 10 mm). Para el caso bidimensional, el tamaño del elemento finito se ha tomado como ${\textstyle h={\left(4/\pi \cdot A\right)}^{\frac {1}{2}}}$ siendo A   el área del elemento finito correspondiente. En el caso tridimensional se ha tomado ${\textstyle h={\left(6/\pi \cdot V\right)}^{\frac {1}{3}}}$ donde V el volumen del elemento finito. Como método de estabilización se emplea el OSS con c_u  = 1.0, c_ɛ  = 1.0 y L₀  = 50 mm. La sub-escala de los desplazamientos ${\textstyle {\tilde {\boldsymbol {u}}}}$ se computa empleando la ecuación (30) . En la integración temporal de la ecuación de movimiento se ha empleado un paso de tiempo Δt   constante. Los resultados obtenidos con la formulación propuesta se comparan con la formulación estándar en desplazamientos y la formulación mixta explícita estándar (Mex-Fem estándar ${\textstyle {\tilde {\boldsymbol {u}}}={\boldsymbol {0}}}$ ) [23] , es decir sin considerar la sub-escala de los desplazamientos. Los análisis se han realizado con el programa de elementos finitos KRATOS [13]  ;  [14] , desarrollado en el Centro Internacional de Métodos Numéricos (CIMNE). Como pre y post-procesador se ha utilizado GiD [16] , también desarrollado en CIMNE.

Figura 1. Membrana de Cook . Geometría.

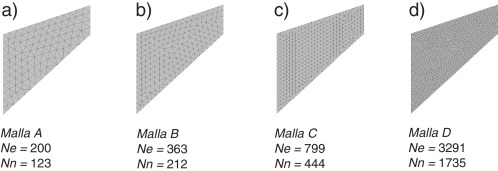
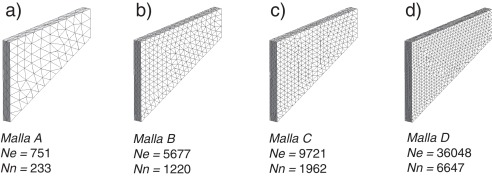
En la discretización espacial se emplean 4 mallas de elementos finitos triangulares y tetraédricos mostradas en las figuras 2 y 3 , respectivamente. Para eliminar las frecuencias espurias que pueden aparecer en la integración temporal sin degradar la respuesta dinámica se emplea un amortiguamiento de Rayleigh con un coeficiente disipación en la sub-escala ${\textstyle {\tilde {\xi }}=0.1}$ . Asimismo, con el fin de obtener la respuesta estacionaria del problema quasi-estático se emplea un amortiguamiento de Rayleigh con un coeficiente de amortiguamiento de ξ  = 0.1. La carga impuesta F de valor unitario se aplica de una manera instantánea y constante en el tiempo.

Figura 2. Membrana de Cook. Mallas de elementos finitos empleada en el análisis bidimensional. Nn: número de elementos y Nn: número de nodos.

Figura 3.

Membrana de Cook. Mallas de elementos finitos empleada en el análisis tridimensional. Nn: número de elementos y Nn: número de nodos.

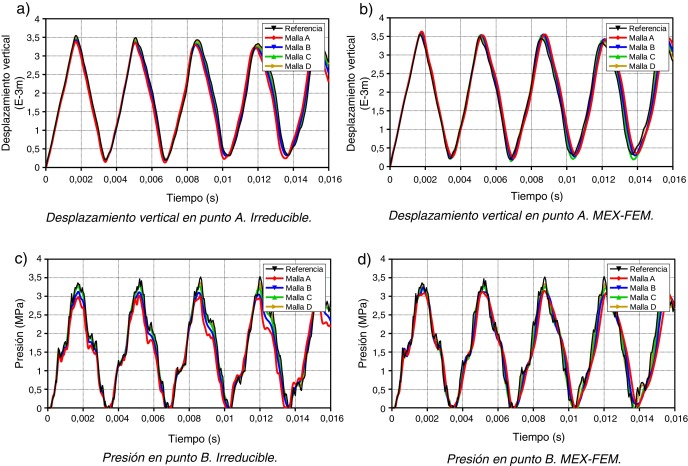
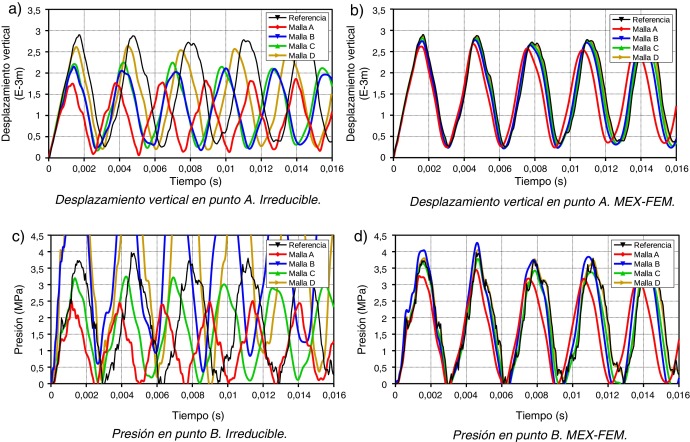
La evolución del desplazamiento vertical en la esquina superior derecha (punto A) para un análisis 2D de deformación plana se muestra en las figuras 4 y 5 para valores de Poisson de ν  = 0.3 y ν  = 0.499, casos compresible y quasi-incompresible, respectivamente. Se puede observar que para ν  = 0.3, ambas formulaciones presentan resultados similares en el campo de los desplazamientos y presiones, aunque MEX-FEM es más preciso. Sin embargo, nótese como en el caso quasi-incompresible ν  = 0.499, la formulación propuesta claramente supera a la irreducible. La figura 5 a muestra el pobre comportamiento del elemento triangular estándar en el campo de los desplazamientos debido al efecto de bloqueo volumétrico. El desplazamiento predicho por este elemento, incluso utilizando mallas finas, está muy por debajo del valor correcto. Nótese además que el error de fase en la formulación irreducible es notoriamente mayor que el obtenido con la presente formulación para una misma malla de elementos finitos. La evolución del campo de las presiones para ν  = 0.499 (punto B de la figura 1 ) se aprecia en las figuras 5 c y 5 d, tanto para la formulación irreducible como para la presente formulación. Dado que el valor de la presión es constante dentro del elemento lineal irreducible, el valor nodal se ha obtenido mediante la proyección ${\textstyle L_{2}}$ , o sea, ${\textstyle p_{h}=P_{h}(p)}$ . Obsérvese cómo el efecto del bloqueo volumétrico en la formulación irreducible provoca oscilaciones el campo de las presiones que desvirtúan completamente la solución. En la figura 5 d se puede comprobar que la presente formulación produce resultados satisfactorios y razonablemente precisos en el campo de las presiones.

Figura 4. Membrana de Cook 2D . Formulación Irreducible vs MEX-FEM con ν  = 0.3.

Figura 5. Membrana de Cook 2D . Formulación Irreducible vs MEX-FEM con ν  = 0.499.

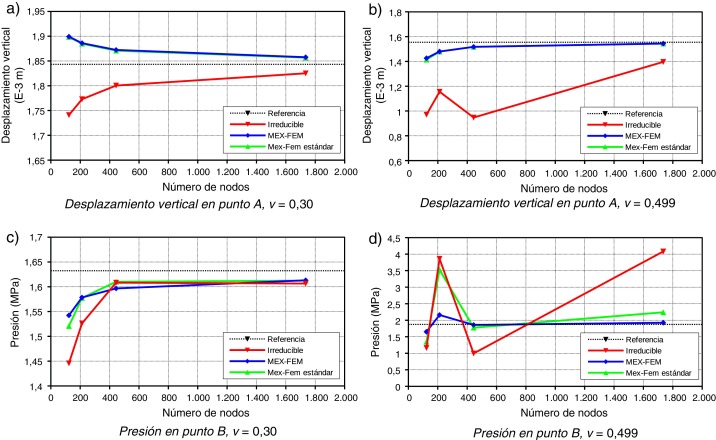
Las curvas de convergencia para el caso estacionario para los valores de coeficiente de Poisson mencionados se muestran en la figura 6 . Nuevamente para valor ν  = 0.3, la formulación irreducible, MEX-FEM con ${\textstyle {\tilde {\boldsymbol {u}}}=0}$ y MEX-FEM convergen al valor correcto del desplazamiento (1.843 mm) y presión (1.632 MPa) a media que se refina la malla. Además, puede verse que las formulaciones mixta estándar y la propuesta convergen a la misma velocidad pero más rápido que la formulación irreducible. Por otra parte, cuando ν  = 0.499, se observa la capacidad de MEX-FEM para predecir el valor correcto del desplazamiento vertical (1.554 mm) y la presión (1.872 MPa). Obsérvese también que la formulación mixta explícita estándar, a pesar de dar un resultado satisfactorio del campo de los desplazamientos, presenta inestabilidades en el campo de las presiones que desvirtúan completamente la solución. En el mismo sentido, nótese que el valor del desplazamiento y de la presión predicho por la formulación irreducible están subestimados.

Figura 6. Membrana de Cook 2D . Curvas de convergencia.

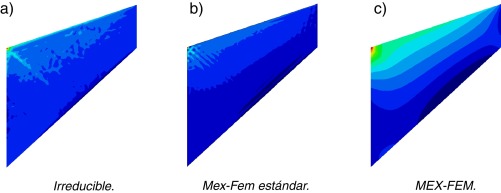
La figura 7 muestra el campo de las presiones de las formulaciones mencionadas en la Malla D para un valor de ν  = 0.499. Obsérvese como MEX-FEM es capaz de dar una solución estabilizada del campo de las presiones, no siendo así para el caso irreducible y el caso mixto explícito sin sub-escala de desplazamientos.

Figura 7. Membrana de Cook 2D . Campo de presiones. Malla D.

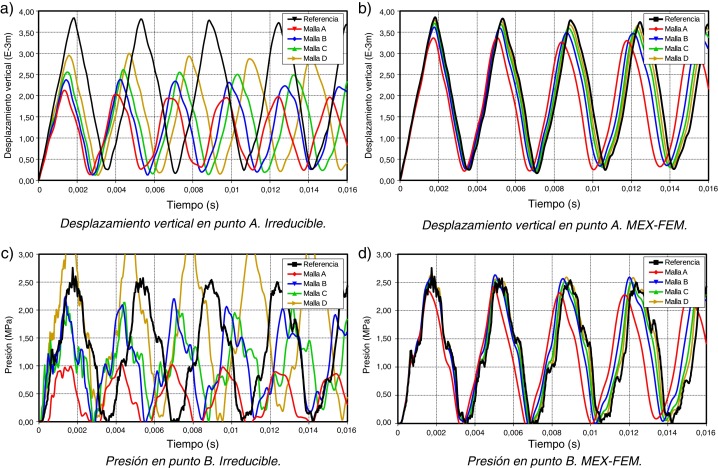
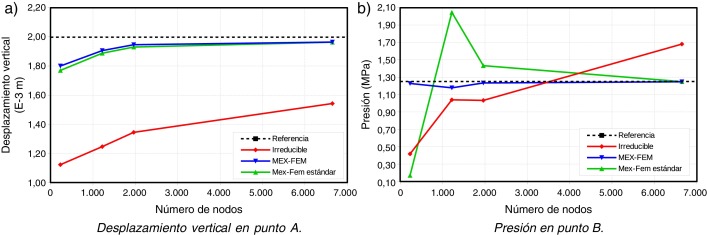
Los resultados para el análisis dinámico tridimensional quasi-incompresible de la membrana de Cook se muestran en la figura 8 . El caso compresible, no mostrado, tiene un comportamiento similar al caso bidimensional. Nuevamente, se observa el pobre rendimiento del elemento tetraédrico estándar en el campo de los desplazamientos debido al efecto de bloqueo volumétrico. El desplazamiento predicho por este elemento, incluso utilizando mallas tupidas, está muy por debajo del valor correcto. Nótese otra vez que el error en el periodo en la formulación irreducible es notoriamente mayor que con el obtenido de la presente formulación para una misma malla de elementos finitos. Las curvas de convergencia para el caso tridimensional se muestran en la figura 9 . Sobresale la capacidad de MEX-FEM para predecir el valor correcto del desplazamiento vertical (1.998 mm) y la presión (1.251 MPa).

Figura 8. Membrana de Cook 3D . Formulación Irreducible vs MEX-FEM con ν  = 0.499.

Figura 9. Membrana de Cook 3D . Curva de convergencia.

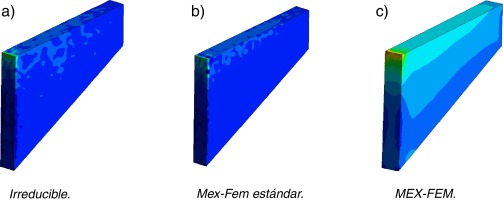
Finalmente, la figura 10 muestra el campo de las presiones de las formulaciones mencionadas en la Malla D para un valor de ν  = 0.499. Adviértase como MEX-FEM es capaz de dar una solución estabilizada del campo de las presiones en un problema tridimensional.

Figura 10. Membrana de Cook 3D . Campo de presiones. Malla D.

4. Conclusión

Ese trabajo propone una formulación mixta explícita de elementos finitos en desplazamientos y deformaciones estabilizadas con sub-escalas, aplicable a elementos con igual orden de interpolación, y en particular, con interpolaciones lineales. Esta formulación se ha desarrollado en el marco del método de las sub-escalas ortogonales, eludiendo de forma efectiva la condición de estabilidad LBB sobre las formulaciones mixtas. En comparación con la formulación irreducible y la formulación mixta sin sub-escala de desplazamientos, la formulación propuesta es más precisa y robusta, no requiere la resolución de un sistema acoplado de ecuaciones y es capaz de abordar problemas quasi-estáticos y dinámicos en situaciones quasi-incompresibles. Por otra parte, el esquema de resolución es análogo al de la formulación irreducible y es muy fácil de integrar la formulación propuesta en un código explícito.

Agradecimientos

Nelson Lafontaine agradece a la Agencia Española De Cooperación Internacional Para El Desarrollo (AECID) por el soporte económico dado en el programa de Becas MAEC-AECID y a los profesores M.W Yuan y Chen Pu por su generoso y valiosísimo apoyo. Riccardo Rossi agradece a los fondos donados por The Seventh Framework Programme (FP7/2007-2013) del ERC bajo el acuerdo n^o 611636 (NUMEXAS) para el desarrollo de este proyecto. Agradecimientos al programa “Excellence Programme for Knowledge Generation by MINECO” del proyecto EACY (Enhanced accuracy computational and experimental framework for strain localization and failure mechanisms, ref. MAT2013-48624-C2-1-P).

References

1. [1] I. Babuska; Error-bounds for finite element method; Numerische Mathematik, 16 (4) (1971), pp. 322–333
2. [2] M. Cervera, M. Chiumenti, L. Benedetti, R. Codina; Mixed stabilized finite element methods in nonlinear solid mechanics. part iii: Compressible and incompressible plasticity; Computer Methods in Applied Mechanics and Engineering, 285 (0) (2015), pp. 752–775
3. [3] M. Cervera, M. Chiumenti, R. Codina; Mixed stabilized finite element methods in nonlinear solid mechanics: Part i: Formulation; Computer Methods in Applied Mechanics and Engineering, 199 (37-40) (2010), pp. 2559–2570
4. [4] M. Cervera, M. Chiumenti, R. Codina; Mixed stabilized finite element methods in nonlinear solid mechanics: Part ii: Strain localization; Computer Methods in Applied Mechanics and Engineering, 199 (37–40) (2010), pp. 2571–2589
5. [5] M. Chiumenti, M. Cervera, R. Codina; A mixed three-field FE formulation for stress accurate analysis including the incompressible limit; Computer Methods in Applied Mechanics and Engineering, 283 (0) (2015), pp. 1095–1116
6. [6] M. Chiumenti, Q. Valverde, C. Agelet de Saracibar, M. Cervera; A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations; Computer Methods in Applied Mechanics and Engineering, 191 (46) (2002), pp. 5253–5264
7. [7] R.W. Clough, J. Penzien; Dynamics of structures; Earthquake Engineering & Structural Dynamics (1976)
8. [8] R. Codina; Stabilization of incompresssibility and convection through orthogonal sub-scales in finite elements methods; Comput. Meth Appl Mech Eng, 190 (2000), pp. 1579–1599
9. [9] R. Codina; Stabilized finite element approximation of transient incompressible flows using orthogonal subscales; Computer Methods in Applied Mechanics and Engineering, 191 (39–40) (2002), pp. 4295–4321
10. [10] R. Codina; Analysis of a stabilized finite element approximation of the oseen equations using orthogonal subscales; Appl. Numer. Math., 58 (3) (2008), pp. 264–283
11. [11] R. Codina, J. Blasco; A finite element method for the stokes problem allowing equal velocity-pressure interpolations; Comput. Meth Appl Mech Eng, 143 (1997), pp. 373–391
12. [12] R. Codina, J. Principe, O. Guasch, S. Badia; Time dependent subscales in the stabilized finite element approximation of incompressible flow problems; Computer Methods in Applied Mechanics and Engineering, 196 (21–24) (2007), pp. 2413–2430
13. [13] P. Dadvand, R. Rossi, M. Gil, X. Martorell, J. Cotela, E. Juanpere, S.R. Idelsohn, E. Oñate; Migration of a generic multi-physics framework to hpc environments; Computers & Fluids, 80 (0) (2013), pp. 301–309
14. [14] P. Dadvand, R. Rossi, E. Oñate; An object-oriented environment for developing finite element codes for multi-disciplinary applications; Archives of Computational Methods in Engineering, 17 (3) (2010), pp. 253–297
15. [15] F. Brezzi, M. Fortin, D. Marini; Mixed finite element methods; Springer (1991)
16. [16] GiD. The personal pre and post processor. http://gid.cimne.upc.es. 2009.
17. [17] A.J. Gil, C.H. Lee, J. Bonet, M. Aguirre; Stabilised petrov-galerkin formulation for linear tetrahedral elements in compressible, nearly incompressible and truly incompressible fast dynamics; Computer Methods in Applied Mechanics and Engineering, 276 (0) (2014), pp. 659–690
18. [18] T.J.R. Hughes; Equivalence of finite elements for nearly incompressible elasticity; J. Appl. Mech., 44 (1977)
19. [19] T.J.R. Hughes; Generalization of selective integration procedures to anisotropic and nonlinear media; International Journal for Numerical Methods in Engineering, 15 (9) (1980), pp. 1413–1418
20. [20] T.J.R. Hughes, G. Scovazzi, L.P. Franca; Multiscale and Stabilized Methods; John Wiley & Sons, Ltd (2004)
21. [21] T.J.R. Hughes; Multiscale phenomena: Greens functions, the dirichlet-to-neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods; Computer Methods in Applied Mechanics and Engineering, 127 (1–4) (1995), pp. 387–401
22. [22] T.J.R. Hughes, G.R. Feijóo, L. Mazzei, J.-B. Quincy; The variational multiscale method-a paradigm for computational mechanics; Computer Methods in Applied Mechanics and Engineering, 166 (1–2) (1998), pp. 3–24 Advances in Stabilized Methods in Computational Mechanics.
23. [23] N.M. Lafontaine, R. Rossi, M. Cervera, M. Chiumenti; Explicit mixed strain-displacement finite element for dynamic geometrically non-linear solid mechanics; Computational Mechanics (2015), pp. 1–17
24. [24] D.S. Malkus, T.J.R. Hughes; Mixed finite element methods - reduced and selective integration techniques: A unification of concepts; Computer Methods in Applied Mechanics and Engineering, 15 (1) (1978), pp. 63–81
25. [25] E. Oñate, A. Valls, J. García; Fic/fem formulation with matrix stabilizing terms for incompressible flows at low and high reynolds numbers; Computational Mechanics, 38 (4–5) (2006), pp. 440–455
26. [26] E. Oñate, J. Rojek, R.L. Taylor, O.C. Zienkiewicz; Finite calculus formulation for incompressible solids using linear triangles and tetrahedra; International Journal for Numerical Methods in Engineering, 59 (11) (2004), pp. 1473–1500
27. [27] G. Scovazzi; Lagrangian shock hydrodynamics on tetrahedral meshes: A stable and accurate variational multiscale approach; Journal of Computational Physics, 231 (24) (2012), pp. 8029–8069
28. [28] J.C. Simo, R.L. Taylor, K.S. Pister; Variational and projection methods for the volume constraint in finite deformation elasto-plasticity; Computer Methods in Applied Mechanics and Engineering, 51 (1–3) (1985), pp. 177–208
29. [29] R.L. Taylor; A mixed-enhanced formulation tetrahedral finite elements; International Journal for Numerical Methods in Engineering, 47 (1-3) (2000), pp. 205–227
30. [30] Q. Valverde, M. Chiumenti, M. Cervera, C. Agelet de Saracibar; Formulación estabilizada de elementos finitos triangulares y tetraédricos para problemas de incompresibilidad en pequeñas deformaciones; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 21 (4) (2005)