Experimental measurements of subsoil–structure interaction and 3D numerical models

Summary

Use of combination of experimental measurements, tests in situ and numerical modelling is optimal approach to obtain reliable results of subsoil–structure interaction. Input data for numerical analyses were obtained by experimental loading tests of three different types of concrete slabs. Loading was performed out using experimental equipment. The unique experimental equipment was constructed in the area of Faculty of Civil Engineering, VŠB-TU Ostrava. Analyses of interaction of reinforced concrete slabs with subsoil were solved by application of inhomogeneous half-space. The main focus was to verify the aptness of application of inhomogeneous half-space in relation to the slab deformations in comparison of different types of reinforcements of concrete slab.

Keywords

Foundation structure ; Soil–structure interaction ; Interaction models ; 3D finite elements ; FEM

Introduction

Geological profile can be different in various parts of the area under the foundations. Unambiguous description of geological profile is very difficult. Experimental measurements of subsoil–structure interaction are carried out throughout the world (Aboutalebi et al., 2014 , Alani and Aboutalebi, 2012  and Huang et al., 2013 ) and also in the Czech Republic and Slovakia. Methology, results and conclusions of the performed loading tests performed out at the Faculty of Civil Engineering, VŠB-TU Ostrava are described in (Cajka et al., 2014 , Buchta and Mynarcik, 2014  and Janulikova and Stara, 2013 ). Inadequate theoretical basics and an absence of appropriate calculation software also prevent the determination of an unambiguous solution of subsoil–structure interaction. Numerical modelling of the subsoil–structure interaction is also described in (Frydrysek et al., 2013 , Janda et al., 2013  and Kralik, 2013 ).

Experimental loading test

In 2010, testing equipment was constructed in areal of the Faculty of Civil Engineering, VŠB – Technical University of Ostrava (Cajka et al., 2011 ). The testing equipment is used for experimental for monitoring of the stress–strain relationships of the interaction of the foundation structures and subsoil. The load is applied by a hydraulic press which pushes the test sample into subsoil. For more details about the structure of the test equipment see (Cajka et al., 2011 ). The testing equipment was used for testing of several different types of foundation slabs. The slabs are different, e.g. from the point of view of concrete mixture, reinforcement, slab dimensions and its thickness or size of the load area. In 2014, the steel-fibre reinforced concrete slab, the post-tensioned concrete slab and the reinforced concrete slab were loaded there. The ground plan dimensions of all slabs were 2000 mm × 2000 mm. Dimensions of the load area were 200 mm × 200 mm. All types of concrete foundation slabs were subjected to punching shear. The failure of the slabs by punching shear is also described in (Halvonik and Fillo, 2013 ).

Experimental loading test of the steel-fibre reinforced concrete slab

The dimensions of the steel-fibre reinforced concrete slab were 2000 mm × 2000 × 170 mm. The C25/30 concrete was used. The concrete was reinforced with scattered reinforcement. The reinforcement consisted of steel fibres 3D DRAMIX 65/60B6–25 kg m⁻³ . From the geologic point of view, the upper layer of subsoil consists of loess loam (F4). The thickness of the layer is approximately 5 m. The Poisson coefficient of the subsoil was μ  = 0.35 and modulus of deformability was E_def  = 2.65 MPa. The loading was performed out sequentially in steps: 20 kN/60 min. Despite of assumptions, the slab did not fail even after nine loading cycles (the load was 180 kN) and the test was interrupted. During repeated loading test of the steel-fibre reinforced concrete slab was loaded with new cycle: 50 kN/30 min. The slab failed during the 6th cycle. The loading force was 250 kN. Fig. 1 shows casting of the slab and cracks at the lower surface of the failed steel-fibre reinforced concrete slab after its lifting up.

Figure 1. Casting of the steel-fibre reinforced concrete slab and cracks at the lower surface of the failed steel-fibre reinforced concrete slab after its lifting up.

Experimental loading test of the reinforced concrete slab

The reinforced concrete slab dimensions were 2000 mm × 2000 mm × 120 mm. The C25/30 concrete was used. 38 steel bars of length 1.9 m and a diameter 8 mm was used for reinforcing of concrete slab. Steel bars were bound to grid with a mesh size 100 mm × 100 mm. Cover of concrete of 20 mm for the lower bars was achieved through concrete spacers. From the geologic point of view, the upper layer of subsoil consists of loess loam (F4). The thickness of the layer is approximately 5 m. 10 cm of the original soil was removed before experimental loading test of reinforced concrete slab. The footing bottom was filled with gravel fraction 0–4 mm along the edge of the surrounding terrain. Gravel was evenly compacted by vibrating plate. The Poisson coefficient of the subsoil was μ  = 0.35 and modulus of deformability was E_def  = 33.1 MPa. The slab was loaded at half-hour intervals by vertical force of 50 kN. The slab was infringed at load of 350 kN. The slab was infringed by punching shear. Fig. 2 shows casting of the slab and cracks at the lower surface of the failed reinforced concrete slab after its lifting up.

Figure 2. Casting of the reinforced concrete slab and cracks at the lower surface of the failed reinforced concrete slab after its lifting up.

Experimental loading test of the post-tensioned concrete slab

Post-tensioned concrete slab had the dimensions 2000 mm × 2000 mm × 150 mm. Concrete class C35/45 was used. Slab was post-tensioned by six threaded prestressing bars. The bars were from steel Y 1050 and their diameter was 18 mm. Each bar was tensioned by force of 100 kN. From the geologic point of view, the upper layer of subsoil consists of loess loam (F4). The thickness of the layer is approximately 5 m. The 300 mm layer of clay soil was removed before loading test of post-tensioned concrete slab. The footing bottom was filled with gravel fraction 0–4 mm to the edge of the surrounding terrain. The Poisson coefficient of the subsoil was μ  = 0.35 and modulus of deformability was E_def  = 33.86 MPa. Loading was carried out in parts, 75 kN/30 min. The slab failed during the 7th cycle during this method of loading. The maximum level of load was 525 kN. The slab was infringed by punching shear. Fig. 3 shows casting of the slab and cracks at the lower surface of the post-tensioned concrete slab after its lifting up.

Figure 3. Casting of the post-tensioned concrete slab and cracks at the lower surface of the post-tensioned concrete slab after its lifting up.

Numerical analysis

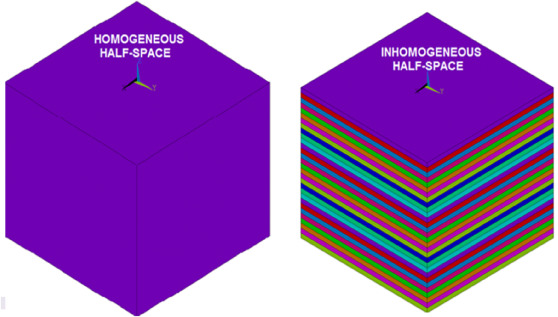
Numerical models were created for all experimental loading tests. It means for steel-fibre reinforced concrete slab, reinforced concrete slab and also post-tensioned concrete slab. 3D numerical models of these three contact tasks were created using ANSYS. 3D subsoil model was created as a half-space. Soil is heterogeneous material and its properties are different from idealization linear elastic isotropic homogeneous substance. Therefore, the calculated values of the settlement do not correspond with the real values measured in real buildings or during the experiments (Labudkova and Cajka, 2014  and Cajka and Labudkova, 2015 ). Inhomogeneous half-space was used for the analysis of the interaction of subsoil and loaded steel-fibre reinforced concrete slab, reinforced concrete slab and also post-tensioned concrete slab. In the inhomogeneous half-space the concentration of vertical stress is different than in the homogeneous half-space and modulus of deformability increases with increasing depth of the subsoil. This is the reason why the material properties of inhomogeneous half-space are more closer to the real conditions than material properties of homogeneous half-space. All three subsoil models were divided into 30 layers (Fig. 4 ). Inhomogeneity of the subsoil was taken into consideration with an increasing modulus of deformability E_{def ,2} (Fig. 4 ). Self weight of soil massif and concrete slabs were neglected. The computational models of all types of subsoil models were created using the element SOLID 45 (3D). When creating a 3D model, the chosen finite elements in the mesh were hexahedral and their dimensions were 0.20 m × 0.20 m × 0.20 m.

Figure 4. Homogeneous half-space (left) and inhomogeneous half-space (right). Inhomogeneous half-space was divided into 30 layers with different material properties – modulus of deformability increases with increasing depth of the subsoil model.

Horizontal nodes displacements in vertical edges of subsoil model were hindered by boundary conditions and vertical nodes displacements in the lower base of the subsoil model were hindered by boundary conditions. No boundary conditions hindered the nodes displacements in the upper level of the subsoil model because it represented the terrain.

Structural and physical nonlinearity were used in the FEM analysis. Structural nonlinearity is caused by interaction between the subsoil and slab (contact task). Definition of the contact area is necessary for the transmission of load effects from the foundation slab to the subsoil. Contact was made using a contact pair TARGE170 and CONTA173. The influence of friction between the slab and the subsoil was neglected. The nonlinear material model was performed by application of Drucker–Prager model which describe the difference between the tensile strength and compressive strength of the soil. The load was applied in a centre of all types of slabs onto the 200 mm × 200 mm area. The load was modelled in several points of the mesh of the slab model. Slab models were a bit different in the creation of numerical models in relation to the type of slab (steel-fibre reinforced concrete slab, reinforced concrete slab, post-tensioned slab). Modulus of elasticity E was according to the strength class of concrete of all slabs and the Poisson coefficient μ  = 0.2.

Results

Resulting deformations were influenced by type of concrete slab. The forces at the moment of the slab failure were different because of different strength class of concrete, different slab thickness, etc. The steel-fibre reinforced concrete slab failed at the load of 250 kN, the reinforced concrete slab failed at the load of 350 kN and the post-tensioned concrete slab failed at the load of 525 kN. Deformation behaviour of slabs was compared at the load of 200 kN at which there was no slab damaged.

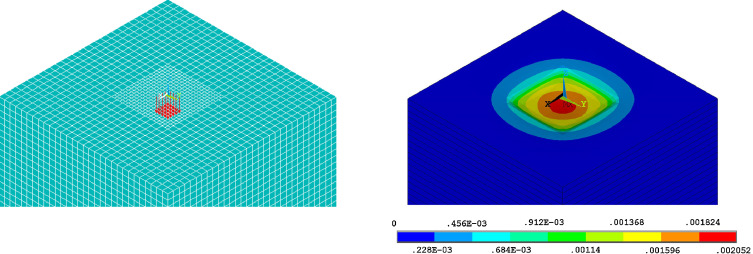
Numerical analysis of the steel-fibre reinforced concrete slab (Fig. 5 )

The computational model was created using the element SHELL 181 (2D). The slab thickness 0.170 m was added to the 2D element SHELL 181 properties. When creating a 2D model, the chosen finite elements in the mesh were 4-nodes and their dimensions were 0.10 m × 0.10 m.

Figure 5. Computational model of steel-fibre reinforced concrete slab (left), deformations of steel-fibre reinforced concrete slab (right), [m].

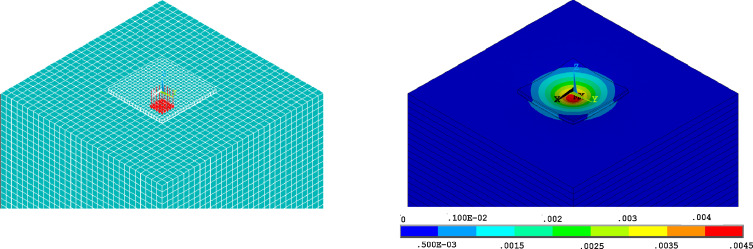
Numerical analysis of the reinforced concrete slab (Fig. 6 )

Reinforced concrete slab model was created using finite elements SOLID 45. Reinforcement was also reflected in the spatial model of reinforced concrete slab. The model slab was divided into four layers. The lowest layer represents the plain concrete and its thickness is equals to the cover of concrete. There is a layer with different material properties which represents the reinforcement above the lowest layer (above the cover of concrete). Another two layers above the reinforcement represent concrete disturbed by cracks. Modulus of elasticity of cracked concrete was derived and it was used in lower layers representing the part of concrete with cracks. Poissons ratio in these layers was μ  = 0.

Figure 6. Computational model of reinforced concrete slab (left), deformations of reinforced concrete slab (right), [m].

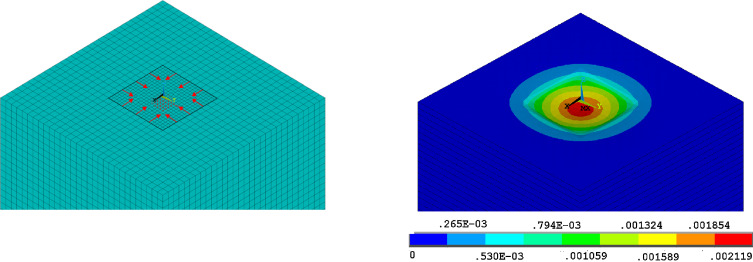
Numerical analysis of the post-tensioned concrete slab (Fig. 7 )

The computational model was created using the element SHELL 181 (2D). The slab thickness 0.120 m was added to the 2D element SHELL 181 properties. When creating a 2D model, the chosen finite elements in the mesh were 4-nodes and their dimensions were 0.10 m × 0.10 m. Prestressing was placed in quarters of all sides of slab model. Force in prestressed reinforcement was 100 kN as well as during the experiment.

Figure 7. Computational model of post-tensioned concrete slab (left), deformations of post-tensioned concrete slab (right), [m].

Discussion

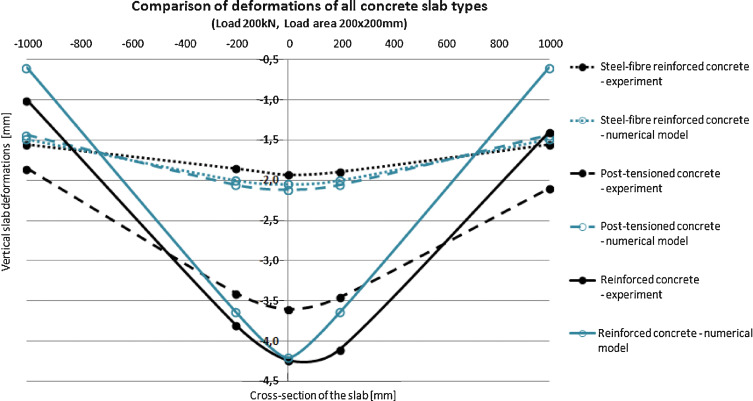
Resulting deformations of all slabs calculated by numerical analyses are shown in the following graph (Fig. 8 ), by blue curves. Deformations measured during experimental loading test are marked by black curves. Deformations of steel-fibre reinforced concrete slab are marked by dotted curve (blue – deformations calculated by numerical analysis, black – deformation measured during experiment). Deformations of reinforced concrete slab are marked by dashed curve (blue – deformations calculated by numerical analysis, black – deformation measured during experiment). Deformations of post-tensioned concrete slab are marked by dashed curve (blue – deformations calculated by numerical analysis, black – deformation measured during experiment). The shapes of calculated deformations of all slabs are similar with shapes of measured deformations. The difference between calculated deformation and the measured deformation in the middle of the post-tensioned slab is about 70.0%. It is the biggest difference. The difference between calculated deformation and the measured deformation in the middle of the steel-fibre reinforced concrete slab is about 5.0%. The difference between calculated deformation and the measured deformation in the middle of the reinforced concrete slab is only about 0.7%.

Figure 8. Comparison of deformations of all concrete slab types at moment of the load of 200 kN. Slabs were loaded at the area of 200 mm × 200 mm. (For interpretation of the references to color in the text, the reader is referred to the web version of this article.)

Conclusions

Comparison of three types of reinforcements of concrete slabs was carried out. The slabs had different thickness, the type of concrete and the subsoil, beside of reinforcements. The main focus was to verify the aptness application inhomogeneous half-space in relation to the slab deformations. The steel-fibre reinforced concrete slab failed at the load of 250 kN, the reinforced concrete slab failed at the load of 350 kN, the post-tensioned concrete slab failed at the load of 525 kN. Deformation behaviour of slabs was compared at the load of 200 kN at which there was no slab failed. Calculated deformations of steel-fibre reinforced concrete slab correlates to the measured deformations very well, because the slab was not disrupted by cracks as in the numerical model. Calculated deformations of reinforced concrete slab correlates to the measured deformations very well, because the slab was disrupted by cracks as in the numerical model. Calculated deformations of post-tensioned concrete slab do not correlates to the measured deformations very well. During the experiment, no cracks were evident at the moment of load of 200 kN, so numerical slab model was created without influence of cracks. The resulting deformations are different about 70%, and one of the reasons may be the developed cracks inside of the slab, which was not evident on the surface of the slab.

Conflict of interest

The authors declare that there is no conflict of interest.

Acknowledgements

This outcome has been achieved with the financial support by Student Grant Competition VSB-TUO. Project registration number is SP2015/108.

References

1. Aboutalebi et al., 2014 M. Aboutalebi, A. Alani, J. Rizzuto, D. Beckett; Structural behaviour and deformation patterns in loaded plain concrete ground-supported slabs; Struct. Concr., 15 (1) (2014), pp. 81–93
2. Alani and Aboutalebi, 2012 A. Alani, M. Aboutalebi; Analysis of the subgrade stiffness effect on the behaviour of ground-supported concrete slabs; Struct. Concr., 13 (2) (2012), pp. 102–108
3. Buchta and Mynarcik, 2014 V. Buchta, P. Mynarcik; Experimental testing of fiberconcrete foundation slab model; Appl. Mech. Mater., 501–504 (2014), pp. 291–294 Trans Tech Publications, Switzerland
4. Cajka et al., 2014 R. Cajka, K. Burkovic, V. Buchta, R. Fojtik; Experimental soil – concrete plate interaction test and numerical models; Key Eng. Mater., 577–578 (2014), pp. 33–36 Trans Tech Publications, Switzerland
5. Cajka and Labudkova, 2015 R. Cajka, J. Labudkova; Fibre concrete foundation slab experiment and FEM analysis; Key Eng. Mater., 627 (2015), pp. 441–444 Trans Tech Publications, Switzerland
6. Cajka et al., 2011 R. Cajka, V. Krivy, D. Sekanina; Design and Development of a Testing Device for Experimental, Measurements of Foundation Slabs on the Subsoil, Transactions of the VSB – Technical University of Ostrava, Construction Series, Vol. XI, Number 1/2011, VSB – TU Ostrava (2011), pp. 1–5 ISSN (Online) 1804–4824, ISSN (Print) 1213–1962
7. Frydrysek et al., 2013 K. Frydrysek, R. Janco, H. Gondek; Solutions of beams, frames and 3D structures on elastic foundation using FEM; Int. J. Mech., 7 (4) (2013), pp. 362–369
8. Halvonik and Fillo, 2013 J. Halvonik, L. Fillo; The maximum punching shear resistance of flat slabs; Proc. Eng., 65 (2013), pp. 376–381
9. Huang et al., 2013 X. Huang, X. Liang, M. Liang, M. Deng, A. Zhu, Y. Xu, X. Wang, Y. Li; Experimental and theoretical studies on interaction of beam and slab for cast-in-situ reinforced concrete floor structure; J. Build. Struct./Jianzhu Jiegou Xuebao, 34 (5) (2013), pp. 63–71 2013
10. Janda et al., 2013 T. Janda, M. Sejnoha, J. Sejnoha; Modeling of soil structure interaction during tunnel excavation: an engineering approach; Adv. Eng. Softw. (2013), pp. 51–60
11. Janulikova and Stara, 2013 M. Janulikova, M. Stara; Reducing the shear stress in the footing bottom of concrete and masonry structures; Proc. Eng., 65 (2013), pp. 284–289
12. Kralik, 2013 J. Kralik; Optimal design of NPP containment protection against fuel container drop; Adv. Mater. Res., 688 (2013), pp. 213–221 Trans Tech Publications, Switzerland
13. Labudkova and Cajka, 2014 J. Labudkova, R. Cajka; Comparison of measured deformation of the plate in interaction with the subsoil and the results of 3D numerical model; Adv. Mater. Res., 1020 (2014), pp. 204–209 Trans Tech Publications Switzerland