Summary
This work covers a contribution to two most interesting research fields in aerodynamics, the finite element analysis of high-speed compressible flows (Part I) and aerodynamic shape optimization (Part II).
The first part of this study aims at the development of a new stabilization formulation based on the Finite Increment Calculus (FIC) scheme for the Euler and Navier-Stokes equations in the context of the Galerkin finite element method (FEM). The FIC method is based on expressing the balance of fluxes in a space-time domain of finite size. It is tried to prevent the creation of instabilities normally presented in the numerical solutions due to the high convective term and sharp gradients.
In order to overcome the typical instabilities happening in the numerical solution of the high-speed compressible flows, two stabilization terms, called streamline term and transverse term, are added through the FIC formulation in space-time domain to the original conservative equations of mass, momentum and energy. Generally, the streamline term holding the direction of the velocity is responsible for stabilizing the spurious solutions produced from the convective term while the transverse term smooths the solution in the high gradient zones. An explicit fourth order Runge-Kutta scheme is implemented to advance the solution in time.
In order to investigate the capability of the proposed formulation, some numerical test examples corresponding to subsonic, transonic and supersonic regimes for inviscid and viscous flows are presented. The behavior of the proposed stabilization technique in providing appropriate solutions has been studied especially near the zones where the solution has some complexities such as shock waves, boundary layer, stagnation point, etc. Although the derived methodology delivers precise results with a nearly coarse mesh, the mesh refinement technique is coupled in the solution to create a suitable mesh particularly in the high gradient zones.
The comparison of the numerical results obtained from the FIC formulation with the reference ones demonstrates the robustness of the proposed method for stabilization of the Euler and Navier-Stokes equations. It is observed that the usual oscillations occur in the Galerkin FEM, especially near the high gradient zones, are cured by implementing the proposed stabilization terms. Furthermore, allowing the adaptation framework to modify the mesh, the quality of the results improves significantly.
The second part of this thesis proposes a procedure for aerodynamic shape optimization combining Genetic Algorithm (GA) and mesh refinement technique. In particular, it is investigated the effect of mesh refinement on the computational cost and solution accuracy during the process of aerodynamic shape optimization. Therefore, an adaptive remeshing technique is joined to the CFD solver for the analysis of each design candidate to guarantee the production of more realistic solutions during the optimum design process in the presence of shock waves.
In this study, some practical transonic airfoil design problems using adaptive mesh techniques coupled to Multi-Objective Genetic Algorithms (MOGAs) and Euler flow analyzer are addressed. The methodology is implemented to solve three practical design problems; the first test case considers a reconstruction design optimization that minimizes the pressure error between a predefined pressure curve and candidate pressure distribution. The second test considers the total drag minimization by designing airfoil shape operating at transonic speeds. For the final test case, a multi-objective design optimization is conducted to maximize both the lift to drag ratio (L/D) and lift coefficient (Cl). The solutions obtained with and without adaptive mesh refinement are compared in terms of solution accuracy and computational cost. These design problems under transonic speeds need to be solved with a fine mesh, particularly near the object, to capture the shock waves that will cost high computational time and require solution accuracy.
By comparison of the the numerical results obtained with both optimization problems, the obtainment of direct benefits in the reduction of the total computational cost through a better convergence to the final solution is evaluated. Indeed, the improvement of the solution quality when an adaptive remeshing technique is coupled with the optimum design strategy can be judged.
Resumen
El presente trabajo pretende contribuir a dos de los campos de investigación más interesantes en la aerodinámica, el análisis numérico de flujos compresibles a alta velocidad (Parte I) y la optimización de la forma aerodinámica (Parte II).
La primera parte de este estudio se centra en la solución numérica de las ecuaciones de Navier-Stokes, que modelan el comportamiento de flujos compresibles a alta velocidad. La discretización espacial se lleva a cabo mediante el método de elementos finitos (FEM) y se pone especial énfasis en el desarrollo de una nueva formulación estabilizada basada en la técnica de cálculo de Incremento finitos (FIC). En este última, los términos de estabilización convectiva se obtienen de manera natural de las ecuaciones de gobierno a través de postulados de conservación y equilibrio de flujos en un dominio espacio-tiempo de tamaño finito. Ello lleva a la obtención de dos términos de estabilización que funcionan de manera complementaria. Uno actúa en dirección de las líneas de corriente proporcionando la estabilización necesaria para contrarestrar las inestabilidades propias de la forma discreta de Galerkin y el otro término, de tipo shock capturing, actúa de manera transversal a las líneas de corriente y permite mejorar la solución numérica alrededor de discontinuidades y otro tipos de fenómenos localizados en el campo de solución de problema. La forma discreta de las ecuaciones de gobierno se completa mediante un esquema de integración temporal explícito de tipo de Runge-Kutta de 4to orden. El esquema de solución básico propuesto se complementa con una técnica de refinamiento adaptativo de malla que permite mejorar automáticamente la solución numérica en zonas localizadas del dominio en que, dadas las características del flujo, se necesita una mayor resolución espacial.
Con el propósito de investigar el comportamiento de la formulación numérica se estudian diferentes casos de análisis que implican flujos viscosos y no viscosos en régimen subsónico, transónico y supersónico y se estudia con especial detalle el funcionamiento de la técnica de estabilización propuesta. Los resultados obtenidos demuestran una exactitud satisfactoria y una buena correlación con resultados presentes en la literatura, incluso cuando se trabaja con discretizaciones espaciales relativamente gruesas. Adicionalmente, los estudios numéricos realizados demuestran que el empleo del esquema adaptativo de malla es eficaz para incrementar la exactitud de la solución numérica manteniendo un bajo coste computacional.
En la segunda parte de este estudio se propone un método para la optimización de formas aerodinámicas que combina algoritmos genéticos multi-objetivo (MOGAs) y remallado adaptativo con el objetivo de asegurar, con un coste computacional mínimo, la calidad de la solución numérica empleada en el proceso de búsqueda de un determinado diseño objetivo, particularmente cuando el flujo presenta discontinuidades y gradientes muy localizados, típicos de flujos a alta velocidad. La metodología se aplica a resolver tres problemas prácticos de diseño de perfiles aerodinámicos en flujo transónico que implican la optimización de la distribución de presiones, minimización de la resistencia de onda y maximización conjunta de la sustentación y la relación sustentación/resistencia. Para cada uno de ellos se estudia el efecto del refinamiento en la calidad de la solución numérica así como también en el coste computacional y la convergencia del problema. Los estudios realizados demuestran la eficacia de la metodología propuesta.
Acknowledgment
I would like to express my sincere and heartfelt gratitude to all my teachers whose dedication and hard work have paved my academic path. I owe special thanks to my advisors, Professor Eugenio Oñate and Professor Gabriel Bugeda, whose patience and guidance were instrumental in kindling the flame of my curiosity and whose encouragements gave me the courage to challenge my own limitations.
During my Ph.D., I was blessed with the kindly help of Dr. DongSeop Lee and Dr. Jordi Pons in the aerodynamic design part and Dr. Roberto Flores and Enrique Ortega in the high-speed flow part. I learned a lot from them and never forget their help.
I want to appreciate Dr. Pooyan Dadvand and Dr. Riccardo Rossi who provided me the possibility of writing my codes in KRATOS and consistently solved my programming problems. It was a grate chance for me to get familiar with different aspects of the serial and parallel computing based on the C++ and Python languages.
I must also thank my family who bore the difficulty of separation for the last five years and whose love and support gave purpose to all my endeavors. A special thanks to all my friends, without whom life at Barcelona would be utterly miserable.
Last but not least, I would like to thank again Professor Eugenio Oñate, as the director of CIMNE, for giving the chance of doing my Ph.D. in such a high level center and for the scholarship that funded my work during the last 5 years. Your support enables plenty of interesting research to be carried out by young students and represents a firm example of faith in the next generations.
1 Introduction
1.1 Motivation
Advances in computational methods over the past two decades have firmly motivated researchers to implement these schemes as a powerful tool to handle the existing problems in different engineering areas. Aerodynamics is one of the most important branch of engineering which always has been considered as a highly interesting application topic for computational methods.
Applications of aerodynamics are common in the design of aircraft in aeronautical engineering, the design of race cars and railway trains in the automotive engineering, the study of wind effect on slender bridges and tall buildings in structural engineering and many other engineering problems. Regarding the different aspects appearing in this area, a huge amount of investigation fields have been created. The implementation of the numerical methods in two important areas, high-speed compressible flows (Part I) and aerodynamic shape optimization (Part II), is investigated in this thesis, separately, and new methodologies are developed for each one. A detailed introduction to each specific part follows.
Part I: High-Speed Compressible Flow
The theory of high speed flow is concerned with flows of fluid at speeds high enough that the fluids compressibility must be taken into account. The theory finds application in many branches of science and technology such as aerodynamics of aircrafts and vehicles. In general, the physical behavior of compressible flows is more complicated than in incompressible flows. Compressible flows may be viscous or inviscid depending on the flow viscosity. Compressible inviscid flows are analyzed using the potential or Euler equations, whereas compressible viscous flows are solved via the Navier-Stokes system of equations. Air flows in the range () may be considered as compressible. This range is usually subdivided into regions identified as subsonic (), transonic (), and supersonic ().
In high speed flow, the variables in the mass, momentum and energy equations are coupled to the thermodynamic variables, because changes in pressure compress or expand the fluid and alter its temperature. Equally, changes in temperature affect the pressure, via the equation of state. Therefore, in the study of high speed flow there is no escape from some thermodynamics.
The theory of shock waves is an important part of the subject of high speed flow and occupies an appreciable proportion of the researches carried out in this field. Furthermore, shock wave turbulent boundary layer interactions in compressible viscous flows constitute one of the most important physical phenomena in computational fluid dynamics. The occurrence of these complexities have made a wide range of investigations in the classical levels of experimental, theoretical and numerical computation.
An intense research effort into the technology of high speed flow has been performed by some brilliant mathematicians, including Lighthill, Von Neumann and Prandtl. A feature of research work on high speed flow has been the increasing use of high speed computers, hand-in-hand with the creation of a new subject, computational fluid dynamics (CFD). Among many successes has been the numerical computation of transonic flow fields, as required for the design of transonic airfoils. The use of high speed computers now pervades all aspects of research into high speed flow and, indeed, other types of flow.
The classical numerical methods such as central finite difference (FD), finite volume (FV) and Galerkin finite element (FE) are the most popular methods in the area of high-speed compressible flows. It has been studied that these discretization methods suffers from the occurrence of the spurious solutions in the numerical results due to the the presence of convective terms [1]. To prevent the occurrence of these non-physical solutions, some stabilization terms must be added to the basic scheme. Also, in order to model and capture the complexities of the high-speed compressible flows (specially near the high gradient zones such as shock waves), extra stabilization terms, called shock capturing terms, is needed in the numerical simulation.
As the stabilization terms play an important role in the quality of the results obtained from the numerical methods, a huge amount of research has been done in this area for predicting an appropriate stabilization term. In order to address this challenge, the Finite Increment Calculus (FIC) method is employed in conjunction with Galerkin FE as the basis for the derivation of stabilization terms in this work. This method is capable of generating accurate results for both inviscid and viscous high-speed compressible flows. In addition, the FIC formulation has a sound mathematical foundation that differs from the ad hoc procedures for introducing the stabilization term in many alternative stabilization procedures.
The FIC method is based in invoking the balance of fluxes in a fluid domain of finite size. This introduces naturally additional terms in the classical differential equations of infinitesimal fluid mechanics which are a function of the balance domain dimensions. The new terms in the modified governing equations provide the necessary stabilization to the discrete equations obtained via the standard Galerkin finite element method. The implementation of the FIC procedure in the stabilized form of the advective-diffusive transport and incompressible fluid flow problems is investigated by Oñate and co-workers [FIC1, FIC2, FIC3, FIC4, FIC5, FIC6,FIC7, FIC8]. The obtained results exhibit the robustness and efficiency of the FIC formulation in the mentioned problems. Hence, the extension of the FIC procedure to derive stabilized finite element schemes for high-speed compressible ̄flow problems is investigated in this thesis.
Besides an appropriate stabilization technique, a suitable computational mesh can enhance magnifically the quality and the precision of the numerical results, specially around the zones where the gradient of the solution is high. This fact motivated us to develop powerful technologies, generally called mesh refinement, to improve the mesh quality around these zones. When using mesh refinement methodologies, a minimum level of error is obtained by paying a reasonable amount of computational cost using a number of degrees of freedom as small as possible. This is achieved by placing much more elements in the zones where the solution has a greater gradient value or discretization error. Also, the elements are removed from the regions where the solution has a smaller gradient value or discretization error to have a minimum computational cost. In this thesis, the mesh refinement technique developed by Löhner [2] is implemented in conjunction with the FIC formulation in order to obtain a better enrichment level.
Part II: Aerodynamic Shape Optimization
Aerodynamic design is one the most important challenges in the engineering problems. The main goal of aerodynamic design is to efficiently and accurately determine an aircraft configuration that attains the optimal aerodynamic performance. The most significant parts of each configuration are the wings and gas-turbine engines which are commonly subjected to be optimized.
According to the complexity of aerodynamic design, several methodologies are developed in this field by scientists. Experimental methods, using wind tunnel and flight testing, provide the basis of the traditional ``cut and try'' approach for the design of new aerodynamic shapes. This approach alone, however, is too expensive, which has motivated the continuous development of sophisticated computational methods for flow simulation [3] and established the field of computational fluid dynamics (CFD). These methods, along with performance gains in computer technology, complement and in some instances even replace the use of the wind tunnel during the design process. In this setting, the experimental and computational techniques are analysis tools that provide reliable estimates of aerodynamic performance for given configurations and operating conditions. A good physical insight of the designer is required to select and evolve the candidate aerodynamic shapes and provide an overall control for the design process.
The ``cut and try' approach does not result in an inefficient design process. Consequently, a significant research effort has been devoted to the development of computational methods for the solution of the design problem. This leads to the creation of ``aerodynamic shape optimization' concept which is the coupling of CFD with numerical optimization. The methods developed based on this concept are efficient at producing aircraft shape configurations with improved performance characteristics at a given aircraft operating condition.
In the early years, the lack of computational resources and robust algorithms limited the overall impact of CFD on the design process. For a while, challenges in accurately predicting fluid dynamic phenomena within reasonable amounts of time were considered to be the foremost shortcoming hindering the widespread use of numerical simulations.
The primary challenge of CFD in the aerodynamic shape optimization is the underlying complex nature of the fluid flow. For cruise configurations of commercial aircraft, the flow is compressible, usually transonic, and may contain features such as shock waves, shock-induced boundary-layer separation and boundary-layer transition which imply using a fine mesh around the zones where these complexities occur. Hence, mesh refinement seems to be interesting for the aerodynamic shape optimization of some real test cases where the control of the mesh is extremely significant. Hence, by utilizing mesh refinement, a suitable mesh is generated around these zones to predict these complexities of the flow in an accurate manner keeping the computational cost reasonable.
Although the most conventional approach of aerodynamic design problems is to use a fixed uniform mesh during the optimization iterations [4,5,6,7], a few researches have been performed on implementing adaptive mesh for each design candidate of the optimization. In this category, the works done by Bugeda and Oñate [8,9] can be mentioned where they developed a methodology which utilizes adaptive mesh for each design in a suitable manner for a full potential flow and Euler equation without shock waves. Their methodology is based on the derivation of the sensitivity of the nodal coordinates and some flow variables with respect to the design variables to project the remeshing parameters from the old design to the new one.
The goal of this research is the integration of adaptive mesh refinement technique with aerodynamic shape optimization under transonic flow regime in order to show the benefits of using mesh adaptation in terms of computational cost and solution accuracy when the solution of the fluid has the previously mentioned complexities.
The rest of this chapter is organized as follows: In Section 1.2 a summary on stabilization methodologies developed in the field of high-speed compressible flows is presented. An overview of algorithms for aerodynamic shape optimization problems is given in Section 1.3 containing different aspects required in a practical problem. Section 1.4 describes the concept of mesh refinement in the engineering problems. The objectives of this thesis are stated in Section 1.5 which also provides an outline of the document.
1.2 Stabilization Methods for High-Speed Compressible Flows
In the past decades, computational resources and algorithms have matured to a state such that numerical modeling is an essential component of engineering analysis and design. This is certainly true for computational fluid dynamics (CFD), which has grown into the ability to solve flow fields with sophisticated geometries and complex physical processes. While experimental measurements will always have a role in the design process, CFD offers advantages in terms of cost, test time, ease of use and quality of output data. Nevertheless, despite the advances in the usage and capabilities of CFD, there is still room for improvement. One area of CFD growth is in the development of accurate schemes and their application to an expanding diversity of flow regimes and problems. Because of the large amount of demands from the aerospace industry, the application of CFD schemes in the regime of high-speed compressible flows always has been interested for the investigators.
As mentioned before, the main difficulties regarding the numerical methods in high-speed compressible flows is the occurrence of numerical instability which has two main sources, the high value of convective term in the original partial differential equation and the sharp gradients in the solution. Much effort has been spent in developing the so called stabilized numerical schemes for all the standard numerical methods such as FD, FV and FE. The following is a brief overview with an historical perspective of two main categories of the stabilization methods, artificial diffusion and limiters.
Artificial diffusion
To overcome the instabilities, the key idea is to introduce more diffusion in the flow equations by adding viscous terms to the governing partial differential equations explicitly. This concept formed the base of a well known family of stabilization methods called artificial diffusion technique proposed by Von Neumann and Richtmyer in 1950 [10].
Within this context, the finite difference method was investigated by Courant et al. in 1952 [11] and Lax in 1954 [12] to solve the high-speed compressible flow problems numerically. Courant et al. [11] introduced the upwind family of finite difference methods which was continued by Godunov in 1959 [13] for developing a new finite difference method based on the solution of the so-called Riemann problem. This original approach generated a series of schemes, known as flux difference splitting methods, that introduce different approximate Riemann solvers proposed by Engquist and Osher [14], Roe [15,16] and Osher [17].
Lax [12] implemented the traditional first order finite difference as the numerical methods for discretization of the Euler and Navier-Stokes equations whereas the development of the second order finite difference methods was provided by Lax and Wendroff [18] and Mac-Cormack [19] implementing an explicit time integration while Lerat [20] presented the implicit one.
Based on the finite volume scheme, following the idea of artificial diffusion, an important numerical improvement was conducted by Jameson et al. [21] using a series of second and fourth order stabilization methods. The study of finite volume flux vector splitting for the Euler equations was presented by Anderson et al. [22] where several advantages of the MUSCL-type approach over standard flux-differencing one is discussed.
The Galerkin finite element method is an alternative numerical procedure which has been widely applied for the Euler and Navier-Stokes equations. Hughes and his group [23] developed the classical Streamline-Upwind/Petrove-Galerkin (SUPG) finite element method, initially proposed by Brooks and Hughes [24] for incompressible flows, for high-speed compressible flows in the context of conservation variables. After that, in order to prevent the instabilities around the discontinuities, they utilized a set of entropy variables in conjunction with a new shock capturing operator depending on the residual of the corresponding equation [25].
Beau and Tezduyar [26] have shown that by considering the same shock capturing operator, the results obtained from [25] can be recovered by entropy variables with the similar level of accuracy. Following the idea of the conservative variable formulation, Mittal and Tezduyar [27] presented a unified finite element method for incompressible and compressible flows where a parameter , based on the local Mach number, was introduced that governs the choice of equations for compressible and incompressible flows.
Based on the concept of the SUPG method, several stabilization techniques were introduced such as Taylor-Galerkin [28] and Galerkin least squares (GLS) methods [29,30] which coincided with the original SUPG method under some specified conditions. Also, the implementation of the GLS method with different sets of variables can be found in the work of Hauke and Hughes [31] where they mentioned that the choice of entropy variables leads to the most robust results in the presence of singularities.
Peraire et al. [32] and Morgan et al. [33] developed a new artificial diffusion scheme based on the mesh size, , and second order gradient of pressure. Zienkiewicz and Wu [34] derived a new formulation by adding a pressure switch obtained from the nodal pressure values inside the element. Using of fractional step method [35,36], Zienkiewicz and co-workers introduced a general fluid mechanics algorithm, called characteristic-based split (CBS) algorithm, for incompressible and compressible flows [37,38] which benefited from the anisotropic shock capturing term presented by Codina [39]. The semi-implicit form of the CBS algorithm for compressible and incompressible flow is investigated by Codina and co-workers [40].
Limiters
Besides the artificial diffusion methods, a modern family of stabilization methods, based on the so-called limiters, was derived and has been commonly used in finite volume and finite difference schemes. This method is based on a concept aimed at preventing the generation of new extrema in the flow solution in such a way that the values of local minima do not decrease, and the values of local maxima do not increase [41,42,43]. This method induced to the Flux Corrected Transport (FCT) scheme, developed by Boris and Book [44], and the Total Variation Diminishing (TVD) method introduced by Harten [45].
A fully multidimensional generalization of the FCT algorithm was proposed by Zalesak [46] and carried over to the finite element method by Parrott [47], Löhner et al. [48] and Luo et al. [49].
Sanderos [50] developed the original TVD method from the explicit/implicit fully discrete scheme to a semi-discrete one, whereas Jameson and Lax [51] derived a general TVD characterization and the necessary conditions for multipoint support in explicit, implicit and semi-discrete formulations. Although the FCT scheme has not got a significant popularity, the TVD method has been used mostly in finite difference [52,53,54], finite volume [55] and finite element [56,57] methods.
1.3 Aerodynamic Shape Optimization
Aerodynamic shape optimization methods can be divided into two categories, namely, inverse design methods and numerical optimization methods. Inverse design methods, first introduced in 1945 by Lighthill [58], are an established approach for the determination of an airfoil shape that attains a given pressure distribution. For example, an experienced designer is able to specify a lift-preserving pressure distribution that is shock-free for transonic flow conditions, thereby achieving significant drag reductions. Inverse methods were also used to design the well-known Liebeck high-lift airfoils [59]. An advantage of this approach is its low computational cost. Giles and Drela [60] developed an inverse design method using the two-dimensional, coupled Euler and boundary layer equations with a computational cost equivalent to the solution of just one analysis problem. Although inverse design methods have been applied to three-dimensional problems [61], their primary limitation is the specification of desirable pressure distributions that lead to optimal designs, especially for problems with multiple operating conditions and turbulent and separated flow.
Numerical optimization methods provide a more general approach for solving design problems. The creativity and insight of an experienced designer are required to reduce the design problem to a well-posed optimization problem. This involves the definition of objective functions that specify the goals of the optimization, design variables that determine the aerodynamic shape, as well as constraints that qualify a feasible region of the design space. Note that for practical problems, it is very likely that the objectives are competing and that changes in the specification of the optimization problem occur as the design evolves. Typically, the problem is cast as a minimization one, where the objective functions include lift, drag and moment functionals. Inverse design can be considered a subset of numerical optimization by defining an objective function that represents the difference between the target and the actual pressure distributions.
Once an aerodynamic shape optimization problem is defined , the following steps provide the aerodynamic optimization process. A flow solver is used to determine the properties of the flow field around an aerodynamic shape such as lift, drag and pressure coefficient at a given set of operating conditions. Then, the formulated objective function evaluates the performance of the shape with respect to the design objectives. A mathematical representation of the geometry of the shape provides a mean to make alterations to the shape via design variables. An optimization algorithm uses information about the objective function at the current design iteration to determine how to modify the design variables to improve the performance of the shape. The updated shape specified by the modified design variables is presented to the flow solver and the process is repeated iteratively until the specified criteria are satisfied indicating that an optimal solution has been achieved and no further improvement in the performance is possible.
1.3.1 Numerical Optimization Methodologies
Despite the fact that numerical optimization methods have been successfully used for a countless number of design problems, an application of numerical optimization to aerodynamic design still remains as a formidable challenge because of the following two difficulties: 1) objective function landscape of an aerodynamic optimization is often multi-modal and nonlinear because the flow field is governed by a system of nonlinear partial differential equations. and 2) function evaluations using a CFD code, especially a three-dimensional Euler or Navier-Stokes code, are very expensive. Due to the above difficulties, aerodynamic design problems require a numerical optimization tool to be very robust and efficient as well.
Typical optimization problems involve the determination of the minimum of a given function. The goal is to identify the values of the parameters that are inputs for the function such that the output of the function is a minimum. If the slope (or gradient) of the function at any point is known, it becomes possible to move toward the minimum by moving in the direction of negative slope. The gradient can also be interpreted as the sensitivity of the functional output to the parameters that control the function. In the context of aerodynamic shape design, functional quantities of interest are usually surface integrated values such as the lift, drag, or moment. Design parameters usually are the variables that control the shape of the geometry and the governing flow equations form the function relating the design variables to the output functional. If gradient-based optimization is to be employed for the purpose of reducing the output functional, the goal then is to determine the gradient or sensitivity of the output with respect to the design variables.
The obvious choice for determining such sensitivities is to perturb the design variables individually and run the numerical simulation (evaluation of the function) for each perturbation in order to determine the effect of the perturbation on the quantity of interest. The method, known as finite-differencing, becomes inefficient as the number of design variables increases since the number of times the simulation has to be performed is directly dependent on the number of design variables. The sensitivity or the gradient determined in this manner is also highly dependent on the magnitude of the perturbation, since for large perturbations the wrong slope may be predicted due to nonlinear effects, while very small perturbations are susceptible to machine precision related issues. In a perfect world using a computer with infinite precision, an infinitesimally small perturbation would recover the analytically exact value of the gradient. Hicks et al. [62] used the finite-difference method to evaluate sensitivities.
Using control theory, the gradient can be calculated indirectly by solving an adjoint equation. This methodology significantly lowers the computational cost and is clearly an improvement over classical finite-difference methods. Although there is the additional overhead of solving the adjoint equation, once it has been solved the cost of obtaining the derivatives of the cost function with respect to each design variable is negligible. Consequently, the total cost to obtain these gradients is independent of the number of design variables and amounts to the cost of one flow solution and one adjoint solution. The adjoint problem is a linear partial differential equation of lower complexity than the flow solver. Jameson was the first to apply control theory for transonic design problems [63,64,65]. Subsequently, Jameson et al. [66] pioneered the shape optimization method for Euler and Navier-Stokes problems. Automatic aerodynamic design of aircraft configurations has yielded optimized solutions of wing and wing-body configurations by Reuther et al. [67,68], Burgreen et al. [69] and Löhner et al. [70,71].
Evolutionary Algorithms (EAs) are alternative optimization algorithms mimicking mechanism of the natural evolution, where a biological population evolves over generations to adapt to an environment by selection, recombination and mutation. When EAs are applied to optimization problems, fitness, individual and genes usually correspond to an objective function value, a design candidate, and design variables, respectively. One of the key features of EAs is that they search from multiple points in the design space, instead of moving from a single point like gradient-based methods do. Furthermore, these methods work on function evaluations alone and do not require derivatives or gradients of the objective function. These methods also offer the benefit of being able to navigate through highly nonlinear, noisy and discontinuous design environments. However, such methods usually require very large numbers of function evaluations and present their own set of difficulties. These features lead to the advantages such as robustness, suitability to parallel computing and simplicity in coupling CFD codes. Owing to these advantages over the analytical methods, EAs have become increasingly popular in a broad class of design problems (for example, see [72]). EAs have been also successfully applied to aerodynamic shape optimization problems such as airfoil shape design [73,74], Multi-element airfoil shape design [75], subsonic wing shape design [6] and supersonic wing shape design [76].
1.4 Adaptive Mesh Refinement
Adaptive methods for the solution of the governing flow equations are means of reducing the overall cost of simulations. The basic principle behind adaptive solutions is the efficient deployment of computational resources.
In the case of finite volume or finite element discretizations of the governing flow equations, the computational expense of obtaining a solution is directly proportional to the resolution of the mesh. However, for two different meshes that have the same number of points, it is possible to obtain different error levels in the overall solution due to different distributions of the mesh points. Non-adaptive solutions rely on user judgment for the clustering of mesh points in various regions of the computational domain in order to capture flow phenomena. The normal practice consists of using some predetermined clustering of points in high gradient regions such as boundary layers, wakes, stagnation points, shock waves and contact discontinuities. Since the flow field being solved for is unknown, the user has to rely on engineering judgment for the determination of regions where clustering may be required. Adaptive solvers approach this problem by starting with a coarse resolution mesh and then add points on-the-fly during the solution process in relevant regions of the computational domain.
The core of any adaptation algorithm is the determination of relevant regions to target for increased resolution. A common adaptation method is to use the spatial gradients of the evolving flow solution to refine regions of high gradients in the hopes that the overall solution error level is reduced. If mesh adaptation is implemented during the process of optimization, while the approach may capture interesting flow phenomena such as vortices and shock waves, there is no guarantee that the solution obtained in this manner necessarily results in improved estimates for specific objective values of interest such as lift or drag. To this end, goal-based or adjoint-based methods for the adaptation of the computational domain have been developed to specifically target the error in objective scalars of interest [77,78]. Goal-based methods use a posteriori estimates of the error in a functional computed using a flow solution to identify regions in the computational domain that are most relevant to the accuracy of the functional. For different scalars of interest computed using the same flow solution (i.e. identical flow conditions and geometry), it is entirely possible that goal-based adaptation produces significantly different adaptations.
In each adaption problem two main features must be considered; (i) A reliable error indicator, and (ii) A refinement methodology, where two features are explained in the following.
Error indicator
In most adaptivity problems, the aim is to reach a uniform level of error in the domain. This error can be evaluated in different manners. A major difficulty in achieving definite improvements using adaptation for Euler and Navier-Stokes calculations is the lack of a reliable error indicator [2,79]. A common strategy is to adapt to certain physical features of the flow, such as shock waves, boundary layers, wakes, slip lines, or stagnation points, by employing error indicators. Normally, the error indicators depend on the gradient of a solution variable like the Mach number, density or entropy. It is typical to classify the error indicators based on the order of the gradient. The indicators obtained from the first order gradients performs well when the problem considered is inviscid in nature [80,81,82]. Also, one can approximate the error in the domain using a derivative one order higher than the shape function of the solution where the derivatives are obtained by some recovery procedures [83].
Refinement methodology
Some powerful refinement strategies are introduced in the literature to properly refine the mesh. Four main directions are followed:
1. p-refinement that adds further degrees of freedom with hierarchical shape functions or with the addition of higher order shape functions[84,85]. This method is more commonly used in variational frameworks such as Discontinuous-Galerkin discretizations, which use a high-order polynomial representation of the solution within each element.
2. r-refinement (or mesh movement) that maintains the mesh topology but allows mesh lines to move, thus contracting some cells while simultaneously expanding others. This technique has the advantage that the number of mesh cells and hence computational cost does not increase when a new flow field is calculated on the adapted mesh [86].
3. h-refinement (mesh enrichment or subdivision) where individual elements are subdivided without altering their original position [87,88,79].
4. Adaptive remeshing that regenerates a new mesh by applying new element sizes obtained from error indicators. A grid generator must be utilized in order to regenerate the mesh [82,89].
1.5 Overview of Thesis
1.5.1 Objectives
As mentioned at the beginning of this chapter, two important research fields in aerodynamics, high-speed compressible flows (Part I) and aerodynamic shape optimization (Part II), are considered as the main contributions of this thesis. An overview of the methodologies proposed in each part of the thesis is presented in the following lines:
Part I: High-Speed Compressible Flow
The first part of this research is dedicated to the development of the FIC formulation for stabilization of the Euler and Navier-Stokes equations in the context of the Galerkin FEM. The FIC method is based on expressing the balance of fluxes in the momentum, mass balance and energy conservation equations in a space-time domain of finite size. It is intended to prevent the creation of instabilities usually presented in the numerical solutions due to the high convective terms and sharp gradients. To reach this aim, two stabilization terms, called the streamline term and the transverse term, are added through the FIC formulation.
Generally, the streamline term which is in the direction of the velocity is responsible for stabilizing the spurious solutions produced from the convective terms while the transverse term smooths the solution in the high gradient zones inside the domain. A fourth order Runge-Kutta scheme has been implemented to advance the solution in time.
In order to investigate the capability of the proposed FIC-FEM formulation, some numerical test examples corresponding to subsonic, transonic and supersonic regimes for inviscid and viscous flows are presented. The behavior of the stabilization terms in providing appropriate solutions has been studied especially near the zones where the solution has some complexities such as shock waves, boundary layer, stagnation point, etc. Although the derived methodology delivers precise results with a nearly coarse mesh, the mesh refinement technique is coupled with the solution to create a suitable unstructured mesh particularly near the high gradient zones.
The comparison of the numerical results obtained from the FIC-FEM formulation with the reference ones demonstrates the robustness of the proposed method for stabilization of the Euler and Navier-Stokes equations for compressible flows. It is observed that the usual oscillations observed in the Galerkin FEM, especially near the high gradient zones, are eliminated by implementing the proposed stabilization terms without introducing an excessive numerical dissipation. Furthermore, allowing the adaptation framework to modify the mesh, the quality of the results improves significantly.
Part II: Aerodynamic Shape Optimization
The second part of this thesis investigates the effect of mesh refinement on the computational cost and solution accuracy during the process of aerodynamic shape optimization. Therefore, an adaptive remeshing technique is linked to the CFD solver for the analysis of each design candidate to guarantee the production of more realistic solutions during the optimum design process in the presence of shock waves.
In this study, some practical transonic airfoil design problems using adaptive mesh techniques coupled to Multi-Objective Genetic Algorithms (MOGAs) and an Euler flow analysis code are addressed. The methodology is implemented to solve three practical design problems; the first test case considers a reconstruction design optimization that minimizes the pressure error between a predefined pressure curve and a candidate pressure distribution. The second test considers the total drag minimization by designing the airfoil shape operating at transonic speeds. For the final test case, a multi-objective design optimization is conducted to maximize both the lift to drag ratio and the lift coefficient . The mentioned design problems under transonic speeds need to be solved with a fine mesh, particularly near the object, to capture the shock waves that will cost high computational time and require solution accuracy.
The solutions obtained with and without adaptive mesh refinement are compared in terms of solution accuracy and computational cost. By comparison of the numerical results, the direct benefits in the reduction of the total computational cost through a better convergence to the final solution are evaluated. Indeed, the improvement of the solution quality when an adaptive remeshing technique is coupled to the optimum design strategy is evident.
1.5.2 Structure
The structure of the thesis is as followings: Chapter 2 presents the derivation of the stabilized Galerkin FEM based on the FIC formulation for analysis of compressible flows. Next, the mesh refinement technique is introduced and some numerical results for inviscid and viscous compressible flows are shown at the end of the chapter. Chapter 3 addresses the aerodynamic shape optimization part of the thesis. First, the optimization tools such as the GA technique and the parametrization method are presented. Then, the validation of the CFD solver chosen for the solution of the compressible flow equations in conjunction with the presented mesh refinement technique is demonstrated and finally a number of optimum shape design examples are shown. Conclusions and areas of future work are summarized in Chapter 4.
2 A Stabilized FEM for High-Speed Compressible Flows
In this chapter, the FIC formulation is applied to finite element discretization of the Euler/Navier-Stokes equations for compressible flows. The proposed method is demonstrated on a series of two-dimensional subsonic, transonic and supersonic test cases involving various configurations. A commonly used error indicator [2] in conjunction with the h-refinement methodology is implemented to comparatively assess the performance of the proposed stabilized formulation. In all the delivered test cases, the FIC scheme avoids the creation of instabilities which are inherently inside the solution due to the high convective term and sharp gradients.
The first part of this chapter, Section 2.1, describes the original equations of the Euler and Navier-Stokes. Section 2.2 presents the development of the FIC stabilized formulation for the mentioned equations. The discretization of the general formulation in space and time is delivered in Section 2.3. The different kind of boundary conditions considered in this thesis are studied in Section 2.4. Additional techniques for enhancing the performance of the method via local time stepping and residual smoothing are presented in Section 2.5 while the mesh refinement methodologies are described in Section 2.6. The numerical test examples containing inviscid and viscous flows are shown in Section 2.7.
The Euler/Navier-Stokes equations are a system of partial differential equations that describe the behavior of a compressible, inviscid/viscous fluid. They are derived from the integral form of the laws of conservation of mass, momentum and energy in an inertial frame of reference.
For an arbitrary fixed control volume with the boundary , the law of conservation of mass can be expressed as
|
|
(1) |
where is the density, is the fluid velocity, expressed using indicial notation and is the outward-pointing unit normal vector at the surface of the control volume. This states that the rate of change of the mass of the fluid in the control volume is equal to the transport of mass across the control volume boundary . Gauss' divergence theorem is used to transform the surface integral into a volume integral over . Then, by requiring the resulting integral equation to hold for any infinitesimal control volume, the differential form of mass conservation law is found to be
|
|
(2) |
which holds everywhere that the flow quantities are continuous and differentiable. At discontinuities, only the integral form is valid.
The integral form of the law of conservation of momentum can be written as
|
|
(3) |
where and are the static pressure and the viscous stress tensor of the fluid respectively. The index spans the two equations, and the repeated index indicates summation. These equations state that the momentum of the fluid within the control volume is changed by the transport of momentum across the surface, and by the action of fluid pressure on the surface . Again, the divergence theorem is used to transform the surface integral terms. The differential form of the momentum equation is
|
|
(4) |
Again, the differential form is not valid at flow discontinuities.
The integral form of energy conservation law can be written as
|
|
(5) |
with standing for the total internal energy per unit mass, for the absolute static temperature and for the thermal conductivity coefficient. This states that the energy within the control volume is changed by the transport of energy across the surface, and by the work done by the action of the fluid pressure upon the surface of . By application of the divergence theorem, the energy equation can be transformed into its differential form,
|
|
(6) |
which is only valid in continuous regions of the flow.
Since the three conservation laws have analogous terms, they can be grouped together to form a system of equations,
|
|
(7) |
where is the vector of conservative variables. By defining , this vector has the following form
|
|
(8) |
with and being the vectors of inviscid and viscous flux respectively,
|
|
(9) |
The Navier-Poisson law for a Newtonian fluid leads to the components of the viscous stress tensor in term of the velocity. For an isotropic media
|
|
(10) |
where a bulk viscosity of is assumed, which is justified by the validity of the Stokes hypothesis for reversible processes under compression. is the dynamic coefficient of viscosity which is calculated from Sutherlands equation.
The momentum and energy equations are coupled by the pressure which is defined by assuming that the fluid behaves as a perfect gas. Hence, the pressure is obtained from the equation of state for a perfect gas as
|
|
(11) |
where the ratio of specific heats is defined as
|
|
(12) |
In the present computations is taken to be equal to for the simulation of the air, which is an adequate choice for subsonic, transonic and supersonic flow where the Mach number is no excessively high and where chemical reactions can be neglected.
It is necessary to mention that the Euler equations can be recovered from the Navier-Stokes equations by neglecting the viscous stress and the heat conduction terms. i.e. .
2.2 A FIC-based Stabilization Formulation
In this section the FIC formulation for stabilization of the Euler/Navier-Stokes equations for compressible flows will be presented. The FIC formulation in space is developed for the the momentum and energy conservation equations whereas the representation of the FIC in space-time is suggested for the mass conservation equation. By joining the three conservation equations, the general stabilized formulation of the Euler/Navier-Stokes equations will be finally presented.
2.2.1 FIC in Space
We define and as the residuals of the momentum and energy equations, respectively, as
|
|
(13) |
|
|
(14) |
where with is the number of space dimensions ( for 2D flow problems), the FIC formulation in space for stabilization of the momentum and energy equations can be found by applying Taylor series expansions to the conservation laws of momentum and energy over a space domain as [90,91]
|
|
(15) |
|
|
(16) |
where and are characteristic length parameters that will be discussed later.
It can be seen that the modified equations via the FIC method introduces naturally an additional term into the standard momentum and energy equations. The definition of the the characteristic length arises from the two main sources of the instabilities in the numerical solutions of high-speed compressible flows, namely the high value of the convective terms and the sharp gradients. By considering this fact, the general form of the characteristic length is expressed as
|
|
(17) |
where the streamline length is responsible for smoothing the instabilities due to the high convective terms by adding extra diffusion in the streamline direction, whereas the transverse length stabilizes the oscillations near the sharp gradient zones by applying extra diffusion in the transverse direction to the gradient.
Definition of the streamline length . The basic idea behind the evaluation of is extracted from the traditional SUPG scheme for stabilization of the incompressible/compressible flow problems, where the diffusion is added in the direction of the velocity. Hence, the characteristic length corresponding to the momentum and energy equations can be represented as
|
|
(18) |
where and are constant coefficients, and are characteristic element sizes corresponding to the momentum and energy equations. Also, is the module of the velocity and is the speed of the sound in the flow.
Definition of the streamline length . As the transverse term is supposed to get involved in the zones where there are some high gradients in the solution, can be defined as
|
|
(19) |
By considering Equation 17, the summation of Equations 18 and 19 gives
|
|
(20) |
|
|
(21) |
Substituting the characteristic lengths and in Equations 15 and 16, the FIC formulation in space for the momentum and energy equations is obtained as
|
|
(22) |
|
|
(23) |
2.2.2 FIC in Space-Time
The residual of the mass conservation equation can be expressed as
|
|
(24) |
with where is the number of space dimensions ( for 2D flow problems).
As mentioned before, the FIC formulation in space-time is written in order to derive the stabilization terms corresponding to the mass equation. In the same manner as for the derivation of the FIC equations in space domain, the space-time formulation can be introduced by considering the mass balance equation in a space-time domain. Hence, after relatively simple algebra, the FIC formulation for mass balance equation can be expressed as [90,91]
|
|
(25) |
where and are the characteristic length vector and the time stabilization parameter corresponding to the mass balance equation, respectively, which will be defined later.
It can be seen that the space and time derivatives of the residual corresponding to the mass equation are coupled together in the stabilized equation. By substituting from Equation 24 in the time-derivative part of Equation 25 and retaining the term related to the space derivatives, the following expression can be obtained
|
|
(26) |
In Equation 25, although the term corresponding to the second derivative of the density respect to time can be obtained explicitly using a simple backward finite difference scheme, it is found that this term does not play an important role in the stabilized formulation and will be neglected here onwards.
Replacing the term from Equation 13 into Equation 25 gives
|
|
(27) |
where is the the divergence of the flux term corresponding to the momentum equation with the form of
|
|
(28) |
Considering the same idea as the one used for the momentum and energy equations to define the characteristic lengths, the expressions of and for the mass balance equation can be defined as
|
|
(29) |
where is a constant and is the characteristic element size related to the mass balance equation.
Substituting Equation 29 into Equation 27, the FIC stabilized formulation for the mass equation is obtained as
|
|
(30) |
2.2.3 The General FIC-based Formulation
Having introduced the stabilized formulation for the mass, momentum and energy equations, we present the general formulation for the Euler/Navier-Stokes equations. In the current thesis, accurate results have been obtained by considering the assumptions
|
|
(31) |
|
|
(32) |
where is a characteristic element size defined as where is the element area for 2D problems and .
By using Equations 31 and 32 and joining Equations 30, 22 and 23, the general FIC-based stabilized formulation can be expressed as
Mass balance
|
|
(33) |
Momentum
|
|
(34) |
Energy
|
|
(35) |
Equations 33, 34 and 35 are the starting point for deriving the discrete form of the stabilized Euler/Navier-Stokes equations in space and time. Clearly, for the infinitesimal case , the standard balance equations 24, 13 and 14 can be recovered from the general stabilized formulation. It is noticeable that expressing the stabilization terms as a function of the residuals of the corresponding balance equations enforces the consistency of the proposed FIC method.
2.3 Space-Time Discretization
2.3.1 Galerkin FE
Now, we can introduce a standard finite element discretization of the conservative variables by choosing continuous linear interpolation over triangle elements as
|
|
(36) |
where for the case of triangle elements, is the vector containing the approximation of the conservative variables , is the matrix of the linear interpolating shape functions and denotes th nodal values inside the elements.
By taking as the vector of weight functions and applying the standard weighted residual method to Equations 33, 34 and 35 and integrating by parts the stabilization terms, neglecting the boundary terms, the variational form of the discretized equations is found as
|
|
(37) |
where is the number of the elements and . In the following, each part of Equation 37 will be defined. The residual vectors and presented in Equation 37 are
|
|
(38) |
where , , and denote the approximate finite element residuals for the mass, momentum and energy equations, respectively, and is the divergence of the approximate finite element flux term corresponding to the momentum equation.
Furthermore, in Equation 37 is the vector of approximated primitive variables of the form
|
|
(39) |
Also, is the the time stabilization parameter and the matrices and have the following form
|
|
(40) |
|
|
(41) |
where denotes the absolute value.
Based on the Galerkin approximation, the weighting functions are assumed to be equal to the interpolation ones, . Indeed, by applying integration by parts on the first term of Equation 37 we obtain
|
|
(42) |
with and and are the approximated inviscid and viscous flux terms applied on the boundaries. In Section 2.4, the different types of the boundary conditions will be defined.
It can be seen that in the right hand side of Equation 42, the first integral represents the Galerkin term in a weak form, the third integral corresponds to the elemental contribution of the streamline stabilization term and the last integral is the elemental contribution of the shock capturing stabilization term.
2.3.2 The Fourth Order Runge-Kutta
After discretization of the Euler/Navier-Stokes equation in space and assembling the element contributions from Equation 42, the found global system of discretized equations can be written as
|
|
(43) |
with where is the total number of nodes inside the domain and means the value computed in time step . In the above equation, is the consistent finite element mass matrix
|
|
(44) |
Also, is the contribution of the th global node from the right hand side of Equation 42 in time step which has the form
|
|
(45) |
To avoid solving a linear system of equations at each time step, the consistent mass matrix is usually replaced by its lumped expression . Furthermore, as the focus of this thesis is on stationary problems, an explicit multi-stage Runge-Kutta algorithm is implemented in order to obtain a converged steady state solution,
Assuming that the nodal values and are known at time , the advance of the solution over the time step to is according to
|
|
(46) |
with being the number of stages of the scheme. Each particular scheme is characterized by a choice of and the constant coefficients . The appropriate choose of these coefficients improves the stability of the time integration and provides accurate numerical solutions. Reasonable results can be obtained by
|
|
(47) |
The scheme presented here is explicit and therefore only conditionally stable. There is an upper limit on the allowable time step. For an inviscid problem, the stability limit for an element could be calculated as [1]
|
|
(48) |
where denotes the allowable Courant number and is the characteristic element size. Except which is global, the remaining variables in the above equation are calculated at the elemental level. If a time accurate solution is sought, the global time step equals to the minimum allowable one for all the elements in the mesh. Including the viscous terms, the critical time step can be represented as
|
|
(49) |
with is the minimum density within the element, is the free stream Mach number, is the non dimensional Prandtl number and is the free stream Reynold number. The other variables have the same meaning as defined above. Details can be found in [1]. In this thesis, the Prandtl number is assumed to be constant and equal to .
In order to enhance the performance of the presented time integration scheme, the methods of local time stepping and residual smoothing are coupled to the solver. A brief review of these schemes is presented in Section 2.5.
2.4 Boundary Conditions
2.4.1 Euler Equation
The discretized equation system of Equation 42 assumes a computational domain surrounded by a boundary with unit normal . So far, the algorithm only describes the contributions of each element across the integral but does not yet states how to incorporate the boundary conditions at the boundary .
In this thesis, two types of boundaries exist: the slip boundary through which mass flux is not possible and the far field (inflow/outflow) boundary through which mass flux is possible. The boundary condition must be applied in a compatible form with the equations to be solved.
Slip Boundary
The normal component of the velocity must vanish on it. This condition can be enforced by considering the normal component of the velocity equal to zero after each stage, k, of the time integration scheme as
|
|
(50) |
Far Field Boundary
Depending on the regime of the flow, the components of the solution which enter the domain are to be enforced and the ones leaving the domain have to be set free. By using Roes approximation Riemann solvers, the appropriate boundary flux for node located at the far field boundary is computed as
|
|
(51) |
where the superscript represent the freestream and is the Roe matrix computed in the direction normal to the boundary. More details about the derivation of the Roe matrix can be found in [92,1].
The treatment of the boundary condition for the Navier-Stokes equations is similar than for the Euler equations. However the steady momentum and energy equations are elliptic and its modeling is more complex. Details are given in [1].
Far Field Boundary
Numerically, for a node located at the far field boundary, the flux for node belongs to the far field boundary, can be obtained by applying the far field values at the boundary, i.e. .
No Slip Boundary
In the case of the Navier-Stokes equations, in addition to the conditions on the normal velocity, some conditions must be considered for the temperature. The physical no slip boundary conditions for the velocity is
|
|
(52) |
where . For temperature boundary conditions, if an adiabatic wall is modeled, then the heat flux across the wall is zero as
|
|
(53) |
whereas, if an isothermal wall is given, the temperature is set
|
|
(54) |
where is a specified wall temperature.
2.5 Performance Enhancement
2.5.1 Local Time Stepping
In order to enhance the performance of the program and to accelerate the solution towards steady state, local time stepping can be used. Hence, time steps of different sizes are used within each element, individually, according to the local stability limit. As the mesh size increases, ie. with the distance from the body, the time increment will also increase. However, this option is only permissible if the transient solution is not of interest.
The local time stepping is implemented at the nodal level. For th node in the mesh, a nodal size is calculated as
|
|
(55) |
where is the size of the th element connected to the th node. The above equation states that the size of node is the minimum size of all the elements to which belongs. The allowable step at each node is then calculated by substituting Equation 55 in to Equations 48 and 49 while the rest of the variables are calculated at the nodal level.
2.5.2 Residual Smoothing
To increase the allowable time step, the residual smoothing technique can be implemented. A Laplacian smoothing is included to extend the support of the interpolation functions, yielding an increase in the allowable Courant number. Hence, the smoothed residual is defined as
|
|
(56) |
where is the residual of the th node defined in Equation 38 and is the smoothing coefficient assuming to .
It can be seen that solving the Equation 56 exactly for the smoothed residual would require solving a linear system of equations negating the advantages of the explicit scheme. However, the smoothing is only used as a mean to achieve faster convergence and has no effect on the steady state solution. Therefore, a rough approximation to the value of is enough to obtain the desired result. The approximate value of the smoothed residual is computed by means of a Jacobi iteration scheme as
|
|
(57) |
where subscript denotes the iteration step.
In common applications a good result can be obtained by running two passes of the Jacobi iteration scheme. The residual smoothing does not need to be applied at each stage of the Runge-Kutta scheme. For example, in the case of the four-stage scheme, smoothing just in the first and third stages is usually enough to produce a twofold increase in the allowable Courant number.
2.6 Mesh Refinement
A powerful error indicator introduced by Löhner [2] is implemented in this research. For each variable of interest U, we define the error as
|
|
(58) |
By dividing the second derivatives of the variable of interest by the absolute value of the first derivatives, the error indicator becomes bounded, dimensionless and the "eating up" effect of strong features is avoided. The term following is added as a noise filter in order not to refine wiggles or ripples which may appear due to loss of monotonicity. The error value thus depends on the algorithm chosen to solve the PDEs describing the physical process at hand. The variable is one of the flow variables such as the density, the Mach number, the velocity modulus, etc. In the current thesis, the density has been chosen.
In the following, a brief overview of two methodologies for mesh refinement implemented in this research, h-refinement and adaptive remeshing, is presented.
2.6.1 h-refinement
By far the most successful mesh enrichment strategy has been h-refinement [2,93,89]. In the present research, this strategy has been implemented in combination with the error indicator mentioned above. The multidimensional form of this error indicator is
|
|
(59) |
where denotes the shape function of node and . The fact that this error indicator is dimensionless allows the simultaneous of several indicator variables. Because the error indicator is bounded , it can be used for whole classes of problems without having to be scaled to the problem at hand. This results in an important increase in user-friendliness, allowing non- expert users access to automatic self-adaptive procedures. This error indicator has been used successfully for many years on a variety of applications [93,89,94].
The main variant used to date achieve mesh enrichment/coarsening through is the classic subdivision of elements into four (2D) by dividing each edge of element into two.
The first step in the h-refinement methodology is to identify the element required refinement or coarsening. By subdividing or removing the elements corresponding to the refinement or coarsening, respectively, the new mesh is created. Finally, the flow variables are interpolated from the old mesh to the new one.
2.6.2 Adaptive Remeshing
The third family of refinement strategies is based on the existence of automatic grid generators. This strategy is based on the existence of automatic grid generators. The grid generator is used in combination with an error indicator based on the present solution technique to remesh the computational domain, either globally or locally, in order to produce a more suitable discretization.
In adaptive remeshing strategy, it is necessary to obtain a more precise estimation of the required element size and shape. The non-dimensional error indicator introduced in Equation 58 can also be generalized for this strategy. By defining the following derivative tensors
|
|
(60) |
The error indicator on the present (old) grid is given by
|
|
(61) |
which yields an error matrix of the form
|
|
(62) |
It is assumed that the new element size is proportional to old element size by a factor which is defined as
|
|
(63) |
The improved error related to the new mesh has the form shown in the following equation, i.e.
|
|
(64) |
Given the desired error indicator value for the improved mesh, the mesh reduction factor is given by
|
|
(65) |
In 2D case, and are obtained for each element, the minimum of these two values is replaced in Equation 63 to calculate the new element size . It is worth noting that in the current methodology only a new element size is prescribed for each element and stretching is not considered. This value is assigned to the corresponding element in the background mesh to generate a new one. By predefining the minimum and maximum element sizes, the computed element size is checked to be in this desirable range. If this condition is not satisfied, the minimum or maximum element size is considered.
An automatic grid generator is needed to generate the new mesh using the information obtained from the old mesh. Any of the automatic grid generation techniques currently available (advancing front [95,96], Delaunay triangulations [97,81] and modified quadtree/octree [98,99]) may be employed to regenerate the mesh. The most robust one which is implemented here and uses the advancing front technique. In this work, given the minimum element size and the desired error, several remeshing steps are performed every predefined time steps of the solution process in order to guarantee a fine mesh at the final step of the analysis.
The first step of each remeshing level is to evaluate the indicator corresponding to each element. Utilizing the obtained indicators, the new element size is calculated for each element. The new mesh in created by implementing the advancing front technique considering the old mesh as the background mesh. Finally, the flow variables are interpolated from the old mesh to the new one.
2.7 Test Examples
In order to assess the performance of the outlined stabilization methodology, this section presents several numerical examples of compressible inviscid/viscous flow in subsonic, transonic and supersonic regimes for steady-state problems. All the tests are performed with triangular meshes utilizing an explicit Runge-Kutta time integration scheme where the relative norm of the density residual is taken as a criterion to check convergence. It is to mention that the computations start by using the upstream values as the initial solution and they are stopped after a reduction of four order of magnitude in the relative norm of the density residual.
For the cases for which the analytical solution exists, the obtained numerical results are compared with exact solutions whereas for the ones that there is not an analytical solution, the comparison is carried out with some numerical references.
2.7.1 Inviscid Flow
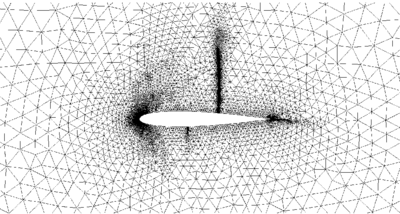
The computations of the inviscid test cases are performed through the entirely unstructured mesh which is enhanced by the h-refinement technique, presented in Section 2.6.1. It is to mention that the refinement is not implemented in the subsonic example as no shock wave happens in the solution.
At the beginning stage of the refinement, the solution starts using an unstructured mesh. Having reached the stationary solution, consecutive refinement levels are carried out every 200 time-steps. By obtaining the final adaptive mesh, the solution stops when the stationary point is gotten. It is notable that the initial mesh, considered for the inviscid examples, must be fine enough to be able to capture the main characteristics of the flow in order to detect the regions where the refinement is needed.
Example I: Reflected shock
A popular example for supersonic regime is the reflected shock problem involving an oblique shock at the angle of and its reflection from the boundary. The main feature of this example is that it can be solved analytically. Hence, it is possible to test the accuracy of the numerical results.
The problem consists in an uniform flow with Mach at the angle of in a rectangle domain of height and length which involves three flow regions, plotted in Figure 1 schematically, as
| Region 1 | Region 2 | Region 3 |
|
| Figure 1: Reflected shock example. Problem definition. |
The initial mesh, shown in Figure ex1_mesh0, is generated by using an unstructured mesh consisting of nodes and 3-noded triangular elements. The final adaptive mesh of nodes and elements is obtained after five steps of refinement as shown in Figure ex1_mesh1. The form of this mesh clearly demonstrates that the refinement has been carried out along the flow discontinuities.
|
|
| Reflected shock. (a) Initial mesh and (b) adaptive mesh after refinement levels. | |
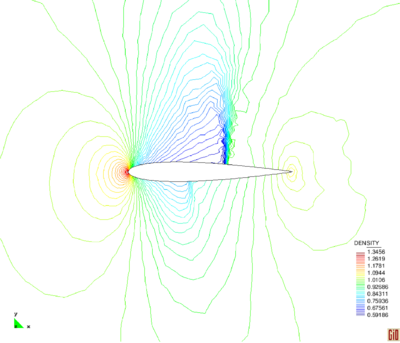
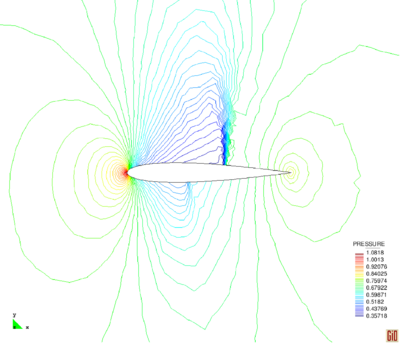
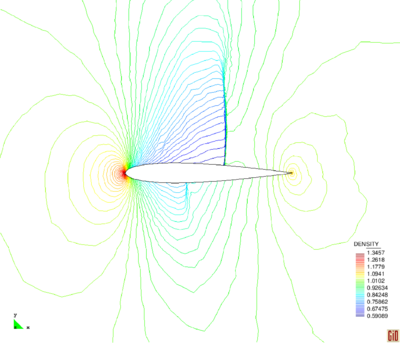
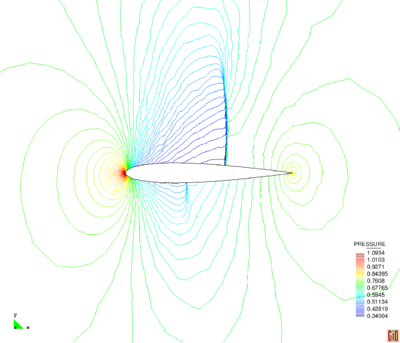
Figures 3 and 4 display numerical results corresponding to the initial and final mesh, respectively, which indicate the smoothness of the solution in all over the domain especially near the shocks. It can be seen that although the FIC method is capable to predict appropriate results by using a coarse discretization, the refinement enhances the resolution of the shocks. An angle of approximately is obtained by using both discretizations which means that the shock locations are captured accurately. It can be mentioned that the shocks are captured within four or five elements for both discretizations.
|
|
| Figure 3: Reflected shock. The results using initial mesh (a) density contours and (b) pressure contours. | |
|
|
| Figure 4: Reflected shock. The results using adaptive mesh (a) density contours and (b) pressure contours. | |
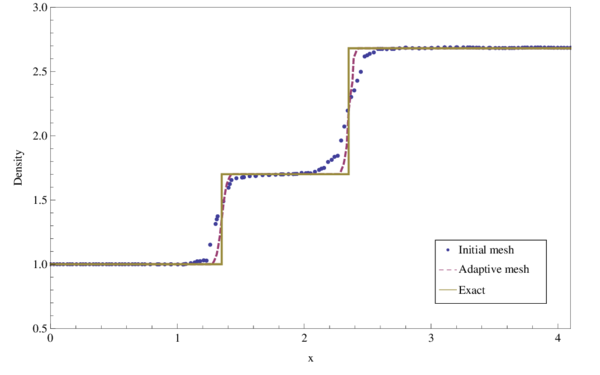
The comparison of the density profiles at corresponding to the exact solution and the numerical solution obtained using the initial and the adaptive meshes is depicted in Figure 5. Good agreement with the exact solution is obtained.
|
| Figure 5: Reflected shock example. Comparison of the density profiles at . |
The capability of the present method for different values of the constant coefficient is tested in this test case. The numerical results corresponding to and are displayed in Figures 6 and 7, respectively, containing the final adapted meshed, density contours using the uniform and the adapted meshes and the comparison of the density profiles at . It can be found that the choice of results in a more diffusive solution while a sharper shock is obtained by assuming . Although the shock positions are almost captured by the both uniform and adapted meshes, some oscillations are seen in the solutions near the shocks. These figures justify the choice of .
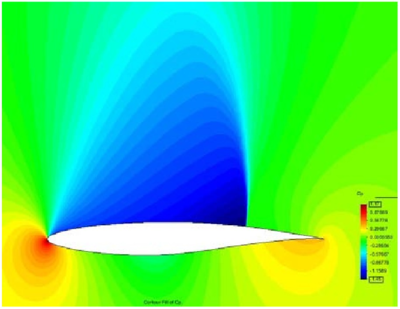
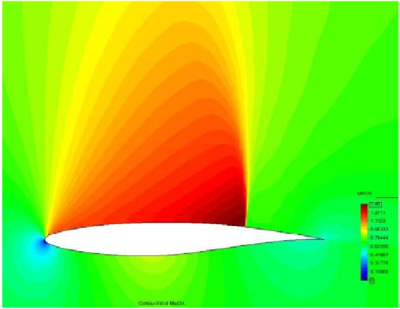
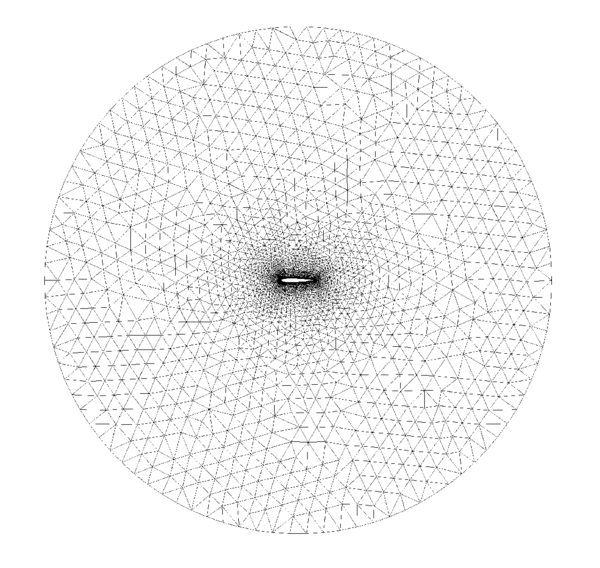
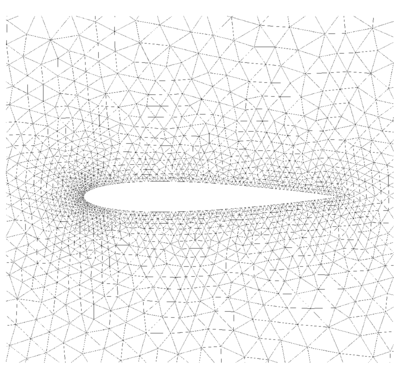
Example II: Subsonic inviscid flow around a NACA0012 airfoil
This example, taken from [38], illustrates the quality of the flow solution for an inviscid subsonic compressible flow past a NACA0012 airfoil at and . A circular computational domain is considered which is discretized by a mesh of nodes and 3-noded triangular elements as shown in Figure 8. Since the flow does not involve any shock waves, mesh refinement is not employed in this example. The slip boundary condition is applied on the surface of the airfoil whereas the far field boundary condition is considered on the outer boundary.
./0.5//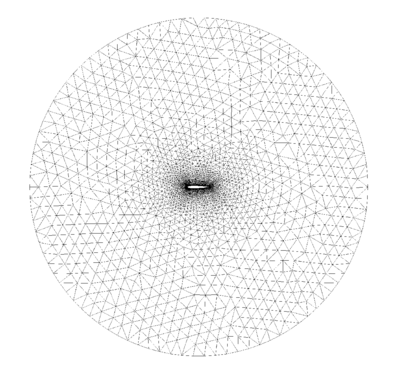
|

|
| Figure 8: Subsonic inviscid flow around around a NACA0012 airfoil example. (a) Domain discretization and (b) airfoil close-up. | |
In Figure 9 the density contours with a zoom at the stagnation point are presented demonstrating that no oscillations are observed, neither in the global solution nor at the stagnation point. A test for accuracy is the value of the density at the stagnation point for which the analytical solution is known, as
|
|
(66) |
where and for this example. Inserting , we obtain as the analytical value. The numerical result for this test case was obtained as which differs about from the analytical value.
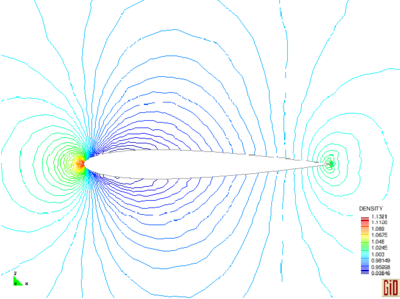
|

|
| Figure 9: Subsonic inviscid flow around around a NACA0012 airfoil example. (a) Density contours and (b) close-up density lines in the stagnation area. | |
The convergence history of the density at the stagnation point is presented in Figure ex2_conv showing that the FIC formulation does not present spurious oscillations in the density values at the stagnation point. The corresponding value along the stagnation streamline is given in Figure ex2_stag_stream proving that a smooth solution is obtained in this zone. The pressure coefficient obtained can be observed in Figure 11.
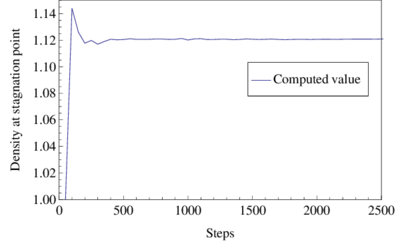
|

|
| Subsonic inviscid flow around around a NACA0012 airfoil example. (a) Convergence of the density at the stagnation point and (b) density value along the stagnation streamline. | |
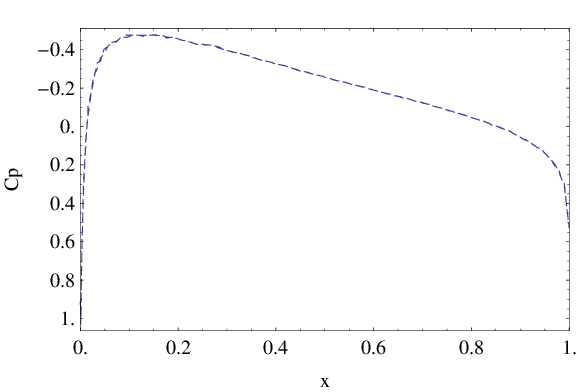
|
| Figure 11: Subsonic inviscid flow around around a NACA0012 airfoil example. Pressure coefficient contours. |
Example III: Transonic inviscid flow around a NACA0012 airfoil
This example demonstrates the ability of the FIC-FEM formulation for the analysis of the transonic compressible flow around a NACA0012 airfoil at and . This example is taken from the reports of the AGARD working group [100]. The initial mesh utilized for this example is the same as the one shown in Figure 8. The slip boundary condition is assigned on the surface of the airfoil whereas the far field boundary condition is applied on the outer boundary. The adapted mesh after five steps of refinement, containing nodes and elements, is shown in Figure 12 where the concentration of the elements in the vicinity of the high gradient zones is clearly seen.
./0.8//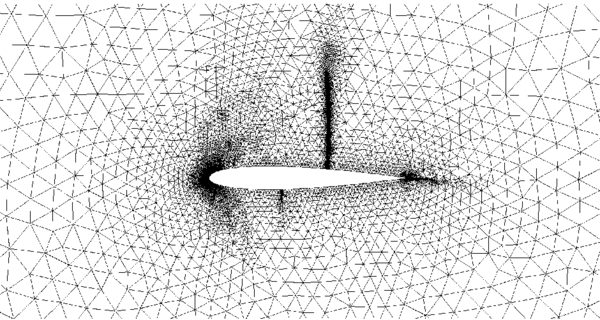
|
| Figure 12: Transonic inviscid flow around a NACA0012 airfoil. Final adapted mesh. |
The solution variables corresponding to the initial mesh and the adaptive mesh are presented in Figures 13 and 14 from which the effect of mesh refinement in improving the quality of the results can be observed. It can be found that, using both initial and adaptive discretizations, the stronger shock at the upper side of the airfoil is captured with minor oscillations as well as the weaker one at the lower side.

|

|
| Figure 13: Transonic inviscid flow around a NACA0012 airfoil. Obtained solution for the initial mesh. (a) density contours and (b) pressure contours. | |

|

|
| Figure 14: Transonic inviscid flow around a NACA0012 airfoil. Obtained solution for the adaptive mesh. (a) density contours and (b) pressure contours. | |
The pressure coefficient distribution over the airfoil resulting from the initial and adaptive meshes is graphically compared with the results of [100] in Figure 15 proving that accurate results have been obtained. Although the position of the shock does not change using the remeshing scheme, the adapted mesh improves the solution in the high-gradient zones.

|
| Figure 15: Transonic inviscid flow around a NACA0012 airfoil. The comparison of the distributions with the reference values. |
Example IV: Supersonic inviscid flow around a NACA0012 airfoil
The examples involves the supersonic flow around a NACA0012 at and which is again evoked from the AGARD working group 07 [100]. The domain, the initial mesh and the boundary conditions are the same as for the Example II. Using a similar scheme for the mesh refinement, the final refined mesh is presented in Figure 16 containing nodes and elements. ./1.2//
The obtained solution from initial and adapted mesh are presented in Figures 17 and 18, respectively. It can be found that although suitable results have been obtained using the initial mesh, the refinement scheme improves the quality of the results, especially near the shock waves. Also, both meshes are able to capture the shock waves near the leading and trailing edge of the airfoil.

|
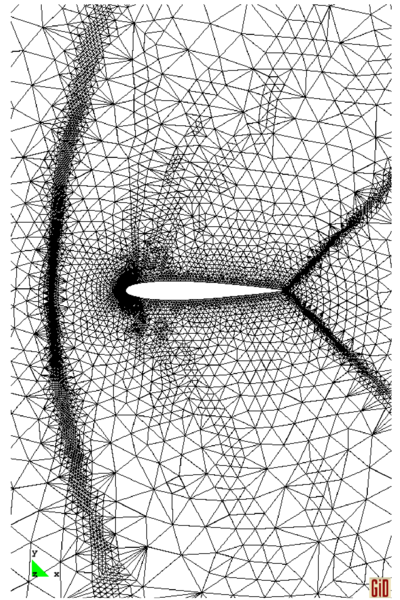
|
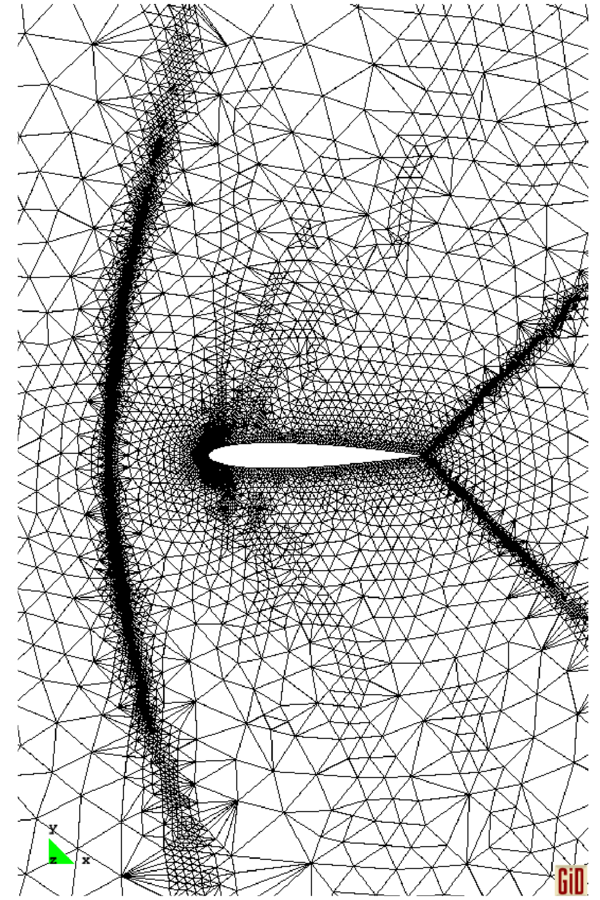
| |
| Figure 16: Supersonic inviscid flow around a NACA0012 airfoil. The adaptive mesh after (a) one level, (b) three levels and (c) five levels of refinement. | |

|
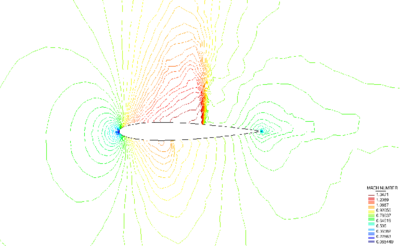
|
| Figure 17: Supersonic inviscid flow around a NACA0012 airfoil. Obtained solution for the initial mesh. (a) density and (b) mach number contours. | |

|
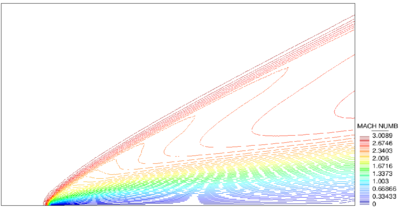
|
| Figure 18: Supersonic inviscid flow around a NACA0012 airfoil. Obtained solution for the refined mesh. (a) density and (b) mach number contours. | |
The pressure coefficient distributions over a NACA0012 surface obtained for this example are shown in Figure 19. A good agreement with the reference results can be observed using both meshes.

|
| Figure 19: Supersonic inviscid flow around NACA0012 airfoil. The comparison of the distributions with the reference values. |
2.7.2 Viscous Flow
For the viscous examples, the computational mesh is generated by a combination of unstructured and structured meshes in such a way that a structured mesh is created a priori near the solid boundaries merging with an unstructured mesh at the remaining parts of the domain. This approach has been widely used for viscous flow problems [101,102]. However, the method has not enough flexibility for the inclusion of mesh refinement or for the extension to general complex 3D configurations. It is to mention that if the domain problem in small enough, the structured mesh is generated in all over the domain without embedding the unstructured mesh.
Example V: Subsonic laminar flow past a NACA0012 airfoil
The subsonic viscous flow around a NACA0012 airfoil is presented here for demonstrating the behavior of the developed stabilized formulation in viscous regime. The flow conditions are , and . The assumed circular domain is discretized into nodes and 3-noded triangle elements including a structured mesh of layers near the airfoil boundary which is merged with an unstructured mesh in the remaining of the computational domain. For the first layer of elements at the boundary, the normal element size has the value of which is increased by a geometric progression for the following layers. The details of the mesh near the airfoil are shown in Figure 20. The no slip adiabatic wall condition is imposed at the airfoil surface, whereas the far field condition is applied at the outer boundary.
./0.5_vis//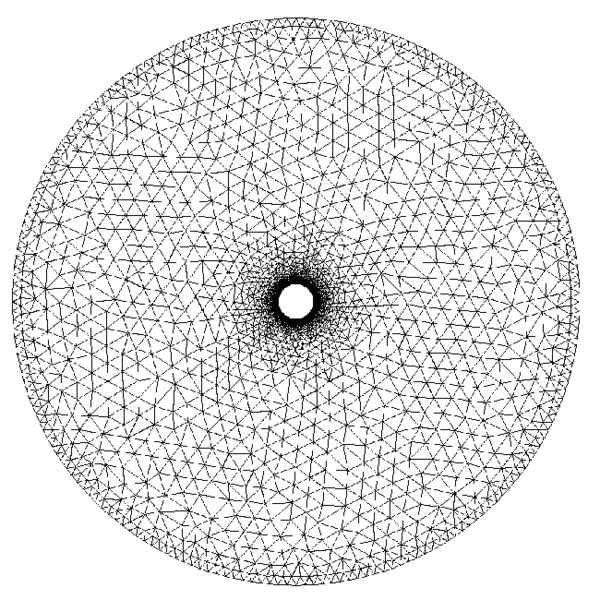
|
| Figure 20: Subsonic laminar flow past NACA0012 airfoil. Detail of the mesh. |
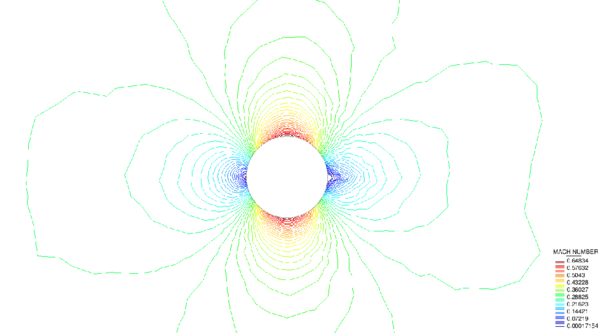
|
| Figure 21: Subsonic laminar flow past a NACA0012 airfoil. Mach number contours. |
The obtained Mach number contour is presented in Figure 21 showing an overall excellent agreement with the reference result [103]. Figure ex5_recirculation illustrates the recirculation bubble at the trailing edge. Each vector of the figure represents the modulus and direction of velocity at each node of the mesh. Pressure contours are shown in Figure ex5_pre. The fact that the lines are parallel to each other with almost no oscillations indicates the good quality of the results.

|
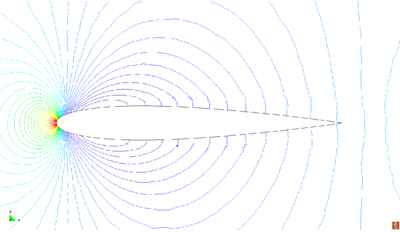
|
| Subsonic laminar flow past a NACA0012 airfoil. (a) Close-up of computed velocity vectors near the trailing edge and (b) details of pressure contours. | |
A more severe test of accuracy is the plot of the pressure coefficient and the skin friction along the airfoil, presented in Figures 23 and 24, respectively, showing the accuracy of the obtained results in comparison with the reference ones [103]. It is to be noted that the peak value of is slightly underestimated. Better results can be obtained by using a finer mesh near the leading edge.
![Subsonic laminar flow past a NACA0012 airfoil. Comparison of the obtained pressure coefficient Cₚ distribution with the numerical results of reference [103].](/wd/images/f/f7/Draft_Content_873167254-cp.png)
|
| Figure 23: Subsonic laminar flow past a NACA0012 airfoil. Comparison of the obtained pressure coefficient distribution with the numerical results of reference [103]. |
![Subsonic laminar flow past a NACA0012 airfoil. Comparison of the obtained skin-friction coefficient Cf distribution with the numerical results of reference [103].](/wd/images/thumb/3/3b/Draft_Content_873167254-cf.png/600px-Draft_Content_873167254-cf.png)
|
| Figure 24: Subsonic laminar flow past a NACA0012 airfoil. Comparison of the obtained skin-friction coefficient distribution with the numerical results of reference [103]. |
The variation of the accuracy and the convergence with the change in the constant coefficient is investigated in this example. Table 1 presents an estimate of the solution accuracy as measured by the computed values of the separation location versus using three different values of 0.25 0.50 and 0.75 for . It can be found that the values obtained from and have a good agreement with the results presented in the reference paper [103], ranging from chord.
| Separation Location | 82.4% | 83.0% | 91.0% |
The variation of the convergence history of the density at the stagnation point with the change in is presented in Figure 25 showing that the choice of does not present spurious oscillations in the density values at the stagnation point.
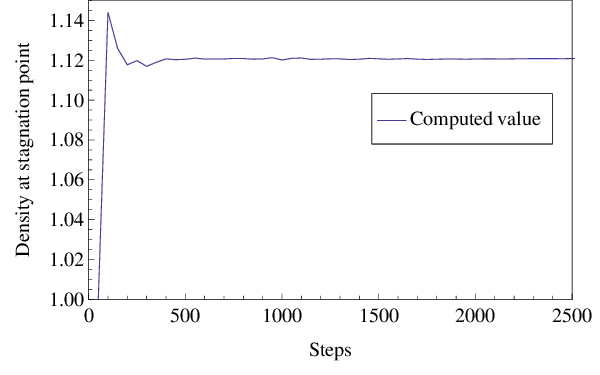
|
| Figure 25: Subsonic laminar flow past a NACA0012 airfoil. Convergence of the density at the stagnation point for different values of |
Example VI: Supersonic flow over flat plate
The Carter's flat plate example with the flow conditions of , and is selected here to examine the capability of the current method in the presence of shock waves and boundary layers. A rectangular domain is presented in Figure 26, with the dimensions of and along the and directions, respectively, where the leading edge of the plate is located at and . The Reynolds number is calculated based on the free stream values and unique length. A structured mesh is created for the example by division of the domain in parts and parts in and directions, respectively.
./flat//
|
| Figure 26: Supersonic flow over flat plate. Problem definition. |
As shown in Figure 26, all the characteristic variables of , , and are fixed at the inflow and upper sides of the domain since these boundaries behave as a supersonic inlet. The no slip boundary condition is applied on the surface of the plate whereas the stagnation temperature of
|
|
(67) |
is imposed there, as well. Although a prescription of the density is needed at the subsonic part of the outflow boundary, the flow variables are left free there.
The obtained density, pressure, temperature and Mach number contours are plotted in Figure 27 proving the appropriate behavior of the presented formulation in capturing the shock wave and boundary layer.
|

|
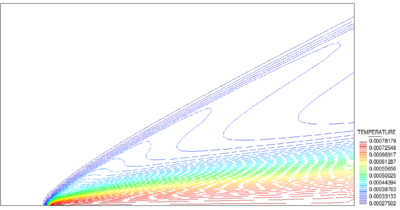
|

|
| Figure 27: Supersonic flow over flat plate. (a) Density, (b) pressure, (c) temperature and (d) Mach number contours. | |
In order to have a more precise test, the obtained density value and the component of the velocity profiles along the line are compared in Figures ex6_den and ex6_vel, respectively, with the ones presented in [104]. Although the obtained peak point values of both the density and component of the velocity profiles are not coincident with the reference ones, a good agreement with the reference results can be observed.
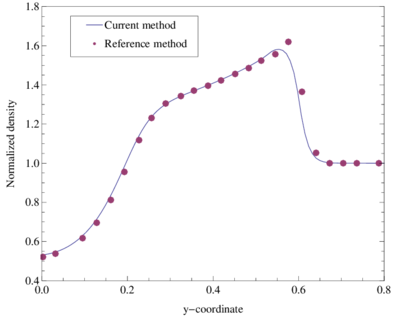
|
![Supersonic flow over flat plate. Comparison of the obtained (a) density (b) vertical velocity profiles along the line x=1.2 with the reference results [104].](/wd/images/thumb/5/5b/Draft_Content_873167254-vel_gr.png/400px-Draft_Content_873167254-vel_gr.png)
|
| Supersonic flow over flat plate. Comparison of the obtained (a) density (b) vertical velocity profiles along the line with the reference results [104]. | |
Example VII: Compression corner
This example is another benchmark of the FIC-FEM formulation for supersonic viscous regimes again extracted from the reference [104] where the flow with the conditions of , and enters the domain passing over a flat plate and then a compression corner of including the shock wave and boundary layers initiated from the leading edge of the plate. The Reynolds number is calculated based on the free stream values and the distance between the leading edge of the plate and the compression corner.
As shown in Figure 29 schematically, the computational domain of and is assumed where the leading edge of the flat plate is located at and the compression corner starts from .
The flow variables of density, velocity and temperature are fixed at the inflow and upper boundaries where no condition is prescribed on the outflow boundary. On the plate surface, the no-slip boundary condition, as well as the specification of the temperature as the stagnation temperature, calculated from Equation 67, are applied.
./comp//
|
| Figure 29: Compression corner. Problem definition. |
The domain is discretized using a structured mesh of 3-noded triangles, shown in Figure 30, containing points in the streamline direction and points in the vertical direction where the minimum element size above the plate is taken as giving the maximum aspect ratio of almost .
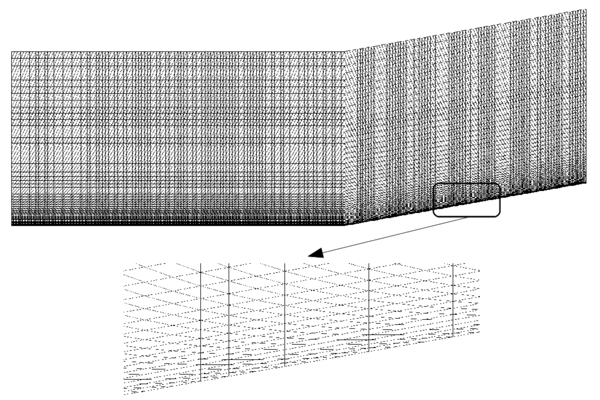
|
| Figure 30: Compression corner. Detail of the structured mesh. |
The obtained density, pressure, temperature and Mach number contours are presented in Figure 31. The figure shows that the methodology developed in this thesis is able to provide smooth results in all over the domain especially near the shock wave as well as near the boundary layers. The only inaccuracy observed in the results is the presence of non-realistic values at the zone close to the stagnation point which is a point of singularity. It can be seen that the weakness of the formulation in determining the temperature at the stagnation point results in an overestimation of the Mach number there. This problem can be resolved by using elements with less aspect ratio around that region.
The comparison of the obtained and distributions along the plate surface with the ones presented by Carter [104] is shown in Figure 32 and Figure 33, respectively. Generally, a good agreement is observed except for the peak values at the stagnation point, as mentioned before. The location of the separation point happens at showing an appropriate compatibility with the results presented in the [104], [105] and [106] ranging from to .

|

|

|

|
| Figure 31: Compression corner. (a) density, (b) pressure, (c) temperature and (d) Mach number contours. | |
![Compression corner. Comparison of the obtained pressure coefficient Cₚ distribution with the numerical results of reference [104].](/wd/images/f/f7/Draft_Content_873167254-cp.png)
|
| Figure 32: Compression corner. Comparison of the obtained pressure coefficient distribution with the numerical results of reference [104]. |
![Compression corner. Comparison of the obtained skin-friction coefficient Cf distribution with the numerical results of reference [104].](/wd/images/thumb/3/3b/Draft_Content_873167254-cf.png/600px-Draft_Content_873167254-cf.png)
|
| Figure 33: Compression corner. Comparison of the obtained skin-friction coefficient distribution with the numerical results of reference [104]. |
3 Aerodynamic Shape Optimization Using Genetic Algorithm And Adaptive Remeshing
The main objective of this chapter is to compare the solutions obtained from different optimization methods with and without the use of adaptive remeshing technique. The solutions will be compared in terms of accuracy and computational cost. Two different methods are considered. The first uses the Multi-Objective Genetic Algorithm (MOGA) technique associated with adaptive mesh refinement technique while the second uses the MOGA coupled with a conventional mesh technique (uniform mesh). Both use an Euler flow code [107] and a multi-objective optimization software [108,109,110] developed at CIMNE in recent years and they are implemented to three practical CFD design problems of the airfoils in transonic regime. The main objective is to compare the solutions obtained with and without adaptive mesh refinement in terms of solution accuracy and computational cost.
This chapter is organized as follows. Section 3.1 presents the overall design process. Section 3.2 describes the fluid solver and the mesh refinement techniques which are coupled to it, including a validation test example. Section 3.3 presents the numerical optimization methods implemented in this thesis, i.e., the MOGA technique and the parametrization methodology. A number of optimization test cases are presented in Section 3.4.
3.1 Overall Design Process
A design code is developed in the current thesis which can be modularized into several components such as the flow solver, the adaptive mesh refinement solver, the parametrization algorithm and the optimization algorithm. The CIMNE in-house codes named PUMI and RMOP are used as the flow solver and the optimization algorithm, respectively, while the adaptive mesh refinement solver and the parametrization algorithm are written in this thesis.
For the uniform mesh method, the design procedure can be described as follows
1. Define initial design variables.
2. Parameterize the configuration of interest using a set of design variables.
3. Generate the fine mesh around the modeled configuration.
4. Solve the flow equations for flow variables initiating from upstream flow variables.
5. Calculate objective functions and constraints.
6. Optimize the current geometry using GA and update design variables.
7. Return to 2. and repeat until an optimum has been reached.
By adding the mesh refinement step to the above algorithm, the design procedure of the adaptive mesh method can be described as follows
1. Define initial design variables.
2. Parameterize the configuration of interest using a set of design variables.
3. Generate the coarse mesh around the modeled configuration.
4. Solve the flow equations for flow variables initiating from upstream flow variables.
5. Refine the coarse mesh by evaluating the error indicator from the obtained flow variables.
6. Interpolate the solution from the coarse mesh to the adapted one.
7. Resolving the flow equations initiating from interpolated flow variables.
8. Calculate objective functions and constraints.
9. Optimize the current geometry using GA and update design variables.
10. Return to 2. and repeat until an optimum has been reached.
A summary of the design process for the both uniform mesh and adaptive mesh methods is illustrated in Figure 34.
3.2 Flow Analysis
3.2.1 CFD Solver Enhanced by Adaptive Refinement
The investigation carried out in this chapter makes use of the PUMI code developed in CIMNE [107]. The reason for this choice is that the focus of this research work is on the optimization algorithm rather than on the flow solver. Hence, it is decided to use a validated solver for the flow equations. PUMI is a 3-D flow solver for high speed inviscid applications. The Galerkin finite element method in conjunction with the upwind stabilization technique is implemented in this code. To achieve optimum performance and reduce the memory requirements an edge based data structure is selected. For time integration, an explicit multi-stage Runge-Kutta scheme is chosen in order to increase the allowable time step. More information about the PUMI CFD solver can be found in [107].
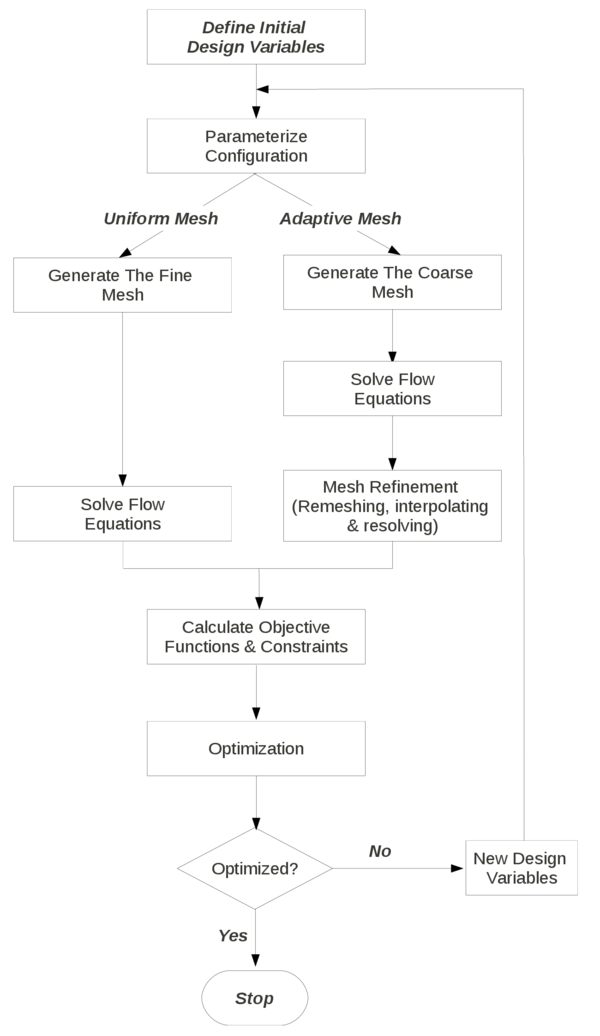
|
| Figure 34: Flowchart of the design process. |
The main goal of this part of the thesis is to compare the optimized results coupled with the uniform and adaptive meshes. The adaptive remeshing technique introduced in Section 2.6 is joined to the CFD solver. Two transonic test cases are presented in the next section to validate the CFD solver and the adaptive refinement techniques implemented.
3.2.2 Validation of the mesh refinement technique
In this section some numerical examples are presented in order to illustrate the performance of the refinement procedures (adaptive remeshing methodologies) in conjunction with the PUMI solver. The mesh generation is carried out using the GiD pre/post processing system via an advanced front technique.
All the examples are related to the solution of an inviscid transonic flow over a NACA 0012 airfoil at different Mach numbers and angles of attack. When the simulation starts, some time steps are performed in order to get a value of the density temporal residual of . Then, the first refinement level is done. Consecutive refinement levels are carried out every 200 time steps. The computational domain is discretized by an unstructured distribution of nodes and 3-noded triangle elements. The initial mesh is shown in Figure 35 which is the same for all the test cases.
|
| Figure 35: Initial mesh containing 2084 nodes and 3970 3-noded triangle elements. |
Test 1
The first example concerns a subsonic flow with a freestream Mach number and angle of attack . After 2, 4, 6, 10, 20 and 30 levels of remeshing, the final meshes are shown in Figure 36. Note that the adaptive procedure captures all the flow features with precision. The shock wave on the upper and lower sides of the airfoil and the leading and trailing edge regions are appropriately captured via the refinement procedure. In Figure 37, the field around the airfoil is introduced using the final adaptive mesh.

|

|

|

|

|

|
| Figure 36: The obtained mesh after (a) 2 (b) 4 (c) 6 (d) 10 (e) 20 (f) 30 remeshing levels for and . | |
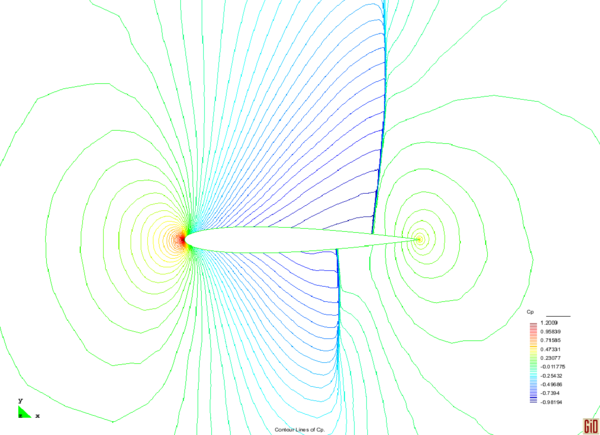
|
| Figure 37: field after 20 refinement levels for and . |
Figure 38 shows the distribution around the airfoil after 30 levels of remeshing compared with numerical results [111] where a good agreement is obtained. As shown in Figure 39, the variation of total number of nodes and elements decrease while the refinement goes forward. Assuming 0.001 as the minimum elem et size, after 30 levels of remeshing, the mesh contains 7782 nodes and 15289 elements. It is noticeable that the total number of nodes and elements do not change much while the refinement progresses.
![Comparison between the Cₚ distribution after 30 remeshing levels and numerical results reported in [111] for M∞=0.8 and α=0.0∘ .](/wd/images/f/f7/Draft_Content_873167254-cp.png)
|
| Figure 38: Comparison between the distribution after 30 remeshing levels and numerical results reported in [111] for and . |
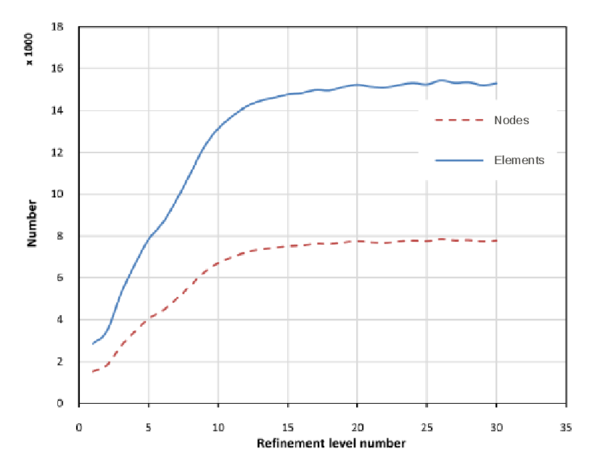
|
| Figure 39: Total number of nodes and elements versus the refinement level number for and . |
Test 2
In this example the freestream Mach number and the angle of attack are considered and . The refined meshes after 2, 4, 6, 10, 20 and 30 levels of remeshing are shown in Figure 40. It is clear that the upper and lower shockwaves are captured exactly as well as the leading and trailing edges.
./0.85_1_a//

|

|

|

|

|

|
| Figure 40: The obtained mesh after (a) 2 (b) 4 (c) 6 (d) 10 (e) 20 (f) 30 remeshing levels for and . | |
Figures 41 and 42 show the field of the refined mesh and the comparison between obtained distribution with numerical results reported in [112], respectively. A good agreement is found between the adaptive remeshing results and the reference ones.

|
| Figure 41: field after 20 refinement levels for and . |
![Comparison between the Cₚ distribution after 30 refinement levels and numerical results reported in [112] for M∞=0.85 and α=1.0∘ .](/wd/images/f/f7/Draft_Content_873167254-cp.png)
|
| Figure 42: Comparison between the distribution after 30 refinement levels and numerical results reported in [112] for and . |
As shown in Figure 43, a suitable convergence is obtained for the total number of nodes and elements during the remeshing process.

|
| Figure 43: Total number of nodes and elements versus the refinement level number for and . |
3.3 Optimization Methodology
Gradient-based methods are well-known optimization algorithms, which find the optimal design using local gradient information. On the other hand, Genetic Algorithms (GAs) are known to be robust optimization algorithms. Even though GAs take more computational time to converge to optimal design when compared to the traditional Gradient-based methods, GAs have capabilities to escape from local optima and to find the global solution. In addition, GAs are based on a fitness function evaluations and no gradients are needed during the optimization process.
Indeed, most of the real-world optimization problems are multi objective optimization and GAs have unique benefits for solving these type of problems because multiple Pareto solutions can be obtained simultaneously without specifying weights between objectives [6]. Beside its applications in a wide range of engineering design problems, GAs have been successfully applied to solve aerodynamic shape optimization problems [73,74].
3.3.1 Multi-Objective Genetic Algorithm
In the Origin of Species [113], Charles Darwin stated the theory of natural evolution. Over many generations, biological organisms evolve according to the principles of natural selection like survival of the fittest to reach some remarkable forms of accomplishment. In nature, individuals in a population have to compete with each other for vital resources. Because of such selection, poorly performing individuals have less chance to survive, and the most adapted, or fit individuals produce a relatively larger number of offsprings. After a few generations, species evolve spontaneously to become more and more adapted to their environment. In 1975, Holland developed this idea in Adaptation in Natural and Artificial system [114]. By describing how to apply the principles of natural evolution to optimization problems, he laid down the first Genetic Algorithm. Hollands theory has been further developed and now Genetic Algorithms (GAs) accepted as a powerful adaptive method to solve search and optimization problems. Some evidences of these results can be found in [115,116].
In GAs, we use the term individual to denote one configuration of the optimal shape. The feasibility of the shape is judged by a fitness function, reflecting the minimized cost functional and penalizing geometrically unfeasible individuals. The shape parameters of one individual are encoded in the individuals chromosome. The GA operates simultaneously on an entire population of individuals (shapes), the initial population being generated either randomly or as a set of feasible individuals using an a-priori engineering guess.
GAs are stochastic iterative processes that are not guaranteed to converge. They have a great potential to explore the whole search space and identify multiple local maxima and to converge to the global optimum while a point to point method will generally stall in a local optimum only. They are found more robust in the case of non differentiable, multi-modal or non convex functions, and are particularly interesting for search of a trade-off optimum with respect to several criteria (Pareto front, Nash game).
The core of the GA consists in selection, crossover and mutation operators, whose role is to mimic natural empiric laws of survival of the fittest (selection), their precreations (crossover) and occasional mutations. The generation operators are usually not deterministic, they implement their operators in the probabilistic sense, with a given probability distribution. The crossover is performed with a crossover probability (or crossover rate); two selected individuals (parents) exchange parts of their chromosome to create two offsprings. This operator tends to enable the evolutionary process to move towards promising regions of the search space. The mutation operator is introduced to prevent premature convergence to local optima by randomly sampling new points in the search space. It is carried out by flipping bits at random, with some (small) probability .
For multi-objective optimization problems, it is necessary to make some modifications to the basic GAs. There exist several variants of GAs for this kind of problem. For the multi-objective GA, the CIMNE in-house software named Robust Multi-objective Optimization Platform (RMOP) is utilized. It is a distributed/parallel computational intelligence framework which is a collection of population based algorithms including GA [117,118] and Particle Swarm Optimization (PSO) as shown in Figure 44. In this work, a GA searching method in RMOP is used and it is denoted as MOGA. MOGA uses a Pareto tournament selection operator which ensures that the new individual is not dominated by any other solutions in the tournament.
|
| Figure 44: Topology of Robust Multi-objective Optimization Platform. |
For the constraint handling, the linear penalty method is used in such a way that a weighted sum of the individual constraint violation is added to its fitness value if the constraint is not satisfied. In this work, each generation consists of 20 individuals and the termination criterion is predefined by the number of generation. In all the test cases of this research, the initial population is created randomly.
RMOP is easily coupled to any analysis tools such as Computation Fluid Dynamic (CFD), Finite Element Analysis (FEA) and/or Computer Aided Design (CAD) systems. Details of RMOP and its engineering design applications can be found in References [108,109,110]. In this work, MOGA is coupled with both conventional mesh technique and an advanced adaptive mesh refinement strategy mentioned in Section 3.2.1.
3.3.2 Parametrization
Bezier curves [119] are used to represent the geometry of the airfoil as a linear combination of the so called Bezier polynomials. Given a set of control points, the corresponding Bezier curve is defined as
|
|
(68) |
where denotes the curve parameter, are the Bezier polynomials of order and are the coordinates of the control points. The different smooth curves are created by changing these control points.
The geometries of the airfoils used in this work (NACA 0012 and RAE 2822) are represented using 24 control points as shown in Figure 45. To represent the airfoil geometry accurately, a bigger density of control points is placed close to the zone where the airfoil curve has a bigger curvature. The coordinates of the control points are considered as the design variables while fixing coordinates. Two control points, at the leading edge and trailing edge, have fixed values during the optimization to keep the chord length constant. Also, two other control points near the leading edge are fixed to obtain enough curvature in that zone. In total, 20 design variables are considered for the optimization test cases.
Figure 45 also shows the upper and lower bounds for the design variables corresponding to both airfoils. This defines a wide range of different geometries which are sufficient for the optimization.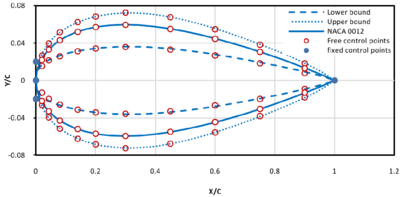
|
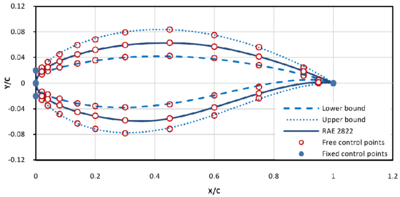
|
| Figure 45: Upper and lower bound of design variables for NACA 0012 (top) and RAE 2822 (bottom) in comparison to the original ones and corresponding free and fixed control points. | |
3.4 Realistic Optimization Test Cases
Having introduced the components of the current optimization algorithm in Section 3.2 and Section 3.3, the obtained results are presented in this section in order to demonstrate the application of mesh refinement in transonic airfoil design optimization for reconstruction design and drag minimization and multi-objective design. Adaptive remeshing, described in Section 2.6, is selected as the refinement methodology in all the results presented in this section.
In this research the flight conditions of Mach number and angle of attack are treated as constant values with a thickness constraint. To demonstrate the benefit of mesh refinement, the results obtained with and without adaptive remeshing are compared. By assuming fixed values for the minimum element size and the number of refinement steps in the process of adaptive remeshing, it is possible to limit the computational cost of adaptive remeshing. By investigating the computational costs related to some random geometries in the assumed flight conditions, it can be found that the computational time do not vary more than around the average one.
Hence, the uniform mesh is constructed in such a way that the same computational cost as the average value of the adaptive mesh tests would be required. Therefore, the characteristics of uniform mesh (such as minimum element size and the variation of element size far from the airfoil) are defined a priori and they are considered the same for all the individuals of each optimization problem. Hence, the computational costs for the CFD analysis of the uniform and adaptive meshes are the same in both reconstruction and drag minimization design problems. It is notable that the additional costs due to the adaptive algorithm and the grid regeneration algorithm are also taken into account.
A very fine uniform mesh is considered as the baseline mesh to compare the final results presented in this research for both reconstruction and drag minimization designs. A mesh independent study has been carried out in several flight conditions in order to find a suitable baseline mesh. The minimum element size considered for the baseline mesh is times finer than the one implemented for the uniform mesh and adaptive mesh used during the optimization. Indeed, it is dense enough in the vicinity of the airfoil to predict the results in an accurate manner. Figure 46(a) exhibits the baseline mesh on NACA 0012 consisting of 23968 nodes and 47006 3-noded triangle elements and that one on RAE 2822 in shown in Figure 46(b) including 24017 nodes and 47091 elements.
./
|
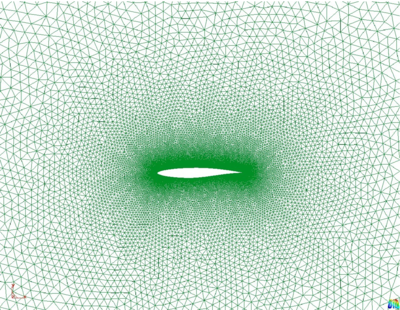
|
| Figure 46: The baseline mesh around NACA 0012 5(a) and RAE 2822 5(b). | |
3.4.1 Reconstruction Design
Statement of the problem
This test case considers a single-objective reconstruction design of NACA 0012 at the flow conditions and . The main objective is to minimize the pressure error between the target pressure coefficient and the candidate one. The fitness function (the least square error of the pressure) is shown in Equation 69. inverse1//
|
|
(69) |
where represents the number of pressure points on the airfoil . As shown in section 2.3.2, the coordinate of the control points assumed around the airfoil are considered as the design variables.
The target pressure coefficient shown in Figure 47 is obtained by constructing the baseline mesh around NACA 0012. In the assumed flight conditions, a strong shock wave appears at the upper edge of NACA 0012 profile which makes this test case suitable to investigate the effect of an adaptive mesh versus uniform mesh during the reconstruction design of the assumed airfoil.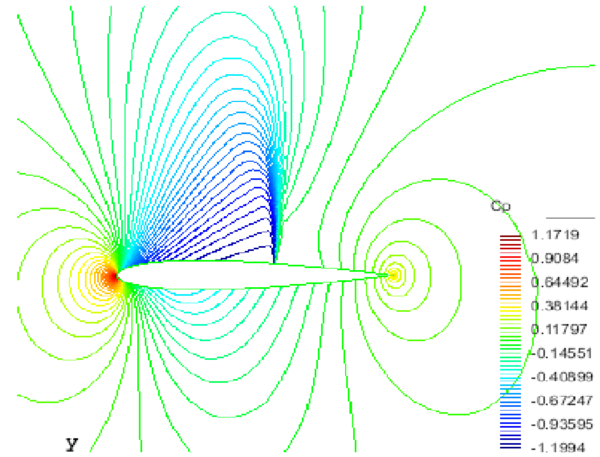
|
| Figure 47: contours around NACA 0012 at the flow conditions and . |
Numerical results
Figure 48 compares the convergence history for the pressure error obtained by MOGA coupled with the uniform mesh and adaptive remeshing approaches. Both test cases were allowed to run for 133 hours and 400 generation using a single 1 2.8 GHz processor. The uniform mesh approach achieves an optimal airfoil with pressure error of 0.0273 after 222 generations (74 hours). The adaptive remeshing technique coupled with MOGA converged to the pressure error of 0.0213 after 208 generations. This reflects that the adaptive remeshing technique produces a 22% more accurate solution. In addition, the adaptive remeshing technique captures the converged value of the uniform mesh method after 99 generations (33 hours) which is only 45% of uniform mesh computational cost. In other words, the adaptive remeshing method saves 55% of the computational cost of the uniform mesh approach. The main reason that the adaptive remeshing method can produce accurate solution within low computational cost, is that the final adapted mesh conditions provide a better environment to simulate flow phenomena when compared to the uniform mesh approach.
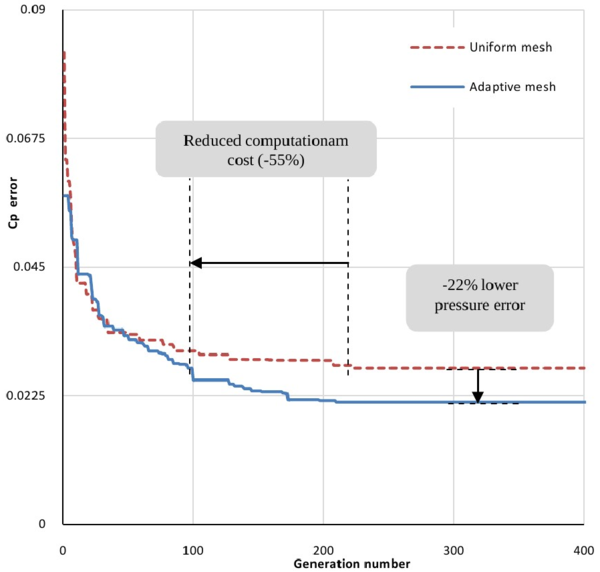
|
| Figure 48: Convergence history of reconstruction design of uniform and adaptive mesh test cases. |
Table 2 compares the final pressure errors obtained for the uniform and the adaptive mesh test cases. It is shown that the adaptive remeshing test case airfoil produces 22% lower pressure error than the one resulting from the uniform mesh test case.
| Adaptive mesh | Uniform mesh | |
| Pressure error | 0.0213 (-22%) | 0.0273 |
It is noticeable that the pressure errors presented in Figure 48 are obtained by constructing the uniform mesh and the adapted mesh on the optimized airfoils. Since these two meshes are completely different, it can be found that a portion of the difference in the final pressure error is due to the use of different meshes.
In order to neglect the effect of mesh difference on the comparison of the computational cost, the baseline mesh is utilized. By constructing the baseline mesh on the final airfoil obtained from uniform mesh test case, the pressure error of 0.023 is obtained. It can be found that this value is captured by constructing the baseline mesh on the airfoil obtained from the adaptive mesh test case after 144 generations which is 65% of the computational cost of the uniform mesh test case. This expresses that the adaptive remeshing technique improves the efficiency of the optimization by 35%
Also, In order to have a fairer comparison on the pressure error, the baseline mesh is constructed on each optimized airfoil to obtain the final pressure error. The corresponding values using the baseline mesh for both optimized airfoils are presented in Table 3 which shows a reduction of the order of 24% in the pressure error.
| Adaptive mesh | Uniform mesh | |
| Pressure error | 0.0174 (- 24%) | 0.0230 |
The geometries of the target and optimal airfoils obtained by the uniform mesh and adaptive remeshing approaches are compared in Figure 49. Even though both approaches can capture the target geometry, the adaptive remeshing technique produces a geometry which has a good agreement to the target airfoil when compared to the optimal airfoil using the uniform mesh approach.
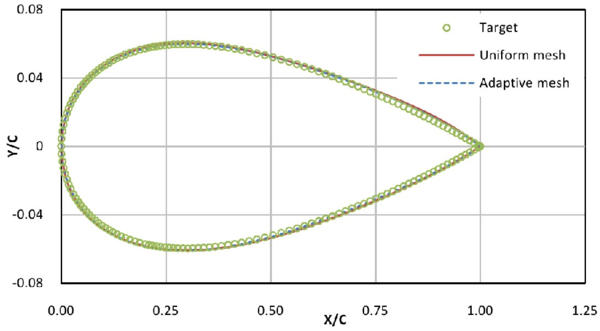
|
| Figure 49: Comparison between target, uniform mesh and adaptive mesh test case airfoils. |
distributions corresponding to target airfoil and two optimized test cases by constructing the baseline mesh for the discretization of each domain are shown in Figure 50. It can be seen that the target pressure distribution on the lower surface of the airfoil is achieved by the uniform and adaptive mesh test cases while the adaptive mesh one creates a closer pressure distribution to the target one on the upper surface due to the more accurate results obtained from adaptive mesh during the optimization. It is noticeable that the shock wave is captured by both methodologies in an accurate manner.

|
| Figure 50: Comparison between target, uniform mesh test case and adaptive mesh test case distributions. |
The corresponding contours and the Mach number contours for the target airfoil and the two optimized test cases are presented in Figures 51a and 51. A good agreement in the pressure and Mach numbers and their corresponding minimum/maximum values around the airfoils is obtained versus the target one.
3.4.2 Drag Minimization
Statement of the problem
The test case considers a single-objective design problem for RAE 2822 to improve aerodynamic efficiency at the fixed flow conditions and . This flow conditions have been selected in order to avoid a possible shock free solution of the optimization problem. The presence of the shock wave justifies the use of the technique proposed in this work. The fitness function is shown in Equation 70 with thickness constraint 71.
|
|
(70) |
subject to
|
|
(71) |
where and represent the lift to drag ratio and the thickness ratio of the airfoil, respectively.
In other words, the inverse of lift to drag ratio is minimized at specified flight conditions while maintaining the maximum thickness of the baseline design (RAE 2822). The design variables selected for drag minimization are the same as the ones assumed in the reconstruction design.
Numerical results
As illustrated in Figure 52, both MOGA coupled with the uniform mesh and the adaptive remeshing techniques are allowed to run for 150 generations (50 hours) using a single 4 2.8 GHz processor. The uniform mesh test case has converged to after 142 generations (47.3 hours). This value is captured by the adaptive remeshing approach after 8 generations (2.67 hours). In other words, the adaptive remeshing method improves the optimization efficiency by 95% when compared to the adaptive remeshing technique.
./drag1//
|
| Figure 52: Convergence history for drag minimization for the uniform and adaptive mesh test cases. |
The fitness value resulted from the target design and the optimized ones are compared in Table 1. It is clear that both optimal airfoils obtained by the uniform and adaptive mesh techniques improve the aerodynamic behavior significantly. By comparing the final fitness function of uniform and adaptive test cases, it can be found that the adaptive one improves the aerodynamic performance by 48% when compared to the baseline design while the uniform one only can make improvements of the order of 30% This improvement on the reduction of objective function is because of the better CFD results obtained from the adaptive mesh during the optimization process.
| Baseline | Adaptive mesh | Uniform mesh | |
| 0.04232 | 0.02221 (-48%) | 0.02979 (-30%) |
As the reconstruction test case, in order to eliminate the effect of the mesh quality on the values presented in Figure 52 and Table 1, the objective functions can be recalculated by constructing the baseline mesh on each optimized airfoil. This leads to a fairer comparison on the final objective function for the uniform mesh and the adaptive mesh test cases.
The final objective function corresponding to the final airfoil resulted from uniform mesh test case has the order of 0.0242 if the baseline mesh is used for the discretization of the domain. This value is captured by constructing the baseline mesh on the optimized airfoil obtained from the adaptive mesh test case on the 36th generation. This computational cost is only 25% of the one for the uniform mesh test case. This shows that the adaptive remeshing technique improves the efficiency of the optimization by 75%
The objective function corresponding to the final airfoils resulting from both test cases (using the baseline mesh) are presented in Table 5. It can be seen that the adaptive remeshing increases the quality of the optimal airfoil by 53% and 20% when compared to the baseline design and the optimal airfoil obtained by using the uniform mesh. Hence, even though the baseline mesh is used for each optimized airfoil, the adaptive mesh test case airfoil yields a more improved objective function.
| Baseline | Adaptive mesh | Uniform mesh | |
| 0.0439 | 0.02050 (-53%) | 0.0242 (-45%) |
The geometries of baseline and optimal airfoils obtained by the uniform and adaptive mesh techniques are compared as shown in Figure 53. The difference between the baseline airfoil and the optimized ones can be seen in this figure. The effect of adaptive remeshing on the optimized airfoil is different in the lower surface as well as in the upper surface.

|
| Figure 53: The comparison between the baseline RAE 2822, the adaptive mesh and uniform mesh test case. |
Table 6 compares the airfoil characteristics such as the maximum thickness, maximum camber for the baseline design and optimal airfoils for the uniform and adaptive mesh techniques. Both optimal airfoils obtained using the uniform and adaptive mesh techniques have lower camber while maintaining similar thickness ratio when compared to the baseline design.
| Baseline | Adaptive mesh | Uniform mesh | |
| 12.11% (@ 37%) | 12.14% (@ 37%) | 12.48% (@ 37%) | |
| 1.26% (@ 75%) | 1.17% (@ 78%) | 1.11% (@ 26%) |
distributions obtained with the baseline design, uniform mesh and adaptive mesh techniques are compared in Figure 54 using the baseline mesh for each one. It can be seen that both test cases reduce the intensity of the shock wave efficiently while the optimal airfoil obtained with the adaptive remeshing technique has a weaker shock wave, when compared to the uniform mesh optimal solution.

|
| Figure 54: distribution obtained from baseline, adaptive mesh and uniform mesh test cases. |
Figures 55a and 55 compare and Mach number contours obtained by the baseline design and the optimal airfoils from the optimization. It can be seen that the strong shock wave on the upper surface of the baseline design is weaker in the optimized airfoil geometry especially in the lower camber (as deduced from Table 6). Therefore, the drag minimization approach has succeeded to decrease the strength of the shock wave on the upper surface of the baseline design.
3.4.3 Multi-Objective Design
Statement of the problem
In this case, a multi-objective transonic airfoil shape design optimization is conducted to improve the transonic aerodynamic characteristics of a NACA 0012 profile especially the lift to drag ratio and lift coefficient . The fitness functions are defined as shown in Equations 72 where and are maximized to extend the aircraft range and to improve its maneuverability, respectively. The optimization has two constraints for geometry (thickness ratio: ) and aerodynamic performance . The geometry constraint is to maintain the fuel tank size of the aircraft and the aerodynamic performance constraint is to keep a flight level at flight conditions of and . This example involves the minimization of two objective functions
|
|
(72) |
subject to
|
|
(73) |
The lift coefficient constant is calculated using Equation 74 which represents the minimum lift coefficient for the aircraft at level flight, as
|
|
(74) |
where is the weight force of the aircraft: mass and acceleration of gravity , is the air density at : , is the wing area: . In this case, the design parameters for the NACA0012 airfoil defined in Section 3.3.2 are used. Twenty design variables for the airfoil design are considered in total.
Numerical results
Two optimization algorithms using the MOGA technique coupled with uniform and adaptive remeshing procedures have run over 50 hours of computer time (150 generations). Figure 56 compares the Pareto front obtained by the baseline design (NACA0012 airfoil), uniform mesh and adaptive remeshing approaches. It can be seen that all Pareto members obtained by both methods dominate the baseline design and the Pareto front obtained by MOGA technique with adaptive remeshing technique has a better convergence when compared to the Pareto front obtained by MOGA coupled with uniform mesh. Also, the use of adaptive remeshing technique speeds up the optimization process while improving the solution accuracy. From the Pareto front obtained by MOGA with adaptive remeshing techniques, the best solutions (Pareto members 1 and 40) for fitness functions 1 and 2, and one of the compromised solutions (Pareto member 25) are selected for further comparisons.
./multi1//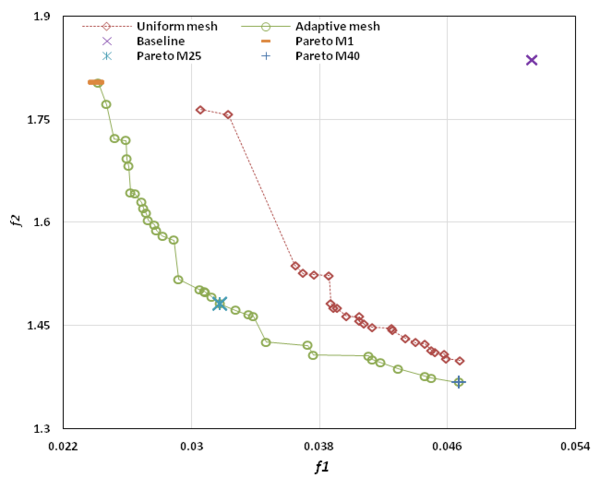
|
| Figure 56: Optimized Pareto fronts after 150 generations and baseline design. |
Table 7 compares the aerodynamic characteristics obtained by the baseline design, Pareto members 1, 25 and 40. The best solution for the fitness function 1 (Pareto member 1) reduces the total drag by 51.97% while improving 112% the lift to drag ratio. The best solution for the fitness function 2 (Pareto member 40) produces 34.01% and 21.46% higher and . The compromised solution (Pareto member 25) produces 23.69% higher and 23.29% lower which results in 61.21% improvement.
| Baseline | 0.5457 | 0.0279 | 19.57 |
| Pareto M1 | 0.5540 (+1.52%) | 0.0134 (-51.97%) | 41.49 (+112.00%) |
| Pareto M25 | 0.6750 (+23.69%) | 0.0214 (-23.29%) | 31.55 ( +61.21%) |
| Pareto M40 | 0.7313 (+34.01%) | 0.0341 (+22.22%) | 21.46 ( +9.66%) |
Figure 57 compares the geometries obtained by the baseline design and Pareto members 1 (the best solution for f1), 25 (compromised solution) and 40 (the best solution for f2). It can be seen that Pareto optimal solutions 1, 25 and 40 have slightly higher camber compared to the baseline design. The geometric characteristics; maximum thickness ration (t/c) and maximum camber, are compared in Table 8. It can be found that there is similarity on the thickness ratio and its position due to the first geometry constraint, while three solutions have different maximum cambers and its positions.

|
| Figure 57: Geometry comparison between the baseline NACA 0012 and optimal airfoils. |
| Baseline | Pareto M1 | Pareto M25 | Pareto M40 | |
| 12.00% (@30%) | 12.03% (@35%) | 12.01% (@ 33%) | 12.08% (@32%) | |
| 0 | 0.86% (@15%) | 0.78% (@67.44%) | 1.11% (@56%) |
Figure 58 compares the pressure coefficient distributions obtained by the baseline design and the compromised solution (Pareto member 25). The same comparison for the contours has been performed in Figures pareto_contoura and pareto_contourb. It can be seen that the shock position on the suction side of airfoil is moved towards the trailing edge when compared to the baseline design while reducing the strength of the shock. It results in improving the values of and by 23.69% and 61.21%, respectively.

|
| Figure 58: distribution obtained from baseline design and compromised solution. |
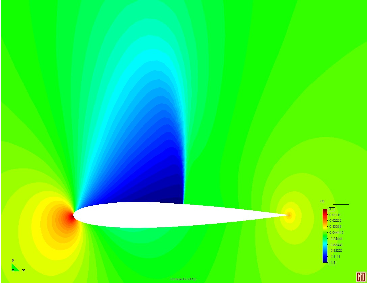
|
![Cₚ contours obtained by the baseline design (a) and compromised solution (b) at Cₚ range of [-1.37:1.20].](/wd/images/4/45/Draft_Content_873167254-pressure_comp.png)
|
| contours obtained by the baseline design (a) and compromised solution (b) at range of . | |
4 Concluding Remarks and Future Work
In this chapter, the conclusions from the current work in this thesis and some recommendations for future work will be presented. They can be divided into two categories: contributions in terms of the stabilized FE formulation aspects and contributions in terms of the aerodynamic shape optimization aspects.
Part I: Development of a Stabilized Formulation For Compressible Flows
Based on the concept of Finite Calculus (FIC), a new algorithm for stabilization of the compressible Euler and Navier-Stokes equations is presented in two-dimensional domains for linear structured/unstructured triangles. Different types of numerical examples have been studied to validate the features of the new methodology for subsonic, transonic and supersonic flows. Some results have been compared to the analytical values, whereas others have been compared to some reference numerical solutions.
The developed FIC-FEM stabilized formulation has led to stable and accurate solutions in regions where the flow has some complexities such as shock wave, boundary layer, stagnation point, etc. It was found that shocks were resolved within four or five elements. Indeed, the boundary layer is captured through an accurate velocity profiles in the boundary layer zone as well as the appropriate pressure coefficient distribution and the skin-friction coefficient distribution along the boundary.
For inviscid flows, error estimation and adaptive mesh refinement have improved the relation cost and accuracy, especially for the flows with shocks. In the case of viscous flows, the formulation has worked well using structured elements with maximum aspect ratio about , except in the zone of singularity where the formulation is not able to control the temperature causing a increase in the Mach number, locally.
For future work, we intend to enhance the accuracy of the proposed formulation for estimating the temperature inside the elements with high aspect ratio. Consideration of the turbulence inside the governing equations can advance the methodology for solving more realistic flow problems. The extension of the current formulation to three-dimensional domains is another target of the future developments in the research.
Part II: Aerodynamic Shape Optimization Using Adaptive Remeshing
In the second part of the thesis, a methodology coupling the MOGA and an adaptive remeshing technique has been developed and has been implemented for three practical aerodynamic shape optimization problems in a single- and multi-objective manner. From numerical studies, both the MOGA technique coupled to uniform mesh and adaptive remeshing approaches have been validated through reconstruction/inverse test case and implemented to solve two complex aerodynamic shape design optimizations, namely, drag minimization and multi-objective shape design. It is noticed that despite using the same MOGA technique and CFD analyzer, the use of adaptive remeshing approach accelerates the optimization process while increasing the solution accuracy when compared to the solution using a uniform mesh technique.
Future works will focus on implementation of the adaptive remeshing technique in a multi-point design optimization considering uncertain design parameters (robust/uncertainty). Also, by implementing gradient-based optimization methodologies, the capability of the adjoint method for predicting sensitivities of the objective function can be studied. Indeed, the development of the current method for three-dimensional optimization test cases will improve the generalization of this optimization framework.
BIBLIOGRAPHY
[1] C. Hirsch. Numerical Computation of Internal and External Flow, vol. 1. J. Wiley, 1988 (vol. 2, 1990)
[2] Lohner, R.. Mesh adaptation in fluid mechanics, Volume 50(5/6). Engineering Fracture Mechanics 819–847, 1995
[3] H. Lomax and T. H. Pulliam and D. W. Zingg. Fundamentals of Computational Fluid Dynamics. Springer-Verlag, 2001
[4] G. Volpe and R. E. Melnik. The design of transonic airfoils by a wellposed inverse method, Volume 22. International Journal for Numerical Methods in Engineering 341–361, 1984
[5] J. Periaux and D.S. Lee and L.F. Gonzalez and K. Srinivas. Fast Reconstruction of Aerodynamic Shapes using Evolutionary Algorithms and Virtual Nash Strategies in a CFD Design Environment, Volume 232. Journal of Computational and Applied Mathematics 61–67, 2009
[6] Obayashi, S. and Oyama, A.. Three- Dimensional Aerodynamic Optimization with Genetic Algorithms 420–424, 1996
[7] Holst, T. L. and Pulliam, T. H.. Aerodynamic Shape Optimization Using a Real- Number-Encoded Genetic Algorithm, 2001
[8] Bugeda, G. and Oñate, E.. Optimum aerodynamic shape design including mesh adaptivity, Volume 20. International Journal for Numerical Methods in Fluids 915–934, 1995
[9] Bugeda, G. and Oñate, E.. Optimum aerodynamic shape design for fluid flow problems including mesh adaptivity, Volume 30. International Journal for Numerical Methods in Fluids 161–178, 1998
[10] Von Neumann and J. and R. D. Richtmyer. A method for the numerical calculation of hydrodynamic shocks, Volume 21. J. Appl. Phys 232-237, 1950
[11] Courant, R. and Isaacson, E.. On the solution of nonlinear hyperbolic differential equations by finite differences, Volume 5. Comm. Pure and Applied Mathematics 243-255, 1952
[12] P.D. Lax. Weak solutions of non-linear hyperbolic equations and their numerical approximations, Volume 7. Communications on Pure and Applied Mathematics 159-193, 1954
[13] Godunov, S. K.. A difference scheme for numerical computation of discontinuous solution of hydrodynamic equations, Volume 47. Matematicheskii Sbornik 271-306, 1959
[14] Engquist, B. and Osher, S.. Stable and entropy satisfying approximations for transonic flow calculations, Volume 34. Mathematics of Computation 45-75, 1980
[15] Roe, P. L.. The use of the Riemann problem in finite differenceschemes, Volume 141. Lecture Notes in Physics 354-359, 1981
[16] Roe, P. L.. Approximate Riemann solvers, parameter vectors and difference schemes, Volume 43. Journal Computational Physics 357-372, 1981
[17] Osher, S.. Shock modelling in aeronautics. In, K. W. Morton and M. J. Baines(eds), NumericalMethodsfor Fluid Dynamics, London: AcademicPress 179-218, 1982
[18] Lax, P. D. and and Wendroff, B.. Difference schemes for hyperbolic equations with high order of accuracy, Volume 17. Comm. Pure and Applied Mathematics 381-398, 1964
[19] R.W. MacCormack. The effect of viscosity in hypervelocity impact cratering. AIAA paper 69-0354, April-May, 1969
[20] Lerat, A. and Peyret, R.. Non centered schemes and shock propagation problems, Volume 2. Computers and Fluids 35-52, 1969
[21] A. Jameson and W. Schmidt and E. Turkel. Numerical solution of the Euler equations by finite volume methods using Runge-Kutta time stepping schemes, Volume 81-1259. AIAA paper, June 1981
[22] W.K. Anderson and J.L. Thomas and B. Van Leer. Comparison of finite volume flux vector splittings for the Euler equations, Volume 24 (9). AIAA Journal 1453-1460, 1986
[23] T.J.R. Hughes and T.E. Tezduyar. Finite element methods for first-order hyperbolic systems with particular emphasis on the compressible Euler equations, Volume 45. Comput. Methods Appl. Mech. Engrg 217-284, 1984
[24] A.N. Brooks and T.J.R. Hughes. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations, Volume 32. Comput. Methods Appl. Mech. Engrg 199-259, 1982
[25] T.J.R. Hughes and L.P. Franca and M. Mallet. A new finite element formulation for computational fluid dynamics: VI. Convergence analysis of the generalized SUPG formulation for linear time-dependent multi-dimensional advective-diffusive systems, Volume 63. Comput. Methods Appl. Mech. Engrg 97-112, 1987
[26] G.J. Le Beau, T.E. Tezduyar. Finite element computation of compressible flows with the SUPG formulation, Volume 123. in: Advances in Finite Element Analysis in Fluid Dynamics, ASME, New York 21-27, 1991
[27] S. Mittal and T. Tezduyar. A unified finite element formulation for compressible and incompressible flows using augmented conservation variables, Volume 161. Comput. Methods Appl. Mech. Engrg 229-243, 1998
[28] J. Donea. A Taylor-Galerkin method for convective transport problems, Volume 20. Int. J. Numer. Methods Engrg 101-120, 1984
[29] F. Chalot and T.J.R. Hughes. A consistent equilibrium chemistry algorithm for hypersonic flows, Volume 112. Comput. Methods Appl. Mech. Engrg 25-40, 1994
[30] F. Shakib and T.J.R. Hughes and Z. Johan. A new finite element formulation for computational fluid dynamics: X. The compressible Euler and Navier-Stokes equations, Volume 89. Comput. Methods Appl. Mech. Engrg 141-219, 1991
[31] G. Hauke and T.J.R. Hughes. A unified approach to compressible and incompressible flows, Volume 113. Comput. Methods Appl. Mech. Engrg 389-395, 1994
[32] J. Peraire and J. Peiro and L. Formaggia and K. Morgan and O.C. Zienkiewicz. Finite element Euler computations in three dimensions, Volume 26. Int. J. Numer. Methods Eng. 2135-2159, 1988
[33] K. Morgan and J. Peraire and J. Peiro and O.C. Zienkiewicz. ‘Adaptive remeshing applied to the solution of a shock interaction problem on a cylindrical leading edge. in P. Stow (ed.), Computational Methods in Aeronautical Fluid Dynamics, Clarenden Press, Oxford 327-344, 1990
[34] O.C. Zienkiewicz and J. Wu. A general explicit of semi-explicit algorithm for compressible and incompressible flows, Volume 35. Int. J. Numer. Methods Eng. 457-479, 1992
[35] A. J. Chorin. Numerical solution of the Navier Stokes equations, Volume 22. Math. Comput. 745-762, 1968
[36] A. J. Chorin. Sur l'approximation de la solution des equations de Navier-Stokes par la methode des pas fractionaires (I), Volume 32. Arch. Rat. Mech. Anal. 135-153, 1969
[37] O.C. Zienkiewicz and R. Codina. A general algorithm for compressible and incompressible flow. Part I. The split characteristic based scheme, Volume 20. Int. J. Numer. Methods Fluids. 869-885, 1995
[38] O.C. Zienkiewicz and B.V.K. Satya Sai and K. Morgan and R. Codina and M. Vazquez. A general algorithm for compressible and incompressible flow. Part II. Tests on the explicit form, Volume 20. Int. J. Numer. Methods Fluids. 887-913, 1995
[39] R. Codina. A discontinuity-capturing crosswind-dissipation for the finite element solution of the convection diffusion equation, Volume 110. Comput. Methods Appl. Mech. Eng 325-342, 1993
[40] R. Codina and M. Vasquez and O.C. Zienkiewicz. A general algorithm for compressible and incompressible flow. Part III: The semi-implicit form, Volume 27. Int. J. Numer. Methods Fluids. 13-32, 1998
[41] Van Leer, B.. Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme, Volume 14(4). J. Comput. Phys. 361-370, 1974
[42] Van Leer, B.. Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow, Volume 23 (3). J. Comput. Phys. 263-275, 1977
[43] LeVeque, R. J.. Numerical methods for conservation laws (Second ed.). Birkhauser, 1992
[44] Boris, J. P. and Book, D. L.. Flux corrected transport I. SHASTA, a fluid transport algorithm that works, Volume 11. J. Comput. Phys. 38-69, 1973
[45] A. Harten. High resolution schemes for hyperbolic conservation laws, Volume 49. J. Comput. Phys. 357-393, 1983
[46] Zalesak, S.T.. Fully Multidimensional Flux-Corrected Transport Algorithm for Fluids, Volume 31. J. Comput. Phys. 335-362, 1979
[47] Parrott, A. K. and Christie, M. K.. FCT applied to the 2D finite element solution of tracer transport by single phase flow in a porous medium. Numerical Methods for Fluid Dynamics, Oxford: Oxford University Press 27-53, 1986
[48] R. Lohner and K. Morgan and J. Peraire and M. Vahdati. Finite element flux-corrected transport (FEM-FCT) for the Euler and Navier-Stokes equations, Volume 7. Int. J. Num. Methods Fluids 103-109, 1987
[49] H. Luo and J. D. Baum and R. Lohner and J. Cabello. Adaptive Edge-Based Finite Element Schemes for the Euler and Navier-Stokes Equations. AIAA-93-0336, 1993
[50] R. Sanders. On convergence of monotone finite difference schemes with variable spatial differencing, Volume 40. Math. Comp. 91-106, 1983
[51] Jameson, A. and Lax, P.D.. Conditions for the Construction of Multi-Point Total Variation Diminishing Difference Schemes. MAE Report 1650, Dept . of Mechanical and Aerospace Engineering, Princeton University, 1984
[52] Davis, S.F.. TVD Finite Difference Schemes and Artificial Viscosity. ICASE Report No. 84-20, 1984
[53] Yee, H.C.. Construction of Implicit and Explicit Symmetric T V D Schemes and Their Applications, Volume 68. J. Comput. Phys. 151-179, 1987
[54] Yee, H.C. and Kutler, P.. Application of Second-Order Accurate Total Variation Diminishing (TVD) Schemes to the Euler Equations in General geometries. NASA TM-85845, 1983
[55] Aftosmis, M. and N. Kroll. A Quadrilateral Based Second-Order TVD Method for Unstructured Adaptive Meshes. AIAA-91-0124, 1991
[56] P. R. M. Lyra1 and K. Morgan1 and J. Peraire and J. Peiró. TVD algorithms for the solution of the compressible Euler equations on unstructured meshes, Volume 19(9). Int. J. Numer. Methods Flu. 827-847, 1994
[57] D. Kuzmin and S. Turek. High-resolution FEM-TVD schemes based on a fully multidimensional flux limiter, Volume 198. J. Comput. Phys. 131-158, 2004
[58] Lighthill, M. J.. A new method of two-dimensional aerodynamic design. Aeronautical Research Council, 1945
[59] Liebeck, R. H.. A class of airfoils designed for high lift in incompressible flow, Volume 10. Journal of Aircraft 610–617, 1973
[60] Giles, M. B. and Drela, M.. Two-dimensional transonic aerodynamic design method, Volume 25. AIAA Journal 1199–1206, 1987
[61] I. Fejtek and D. Jones and G. Waller and E. Hansen and S. Obayashi. A transonic wing inverse design capability for complete aircraft configurations, 2001
[62] Hicks, R. M. and Henne, P. A.. Wing design by numerical optimization, Volume 15(7). Journal of Aircraft 407–412, 1977
[63] Jameson, A.. Aerodynamic design via control theory, Volume 3. Journal of Scientific Computing 233–260, 1988
[64] Jameson, A.. Computational aerodynamics for aircraft design, Volume 245. Science 361–371, 1989
[65] Jameson, A.. Automatic design of transonic airfoils to reduce the shock induced pressure drag 5–17, 1990
[66] A. Jameson and L. Martinelli and N. Pierce. Optimum aerodynamic design using the navier-stokes equations, 1997
[67] Reuther, J. and Jameson, A.. Aerodynamic shape optimization of wing and wing body configurations using control theory, 1995
[68] J. Reuther and A. Jameson and J. J. Alonso and M. J. Rimlinger and D. Saunders. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, 1997
[69] Burgreen, G. W. and Baysal, O.. Three-dimensional aerodynamic shape optimization of wings using sensitivity analysis, 1994
[70] R. Löhner, O. Soto and Chi Yang. An Adjoint-Based Design Methodology for CFD Optimization Problems. AIAA-03-0299, 2003
[71] O. Soto and R. Lohner. CFD Optimization Using an Incomplete-Gradient Adjoint Approach. AIAA-00-0666, 2000
[72] K. Miettinen and M. M. Makela and P. Neittaanmaki and J. Periaux. Evolutionary Algorithms in Engineering and Computer Science. John Willey and Sons Ltd, 1999
[73] Quagliarella, D. and Cioppa, A. D.. Genetic Algorithms applied to the Aerodynamic Design of Transonic Airfoils 686–693, 1994
[74] Yamamoto, K. and Inoue, O.. Applications of Genetic Algorithm to Aerodynamic Shape Optimization 43–51, 1995
[75] Cao, H. V. and Blom, G. A.. Navier-Stokes/Genetic Optimization of Multi-Element Airfoils, 1996
[76] Oyama, A. and Obayashi, S. and Nakahashi, K. and Nakamura, T.. Euler/Navier-Stokes Optimization of Supersonic Wing Design Based on Evolutionary Algorithm, Volume 37(10). AIAA Journal 1327–1329, 1999
[77] N. K. Burgess and D. J. Mavriplis. An hp-adaptive discontinuous galerkin solver for aerodynamic flows on mixed-element meshes. In Proceeding of the 49th Aerospace Sciences Meeting, Orlando, FL, Jan 2011. AIAA Paper 2011-490, 2011
[78] Mani, K. and Mavriplis, D. J.. “Unsteady Discrete Adjoint Formulation for Two-Dimensional Flow Problems with Deforming Meshes, Volume 46-6. AIAA Journal 1351–1364, 2008
[79] D. J. Mavriplis. Adaptive Meshing Techniques for Viscous Flow Calculations on Mixed Element Unstructured Meshes, Volume 34(2). International Journal for Numerical Methods in Fluids 93–111, 2000
[80] Palmerio, B. and A. Dervieux. Application of a FEM Moving Node Adaptive Method to Accurate Shock Capturing. First Int. Conf. on Numerical Grid Generation in CFD, Landshut, W. Germany, July 14–17, 1986
[81] D.J. Mavriplis. Adaptive mesh generation for viscous flows using delaunay triangulation, Volume 90. Journal of Computational Physics 271–291, 1990
[82] Mavriplis, D.J.. Turbulent Flow Calculations Using Unstructured and Adaptive Meshes, Volume 13. Int. J. Num. Meth. Fluids 1131–1152, 2008
[83] Schönauer, W. K.. The Principle of Difference Quotients as a Key to the Self-Adaptive Solution of Nonlinear Partial Differential Equations, Volume 28. Comp. Meth. Appl. Mech. Eng. 327–359, 1981
[84] K. J. Fidkowski and D. L. Darmofal. A triangular cut-cell adaptive method for high-order discretizations of the compressible Navier-Stokes equations, Volume 225(2). Journal of Computational Physics 1653–1672, 2007
[85] L. Wang and D. J. Mavriplis. Adjoint Based h-p Adaptive Discontinuous Galerkin Methods for Aerospace Applications, 2009
[86] J. V. Rosendale. Floating Shock Fitting via Lagrangian Adaptive Meshes. ICASE Report, No. 94-89, 1994
[87] D. Vendetti and D. Darmofal. Grid Adaptation for Functional Outputs: Application to Two-Dimensional Inviscid Flows, Volume 176. Journal of Computational Physics 40–69, 2002
[88] D. Vendetti and D. Darmofal. Anisotropic grid adaptation for functional outputs: application to two-dimensional viscous flows, Volume 187. Journal of Computational Physics 22–46, 2003
[89] R. Lohner. An adaptive finite element solver for transient problems with moving bodies, Volume 30. Comput. and Structures 303–317, 1988
[90] Oñate, E.. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems, Volume 151. Comput. Meth. Appl. Mech. Engng. 233–267, 1998
[91] Oñate, E.. Possibilities of finite calculus in computational mechanics, Volume 60. Int. J. Num. Meth. Engng 255-281, 2004
[92] E. Turkel. Improving the Accuracy of Central Difference Schemes. ICASE Report 8853, 1988
[93] R. Lohner. Three-dimensional grid generation by the advancing front method, Volume 8. International Journal for Numerical Methods in Fluids 1135–1149, 1988
[94] R. Lohner and J. D. Baum. Adaptive H-refinement on 3-D unstructured grids for transient problems, Volume 14(12). International Journal for Numerical Methods in Fluids 1407–1419, 1992
[95] J. Peraire and M. Vahdati and K. Morgan and O. C. Zienkiewicz. Adaptive remeshing for compressible flow computations, Volume 72. Journal of Computational Physics 449–466, 1987
[96] J. Peraire and K. Morgan and J. Peiro. Unstructured finite element mesh generation and adaptive procedures for CFD. AGARD-CP-464, 1990
[97] T. J. Baker. Developments and trends in three-dimensional mesh generation, Volume 5. Applied Numerical Mathematics 275–304, 1989
[98] M. A. Yerry and M. S. Shepard. Automatic three-dimensional mesh generation by the modified-octree technique, Volume 20. International Journal for Numerical Methods in Engineering 1965–1990, 1984
[99] M. S. Shepard and M. K. Georges. Automatic three-dimensional mesh generation by the finite octree technique, Volume 32. International Journal for Numerical Methods in Engineering 709–749, 1991
[100] T. H. Pulliam and J. T. Barton. Euler Computations of AGARD Working Group 07 Airfoil Test Cases. AIAA Paper 85-0018, AIAA 23rd Aerospace Sciences Meeting, Nev. 1985
[101] J. Peraire, K. Morgan, and J. Peiro. Unstructured mesh methods for CFD. Technical Report 90–04, Imperial College Aeronautics Department, 1990
[102] O. Hassan. Finite Element Computation of High Speed Viscous Compressible Flows. PhD Thesis, University of Wales Swansea, 1990
[103] D. J. Mavriplis, A. Jameson and L. Martinelli. Multigrid Solution of the Navier-Stokes Equations on Triangular Meshes. ICASE Rep. No. 89-11, February 1989
[104] J.E. Carter. Numerical solutions of the Navier-Stokes equations for the supersonic laminar flow over a two-dimensional compression corner, Volume TR R-385. NASA Technical Report, 1972
[105] F. Shakib. Finite element analysis of the compressible Euler and Navier-Stokes equations. PhD thesis, Department of Mechanical Engineering, Stanford University, 1988
[106] C.M. Hung and R.W. MacCormack. Numerical solutions of supersonic and hypersonic laminar compression corner flows, Volume 14 (4). AIAA J. 475-481, 1976
[107] R. Flores and E. Ortega and E. Oñate. PUMI: an explicit 3D unstructured finite element solver for the Euler equations. Publication CIMNE, PI 326, 2008
[108] D. S. Lee, J. Periaux, E. Onate and L. F. Gonzalez. Advanced Computational Intelligence System for Inverse Aeronautical Design Optimization. International Conference on Advanced Software Engineering (ICASE-11), Proceedings of the 9th IEEE International Symposium on Parallel and Distributed Processing with Applications Workshops, ISPAW 2011 - ICASE 2011, SGH 2011, GSDP 2011, pp. 299-304, ISBN (978-1-4577-0524-3), DOI (10.1109/ISPAW.2011.46), Busan, Korea, 26-28 May, 2011
[109] D. S. Lee, G. Bugeda, J. Periaux and E. Onate. Robust Active Shock Control Bump Design Optimization using Parallel Hybrid-MOGA. The 23rd International Conference on Parallel Computational Fluid Dynamics 211, Barcelona, Spain, 16-20 May, 2011
[110] D. S. Lee, C. Morillo, G. Bugeda, S. Oller, E. Onate. Multilayered Composite Structure Design Optimization using Distributed/Parallel Multi-Objective Evolutionary Algorithms, Volume 94(3). Journal of Composite Structures 1087-1096, 2012
[111] A. Jameson. The Evolution of Computational Methods in Aerodynamics, Volume 50. Journal of Applied Mathematics 1052–1070, 1983
[112] A. Jameson. Positive schemes and shock modeling for compressible flows, Volume 20. International Journal for Numerical Methods in Fluids 743–776, 1995
[113] C. Darwin. On the origin of species by means of natural selection. John Murray, 1859
[114] J. H. Holland. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. University of Michigan Press, 1975
[115] N. Marco and S. Lanteri. A Two-Level Parallelization Strategy for Genetic Algorithms Applied to Shape Optimum Design. INRIA Research Report, No. 3463, 1998
[116] N. Marco and J.A. Desideri. Numerical solution of optimization test-case by Genetic Algorithms. INRIA Research Report, No. 3622, 1999
[117] Goldberg D.E.. Genetic Algorithm in Search, Optimization and Machine Learning. Addison-Wesley, 1989
[118] K. Deb, A. Pratap, S. Agrawal and T. Meyarivan. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II, Volume 6 (2). IEEE Transactions on Evolutionary Computation 182–197, 2002
[119] I.D. Faux and M.J. Pratt. Computational Geometry for Design and Manufacture. Ellis Horwood Limited, 1887
Document information
Published on 01/01/2013
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?


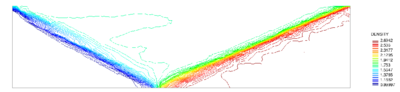
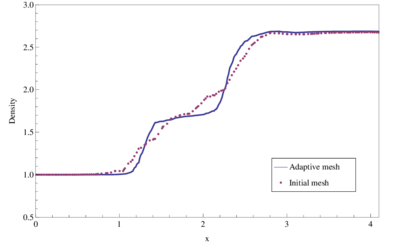



![Cₚ contours around target airfoil (a), uniform mesh test case (b) and adaptive mesh test case (c) in Cₚ range of [-1.21:1.19].](/wd/images/thumb/7/7f/Draft_Content_873167254-pressure_ada.png/400px-Draft_Content_873167254-pressure_ada.png)
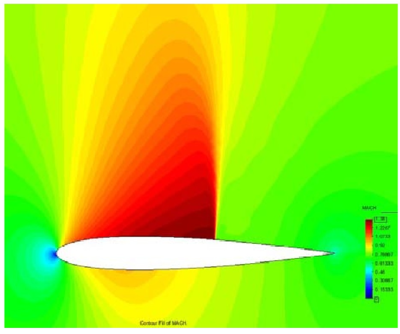
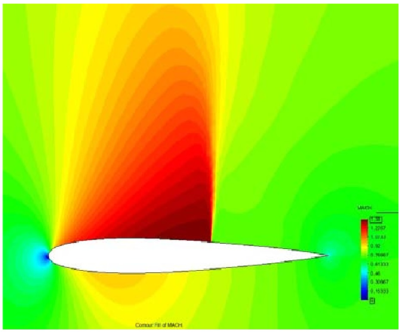
![Mach number contours around target airfoil (a), uniform mesh test case (b) and adaptive mesh test case (c) in Mach range of [0.0:1.38].](/wd/images/thumb/a/ad/Draft_Content_873167254-mach_ada.png/400px-Draft_Content_873167254-mach_ada.png)