Abstract
The main influencing parameter on the efficiency of adsorptive thermochemical energy storage is the efficiency of the desorption process, which is influenced by the process conditions, for example, desorption time and desorption temperature, and the working pair (adsorbent–adsorbate). Due to constrained process requirements, for example, hours of sun shine and low desorption temperatures available from a flat plate solar collector (333–373 K), the only possibility to increase the efficiency is to change the working pair. The reference working pair water–zeolite 13X needs high desorption temperatures of 500 K and high heat inputs per mass adsorbent (1080 kJ kg−1) in the desorption process to reach the maximum efficiency of 79 % and maximum energy density of 844 kJ kg−1. Therefore, the goal is to reach efficiencies in the same range as the maximum efficiency of water–zeolite 13X for desorption temperatures lower than 500 K with the usage of different adsorbates. Four systems of alcohol as adsorbate on activated carbon are compared with the reference working pair. The usage of alcohols on activated carbon allows for highly efficient adsorptive storage even at low desorption temperatures between 360 and 450 K. The maximum efficiency is shifted to higher desorption temperatures with increasing carbon chain length of the alcohol. At low desorption temperatures, the energy density and efficiency of methanol, ethanol, and propanol are higher than the energy density of the reference system. Hence, the alcohol systems on activated carbon are viable alternative approaches for regulating these process parameters.
Introduction
Thermal energy storage can be divided in three main categories: the storage of sensible heat, latent heat, and thermochemical heat [1]. Thermochemical heat storage is divided into storage by adsorption and storage by reaction [2]. In this work, the focus lies on the thermochemical adsorptive heat storage, which follows the mechanism shown in Scheme 1, where two components A (adsorbent) and B (adsorbate) either interact physically or react chemically [3]. The interaction or reaction of the surface A and the adsorbate B to the adsorbed species AB is exothermic and therefore releases heat which can be utilized. If energy in form of heat has to be stored, the endothermic reverse process of AB to A and B is performed.
|
|
|
Scheme 1. Reaction/interaction system of a thermochemical adsorption energy storage process. |
All examined adsorption systems in this work follow the mechanism of physisorption only. The energy is stored through the enthalpy of adsorption, which results from attractive forces between the adsorbate and the adsorbent (plus contributions from interactions between molecules of the adsorbate). Under the assumption of an adiabatic adsorbent fixed bed, the only loss in the process is the sensible heat, which is needed to heat the adsorbent in the adsorption and desorption process. This loss is mainly effected by the isobaric heat capacity of the adsorbent. The operation of an adsorptive energy storage system is shown in Scheme 2. If energy, in this case heat, is needed, a gas stream which is saturated with the adsorbate flows through the adsorber (A). The adsorption of the adsorbate releases heat, which heats the gas stream. The hot and dry gas stream at the outlet can then be used directly or the heat can be transferred via a heat exchanger. The process of adsorption can be considered as the discharging of the energy storage. If heat is available for regeneration, a hot gas stream flows through the loaded adsorber (B). The gas stream is cooled by the desorption, which can be considered as the loading process of the storage [2].
|
|
|
Scheme 2. Flow scheme of the adsorption (A) and the desorption (B) in the adsorptive energy storage process. |
The efficiency of the energy storage is influenced by a number of factors, for example, the isobaric heat capacity of the materials involved (i.e. primarily adsorbent and adsorbate) and the heat of adsorption. However, as shown in our previous work, the most important factor for a high efficiency is the efficiency of the desorption process. This implies an adsorption characteristic (isotherm) that allows for more complete desorption at the same desorption conditions. This can be achieved by a steeper rise of bed loading at lower partial pressure ratios. The higher desorption efficiency results in a higher amount of heat that can be released in the following adsorption and therefore high efficiencies and high energy densities of the overall process. The efficiency is defined as the ratio of the heat released in the adsorption process to the heat needed in the desorption step. The energy density is defined as the heat released in the adsorption process per mass of the adsorbent.
Desorption is mainly affected by the desorption temperature, the desorption time, and the working pair (adsorbate–adsorbent). As desorption time and temperature are process parameters that are determined by the respective application, the only parameter that can be changed to achieve higher efficiencies is the working pair. Much previous work conducted focused on using alternative adsorbents in order to achieve higher energy densities [4-6]. However, the efficiency of the desorption, which can only be optimized with the change of the isotherm, is rarely considered. The variety of commonly used adsorbent classes for adsorptive energy storage systems is limited. Mostly used are activated carbon, zeolite, and silica gel [5]. New potential adsorbent materials include SAPO and ALPO [7] as well as MOFs (metal organic frameworks) like MIL-101, which net high water uptakes [4, 8]. Although these adsorbents have potential for thermochemical energy storage, most of them have only been used in laboratory scale or are implemented in systems that are just starting in market deployment [4]. A working pair that is highly studied and already used in commercial adsorption heating systems is water on zeolite 13X [5, 9]. This adsorption pair is for example implemented in a building heating system in Munich [10] Furthermore, the cycle stability of the working pair is known [11]. Therefore, this working pair is used as the reference adsorption pair in this work.
However, the progression of the isotherm is influenced by the adsorbent and the adsorbate. In order to have a higher variability to find the ideal isotherm for each desorption temperature and time (i.e., corresponding to specific heat power), the focus has to lie on the change in the adsorbate. For example, the usage of methanol instead of water on zeolite 13X leads to higher efficiencies in the desorption process at 120 °C and 6-h desorption, which is equal to a heat input of 562 kJ kg−1. In comparison with other parameters that influence the efficiency like the heat of adsorption or the isobaric heat capacities of the adsorbent and the adsorbate, an isotherm, which shows a steep rise in bed loading at lower partial pressure ratio, increases the efficiency of the whole process by far the most. That result indicates that the influence of the adsorbate on the efficiency of the process is significant. There is some literature about the usage of different adsorbates in adsorption heating and cooling applications. The most commonly used adsorbates are water, ammonia, methanol, and ethanol [12-15]. However, to the best of our knowledge, a systematic way to analyze the effect of different adsorbates on the efficiency and the energy density is not presented in any of the published work investigated.
In this work, the process of adsorptive energy storage is modeled in a detailed one-dimensional simulation. Afterwards, the two key performance indices efficiency and energy density are calculated. Methanol and ethanol are already mentioned in literature as potential adsorbates on the adsorbent activated carbon. Therefore, the first four members of the homologous series of alcohols (methanol, ethanol, propanol, butanol) on BPL activated carbon are used for a systematic evaluation of the influence of the adsorbate on efficiency and energy density. The efficiencies and energy densities of these systems are then compared to the reference system water on zeolite 13X.
Modeling Section
The process has been modeled using the software MATLAB® in the Version 8.3 (R2014a). All partial differential equations are solved by discretization of the process into several time and length steps. The time step was set to 0.01 sec and length step to 0.1 m. The mass balance of the adsorbate and of the adsorbent are calculated using equations (1) and (2). In this model, no dispersion terms are considered as they do not influence the efficiency and the energy density in the way calculated in this work. The dispersion would only change the differential temperature levels at different time steps, but does not have an influence on the integral heat balance. Furthermore, Simo et al. [16] stated that dispersion can be neglected in large-scale adsorbent fixed beds. We validated this by calculating Bodenstein number, which is 800 for the modeled process. The released and needed heats of adsorption and desorption are proportional to the temperature difference between the inlet and outlet gas stream over the whole process duration (eq. (10)).
|
|
(1) |
|
|
(2) |
εG and εS stand for the gas and solid volume fractions of the adsorbent bed, respectively. ρG and ρS stand for the density of the gas phase and of the adsorbent, respectively. describes the mass flow of the gas phase and qG, and qS stand for the gas and bed loading, respectively. The mass exchange between the gas and the adsorbent was calculated with the linear driving force (LDF) approximation (eq. (3)) [17].
|
|
(3) |
In equation (3), β stands for the mass transfer coefficient, which was calculated with the correlation by Kast [18] (eq. (4)). In equation (4), αGS stands for the heat transfer coefficient and cP,G for the isobaric heat capacity of the gas phase.
|
|
(4) |
aS describes the specific surface area of the adsorbent. The theoretical gas loading qG,theoretical at each temperature and bed loading, which is needed for the LDF, was calculated with the potential theory of adsorption by Polányi [19]. qG,theoretical equals the gas loading at equilibrium. In this model, the isotherms are transformed to a temperature independent form called the “characteristic curve of adsorption.” The gas loading is transformed to change in free energy ∆F and the bed loading to the adsorption volume W. The progression of the curve is described with the equation by Dubinin and Astakhov (eq. (5)) [20]. The parameters W0 (saturation adsorption volume), E (adsorption energy), and n (empirical parameter) were fitted to the characteristic curves of adsorption calculated from the isotherm data taken from literature at different temperatures for the examined adsorption systems.
The fundamentals of the adsorption model and of the characteristic curve of adsorption can be taken from Polányi [19] and Dubinin [21]. The energy balances for the adsorbate and the adsorbent are given in equations (6) and (7).
|
|
(5) |
|
|
(6) |
|
|
(7) |
In equations (6) and (7), TG and TS are the temperatures of the gas stream and of the adsorbent, respectively. cP,mix,G and cP,mix,S are the mixed isobaric heat capacities of the gas phase and the solid phase, which were calculated from the heat capacity of the carrier gas or the adsorbent and the heat capacity of the adsorbate in the gas phase or adsorbed on the adsorbent. The heat transfer coefficient αGS was estimated using a Nusselt correlation for the flown through pebble bed (eq. (8)). [11]
|
|
(8) |
In equation (8), λG is the thermal conductivity of the gas phase and dP the diameter of the adsorbent. The enthalpy of adsorption hads depends on the temperature and on the bed loading [22]. The calculation was performed with the equation proposed by Bering et al. [23] where α’ is the expansion coefficient of the adsorbate and ∆hLV the enthalpy of vaporization (eq. (9)).
|
|
(9) |
Examined Adsorption Systems and Process Evaluation Criteria
In this study, five adsorption systems were examined. The reference working pair zeolite 13X–water was compared to four systems of alcohols on activated carbon. The experimental data for the adsorption of water on zeolite 13X contains five adsorption isotherms measured up to the normal boiling point of water (0°C, 25°C, 50°C, 75°C, 100°C) [24]. The data sets for alcohols on BPL activated carbon contain adsorption isotherms at four temperatures (25°C, 50°C, 75°C, 100°C) [25] for methanol, ethanol, propanol, and butanol on BPL activated carbon. All material data needed for the simulation are published in the Appendix. In order to evaluate the process, two main evaluation criteria were chosen. First, the efficiency of the adsorption/desorption process is studied (eq. (10)). In equation (10), Tgas,in and Tgas,out stand for the temperature of the gas stream entering and leaving the adsorber.
|
|
(10) |
As described above, the efficiencies contain the heating of the adsorbent as well as a nonconstant adsorption enthalpy. Furthermore, the heat transport between the adsorbent and the gas phase is taken into account. No peripheral plant components, for example, pumps and compressors and no heat losses over the wall of the adsorber are considered. As the heat capacity of the gas stream in the investigated temperature range only changes from 1038 kJ kg−1 K−1 (298 K) to 1065 kJ kg−1 K−1(500 K), it is considered independent from temperature. The process parameters of the simulation are shown in Table 1. These parameters are very close to an existing sorption energy storage system, which heats a school building in the city of Munich.
| Parameter | Value |
|---|---|
| Volume flow gas | 6000 m3 h−1 |
| Volume adsorber | 3.5 m3 |
| Length adsorber | 2 m |
| Carrier gas | Nitrogen |
| Dew point adsorption | 298.15 K |
| Particle diameter adsorbent | 2 mm |
Another important parameter for the evaluation of thermochemical energy storages is the energy density ρQm, which is calculated for each adsorption system (eq. (11)). In equation (11), the released heat Qads is related to the mass of the adsorbent in the adsorber madsorbent.
|
|
(11) |
Results and Discussion
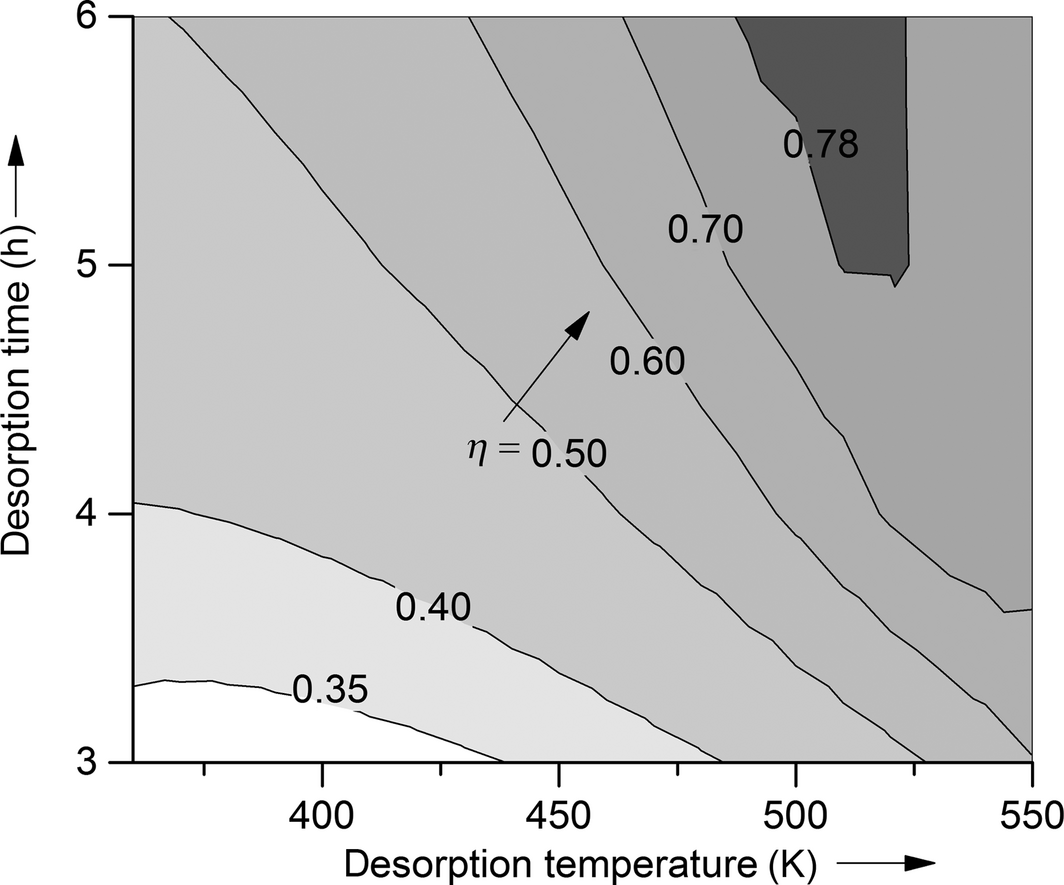
For reasons of comparison, the efficiencies and energy densities of the reference system water on zeolite 13X as a function of desorption temperature and time are presented first. Normally other adsorbates than water cannot be used in open adsorption energy storage systems. However, most literature data on energy densities and efficiencies for adsorption energy storage systems which are available on the market are published for open storage systems. In order to be able to compare the presented results with experimental values, the calculations are performed for an open storage system. All results shown in this work are valid for the process parameters and adsorber dimensions shown in Table 1, but the overall trend of the calculated efficiencies and energy densities can be transformed to other process parameters via the given specific heat inputs per mass adsorbent. Figure 1 shows the efficiency plotted against desorption time (for the range between 3 and 6 h) and desorption temperature (for the range between 340 K and 550 K). The efficiency of the process rises with rising desorption time and desorption temperature until the maximum efficiency is reached, when complete desorption is achieved. With rising desorption time, which equals the charging time of the energy storage, more adsorbate desorbs from the adsorbent as the thermal energy is introduced longer into the adsorbent. With rising desorption temperature (e.g., charging temperature), the driving force of the desorption rises. Therefore, more adsorbate is desorbed in the same desorption time. A first look at the efficiencies in Figure 1 shows that for desorption times below 4 h, even desorption temperatures of 550 K are not sufficient for total desorption. The maximum possible efficiency for the system water–zeolite 13X for a 3-h desorption (specific heat input of 1014 kJ kg−1) is only 59%. In comparison with the desorption time of 3 h, the bed loading of zero can be reached within the shown temperature range for desorption times of 4, 5, and 6 h, which equal specific heat inputs of more than 1080 kJ kg−1.
|
|
|
Figure 1. Efficiency of the adsorption system water–zeolite 13X for desorption temperatures between 340 and 550 K and desorption times between 3 and 6 h. |
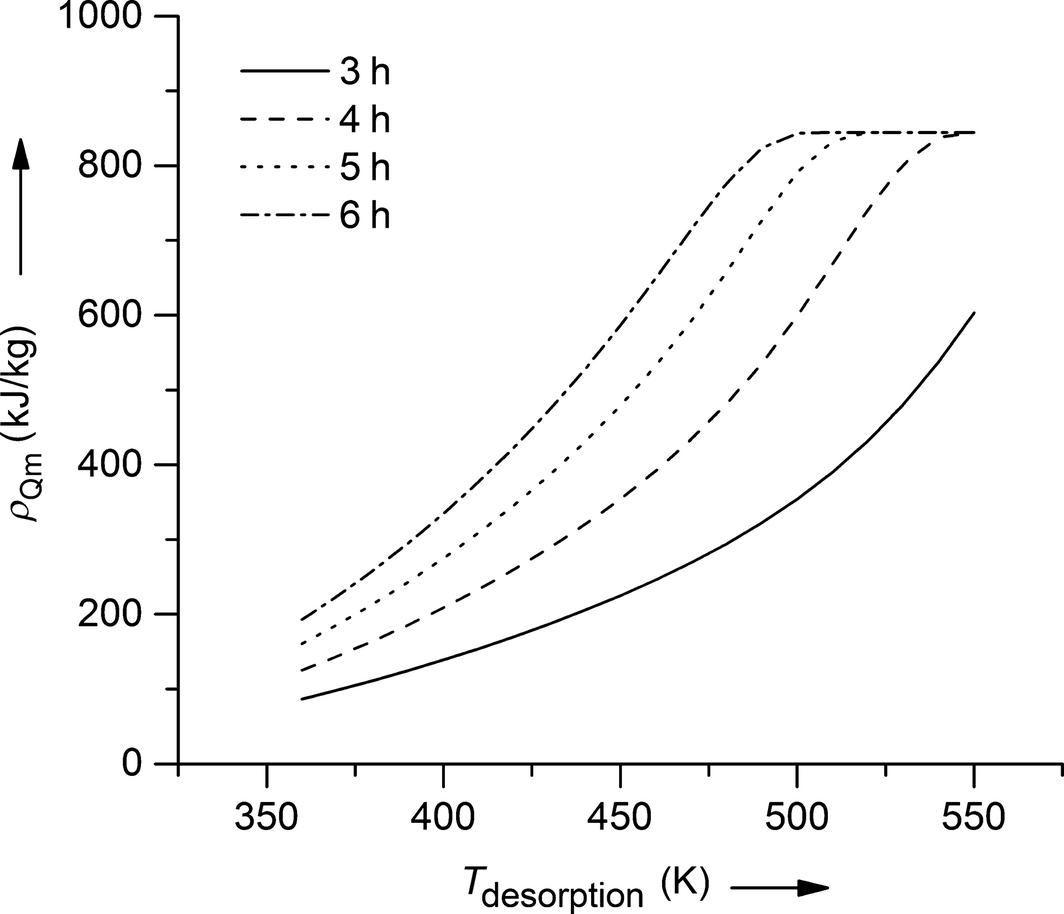
The adsorbate is fully removed at temperatures of 540 K after 4-h desorption, at 520 K after 5-h desorption, and at 500 K after 6-h desorption. These desorption temperatures result in the maximum possible efficiencies of 77%, 78%, and 79% for the respective desorption time. If the desorption temperature is further increased (for fixed desorption times), efficiency goes down, because no lower bed loading can be achieved in the desorption process and therefore, the amount of energy stored stays constant. In order to analyze the net heat released per mass adsorbent during the adsorption process, Figure 2 shows the energy densities of the system zeolite 13X as a function of desorption temperature for different desorption times. If the adsorbent is fully regenerated in the desorption process, the energy density of the system water on zeolite 13X is calculated to 844 kJ kg−1, which is by far the highest value for any of the tested adsorption systems. The calculated value is in good agreement with experimental values from literature (e.g., Ahlefeld et al. 900 kJ kg−1). [5, 10, 26] This energy density can be reached within the tested desorption temperatures for desorption times of 4, 5, and 6 h. If the desorption lasts for only 3 h, the maximum energy density cannot be reached for desorption temperatures under 550 K.
|
|
|
Figure 2. Energy densities of the adsorption pair water–zeolite 13X for different desorption times (3–6 h) and temperatures (350–550 K). |
The results of the efficiency and energy density calculations show, that the system water–zeolite 13X is extremely efficient and nets high energy densities at long desorption times of 4–6 h and high desorption temperatures of at least 500 K. However, the efficiency of the process is significantly lower if desorption time, which corresponds to the specific heat input, and temperature are not high enough. The problem of the low efficiency at low desorption temperatures can be overcome with the usage of a different adsorption system.
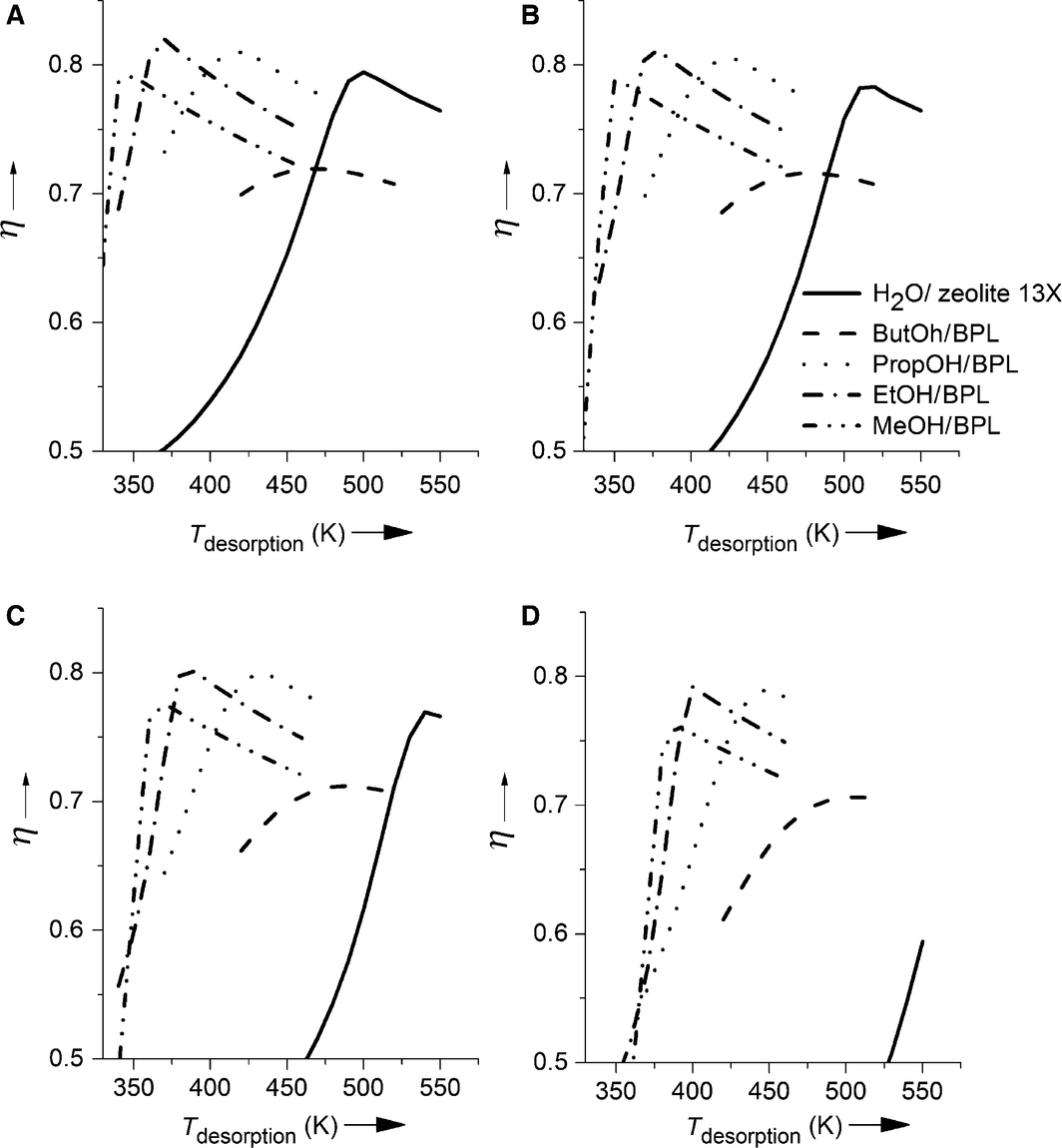
The efficiencies of the systems methanol, ethanol, propanol, and butanol on BPL activated carbon for different desorption times are given in Figure 3A–D. In order to classify these results, the efficiency of water on zeolite 13X is also shown. In Figure 3A–D it can be seen that the maximum efficiencies of the systems based on the adsorption of alcohols are achieved at lower desorption temperatures compared to the reference system. The shorter the chain length of the alcohol, the deeper can the temperature of maximum efficiency be decreased. The maximum efficiency of the alcohol–activated carbon systems slightly increases with increasing chain length from methanol to propanol. These efficiencies are with exception of the system butanol–BPL activated carbon in the same range as the maximum efficiency of water on zeolite. In case of butanol, the maximum efficiency drastically decreases, which mainly results from the relatively low enthalpy of adsorption of butanol on BPL activated carbon. The main reason for the lower heat of adsorption is the low heat of vaporization of butanol.
|
|
|
Figure 3. Efficiencies of different desorption times (A 6 h, B 5 h, C 4 h, D 3 h) and temperatures for water on zeolite (—) butanol (__), propanol (●●●), ethanol (-●-), and methanol (-●●-) on BPL activated carbon. |
From the results shown in Figure 3A, a temperature range can be identified for each of the systems (except for butanol on activated carbon) in which this system reaches the highest efficiency of all systems under consideration. The system butanol on activated carbon has by far the lowest efficiencies of all tested systems and therefore is never the ideal system. As can be seen by comparison of Figure 3A–D, the desorption time influences the maximum efficiencies possible. The shorter the desorption lasts, the lower are the maximum efficiencies, as the desorption process cannot be completed. Furthermore, the desorption temperatures at which the maximum efficiency is observed rise to higher temperatures, as the same amount of the adsorbate is desorbed in a shorter desorption time.
For example, for the system methanol on activated carbon the maximum efficiency is reached at a specific heat input in the desorption of 506 kJ kg−1, which equals a desorption temperature of 350 K for 6-h desorption, 355 K for 5-h desorption, 370 K for 4-h desorption, and 390 K for a 3-h desorption.
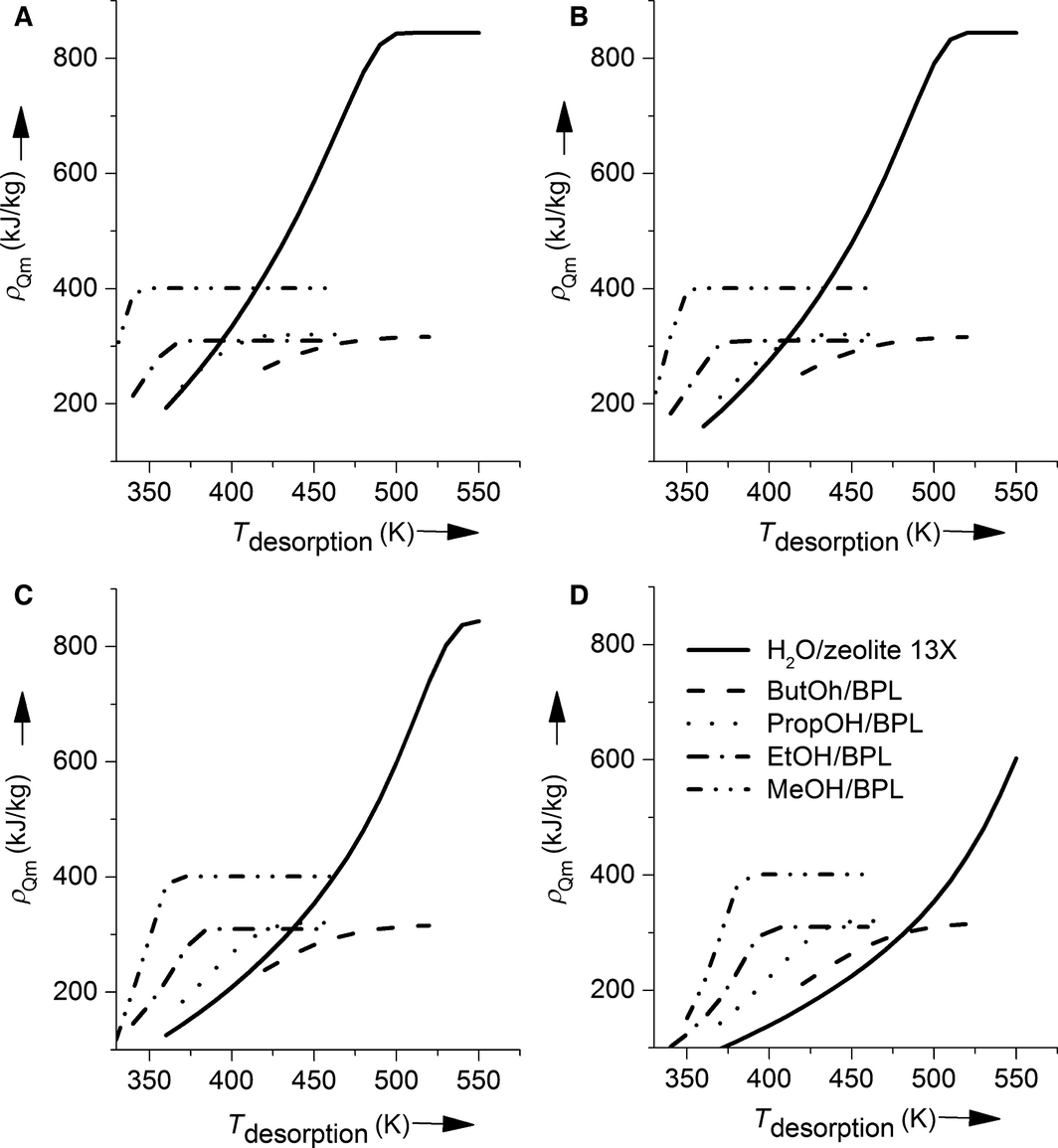
Concerning efficiency, the systems based on adsorption of short-chain alcohols on activated carbon represent a possible alternative to the reference system water on zeolite 13X. This holds especially, if the heat that has to be stored is only available for a short time or at low temperatures. However, the energy density is a further criterion of importance. In Figure 4, the energy densities of the examined working pairs for a six (4A)-, five (4B)-, four (4C)-, and three (4D)-hour desorption at desorption temperatures between 350 and 550 K are shown. The maximum energy density of the system water on zeolite 13X (840 kJ kg−1) is significantly higher than the values for all alcohols on activated carbon systems. From these systems, the system based on methanol shows the highest energy density with 402 kJ kg−1 followed by propanol (320 kJ kg−1), butanol (316 kJ kg−1), and ethanol (310 kJ kg−1). The big difference in energy densities between the water and the alcohol systems results mainly from the high enthalpy of adsorption of the system water on zeolite 13X.
|
|
|
Figure 4. Energy densities for different desorption times (A 6 h, B 5 h, C 4 h, D 3 h) and temperatures for water on zeolite (—) butanol (__), propanol (●●●), ethanol (-●-), and methanol (-●●-) on BPL activated carbon. |
Furthermore, the energy density is influenced by the amount of mass adsorbed and the heat capacities of the adsorbate and the adsorbent. If these components are not taken into account and the energy is only calculated out of the heat of adsorption, the energy densities would be significantly overestimated. In Table 2, the energy densities calculated in the simulation ρQm,model are compared to the energy densities that are calculated with constant enthalpy of adsorption and without considering the energy demand for heating the adsorbent and the adsorbate. The change in enthalpy of adsorption with bed loading has a big influence on the energy density. To demonstrate this effect, two different constant values of the differential enthalpies of adsorption were used to additionally calculate the energy density. is the energy density calculated with the maximum differential enthalpy of adsorption, which occurs at zero bed loading. is the energy density at a bed loading, where the differential enthalpy of adsorption reaches a saturation level.
| Adsorption pair | ρQm,model/kJ kg−1 | /kJ kg−1 | /kJ kg−1 |
|---|---|---|---|
| Water–zeolite 13X | 840 | 1272 | 597 |
| Methanol–BPL activated carbon | 402 | 667 | 475 |
| Ethanol–BPL activated carbon | 310 | 561 | 344 |
| Propanol–BPL activated carbon | 320 | 579 | 355 |
| Butanol–BPL activated carbon | 316 | 638 | 336 |
From the results in Table 2, it can be seen that the energy densities which are calculated just with the maximum differential enthalpy of adsorption are far higher than the results from the detailed simulation. Even the values for the assumption of the lowest differential enthalpy of adsorption are higher for all systems, due to the lack of consideration of energy demand for heating of the materials. These results should remind of the importance of considering the heat capacities and the nonconstant enthalpy of adsorption for process simulations. A closer look at the dependency of energy density on desorption temperature for all examined desorption times makes clear that the systems with alcohols as adsorbates reach higher energy densities than the reference system at low desorption temperatures.
However, the energy density of the system methanol on BPL activated carbon is higher than for the other alcohol systems for every desorption temperature. The discrepancy between the high efficiency and the lower energy density of the alcohol on activated carbon systems results from the definition of efficiency (eq. (9)), where the heat of desorption and adsorption is calculated with the temperature difference of the gas stream at the inlet and outlet of the adsorber. If heat is available for a given time that cannot be used otherwise, the efficiency of the process plays a less important role and therefore, the more reasonable goal is to net high amounts of energy in the adsorption process.
At low desorption temperatures or low desorption times and therefore low specific heat inputs, the energy density of the adsorbate methanol on activated carbon is higher than the energy density of the reference system. If energy has to be stored at these process conditions, the adsorbate methanol on the adsorbent activated carbon results in significantly higher efficiencies and higher energy densities than the reference system water on zeolite 13X and therefore represents a real alternative for the thermochemical energy storage at low desorption temperatures and low specific heat inputs in the desorption process.
Conclusion
The efficiency and the energy density of thermochemical adsorptive energy storage with different working pairs (adsorbate–adsorbent) was examined for different desorption temperatures (350–550 K) and specific heat inputs. The state of the art working pair water on zeolite 13X nets the highest maximum energy density of the tested systems with 844 kJ kg−1, but needs desorption temperatures above 500 K to reach this value and its maximum process efficiency. The other working pairs under consideration were methanol, ethanol, propanol, and butanol on activated carbon. These systems reach their highest efficiencies and therefore maximum energy densities at lower desorption temperatures and specific heat inputs than the state of the art system. Therefore, they offer a high potential for low-grade solar energy storage systems, which only reach charging temperatures below 500 K. The maximum efficiency of the process rises with increasing chain length of the alcohol to higher desorption temperatures. The working pair methanol on activated carbon has the highest energy density (402 kJ kg−1) of the alcohol systems over the whole examined range of desorption temperature and is therefore best suited to be an alternative to the reference system at low desorption temperatures and times. The efficiency and the energy density of this working pair is significantly higher for low desorption temperatures or low specific heat inputs.
Acknowledgments
The authors wish to thank Prof. Wolfgang Arlt for fruitful discussions.
Conflict of Interest
None declared.
Appendix
Parameters of the Dubinin-Astakhov equation
| Adsorption pair | W0/cm3 kg−1 | E/kJ kg−1 | n/- |
|---|---|---|---|
| Water–zeolite 13X | 245.9 | 1038 | 2.11 |
| Methanol–BPL activated carbon | 437.3 | 250.5 | 1.92 |
| Ethanol–BPL activated carbon | 438.9 | 240.8 | 1.99 |
| Propanol–BPL activated carbon | 452.2 | 251.7 | 1.84 |
| Butanol–BPL activated carbon | 471.9 | 254.8 | 1.61 |
Parameter adsorbate
| Parameter | Temperature dependent | Method |
|---|---|---|
| Density liquid | Yes | DIPPR-equation 105/116 |
| Density gas | Yes | Redlich-Kwong EoS |
| cp liquid | Yes | DIPPR-equation 107 |
| cP gas | Yes | DIPPR-equation 100 |
| Vapor pressure | Yes | Wagner 25-equation |
| Heat of vaporization | Yes | DIPPR-equation 106 |
| Thermal conductivity gas | Yes | DIPPR-equation 101 |
Parameter adsorbent (constant with temperature in the simulation) [27]
| Parameter | Zeolite 13X | Activated carbon |
|---|---|---|
| Density/kg m−3 | 2100 | 1880 |
| Porosity/- | 0.5 | 0.45 |
| Particle diameter/m | 0.005 | 0.005 |
| Specific surface/m2 g−1 | 350 | 500 |
| cP solid/J kg−1 K−1 | 1200 | 760 |
References
- Zhang, H., J. Baeyens, G. Cáceres, J. Degrève, and Y. Lv. 2016. Thermal energy storage: Recent developments and practical aspects. Prog. Energy Combust. Sci.53:1–40.
- Zhang, H., K. Huys, J. Baeyens, J. Degrève, W. Kong, and Y. Lv. 2016. Thermochemical Energy Storage for Power Generation on Demand. Energy Technol.4:341–352.
- N'Tsoukpoe, K. E., H. Liu, N. Le Pierrès, and L. Luo. 2009. A review on long-term sorption solar energy storage. Renew. Sustain. Energy Rev.13:2385–2396.
- Henninger, S., F. Jeremias, H. Kummer, P. Schossig, and H.-M. Henning. 2012. Novel Sorption Materials for Solar Heating and Cooling. Energy Procedia30:279–288.
- Dicaire, D., and F. H. Tezel. 2013. Use of adsorbents for thermal energy storage of solar or excess heat: improvement of energy density. Int. J. Energy Res.37:1059–1068.
- Jänchen, J., and H. Stach. 2012. Adsorption properties of porous materials for solar thermal energy storage and heat pump applications. Energy Procedia30:289–293.
- Ng, E.-P., and S. Mintova. 2008. Nanoporous materials with enhanced hydrophilicity and high water sorption capacity. Microporous Mesoporous Mater.114:1–26.
- Aristov, Y. I.2015. Current progress in adsorption technologies for low-energy buildings. Future Cities Environ.1:[e-pub ahead of print] https://futurecitiesenviro.springeropen.com/articles/10.1186/s40984-015-0011-x.
- Hauer, A.2007. Evaluation of adsorbent materials for heat pump and thermal energy storage applications in open systems. Adsorption13:399–405.
- Hauer, A.2007. Thermal energy storage for sustainable energy consumption. Springer, Dordrecht, Netherlands.
- Storch, G., G. Reichenauer, F. Scheffler, and A. Hauer. 2008. Hydrothermal stability of pelletized zeolite 13X for energy storage applications. Adsorption14:275–281.
- Mugnier, D., and V. Goetz. 2001. Energy storage comparison of sorption systems for cooling and refrigeration. Sol. Energy71:47–55.
- Askalany, A. A., M. Salem, I. M. Ismail, A. H. H. Ali, and M. G. Morsy. 2012. A review on adsorption cooling systems with adsorbent carbon. Renew. Sustain. Energy Rev.16:493–500.
- Chan, C. W., J. Ling-Chin, and A. P. Roskilly. 2013. A review of chemical heat pumps, thermodynamic cycles and thermal energy storage technologies for low grade heat utilisation. Appl. Therm. Eng.50:1257–1273.
- Srivastava, N. C., and I. M. Eames. 1998. A review of adsorbents and adsorbates in solid + vapour adsorption heat pump systems. Appl. Therm. Eng.18:707–714.
- Simo, M., S. Sivashanmugam, C. J. Brown, and V. Hlavacek. 2009. Adsorption/Desorption of Water and Ethanol on 3A Zeolite in Near-Adiabatic Fixed Bed. Ind. Eng. Chem. Res.48:9247–9260.
- Sircar, S.1983. Linear-driving-force model for non-isothermal gas adsorption kinetics. J. Chem. Soc.79:785–796.
- Kast, W.1988. Adsorption aus der gasphase. VCH, Weinheim.
- Polányi, M.1916. Adsorption von Gasen (Dämpfen) durch ein festes nichtföüchtiges Adsorbens. Verh. Dtsch. Phys. Ges.18:55–80.
- Dubinin, M. M., and V. A. Astakhov. 1971. Description of Adsorption Equilibria of Vapors on Zeolites over Wide Ranges of Temperature and Pressure. Am. Chem. Soc.60:235–241.
- Dubinin, M. M.1967. Adsorption in Micropores. J. Colloid Interface Sci.23:487–499.
- Thamm, H.1989. Calorimetric Study on the state of C1-C4 Alcohols sorbed on silicalite. J. Chem. Soc.85:1–9.
- Bering, B. P., M. M. Dubinin, and V. V. Serpinsky. 1966. Theory of volume filling for vapor adsorption. J. Colloid Interface Sci.21:378–393.
- Wang, Y., and M. D. Le Van. 2010. Adsorption Equilibrium of Carbon Dioxide and Water Vapor on Zeolites 5A and 13X and Silica Gel: Pure Components. J. Chem. Eng. Data54:2839–2844.
- Taqvi, S. M., W. S. Appel, and M. D. Le Van. 1999. Coadsorption of Organic Compounds and Water Vapor on BPL Activated Carbon. 4. Methanol, Ethanol, Propanol, Butanol, and Modeling. Ind. Eng. Chem. Res.38:240–250.
- Alefeld, G., P. Maier-Laxhuber, and M. Rothmeyer. 1981. Proceedings of the IEA Conference on New Energy Conservation Technologies and their Commercialization, Berlin. Pp. 796–819.
- Bathen, D., and M. Breitenbach. 2001. Adsorptionstechnik. Springer, Heidelberg.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?