Abstract
The effect of vertical throughflow and internal heating effects on fluid saturated porous medium under gravity modulation is investigated. The amplitude of modulation is considered to be very small and the disturbances are expanded in terms of power series of amplitude of convection. A weakly nonlinear stability analysis is proposed to study stationary convection. The Nusselt number is obtained numerically to present the results of heat transfer while using Ginzburg–Landau equation. The vertical throughflow has dual effect either to destabilize or to stabilize the system for downward or upward directions. The effect of internal heat source () enhances or sink () diminishes heat transfer in the system. The amplitude and frequency of modulation have the effects of increasing or diminishing heat transport. For linear model Venezian approach suggested that throughflow and internal heating have both destabilizing and stabilizing effects for suitable ranges of . Further, the study establishes that heat transport can be controlled effectively by a mechanism that is external to the system throughflow and gravity modulation.
Keywords
Throughflow; Gravity modulation; Linear and weakly nonlinear model; Internal heating
Nomenclature
Latin Symbols
- amplitude of convection
- amplitude of gravity modulation
d- depth of the fluid layer
- acceleration due to gravity
- critical wave number
K- permeability of porous medium
Nu- Nusselt number
Pe- Péclet number
p- reduced pressure
Ra- thermal Rayleigh number,
- internal Rayleigh number,
- critical Rayleigh number
T- temperature
- Prandtl Darcy number
- temperature difference across the porous layer
t- time
- horizontal and vertical co-ordinates
Greek symbols
- coefficient of thermal expansion
- square of horizontal wave number
- perturbation parameter
- effective thermal diffusivity
- heat capacity ratio
- frequency of modulation
- dynamic viscosity of the fluid
- porosity
- kinematic viscosity,
- fluid density
- stream function
- slow time
- phase angle
- perturbed temperature
Other symbols
-
Subscripts
b- basic state
c- critical
0- reference value
Superscripts
- perturbed quantity
- dimensionless quantity
1. Introduction
Natural convection (buoyancy driven convection, in which gravitational force plays a main role) in fluid saturated porous medium is of interest due to its importance in various practical applications such as oil recovery process in petroleum industry, geothermal energy extraction, and insulation of reactor vessels. The above mentioned applications along with porous media occur in many natural situations. In these applications control of convective instability plays an important role. It is fact that, one of the effective mechanisms which control convective instability is to maintain a nonlinear temperature gradient. Such a gradient may be achieved by the following: time dependent heating or cooling at the boundaries, suitable thermal and rotation modulation, vibrating the porous medium periodically, volumetric distribution of internal heat sources and radiative heat transfer.
A modified complex body force (gravity modulation) is important when the system is under vertical vibrations. In this case the density gradient is subjected to vibrations, and the resulting buoyancy forces which are produced by the interaction of the density gradient with gravitational field have a complex spatiotemporal structures. The time dependent gravity field is of interest in space laboratory experiments, in areas of crystal growth and large-scale convection of atmosphere other applications. Many theoretical and experimental studies dealing with materials processing or physics of fluids under the microgravity conditions aboard an orbiting spacecraft have been carried out by Nelson [1]. According to Wadih et al. [2] and [3], the vibrations can either substantially enhance or retard heat transfer and thus drastically affect the convection. The effect of modulated gravity on a convectively stable configuration can significantly influence the stability of a system by enhancing or decreasing its susceptibility to convection. Gershuni et al. [4] and Gresho and Sani [5] were the first to study the gravity modulation on the stability of a heated fluid layer. Their results show that the stability of the layer being heated from below is enhanced by g-jitter and being heated from below is enhanced by g-jitter. The instability of a viscoelastic fluid layer heated from below in a modulated gravitational field is studied numerically by Yang [6]. It is found that, modulation has a destabilization effect at low frequencies and a slight stabilization effect at high frequencies, which increases with increasing the amplitude of modulation. It is also pointed that, for viscoelastic fluid acted on by a modulated gravity, modulation has the same effects at both very low and very high frequencies, as those of Newtonian fluids. Using Venezian model the onset of convection in both fluid and porous layers is investigated by Malashetty and Padmavathi [7]. It is found that the low frequency g-jitter can have a significant effect on the stability of the problem. The Darcy limit and viscous flow limit are obtained as degenerate cases of the Brinkman model. The boundary-layer flow induced by a constant temperature vertical surface embedded in a vibrating porous medium is studied by Rees and Pop [8]. The amplitude of g-jitter is assumed to be small compared with the mean acceleration. It is found that, the effect of g-jitter is eventually confined to a thin layer embedded within the main boundary layer, but it becomes weak at increasing distances from the leading edge. A weakly nonlinear analysis in a porous medium under gravity modulation is investigated by Govender [9]. It is found that, the vibration frequency causes the convection amplitude to approach zero which means increasing the vibration frequency stabilizes the system. Kuznetsov [10] investigated bioconvection in a shallow horizontal fluid-saturated porous layer that contains a suspension of oxytactic bacteria, such as Bacillus subtilis. It is found that, linear stability analysis indicates g-jitter has a stabilizing effect on the suspension. Some of the relevant and documented works on gravity modulation are [11], [12], [13], [14] and [15].
Several geophysical and technological applications involve non-isothermal flow of fluids through porous media, called throughflow where the basic flows not quiescently. In situ processing of energy resources such as coal, geothermal energy, oil shale and many practical problems often involves the throughflow in the porous medium. The importance of buoyancy-driven convection in such problem may become significant when precise processing is required. Moreover, the throughflow effect in such circumstances may be of interest because of the possibility of controlling the convective instability by adjusting the throughflow in addition to the gravitational force due to gravity. Throughflow alters the basic state temperature from linear to nonlinear with layer height, which in turn affects the stability of the system significantly. It is found that the throughflow is stabilizing if the bounding surfaces of the porous layer are of the same type but destabilizing in one particular direction if the boundaries are not of the same type [16], [17], [18] and [19]. However, it has been shown that the throughflow is destabilizing even if the boundaries are of the same type if the porous layer is heated internally [20] and also in the presence of an additional diffusing component. The effect of throughflow on the onset of convection in a horizontal porous layer for a Newtonian fluid has been studied by Nield [21]. The effect of throughflow and variable gravity field on thermal convection in a porous layer is investigated by Suma et al. [22]. The Darcy–Forchheimer model was considered for insulating boundaries. It is found that, stabilizing or destabilizing the system depends on types of boundary conditions, direction of throughflow and variable gravity field. Nonlinear throughflow and g-jitter effects on porous medium for stationary and oscillatory mode of convection are investigated by Kiran [23] and [24]. Weakly nonlinear model was developed in order to study heat and mass transfer across the porous layer, while deriving the non-autonomous Ginzburg–Landau equation. The similar problem for temperature modulation is studied by Kiran [25]. Where three types of temperature profiles considered and found that, when the boundaries are at out of phase modulation the heat or mass transfer is maximum. The stationary mode nonlinear Darcy convection is investigated. Throughflow and internal heating effect on onset of convection in a porous medium is investigated by Vanishree [26]. The effect of throughflow and internal heat generation on onset of convection is discussed. It is also found that, the onset of convection may stabilize or destabilize depending on the direction of the flow and internal heat generation.
In experiments like injection of the energy in a system is controlled by the flow rate of fluid (since the granular materials are dissipative injection of the energy is necessary to preserve steady states). The system is in the fixed phase at low flow rate, where particle rests at the bottom. When the flow rate exceeds the critical value, the particles start moving, this state is called the fluidized phase. These fluidized beds may be employed and are created by throughflow through solid particles. Throughflow is important for industrial applications in that it yields a potential method to control the onset behavior of convection, since many practical problems involve more than a Boussinesq approximation in the system of equations. The aim of throughflow is to develop a nonlinear energy stability analysis which yields unconditional stability bounds which are closed to linear theory. It is quite important for understanding these nonlinear effects in nonlinear thermal instability to finite amplitude convection.
The study of heat transfer with internal heat generation arises at consideration of heat dissipation in porous layers exposed to radioactive radiation at storage of nuclear waste materials or transmitting high energy particle beams. There are several situations where porous material offers its own heat source and set up convective flow through the local heat generation. This kind of problem may occur through radioactive decay, a relatively weak exothermic reaction which can take place within the porous material. To be specific, it is the main source of energy for celestial bodies caused by nuclear fusion and decaying of radioactive materials, which keeps them warm and active. Therefore, internal heating of is important in several applications that include reactor safety analyses, geophysics, fire and combustion studies, metal waste form development for spent nuclear fuel, and nuclear reactions, nuclear heat cores, nuclear energy, nuclear waste disposals, oil extractions and crystal growth. The heat transfer in a window for transmission of high-energy beams with a metal foam porous layer is studied by Hetsroni et al. [27]. The image processing of thermal maps on the surface of open-cell porous layer revealed that, the boundary condition with constant heat flux became more relevant for numerical model than those with constant temperature at high values of Reynolds numbers based on the permeability. It is also found that, heat transfer at natural convection in the strip of metal foam was increased drastically (up to 1820 times for metal foam of 20 ppi) relative to the flat plate of the same overall dimensions. Bhadauria et al. [28] performed a weakly nonlinear thermal instability in a porous medium in the presence of internal heating and gravity modulation. An amplitude of convection is derived using Landau equation and found gravity modulation used, to alter the heat transfer, whereas internal heating is to enhance the heat transfer. The studies related to internal heat generation were recently investigated by Bhadauria et al. [29] and Saravanan [30].
It is observed that, in the literature many models being implemented with throughflow for linear theory. But, for nonlinear models with modulation it is scary. It is due to Kiran et al. [23], [24] and [25] that, throughflow effects are considered under gravity or temperature modulation. These are the first papers which contribute the nonlinear throughflow effects under modulation using stationary and oscillatory mode of convections. The conduction state temperature is nonlinear in terms of Péclet number which measures the strength of throughflow and it affects the system through coupled equations of momentum and energy. It is found that, this nonlinear throughflow has duel effect on heat transfer in the system. Also three types of temperature modulation are discussed and presented a significant results for out of phase modulation. A linear stability analysis is performed by Vanishree [26] to study the effect of throughflow and internal heat generation on the preferred mode of stationary thermal convection in a variable viscosity liquid saturating an anisotropic porous medium. The results are presented corresponding to the onset of convection. But, unfortunately the nonlinear part is missing therefore heat transfer analysis. With this concussion the present article is motivated to continue the previous works of Kiran et al. [25] and [39] and Vanishree [26] for nonlinear model. Hence the present paper contributes nonlinear throughflow effects under gravity modulation in the presence of internal heat source and sink, while employing weakly nonlinear model.
2. Mathematical formulation
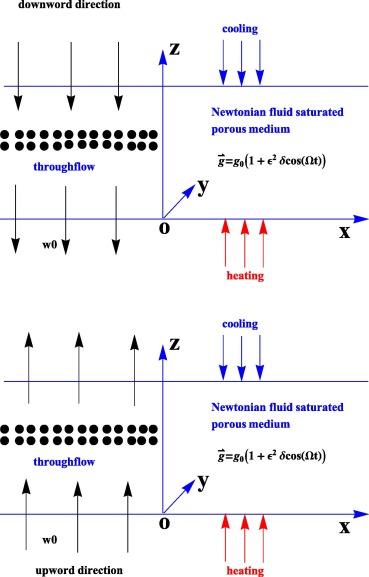
Consider an infinitely extended horizontal porous medium saturated by Newtonian fluid, confined between two free-free boundaries at and , and heated from below. The temperature difference across the porous medium is kept at . The Cartesian frame of reference is chosen, origin in the lower boundary and the z axis in vertically upward direction. The schematic diagram is given in the Fig. 1. Throughflow has been considered in vertical, both upward and downward directions. Further Darcy law and the Oberbeck–Boussinesq approximation are considered, under these assumptions, the equations which describe the flow model are given by Bhadauria and Kiran [31]:
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
The physical variable has their usual meanings and is given in Nomenclature. For simplicity thermal expansion coefficient is taken to be unity in this paper. The externally imposed thermal boundary conditions and time periodic gravity field considered in this paper are:
|
|
(5) |
|
|
(6) |
where and represent the amplitude and frequency of gravity modulation, respectively. The basic state is assumed to be quiescent and the quantities in this state are given by:
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
The basic state temperature defined numerically by solving the Eq. (9). The finite amplitude perturbations on the basic state are superposed in the form,
|
|
(11) |
For two dimensional flow model the following stream function introduced as . The non-dimensional physical variables re-scaled as . Substituting the Eq. (11) in Eqs. (1), (2), (3) and (4), and using the basic state results, while eliminating the pressure term, the following dimensionless governing equations arrived (dropping the asterisk):
|
|
(12) |
|
|
(13) |
where . The dimensionless parameters which appear in Eq. (12) and (13) are given in Nomenclature. The Eq. (13) shows the basic state solution and influences the stability problem through the factor , which is given by Eq. (14). Assuming small variation in time, and re-scaling it as , the stationary mode of convection is studied. The basic state temperature appears in Eq. (13) is derived from the Eq. (9) numerically and it is given by:
|
|
(14) |
The nonlinear system of Eqs. (12) and (13) may be written in the following matrix form:
|
|
(15) |
|
|
|
Figure 1. A schematic diagram of the problem. |
The solution of the system Eq. (15), is evaluated by considering impermeable boundary conditions as given (Bhadauria and Kiran [31]):
|
|
(16) |
3. Heat transport for stationary instability
The solution of the above system Eq. (15) is derived using an asymptotic expansions (given by Malkus and Veronis [32]):
|
|
(17) |
where is the critical value of the Rayleigh number at which the onset of convection takes place in the absence of gravity modulation. The above expansion was earlier used by Malkus and Veronis [32] and Venezian [33]. Now the solution of the system evaluated for different orders of .
3.1. Lowest-order system
This lowest order system is similar to linear model where the nonlinear effects do not occur. At this order the system takes the following form:
|
|
(18) |
The solution of the lowest order system is subject to the boundary conditions Eq. (16) is:
|
|
(19) |
|
|
(20) |
where and . The critical value of the Rayleigh number for stationary convection is given by
|
|
(21) |
and the corresponding wavenumber for the onset of convection is obtained while minimizing with respect to .
3.2. Second-order system
In this order the nonlinear effects enter through the Jacobian terms where the interaction of the fluid motion and thermal diffusivity take place. At this order the system take the following form:
|
|
(22) |
where
|
|
(23) |
|
|
(24) |
The second order solutions subjected to the boundary conditions Eq. (16) is given by:
|
|
(25) |
|
|
(26) |
The horizontally averaged Nusselt number Nu, for the stationary mode of convection is determined numerically by using the definition
|
|
(27) |
In the above Eq. (27) 1 indicates, heat transport in conduction form and second term represents the heat transfer in convection form.
3.3. Third-order system
At this order the system takes the following form:
|
|
(28) |
where
|
|
(29) |
|
|
(30) |
Substituting the expressions of and into Eqs. (29) and (30), the expressions of and easily simplified. But, finding the solution at this order is very difficult due to complexity. The solvability condition being used for the existence of third order solution, and consequently the Ginzburg–Landau amplitude equation is derived for stationary mode of convection with time-periodic coefficients in the following form:
|
|
(31) |
where , . The Ginzburg–Landau equation given by Eq. (31) is a Bernoulli equation and obtaining its analytical solution is difficult due to its non-autonomous nature. So that it has been solved numerically using the in-built function NDSolve of mathematica subjected to the initial condition , where is the chosen initial amplitude of convection. Without loss of generality , is assumed in the calculations and this is done to keep the parameters to a minimum. For unmodulated case, the analytical solution of the above Eq. (31) takes the form:
|
|
(32) |
where same as in Eq. (31), and which appears in Eq. (32) is an integration constant, can be found by using suitable initial condition.
4. Linear stability
For linear stability analysis the nonlinear terms excluded from the Eqs. (12) and (13) thus obtain the linear model in the following form:
|
|
(33) |
|
|
(34) |
Eliminating T from the above equations we get single equation for in the form:
|
|
(35) |
where the gravity modulation term takes the form for linear case.
4.1. Method of solution
We obtain the perturbation technique to obtain eigen functions and eigen values Ra by introducing a small perturbation parameter (Venezian [33]).
|
|
(36) |
Substituting the equation Eq. (36) into equation Eq. (35) the system will be solved for every order of .
4.2. Zeroth order system
The marginally stable solutions will be considered of the following form
|
|
(37) |
Since is independent of y therefore a is the wave number in x direction, the corresponding eigen values are given by
|
|
(38) |
where and . In the absence of internal heat, the expression of similar with the result of Kiran et al. [24] and [25].
4.3. First order system
At this order we obtain the following relation:
|
|
(39) |
where . The solution of the homogeneous equation corresponding to the equation Eq. (39), one must have a term which is orthogonal to . Note that we already apply the theory of minimal Rayleigh number therefore right hand side of equation Eq. (39) is complete orthogonal function to . Using L operator it is found that
|
|
(40) |
|
|
(41) |
The solution for will be derived by inverting the operator L in the following form
|
|
(42) |
where is the complex conjugate of .
4.4. Second order system
At this order the following relation is obtained:
|
|
(43) |
We will not solve the Eq. (43), but using this equation we determine . For the existence of a solution of the Eq. (43), it is necessary that, the steady part of its right hand side must orthogonal to . This gives,
|
|
(44) |
where the upper bar denotes the time average,
|
|
(45) |
5. Results and discussion
The combined effect of gravity modulation and vertical throughflow is investigated in the presence of internal heat source and sink. Both linear and weakly nonlinear theories are investigated. A weakly nonlinear study investigates heat transfer analysis and linear model investigates onset convection in the medium. Firstly the result related nonlinear theory will be discussed. The gravity modulation is assumed to be of third order , which means only small amplitude of gravity modulation is considered. This assumption will help us in obtaining the amplitude equation of convection in simple and elegant manner and is much easier to obtain than Lorenz model. The purpose of weakly nonlinear theory is to study heat transfer, which is not possible in linear theory. External regulations (like thermal, gravity, rotation, and magnetic field modulations) of the current problem is important due to its numerous applications in thermal and engineering sciences. The objective of the problem is to consider, gravity modulation and vertical throughflow for either enhancing or diminishing heat transfer. Since the porous medium is assumed to be closely packed, the Darcy-model is considered in momentum equation. The additional important topic is internal heat source or sink which was realized by energy equation. This concept is most important where the system offers its own internal heat generation. The moderate values of are considered due to its dominant effect on convection.
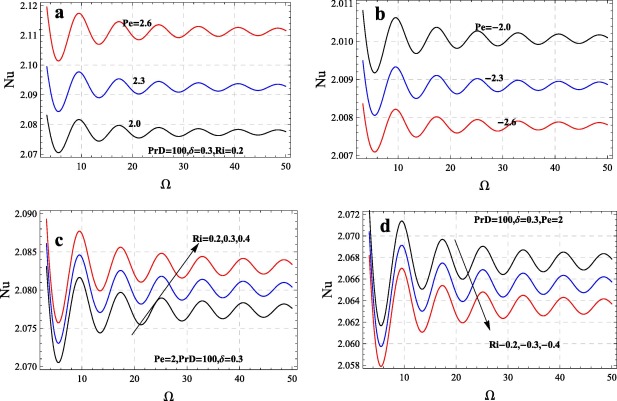
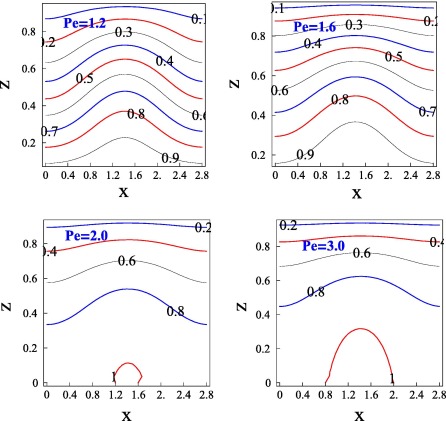
The values of may consider (modern porous medium applications, such as mushy layer in solidification of binary alloys and fractured porous medium) around 1, and also for low porosity medium, the large values considered for . The values of and are considered to be small. For small values of amplitude and frequencies, the heat transfer can reach the maximum. The numerical results for Nu obtained from the Eq. (27) in connection with amplitude Eq. (31), and the results have been presented in Figure 2, Figure 3 and Figure 4. The effect of each parameter on heat transport is shown in Figure 2, Figure 3 and Figure 4 where the plots of Nusselt number Nu versus are presented. It is found from the figures that the value of Nu oscillates maximum for low frequencies and further values of no oscillations can be observed, which means that, low frequencies of modulation enable the system to convect faster. The oscillatory nature of the figures is due to modulation only.
|
|
|
Figure 2. Effect of Pe and on heat transport. |
|
|
|
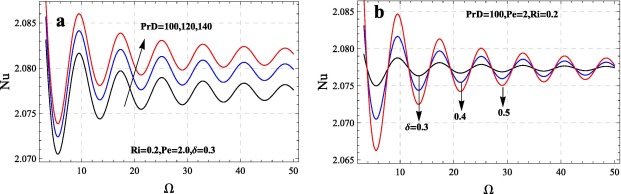
Figure 3. Effect of and on heat transport. |
|
|
|
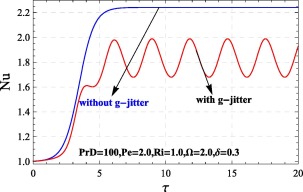
Figure 4. Comparison between modulated and unmodulated system. |
Let us discuss the results of gravity modulation: in Fig. 2 the results corresponding to Péclet and internal Rayleigh number present. The effect of Pe on heat transfer is investigated for the cases of upward and downward directed flows. The upward throughflow (also known as pro-gravity) , given in Fig. 2a has destabilizing effect whereas downward throughflow (also known as anti-gravity) , given in Fig. 2b has stabilizing effect. The related results for linear theory are due to Vanishree [26], this is because of temperature dependence of viscosity. When Pe varies in either directions the nonlinear temperature distribution significantly matters at conduction state and there is significant or drastic variation in the energy supply to the disturbance. The corresponding results are also obtained by Nield [21] in the case of fluid layer for small amount of throughflow. The present results are computable with the results obtained by Shivakumara et al. [19] and Suma et al. [22]. Shivakumara et al. [19] pointed that, the destabilization effect may be due to the distortion of basic state temperature distribution from linear to nonlinear throughflow. The corresponding results of throughflow under modulation the reader may look at the articles [25] and [26]. It is noted that, for nonlinear theories Pe has duel effect [25] but, for linear case only stabilizing effect [26], the reason could be guessed as the finite amplitude interaction in the fluid flow through coupled formation of momentum and energy equations.
The effect of the internal Rayleigh number , for both heat source and heat sink cases, on heat transfer presented in Fig. 2c for heat source and Fig. 2d for heat sink. The reason behind internal heat is that, for many industrial and chemical experiments during their process the system may release or absorb energy in such a situation one needs understand how to control these fluctuations in the system. It is given figures that positive values of (heat source) increase or negative values of (heat sink) decreases the heat transfer in the system. The reader may refer [13], [26], [27], [28], [29], [30] and [31] for internal heat generation. In Astrophysics provides an example of internally driven convection for uniformly heated medium. In the cores of stars heat is produced by thermonuclear reactions. In such situation the heating rate is very sensitive to temperature, and this sensitivity creates steep thermal gradients that drive powerful convection in the cores (Kippenhahn et al. [36]). Clearly, this and many other instances (related space science) of internally driven convection contain more complications. It is observed that, for low porosity medium, large values [29] considered for . The Nusselt number Nu increases with showing heat transfer increases (see Fig. 3a). The results could be gained for lower values of Prandtl Darcy number. The related articles which presents the results corresponding to heat transfer in a porous medium under modulation may be observed in the following studies [12], [13] and [31].
From the Figure 2, Figure 3 and Figure 4, it is observed that as increase decreases the magnitude of Nu, and so the effect of frequency of modulation on heat transport diminishes heat transfer. At high rates of frequency, the gravity modulation on thermal instability disappears altogether. The above results agree quite well with the linear theory of Venezian [33] for temperature modulation, where the correction in the critical value of Rayleigh number due to thermal modulation becomes almost zero at high frequencies. The results for gravity modulation on weakly nonlinear studies see [7], [11], [23], [24], [25], [26], [27], [28] and [29]. In general the frequency of modulation shortens the wavelength and minimizes the magnitude of Nu, due to this reason heat transfer reduces. It is quite intrusting to see even this frequency of modulation play critical role in controlling chaos [24]. The effect of amplitude of modulation is presented in Fig. 3b, and it is found that heat transfer increases as increases. Hence amplitude of modulation is to enhance the heat transfer. The comparison between modulated and unmodulated case is presented in Fig. 4. It is found that gravitationally modulated system flows transport less heat transfer than unmodulated systems the corresponding results obtained from the studies of [34] and [35]. The effect of magnetic field [37] modulation and rotational speed [38] modulation on thermal instability shows similar results for modulated systems. It is to be noted that, the analytical solution for unmodulated case obtained from the Eq. (32).
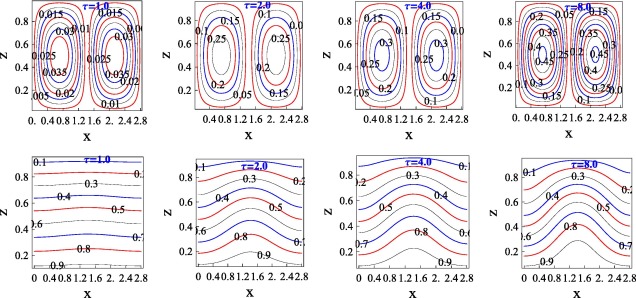
Finally the nature of stream lines and corresponding isotherms presented in Figure 5 and Figure 6. Fig. 5 shows the variation of stream lines and isotherms at different instants of times, respectively. Fig. 5 shows the magnitudes of stream lines increase as time increases. Also, initially the isotherms are flat and parallel, thus heat transport is due to conduction only. However, as time increases, isotherms form contours, showing convective regime is taking place, after reaching certain instant there is no change in the magnitude of stream lines and isotherms, thus showing the steady state. In particular Fig. 6 is drawn to see the effect of throughflow on isotherms. While strengthening the throughflow there forms a boundary layer at the bottom plate, then the significant results may observe at corresponding isotherms, where isotherms are missing at the bottom plate due to throughflow disturbances. The reason would be, when there is flow at the bottom plate there may not be stream line flow due to heavy boundary layer and hence the nature of the Fig. 6.
|
|
|
Figure 5. Streamlines and Isotherms for Pe = 0.3, . |
|
|
|
Figure 6. Isothermas for . |
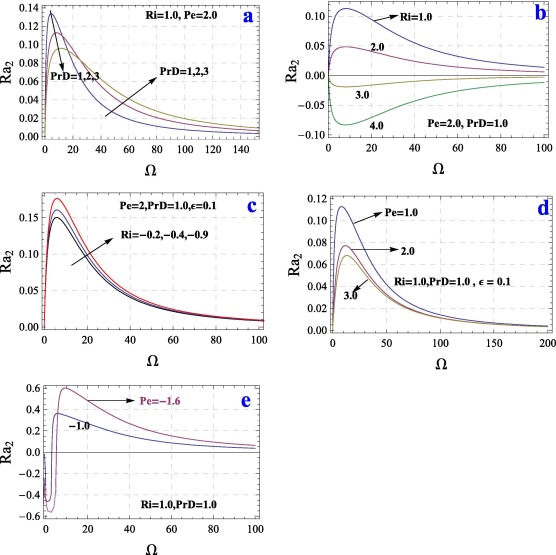
In order to make the article self contained the results corresponding to linear theory also presented in Fig. 7. It is examined that, how this correction Rayleigh number affected by the modulation frequency . Analytical study of gravity modulation on onset of thermal convection in a porous layer using Venezian approach is presented. The regular perturbation method based on small amplitude of modulation is employed to compute the critical value of Rayleigh number and wavenumber. The expression for the critical correction Rayleigh number is computed as a function of the frequency of modulation . The sign of characterizes the stabilizing or destabilizing effect of modulation. A positive indicates that the modulation effect is stabilizing while a negative indicates destabilizing effect.
|
|
|
Figure 7. Variations of with for different values of , Pe and . |
In Fig. 7a the effect of DarcyPrandtl number on the stability of the system is displayed. It is found that the magnitude of critical correction Rayleigh number decreases positively with increasing PrD when frequency is small. However, the trend reverses for moderate and high frequency. Therefore, increase of DarcyPrandtl number enhances the destabilizing effect of gravity modulation when frequency is small whereas it enhances the stabilizing effect of modulation for moderate and high frequency. The results of the present model may be compared with the studies of Malashetty and Padmavathi [7], Vanishree [26] and Kiran et al. [39]. Fig. 7b presents result corresponding to internal Rayleigh number , as increases positively (heat source), decreases positively when and 2. When the value of increases negatively show destabilizing effect. But, for heat sink (Fig. 7c) i.e. when the magnitude of increases showing stabilizing effect of the system. In Fig. 7d and e, the effect of throughflow is presented. For up-directed flow the value of decreases positively showing destabilizing effect. While for inflow the value of negative for lower values of and decreasing the value of showing stabilizing effect. Further moderate values of the stabilizing effect is more and approaching to zero. The result related to linear theory may be compared with the studies of Kiran et al. [39].
6. Conclusions
The effect of gravity modulation and vertical throughflow on Bénard–Darcy convection is investigated for linear and weakly nonlinear studies. The porous medium is internally heated. The Ginzburg–Landau model used for weakly nonlinear theory and Venezian approach is used for linear theory. The following conclusions are drawn on previous analysis:
- Effect of is to enhance the heat transport for lower values of and diminishes for large values of .
- Effect of anti-gravity flow Pe > 0 increases heat transfer and pro-gravity flow Pe < 0 diminishes heat transfer.
- Upon increasing , heat transport increases.
- Upon increasing the value of frequency of gravity modulation , the amplitude of convection decreases, thus effect of g-jitter becomes negligible at higher values of .
- The magnitude of streamlines increases with time and archives maximus size for further values of time.
- Initially isotherms are flat due to conduction state, becomes contour showing the convective regime.
- Low frequency of g-jitter shows its maxim either stabilizing or destabilization effect but, high frequency stabilizes the system.
- Heat source () and anti-gravity flow () have destabilizing effect, heat sink () and pro-gravity flow () have stabilizing effect on the system.
Acknowledgements
The author thank the referees for their valuable suggestions that made the paper into its current form. The author Dr. P. Kiran would like to thank Professor Y. Narasimhulu (Vice Chancellor, RU) for providing research specialities in the department and his encouragement toward research. The author thank Prof. BS. Bhadauria, Ph.D. Supervisor, Institute of Science, Dept of Mathematics, BHU, Varanasi; for motivation toward research.
References
- [1] E.S. Nelson; An examination of anticipation of g-jitter on space station and its effects on materials processes; NASA TM (1991), p. 103775
- [2] M. Wadih, B. Roux; Natural convection in a long vertical cylinder under gravity modulation; J. Fluid Mech., 193 (1988), pp. 391–415
- [3] H. Wadih, N. Zahibo, B. Roux; Effect of gravity jitter on natural convection in a vertical cylinder; Low-gravity fluid dynamics and transport phenomena (A92-17051 04-29). Washington, DC, American Institute of Aeronautics and Astronautics, Inc. (1990), pp. 309–354
- [4] G.Z. Gershuni, E.M. Zhukhovitskii, I.S. Iurkov; On convective stability in the presence of periodically varying parameter; J. Appl. Math. Mech., 34 (1970), pp. 442–452
- [5] P.M. Gresho, R.L. Sani; The effect of gravity modulation on the stability of a heated fluid layer; J. Fluid Mech., 40 (1970), pp. 783–806
- [6] W.M. Yang; Stability of viscoelastic fluids in a modulated gravitational field; Int. J. Heat Mass Transf., 40 (1997), pp. 1401–1410
- [7] M.S. Malashetty, V. Padmavathi; Effect of gravity modulation on the onset of convection in a fluid and porous layer; Int. J. Eng. Sci., 35 (1997), pp. 829–839
- [8] D.A.S. Rees, I. Pop; The effect of G-jitter on vertical free convection boundary-layer flow in porous media; Int. Commun. Heat Mass Transf., 27 (2000), pp. 415–424
- [9] S. Govender; Weak non-linear analysis of convection in a gravity modulated porous layer; Transp. Porous Media, 60 (2005), pp. 33–42
- [10] A.V. Kuznetsov; Linear stability analysis of the effect of vertical vibration on bioconvection in a horizontal porous layer of finite depth; J. Porous Media, 9 (2006), pp. 597–608
- [11] B.S. Bhadauria, P. Kiran; Weak nonlinear double diffusive magneto-convection in a Newtonian liquid under gravity modulation; J. Appl. Fluid Mech., 8 (4) (2014), pp. 735–746
- [12] B.S. Bhadauria, P.G. Siddheshwar, K. Jogendra, Om.P. Suthar; Nonlinear stability analysis of temperature/gravity modulated Rayleigh–Beńard convection in a porous medium; Transp. Porous Media, 92 (2012), pp. 633–647
- [13] B.S. Bhadauria, I. Hashim, P.G. Siddheshwar; Study of heat transport in a porous medium under G-jitter and internal heating effects; Transp. Porous Media, 96 (2013), pp. 21–37
- [14] B. S Bhadauria, P. Kiran; Nonlinear thermal Darcy convection in a nanofluid saturated porous medium under gravity modulation; Adv. Sci. Lett., 20 (2014), pp. 903–910
- [15] P. Kiran; Nonlinear thermal convection in a viscoelastic nanofluid saturated porous medium under gravity modulation; Ain Shams Eng. J. (2015) http://dx.doi.org/10.1016/j.asej.2015.06.005
- [16] G.M. Homsy, A.E. Sherwood; Convective instabilities in porous media with throughflow; AIChE J., 22 (1976), pp. 168–174
- [17] M.C. Jones, J.M. Persichetti; Convective instability in packed beds with throughflow; AIChE J., 32 (1986), pp. 1555–1557
- [18] I.S. Shivakumara, S. Sureshkumar; Convective instabilities in a viscoelastic-fluid-saturated porous medium with throughflow; J. Geophys. Eng., 4 (2007), pp. 104–115
- [19] I.S. Shivakumara, S. Sureshkumar; Convective instabilities in a viscoelastic-fluid-saturated porous medium with throughflow; J. Geophys. Eng., 4 (2007), pp. 104–115
- [20] A. Khalili, I.S. Shivakumara; Onset of convection in a porous layer with net throughflow and internal heat generation; Phys. Fluids, 10 (1998), pp. 315–317
- [21] D.A. Nield; Convective instability in porous media with throughflow; AIChE J., 33 (1987), pp. 1222–1224
- [22] S.P. Suma, Y.H. Gangadharaiahand, R. Indira; Effect of throughflow and variable gravity field on thermal convection in a porous layer; Int. J. Eng. Sci. Technol., 3 (2011), pp. 7657–7668
- [23] P. Kiran; Throughflow and g-jitter effects on binary fluid saturated porous medium; Appl. Math Mech., 36 (10) (2015), pp. 1285–1304
- [24] P. Kiran; Throughflow and gravity modulation effects on heat transport in a porous medium; J. Appl. Fluid Mech., 9 (4) (2015)
- [25] P. Kiran, B.S. Bhadauria; Nonlinear throughflow effects on thermally modulated porous medium; Ain Shams Eng. J. (2014) http://dx.doi.org/10.1016/j.asej.2015.03.010
- [26] R.K. Vanishree; Effects of throughflow and internal heat generation on a thermo convective instability in an anisotropic porous medium; J. Appl. Fluid Mech., 7 (2014), pp. 581–590
- [27] G. Hetsroni, M. Gurevich, R. Rozenblit; Natural convection in metal foam strips with internal heat generation; Exp. Therm. Fluid Sci., 32 (2008), pp. 1740–1747
- [28] B.S. Bhadauria, I. Hashim, P.G. Siddheshwar; Study of heat transport in a porous medium under G-jitter and internal heating effects; Transp. Porous Media, 96 (2013), pp. 21–37
- [29] B.S. Bhadauria, A. Kumar, J. Kumar, N.C. Sacheti, P. Chandran; Natural convection in a rotating anisotropic porous layer with internal heat; Transp. Porous Media, 90 (2011), pp. 687–705
- [30] S. Saravanan; Thermal non-equilibrium porous convection with heat generation and density maximum; Transp. Porous Media, 76 (2009), pp. 35–43
- [31] B.S. Bhadauria, P. Kiran; Heat transport in an anisotropic porous medium saturated with variable viscosity liquid under temperature modulation; Transp. Porous Media, 100 (2013), pp. 279–295
- [32] W.V.R. Malkus, G. Veronis; Finite amplitude cellular convection; J. Fluid Mech., 4 (1958), pp. 225–260
- [33] G. Venezian; Effect of modulation on the onset of thermal convection; J. Fluid Mech., 35 (1969), pp. 243–254
- [34] S.H. Davis; The stability of time periodic flows; Annu. Rev. Fluid Mech., 8 (1976), pp. 57–74
- [35] A. Srivastava, B.S. Bhadauria, P.G. Siddheshwar, I. Hashim; Heat transport in an anisotropic porous medium saturated with variable viscosity liquid under G-jitter and internal heating effects; Transp. Porous Media, 99 (2013), pp. 359–376
- [36] R. Kippenhahn, A. Weigert; Stellar Structure and Evolution; Springer (1994)
- [37] B.S. Bhadauria, P. Kiran; Weak nonlinear analysis of magnetoconvection under magnetic field modulation; Phys. Scripta, 89 (9) (2014), p. 095209
- [38] B.S. Bhadauria, P. Kiran; Effect of rotational speed modulation on heat transport in a fluid layer with temperature dependent viscosity and internal heat source; Ain Shams Eng. J., 5 (4) (2014), pp. 1287–1297
- [39] P. Kiran, B.S. Bhadauria, V. Kumar; Thermal convection in a nanofluid saturated porous medium with internal heating and gravity modulation; J. Nanofluid (2016) accepted
Document information
Published on 12/04/17
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?