Implementation of a moving finite element mesh within the catenary-pantograph dynamic interaction

Resumen

En este artículo se presenta la aplicación tecnológica a la interacción dinámica catenaria-pantógrafo de una metodología propuesta para estructuras flexibles sometidas a cargas móviles. En primer lugar se describe el modelado de una malla móvil de elementos finitos que se desplaza sobre el hilo de contacto de forma solidaria al pantógrafo que recorre la catenaria y, posteriormente, se presenta la comparación de esta metodología frente a un modelo de elementos finitos convencional de malla fija. El caso simulado corresponde al propuesto por la norma EN-50318, obteniendo resultados acordes a los intervalos de validación propuestos por dicha norma. La principal ventaja del método de malla móvil reside en que para precisiones análogas el tiempo de cálculo es del orden de 4 veces menor que el modelo clásico.

Abstract

This paper presents a technological application of a general methodology to analyze cable structures under moving loads, particularly on the catenary-pantograph dynamic interaction. This work firstly describes the modeling of a finite element moving mesh which integrally moves over the contact wire following the pantograph along the whole catenary, prior focusing on its comparison against the classical finite element mesh. The case study corresponds to the standard EN-50318 one, whose results fulfill the ranges proposed by this validation rule. The main advantage of the moving mesh method is presented in the falling of computational costs about 4 times lower than the classic model with similar precision.

Palabras clave

Dinámica ; Carga móvil ; Catenaria ; Pantógrafo ; Análisis no lineal ; Malla móvil

Keywords

Dynamic ; Moving load ; Catenary ; Pantograph ; Non-linear analysis ; Moving mesh

1. Introducción

La simulación de la interacción dinámica catenaria-pantógrafo es en la actualidad uno de los aspectos más relevantes de la investigación en el ámbito de la alta velocidad y la interoperabilidad ferroviaria europea. En los últimos años se han desarrollado diferentes modelos de simulación. No obstante, los requerimientos en precisión y tiempos de cálculo hacen que la investigación en este campo continúe presentando gran actividad. Este trabajo propone la aplicación del mallado móvil presentado en Such et al. [1] como una vía novedosa para favorecer la simulación precisa de la interacción no lineal entre la catenaria y el pantógrafo con una reducción sustancial de los tiempos de cálculo.

Durante los últimos años se ha invertido un gran esfuerzo en analizar el comportamiento dinámico de este sistema, algo que hace decenios comenzó a ser objeto de estudio desde distintas perspectivas. Ockendon y Tayler [2] proporcionan una aproximación analítica de la fuerza de contacto, [3] analiza mediante el método de los elementos finitos su variación, [4] determinan las frecuencias y modos propios, etc. Dentro de este contexto uno de los trabajos más notables y que cuenta además con una vasta revisión del estado del arte es el publicado dos Poetsch et al. [5] .

Entre los modelos que se denominan simplificados, destaca como uno de los más usados el presentado por Wu y Brennan [6] , en el que, partiendo de las propiedades dinámicas de la catenaria vistas por el pantógrafo y de una aproximación senoidal de la rigidez, se propone un modelo simplificado unidimensional del sistema catenaria-pantógrafo. Estos mismos autores analizan el efecto que la propagación de ondas tiene sobre la rigidez de la catenaria [7] . Lopez-Garcia et al. [8] incorporan al modelo presentado por Wu y Brennan [6] un modelo de fuerza de contacto basado en multiplicadores de Lagrange, además de incluir como aportación más relevante la distribución real de la rigidez de la catenaria. Finalmente, entre las simplificaciones más comunes también destaca la linealización de la catenaria mediante métodos de superposición modal como las desarrolladas en Zhang et al. [9] , [10]  and [11] .

Por otra parte, entre los modelos que se pued en denominar complejos existen 2 enfoques principales: los métodos de elementos finitos y los sistemas de ecuaciones diferenciales algebraicas. El modelo propuesto por Collina y Bruni [12] presenta elementos de tipo viga para el hilo de contacto y sustentador, elementos no lineales con ley de comportamiento no lineal para reproducir el comportamiento del aflojamiento para las péndolas, un modelo de pantógrafo que incluye grados de libertad como sólido-rígido y de flexión, así como un modelo de contacto basado en la técnica de penalización de la interpenetración. Park et al. [13] , empleando un método de elementos finitos convencional basado en elementos viga, obtienen las ecuaciones de la dinámica del pantógrafo para realizar un análisis de sensibilidad. La aplicación de dicho análisis paramétrico de sensibilidad a la fuerza de contacto permite modificar las variables de diseño del pantógrafo para reducir las pérdidas de contacto. Otros trabajos de gran relevancia en este contexto son los de Arnold [14] , Arnold y Simeon [15] , y Teichelmann et al. [16] , con un enfoque eminentemente matemático en el que se formula el problema mediante sistemas de ecuaciones diferenciales algebraicas.

La principal ventaja de los modelos de elementos finitos reside en su mayor concordancia entre el modelado y la realidad física del problema. Cuando la fidelidad con el fenómeno físico modelado y la precisión en los cálculos son factores clave, la calidad del mallado es importante en la medida en que determina el error de simulación, ver por ejemplo Babuška y Aziz [17] . Hay que considerar 2 aspectos, por una parte que el número de elementos es relevante por el elevado coste computacional asociado a elevadas densidades de malla, y por otra parte, que el tamaño de los elementos influye en la definición del paso de tiempo a emplear para garantizar la estabilidad dinámica.

Tal y como se ha comentado anteriormente, en este artículo se propone un modelo de elementos finitos con una malla gruesa para todo el continuo sobre la que se superpone una malla móvil fina. El propósito de esta malla móvil es refinar dinámicamente el hilo de contacto en torno al punto de interacción entre la catenaria y el pantógrafo. Donde existe un «contacto móvil»equivalente a las cargas móviles referidas anteriormente. La principal aportación de este artículo es precisamente la aplicación de una metodología para analizar el contacto entre un continuo unidimensional sobre el que actúa un contacto móvil.

Entre los trabajos específicos en dinámica de catenarias bajo el efecto de cargas móviles hay que reseñar los trabajos de Metrikine [18] y Metrikine y Bosch [19] , donde se estudia el régimen permanente de este fenómeno para catenarias de uno y 2 cables longitudinales respectivamente. No obstante, el presente trabajo aporta, con la metodología propuesta por Such et al. [1] , la aplicación de un contacto nodo-nodo con un elemento viga con no linealidad geométrica empleando una malla móvil. En general, el problema se suele resolver haciendo mover el continuo estructural en vez de mover la carga, mientras que lo que se plantea en este artículo es que el mallado se localiza en torno a dicha carga, moviéndose solidariamente con la carga. Las ventajas que aporta esta metodología son que contempla de forma natural las principales no linealidades presentes en el problema del contacto, que proporciona un nivel de precisión muy notable y, sobre todo, que permite obtener soluciones en tiempos de simulación notablemente inferiores cuando es comparada con otros métodos convencionales.

El presente artículo está estructurado de la siguiente forma: en primer lugar se presenta en la sección 2 una propuesta de discretización dinámica de la catenaria para su interacción con el pantógrafo, para ello se define el entorno del dominio local de la malla móvil sobre el hilo de contacto y el acoplamiento entre esta y la malla global estática de la estructura. Después, como principal aportación de este artículo, se aplica la metodología propuesta por Such et al [1] al estudio en la sección 3 de la interacción catenaria-pantógrafo como problema arquetipo de estructura de cables sometida a una carga móvil así como su comparación con un método de elementos finitos clásico y su verificación de acuerdo a la norma EN-50318 [20] . Finalmente se presentan las principales conclusiones que se pueden extraer del método propuesto y su aplicación.

2. Discretización dinámica del sistema catenaria-pantógrafo

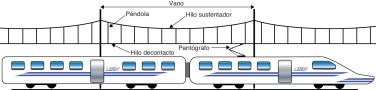
En los sistemas ferroviarios se denomina comúnmente catenaria al sistema de alimentación eléctrica por vía aérea. En la figura 1 se muestra un esquema de una catenaria, la cual es una estructura de cables tensionada y compuesta por el hilo de contacto, elemento a través del cual y por medio de frotación se produce la transmisión de energía al pantógrafo del tren, el hilo sustentador, encargado de soportar el peso del conjunto de cables y las péndolas, elementos que junto con el hilo sustentador sitúan el hilo de contacto a la altura deseada. El conocimiento de la dinámica del sistema catenaria-pantógrafo es crucial para el correcto diseño de líneas de alta velocidad ya que la calidad de la captación de energía depende de la capacidad de conseguir mantener un buen contacto entre catenaria y pantógrafo. Para ello es necesario que, por un lado, no se produzcan despegues entre el pantógrafo y el hilo de contacto que interrumpan la captación de energía y que, por otro, la fuerza de contacto no alcance valores excesivamente elevados que conduzcan a una vida útil más corta tanto para el hilo de contacto como para las pletinas del pantógrafo.

Figura 1. Esquema del sistema de captación de energía por vía aérea de un sistema ferroviario.

El análisis de la respuesta dinámica de la catenaria conlleva un elevado coste computacional debido no solo a las propias no linealidades asociadas a la interacción catenaria-pantógrafo sino también a la no linealidad inherente a las estructuras de cables y a la aparición de ondas y sus efectos sobre la estructura. Para mejorar el modelado del fenómeno tanto desde el punto de vista de la precisión como de las actuaciones del método numérico, se ha desarrollado una técnica de remallado móvil que representa una novedad en el modelado de este tipo de sistemas. Esta técnica de remallado móvil conserva el número de grados de libertad del problema al igual que el remallado de refinado-r , sin embargo, el concepto es esencialmente diferente a la mayoría de otros remallados ya que en cada instante de la simulación dinámica, el método propuesto por Such et al [1] aumenta la densidad de elementos del mallado solo en la zona del contacto. Concretamente la malla móvil correrá por el hilo de contacto siguiendo al pantógrafo, lo cual permite concentrar la mayor parte del esfuerzo computacional en el subdominio del modelo con mayor predominancia de no linealidad permitiendo obtener la precisión deseada y limitando el coste computacional. Hay que destacar 2 aspectos complementarios e igualmente relevantes en la implementación de la malla móvil: en primer lugar la configuración y distribución de nodos en el subdominio de malla móvil y, en segundo lugar, su ensamblado y seguimiento del contacto sobre el mallado grueso original.

En este trabajo la malla móvil seguirá una distribución exponencial de los nodos, permitiendo concentrar más nodos en las proximidades de la zona de contacto y menos en los extremos del subdominio de remallado. El algoritmo implementado parte de la hipótesis de que existe igual número de nodos a uno y otro lado del punto de contacto, lo cual no implica una distribución simétrica ya que los límites inferior, ξ_ri , y superior, ξ_rs , del intervalo Ω no son necesariamente simétricos. Sin embargo, el algoritmo sí conlleva un número impar de nodos en el subdominio de remallado para conseguir un contacto nodo-nodo, es decir, siempre existirá un nodo siguiendo el contacto móvil entre catenaria y pantógrafo, distribuyéndose a ambos lados del mismo n_s nodos de forma que

$n_{s}=\left\{{\begin{array}{cc}(n-1)/2&si\quad n\quad es{\mbox{   }}impar\\n/2-1&si\quad n\quad es{\mbox{   }}par\end{array}}\right.$

La distribución nodal exponencial implementada define la localización ξ_k de los nodos, respecto del sistema móvil, según

$\xi _{k}=\left\{{\begin{array}{cc}exp\left(1/c\right)-exp\left(1/c\right)exp\left(A(\xi _{ri})\right)&\quad \forall \quad \xi _{k}\in \left[\xi _{ri},0\right){\mbox{   }}\vert {\mbox{   }}k\leq n_{s}\in \mathbb {N} ,\\exp\left(1/c\right)exp\left(A(\xi _{rs})\right)-exp\left(1/c\right)&\quad \forall \quad \xi _{k}\in \left(0,\xi _{rs}\right]{\mbox{   }}\vert {\mbox{   }}k\leq n_{s}\in \mathbb {N} ,\end{array}}\right.$

( 1)

donde A (ξ ) es

$A(\xi )={\frac {k\left(c\quad ln\left(\xi +exp\left(1/c\right)\right)-1\right)}{c\quad n_{s}}}.$

Finalmente es posible definir la función ${\textstyle s\left(\Omega ,n,\xi _{i},c\right)}$ del tamaño de los elementos de la malla móvil, como una simple diferencia entre los nodos que componen el elemento que ocupa la posición ξ_i , es decir el tamaño del mismo, s , queda definido como

$s\left(\Omega ,n,\xi _{i},c\right)=\xi _{ki^{+}}-\xi _{ki^{-}},$

( 2)

siendo ${\textstyle \xi _{ki^{-}}}$ y ${\textstyle \xi _{ki^{+}}}$ las localizaciones horizontales de los nodos izquierdo y derecho que definen el elemento i , respectivamente.

Por último, cabe hacer mención al acoplamiento de la malla móvil con la malla gruesa fija presente en todo el continuo. El hecho de que el proceso de remallado no sea demasiado costoso computacionalmente en comparación con el posible remallado del sistema completo, permite plantear la ejecución de este procedimiento paso a paso sin incurrir en tiempos de cálculo inaceptables. No obstante, los argumentos no son solo de tiempo de ejecución sino también de precisión de cálculo. En este sentido son 2 los aspectos que resultan claves en la simulación y que justifican el remallado móvil: el tamaño de los elementos en la zona de contacto y la dinámica del contacto. Concretamente y debido a las particularidades de la interacción dinámica catenaria-pantógrafo, el método de contacto óptimo para la simulación bidimensional de este fenómeno es el nodo-nodo, ya que un método nodo-segmento (perteneciendo el nodo al pantógrafo y el segmento a la catenaria) puede ser fuente de fenómenos numéricos de alta frecuencia asociados a las pérdidas de contacto y a la aparición de percusiones cuando el tamaño de la malla no es suficientemente fino.

Tal como describen Such et al. [1] para cada paso de tiempo los vectores globales de desplazamientos, velocidades y aceleraciones se construyen a partir de la interpolación mediante las funciones de forma del elemento finito a emplear, las funciones de la posición y los parámetros de la malla móvil. Una vez que se establece la malla gruesa, se construyen las matrices globales de masa, amortiguamiento y rigidez, así como las fuerzas internas y externas. El algoritmo de reensamblado se caracteriza por 3 aspectos. En primer lugar, la malla fina introduce un aumento de las dimensiones de las matrices globales. En segundo lugar, es el responsable de añadir las nuevas contribuciones a las correspondientes matrices y vectores globales del sistema a partir de las nuevas interconectividades creadas en la construcción de los nuevos elementos. En tercer lugar, el algoritmo de reensamblado modifica en cada paso de tiempo las contribuciones a las matrices y vectores globales correspondientes a los nuevos elementos en su movimiento. Finalmente, en el proceso de reensamblado, las distintas discretizaciones originales y el mismo integrador temporal resultan opacos para la formación de las matrices y vectores globales.

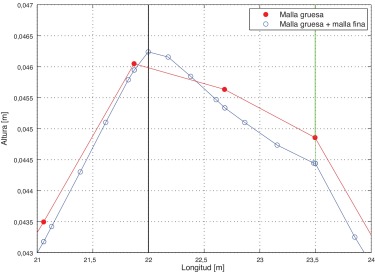
La formulación de una malla móvil sobre el hilo de contacto en el punto donde actúa el pantógrafo permite un mejor modelado de la física del problema sin incurrir en un coste computacional excesivo. Así en la figura 2 se muestra en detalle una comparación entre el efecto estático de una carga (aplicada a 22 m) que actúa sobre un cable suspendido (en 23.5 m), discretizado con una malla gruesa, representada con círculos, o habiendo adaptado sobre ésta la malla móvil, con circunferencias. Puede apreciarse claramente cómo el comportamiento del remallado se ajusta de forma más fiel a la deformación de un cable sometido a su propio peso y a cargas concentradas.

Figura 2. Comparación de la deformada del cable en el que se produce el contacto con la carga móvil para los casos de emplear una malla gruesa y una malla adaptada con malla móvil

3. Análisis de la interacción dinámica catenaria-pantógrafo

El modelado de la interacción dinámica catenaria-pantógrafo requiere de una discretización suficientemente fina como para ser capaz de recoger la dinámica no lineal del sistema. De ahí que la implementación de una malla móvil, asociada al punto de contacto entre el pantógrafo y la catenaria, que recorre el hilo de contacto es fundamental para no incurrir en tiempos de cálculo inaceptables. Los criterios de evaluación seguidos para discernir la precisión del modelo han sido aquellos establecidos en la norma EN-50318. Una discretización de este tipo requiere de una elevada capacidad de computación, ya que la estructura cuya dinámica se quiere estudiar, por un lado presenta no linealidades, como son el propio fenómeno de contacto, la no linealidad geométrica asociada a la estructura flexible que es la catenaria y la nula resistencia a compresión de las péndolasy, por otro lado, están las dimensiones espaciales de la estructura, que pueden alcanzar fácilmente longitudes del orden de 1.000 m.

A modo de referencia se ha realizado una simulación empleando un modelo de elementos finitos clásico con una malla suficientemente densa para verificar los criterios establecidos en el estándar europeo anteriormente citado. La discretización de la catenaria se realiza con elementos unidimensionales, empleando la formulación corrotacional desarrollada en el Crisfield [21] y tanto sus propiedades geométricas como estructurales se definen en la norma. El hilo sustentador y el de contacto se han modelado con elementos tipo viga con formulación corrotacional. Las péndolas emplean elementos corrotacionales tipo barra sin capacidad para soportar compresión, con los que poder simular su posible aflojamiento o pandeo. Para esta malla convencional se han empleado entre cada 2 péndolas: 3 elementos en el hilo sustentador; 21 elementos en el hilo de contacto; y un único elemento para las propias péndolas. El pantógrafo se ha modelado mediante un sistema discreto de masas y muelles con grados de libertad translacionales y propiedades estructurales tal y como se describe en la normativa de validación.

El modelo de elementos finitos que implementa la metodología propuesta se ha realizado con una malla estática gruesa para todo el continuo sobre la que se superpone la malla móvil. Como ya se ha comentado anteriormente el propósito de esta es refinar dinámicamente el hilo de contacto en torno al punto de interacción entre la catenaria y el pantógrafo. Dicho contacto móvil se ha modelado con un método clásico de penalización. La malla fija se ha definido de forma análoga a la malla convencional anteriormente descrita, empleando para esta simulación entre cada 2 péndolas 3 y 4 elementos en los hilos sustentador y de contacto respectivamente, mientras que para la malla móvil se ha optado por un dominio de 6 m de longitud con 20 elementos distribuidos según una función exponencial con un índice de concentración c  = 3.

Ambos modelos de elementos finitos emplean el conocido método de integración temporal HHT desarrollado por Hilber, Hughes y Taylor [22] . A su vez, el método de contacto empleado consiste en un método de penalización sencillo con la constante de penalización, k_p  = 50 kN/m, definida por la norma EN-50318.

El problema de la interacción catenaria-pantógrafo no presenta soluciones analíticas ni tampoco casos de referencia que representen un estándar aceptado por la comunidad científica con los que validar un determinado modelo. En cambio, a nivel tecnológico la norma define una prueba de verificación con la que contrastar los resultados de cualquier modelo. Dicha norma establece los intervalos en los que se deben encontrar diversos resultados de una simulación para considerar el modelo como válido. La tabla 1 recoge los indicadores propuestos por la norma y los resultados que se han obtenido en la simulación empleando el modelo de elementos finitos convencional, esto es, sin malla móvil. Por otra parte en la tabla 2 , se muestran los correspondientes al modelo de malla móvil propuesto. Ambos resultados muestran los valores de dichos indicadores para las 2 velocidades de marcha del tren especificadas por la norma, esto es 250 y 300 km/h. Además en ambas tablas, 1 y 2 , se muestran los tiempos de cálculo empleados por un ordenador con Procesador Intel(R) Core(TM) 2 Duo CPU T8100 - 2 × 2, 10 GHz y en ellas se puede observar que para resultados parecidos, es decir nivel de precisión comparable con respecto a los valores aceptados por la norma, el método de elementos finitos con malla móvil es del orden de 4 veces más rápido que el modelo de elementos finitos convencional.

Tabla 1. Validación del modelo MEF clásico según la norma EN-50318 [20]

Velocidad	250 km/h	EN-50318	300 km/h	EN-50318
Fuerza media de contacto [N]	116,4	[110, 120]	116,1	[110, 120]
Desviación estándar [N]	27,6	[26, 31]	35,2	[32, 40]
Máximo estadístico [N]	199,2	[190, 210]	221,7	[210, 230]
Mínimo estadístico [N]	33,5	[20, 40]	10,4	[-5, 20]
Máximo real [N]	171,3	[175, 210]	208,9	[190, 225]
Mínimo real [N]	60,8	[50, 75]	38,7	[30, 55]
Máx. elevación en 1.er soporte [mm]	51,2	[48, 55]	57,3	[55, 65]
Máx. elevación en 2.o soporte [mm]	48,0	[48, 55]	56,9	[55, 65]
Máx. elevación en 3.er soporte [mm]	48,2	[48, 55]	56,2	[55, 65]
Pérdida de contacto [%]	0	0	0	0
Tiempo de cálculo [h]	11, 7		11, 8

Tabla 2. Validación del modelo MEF con malla móvil según la norma EN-50318 [20]

Velocidad	250 km/h	EN-50318	300 km/h	EN-50318
Fuerza media de contacto [N]	116,2	[110, 120]	115,8	[110, 120]
Desviación estándar [N]	27,6	[26, 31]	35,4	[32, 40]
Máximo estadístico [N]	199,0	[190, 210]	222,1	[210, 230]
Mínimo estadístico [N]	33,5	[20, 40]	9,4	[-5, 20]
Máximo real [N]	176,7	[175, 210]	212,8	[190, 225]
Mínimo real [N]	61,2	[50, 75]	41,2	[30, 55]
Máx. elevación en 1.er soporte [mm]	54,2	[48, 55]	61,5	[55, 65]
Máx. elevación en 2.o soporte [mm]	50,4	[48, 55]	60,9	[55, 65]
Máx. elevación en 3.er soporte [mm]	51,4	[48, 55]	60,4	[55, 65]
Pérdida de contacto [%]	0	0	0	0
Tiempo de cálculo [h]	2, 9		3, 0

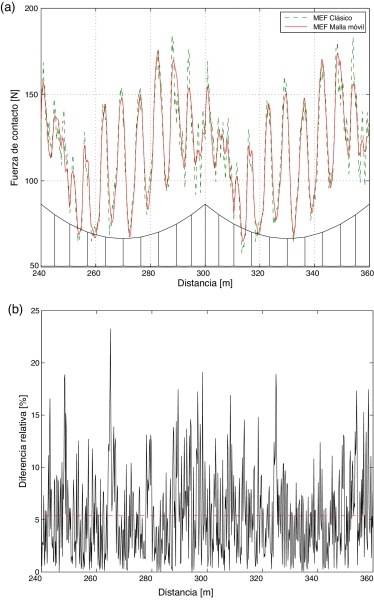
En la figura 3 se presenta una comparación de la evolución de la fuerza de contacto para la velocidad de 250 km/h para los 2 modelos de elementos finitos así como la diferencia relativa entre ambos en los 2 vanos centrales especificados por la norma. Se puede comprobar que ambos resultados son muy parecidos y que el valor medio de la diferencia a lo largo de los 2 vanos es de 5.4% alcanzando diferencias puntuales del orden del 12% como máximo.

Figura 3. (a) Comparación de fuerzas de contacto a 250 km/h (b) diferencia relativa entre ambas.

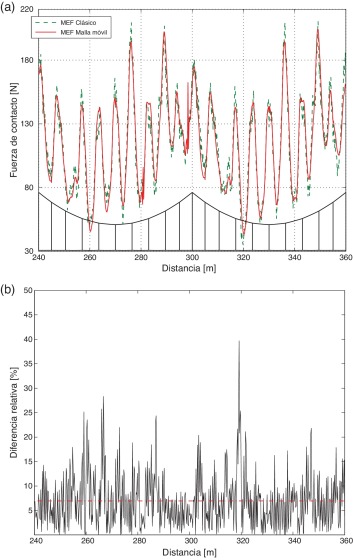
Igualmente en la figura 4 se presentan las fuerzas de contacto para los 2 modelos de elementos finitos así como su diferencia relativa para una velocidad de paso de tren de 300 km/h. Los resultados obtenidos por ambos modelos presentan diferencias máximas locales del orden del 13% y el valor medio de la diferencia a lo largo de los 2 vanos es del 6, 9%.

Figura 4. (a) Comparación de fuerzas de contacto a 300 km/h (b) diferencia relativa entre ambas

Las 2 figuras 3 y 4 muestran una evolución cualitativamente similar para los distintos modelos analizados: tanto a baja frecuencia, regida por los cambios de vano, como a más alta frecuencia, asociada a los pasos por péndolas. Además ambos modelos reproducen una mayor variabilidad en la fuerza de contacto asociada a la velocidad de 300 km/h cuando se compara con la de 250 km/h. Finalmente, se puede comprobar que para ambas velocidades de marcha del tren los 2 modelos producen resultados similares y el método de elementos finitos con malla móvil es capaz de reproducir toda la dinámica que retiene el modelo de elementos finitos convencional.

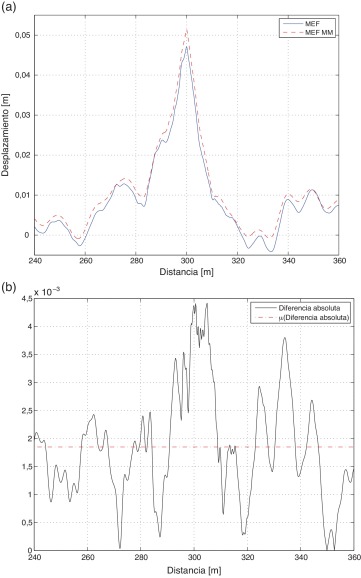
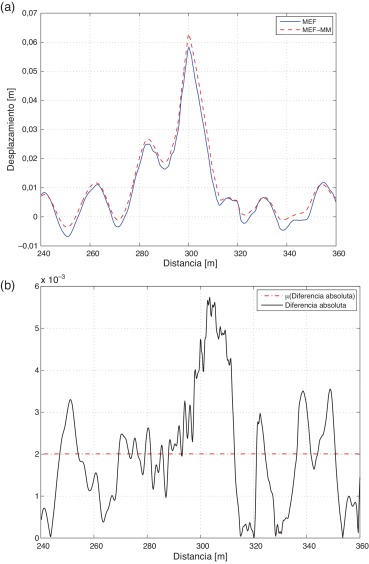
Respecto a la comparación de los desplazamientos en el hilo de contacto, en las figuras 5 y 6 se muestra la evolución temporal de la elevación del segundo soporte para 250  y 300 km/h respectivamente, entre los vanos quinto y sexto, al paso del pantógrafo. Se representan superpuestas las evoluciones temporales de dicha elevación según ambos modelos de elementos finitos, mostrándose también la diferencia absoluta entre los mismos. Nótese que las gráficas representan la elevación del hilo de contacto en dicho punto durante el periodo de tiempo en que el pantógrafo recorre estos vanos centrales. Los resultados muestran un comportamiento similar para los 2 modelos comparados y, aunque el modelo de elementos finitos sin malla móvil refleja valores de elevación ligeramente inferiores, la diferencia absoluta entre ambos desplazamientos para velocidades de paso de tren a 250  y 300 km/h es del orden de 1, 9 mm y de 2 mm, respectivamente.

Figura 5. (a) Comparación de la elevación en el 2.o soporte a 250 km/h y (b) diferencia en desplazamientos para ambos modelos.

Figura 6. (a) Comparación de la elevación en el 2.o soporte a 300 km/h y (b) diferencia en desplazamientos para ambos modelos.

4. Conclusiones

En este artículo se ha presentado la aplicación tecnológica de una metodología basada en el método de los elementos finitos para la interacción dinámica catenaria-pantógrafo. El fin de dicha metodología es el acoplamiento de una malla móvil situada en torno al punto de contacto entre una carga móvil y una estructura, concretamente entre el pantógrafo y el hilo de contacto de la catenaria respectivamente. Mientras que la malla móvil presenta una elevada densidad de elementos en torno al punto de contacto, el resto del continuo presenta una malla con una menor densidad de elementos, lo cual principalmente ha revelado en este trabajo importantes ventajas en coste computacional.

El problema abordado presenta como dificultades propias el modelado de una estructura compleja de cables con una rigidez estática con elevadas variaciones sobre la que actúa la acción del pantógrafo a través de la incorporación del contacto con la catenaria. La verificación del modelo propuesto se ha realizado a 2 niveles: (i) por un lado se han comparado los resultados y prestaciones del modelo de malla móvil con un modelo de elementos finitos clásico, es decir, solo empleando una malla fija con una discretización tal que fuera capaz de producir resultados dentro de los intervalos especificados por los indicadores definidos en la norma EN-50318; y (ii) por otro lado se han comparado los resultados de distintos modelos de malla móvil con relación a los indicadores definidos por dicha norma.

Las principales conclusiones que se pueden extraer de la comparación son las siguientes: (i) en primer lugar el modelo de malla movil presenta la precisión necesaria para producir resultados dentro de los intervalos definidos por el citado estándar europeo; (ii) en segundo lugar el modelo de malla movil muestra un excelente nivel de acuerdo con los resultados obtenidos por el modelo de elementos finitos clásico, alcanzando niveles de diferencias relativas en valor medio a lo largo de 2 vanos en la fuerza de contacto del orden del 7% y en el desplazamiento diferencias medias inferiores a 2 mm, por lo que se puede afirmar que la precisión del modelo de malla móvil es adecuada para propósitos de simulación; (iii) y finalmente, la principal ventaja del modelo de malla móvil se pone de manifiesto cuando se comparan los tiempos de cálculo requeridos. Se observa que la metodología propuesta presenta reducciones del tiempo de simulación en torno a 4 veces el tiempo empleado por un modelo convencional de elementos finitos. Este aspecto es decisivo para lograr una simulación dinámica con el método de los elementos finitos, actualmente de amplia aplicación en investigación, con una reducción sustancial de coste computacional. Esto requiere el desarrollo de metodologías como la aquí propuestata que, por la elevada relación entre la precisión y el tiempo de cálculo, abren la puerta al uso de técnicas de optimización, análisis de sensibilidad, estudios sobre la estabilidad dinámica, etc.

Agradecimientos

Los resultados aquí presentados han sido obtenidos en el desarrollo de diversos proyectos financiados parcialmente por el Colegio Nacional de Ingenieros del ICAI, Cosemel Ingeniería y el Ministerio de Ciencia y Tecnología a través de los proyectos de Plan Nacional TRAN2009-13912-C02-02/TREN y TRA2012-37940.

References

1. [1] M. Such, J.R. Jiménez-Octavio, A. Carnicero, C. Sanchez-Rebollo. Simulación de cargas móviles sobre estructuras mediante un mallado móvil de elementos finitos. Rev. Int. Metod. Numer. Calc. Dise. Online, 2014.
2. [2] J.R. Ockendon, A.B. Tayler; The dynamics of a current collection system for an electric locomotive; Proceedings of the Royal Society of London, Series A (Mathematical and Physical Sciences), 322 (1551) (1971), pp. 447–468
3. [3] T. Vinayagalingam; Computer evaluation of controlled pantographs for current collection from simple catenary overhead equipment at high speed; J. Dyn. Syst.-T. ASME, 105 (1983), pp. 287–294
4. [4] S.D. Eppinger, D.N. O’Connor, W.P. Seering, D.N. Wormley; Modeling and experimental evaluation of asymmetric pantograph dynamics; J. Dyn. Syst.-T. ASME, 110 (2) (1988), pp. 168–174
5. [5] G. Poetsch, J. Evans, R. Meisinger, W. Kortüm, W. Baldauf, A. Veitl, J. Wallaschek; Pantograph-catenary dynamics and control; Vehicle Syst. Dyn., 28 (1997), pp. 159–195
6. [6] T.X. Wu, M.J. Brennan; Basic analytical study of pantograph-catenary system dynamics; Vehicle Syst. Dyn., 30 (1998), pp. 443–456
7. [7] T.X. Wu, M.J. Brennan; Dynamic stiffness of a railway overhead wire system and its effect on pantograph-catenary system dynamics; J. Sound Vibr., 219 (3) (1999), pp. 483–502
8. [8] O. Lopez-Garcia, A. Carnicero, J.L. Maroño; Influence of stiffness and contact modelling on catenary-pantograph system dynamics; J. Sound Vibr., 299 (4-5) (2007), pp. 806–821
9. [9] W. Zhang, G. Mei, X.J. Wu, Z. Shen; Hybrid simulation of dynamics for the pantograph-catenary system; J. Sound Vibr., 38 (6) (2002), pp. 393–414
10. [10] W. Zhang, G. Mei, J. Zeng; A study of pantograph/catenary system dynamics with influence of presag and irregularity of contact wire; Vehicle Syst. Dyn., 37 (2002), pp. 593–604
11. [11] W. Zhang, Y. Liu, G. Mei; Evaluation of the coupled dynamical response of a pantograph-catenary system: contact force and stresses; Vehicle Syst. Dyn., 44 (8) (2006), pp. 645–658
12. [12] A. Collina, S. Bruni; Numerical simulation of pantograph-overhead equipment interaction; Vehicle Syst. Dyn., 38 (4) (2002), pp. 261–291
13. [13] T.J. Park, C.S. Han, J.H. Jang; Dynamic sensitivity analysis for the pantograph of a high-speed rail vehicle; J. Sound Vibr., 266 (2) (September 2003), pp. 235–260
14. [14] M. Arnold; A pre-conditioned method for the dynamical simulation of coupled mechanical multibody systems; Z. Angew. Math. Mech., 81 (2000), pp. 7–818 Supplement 3 to Vol 8
15. [15] M. Arnold, B. Simeon; Pantograph and catenary dynamics: a benchmark problem and its numerical solution; Appl. Numer. Math., 34 (4) (2000), pp. 345–362
16. [16] G. Teichelmann, M. Schaub, B. Simeon; Modelling and simulation of railway cable systems; Z. Angew. Math. Mech., 85 (12) (2005), pp. 864–877
17. [17] I. Babuška, K. Aziz; On the angle condition in the finite element method; SIAM J. Numer. Anal., 13 (1976), pp. 214–226
18. [18] A.V. Metrikine; Steady state response of an infinite string on a non-linear visco-elastic foundation to moving point loads; J. Sound Vibr., 272 (3) (2004), pp. 1033–1046
19. [19] A.V. Metrikine, A.L. Bosch; Dynamic response of a two-level catenary to a moving load; J. Sound Vibr., 292 (2) (2006), pp. 676–693
20. [20] EN-50318 Validation of simulation of the dynamic interaction between pantographs and overhead contact line. Railway Applications. Current Collection Systems CENELEC, 2002.
21. [21] M.A. Crisfield; Non-linear finite element analysis of solids and structures, Vol. 1: Essentials; John Wiley & Sons, Baffins Lane, Chichester West Sussex PO19 IUD, England (1991)
22. [22] H. Hilber, T. Hughes, R. Taylor; Improved numerical dissipation for time integration algorithms in structural dynamics; Earthquake Eng. Struc., 5 (1977), pp. 283–292