Relation between the raise to span ratio and the real ultimate lateral strength for parabolic clamped arches considering different calculation hypothesis

Resumen

En este artículo se proponen gráficas que relacionan los parámetros f/L y λ = qL³ /EI_y para arcos biempotrados con diferentes secciones transversales y para diferentes hipótesis de cálculo.

Para ello es necesario determinar la carga crítica lateral de una serie de arcos biempotrados considerando diferentes hipótesis de cálculo en lo que se refiere a la linealidad geométrica y a las características del material acero.

La hipótesis de material elastoplástico con no linealidad geométrica considera la existencia de tensiones residuales e imperfecciones geométricas iniciales.

Abstract

Curved graphs that relate the f/L ratio and the λ = qL³ /EI_y parameter for clamped arches with the different calculation hypothesis are going to be proposed in this article.

It has been necessary to determine the real critical lateral strength of a series of clamped arches considering different calculation hypothesis respect to geometrical linearity and a steel material characteristic.

The elastic-plastic material hypothesis with non geometrical linearity considers the existence of residual stresses and initial lateral deflection.

Palabras clave

Parámetro crítico de pandeo ; Arcos parabólicos biempotrados ; Esbeltez reducida del arco con respecto al eje «y» ; Límite elástico ; Esbeltez de Euler

Keywords

Critical buckling parameter ; Clamped parabolic arches ; Reduced slenderness of the arches respect to the ‘y’ axis ; Yielding stress ; Euler slenderness

Notación

A- Rigidez a flexión de la sección transversal con respecto al eje «y» = E*I_y

b- Ancho del cajón

C- Rigidez a torsión de la sección transversal = G*J

λ- Parámetro crítico de pandeo = (q*L³ /A)

d- Longitud del alma

E- Módulo de deformación longitudinal del acero, de valor 210.000 MPa

ɛ- ${\textstyle {\sqrt {\frac {235}{f_{y}}}}}$ , con f_y en MPa

f- Flecha del arco

f_y  = σ_y- Límite elástico del acero

h- Altura del cajón

i_y- Radio de giro de la sección transversal con respecto al eje «y»

I_y- Momento de inercia de la sección transversal con respecto al eje «y»

I_z- Momento de inercia de la sección transversal con respecto al eje «z»

K_x- Restricción de la corona con respecto al eje «x»

K_z- Restricción de la corona con respecto al eje «z»

L- Longitud del arco

q- Carga uniformemente distribuida en planta (en t/ml)

t- Espesor de las chapas del cajón

t_w- Espesor del alma

λ_y- Esbeltez mecánica con respecto al eje «y» = L/i_y

${\textstyle {\overline {\lambda }}_{y}}$- Esbeltez reducida de Euler con respecto al eje ${\textstyle {\mbox{«}}y{\mbox{»}}={\frac {{\lambda }_{y}}{\sqrt {\frac {{\pi }^{2}E}{f_{y}}}}}}$

1. Introducción

En el presente artículo se resume de forma breve y concisa la investigación realizada por los autores con el fin de determinar la relación existente entre el parámetro f/L y la carga crítica de pandeo lateral para arcos parabólicos biempotrados sometidos a una carga uniformemente distribuida en planta.

La carga crítica se calcula bajo 3 hipótesis de cálculo:

• Cálculo elástico lineal.
• Cálculo elástico no lineal.
• Cálculo elastoplástico no lineal o carga última.

En el caso de las 2 primeras hipótesis, la modelización se realiza con elementos finitos lineales tipo «viga» y «lámina»; en el tercer caso, con elementos superficiales tipo «lámina», que permiten obtener resultados más ajustados a la realidad.

La primera época de los estudios de arcos metálicos se ha caracterizado por el exclusivo interés hacia el análisis de la estabilidad elástica lineal. Una vez asentado este conocimiento, el afán investigador dio un paso más para centrarse en la estabilidad elástica no lineal. El tercer grupo de trabajos aparece cuando los estructuralistas se preocupan por incluir los efectos en la inestabilidad del comportamiento no lineal del acero que, junto con la potencia de cálculo del ordenador, permite tener en cuenta hipótesis antes obviadas y abordar el problema de la determinación de la carga última de colapso de los arcos.

El objetivo de la presente investigación se integra en este último grupo de trabajos. La estabilidad elástica, lineal o no lineal, tiene un exclusivo interés académico toda vez que las cargas críticas que proporciona constituyen siempre una cota superior de la capacidad resistente de los arcos. Durante muchos años ha centrado el interés de muchos investigadores porque sus hipótesis simplificadoras permitían el estudio analítico y no requerían el empleo de una herramienta de la que entonces se carecía: el ordenador.

En lo que respecta a la estabilidad elástica lineal, Tokarz y Sandhú [1] calcularon la carga última de pandeo lateral torsional para arcos parabólicos biapoyados y biempotrados; Sakimoto y Komatsu [2] estudiaron la rigidez de las diagonales de arriostramiento necesaria para la estabilidad lateral de los arcos, y un análisis del mismo parámetro fue realizado por Kuranishi y Yabuki [3] , con el que obtuvieron resultados similares.

Con relación a la estabilidad elástica no lineal, la «no linealidad geométrica» se debe evaluar para las deformaciones en y fuera del plano y la torsión del arco. Wen y Lange [4] desarrollaron un modelo de elementos finitos para calcular las cargas elásticas de bifurcación de pandeo en y fuera del plano para arcos de diferente geometría.

La determinación de la carga real de colapso «fuera del plano» de un arco metálico debe considerar, entre otros, el comportamiento no lineal geométrico de la estructura, el carácter elastoplástico del acero, la presencia de autotensiones, las imperfecciones geométricas constructivas y la propagación de zonas plastificadas a lo largo de la directriz, que no pueden ser asimiladas a rótulas plásticas. La única herramienta válida para su cálculo es el método de los elementos finitos. Esta técnica analítica ha sufrido un fuerte desarrollo en los últimos 30 años, por lo que se ha conseguido la exactitud en la formulación empleada y, consecuentemente, se ha mejorado la precisión de los resultados: la resolución del problema no lineal se realiza de forma incremental, linealizando cada pequeño escalón de carga y ajustándolo iterativamente.

Casi todos los trabajos de análisis han comenzado por la elaboración de su propia herramienta numérica, hecho que ha restado eficacia a los resultados obtenidos, ya que el desarrollo del programa se convertía en el objetivo principal del trabajo de investigación en lugar de serlo sus resultados. Hoy en día la «tarea programadora» ha remitido debido a la aparición de software especializado en el cálculo de estructuras, lo que permite a los investigadores centrar sus esfuerzos en el estudio «estructural».

Para arcos exentos, Sakimoto y Komatsu [5] investigaron la carga última de colapso de arcos parabólicos exentos debido a una inestabilidad inelástica lateral producida por deformación flexo-torsional fuera del plano, y posteriormente estudiaron las características espaciales elastoplásticas y la carga última de 2 arcos conectados sujetos a la combinación de cargas verticales y horizontales laterales. Asimismo, determinaron la relación existente entre la carga última lateral y la esbeltez del arco con respecto al eje «y».

Para arcos con tablero, Sakimoto y Komatsu [6] estudiaron el efecto de las diagonales en los puentes arco de tablero inferior; Kuranishi y Yabuki [3] analizaron el efecto de las diagonales en los arcos de tablero superior en la carga última espacial de colapso, y obtuvieron conclusiones similares a las deducidas por Sakimoto y Komatsu. Ellos mismos fueron quienes más tarde [5] trataron de establecer parámetros que determinasen la carga última de fallo por inestabilidad lateral de arcos de acero arriostrados lateralmente (arcos apoyados paralelos conectados por vigas y/o diagonales) con cargas uniformemente distribuidas en planta. Continuando con ese mismo trabajo, determinaron la carga última lateral de arcos de tablero inferior con sección cajón utilizando una analogía entre un arco y una columna a través de una función de esbeltez equivalente λ_a .

También se ha investigado recientemente de forma pormenorizada el efecto de las cargas laterales en la carga última de colapso de arcos con o sin tablero. Los 3 trabajos de investigación más relevantes son los de Stussi [7] , Ostlund [8] y Wästlund [9] , ya que propusieron un factor de amplificación que permitía determinar las deformaciones y tensiones «mayoradas» en el caso de acciones perpendiculares (normales) al plano del arco debido a la contribución de la carga axial que interactúa con los desplazamientos laterales. Kuranishi y Yabuki [10] estudiaron el efecto de la fuerza horizontal lateral en la carga última de puentes arco, y posteriormente definieron la rigidez necesaria en los arriostramientos laterales para asegurar que arcos biapoyados sometidos a cargas laterales se comportan básicamente como estructuras en su plano.

Tal y como se aprecia en la descripción realizada del estado del arte, se puede observar que si bien existen investigaciones correspondientes a las 3 hipótesis de cálculo, en ningún caso se ha realizado un estudio paramétrico comparativo de los 3 casos que permita contrastar los resultados obtenidos. Este punto es innovador y se describe en los apartados siguientes del presente artículo.

Con el fin de determinar la carga crítica objeto del estudio bajo las 3 hipótesis de cálculo, se modeliza un arco de eje parabólico, biempotrado, con imperfección geométrica inicial de tipo cosenoidal con valor máximo L/1000 en el centro del arco, sección transversal cajón compacta (clase 2) formada por chapas soldadas, con diafragmas tipo marco ubicados cada 5 m y carga aplicada uniformemente distribuida en planta (sin considerar el peso propio). En el caso de cálculo elastoplástico, se consideran tensiones residuales.

La comparativa de los resultados obtenidos en las 3 hipótesis permite concluir la relación estudiada y la influencia del tipo de cálculo en la misma.

2. Inestabilidad elástica lineal global lateral de arcos parabólicos biempotrados

Tokarz y Sandhú [1] estudiaron de forma detallada el pandeo «lateral-torsional» de los arcos parabólicos sometidos a una carga uniformemente distribuida en planta. El criterio de pandeo que utilizaron se basa en la posibilidad de que, para un cierto valor de carga crítica, la bifurcación de equilibrio ocurre de tal forma que el «pandeo fuera del plano» se inicia con una flecha lateral y un giro del arco.

Las hipótesis adoptadas son:

• El material del arco es homogéneo y elástico lineal.
• El cálculo de esfuerzos se realiza sobre la geometría inicial.
• El eje del arco es inextensible.
• El radio de curvatura es grande en comparación con las dimensiones de la sección transversal.
• Coinciden el centroide y el centro de cortante de la sección transversal.
• Todas las cargas externas se encuentran en el plano del arco.

Los resultados se presentan de forma adimensional, en función de los siguientes parámetros:

• Parámetro crítico de pandeo (menor) ${\textstyle \lambda ={\frac {qL^{3}}{A}}}$ .
• Relación ${\textstyle {\mbox{flecha}}-{\mbox{luz}}={\frac {f}{L}}}$ .
• Relación entre la rigidez a torsión y a ${\textstyle {\mbox{flexión}}={\frac {C}{A}}}$ .
• Parámetro de restricción de la corona ${\textstyle {\frac {K_{z}\cdot L}{C}}y{\frac {K_{x}\cdot L}{A}}}$ .

Los valores de λ se han obtenido para diferentes valores de C/A/, f/L, K_Z L/C y k_x L/C.

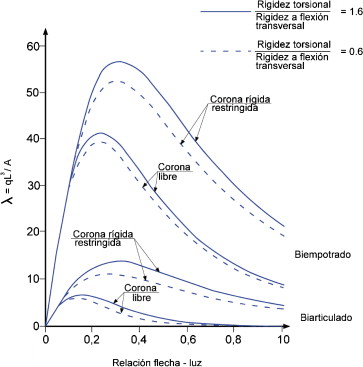
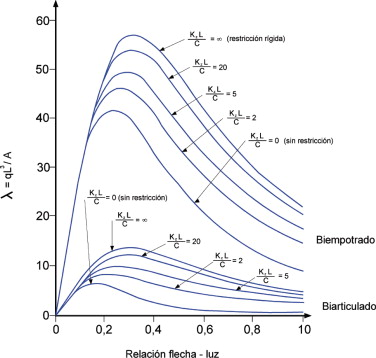
En las Figura 1  and Figura 2 se representan los valores del parámetro de pandeo λ para diferentes relaciones flecha-luz [f/L] en función de K_Z L/C y C/A tanto para arcos biapoyados como biempotrados.

Figura 1. Parámetro crítico de pandeo λ frente a la relación flecha-luz para diferentes valores de KZ L/C y con C/A = 1,6.

Figura 2. Parámetro crítico de pandeo λ frente a la relación flecha-luz para arcos de corona libre o restringida con C/A = 0,6 Y 1,6.

En la figura 1 se observa el efecto de la rigidez a torsión en el comportamiento a pandeo de los arcos, mientras que en la figura 2 se pone de manifiesto el efecto de la restricción de la corona. Asimismo, se concluye que la carga crítica alcanza un valor máximo para relaciones flecha-luz comprendidas entre 0,15 y 0,30 aproximadamente, según los ratios C/A, K_Z L/C y las condiciones de contorno.

En la tabla 1 se tabulan parte de los resultados mostrados anteriormente en las Figura 1  and Figura 2 obtenidos por Tokarz y Sandhú [1] en lo que respecta al pandeo elástico lineal lateral de arcos parabólicos biempotrados, reflejando el caso de los arcos con corona libre biempotrados sin restricciones. Estos se utilizan para validar los modelos empleados en el desarrollo de la presente investigación. Se incluyen los parámetros de pandeo tanto simétricos como antimétricos, aunque en todos los casos el modo simétrico resulta de menor valor.

Tabla 1. Parámetro crítico de pandeo λ para valores de f/L comprendidos entre 0,10 y 1,00 con diferentes valores de C/A para arcos biempotrados (el valor entre paréntesis se refiere al modo de pandeo antimétrico)

f/L (1)	C/A
	0,6 (2)	0,8 (3)	1,0 (4)	1,2 (5)	1,4 (6)	1,6 (7)
0,1	27,70 (58,68)	27,87 (58,86)	27,97 (58,97)	28,044 (59,05)	28,09 (59,10)	28,13 (59,14)
0,2	39,16 (90,67)	39,84 (91,67)	40,29 (92,29)	40,60 (92,72)	40,84 (93,03)	41,03 (93,27)
0,3	37,17 (96,13)	38,07 (98,06)	38,72 (99,31)	39,20 (100,2)	39,58 (100,9)	39,88 (101,4)
0,4	30,70 (88,57)	31,49 (91,06)	32,08 (92,77)	32,55 (94,06)	32,93 (95,11)	33,24 (95,99)
0,5	24,32 (77,58)	24,90 (80,29)	23,36 (82,27)	25,74 (83,85)	26,05 (85,19)	26,32 (86,38)
0,6	19,20 (67,00)	19,61 (69,80)	19,94 (71,93)	20,21 (73,72)	20,45 (75,30)	20,66 (76,75)
0,7	15,31 (58,00)	15,59 (60,75)	15,82 (62,98)	16,02 (64,92)	16,20 (66,62)	16,36 (68,34)
0,8	12,38 51,56	12,58 (53,28)	12,75 (55,56)	12,90 (57,60)	13,03 (59,49)	13,14 (61,28)
0,9	10,18 (44,49)	10,32 (47,16)	10,45 (49,45)	10,55 (51,55)	10,65 (53,51)	10,74 (55,38)
1,0	8,508 (39,52)	8,616 (42,13)	8,710 (44,42)	8,793 (46,53)	8,869 (48,51)	8,939 (50,40)

La determinación en la presente investigación de la carga crítica elástica lineal global lateral de los arcos se lleva a cabo utilizando el método de los autovalores con ayuda de los ordenadores. Se ha calculado el valor de la carga crítica de pandeo elástica lineal global lateral del arco para diferentes casos de luz y flecha, mediante los modelos BEAM (lineal) y SHELL (espacial) incorporados en el programa de cálculo de estructuras Ansys.

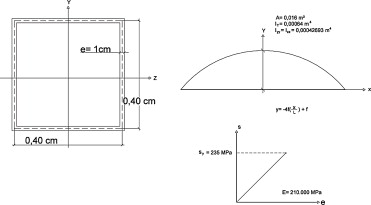
Las luces empleadas son 20, 25, 30, 35 y 40 m para relaciones flecha-luz de 0,1, 0,2, 0,3, 0,4 y 0,5. La sección transversal es un cajón cuadrado de 40 × 40 cm con un espesor uniforme de 1 cm.

2.1. Modelización con elementos BEAM

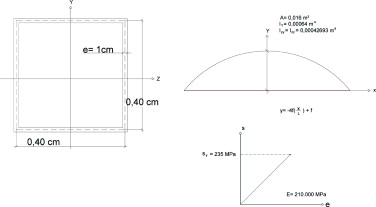
La figura 3 incluye un esquema con los datos más relevantes necesarios para el cálculo.

Figura 3. Directriz parabólica de arco, características mecánicas de la sección y características del material acero.

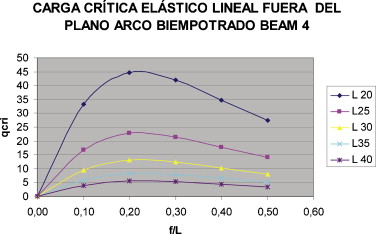
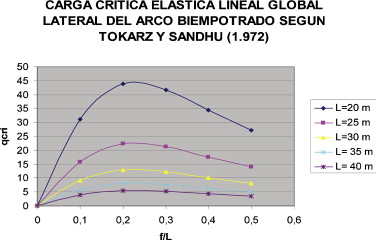
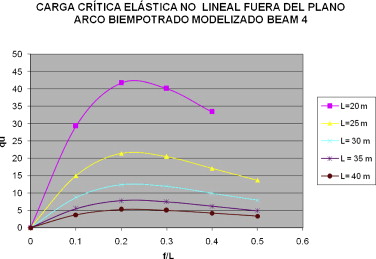
La tabla 2 recoge los resultados obtenidos en la presente investigación para arco parabólico biempotrado, en la que se ha utilizado un modelo con elementos BEAM 4, en función de la longitud del arco y de la relación flecha-luz, la cual se resume en la figura 4 .

Tabla 2. Valor de la carga crítica (en t/ml) elástica lineal fuera del plano para arcos parabólicos biempotrados con diferentes longitudes y relaciones flecha-luz calculada con un modelo con elementos tipo BEAM 4

f/L	L = 20 m qcri	L = 25 m qcri	L = 30 m qcri	L = 35 m qcri	L = 40 m qcri
0,1	33,27	16,63	9,50	5,93	3,95
0,2	44,66	22,75	13,12	8,25	5,52
0,3	42,03	21,48	12,42	7,81	5,23
0,4	34,62	17,71	10,24	6,45	4,32
0,5	27,39	14,01	8,11	5,11	3,42

Figura 4. Valor de la carga crítica (en t/ml) elástica lineal global lateral del arco biempotrado modelizado con elementos BEAM 4.

La investigación realizada por Tokarz y Sandhú [1] recogida en la tabla 1 arroja los valores de carga crítica de pandeo elástico lineal global lateral para arcos biempotrados que se muestran en la tabla 3 y en la figura 5 .

Tabla 3. Valores de la carga crítica (en t/ml) elástica lineal global lateral del arco biempotrado según Tokarz y Shandhú [1]

f/L	L = 20 m qcri	L = 25 m qcri	L = 30 m qcri	L = 35 m qcri	L = 40 m qcri
0,1	31,04	15,89	9,19	5,79	3,88
0,2	43,89	22,47	13,00	8,19	5,49
0,3	41,661	21,33	12,34	7,77	5,21
0,4	34,40	17,61	10,19	6,42	4,31
0,5	27,25	13,95	8,07	5,08	3,41

Figura 5. Valor de la carga crítica (en t/ml) elástica lineal global lateral del arco biempotrado según Tokarz y Sandhú [1] .

Si se comparan los valores calculados en la presente investigación y los obtenidos por Tokarz y Sandhú [1] , se observa que las diferencias existentes son mínimas y se encuentran dentro de los límites admisibles. Se incluyen en la tabla 4 .

Tabla 4. Diferencias existentes entre los valores calculados en la presente investigación y los obtenidos por Tokarz y Sandhú [1]

f/L	L = 20 m%	L = 25 m%	L = 30 m%	L = 35 m%	L = 40 m%
0,1	6,70%	4,42%	3,14%	2,35%	1,84%
0,2	1,74%	1,21%	0,92%	0,74%	0,64%
0,3	0,89%	0,70%	0,60%	0,53%	0,50%
0,4	0,62%	0,53%	0,49%	0,46%	0,42%
0,5	0,48%	0,43%	0,41%	0,40%	0,38%

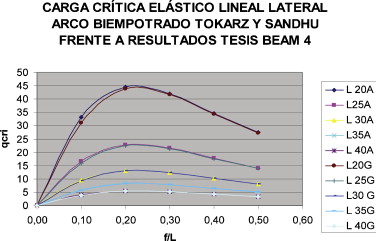
En la figura 6 se representa la comparativa entre la carga crítica de pandeo elástico lineal global lateral del arco biempotrado obtenida por Tokarz y Sandhú [1] y la calculada en la presente investigación con un modelo de elementos BEAM en Ansys.

Figura 6. Comparativa entre la carga crítica (en t/ml) de pandeo elástico lineal global del arco biempotrado obtenida por Tokarz y Sandhú [1] y la calculada en la presente investigación con un modelo de elementos BEAM en Ansys.

Se destacan las siguientes conclusiones:

• Las diferencias porcentuales son reducidas y se encuentran dentro de los límites admisibles. Solo para el arco de 20 m de longitud y relación flecha-luz 0,10 la diferencia es superior al 5% (6,70%).
• Las diferencias existentes se deben a que en los cálculos de Tokarz y Sandhú [1] se desprecia el acortamiento por axil del arco y los momentos derivados del mismo, y en los de la presente investigación, no: cuanto más esbelto es el arco, las flexiones provocadas por los acortamientos por axil son menores y las diferencias se hacen casi nulas. Por ello, el valor absoluto de la diferencia decrece con el aumento de la luz del arco y de la relación flecha-luz.

2.2. Modelización con elementos SHELL

Puede aplicarse todo lo indicado anteriormente en la modelización con elementos BEAM relativo a la directriz del arco, la sección transversal, las características mecánicas de la sección transversal, las propiedades del material acero o la inexistencia de imperfecciones geométricas.

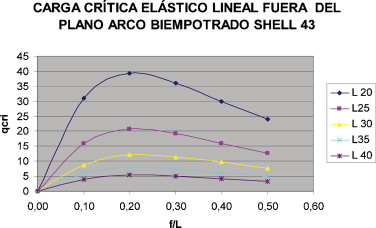
Los resultados obtenidos (en t/ml) se presentan en la tabla 5 y en la figura 7 , agrupados por la longitud del arco y la relación flecha-luz.

Tabla 5. Carga crítica (en t/ml) elástica lineal global lateral del arco biempotrado modelizado con elementos SHELL 43

f/L	L = 20 m qcri	L = 25 m qcri	L = 30 m qcri	L = 35 m qcri	L = 40 m qcri
0,1	31,12	15,90	8,84	5,79	3,88
0,2	39,30	20,82	12,30	8,18	5,528
0,3	36,10	19,30	11,46	7,34	4,98
0,4	29,92	15,96	9,93	6,06	4,11
0,5	24,06	12,76	7,55	5,02	3,26

Figura 7. Valor de la carga crítica (en t/ml) elástica lineal global lateral del arco biempotrado modelizado con elementos SHELL 43.

Si se comparan los valores calculados con el modelo SHELL y los obtenidos por Tokarz y Sandhú [1] (fig. 7 ), se observa que las diferencias existentes son pequeñas y se encuentran dentro de los límites admisibles. Las diferencias en porcentaje se muestran en la tabla 6 .

Tabla 6. Valores de las diferencias porcentuales entre los resultados obtenidos con el modelo SHELL y los resultados obtenidos por Tokarz y Sandhú [1]

f/L	L = 20 m %	L = 25 m %	L = 30 m %	L = 35 m %	L = 40 m %
0,1	0,26%	0,04%	–4,01%	–0,06%	–0,06%
0,2	–11,67%	–7,93%	–5,76%	–0,17%	0,69%
0,3	–15,40%	–10,51%	–7,68%	–5,89%	–4,66%
0,4	–14,99%	–10,38%	–2,70%	–5,93%	–4,74%
0,5	–13,28%	–9,35%	–7,00%	–1,24%	–4,44%

De todo ello se concluye:

• Los valores de las diferencias porcentuales son superiores para la modelización con elementos SHELL que para la realizada con elementos BEAM, ya que el modelo con elementos SHELL 43 tipo lámina permite un mayor acercamiento a la realidad que aquel con elementos tipo BEAM 4 (modelo «espacial» frente a modelo «lineal»).
• Los mayores valores porcentuales corresponden a los arcos de menor longitud (con L = 20 m, 15,40%), lo que se justifica por el hecho anteriormente comentado de que en los cálculos de Tokarz y Sandhú [1] se desprecia el acortamiento por axil del arco y los momentos derivados del mismo y en los de la presente investigación, no. Las diferencias porcentuales decrecen con el aumento de la luz.

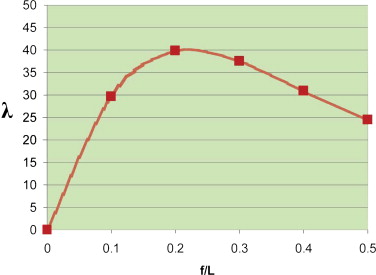
Si se analizan los resultados obtenidos para los arcos biempotrados representando la gráfica que relaciona el cociente f/L con el parámetro ${\textstyle \lambda ={\frac {qL^{3}}{EI_{y}}}}$ (fig. 8 ), se observa que el valor de λ es constante independientemente de la luz, tal y como habían deducido Tokarz y Sandhú [1] . El valor de EI_y (rigidez a flexión transversal) es de 8.965,33 t m² para la sección estudiada de 40 × 40.

Figura 8. Valor del parámetro λ para diferentes relaciones flecha-luz comprendidas entre 0,1 y 0,5 en la hipótesis de cálculo elástico lineal para secciones cajón cuadradas con relación rigidez torsional-rigidez a flexión de 0,60.

3. Inestabilidad elástica no lineal global lateral de arcos parabólicos biempotrados

En la hipótesis de comportamiento elástico no lineal la modelización del arco se realiza con elementos BEAM. Las luces, las flechas, la sección transversal, la geometría del arco y las características del material coinciden con lo expuesto anteriormente para los cálculos elástico-lineales. Se adopta una imperfección inicial geométrica:

$z(x)={\frac {L}{1.000}}\cdot cos\left({\frac {\pi x}{L}}\right)$

( 1)

En la figura 9 se incluye un resumen de las características del arco utilizado en los cálculos de la carga crítica elástica no lineal fuera del plano.

Figura 9. Características del arco empleado en los cálculos elásticos no lineales relativos a la inestabilidad fuera del plano.

Se considera la «no linealidad geométrica», con lo que se permite un cálculo con grandes deformaciones. El método empleado para resolver el problema matemático es el de Newton-Raphson.

Los cálculos se realizan para el caso de arco biempotrado.

Los resultados obtenidos (en t/ml) se presentan en la tabla 7 , agrupados por longitud del arco y relación flecha-luz, y se resumen en la figura 10 .

Tabla 7. Valores de la carga crítica (en t/ml) elástica no lineal fuera del plano para arcos biempotrados modelizados con elementos BEAM–4

f/L	L = 20 m qcri	L = 25 m qcri	L = 30 m qcri	L = 35 m qcri	L = 40 m qcri
0,1	29,3	15	8,7	5,5	3,7
0,2	41,7	21,4	12,4	7,8	5,25
0,3	40,1	20,5	11,9	7,5	5,0
0,4	33,4	17,1	9,9	6,2	4,20
0,5	26,6	13,7	7,9	4,9	3,30

Figura 10. Valor de la carga crítica (en t/ml) elástica no lineal fuera del plano del arco biempotrado modelizado con elementos BEAM 4.

Para los arcos biempotrados, el análisis de la gráfica que relaciona el cociente f/L con el parámetro ${\textstyle \lambda ={\frac {qL^{3}}{EI_{y}}}}$ (tabla 8 ) permite concluir que el valor de λ es constante independientemente de la luz y ligeramente inferior al caso de cálculo elástico lineal, hipótesis más separada de la realidad.

Tabla 8. Valores del parámetro λ en un cálculo elástico no lineal fuera del plano para arcos parabólicos biempotrados modelizados con elementos BEAM–4

f/L	L = 10 m	L = 20 m	L = 25 m	L = 30 m	L = 35 m	L = 40 m
0	0	0	0	0	0	0
0,1	27,26	26,14	26,14	26,20	26,30	26,41
0,2	37,35	37,21	37,30	37,34	37,30	37,48
0,3	35,45	35,78	35,73	35,83	35,87	35,6922569
0,4	29,51	29,80	29,80	29,81	29,65	29,98
0,5	23,61	23,73	23,88	23,79	23,43	23,55

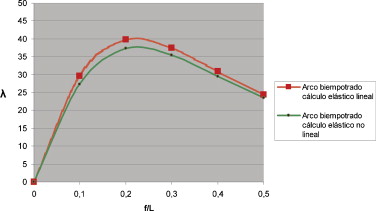
En la figura 11 se representa la comparativa entre los cálculos elástico lineal y elástico no lineal para el caso de arcos biempotrados. El valor de EI_y (rigidez a flexión transversal) es de 8.965,33 t · m² .

Figura 11. Valor del parámetro λ para diferentes relaciones flecha-luz comprendidas entre 0,1 y 0,5 en las hipótesis de cálculo elástico lineal y cálculo elástico no lineal.

4. Carga última de colapso lateral de arcos parabólicos biempotrados

En la hipótesis de comportamiento elastoplástico no lineal, la modelización del arco se realiza con elementos tipo lámina SHELL. La geometría del arco coincide con lo expuesto anteriormente para los cálculos elástico-lineales y no lineales. Se adopta una imperfección inicial geométrica cosenoidal coincidente con la empleada en el caso elástico no lineal.

Las secciones transversales que se emplean son cajones rectangulares y/o cuadrados de dimensiones variables con espesores tales que pertenecen a secciones con almas compactas, con lo que se asegura la no existencia de abolladura en ninguna de las chapas que conforman la estructura (t/d ≤ 38ɛ, fig. 12 ).

Figura 12. Relación entre longitud y espesor de una chapa según la RPM-95 [11] para secciones con almas compactas.

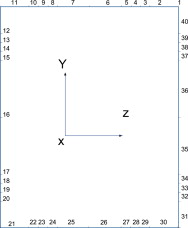
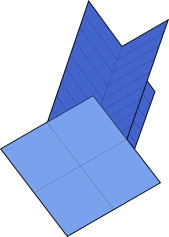
El modelo tridimensional se define a partir de una sección en el espacio con 40 puntos, perpendicular a la directriz en el origen de esta, tal y como se define en la figura 13 .

Figura 13. Puntos y líneas que definen la sección transversal del arco perpendicular a la directriz.

La posición de los puntos que constituyen la sección viene determinada por la introducción del estado de autotensiones.

Los puntos se unen por 40 líneas, tal y como se observa en la figura 13 .

Las coordenadas de cada punto de la sección se obtienen a partir del centro de gravedad con el fin de que la sección permanezca siempre perpendicular a la directriz.

En cualquier punto (x_i , y_i ) de la directriz se cumple que:

$tg{\alpha }_{i}=y^{'}(x_{i})=-{\frac {8f}{L^{2}}}x_{i}^{2}+{y^{'}}_{0}(x_{i})$

( 2)

Las coordenadas del punto 1 de la sección serán:

${\begin{array}{c}x(1)=x_{i}+{\frac {H}{2}}\cdot sen{\alpha }_{i}\\y(1)=y_{i}+{\frac {H}{2}}\cdot cos{\alpha }_{i}\\z(1)={\frac {B}{2}}\end{array}}$

( 3)

Análogamente se procede a dar coordenadas a todos los puntos de la sección.

La directriz se genera mediante 41 puntos de la ecuación de la parábola con una curva SPLINE que pasa por dichos puntos. En Ansys [12] , esta curva se representa mediante una sola línea.

A continuación se extruye la sección a lo largo de la curva directriz generando en el cálculo tantas áreas como líneas hay en la sección (40 áreas).

En lo que respecta al mallado de las áreas resultantes, cabe destacar:

• Se considera un elemento por cada línea generada en la sección transversal inicial perpendicular a la curva directriz.
• Se consideran «n» elementos por cada línea longitudinal existente, siendo n = entero (L/12t), donde L es la longitud del arco y t el espesor de la sección cajón (fig. 14 ).

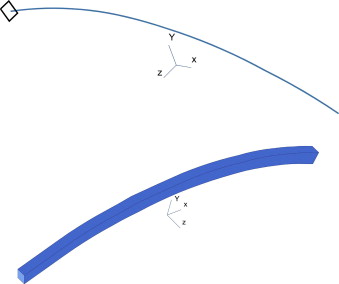
Figura 14. Génesis del arco.

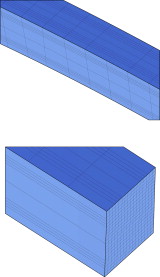
En las siguientes figuras se muestra la génesis del arco por extrusión de la sección transversal inicial a lo largo de la directriz y la densidad de mallado resultante (fig. 15 ).

Figura 15. Arco resultante y densidad de mallado.

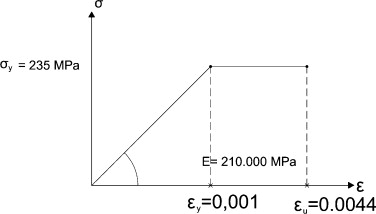
La curva de comportamiento del material es la correspondiente a un Bilineal Kinematic Hardening (material bilineal kinemático), tal y como se muestra en la figura 16 .

Figura 16. Curva de comportamiento del acero.

La modelización del empotramiento se realiza imponiendo en todos los nodos correspondientes a las 4 aristas que conforman las secciones extremas de cada apoyo que los desplazamientos según los 3 ejes coordenados son nulos: u_x  = u_y  = u_z  = 0 (fig. 17 ).

Figura 17. Condiciones de contorno del arco biempotrado.

Es imprescindible rigidizar los apoyos con chapas de grosor elevado que simulen la realidad, para evitar la rotura por plastificación local de las chapas en los arranques. Se ha asegurado la compatibilidad de movimientos de todos los nodos del refuerzo por medio de la aplicación de condiciones de compatibilidad que garanticen su movimiento como sólido rígido.

En la figura 18 se muestra el esquema de rigidización utilizado.

Figura 18. Esquema de rigidización de apoyo utilizado.

Este esquema de rigidización del apoyo hace que la sección extrema gire ante la acción de la carga de forma solidaria. Este refuerzo no altera la carga de colapso real, al representar el apoyo realmente empleado en el diseño de arcos; cabe mencionar que la zona reforzada es tan corta que no afecta a la rigidez global de la estructura. Por otro lado, las secciones pésimas están en riñones o en clave, lejos de los apoyos.

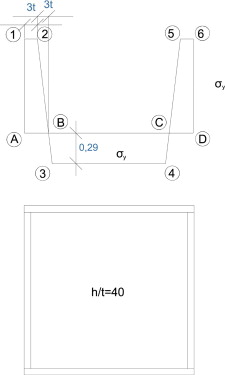
Se adopta la distribución de autotensiones recomendada por la ECCS [13] para secciones en cajón soldadas de relación h/t = 40, la cual se muestra en la figura 19 .

Figura 19. Distribución de autotensiones adoptada en el modelo de la investigación.

Esta distribución de autotensiones se simula mediante un estado térmico que provoca el mismo efecto que la soldadura. El modelo de autotensiones se define dando a cada nodo de la directriz del arco que pasa por el punto A la temperatura ${\textstyle \Delta T_{A}={\frac {2,29\sigma y}{E\alpha }}}$ , a los de los puntos B, C e intermedios la temperatura ${\textstyle \Delta T_{B}={\frac {0,29\sigma y}{E\alpha }}}$ y a los nodos que quedan entre los puntos (2) y (3) y (4) y (5) una temperatura lineal entre ambos de valor ${\textstyle \Delta T_{\left(x\right)}=\left({\frac {\Delta T_{A}+\Delta T_{B}}{6t}}\right)X-}$$\Delta T_{B}$ , con X = 0 en el punto B.

La determinación de la carga última de colapso fuera del plano se realiza para una carga lineal uniformemente distribuida en planta. En el estudio del comportamiento del arco con pandeo lateral no se considera el peso propio del arco .

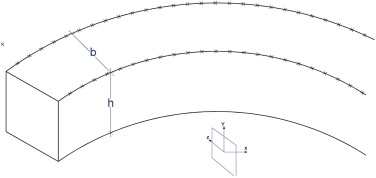
Dado que el arco, al ser una estructura espacial, presenta un determinado espesor según el eje «z», es necesario definir un procedimiento simplificado que regule la introducción de las cargas actuantes.

Si se considera una carga «q» actuante definida en t/ml, su aplicación se lleva a cabo sobre los nodos pertenecientes a las aristas extremas sitas en la cara superior de la estructura con valores de «z» iguales a «–b/2» y a «+b/2», siendo «b» la dimensión horizontal del cajón.

En la figura 20 se muestran los nodos objeto de aplicación de las cargas.

Figura 20. Distribución de las cargas actuantes sobre el arco.

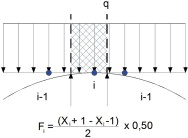
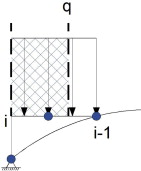
Una vez definidos los nodos sobre los que se aplican las cargas, es necesario calcular el valor de estas. Siendo q el valor de la carga lineal uniformemente distribuida, si se considera el nodo «i», la magnitud de la carga asignada al nodo viene dada por:

$F_{i}={\frac {\left(X_{i+1}-X_{i-1}\right)}{2}}\cdot {\mbox{0,5}}$

( 4)

donde X_i+1 y X_i-1 son las coordenadas x de los nodos i + 1 e i – 1, respectivamente. El factor 0,50 reparte la carga total entre las 2 aristas extremas. En la figura 21 se define el esquema de reparto de las fuerzas.

Figura 21. Reparto nodal de las cargas actuantes.

Esta asignación de cargas solo presenta una singularidad, correspondiente al caso de los nodos extremos. En este caso la magnitud de la fuerza viene dada por:

$Fi^{\ast }={\frac {\left(X_{i+1}-X_{i}\right)}{2}}\cdot {\mbox{0,5}}$

( 5)

Donde X_i es el valor de la coordenada x del nodo i. En la figura 22 se muestra el esquema de reparto para nodos extremos.

Figura 22. Reparto nodal de las cargas actuantes en el caso de nodos extremo.

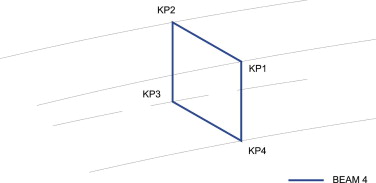
Con el fin de evitar el fenómeno de la distorsión se utilizan diafragmas tipo «marco» modelizados con elementos tipo BEAM que unen cuatro keypoints situados en los extremos de la sección transversal, tal y como se indica en la figura 23 .

Figura 23. Modelización de los diafragmas intermedios.

Las características de los diafragmas empleados son independientes del canto de la sección transversal, tal y como puede verse en la tabla 9 .

Tabla 9. Características de los diafragmas utilizados

Canto de sección transversal (m)	Distancia entre diafragmas (m)	Sección (m2 )	Iy (cm4 )	Iz (cm4 )	It (cm4 )
0,50/1	5	0,0026	449,50	167,30	9,25

Se ha calculado la carga última para relaciones flecha-luz comprendidas entre 0,1 y 0,5 para secciones transversales de ancho 0,50, 1 y 1,50 m, canto de 1 m y diferentes longitudes de arco biempotrado.

En las Tabla 10 , Tabla 11  and Tabla 12 se incluyen las cargas últimas (en t/ml) obtenidas.

Tabla 10. Carga última (en t/ml) de colapso lateral de arcos parabólicos biempotrados de sección transversal 0,50 × 1,00 m y espesor 2,50 cm

f/L	L = 30 m	L = 60 m	L = 90 m	L = 120 m	L = 150 m	L = 180 m
0,1	37,60	9,10	2,80	1,20	0,55	0,30
0,2	66,80	14,00	4,10	1,75	0,90	0,50
0,3	82,00	14,80	4,40	1,9	1,00	0,55
0,4	82,50	13,80	3,90	1,7	0,85	0,50

Tabla 11. Carga última (en t/ml) de colapso lateral de arcos parabólicos biempotrados de sección transversal 1,00 × 1,00 m y espesor 2,50 cm

f/L	L = 30 m	L = 45 m	L = 60 m	L = 90 m	L = 120 m	L = 150 m	L = 180 m
0,1	56,4	31,4	19,5	8,8	4,2	2,4	1,4
0,2	100,8	56,4	34,9	14,4	6,4	3,3	1,85
0,3	130,3	70,2	40,2	15,2	6,5	3,1	2
0,4	145,3	73,3	39,5	14	5,6	2,7	1,8
0,5	132,3	71	36,9	11,7	4,3	2,1	1,5

Tabla 12. Carga última (en t/ml) de colapso lateral de arcos parabólicos biempotrados de sección transversal 1,50 × 1,00 m y espesor 4,00 cm

f/L	L = 30 m	L = 60 m	L = 90 m	L = 120 m	L = 150 m	L = 180 m
0,1	115,60	52,10	29,30	17,20	10,10	6,00
0,2	229,50	98,00	50,90	28,00	15,40	9,20
0,3	284,60	116,80	58,00	32	18	10,3
0,4	304,00	115,30	56,50	30,50	16,4	9,5

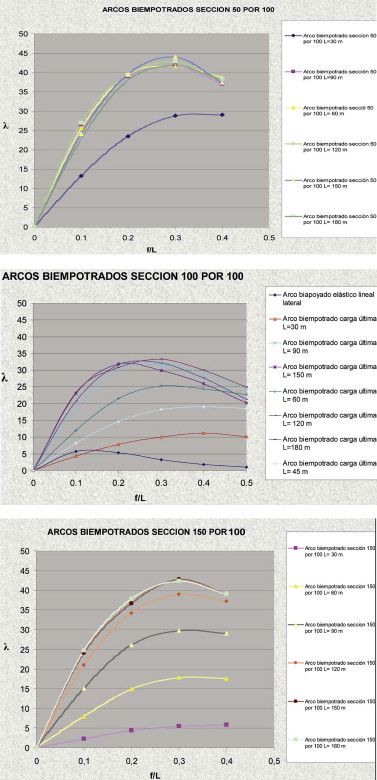
Se ha calculado y representado para los diferentes valores de f/L el parámetro ${\textstyle \lambda ={\frac {qL^{3}}{EI_{y}}}}$ con el fin de analizar y comparar los resultados para las diferentes secciones transversales en la hipótesis de cálculo elastoplástico no lineal.

En la figura 24 se muestran los resultados obtenidos para las diferentes longitudes de arco en los cálculos correspondientes a carga última.

Figura 24. Valor de λ en función de f/L para el caso de varios arcos biempotrados.

En la figura se observa que, si bien el valor de λ permanece más o menos constante para arcos con longitudes superiores a un determinado valor según la sección transversal, para longitudes menores la variación es importante, puesto que aumenta el valor de λ con el incremento de la longitud. El valor de la longitud del arco por debajo del cual el parámetro λ no es constante coincide para cada sección transversal con el correspondiente a la esbeltez de Euler.

Con todo ello, se propone la siguiente expresión para el cálculo de carga última en arcos biempotrados:

$Si{\mbox{ }}{\overline {\lambda }}_{y}>1\rightarrow {\lambda }_{y}>{\lambda }_{EULER}{\mbox{ }}\lambda =$${\frac {qL^{3}}{EI_{y}}}$

( 6)

Si ${\textstyle {\overline {\lambda }}_{y}\leq 1\rightarrow {\lambda }_{y}\leq {\lambda }_{EULER}}$ , λ no es constante y crece con el aumento de la longitud [14] , siendo ${\textstyle {\overline {\lambda }}_{y}}$ la esbeltez reducida con respecto a la de Euler, λ_y  = L/i_y (con i_y radio de giro de la sección transversal con respecto al eje «y») y ${\textstyle {\lambda }_{\mbox{EULER}}={\sqrt {\frac {{\pi }^{2}E}{{\sigma }_{y}}}}}$

Para ${\textstyle {\overline {\lambda }}_{y}>1}$ , las tensiones críticas son inferiores a σ_y , siendo el fenómeno equiparable a los cálculos elástico lineal y elástico no lineal y resultando un parámetro λ independiente de la longitud.

Para ${\textstyle {\overline {\lambda }}_{y}\leq 1}$ , las tensiones críticas son superiores a σ_y , apareciendo plastificaciones que alejan el cálculo de la carga última de los cálculos elástico lineal y elástico no lineal, con lo que el valor de λ no permanece constante.

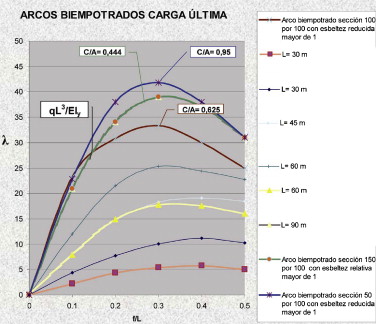
En la figura 25 se representa la comparativa entre los valores del parámetro λ para diferentes relaciones rigidez torsional-rigidez a flexión transversal para arcos biempotrados bajo el supuesto de carga última.

Figura 25. Comparativa entre los valores del parámetro λ para diferentes relaciones rigidez torsional-rigidez a flexión transversal para arcos biempotrados bajo el supuesto de carga última.

5. Conclusiones

De los trabajos de investigación desarrollados se obtienen las siguientes conclusiones:

• En las hipótesis de cálculo elástico lineal y no lineal para arcos parabólicos biempotrados, dada una relación entre la rigidez a torsión y la rigidez a flexión transversal de la sección transversal, el valor del parámetro ${\textstyle \lambda ={\frac {qL^{3}}{EI_{y}}}}$ es constante e independiente de la luz para cada ratio f/L, hecho esperado al no existir plastificación del acero. Los resultados obtenidos confirman la anterior afirmación. Los valores para el caso elástico lineal son superiores a los del caso elástico no lineal.
• En la hipótesis de cálculo elastoplástico no lineal, para una relación entre la rigidez a torsión y la rigidez a flexión transversal dada, en arco con longitud superior a la correspondiente a la esbeltez de Euler, el valor del parámetro λ permanece constante; para longitudes inferiores, el valor de λ decrece. Analíticamente se puede expresar:

Si ${\textstyle {\overline {\lambda }}_{y}>1\rightarrow {\lambda }_{y}>{\lambda }_{EULER}\rightarrow \lambda =}$${\frac {qL^{3}}{EI_{y}}}={\mbox{cte}}$ para f/L dado

Si ${\textstyle {\overline {\lambda }}_{y}\leq 1\rightarrow {\lambda }_{y}\leq {\lambda }_{EULER}\rightarrow \lambda \not =}$${\mbox{cte}}$ . Crece con el incremento de L.

En cualquier caso, los valores de λ para un f/L dado son inferiores a los correspondientes para la misma relación rigidez torsional-rigidez a flexión transversal en los casos de cálculos elástico lineal y no lineal.

La explicación es sencilla: para ${\textstyle {\overline {\lambda }}_{y}>1}$ , con esbelteces grandes, las tensiones críticas son inferiores al límite elástico y el comportamiento es similar al de los cálculos elástico lineal y no lineal; para ${\textstyle {\overline {\lambda }}_{y}\leq 1}$ , con pequeñas esbelteces, las tensiones críticas son superiores al límite elástico y aparecen plastificaciones que alejan el cálculo de la carga última de los cálculos elástico lineal y no lineal, por lo que λ no permanece constante.

Las conclusiones extraídas de la presente investigación ahondan en la no linealidad del material acero. Los arcos esbeltos colapsan para valores menores de la tensión, con λ constante; los arcos menos esbeltos colapsan para valores de tensión cercanos a σ_y , con valores de λ dependientes de la longitud del arco.

La potencia y la facilidad de cálculo aportada por los ordenadores permiten contrastar los resultados actuales para el caso de cálculo elastoplástico no lineal de arcos metálicos: no linealidad del material y no linealidad geométrica.

Bibliografía

1. [1] F.J. Tokarz, R.S. Shandhú; Lateral torsional buckling of parabolic arches; Journal of the Structural Division, ASCE, 98 (ST5) (1972), pp. 1161–1179
2. [2] S.Y. Komatsu, T. Sakimoto; Ultimate load carrying capacity of steel arches; Journal of the Structural Division, ASCE, 103 (ST2) (1977), pp. 2323–2336
3. [3] S. Kuranishi, T. Yabuki; Effect of lateral bracing rigidities on the ultimate strenght of steel arch bridges; Proceedings of the Japan Society of Civil Engineers (305) (1981), pp. 139–149
4. [4] K.R. Wen, J. Lange; Ultimate curved BEAM element for arch buckling analysis; Journal of the Structural Division ASCE, 107 (ST11) (1981), pp. 2053–2069
5. [5] S. Komatsu, T. Sakimoto; A possibility of total break-down of bridge arches due to buckling of the lateral bracing; Final Report of the 2nd International Colloquium on Stability of Steel Structures (1977), pp. 299–301
6. [6] S. Komatsu, T. Sakimoto; Ultimate strength of steel arches under lateral loads; Proceedings of the Japan Society of Civil Engineers (292) (1979), pp. 83–94
7. [7] F. Stussi; Lateral buckling and vibration of arches; Proceedings of International Association of Bridge and Structural Engineering, 7 (1943), pp. 327–343
8. [8] S. Ostlund; Lateral Stability of Bridge Arches Braced With Transverse Bars; Transactions of Royal Institute of Technology, Stockholm, Sweden (1954) N 84
9. [9] G. Wastlund; Stability problems of compressed steel members and arch bridges; Journal of the Strucutral Division, ASCE, 86 (ST6) (1960), pp. 47–71
10. [10] S. Kuranishi, T. Yabuki; Required out-of-plane rigidities of steel arch bridges with two main arch ribs subjected to vertical and lateral loads; The Technology Reports of Tohoku University, 46 (1977), pp. 47–72
11. [11] RPM-95. Recomendaciones para el proyecto de puentes metálicos para carreteras, Centro de publicaciones Ministerio de Fomento. Serie Normativas. Instrucciones de Construcción, Madrid, 1995.
12. [12] P. Ariza, A. Y Sáez; Método de los elementos finitos. Introducción a Ansys; Publicaciones de la Universidad de Sevilla, Manuales Universitarios (1999)
13. [13] ECCS N° 22, 1976. Manual on Stability of Steel Structurees, APTA, Madrid.
14. [14] T.V. Galambós; Guide to Stability Design Criteria for Metal Structures; (5td ed.)John Wiley and Sons, New York (1998)