Numerical investigation of the effects of dwell time duration in a two-stage injection scheme on exergy terms in an IDI diesel engine by three-dimensional modeling

Abstract

Dwell duration of multiple-injection scheme is an important parameter, which makes it possible to shift the tradeoff curve between soot and NOx closer to the origin. In this investigation, therefore, energy and exergy analyses are carried out for various two-step injection schemes in which 25% of the total fuel is injected during the second pulse and the dwell time is increased from 5°CA (crank angle) to 30°CA by 5°CA increments. The calculations are performed for a Lister 8.1 indirect injection (IDI) diesel engine at full load operation. The energy analysis for these schemes is performed during a closed cycle by using a three-dimensional CFD code. The cylinder pressure results for the baseline engine are compared with the corresponding experimental data and they show good agreement. For the exergy analysis, an in-house computational code has been developed, which uses the results of energy analysis in various cases. With crank angle positions and dwell durations set for different injection schemes, various rates of exergy are calculated and the cumulative exergy components are identified separately. The results show that the values of work exergy and exergy efficiency decrease when the dwell duration is changed from 5°CA to 30°CA. Also, there is a sharp change in the exergy parameters when the dwell time reaches 25°CA.

Introduction

The major pollutants from diesel engines are NOx and soot. NOx and soot emissions are of concern to the international community. Stringent exhaust emission standards require the simultaneous reduction in soot and NOx for diesel engines; however, it seems to be very difficult to reduce NOx emission without increasing soot emission. The reason is that there always is a contradiction between NOx and soot emissions whenever the injection timing is retarded or advanced. Split injection has been shown to be a powerful tool to simultaneously reduce soot and NOx emissions for direct injection (DI) and indirect injection (IDI) diesel engines when the injection timing is optimized. Split injection is defined as splitting the main single injection profile into two or more injection pulses with definite delay dwell between the injections. However, an optimum injection scheme of split injection for DI and IDI diesel engines has been always under investigation. Generally, the exhaust of IDI diesel engines is less smoky when compared to DI diesel engines [1]. Hence, investigation of the effect of split injection on combustion process and pollution reduction of IDI diesel engines can be quite valuable.

In recent years, some researchers have already spent significant effort on the effect of the split injection on the combustion process and pollution of DI and IDI diesel engines [2-11].

In a very competitive world, the improvement of engine performance has become an important issue for automotive manufacturers. In order to improve engine performance, the combustion and emission processes are studied more thoroughly these days by simultaneously applying the first and second laws of thermodynamics. Exergy is the key concept in the second law analysis; it is a special case of the more fundamental concept, the available energy, which has been introduced in [12]. For analyzing the performance of engine subsystems, exergy analysis can be a useful alternative to energy analysis, because it is able to reveal more information about engine processes [13-15]. Over the years, many reports have been published on the detailed use of the second law of thermodynamics with respect to internal combustion engines [16-19]. A summary of other studies on the subject has been provided below.

Rakopoulos et al. [20] developed a code for studying the effects of cylinder wall temperature on the second-law transient performance of an IDI turbocharged multi-cylinder diesel engine following a load increase, which had a special emphasis on the case of low heat rejection. The result of this work shows that the transient first-law properties are almost unaffected by the applied wall temperature scheme, while the second-law terms of engine and turbocharger are greatly affected, especially when a low heat rejection cylinder wall is chosen.

Rakopoulos et al. [18] carried out a second-law analysis for a multi-cylinder turbocharged diesel engine and all its components by using a single-zone thermodynamic model. It was demonstrated that exergy analysis offers a more well-rounded and comprehensive insight into the processes occurring in a diesel engine than its traditional first-law counterpart.

Ghazikhani et al. [21] carried out an experimental study about the effect of exhaust gas recirculation (EGR) on various exergy terms of an IDI diesel engine cylinder. Their results indicated that the application of EGR to engine mainly increases the total in-cylinder irreversibility due to the extension of the flame region, thereby raising the combustion temperature. Also, the results revealed that the behaviors of the total in-cylinder irreversibility and engine brake specific fuel consumption (BSFC) are the same, especially at high load conditions.

Rakopoulos et al. [22] carried out an experimental investigation on a six-cylinder, IDI, turbocharged and aftercooled, medium-high-speed marine-type diesel engine coupled to a hydraulic brake. The irreversibility components of every transient cycle were calculated for the diesel engine and its subsystems. Also, for the sake of comparison, the rate and the cumulative value of all the important exergy components were given for the first and last cycles of the transient event. The importance of combustion irreversibility as well as exhaust manifold irreversibility was revealed.

Amjad et al. [23] used a single-zone model to perform a numerical availability analysis of the combustion of n-heptane and natural gas blends in homogenous charge combustion ignition (HCCI) engines. They showed that as the mass percentage of natural gas in the fuel blend increases, irreversibility decreases and the second-law efficiency increases. Adding the EGR to the intake charge of the dual-fuel HCCI engine, up to an optimum value, enhances the exergy efficiency. EGR values above this point could deteriorate engine performance.

Hosseinzadeh et al. [24] carried out a numerical study by comparing the thermal, radical, and chemical effects of EGR gases using a single-zone model to analyze availability in dual-fuel engines operating at 50% loads. They showed that the chemical effect of EGR causes an increase in the unburned chemical availability and a decrease in the work availability, in comparison with the baseline engine (without EGR); while the thermal and radical effects are positive on the availability terms, especially on the unburned chemical and work availabilities. They also demonstrated that by using low values for the radical and thermal components of EGR, the exergy efficiency increases.

Jafarmadar [25] carried out a numerical exergy analysis in pre and main chambers of an IDI diesel engine using three-dimensional modeling.

Jafarmadar [26] carried out a numerical analysis about the effect of engine load on the exergy terms of an IDI diesel engine using three-dimensional modeling. The results show that when the load increases from 25% to full load in steps by 25%, the percentage of combustion irreversibility decreases from 33.7% to 25% of fuel burn exergy. Also, exergy efficiency reaches its peak of 36.7% at 75% load.

Jerald [27] carried out an overview about quantitative levels of exergy destruction during the combustion process in a spark-ignition engine. He presented the detailed results for various operative conditions and design parameters.

Sivadas et al. [28] studied the effects of EGR on exergy destruction due to isobaric combustion for a range of conditions and fuels. Both cooled and adiabatic cases of EGR were studied.

Sayin et al. [29] carried out a comparative energy and exergy analyses of a four-cylinder, four-stroke spark-ignition engine using gasoline fuels of three different research octane numbers (RONs), namely 91, 93, and 95.3.

Jafarmadar et al. [30] carried out a numerical analysis about the exergy analysis in a low heat rejection IDI Diesel Engine by three-dimensional modeling. The comparison of the results for baseline and low heat rejection (LHR) cases shows that when the load increases from 25% to 100% (in 25% increments), heat loss exergy decreases by 68.73%, 80.24%, 91.38%, and 74.97%, respectively, in LHR engine, in comparison to baseline engine. Also, exergy efficiency increases by 17.2%, 12.4%, 6.07%, and 11.81% in LHR engine.

As can be seen in relevant literature, so far, no attempt has been made to use a three-dimensional model to study the effect of dwell duration in two-step injection schemes on various exergy terms in IDI diesel engines from the second-law viewpoint. In this study, a computational fluid dynamic (CFD) code along with an in-house code have been used to predict various exergy terms at different dwell times of a two-step injection scheme for an IDI engine operating at full load.

Initial and Boundary Conditions

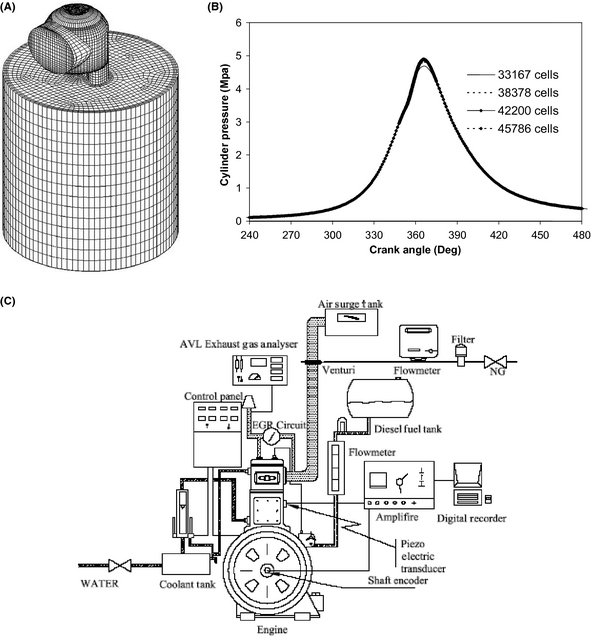
Numerical calculations are conducted at closed system from intake valve closure (IVC) at 165°CA (crank angle) before top dead center (BTDC) to exhaust valve open (EVO) at 180°CA after top dead center (ATDC). The numerical grid for modeling of geometry engine includes a maximum of 42,200 cells at 165°CA BTDC and generated by automated mesh generation of AVL FIRE Software. The present resolution was found to give adequately grid-independent results. Figure 1A shows the numerical grid which is designed to model the geometry of combustion chamber. Also, Figure 1B shows that grid dependency is based on the in-cylinder pressure and present resolution is found to give adequately grid-independent results. Initial pressure in the cylinder is set to 86 kPa and initial temperature is designed to be 384 K. This value for pressure in-cylinder was chosen according to experimental data and for temperature in-cylinder is calculated by air-fuel ratio. All boundaries temperatures were assumed to be constant throughout the simulation, but allowed to vary at various combustion chamber surfaces. Boundary temperatures for two cases in the combustion chamber are as follows:

• Head temperature: 550 K.
• Piston temperature: 590 K.
• Cylinder temperature: 450 K.

Figure 1. (A) Mesh of the Lister 8.1 indirect injection diesel engine. (B) Grid dependency based on the in-cylinder pressure. (C) Schematic diagram of experimental set-up.

This work is studied at full load mode and the engine speed is 730 rpm. All boundary temperatures were assumed to be constant throughout the simulation, but allowed to vary with the combustion chamber surface regions.

First Law and Energy Analysis

The numerical model is carried out for Lister 8.1 IDI diesel engine with the specifications shown in Table 1.

Table 1. Specifications of Lister 8.1 IDI diesel engine

Cycle type	Four stroke
Number of cylinders	1
Injection type	IDI
Cylinder bore × stroke	0.1141 × 0.1397 (m^2)
L/R	4
Displacement volume	1.43 × 10−3 (m^3)
Compression ratio	17.5: 1
Vpre-chamber/VTDC	0.7
Full load injected mass	6.4336 × 10−5 kg per cycle
Injection pressure	88.8 (bar)
Start injection timing	20° BTDC
Nuzzle diameter at hole center	0.003 m
Number of nuzzle holes	1
Nuzzle outer diameter	0.0003 m
Spray cone angle	10°
Valve timing	IVO = 5° BTDC
	IVC = 15° ABDC
	EVO = 55° BBDC
	EVC = 15° ATDC

The governing equations include species, momentum, and energy with appropriate turbulent model (RNG k − ɛ) [31] and solved from IVC to EVO. Standard WAVE breakup model [32] is used in order to simulate the primary and secondary atomization of the spray and resulting droplets. Also, drop parcels are injected in-cylinder with diameters equal to the diameter of nozzle exit. The Dukowicz model [33] is used for modeling of the heat up and evaporation of the droplets. A Stochastic dispersion model is employed to take the effect of interaction between the droplets and the turbulent eddies into account by adding a fluctuating velocity to the mean gas velocity [34]. This model assumes that the fluctuating velocity has a randomly Gaussian distribution. Modeling of the autoignition is based on Shell autoignition [35]. This generic mechanism includes six species as hydrocarbon fuel, oxidizer, total radical pool, branching agent, intermediate species, and products. Also, the important stages of autoignition such as initiation, propagation, branching, and termination were presented by generalized reactions [34, 36].

The Eddy Break-up model (EBU), which is based on turbulent mixing, is used for modeling of the combustion process [30] as follows:

${\overline {\rho {\dot {r}}_{fu}}}={\frac {C_{fu}}{{\tau }_{R}}}{\overline {\rho }}min\left({\overline {y}}_{fu},{\frac {{\overline {y}}_{ox}}{S}},{\frac {C_{pr}.{\overline {y}}_{pr}}{1+S}}\right),$

(1)

where it is assumed in this model that in premixed turbulent flames, the reactants are contained in the same eddies and are separated from eddies containing hot combustion products. The rate of dissipation of these eddies determines the rate of combustion. Because chemical reaction occurs fast, it is assumed that the combustion is mixing controlled. The first two terms in the “minimum value of” operator determine whether fuel or oxygen is present in limiting quantity, and the third term is a reaction probability which ensures that the flame is not spread in the absence of hot products. The above equation also includes two constant coefficients (C_fu, C_pr) and τ_R is the turbulent mixing time scale for chemical reaction.

The governing equations for unsteady, compressible, turbulent reacting multi-component gas mixtures flow and thermal fields were solved from IVC to EVO using the commercial AVL FIRE CFD code [34].

Second Law and Exergy Analysis

The exergy of a system is defined as the maximum value of work obtainable when a system reaches thermal, mechanical, and chemical equilibrium with its environment by means of reversible processes while exchanging heat with only the environment. This state of equilibrium is defined as the dead state of the system and it depends on pressure, temperature, and composition of environment. In this study, the pressure and temperature are assumed equal P₀ =1 bar and T₀ = 298.2 K, respectively. When there is no heat exchange between the system and the environment, that is, the system is at temperature T₀, thermal equilibrium is achieved. Similarly, mechanical equilibrium is achieved when there is no work exchange between the system and its environment. Chemical equilibrium is achieved when no system component can react with the environment. For the present case, this means that in the dead state all species of the working medium have been either oxidized or reduced to N₂, O₂, CO₂, and H₂O. It is shown in Refs. [36, 37] that the total exergy, that is, thermo-mechanical plus chemical exergies of a closed system is equal to:

$Ex=Ex_{ch}+Ex_{tm}=E-P_{0}V-T_{0}S-\sum _{i=1}^{kk}{{\mu }_{i}}^{0}m_{i}$

(2)

where ${\textstyle {\mu }_{i}^{0}}$ is the chemical potential of species i at the true dead state, and m_i is the mass of species i.

The exergy balance equation applied for the closed system inside the cylinder, on CA basis, is expressed as follows [36, 37]:

${\frac {dEx}{d\theta }}={\frac {dEx_{w}}{d\theta }}-{\frac {dEx_{q}}{d\theta }}-$${\frac {dI}{d\theta }}+{\frac {dEx_{f}}{d\theta }}$

(3)

where Ex_w is exergy associated with work done by the system and it can be defined as follows:

${\frac {dEx_{w}}{d\theta }}=\left(P-P_{0}\right){\frac {dV}{d\theta }}$

(4)

This equation illustrates that the rate of work exergy is equal to the rate of useful work done by the system.

Also, Ex_q is exergy pertained to heat losses from across the system boundary. Its variation with CA is given as:

${\frac {dEx_{q}}{d\theta }}=\left(1,-,{\frac {T_{0}}{T}}\right){\frac {dQ}{d\theta }}$

(5)

I is destruction exergy associated with combustion process and it can be defined as follows:

${\frac {dI}{d\theta }}=-{\frac {T_{0}}{T}}\sum _{i=1}^{kk}{\mu }_{i}{\frac {dm_{i}}{d\theta }}$

(6)

where index i includes all reactants and products. For perfect gases μ_j = g_j and for the fuel μ_f = a_f. The above equation reveals that both heat transfer and work production inside the cylinder only indirectly influence the irreversibility value.

Exergy of liquid fuels C_yH_z which are used in compression ignition engines is approximated as follows [38]:

$a_{f}={\mbox{LHV}}\left(1.04224,-,0.011925,{\frac {y}{z}},+\right.$$\left.,{\frac {0.042}{z}}\right)$

(7)

and

${\frac {dEx_{f}}{d\theta }}=a_{f}{\frac {dm_{f}}{d\theta }}$

(8)

is the burned fuel availability, with a_f being the fuel chemical exergy, and ${\textstyle {\frac {dm_{f}}{d\theta }}}$ is the fuel burning rate.

The second-law efficiency can be defined as the ratio of indicated work over total input chemical exergy. For the closed part of the cycle in an engine, the second-law efficiency is defined as:

${\eta }_{II}={\frac {W_{net}}{M_{fi}a_{f}}}$

(9)

Results and Discussion

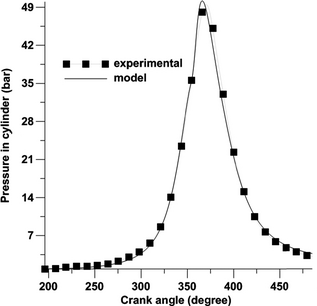
The calculations of exergy terms are carried out for the combustion chamber of a single-cylinder Lister 8.1 IDI diesel engine operating under different two-step injection schemes, at a constant speed of 730 rpm and full load conditions. For routine sampling of the cylinder pressure traces, a piezoelectric-type pressure transducer (Indi Modul 621) was flush-mounted with the combustion chamber. Cylinder pressure was measured at every 0.1 CAs. Figure 1C shows Schematic diagram of experimental setup. Figure 2 shows the computed and the measured [9] mean in-cylinder pressures for the baseline engine. The results presented in these figures are global (cylinder-averaged) quantities and are shown as a function of time (CA). The parameters of fuel injection timing and the amount of injected mass are adjusted according to experimental data. This figure indicates that the computational and experimental pressures during the compression, combustion, and expansion strokes are in excellent agreement. The peak cylinder pressure is 48.8 bars, which occurs at 366°CA (4°CA after TDC). The discrepancy between peak pressures obtained via experiment and computation is less than 0.2%.

Figure 2. Comparison of measured [26] and calculated pressure for baseline at single-injection case for full load operation and engine speed 730 rpm.

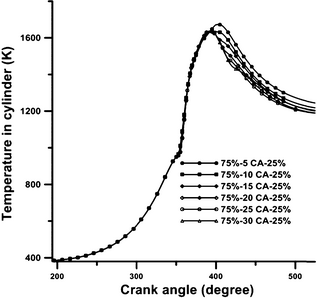
Temperature trend for different cases is illustrated in Figure 3. As can be seen in this figure, when the dwell time increases, the in-cylinder peak temperature diminishes as a result of late injection and the late combustion of fuel injected in the second pulse. The higher rise of peak temperature in the 75%-5°CA-25% case, compared to the other cases, is due to the injection of the second pulse during the ignition period and before the start of combustion. In other cases, similar peak temperatures are observed due to the same amount of fuel injection during the ignition delay period. In the 75%-30°CA-25% scheme, a second peak of temperature can be observed due to the late injection of the second pulse. It causes the in-cylinder temperature to go higher in the expansion stroke, relative to the 75%-20°CA-25% and 75%-25°CA-25% schemes. The peak temperature values for different cases, as the dwell time varies from 5°CA to 30°CA are 1674, 1636, 1934, 1637, 1637, and 1636 K, respectively.

Figure 3. Variation in in-cylinder temperature with crank angle position at various schemes in full load operation and engine speed 730 rpm.

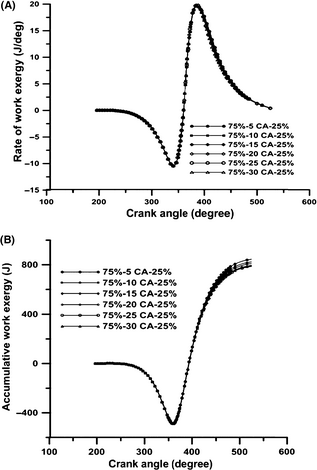
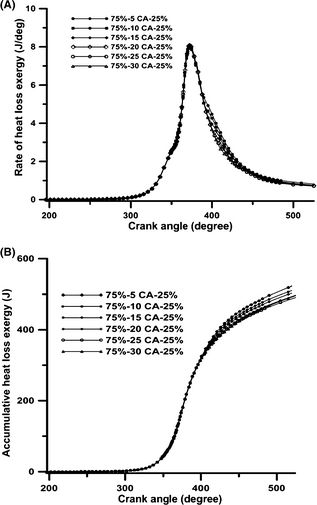
The trend of work exergy rates under various schemes are illustrated in Figure 4A and B. It can be seen that in the compression stroke, the rates of work exergy are negative for all the cases as a result of the compression work. At the start of the combustion process, the rates of work exergy increase for all the cases due to the increase in the in-cylinder pressure and temperature. These figures clearly show that the peak values of work exergy rate remain almost constant for various schemes because of the almost same amount of fuel burned and the same in-cylinder peak pressure created. These figures also indicate that when the dwell duration increases from 5°CA to 30°CA in increments of 5°CA, the rates of work exergy following the start of combustion decreases slightly, except for the dwell time of 30°CA. During this dwell time, the combustion of the fuel injected by the second pulse at the end of the expansion stroke improves the combustion and increases the rate of work exergy. As is shown in Figure 3, this increase in work exergy rate is caused by the higher in-cylinder temperature gradients in the expansion stroke of the 75%-30°CA-25% scheme. According to Figure 4B, the amounts of cumulative work exergy for dwell times from 5°CA to 30°CA are 31.7%, 31.7%, 31.8%, 31.7%, 31.5%, and 31.3% of the exergy of fuel burned, respectively. These values are in good agreement with the result of Rakopoulos and Giakoumis [18]. They showed that the value of work exergy for IDI turbocharged diesel engine is 35%. Slight difference between the two values is due to turbocharging.

Figure 4. The variation in (A) rate of work exergy (B) accumulated work exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

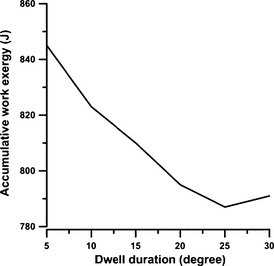
Figure 5 shows the variation in cumulative work exergy with dwell duration under various injection schemes. According to this figure, the cumulative work exergy decreases continuously with the increase in dwell duration up to 25°CA. During the dwell duration of 30°CA, this value increases because of the improved combustion at the end of the combustion cycle when more fuel is injected in the second pulse.

Figure 5. The variation in accumulative work exergy with dwell duration in full load operation and engine speed 730 rpm.

Figures 6A and B, respectively, show the rates of heat loss exergy and cumulative heat loss exergy in the combustion chamber, under various schemes, and during the engines closed cycle. At CAs larger than those at the start of combustion, because of the chambers lower pressure and temperature, the rate of heat loss exergy decreases slightly as the dwell duration increases from 5°CA to 25°CA. During the dwell duration of 30°CA, the rate of heat loss exergy increases due to the improvement in the combustion process in the latter part of the expansion stroke. The peak rates of heat loss exergy are almost the same for various schemes, while the rates of heat loss exergy at the point of EVO are 0.822, 0.762, 0.741, 0.722, 0.710, and 0.756 J/deg, respectively, for dwell durations ranging from 5°CA to 30°CA. The increased rate of heat loss exergy in the 30°CA dwell duration is the result of higher temperature in the latter part of the expansion stroke. As is shown in Figure 6B, the amounts of cumulative heat loss exergy for dwell durations ranging from 5°CA to 30°CA are 525.42, 511.09, 503.56, 497.44, 491.05, and 496.1 J, which constitute 19.1%, 19.7%, 19.7%, 19.8%, 19.7%, and 19.7% of the burned fuel exergies, respectively. These values are in good agreement with the result of Rakopoulos and Giakoumis [18]. They showed that the value of heat loss exergy for IDI turbocharged diesel engine is 18.95%.

Figure 6. The variation in (A) rate of heat loss exergy (B) accumulated heat loss exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

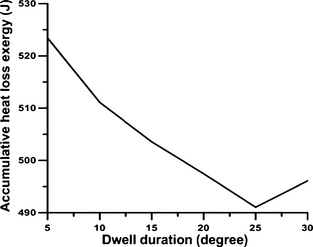
Figure 7 illustrates the changes of cumulative heat loss exergy with dwell duration under various injection schemes. According to this figure, the value of cumulative heat loss exergy decreases continuously with the increase in dwell duration up to 25°CA. During the dwell duration of 30°CA, this value increases because of improved combustion in the latter part of the combustion cycle due to the combustion of fuel injected in the second pulse.

Figure 7. The variation in accumulative heat loss exergy with dwell duration in full load operation and engine speed 730 rpm.

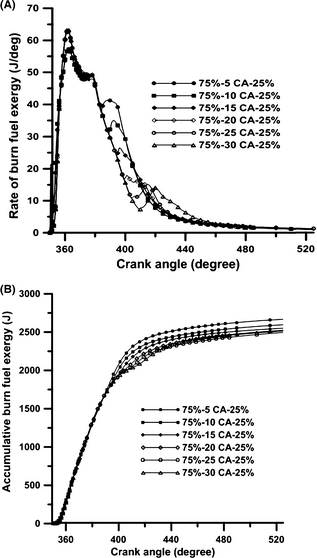
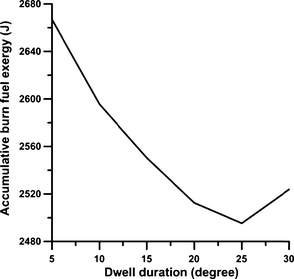
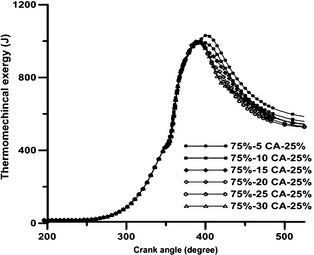
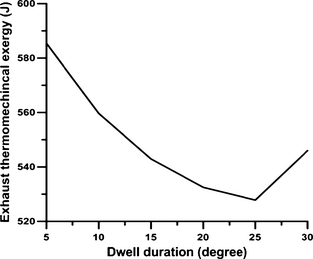
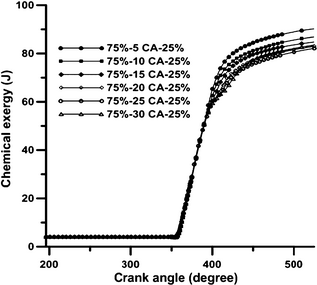
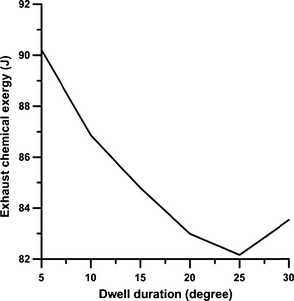
Figures 8A and B, respectively, show the exergy rates of burned fuel and cumulative exergy rates of burned fuel in the chamber under various schemes during the engines closed cycle. As is shown in Figure 8A, the first peak values in the premixed combustion phase in the dwell durations of 15, 20, 25, and 30°CA are higher than those in the 5 and 10°CA durations, as a result of longer ignition delays. In the diffusion combustion phase, similar peak values can be observed for all the schemes. The third peak in the exergy rate of burned fuel indicates the combustion of the injected fuel in the second pulse. For the split injection case, the second peak in the exergy rate of burned fuel occurs at 410°CA and it indicates a rapid diffusion burn in the latter part of the combustion and affects the in-cylinder pressure, temperature, and soot oxidation. As is shown in Figure 8B, the amounts of cumulative burned fuel exergy for dwell durations ranging from 5°CA to 30°CA are 2667, 2595, 2550, 2512, 2495, and 2524 J, respectively. Figure 9 shows the changes of cumulative burned fuel exergy with dwell duration under different injection schemes. According to this figure, the value of cumulative burned fuel exergy decreases continuously with the increase in dwell duration up to 25°CA. During the dwell duration of 30°CA, this value increases because of improved combustion in the latter part of the combustion phase as a result of the combustion of fuel injected in the second pulse. Figure 10 shows the changes of thermo-mechanical exergy in the cylinder with CA positions under various injection schemes. In the compression stroke, before the injection of fuel, the thermo-mechanical exergy increases in the chamber, because of the work done by the piston. The value of thermo-mechanical exergy in the chamber increases at the beginning of the combustion process due to the rise in temperature and pressure, and this increase is more pronounced in lower dwell durations. At the end of the combustion phase and in the expansion stroke, the rate of thermo-mechanical exergy diminishes due to the gas temperature reduction during the expansion stroke. The increase in thermo-mechanical exergy during the dwell duration of 30°CA, as compared to the dwell durations of 25 and 20°CA, is due to the improved combustion at the end of the expansion stroke as a result of fuel injection in the second pulse. As Figure 11 illustrates, the exhaust thermo-mechanical exergy diminishes with the increase in dwell duration from 5°CA to 25°CA and then it increases again during the dwell duration of 30°CA. This increase is due to the higher pressure and temperature resulting from EVO during the dwell duration of 30°CA (as shown in Fig. 3). Figure 12 shows the changes of cumulative chemical exergy in the cylinder with CA positions in various injection schemes. As is shown in this figure, the chemical exergy does not change during the compression stroke. The chemical exergy in the chamber increases at the start of the combustion process due to the rise in temperature and pressure and the concentration of complete combustion products; and this increase is more pronounced for shorter dwell durations. Toward the end of the combustion phase, the amount of chemical exergy remains constant, because of the constant concentration of combustion products. As is shown in Figure 13, the amounts of cumulative chemical exergy for various schemes using dwell durations from 5°CA to 30°CA are 90.21, 86.86, 84.79, 82.99, 83.16, and 83.53 J, respectively.

Figure 8. The variation in (A) rate of fuel burn exergy (B) accumulated fuel burn exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

Figure 9. The variation in accumulative fuel burn exergy with dwell duration in full load operation and engine speed 730 rpm.

Figure 10. The variation in accumulated thermo-mechanical exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

Figure 11. The variation in accumulative thermo-mechanical exergy with dwell duration in full load operation and engine speed 730 rpm.

Figure 12. The variation in accumulative chemical exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

Figure 13. The variation in chemical exergy with dwell duration in full load operation and engine speed 730 rpm.

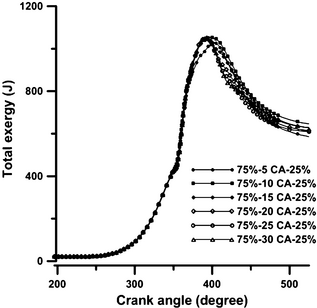
Figure 14 shows the total exergy, which is defined as the sum of chemical and thermo-mechanical exergies. The changes of this value are similar to those of the chemical and thermo-mechanical exergies. The amounts of exhaust gas exergies for dwell times from 5°CA to 30°CA are 25.3%, 24.87%, 24.62%, 24.52%, 23.46%, and 24.98% of the exergy of fuel burned, respectively. These values are in good agreement with the result of Rakopoulos and Giakoumis [18]. They showed that the value of accumulative irreversibilities for IDI turbocharged diesel engine is 21.38%.

Figure 14. The variation in total exergy with crank angle position at various schemes in full load operation and engine speed 730 rpm.

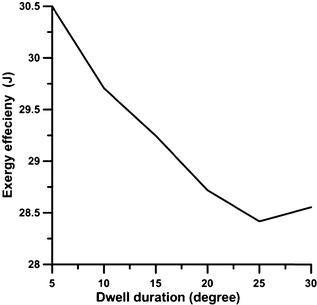
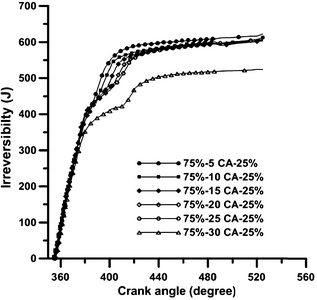
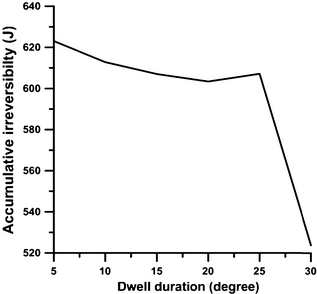
The variation in the second-law efficiency with dwell duration is shown in Figure 15. According to this figure, the value of the second-law efficiency diminishes with the increase in dwell duration from 5°CA to 25°CA, due to the reduction in work exergy, and then it increases during the dwell duration of 30°CA, due to the rise in work exergy. The combustion process makes the highest contribution to the total in-cylinder irreversibility in a diesel engine, which according to the research by Primus and Flynn [39], is more than 90%. Figure 16 illustrates the trend for the cumulative irreversibility arising from the in-cylinder combustion during an engines closed cycle, under different injection schemes. It is clear from Figures 16 and 17 that when the dwell duration increases from 5°CA to 20°CA (Fig. 17), the value of cumulative irreversibility decreases slightly due to the lower temperature of combustion. In the dwell duration of 25°CA, cumulative irreversibility increases slightly and then it diminishes considerably during the dwell duration of 30°CA. This sharp decline of irreversibility is due to the rise of combustion temperature in the expansion stroke. A rise in the cylinder charge gas temperature reduces the relative heat transfer from the reacting gas to the yet unburned mixture, which causes the irreversibility of the combustion process to diminish. The amounts of cumulative irreversibilities for dwell times from 5°CA to 30°CA are 23.3%, 23.6%, 23.8%, 24.1%, 24.3%, and 20.8% of the exergy of fuel burned, respectively. These values are in good agreement with the result of Rakopoulos and Giakoumis [18]. They showed that the value of accumulative irreversibilities for IDI turbocharged diesel engine is 23.3%.

Figure 15. The variation in second-law efficiency with dwell duration in full load operation and engine speed 730 rpm.

Figure 16. The variation in irreversibility with crank angle position at various schemes in full load operation and engine speed 730 rpm.

Figure 17. The variation in accumulative irreversibility with dwell duration in full load operation and engine speed 730 rpm.

Conclusion

In this study, a three-dimensional CFD code has been used to study the combustion processes within the chamber of an IDI diesel engine, for various two-step injection schemes, from the perspective of the second law of thermodynamics. The calculated pressure results for the baseline engine are compared with the corresponding experimental data, showing a good agreement. Such correlations between the experimental and the computed results make the model reliable for the prediction of exergy terms under various two-step injection schemes. Various exergy terms including the fuel, heat loss, irreversibility, work, exhaust loss, and the chemical and thermo-mechanical exergies are presented for different two-step injection schemes. The findings of this study, when the dwell duration increases from 5°CA to 30°CA are as follows:

1. All exergy terms diminish with the increase in dwell duration from 5°CA to 25°CA and then increase during the dwell duration of 30°CA.
2. The cumulative heat loss exergy decreases by 5.2%.
3. The cumulative work exergy decreases by 6.32%.
4. The cumulative burned fuel exergy diminishes by 5.67%.
5. The exhaust exergy diminish by 6.82%.
6. The irreversibility diminishes by 1.45%.
7. The exergy efficiency diminishes by 6.32%.

This study demonstrates that CFD simulations can be used to greatly improve and facilitate the understanding and analysis of combustion, from the second-law viewpoint, in multi-chamber diesel engines operating under different injection modes. It should be acknowledged that in this study, only an optimum split injection scheme has been considered for an engine operating at full load and with a single maximum torque speed of 730 rpm. Further studies are required to address the effects of different ratios of injected fuel mass in two pulses, engine speeds, and pressures on the exergy terms and exergy efficiency. The studying of literatures shows that by split injection concept, a reduction can be established in NOx and particulate matter emissions [9, 10]. Therefore, this simulation is carried out as exergoenvironmental optimization in IDI diesel engine according to Ahmadi et al. [40].

Conflict of Interest

None declared.

References

1. Gomaa, M., A. J. Alimin, and K. A. Kamarudin. 2010. Trade-off between NOx, soot and EGR rates for an IDI diesel engine fuelled with JB5. World Acad. Sci. Eng. Technol.62:449–450.
2. Bianchi, G. M., P. Peloni, F. E. Corcione, and F. Lupino. 2001. Numerical analysis of passenger car HSDI diesel engines with the 2nd generation of common rail injection systems: the effect of multiple injections on emissions. SAE Paper No. 2001-01-1068.
3. Shayler, P. j., and H. K. Ng. 2004. Simulation studies of the effect of fuel injection pattern on NOx and soot formation in diesel engines. SAE Paper No. 2004-01-0116.
4. Chryssakis, C. A., D. N. Assanis, S. Kook, and C. Bae. 2005. Effect of multiple injections on fuel-air mixing and soot formation in diesel combustion using direct flame visualization and CFD techniques. Spring Technical Conference, ASME No. ICES2005-1016.
5. Ehleskog, R.2006. Experimental and numerical investigation of split injections at low load in an HDDI diesel engine equipped with a piezo injector. SAE Paper No. 2006-01-3433.
6. Sun, Y. D., and R. Reitz. 2006. Modeling diesel engine NOx and soot reduction with optimized two-stage combustion. SAE Paper No. 2006-01-0027.
7. Abdullah, N., A. Tsolakis, P. Rounce, M. Wyszinsky, H. Xu, and R. Mamat. 2009. Effect of injection pressure with split injection in a V6 diesel engine. SAE Paper No. 2009-24-0049.
8. Jafarmadar, S., and A. Zehni. 2009. Multi-dimensional modeling of the effects of split injection scheme on combustion and emissions of direct-injection diesel engines at full load state. IJE22:369–378.
9. Jafarmadar, S., and A. Zehni. 2012. Multi-dimensional modeling of the effects of spilt injection scheme on performance and emissions of IDI diesel engines. IJE25:135–146.
10. Showry, K., and A. Raju. 2010. Multi-dimensional modeling and simulation of diesel engine combustion using multi-pulse injections by CFD. Int. J. Dyn. Fluids ISSN 0973-1784, 6:237–248.
11. Iwazaki, K., K. Amagai, and M. Arai. 2005. Improvement of fuel economy of an indirect (IDI) diesel engine with two-stage injection. Energy Convers. Manage.30:447–459.
12. Gibbs, J. W.1961. The scientific papers. Vol. 1. Dover, New York, NY.
13. Dunbar, W. R., N. Lior, and R. A. Gaggioli. 1992. The component equations of energy and exergy. Trans. ASME J. Energy Resour. Technol.114:75–83.
14. Dunbar, W. R., and N. Lior. 1994. Sources of combustion irreversibility. Combust. Sci. Technol.103:41–61.
15. Obert, E. F.1993. Internal combustion engines and air pollution. Intext Educ. Publ, New York, NY.
16. Rakopoulos, C. D., and E. G. Giakoumis. 1997. Simulation and exergy analysis of transient diesel engine operation. Energy22:875–885.
17. Caton, J. A.2000. On the destruction of availability (exergy) due to combustion processes – with specific application to internal combustion engines. Energy25:1097–1117.
18. Rakopoulos, C. D., and E. G. Giakoumis. 1997. Development of cumulative and availability rate balances in a multi-cylinder turbocharged IDI diesel engine. Energy Convers. Manage.38:347–369.
19. Kyritsis, D. C., and C. D. Rakopoulos. 2001. Parametric study of the availability balance in an internal combustion engine cylinder. SAE paper 2001-01-1263.
20. Rakopoulos, C. D., and D. C. Kyritsis. 2005. The influence of cylinder wall temperature profile on the second-law diesel engine transient response. Appl. Therm. Eng.25:1779–1795.
21. Ghazikhani, M., M. E. Feyz, A. Joharchi. 2010. Experimental investigation of the exhaust gas recirculation effects on irreversibility and brake specific fuel consumption of indirect injection diesel engines. Appl. Therm. Eng.30:1711–1718.
22. Rakopoulos, C. D., and E. G. Giakoumis. 2004. Availability analysis of a turbocharged diesel engine operating under transient load conditions. Energy29:1085–1104.
23. Amjad, A. K., R. Khoshbakhi Saray, S. M. S. Mahmoudi, and A. Rahimi. 2011. Availability analysis of n-heptane and natural gas blends combustion in HCCI engines. Energy36:6900–6909.
24. Hosseinzadeh, A., R. Khoshbakhti Saray, and S. M. Seyed Mahmoudi. 2010. Comparison of thermal, radical and chemical effects of EGR gases using availability analysis in dual-fuel engines at 50% loads. Energy Convers. Manage.51:2321–2329.
25. Jafarmadar, S.2013. Three-dimensional modeling and exergy analysis in combustion chamber of an indirect injection diesel engine. Fuel107:439–447.
26. Jafarmadar, S.2013. Multidimensional modeling of the effect of engine load on various exergy terms in an indirect injection diesel engine. Int. J. Exergy, in press.
27. Caton, J. A.2012. Exergy destruction during the combustion process as functions of operating and design parameters for a spark-ignition engine. Int. J. Energy Res.36:368–384.
28. Sivadas, H. S., and J. A. Caton. 2008. Effects of exhaust gas recirculation on exergy destruction due to isobaric combustion for a range of conditions and fuels. Int. J. Energy Res.32:896–910.
29. Sayin, C., M. Hosoz, M. Canakci, and I. Kilicaslan. 2007. Energy and exergy analyses of a gasoline engine. Int. J. Energy Res.31:259–273.
30. Jafarmadar, S., R. Tasoujiazar, and B. Jalilpour. 2013. Exergy analysis in a low heat rejection IDI diesel engine by three dimensional modeling. Int. J. Energy Res. 3 SEP 2013, doi: 10.1002/er.3100
31. Han, Z., and D. Reitz. 1995. Turbulence modeling of internal combustion engines using RNG k−ɛ models. Combust. Sci. Technol.106:267–295.
32. Liu, A. B., and R. D. Reitz. 1993. Modeling the effects of drop drag and break-up on fuel sprays. SAE Paper No. 930072.
33. Dukowicz, J. K.1979. Quasi-steady droplet change in the presence of convection. Informal report Los Alamos Scientific Laboratory, Los Alamos, NM. LA7997-MS.
34. AVL FIRE user manual V. 8.5. 2006.
35. Halstead, M., L. Kirsch, and C. Quinn. 1977. The auto ignition of hydrocarbon fueled at high temperatures and pressures – fitting of a mathematical model. Combust. Flame30:45–60.
36. Van Gerpen, J. H., and H. N. Shapiro. 1990. Second law analysis of diesel engine combustion. Trans. ASME J. Eng. Gas Turb. Power112:129–137.
37. Rakopoulos, C. D., and E. G. Giakoumis. 2006. Second-law analyses applied to internal combustion engines operation. Prog. Energy Combust. Sci.32:2–47.
38. Rodriguez, L.1980. Calculation of available-energy quantities. Pp. 39–59inR. A. Gaggioli, ed. Thermodynamics: second law analysis. American Chemical Society, Symposium Series No. 122, Washington, DC.
39. Primus, R. J., and P. F. Flynn. 1986. Pp. 61–68inThe assessment of losses in diesel engines using second law analysis. ASME WA-Meeting, Proc. AES, Anaheim, CA.
40. Ahmadi, P., A. Almasi, M. Shahriyari, and I. Dincer. 2012. Multi-objective optimization of a combined heat and power (CHP) system for heating purpose in a paper mill using evolutionary algorithm. Int. J. Energy Res.36:46–63.