Abstract
The development of high-speed train lines has increased significantly during the last twenty-five years, leading to more demanding loads in railway infrastructures. Most of these infrastructures were constructed using railway ballast, which is a layer of granular material placed under the sleepers whose roles are: resisting to vertical and horizontal loads and facing climate action. Moreover, the Discrete Element Method was found to be an effective numerical method for the calculation of engineering problems involving granular materials. For these reasons, the main objective of the work is the development of a numerical modelling tool based on the Discrete Element Method which allows the users to understand better the mechanical behaviour of railway ballast.
The first task was the review of the specifications that ballast material must meet. Then, the features of the available Discrete Elements code, called DEMPack, were analysed. After those revisions, it was found that the code needed some improvement in order to reproduce correctly and efficiently the behaviour of railway ballast. The main deficiencies identified in the numerical code were related to the contact between discrete element particles and planar boundaries and to the geometrical representation of such a irregular material as ballast.
Contact interactions between rigid boundaries and Discrete Elements are treated using a new methodology called the Double Hierarchy method. This new algorithm is based on characterising contacts between rigid parts (meshed with a Finite Element-like discretisation) and spherical Discrete Elements. The procedure is described in the course of the work. Moreover, the method validation and the assessment of its limitations are also displayed.
The representation of irregular particles using the Discrete Element Method is a very challenging issue, leading to different geometrical approaches. In this work, a deep revision of those approaches was performed. Finally, the most appropriate methods were chosen: spheres with rolling friction and clusters of spheres. The main advantage of the use of spheres is their low computational cost, while clusters of spheres stand out for their geometrical versatility. Some improvements were developed for describing the movement of each kind of particles, specifically, the imposition of the rolling friction and the integration of the rotation of clusters of spheres.
In the course of this work the way to fill volumes with particles (spheres or clusters) was also analysed. The aim is to control properly the initial granulometry and compactness of the samples used in the calculations.
After checking the correctness of the numerical code with simplified benchmarks, some laboratory tests for evaluating railway ballast behaviour were computed. The aim was to calibrate the ballast material properties and validate the code for the representation of railway ballast. Once the material properties were calibrated, some examples of a real train passing through a railway ballast track were reproduced numerically. This calculations allowed to prove the possibilities of the implemented tool.
This publication is a revised version of the text of the PhD Thesis “Numerical analysis of railway ballast behaviour using the Discrete Element Method” of Joaquín Irazábal, presented at the Technical University of Catalonia on October 6th 2017
Acknowledgements
I would like to thank all people who contributed in one way or the other to the achievement of this work.
First of all I want to express my gratitude to my PhD advisors, Prof. Eugenio Oñate, for his support all over these years. It has been a pleasure to work with him.
I want to specially thank Fernando Salazar, the Director of CIMNE Madrid. He has been not only my boss but also my college. Without his invaluable help and advices this work would not be what it is. I want to thank also my other colleges in the CIMNE Madrid's office, David and Javier, for the good times we have spent and for letting me share my experiences with them, always giving me useful opinions.
Thanks to Miguel Ángel and Salva for their cooperation and assistance and also for making me feel one more of the team when I go to Barcelona. I can not forget to thank the other DEM Team members: Guillermo and Ferran for their outstanding work, which has been fundamental for the code developments implemented during this work. Thanks to Miquel Santasusana for making our collaboration so enjoyable, we shared an article and many hours of work, but also great moments out of the office. I should also thank Pablo and his patience with me during my first months in CIMNE helping me to start understanding KRATOS, Antonia who helped me always since I started studying the Master and the colleges in CIMNE Cuba, Roberto and Carlos, who assisted me from the moment I asked for help. I also want to thank Merce for her kind help in the difficult administrative issues. May be because I am in Madrid I am missing some people in Barcelona, but my intention is to thank everybody belonging to CIMNE family.
Last but not least to all my friends and family, specially my parents, Juanjo and Charo, and my sister, Lucía, for being always at my side. Finally, I would like to thank the person with whom I have shared more time and experiences the last ten years: thanks Patry for supporting me everyday but above all making me happy.
This work was carried out with the financial support of CIMNE via the CERCA Programme / Generalitat de Catalunya and the Spanish MINECO within the BALAMED (BIA2012-39172) and MONICAB (BIA2015-67263-R) projects.
Resumen
El desarrollo de las líneas de alta velocidad ha aumentado significativamente durante los últimos veinticinco años, dando lugar a cargas más exigentes sobre las infraestructuras ferroviarias. La mayor parte de estas infraestructuras se construyen con balasto, que es una capa de material granular colocada bajo las traviesas cuyas funciones principales son: resistir las cargas verticales y horizontales repartiéndolas sobre la plataforma y soportar las acciones climáticas. Por otra parte, se encontró que el Método de los Elementos Discretos es muy eficaz para el cálculo de problemas de ingeniería que implican materiales granulares. Por estas razones se decidió que el objetivo principal de la tesis fuera el desarrollo de una herramienta de modelación numérica basada en el Método de los Elementos Discretos que permita a los usuarios comprender mejor el comportamiento mecánico del balasto ferroviario.
La primera tarea fue la revisión de las especificaciones que el balasto debe cumplir. A continuación, se analizaron las características del código de Elementos Discretos disponible, denominado DEMPack. Después de esas revisiones, se encontró que el código necesitaba alguna mejora para poder reproducir correcta y eficientemente el comportamiento del balasto ferroviario. Las principales deficiencias identificadas en el código numérico están relacionadas con el contacto entre partículas y contornos planos y con la representación geométrica de un material tan irregular como es el balasto.
Los contactos entre contornos rígidos y elementos discretos se tratan usando una nueva metodo-logía llamada el Double Hierarchy method. Este nuevo algoritmo se basa en la caracterización de contactos entre elementos rígidos (discretizados de forma similar a los elementos finitos) y elementos discretos esféricos. El procedimiento de búsqueda y caracterización de contactos se describe detalladamente a lo largo de la tesis. Además, también se muestra la validación del método y se evalúan sus limitaciones.
La representación de partículas irregulares utilizando el Método de los Elementos Discretos se puede abordar desde diferentes enfoques geométricos. En este trabajo, se realizó una revisión de estos enfoques. Finalmente, se escogieron los métodos más adecuados: esferas con resistencia a la rodadura y clusters de esferas. La principal ventaja del uso de las esferas es su bajo coste computacional, mientras que los clusters de esferas destacan por su versatilidad geométrica. Se han desarrollado algunas mejoras para describir el movimiento de cada uno de los tipos de partículas, concretamente, la imposición de la resistencia a la rodadura y la integración de la rotación de clusters de esferas.
En el curso de este trabajo también se analizó la forma de llenar volúmenes con partículas (esferas o clusters). El objetivo es controlar adecuadamente la granulometría inicial y la compacidad de las muestras utilizadas en los cálculos.
Después de comprobar el comportamiento del código numérico con tests simplificados, se emularon numéricamente algunos ensayos de laboratorio con balasto ferroviario. El objetivo era calibrar las propiedades del balasto y validar el código para representar con exactitud su comportatimiento. Una vez calibradas las propiedades del material, se reprodujeron numéricamente algunos ejemplos de un tren pasando sobre una vía con balasto. Estos cálculos permiten demostrar las posibilidades de la herramienta numérica implementada.
1 Introduction
The railway line system plays an important role in the transport network of any country, and its maintenance is essential. Among other solutions, ballast is traditionally used to support railway tracks as it is relatively inexpensive and easy to maintain [1].
Before the advent of high-speed trains, most attention was given to the track superstructure (consisting of rails, fasteners and sleepers) than to the substructure (consisting of ballast, subballast and subgrade). However, the maintenance cost of the substructure is not negligible at all [2], and a better knowledge of railway ballast behaviour may allow a more efficient use of it, saving money and increasing rail transport safety.
Besides the importance of studying ballast properties, in economic and safety terms, it should be pointed that a new variable appeared in the last two decades: the increase of trains speed. High-speed trains improved people mobility all around the world, at the cost of increasing vibrations and loads on the railway track [3], making its behaviour more uncertain.

|
| Figure 1: High-speed train travelling over a ballasted railway track. |
Efficiency, safety and the more demanding loads and vibrations raised the interest on studying railway infrastructures deeply. Within those infrastructures, the ballast layer is one of the elements whose behaviour is more uncertain, due to its granular nature. For this reason, railway ballast laboratory tests are being preformed by different construction companies and research teams. However, real tests are difficult and expensive to carry out. In addition, there are parameters that can not be easily measured in the laboratory.
To overcome these problems, the calculation of railway ballast and other granular materials is being addressed by means of the development of different computational methods. Regarding the computational analysis, granular materials can be considered either as discrete individuals that interact through proper contact laws, or as a continuum, whose behaviour is governed by some constitutive law.
1.1 Numerical analysis of granular materials
Although, in general, granular materials can be defined as numerous collections of rigid or deformable bodies that interact with one another [4], they can be classified based on various criteria. There are granular materials whose particles can be of different grain sizes, from nanoscale powders to groups of stones; there are granular materials whose particles appear round and others with very sharp particles; and, there also exist very compacted granular materials and others whose particles appear disperse. These and other characteristics lead to no single predictive behaviour of granular materials, and their calculation must be addressed from diverse numerical perspectives depending on their properties.
In this particular case, the interest lies in the calculation of railway ballast behaviour. Railway ballast refers to the layer of crushed stones placed between and underneath the sleepers whose purpose is to provide drainage and structural support for the dynamic loading applied by trains. Railway ballast forms a dense collection of particles with relatively large grain size, as compared to the depth of the ballast bed. It typically works under high frequency loads exerted by high-speed trains travelling over the rails.
Traditionally, complex geomechanic problems were addressed using refined constitutive models based on continuum assumptions. Although these models may be accurate in the evaluation of the critical state of soils [5,6,7,8], or the flow of bulk material masses [9], they are not able to represent local discontinuities which typically play a fundamental role in the behaviour of granular materials. This discontinuous nature induces special features such as anisotropy or local instabilities, which are difficult to understand or model based on the principles of continuum mechanics [10].
The most natural choice to represent granular materials is the use of discrete techniques, intrinsically appropriate to account for their discontinuity and heterogeneity. The two principal approaches within the discrete framework are: Non-smooth and Smooth Discrete Element Methods [11].
Within Non-smooth Discrete Element Methods, interactions are described by shock laws and Coulomb friction, written as non-differentiable relations. Meanwhile, Smooth Discrete Element Methods describe the interactions between grains by regular functions involving gaps, relative velocities and reaction forces.
The most popular Non-smooth discrete element methods are:
- Event Driven (ED) methods, which are used for collections of rigid bodies distanced from each other that collide by pairs (these methods assume that the contact time is implicitly zero). Collisions are governed by shock laws with restitution coefficients, not always considering friction [12].
- Non-Smooth Contact Dynamics (NSCD) method, which is normally applied to dense collections of rigid or deformable bodies. Contact laws are described by non-continuous functions within the frame of convex analysis. Time integration is carried out using implicit schemes, contrary to ED methods [13,14].
Smooth Discrete Element Methods can also be addressed by different approaches, where two methods can be highlighted:
- Molecular Dynamics (MD) considers grains as rigid particles submitted to contact forces calculated from potential functions. Since this method was initiated to deal with colliding gas particles, their particles rotation is discarded. Explicit time integration schemes, together with simple interaction modelling, allow fast flows of data to be managed for numerous collections of particles.
- Discrete Element Method (DEM) is the result of considering rotational degrees of freedom and contact mechanisms to MD [15]. Presented by Cundall and Strack [16] in 1979, each material grain is calculated as a rigid particle. The deformation of the material is represented by the interaction between the particles, allowing small overlaps. The normal and tangential contact between the rigid particles define the material constitutive behaviour. The dynamic equation is solved by means of explicit integration schemes.
The main features of the four mentioned methods are summarised in Table 1.
| Non-smooth DEM | Smooth DEM | |||
| ED | NSCD | MD | DEM | |
| Valid for dense collections of particles | ⨉ | ✓ | ⨉ | ✓ |
| Valid for loose collections of particles | ✓ | ⨉ | ✓ | ✓ |
| Contact mechanism accurately characterised | ⨉ | ✓ | ⨉ | ✓ |
| Allows multiple contacts | ⨉ | ✓ | ✓ | ✓ |
| Implicit scheme for time integration | ⨉ | ✓ | ⨉ | ⨉ |
| Explicit scheme for time integration | ✓ | ⨉ | ✓ | ✓ |
DEM can be used for the calculation of loose collections of particles, but the computational time would be very high compared to ED method or MD.
In this research, ED and MD methods are discarded because they are not conceived for the calculation of dense collections of particles and the contact mechanism in both methods is not accurately treated. Between DEM and NSCD the main difference is the use of explicit and implicit time integration schemes respectively. Explicit algorithms are more straightforward than implicit ones, but their computational stability limits the calculation time step. On the other hand, the time step for implicit schemes is not limited by the system stability, at the cost of a higher computational demand.
Many studies [17,18,19] tried to evaluate which of DEM or NSCD is better for the calculation of dense collections of particles. In all of them the conclusion is that it depends on the case study, so there is not a general rule to choose one or another.
In this particular case, considering that high-speed trains exert high frequency loads over the ballast bed, the use of explicit time integration schemes could be computationally advantageous [20,21]. These schemes do not need to include any additional term to take into account the frequency of the input load. In order to correctly capture the dynamic response, the calculation time step should be several times smaller than the input load period. Under this condition, the explicit integration yields sufficient accuracy and the time step is generally below its stability limits. Another important outcome of the use of an explicit integration is the easier parallelisation of the code and the avoidance of linearisation and employment of system solvers. Such considerations induce to conclude that, although NSCD is an interesting method to address this problem, the DEM is more appropriate.
1.2 Objectives
This work falls within the framework of two research projects funded by the Spanish Ministry of Economy, Industry and Competitiveness (MINECO):
- BALAMED (BIA2012-39172): Numerical modelling of rail-sleeper-ballast interaction using the Discrete Element Method.
- MONICAB (BIA2015-67263-R): Numerical modelling of sand-fouled ballast in high-speed railways.
BALAMED project aims to develop a numerical tool, based on the DEM, for calculating the response of the rail-sleeper-ballast system under the loads of the high speed trains. It started in 2013 and finished in 2015. Meanwhile, MONICAB project started in 2016 and will finish in 2018. Its main objective is the development of a numerical modelling tool, based on the DEM for the analysis of the behaviour of the sand-fouled railway ballast.
Current thesis shows most of the progresses made within those projects. The research is conducted in parallel with the improvements performed in the open-source DEM code developed in CIMNE1, the so-called DEMPack (www.cimne.com/dempack/). The data structures and algorithms, used in DEMPack are implemented through the Kratos multiphysics software suite [22], an Open-Source framework for the development of numerical methods for solving multidisciplinary engineering problems.

|
| Figure 2: DEMpack logo. |
From all the above-mentioned, the general objective of this thesis can be stated as follows: develop a numerical tool based on the DEM, within DEMpack, able to reproduce ballast behaviour, including its interaction with other structures. To reach this goal some partial objectives should be fulfilled.
- Conduct a literature review on railway ballast, studying its physical properties, and the specifications it should meet. The aim is to determine the necessities of a numerical code able to reproduce railway ballast behaviour.
- Identify the limitations of the available DEM code for reproducing railway ballast, such as, the interaction between Discrete Elements (DEs) and rigid boundaries and the geometrical representation of irregular particles.
- Implement an accurate and efficient method to search neighbours and evaluate forces in calculations involving DEs and rigid boundaries.
- Evaluate the alternatives for the geometrical representation of granular materials. Choose the most suitable approaches for replicating railway ballast behaviour taking into account accuracy and computational efficiency.
- Explore and define suitable methodologies to generate samples of granular material with the desired granulometry, particle shape and compaction.
- Develop contact constitutive models for railway ballast particles interaction, taking into account the singularities of each geometrical approach chosen.
- Calibrate and validate the contact constitutive models by reproducing different laboratory tests previously identified.
- Finally, the usefulness of the numerical code was verified by calculating full scale cases where a train passes through different ballasted track sections.
(1) Centre Internacional de Metodes Numerics en Enginyeria.
1.3 Outline
The work is divided into eight chapters, including current one:
- Chapter 2 introduces the literature review on railway infrastructures, focusing mainly on railway ballast. The aim is to have as much information as possible to define the material properties in the most accurate manner. In this chapter, laboratory tests for the calibration and validation of the numerical code are also reviewed.
- Chapter 3 describes the basic aspects of the DEM with spherical particles, including the neighbour search and force evaluation strategies followed, the contact constitutive models used and the time integration schemes adopted.
- Chapter 4 is dedicated to the strategy followed to detect and solve contact between spherical particles and planar surfaces. The novel Double Hierarchy Method for contact with rigid boundaries is described. Validation examples and limitations analysis are also displayed.
- Chapter 5 presents the geometric alternatives to represent railway ballast particles within the DEM. The two approaches finally chosen were the use of spherical particles and sphere clusters. Special features regarding spherical and non-spherical particles rotation are deeply described, detailing the new developments carried out during this research. The main improvements implemented concern rolling friction application to spherical particles and non-spherical particles rotational integration of motion. The validation procedure of those improvements is also presented.
Regarding particles arrangement, the generation of compacted groups of spherical particles and sphere clusters is also addressed in Chapter 5.
- Chapter 6 starts with the review of the material properties needed to accurately define railway ballast in the numerical calculations. Then, aiming to calibrate and validate the numerical code, some laboratory tests are reproduced.
- Chapter 7 shows the calculation of a real train passing through different ballasted track sections: the first one correctly compacted, the second including a bump and the third eroded laterally.
- Finally, Chapter 8 refers to the conclusions that can be drawn from this research and the future work that can be derived from its findings.
1.4 Related publications
1.4.1 Articles in scientific journals
- M. Santasusana, J. Irazábal, E. Oñate, J.M. Carbonell. The double hierarchy method. A parallel 3D contact method for the interaction of spherical particles with rigid FE boundaries using the DEM, Comp Part Mech 3 (3) (2016) 407–428.
- J. Irazábal, F. Salazar, E. Oñate. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Comput Geotech 85 (2017) 220–229.
1.4.2 Communications in congresses
- M. Santasusana, E. Oñate, J.M. Carbonell, J. Irazábal, P. Wriggers. Combined DE/FE Method for the simulation of particle-solid contact using a Cluster-DEM approach, 4 International Conference on Computational Contact Mechanics (ICCCM 2015), Hannover.
- J. Irazábal, F. Salazar, E. Oñate. Numerical modelling of railway ballast behaviour using the Discrete Element Method (DEM) and spherical particles, IV International Conference on Particle-Based Methods (Particles 2015), Barcelona.
- M. Santasusana, E. Oñate, J.M. Carbonell, J. Irazábal, P. Wriggers. A Coupled FEM-DEM procedure for nonlinear analysis of structural interaction with particles, IV International Conference on Particle-Based Methods (Particles 2015), Barcelona.
- J. Irazábal, F. Salazar, E. Oñate. Geometrical representation of railway ballast using the Discrete Element Method (DEM), 7 European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress 2016), Crete Island.
- M. Santasusana, J. Irazábal, E. Oñate, J.M. Carbonell. Contact Methods for the Interaction of Particles with Rigid and Deformable Structures using a coupled DEM-FEM procedure, 7 European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress 2016), Crete Island.
- J. Irazábal, F. Salazar, E. Oñate. Shape characterisation of railway ballast stones for discrete element calculations, V International Conference on Particle-Based Methods (Particles 2017), Hannover.
2 Introduction to railway tracks
This chapter is divided in three different sections. The first one presents a brief introduction of railway infrastructures and a review of its components, from the superstructure to the substructure, focusing on the ballast layer. Meanwhile, section 2.2 describes the main features of ballast and sleepers. Finally, section 2.3 is a review of the state of the art of the laboratory tests used to evaluate railway ballast behaviour.
2.1 Railway infrastructures
Railway infrastructures can be split in two parts: the superstructure, that transmits the train loads to the substructure and the substructure, that distributes those loads to the soil. The superstructure is directly in contact with the train wheels, while the substructure is in contact with the superstructure via the sleepers, that are embedded in the ballast layer as it is shown in Figure 3.

|
| Figure 3: Scheme showing the position of the rails, the sleepers and the ballast layer. |
2.1.1 Railway substructure
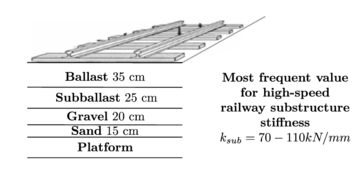
Traditionally, the cross-section of the substructure of conventional railway tracks consisted of a simple ballast layer over the platform. Besides distributing traffic loads, the ballast layer contributes to rainwater evacuation, platform protection to moisture variance, longitudinal and lateral stabilisation and high loads damping [23].
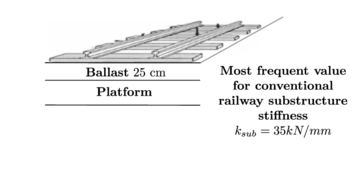
The typical cross-section of conventional and high-speed railway tracks is presented in Figure 4. The differences between both are due to the more demanding loads exerted by high-speed trains. Although the function of the ballast layer is the same in both types of tracks, in high-speed railway infrastructures the ballast layer is thicker and more layers of various materials (subballast, gravel and sand) are placed over the platform, in order to distribute more efficiently train loads and prevent the platform damage due to erosion. These differences lead to a higher stiffness of the substructure in high-speed railway tracks.
|
|
| (a) Conventional railway substructure. | (b) High-speed railway substructure. |
| Figure 4: Typical cross-section of conventional and high-speed railway tracks. Scheme including typical values for the vertical stiffness of the platform and subgrades (). Source: López Pita [28]. | |
2.1.2 Railway superstructure
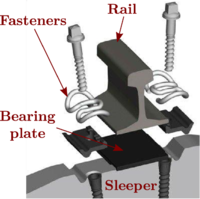
Railway superstructure primary role is to transmit loads from train wheels to the substructure. Figure 5 shows its main components.
- Rails are directly responsible of supporting the vehicles passing. Modern rails are typically manufactured from hot-rolled steel due to the high stresses they have to bear with. Their weight used to be about 60 kg/m [24].
- Fasteners are elements that fix the rails to the sleepers. There are four per sleeper, which corresponds to two per rail.
- Bearing plates are elastic pads collocated between the sleepers and the rails that provide greater vertical elasticity to the whole structure.
- Sleepers are fixed to the rails through the fasteners and are directly in contact with the ballast layer. Sleepers main features will be deeply commented in section 2.2.
|
| Figure 5: Superstructure configuration. |
In addition to the components shown in Figure 5, there is another significant element , called rubber sole, that forms the superstructure. Rubber soles are elastic elements located under the sleepers to modify track stiffness and increase elasticity. They are normally used in viaducts where track elasticity should be increased in order to reduce its rapid damage.
2.1.3 Railway geometrical quality
When a train travels over the track, it has three degrees of freedom corresponding to the displacement along its principal axes, which are: longitudinal (travelling direction), vertical and lateral. In addition, the train has other three degrees of freedom corresponding to the rotation about those axes, which are called: roll (about the longitudinal axis), yaw (about the vertical axis) and pitch (about the lateral axis). Figure 6 shows a diagram of those movements.

|
| Figure 6: Train translational and rotational degrees of freedom. The vehicle travels in the longitudinal direction. |
These displacements and rotations produce a set of loads that have to be taken into account for dimensioning the railway track. Vertical loads are the main criteria for designing the components of the track, lateral loads determine the maximum speed of vehicles movement, whereas longitudinal loads can cause horizontal buckling of the track.
The high loads to which the railway track is subjected, in any of the three directions, can trigger defects in the railway infrastructure. To measure the impact of this defects, in safety and comfort terms, it is important to quantify the track quality, which can be achieved by the following parameters [25]:
- Vertical alignment: this parameter defines the variations in height of the rail upper surface, relative to a reference plane.
- Cross level: this parameter sets the difference in height between the upper surface of both rails on a section normal to the axis of the road.
- Track gauge: parameter determining the distance between the active faces of the heads of the rails 14 mm below the rolling surface.
- Horizontal alignment: parameter which, for each rail, represents the distance, from above, compared to the theoretical alignment.
- Track twist: represents the distance between a point of the track and the plane formed by three points belonging to the same railway. It has an impact on possible derailments.
Figure 7 shows schematically some of these defects.
![Typical railway track alignment defects. Source: López Pita [28].](/wd/images/thumb/8/81/Draft_Samper_552093892-test-Ch2Fig5.png/600px-Draft_Samper_552093892-test-Ch2Fig5.png)
|
| Figure 7: Typical railway track alignment defects. Source: López Pita [28]. |
2.1.4 Railway stiffness
Railway stiffness refers to the resistance of the whole track against deformations in the vertical direction [26]. Burrow [27] highlighted that the magnitude of the railway stiffness is mainly influenced by the substructure. Considering only the layers that compose the substructure, ballast is the most relevant material. It should be noted that, comparatively, the platform influences more, but its stiffness is almost imposed and can not be adjusted.
From Burrow's developments [27], it can be concluded that there is an optimal railway stiffness (at least from the theoretical point of view). When railway stiffness is excessively low, too much rail deformation may occur, while, if it is high, the infrastructure would be damaged rapidly. López Pita et al. [28] proposed a range of optimal values for railway stiffness. Their work was based on optimizing maintenance costs and energy dissipation costs (due to excessive deformations). They used data from the high-speed tracks Paris-Lyon and Madrid-Sevilla. The study concluded that the overall railway stiffness must be between 70 and 80 kN/mm.
The EUROBALT II European project also dealt with the deterioration of railway tracks. Its main objective was to identify the parameters that should be controlled to reduce damage in railway tracks. The findings of this study were that the most influencing parameters to the track behaviour were: the stiffness, the displacement of the rails and the settlement of the different layers.
2.2 Ballasted tracks components
Railway ballast is the material under consideration in this thesis, for that reason it is important to perform a deep study of its properties. In the first part of this section, ballast specifications are described. Moreover, in the second part the main features of sleepers used in Spain are defined. Sleepers characteristics are significant in this research due to the fact that they directly interact with ballast. Finally, some aspects about the fasteners will be commented briefly.
2.2.1 Ballast specifications
Ballast, as structural element, is formed by a set of particles of different size and shape. The ballast is, thus, a layer of granular material which is placed under the sleepers and therefore develops important roles: resisting to vertical and horizontal loads (produced by the passing train over the rail) and facing climate action.

|
| Figure 8: Ballast stones. |
The Standard UNE-EN 13450:2015 [29] specifies the technical characteristics of the ballast used as a supporting layer in railway tracks. The Standard defines quality controls to which ballast should be subjected. Those quality controls have to do with five material properties: granulometry, Los Angeles coefficient (CLA)1, micro-Deval coefficient (MDS)2, flakiness index and particle length.
The size distribution of particles established by the Standard UNE-EN 13450:2015 is presented in Table 2. Ballast particles size should be between and . In addition, the presence of angular stones is discouraged, because those kind of particles slip easily and can obstruct tamping operation.
| Sieve size (mm) | Cumulative % passing through each sieve |
| 63 | 100 |
| 50 | 70-100 |
| 40 | 30-65 |
| 31.5 | 0-25 |
| 22.4 | 0-3 |
| 32-50 | 50 |
Tamping operation is performed by the tamping machine which moves each sleeper and rail into their correct vertical and horizontal position. Then, it introduces its tines into the ballast layer. When the tines reach the required depth they start to vibrate, in order to arrange the ballast stones under the sleeper in the most compacted manner. The need to carry out this operation lies in the necessity of correcting track misalignments by compacting the ballast under the sleepers, providing a solid foundation. If the track is not rigid enough when a vehicle is travelling through it, two different phenomenon can appear simultaneously: vertical deflection and lifting wave [24]. Vertical deflection affects a rail length of to approximately. Its maximum value in the point of application of the load ranges from to , considering a load of per wheel. Otherwise, lifting wave refers to the lift of the front part of the railway track in the direction of movement, the magnitude use to be about the of vertical deflection.
Regarding the train passage, it has to be said that each train axle produces a sleeper stroke to the ballast layer (on a freight train 150 strokes can be reached) which, together with the increasing weight of the sleepers (about ) may lead to a rapid deterioration of ballast stones. Aiming to minimise this deterioration and to resist tamping operation, a hard enough rock, difficult to break, is needed. According to the Railway Standard UNE 22950-1:1990 [31], this requirement is met if the original rock has a compression resistance of . The Standard UNE-EN 13450:2015 established a maximum value for the coefficient of Los Angeles, which should be less than . Abrasion needs are achieved by requiring the ballast a value over 15 in the Deval coefficient.
Particle shape also affects ballast behaviour, that is why flakiness index and particle length are evaluated. The flakiness index test is performed to determine the number of slabs in the granular material used in the construction of railway tracks. Stretched particles can break, leading to modifications of the particle size and decreasing the load capacity. In this context, slabs are the fraction of granular material whose minimum dimension (thickness) is less than 3/5 of the average size of the considered material fraction. The test consists of two sifting operations, the first to separate particles into groups, depending on their size, and the second with a parallel bars sieve. The bars of the second sieve are separated times the size of the first sieve. The flakiness index is expressed as the weight percentage of ballast passing through the bars sieve. According to the regulations, this index must be less than or equal to .
The particle length index is defined as, the mass percentage of ballast particles greater than or equal to 100 mm length, in a ballast sample weighting more than 40 kg. The test is performed by measuring each of the particles with a calliper. According to the legislation the particle length index must be lower than 4%
| Actions | Functions | Property | Property evaluation | |||||
| Vertical | Elasticity and damping | Elastic modulus | Load plate test | |||||
| Ballast thickness | Minimum thickness | |||||||
| Abrasion resistance | Resistance to abrasion | Wet MicroDeval | ||||||
| Alleviate pressure on the railway platform | Ballast thickness | Minimum thickness | ||||||
| Withstand rail shocks | Impact resistance | Los Angeles coefficient | ||||||
| Horizontal | Longitudinal resistance | Granulometry |
| |||||
| Transversal resistance | ||||||||
| Climate | Assist the drainage | Granulometry |
| |||||
| Ice resistance | Frost resistance |
|
Table 3 summarises other features required for materials used as ballast. To comply all those functions, the layer thickness should be between 25 and 35 cm [24]. The lower limit is set by the need of achieving the loads resistance objectives, with less ballast the specifications could not be met, while the upper value is set by the need to restrict seats and geometrical defects on the railway track.
From all the above-mentioned, it can be concluded that, in addition to deal with climate actions, the main functions of the ballast layer are:
- Help to provide stability and damping capacity to the railway track, which reduces the dynamic loads exerted by trains passage.
- Distribute pressures in the platform to avoid reaching the bearing capacity of the ground.
- Withstand particles abrasion that can be consequence of their successive contact with rigid infrastructures such as, for example, concrete bridges.
(1) Wear coefficient of Los Angeles (CLA). It measures wear resistance by attrition and impact of aggregates. It is the ratio of the difference in weight of the initial sample and the material retained by the sieve 1.6 UNE (once subjected to an abrasive and standardised process using iron balls), divided by the initial weight of the sample.
(2) Deval coefficient: determined by the value obtained in the Deval test, consisting of introducing 44 stones of 7 weighing 5 , in a cylinder that rotates around an inclined axis. The cylinder rotates for 5 hours until 10000 turns. Then the set of dispersed materials are weighed getting "P" in grams. The Deval coefficient is given by the ratio 400/P [30].
2.2.2 Sleepers
The elongated pieces made of various materials, located between the rails and the ballast layer are called sleepers, whose main functions are [32]:
- Keep rail position, supporting them and maintaining their separation and inclination.
- Distribute vertical, lateral and longitudinal loads from the rails to the ballast layer.
- Contribute (along with fasteners) to maintain electrical isolation between the two rails, in railway tracks with electrical signals.
- Preserve the horizontal stability of the track (in lateral and longitudinal direction) against stresses due to temperature variations or dynamic loads due to trains passage. Sleepers prevent buckling and ripping (lateral displacement) of rails.
- Preserve the stability of the track in the vertical plane, against static and dynamic loads produced by trains.
The variables that influence in a more significant way the sleepers behaviour are [32]: their dimensions, weight and elasticity.
Sleepers dimensions are important because they affect the supporting area available, which can reduce the stresses transmitted to the ballast layer. A high weight contributes to increase longitudinal and lateral stability of the track, however, heavier sleepers are more difficult to install in the construction phase. Regarding sleepers elasticity, it provides stability absorbing mechanical forces and preventing deterioration, which minimizes maintenance costs.
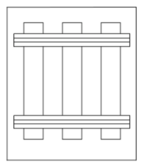
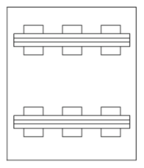
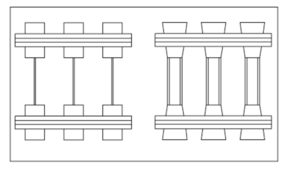
Different types of sleepers can be classified according to the material they are made of or based on their shape. Sleepers can be made of wood, steel, cast iron, reinforced concrete, pre-stressed concrete or synthetic materials. According to their shape, sleepers can be monoblock, semi-sleepers or twin block, as it is shown in Figure 9.
|
|
|
| (a) Monoblock. | (b) Semi-sleeper. | (c) Bi-block. |
| Figure 9: Different types of sleepers depending on their shape. Source: Álvarez and Luque [32]. | ||
Although the list of different sleepers may seem large, in Spain, basically three types are used:
- Wood sleepers (Figure 10a).
- Two different concrete sleepers: monoblock (Figure 10b) and twin block (Figure 10c).

|

|

|
| (a) Wood sleepers. | (b) Monoblock concrete sleepers. | (c) Twin block concrete sleepers. |
| Figure 10: Different kinds of sleepers, by material and shape. | ||
Wood sleepers, defined in the Standard NRV 3-1-0.0 [33], may be of different kinds of trees such as oak, beech or pine. These sleepers must comply the established regulations, which came from 1966 [34].
In the first railway tracks, constructed in the nineteenth century, the only material used to manufacture sleepers was wood, since their physical and mechanical properties, added to its abundance, made this material the best choice. However, time passes and the possibility of using concrete to build sleepers make wood sleepers almost disappear. Nowadays, wood sleepers are used very rarely and never in high-speed tracks. Wood sleepers can be used, for example, in tracks where the stiffness is very high, like in metal bridges.
Prestressed concrete displaced wood as a material for sleepers manufacturing. These are the most well-known advantages and drawbacks of concrete sleepers over wood sleepers [35]:
- Advantages:
- Concrete sleepers have a longer life, about two or three times more than wood sleepers.
- Their physical conditions are preserved all over the railway track.
- Better track resistance against displacement in its horizontal plane.
- Their greater weight provides higher lateral and longitudinal resistance against different forces.
- Their design can be easily changed to improve track properties.
- Concrete sleepers cost less than treated wood sleepers.
- Disadvantages:
- Concrete sleepers need special insulation to electrically isolate the two rails.
- Its weight, about for monoblock sleepers, compared to the weight of wood sleepers, about , make them an element difficult to handle.
- They are more brittle.
- They present a structural weakness at their centre (in case of monoblock sleepers) because their uniform support on ballast produce stresses on their upper face, being able to originate cracks in concrete.
The Standards N.R.V. 3-1-2.1 [36] and N.R.V. 3-1-3.1 [37] describe, respectively, the main features of monoblock and twin block sleepers. In Spain, monoblock sleepers are widely used because of their resistance (monoblock sleepers can be prestressed) and their bigger bearing surface, that allows a better distribution of loads. The advantages of twin block sleepers are that they are lighter and their behaviour to lateral movement is good (in France they are still used frequently). Twin block sleepers main problems are [38]:
- Its high cost due to the steel used in its central zone.
- They are not the best sleeper in maintaining rail track width, mainly due to its low vertical and horizontal stiffness.
- Their central strut may be corroded easily.
- Their behaviour against derailment is poor.
Regarding the materials used, technical specifications require a high quality cement with high strength and uniform size aggregates and siliceous. The compressive strength of the concrete must be greater than , and the tensile strength of the steel should be about .
There are many types of concrete sleepers depending on their dimensions which can be modified if it is necessary. If a new sleeper design wants to be used, it should be fully defined in a draft drawing signed by the applicant. The draft drawing must include basic dimensions that the department responsible for the railway infrastructure administration determines. Sleeper length should be about and the base width in the outer part is equal to , excluding very few exceptions.
For monoblock sleepers, which will be the object of study in this work as they are the most used in Spain, technical specification ET 03.360.571.8 [39] establishes the parameters that should be defined in the draft. Those parameters are displayed in in Table 4. Figure 11 shows graphically those parameters.
| Dimension | Description |
| Concrete element total length | |
| , | Concrete element lower and upper part thickness |
| Height in each position along the entire concrete element | |
| Distance from the outer reference point to the fasteners | |
| Distance between the outer reference point and the end of the concrete element | |
| Tilting of the rail support plane | |
| Flatness of each supporting area to two points far away 150 mm | |
| Relative torsion between the supporting planes of both rails |
![Sleeper geometry parameters [39].](/wd/images/thumb/4/42/Draft_Samper_552093892-test-Ch2Fig9.png/600px-Draft_Samper_552093892-test-Ch2Fig9.png)
|
| Figure 11: Sleeper geometry parameters [39]. |
2.2.2.1 Friction between ballast and sleepers
Direct interaction between ballast and sleepers makes ballast-sleeper friction a key parameter that affects greatly the behaviour of the whole track. Specifically, it is fundamental in the evaluation of the resistance of the track, mainly against loads in the lateral and longitudinal directions. However, it is a feature very difficult to obtain.
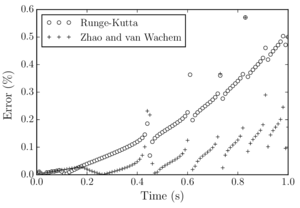
Zand and Moraal [40] compared the variation of the lateral force (force needed to move the sleeper laterally) with the variation of vertical load (weight on the sleeper), obtaining a friction coefficient value of 0.7247. They also compared their results with other previous studies whose conclusion was that the value of the ballast-sleeper friction coefficient used to be between 0.665 and 0.872.
2.2.3 Fasteners
The interaction between rails and sleepers is performed through the fasteners. There are many different types of fasteners since each administration uses the most convenient ones. Regardless of the model, they attach each rail to the sleepers in two points. The fasteners are elastic and their main function is fixing the foot of the rail to the sleeper that has to be prepared for the inclusion of these devices.
2.3 Railway ballast laboratory tests
Well-defined numerical and laboratory tests are available in the literature. These laboratory tests are suitable for validating the numerical code. In this section, some of the most used tests are briefly described.
2.3.1 Ballast lateral resistance
One of the problems that may appear in railway infrastructures is lateral buckling, which is one of the most critical troubles in railway tracks [41]. It can greatly affect the circulation and may cause catastrophic derailments [42]. Lateral buckling can be caused by mechanical or thermal loads, being relatively common in countries with large deviations in temperature between winter and summer. For this reason, lateral resistance of the track is one of the most important parameters regarding track stability, being the design of the ballast layer a key aspect.
The evaluation of the ballast layer lateral resistance was studied by several researchers. Zand and Moraal [40] carried out some tests that consist of pulling on laterally a track panel with five sleepers inside a ballast bed, measuring the necessary force to move it. Moreover, Kabo [41] developed a numerical study, using the FEM, evaluating the influence of the ballast layer geometry on its lateral resistance. Figure 12 shows one of the analysed geometries.
![Perspective view of FE model of a sleeper embedded inside a ballast bed. Source: Kabo [41].](/wd/images/thumb/6/6b/Draft_Samper_552093892-test-Ch2Fig10.png/600px-Draft_Samper_552093892-test-Ch2Fig10.png)
|
| Figure 12: Perspective view of FE model of a sleeper embedded inside a ballast bed. Source: Kabo [41]. |
2.3.2 Box compression test
Repeated train loading implies ballast deterioration, which triggers undesired seats in the railway track and fouling of the ballast layer because of breakage. One of the available tests to evaluate the consequences of cyclic loading in the ballast layer is the box compression test (Figure 13).

|

|
| (a) Test set-up, top view. | (b) Test set-up, front view. |
| Figure 13: Box compression test set-up. Source: Lim [3]. | |
The box compression test consists of applying a cyclic load on a ballast bed inside a rigid box. The ballast deformation is measured comparing it with the number of load cycles. Indraratna et al [43] reproduced this test using a two-dimensional breakable DE model for ballast.
2.3.3 Large-scale direct shear test
Figure 14 shows the layout of the typical large-scale direct shear test. This laboratory test consists of introducing ballast inside a box divided in two halves, pulling from the lower box and computing the stress-strain curve of the ballast sample. Ballast can be confined, in order to reproduce more accurately railtrack ballast conditions.
![Box shear test sample. Source: Huang and Tutumluer [45].](/wd/images/thumb/1/16/Draft_Samper_552093892-test-Ch2Fig12.png/300px-Draft_Samper_552093892-test-Ch2Fig12.png)
|
| Figure 14: Box shear test sample.
Source: Huang and Tutumluer [45]. |
This test was already reproduced using the DEM by Indraratna et al. [44] and Huang and Tutumluer [45], among other authors. Numerically, the major interest of this test is that it is performed on a relatively small domain. This implies that the computational cost is moderate, so it can be very useful to perform multiple tests in the calibration phase.
2.3.4 Triaxial tests
The most frequently used test to characterize railway ballast is the triaxial test. The reason is that, in the triaxial test, the ballast sample is confined to a certain pressure, simulating its working conditions under the track. There exist several research works in which ballast triaxial tests were developed using the DEM [46,47,1,48].
One of the difficulties in the simulation of triaxial tests using the DEM is the introduction of the confinement pressure. In laboratory tests, this pressure is applied on a membrane that confines the sample, as it can be seen in Figure 15. Some authors use simplifications to introduce pressure on the sample, but there are methods for calculating discrete (for ballast particles) and finite (for the membrane) elements coupled, using explicit schemes [49]. The possibility of considering the DEs and FEs totally coupled would increase the possibilities of practical application of the model.
![Triaxial test device with ballast inside. Source: Harkness et al. [48].](/wd/images/thumb/8/89/Draft_Samper_552093892-test-Ch2Fig13.png/150px-Draft_Samper_552093892-test-Ch2Fig13.png)
|
| Figure 15: Triaxial test device with ballast
inside. Source: Harkness et al. [48]. |
3 Introduction to the Discrete Element Method with spherical particles
Since Cundall and Strack [16] presented the first ideas of the DEM in 1979, this numerical technique has increased its popularity being known, nowadays, as a powerful and efficient tool to reproduce the behaviour of granular materials.
For the analysis of granular materials with the DEM, each grain is represented as a rigid particle. In the first DEM approaches, those particles used to be spheres (3D) and circles (2D), but now, numerous advances were developed, in order to represent different geometries. Regardless the geometry of the particles, they interact among themselves in the normal and tangential directions, assuming material deformation concentrated at the points of contact. Material properties are defined by appropriate contact laws that can be seen as the formulation of the material model at the microscopic level.
In this chapter, the main features of the classical DEM, with spheres, is presented. The solving strategy is based on three main steps: contact detection, evaluation of forces and integration of motion.
3.1 Contact detection algorithm
Due to the method formulation, the definition of the appropriate contact laws is fundamental and a fast contact detection is something of significant importance in DEM calculations. Contact status between two DE particles can be calculated from their relative position in the previous time step and it is used for updating the contact forces at the current step. The relative computational cost of the contact detection over the total computational cost is high in most of DEM simulations, and so, the problem of how to recognize all contacts precisely and efficiently has received considerable attention in the literature [50,51].
Contact detection for non-spherical particles may involve the resolution of a non-linear system of equations (see the case of superquadrics [49,52] or polyhedra [53,54,55]), for that reason, the use of spheres is the most efficient choice.
Traditionally, the contact detection is split into two stages:
- Global Neighbour Search (GNS) consists in determining potential contact objects for each given particle (target). In this stage the computational cost can be reduced from in an all-to-all check to a . Han et al. [56] compared the most common Global Neighbour Search algorithms, cell based and tree based, in simulations with spherical particles.
Cell based algorithms [57,58] divide the entire calculation domain in rectangles (2D) or cuboids (3D). Meanwhile, the target particle is surrounded by a simple bounding box, that is used to check rapidly which cells intersects with it. The list of intersecting cells are stored for each particle (see Figure 16). The potential neighbours for every target particle are all the elements stored in the different cells to which the bounding box belongs.
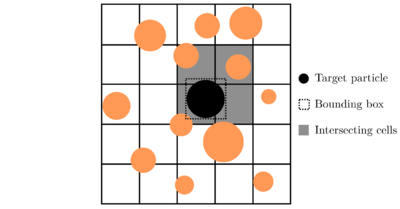
|
| Figure 16: Cell based algorithm scheme in 2D. |
Tree based algorithms [59,60] start splitting the entire domain into two sub-domains, taking into account the position of a centred particle. Then, two particles, one in each of those sub-domains, are used to divide them into smaller regions, alternating the splitting dimension (X, Y and Z in 3D). The process continues till the required number of sub-domains is obtained (see Figure 17). The potential neighbours are determined following the tree in upward direction.
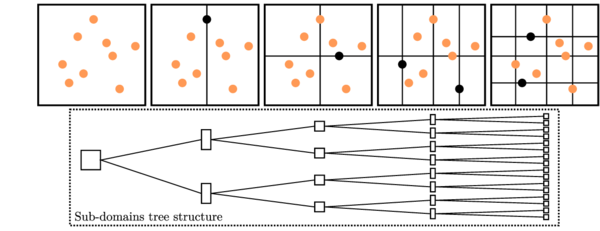
|
| Figure 17: Two-dimensional sub-domain decomposition of tree based algorithm. |
Numerical tests showed better performance for the cell based algorithms (D-Cell [57] and NBS [58]) over the tree based ones (ADT [59] and SDT [60]), specially for large-scale problems. It should also be noted that the efficiency is dependent on the cell dimension and, in general, the size distribution can affect the performance. Han et al. [56] suggest a cell size of three times the average discrete object size for 2D and five times for 3D problems. It is worth noting that (using these or other efficient algorithms) the cost of the GNS represents typically less than 5 percent of the total computation while the total cost of the search can reach values over 75 percent [61]. In this sense the focus should be placed on the next stage rather than on optimizing the GNS algorithms.
- Local Contact Resolution (LCR) consists in defining the actual contacting particles from the potential neighbours. If the particles are in contact, the normal and tangential force directions, the position of the point of contact and the characteristics of the overlap may also need to be determined at this stage.
Figure 18 shows the LCR stage for spherical particles. It can be seen that the only data needed to completely define the contact are the centres of the spheres and their radius. In the example of Figure 18, contact exists between the target particle and particle because the distance between their centres is less than the sum of their radius
|
|
(3.1) |
where , are the centres and , the radius of the particles and respectively.
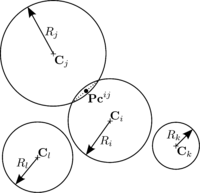
|
| Figure 18: Local Contact Resolution (LCR). |
On the other hand, Figure 18 shows that potential contact between particles , and , , which were found in the GNS stage, are discarded in the LCR stage.
The computation of contact characteristics is explained in section 3.2.2. For non-spherical particles, LCR may be more complex. This topic will be further discussed in chapters 4 and 5.
It is worth mentioning that, depending on the nature of the calculation, it may be advantageous not to perform contact detection at every time step, due to its computational cost. In most of the numerical calculations, contact duration lasts several time steps because particles position varies very little, specially in the computation of dense collections of particles, such as railway ballast numerical calculations. In this regard, computational efficiency can be improved by developing contact detection after several time steps, only updating the characteristics of previous contacts (point of contact, normal and tangential force direction and penetration). However, numerical stability should be taken into account, because if contacts are detected late, indentations (and forces) will achieve high values, leading to instabilities and inaccurate results.
In this work, GNS stage is carried out using a basic cell-based algorithm parallelised using OMP. Meanwhile, LCR is developed between spheres, leading to an efficient contact characterisation. In this work, LCR is always performed between spheres because particles used are spheres and clusters of spheres (rigid particles formed by groups of spheres overlapped in a rigid way, see Section 5.3). Issues related with contact between DEs and planar boundaries are explained in detail in chapter 4.
3.2 Force evaluation
The behaviour of granular materials is governed by grain-grain contact interactions. This is the basis of the DEM approach, where the material is characterised by means of defining the interactions between its constituent particles.
3.2.1 Equations of motion
In the basic DEM formulation, standard rigid body dynamic equations define the translational and rotational motion of particles. For the special case of spherical particles these equations, for the -th particle, can be written as
|
|
where , and are respectively the particle centroid displacement and its first and second derivative in a fixed coordinate system , is the angular acceleration, is the particle mass, is the second order inertia tensor with respect to the particle centre of mass, is the resultant force, and is the resultant moment about the central axes.
and are computed as the sum of:
- the forces and moments applied to the -th particle due to external loads and moments, and , respectively,
- the contact interaction forces from other particles , where is the index of the neighbouring particle ranging from to the number of elements in contact with the particle under consideration .
From the above-mentioned, and can be expressed as
|
where is the vector connecting the centre of mass of the -th particle and the point of contact with the -th particle (Fig. 19). The contact between the two interacting spheres can be represented by the contact forces and , which satisfy .
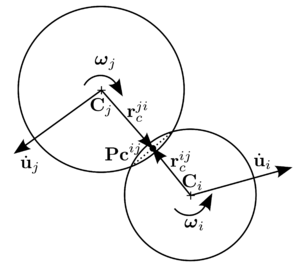
|
| Figure 19: Contact between two spherical particles. |
3.2.2 Contact characteristics
The contact force can be decomposed into the normal and tangential components at the point of contact . The local reference frame in the point of contact is defined by normal and tangential unit vectors, as it is shown in Figure 20.
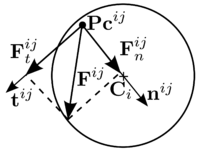
|
| Figure 20: Decomposition of the contact force into normal and tangential components. |
The unit normal vector is defined along the line connecting the centres of the two particles. Its direction is towards the centre of particle .
|
|
(3.8) |
The indentation or inter-penetration is calculated from the distance between the centres of the particles and their radius (Figure 21).
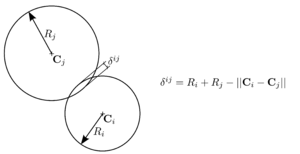
|
| Figure 21: Indentation or inter-penetration . |
Vectors from the centre of particles to the point of contact and depend on the contact model. Therefore, the position of the point of contact is influenced by the contact model used.
The relative velocity between both contacting particles at the point of contact is determined by
|
|
(3.9) |
which can be decomposed in the local reference frame as:
|
The tangential unit vector can be obtained from the tangential component of the relative velocity between the particles and .
|
|
(3.12) |
Now the contact force between the two interacting spheres and can be decomposed into its normal and tangential components, as it can be seen in Figure 20 and eq. 3.13.
|
|
(3.13) |
The forces and are obtained from the contact constitutive model.
3.2.3 Contact constitutive models
Contact between granular material particles is, in general, a complex and highly non-linear problem, which, in the DEM framework, is simplified. For spherical particles, the constitutive contact models used depend on a few parameters such as the particles relative velocity, inter-penetration, radius and material properties. To take into account energy losses, some damping parameters need to be defined.
The main parameters used in standard constitutive models in the DEM are shown in Figure 22.
![Standard DEM contact interface [Onate2013].](/wd/images/thumb/5/55/Draft_Samper_552093892-test-Ch3Fig7.png/300px-Draft_Samper_552093892-test-Ch3Fig7.png)
|
| Figure 22: Standard DEM contact interface [Onate2013]. |
Those parameters are:
- : normal contact stiffness.
- : tangential contact stiffness.
- : normal local damping coefficient at the contact interface
- : tangential local damping coefficient at the contact interface.
- : friction coefficient.
The first contact model presented by Cundall and Strack [16] was the linear spring-dashpot model. It uses, for both normal and tangential direction, a linear elastic stiffness device and a damper to introduce viscous energy dissipation. Within the commonly used contact constitutive models, this is the simplest one.
Other contact models consider the relationship between force and displacement non-linear. The most popular non-linear contact models come from the Hertz-Mindlin and Deresiewicz theory. Hertz [62] proposed the relationship between normal force and normal displacement. Deresiewicz and Mindlin [63] requested a general tangential force model where the force-displacement relationship depends on the whole loading history as well as on the instantaneous rate of change of the normal and tangential force or displacement.
In the literature, there can be found other contact models, but the model used in this work is the Hertz-Mindlin model simplified by Thornton et al. [64], due its balance between simplicity and accuracy [15].
3.2.3.1 Normal contact force calculation within the Hertz theory
Throughout the Hertzian theory, the normal contact force is decomposed into the elastic part and the damping contact force :
|
|
(3.14) |
The elastic part of the normal compressive contact force is calculated as:
|
|
(3.15) |
while the contact damping force is assumed to be of viscous type and given by:
|
|
(3.16) |
The damping coefficient is taken as a fraction of the critical damping , which depends on the particles mass and on the contact stiffness :
|
|
(3.17) |
The fraction is related with the coefficient of restitution , which is a material property that defines the kinetic energy that remains after a collision between two objects. It can also be defined as the fractional value representing the ratio of speeds after and before an impact
|
|
(3.18) |
Taking this into account, can be expressed as a function of through the following expression [64]:
|
|
(3.19) |
However, as the coefficient of restitution is a material parameter and the parameter to be used in the DEM contact force evaluation, is more convenient to express as a function of . The solution can be accurately fitted by a curve of the form
|
|
(3.20) |
where
|
|
(3.21) |
Thornton et al. [64] defined which are the appropriate values of the parameters for each linear or Hertzian contact model respectively.
3.2.3.2 Tangential contact force calculation within the Deresiewicz and Mindlin theory
The elastic tangential force at time step depends on the previous elastic tangential force, at time step . It should be noted that the tangential stiffness will be different if the normal force is increasing (loading phase) or decreasing (unloading case). For the loading phase, the relationship between the elastic tangential force and the relative tangential displacement is defined through a regularised Coulomb model. On the other hand, in the unloading phase, the elastic tangential force must be reduced due to the reduction in the contact area, which implies that the previous tangential force can not be longer supported.
|
|
(3.22) |
The increment of tangential displacement is computed from the integration of the relative displacement of the point of contact in the local frame , due to particles translation and rotation.
|
|
(3.23) |
For the calculation of the tangential contact force , not only the elastic contact force but also the damping contact force should be considered. The damping coefficient is, as for the normal direction, a fraction of the critical damping :
|
|
(3.24) |
After calculating the elastic and damping tangential forces at time step , it has to be ensured that the total tangential force does not exceed the Coulomb's friction limit:
|
|
(3.25) |
|
|
(3.26) |
3.2.3.3 Contact parameters of the Hertz-Mindlin and Deresiewicz theory
Till this point, forces have been expressed as a function of contact parameters. However, when the numerical model is applied to a real case, those contact parameters should be computed from the material properties and particles geometry. For the calculation of the contact stiffness, the Hertz theory considers the curvature of the contacting surfaces [65]. When two particles with radius and are in contact, the contact area is a circle of radius , as shown in Figure 23.
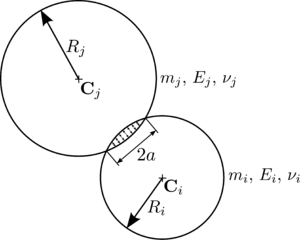
|
| Figure 23: Hertz contact model scheme. |
Which leads to the definition of and [66]
|
Meanwhile, the damping parameters are defined as:
|
Considering the contact between the two spheres and from Figure 23, if the material they are composed of has different Young modulus (, ), Poisson's ratio (, ), radius (, ) and damping coefficient (, ), the equivalent contact properties are computed as:
|
The value of the shear modulus for each particle can be obtained from its Young modulus and the Poisson's ratio :
|
|
(3.30) |
3.3 Time integration
As it was introduced in section 1.1, equations 3.2 and 3.3 are integrated in time using an explicit scheme, where the information at the previous step suffices to predict the solution at the next step. Explicit integration schemes require the time step to be below a certain limit in order to achieve computational stability. The critical time step depends on the material properties, particles geometry and constitutive model [67].
There exist several integration schemes, which can be of different order. In this work, low order (first and second) integration schemes are used, due to the fact that with such small computational time steps the use of higher order methods would not increase the accuracy significantly.
3.3.1 Explicit integration methods
The explicit methods to be described below come from the application of the Taylor series approximation of the equations that describe the problem (second order differential equations of motion 3.2 and 3.3).
|
|
(3.31) |
It should be mentioned that, the time integration of equation 3.3 is only applicable to spherical particles, due to the fact that spheres inertia tensor is independent of the orientation, furthermore, because of the symmetry of the sphere, the moment of inertia taken about any diameter is
|
|
(3.32) |
and the angular acceleration can be directly computed
|
|
(3.33) |
As for spheres, the orientation of the particle is not a key parameter, the use of the following explicit integration schemes, for calculating rotation increments, can be acceptable. However, in Section 5.3.1 the weaknesses of this schemes will be highlighted.
3.3.1.1 Forward Euler scheme
The forward Euler scheme is referred to as a first order approximation of the displacement and velocities.
|
Regarding the rotational motion, the angular velocity is also approximated using a first order approach
|
|
(3.36) |
such as the vector of incremental rotation
|
|
(3.37) |
3.3.1.2 Symplectic Euler scheme
The Symplectic Euler is a modification of the previous method which uses a backward difference approximation for the derivative of the position and the increment of rotation.
|
3.3.1.3 Taylor scheme
The Taylor scheme applies a first order integrator for the linear and angular velocities and a second order integrator for the position and rotation increment.
|
3.3.1.4 Velocity Verlet scheme
This algorithm is also known as the Central Differences algorithm [68]. Within this approach, the approximate velocity at instant is computed in order to calculate the displacement along this time step.
|
The velocity and the displacement are then used to estimate the force in the following time step.
|
|
(3.48) |
Finally the velocity is updated.
|
For the rotational motion, the procedure is the same as for the translational motion.
|
The torque in the following time step is estimated.
|
|
(3.53) |
And the angular velocity is updated.
|
3.3.2 Accuracy, stability and computational cost
Santasusana [15] developed different benchmark cases in order to evaluate which is the better scheme to use, for the translational motion. From this study it was concluded that, Symplectic Euler and Velocity Verlet accurately approximate the indentation, however, regarding the velocity, the Velocity Verlet scheme is superior to the other schemes. From the tests concerning the numerical stability, the results showed that Velocity Verlet scheme is the only one which has an acceptable performance in the limit of the critical time step, as it is a second order scheme.
Concerning the computational cost, it was found that the difference in computational time between the quickest (Forward Euler) and the slowest (Velocity Verlet) is lower than 3%
From the above-mentioned it was concluded that the better performance is obtained with the Velocity Verlet scheme, which is the scheme chosen in the calculations along this work.
Regarding the integration of the rotational motion, these schemes can be assumed accurate enough for calculating rotation increments of spherical particles in most of the cases. However, if the orientation of the particle needs to be tracked, the use of specific schemes would be recommended. Those numerical schemes are presented in Section 5.3.1.
4 Interaction of spherical particles with rigid boundaries
Till this point, the basic features of the DEM with spherical particles, were explained. However, it was realised that a greater adaptability of the numerical code would be achieved if there exist the possibility of computing the contact between planar boundaries and DEs. Talking about railway ballast, the boundaries refer to the soil, the sleeper or, in case of representing laboratory tests, the walls of the corresponding device.
Regarding the characterisation of railway ballast, most of the deformation will occur in the layer of granular material and a small deformation will occur in the boundaries interacting with it. Thus, a new methodology for the treatment of the contact interaction between spherical DEs and rigid boundaries is developed. The parts of the rigid body are defined from surfaces meshed with a Finite Element-like discretisation. The detection and calculation of contacts between those DEs and the discretised boundaries is not straightforward and, during the last years, it was addressed by different approaches.
The algorithm presented in this chapter considers the contact of DEs with geometric primitives of a Finite Element (FE) mesh (facets, edges or vertices). To do so, the original hierarchical method presented by Horner in 2001 [61] is extended with a new insight leading to a robust, fast and accurate 3D contact algorithm which is fully parallelisable. The implementation of the method is developed in order to deal ideally with triangles and quadrilaterals. If the boundaries are discretised with another type of geometries, the method can be easily extended to higher order planar convex polyhedra.
In the following sections, a review of the state of the art of the existing methods for modelling the contact between DEs and rigid boundaries is presented. Next, the proposed strategy for the DE/FE contact search is described. Finally, some validation analysis together with examples of performance in critical situations (where most of the literature methods would fail) are shown.
Most of the ideas presented in this chapter are based on the published article The double hierarchy method. A parallel 3D contact method for the interaction of spherical particles with rigid FE boundaries using the DEM[69].
4.1 State of the art
Particle-solid interaction problems were resolved by different approaches. Among the simplest ones is the glued-sphere approach [70], which approximates any complex geometry (i.e. a rigid body or boundary surface) by a collection of spherical particles, retaining the simplicity of particle-to-particle contact interaction. This approach, however, is geometrically inaccurate and computationally intensive due to the introduction of an excessive number of particles. Another easy approach (used in some numerical codes, e.g., ABAQUS) is to define the boundaries as analytical surfaces. This approach is computationally inexpensive, but it can only be applied in certain specific scenarios, where the use of infinite surfaces do not disturb the calculation. A more complex approach which combines accuracy and versatility is to resolve the contact of particles (spheres typically) with a finite element boundary mesh. These methods take into account the possibility of contact with the primitives of the FE mesh surface, i.e., facet, edge or vertex contact.
Horner et al. [61] and Kremmer et al. [71] developed the first hierarchical resolution algorithms for contact problems between spherical particles and triangular elements, while Zang et al. [72] proposed similar approaches accounting for quadrilateral facets. Dang et al. [73] upgraded the method introducing a numerical correction to improve smoothness and stability. Su et al. [74] developed a complex algorithm involving polygonal facets under the name of RIGID method which includes an elimination procedure to resolve the contact in different non-smooth contact situations. This approach, however, does not consider the cases when a spherical particle might be in contact with the entities of different surfaces at the same time (multiple contacts) leading to an inaccurate contact interaction. The upgraded RIGID-II method presented later by Su et al. [75] and also the method proposed by Hu et al. [76] account for the multiple contact situations, but they have a complex elimination procedure with many different contact scenarios to distinguish, which is difficult to code in practice. Recently, Chen et al. [77] presented a very simple and accurate algorithm which covers many situations. Their elimination procedure, however, requires a special database which can not be computed in parallel.
Therefore, the proposed Double Hierarchy () method consists in a simple contact algorithm based on the FE boundary approach. The method is specially designed to resolve efficiently the intersection of spheres with triangles and planar quadrilaterals but it can also work fine with any other higher order planar convex polyhedra. A two layer hierarchy is applied upgrading the classical hierarchy method presented by Horner [61]; namely hierarchy on contact type followed by hierarchy on distance. The first one, classifies the type of contact (facet, edge or vertex) for every contacting neighbour in a hierarchical way, while the distance-based hierarchy determines which of the contacts found are valid or relevant and which ones have to be removed.
Although code parallelisation lies outside the scope of this thesis it is worth to mentioning that the method is designed in a way that the code can work efficiently in parallel computations, which is crucial for practical purposes of a DEM code. This is a clear advantage over the above-mentioned publications. Nakashima [78] whose method is presumably parallelisable and Zang [72] and Su [75] who remark the importance of the future parallelisation of their algorithms are exceptions.
Summarising, the contact search framework presented is designed to satisfy the following requirements:
- Include poly-disperse elements for both FEs and DEs.
- Allow different FE geometries and primitives (triangle, quadrilateral, polygon).
- Ensure contact continuity in non-smooth regions (edges and vertices).
- Resolve multiple contacts and contact with different entities simultaneously.
- Need low memory storage.
- Be simple, fast and accurate.
- Be fully parallelisable.
| Glued | Anal. | Hierarchical | RIGID | RIGID-II | Hu | Chen | ||
| [70] | [61,72,73] | [74] | [75] | [76] | [77] | |||
| Wide size rate DEs/FEs | - | - | ⨉ | ✓ | ✓ | ✓ | ⨉ | ✓ |
| Contact elem. typologies | ⨉ | - | ✓ | ✓ | ✓ | ⨉ | ⨉ | ✓ |
| Boundary shape variety | ✓ | ⨉ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Multi-contact | ✓ | - | ✓ | ⨉ | ✓ | ✓ | ✓ | ✓ |
| Simple | ✓ | ✓ | ✓ | ⨉ | ⨉ | ⨉ | ✓ | ✓ |
| Efficient | ⨉ | ✓ | ⨉ | ✓ | ⨉ | ⨉ | ✓ | ✓ |
| Accurate | ⨉ | ⨉ | ✓ | ⨉ | ✓ | ✓ | ⨉ | ✓ |
| Low storage | ✓ | ✓ | ⨉ | ⨉ | ⨉ | ⨉ | ✓ | ✓ |
| Contact with deform. FEs | ⨉ | ⨉ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Large indentation | ⨉ | ✓ | ⨉ | ⨉ | ✓ | ✓ | ⨉ | ✓ |
| Contact continuity | ⨉ | - | ✓ | ⨉ | ✓ | ✓ | ✓ | ✓ |
Symbol (✓) implies that the method satisfies the property. On the other hand, symbol (⨉) means that the method does not satisfy the property. Symbol (-) denotes that the property does not apply to that method and (✓) means that, although the method satisfies the property, there are some limitations.
Table 5 summarises the strengths and drawbacks of the reviewed contact detection methods. Methods based on storing all the potential contacts to lately remove the invalid ones (RIGID-II [75], Hu et al. [76], Chen et al. [77] and ) are the most accurate. They treat the cases with large indentations (relative to the size of the FE) and give a solution for the contact continuity in non-smooth regions of the boundary. These methods have, however, some limitations due to the fact that the real deformed geometry of the sphere is not being represented in the DEM. The indentation emulates, instead, the local deformation near the contact region. Due to this fact, in concave transitions of the boundary, error in the contact detection is common for all these methods including the method here presented. In Section 4.4 this error is analysed under the framework.
4.2 DE/FE contact
As it was already mentioned, within the method, boundaries are discretised with a FE-like mesh. However, this discretisation is only for contact detection purposes and each FE entity is, indeed, a rigid element. Therefore, the boundaries are not calculated by means of a FE procedure.
4.2.1 DE/FE contact constitutive laws
Similarly to the scheme shown in Figure 22, the rheology of a particle contacting a FE is presented in Figure 24.
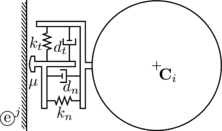
|
| Figure 24: DE/FE standard contact interface. |
The adaptation of constitutive contact laws for DE/DE contact computation (section 3.2.3) to the case of DE/FE contact is straightforward. It is only necessary to take into account that:
- .
- .
- The normal stiffness of the walls can be set by the user so that the deformation of the rigid wall can be concentrated in the point of contact.
- , since the tangential displacement of the wall will be, in most cases, much smaller than the particle's one [66].
Leading to the following equivalent contact properties:
|
The application of constitutive contact laws, such as Hertz-Mindlin [79], requires that the contact surfaces are smooth and present a unique normal at each point. In the DE/FE contact, usually, the original geometry presents regions where this requirement is not fulfilled. Moreover, even smooth surfaces loose this feature when they are discretised by means of FEs. In these situations a special treatment of the non-smooth regions should be applied under the requirement of some conditions to ensure reasonable results. Those conditions were analysed in the work by Wellmann [49]:
- The contact constitutive model will be applied normally when the contact is on the facet and will vanish when there is no interpenetration between the elements.
- There should be no discontinuities in the contact force when a point of contact evolves from facet to edge and the other way round in order to avoid unphysical results and numerical instabilities.
- The energy should be conserved in an elastic frictionless impact.
The use of the present contact algorithm helps the selected contact model ensuring these objectives. Additionally, it should be noted that this method is not mesh dependent, with the limitations detailed in section 4.4.
4.2.2 DE/FE contact search algorithm
The DE/FE contact search differs from the DE/DE in the sense that the search is between two different groups of geometries whose intersection is generally more complex and computationally more expensive than the trivial sphere-sphere case. The choice of spheres for the DEs and triangles or quadrilaterals for the FEs is a clever choice since this particular check can be done in an efficient way. As in the DE/DE contact detection, the contact search is also split into a GNS and a LCR.
In other works developed in parallel to this thesis [69] [15], the LCR stage is split into a Fast Intersection Test and method. However, the aim of this work is improving the method and prove that it can be used correctly and efficiently as a full LCR algorithm. The contact search scheme is shown in Figure 25.
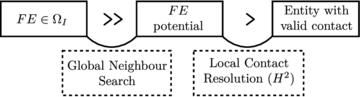
|
| Figure 25: Neighbour search scheme. |
4.2.2.1 Global Neighbour Search algorithm
For the GNS, a basic cell-based algorithm [57] is chosen, parallelised in OMP and adapted for the DE/FE search. The FE domain () is selected to search taking advantage of the fact that, usually, the spatial distribution of the FEs is more regular than the spatial distribution of the DEs and in some cases fixed. Moreover, the search is carried out considering only the FEs belonging to the intersection of the bounding boxes of the DEs () and FEs () domains. Figure 26 shows how the intersection evolves as long as the calculation goes on. On the other hand, only the DEs inside the intersection domain () will look for their FE neighbours. This reduces significantly the contact pairs to be checked and, therefore, the global search performance is improved.
|
| Figure 26: Evolution of the bounding box of the intersection . |
In the GNS, every FE and DE has an associated Bounding Box (, as shown in Figures 27a and 27b) that is used to tag the position of the elements on the Search Bins and rapidly check for potential neighbours. This is done using a hash table structure as depicted in Figure 27c which relates each cell to the bounding box that falls into it. Rectangular (in 2D) or hexahedral (in 3D) bounding boxes, encompassing both types of elements, are chosen here. The process continues with the LCR (Figure 27d).
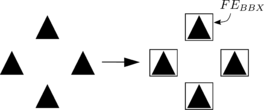
|
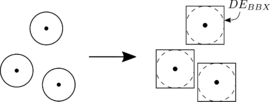
|
| (a) Bounding box of the FEs . | (b) Bounding box of the DEs . |
|
|
| (c) Intersection cells. | (d) Local Contact Resolution. |
| Figure 27: Sketch showing the search algorithm at the basic contact level. | |
4.2.2.2 Local Contact Resolution
As it was already commented, the LCR can be split in two stages being the first one the Fast Intersection Test where it is determined which potential FE neighbours are in actual contact with each particle. A detailed description of this procedure can be found in [69] and [15].
In this work, the main effort was made in improving the second stage, the method as a full LCR check itself.
4.3 Double Hierarchy Method
The first ideas about the method were presented in Irazábal's [80] work. Since then, the development has been focused in improving the efficiency for the characterisation of contacts.
The algorithm is split in two different stages:
- Contact Type Hierarchy (Section 4.3.1): where, for every contacting FE, the contact entity (facet, edge or vertex) with higher priority is determined.
- Distance Hierarchy (Section 4.3.2): where the elimination procedure takes place, determining which points of contact have distance priority over others and which are redundant or false and have to be eliminated.
4.3.1 Contact Type Hierarchy
The basis of this procedure is that each primitive has hierarchy over its sub-entities, i.e., a facet of a -sides polygon has hierarchy over the edges that compose it. In turn each of the edges has hierarchy over its two vertices . Figure 28 outlines the Contact Type Hierarchy for a triangle.

|
| Figure 28: Contact Type Hierarchy for a triangle: the facet has higher hierarchy than its edge and vertices, while the edges have higher hierarchy than its vertices. |
The algorithm is organised as a sequence of three entity-checking levels. If a particle is in contact with the facet of a FE, the contact search over its edges and vertices, which are at a lower hierarchy level, is discarded (See Figure 29). Otherwise, if contact with the FE facet does not exist, the contact check should continue over the sub-entities.
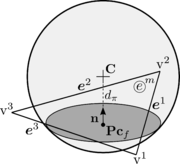
|
| Figure 29: Contact with facet. Edges and vertices are discarded from contact check. |
Similarly, at the edges level, any contact with an edge cancels out further contact checks for those two vertices belonging to that edge. As shown in Figure 30, when contact with the edge is found, the check at the lower level for the vertices associated to it, and , is discarded. However, the contact check with the following edges can not be discarded, since they are at the same hierarchy level in terms of Contact Type.
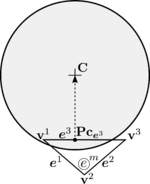
|
| Figure 30: Contact with edge. Vertices belonging to that edge are discarded from contact check. |
Figure 31 illustrates why the edge has hierarchy over its two vertices but not over the non-contiguous one .
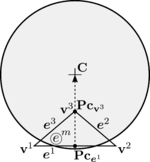
|
| Figure 31: Contact with edge and vertex. When contact exist with edge it can also exists with vertex . |
For any of the entities, if the contact is detected and it is valid, the following characteristics are stored:
- The point of contact .
- The FE nodal weights.
- The contact type: facet, edge or vertex.
The procedure to determine each contact type (facet, edge, vertex or no contact), the computation of the position of and the calculation of the FE nodal weights are explained in the following paragraphs.
4.3.1.1 Contact with facet
To know if the DE particle is in contact with a facet, the first check is to determine whether the particle intersects the plane formed by the -th planar finite element ![]() . This is represented in Figure 32.
. This is represented in Figure 32.
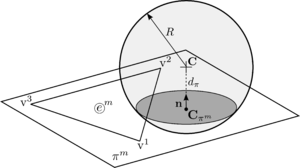
|
| Figure 32: Intersection of a DE particle with a plane formed by a planar FE. |
The outward-pointing normal of the plane can be calculated with the cross product of any pair of edges taken counter-clockwise. This can be written in the following form, using the permutation tensor on two edges formed, for example, by the three consecutive vertices , , :
|
|
(4.2) |
which has to be normalised to obtain the normal to the plane
|
|
(4.3) |
In the case of a zero-thickness wall which can contact for both sides of the FE, the sense of the normal will be set such that points towards the particle centre. Once the normal is defined, the distance of the DE centre to the plane can be determined taking any known point of the plane, namely a vertex , as
|
|
(4.4) |
and the projection of the centre onto the plane can be calculated as
|
|
(4.5) |
The distance should be compared to the radius of the DE. If and only if , the contact between the sphere and the FE is possible. If this condition is fulfilled, the next step is to evaluate whether the projection lies inside or outside the FE ![]() .
.
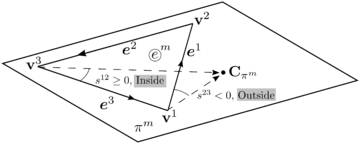
|
| Figure 33: Inside-Outside check of the projection point edge by edge. |
Considering the edge formed by the vertices and ()
|
|
(4.6) |
the cross product sign , shown in Figure 33, is computed as
|
|
(4.7) |
If the product is positive, the projection point turns to be inside the triangle with respect to that edge. The loop proceeds with the next edges. If the same result is found for every edge, contact occurs with the facet of the FE and so the contact is assured. Figure 34 shows two examples where the projection is inside and outside the FE facet.
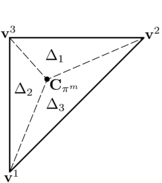
|
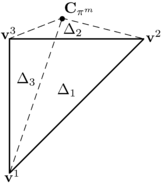
|
| (a) inside the facet. | (b) outside the facet. |
| Figure 34: Example of projection inside and outside the FE facet for a triangle. | |
The values of the cross product sign , obtained from equation 4.7 for every edge , are used to obtain the weights of the shape function at the point of contact. The areas needed for the calculation are simply one half of the cross product sign: . The weights of the nodal shape functions on the point of contact are then calculated. For a triangle:
|
|
(4.8) |
where
|
|
(4.9) |
For 4-node convex quadrilaterals (Figure 35) the following expression can be applied as introduced in Zhong [81]:
|
|
(4.10) |
where
|
|
(4.11) |
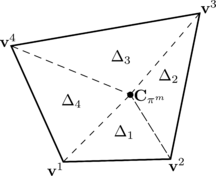
|
| Figure 35: Triangular areas for the calculation of shape function values in a planar convex quadrilateral. |
The general formula for calculating the nodal weights for -side polygons can be found in Santasusana et al. [69].
If the projection (equation 4.5) lies inside the facet, it becomes the point of contact . Due to the highest hierarchy level of the facet, the Contact Type Hierarchy finishes here for this FE. The Distance Hierarchy is now called and all the necessary contact characteristics are saved.
4.3.1.2 Contact with edge
Checking contact with edges is needed for the cases where lies outside the facet. Here, to improve the efficiency of the algorithm, it is considered that the edge contact can not occur with the edges for which was found inside. Therefore, it is recommendable to test the edges with starting from the vertex for which is outside and skipping the previous ones (note that the edge check is the most expensive one). This approach was also used by Chen et al. [77].
First, the shortest distance between the edge and the particle centre should be calculated and compared to the radius .
|
|
(4.12) |
The distance is calculated finding out the point of contact , as
|
|
(4.13) |
where
|
|
(4.14) |
and is the distance resulting from the projection of the vector connecting the centre and the vertex onto the edge :
|
|
(4.15) |
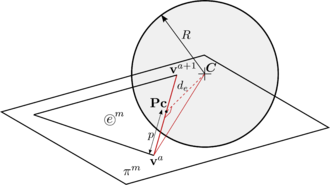
|
| Figure 36: Intersection of a DE particle with an edge. |
If , the contact with this edge is not possible and the check starts again with the next edge . Otherwise, if , position is determined along the edge using the parameter , defined as
|
|
(4.16) |
The case of implies edge contact. However, the contact check with the following edges can not be discarded since they are at the same hierarchy level in terms of Contact Type. The Distance Hierarchy will determine the validity of the new contact and eliminate or substitute previous ones.
If or , for the current edge , the connecting vertices ( and ) have to be evaluated. A value of indicates that the check has to be done with ; on the other hand, for the vertex to be tested is .
The nodal weights can be obtained from the parameter (equation 4.16) at the edge . Figure 37 shows graphically how is determined,
|
|
(4.17) |
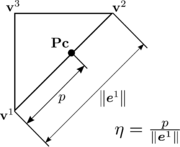
|
| Figure 37: Weights for a edge contact in a triangle. |
Equation 4.17 shows the values at the nodes connected to the edge . The rest of the nodes have a null value for its shape functions.
4.3.1.3 Contact with vertex
For the vertex under consideration the squared distance to the DE centre should be calculated:
|
|
(4.18) |
If , contact exists, being the vertex itself with a nodal weight equal to one. Otherwise the test moves on with the check of the next edge and its subsequent vertices.
As usual, the Distance Hierarchy is called after the contact is detected. If the contact is valid, its characteristics are stored.
4.3.1.4 Contact Type Hierarchy scheme
The scheme of Table 6 presents the Contact Type Hierarchy algorithm. For every DE the first loop is over the potential neighbours found during the Global Search. The check can be performed in parallel for every particle in the model.
| loop over every FE potential neighbour |
| Facet level |
| Perform Facet check. |
| if Contact: Go to Distance Hierarchy (Table 7) and Stop! |
| else: Go to . |
| Edge level |
| loop over every edge . |
| Perform the Edge Check. |
| if Contact Go to Distance Hierarchy (Table 7). |
| else if ( and ) Go to (3) with . |
| else if ( and ) Go to (3) with . |
| Continue with the next edge. |
| Vertex level |
| Perform Vertex check. |
| if Contact Go to Distance Hierarchy (Table 7). |
| Go To Edge level and check next edge. |
4.3.2 Distance Hierarchy
A spherical particle can be in contact with many different FE entities. These contacts are result of the penetrations introduced by the penalty method. In some cases, those contacts give redundant or invalid information and should be eliminated. This is the scenario shown in Figure 38 where contact with elements ![]() ,
, ![]() and
and ![]() is detected.
is detected.
In a collision between a sphere and a plane, the force applied by the plane surface to the sphere must have the same direction as the normal of the plane and its magnitude must only depend on the penetrations, being independent of the position of the point of contact on the plane. Therefore, the contact force coming from the edges of elements ![]() and
and ![]() of Figure 38 should not be taken into account. This is solved by the Distance Hierarchy which is an elimination procedure that takes place every time a new contact entity is found at the Contact Type Hierarchy.
of Figure 38 should not be taken into account. This is solved by the Distance Hierarchy which is an elimination procedure that takes place every time a new contact entity is found at the Contact Type Hierarchy.
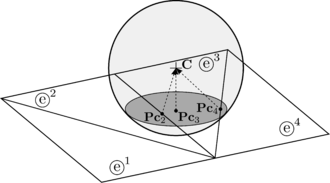
|
| Figure 38: Contact between a DE and a FE mesh whose elements are smaller than the indentation. |
The procedure basically compares the contact vectors against their projections one another. The new contact vector is projected onto the previously found contact vector and vice versa. The following expressions are obtained:
|
|
(4.19) |
The contact check is performed using the algorithm presented in Table 7:
| Given a new found contact by the Contact Type Hierarchy: |
| loop over every existing contact |
| Project on : |
| Project on : |
| if ( ): is an invalid contact. |
| Go to (2) () and break loop. |
| else if ( ): is an invalid contact. |
| Discard ! Continue loop. |
| Go to (2) (). |
| Valid contact () |
| if ( ): is valid contact! Save contact details. |
| else ( ): is an invalid contact! Discard !. |
Table 4.3.2 shows an example of how the elimination procedure is performed for two different scenarios. On the left side all the found contact vectors are represented. A graphical interpretation of the projections is also given. On the right side only the final relevant contact vectors, that the Distance Hierarchy yields, are shown.
In the first situation, no contact with edges of elements ![]() and
and ![]() is taken into account, since their projections, and , over the contact vector with element
is taken into account, since their projections, and , over the contact vector with element ![]() have the same module as the contact vector itself.
have the same module as the contact vector itself.
In the second situation, the sphere has contact with the facet of element ![]() , the edge of element
, the edge of element ![]() and the shared edge of elements
and the shared edge of elements ![]() and
and ![]() which will be appearing as two different contact vectors and given by the Contact Type Hierarchy stage. These vectors do not appear directly in the figures in Table 4.3.2 but they are calculated by and respectively. First, note that either contact with or will be arbitrarily discarded by the elimination procedure since they are mathematically the same vector. Let us assume the is kept and discarded. On the other hand, the projection of the contact vector over the contact vector discards contact with element
which will be appearing as two different contact vectors and given by the Contact Type Hierarchy stage. These vectors do not appear directly in the figures in Table 4.3.2 but they are calculated by and respectively. First, note that either contact with or will be arbitrarily discarded by the elimination procedure since they are mathematically the same vector. Let us assume the is kept and discarded. On the other hand, the projection of the contact vector over the contact vector discards contact with element ![]() . Finally, contacts with elements
. Finally, contacts with elements ![]() and
and ![]() do not discard each other since their projections one another have a value of and (they form a 90 degrees angle) and therefore are smaller than the contact vectors length. Hence both contacts are taken into account, as it is expected.
do not discard each other since their projections one another have a value of and (they form a 90 degrees angle) and therefore are smaller than the contact vectors length. Hence both contacts are taken into account, as it is expected.
Contact elimination cases.
| Found Points of Contact and Vectors | Relevant Contact Vectors | |
| 1 | 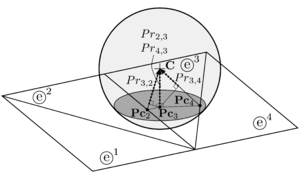
|
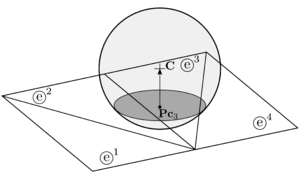
|
| 2 | 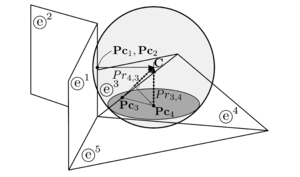
|
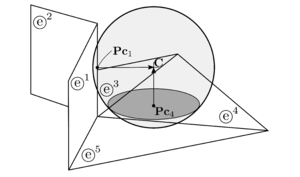
|
The main advantage of this method lies in its wide generality. It works fine for most of the traditional conflictive situations where multi-contacts and FE transitions are present. It is consistent and so the order in which the neighbours have been found and stored does not affect the final result. The tests carried out in the validation (Section 4.5) show that the force vector always has the appropriate direction.
4.4 Method limitations
4.4.1 Extension to deformable FE
Although the method was conceived for calculating contacts between DEs and rigid boundaries, it can be easily upgraded to be coupled with deformable FEs. The contact forces can be transferred to the finite element nodes through interpolation based on FE shape functions [61]. For linear triangles, a simple linear interpolation is used as
|
|
(4.20) |
where is the position of the point of contact and is the area of the triangle formed by the point of contact and the opposite vertices to vertex in the FE, as it is shown in Figure 39.

|
| Figure 39: Punctual force and its nodal interpolation to a three noded triangle by means of linear shape functions expressed using its area coordinates. |
However, this linear interpolation may yield to inaccurate results if a detailed analysis of strain and stress in the deformable FEs is being conducted. In that case, more precise schemes should be used.
Figure 40 shows an scenario where the non-smooth contact detection introduces a calculation error. In Figure 40a the DE is in contact with an edge at time , the indentation is and the contact force is F. At time (Figure 40b), the DE is in contact with two surfaces, because now the normal to those two surfaces is not the same. Since the time-step size, in explicit time integration algorithms, is usually very small, it is reasonable to suppose that the penetration vectors between the DE and surface 1 () and surface 2 () at time are similar to . Then, the resultant contact is approximately: F = 2 F.
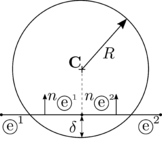
|
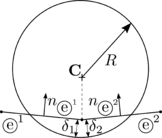
|
| (a) Time . | (b) Time . |
| Figure 40: Non-smoothness of the contact force with elastic elements. | |
Notwithstanding the importance of this error, it should be mentioned that, for quasi-static calculations with small time steps and where the importance of the analysis lies on the DEs behaviour, the error introduced by the non-smoothness can be neglected [72].
Han et al [82,83], Wellmann [49] and Santasusana [15] developed algorithms to overcome the non-smoothness of the contact between DEs and deformable FEs. The computational cost of this new algorithms will be higher, so, it should be evaluated, for each case, if it is worth using them.
4.4.2 Normal force in concave transitions
A limitation of this method, which is common to the revised penalty-based contact algorithms, occurs when a DE contacts with a slightly non-convex surface.
The penalty method introduces an indentation which accounts for the local elastic deformation of the DE during a contact event and allows the imposition of the contact condition in a weak form. This indentation is not problematic when the contact is with convex surfaces, however, for non-smooth concave regions the basic assumptions are not met and contact detection errors may arise.
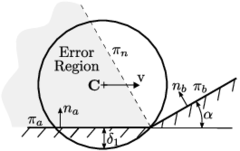
|
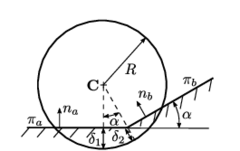
|
| (a) Error region. | (b) Contact with 2 planes. |
| Figure 41: Error emerging in concave transitions. | |
In the example of Figure 41 a sphere moves horizontally in a plane until it reaches a transition with other plane (planes and form an acute angle ). In this situation a region formed by the common edge of both planes and the normal of the second plane can be defined. Whenever the sphere centre is in that region a discontinuity in forces will occur. The contact with plane is detected only when the centre has a normal projection onto the plane forming a tangential contact. Figure 41b shows that when the new contact is detected, some indentation is existing already and, therefore, the new contact force value introduces a discontinuity.
It was found that for an indentation of of the radius of the DE, even with a small change in the angle ( degrees) no error is produced. However, for higher indentations the error increases, being higher for lower changes of the angle . An error of is reached in the extreme case of coplanar transition. Luckily, this very frequent case is considered by the Distance Hierarchy where a tolerance is used to detect coplanar cases. Note that the error depends only on geometrical conditions and the indentation and not on the boundary FE mesh quality.
Santasusana et al. [69] studied exhaustively this error, presenting it as a function of the change of and the indentation for different constitutive models.
4.4.3 Tangential force across elements
The tangential force is applied by means of an incremental scheme which requires to keep track of the forces between the particle and each of its neighbours. The problem arises when a particle moves across two elements and the historical tangential force resets to zero because the contact is determined with the new element. This is common to all reviewed contact algorithms. Even though it could be solved with a complex data structure, the error introduced is very low for practical situations.
The cases with larger error will be the ones with sliding where the tangential force is kept at its maximum (generally Coulomb friction value) and are much higher than during a rolling event. In this situation the error can be measured in terms of the missing work in a force-displacement diagram. After studying the error, Santasusana et al. [69] came to the conclusion that a large indentation equal to the of the characteristic size of the FE, yields only an error about the , meanwhile, if the Hertz-Mindlin contact law is used, the error would be very similar.
4.5 Validation
In this section, several examples are carried out to test the performance of the algorithm in critical situations. The following tests do not correspond to practical situations, but they serve instead to validate the contact calculation procedure. All benchmarks have been carried out using a Hertzian contact law and Velocity Verlet integration scheme.
4.5.1 Benchmark 1: facet, edge and vertex contact
The first benchmark is represented by three spheres with low stiffness in order to achieve large indentation. Each sphere contacts a different boundary structure meshed with triangles. In every case the sphere falls from the same height (1 ) vertically and perpendicular to the contact entity which is respectively a facet, an edge or a vertex. Figure 42 shows the layout of the three sphere and boundary cases, while the material properties and calculation parameters are detailed in table 8.
|
| Figure 42: Benchmark 1 layout. |
| Material properties | Calculation parameters | ||
| Radius () | Initial velocity (DE) () | ||
| Density () | Gravity () | ||
| Friction coefficient DE/FE | Time step () | ||
| Young modulus () | Neighbour search frequency | ||
| Poisson ratio | |||
Since there is no damping applied, the energy should be conserved and the ball must return to the initial position after the rebound. The sphere is expected to follow a vertical trajectory with identical results for the three cases.
|
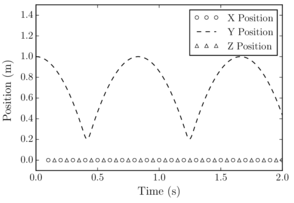
|
| (a) Force exerted by the FEs to the DE. | (b) Position of the centre of the DE. |
| Figure 43: Results obtained in the first benchmark test. | |
The contact indentation in the three cases is greater than the of the sphere radius, leading to multiple contacts with all kind of entities. Besides that, graph in Figure 43a shows that the force is applied only in the vertical direction (Y direction). From this, it can be concluded that the contact elimination procedure performs correctly. The results are exactly the same in the three different scenarios (facet, edge and vertex contact). It verifies also that there is no energy gain or dissipation since the rebound maximum height is always the same, as it can be observed in Figure 43b. This is a good test to see that the method works properly for normal contacts of all three types: with facet, with edge and with vertex, independently of the mesh and the indentation achieved (always lower than the radius).
4.5.2 Benchmark 2: continuity of contact
It is essential to ensure the continuity of the contact force in the non-smooth contact regions and FEs transitions. In the following example the continuity of the normal force is presented.
A DE is set to move along the boundary and its contact transfers from the surface of a triangular element (facet contact) to one of its edges or vertices. In particular, a frictionless and rotation free sphere has a trajectory path enforced (as shown in Figure 44) so that the indentation is always constant ( either in contact with the facets and or with the edge ). The material properties and calculation parameters are the ones presented in the table 8.
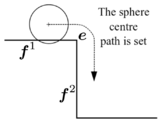
|
|
| (a) | (b) |
| Figure 44: Scheme of benchmark 2. | |
If continuity is met, the force module must always be the same. The direction of the contact force should evolve from vertical (normal to ) to horizontal (normal to ) with a smooth transition. This is achieved due to the fact that the algorithm gives higher hierarchy to the edge and the vector is calculated joining the point of contact and the centre of the sphere.
|

|
|
|
| (a) Contact . | (b) Contact . | (c) Contact . | (d) Contact . |
| Figure 45: Force applied by the surface and the edge to the sphere at different instants. | |||
The results show that no discontinuities arise when the contact evolves from facet contact to edge contact and vice versa, being the contact force constant along all the calculation and equal to 76.063 N, as expected.
The continuity of the normal forces in a concave transition and the tangential forces across different elements is not fully assured, as it was commented in Section 4.4.2. Even though the error is very small for practical situations.
4.5.3 Benchmark 3: multiple contacts
The goal of this test is to check that the method determines correctly the case of a sphere contacting more than one element. The set up of the example consists of three spheres falling onto a plane with three different shape holes, as shown in Figure 46. Material properties and calculation parameters are presented in table 9. In this example damping is applied.
|
|
| (a) | (b) |
| Figure 46: Geometry of benchmark 3. | |
| Material properties | Calculation parameters | ||
| Radius () | |||
| Density () | Initial velocity (DE) () | ||
| Friction coefficient DE/FE | Gravity () | ||
| Young modulus () | Time step () | ||
| Poisson ratio | Neighbour search frequency | ||
| Restitution coefficient | |||
Graph in Figure 47 shows the velocity modulus of each of the DEs involved in the numerical test. It can be seen that the spheres velocity after 2.5 seconds of calculation is close to 0. All the spheres reach their final equilibrium position, contacting vertices and edges simultaneously.
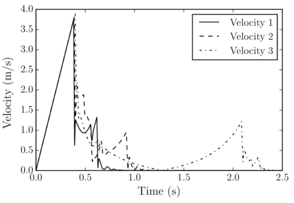
|
| Figure 47: DEs velocity. |
4.5.4 Benchmark 4: mesh independence
The following example represents two balls sliding on a plane with friction and is used to evaluate if the algorithm is independent of the mesh. The spheres are set in vertical equilibrium upon the plane and an horizontal velocity is imposed. The spheres should start sliding while their angular velocity will progressively increase up to a constant value at which the sliding event finishes and only rolling occurs thereafter. This is schematically depicted in Figure 48a.
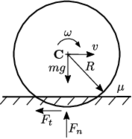
|
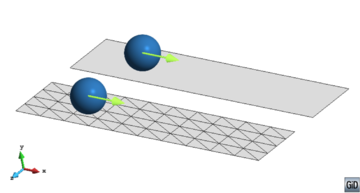
|
| (a) Problem definition. | (b) Calculation set up. |
| Figure 48: Benchmark 4 layout. | |
The analytical solution can be determined to validate the calculation using equilibrium equations with kinematic compatibility conditions and the basic Coulomb friction law. The moment of inertia of a sphere is . In this case a high value of the Young modulus () was chosen, in order to avoid large indentations, which will allow to assume that the sphere radius is equal to the rotational radius (). The following is obtained for the combined sliding and rotation phase:
|
|
(4.21) |
|
|
(4.22) |
|
|
(4.23) |
Equation 4.23 comes from integrating the angular acceleration for the case of zero initial angular velocity. The constant rolling event occurs when the tangential velocity matches the angular velocity times the radius :
|
|
(4.24) |
Leading to a critical time equal to:
|
|
(4.25) |
For time the equations of motion are:
|
|
(4.26) |
|
|
(4.27) |
|
|
(4.28) |
The set up of the numerical test is shown in Figure 48b. Two cases are compared, one involves sliding on a plane discretised by a single quadrilateral element while in the other case the plane is discretised by 80 triangular elements. The spheres are given a initial velocity of in the direction and the computational time is one second. Other calculation and material parameters are detailed in Table 10.
| Material properties | Calculation parameters | ||
| Radius () | |||
| Density () | Initial velocity (DE) () | ||
| Friction coefficient DE/FE | Gravity () | ||
| Young modulus () | Time step () | ||
| Poisson ratio | Neighbour search frequency | ||
| Restitution coefficient | |||
The numerical results and the analytical solution are plotted in Figure 49. This plot, together with the information presented in Table 11, shows that the difference between meshes turned to be negligible. In Table 11 the values of the displacement (), velocity (), angular velocity () and computational error at the end of the calculation () are presented.
| Triangle | Quadrilateral | Analytical | |
| (m) | |||
| Error() | - | ||
| Meshes difference () | - | ||
| (m/s) | |||
| Error () | - | ||
| Meshes difference () | - | ||
| (rad/s) | |||
| Error () | - | ||
| Meshes difference () | - | ||
This example shows how the results on the DE are practically independent on the boundary mesh selected. Moreover, for the calculation performed, the numerical results agreed perfectly with the theoretical solution. This case does not show any noticeable discontinuity in the normal and tangential contact forces in the transition between boundary FEs.
5 Geometric representation of railway ballast
Railway ballast is a layer of granular material composed of particles of different sizes with notorious irregularities. Those irregularities greatly affect the material behaviour. With this in mind, it may be though that the use of spherical particles for the representation of this material can be too simplistic. However, the computational advantages of using spheres have to be taken into account.
From the point of view of micro-scale analysis, it is essential to represent the exact geometry of the particle. On the other hand, if the interest lies in the behaviour of the granular material as a whole, it is thought that the geometry of each particle is not a determining factor. The key point is to find an approach accurate enough without being too much computationally intensive.
In this chapter, different approaches for characterising the geometry of railway ballast, and other granular materials, are presented. After evaluating each of them in section 5.1, two approaches were chosen, which are spheres with rolling friction and sphere clusters. In sections 5.2 and 5.3 respectively, the way spheres with rolling friction and sphere clusters are implemented in Kratos is described.
5.1 State of the art
DEM has proven to be a very useful tool to obtain complete qualitative information on calculations of groups of particles [10], however, the computational cost of contact evaluation between DEs is high and limits the calculation capability. On this subject, it should be noted that particles shape greatly affects contact calculation computational cost, being spherical DEs the less computational demanding particles. This limitation, together with the uncertainty about the real contact mechanics and particle properties [84], led to different particle shape simplifications [85,86].
- Rolling friction refers to an additional torque (rolling resistance torque) that is applied to each particle pair in contact and resists the rolling motion. This approach is typically applied to spherical DEs to avoid excessive rotation. Its main advantage is the low computational cost, since only the radii and the position of the centre of the spherical particles are required for the contact detection, as it was described in Chapter 3. Other advantage of the use of spherical particles is the proper calculation of its contact with rigid boundaries, detailed in Chapter 4.
In the literature, different algorithms can be found to implement rolling friction. Section 5.2 presents them and describes the new algorithm proposed in this work, which was previously published in the article Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast [87].

|
| Figure 50: Repose angle of a granular material represented by spheres with rolling friction. |
- Sphere clusters approach consists of representing each DE particle as a group of overlapping spheres joined rigidly, thereby allowing the use of algorithms that are straightforward extensions of the efficient methods used for spheres. This approach was used to represent geomaterials [88,89,90,91,92] formed by non-spherical particles. The total amount of spheres in the model is , where is the number of spheres per cluster, and is the number of particles to be considered in the model. Depending on the material under consideration and the problem addressed, in engineering calculations, where only macroscopic results are searched for, particles with spheres could be appropriate [44]. Anyway, there is a relevant increase of contact detection time that grows, at least, proportionally to the increase in the total amount of spheres in the model, compared to the same calculation using spherical particles.

|
| Figure 51: Simplification of the geometry if six different ballast particles using sphere clusters. |
It should also be noted that this approach introduces geometric friction due to the undesired cavities between overlapped spheres. This issue will be further analysed in Section 6.3.
- Superquadrics are a family of geometric shapes defined by formulas that resemble those of ellipsoids and other quadrics, except that the squaring operations are replaced by arbitrary powers. Contact calculation between two superquadrics was addressed by different authors in the last ten years [93,94,95].
![Examples of superquadrics. Source: Chakraborty et al. [93].](/wd/images/thumb/1/1d/Draft_Samper_552093892-test-Ch5Fig3.png/400px-Draft_Samper_552093892-test-Ch5Fig3.png)
|
| Figure 52: Examples of superquadrics. Source: Chakraborty et al. [93]. |
Although superquadrics are a promising option to represent granular materials with the DEM, the computational cost of contact detection is high. Boon et al. [52] reported that the computation of the contact between superquadrics is 48 times higher than for spheres.
It is worth mentioning that superquadrics are very flexible in order to represent a large number of different particle shapes, however, they can not properly reproduce the numerous irregularities and concavities of ballast particles.
- Polyhedral particles representation allows the use of sharp edges and corners, which can be useful to reproduce many kinds of granular material particles. However, this approach leads to an increase of GNS and LCR computational time.
An extensive effort was made to use polyhedral particle shapes. Cundall et al. [96,97] developed a technique to detect contact forces between polyhedra called the common plane method. It is a computationally expensive iterative method that replaces the contact between two polyhedra with two plane-polyhedron contacts. This method was further improved by fast determination of the common plane [98]. Elias [55] presented a new method of estimating the contact force between two polyhedra based on calculating the intersecting volume, and applied it to the calculation of railway ballast behaviour. Although the results obtained were promising, the simulations involved only 120 particles, due to computational time issues.
![Oedometric test calculation of a ballast sample carried out with polyhedral particles. Source: Elias [55].](/wd/images/thumb/d/d9/Draft_Samper_552093892-test-Ch5Fig4.png/250px-Draft_Samper_552093892-test-Ch5Fig4.png)
|
| Figure 53: Oedometric test calculation of a ballast sample carried out with polyhedral particles. Source: Elias [55]. |
Aiming to improve contact detection and force evaluation, Alonso-Marroquín and Wang [99,100] developed the spheropolygons approach in 2D. It is based on sweeping a sphere around a polygon, which leads to an easier force evaluation, and a decrease in LCR computational time. Galindo-Torres and Pedroso [101] extended it to more complex interactions in 3D, resulting in the spheropolyhedra approach, which was used to predict granular materials behaviour [102].
![From polyhedron to spheropolyhedron. Source: Galindo-Torres and Pedroso [101].](/wd/images/thumb/4/49/Draft_Samper_552093892-test-Ch5Fig5.png/300px-Draft_Samper_552093892-test-Ch5Fig5.png)
|
| Figure 54: From polyhedron to spheropolyhedron. Source: Galindo-Torres and Pedroso [101]. |
Ahmed et al. [1] presented a new algorithm called the potential particle shapes approach. It is based on representing the particles as adjustably rounded polyhedra. The limitation of this approach is that it is only able to represent convex particles.
![Ballast sample represented with potential particles. Source: Ahmed et al. [1].](/wd/images/thumb/7/72/Draft_Samper_552093892-test-Ch5Fig6.png/600px-Draft_Samper_552093892-test-Ch5Fig6.png)
|
| Figure 55: Ballast sample represented with potential particles. Source: Ahmed et al. [1]. |
Table 12 presents the strengths and weaknesses of each geometrical approach. The most efficient contact calculation is done with spheres with rolling friction and sphere clusters, however, compared to spherical particles calculations the computational time using sphere clusters augments proportionally to the increase of the amount of spheres in the model. For superquadrics, polyhedra, spheropolyhedra and potential particles, the computational time strongly depends on the number of DEs and contacts, being difficult to compare them with spherical particles. Anyway, it should be noted that the calculations found in published works [95,1,55,103] are limited only to a few thousands of particles. Regarding the particles shape, sphere clusters are the only geometric type that can reproduce easily concave particles (calculations with concave polyhedra will increase dramatically the computational cost). On the other hand, as sphere clusters are a conglomerate of spheres joined rigidly, they do not ensure contact tangential continuity when contact changes from one sphere to other that belongs to the same cluster, similarly to the case exposed in Section 4.5.2 for planar boundaries. Even though, considering the irregular nature of ballast particles, the error introduced by this fact can be assumed.
| Spheres with RF | Sphere Clusters | Superquadrics | Polyhedra | Sphero-polyhedra | Potential Particles | |
| Low computational cost | ✓ | ⨉ | ⨉ | ⨉ | ⨉ | ⨉ |
| Efficient | ✓ | ✓ | ⨉ | ⨉ | ✓ | ⨉ |
| Geometrical variety | ⨉ | ✓ | ⨉ | ✓ | ✓ | ✓ |
| Concave particles | ⨉ | ✓ | ⨉ | ✓ | ✓ | ⨉ |
| Contact continuity | ✓ | ⨉ | ✓ | ✓ | ✓ | ✓ |
Symbol (✓) implies that the geometrical approach satisfies the property. On the other hand, symbol (⨉) means that the geometrical approach does not satisfy the property. Symbol (✓) means that, although the geometrical approach satisfies the property, there are some limitations.
Considering all the above-mentioned, in this work, the two types of particles chosen are: spheres with rolling friction, due to their simplicity and lower computational requirements, and sphere clusters, because their calculation is based on an extension of the spherical particles algorithms yielding to an efficient contact calculation. Another important advantage of using sphere clusters is their versatility in terms of particle shape. Angularities and concavities can be naturally included, which may be useful for representing railway ballast stones.
5.2 Representation of irregular particles using spheres
The low computational demand of spheres, compared to other geometrical shapes, makes them very attractive for DEM calculations. On the other hand, the special characteristics of spheres may be an obstacle to reproduce the behaviour of irregular granular materials, such as railway ballast.
The main drawback of using spheres is controlling their excessive rotation; to that end, the rolling friction approach is used, which consist on applying a virtual torque against particles rotation, the so-called rolling resistance torque. In this section a new insight for the application of this virtual torque, called the Bounded Rolling Friction (BROF) model, is presented. Some validation tests are included in order to check its correctness and robustness.
5.2.1 Bounded Rolling Friction (BROF) Model
Rolling friction calculation can be addressed by different formulations. Ai et al. [104] presented the four most popular models:
- Models type A: the direction of the rolling resistance torque is always against the relative rotation between the two contacting entities, its magnitude depends on the material properties and the contact normal force [105].
- Models type B: the magnitude of the rolling resistance torque depends on the angular velocity [105]. There are some situations where these models do not predict rolling friction when it is required, due to its dependence on surface velocity difference between two particles, making them inaccurate.
- Models type C: the rolling resistance torque is the sum of a mechanical spring torque and a viscous damping torque [106]. In a dynamic situation, models A and C (without damping) should converge to the same behaviour. Ai et al. [104] showed that model C is superior in a static situation.
- Models type D: the rolling resistance torque is dependent on the total rotation or rotational velocity of a particle [107]. These models are clearly inefficient, not representing reality [104].
Models B and D will not be further commented due to their limitations.
A and C are the most commonly used rolling friction model types [84]. In this work, model A has been improved to avoid the inconsistencies appearing in static situations. The main advantage of model A compared to model C is that it only needs one parameter to be defined.
In model type A the rolling resistance torque of particle in contact with particle () is given by
|
|
(5.1) |
where is the resistance parameter that defines the contact rolling friction, which depends on the size and material properties of the particles in contact. is the normal contact force and is the relative angular velocity between the two particles. Figure 56 shows schematically the implementation of the rolling friction model type A.
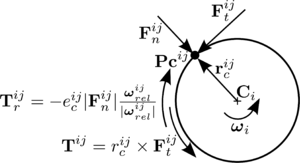
|
| Figure 56: Scheme of rolling resistance model type A. |
The material property that influences the rolling behaviour of the DE particles is called rolling friction coefficient (), which depends on the shape of the granular material particles: it will be higher for sharp stones than for pseudo-spherical ones. The rolling resistance parameter, , depends on the rolling friction coefficient and the radius of both contacting spheres.
Till this point, was treated as the rolling resistance parameter. However, it can also be defined as the eccentricity of the contact. The need of this parameter is based on the fact that, when dealing with non-spherical particles contact, the line of action of the contact normal force does not pass through the centroid of the particles [84]. In the classical model A, the rolling resistance parameter for the contact between particles and () is considered as the product of the rolling friction coefficient of the particle under consideration () and the effective rolling radius () [84,104], which, for those particles in contact, is calculated as
|
|
(5.2) |
leading to the expression
|
|
(5.3) |
Figure 57 shows schematically how is the rolling friction applied into particle , considering the eccentricity of the normal contact force.
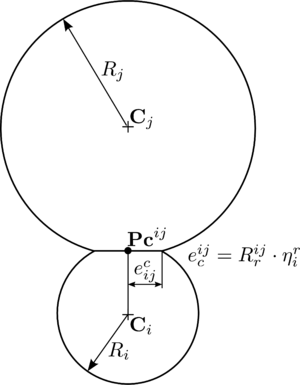
|
| Figure 57: Schematic representation of the effect of the rolling friction parameter . |
Ai et al. [104] outlined that model A should be used with caution in static situations, because rapid oscillations in the rolling resistance torque can appear due to the discontinuity in Eq. 5.1 at . To avoid this drawback, the BROF model limits the rolling resistance torque () to the necessary moment to stop the sphere rotation in one time step ()
|
|
(5.4) |
where is the angular velocity of the sphere in the previous time step.
Finally, the BROF model conditions read:
|
|
(5.5) |
This improvement, based on the work of Tasora and Anitescu [108], avoids undesirable oscillations in the spheres spin.
It should be noted that, within the BROF model, the rolling resistance torque is applied in the direction of the necessary moment to stop the sphere rotation in one time step (), and not in the direction of the relative angular velocity of the two particles in contact (). This was set in order to avoid discrepancies, making the algorithm frame-independent.
Figure 58 shows how all the particles in contact with particle applied the rolling resistance torque in the same direction, against the sphere rotation.
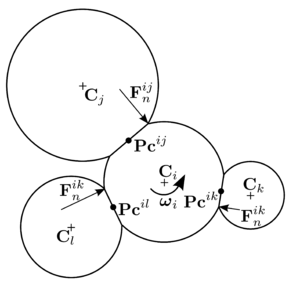
|
| Figure 58: Rolling friction from various particles acting against particle rotation. |
Eq. 5.6.a highlights the differences in the computation of the rolling resistance torque between the classical model A and the BROF model.
|
5.2.2 BROF model validation
Two test cases were selected for the validation of the BROF model. They were chosen from Ai et al. reference study [104]. Both tests were reproduced setting the same material properties and simulation parameters as in the reference tests. It should be noted that, although in the reference study the rolling particle is a disk, its thickness was chosen in order to have the same moment of inertia as a sphere, allowing the comparison between the BROF model results and those presented by Ai et al.
5.2.2.1 Test case 1: sphere with initial velocity rotating over a flat surface [104]
The first test adopted is a single sphere (with rolling friction) rotating over a flat surface. To develop the simulation, a sphere is placed over a rigid surface letting it move by its own weight until it achieve equilibrium. Then, an initial translational velocity () is applied to the sphere.
The material properties and simulation parameters of the test case are summarised in Table 13, while the initial layout is shown in Fig. 59.
| Material properties | Calculation parameters | ||
| Density () | |||
| Young modulus () | Gravity () | ||
| Poisson ratio | Time step () | ||
| Restitution coefficient | Neighbour search frequency | ||
| Friction coefficient DE/FE | |||
| Rolling friction coefficient | |||
|
| Figure 59: Initial layout of test case 1. |
Fig. 60 shows the rolling resistance torque over time using the BROF model, as compared to that obtained with the classic model type A [104]. In the dynamic part of the simulation, the rolling resistance torque in both models is a constant value. However, once the sphere reaches its final position, differences between both models arise. In the classic model A, the torque oscillates between a positive and a negative value with the same magnitude. The BROF model overcomes this inconvenience thanks to the limitation imposed, defined in equation 5.5, and leads to an equilibrium situation where the rolling resistance torque and the particle angular velocity are zero.
![Comparison between rolling resistance torque obtained applying the classic rolling friction model A [104] and the BROF model.](/wd/images/thumb/e/e1/Draft_Samper_552093892-test-Ch5Fig11.png/300px-Draft_Samper_552093892-test-Ch5Fig11.png)
|
| Figure 60: Comparison between rolling resistance torque obtained applying the classic rolling friction model A [104] and the BROF model. |
The comparison between the angular velocity of both models is not presented because, although oscillations exist when the classic rolling friction model A is applied, their magnitude is very low. It can be assumed that those angular velocity oscillations can not affect the system response due to their small magnitude, however, if the simulation involves a big amount of particles, the kinetic energy introduced by the angular velocity changes may not be neglected.
Differences between the classic model C and the BROF model are displayed in Fig. 61. The first fact to point out about model C is that it is defined by two key parameters: the rolling damping and the rolling stiffness. Damping is necessary to avoid oscillations in a static situation. Without damping, the behaviour would be similar to the behaviour of model A, but the oscillating frequency in that case would depend on the rolling stiffness and the mass of the sphere and not on the time step.
The graph in Fig. 61 shows the response of the BROF model and the classic rolling friction model C with a damping ratio . It can be appreciated that, in model C, some oscillations already appear although damping is applied. The amplitude of the oscillation decreases gradually with time.
![Comparison between rolling resistance torque obtained applying the classic rolling friction model C with a damping ratio δr= 0.3 [104] and the BROF model.](/wd/images/thumb/5/5a/Draft_Samper_552093892-test-Ch5Fig12.png/300px-Draft_Samper_552093892-test-Ch5Fig12.png)
|
| Figure 61: Comparison between rolling resistance torque obtained applying the classic rolling friction model C with a damping ratio [104] and the BROF model. |
From the results obtained in test number 1 it can be concluded that the new rolling friction model proposed in this thesis avoids oscillations when the angular velocity of the sphere is almost zero, but it behaves in a similar manner to classic rolling friction models when the sphere is rotating. It is also worth noting that this new approach only needs one parameter to be defined, an advantage compared to the classic rolling friction model C.
5.2.2.2 Test case 2: sphere with initial angular velocity rotating over an inclined surface [104]
The first test case was used to compare the BROF model with the classic model types A and C. The aim of the second test case is to evaluate the influence of varying the rolling friction coefficient in the BROF model.
Test case 2 consists of a sphere rolling up a slope with an angle degrees, as shown in Fig. 62. The sphere has the same properties as in test case 1 (see Table 13). In this case the sphere is positioned over the rigid surface allowing it to move by its own weight, but restraining its movement in the direction (see Fig. 62). When the sphere comes to rest, the restriction of movement in the direction is removed and an initial translational velocity , parallel to the slope, is applied.
|
| Figure 62: Initial layout of test case 2. |
In this test case, in order to evaluate the influence of the rolling friction coefficient in the sphere response, two other values of the rolling friction coefficient are considered. When is small (less than 0.176, which corresponds to a rolling friction angle degrees), the sphere should roll back downwards after reaching its highest point. When is sufficiently large (more than 0.176), the sphere should be stopped by a resistance torque that prevents the downward rolling due to gravity.
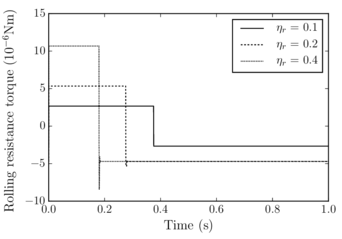
|
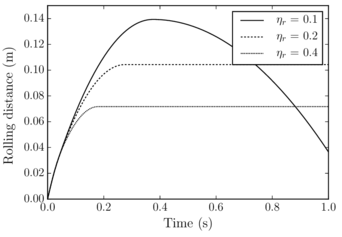
|
| (a) | (b) |
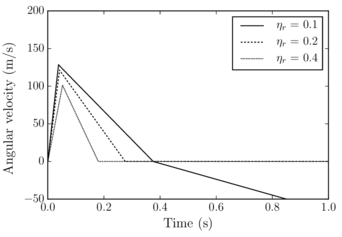
| |
| (c) | |
| Figure 63: Test case 2 results for three different rolling friction coefficients and applying the BROF model. | |
Fig. 63a shows the evolution of the rolling resistance torque over time. It is worth noting that applying the BROF model, the rolling resistance torque in dynamic situations is constant for a specific value of the rolling friction coefficient. However, when the particle comes to rest, the rolling resistance torque is set to a specific value, which is the necessary torque to stop the sphere rotation in one time step. This feature can be clearly appreciated in the last part of the graph of Fig. 63a, for and , where the rolling resistance torque is the same, independently of the value of the rolling friction coefficient.
From Fig. 63b, which shows the sphere rolling distance over time, it can be concluded that, with a higher rolling friction coefficient, the sphere spin stops faster. As it was already commented, it can be seen that, for a rolling friction coefficient smaller than 0.176, the sphere rolls back downwards after reaching its highest point. This fact is reinforced in Figure 63c where the evolution of the angular velocity over time is displayed.
Fig. 64 presents the results obtained by Ai et al. [104] when they use the classic rolling friction model C with a damping ratio . From the graphs, it can be concluded that the rolling resistance torque using the BROF model and the classic rolling friction model C are similar, but the BROF model avoids oscillations.
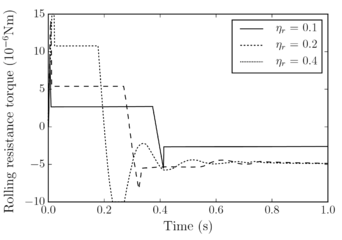
|
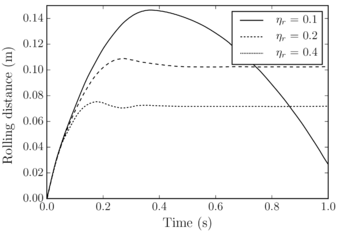
|
| (a) | (b) |
| Figure 64: Test case 2 results for three different rolling friction coefficients and applying the classic rolling friction model C with a damping ratio [104]. | |
To summarise, it can be remarked that the BROF model, besides providing similar results than the previous rolling friction models in dynamic situations, it includes a limitation to the angular velocity in order to avoid undesirable sphere rotation when the particle is almost at rest, outperforming previous approaches and only needing one parameter () to be defined.
5.2.3 Spherical particles arrangement
One important feature which was not already mentioned is the generation of particle packings. Different methods are proposed in the literature to generate these assemblies. Bagi [109] divided them into two different types: dynamic and constructive methods.
- Dynamic methods are based on generating groups of separated particles with the desired granulometry, needing to develop a pre-calculation to arrange the particles correctly packed.
- Constructive methods prepare the material assemblies using purely geometrical calculations, without needing to develop any pre-calculation. Constructive methods can be based on different algorithms such as: sequential inhibition, triangulation, dropping and advancing front [110].
In this work, the algorithm used to create the spheres assembly is the method developed by Roselló et al. [110], which is based on the advancing front packing technique in 2D but modified for obtaining high density sets of spherical particles (3D) in an efficient way. Advancing front techniques collocate the particles layer by layer starting from the boundaries or the interior of the domain controlling the desired size distribution.
![Example of a cube of side 90 \hbox m filled with spheres with radii between 0.01 \hbox m and 0.02 \hbox m. Source: Roselló et al. [110].](/wd/images/thumb/0/0d/Draft_Samper_552093892-test-Ch5Fig16.png/300px-Draft_Samper_552093892-test-Ch5Fig16.png)
|
| Figure 65: Example of a cube of side filled with spheres with radii between and . Source: Roselló et al. [110]. |
Although the new advancing front approach allows the generation of dense distributions of spherical particles, the result do not always meet the desired compactness for railway ballast. As a result, new alternatives need to be considered to address the problem. Tran [111] proposed the dynamic method called gravitational packing technique to generate DE samples for granular material simulations. It consists in assigning the particles a small friction coefficient value, and letting them to freely fill the volume under consideration. The friction coefficient used to be zero, but depending on the desired compactness of the sample, it can be other value. This leads to a high particle compactness, though requires a pre-calculation.
5.3 Sphere clusters
Clusters of spheres are a widely used alternative to spherical particles for representing granular materials. The contact forces and torques are evaluated as usual on the spheres, through equations 3.4 and 3.5. The force and torque contribution from every sphere is then summed up and translated to the centre of mass of the cluster, adding also the additional torque from the application of each force in the centre of every sphere .
For a body enclosed by the domain , supposing constant density, the centre of mass of the cluster is calculated with the formula:
|
|
(5.7) |
the distance vector can be calculated as
|
|
(5.8) |
yielding to the following expressions for the force and the torque over the cluster particle:
|
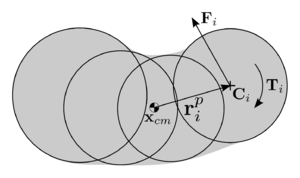
|
| Figure 66: Forces and torques applied over a rigid body discretised as a cluster with overlapped spheres. |
Once the total force is obtained, the classical Newton's second law for the translational motion have to be solved and integrated in an explicit way, as it was detailed in Section 3.3.1. Regarding the rotational motion, the resolution of the Euler rotation equations is needed and, due to the complexity of the equations, the integration is preferably developed with a second or higher order scheme.
5.3.1 Particles rotation
DEs are rigid bodies, which means that the distance between two material points belonging to a DE is constant over time, and their movement can be described with the displacement of the centre of mass plus a rotation.
Aiming to describe the motion of a rigid DE, two reference frames are introduced (see Figure 67). The first is an inertial frame which does not move with the DE. From now on, this will be referred to as the inertial reference frame, which is denoted , and . The second frame, referred to as the element frame, has its origin fixed to the centre of mass of the DE and it is defined as , and . The axes of the coordinate system associated with the element frame are assumed to coincide with the principal axes of inertia [112].
5.3.1.1 Equations of motion
The spatial description of the body is defined identifying the position of every material point in time . The spatial position refers to the inertial reference system, while denotes the same quantity expressed with respect to the element frame (in the following developments, the temporal dependence will be excluded for clarity purposes).
|
| Figure 67: Inertial () and element () frames of reference. |
The inertia of a body enclosed by the domain supposing constant density in translational motion is defined by its mass, while, in rotational motion, the inertia of the same body is defined by its inertia tensor
|
|
(5.11) |
where the moments of inertia are
|
and the products of inertia are
|
As the axes of the element frame coincide with the principal axes of inertia, the products of inertia are zero, and the inertia tensor in the element frame is represented by a diagonal matrix
|
|
(5.14) |
Defining . The velocity and acceleration of point can be obtained:
|
The linear and angular momentum are defined as:
|
In the inertial reference frame, the motion of the body is governed by the Euler equations
|
Leading to the expression for the translational motion (Newton's second law) which is best resolved in the inertial reference frame:
|
|
(5.21) |
On the other hand, the equation of the Euler equations for the rotational motion is best expressed in the element frame as the inertia tensor has constant components:
|
|
(5.22) |
which can be expressed component-wise as:
|
5.3.1.2 Rotation operators
To work with the above equations of motion is essential to know how to develop the transformation from the inertial to the element reference frame, and vice versa, in an efficient way. The three most popular ways to represent rotations are:
- Euler angles define the orientation by three successive rotations on different axes. The roll, pitch and yaw angles represent the three rotations on the , and axes, respectively. Euler angles are a similar representation, however, there is not only one way to express the orientation. Changing the rotation axes and the order in which those rotations are taken into account, more than twelve different permutations can be developed [113].
Figure 68 shows an example of an object orientation expressed with Euler angles using a permutation , where the axis represents the direction of the axis after the first rotation. The second rotation is made around that axis, and the third, around the axis.
Although the orientation of any rigid body can be determined knowing the permutation used and the angles , and , Euler angles present a singularity when the angle of the second rotation () is or radians. In that case, the first and third rotations will be in the same direction, leading to the so-called Gimbal lock, which is explained in Figure 69.
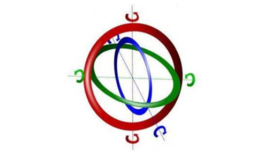
|
|
| (a) Rotation represented with Euler angles. | (b) Circles aligned, rotation allowed only in two dimensions. |
| Figure 69: Gimbal lock. | |
- Rotation matrices are 3x3 matrices, whose columns represent the unit vectors of the element reference frame projected on the axes of inertial reference system, as it is shown in Figure 70.
This leads to the following rotation matrix:
|
|
(5.24) |
- Quaternions consider the orientation as a single rotation of a unit vector defined in the inertial reference system. A quaternion is a four-dimensional vector whose elements are: the three components of the unit vector and the magnitude of the rotation. Given the rotation angle over the unit vector of Figure 71, the resulting unit quaternion reads:
|
|
(5.25) |
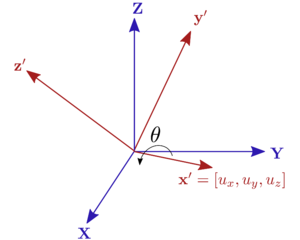
|
| Figure 71: Example of Quaternion rotation. |
As it was previously commented, Euler angles present the limitation of the Gimbal lock. Besides that, these angles involve a combination of non-linear sine and cosine functions, being their mathematical treatment tedious [114]. For those reasons, Euler angles were found not suitable.
Considering rotation matrices and quaternions, it should be noted that the use of quaternions represents a clear advantage. Both methods avoid the singularity problems that Euler angles present, however, quaternions are more compact, requiring less memory and being computationally more efficient than the rotation matrices for transformation operations.
To transform a vector and a tensor with a rotation matrix , from one coordinate system to another, it is necessary to proceed as follows:
|
The rotation matrix representing a rotation of degrees over a unit vector is constructed as:
|
|
(5.28) |
while a quaternion can summarize the same information in the more compacted way, using the unit quaternion shown in equation 5.251.
Quaternions can be expressed as a complex number with three imaginary components:
|
|
(5.29) |
or in a compact form:
|
|
(5.30) |
Defining the quaternion conjugate as , the norm is
|
|
(5.31) |
and its inverse
|
|
(5.32) |
Now, the vector can be rotated in the following way:
|
|
(5.33) |
which implies quaternion-vector multiplications. The multiplication operation between two quaternions and is
|
|
(5.34) |
while, to multiply a vector by a quaternion, the vector should be treated as a quaternion with a null scalar part . It should be noted that, since this operation involves a cross product, the multiplication of quaternions is not commutative.
The canonical way of rotating a vector with a quaternion was given by equation 5.33, which turns to two computationally expensive quaternion multiplications. Luckily, equation 5.33 can be developed in a less computationally intensive manner.
|
|
(5.35) |
where the vector is
|
|
(5.36) |
Regarding the rotation of second order tensors, Zhao and van Wachem [114] proposed a new model for determining a tensor in the rotated framework using unit quaternions. To that end the tensor should be considered as three column vectors , and :
|
|
(5.37) |
Leading to the following transformation:
|
|
(5.38) |
Concerning the change of the orientation of the element frame over time, it can also be developed directly with quaternions. The way to proceed is multiplying the rotational variation by the previous orientation [115].
Hereafter, the quaternions expressed in the form represent incremental rotations that are derived from the application of constant angular velocities during a fraction of time .
|
|
(5.39) |
5.3.1.3 Time integration of rotational motion in rigid bodies
Although Section 3.3.1 presented different methods for integrating the rotation of particles, those schemes are only applicable for spherical particles when just the variation of the rotation in each time step is calculated. On the other hand, if the orientation of the spherical particles needs to be tracked, those methods are not accurate enough and their use is not recommended. In the same way, if the particles used are not spheres, with their inertia tensor in the inertial frame depending on the orientation, higher order numerical integration methods should be used for calculating the rotation.
In the following paragraphs, firstly, an extension of the direct explicit integration presented in Section 3.3.1 for non-spherical particles is described. Then, two different strategies for the integration of the rotational motion will be explained: (1) an adaptation of the order scheme presented by Munjiza et al. [112], but using quaternions instead of rotation matrices; (2) the order scheme developed by Zhao and van Wachem [114] which is a predictor-corrector direct multiplication method based on the numerical integration of unit quaternions.
- Direct explicit integration: some numerical codes perform a direct forward explicit integration as it was detailed in Section 3.3.1. However, for non-spherical particles, the angular acceleration from equation 3.33 should by calculated using the Euler equation of motion 5.49. Then, the angular acceleration components are calculated as:
|
- order Runge-Kutta scheme: Munjiza et al. [112] introduced the idea that the change in angular momentum can be approximated by increments due to the change in the external torques at every time step
|
|
(5.41) |
Yielding to a constant angular momentum throughout a time step
|
|
(5.42) |
As the torques and angular momentum are usually expressed in global coordinates while the inertia tensor is naturally stored in the element frame, the inertia tensor has to be transformed using the quaternion tensor rotation, leading to:
|
|
(5.43) |
where is the quaternion defining the transformation between the element and the inertial reference frames.
Aiming to achieve higher accuracy, instead of calculating the angular velocity directly, this algorithm approximates the angular velocities through a 4 order Runge-Kutta scheme, to determine an average angular velocity during the time step:
|
where the values of the transformation quaternions are:
|
Once the average angular velocity during the time step is obtained, the final update calculates the orientation, angular velocity and rotation angle variation at the new step as:
|
- Scheme based on the numerical integration of unit quaternions: Zhao and van Wachem [114] proposed a predictor-corrector algorithm. Within this method the variables that describe the rotational motion of the particles have to be transformed into the element frame at instant :
|
The angular velocity at instants and are calculated as:
|
where the angular acceleration is determined using the Euler equation derived from equation 5.22
|
|
(5.49) |
Then, the predicted angular velocity in the inertial reference frame at instant is approximated based on the orientation at instant
|
|
(5.50) |
Leading to the prediction of the quaternion at instant
|
|
(5.51) |
which is used to calculate the angular velocity in the inertial reference frame at instant
|
|
(5.52) |
Finally, the corrected unit quaternion is
|
|
(5.53) |
and the angular velocity at instant in the element and inertial reference frames reads:
|
while the variation of the rotation angle is:
|
|
(5.55) |
(1) It is important to recall that the quaternions used to develop these transformations have to be unitary, in order to preserve lengths during rotations.
5.3.2 Comparison of the rotation integration schemes
In the following paragraphs, the three different methods discussed above are compared, in order to evaluate the quality of the results of each scheme. The first two tests analyse the rate of convergence of each method, comparing the numerical with the analytical results. The third and fourth test are developed to check if the energy is being conserved.
In the first two benchmark tests, translational motion is not considered. However, in the two tests that evaluate the conservation of energy, the error in both translation and rotation is going to be considered. To avoid discrepancies, the translation of the particles is determined by a Velocity Verlet scheme along with the different methods for integrating the rotation.
5.3.2.1 Test case 1: cylinder rotating freely [112]
Munjiza et al. [112] evaluated the behaviour of a cylinder set to freely rotate in the space during . The interest of this example lies in the fact that it can be solved analytically.
The angular velocity in the inertial reference frame was set to leading to an initial angular velocity in the element frame , as it is shown in Figure 72.
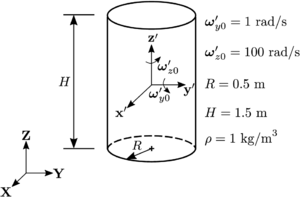
|
| Figure 72: Test case of a cylinder rotating freely. |
Since the initial axis of rotation does not coincide with any of the principal directions in the element frame, the resulting rotational motion presents the so called torque free precession which is characterised by a varying rotational velocity and inertia tensor (in the inertial reference frame).
The analytical solution for the angular velocity in the element frame is:
|
Figures 73 and 74 compare the analytical and numerical solutions of the angular velocity in the axis and respectively, for the three integration schemes. The time step of each numerical calculation is .
From the graphs presented in Figures 73 and 74, it can be concluded that the direct integration scheme is not accurate enough, giving erroneous results from the first steps that increase along time. However, it should be mentioned that the numerical results converge to the analytical solution when smaller time steps are used. On the other hand, the order Runge-Kutta scheme and the method developed by Zhao and van Wachem are much more accurate, yielding accurate outcome even when the time step is .
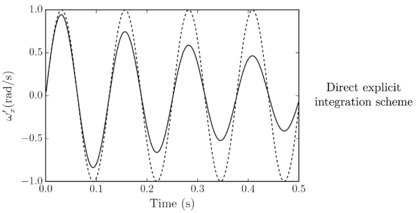
|
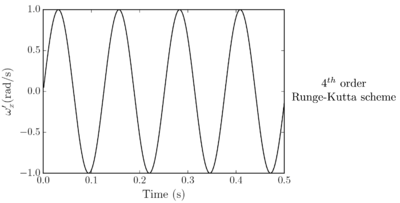
|
| (a) | (b) |
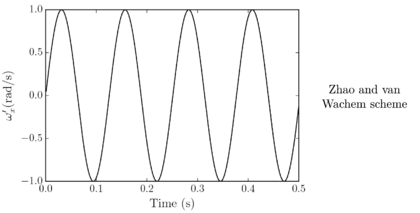
| |
| (c) | |
| Figure 73: Analytical and numerical results of the angular velocity in the element frame using the different integration schemes to calculate the rotational motion. | |
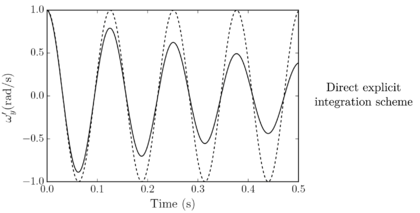
|
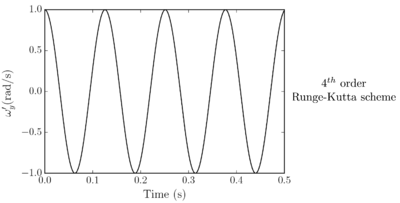
|
| (a) | (b) |
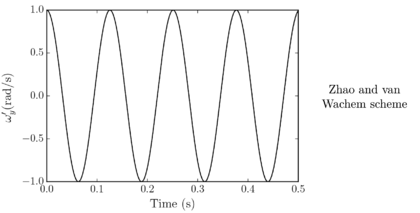
| |
| (c) | |
| Figure 74: Analytical and numerical results of the angular velocity in the element frame using the different integration schemes to calculate the rotational motion. | |
5.3.2.2 Test case 2: rotation of a fixed particle with an applied variable torque [114]
Although interesting conclusions were addressed from the previous test, it should be noted that it did not consider the application of any torque to the particle, which is important to be checked due to the non-linearity of the equations. To that end, the second test case considers the rotation of a fixed particle with an applied variable torque. The particle considered, shown in Figure 75, is a sphere with radius and density equal to . The prescribed torque is , where represents time.
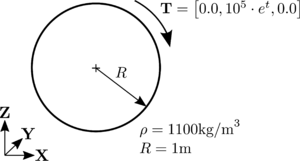
|
| Figure 75: Rotation test case 2 set-up. |
Due to the symmetry of the sphere, the equation can be solved analytically. The rotated angle obtained by integrating the torque function is
|
|
(5.57) |
The graph in Figure 76 presents the difference of the angle rotated between the analytical solution and the solution obtained with the order Runge-Kutta scheme and with the method developed by Zhao and van Wachem, using a time step .
The results obtained with the direct method are not shown, due to the fact that they do not converge. The results from the method developed by Zhao and van Wachem are clearly better than those obtained with the order Runge-Kutta scheme.
It is worth mentioning that there are some points where the difference between the analytical and the numerical solution suddenly increases. Those points always appear when the rotated angle is a multiple of , so, the unexpected increases are due to the numerical error in the calculation of trigonometrical functions used for transforming quaternions into rotated angles.
5.3.2.3 Test case 3: single fibre bouncing without energy dissipation [114]
The following two test cases are based on the energy conservation, to that end no friction nor damping is applied to the numerical model. In both tests, the particles are clusters representing the fibre shown in Figure 77. The construction and definition of the geometrical properties of clusters was not commented yet in this work, it is explained in Section 5.3.3.
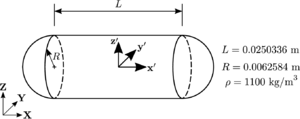
|
| Figure 77: Fibre used in the third and fourth rotation test cases. |
In the third test case, a single fibre, placed in the middle of a box , falls down under the effect of gravity. Initially, the axis of the fibre is oriented in the direction of the inertial frame. An interesting fact of this test is that, as a result of the initial orientation of the fibre, its collision with the bottom wall of the box introduces a torque, making the fibre rotate. This allows the evaluation of the rotational kinetic energy, which may be used for assessing the correctness of each rotational integration scheme.
The initial configuration of test case 3 is presented in Figure 78, while the material properties and the calculation parameters are summarised in Table 14. Contact forces are computed using the Hertz contact model, as in previous calculations.
|
| Figure 78: Initial configuration of the rotation test case 3. |
| Material properties | Calculation parameters | ||
| Young modulus of the fibre () | |||
| Poisson ratio of the fibre | Gravity () | ||
| Young modulus of the walls () | Time step () | ||
| Poisson ratio of the walls | Neighbour search frequency | ||
| Friction coefficient (all contacts) | |||
| Restitution coefficient (all contacts) | |||
The energy of the fibre along the calculation, for the three different integration schemes evaluated, is presented in Figure 79. As no friction nor damping is applied, the total energy is expected to be conserved. This feature can be observed in the calculations where the order Runge-Kutta and Zhao and van Wachem schemes are used. On the other hand, for the direct scheme, the total energy of the fibre oscillates when it bounces off the bottom wall. The kinematic, gravitational and elastic energy are also plotted separately. It can be seen that the elastic energy appears only when the fibre is in contact with the wall. At time , as the initial velocity of the fibre is zero, all the energy is gravitational.
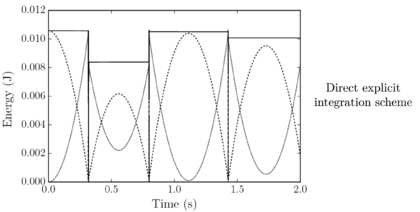
|
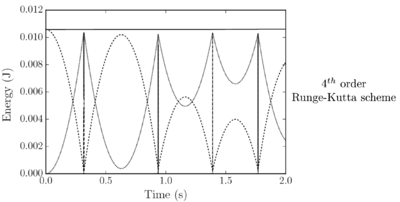
|
| (a) | (b) |
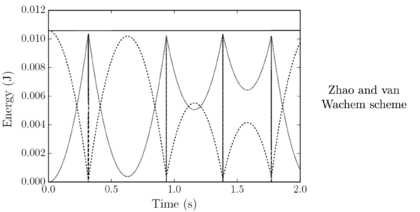
| |
| (c) | |
| Figure 79: Energy v time for the different rotation integration schemes in test case 3. | |
Figure 80 shows the error in the total energy as a function of time for the different integration schemes. The error using the direct method rapidly goes beyond the limits, for the other methods, the error remains below being lower for the Zhao and van Wachem scheme.
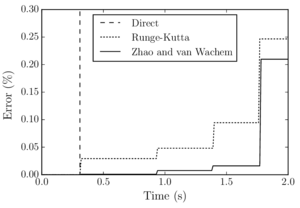
|
| Figure 80: Error in the energy conservation between the different rotation integration schemes for test case 3. |
5.3.2.4 Test case 4: multiple fibres bouncing without energy dissipation [114]
The fourth test case involves nine fibres equal to the previous one shown in Figure 77. The bounding box is the same as in the previous test and the material properties and simulation parameters are the ones presented in Table 7.
Figure 81 presents the test set-up at the initial instant () of the calculation. In this case, the nine fibres fall under the action of gravity force and have an initial velocity . They are distributed evenly along the vertical half plane of the box, with coordinates equal to and coordinates equal to . The axis of the fibres is oriented in the direction of the inertial frame. Compared to the previous test, it is important to mention that, now, there are not only particle-wall contacts, occurring several particle–particle collisions.
|
| Figure 81: Initial configuration of the rotation test case 4. |
Figure 82 plots the energy of the fibres during the calculation, for the three rotation integration algorithms. As in the third test case, the total energy using the order Runge-Kutta and Zhao and van Wachem schemes is almost constant. However, when the direct scheme is applied, great oscillations appear. From the plots showing the elastic energy, it can be appreciated that, in this case, there are a lot more contacts than in the third test. Other difference between this and the previous test is that, now, due to the initial velocity of the fibres, the initial energy is the sum of the gravitational and kinetic energy.
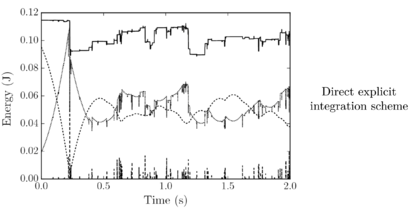
|
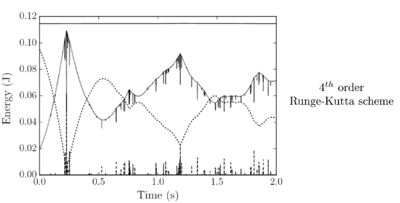
|
| (a) | (b) |
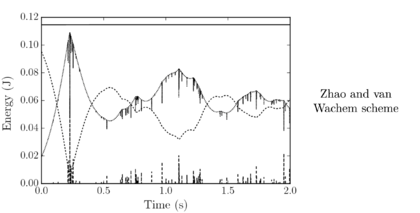
| |
| (c) | |
| Figure 82: Energy against time for the different rotation integration schemes in test case 4. | |
The error in the conservation of energy is presented in Figure 83 where it can be noted that the Zhao and van Wachem scheme yields lower discrepancies than the order Runge-Kutta method. Regarding the direct method, the error goes beyond the limits after the first contacts.
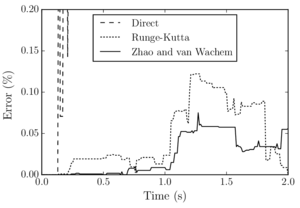
|
| Figure 83: Error in the energy conservation between the different rotation integration schemes for test case 4. |
5.3.2.5 Computational efficiency of the rotational schemes
As the fourth test case implies several DEs contacting with each other, it was considered to measure the computational time of each method. From the results, it was found that the difference in computational time between the quickest (Zhao and van Wachem) and the slowest ( order Runge-Kutta) is about the .
From the test case results, it can be concluded that the direct method is not appropriate to reproduce particle rotation, so, more sophisticated methods should be used. With the two other integration methods evaluated, good results were obtained, however, in all the tests, the method proposed by Zhao and van Wachem [114] provides better results than the order Runge-Kutta scheme [112]. Although the difference in computational time is not significant, it is interesting to note that the Zhao and van Wachem method was the quickest one in the test case considered.
It should be mentioned that the method proposed by Zhao and van Wachem and the Velocity Verlet scheme (see Section 3.3.1) for the integration of the rotational and translational motion, respectively, are both predictor-corrector methods, making the computational implementation of both methods together feasible and simple.
5.3.3 DEM flowchart after code improvements
To summarise, the basic DEM flowchart after the improvements commented in the Chapters 4 and 5 is presented in Figure 84. The chart has been modified from the work of Santasusana [15] with the improvements developed in this work regarding the rotational integration of motion.
![DEM flowchart. Modified from Santasusana [15].](/wd/images/thumb/a/a4/Draft_Samper_552093892-test-Ch5Fig35.png/600px-Draft_Samper_552093892-test-Ch5Fig35.png)
|
| Figure 84: DEM flowchart. Modified from Santasusana [15]. |
In the original flowchart, the scheme used for integrating the rotational motion was the order Runge-Kutta method. On the other hand, in this work, the Zhao and Van Wachem method was implemented. Another difference is that Santasusana [15] included the Fast Intersection Test before performing the Double Hierarchy method, which was not included in this work.
5.3.4 Sphere clusters construction
The use of spheres to represent granular materials is attractive for several reasons already commented along this work. However, the easiness of constructing the particles was not mentioned yet.
Spheres are defined by means of the coordinates of their centres and the radii. By contrast, sphere clusters require additional information. First of all, the agglomerate of spheres should be created from the real geometry of the particle. Then, as the geometrical properties are difficult to define from the spheres geometries, due to the overlaps, the position of the centre of mass, the volume and the inertia tensor of the particle should be calculated.
5.3.4.1 Geometry creation
In this work, the creation of the agglomerate of spheres from the real geometry of the particle is developed using the Sphere-Tree Construction Toolkit (STCT) (http://isg.cs.tcd.ie/spheretree/), which is an Open-Source software that allows the use of a number of algorithms for filling volumes with overlapped spheres in an efficient way [116,117,118].
The starting point should always be the geometry of the particle, which may be generated by the user or obtained by scanning real particles. For introducing this geometry in the STCT, a triangular surface mesh from the outer surface of the particle (Figure 85) should be created. Particles geometry and surface triangular meshes are generated using GiD1 software.
|

|
| (a) Original geometry. | (b) Triangle surface mesh. |
| Figure 85: Original geometry and triangular surface mesh used for creating a sphere cluster. | |
The agglomerate of spheres can be created from the triangular surface mesh with the STCT. The software allows the use of different algorithms, and in this work the reduced Hubbard method is chosen [116,119]. Figure 86 shows two sphere clusters generated from the same geometry, the one presented in Figure 85. The cluster in Figure 86a has 16 spheres, while the cluster in Figure 86b is formed by 45 spheres.

|

|
| (a) 16 spheres cluster. | (b) 45 spheres cluster. |
| Figure 86: Same particle cluster generated with 16 and 45 spheres. | |
The cluster with 45 spheres fits better in the original volume of the particle, however, the use of more spheres would increase the computational time. In Chapter 6 a procedure to chose the appropriate cluster to reproduce railway ballast, combining accuracy and computational efficiency, is proposed.
Till this point, the cluster geometry is already generated. Now, the next step is to calculate the geometric features, required for the physical calculations.
5.3.4.2 Calculation of the cluster properties
To calculate the geometrical properties of the clusters, the volume of the cluster should be generated. To that end, all the spheres of the cluster are collapsed, leading to a single volume. This volume is meshed with tetrahedral elements (Figure 87). It should be noted that the finer is the tetrahedra mesh, the best the properties of the cluster will be defined.
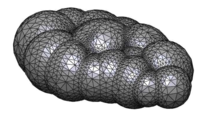
|

|
| (a) 16 spheres cluster. | (b) 45 spheres cluster. |
| Figure 87: Tetrahedra mesh of two volumes generated after collapsing the spheres of the corresponding cluster geometries. | |
The generated tetrahedra mesh is used to calculate the centre of mass, the volume and the inertia tensor of the cluster. The volume is the sum of the volumes of all tetrahedra, while the centre of mass and the inertia tensor are calculated from equations 5.7 and 5.11, respectively, considering the discretised volume.
Finally, it should be considered that the centre of mass of the cluster has to be located in the origin of coordinates, if this condition is not met, the translation of the spheres that make up the cluster is necessary. Moreover, the inertia tensor of the particle should be oriented parallel to its principal axis, so as, the spheres may need to be rotated around the centre of mass of the cluster.
In this work, the geometry of six different ballast particles is considered. For each of the geometries, two different clusters are generated, one with a number of spheres between and and others between and . The geometry of two of the stones was provided by Noura Ouhbi (Figures 88a and 88b), from the Innovation and Research Department of SNCF in France. The procedure they use to obtain the scanned geometry of the stones is explained in Ouhbi et al. [103]. The other four particles (Figures 88c, 88d, 88e and 88f) are user-defined according to the regulations presented in section 2.2.1.

|

|

|
| (a) Cluster 1. | (b) Cluster 2. | (c) Cluster 3. |

|

|

|
| (d) Cluster 4. | (e) Cluster 5. | (f) Cluster 6. |
| Figure 88: Different clusters generated to reproduce railway ballast. | ||
It is worth mentioning that in Figure 88 the geometry of the stones is not oriented in the same direction as the corresponding clusters, due to the transformation operations (translations and rotations) needed to locate the centre of mass in the origin and the inertia tensor parallel to to its principal axis.
(1) GiD is a universal, adaptive and user-friendly pre and postprocessor for numerical simulations in science and engineering. It was designed to cover all the common needs in the numerical simulations field from pre to post-processing: geometrical modeling, effective definition of analysis data, meshing, data transfer to analysis software, as well as the visualisation of numerical results. GiD is developed in CIMNE
5.3.5 Sphere clusters arrangement
As with spheres, the availability of an automatic generator of groups of clusters to fill specific volumes is fundamental. The algorithm used in this work is the method developed by Recarey et al. [120] [121], which is based on the technique used for creating sphere meshes, but improved to generate meshes of non-spherical particles.
![Cube filled with 5901 non-spherical particles. Source: Recarey et al. [120].](/wd/images/thumb/f/f9/Draft_Samper_552093892-test-Ch5Fig40.png/300px-Draft_Samper_552093892-test-Ch5Fig40.png)
|
| Figure 89: Cube filled with 5901 non-spherical particles. Source: Recarey et al. [120]. |
As it was mentioned before in the case of the spheres, the new advancing front technique creates dense packings of non-spherical particles with the desired granulometry, however, for representing railway ballast, the high compaction necessary can not be met, and the use of dynamic methods, to compact the assembly, may be also necessary.
To use the advancing front technique it is necessary to know the radius of the sphere that circumscribes the entire cluster, in order to avoid overlaps between particles and to generate the desired granulometry. The calculation of the sphere that circumscribes the cluster may be easy for several cluster geometries, such as ellipsoids or fibres, however, in case of very irregular particles, such as railway ballast, its calculation can be troublesome.
Aiming to facilitate the task of calculating the sphere that circumscribes each cluster, a new iterative algorithm was developed. As an example, the procedure for a 2D cluster composed by 3 circles (see Figure 90) is explained:
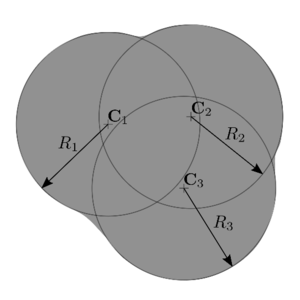
|
| Figure 90: Clusters composed by three circles. |
- Knowing the centres of the spheres (, and ) and their radius (, and ), the distance between the outer points of the circles can be computed as
|
|
(5.58) |
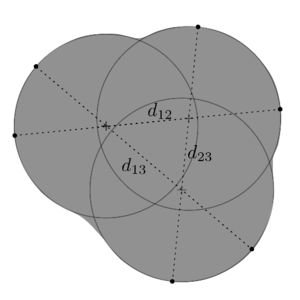
|
| Figure 91: Distance between the outer points of the circles. |
- Those distances are compared, saving the largest. In the case shown in Figure 91, the longest distance is .
The coordinates of the two most distant points in the cluster (in this case and ) is
|
|
(5.59) |
which are used to calculate the centre of the circle that circumscribes the two most distant points in the cluster
|
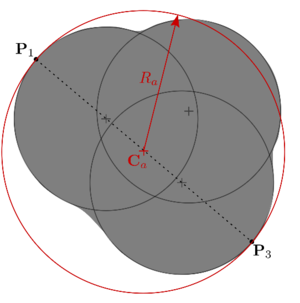
|
| Figure 92: Circumference that circumscribes the two most distant points in the cluster. |
- The next step is checking if all the circles of the cluster lie inside the circumference. If all the spheres fit inside the circumference the process finishes here. However, in most of the cases, such as the situation presented in Figures 92 and 93, this condition is not met. To correct this, the furthest point to should be calculated. As the sphere lying outside the circumference belongs to circle , is calculated as
|
|
(5.62) |
The centre of the next circumference is in a point where, with the radius , lies inside the circumference
|
|
(5.63) |
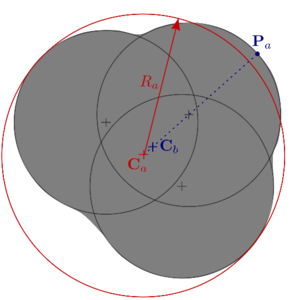
|
| Figure 93: Centre of the next circumference used to fit the cluster inside. |
The radius of this new circumference is the distance from its centre to the furthest point of the cluster, as it is shown in Figure 94. As the entire cluster lies inside it, the process finishes.
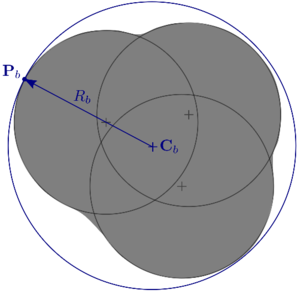
|
| Figure 94: New circumference that circumscribes the full cluster. |
Although the calculation of the sphere that circumscribes the cluster can be calculated without this iterative method, in three dimensions the operations become complicated and this iterative model leads to good results in a simple and efficient way.
6 Railway ballast modelling within the DEM
A review of the conditions that the ballast layer should meet were presented in Chapter 2. However, regulations do not specify clearly the material properties of each ballast stone. Moreover, the geometry simplifications introduced in the DEM model and the unpredictability of the contact mechanisms, lead to some uncertainties in the assignment of material properties.
In this Chapter, a review of the material parameters needed to define the railway ballast grains is presented. As not all the material properties are perfectly known, three different laboratory tests are performed using the numerical code. Specifically, the angle of repose of a group of ballast particles (Section 2.3.1), the large-scale direct shear test (Section 2.3.2) and the lateral resistance test (Section 2.3.3) are carried out. The aim is not only validating the numerical code, but also calibrating the parameters that should be applied to emulate the behaviour of railway ballast and evaluate the potential of the developed software.
6.1 Railway ballast material properties
Railway ballast behaviour is characterised by different material properties. Some of them are well documented in technical literature and can be assigned to the DEM model directly. However, other properties are influenced by the contact mechanism and should be modified in the numerical calculations due to the simplifications of the model:
- Ballast density is well known. It used to be between and [122].
- Sample size distribution is clearly defined in the regulations of each region. Railway tracks granulometry, obtained from the European standards, was presented in Table 2 [29]. The sample size distribution can be accurately defined with the available meshers: see Section 5.2.3 for spheres and Section 5.3.5 for clusters.
- Particle contact stiffness within the DEM model is difficult to determine. Figure 95 shows the difference between the microscopic real contact geometry and the simplified contact geometry. Within the Hertzian contact law the contact stiffness depends not only on the material properties but also on the overlapped volume.
|

|
| (a) Real contact geometry. | (b) Hertzian contact geometry. |
| Figure 95: Real and Hertzian contact geometry. | |
Real ballast particles have rough, non-spherical surfaces. As a consequence, there is some scope for uncertainty in the choice of stiffness magnitude [48], which, amongst the material properties, mainly depends on the value of the Young modulus ().
Although ballast Young modulus is about [123,124], for rough surfaces the contact volume is much smaller than for idealised smooth shapes. This leads to the need of using a lower Young modulus for the numerical calculations than the real one. Ahmed et al. [1] used values between and for potential particles, with a value of the Poisson ratio () equal to . The Poisson ratio for ballast used to be between and [125,122].
- The inter-particle friction between ballast stones depends on the time and on the load cycles suffered by the sample. Melis [122] studied that the friction coefficient should always be between 30 and 40 degrees (friction coefficient between 0.577 and 0.839). Chen et al. [91] used a value of .
- Particle-wall friction depends not only on ballast properties, but on the properties of the material of the wall.
- The coefficient of restitution is well documented in the literature, being equal to [125]. However, since in DEM calculations ballast grains used to be considered as perfectly rigid bodies and no wear nor crushing are taken into account (where most of the energy is dissipated) the collisions are assumed to be inelastic. In other words, the restitution coefficient used to be set to [126].
- The initial void ratio greatly affects the behaviour of a ballast sample. As it was mentioned in Sections 5.2.3 and 5.3.5, in most of the cases, the particle packing obtained with the available sphere and cluster meshers is not high enough and dynamic packing methods should be applied.
- The particle shape depends on the geometrical approach considered. If the railway ballast particles were represented as spherical DEs, the parameter that reproduces the irregularities is the rolling friction coefficient. On the other hand, if the geometrical approach chosen is the use of sphere clusters, the particle shape depends on the correctness of the cluster construction.
A simple and efficient way to calibrate the value of the appropriate rolling friction coefficient for spheres or check out if the clusters geometry is accurate, is measuring the angle of repose of the ballast particles. The procedure followed in this work to evaluate the angle of repose is described in the following section.
6.2 Angle of repose of railway ballast
The angle of repose is defined as the slope of a pile of granular material laid up on the ground without any other support [127]. The importance of this material property is that it controls all parameters that affect the behaviour of large amounts of granular material (friction between particles, shape and size of different grains...), allowing their evaluation in a simple way. The angle of repose of railway ballast is always about 40 degrees [91].
As the rolling friction coefficient aims to gather all the geometrical irregularities of the bulk material in one numerical parameter, it should be taken into account that the rolling friction coefficient of the contact between spherical particles and rigid walls, in most cases, should be different than for particle-particle contact. The reason is sketched in Figure 96a where six irregular particles are stacked. It can be seen that the rotation of particles , and is restrained because their entire lower surface is directly in contact with a rigid wall. However, for particles , and , if any disturbance occurs, they can easily rotate, as it is shown in Figure 96b.
|
|
| (a) Particles in equilibrium. | (b) Rotation of particle due to a small disturbance in particle . |
| Figure 96: Rolling friction with walls. | |
6.2.1 Angle of repose of railway ballast using spherical particles
Figure 97 shows the layout of the simulation developed to calibrate the rolling friction coefficient of the material. The geometry of the test is taken from Chen et al. [91], modifying the amount of material, and it is based on measuring the angle of repose of the ballast sample for each of the rolling friction coefficients evaluated. In the calculation, particles are deposited from a hopper with a squared aperture of side, located above the floor.
|
| Figure 97: Calculation layout (dimensions in ). |
Considering that the critical time step of the system depends on the mass and the stiffness of the particles, a first attempt to look for the appropriate rolling friction coefficient of railway ballast is developed using the lowest particles stiffness, which allows the use of a higher time step. Then, it is proven that the results, for this specific test are independent of the stiffness of the particles (considering reasonable values, not too low). Based on the work of Ahmed et al. [1], the value of the Young Modulus used is . The material and calculation parameters are summarised in Table 15. Friction between the ballast and the silo is null while the friction coefficient between ballast particles and the floor is [91], equal to the friction coefficient between ballast stones.
| Material properties | Calculation parameters | ||
| Density () | |||
| Poisson coefficient | |||
| Young modulus () | Time step () | ||
| Friction coefficient ballast | Neighbour search frequency | ||
| Friction coefficient ballast-floor | |||
| Restitution coefficient | |||
| Rolling friction coefficient | |||
Figure 98 shows the angle of repose obtained for each value of the rolling friction coefficient and a Young modulus . Since the angle of repose of ballast is 40 degrees, a rolling friction coefficient value equal to may be appropriate to reproduce railway ballast behaviour.
Till this point, an appropriate rolling friction coefficient for reproducing railway ballast repose angle is obtained. However, the independence of the results from the Young modulus should still be verified.
The material parameters used in this step are the same presented in Table 15, with a rolling friction coefficient equal to and different Young modulus . Since the critical time step depends on the stiffness of the particles, different time steps may be used for each calculation, being for each value of the Young modulus respectively.
Figure 99 shows the angle of repose of railway ballast represented with spheres with rolling friction and various Young modulus. From the results, it can be concluded that the angle of repose is independent of the stiffness of the particles. It should also be noted that, when reproducing the behaviour of ballast in a railway track, the material stiffness would be a key parameter, because the deformation of the track is important, so, further calculations should be developed to calibrate the value of the Young modulus.
After reproducing the angle of repose test, a suitable value of the rolling friction coefficient for representing railway ballast behaviour with spherical particles was found. It was also proven that the contact stiffness of the material is not a key parameter in this particular test. The rolling friction approach can be considered useful to reproduce railway ballast, or other granular materials, with spherical DEs.
In the following Section, the same procedure is used in order to validate the use of two different groups of clusters of spheres to reproduce the behaviour of railway ballast.
6.2.2 Angle of repose of railway ballast using clusters of spheres
Two different groups of clusters of spheres were presented for each ballast stone geometry in Section 5.3.4. One group was composed of clusters with a number of spheres between and and the other between and . The group of clusters with less spheres would be computationally more efficient, however, it is important to prove if their geometry is sharp enough to correctly reproduce the behaviour of railway ballast.
As in the previous Section with the calibration of the rolling friction coefficient, the appropriateness of each group of clusters is evaluated by measuring their angle of repose. The geometry of the tests is shown in Figure 100, while the material and calculation parameters are presented in Table 16.
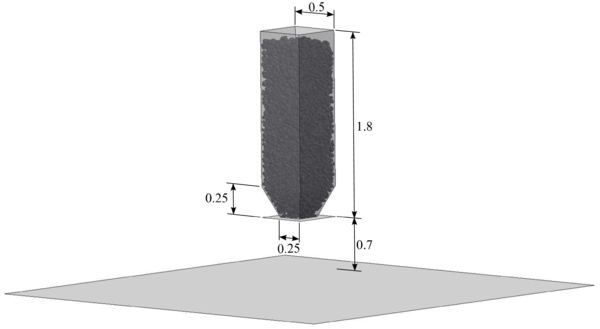
|
| Figure 100: Simulation layout (dimensions in ). |
Taking advantage of the independence of the angle of repose with respect to the Young modulus of the material, a value is set. In Table 16 it can be seen that there is not reference to the rolling friction coefficient. The reason is that within the sphere clusters approach not rolling friction is applied.
| Material properties | Calculation parameters | ||
| Density () | |||
| Poisson ratio | |||
| Young modulus () | Time step () | ||
| Friction coefficient ballast | Neighbour search frequency | ||
| Friction coefficient ballast-floor | |||
| Restitution coefficient | |||
The results are presented in Figure 101. The angle of repose obtained with the clusters with more spheres is almost , so they would be considered convenient for reproducing railway ballast. On the other hand, the angle of repose achieved with the clusters with less spheres is about , so, it can be concluded that, with that geometry, the behaviour of ballast stones is not being reproduced well.

|

|
| (a) Clusters with more spheres. | (b) Clusters with less spheres. |
| Figure 101: Repose angle of railway ballast represented with the different groups of sphere clusters. | |
Hereafter, in the calculations with clusters of spheres, the particles composed by more spheres (between and ) will be used. Clusters with less spheres (between and ) will be discarded.
6.3 Large-scale direct shear test
The large-scale direct shear test used to be performed to evaluate the behaviour of railway ballast under different scenarios. It consists of introducing ballast inside a box divided in two halves, pulling from the lower box and computing the stress-strain curve of the ballast sample. This test is typically carried out to determine the resistance of the ballast layer under different levels of fouling, which decreases its load resistance capacity [128,129]. In this work, it is used to calibrate the material parameters and assess the validity of sphere clusters approach for reproducing railway ballast.
One of the main advantages of this large-scale direct shear test is that it allows the use of laboratory devices with a reasonable size. Regarding numerical calculations, this is also beneficial to evaluate the behaviour of sphere clusters. Firstly, it involves a not so high number of particles compared to an actual section of a railway track, leading to an acceptable computational time. Besides that, to reproduce this kind of experiments where a small number of particles is confined, sphere clusters should be used instead of spheres due to the dependence of the results on the number and distribution of contacts [44].
6.3.1 Reference test
Indraratna et al. [129] conducted a series of large-scale direct shear tests. The apparatus used in this study consisted of a steel square box , high, divided horizontally into two equal halves. On the top part, a free-loading plate was placed. This plate, that allowed the particles to be displaced vertically during shearing, was used to apply normal load and to monitor vertical displacement.
Figure 102 shows schematically the laboratory layout of the large-scale direct shear test.
![Laboratory test layout with dimensions in mm. Modified from Indraratna et al. [129].](/wd/images/thumb/b/b3/Draft_Samper_552093892-test-Ch6Fig8.png/510px-Draft_Samper_552093892-test-Ch6Fig8.png)
|
| Figure 102: Laboratory test layout with dimensions in . Modified from Indraratna et al. [129]. |
To minimise the boundary effects, the size of the ballast particles was slightly smaller than the typical ballast used in railway tracks [44]. The maximum size of the ballast stones () was rather than the of used in typical ballast gradations. The of the tested ballast was and the stones could not be smaller than .
From all the experiments developed in the laboratory, in this work three scenarios are reproduce numerically. Those three tests are the large-scale direct shear tests, for fresh ballast, subjected to normal stresses equal to , and . In the experiments, each specimen was subjected to a maximum horizontal displacement of 37 mm.
The void ratio of the assembly representing the initial condition of the test specimen was controlled at 0.82 (porosity equal to 45%) in the laboratory.
Concerning the applied force, it should be considered that the normal force acting on the shear band is the sum of the load applied by the top plate and the weight of ballast in the upper box. Being and the length and width of the shear box, respectively, the horizontal velocity of the lower box and the time, the contacted shearing area of the shear band incorporating the shear displacement is . Therefore, the normal stress applied is:
|
|
(6.1) |
With regard to the results obtained, the variables evaluated are the shear stress and volumetric strain depending on the horizontal displacement of the lower box. The shear force can be calculated by considering the equilibrium of forces in the horizontal direction. To that end, the normal and shear force over the walls of the upper box and the shear force over the loading plate is computed. Thus, the shear stresses is readily computed as
|
|
(6.2) |
Meanwhile, the volumetric strain can be assessed simply by measuring the vertical displacement of the loading plate.
6.3.2 DE model
Figure 103 shows the DE model of the large-scale direct shear test. To generate the ballast sample, the available cluster mesher (see Section 5.3.5) is used. The mesher allows the user to define the material gradations, however, the void ratio can not be controlled, thus, a pre-calculation should be developed.
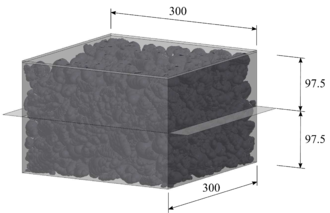
|
| Figure 103: DE model of the large-scale direct shear tests with dimensions in . |
6.3.2.1 Pre-calculation
The material properties of the ballast in the pre-calculation are the same as for the numerical calculation of the angle of repose defined in Table 16.
Regarding the rigid boundary walls, the value of the Young modulus and the Poisson ratio is the same as for ballast, while friction between them and the granular material is set to in order to allow a better particle arrangement. It may be thought that it is not congruent to assign a value of the Young modulus and Poisson ratio to a rigid wall, however, this parameters are necessary in order to define the normal and tangential stiffness of their contact with the DEs (see equation 4.1).
Figure 104 presents the pre-calculation process. As the void ratio of the assembly is 0.82, the total volume of the ballast stones is , so, a ballast sample with the specified granulometry and a volume close to is created using the cluster mesher. However, the cluster mesher can not generate compacted assemblies and the particles are separated from one another, occupying a space larger than the box. The initial configuration of the pre-calculation is shown in Figure 104a. The pre-calculation starts and the ballast stones fall freely placing themselves in an equilibrium position (Figure 104b). Finally, the loading plate is moved down to the proper position (Figure 104c) and the calculation continues during to ensure that all the particles are at rest (Figure 104d).
Particles arrangement when the pre-calculation finishes is the initial particles distribution for the large-scale direct shear test calculations.

|

|

|
| (a) . | (b) . | (c) . |

| ||
| (d) . | ||
| Figure 104: Different instants of the DE pre-calculation of the large-scale direct shear test. | ||
6.3.2.2 Large-scale direct shear test numerical model
The conducted shearing velocity in the laboratory was . Considering that the lower box was moved , this leads to an experiment lasting , which may be computationally too costly. Indraratna et al. [44] had also this problem when performing the numerical calculation of this laboratory test and they imposed a lower box velocity equal to , concluding that this relatively low shearing rate was not enough to unduly disturb the assembly, but can still attain an acceptable convergence rate. Taking advantage of this, in this work, the lower box velocity was set to .
It should be remembered that, as it was shown in Figure 95, the contact geometry between DEs is very different to real contact geometry. This leads to uncertainties in the election of particles stiffness, which, in this kind of calculations where the strain of a bulk material is measured, is a key parameter. For this reason, the Young modulus should be calibrated.
In Sections 6.2.1 it was observed that the angle of repose is not significantly affected by the material Young modulus. It was concluded that, the angle of repose depends on the friction coefficient and, mainly, on the rolling friction coefficient (for spheres) and particles geometry (for clusters). However, in the large scale direct shear test, where material strain is computed, the Young modulus is a key parameter that influences greatly the initial slope of the stress-strain curve.
In a first attempt a value of was chosen, based on the work of Ahmed et al. [1]. With this Young modulus the obtained stress-strain curve was very steep which can be explained due to the use of sphere clusters, while Ahmed et al. used potential particles. Sphere clusters are conglomerates of spheres that include overlaps, leading to more points of contact. This fact, together with the results obtained, suggests that the value of the Young modulus should be lower than .
Three different values for the Young modulus lower than were evaluated in order to find the appropriate one. They were that corresponds to , with a Poisson ratio . After developing those calculations, the case with the initial slope of the stress-strain curve more similar to the experimental one was chosen. The value is .
Table 17 summarises the material and calculation parameters. The Young modulus and Poisson ratio of the rigid walls are the same as for ballast particles, and . Regarding friction between ballast particles and the steel box, Huang and Tutumluer [45] developed a series of numerical calculations of similar large-scale direct shear tests with polyhedral particles concluding that the friction angle between the stones and the rigid box is about , which corresponds to a friction coefficient equal to , the value used in the calculations.
| Ballast properties | Walls contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
6.3.3 Results
The numerical model yields some interesting results that should be carefully analysed. The shear stress-displacement and volumetric strain-displacement curves, obtained with the computational code, are displayed in Figure 105 together with the laboratory outcome.
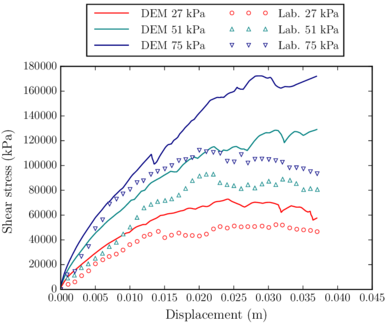
|
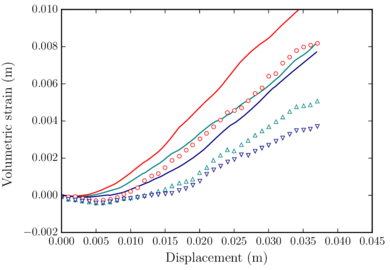
|
| (a) | (b) |
| Figure 105: Large-scale direct shear numerical results. | |
Firstly, it should be mentioned that this test depends highly on the local behaviour of the stones, making impossible the exact replication of the laboratory test with the numerical code. This fact is more pronounced when the lower box was moved several . Moreover, according to Indraratna et al. [44], some differences between the numerical and laboratory results are consequence of the absence of crushing in the numerical model. In the laboratory test, stones crush lead to sudden decreases in the shear stress and volumetric strain, decreases that can not be reproduced with this numerical model.
Notwithstanding the absence of crushing and the dependence of the test on the local behaviour of ballast stones, it can be appreciated that, for the three different normal stresses, the shear stress and volumetric strain are largely overestimated in the numerical model. Moreover, the difference is greater for high values of the normal stress.
6.3.4 Stress-dependent friction contact model
Höhner et al. [130] found that the use of clusters of spheres introduces discontinuities in the force calculation and also artificial friction due to spheres overlap. Although the normal force discontinuities may be a problem when dealing with smooth particles, for such irregular material as ballast, this was not found to be critical. However, the geometric friction may be problematic, and its effects increase with higher confinements. As an example, Figure 106a presents the actual contact force between two smooth particles, while Figure 106b shows the contact force considering those particles sphere clusters. It can be seen that the normal force between those particles does not point in the same direction in each case.
Höhner et al. [130] proposed a new model based on calculating the mean force when more than one sphere is involved in the same contact (see Figure 107). Although this model produces good results for the normal force computation, the problem was already solved decreasing the Young modulus. Besides that, with this new model, each DE can not be in contact with more than one DE or FE simultaneously. For those reasons, the use of the new model is discarded.
![Spheres cluster impacting a flat wall for two different time steps. Source: Höhner et al. [130].](/wd/images/thumb/4/41/Draft_Samper_552093892-test-Ch6Fig13.png/360px-Draft_Samper_552093892-test-Ch6Fig13.png)
|
| Figure 107: Spheres cluster impacting a flat wall for two different time steps. Source: Höhner et al. [130]. |
Trying to solve the problem of the artificial geometric friction introduced by the spheres overlap in clusters, a new contact model is proposed in the following paragraphs.
Harkness et al. [48] tried to reproduce the effects of confining pressure on the behaviour of railway ballast in triaxial tests within the DEM. In their work, they were concerned about the use of unrealistic Young modulus for representing railway ballast within the DEM and also about the dependence of the friction coefficient in relation with the particles confinement. Although they use potential particles instead of sphere clusters, some ideas of their model were found useful.
Regarding the Young modulus, they reported good results in the triaxial tests just lowering its value, however, they wanted to use a realistic value. They proposed a new model, the so-called Conical Damage contact model, based on reproducing the micro-mechanics of the contact. To that end, the new model includes a new parameter , and a minimum contact radius as it is shown in Figure 108.
![Conical Damage contact model. Source: Harkness et al. [48].](/wd/images/thumb/5/5c/Draft_Samper_552093892-test-Ch6Fig14.png/360px-Draft_Samper_552093892-test-Ch6Fig14.png)
|
| Figure 108: Conical Damage contact model. Source: Harkness et al. [48]. |
When the contact stress exceeds a certain value , the contact radius is increased, decreasing the indentation a value , leading to a realistic non-linear contact model (more similar to 95a than the Hertz contact model).
Although Harkness et al. obtained good results, the difficulty to calibrate the new parameters (, and ) and the use of a realistic value of the Young modulus (which will decrease the computational time step increasing the overall computational time) are found to be not operational. Moreover, they conclude that the contact between ballast stones should be considered non-linear, however, the Hertz contact model is already considering the non-linearity of the contact without introducing any new contact parameter.
On the other hand, the findings of Harkness et al. concerning the changes in friction during high compaction due to wear and particle shape inaccuracies were found interesting, even if their contact model was optimised for potential particles (see Section 5.1).
The simplest approach used to achieve realistic results with high compacted particles was based on decreasing the inter-particle friction coefficient globally, however, this would not be adequate for low compression tests. As an alternative to setting the inter-particle friction coefficient globally it was found that determining the friction coefficient for each contact as a function of the contact stress could provide a more generally applicable model. The main advantage of a method that depends on the contact stress is that it is non-dimensional and can be applied at different scales.
The maximum stress () for a Hertzian contact (which occurs at the centre of the contact) can be expressed as a function of the radius of the contact (), the normal force () and the indentation () as:
|
|
(6.3) |
Taking advantage of this, a critical maximum stress () can be set, from which the critical contact force () can be calculated for each contact:
|
|
(6.4) |
The model proposed in this work states that, when the value of is exceeded, the friction coefficient should decrease. Thus, when the sphere clusters are confined, the effect of the geometric friction will be lowered.
Then, the expression relating the friction coefficient with the critical contact force should be suggested. Harkness et al. [48], based on the work of Kogut and Etsion [131], came to the expression
|
|
(6.5) |
where is the friction coefficient, a parameter and a parameter . It should be noted that, in their model, can never exceed due to the use of the Conical Damage contact model mentioned before.
For sphere clusters, as the friction coefficient for non-confined particles () is already known from the angle of repose tests (see Section 6.2.2), the friction coefficient is:
|
|
(6.6) |
The main drawback of this stress-dependent friction contact model is that two new parameters ( and ) should be defined. However, as it was used for changing the friction coefficient when particles are confined, the critical contact stress was considered equal to the contact stress on a point that supports alone all the gravitational force () of a stone.
Since clusters with different amount of spheres and radii are considered, a mean value of should be computed. Being the acceleration of gravity, the mean volume of the particles and their density, the gravitational force can be computed as:
|
|
(6.7) |
which leads to the expression:
|
|
(6.8) |
where is calculated from equation 3.29.a and from equations 3.15, 3.27.a and 3.29.c as
|
|
(6.9) |
It is important to mention that the radius of the spheres involved in this expressions are the mean radius of the spheres that compose all the clusters in the calculation.
For the large-scale direct shear test with , was calculated yielding a value of . On the other hand, the parameter is unknown and has to be calibrated from numerical calculations. Table 18 summarises the material and calculation parameters of the numerical models used to calibrate . It can be appreciated that all the parameters are the same as in the Hertz contact model calculation except and , which should be included to correctly define the stress-dependent friction contact model.
The values of chosen were . The reason is that when computing the analytical equations 6.4 and 6.6 with the material parameters and more negative than , the friction coefficient decreases with respect to the increase of contact stress in a way that seems too sharp.
| Ballast properties | Walls contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Critical contact stress () | |||
| parameter | |||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
It is worth mentioning that this stress-dependent friction contact model is developed in order to minimise the influence of the artificial geometric friction produced by overlapping spheres in clusters. For this reason, the contact between sphere clusters and walls is calculated applying the classical Hertz contact model. As it is shown in Figure 109, in most particle-wall contacts, the spheres overlap do not affect the direction of the normal contact force.
|
|
| (a) Irregular particle-wall normal contact force. | (b) Sphere cluster-wall normal contact force. |
| Figure 109: Normal contact force in a real particle and a sphere cluster collision with a wall. | |
The results presented in the graphs of Figures 110, 111 and 112 suggest that the stress-dependent friction contact model is behaving as expected, decreasing the shear stress and volumetric strain due to the decrease in the friction coefficient.
It can be appreciated that with (see Figure 110), the curves obtained with the numerical model do not coincide with the experimental curves for any of the normal stresses.
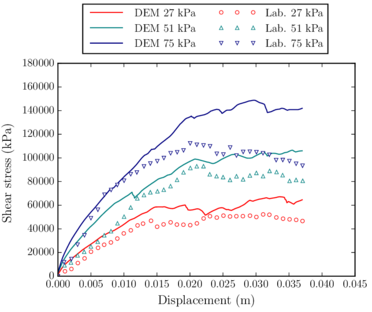
|
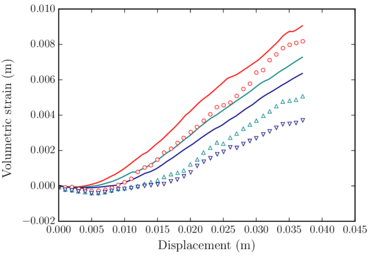
|
| (a) | (b) |
| Figure 110: Large-scale direct shear numerical results with the stress-dependent friction contact model and . | |
The results obtained with the numerical model for (see Figure 111) are very similar to the laboratory test results when the normal stress is , however, when the normal stress is higher, and , the shear stress and volumetric strain are overestimated.
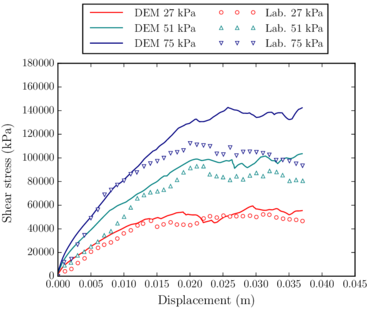
|
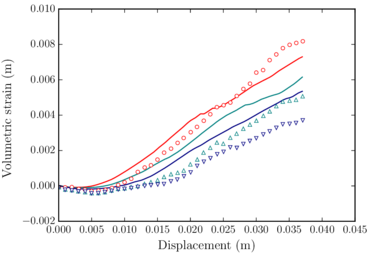
|
| (a) | (b) |
| Figure 111: Large-scale direct shear numerical results with the stress-dependent friction contact model and . | |
The best results are obtained with for the three different normal stresses. It should be mentioned that the volumetric strain is not as accurately captured as the shear stress. This may be explained based on the fact that the volumetric strain depends largely on the sample granulometry and particles arrangement, and may change for each case depending on the ballast used. Notwithstanding the error in the results, it is worth mentioning that the initial contraction and following dilation are captured with the numerical model.
In the case with the normal stress equal to the sear stress experiments a continuous increase when the lower box was moved more than . This behaviour, different from the reference test results, is not considered as an error of the numerical model due to the fact that the more the lower box is moved, the more the results depend on local phenomenon.
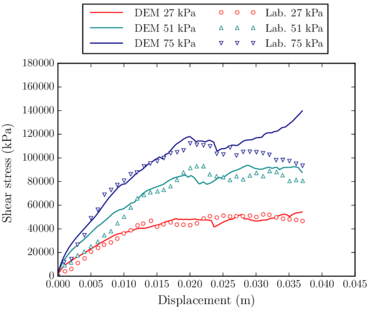
|
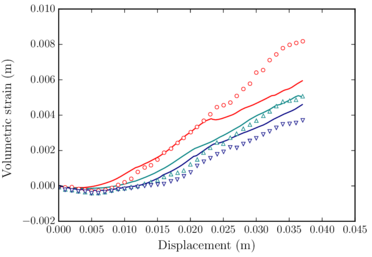
|
| (a) | (b) |
| Figure 112: Large-scale direct shear numerical results with the stress-dependent friction contact model and . | |
After calibrating the new parameter () used in the stress-dependent friction contact model, it should be checked that the angle of repose is still being computed correctly. This test is necessary in order to evaluate if the stress-dependent friction contact model works for non-confined groups of particles.
Ballast properties are the same used in the large scale shear test with , while the friction between particles and floor is set to as in the previous angle of repose tests (see Section 6.2.2). For clarity purposes, the material properties and calculation parameters used in this test are summarised in Table 19.
| Material properties | Calculation parameters | ||
| Density () | |||
| Poisson ratio | |||
| Young modulus () | |||
| Friction coefficient ballast | Time step () | ||
| Friction coefficient ballast-floor | Neighbour search frequency | ||
| Restitution coefficient | |||
| Critical contact stress () | |||
| parameter | |||
In Figure 113, it can be seen that the stress-dependent friction contact model with these material properties results in an angle of repose close to 40 degrees. This leads to the conclusion that railway ballast behaviour can be appropriately characterise with clusters of spheres and the new contact model proposed in this work.

|
| Figure 113: Angle of repose of a pile of ballast represented with sphere clusters and the stress-dependent friction contact model with . |
From all the above-mentioned regarding friction between clusters of spheres, it can be deduced that the Young modulus may affect the angle of repose when using this kind of particles. The reason is the difference in the indentation between overlapped spheres. So, with clusters of spheres, it is advisable to develop again the angle of repose test after calibrating all the parameters in the contact model.
6.4 Ballast layer lateral resistance
The possibility of lateral buckling occurrence in railroad tracks makes the assessment of the lateral resistance of the ballast layer essential. To that end, the laboratory test carried out by Zand and Moraal in 1997 [40] was reproduced numerically. The test consists of measuring the lateral resistance force of the ballast layer against the imposed motion of a sleeper embedded in it.
The large amount of particles involved in this tests makes the use of sphere cluster computationally infeasible, yielding to the necessity of using spherical particles. Thus, this test will allow to asses the potential of spherical particles with rolling friction for reproducing the behaviour of ballast in a railway track.
6.4.1 Reference test
Zand and Moraal [40] conducted a series of three-dimensional ballast resistance tests using a rail track panel. Those tests were performed in the Roads and Railways Research Laboratory of the Delft University of Technology (TU Delft).
![Laboratory test layout. Modified from Zand and Moraal [40].](/wd/images/thumb/d/d7/Draft_Samper_552093892-test-Ch6Fig20.png/252px-Draft_Samper_552093892-test-Ch6Fig20.png)
|
| Figure 114: Laboratory test layout. Modified from Zand and Moraal [40]. |
The tests consisted of a track panel with five prestressed concrete sleepers NS90 [132] inside a ballast bed (Figure 114). The sleepers mass, along with rails and fasteners, is about 360 kg each. Lateral load was applied to the track section by means of two diagonal rods connecting the hydraulic actuator (150 kN). Two connecting beams were welded between the rails to reinforce the track panel enabling a more uniform load application. The motion of the track panel was imposed and the opposing force was measured.
The laboratory tests were performed for different vertical loads. In this work, the test with the sleeper unloaded is used for calibrating the material parameters that should be imposed to reproduce railway ballast behaviour. Then, the numerical calculation of the loaded tests is carried out with the material properties already obtained in the calibration procedure. These calculations allow to evaluate if the particles confinement in real-scale tests influences the behaviour of the numerical model, determining if the use of spheres with rolling friction is an appropriate approach to reproduce railway ballast behaviour.
6.4.2 DE model
The geometry used in the calculations is the same as in the laboratory test, but for only one sleeper instead of five. The geometry of the computational model is shown in Figure 115.
|
| Figure 115: Geometry of the test for calculating ballast lateral resistance force against sleeper movement (distances in ). |
6.4.2.1 Pre-calculation
The initial distribution of spherical particles was already mentioned in Section 5.2.3, emphasizing its importance in calculations where a high particles compactness is required. In this regard, the gravitational packing technique is used aiming to obtain the desired material compactness. The procedure may be slightly different from the process followed in the pre-calculation of the large-scale direct shear test because in this case the void ratio is unknown. It is also worth mentioning that the special geometry of spheres makes the task of filling volumes compactly not straightforward.
Figure 116 shows the geometry of the pre-calculation. To perform properly the gravitational packing technique, a volume bigger than the original should be filled in with the sphere mesher, and the boundaries and sleeper have to be modified. Moreover, as for obtaining a high particles compaction the friction coefficient between particles and between particles and walls should be set to zero, auxiliary surfaces are required to maintain the slope of the embankment.
|
| Figure 116: Geometry of the pre-calculation, a bigger sleeper and auxiliary surfaces are used to maintain the geometry. |
Regarding the material parameters, the density and Poisson ratio chosen are the same as in the calculation of the angle of repose (see Section 6.2.1). For the Young modulus, a value , which allows the use of a time step , is applied. Material and computational parameters for the pre-calculation are summarised in Table 20.
| Ballast properties | Walls contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
Figure 117 shows the procedure followed during the pre-calculation. Firstly, the auxiliary surfaces move downwards pushing the granular material in order to maintain the desired geometry. After , the auxiliary top surfaces are in their final position and the granular material is let to move freely. Then, when time all the particles outside the domain are erased, and those inside it continue moving without restrains till they reach their equilibrium position at .

|

|
| (a) . | (b) . |

|

|
| (c) . | (d) . |
| Figure 117: Pre-calculation along time. | |
In a previous study [80] the lateral resistance force was evaluated without applying the gravitational packing technique; the mesh provided by the sphere mesher was used instead. The lateral resistance force, in that case, when the sleeper was moved was about one half of the value obtained in the laboratory.
6.4.2.2 Lateral resistance test numerical calculation
The particle arrangement at the end of the pre-calculation is the starting point of the lateral resistance test computational model. After developing the gravitational packing technique, the porosity of the ballast sample is (see Figure 118).
|
| Figure 118: Initial configuration for the ballast resistance numerical test. |
Regarding the boundary conditions, it should be noted that the friction between ballast and the boundary lateral walls is considered null to represent a continuous domain with mirrored particles. Hence, the results of the numerical model can be compared to those obtained in the experiment, where the lateral force was applied to 5 sleepers. The value of the friction coefficient between the ballast stones and the sleeper is taken from the reference study [40], where it was computed experimentally. As in the laboratory the ballast bed is placed over a concrete slab, the friction between ballast and the lower surface is the same as the friction between ballast and the concrete sleeper, being equal to .
The material properties and calculation parameters are defined in Table 21. The rolling friction coefficient is set to , based on the results of the angle of repose test (Section 6.2.1). It should be remembered that the rolling friction coefficient between ballast and walls is , as it was explained in Section 6.2.
In this test, the displacement of the sleeper embedded in a ballast sample is measured. This is similar to the case of the large scale direct shear test where the ballast sample strain was controlled, making the contact stiffness a key parameter. In this respect, four values of the Young modulus in the range suggested by Ahmed et al. [1] () for potential particles are proven. As it was already mentioned, the critical time step for the calculations depends on the material properties, so, a different time step should be used in each case.
Unlike the large scale direct shear test where the particles were sphere clusters, in this case the Young modulus is supposed to be between the values proposed by Ahmed et al. for potential particles due to the similarities between their contact mechanism and that of spherical particles (the Young modulus is lower for clusters due to the higher number of contacts due to spheres overlaps, see Section 6.3).
The sleeper and the boundary surfaces are considered completely rigid, they can not be deformed. However, the contact stiffness between ballast and those surfaces depends on their material properties (see equation 4.1). Concrete surfaces are characterised by a Young modulus and a Poisson ratio , while the properties of the boundary lateral walls are taken from the characteristics of the bulk ballast layer with a Young modulus and a Poisson ratio [133].
| Ballast properties | Concrete sleepers contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Lower wall contact properties | Lateral walls contact properties | ||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
6.4.3 Results
The sleeper velocity in the laboratory test is very low, leading to the need of calculating to move the sleeper only . In order to decrease the necessary computational time, the influence of changing the sleeper velocity is tested. To that end, the calculation where the ballast Young modulus is set to is performed with a sleeper velocity equal to (as in the laboratory test) and .
The results obtained with both sleeper velocities are shown in Figure 119. It can be seen that performing the calculation using a sleeper velocity times higher than in the laboratory test does not disturb the results significantly.
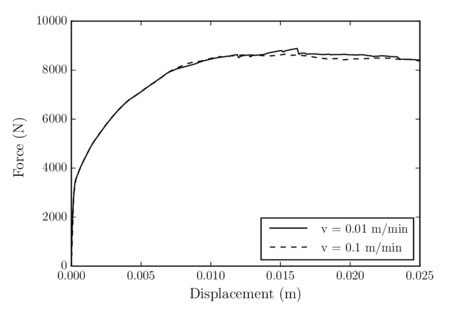
|
| Figure 119: Difference between the results obtained with a velocity of the sleeper equal to the laboratory test and times that velocity. |
From now on, the calculations of the lateral resistance of the ballast layer will be developed with a sleeper velocity , which will decrease the computational time of the calculations, due to the fact that their duration will be times lower.
Figure 120 presents the curves obtained for each value of the Young modulus, together with the experimental results. It can be observed that the results in the first loading stages for and are almost identical, and close to the experimental curve. For lower values of the Young modulus, the slope is also lower. The differences in terms of the maximum resistance force are less relevant, with certain erratic behaviour.
These results suggest that, for this test, the use of a Young modulus between and may be adequate. Since lower values allow for larger time steps and lower computational time, it is advantageous to use .
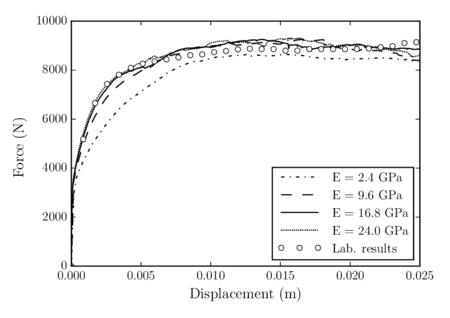
|
| Figure 120: Numerical results of the ballast resistance test for four different values of the Young modulus, and comparison to the experimental test. |
An interesting feature of the numerical methods is that they allow obtaining results difficult to measure in experimental facilities. Figure 121 illustrates the lateral force against sleeper displacement of each particle when the sleeper has been moved 5 mm, while Figure 122 presents the lateral displacement of every particle at the end of the calculation.
It is important to mention that, although this local results may be very useful for understanding the behaviour of the ballast sample, they should be analysed with caution, due to the use of a simplified geometry to represent the ballast particles. For the evaluation of the behaviour of each particle separately the advise is to use sphere clusters.

|
| Figure 121: Lateral force against sleeper displacement of each particle when the sleeper has been moved 5 mm. |
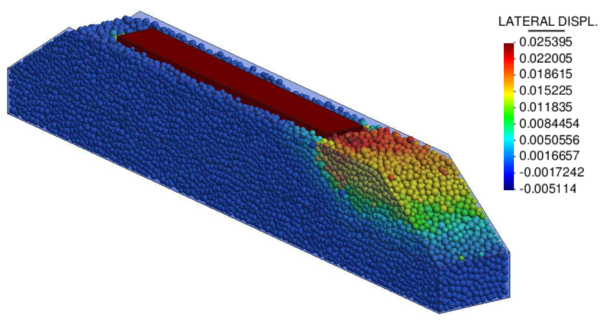
|
| Figure 122: Lateral displacement at the end of the calculation. |
The numerical code provides other possibilities. As an example, the percentage of the lateral resistance force exerted by the ballast sample against each face of the sleeper was computed. The results are shown in Figure 123. This information can be useful to optimise the geometry of the cross-section to, for example, evaluate if it is possible to decrease the amount of ballast used in the infrastructure or improve the sleepers geometry.
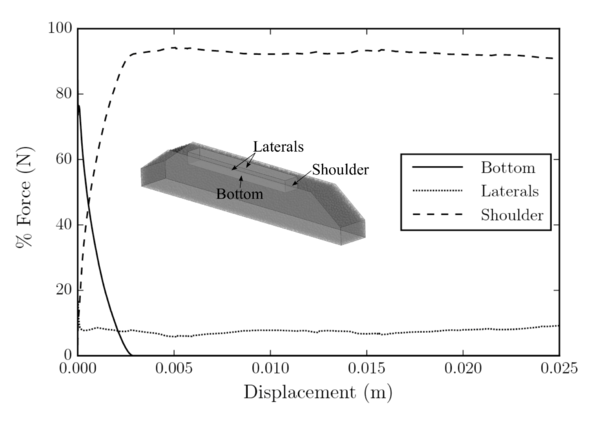
|
| Figure 123: Percentage of the lateral resistance force acting in each sleeper face. |
It can be seen that, at the first instants of the calculation, almost of the resisting force is due to the friction of the bottom face. However, that percentage decays sharply becoming negligible when the displacement is higher than , while it grows for the shoulder, whose influence in the lateral force is about a when the sleeper displacement is greater or equal to .
According to these results, if the lateral movement of the sleeper should be fully restrained, the most effective way to increase the lateral resistance would be to augment the roughness of the bottom face of the sleeper. On the other hand, if lateral displacements greater than were allowed, the geometry of the shoulder should be optimised. It should be remembered that this results are for the unloaded case; the following calculations will be developed for loaded cases, where this percentages would change significantly.
6.4.4 Loaded sleeper
Zand and Moraal also developed tests with loaded scenarios. The variable vertical load was put on the rails by placing concrete slabs (weighing each) over the rails.
In this work, loads equal to , , , , , and were applied. Then, the relation between the peak lateral force and the vertical load is evaluated.
In the reference study, the equation relating the peak lateral force and the vertical load is
|
|
(6.10) |
while the equation obtained with the numerical code is
|
|
(6.11) |
Figure 124 shows the trend line obtained from the laboratory tests developed by Zand and Moraal, and the maximum lateral force for each vertical load obtained with the DEM code.
It can be seen that the numerical and experimental results are very similar. In both cases there is a linear relation between the peak lateral force and the vertical load, with a slope almost proportional to the friction coefficient between ballast stones and the sleepers. The difference in the slope of the trend line between laboratory and numerical results is . The error in the maximum lateral resistance force does not exceed a value of in any of the cases. Taking into account that the force-displacement curve is not totally smooth, having some peaks due to sudden lateral forces from new contacts, and that the laboratory results are obtained from the normalised trend line (not the exact results for each scenario) the outcome from the numerical model can be considered accurate enough.
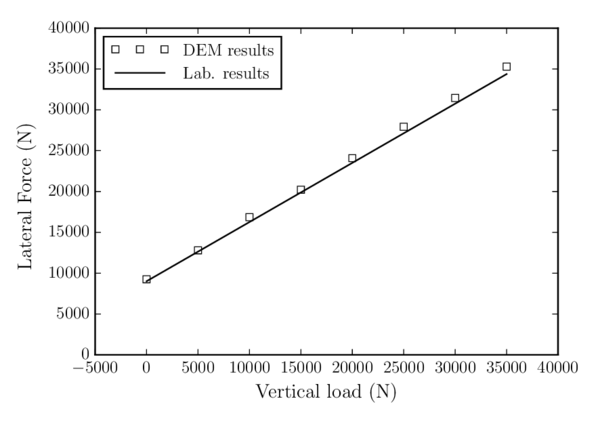
|
| Figure 124: Comparison of the maximum vertical force between the laboratory tests and the DEM calculations. |
As it was previously commented, the resistant force applied over each part of the sleeper would depend on the vertical load. Figure 125 shows the percentage of lateral resistance force exerted on each part of the sleeper for the different vertical loads.
From the results, it can be observed that the higher is the vertical load, the more influence has the friction of the sleeper bottom part with the ballast layer. Taking this into account, the conclusion addressed is that, to improve the lateral resistance of a ballasted track when the train is passing through it, the friction with the sleeper should be increased, weather changing the geometry of the bottom part of the sleeper or its material. On the other hand, if the lateral resistance force has to be increased when the track is unloaded, the geometry of the shoulder of the ballast layer should be improved, because in that scenario the shoulder is the most resisting part. When the train is not passing, lateral resistance is also important due to changes in the rail geometry that may be caused by sudden changes in the temperature.
The most optimised railway track design to support lateral forces may depend on the track section, if it is a straight or curved, and also on the location due to weather actions.
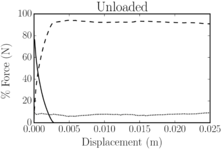
|
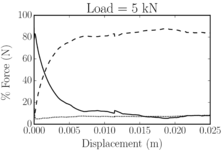
|
| (a) | (b) |
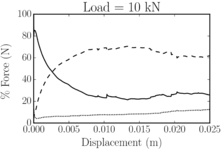
|
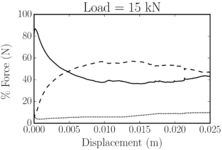
|
| (c) | (d) |
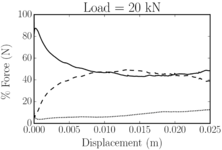
|
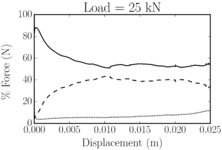
|
| (e) | (f) |
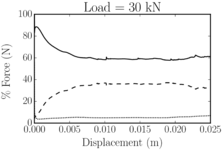
|
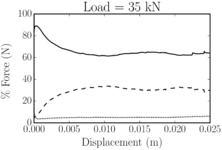
|
| (g) | (h) |
| Figure 125: Lateral resistance force over each part of the sleeper for the different vertical loads. | |
6.4.5 Variation in the ballast layer thickness
One of the main problems that appeared with the increase of train speed is, the so-called, ballast flight. Although the traditional ballasted track was found to be a good solution, the high-speed air fluxes generated by the train, passing at certain velocity, can cause movement of ballast particles. Those particles can hit the underbody of the train, they can be crushed by the wheels against the rail (damaging both elements) or they can be projected laterally outside the railway track. If those stones bounce off causing the release of other particles they could generate a phenomenon called ballast clouds.
A possible solution to this problem is to reduce the thickness of the ballast bed, in order to increase the space between train and ballast, that will lead to the decrease of the air speed fluxes. This solution leaves the sleeper slightly uncovered, which can cause new problems like excessive settlements and horizontal displacements in some sections.
A calculation decreasing the ballast level was carried out to compare its influence in the lateral resistance force. Figure 126 shows the initial geometry of the ballast layer of the original calculation and the new calculation with less ballast. Obviously, the geometries were obtained after a pre-calculation following the gravitational packing technique procedure. The porosity of the sample after the pre-calculation was

|

|
| (a) Original geometry. | (b) low. |
| Figure 126: Front view of the two calculations developed varying the ballast layer thickness. | |
The graph shown in Figure 127 displays the lateral resistance force for the different thickness of the ballast layer. It can be realised that decreasing the thickness of the ballast layer diminish the lateral resistance capacity about a for an unloaded sleeper.
Decreasing the amount of ballast, without making any other change in the track would be dangerous, at least, regarding lateral resistance in unloaded tracks. This could, for example, lead to lateral buckling due to sudden temperature changes.
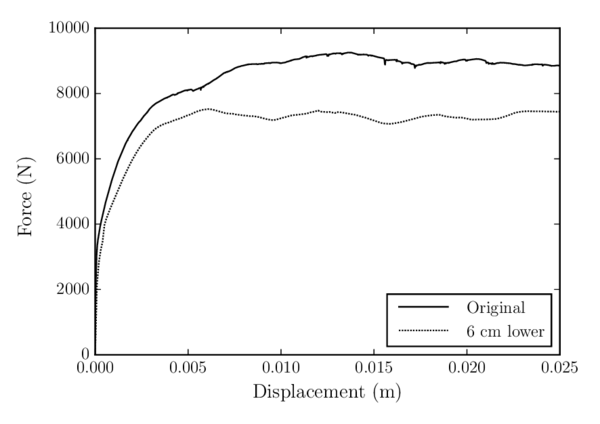
|
| Figure 127: Lateral resistance of the ballast layer for different ballast bed thickness. |
6.5 Concluding remarks
The results of this section show that, although clusters of spheres allow better representation of the actual geometry of ballast stones, it is possible to obtain accurate results with spherical particles when studying real-scale cases. Since the use of clusters implies a very important increase in computational cost, it seems advisable to use spheres when studying the macro behaviour of the ballast layer. On the other hand, for small-scale tests involving highly compacted particles, the use of clusters may be essential due to the fact that their results are greatly influenced by particles and contacts distribution.
In addition, clusters introduce a geometric roughness that is difficult to characterize. The recommendation is to use them only when microscopic results, such as the distribution of contacts, have to be evaluated.
Considering this, the following calculations representing a train passing through a ballasted track section involving sleepers will be developed using spherical particles.
7 Full scale railway track test under dynamic loads
Once the calibration and validation of the numerical model were carried out, some real-scale calculations are developed. The aim is to evaluate the behaviour of a straight section of a ballast layer comprising sleepers under the loads exerted by a high speed train, considering different conditions: a) a conventional ballast layer properly compacted, b) a poorly compacted ballast and c) an eroded layer.
The vertical force is analytically imposed considering how the rails distribute the train loads over the sleepers. Before performing the calculations, the way to introduce the loads has to be carefully analysed, due to the fact that the rail and bearing plate are not being represented in the numerical computation. The detailed consideration of the rail and bearing plate together with the sleepers and ballast layer will be a very interesting improvement for the future.
7.1 Railway track. Vertical stiffness and application of vertical loads
The mechanical behaviour of a ballast track affected by vertical loads can be defined using several parameters:
- Track stiffness () characterizes the track globally. It is the ratio between the applied load by a wheel () in a point of the rail and its settlement ()
|
|
(7.1) |
Considering that the load is applied in the origin of the coordinates system and that the train is travelling in the axis direction, the settlement can be computed using the equation proposed by Zimmermann, based on Winkler's theory [134].
|
|
(7.2) |
where represents the elastic length of the track which is a function of and the bending stiffness () of the rail
|
|
(7.3) |
Figure 128 presents the settlement bulb calculated from equation 7.2. It can be observed that the length of the path affected by the load on each side depends on the parameter .
![Typical settlement bulb, obtained from equation 7.2. Source: Cuéllar [135].](/wd/images/thumb/2/2a/Draft_Samper_552093892-test-Ch7Fig1.png/360px-Draft_Samper_552093892-test-Ch7Fig1.png)
|
| Figure 128: Typical settlement bulb, obtained from equation 7.2. Source: Cuéllar [135]. |
- Track modulus () is a parameter that, multiplied by the rail settlement at any point, provides the unit reaction of the track ()
|
|
(7.4) |
can be computed from and the bending stiffness of the rail as
|
|
(7.5) |
From , the percentage of the load that is transmitted to each sleeper can be obtained immediately, integrating the unit reactions along the length of the track influenced by each sleeper. The load transmitted by the rails to the sleeper is calculated as
|
|
(7.6) |
where is the distance between the centre of two sleepers.
- The whole track stiffness can also be characterised by the ballast coefficient (). It is the ratio between the track modulus and the so-called equivalent width () [135]. For a long time, the ballast coefficient was used for defining the quality of the track, however, in recent times the track stiffness parameter became more relevant.
- Bearing stiffness () relates the load over each sleeper, denoted , with their settlement
|
|
(7.7) |
From equations 7.1 and 7.7, the ratio of the load applied to a sleeper located a distance to the train wheel can be derived:
|
|
(7.8) |
The rail settlement at any point can be decomposed considering the contributions provided by each of the supporting elements: bearing plate (), ballast (), subballast () and platform (). Assuming that the subballast is part of the platform, the rail settlement can be expressed as:
|
|
(7.9) |
And the stiffness of each element can be computed as:
|
|
(7.10) |
Finally, the bearing stiffness can be expressed as a function of the stiffness of each constituent element as:
|
|
(7.11) |
From equation 7.2, it can be concluded that the temporal history of the track settlements produced on a sleeper by a vertical load that passes trough a point located at a distance at with a velocity , is given by the following expression:
|
|
(7.12) |
From 7.8 (considering the temporal history) and 7.12, the following expression for the load over a sleeper can be derived
|
|
(7.13) |
In the numerical calculations, this analytical equation would be used to introduce the vertical loads over the sleepers.
7.2 Numerical model
In this section, the behaviour of a railway track section under different scenarios is evaluated. Figure 129 shows the geometry of the track.

|
| Figure 129: Railway track section. Dimensions in . |
Aiming to decrease the necessary computational time, the symmetry of the geometry is considered. Taking advantage of it, one half of the computational domain can be discarded.
In this case, a pre-calculation should also be developed, just like in the lateral resistance test, in order to obtain a ballast compactness similar to the one that can be found in typical railway tracks. The geometry of the pre-calculation is presented in Figure 130a, while the particles arrangement after developing the pre-calculation is displayed in Figure 130b. At that moment, the porosity of the ballast sample is .
The material and calculation parameters are those summarised in Table 20 for the pre-calculation of the lateral resistance force test. As in that case, the boundaries and sleeper have to be modified and auxiliary surfaces are required to maintain the slope of the embankment, due to the fact that the friction between particles and between particles and walls is set to zero.
Before developing the calculations of the train passing through the railway track, the vertical stiffness should be checked. The reason is that the subballast and platform are represented as a rigid surface and not as two deformable layers. In the numerical model, the deformation of those two layers will be concentrated on the point of contact between the ballast particles located at the bottom and the lower rigid surface.
7.2.1 Vertical stiffness
The material properties of railway ballast represented with spheres are known from previous tests displayed in Chapter 6. However, the lower boundary contour in those cases was almost rigid and practically all the deformation occurred in the granular material. Meanwhile, now, it is assumed that under the ballast there are deformable granular layers.
To calibrate the contact stiffness between ballast particles and the bottom surface, three different values of the Young modulus are evaluated .
is the typical value of the Young modulus for characterizing subballast layers [133]. Then, two lower Young modulus () are chosen due to the fact that here the whole deformation of the subballast layer and platform is going to be concentrated in the ballast-surface contact points, so, the Young modulus is not supposed to be larger than the reference one.
The Poisson ratio is set to and the friction coefficient to , taken from the literature [133]. The remaining parameters are equal to those employed in the lateral resistance test (all of them are summarised in Table 22).
| Ballast properties | Concrete sleepers contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Lower wall contact properties | Lateral walls contact properties | ||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
A numerical calculation for each value of the Young modulus is developed. In those calculations a vertical load that goes from to in is applied on the sleepers and . The aim is to measure the stiffness of the ballast, subballast and platform assembly. It should be recalled that, as the sleepers considered are one half of the real ones, the vertical load applied on them is also one half.
The load is applied on two sleepers following the advice of Fonseca [136], who recommended to measure the vertical stiffness in two points of the track due to the variability among the ballast layer properties. After computing the stiffness in sleepers and , the mean value is calculated.
The graphs in Figures 131 and 132 show the vertical displacement of sleepers and as a function of the vertical load imposed over each one for and respectively. The solid line is the mean value of the force-displacement curve of both sleepers.
The slope of the solid line corresponds to the vertical stiffness of the ballast, subballast and platform assembly , being
|
|
(7.14) |
The typical value of for high-speed train lines is between and [28]. yields a value of which lies outside the range. On the other hand, implies a stiffness which is greater than and lower than .
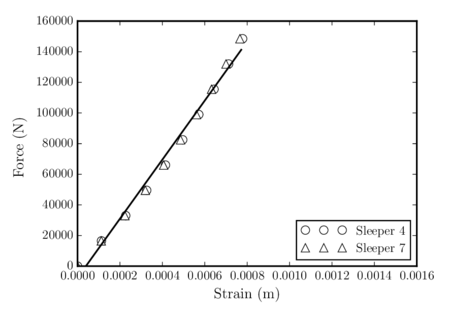
|
| Figure 131: Vertical force against vertical displacement of sleepers and with a lower boundary with . |
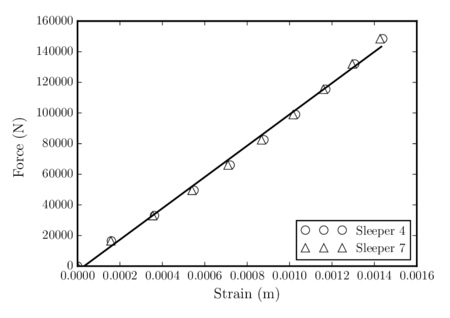
|
| Figure 132: Vertical force against vertical displacement of sleepers and with a lower boundary with . |
The results for are not displayed because the contact stiffness is too low, leading to indentations greater than the particles radius and causing the numerical calculation to fail.
7.2.2 Test case 1. Conventional track
The train chosen for the numerical calculations is an AVE Series 100 [137], whose geometry is sketched in Figure 133. It passes through the railway track section shown in Figure 129 with a velocity equal to .

|
| Figure 133: Geometry of the train passing over the railway track. Dimensions in . |
As it was mentioned in Section 7.1, there exist several parameters that should be set, in order to correctly apply vertical forces. Going over equation 7.13, it can be concluded that the overall track stiffness (), the bearing stiffness () and the elastic length () should be determined.
López Pita et al. [28] stated that, for optimizing maintenance and energy dissipation costs, the overall track stiffness should be between and , consequently, a value of was chosen. In the same study, López Pita et al. suggested to use bearing plates with a stiffness between and . Following their advice a value of was selected, which leads, applying equation 7.11, to a value for the bearing stiffness . Regarding the elastic length, it should be mentioned that the bending stiffness of a rail used to be about [135]. For that value and using equation 7.3, yields .
From equation 7.13, the load from axle over sleeper would be:
|
|
(7.15) |
According to the train specifications [137], the load per axle is . The velocity of the train is (almost ). Finally, equation 7.15 reads:
|
|
(7.16) |
where is the initial distance from the axle to the sleeper .
The weight of the sleeper and rails () should be added to the vertical load exerted by each axle of the bogie over each sleeper.
The calculation was designed so that the train passes over the first sleeper at time . In other words, the distance from the first axle of the train to the first sleeper is when the calculation starts.
As in the calculation of the vertical stiffness, the symmetry of the track is taken into account. The geometry of the numerical model is the same shown in Figure 130b and the load of each axle is divided by two. Due to the symmetry simplification, the lateral displacement of the sleepers is totally restrained.
Table 23 summarises the material properties and calculation parameters. These values are used also in the next two calculations.
| Ballast properties | Concrete sleepers contact properties | ||
| Density () | |||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Lower wall contact properties | Lateral walls contact properties | ||
| Poisson ratio | Poisson ratio | ||
| Young modulus () | Young modulus () | ||
| Friction coefficient | Friction coefficient | ||
| Restitution coefficient | Restitution coefficient | ||
| Rolling friction coefficient | Rolling friction coefficient | ||
| Calculation parameters | |||
| Time step () | |||
| Neighbour search frequency | |||
The following two Figures show results from the numerical model at time , when the axles of the second bogie are almost over the sleepers and .
Figure 134 shows the velocity of the ballast stones. It can be seen that the most affected particles are those surrounding the sleepers under the axles and the maximum velocity of those particles is about . It can also be seen that the particles all along the thickness of the ballast layer are affected by the train disturbance, but the lower the particles are, the less they move.
Meanwhile, Figure 135 displays the force exerted by each ballast stone over the sleepers, also at time . It can be seen that the maximum force does not exceed .
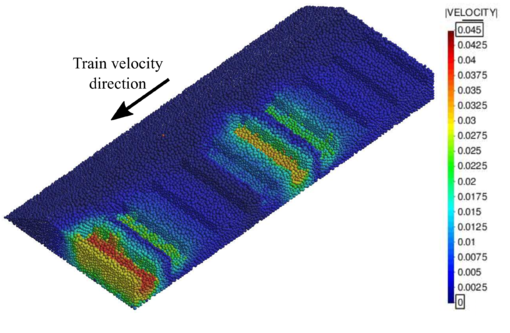
|
| Figure 134: Velocity of the ballast stones for the case of a compacted ballast railway track at time (results in ). |
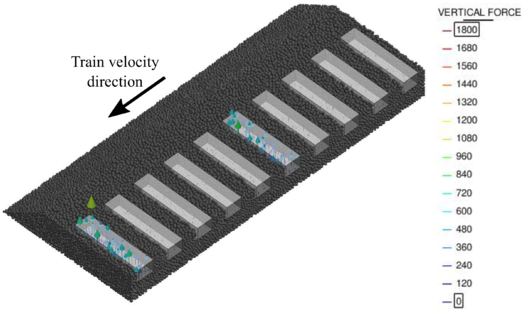
|
| Figure 135: Force exerted by each ballast stone against sleeper movement in the vertical direction for the case of a compacted ballast railway track at time (results in ). |
As it was already mentioned in Chapter 6, results involving the distribution of contacts should be analysed with caution. In this case, as the calculation is developed using spheres to represent irregular ballast stones, the number of contacts is lower than in the real case, and consequently their magnitude is higher. On the other hand, it should be noted that, these results are very useful for understanding the ballast layer behaviour and to compare different scenarios. Moreover, the numerical model yields results that cannot be directly measured in the ballast track or in the laboratory.
The vertical displacement of each sleeper over time is presented in graphs of Figure 138. It can be seen that the settlement of sleeper occurs slightly before the settlement of sleeper and so on. The time lag is , equal to the distance between sleepers divided by the train velocity. It can also be noted that, although the vertical movement of each sleeper is similar for all of them, there are little differences because the vertical stiffness is not exactly the same along all the track. Another interesting feature to point out is that, as this is the first train passing over this track, the sleepers were still settling, and when the first axles pass through the sleepers, they do not return to the initial position.
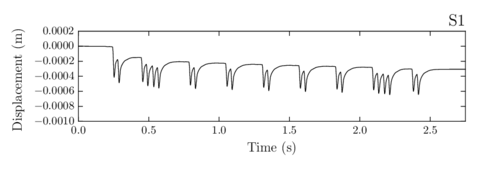
|
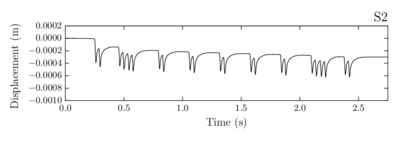
|
| (a) | (b) |
| Figure 136 | |
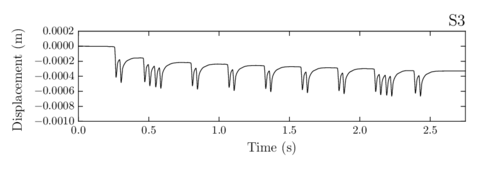
|
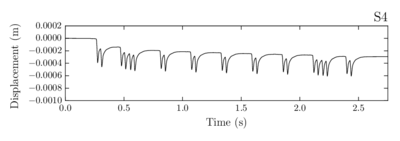
|
| (a) | (b) |
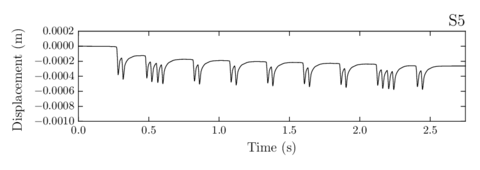
|
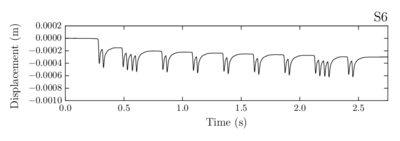
|
| (c) | (d) |
| Figure 137 | |
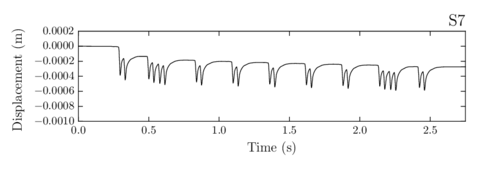
|
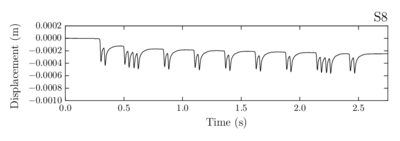
|
| (a) | (b) |
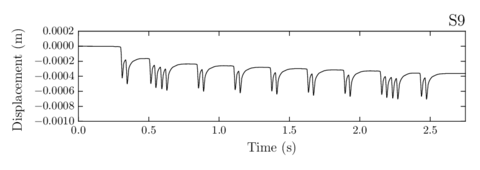
|
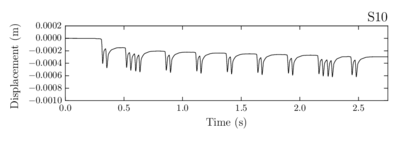
|
| (c) | (d) |
| Figure 138: Displacement of the sleepers (from to ) during the train passage. | |
7.2.3 Test case 2. Poorly compacte ballast
The calculation of a train passing through a bumpy track is explained in the following paragraphs. The train is the same AVE Series 100 presented before in Figure 133. The bumpy track is represented by an area with low compacted ballast. Figure 139 illustrates the part of the track with ballast loosely compacted.

|
| Figure 139: Geometry of the bumpy track used in the numerical calculation. Dimensions in . |
To generate the bump section, the gravitational packing technique assigning a different friction coefficient is used. As in previous cases, in the pre-calculation, the friction between ballast stones in the compacted part is set to zero. However, in this specific case the friction coefficient between particles inside the bump section is . After this procedure, the porosity in the central part of the geometry is , forming the desired bump, while in the other parts of the track the porosity is .
In order to reduce the computational time, the symmetry of the geometry is taken into account again. The material and calculation parameters presented in Table 23 are applied.
This calculation may allow to evaluate the influence of the granulometry and the amount of ballast for maintaining the track geometry in the vertical plane.
The settlement of the sleepers when the train passes through the section with less ballast can significantly affect the train behaviour. The larger this settlement is, the more vibrations will produce in the wagons, being uncomfortable and even insecure for the passengers [35].
Figures 140 and 141 are presented to be compared with Figures 134 and 135, respectively. They show the results obtained with the numerical model at time .
In Figure 140 the dark red particles move faster than . Comparing this with Figure 134, it can be seen that the particles under sleeper , where the ballast is loosely compacted, move faster than in the previous calculation. On the other hand, particles surrounding sleeper behave similar in both cases, as it was expected.
The vertical forces exerted by the ballast particles to the sleepers are shown in Figure 141. Although the contact distribution is not the same as in the reality due to the difference between real and computational particles geometry, Figure 141 and Figure 135 can be compared to understand how the ballast layer behaves in each case. It is found that the force applied by each particle against sleeper movement is higher when the ballast is loosely compacted, being the sleeper in contact with less particles.
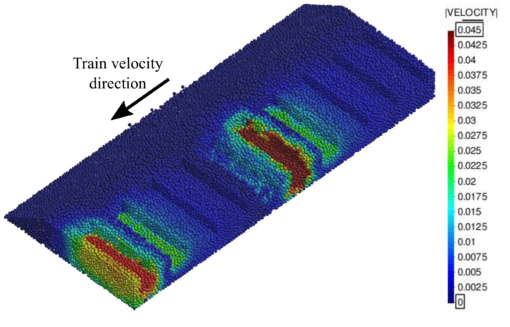
|
| Figure 140: Velocity of the ballast stones for the case of a bumpy ballast railway track at time (results in ). |
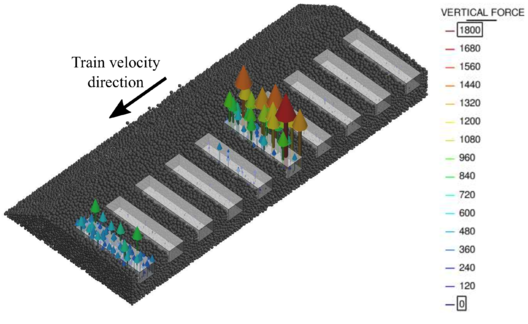
|
| Figure 141: Force exerted by each ballast stone against sleeper movement in the vertical direction for the case of a bumpy ballast railway track at time (). |
In the graphs of Figure 145, a larger settlement on sleepers and can be clearly seen. With a poorly compacted ballast layer, the sleepers move down almost , while, when the ballast is compacted, the sleepers only move down about .
The other sleepers (from to and from to ) behave similarly to the previous case where all the ballast layer is adequately compacted.
|
| Figure 142 |
|
|
| (a) | (b) |
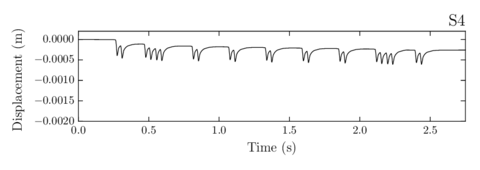
|
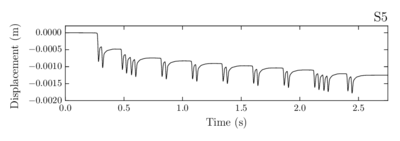
|
| (c) | (d) |
| Figure 143 | |
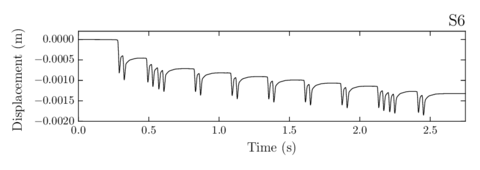
|
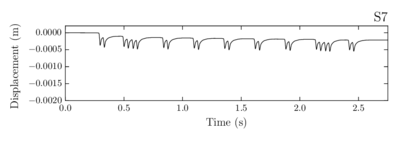
|
| (a) | (b) |
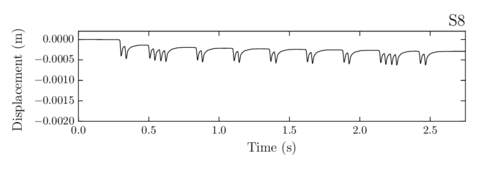
|
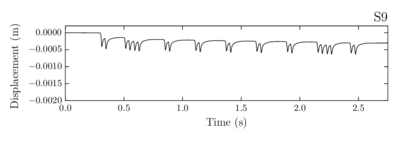
|
| (c) | (d) |
| Figure 144 | |
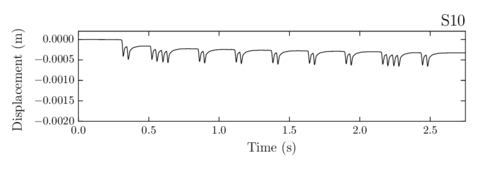
|
| (a) |
| Figure 145: Displacement of the sleepers (from to ) during the train passage through the bumpy track. |
7.2.4 Test case 3. Eroded ballast layer
The following paragraphs introduce the computation of a train passing through a straight railway track section eroded laterally. Figure 146 shows the geometry of the railway track which is similar to the one used previously, but for the erosion in the right embankment.

|
| Figure 146: Geometry of the eroded track used in the numerical calculation for test case 3. |
The aim of this calculation is to evaluate if the lateral erosion of the ballast layer affects significantly the vertical stiffness of the track.
As in the previous cases, the material and calculation parameters used are those presented in Table 23. However, in this case, the entire domain must be considered, since it is not symmetric. Therefore, the entire load of each axle should be applied over the sleepers.
In this example, two different pre-calculations should be developed. The first one is performed based on the classical gravitational packing technique. However, the eroded part can not be generated in this way due to the fact that the geometry of the embankment is unknown and the friction between particles is zero, which would lead to an excessive movement of the particles as the geometry of the eroded embankment can not be controlled by auxiliary boundaries. To correct this, the second pre-calculation is developed, assigning the actual properties to the ballast material and eliminating part of the lower boundary surface to let the particles fall down through it and arrange freely.
Figure 147 shows the particles arrangement after developing the first and the second pre-calculations.

|

|
| (a) Pre-calculation 1. | (b) Pre-calculation 2. |
| Figure 147: Particles arrangement after both pre-calculations. | |
Figures 148 and 149 present the results obtained with the numerical model at time . It is the same moment as in Figures 134 and 135, aiming to compare the eroded and not eroded track behaviour.
From those Figures, it can be concluded that the lateral erosion of the track does not affect significantly its vertical stiffness, being the velocity of the particles and the contact forces near the sleepers where the axle force is applied similar in both cases.
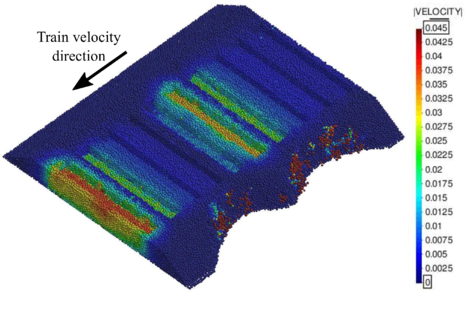
|
| Figure 148: Velocity of the ballast stones for the case of a eroded ballast railway track at time (results in ). |
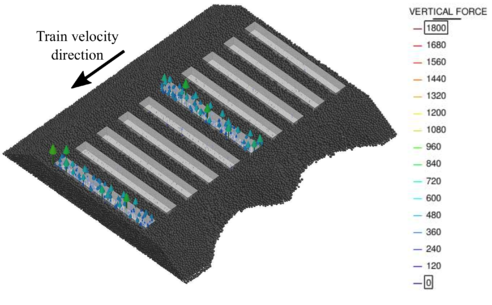
|
| Figure 149: Force exerted by each ballast stone against sleeper movement in the vertical direction for the case of a eroded ballast railway track at time (). |
The idea of the low influence in the vertical stiffness of the lateral erosion is reinforced comparing the graphs in Figure 152 with those in Figure 138. In both models the maximum vertical displacement of the sleepers is about . Although some different behaviour in sleepers and , where the track is more eroded, was expected, it can be appreciated that their performance is analogous to the other sleepers.
One interesting thing to notice from Figure 148 is that the stones in the eroded embankment are moving due to their unstable position and the forces exerted by the train. This behaviour suggests that, although the lateral erosion of the ballast layer does not affect significantly the vertical stiffness, the damage would be increased rapidly with the passage of the trains leading to future problems in the infrastructure.
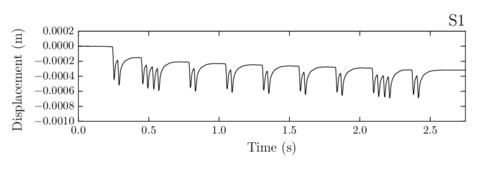
|
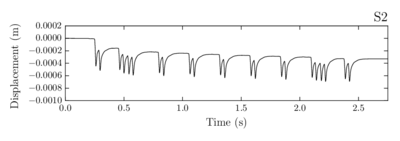
|
| (a) | (b) |
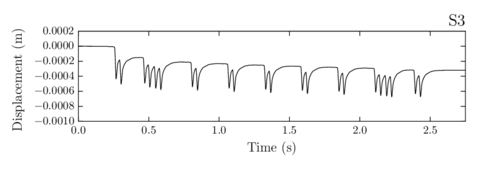
| |
| (c) | |
| Figure 150 | |
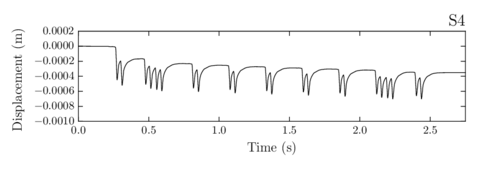
|
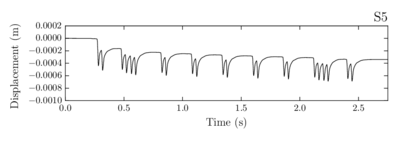
|
| (a) | (b) |
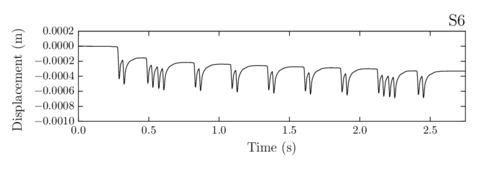
|
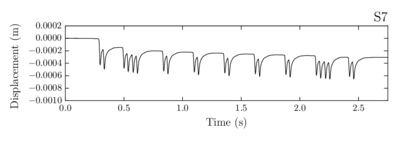
|
| (c) | (d) |
| Figure 151 | |
|
|
| (a) | (b) |
| |
| (c) | |
| Figure 152: Displacement of the sleepers (from to ) during the train passage through the laterally eroded track. | |
8 Conclusions and future work
In this Chapter all the achievements of the thesis are commented emphasising the conclusions drawn. The future lines of research are also presented.
8.1 Summary, achievements and conclusions
Due to new challenges in the railway industry, such as the development of high-speed trains and the construction of train lines in locations with extreme weather, the development of a numerical tool able to reproduce ballast behaviour appeared to be essential. For this reason, the implementation of a numerical code to represent ballast behaviour, including its interaction with other structures, has become the main goal of this thesis. After a bibliographic review, presented in Chapter 1, the most appropriate numerical method to achieve this objective was found to be the Discrete Element Method (DEM).
Chapter 2 presents a brief introduction of railway infrastructures, highlighting railway ballast and sleepers main characteristics and the standards that they should meet, while Chapter 3 analyses the available DEM code called DEMPack. This review led to identify the weaknesses of the available numerical code in order to properly reproduce railway ballast behaviour. The needed improvements are: the development of a method able to find and characterise contacts between DE particles and planar surfaces (typically used to define the boundaries) and the identification of a geometrical approach for DEs which allows the emulation of such irregular particles as ballast stones.
Then, when the numerical code was found convenient for reproducing railway ballast behaviour, some calibration and validation tests were carried out. The thesis finishes with some calculations of a train passing through three different railway track sections.
8.1.1 Contact detection between DE particles and boundary surfaces
Chapter 4 presents a new contact detection algorithm, the so-called Double Hierarchy Method (). The method is based on characterising the contact between spherical DEs and boundary surfaces discretised with a FE-like mesh. Besides being accurate, robust and efficient, the method was developed to perform well in extreme cases, where DEs and FEs sizes are different or where the relative indentation between them can be considerably high. This method can be used with different types of planar geometries providing a high level of accuracy in terms of contact force continuity in transitions. The method also allows multi-contact scenarios with high mesh independence and low effort. It was designed to make it easy to implement and adapt it to an existing DEM code. In addition, the algorithm was conceived to be fully parallelisable, something essential in order to allow the calculation of real cases with a great amount of discrete and finite elements.
Within the method, contact calculation is split into two stages: Global Neighbour Search and Local Contact Resolution, where the Double Hierarchy takes place in order to accurately calculate the contact characteristics and to remove invalid contacts.
The accuracy and robustness of the proposed algorithm was verified carrying out different benchmark tests representing critical situations (where most of the literature methods would fail). The results obtained were satisfactory.
The limitations for the use of this method were clearly defined and analysed. First, any geometry can be used for the contact elements (triangle, quadrilateral, polygon) only if they are convex. In second place it was highlighted that this method is upgradable to work with deformable FEs, but only under certain conditions. Finally it was appointed that the method works perfectly for calculating the normal force with surfaces that present a convex transition, however, when dealing with concave transitions between surfaces that form small angles it may present some discontinuities. Also, in sliding situations across different elements with non small indentations, some error in the continuity of tangential contact forces can arise. The error introduced in these cases, which is most of the times negligible for practical cases, was quantified in Section 4.4.
Notwithstanding those limitations, the proposed algorithm can be used in a wide range of DE/FE simulations.
8.1.2 Particles geometry
In Chapter 5, different approaches for representing granular materials geometry were analysed: spheres with rolling friction, sphere clusters, superquadrics, polyhedra, spheropolyhedra and potential particles. From those geometry types, spheres with rolling friction and sphere clusters were chosen. The main reasons to use spheres with rolling friction is their simplicity and lower computational requirements. Talking about clusters of spheres, the main advantages are that their calculation is based on an extension of the spherical particles algorithms (yielding to an efficient contact calculation) and their versatility in terms of particle shape. Within the sphere clusters approach, angularities and concavities can be naturally included, which may be useful for representing railway ballast stones.
The computation of the rolling friction for spherical DE particles was carried out using a new model called the Bounded Rolling Friction (BROF). This model provides similar results than the previous rolling friction models in dynamic situations. Its fundamental improvement is that it includes a limitation to the angular velocity in order to avoid undesirable sphere rotation when the particle is almost at rest (static situations). The BROF model was compared with previous rolling friction models, concluding that the results were accurate, with only one parameter () to be calibrated. BROF model sensitivity to changes in was also checked. It can be concluded that the BROF model outperforms previous approaches for modelling irregular particle shapes with spherical DEs.
When working with clusters of spheres, it was realised that the integration of the rotation with the same first and second order schemes used for integrating the translation along time, lead to inaccuracies. This results from the high complexity of the rotational equations involved. A typical direct explicit integration scheme for integrating the rotation was compared with other two high order integration schemes: a order Runge-Kutta scheme developed by Munjiza et al. [112] and a scheme based on the numerical integration of unit quaternions firstly presented by Zhao and van Wachem [114].
The benchmarks used to evaluate the performance of the rotation integration methods are extreme cases for particles rotating rapidly and to which large moments are applied. In those benchmarks, the direct explicit integration scheme results yield high errors, so, it was concluded that a higher order integration scheme should be used for rotational motion. The order Runge-Kutta scheme and the scheme based on the numerical integration of unit quaternions provided both accurate results, however, the method based on the numerical integration of unit quaternions performs slightly better. Moreover, it is the less computational demanding method.
For both, spherical particles and clusters of spheres, there exist algorithms that automatically generate groups of particles with the desired granulometry in an specific volume. However, it was found that those methods can not create groups of particles compacted enough to reproduce railway ballast on its working conditions. To solve this, several dynamic methods based on developing a pre-calculation to compact the sample can be used. The most popular one is the gravitational packing technique which consist of assign a zero friction coefficient to the particles and let them arrange freely in the most compacted way. Other methods that used moving boundary walls to pack the granular material were found useful too.
8.1.3 Ballast representation within the DEM
Regardless the geometrical approach used to represent railway ballast particles, calibration is needed to determine some material properties.
When using spherical particles with rolling friction, most of the material properties are known, but not the rolling friction coefficient. To calibrate the value of this parameter, the angle of repose test was found to be an easy and efficient procedure. In case of using clusters of spheres, the evaluation of the angle of repose appeared to be useful in order to assess the correctness of the particles geometry. The only problem of this angle of repose test is that it can not be adopted to determine the particle stiffness.
The material stiffness is unknown because, within the Hertz contact model, the contact force depends also on the contacting volume, which is larger for idealised spherical particles than for rough real stones (this fact is graphically explained in Figure 95). Particles stiffness has to be calibrated with other tests that should imply stress-strain or force-displacement measurements.
Two different laboratory tests were performed numerically in order to calibrate both, clusters of spheres and spheres with rolling friction material properties: large-scale direct shear test and lateral resistance of a ballast layer.
Due to the high dependence of the large-scale direct shear test on the number and distribution of contacts, it should be performed with sphere clusters and not with spherical particles. This test was found to be accurate in the calibration of the Young modulus of sphere clusters. In addition, other interesting feature of this large-scale direct shear test is that it was performed with particles under different confinement pressures. Clusters of spheres introduce artificial geometric friction due to the concavities of the overlapped spheres. This means that the accuracy of the results, with the classical Hertz contact model, depends on the particles confinement. To solve this, a new contact model was developed. The friction coefficient in this new model depends on the stress of each contact and it implies the calibration of a new parameter . After some trial tests, an appropriate value for was found and the accuracy of the results became independent of the particles confinement. The new model was called stress-dependent friction contact model.
Spherical particles with the BROF model were used to reproduce an experimental test on the lateral resistance of ballast against a sleeper with imposed motion. It was concluded that spherical particles have to be used for this kind of real scale tests, due to computational time issues. After calibrating the particles Young modulus (contact stiffness), the initial stiffness of the force-displacement curve was correctly reproduced for the case of an unloaded sleeper and the maximum force was captured with an error lower than the . Then, more calculations with loaded sleepers were carried out, obtaining accurate results. DEM also allows detailed analyses of the system response, which are often difficult to carry out in laboratory. In the calculation presented, the evolution of the relative influence in the resistant force of each part of the ballast layer was identified. Finally, the code was used to assess how was the lateral resistance force affected by the decrease of the ballast level , a solution applied in the high-speed train line Madrid-Valencia aiming to minimise the appearance of ballast flight. The results obtained lead to the conclusion that lowering the ballast level , the lateral resistance for unloaded sleepers decreases about a , which may be dangerous.
Local results impossible to measure in the laboratory, such as particles velocity or contact forces, can be obtained with the numerical model, however, this results should be previously examine with caution before addressing conclusions. The reason is that the simplification in the geometry of the particles can reproduce accurately the macroscopic performance of the bulk material, but not the isolated behaviour of a simple grain.
8.1.4 Numerical model of a train passing through different ballasted track sections
As it was mentioned before, the development of real scale calculations should be carried out with spheres with rolling friction, aiming to reduce the necessary computational time. For that reason, the calculations of a train passing through different straight ballasted track sections composed by ten sleepers was performed with spheres with rolling friction.
Ballast properties are already known from the previous calibration procedure. However, in this case the vertical displacement of the sleepers was measured and the contact stiffness between ballast and the lower surface should be estimated. The reason is that subballast and platform are not being calculated as deformable layers, so their deformation has to be concentrated in the points of contact between the lower ballast particles and the rigid surface.
Three different scenarios were tested, the first one represented the typical well compacted railway track while the second had a section poorly compacted and the third is eroded laterally. From the results obtained, it can be concluded that the ballast compactness influences highly the vertical stiffness of the track. A ballast layer poorly compacted may lead to uncomfortable vibrations and, in the worst case, may imply a fatal train derailment due to an excessive seat of the sleepers. On the other hand, the lateral erosion of the ballast layer does not affect significantly the vertical stiffness of the track, yielding to sleeper seats similar to those in the original track.
8.2 Future lines of research
Although the results obtained are satisfactory, some possible improvements, that can be implemented in the code, were identified:
- It would be interesting to introduce particles wear and crushing in order to develop more realistic calculations. The simplification based on applying a zero restitution coefficient to the material was valid for the cases considered in this thesis. However, for long time calculations, the effects of crushing and wear would be more important and may be interesting to reproduce them.
- Related to the previous point, the introduction of a constitutive model that varies the friction along time would be interesting. This may be useful for introducing not only the influence of wear, but also processes such as sand fouling.
- It is worth mentioning that the bonded DEM is already implemented in the numerical code [138]. The bonded DEM is a modification of the classical DEM which assumes that bonds exist between particles, resisting their separation [139]. With this numerical model, the rails and bearing plates can be reproduced numerically, simplifying the way of imposing loads when a train is passing through a railway track. However, their characterisation requires further investigation. This code improvement may lead to an easier introduction of the loads, making possible to impose dynamic loads in every direction.
Zhang et al. [140] already developed some calculations representing one rail and the bearing plates with DE particles, but in two dimensions. The results obtained were promising.
BIBLIOGRAPHY
[1] Ahmed, S. and Harkness, J. and Le Pen, L. and Powrie, W. and Zervos, A. (2015) "Numerical modelling of railway ballast at the particle scale", Volume 40. Int J Numer Anal Met 5 713–737
[2] Selig, E.T. and Waters, J.M. (1994) "Track Geotechnology and Substructure Management". Thomas Telford
[3] Lim, W.L. (2004) "Mechanics of Railway Ballast Behaviour". University of Nottingham
[4] Jean, M. (2009) "Numerical Simulation of Granular Materials". Micromechanics of Granular Materials. ISTE 149–315
[5] Duncan, J. M. (1996) "State of the Art: Limit Equilibrium and Finite-Element Analysis of Slopes", Volume 122. J Geotech Eng-ASCE 7 577–596
[6] Dafalias, Y .F. and Manzari, M. T. (1997) "A Critical State Two-surface Plasticity Model for Sands", Volume 47. Géotechnique 2 255–272
[7] Indraratna, B. and Nimbalkar, S. and Coop, M. and Sloan, S. W. (2014) "A constitutive model for coal-fouled ballast capturing the effects of particle degradation", Volume 61. Comput Geotech 96–107
[8] Esmaeili, M. and Khodaverdian, A. and Neyestanaki, H. K. and Nazari, S. (2016) "Investigating the effect of nailed sleepers on increasing the lateral resistance of ballasted track", Volume 71. Comput Geotech 1–11
[9] Salazar, F. and Irazábal, J. and Larese, A. and Oñate, E. (2015) "Numerical modelling of landslide–generated waves with the particle finite element method (PFEM) and a non–Newtonian flow model", Volume 40. Int J Numer Anal Met 6 809–826
[10] Belheine, N. and Plassiard, J. P. and Donzé, F. V. and Darve, F. and Seridi, A. (2009) "Numerical Simulation of Drained Triaxial Test using 3D Discrete Element Modeling", Volume 36. Comput Geotech 1–2 320–331
[11] Jebahi, M. and Andre, D. and Terreros, I. and Iordanoff, I. (2015) "Discrete Element Method to Model 3D Continuous Materials". John Wiley & Sons
[12] Rapaport, D. C. (1980) "The event scheduling problem in molecular dynamic simulation", Volume 34. J Comput Phys 2 184–201
[13] Jean, M. (1999) "The non-smooth contact dynamics method", Volume 177. Comput Method Appl M 3–4 235–257
[14] Radjai, F. and Richefeu, V. (2009) "Contact dynamics as a nonsmooth discrete element method", Volume 41. Mechanics of Materials 6 715–728
[15] Santasusana, M. (2016) "Numerical techniques for non-linear analysis of strutures combining Discrete Element and Finite Element Methods". Universitat Politecnica de Catalunya
[16] Cundall, P. A. and Strack, O. D. L. (1979) "A Discrete Numerical Model for Granular Assemblies", Volume 29. Géotechnique 1 47–65
[17] Kleinert, J. and Obermayr, M. and Balzer, M. (2013) "Modeling of large scale granular systems using the discrete element method and the non-smooth contact dynamicsmethod:Acomparison". Proceedings of the ECCOMAS Multibody Dynamics Conference
[18] Kleinert, J. and Simeon, B. and Dreßler, K. (2017) "Nonsmooth Contact Dynamics for the large-scale simulation of granular material", Volume 316. J Comput Appl Math 345–357
[19] Servin, M. and Wang, D. and Lacoursière, C. and Bodin, K. (2014) "Examining the smooth and nonsmooth discrete element approaches to granular matter", Volume 97. Int J Numer Meth Eng 12 878–902
[20] Unger, T. (2004) "Characterization of static and dynamic structures in granular materials". Budapest University of Technology and Economics
[21] Nguyen, N-S. and François, S. and Degrande, G. (2014) "Discrete modeling of strain accumulation in granular soils under low amplitude cyclic loading", Volume 62. Comput Geotech 232–243
[22] Dadvand, P. and Rossi, R. and Oñate, E. (2010) "An object-oriented environment for developing finite element codes for multi-disciplinary applications", Volume 17. Springer. Arch Comput Method E 3 253–297
[23] Centro de Innovación del Transporte, CENIT. (2008) "Reducción de las Variaciones de Rigidez Vertical de la Vía: Establecimiento de Criterios de Diseño, Recepción y Mantenimiento de las Infraestructuras Ferroviarias.". CENIT
[24] López, A. (2006) "Infraestructuras Ferroviarias". Universitat Politecnica de Catalunya
[25] Galván, J. M. (2012) "Estudio por Elementos Finitos de la Transición Vía con Balasto - Vía en Placa". Universitat Politecnica de Catalunya
[26] Selig, E.T. and Li, D. (1994) "Track Modulus: its Meaning and Factors Influencing it", Volume 1470. Transport Res Rec 47–54
[27] Burrow, M. P. N. and Ghataora, G. S. and Stirling, A. B. S. (2005) "A Rational Approach to Track Substructure Design.". Proceedings of the Conference on Excellence in Railway Systems Engineering and Integration
[28] López Pita, A. and Teixeira, P.F. and Robuste, F. (2004) "High Speed and Track Deterioration: the Role of Vertical Stiffness of the Track", Volume 218. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit 31–40
[29] AENOR "Aggregates for railway ballast; UNE-EN 13450:2015"
[30] Sanz, J. J. (1975) "Mecánica de Suelos". Reverte
[31] AENOR "Mechanical properties of rocks. Strength determination tests; UNE-EN 22950-1:1990."
[32] Álvarez, D. and Luque, P. (2003) "Ferrocarriles: Ingeniería e Infraestructura de los Transportes". Universidad de Oviedo
[33] Mantenimiento de Infraestructura Renfe. Dirección Técnica Jefatura de vía. (1981) "N.R.V. 3-1-0.0. Traviesas. Traviesas y Cachas de Madera"
[34] RENFE Explotaciones Forestales. (1966) "Especificación Técnica para el Suministro de Traviesas y Cachas no Inyectadas, de Roble, Haya o Pino". RENFE
[35] Admetlla, N. (2011) "Transición Vía en Placa - Vía con Balasto Mediante Traviesas Cuadro". Universitat Politecnica de Catalunya
[36] Mantenimiento de Infraestructura Renfe. Dirección Técnica Jefatura de vía. (1997) "N.R.V. 3-1-2.1. Traviesas. Traviesas Monobloque de Hormigón"
[37] Mantenimiento de Infraestructura Renfe. Dirección Técnica Jefatura de vía. (1999) "N.R.V. 3-1-3.1. Traviesas. Traviesas Bibloque de Hormigón"
[38] Gimeno, S. (2004) "Una Nueva Problemática: la Renovación de Líneas de Alta Velocidad". Universitat Politecnica de Catalunya
[39] ADIF. (2003) "Homologación de Traviesas Monobloque de Hormigón Pretensado". ADIF
[40] Zand, J. van 't and Moraal, J. (1997) "Ballast Resistance under Three Dimensional Loading". Delft University of Technology
[41] Kabo, E. (2006) "A Numerical Study of the Lateral Ballast Resistance in Railway Tracks", Volume 220. P I Mech Eng F-J RAI 4 425–433
[42] Gallego, J. and Gómez-Rey, D. (2001) "A finite element solution for the lateral track buckling problem". TIFSA-RENFE Group
[43] Indraratna, B. and Ngo, N. T. and Rujikiatkamjorn, C. (2013) "Deformation of Coal Fouled Ballast Stabilized with Geogrid under Cyclic Load", Volume 139. J Geotech Geoenviron Eng 8 1275–1289
[44] Indraratna, B. and Ngo, N. T. and Rujikiatkamjorn, C. and Vinod, J. S. (2014) "Behavior of Fresh and Fouled Railway Ballast Subjected to Direct Shear Testing: Discrete Element Simulation", Volume 14. Int J Geomech 1 34–44
[45] Huang, H. and Tutumluer, E. (2014) "Image-Aided Element Shape Generation Method in Discrete-Element Modeling for Railroad Ballast", Volume 26. J Mater Civil Eng 3 527–535
[46] Indraratna, B. and Thakur, P. K. and Vinod, J. S. (2010) "Experimental and Numerical Study of Railway Ballast Behavior under Cyclic Loading", Volume 10. Int J Geomech 4 136–144
[47] Qian, Y. and Lee, S. J. and Tutumluer, E. and Hashash, Y. M. A. and Mishra, D. and Ghaboussi, J. (2013) "Simulating Ballast Shear Strength from Large-Scale Triaxial Tests: Discrete Element Method", Volume 2374. Transport Res Rec -1 126–135
[48] Harkness, J. and Zervos, A. and Le Pen, L. and Aingaran, S. and Powrie, W. (2016) "Discrete element simulation of railway ballast: modelling cell pressure effects in triaxial tests", Volume 18. Granul Matter 3 65
[49] Wellmann, C. (2011) "A two-scale model of granular materials using a coupled DE-FE appoach". Institut für Kontinuumsmechanik, Leibniz Universität Hannover
[50] Williams, J. R. and O'Connor, R. (1999) "Discrete element simulation and the contact problem", Volume 6. Arch Comput Method E 4 279–304
[51] Munjiza, A. (2004) "The Combined Finite-Discrete Element Method". Wiley, 1 edition Edition
[52] Boon, C. W. and Houlsby, G. T. and Utili, S. (2013) "A new contact detection algorithm for three-dimensional non-spherical particles", Volume 248. Powder Technol 94–102
[53] Nezami, E. G. and Hashash, Y. M. A. and Zhao, D. and Ghaboussi, J. (2004) "A fast contact detection algorithm for 3-D discrete element method", Volume 31. Comput Geotech 7 575–587
[54] Boon, C. W. and Houlsby, G. T. and Utili, S. (2012) "A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method", Volume 44. Comput Geotech 73–82
[55] Eliás, J. (2014) "Simulation of railway ballast using crushable polyhedral particles", Volume 264. Powder Technol 458–465
[56] Han, K. and Feng, Y. T. and Owen, D. R. J. (2007) "Performance comparisons of tree-based and cell-based contact detection algorithms", Volume 24. Eng Computation 2 165–181
[57] Williams, J. R. and Perkins, E. and Cook, B. (2004) "A contact algorithm for partitioning N arbitrary sized objects", Volume 21. Eng Computation 2/3/4 235–248
[58] Munjiza, A. and Andrews, K. R. F. (1998) "NBS contact detection algorithm for bodies of similar size", Volume 43. Int J Numer Meth Eng 1 131–149
[59] Bonet, J. and Peraire, J. (1991) "An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems", Volume 31. Int J Numer Meth Eng 1 1–17
[60] Feng, Y. T. and Owen, D. R. J. (2002) "An augmented spatial digital tree algorithm for contact detection in computational mechanics", Volume 55. Int J Numer Meth Eng 2 159–176
[61] Horner, D. A. and Peters, J. F. and Carrillo, A. (2001) "Large Scale Discrete Element Modeling of Vehicle-Soil Interaction", Volume 127. J Eng Mech-ASCE 10 1027–1032
[62] Hertz, H. (1882) "Ueber die Berührung fester elastischer Körper.", Volume 1882. Journal für die reine und angewandte Mathematik 92 156–171
[63] Deresiewicz, H. and Mindlin, R. D. (1952) "Elastic spheres in contact under varying oblique forces". Columbia University
[64] Thornton, C. and Cummins, S. J. and Cleary, P. W. (2013) "An investigation of the comparative behaviour of alternative contact force models during inelastic collisions", Volume 233. Powder Technol 30–46
[65] Johnson, K.L. (1987) "Contact Mechanics". Cambridge University Press
[66] Tsuji, Y. and Tanaka, T. and Ishida, T. (1992) "Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe", Volume 71. Powder Technol 3 239–250
[67] O'Sullivan, C. and Bray, J. D. (2004) "Selecting a suitable time step for discrete element simulations that use the central difference time integration scheme", Volume 21. Eng Computation 2/3/4 278–303
[68] Belytschko, T. and Liu, W. K. and Moran, B. and Elkhodary, K. (2013) "Nonlinear finite elements for continua and structures". John wiley & sons
[69] Santasusana, M. and Irazábal, J. and Oñate, E. and Carbonell, J. M. (2016) "The Double Hierarchy Method. A parallel 3D contact method for the interaction of spherical particles with rigid FE boundaries using the DEM", Volume 3. Comp Part Mech 407–428
[70] Kodam, M. and Bharadwaj, R. and Curtis, J. and Hancock, B. and Wassgren, C. (2009) "Force model considerations for glued-sphere discrete element method simulations", Volume 64. Chem Eng Sci 15 3466–3475
[71] Kremmer, M. and Favier, J. F. (2001) "A method for representing boundaries in discrete element modelling—part II: Kinematics", Volume 51. Int J Numer Meth Eng 12 1423–1436
[72] Zang, M. and Gao, W. and Lei, Z. (2011) "A contact Algorithm for 3D Discrete and Finite Element Contact Problems Based on Penalty Function Method", Volume 48. Comput Mech 5 541–550
[73] Dang, H. K. and Meguid, M. A. (2013) "An efficient finite-discrete element method for quasi-static nonlinear soil-structure interaction problems", Volume 37. Int J Numer Anal Met 2 130–149
[74] Su, J. and Gu, Z. and Xu, X. Y. (2011) "Discrete element simulation of particle flow in arbitrarily complex geometries", Volume 66. Chem Eng Sci 23 6069–6088
[75] Su, J. and Gu, Z. and Zhang, M. and Xu, X. Y. (2014) "An improved version of RIGID for discrete element simulation of particle flows with arbitrarily complex geometries", Volume 253. Powder Technol 393–405
[76] Hu, L. and Hu, G. M. and Fang, Z. Q. and Zhang, Y. (2013) "A new algorithm for contact detection between spherical particle and triangulated mesh boundary in discrete element method simulations", Volume 94. Int J Numer Meth Eng 8 787–804
[77] Chen, H. and Zhang, Y. X. and Zang, M. and Hazell, Paul J. (2015) "An accurate and robust contact detection algorithm for particle-solid interaction in combined finite-discrete element analysis", Volume 103. Int J Numer Meth Eng 8 598–624
[78] Nakashima, H. and Oida, A. (2004) "Algorithm and implementation of soil–tire contact analysis code based on dynamic FE–DE method", Volume 41. J Terramechanics 2–3 127–137
[79] Mindlin, R. D. (1949) "Compliance of elastic bodies in contact", Volume 16. J Appl Mech 259–268
[80] Irazábal, J. (2015) "Numerical modeling of railway ballast using the discrete element method". Universitat Politecnica de Catalunya
[81] Zhong, Z. H. (1993) "Finite Element procedures for contact-impact problems". Oxford University Press
[82] Han, K. and Peric, D. and Crook, A. J. L. and Owen, D. R. J. (2000) "A combined finite/discrete element simulation of shot peening processes – Part I: studies on 2D interaction laws", Volume 17. Eng Computation 5 593–620
[83] Han, K. and Peric, D. and Owen, D. R. J. and Yu, J. (2000) "A combined finite/discrete element simulation of shot peening processes – Part II: 3D interaction laws", Volume 17. Eng Computation 6 680–702
[84] Wensrich, C. M. and Katterfeld, A. (2012) "Rolling friction as a technique for modelling particle shape in DEM", Volume 217. Powder Technol 409–417
[85] Lane, J. E. and Metzger, P. T. and Wilkinson, R. A. (2010) "A Review of Discrete Element Method (DEM) Particle Shapes and Size Distributions for Lunar Soil". NASA
[86] Lu, G. and Third, J. R. and Müller, C. R. (2015) "Discrete element models for non-spherical particle systems: From theoretical developments to applications", Volume 127. Chem Eng Sci 425–465
[87] Irazábal, J. and Salazar, F. and Oñate, E. (2017) "Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast", Volume 85. Computers and Geotechnics 220–229
[88] Matsushima, T. and Katagiri, J. and Uesugi, K. and Tsuchiyama, A. and Nakano, T. (2009) "3D Shape Characterization and Image-Based DEM Simulation of the Lunar Soil Simulant FJS-1", Volume 22:1. J Aerospace Eng 15 15–23
[89] García, X. and Xiang, J. and Latham, J. P. and Harrison, J. P. (2009) "A clustered overlapping sphere algorithm to represent real particles in discrete element modelling", Volume 59. Géotechnique 9 779–784
[90] Ferellec, J. F. and McDowell, G. R. (2010) "A method to model realistic particle shape and inertia in DEM", Volume 12. Granul Matter 5 459–467
[91] Chen, C. and McDowell, G. R. and Thom, N. H. (2014) "Investigating geogrid-reinforced ballast: Experimental pull-out tests and discrete element modelling", Volume 54. Soils Found 1 1–11
[92] Ngo, N. T. and Indraratna, B. and Rujikiatkamjorn, C. (2014) "DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal", Volume 55. Comput Geotech 224–231
[93] Chakraborty, N. and Peng, J. and Akella, S. and Mitchell, J. E. (2008) "Proximity Queries Between Convex Objects: An Interior Point Approach for Implicit Surfaces", Volume 24. IEEE T Robotic 1 211–220
[94] Lopes, D. S. and Silva, M. T. and Ambrósio, J. A. and Flores, P. (2010) "A mathematical framework for rigid contact detection between quadric and superquadric surfaces", Volume 24. Multibody Syst Dyn 3 255–280
[95] Podlozhnyuk, A. and Pirker, S. and Kloss, C. (2017) "Efficient implementation of superquadric particles in Discrete Element Method within an open-source framework", Volume 4. Comp. Part. Mech. 1 101–118
[96] Cundall, P. A. (1988) "Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks", Volume 25. Int J Rock Mech Min 3 107–116
[97] Hart, R. and Cundall, P. A. and Lemos, J. (1988) "Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks", Volume 25. Int J Rock Mech Min 3 117–125
[98] Nezami, E. G. and Hashash, Y. M. A. and Zhao, D. and Ghaboussi, J. (2006) "Shortest link method for contact detection in discrete element method", Volume 30. Int J Numer Anal Met 8 783–801
[99] Alonso-Marroquín, F. (2008) "Spheropolygons: A new method to simulate conservative and dissipative interactions between 2D complex-shaped rigid bodies", Volume 83. EPL 1 14001
[100] Alonso-Marroquín, F. and Wang, Y. (2009) "An efficient algorithm for granular dynamics simulations with complex-shaped objects", Volume 11. Granul Matter 5 317–329
[101] Galindo-Torres, S. A. and Pedroso, D. M. (2010) "Molecular dynamics simulations of complex-shaped particles using Voronoi-based spheropolyhedra", Volume 81. Phys Rev E 6 061303
[102] Richefeu, V. and Mollon, G. and Daudon, D. and Villard, P. (2012) "Dissipative contacts and realistic block shapes for modeling rock avalanches", Volume 149–150. Eng Geol 78–92
[103] Ouhbi, N. and Voivret, C. and Perrin, G. and Roux, J. N. (2016) "Railway Ballast: Grain Shape Characterization to Study its Influence on the Mechanical Behaviour", Volume 143. Procedia Eng 1120–1127
[104] Ai, J. and Chen, J. F. and Rotter, J. M. and Ooi, Jin Y. (2011) "Assessment of rolling resistance models in discrete element simulations", Volume 206. Powder Technol 3 269–282
[105] Zhou, Y. C. and Wright, B. D. and Yang, R. Y. and Xu B. H. and Yu, A. B. (1999) "Rolling friction in the dynamic simulation of sandpile formation", Volume 269. Phys A 24 536–553
[106] Iwashita, K. and Oda, M. (1998) "Rolling Resistance at Contacts in Simulation of Shear Band Development by DEM", Volume 124. J Eng Mech-ASCE 3 285–292
[107] Sakaguchi, H. and Ozaki, E. and Igarashi, T. (1993) "Plugging of the Flow of Granular Materials during the Discharge from a Silo", Volume 07. Int J Mod Phys B 09n10 1949–1963
[108] Tasora, A. and Anitescu, M. (2013) "A complementarity-based rolling friction model for rigid contacts", Volume 48. Meccanica 7 1643–1659
[109] Bagi, K. (2005) "An algorithm to generate random dense arrangements for discrete element simulations of granular assemblies", Volume 7. Granul Matter 1 31–43
[110] Roselló, R. and Pérez, I. and Vanmaercke, S. and Recarey, C. and Argüelles, L. and Díaz-Guzmán, H. (2015) "Modified algorithm for generating high volume fraction sphere packings", Volume 2. Comp Part Mech 161–172
[111] Tran, V. D. H. and Meguid, M. A. and Chouinard, Luc E. (2014) "Discrete Element and Experimental Investigations of the Earth Pressure Distribution on Cylindrical Shafts", Volume 14. Int J Geomech 1 80–91
[112] Munjiza, A. and Latham, J. P. and John, N. W. M. (2003) "3D dynamics of discrete element systems comprising irregular discrete elements—integration solution for finite rotations in 3D", Volume 56. Int J Numer Meth Eng 1 35–55
[113] Henderson, D. M. (1977) "Euler angles, quaternions, and transformation matrices for space shuttle analysis". NASA
[114] Zhao, F. and Wachem, B. G. M. van. (2013) "A novel Quaternion integration approach for describing the behaviour of non-spherical particles", Volume 224. Acta Mech 12 3091–3109
[115] Whitmore, Stephen A. (2000) "Closed-form integrator for the quaternion (euler angle) kinematics equations" US-PATENT-6,061,611, US-PATENT-APPL-SN-002871
[116] Bradshaw, G. and O'Sullivan, C. (2002) "Sphere-tree Construction Using Dynamic Medial Axis Approximation". Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. ACM 33–40
[117] Bradshaw, G. (2002) "Bounding Volume Hierarchies for Level-of-detail Collision Handling". Trinity College
[118] Bradshaw, G. and O'Sullivan, C. (2004) "Adaptive Medial-axis Approximation for Sphere-tree Construction", Volume 23. ACM Trans Graph 1 1–26
[119] Hubbard, P.M. (1995) "Collision Detection for Interactive Graphics Applications", Volume 1. IEEE T Vis Comput Gr 218–230
[120] Recarey, C. A. and Pérez, I. P. and Muñiz, M. and Oñate, E. and Roselló, R. and Díaz-Guzmán, H. (2016) "General advancing front packing algorithm for the discrete element method". Comp Part Mech 1–21
[121] Pérez, I. and Roselló, R. and Recarey, C. and Muñiz, M. (2017) "Dense packing of general-shaped particles using a minimization technique", Volume 4. Comp. Part. Mech. 2 165–179
[122] Melis, M. (2006) "Embankments and Ballast in High Speed Rail", Volume 153. Revista de Obras Publicas 7–26
[123] Howatson, A. M. and Lund, P. G. and Todd, J. D. (1972) "Engineering tables and data". Chapman and Hall
[124] Aikawa, A. (2015) "Dynamic characterisation of a ballast layer subject to traffic impact loads using three-dimensional sensing stones and a special sensing sleeper", Volume 92. Constr Build Mater 23–30
[125] Farmer, I. W. (1968) "Engineering Properties of Rocks". Spon
[126] Deiros, I. and Voivret, C. and Combe, G. and Emeriault, F. (2016) "Quantifying Degradation of Railway Ballast Using Numerical Simulations of Micro-deval Test and In-situ Conditions", Volume 143. Procedia Engineering 1016–1023
[127] Taylor, D. W. (1948) "Fundamentals of soil mechanics". J. Wiley
[128] Huang, H. and Tutumluer, E. and Dombrow, W. (2009) "Laboratory Characterization of Fouled Railroad Ballast Behavior", Volume 2117. Transportation Research Record: Journal of the Transportation Research Board 93–101
[129] Indraratna, B. and Ngo, N. T. and Rujikiatkamjorn, C. (2011) "Behavior of geogrid-reinforced ballast under various levels of fouling", Volume 29. Geotextiles and Geomembranes 3 313–322
[130] Höhner, D. and Wirtz, S. and Kruggel-Emden, H. and Scherer, V. (2011) "Comparison of the multi-sphere and polyhedral approach to simulate non-spherical particles within the discrete element method: Influence on temporal force evolution for multiple contacts", Volume 208. Powder Technol 3 643–656
[131] Kogut, L. and Etsion, I. (2003) "A Semi-Analytical Solution for the Sliding Inception of a Spherical Contact", Volume 125. J. Tribol 3 499–506
[132] "https://www.spanbeton.nl/en/ns90-sleepers/"
[133] Paderno, C. (2009) "Simulation of ballast behaviour under traffic and tamping process". 9th Swiss Transport Research Conference
[134] Kerr, A. D. (1974) "The Stress and Stability Analyses of Railroad Tracks", Volume 41. J. Appl. Mech 4 841–848
[135] Cuéllar, V. (2016) "Comportamiento dinámico de líneas ferroviarias con balasto bajo cargas verticales", Volume 183. Ingeniería civil 79–108
[136] Fonseca, P. (2004) "Contribución a la reducción de los costes de mantenimiento de vías de alta velocidad mediante la opitimización de su rigidez vertical". Universitat Politècnica de Catalunya
[137] "http://www.renfe.com/viajeros/nuestros_trenes/aves100r_ficha.html"
[138] Oñate, E. and Zárate, F. and Miquel, J. and Santasusana, M. and Celigueta, M. A. and Arrufat, F. and Gandikota, R. and Valiullin, K. and Ring, L. (2015) "A local constitutive model for the discrete element method. Application to geomaterials and concrete", Volume 2. Comp Part Mech 2 139–160
[139] Brown, N. J. and Chen, J-F. and Ooi, J. Y. (2014) "A bond model for DEM simulation of cementitious materials and deformable structures", Volume 16. Granul Matter 3 299–311
[140] Zhang, X. and Zhao, C. and Zhai, W. (2017) "Dynamic Behavior Analysis of High-Speed Railway Ballast under Moving Vehicle Loads Using Discrete Element Method", Volume 17. Int J Geomech 7
Document information
Published on 09/02/18
Submitted on 01/02/18
Licence: CC BY-NC-SA license