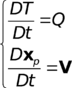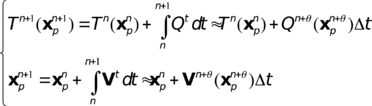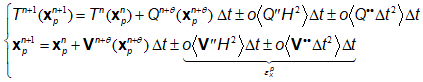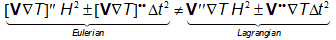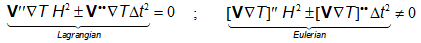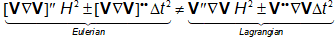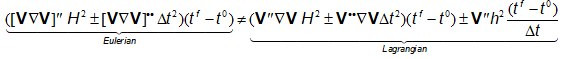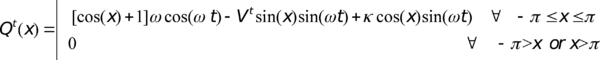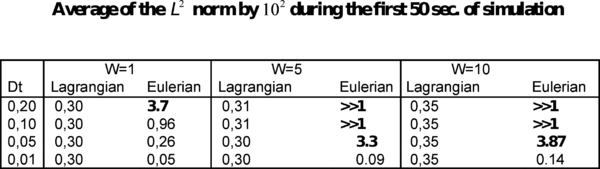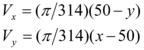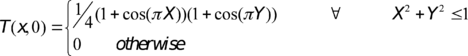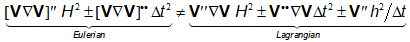Lagrangian versus Eulerian integration errors

Published in Comput. Methods Appl. Mech. Engrg. Vol. 293, pp. 191–206, 2015
doi: 10.1016/j.cma.2015.04.003

Abstract

The possibility to use a Lagrangian frame to solve problems with large time-steps was successfully explored previously by the authors for the solution of homogeneous incompressible fluids and also for solving multi-fluid problems [28-30]. The strategy used by the authors was named Particle Finite Element Method second generation (PFEM-2). The objective of this paper is to demonstrate in which circumstances the use of a Lagrangian frame with particles is more accurate than a classical Eulerian finite element method, and when large time-steps and/or coarse meshes may be used.

1. Introduction

Over the last decades, computer simulation of incompressible fluid flow has been mainly based on the Eulerian formulation of the fluid mechanics equations on fixed domains [1]. During this period, hardware has evolved considerably increasing the speed performance of computations and allowing better facilities for data entry and the display of results. However in these decades there have been no substantial improvements on the numerical methods used concerning the efficiency of the algorithm. In most practical engineering problems, very fine mesh and very small time-steps are needed to reach acceptable results. This handicap exceeds most time the efficiency of current powerful computers.

More recently, particle-based methods in which each particle is followed in a Lagrangian manner have been used for fluid flow problems [2-5]. Monaghan [2] proposed the first ideas for the treatment of astrophysical hydrodynamic problems with the so-called Smoothed Particle Hydrodynamics Method (SPH) which was later, generalized to fluid mechanics problems [2-5]. Koshizuka and coworkers [6,7] developed a similar method to SPH, named Moving Particle Simulation (MPS). SPH and MPS belong to the family of the so-called meshless methods, as well as the Finite Point Method [8-10]. Lately, the meshless ideas were generalized to take into account the finite element type approximations in order to obtain more accurate solutions [11]. This method was called the Meshless Finite Element Method (MFEM) and uses the Extended Delaunay Tessellation [12] to build the mesh in a computing time, which is linear with the number of nodal points.

A natural evolution of the last work was the Particle Finite Element Method (PFEM) [13, 14]. The PFEM combines the particle precept with the Finite Element Method (FEM) shape functions using a background finite element mesh. This mesh may be quickly rebuilt at each time-step (PFEM with moving mesh) or may be a fixed mesh (PFEM with fixed mesh). In the last case, the results from the Lagrangian particles are projected on a fixed mesh at each time-step. The idea of combining fixed meshes with moving particles is not new. It was introduced for convection diffusion problems in [15] and was used in the so-called Particle in Cell method (PIC) [16] and later in its extension called the Material Point Method (MPM) [17]. All these methods use a Finite Element (FE) background mesh. Despite that both the PFEM and the MPM use a fixed FE mesh and a set of Lagrangian particles, there are important differences in the way the particles are employed: thus, while in the MPM all computations are performed on the mesh, in the PFEM the aim is to calculate as much as possible on the particles, leaving small corrections to be performed on the mesh. However, the most important difference is that in the PFEM the particles do not represent a fixed amount of mass, but rather material points that transport only intrinsic properties of the fluid. This allows to use a variable number of particles and therefore simplifying refinement.

The PFEM has been successfully used to solve the Navier-Stokes equations [18-21] and fluid-structure interaction problems [22-25] as well as solid mechanics problems [26]. The advantages of the PFEM concerning the tracking of internal interfaces have also been explored and used to solve fluid mechanics problems including multi-fluid flows [27].

The possibility to use the PFEM to solve non-linear problems with large time-steps in order to obtain an accurate and fast solution was successfully explored by the authors for the solution of the homogeneous incompressible Navier-Stokes equations [28] and multi-fluid problems [29]. This new strategy was named PFEM-2. The objective of this paper is to demonstrate why PFEM-2 is more accurate than a classical Eulerian FEM in certain particular cases when large time-step and/or coarse meshes are used. The authors claim that nowadays, the best way to improve the efficiency of the algorithms in order to take advantages of the increasing computer power is the use of this particle-based method.

The layout of the paper is the following. After a general description in Section 2 of the particular time integration used to allow large time-steps, the PFEM-2 is described in Section 3. The analysis of the space and time integration errors for both the Eulerian and Lagrangian formulations is introduced in Section 4 for the convection-diffusion equation. Section 5 describes the generalization to the Navier-Stokes equations. Finally, prior to the conclusions, some numerical tests are presented to validate the method and the possibilities of using the PFEM-2 for solving convection dominant problem with large time-steps.

1. General description

Let the time variable. The initial value of the time-step will be called , the final value , the difference will be the time-step and some internal time value between and will be named .

Let be the vector defining the position of a spatial point in a three-dimensional (3D) space and let be the vector defining the position of a material point (particle). This particle position may be described on a fixed frame as a function of time. For simplicity will be written as . The particles move according with the velocity field , which is a function of space and time . For simplicity it will be written as or .

The unknown function will be described by for the case of an Eulerian frame and by for a Lagrangian frame. The unknown function may be a scalar function (temperature, pressure, level set position, etc) or a vector function. The particular case in which the unknown function is the velocity field itself (as in the case of the Navier-Stokes equations) will be considered separately.

In a general way, all convective equations may be written in a Eulerian frame as:

(1.1)

where includes the source term , the diffusion term , the reaction term , etc

(1.2)

The same convective equation may written in a Lagrangrian frame as:

(1.3)

where is

(1.4)

Time integration

Equations (1.1) and (1.3) will be integrated in time in an Eulerian frame using the simplest linear in time

-method:

(1.5)

with the definition of any function .

In the same way, in the Lagrangian frame the -method reads:

(1.6)

with the definition .

The time integration error of a function for is proportional to the second derivative of the function and , i.e. :

(1.7)

Other form of time integration for the Lagrangian frame:

It is interesting to note that using the same linear -method, the Lagrangian frame allows different ways to evaluate the integral of a function. For instance, the first equation of (1.6) may be also written as:

(1.8)

in which the functions evaluated at time and are integrated with moving particles following the streamlines at the respective time-steps. Equation (1.8) seems to be more accurate than (1.6) because it takes into account all the intermediate positions of the particles. Another possibility is a mix between (1.6) and (1.8) as:

(1.9)

The advantage of (1.9) over (1.8) is that the integration over the streamlines is performed in the explicit part of the equation and the remaining implicit part is simpler. To perform the first integral in (1.9) a possible numerical strategy is to divide the time step into m time subintervals. The analytical solution to solve this integral for linear unknown approximation was also presented in [30].

The use of (1.9) for the unknown with and the use of (1.9) for the integration of the velocity - second equation of (1.6) – with , has been named X-IVAS+implicit correction in [30].

(1.10)

This integration will be used in all the examples presented using a Lagrangian frame. However, in the present study for the error analysis, the standard -method will be considered, assuming that the X-IVAS integration improves the results and decreases the integration errors, but without evaluating this difference.

2. The Particle Finite Element Method, second generation (PFEM-2)

The Particle Finite Element Method, second generation (PFEM-2) has been described in [28, 29]. Only a summary will be presented here for completeness. Detail can be found in [28, 29].

While PFEM-2 can be used either with fixed or moving mesh, however, in this paper only PFEM-2 with fixed mesh will be described. The reason is that the goal of this work is to compare the errors between Lagrangian and Eulerian formulations, and therefore it is more consistent to work with a fixed mesh in both frameworks.

One of the main characteristics of PFEM-2 with a fixed mesh is the existence of two meshes: one is a fixed mesh which is the standard FE mesh, while the other mesh, which is a fictitious mesh, is the particle distribution. This last mesh may be considered as a moving mesh without connectivities. On the fixed mesh, all the derivatives of the unknown functions will be evaluated and also will be used to interpolate any variable from the FE mesh to the particle mesh. On the particle mesh only the unknown function will be evaluated but not its derivatives. For this reason, the particle mesh does not need connectivities, only the particle positions are enough to represent the unknown function.

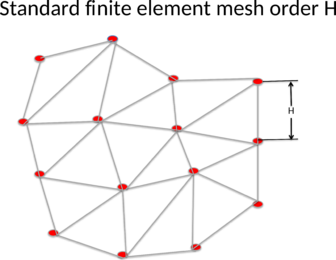
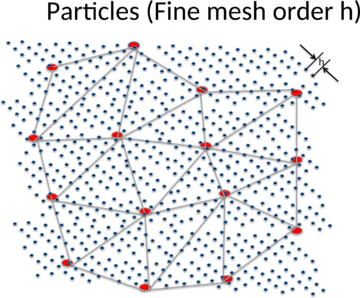
For reasons to be justified later in the error analysis, the particle mesh will be finer than the FE mesh. Let us assume that the FE mesh is of order and the particle mesh is of order with . See Figures 2.1 and 2.2

Figure 2.1. Fixed finite element mesh of order H

Figure 2.2 Moving particle mesh of order h

The steps to solve a problem using PFEM-2 are the following:

1) As a prerequisite, the value of the unknown , the source and the velocity field in all the nodes of the FE mesh must be known from the previous time-step. Also the unknown function is stored on the particles .

2) Evaluate the new particle position using (1.10) with

3) Evaluate the explicit part of (1.9) to give an initial prediction of . Let us call it .

4) Project from the particle to the FE mesh

5) Solve implicitly on the FE mesh, using the standard FEM and the second part of (1.9) to obtain

6) Update the solution on the particles

7) If necessary return to Step 1 with , otherwise go to the next time-step.

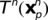It must be noted that the iterative process described in Step 6 is not needed for the case of convection-diffusion equation where the velocity field is known at all times. In this case may be used from the initial step. This situation is different for the Navier-Stokes equations, where the velocity field is the unknown. In this case, the problem is non-linear and the only way to obtain the exact solution is iteratively using at each iteration an approximation of the velocity at time . However, the linearization introduced by imposing on the first step has been enough to obtain accurate results in all the examples tested, making the iteration process unnecessary.

It is important to note also than in the Step 5 the interpolation from the coarse mesh to the particles is performed on the increments of the unknown function and not on the unknown function itself. This is imperative in order to preserve the arbitrary shape of the unknown function on the particles.

3. Lagrangian versus Eulerian integration errors

Eulerian frame:

The time integration using any numerical formula introduces some errors. In particular, the linear -method proposed in (1.5) introduces a minimum error for proportional to the second time derivative of the integrated function and the square of the time-step, i.e.:

(3.1)

with the time integration error

(3.2)

where means .

In the same way the FEM approximation of the functions and the space derivatives of the function introduces spatial error. This means that the sum of the function and some spatial integration errors is integrated in time by:

(3.3)

In this paper only linear finite elements approximations of the unknown are considered. Then, the spatial errors are proportional to the second derivative of the functions and the square of the mesh size, i.e.:

(3.4)

where means .

Avoiding higher order terms the unknown function after a time-step will be:

Hence, the Eulerian error is:

(3.5)

Lagrangian frame:

In the same way, the errors in the numerical evaluation of the unknown function and the particle position for the Lagrangian frame will be:

(3.6)

It must be noted that the error in the evaluation of the particle position introduces an error in the evaluation of the unknown function. Expanding in series around

(3.7)

The first equation of (3.6) remains:

(3.8)

or also calling all the lagrangian errors:

Introducing the value of from (3.6) into (3.8) the Lagrangian errors remains:

(3.9)

Comparing the Eulerian errors in (3.5) with the Lagrangian ones in (3.9), the main differences are in the terms:

(3.10)

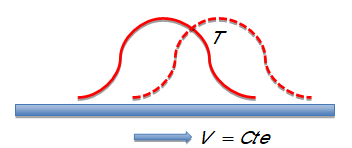
It is interesting to note that, despite the difference between the Eulerian and the Lagrangian errors are problem dependent, in general the errors in the Eulerian frame are higher than those in the Lagrangian one. For instance, in the standard convection-diffusion problem, where the convective field is known and has a constant or nearly constant velocity (See Figure 3.1), Equation (3.10) reads:

This is so because in this case:

, but

(3.11)

Figure 3.1 Convection of a unknown function in a constant velocity field

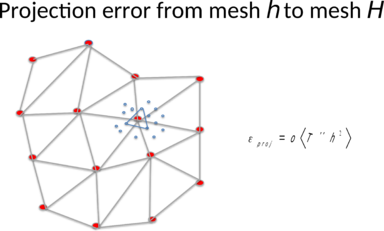
Projection errors:

The Lagrangian frame must add the projection errors to the previous integration ones. Projection errors are introduced while mapping the information from the particle mesh to the FE mesh.

Considering a minimum number of particles surrounding a fixed node (Figure 3.2) a linear interpolation may be used to project the unknown function from the neighboring particles around a node to the node itself. In this case, the error will be proportional to the second derivative of the unknown and the size of the particle mesh .

(3.12)

This projection error is introduced at each projection step independently of the time-step size. Then, in a total period of time , the Lagrangian error becomes:

(3.13)

The importance to use a fine particle mesh with becomes now obvious for decreasing projection errors. Several existing Lagrangian methods, as for instance the Characteristic Galerkin method [31], use a single mesh. In these methods the projection errors are order , the same order as the spatial diffusive error, and therefore they lead to very diffusive methods.

Figure 3.2. Projection errors from mesh h to mesh H

Errors due to adding and removing particles:

Another handicap of PFEM-2 is the permanent need of adding and removing particles from the fine mesh. Effectively, the particle mesh is a moving mesh. This means that particles move accordingly to the velocity field. In such cases in which the velocity field or the fixed mesh size H are not constant, keeping the mesh size sufficiently small in order to obtain the projection errors to acceptable values is not always possible. Adding and sometimes removing particles becomes a need to preserve the accuracy and the computational cost acceptable.

Starting from Equation (3.12), it is possible to obtain guidelines to define the number of particles. Particles must be added or removed accordingly to the following two criteria:

1) when the local size increases or decreases.

2) when the second derivative of the unknown function increases or decreases.

By adding/removing particles it is possible to have a complete control over the h size in order to obtain the desired error value.

During the process of adding a new particle, the unknown function must be interpolated from the neighboring particles. In some cases, for simplicity the unknown function is interpolated from the fixed mesh. In this case, the error introduced is of order

(3.14)

Otherwise, when the surrounding particles are used for compute the new unknown value, the error is of order

(3.15)

This is also the error introduced when a particle is removed.

Adding or removing particles must be performed only in such cases where it is strictly necessary due to the diffusive error introduced at each adding/removing step.

On the other hand, it is important to control the local value of to avoid important projection errors in subsequent time-steps. A good balance between adding particles along time and removing as few as possible is a good strategy.

Advantages and disadvantages of the Eulerian/Lagrangian frames:

Comparing the equations for the errors in the Eulerian and Lagrangian frames the following conclusions may be drawn:

1) Eulerian frames are better for diffusion dominant problems. In these cases, the errors between the Lagrangian and Eulerian approaches are of the same order, but in the Lagrangian frames the projection errors must be added.

2) Lagrangian frames are better for convective dominant problems when the convective flow is constant or nearly constant. The remaining cases, when the convective flow presents high variations the Lagrangian or the Eulerian frame will be better or worse depending on the projection errors.

3) Eulerian frames are better for stationary problems. In these cases,

and there are not projection errors.

Generalization to the Navier-Stokes equations:

It is interesting to analyze it separately the particular case in which the unknown function is the convective term itself as for the Navier-Stokes equations. The errors equations are the same, but the conclusions are fundamentally different.

Generalizing Equation (3.10), the difference between the errors in the Eulerian and Lagrangian frames for convective dominant problems (high Reynolds number) are:

(3.16)

Adding the projection errors for a period reads:

(3.17)

It is not anymore possible to separate the case in which the convective field is constant from the case in which is not constant. Nevertheless, some particular cases may be analyzed in order to draw some conclusions:

1. Eulerian frames are better for low Reynolds number. In these cases, the errors between the Lagrangian and the Eulerian approaches are of the same order, but on Lagrangian frames the projection errors must be added.

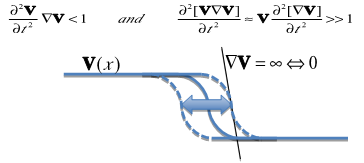
2. Lagrangian frames are better for convective dominant problems when the velocity has a smooth variation in time but the gradient of the velocity has high spatial variations. This case is very common in fluid mechanics problems. See for instance Figure 4.1. The remaining cases are better or worse depending on the projection errors.

3. Eulerian frames are better for stationary problems. In these cases, 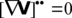and there are not projection errors.

4. Lagrangian frames are better for multi-fluid flows. This is because Eulerian frames need to solve a level set equation to know the position of the interface. The level set equation [32-33] is a convection equation that requires small time-steps to yield accurate results due to the considerations concluded in the previous Section, i.e.:.

Figure 3.3. Case with a small variation of the velocity field and a large variation of the velocity gradient.

4. Numerical examples

Manufactured, one-dimensional problem:

In order to test the validity of the expressions presented in Section 3, a particular 1D problem was tailored to have an analytical solution in order to compare the results.

The velocity field is constant in space but has a variation in time with a constant coefficient such that:

(4.1)

with and

The target solution is a trigonometric function that does not move in the space x, but rather changes its amplitude in time, affected by the parameter  :

(4.2)

An initial value of and periodic boundary conditions were used. For these conditions, the source term becomes (4.3). It is interesting to note that despite the target T(x,t) must not be affected by the velocity, the load actually does depend on in order to obtain the desired solution.

(4.3)

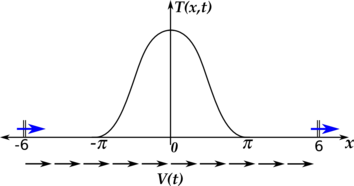
The 1D space was split in equal elements of length . The conductivity coefficient was set to . This gives a Peclet number based on the source length from 1570 to 4700. Figure 4.1 shows a graphic representation of the problem.

Figure 4.1. Manufactured 1D problem

The problem was solved with different time-steps from to . Defining the Courant number as the number of elements that a material point passes by at each time step ( ), the range of this value is 0.125 to 7.5 for this problem. The frequency of the amplitude was also variable from for the nearly stationary case, to for the most transient case. The number of particle used in the Lagrangian frames was set to around 10 particles by element in order to reduce the projection errors to a minimum, leading to h=1/10 H.

This very simple 1D problem is interesting because it represents, to some extent, the problem of a stationary shock wave in a fluid that moves at high speed. As the shock wave can be identified on a fixed part of the domain, this problem is usually solved with an Eulerian method.

Table 4.1 presents the results of the norm of the error averaged for a period of simulation of 50 sec. In this problem, the velocity field in all the different cases tested was the same, with and . The unknown function has a variation in time depending of the frequency . For small values of , small values of the variable will be obtained. Contrary, for high frequencies, this value will be high. Table 4.1 confirms the expected results presented in Section 3. High frequencies introduce high errors in the Eulerian frame. In these cases very small time-steps are needed to obtain acceptable results. However, the Lagrangian frame is independent from the frequency and the time-step size in this problem, because the error depends only on instead of . The Eulerian frame has acceptable results only in the near stationary case ( ) and even in this case, small time-steps are needed. For the other cases ( and ), time-steps 20 times smaller are needed to have acceptable results in the Eulerian frame. Nevertheless, for very small time-steps, the Eulerian frame presents a better convergence to the exact results while in the Lagrangian frame, the error results do not decrease to lower values due to the projection errors.

Table 4.1 Manufactured 1D problem.

Average of theL² norm x10^-2 of the error for different frequencies

Table 4.2 shows the same problem changing the mesh size. The results show a similar behavior. This means that the previous conclusions are independent from the mesh size. The solution in the Eulerian frame depends on the time-step and cannot be improved by decreasing the mesh size.

Table 4.2 Manufactured 1-D problem.

Average of the L²norm of the error for different mesh size

Rigid Body Rotation of Zalesak’s Disk:

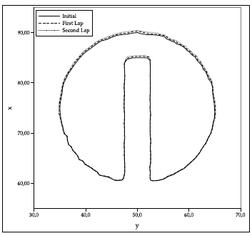
This test consists in the pure convection of a region composed of a circle with a slot [34]. The computational domain is . The convected region is a circle centered at (50; 75) with a radius of 15 and a slot of width 5 and height 25. The velocity field is a rigid body rotation around the center of the domain with a period of 628 time units:

(4.4)

The FE mesh used was 100 points in each direction, conforming a Cartesian mesh with 20,000 triangles and a mesh size H=1. Large time-steps were used in the simulation corresponding to a Courant number approximately to 4.5. The number of particles used in the fine mesh of PFEM-2 was around six particles within each triangular element, leading to an average h of about .

This is an interesting problem for validate the possibility of a numerical method that perfectly convects a shape function. This is important not only for the permanent need to convect functions in practice, but also because in multi-fluid flows it is always necessary to convect the internal interfaces between two fluids. The accuracy of the results depends on a great extent in the accuracy of the convection of the internal interfaces. The particular case of convection without changes in the shapes must be solved exactly; otherwise large errors must be expected in other, more difficult to validate, cases.

The field at the initial step and after one and two revolutions are shown in Fig. 4.2 for two different methods based on two Lagrangian approaches: a) PFEM-2; b) Characteristic-Galerkin method.

In this example, the term is zero, but the term is not. This explains why this problem solved with the Eulerian frame only gives acceptable results for very small time-steps. However, despite that the two methods used for solving this problem of Figure 4.2 are Lagrangian and therefore should have null convective errors, the Characteristic Galerkin Method lies a much more diffusive behavior. This difference is due to projection errors since the Characteristic-Galerkin Method [31] moves the nodes of the mesh in a Lagrangian way to obtain the unknown in the previous position. This is equivalent to use only one particle per node of the mesh. In this case, as expressed in Equation (3.14) the error is the order instead of the order as for PFEM-2. Consequently, not all the Lagrangian methods are able to convect correctly a function. The importance to use several particles to avoid large projection errors is clearly evidenced in this example.

a) PFEM-2 solution	b) Characteristic-Galerkin solution
Figure 4.2 Zalesak’s disk results after one and two full revolutions with 100 grid points per direction and Co=4.5 a) PFEM-2 interface location after one and two revolutions; b) Characteristic-Galerkin solution. White line: Initial interface location. Black line: interface location after one revolution. The interface is located where the distance function is valued zero, plotted with contour fill.

Convection-Diffusion Transport of a Gaussian hill:

The problem consists of transport a Gaussian hill signal with physical diffusion. The velocity field is a flow rotating around the center of a square domain. The initial Gaussian signal is displaced from the center of the domain at a certain radius and its shape makes the transported signal have a non-zero value in a limited region of the domain initially. Figure 4.3 shows the problem definition. Since the velocity field corresponds to a rigid body motion, the solution can be easily decomposed into two parts: The conductivity of the material diffuses the Gaussan hill while the solution is convected; Using the Lagrangian (material) field as a reference system, the problem simply becomes a pure diffusion problem and therefore the analytical solution is trivial.

The initial solution is a Gaussian function with

(4.5)

with . In the example tested and was used. The rotating field had an angular rotation of and the diffusive coefficient was set to

Figure 4.3 Convection-Diffusion Transport of a Gaussian hill. Problem definition

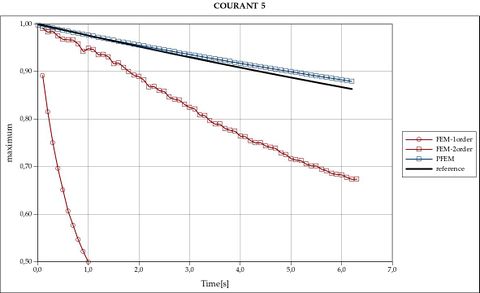
The fixed mesh used was a 30x30 triangular mesh and the time-step was fixed to have a Courant number of 5. Note that this represents a very large time-step for this coarse mesh. The same problem was solved with a very fine mesh and a very small time-step to have a reference solution.

Figure 4.4 show the results of the top of the Gaussian hill during the period studied of seven seconds. The black full line is the reference solution. The two very diffusive curves correspond to the standard FEM using an Eulerian frame. The more diffusive results are obtained using explicit integration ( ). The other curves correspond to the more accurate implicit integration ( ). Both Eulerian solutions are very diffusive for this large time-step. The Eulerian and the Lagrangian solutions coincide if the time-step is reduced to a Courant number of 0.5.

In this example and are null, however and are not. This explains, accordingly with (3.10), the big difference in the error between the Lagrangian and the Eulerian approaches. In PFEM-2 the projection error was decreased using nine particles in each element.

Figure 4.4 Convection-Diffusion Transport of a Gaussian hill. Top value of the Gaussian hill at different time-steps with a constant Courant number=5 for different methods

Rayleigh-Taylor Instability:

This problem simulates the evolution of two fluids initially at rest in a gravity field. The density of the upper fluid is three times larger than the one placed underneath. Due to an initial disturbance the denser fluid moves down and the lighter one does the opposite. A mixture of fluids is created, which is lately segregated. The final state reaches a stable equilibrium with the denser fluid at the bottom layer and the lighter one at the top layer. The evolution of the instability has been investigated by Guermond and Quartapelle [35] among others.

This problem fall in the category of the cases discussed in Section 4, in which the unknown function is the actual velocity field. The main differences in the evaluation of the errors are those included in Equations (3.16-17). Furthermore it is a multi-fluid problem. This means that method based on Eulerian frames must make use of the concept of Level-Set (or Volume of Fluid) to determine the internal interface position. Hence, the evaluation of the interface position is dominated by a convective equation, where the errors are described in Equation (3.10).

The computational domain was . Other physical parameters were selected to give Re=1000. A fixed finite element mesh was generated formed by 80,000 structured triangles ( ). Slip boundary conditions were set on each wall. The time-step was , which allows . Between five and eight particles per element were used which suppose an h between ( ) and .

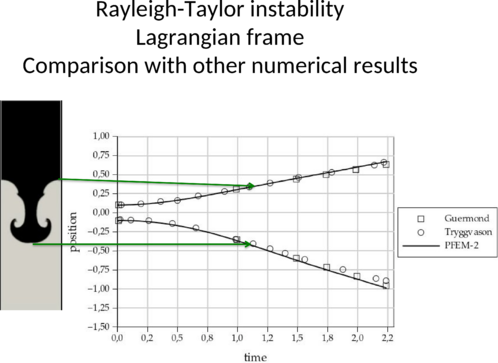
Results for the vertical position of the tip of the falling and rising fluid are shown in Figure 4.5. It can be observed that the current solution is in good agreement with the reference results [35].

Figure 4.5 Rayleigh-Taylor Instability. Vertical position of the tip of the falling and rising fluid

In order to emphasize the differences between the errors introduced in the space-time integration for large time-steps using a Lagrangian or an Eulerian frame, the current case was also simulated with a large range of time-steps using PFEM-2 and comparing with results obtained by the widely known OpenFOAM code. The solver InterFOAM was chosen, which implements a Volume of Fluid (VoF) algorithm for multi-fluid flows [36][37].

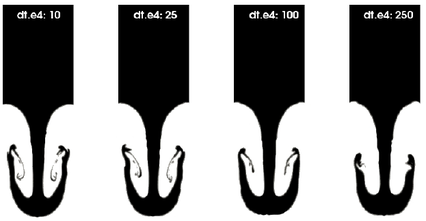
Figure 4.6 presents the comparison of the solutions with PFEM-2 and OpenFOAM

From snapshots it can be concluded that PFEM-2 yields approximately the same solution for the different time-steps. However, OpenFOAM only gives accurate results for . For larger time-steps the evolution of the mushroom-like interface differs from the reference results and this divergence is increased when the time-steps are increased. Moreover, simulations with OpenFOAM diverge when the Courant number > 0.5 is reached. This happens at different times depending on the selected time-step and also on the solver used. For instance, for an implicit solver the solution is more stable, but the results are more diffusive.

1) PFEM-2 (Lagrangian frame)

2) OpenFOAM (Eulerian frame)

Figure 4.6 Rayleigh-Taylor Instability. Different shape of the internal interface at for different time-step sizes

Another relevant feature to take into account when comparing both algorithms is that similar CPU times are required to solve a time-step.

Comparing the CPU times required to complete one second of actual time in the current case, the results show that using the same time-step both solvers have similar performance, being OpenFOAM slightly faster. However, due to the capability of increasing the time-step with PFEM-2, much smaller CPU times are achieved with similar accuracy, being the solution with PFEM-2 one order of magnitude faster than that with OpenFOAM.

5. Conclusions

The errors between the use of an Eulerian or a Lagrangian frame have been studied for the cases of linear interpolation in time and in space.

For a Lagrangian frame, there are projection errors that must be added to the space-time integration. Projection errors are of the order and must be takes into account at each time-step.

The main difference in the evaluation of the errors between the Eulerian and Lagrangian frames are for the cases of convective dominant problems (high Peclet or Reynolds number). For these cases the main conclusion is that the integration errors are proportional to:

The following highlights can be drawn from these expressions:

- Low Reynolds numbers (or low Peclet numbers) have the same integration errors in both frames. Taking into account that Lagrangian errors have also projection errors, the Eulerian frame is more competitive in these cases.

- For moderated or high Reynolds numbers are the cases that a Lagrangian frame may be competitive. In these cases, having big variations of the velocity gradients (in time or in space), but small variations of the velocity itself, improves the competitiveness of the Lagrangian frame. Contrary, stationary problems or near constant in space velocity fields make an Eulerian frame more suitable.

- In all Lagrangian frame-based methods, the use of a strategy to improve the projection errors is essential. Otherwise projection errors overweight the advantages of the accuracy in the Lagrangian integration of the convective terms.

- For heterogeneous fluids (multi-fluid, multi-phase or free-surface flows), the Lagrangian frame is more suitable because the position of the internal interfaces or the free-surface is free from the Eulerian convective errors. In such cases, a reduction of more than one order of magnitude in the total computing time has been obtained using a Lagrangian frame.

- In cases where the physics of the problem imposes very small time-steps, an Eulerian frame is more convenient because the error does not depend on .

Acknowledgements:

This research was supported by the HFLUIDS project of the National RTD Plan of the Spanish Ministry of Science and Innovation I+D BIA2010-15880; by the ERC Advanced Grant projects “REALTIME”, AdG-2009325 and “SAFECON”, AdG-267521; by the F7 PEOPLE-ITN project Multi-scale Modeling of Landslides and Debris Flows “MuMoLaDe”, REA Grant Agreement 289911; by the CONICET(Argentina) and the Universidad Nacional del Litoral (CAI+D Nro 50120110100435LI, (2011)); by the ERC Proof of Concept FORECAST (Ref. 664910) under H2020 Programme and by ANPCyT-FONCyT (Grants PICT 2013 0830). J. Gimenez and N. Nigro gratefully acknowledge also the support of CONICET and the ANPCyT, both from Argentina, through a doctoral grant from the FONCyT program.

References:

[1] J. Donea, A. Huerta, Finite Element Method for Flow Problems, John Wiley (2003)

[2] JJ Monaghan, An introduction to SPH. Comput. Phys. Comm. 48 (1988) 89-96

[3] R.A. Gingold, J.J. Monaghan, Kernel estimates as a basis for general particle methods in hydrodynamics, J. Comput. Phys. 46 (1981) 429–453

[4] R.A. Gingold, J.J. Monaghan. Smoothed particle hydrodynamics, theory and application to non-spherical stars. Mon. Not R. Astron. Soc. 181 (1997) 375–389

[5] WK Liu, S Jun, YF Zhang, Reproducing Kernel particle methods. Int. J. Numer. Meth. Fl., 20 (1995) 1081–1106

[6] S Koshizuka, H Tamako, Y Oka, A Particle Method for Incompressible Viscous Flow with Fluid Fragmentation, Comput. Fluid Dyn. J., 113 (1995) 134-147.

[7] S. Koshizuka and Y. Oka; Moving-Particle Semi-Implicit Method for Fragmentation of Incompressible Fluid; Nucl. Sci. Eng.; Vol: 123, pp: 421-434 (1996).

[8] E. Oñate, S.R. Idelsohn, O.C. Zienkiewicz, A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J. Numer. Meth. in Eng. 39 (1996) 3839-3866

[9] E. Oñate, S.R. Idelsohn, O.C. Zienkiewicz, R.L. Taylor, C. Sacco, A stabilized finite point method for analysis of fluid mechanics problems, Comput. Meth. Appl. Mech. Engrg. 139(1– 4) (1996) 315–346

[10] E. Oñate, C. Sacco, S.R. Idelsohn, A finite point method for incompressible flow problems, Comput. Visual. Sci. 2 (2000) 67–75

[11] S.R. Idelsohn, E. Oñate, N. Calvo, F. Del Pin, The meshless finite element method, Int. J. Numer. Methods Engrg. 58 (6) (2003) 893–912

[12] S.R. Idelsohn, N. Calvo, E. Oñate, Polyhedrization of an arbitrary point set, Comput. Meth. Appl. Mech. Engrg. 192 (22–24) (2003) 2649–2668

[13] S.R. Idelsohn, E. Oñate, F. Del Pin, The Particle Finite Element Method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves, Int. J. Numer. Meth. in Eng. 61(7) (2004) 964-984

[14] S.R. Idelsohn, E. Oñate, F. Del Pin, The particle finite element method a powerful tool to solve incompressible flows with free-surfaces and breaking waves, Int. J. Numer. Methods Eng., 61 (2004) 964-89

[15] S.P. Neuman, Adaptaive Eulerian-Lagrangian Finite Element Method for Advection-Dispersion; Int. J. Nume. Meth. Engineering; 20, 321-337 (1984).

[16] Brackbill and Ruppel, FLIP: A method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions, J. Comput. Phys. 65, 314-343 (1986)

[17] Z. Więckowski, The material point method in large strain engineering problems, Comput. Methods. Appl. Mech. Eng., 193.39 (2004) 4417-4438.

[18] R. Aubry, S.R. Idelsohn, E. Oñate, Particle finite element method in fluid mechanics including thermal convection–diffusion, Comput. Struct. 83 (17–18) (2005) 1459–1475

[19] E. Oñate, J. Garcia, S.R. Idelsohn, Ship Hydrodynamics. Encyclopedia of Computational Mechanics. Eds. E. Stein, R. De Borst and T.J.R. Hughes. J. Wiley (2004)

[20] S.R. Idelsohn, E. Oñate, F. Del Pin, N. Calvo, Lagrangian formulation: the only way to solve some free-surface fluid mechanics problems, H.A. Mang, F.G. Rammerstorfer, J. Eberhardsteiner (Eds.), Fifth World Congress on Computational Mechanics, July 7–12, Vienna, Austria, (2002)

[21] A. Larese, R. Rossi, E. Oñate, S.R. Idelsohn, Validation of the Particle Finite Element Method (PFEM) for Simulation of the Free-Surface Flows. Eng. Comput., 25(4) (2008), pp 385-425

[22] S.R. Idelsohn, E. Oñate, F. Del Pin, N. Calvo, Fluid–structure interaction using the particle finite element method, Comput. Meth. Appl. Mech. Engrg. 195 (2006) 2100 -2113

[23] E. Oñate, S.R. Idelsohn, M.A. Celigueta, R. Rossi. Advances in the Particle Finite Element Method for the Analysis of Fluid-Multibody Interaction and Bed Erosion in Free-surface Flows. Comput. Methods Appl. Mech. Engrg., 197 (2008) 1777-1800

[24] S.R. Idelsohn, J. Marti. A. Limache, E. Oñate, Unified Lagrangian Formulation for Elastic Solids and Incompressible Fluids. Application to Fluid-Structure Interaction Problems via the PFEM. Comput. Methods Appl. Mech. Engrg., 197 (2008), pp 1762-1776

[25] F. Del Pin, S.R. Idelsohn, E. Oñate, R. Aubry, The ALE/Lagrangian particle finite element method: a new approach to computation of free-surface flows and fluid–object interactions, Comput. Fluids 36 (2007) 27–38.

[26] J. Oliver, J.C. Cante, R. Weyler, C. Gonzalez and J. Hernandez. Particle Finite Element Methods in Solid Mechanics Problems. Computational Plasticity. Vol 7, pp 87-103; E. Oñate and R. Owen Eds.; Springer Netherlands, 2007.

[27] S.R. Idelsohn, M. Mier-Torrecilla, E. Oñate, Multi-fluid flows with the Particle Finite Element Method, Comput. Meth. Appl. Mech. Engrg., 198 (2009) 2750-2767

[28] S.R. Idelsohn, N.M. Nigro, A. Limache, E. Oñate, Large time-step explicit integration method for solving problems with dominant convection Comput. Methods Appl. Mech. Engrg., 217-220 (2012) 168-85

[29] S.R. Idelsohn, J. Marti, P. Becker, E. Oñate.; Analysis of multi-fluid flows with large time-steps using the Particle Finite Element Method; Int. J. Numer. Meth. Fl.; Vol 75, pp: 621-644, DOI: 10.1002/fld.3908, (2014).

[30] S.R. Idelsohn, N. M. Nigro, J. M. Gimenez, R. Rossi, J. Marti, A fast and accurate method to solve the incompressible Navier-Stokes equations, Eng. Computations, 30 (2) (2013) 197 – 222.

[31] O. Pironneau and M. Tabata; Stability and convergence of a Galerkin charac-teristics finite element scheme of lumped mass type; Int. J. Numer. Meth. Fl.; Vol 64; pp 1240–1253; (2010).

[32] S.J. Osher, R.P. Fedkiw, Level set methods: an overview and some recent results. J. Comput. Phys., 169 (2001) 463–502

[33] Enright, Douglas, et al. A hybrid particle level set method for improved interface capturing. J. of Comput. Phys., 183.1 (2002): 83-116.

[34] S. Zalesak; Fully multidimensional flux-corrected transport algorithms for fluids; J. Comput. Phys; 31(3); pp: 335 – 362; (1979).

[35] J. Guermond, L. Quartapelle, A projection fem for variable density incompressible flows; J. of Comput. Phys.; Vol:165167-188.; (2000).

[36] E. Berberovich, N. P. van Hinsberg, S. Jakirli, I. V. Roisman, C. Tropea; Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution; Phys. Rev. E 79 (2009) 036306. doi:10.1103/PhysRevE.79. 036306.

[37] S. Marquez Damian, N. Nigro, An extended mixture model for the simultaneous treatment of small-scale and large-scale interfaces; Int. J. Numer. Meth. Fl.; Vol. 75 Number 8, pp: 547-574 (2014); doi:10.1002/fld.3906.