A unified symmetrical formulation for interactions between elastic solids and incompressible fluids

Published in Variational Formulations in Mechanics: Theory and Applications, E. Taroco, E.A. de Souza Neto and A.A. Novotny (Eds.), CIMNE, Barcelona, Spain, 2007

Abstract

We present a general Lagrangian formulation for treating elastic solids and quasi/fully incompressible fluids in a unified form. The formulation allows to treat solid and fluid subdomains in a unified manner in fluid-structure interaction (FSI) situations. The use for both fluid and solid of a Lagrangian formulation avoid convective terms allowing to approximate the problem via a Variational Formulation. In our work the FSI problem is solved via the Particle Finite Element Method (PFEM). The PFEM is an effective technique for modeling complex interactions between floating and submerged bodies and free surface flows, accounting for splashing of waves, large motions of the bodies and frictional contact conditions. Applications of the unified Lagrangian formulation to a number of FSI problems are given.

Keywords Lagrangian formulation, fluid-structure, particle finite element method.

1 INTRODUCTION

Fluid-structure interaction (FSI) problems are typically solved with a staggered scheme [23] by which the relevant variables at the fluid and solid subdomains are separately and sequentially (and iteratively) solved using as boundary conditions at the common fluid-solid boundaries the velocities (for the fluid problem) and the surface tractions (for the solid problems). The staggered scheme is ideal for using existing finite element codes, initially developed for fluid dynamics and solid mechanics problems, and the computing effect is mainly focused on the interfacing of the relevant data between the common fluid and solid boundaries. Indeed the FSI problem typically involves the motion of mesh nodes in both the fluid and solid domains. As a consequence, an arbitrary Lagrangian-Eulerian (ALE) formulation [24] is used to model the governing equations for the fluid, while a standard Lagrangian formulation is used for the equations of the solid part.

In our work we propose a different route for solving FSI problems. Our goal is to solve the equations for both the fluid and solid domains using a unified lagrangian formulation. This basically means that the analysis domain, containing both fluid and solid subdomains which interact with each other, is seen as a single continuum domain with different material properties assigned to each of the interacting subdomains (i.e. the fluid and solid regions). This allows to make no distinction between fluids and solids for the numerical solution and a single computer code can be used for solving the FSI problem.

The governing equations for the fluid and solid domains (in a lagrangian frame of reference) are discretized and solved with the Particle Finite Element Method (PFEM). The PFEM treats the mesh nodes in the fluid and solid domains as moving material points (henceforth called particles) which can freely move and even separate from the main fluid domain representing, for instance, the effect of water drops. A finite element mesh connects the nodes defining the discretized domain where the governing equations are solved in the standard FEM fashion. The motion of the mesh discretizing the total domain (including both the fluid and solid parts) is followed during the transient solution. The PFEM is the natural evolution of recent work of the authors for the solution of FSI problems using Lagrangian finite element and meshless methods. [1],[7],[8],[10],[18],[19],[20],[28],[29],[30]

In summary, the key ingredients of the unified formulation presented in this paper are: a) the definition of a unified constitutive equation for the fluid and solid materials, b) the use of a Lagrangian description to model the kinematic of both fluid and solid domains, and c) the use of the Particle Finite Element Method (PFEM) for redefinition of the domain boundaries and the treatment of frictional contact conditions.

An obvious advantage of the Lagrangian formulation is that the convective terms disappear from the fluid equations. The remaining problem may be obtained via the minimization of a Variational Principle given symmetric operators. The difficulty is however transferred to the problem of adequately (and efficiently) moving the mesh nodes. Indeed for large mesh motions remeshing may be a frequent necessity along the time solution. We use an innovative mesh regeneration procedure blending elements of different shapes using an extended Delaunay tesselation. [7],[9] Furthermore, this special polyhedral finite element needs special shape functions. In this paper, meshless finite element (MFEM) shape functions have been used. [7] Another possibility is the use of a standard mesh generator with sliver elimination. [25] Nevertheless, standard mesh generator are some times too expensive in computational cost. An efficient mesh generator as such presented in ref. [9] is a key issue in a Lagrangian formulation.

The layout of the paper is the following. In the next section the basic ideas of the PFEM are outlined. Next the basic equation for an incompressible flow using a Lagrangian description and the elastic solid using a hypo-elastic approximation are presented. Details of the treatment of the coupled FSI problem are given. The procedures for mesh generation and for identification of the free surface nodes are briefly outlined. Finally, the efficiency of the particle finite element method (PFEM) is shown in its application to a number of FSI problems involving large flow motions, surface waves, moving bodies. etc.

2 THE BASIS OF THE PARTICLE FINITE ELEMENT METHOD

Let us define the collection or cloud of nodes (C) pertaining to the fluid and solid domains, the volume (V) defining the analysis domain for the fluid and the solid and the mesh (M) discretizing both domains.

A typical solution with the PFEM involves the following steps.

1. The starting point at each time step is the cloud of points in the fluid and solid domains. For instance ${\textstyle {}^{n}C}$ denotes the cloud at time ${\textstyle t=t_{n}}$ (Figure 1).
2. Identify the boundaries for both the fluid and solid domains defining the analysis domain ${\textstyle {}^{n}V}$ in the fluid and the solid. This is an essential step as some boundaries (such as the free surface in fluids) may be severely distorted during the solution process including separation and re-entering of nodes. This allows to model splashing of waves. The Alpha Shape method [4] is used for the boundary definition (see Section 6).
3. Discretize the fluid and solid domains with a finite element mesh ${\textstyle {}^{n}M}$. In our work we use an innovative mesh generation scheme based on the extended Delaunay tesselation. [9]
4. Solve the Lagrangian equations of motion for the fluid and the solid domains using the unified formulation proposed in this work. Compute the relevant state variables in both domains at the next (updated) configuration for ${\textstyle t+\Delta t}$: velocities, pressure and viscous stresses in the fluid and displacements, stresses and strains in the solid. Indeed this step requires an iterative scheme as large motion of both the fluid and solid domain may occur during the time step. Also material non linearities may appear in the solid although this situation is not considered in this work.
5. Move the mesh nodes to a new position ${\textstyle {}^{n+1}C}$ where ${\textstyle n+1}$ denotes the time ${\textstyle t_{n}+\Delta t}$, in terms of the time increment size. This step is typically a consequence of the solution process of step 4.
6. Go back to step 1 and repeat the solution process for the next time step.

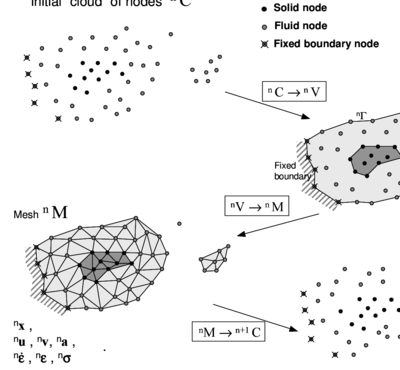
Figure 1: Sequence of steps to update a “cloud” of nodes from time $n$ ($t=t_{n}$) to time $n+1$ ($t=t_{n}+\Delta t$)

3 CONSTITUTIVE EQUATIONS TO BE USED FOR BOTH FLUID AND SOLID MATERIALS

3.1 Constitutive equations for hypo-elastic solids

Let a material with a hypo- elastic constitutive equation like:

$L(\tau _{ij})=\lambda _{s}\delta _{ij}d_{ll}+2\mu _{s}d_{ij}$

(1)

where ${\textstyle \tau _{ij}=J\sigma _{ij}}$ is the Kirchhoff stress tensor, ${\textstyle d_{ij}=\displaystyle {\frac {1}{2}}\left(\displaystyle {\partial V_{i} \over \partial x_{j}}+{\partial V_{j} \over \partial x_{i}}\right)}$ is the rate of deformation tensor, ${\textstyle V_{i}}$ the velocity along the ${\textstyle i}$th axis, ${\textstyle \sigma _{ij}}$ the Cauchy stress tensor, ${\textstyle \lambda _{s}}$ and ${\textstyle \mu _{s}}$ the Lamé parameters, ${\textstyle J={det}(F_{ij})}$ the Jacobian, being ${\textstyle F_{ij}=\displaystyle {\partial x_{i} \over \partial X_{j}}={\partial u_{i} \over \partial X_{j}}+\delta _{ij}}$ the deformation gradient tensor, ${\textstyle u_{i}}$ the ${\textstyle i}$th displacement component and ${\textstyle L(\tau _{ij})=F{\dot {S}}F^{T}}$, the time Lie derivative, with ${\textstyle S=F^{-1}\tau F^{-T}=F^{-1}\sigma F^{-T}J}$, the second Piola-Kirchhoff stress tensor.

Dividing the strain and the stress in their deviatoric (${\textstyle ^{\prime }}$) and the volumetric parts

$d_{ij}=d_{ij}'+{d_{ll} \over 3}\delta _{ij}\quad ;\quad \tau _{ij}=\tau _{ij}'+{\tau _{ll} \over 3}\delta _{ij}$

(2)

Then

$L(\tau _{ij})=\left(\lambda _{s}+{2\mu _{s} \over 3}\right)\delta _{ij}d_{ll}+2\mu _{s}d_{ij}'$

(3)

This may be split as

$L(\tau _{ij}')=2\mu _{s}d_{ij}'$ $L\left({\tau _{ll} \over 3}\right)=\left(\lambda _{s}+{2\mu _{s} \over 3}\right)d_{ll}$

(4)

The volumetric strain rate and the pressure will be written as

$\varepsilon _{v}=tr(d_{ij})=d_{ll}\quad {\hbox{and}}\quad p=tr\left(-{\sigma _{ij} \over 3}\right)=-{\sigma _{ll} \over 3}=-{\tau _{ll} \over 3J}$

(5)

Approaching the derivative in (4) by a finite time step

$\left(F{\Delta S \over \Delta t}F^{T}\right)^{\prime }=2\mu _{s}d'\quad {\hbox{and}}\quad tr\left(F{\Delta S \over 3\Delta t}F^{T}\right)=\left(\lambda _{s}+{2\mu _{s} \over 3}\right)\varepsilon _{v}$

(6)

which may be written as a function of the Cauchy stress:

$\sigma _{ij}^{'(n+1)}={\hat {\sigma }}_{ij}^{'(n)}+{2\Delta t\mu _{s} \over J}{d'}_{ij}\quad {\hbox{and}}\quad p^{n+1}-{\hat {p}}^{n}=-{\Delta t \over J}\left(\lambda _{s}+{2\mu _{s} \over 3}\right)\varepsilon _{v}$

(7)

where:

${\begin{array}{l}{\hat {\sigma }}^{(n)}=\displaystyle {FS^{n}F^{T} \over J}\quad ;\quad {\hat {\sigma }}^{'(n)}=\displaystyle {(FS^{n}F^{T})^{\prime } \over J}\\[.3cm]\displaystyle {\hat {p}}^{(n)}=\displaystyle {-tr\left[F\left(S^{n}/3\right)F^{T}\right] \over J}\quad ;\quad p^{n+1}=\displaystyle {-tr\left[F\left(S^{n+1}/3\right)F^{T}\right] \over J}\end{array}}$

(8)

In the previous equations ${\textstyle {\hat {\sigma }}^{'(n)}}$ and ${\textstyle {\hat {p}}^{(n)}}$ represent the deviatoric stress and the pressure at the beginning of the time step ${\textstyle (n)}$, but referred to the final time step configuration ${\textstyle (n+1)}$.

Finally for the hypo-elastic material the constitutive relations may be written in terms of the following three expressions:

$\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{'(n)}+{2\Delta t\mu _{s} \over J}{d'}_{ij}-p^{n+1}\delta _{ij}$ (9) $\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{(n)}+{2\Delta t\mu _{s} \over J}{d'}_{ij}+{\Delta t \over J}\left(\lambda _{s}+{2\mu _{s} \over 3}\right)\varepsilon _{v}\delta _{ij}$ (10) $\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{(n)}+{2\Delta t\mu _{s} \over J}d_{ij}+{\Delta t \over J}\lambda _{s}\varepsilon _{v}\delta _{ij}$ (11)

3.2 Constitutive relations for incompressible and quasi-incompressible fluids

For Newtonian fluid flows the standard constitutive relations are:

$\sigma _{ij}^{n+1}=2\mu {_{L}d'}_{ij}-p^{n+1}\delta _{ij}$

(12)

where ${\textstyle \mu _{L}}$ is the viscosity.

For quasi-incompressible flows, the volumetric train rate may be written as a strain function of the sound speed by:

${Dp \over Dt}\simeq {\Delta p \over \Delta t}=-C^{2}\rho \varepsilon _{v}\Rightarrow p^{n+1}=p^{n}-\Delta tC^{2}\rho \varepsilon _{v}=p^{n}-\Delta t\kappa _{l}\varepsilon _{v}$

(13)

where ${\textstyle C}$ is the sound speed and ${\textstyle \kappa _{l}=C^{2}\rho }$.

Then, the Cauchy stress tensor may be written in function of the volumetric strain rate by:

$\sigma _{ij}^{n+1}=2\mu {_{L}d'}_{ij}-p^{n}\delta _{ij}+\Delta t\kappa _{l}\varepsilon _{v}\delta _{ij}=2\mu _{L}d_{ij}-p^{n}\delta _{ij}+\left(\Delta t\kappa _{l}-{2\mu _{l} \over 3}\right)\varepsilon _{v}\delta _{ij}$

(14)

From (12-14) Newtonian constitutive relation for incompressible or near incompressible flow may be written in one of the following three manners:

$\sigma _{ij}^{n+1}=2\mu {_{L}d'}_{ij}-p^{n+1}\delta _{ij}\quad {\hbox{ (for incompressible)}}$ (15) $\sigma _{ij}^{n+1}=2\mu {_{L}d'}_{ij}-p^{n}\delta _{ij}+\Delta t\kappa _{l}\varepsilon _{v}\delta _{ij}\,\,{\hbox{ (for quasi-incompressible)}}$ (16) $\sigma _{ij}^{n+1}=2\mu _{L}d_{ij}-p^{n}\delta _{ij}+\left(\Delta t\kappa _{l}-{2\mu _{l} \over 3}\right)\varepsilon _{v}\delta _{ij}\,\,{\hbox{ (for quasi-incompressible)}}\qquad$ (17)

3.3 Unique constitutive equation for fluids and solids

In the following, only a unified constitutive equation will be used for both the elastic solid and the incompressible or nearly incompressible fluid:

$\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{(n)}+2\mu {d'}_{ij}-\Delta p^{n+1}\delta _{ij}\quad {\hbox{ (for incompressible)}}$ (18) $\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{(n)}+2\mu {d'}_{ij}+\Delta t\kappa \varepsilon _{v}\delta _{ij}\quad {\hbox{ (for quasi-incompressible)}}$ (19) $\sigma _{ij}^{n+1}={\hat {\sigma }}_{ij}^{(n)}+2\mu d_{ij}+\lambda \varepsilon _{v}\delta _{ij}\quad {\hbox{ (for quasi-incompressible)}}$ (20)

with the definitions for ${\textstyle {\hat {\sigma }}_{ij}^{(n)}}$, ${\textstyle \mu }$, ${\textstyle \lambda }$ and ${\textstyle \kappa }$ given in Table 1.

Table. 1 Definition of physical parameters

Solid	Fluid	Unique
${\hat {\sigma }}_{ij}^{(n)}$	$-p^{n}\delta _{ij}$	${\hat {\sigma }}_{ij}^{(n)}$
$\displaystyle {\Delta t\mu _{s} \over J}$	$\mu _{L}$	$\mu$
$\displaystyle {\Delta t\lambda _{s} \over J}$	$\Delta t\kappa _{l}-\displaystyle {2\mu _{l} \over 3}$	$\lambda$
$\displaystyle {1 \over J}\left(\lambda _{s}+{2\mu _{s} \over 3}\right)$	$\kappa _{l}$	$\kappa$

Eq.(18) will be used only in such cases in which all the domain or a part of the domain is totally incompressible, while Eq.(19) or (20) will be used in such cases in which all the domain may be considered as compressible or quasi-incompressible.

Then, depending of the material the following definitions will be used:

a) For the fluid

$\mu =\mu _{l}$

(21)

${\hat {\sigma }}_{ij}^{'(n)}\equiv 0$

(22)

${\hat {\sigma }}_{ij}^{(n)}=-p^{n}\delta _{ij}$

(23)

$\kappa =\kappa _{l}=C^{2}\rho _{l}$

(24)

$\lambda =\lambda _{l}=\Delta t\kappa \varepsilon _{v}$

(25)

Totally incompressible flows means ${\textstyle C=\infty }$ and then ${\textstyle \kappa =\kappa _{l}=\infty }$.

b) For the solid part:

$\mu ={\Delta t \over J}\mu _{s}={\Delta t \over J}{E \over 2(1+\nu )}$

(26)

where ${\textstyle E}$ is the Young modulus, ${\textstyle \nu }$ the Poison coefficient and ${\textstyle \lambda _{s}}$ and ${\textstyle \mu _{s}}$ the Lamé parameters.

$\lambda =\lambda _{s}={\nu E \over (1+\nu )(1-2\nu )}$

(27)

$\kappa =\kappa _{s}={1 \over J}\left(\lambda _{s}+{2\mu _{s} \over 3}\right)$

(28)

3.4 Momentum conservation equations

The standard infinitesimal momentum conservation equation may be written in a Lagrangian frame as:

$\rho a_{i}=\rho {DV_{i} \over Dt}={\partial \sigma _{ij} \over \partial x_{j}}+\rho f_{i}$

(29)

The equations are completed with the pressure-volumetric strain equations

$\varepsilon _{v}=-{\Delta p \over \kappa \Delta t}$

(30)

and the boundary conditions:

$\sigma _{ni}={\bar {\sigma }}_{ni}\quad {\hbox{on }}\Gamma _{\sigma }$

(31)

$V_{i}={\bar {V}}_{i}\quad {\hbox{on }}\Gamma _{V}$

(32)

It must be noted that the term ${\textstyle {DV_{i} \over Dt}}$, represents the time material derivative (lagrangian) of the velocity ${\textstyle {DV_{i} \over Dt}={V_{i}^{n+1}-V_{i}^{n} \over \Delta t}}$ where ${\textstyle V_{i}^{n+1}}$ represents the velocity at time ${\textstyle (n+1)}$ in the position ${\textstyle x_{i}^{n+1}}$. The convective term, normally included in the fluid mechanics equations, are not explicitly present in the lagrangian formulation.

A weighted residual method will be used to approximate above equations:

$\int _{V}W_{i}\left(\rho {DV_{i} \over Dt}-{\partial \sigma _{ij} \over \partial x_{j}}-\rho f_{i}\right)dV+\int _{\Gamma _{\sigma }}W_{i}(\sigma _{ni}-{\bar {\sigma }}_{ni})d\Gamma =0$ (33) $\int _{V}W_{p}\left(-\varepsilon _{v}-{\Delta p \over \kappa \Delta t}\right)dV=0$ (34)

In weak form:

$\int _{V}\left(W_{i}\rho {DV_{i} \over Dt}+{\partial W_{i} \over \partial x_{j}}\sigma _{ij}-W_{i}\rho f_{i}\right)dV-\int _{\Gamma _{\sigma }}W_{i}{\bar {\sigma }}_{ni}d\Gamma =0$ (35) $\int _{V}W_{p}\left(-\varepsilon _{v}-{\Delta p \over \kappa \Delta t}\right)dV=0$ (36)

4 TEMPORAL INTEGRATION OF GOVERNING EQUATIONS

Let

$a_{i}^{n+1/2}={V_{i}^{n+1}-V_{i}^{n} \over \Delta t}={a_{i}^{n+1}+a_{i}^{n} \over 2}\Rightarrow a_{i}^{n+1}=2\left({V_{i}^{n+1}-V_{i}^{n} \over \Delta t}\right)-a_{i}^{n}$

(37)

Then, at time ${\textstyle (n+1)}$ the weak form of the weighted residual equation becomes:

$\int _{V}\left(W_{i}2\rho \left({V_{i}^{n+1}-V_{i}^{n} \over \Delta t}\right)-W_{i}\rho a_{i}^{n}+{\partial W_{i} \over \partial x_{j}}\sigma _{ij}^{n+1}-W_{i}\rho f_{i}^{n+1}\right)dV-$ $\qquad -\int _{\Gamma _{\sigma }}W_{i}{\bar {\sigma }}_{ni}d\Gamma =0$ (38) $\int _{V}W_{p}\left(-\varepsilon _{v}^{n+1}-{\Delta p \over \kappa \Delta t}\right)dV=0$ (39)

In the following, the upper index ${\textstyle n+1}$ will be dropped resulting in:

$\int _{V}\left(W_{i}2\rho \left({V_{i}-V_{i}^{n} \over \Delta t}\right)-W_{i}\rho a_{i}^{n}+{\partial W_{i} \over \partial x_{j}}\sigma _{ij}-W_{i}\rho f_{i}\right)dV-\!\int _{\Gamma _{\sigma }}W_{i}{\bar {\sigma }}_{ni}d\Gamma =0$

(40)

$\int _{V}W_{p}\left(-\varepsilon _{v}-{\Delta p \over \kappa \Delta t}\right)dV=0$

(41)

4.1 Case in which all the domain may be considered as quasi-incompressible

In this case, the constitutive equations are the described in Eqs.(19) or (20). The pressure is not a state variable:

$\int _{V}\left(W_{i}2\rho \left({V_{i}-V_{i}^{n} \over \Delta t}\right)-W_{i}\rho a_{i}^{n}+{\partial W_{i} \over \partial x_{j}}({\hat {\sigma }}_{ij}^{(n)}+2\mu d_{ij}+\lambda \varepsilon _{v}\delta _{ij})-W_{i}\rho f_{i}\right)dV$ $-\int _{\Gamma _{\sigma }}W_{i}{\bar {\sigma }}_{ni}d\Gamma =0$

(42)

or

$\int _{V}\left[W_{i}(2\rho )V_{i}+\Delta t{\partial W_{i} \over \partial x_{j}}2\mu d_{ij}+\Delta t{\partial W_{i} \over \partial x_{i}}\lambda \varepsilon _{v}\right]dV=$ $\int _{V}\left[W_{i}(2\rho )V_{i}^{n}+\Delta tW_{i}\rho a_{i}^{n}+\Delta tW_{i}\rho f_{i}-\Delta t{\partial W_{i} \over \partial x_{j}}{\hat {\sigma }}_{ij}^{(n)}\right]dV+\Delta t\int _{\Gamma _{\sigma }}{\bar {\sigma }}_{ni}d\Gamma$

(43)

Spatial discretization

Each of the velocity components ${\textstyle V_{i}}$ is interpolated using the MFEM shape functions [7] as:

$V_{i}=N^{T}Q_{i}$

(44)

where ${\textstyle N^{T}}$ are the MFEM shape functions and ${\textstyle Q_{i}}$ a vector containing the nodal values of the velocity components.

For Galerkin residual approximations, the arbitrary weighting functions ${\textstyle W_{i}}$ are:

$[W_{1},W_{2},W_{3}]=\left[{\begin{matrix}N&0&0\\0&N&0\\0&0&N\end{matrix}}\right]$

(45)

The equation to be solved in matrix form becomes:

$(M_{ij}+\Delta tK_{ij})Q_{j}=G_{i}^{n}$

(46)

with

${\begin{array}{l}K_{ij}=K_{ij}^{1}+K_{ij}^{2}+K_{ij}^{3}\\[.2cm]M_{ii}=\int _{V}N(2\rho )N^{T}dV\quad ;\quad K_{ii}^{1}=\int _{V}\displaystyle {\partial N \over \partial x_{j}}(\mu )\displaystyle {\partial N^{T} \over \partial x_{j}}dV\\[.2cm]M_{ij}=K_{ij}^{1}=0\qquad \forall i\not =j\\[.2cm]K_{ij}^{2}=\int _{V}\displaystyle {\partial N \over \partial x_{j}}(\mu )\displaystyle {\partial N^{T} \over \partial x_{i}}dV\\[.2cm]K_{ij}^{3}=\int _{V}\displaystyle {\partial N \over \partial x_{i}}(\lambda )\displaystyle {\partial N^{T} \over \partial x_{j}}dV\\[.2cm]G_{i}^{n}=\int _{V}\left[N(2\rho )V_{i}^{n}+N(\Delta t\rho )a^{n}-\Delta t\displaystyle {\partial N \over \partial x_{j}}{\hat {\sigma }}_{ij}^{n}+N\Delta t\rho f_{i}\right]dV+\int _{\Gamma _{\sigma }}N\Delta t{\bar {\sigma }}_{ni}d\Gamma \end{array}}$

(47)

4.2 Case in which all the domain or a part of it must be considered as incompressible

In this case, the only possibility is to use a mixed formulation Eq.(18) using the velocity and the pressure as unknown variables. The weighted residual equation remains:

$\int _{V}\left(W_{i}2\rho \left({V_{i}-V_{i}^{n} \over \Delta t}\right)-W_{i}\rho a_{i}^{n}+{\partial W_{i} \over \partial x_{j}}({\hat {\sigma }}_{ij}^{(n)}+2\mu {d'}_{ij}-\Delta p\delta _{ij})-W_{i}\rho f_{i}\right)dV-$ $\qquad -\int _{\Gamma _{\sigma }}{\bar {\sigma }}_{ni}d\Gamma =0$ (48) $\int _{V}W_{p}\left(-\varepsilon _{v}-{\Delta p \over \kappa \Delta t}\right)dV=0$ (49)

or also

$\int _{V}\left[W_{i}(2\rho )V_{i}+\Delta t{\partial W_{i} \over \partial x_{j}}2\mu {d'}_{ij}-\Delta t{\partial W_{i} \over \partial x_{i}}\Delta p\right]dV$ $=\!\!\int _{V}\left[W_{i}(2\rho )V_{i}^{n}+\Delta tW_{i}\rho a_{i}^{n}-\Delta t{\partial W_{i} \over \partial x_{j}}{\hat {\sigma }}_{ij}^{(n)}+\Delta tW_{i}\rho f_{i}\right]dV+\Delta t\int _{\Gamma _{\sigma }}{\bar {\sigma }}_{ni}d\Gamma \quad \qquad$ (50) $\int _{V}\left[\Delta tW_{p}{\partial V_{i} \over \partial x_{i}}+W_{p}{\Delta p \over \kappa }\right]dV=0$ (51)

Taking into account the definition of the deviatoric strain rate:

$\int _{V}\left[W_{i}(2\rho )V_{i}+\Delta t{\partial W_{i} \over \partial x_{j}}\mu {\partial V_{i} \over \partial x_{i}}+\Delta {\partial W_{i} \over \partial x_{j}}\mu {\partial V_{j} \over \partial x_{i}}-\Delta t{\partial W_{i} \over \partial x_{j}}{2\mu \over 3}\varepsilon _{v}\delta _{ij}-\Delta t{\partial W_{i} \over \partial x_{i}}\Delta p\right]dV$ $=\!\!\int _{V}\left[W_{i}(2\rho )V_{i}^{n}+\Delta tW_{i}\rho a_{i}^{n}-\Delta t{\partial W_{i} \over \partial x_{j}}{\hat {\sigma }}_{ij}^{(n)}+\Delta tW_{i}\rho f_{i}\right]dV+\Delta t\int _{\Gamma _{\sigma }}{\bar {\sigma }}_{ni}d\Gamma$ (52) $\int _{V}\left[\Delta tW_{p}{\partial V_{i} \over \partial x_{i}}+W_{p}{\Delta p \over \kappa }\right]dV=0$ (53)

5 SPATIAL DISCRETIZATION

Both the velocity components and the pressure increment are discretized by

$V_{i}=N^{T}Q_{i}\quad {\hbox{and}}\quad \Delta p=N_{p}\Delta P$

(54)

The equation to be solved in matrix form becomes:

$\left\{\left[{\begin{matrix}M_{ij}&0\\0&-{1 \over \kappa }M_{pp}\end{matrix}}\right]+\Delta t\left[{\begin{matrix}K_{ij}&-B_{ip}\\-B_{pj}&0\end{matrix}}\right]\right\}\left[{\begin{matrix}Q_{i}\\\Delta P\end{matrix}}\right]=\left[{\begin{matrix}G_{i}^{n}\\0\end{matrix}}\right]$

(55)

with

${\begin{array}{l}K_{ij}=K_{ij}^{1}+K_{ij}^{2}+K_{ij}^{3}\\[.2cm]M_{ii}=\int _{V}N(2\rho )N^{T}dV\quad ;\quad K_{ii}^{1}=\int _{V}\displaystyle {\partial N \over \partial x_{j}}(\mu )\displaystyle {\partial N^{T} \over \partial x_{j}}dV\quad ;\quad M_{pp}=\int _{V}N_{p}N_{p}^{T}dV\\[.2cm]M_{ij}=K_{ij}^{1}=0\qquad \forall i\not =j\\[.2cm]K_{ij}^{2}=\int _{V}\displaystyle {\partial N \over \partial x_{j}}(\mu )\displaystyle {\partial N^{T} \over \partial x_{i}}dV\\[.2cm]K_{ij}^{3}=\int _{V}\displaystyle {\partial N \over \partial x_{i}}(-{2\mu \over 3})\displaystyle {\partial N^{T} \over \partial x_{j}}dV\\[.2cm]B_{ip}=\int _{V}\displaystyle {\partial N \over \partial x_{i}}N_{p}^{T}dV\quad ;\quad B_{pi}=\int _{V}N_{p}{\partial N^{T} \over \partial x_{i}}dV\\[.2cm]G_{i}^{n}=\int _{V}\left[N(2\rho )v_{i}^{n}+N(\Delta t\rho )a^{n}-\Delta t\displaystyle {\partial N \over \partial x_{j}}{\hat {\sigma }}_{ij}^{n}+N\Delta t\rho f_{i}\right]dV+\int _{\Gamma _{\sigma }}N\Delta t{\bar {\sigma }}_{ni}d\Gamma \end{array}}$

(56)

It must be noted that this equation must be stabilized in order to avoid wiggles in the pressure solution due to the lack of the Babuska-Brezzi conditions. In this paper a Finite Calculus (FIC) formulation will be used to stabilize the solution. [12][13][14][16]

At the end of each time step, the Cauchy stress ${\textstyle \sigma _{ij}^{n+1}}$ are evaluated and saved for the next time step. At the beginning of each time step, the previous Cauchy stress are considered as the second Piola-Kirchhoff stress for the present step and they are evaluated by

$S_{ij}^{n}\Leftarrow \sigma _{ij}^{n+1}$ ${\hat {\sigma }}^{n}=(FS^{n}F)/J$

(57)

where ${\textstyle F}$ is the deformation gradient tensor and ${\textstyle J}$ the ${\textstyle \det(F)}$ defined in Section 3.1.

6 GENERATION OF A NEW MESH AND IDENTIFICATION OF THE BOUNDARY SURFACES

One of the key points for the success of the Lagrangian formulation described here is the fast regeneration of a mesh at every time step on the basis of the position of the nodes in the space domain. In our work the mesh is generated using the so called extended Delaunay tesselation (EDT) presented in [7]-[10]. The EDT allows one to generate non standard meshes combining elements of arbitrary polyhedrical shapes (triangles, quadrilaterals and other polygons in 2D and tetrahedra, hexahedra and arbitrary polyhedra in 3D) in a computing time of order ${\textstyle n}$, where ${\textstyle n}$ is the total number of nodes in the mesh. The ${\textstyle C^{\circ }}$ continuous shape functions of the elements can be simply obtained using the so called meshless finite element interpolation (MFEM). Details of the mesh generation procedure and the derivation of the MFEM shape functions can be found in [7]-[10],[30].

Once the new mesh has been generated the numerical solution is found at each time step using the fractional step algorithm described in the previous section.

One of the main tasks in the PFEM is the correct definition of the boundary domain. Sometimes, boundary nodes are explicitly identified differently from internal nodes. In other cases, the total set of nodes is the only information available and the algorithm must recognize the boundary nodes.

The extended Delaunay partition makes it easier to recognize boundary nodes. Considering that the nodes follow a variable ${\textstyle h(x)}$ distribution, where ${\textstyle h(x)}$ is typically the minimum distance between two nodes, the following criterion has been used. All nodes on an empty sphere with a radius greater than $\alpha h$, are considered as boundary nodes. In practice ${\textstyle \alpha }$ is a parameter close to, but greater than one. This criterion is coincident with the Alpha Shape concept. [4]

Once a decision has been made concerning which nodes are on the boundaries, the boundary surface is defined by all the polyhedral surfaces (or polygons in 2D) having all their nodes on the boundary and belonging to just one polyhedron.

The correct boundary surface is important to define the normal to the surface. Moreover, in weak forms (Galerkin) such as those used here a correct evaluation of the volume domain is important. In the criterion proposed above, the error in the boundary surface definition is proportional to ${\textstyle h}$ which is an acceptable error.

The method described also allows one to identify isolated fluid particles outside the main fluid domain. These particles are treated as part of the external boundary where the pressure is fixed to the atmospheric value. We recall that each particle is a material point characterized by the density of the solid or fluid domain to which it belongs. The mass which is lost when a boundary element is eliminated due to departure of a node (a particle) from the main analysis domain is again regained when the “flying” node falls down and a new boundary element is created by the Alpha Shape algorithm when the lost node is at a distance less than ${\textstyle \alpha h}$ from the boundary.

7 EXAMPLES

The examples chosen show the applicability of the PFEM to solve problems involving large fluid motions and FSI situations.

Only quasi-incompressible materials have been used in all the examples shown in the following sections.

The use of quasi-incompressible formulation to approximate an incompressible flow has been largely used in the literature. The advantage of this approximation is that no stabilization is necessary to obtain smooth solutions. In our unique lagrangian formulation for both, the elastic solid and the incompressible flow, the advantage is more evident because both domains: the solid and the fluid may be solved identical in this case. The only difference between the solid and the fluid is the constitutive equation but both do not need the pressure as a state variable.

There is some type of fluid-structure interaction problems, named gravitational problems in which the introduction of a speed of sound much smaller than the real one do not disturb too much the results. The large majority of free-surface problem where the free-surface is in contact with the atmospheric pressure are inside this kind of gravitational problems and for this reason, the introduction of the real speed of sound is unnecessary and we can take advantage of this factor. The reader is referred to previous publications of the authors [10],[28],[29] to see 2D and 3D examples of FSI between totally incompressible fluid flows and rigid solids.

In all the examples shown bellow, the mesh in the solid domain is generated only once and then the nodes are moved without re-meshing as in a classical finite element method. The PFEM approximation described before is only used in the fluid domain. In this way, the stresses ${\textstyle {\hat {\sigma }}_{ij}^{(n)}}$ from the previous time step remain at the element level for the next time step. Nevertheless the pressure values for the fluid domain are evaluated at the node (particles) to be transmitted to next time step with a new mesh.

7.1 Elastic solid oscillation of a cantilever beam

The unified formulation presented has been widely used in fluid dynamics problems using PFEM [6],[10],[18],[20]. Lecturers are asked to read previous references for PFEM validation on fluid mechanics problems. Nevertheless, for structural problems the solution with PFEM is new. For this reason a simple a pure structural dynamic example has been tested. The free vibration of a cantilever beam subjected to a suddenly applied shear stress across the other end boundary face is shown in Figure 2. A plane strain beam with length ${\textstyle l=20}$m, height ${\textstyle h=5}$, ${\textstyle E=4.00}$GPa, Poisson's ratio = 0.32, ${\textstyle G=1.51}$GPaN/cm${\textstyle ^{2}}$ and density =1450kg/m${\textstyle ^{3}}$ was discretized using 1331 equal space particles . The total shear stress was equal to 1MPa with the upper and lower faces being traction free.

Figure 2: Cantilever beam under a shear stress at the end length: Geometry

This example was presented in [27] and compare with an analytical solution for the 1D beam theory with a correction for longitudinal shear deformation.

The maximum displacement of the beam as time function is represented in Figure 3 and compare with the analytical solution. Different time step were used in order to test de numerical diffusion of the method. Courant number equal 0.5 and 50 were tested. We can conclude that the approximation used in the solid part of the domain has a small numerical diffusion and that time step order of Courant number between 0.5 and 50 are enough to have excellent results.

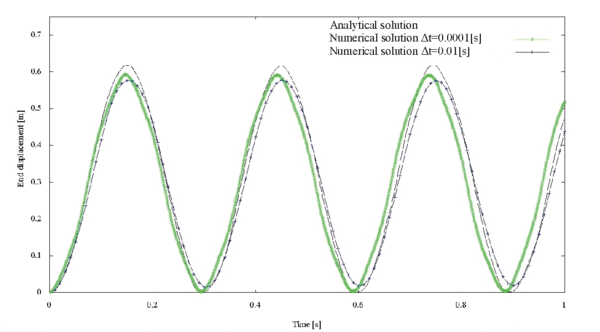
Figure 3: Cantilever beam under a shear stress at the end length: Maximum displacement for Courant numbers 0.5 and 50

7.2 Impact of waves on elastic and rigid objects

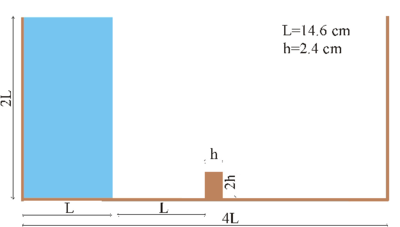
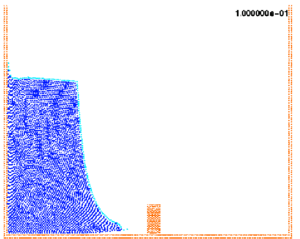
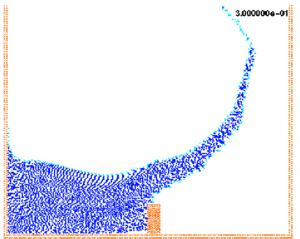
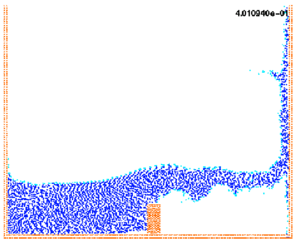
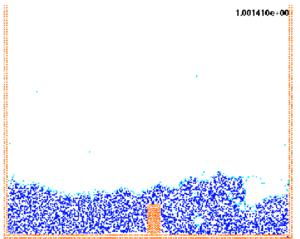
The collapse of a water column illustrated in Figure 4 is calculated using the present formulation and compared with experiment results obtained by S. Koshizuka. [11] Figure 5 shows the experimental and the numerical results at different characteristic time step.

At time 0.1 sec, the right surfaces of the water start the disturbance due to the obstacle. At time 0.2 sec, the water surface is completely disturbed by the obstacle. The results compare very well with the experimental results. At 0.3 sec. the collapsed water crashes to the right wall. At 0.4 sec, the water goes up along the right wall with separations and several drops. Finally, at 1,0 sec, the water along the right wall falls down and a new breaking wave will soon occur on the left wall.

Figure 4: Initial geometry of the water column

Figure 5: Comparison between experimental and numerical results of the collapse of a water column with an obstacle

After 0.4 sec a large deviation between the experimental results and the numerical one is observed. The reason is that the experimental results were performed in recipient with water in contact with the external air. After 0.4 sec, an air bubble is formed with the jet of water and the recipient. This incompressible air bubble changes significantly the experimental results.

In order to improve the numerical results, the same problem was solved including the recipient water and air. Figure 6 shows the new results in which the air is represented by a fluid with their corresponding density and viscosity. The results are now in a better agreement with the experimental ones and show the powerful of the PFEM to handle large differences in fluid physical characteristic.

Figure 6: Comparison between experimental and numerical results of the collapse of a water column with an obstacle. Case with water and air.

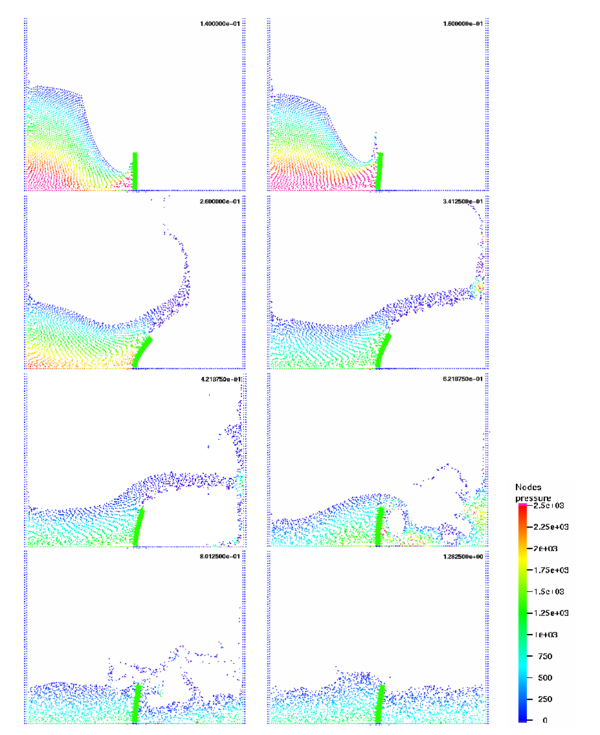
Figure 7 represents the same problem but with a elastic obstacle with density ${\textstyle \rho =2500[kg/m^{3}]}$, Young's modulus ${\textstyle E=10^{6}[kg/s^{2}m]}$ and Poisson's ratio ${\textstyle \nu =0}$. The geometry of the more slender obstacle is of width ${\textstyle h=1.2[cm]}$ and height ${\textstyle 20/3\cdot h}$. This example was also solved in Ref. [26] with a staggered and level-set method for the free surface flow. A unified formulation for incompressible flow and for the flexible obstacle has been used in this paper. No experimental results have been found for this example, but the shape of the deformation of the elastic beam as well as the free surface perturbation seems to be in agreement with the physics of the problem.

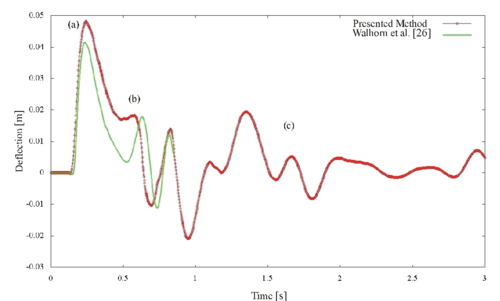
The left upper corner of the solid first gets a defection to the left when the water acts on its lower part and moves to the right while the water rises. It obtains its maximum deflection (mark (a) in Figure 8) when the water jet passes the top and is fully attached to the left side of the solid. Finally, the impact of the fluid causes the thin solid to start oscillating (b). This oscillation is damped (c) by the water located left and right of the wall. The results obtained in Ref. [26] are also presented in Figure 8.

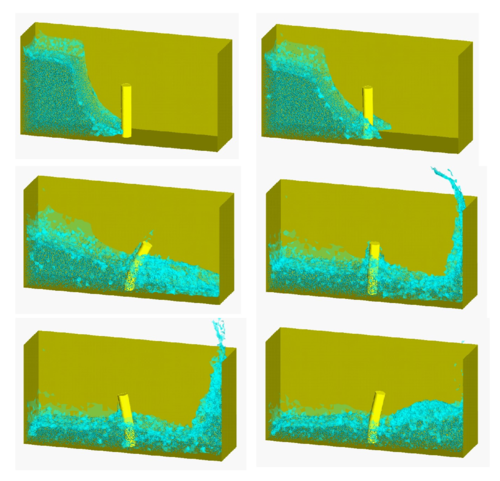
Finally, Figure 9 shows a 3D solution with a cylindrical elastic obstacle. The figure shows the elastic deflection of the beam at different time steps. Experimental results are not finished for this example, but the results seems to be in agreement with the physical of the problem.

Figure 7: Collapse of a water column with an elastic obstacle

]

Figure 8: Collapse of a water column with an elastic obstacle: History of the displacement and comparison with Ref. [26]

Figure 9: 3D collapse of a water column with an elastic cylindrical obstacle

ACKNOWLEDGEMENTS

The authors thank Prof. J. Oliver, Drs. R. Rossi and A. Limache for many useful discussions. This work was partially supported by project SEDUREC of the Consolider Programme of the Ministerio de Educación y Ciencia of Spain. This work was supported by the Programme Alban, the European Union Programme of High Level Scholarships for Latin America, scholarship No.E06D100984AR.

References

[1] R. Aubry, S.R. Idelsohn, E. Oñate. Particle finite element method in fluid mechanics including thermal convection-diffusion. Computer & Structures , 83 (17-18), 1459–1475, (2005).

[2] R. Codina, O.C. Zienkiewicz. CBS versus GLS stabilization of the incompressible Navier-Stokes equations and the role of the time step as stabilization parameter. Communications in Numerical Methods in Engineering, 18 (2), 99–112, (2002).

[3] J. Donea, A. Huerta. Finite element method for flow problems. J. Wiley, (2003).

[4] H. Edelsbrunner, E.P. Mucke. Three dimensional alpha shapes. ACM Trans. Graphics, 13, 43–72, (1999).

[5] J. García, E. Oñate. An unstructured finite element solver for ship hydrodynamic problems. J. Appl. Mech., 70, 18–26 January, (2003).

[6] S.R. Idelsohn, E. Oñate, F. Del Pin, N. Calvo. Lagrangian formulation: the only way to solve some free-surface fluid mechanics problems. Fith World Congress on Computational Mechanics, Mang HA, Rammerstorfer FG, Eberhardsteiner J (eds), July 7–12, Viena, Austria, (2002).

[7] S.R. Idelsohn, E. Oñate, N. Calvo, F. Del Pin. The meshless finite element method. Int. J. Num. Meth. Engng. 58 (6), 893–912, (2003a).

[8] S.R. Idelsohn, E. Oñate, F. Del Pin. A lagrangian meshless finite element method applied to fluid-structure interaction problems. Computer and Structures, 81, 655–671, (2003b).

[9] S.R. Idelsohn, N. Calvo, E. Oñate. Polyhedrization of an arbitrary point set. Comput. Method Appl. Mech. Engng. 192 (22-24), 2649–2668, (2003c).

[10] S.R. Idelsohn, E. Oñate, F. Del Pin. The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Num. Meth. Engng., 61, 964-989, (2004).

[11] S. Koshizuka, H. Tamko, Y. Oka, A particle method for incompressible viscous flow with fluid fragmentation. Comp. Fluid Dynamic Journal, 4, (1), 29–46, (1995).

[12] E. Oñate. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engng., 151, 233–267, (1998).

[13] E. Oñate. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comp. Meth. Appl. Mech. Engng., 182(1–2), 355–370, (2000).

[14] E. Oñate. Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng., 60(1), 255–281, (2004).

[15] E. Oñate, S.R. Idelsohn. A mesh free finite point method for advective-diffusive transport and fluid flow problems. Computational Mechanics, 21, 283–292, (1998).

[16] E. Oñate, J. García. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. Comput. Meth. Appl. Mech. Engrg., 191, 635–660, (2001).

[17] E. Oñate, C. Sacco, S.R. Idelsohn. A finite point method for incompressible flow problems. Comput. Visual. in Science, 2, 67–75, (2000).

[18] E. Oñate, S.R. Idelsohn, F. Del Pin. Lagrangian formulation for incompressible fluids using finite calculus and the finite element method. Numerical Methods for Scientific Computing Variational Problems and Applications, Y Kuznetsov, P Neittanmaki, O Pironneau (Eds.), CIMNE, Barcelona, (2003).

[19] E. Oñate, J. García, S.R. Idelsohn. Ship hydrodynamics. Encyclopedia of Computational Mechanics, E Stein, R de Borst, T.J.R. Hughes (Eds), J. Wiley, (2004a).

[20] E. Oñate, S.R. Idelsohn, F. Del Pin, R. Aubry. The particle finite element method. An overview. Int. J. Comput. Methods, 1(2), 267-307, (2004b).

[21] O.C. Zienkiewicz, R.L. Taylor, P. Nithiarasu. The finite element method for fluid dynamics. Elsevier, (2006).

[22] O.C. Zienkiewicz, R.L. Taylor, The finite element method for solid and structural mechanics. Elsevier, (2005).

[23] Ch. Farhat, G. Kristoffer, V. Zee, Ph. Geozine. Probably second-order time accurate loosely-coupled solution algorithm for transient nonlinear computational aeroelasticity. Comput. Meth. Appl. Mech. Engrg., 195(17–18), 1973–2001, (2006).

[24] Ch. Foster, W.A. Wall, E. Ramm. Artificial added mass instabiliting in sequential staggered coupling of nonlinear structures and incompressible flows. Comput. Meth. Appl. Mech. Engrg., 196, 1278–1293, (2007).

[25] R. Lohner. A parallel advancing front grid generation scheme. AIAA, 00-1005, (2000).

[26] E. Walhorn, A. Kolke, B. Hubner, D. Dinkler. Fluid-structure coupling with monolithic model involving free surface flows. Computers & Structures, 83, 2100–2111, (2005).

[27] C.J. Greenshields, H.G. Weller. A unified formulation for continuum mechanics applied to fluid-structure interaction in flexible tubes. Int. J. Num. Meth. Engng., 64, 1575–1593. (2005).

[28] F. Del Pin, S.R. Idelsohn, E. Oñate, R. Aubry. The ALE/Lagrangian Particle Finite Element Method: A new approach to computation of free-surface flows and fluid-object interactions. Computers and Fluids, 36 (1), 27–38 (2007).

[29] R. Aubry, S.R. Idelsohn and E. Oñate. Fractional step like schemes for free-surface problems with thermal coupling using the Lagranguan PFEM. Computational Mechanics, 38 (4-5), 294–309. (2006).

[30] S.R. Idelsohn and E. Oñate. To mesh or not to mesh. That is the question..., Computer Methods in Applied Mechanics and Engineering, 195 (37-40), 4681–4696, (2006).