Buckling of composite material panels with holes

1. Introduction

Buckling is a key sizing driver on the design process of composite panels used in the aerospace industry. Therefore, a wide variety of methods have been developed to determine the critical buckling load of structures, from simple analytical solutions to more complex finite element methods.

Typically, during the structural sizing process the methodology to be used for panel stability is gradually evolving from simplified closed formulae using basic panel idealization thru mathematical energy based methods with stiffened panel idealization and concluding with complex finite analysis models including detailed component idealization called virtual testing.

The state of the art of mathematical approach is limited to rectangular solid stiffened panels. In this paper an evolution from solid to holed panels, including non-rectangular panels, submitted to any in-plane load combination is proposed.

Several hole shapes and panels with anisotropic lay-ups are considered. Panel thickness evolution is not considered in the theory development, however the capability of doing panel assemblies using this methodology override this limitation.

2. Method description

A brief energy method basis is described below.

2.1. Energy method

The Rayleigh-Ritz procedure is a well know energy method based on the principle of virtual work, which states that a continuous body is in equilibrium if and only if the virtual work of all forces, internal ${\textstyle ({\delta W}_{I})}$ and external ${\textstyle ({\delta W}_{E})}$, acting on the body is zero under a virtual displacement (Ref [1]):

${\delta W=\delta W}_{I}+{\delta W}_{E}=0$

(1)

The virtual work done by actual body forces ${\textstyle {\overset {\rightarrow }{f}}}$ and surface forces ${\textstyle {\overset {\rightarrow }{t}}}$ moving through the virtual displacement ${\textstyle {\overset {\rightarrow }{\delta u}}}$ is:

${\delta W}_{E}=-\left(\int _{\Omega }^{}{\overset {\rightarrow }{f}}\cdot {\overset {\rightarrow }{\delta u}}d\Omega +\right.$$\left.\int _{S\Omega }^{}{\overset {\rightarrow }{t}}\cdot {\overset {\rightarrow }{\delta u}}dS\right)$

(2)

And the total internal virtual work stored in the body is:

${\delta W}_{I}=\int _{\Omega }^{}\sigma \cdot \delta \epsilon d\Omega$

(3)

When the equation is applied to elastic bodies, the strain density function ${\textstyle u}$ exists such that ${\textstyle \sigma =}$${\frac {\delta u}{\delta \epsilon }}$ and the principle of virtual work can be transformed into a minimization problem known as Principle of Minimum Total Potential Energy.

$\delta W=\int _{\Omega }^{}\sigma \cdot \delta \epsilon d\Omega -\left(\int _{\Omega }^{}{\overset {\rightarrow }{f}}\cdot {\overset {\rightarrow }{\delta u}}d\Omega +\right.$$\left.\int _{S\Omega }^{}{\overset {\rightarrow }{t}}\cdot {\overset {\rightarrow }{\delta u}}dS\right)=$$\int _{\Omega }^{}{\frac {\delta u}{\delta \epsilon }}\cdot \delta \epsilon d\Omega +\delta V=\,\delta U+$$\delta V\equiv \delta \Pi$

(4)

The sum ${\textstyle U+V=\Pi }$ is the total potential energy and the body is in equilibrium when the variation of this magnitude is null, reaching ${\textstyle \Pi \,}$ a minimum.

2.2. Rayleigh-Ritz approach

The Rayleigh-Ritz procedure consist on expressing the potential energy functional ${\textstyle \Pi \,}$ as a function of the plate displacements. In the literature, this deflection shape is approximated by a trigonometric series which it must comply with the boundary conditions. For instance for simply supported conditions trigonometric series of sins are recommended.

But other formulations can be used like Chebyshev polynomials (Ref [2]). It has been considered due to their superior rate of convergence and the accumulated experience with them in previous works.

${w}_{0}=\sum _{i}^{}\sum _{j}^{}{w}_{ij}{T}^{i}\left(x\right){T}^{j}\left(y\right)=$$\sum _{i}^{}\sum _{j}^{}{w}_{ij}\,cos\left(i\xi \right)\,cos(j\eta )$

(4)

For the sake of simplicity, only the terms depending on the perpendicular displacements are retained on this paper, but the method is applicable to all the degrees of freedom of the plate including in-plane displacements.

Introducing this deflection shape function into the potential energy function ${\textstyle \Pi \,}$ defined in the previous section a function depending only on the solution unknowns ${\textstyle {w}_{ij}}$ is obtained. The equilibrium of the structure is reached, according to the principle of minimum total potential energy, by obtaining the minimum of the function with respect to the unknown coefficients.

3. Application to holed panels

3.1. Definition of the change of variable

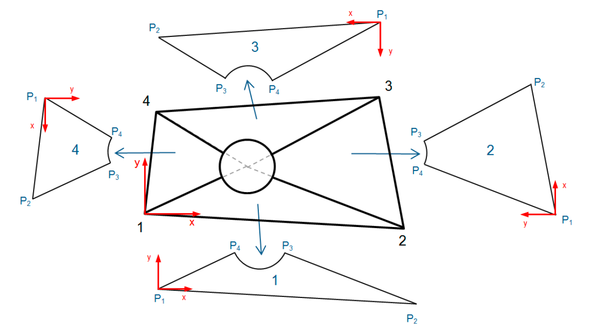
As it was explained in the introduction, the energy methods are typically limited to basic geometries due to the difficulty of finding a shape function that defines the panel deflection along the integration domain while fulfilling the boundary conditions. To solve this constraint, it is necessary to carry out a transformation of the domain of integration, switching from ${\textstyle (x,y)}$ to ${\textstyle (\xi ,\eta )}$ , using a variable change and a panel division that will allow to convert the holed panel into an assembly of 4 basic rectangular panels, which constitutes one of the innovations of this work.

The panel will be divided in four sub-panels so that the holed edge is split in four edges, each one belonging to one of the sub-panels. The division is made joining the center of the hole with the four corners of the panel, as shown in next figure (1).

Figure 1: Panel division into sub-panels

Each of these sub-panels is transformed into an iso-parametric square with sides of length 2, with the new axes ${\textstyle (\xi ,\eta )}$ passing through the midpoint of each edge:

Figure 2: Transformed element

3.2. Strain Energy and work of the external loads

Once the change of variable has been defined to simplify the problem, the Rayleigh-Ritz procedure defined in the previous chapter is now applied to the assembly of the panels. Therefore, the Total Potential energy result from the internal strain energy and the work performed by the external loads:

$\Pi =\sum _{k=1}^{4}(U+V)$

(5)

For a laminated plate of anisotropic material, the internal strain energy including the coupling effect is:

$U={\frac {1}{2}}\int \!\int _{A}^{}({N}_{x}{\epsilon }_{x}+{N}_{y}{\epsilon }_{y}+{N}_{xy}{\epsilon }_{xy}+{M}_{x}{\kappa }_{x}+{M}_{y}{\kappa }_{y}+{M}_{xy}{\kappa }_{xy})dxdy$

(6)

Taking into account the classical laminate theory (Ref [3]), the strain at any ply of the laminate can be expressed as the addition of the mid-plane strain and the curvature contribution:

${\left\{\epsilon \right\}}_{k}=\left\{{\epsilon }^{0}\right\}+{\underline {z}}_{k}\left\{\kappa \right\}$

(7)

${\left\{{\begin{matrix}{\epsilon }_{x}^{0}\\{\epsilon }_{y}^{0}\\{\gamma }_{xy}^{0}\end{matrix}}\right\}}_{k}=$$\left\{{\begin{matrix}{\frac {\partial u}{\partial x}}\\{\frac {\partial v}{\partial y}}\\{\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}\end{matrix}}\right\}\,\,;\,{\left\{{\begin{matrix}{\kappa }_{x}\\{\kappa }_{y}\\{\kappa }_{xy}\end{matrix}}\right\}}_{k}=$$\left\{{\begin{matrix}-{\frac {{\partial }^{2}w}{\partial {x}^{2}}}\\-{\frac {{\partial }^{2}w}{\partial {xy}^{2}}}\\-2{\frac {{\partial }^{2}w}{\partial x\partial y}}\end{matrix}}\right\}\,\,$

(8)

Where the mid-plane strain and the curvature can be expressed in terms of the displacements field as follows:

Joining the last two equations into equation (9), leads to:

$\delta U={\frac {1}{2}}\sum _{k=1}^{N}\int _{0}^{{a}_{k}}\int _{0}^{{b}_{k}}\left[{\left\{{\epsilon }^{0}\right\}}_{k}^{T}{\left[A\right]}_{k}{\left\{{\epsilon }^{0}\right\}}_{k}+2{\left\{{\epsilon }^{0}\right\}}_{k}^{T}{\left[B\right]}_{k}{\left\{\kappa \right\}}_{k}+{\left\{\kappa \right\}}_{k}^{T}{\left[D\right]}_{k}{\left\{\kappa \right\}}_{k}\right]dxdy$

(10)

Where the index k denotes the sub-panel identification and [A], [B] and [D] are the laminate stiffness matrices according to the classical laminate theory.

The same way, the work done by the external loads for each sub-panel is defined as follows:

$V=\,\sum _{k=1}^{4}\left(\int \!\int _{}^{}\left[{N}_{x}{\frac {\partial {u}^{k}}{\partial x}}+{N}_{y}{\frac {\partial {v}^{k}}{\partial y}}+{N}_{x}\left({\frac {\partial {u}^{k}}{\partial y}}+{\frac {\partial {v}^{k}}{\partial x}}\right)\right]\right)+$${\frac {1}{2}}\int \!\int _{}^{}\left[{N}_{x}{\left({\frac {\partial {w}^{k}}{\partial x}}\right)}^{2}+{N}_{y}{\left({\frac {\partial {w}^{k}}{\partial y}}\right)}^{2}+{2N}_{xy}{\frac {\partial {w}^{k}}{\partial x}}{\frac {\partial {w}^{k}}{\partial y}}\right]$

(11)

3.3. Optimization problem

As previously indicated, the minimum potential energy principle leads to an optimization problem to obtain the solution. The boundary conditions are imposed by means of a set of linear equations that the coefficients of the shape function have to fulfill:

$\left[C\right]\left\{S\right\}=\left\{d\right\}$

(12)

Where {S} is a compact form of all the unknown coefficients, d represents the independent term and [C] is the matrix of coefficients derived from the boundary equations imposition.

The minimization of function ${\textstyle \Pi }$ together with the set of constraints in the unknown coefficients lead to a constrained optimization that can be transformed into an unconstrained one by means of the Lagrange multipliers method. This method reduces the problem with n variables and I constraints to a new system with ${\textstyle (n+}$$i)$ variables without any constraints.

A new objective function is defined adding to the original function ${\textstyle \Pi }$ the constraints equations multiplied by arbitrary parameters ${\textstyle {\lambda }_{i}}$ (Lagrange multipliers):

${\Pi }_{2}=\Pi +\sum _{}^{}{\lambda }_{i}\cdot {f}_{i}\left({w}_{1},{w}_{2},\ldots ,{w}_{N}\right)$

(13)

In this case, the structure is composed by 4 interconnected panels, therefore, the modified total potential energy ${\textstyle {\Pi }_{2}}$ has to be computed for the complete structure as the sum of the total potential energy of each individual panel in addition to the terms coming from the Lagrange multipliers method:

${\Pi }_{2}=\sum _{i=1}^{M}{U}_{i}\left({c}_{1}^{i},\ldots ,{c}_{N}^{i}\right)+\sum _{i=1}^{M}{V}_{i}\left({c}_{1}^{i},\ldots ,{c}_{N}^{i}\right)+\sum _{i=1}^{{N}_{c}}{\lambda }_{i}{e}_{i}\left({c}_{1}^{i},\ldots ,{c}_{N}^{i},\ldots ,{c}_{1}^{M},\ldots ,{c}_{N}^{M},{d}_{i}\right)$

(14)

Being the expression of the strain energy and the external forces work quadratic in the coefficients, once they bare derived with respect to these coefficients a linear system of equations is obtained, that can be expressed in matrix form as follows:

$\left[U\right]\left\{{S}_{i}\right\}+\rho \left[C\right]\left\{S\right\}+$${\left[C\right]}^{T}\left\{\lambda \right\}=\left\{T\right\}$	(14)
$\left[C\right]\left\{S\right\}=\left\{d\right\}$	(15)

Some of the unknown coefficients will not be independent but can be derived from the relations imposed by the boundary conditions. To identify the dependent coefficients, the rectangular matrix [C] used to define the restrictions can be transformed by reordering the unknown coefficients rewriting the set of equations as shown below:

$\left[{\begin{matrix}{\left[U\right]}_{d}&{\left[U\right]}_{id}\\{\left[U\right]}_{di}&{\left[U\right]}_{i}\end{matrix}}\right]\left\{{\begin{matrix}{\left\{c\right\}}_{d}\\{\left\{c\right\}}_{i}\end{matrix}}\right\}+$$\rho \left[{\begin{matrix}{\left[V\right]}_{d}&{\left[V\right]}_{id}\\{\left[V\right]}_{di}&{\left[V\right]}_{i}\end{matrix}}\right]\left\{{\begin{matrix}{\left\{c\right\}}_{d}\\{\left\{c\right\}}_{i}\end{matrix}}\right\}+$$\left[{\begin{matrix}{\left[C\right]}_{d}^{T}\\{\left[C\right]}_{i}^{T}\end{matrix}}\right]\left\{\lambda \right\}=$$\left\{{\begin{matrix}{\left\{T\right\}}_{d}\\{\left\{T\right\}}_{i}\end{matrix}}\right\}$

(16)

$\left[{\begin{matrix}{\left[C\right]}_{d}&{\left[C\right]}_{i}\end{matrix}}\right]\left\{{\begin{matrix}{\left\{c\right\}}_{d}\\{\left\{c\right\}}_{i}\end{matrix}}\right\}=$$\lbrace d\rbrace$

(17)

${\textstyle {\left[C\right]}_{d}}$ is a square non-singular matrix and ${\textstyle \,{\left\{c\right\}}_{d}\,\,}$ are the dependent coefficients that can be derived from the independent coefficients ${\textstyle {\left\{c\right\}}_{i}}$:

${\lbrace c\rbrace }_{d}={\left[C\right]}_{d}^{-1}(\left\{d\rbrace +{\left[C\right]}_{i}{\lbrace c\rbrace }_{i}\right)$

(18)

Substituting ${\textstyle \,{\left\{c\right\}}_{d}}$ and removing ${\textstyle \lbrace \lambda \rbrace }$ the following system is obtained to determine ${\textstyle \,\left\{{c}_{i}\right\}}$  :

$\left(\left[{U}_{s}\right]+\rho \left[{V}_{s}\right]\right)\left\{{c}_{i}\right\}=$$\lbrace {d}_{s}\rbrace$

(19)

Where:

$\left[{U}_{s}\right]=\left({\left[U\right]}_{i}-{\left[U\right]}_{di}{\left[C\right]}_{d}^{-1}{\left[C\right]}_{i}+\right.$$\left.{\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}{\left[U\right]}_{d}{\left[C\right]}_{d}^{-1}{\left[C\right]}_{i}-\right.$$\left.{\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}{\left[U\right]}_{id}\right)$	(20)
$\left[{V}_{s}\right]=\left({\left[V\right]}_{i}-{\left[V\right]}_{di}{\left[C\right]}_{d}^{-1}{\left[C\right]}_{i}+\right.$$\left.{\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}{\left[V\right]}_{d}{\left[C\right]}_{d}^{-1}{\left[C\right]}_{i}-\right.$$\left.{\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}{\left[V\right]}_{id}\right)$	(21)
$\left\{{d}_{s}\right\}{=\lbrace T\rbrace }_{i}-{\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}{\left\{T\right\}}_{d}+$${\left[C\right]}_{i}^{T}{\left({\left[C\right]}_{d}^{T}\right)}^{-1}\left({\left[U\right]}_{d}+\right.$$\left.\rho {\left[V\right]}_{d}\right){\left[C\right]}_{d}^{-1}\left\{d\right\}-$$\left({\left[U\right]}_{di}+\rho {\left[V\right]}_{di}\right){\left[C\right]}_{d}^{-1}\left\{d\right\}$	(22)

The buckling onset of the structure is obtained from the indeterminate solution of this system, giving rise to an eigenvalue problem providing the buckling load level corresponding to each buckling mode (eigenvalues) and the corresponding buckling deflection shape (eigenvectors).

$\mathrm {det} \,\left(\left[{U}_{s}\right]+\rho \left[{V}_{s}\right]\right)=$$0$

(23)

4. Results

In order to verify the correctness of the method, the results for a single panel subjected to different loading combinations and imposing different boundary conditions are compared against FE results (NASTRAN).

The following table (1) summarizes the geometry and properties used:

Parameter	Units	Value
Ply thickness	mm	0.184
Layup	-	[45,-45,0,90]s
Loading	N/mm	-1

Table 1: Single panel boundary conditions validation.

The panel is always simply supported for the following scenarios, except for the free edge section where one of the sides has been left free.

The method has been implemented in a software program that has been called BUHO which stands for “BUckling of composite panels with HOles”.

4.1. Rectangular panels

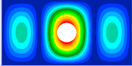
The next table (2) show the first two buckling modes for a 400x200 panel with longitudinal compression loading ( ${\textstyle {N}_{x}}$ = -1 N/mm) and a hole located in the center of the panel, with a radius varying from 10 mm to 70 mm.

Radius	10		30
	Mode 1	Mode 2	Mode 1	Mode 2
BUHO
NASTRAN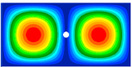
Error	1.5%	0.6%	0.9%	0.7%

Radius	50		70
	Mode 1	Mode 2	Mode 1	Mode 2
BUHO
NASTRAN
Error	1.2%	0.8%	1.4%	0.8%

Table 2: Comparison for a 400x200 rectangular panel with Nx

4.2. Trapezoidal panels

Next table (3) shows a trapezoidal panel loaded with N_x, N_y and N_xy and the same radius as the previous scenario. In this case it can be seen that, when the hole is too close to the edge, the division of the sub-panels is too deformed and could potentially lead to a higher error between Nastran and the method.

Radius	10		30
	Mode 1	Mode 2	Mode 1	Mode 2
BUHO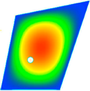
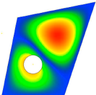
NASTRAN
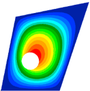
Error	2.5%	1.6%	3.1%	1.8%

Radius	50		70
	Mode 1	Mode 2	Mode 1	Mode 2
BUHO
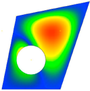
NASTRAN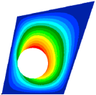
Error	4.3%	3.3%	6.4%	-4.8%

Table 3: Comparison for a trapezoidal panel with Nx, Ny Nxy

4.3. Free Edge

One of the advantages of using Chebyshev polynomials is that the boundary conditions are not imposed, as it was explained in the previous section. In the next table (4) it will be shown an example where one of the edges has been left free to illustrate that the results are equally good. The panel is loaded with N_x.

Radius	10						30
	Mode 1	Mode 2					Mode 1					Mode 2
BUHO
NASTRAN
Error	3.0%	1.3%					2.1%					2.8%
Radius	50										70
	Mode 1					Mode 2					Mode 1					Mode 2
BUHO
NASTRAN
Error	3.7%					4.5%					4.4%					4.6%

Table 4: Comparison for a free-edge panel with Nx

5. Conclusions and future developments

The most significant advantages of using the program instead of Nastran and conventional methods are:

• More accuracy than simple analytical procedures and as same level of FE analysis for simple boundary conditions.

• Less calculation time compared to finite element methods, being remarkable when lots of cases are studied.

• Possibility of making parametric analysis, not depending on any meshing of the geometry.

• Potential integration of the method in more complex tools.

• Cost saving due to the reduction in analysis time and the commercial software licenses.

• Implementation of this failure method in thorough structural analysis of components, such as stringers and skin.

• Local versus global buckling criterion can be implemented.

In order to account for all real scenarios, the number of different shapes of holes should be increased. Accessibility, associated structure and structural requirements are some of the variables when deciding the shape of the hole to be applied on the panel. The methodology to include these shapes will be the same, applying a different change of variable for each case.

In some cases, the panel needs to be reinforced to increase its stiffness, leading to the addition of longitudinal or transverse stiffeners, as it is shown in the next figure (3):

Figure 3: Thickness reinforcement around the web of the hole.

This scenario would be approached by placing the stiffener in one of the edges, so when the panel division is performed, the stringer is not deformed. In addition, the strain energy and the external forces work for each stiffener should be added to the overall solution.

The developed method in this work considers the Classical laminate theory in which the transverse shear effect is neglected. It happens when a high stiffness is supposed, which means that the normal of the mid-plane remains straight according to the curvature radius of the mid-plane after deflection. The hypothesis is valid for thin panels, but implies that results are non-conservative. Therefore, buckling could occur sooner than expected when the relation between the width of the panel and its thickness is high enough. This effect is not significant for the cases studied in the project; however, the addition of this step constitutes a natural next step.

References

[1]	J. Reddy, Energy Principles and variational methods in applied mechanics, Texas: Texas A&M University, 1984.
[2]	D. H. John.C. Mason, Chebysehv Polynomials, 2002.
[3]	S. G. Kollár LP, Mechanics of Composite Structures, Cambridge: Cambridge University Press, 2003.
[4]	M. H. Collado, Buckling Insability of Composite Material Panels with Holes, Master Thesis, 2018.