Non-linear sloshing effect on storage tanks subjected to high earthquake ground motion

Resumen

En este trabajo se propone una técnica numérica para el análisis sísmico de tanques rectangulares y cilíndricos considerando los efectos hidrodinámicos no lineales. Las ecuaciones de movimiento son mapeadas de un dominio físico a un dominio computacional por medio de un cambio de variable y la solución numérica se obtiene por medio de diferencias finitas. El sistema de ecuaciones de segundo orden obtenido en la discretización se linealiza usando el método de Newton y se resuelve empleando el método del gradiente biconjugado. La formulación numérica se aplica en tanques sometidos a movimientos símicos registrados en la ciudad de México en septiembre de 1985. Los resultados de la respuesta están dados en términos de altura de la superficie del líquido, fuerza cortante y momento de volteo en la base de la pared; y se comparan con los obtenidos con la solución lineal.

Abstract

A numerical method is proposed for the seismic response analysis of rectangular and cylindrical tanks accounting for non-linear hydrodynamic effects. The equations of motion are mapped from the physical to the computational domain by means of a change of variable. The numerical solution is then obtained by means of finite differences. The system of second order equations obtained from the finite difference discretization are linearized using the Newton method and solved numerically by means of the biconjugate gradient method. The numerical formulation was applied to study the response of tanks subjected to ground motion records from the Mexico earthquake of 19 September 1985, obtained in Mexico City. Response results are given in terms of wave height on the liquid surface, and shear force and overturning moment at the base wall, and are compared with those obtained for the linear solution.

Palabras clave

Oleaje no lineal ; Tanques cilíndricos ; Tanques rectangulares ; Respuesta sísmica ; Efectos hidrodinámicos no lineales

Keywords

Non-linear sloshing ; Cylindrical tanks ; Rectangular tanks ; Seismic response ; Non-linear hydrodynamic effects

1. Introducción

Debido a su importancia, los tanques de almacenamiento de líquidos se consideran estructuras del grupo A, es decir, en caso de la ocurrencia de un evento sísmico, estos deben permanecer funcionando. La falla de algún contenedor puede ocasionar contaminación atmosférica, pérdida de líquido, explosiones o daños secundarios debido a la pérdida de agua potable en caso de que la contenga. En la literatura se han reportado daños severos en tanques de almacenamiento de líquidos durante temblores como los de Alaska (1964), Nigata (1964), California (1980), Colinga (1983), Northridge (1994) [1] y Kocaeli (1999) [2] . Se observaron daños en la cubierta por la magnitud del oleaje en la superficie libre del líquido, pandeo en las paredes del tanque, daño en soldaduras y roturas entre la pared del tanque y el anillo de cimentación, así como levantamiento de la placa base. El sismo de Kocaeli en Turquía (1999) produjo fallas en las conexiones de las tuberías de alimentación debidas a momentos de volteo excesivos.

Los tanques para almacenar líquidos pueden construirse con concreto armado o con acero estructural y pueden tener forma cilíndrica o rectangular y estar anclados o simplemente apoyados a la cimentación, la cual se puede considerar flexible o rígida. Dependiendo de su relación altura- radio, H/a , se clasifican como anchos si H/a  ≤ 0,50 y como esbeltos cuando dicha relación es mayor. Este tipo de tanques generalmente almacenan un poco menos de su capacidad total, por lo que las presiones hidrodinámicas sobre las paredes y el fondo son prácticamente iguales a las de un recipiente con superficie libre. Graham y Rodríguez (1952) fueron los primeros en resolver el problema hidrodinámico linealizado para el caso de tanques de aeronaves [3] . Retomando el enfoque de los autores anteriores, Housner [4] propuso un procedimiento de análisis basado en un modelo masa-resorte que posteriormente fue modificado por Veletsos y Yang [5] . Wozniak y Michell [6] establecieron que los efectos hidrodinámicos impulsivos en tanques con paredes rígidas son similares a los que presentan los tanques con paredes flexibles, por lo que la diferencia en su comportamiento puede ser despreciable. En la actualidad existe un gran número de referencias que siguen usando la teoría linealizada de la condición cinemática en la superficie libre del líquido; algunos autores emplean la teoría del potencial [7]  and [8] , la analogía de masas concentradas [9]  and [10] o algún software comercial basado en el método de elemento finito [2] , [11] , [12] , [13] , [14]  and [15] . En la práctica profesional es común que los elementos mecánicos de diseño se calculen por medio de la analogía de masas concentradas-resortes [16] , [17]  and [18] .

Existen diversas fuentes de no linealidad que intervienen en el comportamiento sísmico de tanques de almacenamiento: no linealidad cinemática de la superficie libre del líquido, pandeo de las paredes, interacción no lineal suelo-estructura, no linealidad de contacto entre la placa base y la cimentación del tanque, y no linealidad del material de las paredes. En este trabajo se considera que las paredes del tanque son rígidas y ancladas a la cimentación, que se encuentra sometida ante una excitación sísmica de gran intensidad, y que el líquido contenido en el recipiente tiene un comportamiento dinámico no lineal debido principalmente a la ecuación cinemática en la superficie del fluido.

En diversas referencias bibliográficas se encuentra que la ecuación de movimiento que considera los efectos hidrodinámicos no lineales se ha resuelto analíticamente o por métodos numéricos. Las soluciones analíticas existentes se basan en el método de perturbaciones [3] , [19] , [20] , [21] , [22] , [23] , [24] , [25]  and [26] , y las numéricas, principalmente, en los métodos de elementos de frontera (MEF), y de elementos finitos (MEF) y de diferencias finitas (MDF). En la literatura aparecen diferentes algoritmos de solución basados en el llamado método marcador y celda (MMC) [26] . Hirt, Nichols y Romero [27] proponen una versión simplificada del método MAC con los algoritmos de SOLA y SOLA-SURF. Durante el período de 1975 a 1981 se desarrollaron varios algoritmos computacionales simplificados, con el nombre genérico SOLA [28]  and [29] . Ukeguchi, Sakata y Adachi [30] proponen el método llamado FLIC (Fluid Interaction Computer) en el que se combina el MEF con el método del volumen finito (MVF) para calcular el flujo alrededor de un cuerpo estanco. Faltinsen [31] desarrolló un método numérico para el cálculo del oleaje en 2 dimensiones de tanques rectangulares basado en la técnica de integrales en la frontera y el método del panel. Nakayama y Washizu [32] aplican MEF para el análisis no lineal del oleaje en 2 dimensiones de un contenedor rectangular. Basándose en el trabajo de Zakharov [33] , Miles [34]  and [35] y Bridges y Dias [36] , recientemente Gavrilyuk et al. [37] han resuelto el problema de estabilidad del movimiento no lineal del oleaje en tanques por medio de métodos variacionales. Actualmente el MDF se sigue usado para la solución del problema de oleaje no lineal en contenedores sometidos a movimientos de traslación y cabeceo ante cargas armónicas [38] , [39]  and [40] .

En las referencias antes citadas [3] , [19] , [20] , [21] , [22] , [23] , [24] , [25] , [26] , [27] , [28] , [29] , [30] , [31] , [32] , [33] , [34] , [35] , [36] , [37] , [38] , [39]  and [40] se supone que la excitación en la base del tanque es de tipo armónica, es decir, del tipo seno-coseno, con pequeña amplitud y corta duración. En ocasiones los movimientos sísmicos presentan altos niveles de excitación (> 0,2 g), tienen un periodo de duración de 20 a 60 s o mayor, y el movimiento que presentan no es armónico, por lo que las soluciones planteadas dejan de ser válidas para el caso de sismos de gran intensidad.

Existen pocas referencias en las que se considere el efecto no lineal del oleaje en la respuesta sísmica de tanques. Chen et al. [41] aplican la teoría de potencial y resuelven las ecuaciones de movimiento por medio del MDF en contenedores rectangulares sometidos a sismos característicos de Norteamérica. Para estabilizar la solución numérica agregan amortiguamiento por medio de disipación numérica o viscosidad artificial, lo cual podría comprometer la solución. En Hernández-Barrios et al. [42] tratan el problema en tanques cilíndricos sometidos a diversos tipos de registros sísmicos. Las ecuaciones de movimiento se discretizan por el MDF y el método del volumen finito (MVF). Ozdemir et al. [43] desarrollaron una metodología explicita basada en el MEF con el algoritmo Arbitrary Lagrangian-Eulerian (ALE) en tanques cilíndricos de acero anclados o no a la cimentación. En los ejemplos presentados no utilizan registros sísmicos reales. Goudarzi y Sabbagh-Yazdi [44] utilizan el software comercial ANSYS para obtener la solución no lineal en tanques rectangulares; sin embargo, en sus resultados no definen el valor y cómo controlan el amortiguamiento del líquido.

En este trabajo se presenta una extensión de la metodología empleada en Hernández-Barrios et al. [42] aplicada a tanques rectangulares sometidos a sismos de gran intensidad. Se utilizan registros sísmicos que no se utilizaron en [42] . Además, para el caso de tanques cilíndricos no se usa el MVF en la discretización de las ecuaciones de frontera. Se comparan los efectos de las condiciones hidrodinámicas no lineales en la respuesta, en tanques cilíndricos y rectangulares con dimensiones geométricas comunes en la práctica profesional. Los resultados de la respuesta están dados en términos de altura de la superficie del líquido, fuerza cortante y momento de volteo en la base de la pared.

2. Ecuaciones de movimiento

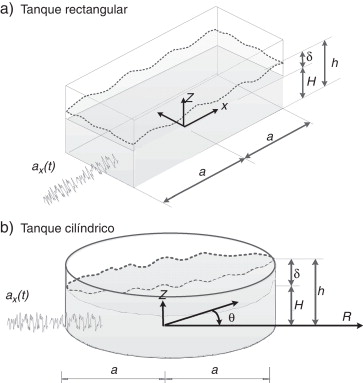
Consideremos un tanque de almacenamiento con forma rectangular (fig. 1 a) o cilíndrica (fig. 1 b) con paredes rígidas y anclado a la cimentación y que está sometido a una aceleración sísmica del terreno en su base: ${\textstyle {\overset {\mbox{ˆ}}{a}}\left(t\right)=a_{x}\left(t\right)}$ . El tanque contiene un fluido ideal e irrotacional, lo que permite considerar un flujo basado en la teoría del potencial [23] , válido para movimientos de fluido cuya ola no rompe. Esta hipótesis tiene el inconveniente de que es válida para movimientos no amortiguados. En este trabajo se incluyó el amortiguamiento en la ecuación dinámica considerándolo del tipo pseudoviscoso [21]  and [29] .

Figura 1. Configuración de los tanques de almacenamiento.

En la figura 1 a se observa un tanque rectangular, con un ancho en su base de 2 a y profundidad del líquido H . La amplitud del oleaje en la superficie, δ, se mide a partir de la superficie media del líquido. Para el tanque cilíndrico ( fig. 1 b) a es su radio, y para ambos casos h es la altura de ola medida desde el fondo. El sistema de ecuaciones que gobierna el comportamiento dinámico del problema para un sistema de referencia no inercial [29] , en términos de un potencial de velocidades relativas en coordenadas cartesianas, ${\textstyle \varphi \left(x,z\right)}$[45] , está dado por la ecuación de Laplace válida en el dominio del líquido, Ω :

$\nabla ^{2}\varphi =0{\mbox{ }}{\mbox{en}}{\mbox{ }}\Omega$

( 1)

en las paredes del tanque:

${\frac {\partial \varphi }{\partial x}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}x=\pm a$

( 2)

y en el fondo:

${\frac {\partial \varphi }{\partial z}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=0$

( 3)

La condición cinemática de la superficie libre del líquido [46] es:

${\frac {\partial h}{\partial t}}+{\frac {\partial h}{\partial x}}{\frac {\partial \varphi }{\partial x}}-{\frac {\partial \varphi }{\partial z}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=h$

( 4)

y para la condición dinámica, que se obtiene de aplicar la ecuación de Bernoulli en la superficie libre del líquido [29] :

${\frac {\partial \varphi }{\partial t}}+{\frac {1}{2}}\left({\frac {\partial \varphi }{\partial x}}\right)^{2}+{\frac {1}{2}}\left({\frac {\partial \varphi }{\partial z}}\right)^{2}+\mu \varphi +gh-gH+xa_{x}(t)=0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=h$

( 5)

Las ecuaciones (1-5) en coordenadas cilíndricas, ${\textstyle \varphi \left(R,\theta ,z\right)}$ , son:

${\frac {\partial ^{2}\varphi }{\partial R^{2}}}+{\frac {1}{R}}{\frac {\partial \varphi }{\partial R}}+{\frac {1}{R^{2}}}{\frac {\partial ^{2}\varphi }{\partial \theta ^{2}}}+{\frac {\partial ^{2}\varphi }{\partial z^{2}}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}\Theta$

( 6)

${\frac {\partial \varphi }{\partial R}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}R=\pm a$

( 7)

${\frac {\partial \varphi }{\partial z}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=0$

( 8)

${\frac {\partial h}{\partial t}}+{\frac {\partial h}{\partial R}}{\frac {\partial \varphi }{\partial R}}+{\frac {1}{R^{2}}}\left[{\frac {\partial \varphi }{\partial \theta }}{\frac {\partial h}{\partial \theta }}\right]-{\frac {\partial \varphi }{\partial z}}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=h$

( 9)

${\begin{array}{l}\displaystyle {\frac {\partial \varphi }{\partial t}}+{\frac {1}{2}}\left({\frac {\partial \varphi }{\partial R}}\right)^{2}+{\frac {1}{2}}\left({\frac {\partial \varphi }{\partial z}}\right)^{2}+{\frac {1}{2}}\left({\frac {1}{R^{2}}}\right)\left({\frac {\partial \varphi }{\partial \theta }}\right)^{2}+\mu \varphi +gh-gH+\\\displaystyle +a_{x}\left(t\right)Rcos\theta =0{\mbox{ }}{\mbox{en}}{\mbox{ }}z=h\end{array}}$

( 10)

donde g es la aceleración de la gravedad y μ es el término que representa el amortiguamiento tipo pseudoviscoso. La presión hidrodinámica se obtiene directamente de la ecuación de Bernoulli:

$P_{h}\left(x,z,t\right)=-{\frac {1}{\rho }}\left[{\frac {\partial \varphi }{\partial t}}+{\frac {1}{2}}\left(\nabla \varphi \right)^{2}+xa_{x}\left(t\right)+\mu \varphi +gz\right]$

( 11)

donde ρ es la densidad del líquido. La fuerza cortante instantánea en la base del tanque se obtiene integrando las presiones en las paredes:

${\begin{array}{l}\displaystyle F_{n}\left(t_{o}\right)=\int _{0}^{\delta \left(-a,t_{o}\right)}P_{h}\left(-a,z,t_{o}\right)dz-\int _{0}^{\delta \left(a,t_{o}\right)}P_{h}\left(a\right.\\\left.\displaystyle z,t_{o}\right)dz\end{array}}$

( 12)

y el momento de volteo instantáneo se obtiene como:

${\begin{array}{l}\displaystyle M_{n}\left(t_{o}\right)=\int _{0}^{\delta \left(a,t_{o}\right)}z{\mbox{ }}P_{h}\left(a,z,t_{o}\right)dz-\int _{0}^{\delta \left(-a,t_{o}\right)}z{\mbox{ }}P_{h}\left(-a\right.\\\left.\displaystyle z,t_{o}\right)dz+\int _{-a}^{a}xP_{h}\left(x,0,t_{o}\right)dx\end{array}}$

( 13)

Nótese que las integrales en (12) y (13) se evalúan hasta la superficie libre del líquido, ${\textstyle \delta \left(x,t_{o}\right)}$ , y no hasta la superficie media, a diferencia de lo que se haría en el caso de un análisis hidrodinámico lineal.

3. Estrategia para la solución no lineal

Una de las principales características del problema hidrodinámico no lineal es que la superficie libre del líquido cambia de posición en cada incremento de tiempo, por lo que si se resuelve el problema en forma numérica, la malla de discretización del dominio debe ajustarse a la nueva configuración. El dominio matemático en el que el sistema de ecuaciones que gobierna el comportamiento hidrodinámico no lineal es válido va cambiando durante la solución del problema debido a que la frontera libre del líquido no permanece plana en cada instante. Como estrategia de solución se propone el siguiente cambio de variable, en coordenadas cartesianas:

$\sigma ={\frac {z}{h\left(x,t\right)}}$

( 14a)

y para el sistema en coordenadas cilíndricas:

$\sigma ={\frac {z}{h\left(R,\theta ,t\right)}}$

( 14b)

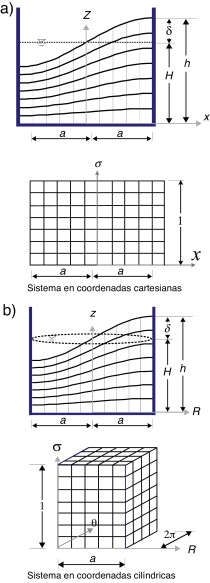
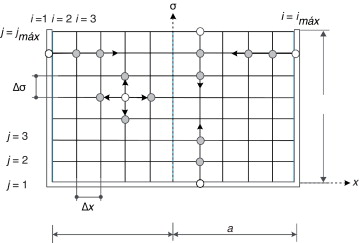
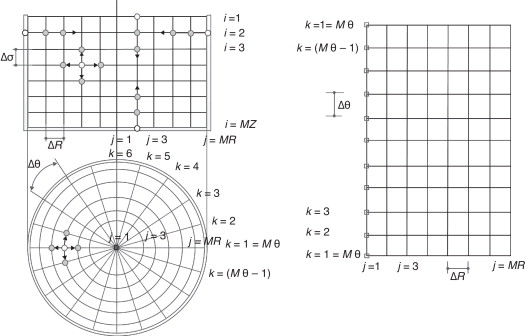
donde h es la elevación de la superficie libre del líquido medida desde el fondo del tanque y z es la variable independiente en el problema físico. Mediante (14) se mapea el dominio físico a un dominio computacional, donde ahora z es la variable dependiente. La ventaja de usar este cambio de variable es que la nueva variable independiente, σ , siempre vale la unidad en la superficie libre del líquido ( fig. 2 a). Para el caso del sistema en coordenadas cilíndricas (fig. 2 b) el dominio físico desconocido se transforma en un dominio computacional, que consiste en un paralelepípedo de dimensiones a , 2π y 1. Sin embargo, el sistema de ecuaciones de frontera en el dominio computacional, Ω^' , tiene un número de elementos considerablemente mayor al que se tendría en el dominio físico, Ω .

Figura 2. Dominio físico y dominio computacional.

Sea ${\textstyle {\tilde {\varphi }}}$ el nuevo potencial en el dominio computacional, ${\textstyle {\tilde {\varphi }}\left(x,\sigma ,t\right)}$ y ${\textstyle {\tilde {\varphi }}(R,\theta ,\sigma ,t)}$ , para el sistema en coordenadas cartesianas y cilíndricas, respectivamente. Se tiene el siguiente sistema de ecuaciones para el tanque rectangular:

${\begin{array}{c}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial x^{2}}}-\sigma \left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)\left({\frac {1}{h}}\right)\left({\frac {\partial ^{2}h}{\partial x^{2}}}\right)+2\sigma \left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)\left({\frac {1}{h^{2}}}\right)\left({\frac {\partial h}{\partial x}}\right)^{2}+\\+\sigma ^{2}\left({\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\right)\left({\frac {1}{h^{2}}}\right)\left({\frac {\partial h}{\partial x}}\right)^{2}+\left({\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\right)\left({\frac {1}{h^{2}}}\right)-2\sigma \left({\frac {1}{h}}\right){\frac {\partial h}{\partial x}}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial x\partial \sigma }}=0{\mbox{ }}en{\mbox{ }}\Omega ^{'}\end{array}}$

( 15)

${\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}\sigma =0$

( 16)

${\frac {\partial {\tilde {\varphi }}}{\partial x}}=\sigma {\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\left({\frac {1}{h}}\right){\frac {\partial h}{\partial x}}{\mbox{ }}{\mbox{en}}{\mbox{ }}x=\pm a$

( 17)

La condición cinemática de la superficie libre del líquido se transforma en:

${\frac {\partial h}{\partial t}}={\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\left({\frac {1}{h}}\right)\left[1+\left({\frac {\partial h}{\partial x}}\right)^{2}\right]-{\frac {\partial {\tilde {\varphi }}}{\partial x}}{\frac {\partial h}{\partial x}}{\mbox{ }}{\mbox{en}}{\mbox{ }}\sigma =1$

( 18)

y la dinámica:

${\begin{array}{l}\displaystyle {\frac {\partial {\tilde {\varphi }}}{\partial t}}=-g\left(h-H\right)-{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial x}}\right)^{2}+{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)^{2}\left({\frac {1}{h^{2}}}\right)\left[1+\left({\frac {\partial h}{\partial x}}\right)^{2}\right]+\mu {\tilde {\varphi }}+\\\displaystyle +xa_{x}\left(t\right)\end{array}}$

( 19)

La presión en las paredes se obtiene con:

${\begin{array}{c}{\frac {P_{H}}{\rho }}=-{\frac {\partial {\tilde {\varphi }}}{\partial t}}-{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial x}}\right)^{2}+{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\left[{\frac {\partial h}{\partial t}}+{\frac {\partial {\tilde {\varphi }}}{\partial x}}{\frac {\partial h}{\partial x}}\right]{\frac {\sigma }{h}}-{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}{\frac {1}{h}}\right)^{2}-\\-{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}{\frac {\partial h}{\partial x}}{\frac {\sigma }{h}}\right)^{2}-\mu {\tilde {\varphi }}-xa_{x}\left(t\right)-g\left(\sigma h-H\right)\end{array}}$

( 20)

Para el tanque con forma cilíndrica las ecuaciones se transforman en:

${\begin{array}{c}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial R^{2}}}+{\frac {1}{R}}{\frac {\partial {\tilde {\varphi }}}{\partial R}}+{\frac {1}{R^{2}}}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \theta ^{2}}}-\sigma \left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)\left({\frac {1}{h}}\right)\left[{\frac {\partial ^{2}h}{\partial R^{2}}}+{\frac {1}{R}}{\frac {\partial h}{\partial R}}+{\frac {1}{R^{2}}}{\frac {\partial ^{2}h}{\partial \theta ^{2}}}\right]+\\+2\sigma \left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)\left({\frac {1}{h^{2}}}\right)\left[\left({\frac {\partial h}{\partial R}}\right)^{2}+{\frac {1}{R^{2}}}\left({\frac {\partial h}{\partial \theta }}\right)^{2}\right]+\sigma ^{2}\left({\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\right)\left({\frac {1}{h^{2}}}\right)\left[\left({\frac {\partial h}{\partial R}}\right)^{2}+\right.\\\left.\displaystyle +{\frac {1}{R^{2}}}\left({\frac {\partial h}{\partial \theta }}\right)^{2}\right]+\\+{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\left({\frac {1}{h^{2}}}\right)-2\sigma \left({\frac {1}{h}}\right){\frac {\partial h}{\partial R}}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial R\partial \sigma }}-2\sigma \left({\frac {1}{h}}\right)\left({\frac {1}{R^{2}}}\right){\frac {\partial h}{\partial \theta }}{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \theta \partial \sigma }}=0{\mbox{ }}en{\mbox{ }}\Omega ^{'}\end{array}}$

( 21)

${\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}\sigma =0$

( 22)

${\frac {\partial {\tilde {\varphi }}}{\partial R}}=\sigma {\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\left({\frac {1}{h}}\right){\frac {\partial h}{\partial R}}{\mbox{ }}en{\mbox{ }}R=a$

( 23)

la condición cinemática:

${\frac {\partial h}{\partial t}}={\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\left({\frac {1}{h}}\right)\left[1+\left({\frac {\partial h}{\partial R}}\right)^{2}+{\frac {1}{R^{2}}}\left({\frac {\partial h}{\partial \theta }}\right)^{2}\right]-{\frac {\partial {\tilde {\varphi }}}{\partial R}}{\frac {\partial h}{\partial R}}-{\frac {1}{R^{2}}}\left({\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right)\left({\frac {\partial h}{\partial \theta }}\right){\mbox{ }}{\mbox{en}}{\mbox{ }}\sigma =1$

( 24)

y la dinámica:

${\begin{array}{c}{\frac {\partial {\tilde {\varphi }}}{\partial t}}=-g\left(h+H\right)-{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial R}}\right)^{2}-{\frac {1}{2}}\left({\frac {1}{R^{2}}}\right)\left({\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right)^{2}+{\frac {1}{2}}\left({\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right)^{2}\left({\frac {1}{h^{2}}}\right)\left[1+\right.\\\left.\displaystyle +\left({\frac {\partial h}{\partial R}}\right)^{2}+\left({\frac {1}{R^{2}}}\right)\left({\frac {\partial h}{\partial \theta }}\right)^{2}\right]-\\-\mu {\tilde {\varphi }}-a_{x}\left(t\right)Rcos\theta {\mbox{ }}{\mbox{en}}{\mbox{ }}\sigma =1\end{array}}$

( 25)

Las ecuaciones (15-19) y (21-25) forman los 2 nuevos sistemas de ecuaciones de frontera en el dominio computacional. El sistema de ecuaciones no lineales se resuelve utilizando el MDF. El esquema temporal utilizado para la solución del sistema de ecuaciones es el de Crank-Nicholson, por considerarse estable para la mayoría de los registros sísmicos empleados. El esquema de Crank-Nicholson está centrado en el espacio y en el tiempo, lo que lo hace incondicionalmente estable, además de tener poco amortiguamiento numérico implícito [47] . El sistema de ecuaciones no lineales se resolvió por medio del método de Newton. El éxito de este método depende de que la condición inicial de la iteración de las raíces sea próxima a la raíz verdadera; esta consideración se toma en cuenta en la solución no lineal del oleaje considerando que el cambio numérico de la respuesta entre 2 intervalos de tiempo es continua y pequeña; además, el incremento temporal de los registros sísmicos, Δt, es suficientemente pequeño. El sistema de ecuaciones algebraicas simultáneas resultantes se resolvió por medio del método del gradiente biconjugado (MGB) [48] .

La discretización del sistema de ecuaciones (15-19) se muestra en el Appendix A apéndice A, y la estrategia de la solución temporal para el sistema de ecuaciones (21-25), en el Appendix B apéndice B.

4. Respuesta sísmica

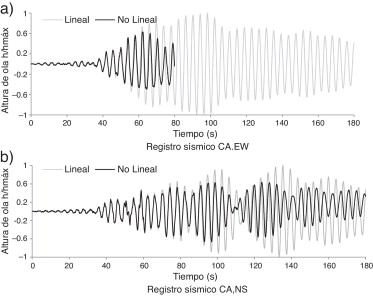
Considerando un tanque cilíndrico que contiene agua con radio a  = 5,5 m, altura media del líquido H  = 2,75 m y un valor del amortiguamiento de ξ = 0,5%, sometido en su base al evento sísmico registrado en Central de Abasto (CA), en las direcciones este-oeste (EO) y norte-sur (NS) durante el sismo de septiembre de 1985, en el Valle de México. El periodo fundamental del líquido contenido en el tanque es de T  = 4,06 s. En la figura 3 se muestra la historia de la altura de ola normalizada al valor máximo obtenido. No fue posible calcular la altura de ola máxima generada con el registro CA.EO (fig. 3 a) después del segundo 81,05 del registro. Esto se debe a que la excitación tiene un periodo característico de T  = 3,93 s, casi similar al periodo del líquido, por lo que se puede estar presentando el fenómeno de resonancia [41] . En algunas referencias [3] , [19] , [20] , [21] , [22] , [23] , [24] , [25] , [26] , [27] , [28] , [29] , [30] , [31] , [32] , [33] , [34] , [35] , [36] , [37] , [38] , [39]  and [40] se reportan resultados similares cuando la excitación en la base del tanque es del tipo armónica con frecuencia próxima a la del sistema dinámico. Para estabilizar la solución es necesario agregar amortiguamiento numérico, lo cual no se consideró adecuado ya que se compromete la solución del problema. Para el caso del registro CA.NS, con periodo característico de T  = 3,81 s, la altura de ola máxima obtenida con la solución no lineal es de 1,74 m, y con la solución lineal resultó de 2,60 m. En este caso, la altura de ola obtenida con la solución lineal resultó ser mayor que la obtenida con la solución no lineal.

Figura 3. Historia de la altura de ola (a = 5,5 m, H = 2,75 m, ξ = 0,5%), tanque cilíndrico.

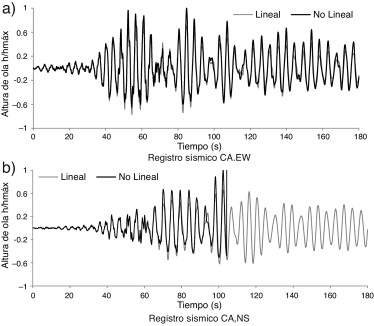
Ahora se considera un tanque rectangular con la misma relación H/a que el tanque cilíndrico y sometido en su base al mismo evento sísmico (CA). El tanque tiene un semiancho a  = 5,5 m, altura media del líquido H  = 2,75 m y un valor del amortiguamiento del 0,5%. El periodo fundamental del líquido contenido en el tanque es de T  = 4,63 s. En la figura 4 se muestra la historia de la altura de ola normalizada al valor máximo obtenido. Cuando se aplica el registro sísmico CA.EO en la base del tanque (fig. 4 a), la solución no lineal predice un valor de altura de ola de 1,36 m y la solución lineal de 1,06 m. En este caso la solución no lineal resultó ser del orden del 28% mayor que la altura de ola con la solución linealizada del problema. Para el caso de registro sísmico CA.NS, la historia de ola se muestra en la figura 4 b. Para este caso no fue posible calcular la altura de ola con la solución no lineal después del segundo 110 del registro. Esto ocurre porque a partir de ese tiempo se presenta inestabilidad numérica, debido a que el sistema se encuentra en cuasi resonancia, así como al bajo valor del amortiguamiento del líquido, lo que físicamente significa que la altura de ola es grande y tiende a romper. La solución numérica se logra estabilizar si al sistema se le agrega amortiguamiento externo por medio de disipación numérica o viscosidad artificial. Existen varios métodos para agregar disipación numérica al sistema. El más usado es el conocido como «upwind» [47] , pero en este trabajo no se agregó para no comprometer la exactitud de la solución.

Figura 4. Historia de la altura de ola (a = 5,5 m, H = 2,75 m, ξ = 0,5%), tanque rectangular.

Como segundo caso de aplicación se consideró un tanque rectangular y uno cilíndrico, ambos con una relación H/a  = 0,35, donde para el tanque rectangular a es el semiancho y para el tanque cilíndrico a es el radio. El periodo fundamental del líquido contenido en el tanque cilíndrico es de T  = 5,5 s, y el del tanque rectangular, de T  = 6,34 s.

En la tabla 1 se muestran los resultados de la altura de ola máxima obtenida con la solución lineal y con la solución no lineal, cuando los tanques son sometidos a los eventos sísmicos registrados en el Valle de México durante el sismo de septiembre de 1985, en sus direcciones NS y EO. Los registros sísmicos empleados son el registrado en terreno duro de Ciudad Universitaria (CU), el obtenido en suelo de transición en la estación Viveros (VIV ) y los obtenidos en suelo considerado como blando: en la Secretaría de Comunicaciones y Transportes (SCT) y en Tacubaya (TACY). Para ambas configuraciones de los tanques, la altura de ola calculada con la teoría lineal es menor que la altura de ola calculada con la teoría no lineal; para el caso del tanque rectangular los registros sísmicos SCT y TACY son los más desfavorables, subestimándose la altura de ola hasta en un 34%. Para el tanque cilíndrico la altura de ola calculada con la teoría lineal es subestimada en un 25% para el caso del registro TACY.NS. Subestimar la altura de ola en el cálculo de la respuesta sísmica puede ocasionar derramamiento de líquido, contaminación ambiental, explosiones o pérdida de agua potable.

Tabla 1. Altura de ola máxima (m) lineal y no lineal en la pared de los tanques (H/a = 0.35)

Registro sísmico	Tanque cilíndrico			Tanque rectangular
	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$
CU.NS	0,2605	0,2801	7	0,4164	0,4043	−3
CU.EW	0,3205	0,3348	4	0,3047	0,3745	22
VIV .NS	0,3761	0,4144	10	0,4523	0,4974	10
VIV .EW	0,3728	0,3855	3	0,3022	0,3534	17
SCT.NS	0,9996	1,0907	13	1,4125	1,8867	34
SCT.EW	1,2287	1,3070	6	1,9227	2,5476	33
TACY.NS	0,4551	1,098	25	0,2686	0,3292	23
TACY.EW	0,2862	0,3398	19	0,3853	0,4866	26

En la tabla 2 se compara la fuerza cortante máxima en la pared de los tanques cilíndrico y rectangular, con las características mencionadas. Se puede ver que el efecto no lineal del oleaje es despreciable en la cuantificación de la fuerza cortante en el tanque rectangular para los movimientos sísmicos empleados, excepto para el registro TACY.EO, cuya diferencia entre las soluciones es del orden del 10%. Para el caso del tanque cilíndrico la fuerza cortante no lineal es mucho más importante, principalmente para los eventos sísmicos registrados en terreno blando (SCT y TACY).

Tabla 2. Fuerza cortante máxima (kN) lineal y no lineal en la pared del tanque (H/a = 0,35)

Registro sísmico	Tanque cilíndrico			Tanque rectangular
	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$
CU.NS	45,76	51,98	14	44,46	45,15	2
CU. EW	26,92	28,41	6	41,51	41,24	−1
VIV .NS	51,22	55,35	8	45,20	45,70	1
VIV . EW	38,20	46,89	23	41,13	41,42	1
SCT.NS	128,08	144,22	13	56,37	55,16	−3
SCT. EW	143,84	144,51	3	55,42	56,20	2
TACY.NS	74,53	111,60	50	44,68	42,13	−6
TACY. EW	51,36	65,25	28	41,52	45,62	10

En la tabla 3 se muestran los resultados del momento de volteo máximo obtenidos con los registros sísmicos antes mencionados. En este caso, para ambas configuraciones de tanques los efectos no lineales del oleaje son importantes en la respuesta, de manera que despreciarlos puede ocasionar daños en las paredes de los tanques y fallas estructurales en las mismas.

Tabla 3. Momento de volteo máximo (kN m) lineal y no lineal, en la pared del tanque

Registro sísmico	Tanque cilíndrico			Tanque rectangular
	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$	Lineal	No lineal	${\textstyle \Delta \left(\%\right)}$
CU.NS	184,62	223,17	21	94,16	130,11	38
CU.EW	99,99	118,76	19	84,55	114,32	35
VIV .NS	199,54	235,69	18	97,62	133,96	37
VIV .EW	153,94	205,23	33	82,60	118,26	40
SCT.NS	503,83	768,73	52	146,23	178,48	22
SCT.EW	597,08	787,54	32	146,40	198,13	35
TACY.NS	292,80	514,85	76	94,88	117,95	24
TACY.EW	202,47	286,31	41	83,75	132,94	58

5. Conclusiones

Se presenta una metodología numérica para cuantificar los efectos de la no linealidad del oleaje en la respuesta sísmica de tanques de almacenamiento con forma cilíndrica y rectangular, sometidos a eventos sísmicos intensos con larga duración y periodo característico grande. Los registros sísmicos empleados en este trabajo corresponden a los que se registraron en septiembre de 1985, en la Ciudad de México, que tienen una duración de 180 s, amplitudes del orden de 0,169 g, con frecuencias dominantes que pueden ser cercanas a la frecuencia fundamental del oleaje de los tanques con dimensiones convencionales en la infraestructura civil. La respuesta hidrodinámica no lineal se compara con la solución lineal tradicional en cuanto a las fuerzas cortantes, momento de volteo y altura de ola.

Es posible que para tanques con dimensiones usuales en la práctica profesional (a  = 5,5 m y H  = 2,75 m) que almacenen líquidos con bajos valores de amortiguamiento se presente el fenómeno de resonancia cuando son excitados por registros sísmicos con las características que se presentan en el Valle de México. Para los tanques con relación H/a  = 0,35, la altura de ola calculada con la teoría no lineal resulta ser mayor que la calculada con la teoría lineal. Subestimar la altura de ola en el cálculo de la respuesta sísmica puede ocasionar derramamiento de líquido, contaminación ambiental, explosiones o pérdida de agua potable. El efecto no lineal del oleaje puede considerarse despreciable en la cuantificación de la fuerza cortante en el tanque rectangular; para el caso del tanque cilíndrico la fuerza cortante no lineal es más importante, principalmente para los eventos sísmicos registrados en terreno blando (SCT.NS y TACY). Los momentos de volteo en la base del tanque calculándolos con la teoría lineal son subestimados para ambas configuraciones de tanques, llegando a ser del orden de un 58% mayores para el tanque rectangular y de un 76% para el tanque cilíndrico.

Agradecimientos

Se agradece a la Universidad Michoacana de San Nicolás de Hidalgo quien, por medio de la Coordinación de la Investigación Científica y de la Facultad de Ingeniería Civil, proporcionó las facilidades para la realización de este trabajo. De igual forma, se agradece a la Dirección General de Apoyo al Personal Académico (DGAPA) de la UNAM por el apoyo brindado a través del proyecto PAPIIT IT101513 «Riesgo Sísmico del Municipio de Naucalpan».

Apéndice A. 

En la figura A1 se muestra el dominio matemático en el que se discretizaron las ecuaciones en diferencias finitas de segundo orden para el caso del tanque rectangular.

Figura A1. Discretización por medio de diferencias finitas para el tanque rectangular.

La ecuación (15) se aproxima por medio de diferencias finitas de segundo orden como: rectangular.

${\begin{array}{c}-2\left(k_{1}+k_{2}\right){\tilde {\varphi }}_{i,j}+k_{1}{\tilde {\varphi }}_{i+1,j}+k_{1}{\tilde {\varphi }}_{i-1,j}+\left(k_{2}-\right.\\\left.\displaystyle -k_{3}\right){\tilde {\varphi }}_{i,j-1}-k_{4}{\tilde {\varphi }}_{i+1,j-1}+k_{4}{\tilde {\varphi }}_{i-1,j-1}\\+\left(k_{2}+k_{3}\right){\tilde {\varphi }}_{i,j+1}+k_{4}{\tilde {\varphi }}_{i+1,j+1}-k_{4}{\tilde {\varphi }}_{i-1,j+1}=0\\para{\mbox{ }}i\in \left[2,i_{max-1}\right],{\mbox{ }}j\in \left[2,j_{max-1}\right]\end{array}}$

( A1)

La ecuación (19), válida en la superficie libre del líquido, se discretiza como:

${\begin{array}{c}\left(1+k_{5}\right){\tilde {\varphi }}_{i,j}^{n+1}+k_{6}\left.\left[\left({\tilde {\varphi }}_{i+1,j}\right)^{2}-2{\tilde {\varphi }}_{i+1,j}+\right.\right.\\\left.\left.\displaystyle +{\tilde {\varphi }}_{i-1,j}\right]\right|^{n+1}+\\+k_{7}\left.\left[9\left({\tilde {\varphi }}_{i,j}\right)^{2}-24{\tilde {\varphi }}_{i,j}{\tilde {\varphi }}_{i,j-1}+6{\tilde {\varphi }}_{i,j}{\tilde {\varphi }}_{i,j-2}+\right.\right.\\\left.\left.\displaystyle +16\left({\tilde {\varphi }}_{i,j-1}\right)^{2}-8{\tilde {\varphi }}_{i,j-1}{\tilde {\varphi }}_{i,j-2}+\left(\varphi _{i,j-2}\right)^{2}\right]\right|^{n+1}=\\\left(1-k_{5}\right){\tilde {\varphi }}_{i,j}^{n}-\left.k_{5}\left[{\tilde {\varphi }}_{i+1,j}-{\tilde {\varphi }}_{i-1,j}\right]^{2}\right|^{n}-\left.k_{7}\left({\tilde {\varphi }}_{i,j}-\right.\right.\\\left.\left.\displaystyle -4{\tilde {\varphi }}_{i,j-1}+{\tilde {\varphi }}_{i,j-2}\right)^{2}\right|^{n}-\\-\Delta tx\left({\frac {a_{x}\left(t\right)^{n+1}+a_{x}\left(t\right)^{n}}{2}}\right)-{\frac {\Delta tg}{2}}\left(h^{n}-H\right)-{\frac {\Delta tg}{2}}\left(h_{i}^{n+1}-H\right)\end{array}}$

( A2)

La altura de ola (18) se puede aproximar como:(A3)${\textstyle {\begin{array}{c}\left.h_{i}+\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)\left({\frac {{\tilde {\varphi }}_{i+1,j}-{\tilde {\varphi }}_{i-1,j}}{2\Delta x}}\right){\frac {\Delta t}{2}}-\right.\\\left.\displaystyle -\left[\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)^{2}+1\right]\left({\frac {3{\tilde {\varphi }}_{i,j}-4{\tilde {\varphi }}_{i,j-1}+{\tilde {\varphi }}_{i,j-2}}{2\Delta \sigma }}\right){\frac {\Delta t}{2h_{i}}}\right|^{n+1}=\\\left.h_{i}-\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)\left({\frac {{\tilde {\varphi }}_{i+1,j}-{\tilde {\varphi }}_{i-1,j}}{2\Delta x}}\right){\frac {\Delta t}{2}}+\right.\\\left.\displaystyle +\left[\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)^{2}+1\right]\left({\frac {3{\tilde {\varphi }}_{i,j}-4{\tilde {\varphi }}_{i,j-1}+{\tilde {\varphi }}_{i,j-2}}{2\Delta \sigma }}\right){\frac {\Delta t}{2h_{i}}}\right|^{n}\\{\mbox{para}}{\mbox{ }}i\in \left[2,i_{max-1}\right],{\mbox{ }}j=j_{max}\end{array}}}$ donde:

${\begin{array}{c}k_{1}={\frac {1}{\left(\Delta x\right)^{2}}}\\k_{2}={\frac {1}{\left(\Delta \sigma \right)^{2}h_{i}^{2}}}\left[\sigma ^{2}\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)+1\right]\\k_{3}={\frac {\sigma }{2h_{i}\Delta \sigma }}\left[{\frac {2}{h_{i}}}\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)^{2}-\left({\frac {h_{i+1}-2h_{i}+h_{i-1}}{\left(\Delta x\right)^{2}}}\right)\right]\\k_{4}={\frac {\sigma }{2h_{i}\Delta x\Delta \sigma }}\left({\frac {h_{i+1}-h_{i-1}}{2\Delta x}}\right)\\k_{5}={\frac {\Delta t}{2}}\mu \\k_{6}={\frac {\Delta t}{16\left(\Delta x\right)^{2}}}\\k_{7}={\frac {\Delta t}{16\left(\Delta \sigma \right)^{2}\left(h_{i}^{n+1}\right)^{2}}}\left[\left({\frac {h_{i+1}^{n+1}-h_{i-1}^{n+1}}{2\Delta x}}\right)+1\right]\\k_{8}={\frac {\Delta t}{16\left(\Delta \sigma \right)^{2}\left(h_{i}^{n}\right)^{2}}}\left[\left({\frac {h_{i+1}^{n}-h_{i-1}^{n}}{2\Delta x}}\right)+1\right]\\-3h_{i}+4h_{i+1}-h_{i+2}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}i=1\\3h_{i}-4h_{i-1}+h_{i-2}=0{\mbox{ }}{\mbox{en}}{\mbox{ }}i=i_{max}\end{array}}$

El sistema de ecuaciones no lineales se resolvió por medio del método de Newton. Las primeras derivadas de estas ecuaciones se pueden calcular analíticamente para formar la matriz jacobiana y la solución del sistema de ecuaciones lineales simultáneas que resultan durante el proceso se resolvió por medio del MGB.

Apéndice B. 

Para obtener la solución temporal usando el esquema Crank-Nicholson, la condición dinámica equivalente (25) se discretiza de la siguiente forma:

${\begin{array}{c}\left(g_{1}\right)_{j,k,1}^{n+1}=-U_{j,k,1}\left[{\frac {2}{\Delta tg}}\right]\left[1+{\frac {\mu \Delta t}{2}}\right]-\left[{\frac {1}{2g}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right]^{2}-\\\displaystyle -\left[{\frac {1}{2g}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right]^{2}+\\+\left[{\frac {1}{2g}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}+\left[{\frac {1}{2g}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}\left[{\frac {\partial h}{\partial R}}\right]^{2}+\\+\left.\left[{\frac {1}{2g}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}\left[{\frac {\partial h}{\partial \theta }}\right]^{2}-h_{j,k}\right\|^{n+1}-f_{1}^{n}({\tilde {\varphi }},h)=0\end{array}}$

( B1)

donde:

${\begin{array}{c}f_{1}^{n}\left({\tilde {\varphi }}\right.\\\left.\displaystyle h\right)=-U_{j,k,1}\left[{\frac {2}{\Delta tg}}\right]\left[1-{\frac {\mu \Delta t}{2}}\right]+\left[{\frac {1}{2g}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right]^{2}+\left[{\frac {1}{2g}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right]^{2}-\\-\left[{\frac {1}{2g}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}-\left[{\frac {1}{2g}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}\left[{\frac {\partial h}{\partial R}}\right]^{2}-\\\left.\left[{\frac {1}{2g}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {1}{h_{j},k^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]^{2}\left[{\frac {\partial h}{\partial \theta }}\right]^{2}-h_{j,k}-2H\right\|^{n}+\\\displaystyle +{\frac {2R_{j}}{g}}cos\theta \left[a_{x}\left(t\right)\right]^{n+1/2}\end{array}}$

( B2)

Una vez conocidos los valores de ${\textstyle h_{j,k}^{n}}$ y de ${\textstyle U_{j,k,1}^{n}}$ , que representan la aproximación de ${\textstyle {\tilde {\varphi }}}$ , el término ${\textstyle f_{1}^{n}({\tilde {\varphi }},h)}$ definido por la expresión B2 es una constante. Al discretizarse la ecuación B1 en diferencias finitas para cada uno de los puntos del dominio, se convierte en una ecuación algebraica no lineal de segundo orden cuyas derivadas parciales, con respecto a las variables espaciales, se pueden evaluar en forma analítica para formar la matriz jacobiana utilizada en el método de Newton. De manera similar la ecuación cinemática equivalente se puede escribir:

${\begin{array}{c}\left(g_{2}\right)_{j,k,1}^{n+1}=h_{j,k}-\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]-\\\displaystyle -\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\left[{\frac {\partial h}{\partial R}}\right]^{2}-\\-\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\left[{\frac {\partial h}{\partial \theta }}\right]^{2}+\left[{\frac {\Delta t}{2}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right]\left[{\frac {\partial h}{\partial R}}\right]+\\\displaystyle +\left.\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right]\left[{\frac {\partial h}{\partial \theta }}\right]\right\|^{n+1}-\\-f_{2}^{n}({\tilde {\varphi }},h)=0\end{array}}$

( B3)

donde:

${\begin{array}{c}f_{2}^{n}\left({\tilde {\varphi }},h\right)=h_{j,k}+\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]+\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\left[{\frac {\partial h}{\partial R}}\right]^{2}+\\+\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {1}{h_{j},k}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\left[{\frac {\partial h}{\partial \theta }}\right]^{2}-\left[{\frac {\Delta t}{2}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right]\left[{\frac {\partial h}{\partial R}}\right]-\\\displaystyle -\left.\left[{\frac {\Delta t}{2}}\right]\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial {\tilde {\varphi }}}{\partial \theta }}\right]\left[{\frac {\partial h}{\partial \theta }}\right]\right\|^{n}\end{array}}$

( B4)

Nuevamente el término ${\textstyle f_{2}^{n}({\tilde {\varphi }},h)}$ es una constante, una vez conocidos los valores de ${\textstyle h_{j,k}^{n}}$ . El potencial de velocidad, ${\textstyle {\tilde {\varphi }}}$ , en el dominio computacional, se puede escribir como:

${\begin{array}{c}\left(g_{3}\right)_{j,k,l}^{n+1}=\left[\left[{\frac {1}{R_{j}}}\right]{\frac {\partial }{\partial R}}\left[R{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right]+\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \theta ^{2}}}\right]\right]+\left[{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\right]\left[{\frac {1}{h_{j,k}^{2}}}\right]-\\-\sigma \left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\left[{\frac {1}{h_{j,k}}}\right]\left[\left[{\frac {1}{R_{j}}}\right]{\frac {\partial }{\partial R}}\left[R{\frac {\partial h}{\partial R}}\right]+\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial ^{2}h}{\partial \theta ^{2}}}\right]\right]+\\+\left[2\sigma \left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]+\sigma ^{2}\left[{\frac {\partial ^{2}{\tilde {\varphi }}}{\partial \sigma ^{2}}}\right]\right]\left[{\frac {1}{h_{j,k}^{2}}}\right]\left[\left[{\frac {\partial h}{\partial R}}\right]^{2}+\left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial h}{\partial \theta }}\right]^{2}\right]-\\\left.-2\sigma \left[{\frac {\partial }{\partial R}}\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\right]\left[{\frac {1}{h_{j,k}}}\right]\left[{\frac {\partial h}{\partial R}}\right]-2\sigma \left[{\frac {1}{R_{j}^{2}}}\right]\left[{\frac {\partial }{\partial \theta }}\left[{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right]\right]\left[{\frac {1}{h_{j,k}}}\right]\left[{\frac {\partial h}{\partial R}}\right]\right\|^{n+1}=0\end{array}}$

( B5)

Para el fondo del tanque en el dominio computacional,

$\left(g_{4}\right)_{j,k,MZ}^{n+1}=\left.{\frac {\partial {\tilde {\varphi }}}{\partial \sigma }}\right|^{n+1}=0$

( B6)

y la condición de frontera en la pared,

$\left(g_{5}\right)_{MR,k,l}^{n+1}=\left.{\frac {\partial {\tilde {\varphi }}}{\partial R}}\right|^{n+1}=0$

( B7)

Las condiciones de frontera del problema transitorio quedan definidas por las ecuaciones no lineales (B1), (B3) y (B5) conjuntamente con las lineales (B6) y (B7). Las primeras derivadas de estas ecuaciones formarán la matriz jacobiana utilizada en el método de Newton.

$\left[J\left(x^{\left(k\right)}\right)\right]_{i,j}=\left[{\begin{array}{cccccc}{\frac {\partial g_{1}(x)}{\partial x_{1}}}&{\frac {\partial g_{1}(x)}{\partial x_{2}}}&.&.&.&{\frac {\partial g_{1}(x)}{\partial x_{n}}}\\{\frac {\partial g_{2}(x)}{\partial x_{1}}}&{\frac {\partial g_{2}(x)}{\partial x_{2}}}&.&.&.&{\frac {\partial g_{2}(x)}{\partial x_{n}}}\\.&.&{\mbox{ }}&{\mbox{ }}&{\mbox{ }}&.\\.&.&{\mbox{ }}&{\mbox{ }}&{\mbox{ }}&.\\.&.&{\mbox{ }}&{\mbox{ }}&{\mbox{ }}&.\\{\frac {\partial g_{n}(x)}{\partial x_{1}}}&{\frac {\partial g_{n}(x)}{\partial x_{2}}}&.&.&.&{\frac {\partial g_{n}(x)}{\partial x_{n}}}\end{array}}\right]$

( B8)

El éxito del método de Newton depende de que la condición inicial de la iteración de las raíces sea próxima a la raíz verdadera; esta consideración se tiene en cuenta en la solución no lineal del oleaje considerando que el cambio numérico de la respuesta entre 2 intervalos de tiempo es continua y pequeña, además de que Δt es suficientemente pequeño. El sistema de ecuaciones algebraicas simultáneas resultantes (6.000 × 6.000) se resolvió por medio del MGB. El dominio computacional se discretizó tal como se muestra en la figura B1 .

Figura B1. Esquema de discretización del dominio en diferencias finitas.

Bibliografía

1. [1] H. Hernández-Barrios, E. Heredia-Zavoni; Respuesta sísmica de tanques cilíndricos para almacenamiento de líquidos; Revista de Ingeniería Sísmica, Sociedad Mexicana de Ingeniería Sísmica, 62 (2000), pp. 63–88
2. [2] H. Sezen, R. Livaoglu, A. Dogangun; Dynamic analysis and seismic performance evaluation of above-ground liquid-containing tanks; Eng. Struct., 30 (2008), pp. 794–803
3. [3] H.N. Abramson; The Dynamic Behavior of Liquids in Moving Containers, with Applications to Space Vehicle Technology; NASA SP-106, San Diego (1966)
4. [4] G.W. Housner; Dynamic Pressures on Accelerated fluid containers; B. Seismol. Soc. Am., 47 (1957), pp. 15–35
5. [5] A.S. Veletsos, J.Y. Yang; Earthquake response of liquid storage tanks, Advances in Civil Engineering through Engineering Mechanics, Proceedings Second Annual Eng. Mech; Div-ASCE (1977), pp. 1–24
6. [6] R.S. Wozniak, M. Mitchell; Basis of Seismic Design Provision for Welded Steel Oil Storage Tanks; Proceedings–Refining Department, 57 (1978), pp. 485–501
7. [7] S. Hashemi, M.M. Saadatpour, M.R. Kianousk; Dynamic analysis of flexible rectangular fluid containers subjected to horizontal ground motion; Earthquake. Eng. Struc., 42 (2013), pp. 1637–1656
8. [8] D. James, G. Thanigaiarasu; Seismic analysis on cylindrical tanks subjected to horizontal acceleration; IJARME, 1 (2011), pp. 44–47
9. [9] A. Saif; Seismic analysis of liquid storage tanks; International Journal of Advanced Tends in Computer Science and Engineering., 2 (2013), pp. 357–362
10. [10] Y. Li, J. Wang; A supplementary, exact solution of an equivalent mechanical model for sloshing fluid in rectangular tank; J. Fluid. Struct., 31 (2012), pp. 147–151
11. [11] U. Chaduvula, D. Patel, N. Gopalakrishnan; Fluid-structure-soil interaction effects on seismic behaviour of elevated water tanks; Procedia Eng., 51 (2013), pp. 84–91
12. [12] M. Mirzabozorg, M.A. Hariri, R. Nateghi; Free surface sloshing effects on dynamic response of rectangular storage tanks; Am. J. Fluid. Dyn., 2 (4) (2012), pp. 23–30
13. [13] M.R. Kianoush, A.R. Ghaemmaghami; The effect of earthquake frequency content on the seismic behavior of concrete rectangular liquid tanks using the finite element method incorporating soil-structure interaction; Eng. Struct., 33 (2011), pp. 2186–2200
14. [14] M. Moslemi, M.R. Kianoush, W. Pogorzelski; Seismic response of liquid-filled elevated tanks; Eng. Struct., 33 (2011), pp. 2074–2084
15. [15] Z. Yang, B. Shou, L. Sun, J. Wang; Earthquake response analysis of spherical tanks with seismic isolation; Procedia Eng., 14 (2011), pp. 1879–1886
16. [16] EN 1998-4 Eurocode 8, Design of structures for earthquake resistance, Part 4: Silos, Tanks and pipelines, 2006.
17. [17] IITK-GSMA Guidelines for seismic design of liquid storage tanks-provisions with commentary and explanatory examples; Indian Institute of Technology, Kapur (2005)
18. [18] American Petroleum Institute, API 650, Welded Tanks for Oils storage, 11th edition, Addendum 3, October, 2012.
19. [19] H.F. Harlow, J.E. Welch; Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface; Phys. Fluids, 8 (12) (1965), pp. 2182–2189
20. [20] R.E. Hutton; An Investigation of Resonant, Nonlinear Nonplanar Free Surface Oscillations of a Fluid; NASA TN D-1870 (1963)
21. [21] O.M. Faltinsen; A nonlinear Theory of Sloshing in rectangular tanks; J. Ship. Res., 18 (4) (1974), pp. 224–241
22. [22] S. Froydis; Analytical and Numerical Studies of Sloshing in Tanks; Norges Teknisk-Naturvitenskapelige, Univ. Trondheim, Norway (1995)
23. [23] F.T. Dodge; The New Dynamic Behavior of Liquids in Moving Containers; Southwest Research Institute, San Antonio, Texas, (2000) NASA SP-106
24. [24] R.A. Ibrahim; Liquid Sloshing Dynamics, Theory and Applications; Cambridge University Press (2005)
25. [25] H. Zhang, W. Peing-fei, L. Wen-bai; The analysis of second-order sloshing resonance in a 3-D tank; J. Hidrodyn., 26 (2) (2014), pp. 309–315
26. [26] H.F. Harlow, J.E. Welch; Numerical study of large-amplitude free-surface motions; Phys. Fluids, 9 (5) (1966), pp. 842–851
27. [27] C.W. Hirt, B.D. Nichols, N.C. Romero; SOLA: A Numerical Solution Algorithm for Transient Fluid Flows; Los Alamos Scientific Laboratory Report LA-5852 (1975)
28. [28] C.W. Hirt; SOLA. A Basic Solution Algorithm for Flow Analysis, Applications of SOLA to Free Surface Flows; Von Karman Institute for Fluid Dynamics, Lecture Series 1986-07, Introduction to Numerical Solution of Industrial Flows (1986), pp. 12–16
29. [29] H. Hernández-Barrios; Análisis sísmico no lineal de tanques cilíndricos de almacenamiento [Ph. D. thesis]; DEPFI, Facultad de Ingeniería, Universidad Nacional Autónoma de México, México (2003)
30. [30] N. Ukeguch, H. Sakata, T. Adachi; On the numerical analysis of compressible flow problems by the modified flic method; Comput. Fluids, 8 (1980), pp. 251–263
31. [31] O.M. Faltinsen; A numerical nonlinear method of sloshing in tanks with two-dimensional flow; J. Ship. Res., 22 (3) (1978), pp. 193–202
32. [32] T. Nakayama, K. Washizu; The boundary element method applied to the analysis of two-dimensional nonlinear sloshing problems; Int. J. Numer. Meth. Eng., 17 (1981), pp. 1631–1646
33. [33] V.E. Zakharov; Stability of periodic waves on finite amplitude on the surface of a deep fluid; J. Appl. Mech. Technol. Phys., 9 (1968), pp. 190–194
34. [34] J.W. Miles; Stability of forced oscillations of a spherical pendulum; Quart. Appl. Math., 20 (1962), pp. 21–32
35. [35] J.W. Miles; Surface waves in basins of variable depth; J. Fluid. Mech., 152 (1985), pp. 379–389
36. [36] T.J. Bridges, F. Dias; An analysis of two-dimensional water waves based on O₂ symmetry  ; Nonlinear Analysis, Theory, Methods and Applications, 14 (1990), pp. 733–764
37. [37] I.P. Gavrilyuk, I.A. Lukovsky, A.N. Timokha; Linear and nonlinear sloshing in a circular conical tank; Fluid. Dyn. Res., 37 (2005), pp. 399–429
38. [38] B. Chen, R. Nokes; Time-independent finite difference analysis of fully non-linear and viscous sloshing in a rectangular tank; J. Comput. Phys., 209 (2005), pp. 47–81
39. [39] C. Wu, B. Chen; Sloshing waves and resonance modes of fluid in a 3 D tank by a time-independent finite difference method; Ocean Eng., 36 (2009), pp. 500–510
40. [40] W. Chih-Hua, B. Chen, H. Tin-Kan; Hydrodynamic forces induced by transient sloshing in a 3 D rectangular due to oblique horizontal excitation; Comput. Math. Appl., 65 (2013), pp. 1163–1186
41. [41] W. Chen, M.A. Haroun, F. Liu; Large amplitude liquid sloshing in seismically excited tanks; Earthquake Eng. Struc., 25 (1996), pp. 653–669
42. [42] H. Hernández-Barrios, E. Heredia-Zavoni, A.A. Aldama-Rodríguez; Nonlinear sloshing response of cylindrical tanks subjected to earthquake ground motion; Eng. Struct., 29 (2007), pp. 3364–3376
43. [43] Z. Ozdemir, M. Souli, Y.M. Fahjan; Application of nonlinear fluid-structures interaction methods to seismic analysis of anchored and unanchored tanks; Eng. Struct., 32 (2010), pp. 409–423
44. [44] M.A. Goudarzi, S.R. Sabbagh-Yazdi; Investigation of nonlinear sloshing effects in seismically excited tanks; Soil Dynam. Earthquake Eng., 43 (2012), pp. 355–365
45. [45] A. Hernández; Análisis sísmico no-lineal de tanques rectangulares [MS thesis]; Facultad de Ingeniería, Universidad Michoacana de San Nicolás de Hidalgo, México (2012)
46. [46] B. Le Méhauté; An Introduction to Hydrodynamics and Water Waves; Springer-Verlag, New York (1976)
47. [47] Thomas J.W. Numerical partial differential equations, Finite Difference Methods, Text in Applied Mathematics, Vol. 22, Springer, 1998.
48. [48] W.H. Press, S.A. Teukolosky, W.T. Vettering, B.P. Flannery; Numerical Recipes in Fortran, The Art of Scientific Computing; (2 nd ed)Cambridge University Press (1992)