New thermal compensation algorithm for piezoresistive pressure sensors based on the linear approximation by segments

Resumen

Los sensores de presión piezorresistivos son ampliamente utilizados en aplicaciones de control y monitorización dentro del sector industrial. Estos sensores presentan problemas de dependencia térmica y no linealidades que afectan la exactitud de la medición. Por esta razón, es necesario utilizar circuitos de acondicionamiento de señales para obtener salidas de alta exactitud. Una de las técnicas más empleadas actualmente para acondicionar las señales provenientes de los sensores se basa en la utilización de procesadores digitales de señales y algoritmos de compensación.

Este trabajo propone un nuevo algoritmo de calibración y compensación para sensores de presión piezorresistivos basado en la aproximación lineal por segmentos con compensación térmica. El algoritmo fue simulado empleando el software matemático MathCAD y utilizando datos de un sensor de presión piezorresistivo ficticio. El algoritmo fue validado experimentalmente implementándolo en 2 procesadores digitales de señales y utilizando sensores de presión manométricos ventilados de 10 bar en el intervalo de temperaturas de 0 a 80 °C. Se obtuvo como resultado que el máximo error a la salida del sensor, debido a la dependencia térmica del offset, fue de 0,081% del intervalo de medida. El error máximo obtenido a la salida provocado por la dependencia térmica de la sensibilidad fue de 0,106% del intervalo de medida. Se demostró la efectividad del algoritmo en la compensación térmica de los sensores de presión piezorresistivos. Este algoritmo puede ser aplicado a otros tipos de sensores que posean dependencias térmicas y que incorporen un microprocesador o un procesador digital de señales.

Abstract

The piezoresistive pressure sensors are widely used in monitoring and control applications within the industrial sector. These sensors have problems of temperature dependence, and non-linearities that affect the measurement accuracy. For this reason, it is necessary to use signal conditioning circuits for to obtain high accuracy outputs. One of the most common techniques currently used to conditioning the signals from the sensors is based on the use of digital signal processors and compensation algorithms.

This paper proposes a new calibration and compensation algorithm for piezoresistive pressure sensors based on the linear segment approximation with thermal compensation. The algorithm was simulated using the mathematical software MathCAD and using data from a piezoresistive pressure dummy sensor. The algorithm has been validated experimentally implementing it into two digital signal processors using vented piezoresistives pressure sensors of 10 bar in the range of temperatures from 0 °C to 80 °C. The result was that the maximum error in the sensor output due to the temperature dependence of the offset was 0,081% of full scale output. The maximum error obtained at the output caused by the temperature dependence of the sensitivity was 0,106% of full scale output. The effectiveness of the algorithm is demonstrated in the thermal compensation of piezoresistive pressure sensors. This algorithm can be applied to other types of sensors having thermal dependencies and incorporating a microprocessor or digital signal processor.

Palabras clave

Sensores de presión ; Algoritmos de compensación y calibración ; Compensación térmica ; Aproximación lineal por segmentos

Keywords

Pressure sensors ; Calibration and compensation algorithms ; Thermal compensation ; Linear approximation using segments

1. Introducción

Los sensores juegan un importante rol dentro de las tecnologías de vanguardia del mundo moderno, representando un elemento importante dentro de las tecnologías de la información, las comunicaciones y la computación [1] . Las aplicaciones más comunes de los sensores de presión están: en la rama aeroespacial, en la automotriz, en la hidráulica y en general en la industria. La automatización industrial ha traído consigo el desarrollo de una amplia gama de sensores de presión basados en diferentes tecnologías de fabricación para el control y la monitorización de procesos.

Dentro de las tecnologías de fabricación, han tenido un creciente desarrollo los sensores integrados construidos en base a semiconductores cristalinos, particularmente en base a silicio, debido fundamentalmente a que este material es el más usado en la fabricación de circuitos integrados y a que presenta propiedades elásticas casi ideales. Desde el surgimiento de los sensores piezorresistivos, el puente de Wheatstone ha sido una de las configuraciones circuitales más empleadas para transformar magnitudes físicas como la presión, en señales eléctricas [2] . En estos sensores la exactitud de su señal de salida se ve afectada por un comportamiento no lineal de esta, por la presencia de un offset y por una marcada dependencia de este offset y la sensibilidad con la temperatura [3] . Es por ello que es necesario utilizar circuitos de acondicionamiento de señales para compensar estas características no deseadas y minimizar sus efectos en la señal de salida de los sensores.

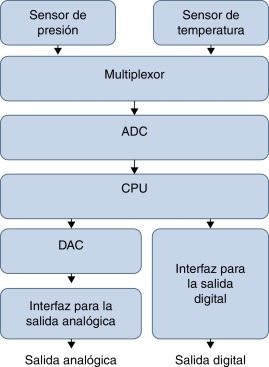
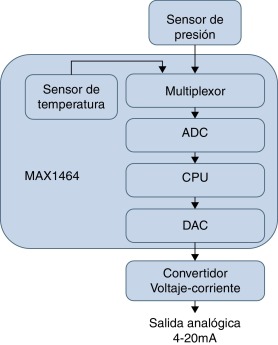
Una de las técnicas más novedosas para realizar el acondicionamiento de las señales provenientes de los sensores se basa en la utilización de Digital Signal Processor (DSP) [1] , [4]  and [5] . Esta técnica brinda gran flexibilidad y exactitud debido a que la corrección de los sensores se realiza en el dominio digital mediante algoritmos de compensación que son implementados en la Central Processing Unit (CPU) que poseen estos DSP. En la figura 1 se observa el diagrama en bloques general y simplificado de los sensores inteligentes de presión que utilizan compensación digital.

Figura 1. Diagrama en bloques funcional y simplificado de sensores inteligentes de presión que utilizan compensación digital.

Las señales del sensor de presión y el sensor de temperatura son multiplexadas y digitalizadas utilizando un Analog to Digital Converter (ADC). En la CPU se implementa un algoritmo de compensación de las características no deseadas de la señal de salida del transmisor y se obtiene el valor corregido de presión que es enviado a través de la salida digital. La señal de salida analógica se obtiene utilizando un Digital to Analog Converter (DAC) y un circuito analógico encargados de garantizar a la salida del transmisor una señal de tensión o corriente proporcional a la presión medida. Los 2 sensores y el canal de entrada hasta la CPU deben ser compensados térmicamente, al igual que el DAC y el circuito que conforma la interfaz para obtener la salida analógica.

De forma general, cuando se utilizan técnicas de compensación digital, el proceso de corrección de las características no deseadas del sensor se encuentra dividido en 2 etapas fundamentales. Una de ellas es ejecutada in factory , o sea, durante la fabricación del transmisor de presión. Esta primera etapa consiste en aplicar una metodología que permite obtener en un banco de calibración los coeficientes específicos que compensan el comportamiento del sensor y las dependencias térmicas del circuito de acondicionamiento de la señal. A esta etapa se la conoce normalmente como proceso de calibración. La segunda etapa es ejecutada in service , o sea, cuando el transmisor se encuentra midiendo la presión en tiempo real. Este proceso consiste en ejecutar en la CPU un algoritmo de compensación para obtener en la salida del transmisor una señal corregida y proporcional a la presión sensada.

En la literatura han sido reportados gran variedad de algoritmos de compensación y calibración para la linealización y corrección de sensores [6] , [7] , [8]  and [9] . Estos algoritmos varían en cuanto a complejidad, cantidad de procesamiento requerido y en el modelo matemático que utilizan para realizar la compensación de las características no deseadas. Varios de estos algoritmos se basan en la implementación de ecuaciones polinomiales que son obtenidas a partir de la interpolación de 3 o más datos conocidos de las respuestas de los sensores [7] . Utilizando este tipo de algoritmo es posible generar una función de calibración a partir de un número reducido de datos (puntos de calibración) y obtener en la salida valores de exactitud menores que 0,5% del intervalo de medida [8] .

Resulta muy ventajoso contar con algoritmos sencillos de compensación térmica que requieran la menor cantidad de recursos para su implementación, pero que a la vez garanticen los niveles de exactitud requeridos. Esto permitiría utilizar un hardware de menor complejidad para realizar la compensación de los sensores y con ello disminuir los costos de fabricación de los transmisores de presión.

En este artículo se presenta un nuevo algoritmo de compensación y calibración para sensores de presión piezorresistivos que consiste en una aproximación lineal por segmentos con compensación térmica. El algoritmo fue simulado empleando el software matemático MathCAD y utilizando datos de un sensor de presión piezorresistivo ficticio. Posteriormente fue validado experimentalmente implementándolo en 2 procesadores digitales de señales y utilizando sensores de presión manométricos ventilados de 10 bar en el intervalo de temperaturas de 0 a 80 °C. Después de implementado el algoritmo, se obtuvo como resultado que el máximo error en la señal de salida del sensor debido a la dependencia térmica del offset fue de 0,081% del intervalo de medida, y debido a la dependencia térmica de la sensibilidad fue de 0,106% del intervalo de medida. Fue demostrada la efectividad del algoritmo en la compensación térmica de los sensores de presión piezorresistivos. Este algoritmo puede ser aplicado a otros tipos de sensores inteligentes que sus señales de salida posean dependencias térmicas y que incorporen un microprocesador o un procesador digital de señales.

2. Algoritmo de compensación

El algoritmo de compensación desarrollado para el sensor de presión consiste en una aproximación lineal utilizando 4 segmentos de rectas en todo su intervalo de medición. Los objetivos fundamentales de este algoritmo son obtener una respuesta lineal a la salida del transmisor de presión y compensar las dependencias térmicas tanto del sensor de presión como del circuito de acondicionamiento. Este algoritmo de compensación fue implementado en la CPU del dispositivo inteligente utilizado para realizar la corrección digital. La modelación y compensación de la señal del sensor de temperatura fue realizada de forma similar a la reportada por Maxim en [10] , utilizando como modelo un polinomio de segundo orden.

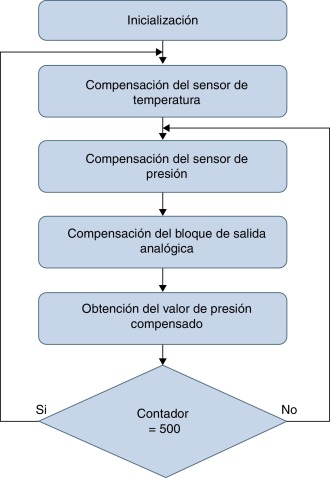
En la figura 2 se muestra el diagrama en bloques general del algoritmo desarrollado. Entre los bloques principales se encuentran el que realiza la compensación de la señal proveniente del sensor de temperatura, otro donde se compensa la señal proveniente del sensor de presión y por último uno encargado de realizar la compensación del bloque de salida analógico. Este trabajo se centra principalmente en el bloque relacionado con la compensación del sensor de presión, ya que la compensación del sensor de temperatura y del bloque de salida analógico se realiza de forma similar a lo reportado en [10] .

Figura 2. Diagrama en bloques general del algoritmo de compensación desarrollado.

Como puede apreciarse en la figura 2 , el primer paso es realizar la configuración inicial de los diferentes bloques y variables. Posteriormente se ejecuta la compensación de la señal proveniente de un sensor de temperatura para obtener un valor compensado de esta variable. Partiendo del valor obtenido se calculan varios coeficientes que solo dependen de la temperatura y que son utilizados posteriormente en la compensación del sensor de presión. Después de determinar el valor de estos coeficientes se realiza la compensación de la señal del sensor de presión.

La compensación del sensor de presión tiene como base un modelo de aproximación lineal utilizando 4 segmentos de rectas para modelar el comportamiento del sensor en todo el intervalo de medición. Los parámetros de estas rectas (la pendiente y el intercepto) poseen una marcada dependencia con la temperatura. Por esta razón es necesario calcular los valores de estos parámetros para la temperatura real a la que se encuentra el transmisor y utilizarlos para determinar el valor teórico esperado a la salida. Posteriormente se debe realizar un ajuste para lograr la compensación del sensor ante cambios de la temperatura. Finalmente se realiza la compensación del bloque de salida analógico del transmisor de presión para minimizar su dependencia con la temperatura.

En la mayoría de las aplicaciones donde se desea medir presión se cumple que la temperatura varía de forma mucho más lenta que la propia presión aplicada al sensor. Como se puede observar en la figura 2 , en el programa desarrollado se realiza un lazo de temperatura por cada 500 de presión. La elección de este valor fue un criterio de diseño teniendo como base el hecho de que la temperatura constituye un parámetro que varía mucho más lentamente en el tiempo, y además que la presión es la magnitud física fundamental a medir. Esta decisión trae consigo la ventaja de que durante el funcionamiento del transmisor se estará ejecutando solo una pequeña parte del algoritmo, que tiene un reducido número de instrucciones, mejorando con esto los tiempos de respuesta del transmisor ante los cambios de la presión. Esta relación es ajustable en función de la aplicación específica donde se utilice transmisor.

2.1. Modelación y compensación del sensor de temperatura

La modelación del comportamiento del sensor de temperatura se realizó utilizando un polinomio de segundo orden de forma similar a lo reportado en [10] . Para ello se utilizaron 3 pares de puntos obtenidos experimentalmente durante el proceso de calibración al aplicar 3 temperaturas de referencia. Estos puntos son representados como (TrefMin; TsenMin ), (TrefMed; TsenMed ) y (TrefMax, TsenMax ). La expresión que describe el comportamiento del sensor de temperatura Temp(T) está dada por la ecuación (1). Los coeficientes a₀ , a₁ y a₂ son calculados resolviendo un sistema lineal de ecuaciones a partir de los 3 puntos obtenidos experimentalmente. El parámetro «T» representa la temperatura de referencia

$Temp\left(T\right)=a_{0}+a_{1}\cdot T+a_{2}\cdot T^{2}$

( 1)

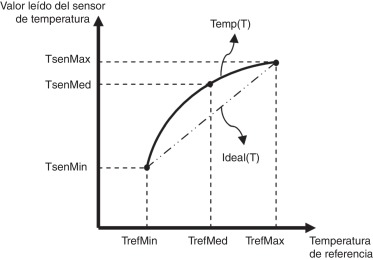
Con el objetivo de determinar la no linealidad de la señal del sensor de temperatura se obtuvo la función Ideal(T) que representa la recta que une los puntos extremos de Temp(T) . En la figura 3 se representan gráficamente estas 2 funciones.

Figura 3. Representación de las funciones Temp(T) e Ideal(T) .

A partir de la ecuación (1) y la función Ideal(T) se obtiene Nl(T) mediante la ecuación (2). Esta función representa el error de no linealidad del sensor de temperatura

$Nl\left(T\right)=Temp\left(T\right)-Ideal(T)$

( 2)

Posteriormente se halla la función Tnl(T) utilizando interpolación cuadrática y tomando como nodos de interpolación 3 puntos que pertenecen a Nl(T) . El objetivo de este procedimiento es obtener una expresión analítica en forma de polinomio, como se muestra en la ecuación (3), y que represente la no linealidad del sensor de temperatura

$Tnl\left(T\right)=ac_{0}+ac_{1}\cdot T+ac_{2}\cdot T^{2}$

( 3)

siendo ac₀, ac₁y ac₂ los coeficientes que se utilizarán para la corrección de las no linealidades de la señal de temperatura en tiempo real. Almacenando estos 3 coeficientes es posible conocer el error de linealidad del sensor para cualquier temperatura a la que se encuentre el transmisor, facilitando de este modo el proceso de compensación. Calculando la diferencia entre la función que representa el comportamiento real del sensor (1) y la función que modela la no linealidad del mismo (3), es posible realizar una compensación de la no linealidad como se muestra en la ecuación (4)

$TempNlC(T)=Temp(T)-Tnl(T)$

( 4)

Una vez ejecutada la compensación de la no linealidad del sensor de temperatura se procede a realizar el ajuste de su sensibilidad. Para realizar esta operación es necesario multiplicar la ecuación (4) por un coeficiente que también debe ser calculado en el proceso de calibración. Este coeficiente se calcula utilizando la ecuación (5) y también debe ser almacenado para la compensación en tiempo real

$AjSpan={\frac {\left({\frac {SpanMax-SpanMin}{TrefMax-TrefMin}}\right)}{\left({\frac {TsenMax-TsenMin}{TrefMax-TrefMin}}\right)}}={\frac {SpanMax-SpanMin}{TsenMax-TsenMin}}$

( 5)

donde SpanMax y SpanMin son los valores máximo y mínimo a los que se desea ajustar el intervalo de medida del sensor de temperatura. El resto de los parámetros fueron definidos anteriormente. El ajuste de la sensibilidad de la señal proveniente del sensor de presión se realiza utilizando la ecuación (6)

$TempNlSpC(T)=TempNlC(T)\cdot AjSpan$

( 6)

Finalmente se realiza la compensación del offset según la ecuación (7)

$TempComp\left(T\right)=TempNlSpC\left(T\right)-CompOffset$

( 7)

donde CompOffset es un coeficiente que también debe ser calculado en el proceso de calibración a través de la ecuación (8)

$CompOffset=TempNlSpC\left(TrefMin\right)-SpanMin$

( 8)

La función TempComp(T) representa la señal del sensor de temperatura con compensación de la no linealidad, la sensibilidad y el offset . Esta función es utilizada para calcular el valor compensado de presión.

2.2. Modelación y compensación del sensor de presión

El diseño de un algoritmo de compensación basado en un modelo completamente lineal en todo el intervalo de medición del sensor de presión imposibilita la compensación de los errores de no linealidad del mismo y afecta considerablemente la exactitud de la medida. La principal causa se debe a que varios factores influyen sobre estos dispositivos y provocan desviaciones en su comportamiento respecto a una función lineal ideal. Una forma sencilla y eficiente de minimizar estos errores consiste en utilizar varios segmentos de rectas para modelar y compensar el comportamiento del sensor en todo el intervalo de medición. Cada uno de estos segmentos deberá tener diferente pendiente e intercepto, lo que permitirá realizar una modelación más exacta del comportamiento real del sensor de presión y compensar los errores de no linealidad. Partiendo de estas ideas se implementó un algoritmo de compensación basado en una aproximación lineal utilizando 4 segmentos para la compensación del offset , la sensibilidad y la no linealidad en el comportamiento del sensor de presión. Adicionalmente se desarrolló un método para compensar las dependencias térmicas de la pendiente y el intercepto de cada uno de estos segmentos. De esta forma se logró minimizar una de las principales fuentes de error en los sensores de presión piezorresistivos, contribuyendo notablemente a mejorar la exactitud en la medición.

La selección de la cantidad de segmentos que se deben utilizar para modelar el comportamiento del sensor de presión se basa en la relación entre la exactitud que se desea obtener en la medición y la complejidad del proceso de calibración. Mientras mayor sea la cantidad de segmentos utilizados, mayor será la exactitud lograda en la medición, pero se hará más complejo el proceso de calibración, ya que se deberá caracterizar el sensor de presión para una mayor cantidad de presiones de referencias. Teniendo en cuenta la relación anterior se decidió realizar la modelación del sensor de presión utilizando 4 segmentos de rectas, a partir de 15 puntos obtenidos experimentalmente en el proceso de calibración del sensor. Estos puntos son tomados por la CPU cuando se aplican al sensor 5 presiones de referencias para cada una de las 3 temperaturas de referencias. Partiendo de estos puntos es posible realizar una interpolación y obtener un modelo basado en un polinomio de orden 4, donde los 5 coeficientes del mismo dependen de la temperatura, como se muestra en la ecuación (5)

$Sdata\left(T,P\right)=\sum _{n=0}^{4}\left[\sum _{i=0}^{2}C_{ni}\cdot T^{i}\right]\cdot P^{n}$

( 5)

Los 15 coeficientes C_ni son calculados resolviendo un sistema lineal de ecuaciones. La función Sdata(T,P) representa el comportamiento del sensor de presión en todo el intervalo de temperaturas y, por tanto, también las características no deseadas del mismo, como el offset , la no linealidad y la dependencia térmica del offset y la sensibilidad.

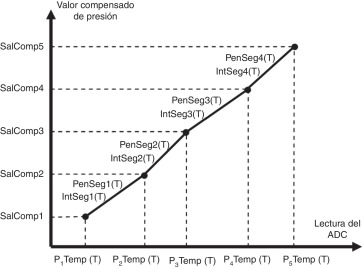
Para realizar la corrección de sensor de presión es necesario obtener 5 polinomios de segundo orden que representen la variación de la salida del sensor de presión con los cambios de la temperatura cuando son aplicadas cada una de las 5 presiones de referencia. O sea, se deben obtener 5 ecuaciones cuadráticas (una para cada presión de referencia aplicada en la calibración) en las que se caractericen las variaciones de cada una de estas presiones con la temperatura. En la figura 4 se representan los 4 segmentos, con la pendiente y el intercepto de cada uno de ellos.

Figura 4. Modelación y compensación de la señal del sensor de presión.

Las ecuaciones (6) a (10) permitirán obtener 5 puntos a partir de los cuales se calcularán la pendiente y el intercepto de cada uno de los 4 segmentos que se utilizarán para compensar la salida del sensor de presión

${\begin{array}{l}\displaystyle P_{1}Temp\left(T\right)=A_{10}+A_{11}\cdot TempComp\left(T\right)+A_{12}\cdot \\\displaystyle \cdot TempComp\left(T\right)^{2}\end{array}}$

( 6)

${\begin{array}{l}\displaystyle P_{2}Temp\left(T\right)=A_{20}+A_{21}\cdot TempComp\left(T\right)+A_{22}\cdot \\\displaystyle \cdot TempComp\left(T\right)^{2}\end{array}}$

( 7)

${\begin{array}{l}\displaystyle P_{3}Temp\left(T\right)=A_{30}+A_{31}\cdot TempComp\left(T\right)+A_{32}\cdot \\\displaystyle \cdot TempComp\left(T\right)^{2}\end{array}}$

( 8)

${\begin{array}{l}\displaystyle P_{4}Temp\left(T\right)=A_{40}+A_{41}\cdot TempComp\left(T\right)+A_{42}\cdot \\\displaystyle \cdot TempComp\left(T\right)^{2}\end{array}}$

( 9)

${\begin{array}{l}\displaystyle P_{5}Temp\left(T\right)=A_{50}+A_{51}\cdot TempComp\left(T\right)+A_{52}\cdot \\\displaystyle \cdot TempComp\left(T\right)^{2}\end{array}}$

( 10)

Los coeficientes desde A₁₀ hasta A₅₂ son obtenidos en el proceso de calibración resolviendo un sistema lineal de ecuaciones y deben ser grabados en la memoria de programa del CPU para realizar la compensación del sensor de presión en tiempo real. Una vez caracterizado el comportamiento de la variación de las presiones de referencias con la temperatura, se procede entonces a calcular la pendiente de cada uno de los segmentos utilizando las ecuaciones (11) a (14)

$PenSeg1(T)={\frac {SalComp2-SalComp1}{P_{2}Temp\left(T\right)-P_{1}Temp\left(T\right)}}$

( 11)

$PenSeg2(T)={\frac {SalComp3-SalComp2}{P_{3}Temp\left(T\right)-P_{2}Temp\left(T\right)}}$

( 12)

$PenSeg3\left(T\right)={\frac {SalComp4-SalComp3}{P_{4}Temp\left(T\right)-P_{3}Temp\left(T\right)}}$

( 13)

$PenSeg4\left(T\right)={\frac {SalComp5-SalComp4}{P_{5}Temp\left(T\right)-P_{4}Temp\left(T\right)}}$

( 14)

Los coeficientes SalComp1, SalComp2, SalComp3, SalComp4 representan los valores compensados de presión que se desean obtener a la salida del transmisor para cada una de las 5 presiones de referencia aplicadas en el proceso de calibración.

Posteriormente se procede a calcular el intercepto de cada uno de los segmentos utilizando las ecuaciones (15) a (18)

$IntSeg1\left(T\right)=SalComp1-PenSeg1\left(T\right)\cdot P_{1}Temp\left(T\right)$

( 15)

$IntSeg2\left(T\right)=SalComp2-PenSeg2\left(T\right)\cdot P_{2}Temp\left(T\right)$

( 16)

$IntSeg3\left(T\right)=SalComp3-PenSeg3\left(T\right)\cdot P_{3}Temp\left(T\right)$

( 17)

$IntSeg4\left(T\right)=SalComp4-PenSeg4\left(T\right)\cdot P_{4}Temp\left(T\right)$

( 18)

De esta forma es posible obtener una ecuación que representa el valor de presión compensado para cada uno de los 4 segmentos de recta, como se muestra en las ecuaciones (19) a (22). La ecuación específica que se utilizará para el cálculo de la presión compensada está estrechamente relacionada con el valor obtenido del sensor.

Para seleccionar la recta específica a utilizar fue desarrollado un algoritmo comparativo entre el valor obtenido del sensor y los valores calculados utilizando las ecuaciones (6) a (10)

${\begin{array}{l}\displaystyle SalComp1\left(T,P\right)=PenSeg1\left(T\right)\cdot Sdata\left(T\right.\\\left.\displaystyle P\right)+IntSeg1\left(T\right)\end{array}}$

( 19)

${\begin{array}{l}\displaystyle SalComp2\left(T,P\right)=PenSeg2\left(T\right)\cdot Sdata\left(T\right.\\\left.\displaystyle P\right)+IntSeg2\left(T\right)\end{array}}$

( 20)

${\begin{array}{l}\displaystyle SalComp3\left(T,P\right)=PenSeg3\left(T\right)\cdot Sdata\left(T\right.\\\left.\displaystyle P\right)+IntSeg3\left(T\right)\end{array}}$

( 21)

${\begin{array}{l}\displaystyle SalComp4\left(T,P\right)=PenSeg4\left(T\right)\cdot Sdata\left(T\right.\\\left.\displaystyle P\right)+IntSeg4\left(T\right)\end{array}}$

( 22)

Donde Sdata(T,P) es el valor correspondiente a la salida del sensor obtenido en el CPU a través del ADC.

2.3. Modelación y compensación del bloque de salida analógica

La modelación y compensación del bloque de salida analógica se realiza de forma similar a la reportada por Maxim en [10] , pero se realizó una modificación importante. En el algoritmo descrito por Maxim solo se compensan las características no deseadas del DAC, mientras que en el algoritmo propuesto en este trabajo también se compensan las características no deseadas de todo el bloque de salida analógica compuesto por el DAC y otros elementos circuitales adicionales.

Como puede observarse en la figura 1 , la CPU recibe los datos de los sensores de presión y temperatura en formato digital, antes del bloque de salida analógica. Dado que la compensación en tiempo real ocurre en la CPU, si en esta se corrigen solamente los errores del sensor de presión y de temperatura, entonces, cuando la señal compensada sea enviada al bloque de salida analógica, este degradará la corrección realizada anteriormente por ser también sensible a la temperatura. Para que lo anterior no ocurra, se caracteriza también el bloque analógico para saber cómo este afectaría la señal. Antes de enviar el dato compensado de presión al DAC, se debe modificar en la CPU este valor en la misma magnitud pero en sentido contrario a cómo será afectado por el bloque analógico. De esta forma es posible obtener en la salida el valor deseado. Los errores de las señales de los sensores de presión y temperatura son corregidos después de que estos ocurren y los errores del DAC y el resto de los componentes que conforman el bloque analógico son corregidos antes de que ocurran.

La ecuaciones representadas en (19) a (22) permiten obtener el valor compensado de presión. Para obtener una salida analógica es necesario utilizar un DAC y un circuito encargado de transformar las variaciones de la tensión a la salida de este dispositivo en variaciones de voltaje o corriente entre niveles estándares. En caso de que el transmisor tuviera solamente salida digital no sería necesario realizar esta compensación.

Para compensar las dependencias térmicas del bloque de salida analógica se caracteriza su comportamiento para cada una de las 3 temperaturas de referencia durante el proceso de calibración. Para cada temperatura se colocan 2 valores digitales de referencia a la entrada de DAC y se mide la salida del bloque analógico. De esta forma se obtienen 6 valores que caracterizan su comportamiento. Estos puntos se nombran SalA1T1 , SalA2T1 , SalA1T2 , SalA2T2 , SalA1T3 y SalA2T3 .

La modelación del bloque de salida analógica se realiza utilizando un modelo trasferencial lineal donde la pendiente y el intercepto dependen de la temperatura que es modelada de forma cuadrática. Para ello primero se calcula la pendiente que tendría la recta para cada una de las temperaturas de referencia según se muestra en las ecuaciones (23) a (25)

$PenT1={\frac {SalA2T1-SalA1T1}{DACref2-DACref1}}$

( 23)

$PenT2={\frac {SalA2T2-SalA1T2}{DACref2-DACref1}}$

( 24)

$PenT3={\frac {SalA2T3-SalA1T3}{DACref2-DACref1}}$

( 25)

Los valores SalA1T1 y SalA2T1 se miden a la salida del bloque analógico para la temperatura de referencia 1 cuando se aplican a la entrada del DAC los valores de referencia DACref1 y DACref2 , respectivamente. Los valores SalA1T2 , SalA2T2, SalA1T3 y SalA2T3 son equivalentes a SalA1T1 y SalA2T1 para las otras 2 temperaturas de referencia, según corresponda. Seguidamente se calcula el valor del intercepto para cada una de estas 3 rectas utilizando las ecuaciones (26) a (28)

$IntT1=SalA1T1-PenT1\cdot DACref1$

( 26)

$IntT2=SalA1T2-PenT2\cdot DACref1$

( 27)

$IntT3=SalA1T3-PenT3\cdot DACref1$

( 28)

Las 3 rectas que representan el comportamiento del bloque analógico de salida para las 3 temperaturas de referencia se representan en las ecuaciones (29) a (31)

$SalT1\left(DACin\right)=PenT1\cdot DACin+IntT1$

( 29)

$SalT2\left(DACin\right)=PenT2\cdot DACin+IntT2$

( 30)

$SalT3\left(DACin\right)=PenT3\cdot DACin+IntT3$

( 31)

Para determinar una única expresión que modele el comportamiento del bloque analógico de salida en función de la temperatura y el valor de entrada del DAC, se determinaron las ecuaciones de segundo orden que caracterizan las variaciones térmicas de la pendiente Pen(T) y del intercepto de la función transferencial lineal Int(T) tomando como base las ecuaciones (29) a (31).

Las ecuaciones (32) y (33) representan estas variaciones

$Pen\left(T\right)=p_{1}+p_{2}\cdot T+p_{3}\cdot T^{2}$

( 32)

$Int\left(T\right)=i_{1}+i_{2}\cdot T+i_{3}\cdot T^{2}$

( 33)

Los coeficientes i₁ , i₂ , i₃ y p₁ , p₂ , p₃ son calculados resolviendo 2 sistemas lineales de ecuaciones a partir de las temperaturas de referencia y los valores de IntT1, IntT2, IntT3 , y PenT1, PenT2, PenT3 , respectivamente. La ecuación (34) representa el comportamiento del bloque analógico de salida para todo el intervalo de temperaturas

$SalA\left(T,DACin\right)=Pen(T)\cdot DACin+Int(T)$

( 34)

3. Simulación del algoritmo

Para comprobar el algoritmo diseñado fue realizada la simulación del mismo en el software matemático MathCAD. Para ello fueron utilizados los datos mostrados en la tabla 1 que caracterizan el comportamiento de un sensor ficticio de 10 bar en el intervalo de temperaturas de 0 a 50 °C. La dependencia térmica del sensor fue magnificada para comprobar la efectividad del algoritmo. Las temperaturas de referencia utilizadas en la simulación del algoritmo para realizar la calibración del sensor de presión fueron 0, 25 y 50 °C.

Tabla 1. Salida en tensión (mV) del sensor ficticio utilizado en la simulación

T (°C)	P(bar)
	0	2,5	5	7,5	10
0	−10,156	25,177	60,384	95,466	130,422
12,5	−5,5071	26,286	57,990	89,604	121,130
25	−2,1668	26,535	55,176	83,756	112,275
37,5	−0,135	25,924	51,942	77,920	103,857
50	0,588	24,453	48,288	72,096	95,875

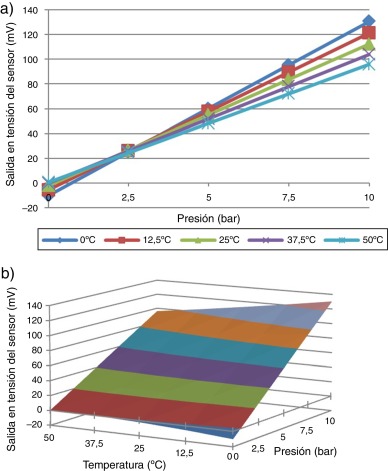
En la figura 5 se muestra la respuesta del sensor antes de la calibración. En estos gráficos se evidencia la dependencia térmica del offset y de la sensibilidad en la salida del sensor de presión. El principal objetivo de la simulación realizada fue comprobar que el algoritmo compensaba los errores provocados por estas dependencias.

Figura 5. a) Característica transferencial de la señal del sensor de presión sin compensar para diferentes temperaturas. b) Superficie que caracteriza la respuesta del sensor sin compensar en el intervalo de temperaturas.

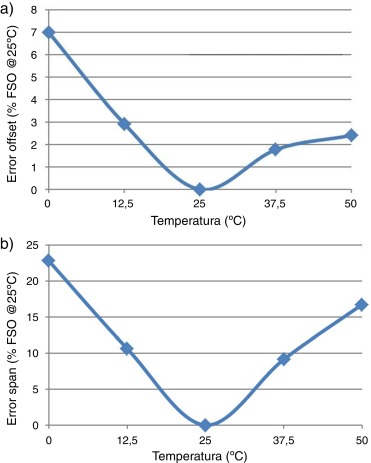
En la figura 6 a,b se muestran los errores en la salida del sensor provocados por las dependencias térmicas del offset y de la sensibilidad, respectivamente, antes de la calibración. Estos errores fueron calculados tomando como referencia el offset y la sensibilidad a 25 °C.

Figura 6. a) Error en la salida del sensor debido a la dependencia térmica del offset. b) Error en la salida del sensor debido a la dependencia térmica de la sensibilidad.

La ecuación (35) muestra cómo fue calculado el error de offset mostrado en la figura 6 a

$ErrorOffsetTempX={\frac {\left|OffsetTempX-Offset25{^{\circ }}C\right|}{Span25{^{\circ }}C}}\cdot 100\%$

( 35)

OffsetTempX representa el offset en la salida del sensor para la temperatura a la que se encuentra, Offset25 °C es el offset a 25 °C que es tomado como referencia, y Span25 °C es la diferencia entre las salidas máxima y mínima del sensor para la temperatura de 25 °C.

La ecuación (36) muestra cómo fue calculado el error de sensibilidad mostrado en la figura 6 b

$ErrorSpanTempX={\frac {\left|SpanTempX-Span25{^{\circ }}C\right|}{Span25{^{\circ }}C}}\cdot 100\%$

( 36)

SpanTempX representa la diferencia entre la salida máxima y mínima del sensor para la temperatura a la que se encuentra el sensor.

En la figura 6 a se observa que el error máximo debido a la dependencia térmica del offset es del 7% del intervalo de medida, aproximadamente. En la figura 6 b se muestra que el error máximo debido a la dependencia térmica del span es del 22% del intervalo de medida, aproximadamente.

Fue simulado el algoritmo partiendo de los datos mostrados en la tabla 1 . La figura 7 muestra la respuesta del transmisor de presión después de realizada la calibración y compensación utilizando el algoritmo de aproximación lineal por segmentos con compensación térmica. Resulta evidente la compensación de las dependencias térmicas de estos parámetros.

Figura 7. a) Característica transferencial del transmisor de presión compensado. b) Superficie que caracteriza la respuesta del transmisor compensado.

En la figura 8 a fue graficado el error debido a la dependencia térmica del offset en la salida del transmisor de presión después de calibrado y compensado. La ecuación (35) fue utilizada nuevamente para determinar estos errores. En la figura 8 b se observa el error provocado por la dependencia térmica de la sensibilidad en el transmisor calibrado para todo el intervalo de temperaturas. Este error fue calculado utilizando la ecuación (36).

Figura 8. a) Error en la salida del transmisor después de calibrado debido a la dependencia térmica del offset . b) Error en la salida del transmisor después de calibrado debido a la dependencia térmica de la sensibilidad.

El error de offset máximo obtenido fue de 0,045% del intervalo de medida, mientras que el error de span máximo fue de 0,084% del intervalo de medida. En la figura 8 se observa que los errores para las temperaturas de 0, 25 y 50 °C son prácticamente nulos. Este resultado es esperado teniendo en cuenta que esas fueron las temperaturas utilizadas como referencias en la simulación del algoritmo. Esto se debe a que en la simulación no se tienen en cuenta varias fuentes de errores que sí están presentes en la vida real, como la histéresis térmica y la repetibilidad. Se puede observar que utilizando el algoritmo de aproximación lineal por segmentos con compensación térmica, se reducen notablemente los errores térmicos del sensor ficticio utilizado en la simulación.

4. Resultados experimentales

Para realizar la validación experimental del algoritmo de aproximación lineal por segmentos con compensación térmica fueron diseñados y construidos 2 transmisores de presión utilizando sensores de presión piezorresistivos. En la figura 9 se muestra el diagrama en bloques simplificado de los transmisores diseñados.

Figura 9. Diagrama en bloques simplificado de los transmisores diseñados.

Como núcleo central de los transmisores fue seleccionado el DSP MAX1464 [11] , que es un procesador digital de bajo ruido y bajo consumo de potencia, optimizado para aplicaciones industriales de control de procesos. Este dispositivo posee un sensor de temperatura integrado en el mismo chip, un multiplexor y un convertidor analógico-digital para digitalizar las señales analógicas provenientes tanto del sensor de presión como del propio sensor de temperatura interno. También posee integrado en el mismo chip una CPU y un conversor digital-analógico, como se muestra en la figura 9 . La CPU del MAX1464 posee 16 registros, 16 puertos, un repertorio de 16 instrucciones y 4 kbytes de memoria de programa para realizar la implementación del algoritmo descrito en este trabajo.

El programa desarrollado en código ensamblador para este DSP se encuentra estructurado en 2 ciclos o lazos fundamentales, como se mostró en la figura 2 . Fue desarrollada una rutina de inicialización donde se realiza la configuración de varios módulos, como por ejemplo la resolución del ADC y su frecuencia de conversión, la frecuencia del oscilador interno del MAX1464, el voltaje de referencia, entre otros. En uno de los lazos se calcula el valor compensado de temperatura, así como otros valores que solo dependen de este parámetro. En el otro lazo es donde se determina el valor compensado de presión utilizando varios parámetros calculados en el lazo de temperatura y los coeficientes calculados en el proceso de calibración.

El lazo que calcula la presión compensada se ejecuta 500 veces por cada vez que se ejecuta el lazo donde se determina el valor compensado de temperatura. A partir de la salida en tensión del DAC se implementó un circuito convertidor voltaje-corriente para obtener una salida estándar 4-20 mA a 2 hilos. Para la construcción de los transmisores fueron utilizados sensores manométricos ventilados de 10 bar fabricados por Keller [12] . Las Tabla 2  and Tabla 3 muestran la respuesta de los sensores de presión en todo el intervalo de temperaturas para las presiones de referencia antes de realizar la calibración.

Tabla 2. Salida en tensión (mV) del sensor 1 antes de la calibración

T (°C)	P(bar)
	0	2,5	5	7,5	10
0	12,635	51,220	89,730	128,18	166,55
20	12,754	51,395	89,980	128,49	166,95
40	13,330	52,120	90,830	129,49	168,09
60	13,969	53,005	92,005	130,94	169,83
80	14,675	54,125	93,545	132,90	172,23

Tabla 3. Salida en tensión (mV) del sensor 2 antes de la calibración

T (°C)	P(bar)
	0	2,5	5	7,5	10
0	9,385	49,520	91,760	133,87	175,89
20	10,251	52,520	94,750	136,75	178,75
40	10,644	53,017	95,325	137,53	179,66
60	10,868	53,595	96,207	138,73	181,18
80	11,040	54,220	97,310	140,29	183,23

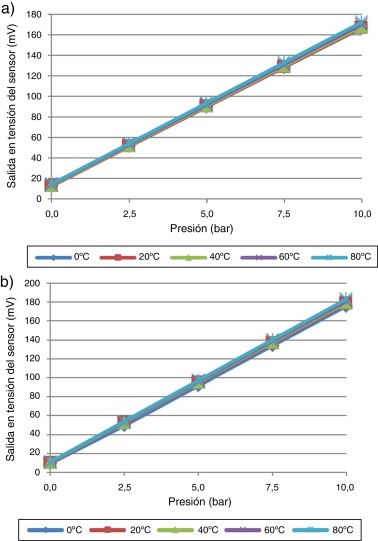
En la figura 10 se muestran las características transferenciales de los 2 sensores de presión utilizados. Se observan las dependencias térmicas de los sensores, aunque estas no son tan marcadas como las mostradas en la figura 5 para el sensor ficticio utilizado para la simulación.

Figura 10. Característica transferencial de los sensores de presión utilizados: a) Sensor 1. b) Sensor 2.

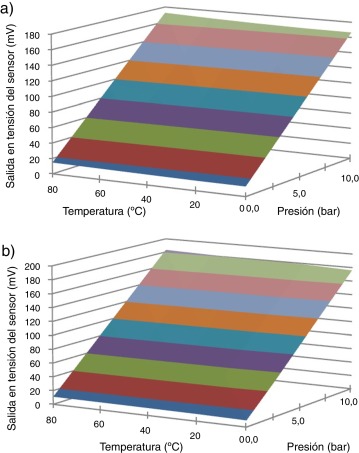
En la figura 11 se observan las superficies que caracterizan las salidas de los 2 sensores utilizados para la construcción de los transmisores. En ellas se puede observar como el offset aumenta ligeramente su valor con el aumento de la temperatura, mientras que la sensibilidad también varía.

Figura 11. Superficies que caracteriza la respuesta de los sensores antes de ser calibrados. a) Sensor 1. b) Sensor 2.

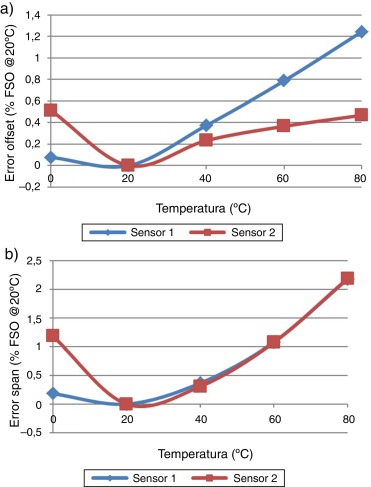
En la figura 12 a fue graficado el error debido a la dependencia térmica del offset para los 2 sensores antes de ser sometidos al proceso de calibración. En este caso se tomó como referencia la temperatura de 20 °C. La ecuación (35) fue utilizada nuevamente para determinar estos errores pero utilizando como temperatura de referencia 20 °C. En la figura 12 b se observa el error a la salida de los transmisores provocado por la dependencia térmica de la sensibilidad antes de calibrados. Estos errores fueron calculados utilizando (36).

Figura 12. a) Errores en las salidas de los sensores debido a la dependencia térmica del offset. b) Errores en las salidas de los sensores debido a la dependencia térmica de la sensibilidad.

En la figura 12 a se observa que el error máximo debido a la dependencia térmica del offset fue del 1,24% del intervalo de medida para el sensor 1, mientras en la figura 12 b se muestra que el error máximo debido a la dependencia térmica de la sensibilidad fue aproximadamente 2,19% del intervalo de medida para ambos sensores. Estos valores demuestran la necesidad de utilizar circuitos de acondicionamiento para estos sensores si se desea obtener salidas con exactitudes superiores al 0,25% del intervalo de medida.

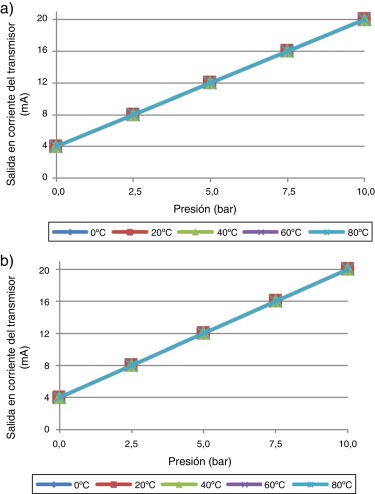
Una vez construidos los transmisores, fueron sometidos a un proceso de calibración. En este proceso de calibración se caracterizaron a 3 temperaturas de referencia (0, 40 y 80 °C) y para cada una de esas temperaturas se aplicaron 5 presiones de referencia (0, 2,5, 5, 7,5 y 10 bar). De esta forman fueron obtenidos 15 valores para cada transmisor que caracterizan el comportamiento de los sensores utilizados. Adicionalmente también fueron caracterizados el sensor de temperatura y el bloque de salida analógica. Para aplicar las temperaturas de referencia fue utilizada la cámara climática VCL 4006 de Vötsch y las presiones de referencias fueron aplicadas con el calibrador de presión DPI 515 de Druck GE. Partiendo de los datos obtenidos en el proceso de calibración fueron obtenidos los coeficientes específicos que compensan a los transmisores construidos. El algoritmo de aproximación lineal por segmentos con compensación térmica fue implementado en los DSP de los transmisores utilizando los coeficientes específicos obtenidos. Posteriormente se caracterizaron las salidas en corriente de los transmisores para comprobar el algoritmo implementado. La figura 13 muestra la respuesta del transmisor de presión después de realizada la calibración y compensación utilizando el algoritmo. Se observa que el algoritmo realizó la compensación de las dependencias térmicas.

Figura 13. Característica transferencial de los transmisores de presión compensados. a) Transmisor 1. b) Transmisor 2.

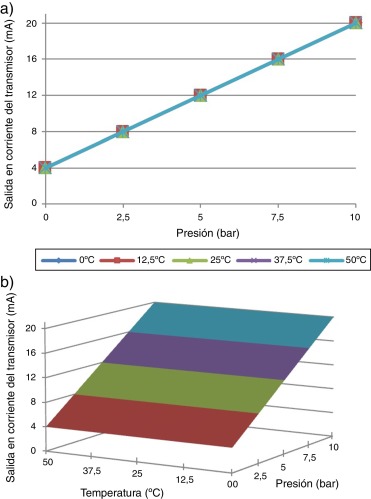
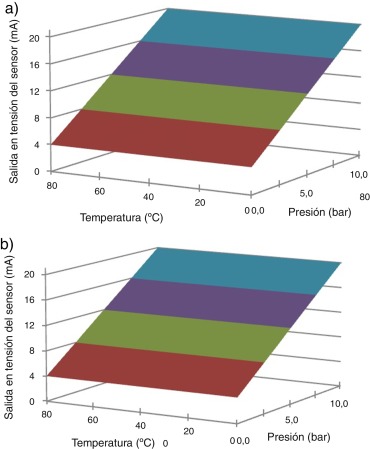
En la figura 14 se muestran las superficies que caracterizan las salidas de los transmisores construidos después de realizada la calibración y compensación, para el intervalo de temperaturas de 0 a 80 °C. Se observa que las superficies son planos prácticamente perfectos, lo que evidencia la compensación térmica de la salida de los transmisores.

Figura 14. Superficies que caracterizan la salida de los transmisores de presión construidos después de la calibración. a) Transmisor 1. b) Transmisor 2.

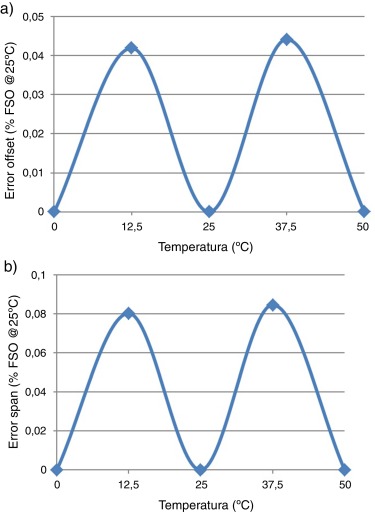
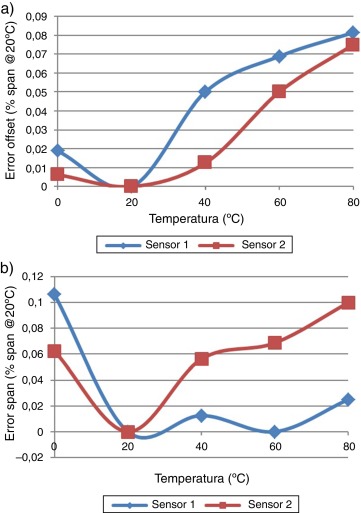
En la figura 15 a fueron graficados los errores debidos a la dependencia térmica del offset en los transmisores de presión después de calibrados y compensados. La ecuación (35) fue utilizada nuevamente para determinar estos errores tomando como referencia la temperatura de 20 °C. En la figura 15 b se observa el comportamiento de los errores provocados por la dependencia térmica de la sensibilidad en los transmisores después de calibrados para todo el intervalo de temperatura. Este error fue calculado utilizando la ecuación (36) y tomando también como referencia la temperatura de 20 °C.

Figura 15. a) Error a la salida de los transmisores debido a la dependencia térmica del offset . b) Error en la salida de los transmisores debido a la dependencia térmica de la sensibilidad.

El máximo error de offset obtenido fue de 0,081% del intervalo de medida, mientras que el error de sensibilidad máximo fue de 0,106% del intervalo de medida. Los valores de errores obtenidos en los experimentos fueron superiores a los obtenidos en la simulación del algoritmo. Este resultado es lógico, ya que en la simulación no se tienen en cuenta varias fuentes de errores que sí están presentes en la vida real como la histéresis térmica, la repetibilidad y el auto-calentamiento. Utilizando el algoritmo de aproximación lineal por segmentos con compensación térmica, se reducen notablemente los errores térmicos de los sensores obteniendo valores inferiores al 0,11% del intervalo de medida.

5. Conclusiones

El algoritmo de aproximación lineal por segmentos con compensación térmica presentado en este trabajo representa un método práctico para realizar la corrección de las dependencias térmicas del offset y la sensibilidad en sensores de presión piezorresistivos. El algoritmo es simple, ya que no es necesario conocer explícitamente la función trasferencial de cada sensor que se desee compensar, y solamente caracterizándolo a 3 temperaturas y 5 presiones de referencia es posible realizar su compensación. Este algoritmo puede ser aplicado a otros tipos de sensores inteligentes que también posean dependencias térmicas y que incorporen un microprocesador o un procesador digital de señales.

El algoritmo fue simulado y probado utilizando el programa computacional matemático MathCAD. La simulación permitió realizar un estudio del algoritmo utilizando datos de un sensor convencional de 10 bar en el intervalo de temperaturas de 0 a 50 °C. Los resultados obtenidos en la simulación fueron comprobados experimentalmente utilizando sensores manométricos ventilados de 10 bar en el intervalo de temperaturas de 0 a 80 °C. Fue validado el algoritmo demostrando su efectividad en la compensación térmica de los sensores de presión piezorresistivos.

Agradecimientos

Agradecemos a las siguientes instituciones brasileras por el apoyo financiero en el desarrollo de este trabajo: CNPq (Programa RHAE), FINEP (Programa de Microelectrónica), FAPESP (Programa PIPE) y a los laboratorios LSI y LME de la EPUSP. Este trabajo fue desarrollado con la colaboración de la empresa MEMS Ltda.

Bibliografía

1. [1] Y. Chuan, L. Chen; The Intelligent Pressure Sensor System Based on DSP; The 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), Chengdu (2010)
2. [2] E.M. Boujamaa, B. Alandry, S. Hacine, L. Latorre, F. Mailly, P. Nouet; A Low Power Interface Circuit for Resistive Sensors with Digital Offset Compensation; The IEEE International Symposium on Circuits and Systems, Paris (2010)
3. [3] J. Ramirez, E. Charry; A CMOS signal conditioning circuit for piezoresistive pressure sensors; The IEEE International Symposium on Circuits and Systems, Phoenix (2002)
4. [4] R. Brown; High precision silicon piezo resistive SMART pressure sensor; J. Phys. Conf. Ser., 15 (2005), pp. 19–26
5. [5] A. Hernández, J. Ramírez, J.F. Trujillo, E. Charry; New Architecture for Intelligent Pressure Sensors with Analog and Digital Outputs; IEEE Lat. Am. Trans., 12 (2014), pp. 116–121
6. [6] M. Pavlin, F. Novak; Yield enhancement of piezoresistive pressure sensor for automotive application; Sens. Actuators, A., 141 (2008), pp. 34–42
7. [7] J. Philip, J. Abhay, S. Pramod, P.D. Ajayakumar, K. Natarajan; Signal Conditioner for MEMS based Piezoresistive sensor; The 5th International Conference on Industrial and Information Systems, India (2010)
8. [8] A.C. Zoric, D. Martinovic, S. Obradovic; A Simple 2D Digital Calibration Routine for Transducers; Ser. Elec. Energ., 19 (2006), pp. 197–207
9. [9] S. Poussier, H. Rabah, S. Weber; Smart adaptable strain gage conditioner: hardware/software implementation; IEEE Sensors J., 4 (2004), pp. 262–267
10. [10] Maxim Integrated Inc., Application Note 3649. MAX1464 Signal-Conditioner, Sensor Compensation Algorithm (2005) [consultado 12 Feb 2014]. Disponible en: http://www.maximintegrated.com
11. [11] Maxim Integrated Inc., MAX1464 Low-Power, Low-Noise Multichannel Sensor Signal Processor (2005) [consultado 12 Feb 2014]. Disponible en: http://www.maximintegrated.com
12. [12] Keller AG Inc., Piezoresistive OEM Pressure Transducers. Series 7S/9S/9FL (2008) [consultado 12 Feb 2014]. Disponible en: http://www.keller-druck.com