Resumen
El comportamiento de elementos de hormigón armado y pretensado sometidos a cortante ha sido tradicionalmente objeto de estudio de las denominadas Teorías de Campos de Compresiones . En los últimos años varios autores han modificado parcialmente el modelo mecánico en que se apoyan dichas teorías a fin de incluir el efecto de la tensorrigidez del hormigón (o capacidad del hormigón de resistir tracciones entre fisuras) en la ecuación de comportamiento del acero; el sistema de ecuaciones resultante es altamente no-lineal e involucra una gran cantidad de variables. El presente artículo plantea, a partir de datos experimentales ya existentes, el ajuste del modelo de cortante propuesto por una de estas teorías, usando para ello algoritmos evolutivos. Los algoritmos evolutivos son una rama emergente de la computación natural, cuyo principal objetivo es la resolución de problemas de optimización y búsqueda, computacionalmente costosos, en un tiempo razonable. Estos métodos se caracterizan por la creación de una población que representa posibles soluciones del problema. Los individuos de la población se combinan y compiten entre sí con el fin de buscar el individuo (solución) más apto para el problema tratado. Los resultados numéricos obtenidos presentan un error relativo inferior al 10% respecto a los valores experimentales considerados, validando así la estrategia evolutiva y situándola como una alternativa seria en problemas de ajuste computacionalmente costosos.
Abstract
The behavior of reinforced and prestressed concrete members subjected to shear has been traditionally studied by the so-called Compression-Field Theories. In the last years several authors have modified the mechanical model of such theories in order to include the tension-stiffening effect of the concrete in the steel constitutive model; the resulting system of equations is highly non-linear and involves a great number of unknowns. From an experimental database of RC beams, this work performs an adjustment of the shear model proposed by one of these theories using evolutionary algorithms. Evolutionary algorithm is a branch of Natural Computing. Its computations start from an initial population of individuals (randomly generated) and proceed according to rules of selection and other operators, such as recombination and mutation. The main objective of such algorithms is to find good solutions in a reasonable time-frame. Numerical results show a relative error between numerical results and experimental data less than 10%, what validates genetic algorithms as a good alternative for solving these computationally-intensive adjustment problems.
Palabras clave
Algoritmos evolutivos ; Cortante en hormigón estructural ; Modelos constitutivos
Keywords
Evolutionary algorithms ; Shear in concrete ; Constitutive models
1. Introducción
La transmisión del esfuerzo cortante a través del alma fisurada de una viga de hormigón armado constituye un fenómeno sumamente complejo que, todavía a día de hoy, es objeto de diversos tipos de estudios. La formulación de un modelo que determine la curva de respuesta a cortante de una viga de hormigón armado requiere tener en cuenta, para cada nivel de solicitación, la inclinación de las fisuras en el alma de la referida viga. En este sentido, las Teorías de Campo de Compresiones [1] ; [2] ; [3] establecen relaciones cinemáticas entre la inclinación de dichas fisuras, las deformaciones de la armadura y del hormigón. Tales relaciones, unidas a unas condiciones de equilibrio y los correspondientes modelos constitutivos de los materiales involucrados, permiten determinar con un grado de aproximación razonable la respuesta carga-deformación en cualquier sección de una viga de hormigón armado y pretensado sometida a cortante.
La validación experimental de las Teorías de Campo de Compresiones [2] ; [3] ; [4] concluye que la consideración del área de rigidez a tracción del hormigón entre fisuras (o área de tensorrigidez) propuesta por la actual normativa, en base a la pérdida de adherencia que acontece entre el hormigón y el acero en la zona próxima a la fisura, subestima notablemente la resistencia a cortante de la viga en los instantes previos al agotamiento. En este sentido, resulta interesante ajustar una función que tenga en cuenta la progresiva degradación resistente que experimenta el hormigón a medida que aumenta la fuerza solicitante y que esté relacionada con la deformación por cortante del elemento estructural.
El ajuste de un parámetro de degradación del área de tensorrigidez que permita estimar en mejor medida la respuesta a cortante de un elemento de hormigón estructural ha sido abordado mediante técnicas clásicas de regresión, obteniéndose bajos coeficientes de correlación debido, entre otras razones, a la alta no linealidad del problema y el gran número de variables involucradas [5] . En este sentido, y a fin de mejorar el ajuste del modelo, este trabajo propone el uso de la computación evolutiva, y en concreto, la estrategia de evolución des-aleatorizada con adaptación de matriz de covarianza (CMA-ES).
Los algoritmos evolutivos son estrategias de optimización y búsqueda de soluciones que toman como inspiración la evolución en distintos sistemas biológicos [6] . La idea fundamental de estos algoritmos es mantener un conjunto de individuos que representan una posible solución del problema. Estos individuos se mezclan y compiten entre sí, siguiendo el principio de selección natural por el cual sólo los mejor adaptados sobreviven al paso del tiempo. Esto redunda en una evolución hacia soluciones cada vez más aptas.
El objetivo de este trabajo es obtener, mediante computación evolutiva y a partir de datos experimentales de vigas de hormigón armado y pretensado disponibles en la bibliografía, una función de degradación que permita ajustar la variación del área de tensorrigidez del hormigón después que éste ha fisurado y, particularmente, en los estadios de deformación previos al agotamiento por cortante. El resto del trabajo está estructurado de la siguiente forma; en la sección 2 presentamos la metodología utilizada para el cálculo la función de degradación mediante algoritmos evolutivos. Posteriormente, se muestran los resultados obtenidos en base a los datos experimentales seleccionados y, finalmente, se emiten unas conclusiones.
2. Metodología
2.1. Teorías de Campo de Compresiones en hormigón estructural
La formulación de las Teorías de Campo de Compresiones en el contexto de la mecánica de medios continuos, habida cuenta de la fisuración (y consiguiente pérdida de «continuidad») del hormigón durante el proceso de aplicación de la carga, pasa por la consideración de deformaciones medias comunes a acero y hormigón, medidas sobre una longitud suficiente que incluya varias fisuras y basadas en una adherencia perfecta entre ambos materiales. En este sentido, se asume un único tensor de deformaciones para el alma fisurada de la viga de hormigón armado, el cual verifica las siguientes relaciones cinemáticas:
|
|
( 1) |
|
|
( 2) |
donde ɛx y ɛt son las deformaciones longitudinal y transversal de la viga, respectivamente, ɛ1 y ɛ2 son las deformaciones principales a tracción y compresión en el hormigón, respectivamente, mientras que θc es el ángulo que mide la inclinación de la dirección principal de deformación a compresión respecto al eje longitudinal de la viga (y se asume igual a la inclinación de la fisura en el alma). El equilibrio a cortante puro del alma de la viga de hormigón armado viene definido por el siguiente conjunto de tres ecuaciones:
|
|
( 3) |
|
|
( 4) |
|
|
( 5) |
donde σ1 es la tensión principal de tracción en el hormigón, θe es el ángulo que forma la tensión principal de compresión con el eje longitudinal de la viga, V es la fuerza cortante, σ2 es la tensión principal de compresión en el hormigón, s es la separación entre cercos, bw es el ancho del alma, z es el brazo mecánico de flexión, Asx , Ast y Ap son las secciones de la armadura longitudinal, transversal y pretensada, respectivamente, y σsx , σst y σp son las tensiones en las barras longitudinales, en los cercos y en la armadura activa, respectivamente (fig. 1 a). Los ángulos θe y θc coinciden aproximadamente [1] y en el marco de las teorías de campo de compresiones se asumen iguales (i.e., θe = θc = θ ) bajo un cierto error aceptable [1] ; [7] . Las dos hipótesis de base indicadas anteriormente (en relación a deformaciones medias y ángulos) han sido validadas por la experimentación desarrollada durante varias décadas [1] ; [2] ; [4] y permiten la predicción de la respuesta a cortante de elementos fisurados de hormigón armado y pretensado con un grado de precisión suficiente y un coste computacional razonable.
|
|
|
Figura 1. a) Diagramas de equilibrio en la viga de hormigón armado (adaptado de [3] ; [8] ); b) Modelos de comportamiento del acero para barra aislada y embebida. Datos: fy = 530 MPa, fct = 4.50 MPa, As = 50.27 mm2 (1 Ø 8), Ac = 9025 mm2 . |
En el caso de paneles de hormigón sometidos a un estado biaxial de tracción y compresión, Vecchio y Collins proponen el siguiente modelo de comportamiento a compresión del hormigón [1] :
|
|
( 6) |
siendo fc la resistencia a compresión del hormigón obtenida mediante ensayo uniaxial de una probeta cilíndrica, ɛc es la deformación a compresión correspondiente a fc , y f2,max es la resistencia máxima a compresión del hormigón sometido a un estado de tensión biaxial. Del mismo modo cuando la deformación supera el valor correspondiente a la resistencia media de tracción (fctm ), la contribución del hormigón a tracción entre fisuras (o tensorrigidez) no es despreciable y condiciona en gran medida la respuesta a cortante del hormigón estructural en la etapa de post-fisuración; Collins y Mitchell proponen el siguiente modelo de tensorrigidez para el hormigón [1] ; [8] :
|
|
( 7) |
donde Ec es el módulo de deformación del hormigón y ɛctm es la deformación asociada a la resistencia media a tracción del hormigón (fctm ). Para barras corrugadas y cargas rápidas no cíclicas (como se ha considerado en el presente trabajo), el coeficiente α toma valor igual a la unidad.
En los últimos años la evolución de las teorías de campo de compresiones ha tenido lugar a través de la formulación de un modelo de comportamiento para el acero que tenga en cuenta la tensorrigidez del hormigón adherido a la barra (modelo de barra «embebida») [3] ; [9] ; [10] ; una de las teorías formuladas en esta línea es la denominada «Teoría Refinada del Campo de Compresiones» (Refined Compression Field Theory, RCFT) [3] ; [4] ; [11] . Según esta teoría, una vez el hormigón ha fisurado la tensión del acero en el punto de fisura debe ser igual, por equilibrio, a la suma de las tensiones a tracción del acero y el hormigón en la zona entre fisuras (véase detalle de fig. 1 a). En base a esta consideración, la relación tensión-deformación (en valores medios) del acero a tracción puede formularse como (fig. 1 b):
|
|
( 8,9) |
donde
|
|
( 10) |
siendo Es el módulo de deformación del acero, fy la tensión de cedencia del acero y ɛmax la deformación aparente de cedencia del acero (o deformación media del acero cuando éste alcanza la tensión de cedencia en el punto de fisura). Los subíndices x1 , x2 y t se refieren a las armaduras longitudinal inferior, longitudinal superior y transversal, respectivamente. Al área de hormigón de la sección de la viga que envuelve a la armadura y aporta, conjuntamente con ésta, rigidez a tracción se la denomina área de tensorrigidez (Ac,i ). Asimismo, en el caso de elementos de hormigón pretensado es preciso considerar dos ecuaciones adicionales, una de compatibilidad y otra de comportamiento, según se indica a continuación:
|
|
( 11) |
|
|
( 12) |
siendo ɛp la deformación unitaria de la armadura activa, Δɛp la deformación impuesta por el sistema de pretensado, σp la tensión de la armadura activa, fyp y Ep su tensión de cedencia y su módulo de deformación longitudinal, respectivamente. El conjunto de ecuaciones (1-6) y (8-12) anteriormente expuesto constituye un sistema no-lineal de 11 ecuaciones y 11 incógnitas: θ , ɛx , ɛt , ɛp , ɛ2 , σ2 , σsx1 , σsx2 , σst , σp y V , si se resuelve para un determinado valor de la deformación principal a tracción (ɛ1 ), el cual permite determinar la respuesta a cortante de un elemento de hormigón armado y pretensado.
2.2. Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
Los algoritmos evolutivos son una familia de métodos de optimización, y como tal, tratan de hallar una tupla de valores (xi,…,xn ) tales que se minimice una determinada función F(xi,…,xn) . Los distintos valores de la n-tupla forman una Población . Sobre esta población se aplican uno o varios operadores genéticos y se fuerza una presión selectiva (los operadores utilizados se aplicarán sobre estos cromosomas, o sobre poblaciones de ellos).
El algoritmo CMA-ES (estrategia de evolución des-aleatorizada con adaptación de matriz de covarianza) [12] es un método de búsqueda evolutivo que basa su heurística en la sucesiva adaptación de la matriz de covarianza completa de una distribución normal (distribución gaussiana) de mutaciones. La figura 2 a muestra el esquema general del algoritmo CMA-ES. Este algoritmo emplea una función gaussiana para generar una descendencia de mu soluciones para luego utilizar lambda mejores candidatos para refinar la propia función de distribución en un proceso iterativo. El bucle principal del algoritmo (ecuaciones (13), (14) y (15)) parte de una distribución gaussiana donde se generan los pesos, afectados por la raíz cuadrada de covarianzas (√C ) que actúa como matriz de transformación sobre los datos
|
|
( 13) |
|
|
( 14) |
|
|
( 15) |
En CMA-ES, la distribución de probabilidad a ser estimada es una distribución normal multivariante N(m, δ2C) , cuyos parámetros son la media m y la matriz de covarianza δ2C . La media representa la localización actual de búsqueda y se moverá en torno a mejores localizaciones a medida que la búsqueda progrese. A continuación, se utilizan esos pesos para perturbar la nueve de puntos, siendo éstos evaluados según su aptitud o fitness . La matriz de covarianza controla las mutaciones y se usa para guiar la búsqueda. CMA-ES descompone la matriz de covarianza total en una matriz de covarianza C y la varianza global δ , llamado control de tamaño de paso (step-size control ). Una vez terminado el proceso de reajuste se realiza la selección ecuación (16) y el cruce ecuación (15) hasta alcanzar el tamaño apropiado indicado por lambda
|
|
|
|
( 16) |
|
|
( 17) |
Este algoritmo además controla el tamaño de los pasos de la mutación δ2 independientemente de la dirección de búsqueda C. Estimar C requiere muchas muestras siendo muy alto el coste computacional de su adaptación. Sin embargo δ2 puede ser adaptada en marcos de tiempo más cortos. Así se reduce el número de generaciones necesarias para obtener buenos individuos, evitando caer en mínimos locales. Posteriormente se procede a auto-adaptar los valores de la propia búsqueda. La ecuación (18) ajusta el vector de dirección (s ) de la búsqueda. El término es un término de memoria (cumulación) que decrece conforme se cumple el criterio de convergencia
|
|
( 18) |
Posteriormente, el vector de dirección s se utiliza para actualizar la matriz C según la ecuación (19):
|
|
( 19) |
|
|
|
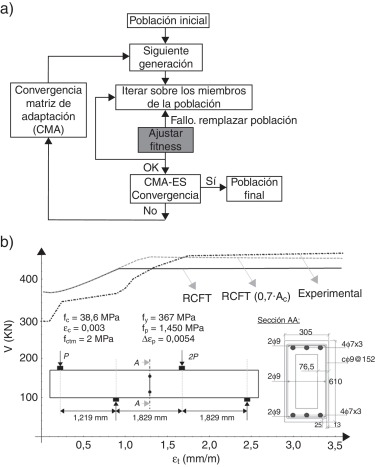
Figura 2. a) Esquema general del algoritmo CMA; b) Curvas teóricas y experimental de respuesta a cortante para la viga ensayada por Abersman y Conte (1973). |
CMA-ES controla el tamaño de los pasos comparándolo con el que tamaño de pasos que tendría si eligiese un camino aleatorio. Si el camino es más corto significa que los pasos son muy largos y se producen ciclos, en cambio si el camino es más largo significa que se dan varios pasos en la misma dirección, por lo que podrían reducirse si los pasos fuesen más largos. La media, el step-size y la matriz de covarianza se actualizan en cada generación t. Por último, las ecuaciones (20) y (21) se encargan de actualizar los parámetros de la distribución de forma que se produce un mejor ajuste como consecuencia del mayor conocimiento del área explorada
|
|
( 20) |
|
|
( 21) |
2.3. Modelo propuesto
En las secciones anteriores hemos presentado el modelo mecánico de una viga de hormigón armado sometida a cortante. Así mismo, se ha realizado una introducción a las técnicas de computación evolutiva; y en concreto a la estrategia CMA-ES. Esta estrategia no requiere un gran número de evaluaciones y funciona relativamente bien con poblaciones pequeñas. Esto es fundamental para la resolución de este problema por su elevado costo computacional, especialmente en el cálculo de la función de aptitud.
El ajuste del modelo de cortante presentado en el apartado 2.1 puede desarrollarse en términos de diferentes parámetros, particularmente de aquéllos involucrados en el efecto de tensorrigidez del hormigón. De acuerdo a los resultados presentados en [3] ; [4] ; [11] , la respuesta a cortante de elementos de hormigón armado resulta eficazmente corregida en estadios avanzados de la deformación cuando se actúa sobre el área de tensorrigidez del hormigón. Así pues, de forma preliminar y bajo el objetivo principal de validar el algoritmo CMA-ES como estrategia de ajuste de la respuesta a cortante en vigas de hormigón armado, se han seguido las directrices planteadas por Gil Martín et al. en [3] y se ha actuado únicamente sobre el área Ac , afectándola de un coeficiente (κ) en las ecuaciones (8)-(10) antes indicadas. Inspirándonos en el modelo de tensorrigidez propuesto por Collins y Mitchell (ecuación (7)), la formulación del coeficiente κ se ha ajustado en base a la siguiente familia paramétrica de funciones:
|
|
( 22) |
con {a, b, c} . Así pues, cada individuo o vector R de la población a evolucionar vendrá representado por una terna de parámetros {a,b,c}. El ajuste de estos parámetros se ha realizado a partir de una base de datos experimental compuesta por un conjunto de vigas de hormigón armado y pretensado ensayadas a cortante hasta su agotamiento por diferentes autores [13] ; [14] ; [15] ; [16] ; [17] ; [18] ; [19] ; [20] ; [21] ; [22] ; [23] ; [24] ; [25] ; [26] ; [27] ; en particular, de cada una de los ensayos analizados se ha tomado en consideración el cortante (Vu ) y la tensión experimental en cercos (σst ,exp ) en el instante de agotamiento. A fin de calcular la idoneidad F(R) de cada individuo se ha utilizado la siguiente función auxiliar:
|
|
( 23) |
donde σst ,X ,exp es el valor experimental de tensión en cercos correspondiente al espécimen X , mientras que σst,X,R es el valor teórico de la tensión en cercos correspondiente a una fuerza cortante igual a la de agotamiento del espécimen considerado (V = Vu ).
3. Resultados y discusión
Para la validación de los resultados obtenidos hemos considerado el ensayo a cortante desarrollado por Abersman y Conte en [28] . La Figura 2 b muestra las curvas de respuesta teórica (según la RCFT, con valor κ = 1) y experimental de dicho ensayo. En el caso particular de la viga ensayada se observa que una disminución del 30% (κ = 0.7) en el área de tensorrigidez propuesta por la actual normativa española [29] reduce significativamente la desviación existente entre los valores teóricos y experimentales para altas deformaciones (en particular, para deformaciones transversales iguales o superiores a 1.5 mm/m).
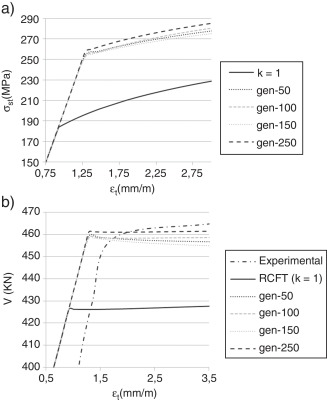
En la figura 3 a se muestra las curvas de comportamiento de la armadura transversal de la viga de Abersman y Conte para el área de tensorrigidez sin corregir (κ = 1) y para el área de tensorrigidez ajustada mediante las mejores funciones de degradación obtenidas en cada generación del algoritmo genético. Como se puede observar, el ajuste del parámetro de degradación (κ) en el modelo constitutivo del acero se traduce en un comportamiento de la armadura coherente con la consideración de equilibrio entre hormigón y acero en que se basa la RCFT, según la cual a medida que aumenta la deformación en el hormigón envolvente (y por ende, su nivel de fisuración) más solicitada se encuentra la armadura.
|
|
|
Figura 3. a) Curvas de comportamiento del acero transversal para el área de tensorrigidez sin corregir (κ = 1) y corregida según las funciones de degradación obtenidas mediante distintas generaciones del algoritmo genético; b) Curvas ajustadas de respuesta a cortante, obtenidas por el algoritmo genético con distinto número de generaciones, curva de respuesta experimental (ensayo de Abersman y Conte) y curva teórica del modelo de cortante sin ajustar (k = 1 ). |
En la figura 3 b se muestra las curvas teóricas de respuesta a cortante de la viga analizada, correspondientes a cada una de las soluciones obtenidas mediante distintas generaciones del algoritmo genético, junto con la curva de respuesta experimental. Como se puede observar, conforme aumenta el número de generaciones, la respuesta a cortante de la viga evoluciona en el entorno de los valores experimentales registrados, siendo el error máximo relativo, correspondiente al mejor individuo de la generación 250 y deformaciones superiores a 1.5 mm/m, inferior al 10%.
4. Conclusiones
La implementación de un parámetro de degradación en el modelo constitutivo del acero permite ajustar de forma efectiva la respuesta a cortante de un elemento de hormigón estructural en los estadios previos a su agotamiento. La formulación de dicho parámetro como una función racional de la deformación por cortante preserva la convergencia del modelo de cortante y proporciona una respuesta regular y estable del mismo para altos niveles de deformación. Los resultados obtenidos demuestran que las estrategias de evolución pueden mejorar notablemente los resultados obtenidos mediante métodos de regresión y tienen una aplicación clara en problemas donde el paisaje de búsqueda no se conoce o es imposible de calcular.
Bibliografía
- [1] F.J. Vecchio, M.P. Collins; The modified compression field theory for reinforced concrete elements subjected to shear; ACI Journal, 83 (1986), pp. 219–231
- [2] A. Belarbi, T.T.C. Hsu; Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete; ACI Structural Journal, 91 (1994), pp. 465–474
- [3] L.M. Gil-Martín, E. Hernández-Montes, M. Aschheim, S. Pantazopoulou; Refinements to Compression Field Theory with Application to Wall-Type Structures; American Concrete Institute Special Publication, 265 (2009), pp. 123–142
- [4] M. Palermo, L.M. Gil-Martín, T. Trombetti, E. Hernández-Montes; In-plane shear behaviour of thin low reinforced concrete panels for earthquake reconstruction; Materials and Structures, 46 (2013), pp. 841–856
- [5] A.M. Hernández Díaz; Revisión de las Teorías de Campo de Compresiones en Hormigón Estructural; Universidad de Granada (2012)
- [6] L. Davis; Handbook of Genetic Algorithms; Van Nostrand Reinhold, New York (1991)
- [7] A.M. Hernández-Díaz, L.M. Gil-Martín; Analysis of the equal principal angles assumption in the shear design of reinforced concrete members; Engineering Structures, 42 (2012), pp. 95–105
- [8] M.P. Collins, D. Mitchell; Prestressed Concrete Structures; Prentice Hall, Nueva Jersey (1991)
- [9] T.C. Hsu; Toward a unified nomenclature for reinforced concrete theory; Journal of Structural Engineering, 122 (1996), pp. 275–283
- [10] B. Martín-Pérez, S.J. Pantazopoulou; Effect of bond, aggregate interlock and dowel action on the shear strength degradation of reinforced concrete; Engineering Structures, 23 (2001), pp. 214–227
- [11] M. Palermo, L.M. Gil-Martín, E. Hernández-Montes, M. Aschheim; Refined compression field theory for plastered straw bale walls; Construction and Building Materials, 58 (2014), pp. 101–110
- [12] N. Hansen, S. Kern; Evaluating the CMA evolution strategy on multimodal test functions. In Parallel Problem Solving from Nature-PPSN VIII; Springer, Berlin Heidelberg (2004), pp. 282–291
- [13] S.H. Ahmad, F. Park, K. El-Dash; Web reinforcement effects on shear capacity of reinforced high–strength concrete beams; Magazine of Concrete Research, 47 (1995), pp. 227–233
- [14] C.J. Bernhardt, C.C. Fynboe; High Strength Concrete Beams, Cement and Concrete Research Institute; The Norwegian Institute of Technology (1986)
- [15] A. Cladera Bohigas, A. Marí Bernat; Shear Design of Reinforced High- Strength Concrete Beams; Universidad Politécnica de Cataluña, Dpto. de Ingeniería de la Construcción, Barcelona (2002)
- [16] W.J. Krefeld, C.W. Thurston; Studies of the Shear and Diagonal Tension Strength Simply Supported Reinforced Concrete Beams; Journal of the American Concrete Institute, 63 (1966), pp. 451–476
- [17] P.Y.L. Kong, B.V. Rangan; Reinforced High Strength Concrete (HSC) Beams in Shear, Australian Civil/Structural Engineering Transactions; CE, 39 (1997), pp. 43–50
- [18] F. Leonhardt, R. Walther, Schubversuche an einfeldrigen Stahlbetonbalken mit und ohne Schubbewehrung zur Ermittlung der Schubtragfähigkeit und der oberen Schubspannungsgrenze, Deutscher Ausschuss für Stahlbeton, Heft 151, Berlin, 1962.
- [19] F. Levi, P. Marro, Shear tests up to failure of beams made with normal and high strength concrete, Special Discussion Session: Design Aspects of High Strength Concrete, Dubrovnik, 1988.
- [20] B.S. Lyngberg; Ultimate Shear Resistance of Partially Prestressed Reinforced Concrete I-Beams; ACI Journal Proceedings, 73 (1976), pp. 214–222
- [21] M. Moayer, E. Regan; Shear Strength of Prestressed And Reinforced Concrete T-Beams; ACI-SP, 42 (1974), pp. 183–213
- [22] M.N. Palaskas, E.K. Attiogbe, D. Darwin; Shear Strength of Lightly Reinforced T–Beams, ACI Journal; Title. No., 78–39 (1981), pp. 447–455
- [23] U. Quast; Zum Einfluβ von Längszugspannungen auf das Schubtragverhalten von Stahlbetonbbalken; Bautechnik, 76 (1999), pp. 646–650
- [24] P. Regan; Shear in Reinforced Concrete–an experimental study, PhD Thesis; Civil Engineering Dept., Imperial College (1971)
- [25] K.H. Reineck, D.A. Kuchma, B. Fitik, Formelsammlumg für die Datenerhebungsdateil Stahlbetonbalken mit Bügel (vsw-RC_DS) unter Einzellasten, 2011.
- [26] H.C. Soerensen; Shear Tests on 12 Reinforced Concrete T- Beams, PhD Thesis; Structural Research Laboratory, Technical University of Denmark (1974)
- [27] Y.-S. Yoon, W.D. Cook, D. Mitchell; Minimum Shear Reinforcement in Normal, Medium, and High-Strength Concrete Beams; ACI Structural Journal, 93 (1996), pp. 1–9
- [28] B. Abersman, D.F. Conte; The Design and Testing to Failure of a Prestressed Concrete Beam Loaded in Flexure and Shear, BASc thesis; Department of Civil Engineering, University of Toronto (1973)
- [29] EHE - 08 Instrucción de Hormigón Estructural. Ministerio de Fomento. Gobierno de España.
Document information
Published on 01/03/17
Accepted on 23/10/15
Submitted on 27/08/15
Volume 33, Issue 1, 2017
DOI: 10.1016/j.rimni.2015.10.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![a) Diagramas de equilibrio en la viga de hormigón armado (adaptado de [3,8]); b) ...](/wd/images/5/58/Draft_Content_860837407-1-s2.0-S0213131515000590-gr1.jpg)