Fe-Cu metastable material as a mesoporous layer for dye-sensitized solar cells

Abstract

This study investigates the performance of dye-sensitized solar cells constructed with a Fe-Cu metastable material as the mesoporous layer on which a natural organic dye is applied. The synthesis of the Fe-Cu material is done via a high throughput process that produces nanosized particles from elemental metallic powders. Xanthophyll is singled out as the organic natural dye of choice among other dyes that were extracted, as it exhibited wider spectral absorptivity in terms of wavelength range and magnitude. Two compact solar cells were constructed and tested; one is a reference cell with a TiO₂ working electrode and the other with a Fe-Cu working electrode. The results show a better power conversion efficiency for the Fe-Cu-based solar cell 0.943% compared to 0.638% for the TiO₂, and the number of carriers in the former is found to be orders of magnitude higher than the latter (10¹⁹ vs. 10³², respectively). A thorough optical, electrical, and thermal analysis of the Fe-Cu material is conducted and used to explain the obtained results.

Introduction

The dye-sensitized solar cells (DSSC) are formidable competitors to the industry-standard silicon-based solar cells due to their low cost, easy fabrication, and relatively high efficiencies, reaching up to 13% in porphyrin dye and cobalt (II/III) DSSC as reported by Grätzel group and others [1, 2]. Sensitizers are key cell components, critical to the widespread adoption of this technology. They possess excellent radiation absorbing properties in the visible wavelength range with their ability to mimic the light harvesting strategies found in nature to generate the required excitons. Many different sensitizers have been investigated for DSSCs applications, most of which use their carboxyl groups to enhance their attachment to the semiconductor [3]. The main types of sensitizers used nowadays are the metal complexes that use the metal to ligand (MTL) charge transfer phenomenon to increase photovoltaic performance, such as ruthenium complex sensitizers. It has been noted that DSSCs sensitized using pure organic sensitizers have higher absorption coefficients due to intramolecular π–π^* transitions. Their redox potentials, LUMO, and HUMO, are easily controlled for better performance and their ease of purification increases the chances of their acceptance in the market. Importantly, organic dyes have the availability aspect that metal complexes lack [4, 5]. Critical to achieving the reported efficiency levels, a proper choice of the nanostructured mesoporous substrate in order to achieve the desired dye molecules adsorption. This substrate is conventionally a metal oxide, usually a thin TiO₂ film, applied to the working electrode to maximize the surface area available for dye adsorption, optimize incident light harvesting, and enhance electrolyte diffusivity. The available molecular structures of TiO₂-containing mesoporous layers include: highly ordered nanorods with PCE of 2.9% [6, 7], spheres [8, 9], rice grain shapes and hollow fibers [10]; all pertaining to nanoscale dimensions. Some references in the literature have reported on the utilization of different materials to replace or be used in conjunction with the mesoporous semiconducting layer, for example, graphene has been used as the transparent conductive photoelectrode to great thermal and chemical stability [11, 12]. The use of organic perovskite electrodes is also a promising third generation solar cell technology employing lead or tin halide-based materials as the light harvesting electrodes, with reported efficiencies of around 20.1% in 2015, according to the National Renewable Energy Laboratory (NREL) [13].

The Fe-Cu intermetallic phase is attractive for many applications due to its high strength and traditionally attractive thermal and electrical properties [14-19]. But similar to other metastable intermetallic systems, for example, Ni-Ag, Cu-V, and Co-Cu, its synthesis suffers from the main drawback of limited immiscibility of its components as solid solutions due to their positive energy of mixing (around 13 kJ/mol for the Fe-Cu system) [20, 21]. Thus they will not form intermetallic compounds and will have negligible mutual solid solubility in equilibrium at temperatures below 700°C [22-26]. One effective and easy method to synthesize the Fe-Cu system with no conventional energy requirement in the form of applied heat or voltage is mechanical alloying (MA), which has the advantages of low-temperature processing, easy control of compositions, the production of relatively large amount of samples [20] and results in a significant extension of mutual solubility of the elements relative to the equilibrium values, which can be observed through X-ray diffraction patterns. This method involves ball-milling powders of the pure constituents to obtain the sought solid solutions. In this process, the coherent lattices of the pure metals undergo simultaneous shear induced deformation and thermal interdiffusion, with the resulting composition being determined by the equilibrium between the mechanically driven alloying and the diffusion-controlled decomposition [27-30]. It was found that low-energy ball milling of FCC and BCC metals leads to a refinement of the crystallite size to the nanometer scale [31-34]. With a work difference (∆E_w) of around 0.43 eV, the Fe-Cu alloy system has a high intrinsic absorption coefficient that further optimizes its optical absorptance [35]. Also, any observed roughness of the microstructure allows the interreflection of incident irradiation in the UV–Vis range that reduces reflection and scattering losses [36], and decreases the impedance between space and the absorber, which also leads to better absorbance properties [37].

In this work an alternative to TiO₂ as a mesoporous substrate of the working electrode of a DSSC in the form of a Fe₅₀-Cu₅₀ binary intermetallic phase is proposed and tested. The structural and optical properties of the obtained alloy are compared with those of TiO₂, and in addition, two DSSCs are constructed to evaluate the power, overall PCE, and fill factor (FF) for tested cells. The natural organic dye sensitizers (chlorophyll, anthocyanin, and xanthophyll) are extracted and processed locally and their absorptivities compared to choose the one with the widest spectral absorptivity in the UV–Vis wavelength. The Fe-Cu metastable alloy is produced via mechanical alloying, which is a facile and economic process that utilizes high-energy ball milling. It is an old but effective technique with high throughput, which will enhance the power-to-price ratio, increasing the appeal of DSSC in general as a third generation photovoltaic option. A comprehensive thermal, optical, and electrical investigation of the properties of the proposed Fe-Cu alloy is presented.

Experimental

Synthesis

The synthesis by MA takes place in a Retsch PM 100 planetary ball mill in a 25 mL stainless steel grinding bowl to mechanically alloy a starting amount of 9 g of high-purity copper (<425 μm, 99.5%) and iron (≥99%) powders, used as received from the supplier (Sigma-Aldrich, http://www.sigmaaldrich.com/united-states.html[United States of America]). A target composition 50:50 of Fe-Cu (% wt.) is used at a controlled milling speed of 600 rpm. Six 10-mm stainless-steel balls are used, making the filling ratio within the bowl 5:1. Milling is carried out for an hour at a time, pausing afterwards to cool the equipment and take a few milligrams of the powder for further characterization and testing. The run is to be terminated once microstructural changes become small, which in the present case took place after 6 h.

Microstructural analysis via SEM-EDX and XRD

The powder X-ray diffraction (XRD) patterns, plotted for five powder samples collected at a 2-h interval for 8 h, provide an insight into extent and progress of crystallization and the composition and grain structure of the developing solid solution. The X-ray patterns are recorded in the 2θ geometry between 40 and 90° at 0.02° 2θ/sec with a Bruker D8 Advance DaVinci multipurpose X-ray diffractometer with Cu Kα radiation operating at λ = 1.5406 Å, 40 kV tube voltage, and 40 mA current. The microstructural results are used to calculate important quantities such as the lattice parameter from Cohens method, grain size by the Full-width half-max (FWHM) analysis with the Hall–Williamson method and Braggs formula. Fused pieces of the material collected after 6 h milling time are examined under a scanning electron microscope (SEM) and the coupled energy dispersive X-ray spectrometer (EDX). The SEM is a VEGA3 XM by TESCAN, operating at 5 kV, whereas the EDX analysis is conducted with both map and point modes at the same operating voltage; the former was acquired during 3 min, whereas the latter was from four different spots of the sample during 30 sec live time.

Thermal analysis

Differential scanning calorimetry (DSC) is performed on the milled powders to provide insight on the energy of formation and mixing of the resulting compounds. The stability of these materials is due to the balance between the effectiveness of the MA process and thermal decomposition at high temperatures. For an endothermic reaction, heat flow indicates the phase shift within the solid solution (a peritectoid reaction). The calorimeter used is a Q20 from TA Instruments, running on 120 V_ac, 47–63 Hz, 500 W (4.5 amps) and equipped with a liquid nitrogen cooling system (LNCS) that allows automatic and continuous temperature control within a full range of −180°C to 550°C. A few milligrams of as-is and 2, 4, 6, and 8 h powders is encapsulated in an aluminum pan, and an empty reference pan sit on a thermoelectric disk surrounded by a furnace. As the temperature of the furnace is changed, heat is transferred to the sample and reference through the thermoelectric disk. The differential heat flow to the sample and reference is measured by area thermocouples. The phase formation, total enthalpy and heat flow through 0–500°C temperatures are examined for the current test.

Optical (spectroscopic) analysis

Spectral measurements of absorption in the ultraviolet, visible, and near-infrared (UV–Vis–NIR) regions were carried out on all the powders (as-is and 2, 4, 6, and 8 h milling time) with an Ocean Optics HR2000 high-resolution spectrometer. The HR2000 has a 300 lines per mm diffraction grating, 10 μm entrance slit, a Sony ILX511 2048-Pixel element linear CCD array detector, and is operating in the effective wavelengths range 300–1100 nm. The spectrometer is connected to a fiber optic reflection probe R200-7-SR, 2-m long, and of a 200-μm-core diameter. The reflection probe consists of a tight bundle of seven optical fibers in a stainless steel ferrule with six illuminating fibers around one axial read fiber, fixed at ~4 mm from the sample where losses due to scattering is assumed to be negligible, and all diffuse reflectance is collected at the probe. The source end of the reflection probe is connected to a tungsten halogen light source (Ocean Optics LS-1-LL). A reference surface in the form of a reflection standard (B0071519) is used to store baseline absorptance (0%) spectra to facilitate comparison between the various compositions. The integration time was set to 30 msec to contain the intensity of the highest acquired peak. The recorded time-resolved spectra were averaged over 10 readings to increase the signal-to-noise ratio.

Electrical impedance and Mott–Schottky analysis

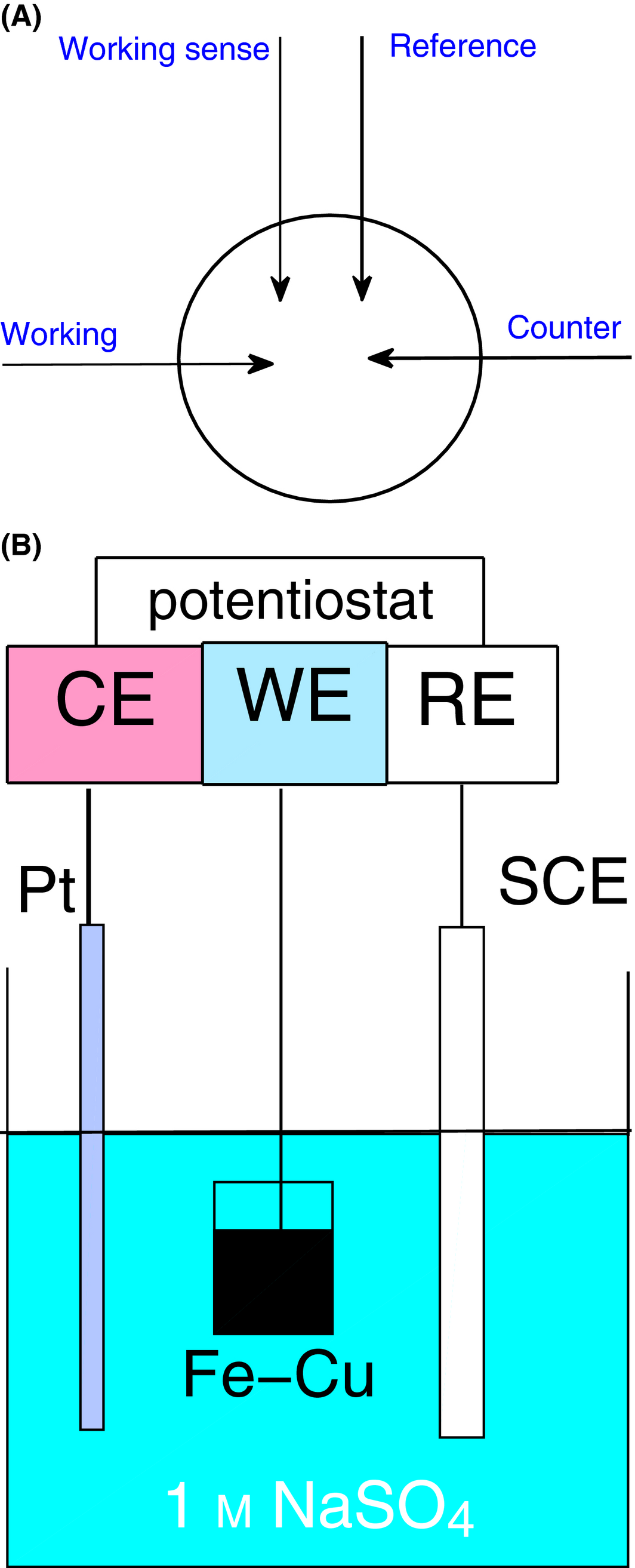
The impedance of the resulting Fe-Cu material is investigated and compared with values obtained for TiO₂ by virtue of the four-probe method impedance spectroscopy. The four probes, arranged as seen in Figure 1A, cover an area of 2 cm² and are connected to a Biologic VSP-300 potentiostat, providing impedance spectroscopy (10 μHz to 7 MHz) ± 12 V compliance, an automatic current range from 1 μA up to 500 mA (seven decades) and a potential resolution down to 750 nV. Impedance parameters were determined by fitting of impedance spectra using Z-view software and generating the pertinent Nyquist plot. The Fe-Cu material and the TiO₂ were deposited on respective glass substrates by spreading an emulsion of each in glycerol (C₃H₈O₃) and subsequently sintering the setup at 450°C for 30 min. It is noted that no phase change was observed afterwards in the postsintered XRD results. To investigate the interaction between the Fe-Cu layer and the electrolyte, a Mott–Schottky analysis was performed with the mesoporous FeCu deposited on ITO glass, which acts as the working electrode and immersed in an aqueous solution of 1 mol/L Na₂SO₄ (pH 8.5) with respect to a standard calomel (SCE) reference electrode and a Pt counter electrode [38]. The three-electrode arrangement for the electrochemical cell is shown in Figure 1B and is connected to a Biologic VSP-300 potentiostat providing an applied voltage range between −1 V and 1 V vs. SCE (20 potential steps recorded every 0.1 sec with waiting interval of 5 sec/step) and a potential resolution of 50 μV. The frequency range was from 0.1 Hz to 200 kHz (10 points per decade) with sinusoidal amplitude of 25 mV.

Figure 1. (A) Four-electrode arrangement for impedance spectroscopy and (B) Mott–Schottky cell setup.

Surface area determination

The surface area of the resulting Fe-Cu material is determined by the BET method in an Autosorb iQ from Quantachrome USA machine, where 1 g of Fe-Cu and 1 g of TiO₂ (for comparison) are degassed for 16 h at 300°C then tested with adsorbent nitrogen at 77.4 K.

Natural organic dye extraction and absorptivity testing

The most commonly used natural organic dyes in literature are chlorophyll, anthocyanin, and xanthophyll. These dyes are extracted from plants rich in them, like spinach, cabbage, and red leaves, respectively. These plants are collected, washed with deionized water, dried by tissue paper and trimmed using scissors to remove the stalk, mid rib, and veins. A container full of sliced leaves is cooled downed by placement in liquid nitrogen to minimize degradation. Immediately after, leaves are soaked completely in a beaker filled with acetone (C₃H₆O). The acetone-leaves mixture is stirred using a stirring rod as the extraction process carries on overnight for 24 h in dim light. Later, liquid dye extracts are filtered through a funnel equipped with small pore filter paper and placed in a centrifuge at 10,000 rpm for 10 min. In the case of chlorophyll, the beaker is covered with punched aluminum foil to allow natural vaporization of the acetone carrier for 48 h in dim light. On the other hand, each of the anthocyanin and xanthophyll are placed in a rotary evaporator to rotate and heat the filtrates up to the boiling point of extraction solution. The final products – chlorophyll, anthocyanin and xanthophyll extracts – are stored in a refrigerator to minimize any light-induced degradation [39-41].

In order to perform the absorptivity test, the dyes are diluted by distilled water, which is taken as the absorptivity baseline. The absorptivity measurement test is conducted using a PerkinElmer EZ301 spectrometer in ultraviolet–visible (UV-VIS) range (250 and 750 nm).

Solar cell fabrication and testing

To compare the effectiveness of utilizing the Fe-Cu material as a mesoporous material in DSSCs, two cells were constructed, one having TiO₂ as the photoelectrode, whereas the other had Fe-Cu. For depositing the former, the process starts with the preparation of TiO₂ paste by adding 1.5 mL of weak acetic acid (CH3COOH) to 1 g of titanium dioxide nanopowder (brookite nanopowder, <100 nm, 99.99%, used as received from Sigma-Aldrich) in a mortar while vigorously grinding by the pestle and then glycerol is added as a surfactant. The prepared homogenous paste is spread as a thin layer by employing the doctor blading technique on ITO-coated glass (15–25 Ω/sq., used as received from Sigma-Aldrich). The photoelectrode is then sintered by heating in a furnace at 450°C in static air for 30 min to remove solvents, surfactants, and any other organic materials.

As for the Fe-Cu photoelectrode, an identical process is applied, but instead of using acetic acid, glycerol is used to evenly spread the homogeneous layer on the ITO glass. The assembled cell is shown in Figure 2.

Figure 2. Assembled Fe-Cu sensitized solar cell.

The electrolyte used is the classic ${\textstyle I^{-}/I_{3}^{-}}$ redox electrolyte prepared from 127 mg iodine crystals, 830 mg potassium iodide, and 10 mL ethylene glycol are mixed thoroughly until they are completely dissolved. This electrolyte will be the diffusion medium for ionic species between the working photoelectrode prepared above and the counter electrode made up of pure copper with carbon deposits on an area of 2.5 × 2.5 cm to enhance the surface area and consequently the conductivity. The operation mechanism (injection of electrons and diffusion of ionic species) of DSSCs is well explained and documented, especially for the ${\textstyle I^{-}/I_{3}^{-}}$ redox electrolyte [40].

The testing of the solar cell to measure its power conversion efficiency, fill factor, and IV characteristics are conducted using a solar simulator Xenon Arc Lamps setup, capable of providing irradiance between 0.1 and 1 suns (up to 1367 W/m²) is used to provide a constant irradiation on the cells, and was kept at a vertical distance of 30 cm at 1.5 AM at 25°C. The cell characterization is conducted using VSP-300 potentiostat from Biologic with a potential resolution of 1 μV and a control voltage of ±10 V up to ±48 V. The voltage was varied at a rate of 10 mV/sec and the current recorded at each point until the measured voltage reached the open circuit voltage, V_OC. A PV cell analysis software built into the potentiostat is also used to determine the power, efficiency, fill-factor (FF), and also the Nyquist plots of impedance for each cell configuration using the Z-fit postprocessor.

Results and Discussion

SEM and EDS

The SEM micrograph of the Fe-Cu system is shown in Figure 3A for a few milligrams removed after 6 h of milling. There is obvious presence of the FCC phase caused by the interdiffusion of Fe and Cu, resulting in different grain size distribution from a few nanometers to around 100 nm. Upon further magnification, Figure 3B shows a homogeneous phase with the apparent shearing effect from milling, which produces a lamellar structure [24]. An EDS analysis at two points (1) and (2) indicated on the figure shows a composition of 53% Fe and 47% Cu (%wt.) as evidence of successful interdiffusion and the formation of the new single phase. This is in contrast to other synthesis methods involving casting [21], deposition or electron-beam forming that reported severely segregated phases when the material is cooled below 700°C.

Figure 3. SEM photomicrographs of the resulting microstructure at (A) 250 × magnification, showing the granular microstructure, and (B) 20 k × magnification, showing homogeneous phases of Fe and Cu, with EDS test locations indicated at 1 and 2.

The lattice strain energy ∆U_strain can be calculated from the relation ${\textstyle \Delta U_{strain}=\left({\overline {E}}\delta \right){\left(2{\overline {r}}\right)}^{2}{\overline {d}}}$ where ${\textstyle {\overline {E}}}$ is the average Young modulus for Cu and Fe, ${\textstyle {\overline {d}}}$ the average displacement of atoms (${\textstyle {\overline {d}}=\delta {\overline {r}}}$) and lattice distortion, δ, is calculated by using the equation ${\textstyle \delta ={\sqrt {\sum _{i=1}^{n}X_{i}{\left(1-{\frac {r_{i}}{\overline {r}}}\right)}^{2}}}}$, where X_i is the fraction of the i^th component (n here equals 2) and r_i and ${\textstyle {\overline {r}}}$ are the i^th and the average atom radii, respectively [42]. The lattice distortion energy is found to be 8.61 kJ/mol. Although the relations are nonlinear and highly dependent on the Cu concentration in the Fe-Cu material, this value is still orders of magnitudes higher compared to the martensitic transformation in iron system (around 751 J/mol) that will form a homogenous single martensite phase with a high density of lattice defects [43].

XRD

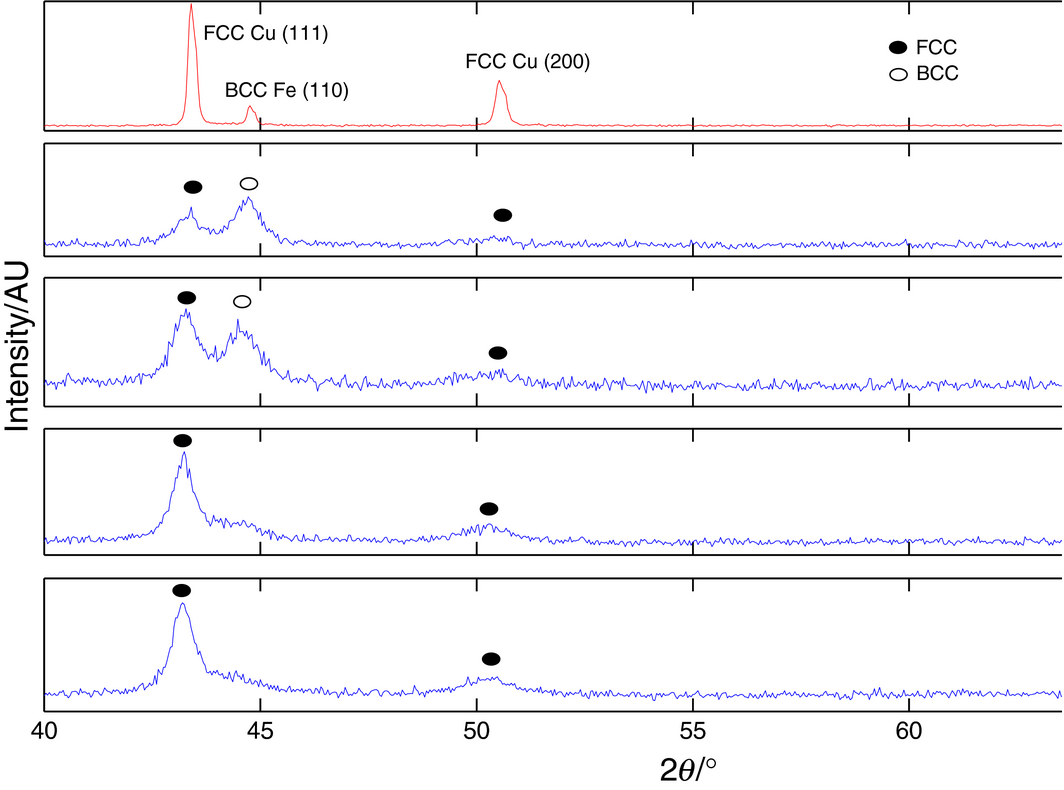
The result of XRD analysis is shown in Figure 4 for the as-is and 2, 4, 6, and 8 h milling time, to follow the evolution of the crystal structure. The as-is patterns show intense sharp peaks of elemental iron and copper are slightly shifted towards lower angles, which are consistent with the similar atomic sizes of Fe and Cu present in the same mixture [24], and the recorded signals are strong with little noise. It is interesting to observe these peaks widening and shifting further as milling proceeds due to the interdiffusion of Fe and Cu atoms caused by the shearing action and the friction-induced temperature increase, promoting larger grain sizes. After 6 h, a single phase is observed in which Fe atoms are diffused in the Cu matrix, or an FCC Cu(Fe) solid solution, as corroborated by the results from SEM analysis in Figure 4B. These results are also consistent with previous reports [24, 44] and indicate the successful formation of the desired homogenous phase.

Figure 4. XRD plots for progression of milling times.

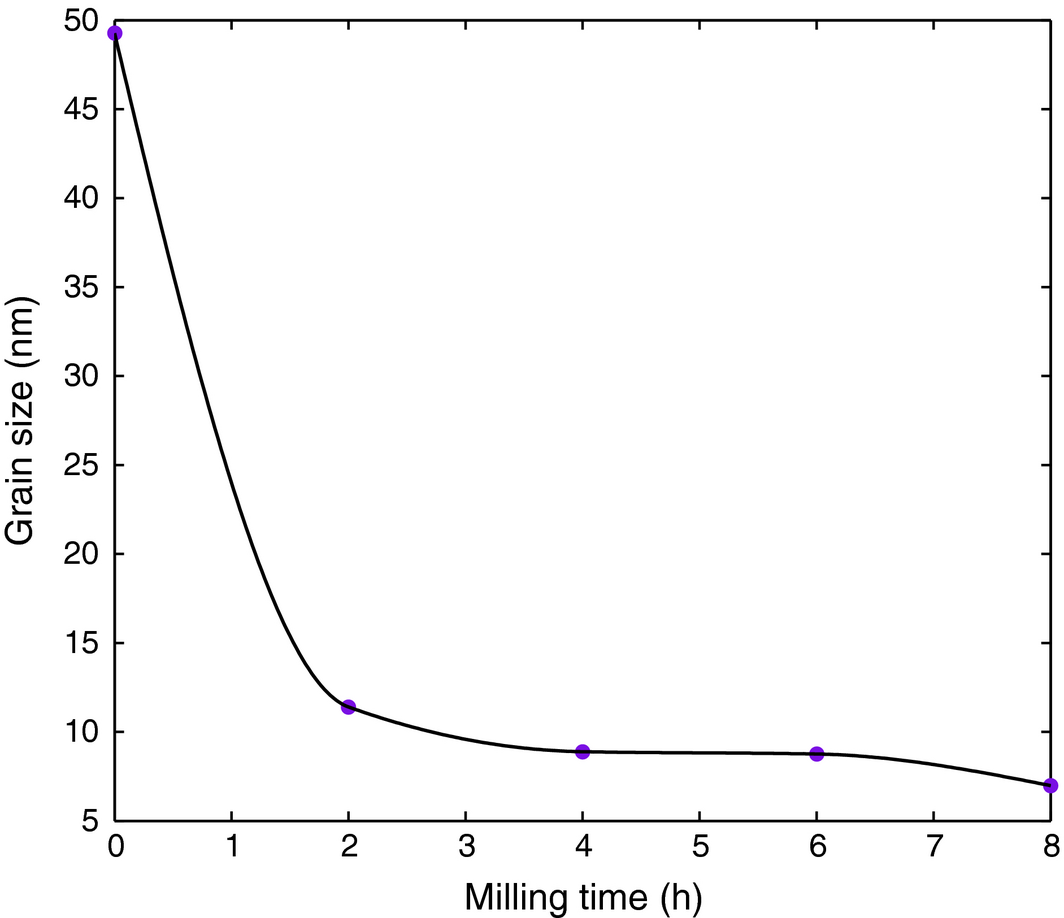
The grain size change with milling time is depicted in Figure 5 calculated from Braggs law and Scherrer formula. It is noted from the figure that the grain size decreases rapidly as milling time increases, then it almost plateaus around 4–8 h, which is consistent with trends reported elsewhere [42, 44, 45].

Figure 5. Grain size variation with milling time.

Thermal analysis results

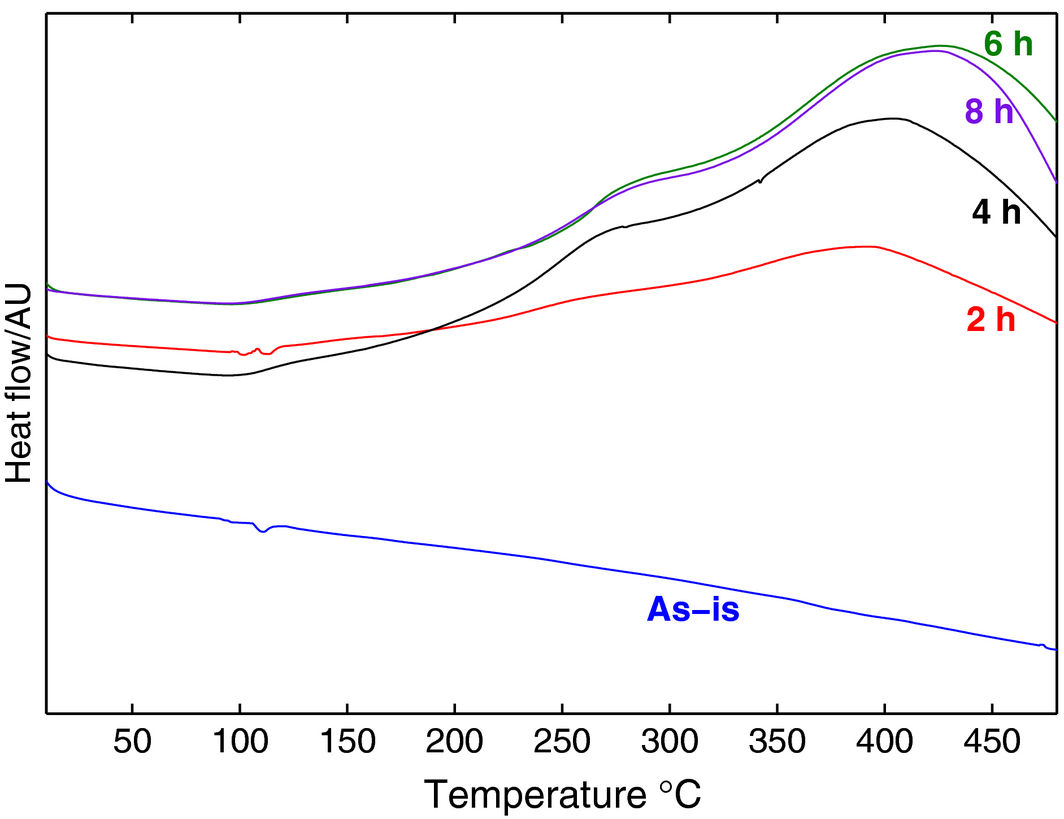
The results obtained from the DSC are shown in Figure 6 for all milling times and also for the as-is specimen. While the latter shows no phase reaction and its thermal response line remains flat, the rest of the samples show a trend that indicates more thermal stability as milling time increases. The results for 6 and 8 h show the least difference between the obtained peaks, indicating a limiting time for the milling process, which can be correlated with the XRD patterns of Figure 4. The results are inverted to show a positive scale and are in line with those found in previous work [18]. The peaks also occur at successively higher temperatures, indicating better phase stability.

Figure 6. Differential scanning calorimetry heat flow plots versus milling times.

Spectroscopy

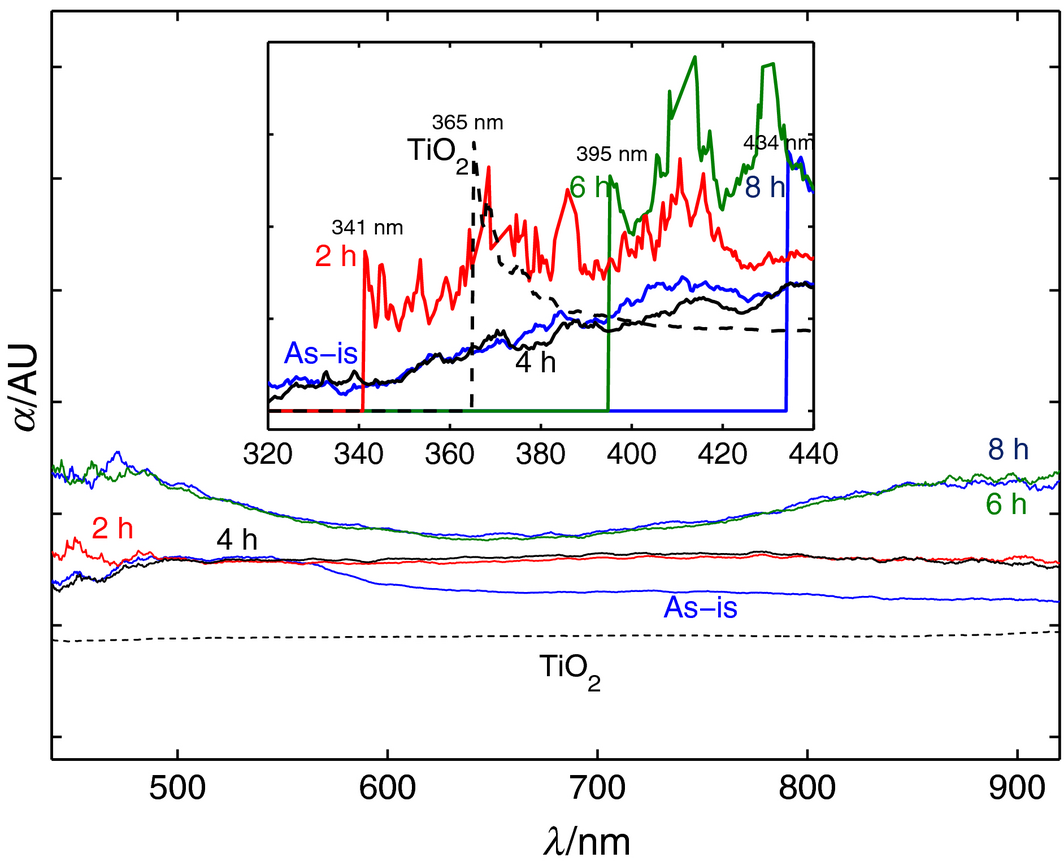
The evolution of the microstructure with milling has impacted the optical absorptivity of the material, as can be seen in Figure 7. The original powder shows a slight increase in absorptivity with respect to the mirror reference up to 500 nm, at which it plateaus until 550 nm, after which absorptivity decreases asymptotically towards 900 nm. As for milling times of 2, 6, and 8 h, the onset of absorptivity is seen to be an abrupt step increase at progressive wavelengths of 341, 396, and 434 nm, respectively. Another interesting observation from the curves can be made in conjunction with the XRD plots of Figure 3 for the 2–4 h on one hand and 6–8 h materials on the other. The former set shows a virtually constant absorptivity across the tested wavelength of Vis–NIR (450–900 nm) due to the existence of both FCC and BCC structures, whereas the latter start with a high onset value, then assumes a flat parabolic shape with an apex at 650 nm, thought to be due to an all-FCC microstructure. Longer milling times of 6 and 8 h, exhibit a 63% and 81%, enhanced absorptivity, respectively, compared to as-is powder if the areas under the absorptivity curves are integrated from 450 to 900 nm. This enhancement is due in part to the roughness in microstructure that augments the probability of absorbing the diffracted and trapped light beams by adjacent grains. Roos et al. [46-48] have reported similar trends of optical properties of copper oxide thin films prepared by thermal and chemical oxidations and plotted against processing time, and the results are in general agreement of what is reported in this work.

Figure 7. Absorptivity results at different milling times with TiO2 superimposed in dotted line.

It is also useful to compare the obtained optical properties of the prepared materials against TiO₂, a known photo catalyst that is used extensively in DSSCs. Thus, the optical absorptivity in the UV–Vis–NIR (280–900 nm) range was measured for an as-received TiO₂ powder (Sigma-Aldrich) and shown as a dashed line in Figure 6. The curve shows standard optical characteristics of the TiO₂ powder as reported in literature [49], where negligible absorptivity below 365 nm is replaced with a sharp increase in absorptivity followed by an exponential decay right before the 400 nm mark where it levels off as Figure 6 depicts. The advantage of using the suggested mesoporous Fe-Cu material is thus twofold, one is in the tuning of absorption response to higher wavelengths that can be well defended in situations where target solar cells are to be operated indoors or at different incident radiation intensities, and the other benefit is the obvious enhanced absorptivity magnitudes over the rest of the Vis–NIR spectrum which has many benefits for both solar thermal and solar photovoltaic applications.

Electrical impedance

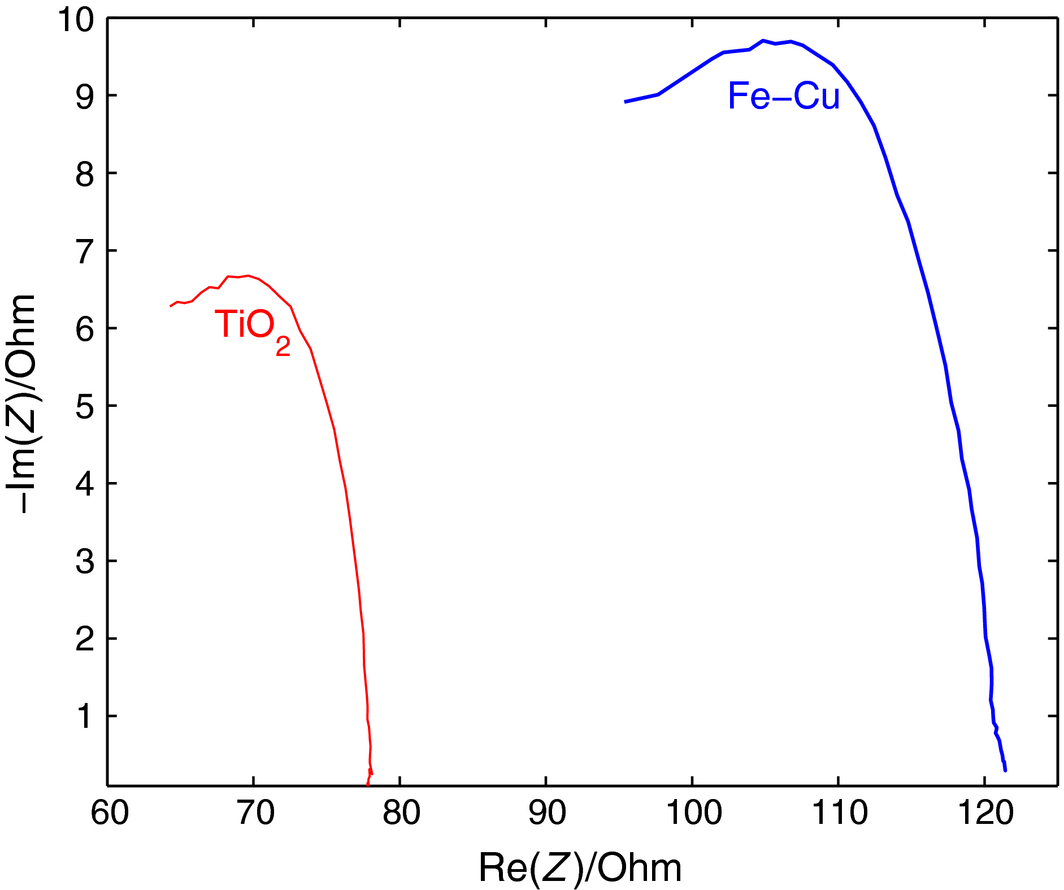
The electrical impedance of a thin film of an 8 h milled Fe-Cu versus TiO₂, each deposited on a glass substrate is shown in the Nyquist plot of Figure 8.

Figure 8. Impedance spectroscopy of 8 h milled Fe-Cu versus TiO2.

Compared with the near zero real impedance of the as-is starting Fe-Cu powder, the 8 h milling time displayed a large impedance value (around 120 Ω), larger than the one measured for titania (around 78 Ω) as seen in the figure, suggesting a fundamental change in the electric behavior of the new Fe-Cu composite compared to the as-is starting mix, akin to the thermal conductivity of an alloy being substantially less than that of its pure components. This result is important, especially that the traces of oxygen observed in the EDX analysis of the components indicates that no oxides were formed from either iron or copper as seen in the mapping of Figure 9, showing that oxygen as only 11% of the elements present, with Fe, Cu, and I as 42%, 43%, and 4%, respectively.

Figure 9. (A) SEM of the Fe-Cu photoanode on ITO with the EDX map for (B) Fe, (C) Cu, and (D) oxygen; being only 11% wt. of the present components.

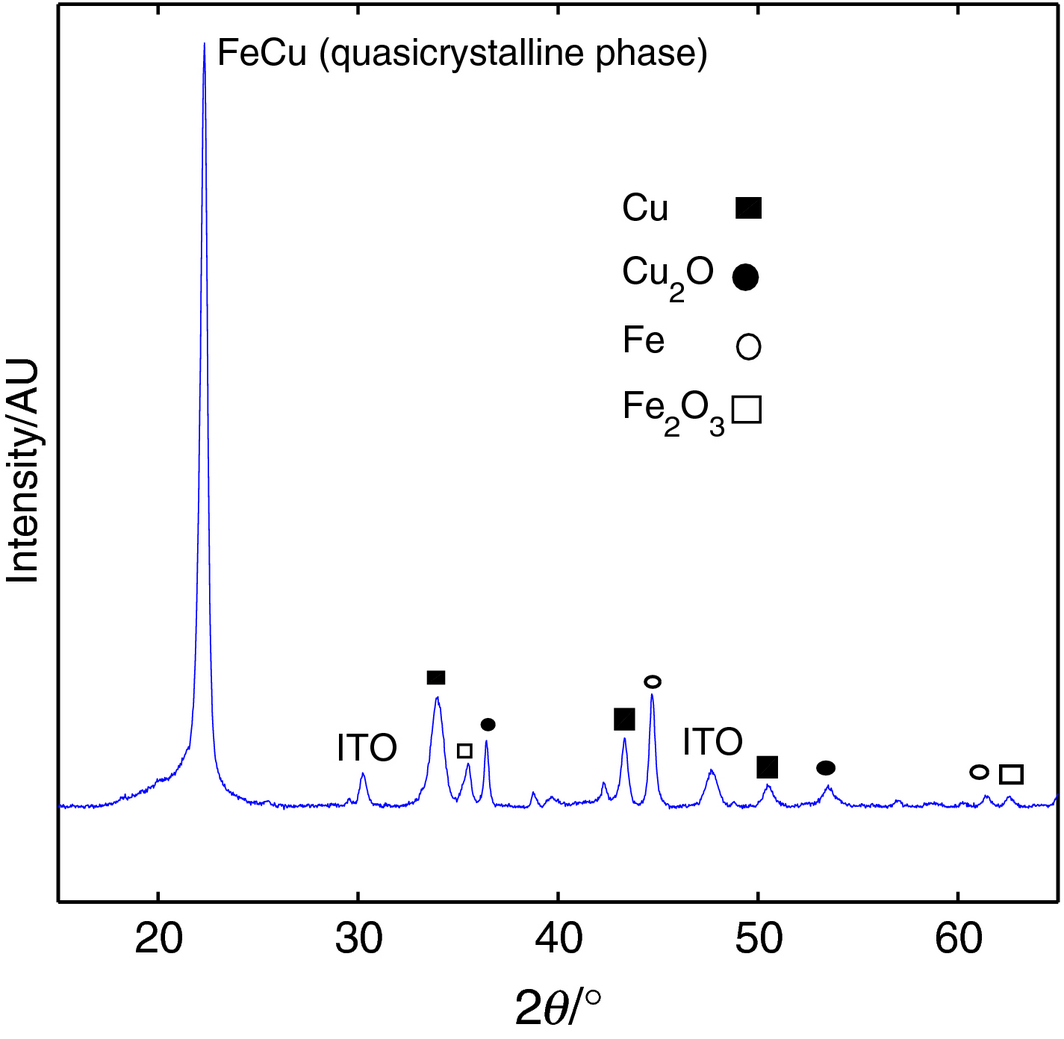
An XRD testing is also performed on the sintered Fe-Cu on ITO, and the results show a significant peak belonging to the FeCu FCC phase that is sharper than the one seen in the original XRD due to sintering on glass at 400°C and a shift towards 2θ = 21°, with minor peaks belonging mostly to elemental Fe and Cu that have been segregated from the unsintered mixture. This has resulted in using up the available oxygen in the form of Cu₂O and Fe₂O₃, with the former being more pronounced and is an intermediate phase of copper oxide that is less stable chemically and structurally than CuO [50]. From the XRD plot of Figure 10, the Fe-Cu materials shows good stability after the 50 cycles of solar cell testing while being in contact with the dye and electrolyte, exhibiting what is believed to be mild oxidation of the surface of the material occupied mostly by the Cu molecules due to the presence of the hydroxyl (OH⁻) species that caused the following pathway to take place [51]:

Figure 10. XRD of the Fe-Cu material deposited on ITO glass after solar testing.

${\mbox{Cu}}+{\mbox{OH}}^{-}\rightarrow {\mbox{CuOH}}$

(1)

$2{\mbox{CuOH}}\rightarrow {\mbox{Cu}}_{2}O+H_{2}O$

(2)

where the copper oxide film is gradually formed on the outer surface of the Fe-Cu material by the adsorption of OH⁻, followed by the dehydration of copper hydroxide into Cu₂O. This is another indication of the formation of the FCC structure with Fe atoms being forced into the structure of the Cu grains, whereas the Fe₂O₃ oxidation takes place on the Fe atoms that diffused out and were segregated from the Fe-Cu material due to the annealing temperature [51-56].

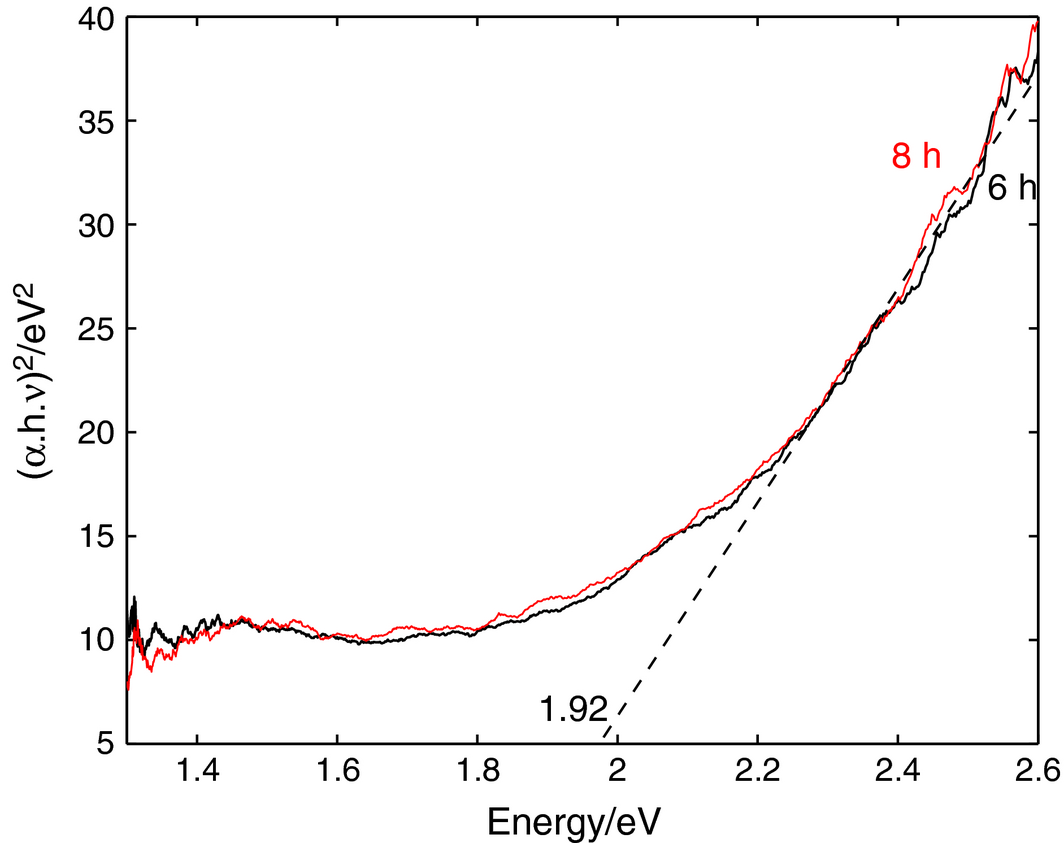
The semiconductive behavior of the resulting material paves the way for using it in place of the more expensive titania that is apparently an inferior absorber in the useful solar spectrum as clearly seen in Figure 7. Since the Fe-Cu material exhibits this semiconductive behavior, an estimation of the resulting bandgap is shown in Figure 11. The band gap is determined from the traditional Tauc relationship; α.hν = A.(h.ν-E_g)ⁿ, by plotting (α.h.ν)^1/n versus the photoenergy h.ν, where α is the absorption coefficient, A is the edge width parameter, E_g is the optical band gap value, and n is a constant dependent on the nature of the transition (n = 1/2 for a direct allowed transition and 2 for an indirect transition) [47, 48]. An extrapolation of the linear region of the plot for when the ordinate equals to zero, gives an absorption edge energy that corresponds to the value of the optical band gap E_g. With n being 1/2 for best fitting, the results in Figure 11 indicate direct transitions in Fe-Cu material with milling time. According to the figure, band gap results start to appear after 6 h of milling as elements diffusion becomes pronounced and the micrsostructure shifts to metastability, which is also inferred from the XRD plots of Figure 4. The obtained optical band gap values is 1.8 eV.

Figure 11. Energy bandgap of the resulting Fe-Cu material.

The semiconductive behavior of quasicrystalline materials has been observed by other researchers; some correlating the change in behavior with the increased role of disorder in the aperiodicity that has a profound effect on the metal-insulator transition [57], and others have reported a 2.2 eV bandgap value for the Fe-Cu solid solution and attributed it to a contribution similar to d transitions in the noble metal and follows the direct transitions from a virtual bound state to the Fermi level [58, 59]. In the particular case of quasicrystalline materials produced by mechanical alloying, the semiconductive behavior is generally attributed to the enhanced interdiffusion of elemental components that creates supersaturated structures that leads to a metallic-covalent bonding conversion, and indeed a bandgap is reported by Takagiwa and Kimura [60] for an aluminum-based quasicrystalline material, and by our group [56].

Mesoporous media surface area

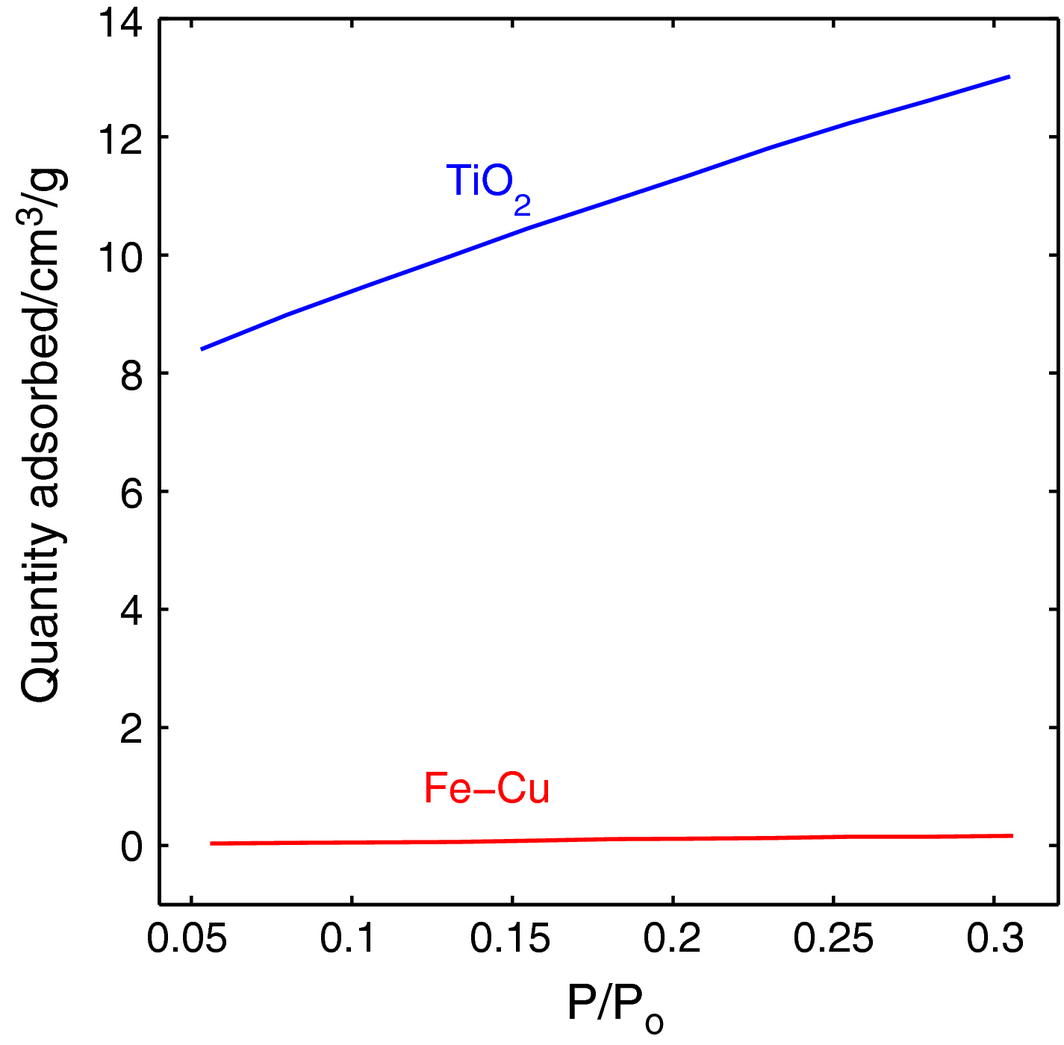
The results obtained from the BET testing show that the surface area of the Fe-Cu material is 0.78 m²/g, whereas that of TiO₂ equals 41.1 m²/g. While the fit for the volume adsorbed versus the differential pressure applied is strictly linear for TiO₂ (R = 0.9995), the variation in grains sizes for the Fe-Cu specimen as seen in the SEM of Figure 9 has caused inconsistencies in its adsorption as shown in Figure 12 and the fitted data shows a deviation from the linear behavior (R = 0.867).

Figure 12. BET surface area for Fe-Cu versus TiO2.

Dye absorptivity results

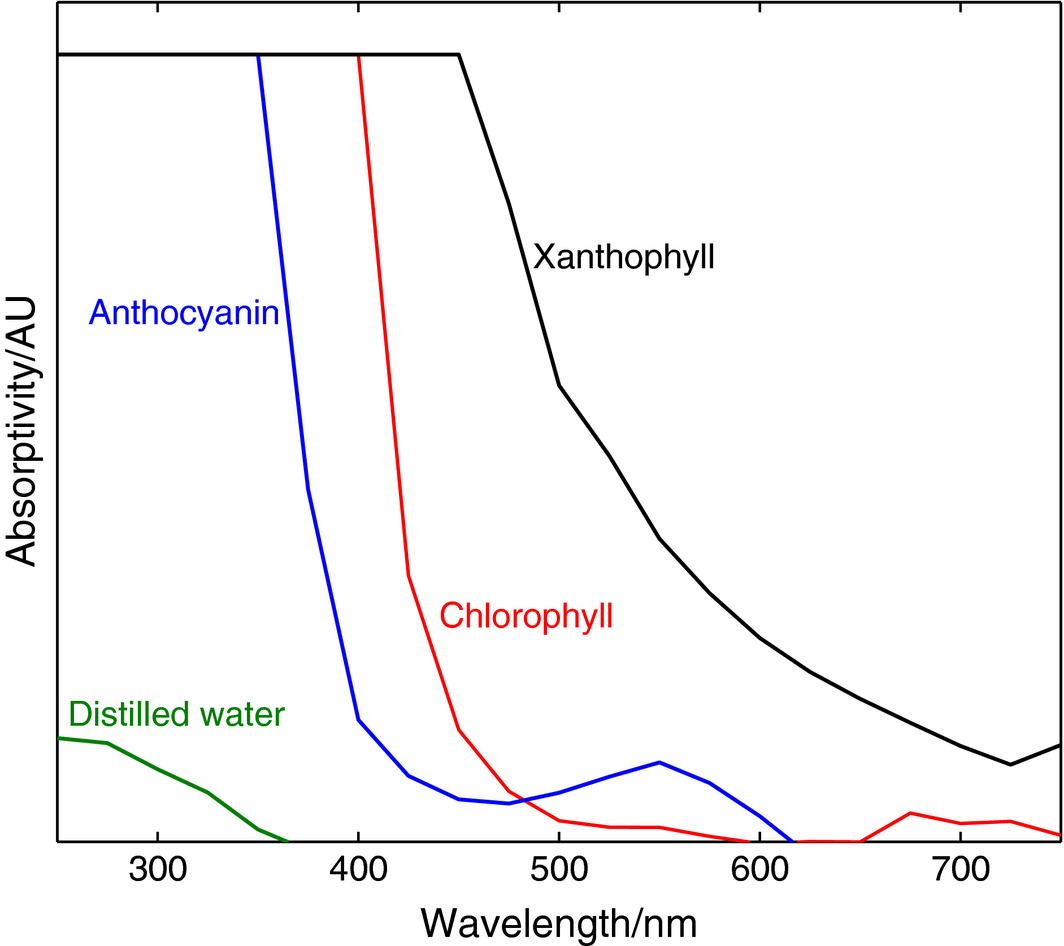
The results obtained from testing chlorophyll, anthocyanin, and xanthophyll are shown in Figure 13. The spectral absorptivity in the UV–VIS range (250–750 nm) for each dye shows a high onset of absorption at the UV spectral range, compared to the distilled water reference. The three curves show a step fall after around 350, 400, and 450 nm for anthocyanin, chlorophyll, and xanthophyll, respectively. Xanthophyll exhibits superior absorptivity behavior, especially in the visible range (400–700 nm) where the drop in absorptivity is seen to be less abrupt than its two counterparts, never reaching zero even at the extreme end of the sampling spectrum (750 nm). This behavior, along with the broad spectral range of absorptivity of xanthophyll makes it an ideal choice for sensitizing the mesoporous materials of the experimental cells.

Figure 13. Absorptivity test of various natural organic dyes against distilled water.

Solar cell test results

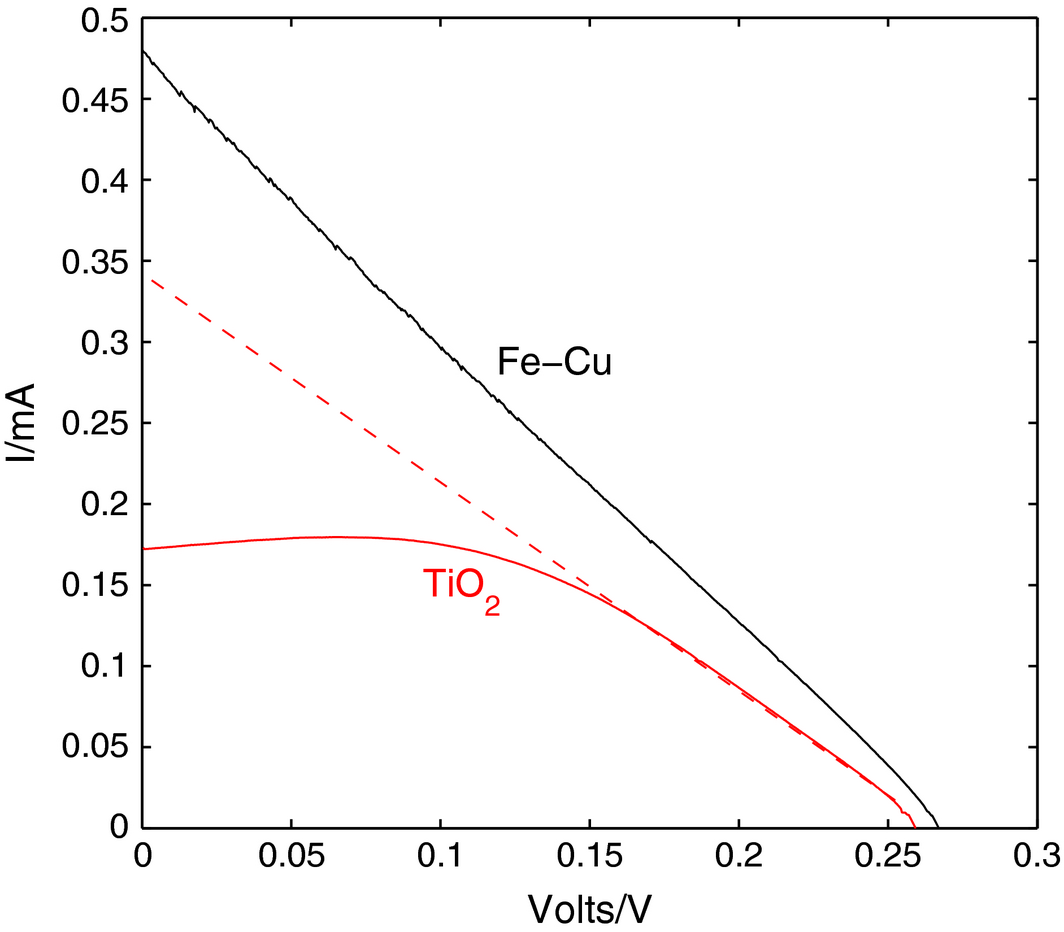
The results of the characteristics test for the manufactured DSSC are shown in Figure 14. It is noted that there is a linear decrease in the voltage of the Fe-Cu cell in proportion to the generated current, which is usually an indication of a large series resistance in multicrystalline silicon solar cells. The series resistance in solar cells is mostly due to contact resistance, and hence the recommendations to mitigate its effects are numerous, like changing the concentration of the electrolyte, the counter electrode or the clips that connect the cell to the load. It is also noted from the curve that the series resistance in both have similar values (as shown from the line tangent to the TiO₂ IV curve in Figure 14).

Figure 14. IV characteristic curves for TiO2 and Fe-Cu xanthophyll-sensitized solar cells.

In general, the Fe–Cu-based solar cell exhibits better performance when other characteristics are calculated, such as the fill factor, power, and efficiency. A summary of these parameters is shown in Table 1.

Table 1. Comparison of parameters for the two DSSCs experimental cells

Parameter	TiO2-based cell	Fe-Cu-based cell
Isc, [mA]	0.173	0.53
Eoc, [V]	0.248	0.269
FF (Pmax/ PTheo)[%]	48.4	25.0
η, [%]	0.638	0.943

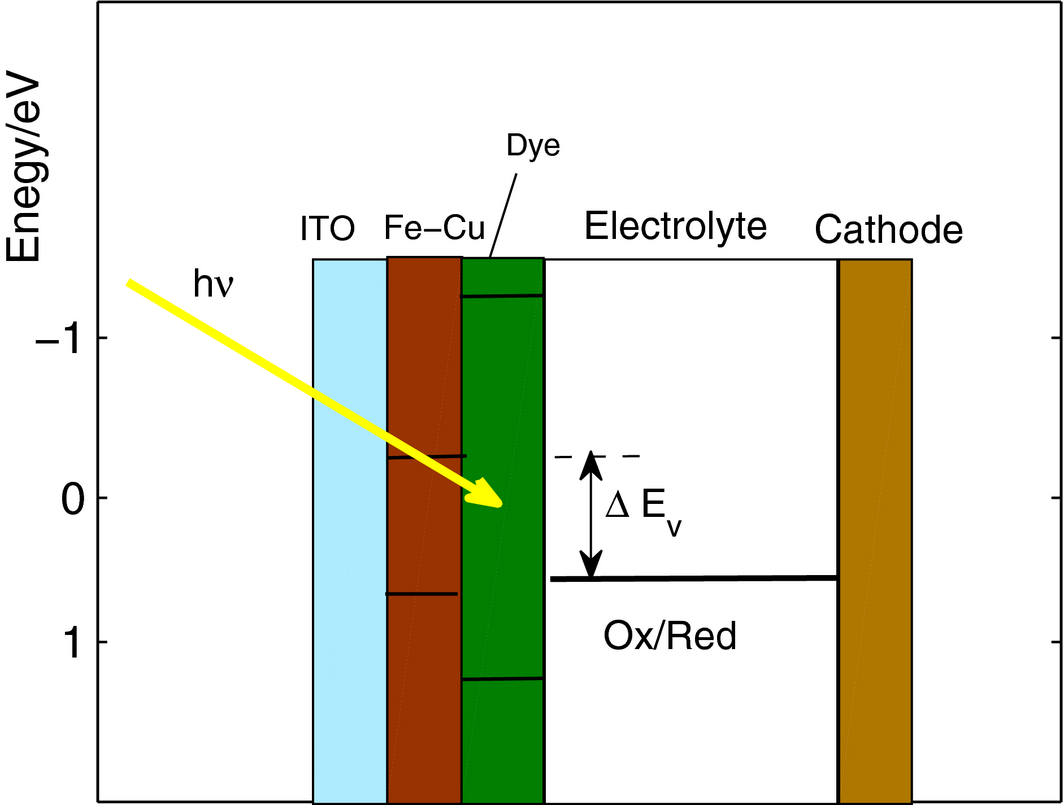
An explanation of the measured enhancement over the TiO₂-based cell is presented with reference to the energy levels diagram in Figure 10 that schematically shows the Fe-Cu bandgap to be around 1.8 eV (±0.9 eV at each side of the 0 eV mark), where the open circuit voltage, measured as ∆E_v is the potential difference between the dye/electrolyte interface and the upper end of the mesoporous material energy gap. The conduction band for the Fe-Cu has to be above 0 V versus normal hydrogen electrode (NHE) for the photovoltaic effect to take place (Fig. 15).

Figure 15. Illustration of energy levels diagram of a DSSC based on Fe-Cu mesoporous material.

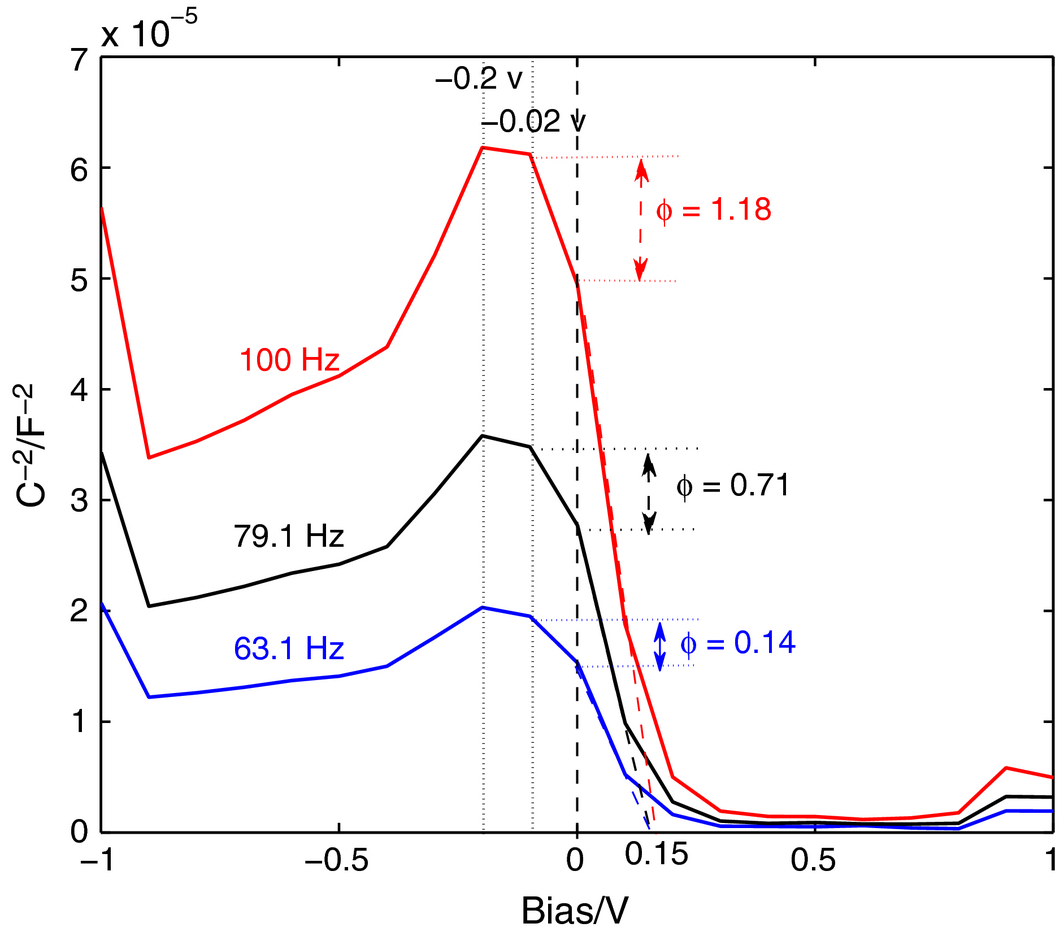
To determine the cell potential behavior at the Fe-Cu/electrolyte interface, a Mott–Schottky (MS) analysis is conducted using the potentiostat at frequencies 63, 79, and 100 Hz. The plots are shown in Figure 16. The MS analysis probes the depletion capacitance at a Schottky or p-n junction which is determined by the width of the bias-dependent depletion region, hence the depletion capacitance, C, is also bias dependent and can be expressed as follows:

Figure 16. Mott–Schottky diagrams for Fe-Cu-based photoelectrode.

${\frac {1}{C^{2}}}={\frac {2(V_{bi}-V)}{A^{2}q\epsilon {\epsilon }_{0}N}}$

(3)

where V is the applied bias, A is the device area, q is the elementary charge, ε is the compound dielectric constant, and ε₀ is the permittivity of free space. The built-in bias and doping density are then found by fitting equation (1) to the linear portion of the C⁻² versus bias voltage plot, as shown by the converging dotted lines in Figure 16. The intersection of the line equals the flat band potential, whereas the slope of the line is used to estimate the carrier density, N, as the slope equals 2/(ε·ε₀·q·N). The Helmholtz capacitance on the electrolyte side of the interface is large enough that it is negligible since the observed capacitance, C, is given by 1/C = 1/C_H+1/C_SC, where C_H, and C_SC, are the capacitances of the Helmholtz layer and the semiconductor, respectively.

The MS plots reveal that the Fe-Cu behaves like a p-type semiconductor (SC), contrary to the n-type TiO₂. When the p-SC is in contact with an electrolyte solution, the electrons in the SC are transported to the vacant level of the electrolyte solution, which makes the SC positively charged and the electrolyte solution negatively charged. Upon irradiation, at the interface between the Fe-Cu layer and the electrolyte solution, the energy of which is larger than the bandgap (E_g) of the semiconductor (for Fe-Cu E_g ~ 0.1.8 eV), excitation of electrons from the valence band to the conduction takes place leaving holes in the valence band. The electron and the hole form the short-lived excitons. The space charge layer, ϕ, which is measured as the difference between the C⁻² value at the inflection point before crossing the zero-voltage bias (see Figure 16) for the three frequency values of 63 Hz, 79 Hz, and 100 Hz is measured as 0.14, 0.71, and 1.18 F⁻², respectively. The physical significance of the space charge layer is that a hole can migrate towards the SC interface, and the electron can migrate toward the inside of the SC bulk so that the chances of their recombination are smaller. When an electron donor is present in the contacted liquid phase, the holes can oxidize the donor in the electrolyte, and the electrons are transported first to the ITO glass conductive layer through Fe-Cu grain boundaries and then to the counter electrode, reducing electron acceptance there. From Figure 14, the flat band potential of the Fe-Cu layer is found to be 0.15 V compared with that of TiO₂ at −0.16 V [52]. To calculate the carrier density, whereas the relative permittivity of Fe-Cu is chosen to be in the order of magnitude of 10³ [53], ε₀ the vacuum permittivity = 8.854 × 10⁻¹² F/m, and q the elementary electric charge = 1.602 × 10⁻¹⁹ C; then the carrier density per meter cube is estimated to be 4.27 × 10³²/cm³. This value is higher than the value reported for TiO₂ (6.96 × 10¹⁹/cm³) in literature [51], proving that the quasicrystalline Fe-Cu thin film can function as an excellent electron conducting material under irradiation conditions when a strong electron donor is present in the electrolyte. This explains the bigger current values in the IV curves of Figure 12 when Fe-Cu is used as a mesoporous layer instead of TiO₂, and with the facile and cheap synthesis procedure of Fe-Cu, the latter is considered a real competitor in the manufacture of dye-sensitized solar cells to drive the cost-per-watt even lower [54-56].

Conclusion

In this study, an economical and facile method for the production of a mesoporous material made from Fe-Cu metastable alloy system is investigated for DSSC photoelectrodes. High-energy ball milling, a mechanical alloying technique, was used to synthesize the alloy and the resulting microstructure was examined using SEM-EDS and XRD at 2 h intervals starting from the as-is powder up to the final duration of 8 h. The resulting alloy is a homogenous, FCC single phase of Fe diffused in Cu with no segregation of elements. The optical absorptivity in the Vis–NIR ranges for the alloy was measured for the same durations and the results show a strong correlation between the microstructural morphology and the optical behavior and enhancement of spectral absorptivity between 400 and 900 nm. The spectral absorptivity is enhanced up to 81% for the 8 h milled alloy compared to the original powder, and around 95% higher than TiO₂, which is the mesoporous material of choice for DSSCs. The increase in the impedance up to 120 Ω is an indication of the fundamental change of the electrical properties of the resulting phase after 8 h of milling, which has created the reported bandgap. Two DSSCs sensitized by the natural organic dye xanthophyll were constructed, one with Fe-Cu and the other with TiO₂ as the mesoporous layer, and the former had better performance in terms of power (0.078 vs. 0.022 mW, respectively) and efficiency (0.638% compared to 0.943%, respectively) for a 6.25 cm² cell. The carrier density for cells was also calculated using Mott–Schottky tests and Fe-Cu had orders of magnitude more carriers (4.27 × 1032 vs. 6.69 × 1019/cm³) for the TiO₂. The Fe-Cu intermetallic phase is a promising mesoporous material due to its cost-effectiveness, mass-production capable synthesis technique, excellent spectral absorptivity in the UV–Vis range, recyclability, and good thermal and mechanical properties.

Conflict of Interest

None declared.

References

1. Green, M. A., K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop. 2015. Solar cell efficiency tables (Version 45). Prog. Photovoltaics Res. Appl.23:1–9.
2. Mathew, S., A. Yella, P. Gao, R. Humphry-Baker, B. F. E. Curchod, N. Ashari-Astani, et al. 2014. Dye-sensitized solar cells with 13% efficiency achieved through the molecular engineering of porphyrin sensitizers. Nat. Chem.6:242–247.
3. Puxeu, L.2014.Exploring novel dye concepts in dye sensitized solar cell, Thesis.
4. Chen, Z., F. Li, and C. Huang. 2007. Organic D-π-A dyes for dye-sensitized solar cell. Curr. Org. Chem.11:1241–1258.
5. Hara, K., and N. Koumura. 2009. Organic dyes for efficient and stable dye-sensitized solar cells. Mater. Matters92:4.4.
6. Mor, G. K., K. Shankar, M. Paulose, O. K. Varghese, and C. A. Grimes. 2006. Use of highly-ordered TiO₂ nanotube arrays in dye-sensitized solar cells. Nano Lett.6(2):215–218.
7. Zhu, K., N. R. Neale, A. Miedaner, and A. J. Frank. 2007. Enhanced charge-collection efficiencies and light scattering in dye-sensitized solar cells using oriented TiO₂ nanotubes arrays. Nano Lett.7(1):69–74.
8. Kim, Y. J., M. H. Lee, H. J. Kim, G. Lim, Y. S. Choi, N.-G. Park, et al. 2009. Formation of highly efficient dye-sensitized solar cells by hierarchical pore generation with nanoporous TiO₂ spheres. Adv. Mater.21:3668–3673.
9. Park, Y.-C., Y.-J. Chang,B.-G. Kum, E.-H. Kong, J. Y. Son,Y. S. Kwon, et al. 2011. Size-tunable mesoporous spherical TiO₂ as a scattering overlayer in high-performance dye-sensitized solar cells. J. Mater. Chem.21:9582–9586.
10. Chen, J., J. Wang, F. Bai, L. Hao, Q. Pan, and H. Zhang. 2013. Connection style and spectroscopic properties: theoretical understanding of the interface between N749 and TiO₂ in DSSCs. Dyes Pigm.99:201–208.
11. Wang, X., L. Zhi, and K. Müllen. 2008. Transparent, conductive graphene electrodes for dye-sensitized solar cells. Nano Lett.8:323–327.
12. Sun, S., L. Gao, and Y. Liu. 2010. Enhanced dye-sensitized solar cell using graphene-TiO₂ photoanode prepared by heterogeneous coagulation. Appl. Phys. Lett.96:083113.
13. NREL. 2015. www.nrel.gov, last accessed 31 December 2015.
14. Liu, J. Z., A. van de Walle, G. Ghosh, and M. Asta. 2005. Structure, energetics, and mechanical stability of Fe-Cu bcc alloys from first-principles calculations. Phys. Rev. B72:144109.
15. Hasebe, M.1981. T. Nishizawa and Further study on phase diagram of the iron-copper system. Calphad5:105–108.
16. Huang, X., and T. Mashimo. 1999. Metastable BCC and FCC alloy bulk bodies in Fe–Cu system prepared by mechanical alloying and shock compression. J. Alloy. Compd.288:299–305.
17. Weeber, A. W.1987. Application of the Miedema model to formation enthalpies and crystallisation temperatures of amorphous alloys. J. Phys. F: Met. Phys.17:809.
18. He, J., J. Z. Zhao, and L. Ratke. 2006. Solidification microstructure and dynamics of metastable phase transformation in undercooled liquid Cu–Fe alloys. Acta Mater.54:1749–1757.
19. Mazzone, G., and M. V. Antisari. 1996. Structural and thermodynamic factors of suppressed interdiffusion kinetics in multi-component high-entropy materials. Phys. Rev. B54:441–446.
20. Ma, E., M. Atzmon, and F. E. Pinkerton. 1993. Thermodynamic and magnetic properties of metastable FexCu100− x solid solutions formed by mechanical alloying. J. Appl. Phys.74:955–962.
21. Xu, J., U. Herr, T. Klassen, and R. S. Averback. 1996. Formation of supersaturated solid solutions in the immiscible Ni–Ag system by mechanical alloying. J. Appl. Phys.79:3935–3945.
22. Hansen, M., and K. Anderko. 1965. Constitution of binary alloys, Issue 1, 2nd ed. McGraw-Hill, New York.
23. Lyasotsky, I., N. Dyakonova, D. Dyakonov, and E. Vlasova. 2008. Metastable phases and nanostructuring of Fe-Nb-Si-B base rapidly quenched alloys. Rev. Adv. Mater. Sci.18:695–702.
24. Fu, G., Z. Hu, L. Xie, X.Jin, Y. Xie, Y. Wang, et al. 2009. Electrodeposition of nickel hydroxide films on nickel foil and its electrochemical performances for supercapacitor. Int. J. Electrochem. Sci.4:1052–1062.
25. Gupta, R., N. Sukiman, M. Cavanaugh, B. Hinton, C. Hutchinson, and N. Birbilis. 2012. Metastable pitting characteristics of aluminium alloys measured using current transients during potentiostatic polarisation. Electrochim. Acta66:245–254.
26. Li, Q.2009. Formation of bulk ferromagnetic nanostructured Fe₄₀Ni₄₀P₁₄B₆ alloys by metastable liquid spinodal decomposition. SP Sci. China Press1:1919–1922.
27. Das, N., J. Mittra, B. Murty, S. Pabi, U. Kulkarni, and G. Dey. 2013. Miedema model based methodology to predict amorphous-forming-composition range in binary and ternary systems. J. Alloy. Compd.550:483–495.
28. Greenfield, M., and C. Pierce. 1973. Postweld aging of a metastable beta titanium alloy. Weld. J.52:524–528.
29. Ravi, C., C. Wolverton, and V. Ozolin¸š. 2006. Predicting metastable phase boundaries in Al–Cu alloys from first-principles calculations of free energies: the role of atomic vibrations. Europhys. Lett.73:719.
30. Xu, J., G. S. Collins, L. S. J. Peng, and M. Atzmon. 1999. Deformation-assisted decomposition of unstable Fe50Cu50 solid solution during low-energy ball milling. Acta Mater. 47:1241–1253.
31. Oleszak, D., and P. Shingu. 1996. Nanocrystalline metals prepared by low energy ball milling. J. Appl. Phys.79:2975–2980.
32. Jartych, E., J. K. Z·urawicz, D. Oleszak, and M. Pe˛kała. 2000. X-ray diffraction, magnetization and Mössbauer studies of nanocrystalline Fe–Ni alloys prepared by low- and high-energy ball milling. J. Magn. Magn. Mater.208:221–230.
33. Roeder, J., J. Sculac, and M. Notis. 1984. The precipitation of iron in early smelted copper from Timna. Microbeam Anal.243:243–246.
34. Ying-Yu, C., S. Rainer, and C. Y. Austin. 1984. Thermodynamic analysis of the iron-copper system I: the stable and metastable phase equilibria. Metall. Trans. A15:1921–1930.
35. Kennedy, C. E.2002. Review of mid- to high-temperature solar selective absorber materials. Technical Report NREL/TP-520-31267. National Renewable Energy Laboratory.
36. Alami, A. H., A. Allagui, and H. Alawadhi. 2015. Synthesis and optical properties of electrodeposited crystalline Cu2O in the Vis–NIR range for solar selective absorbers. Renewable Energy82:21–25.
37. Rephaeli, E., and F. S. 2008. Tungsten black absorber for solar light with wide angular operation range. Appl. Phys. Lett.92:211107–1–3.
38. Geldermon, K., L. Lee, and W. Donne. 2007. Falt-Band potential of a semiconductor: using the Mott-Schottky equation. J. Chem. Educ.84:685–688.
39. Hoerner, L.2013. Photosynthetic solar cells using chlorophyll and the applications towards energy sustainability. Thesis. University of South Florida, St. Petersburg.
40. Chien, C., and B. Hsu. 2013. Optimization of the dye-sensitized solar cell with anthocyanin as photosensitizer. Sol. Energy98:203–211.
41. Patil, G., M. Madhusudhan, B. R. Babu, and K. Raghavarao. 2009. Extraction, dealcoholization and concentration of anthocyanin from red radish. Chem. Eng. Process.48:364–369.
42. Zhang, Y., Y. J. Zhou, J. P. Lin, G. L. Chen, and P. K. Liaw. 2008. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater.10:534–538.
43. Takaki, S., K. Fukunaga, J. Syarif, and T. Tsuchiyama. 2004. Effect of grain refinement on thermal stability of metastable austenitic steel. Mater. Trans.45:2245–2251.
44. Gaffet, E., M. Harmelin, and F. Faudot. 1993. Far-from-equilibrium phase transition induced by mechanical alloying in the Cu-Fe system. J. Alloy. Compd.194:23–30.
45. Lucas, F., B. Trindade, B. Costa, and G. Le Caër. 2003. The influence of pre-milling on the microstructural evolution during mechanical alloying of a Fe₅₀Cu₅₀ Alloy. J. Metastable Nanocrystalline Mater.18:49–56.
46. Roos, A., T. Chibuye, and B. Karlsson. 1983. Properties of oxidized copper surfaces for solar applications I. Solar Energy Mater.7:453–465.
47. Tauc, J., R. Grigorovici, and A. Vancu. 1966. Optical properties and electronic structure of amorphous germanium. Phys. Status Solidi B15:627–637.
48. Erdogan, I. Y., and O. Gullu. 2010. Optical and structural properties of CuO nanofilm: its diode application. J. Alloy. Compd.492:378–383.
49. Kormann, C., D. W. Bahnemann, and M. R. Hoffmann. 1988. Preparation and characterization of quantum-size titanium dioxide. J. Phys. Chem.92:5196–5201.
50. Nakano, Y., S. Saeki, and T. Morikawa. 2009. Optical bandgap widening of p-type Cu₂O films by nitrogen doping. Appl. Phys. Lett.94:022111.
51. Pike, J., S. W. Chan, F. Zhang, X. Wang, and J. Hanson. 2006. Formation of stable Cu₂O from reduction of CuO nanoparticles. Appl. Catal. A303:273–277.
52. Kaneko, M., H. Ueno and J. Nemoto.2011. Schottky junction/ohmic contact behavior of a nanoporous TiO₂ thin film photoanode in contact with redox electrolyte solutions. Beilstein J. Nanotechnol.2:127–134.
53. Brian, Cantor (Book editor). 2005. Novel nanocrystalline alloys and magnetic nanomaterials, Brian Cantor. Institute of Physics Publishing, Sussex, UK.
54. Alami, A. H., A. Alketbi, M. Almheiri, and J. Abed. 2015. The Fe-Cu metastable nano-scale compound for enhanced absorption in the UV-Vis and NIR ranges. Metall. Mater. Trans. E Mater. Energy Syst.2:229–235.
55. Alami, A. H., A. Alketbi, M. Almheiri, and J. Abed. 2016. Assessment of Al-Cu-Fe compound for enhanced solar absorption. Int. J. Energy Res. doi: 10.1002/er.3468 [Epub ahead of press].
56. Alami, A. H., A. Alketbi, and M. Almheiri. 2015. Synthesis and microstructural and optical characterization of Fe-Cu metastable alloys for enhanced solar thermal absorption. Energy Procedia75 C:410–416.
57. Axel, F., F. Denoyer, and J. P. Gazeau. 2000. From quasicrystals to more complex systems, 13, 1, pp. 76. Springer-Verlag, Berlin Heidelberg.
58. Korn, D., H. Pfeifle, and G. Zibold. 1979. Optical properties of metastable CuFe solid solutions. J. Phys. F: Metal Phys.9:1709–1–7.
59. Liu, B. X., C. H. Shang, L. J. Huang, and H.-D. Li. 1990. Fe-Cu icosahedral phase and its thermal and magnetic properties. J. Non-Cryst. Solids117:785–788.
60. Takagiwa, Y., and K. Kimur. 2014. Metallic–covalent bonding conversion and thermoelectric properties of Al-based icosahedral quasicrystals and approximants, a review. Sci. Technol. Adv. Mater.15:044802, (12 pp).