Reliable iterative techniques for solving the KS equation arising in fluid flow

Abstract

In this study, we examine the Kuramoto-Sivashinsky equation which is a nonlinear model that describes several physical and chemical events arising in fluid flow. The approximate analytical solution for the fractional KS (FKS) problem is calculated using the Temimi-Ansari method (TAM) and the natural decomposition method (NDM). The projected procedure (NDM) combines the adomian decomposition method with the natural transform. Each technique can deal with nonlinear terms without making any assumptions. The methodologies under consideration provide $\omega _{n}$-curves that display the convergence window of the power series solution that approaches the exact solution. We explore two distinct examples to confirm the efficiency and applicability of the proposed strategies. The acquired outcomes are compared numerically with the q-homotopy analysis transform method (q-HATM). The numerical investigation is carried out to validate the precision and dependability of the approaches under consideration. Additionally, the nature of the outcomes gained has been displayed in a different order. The obtained results show that the proposed techniques are highly efficient and simple to use to analyze the behavior of other nonlinear models.

Keywords: Kuramoto-Sivashinsky equation, Laplace transform, natural decomposition method (NDM), Temimi-Ansari method (TAM)

1. Introduction

Since nearly three centuries ago, fractional calculus has always been considered a purely mathematical problem [1-3]. Despite having a long history, it was not utilized in both engineering and physics for an extended period of time. In recent decades, fractional calculus has attracted growing interest from a practical perspective among scientists [4-6]. In the disciplines of continuous-time simulation, numerous experts have noted that fractional derivatives are useful for describing linear viscoelasticity, rheology, acoustics, polymerization chemistry, etc. In addition, fractional derivatives have proven to be a useful instrument for describing the memory and inherited properties of diverse substances and procedures. The mathematical principles and practical implications of these operators are currently well-developed, and their applicability to the fields of science and engineering is viewed as a topic of interest. In physics, chemistry, and engineering [7-8], fractional derivatives have appeared in equations used to characterize dynamical processes; consequently, fractional-order differential equations (FDEs) are the subject of an increasing number of studies.

Gregory I. Sivashinsky measured the situation of a laminar flaming front in 1977. When Yoshiki Kuramoto simultaneously designed diffusion-induced chaos in a three-dimensional simulation of the Belousov-Zabotinskii transformation [10-13], he created a certain problem. The result of their collaboration is known as the Kuramoto-Sivashinsky (KS) model. This system describes the variations in the orientation of the combustion front, the flow of a liquid down a circular surface, and a dynamically specific oscillating of chemical compounds in a fluid that is homogeneous [14-16]. It creates chaotic behavior and necessitates a result resembling waves traveling in a finite space domain without changing scale. That has numerous implementations in a variety of concepts, such as response diffusion systems [17], thin film hydrodynamics [18], and front burn instability [19], as well as lengthy waves on functionality in a few noxious fluids [20].

The general Kuramoto-Sivashinsky equation (fractional Kuramoto-Sivashisky equation) is:

$D_{\iota }^{\sigma }\omega {+\omega }{\frac {\partial \omega }{\partial \vartheta }}+\alpha {\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+\gamma {\frac {\partial ^{3}\omega }{\partial \vartheta ^{3}}}+\eta {\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}=0,\quad 0<\mu \leq {1},\quad \vartheta \in [a,b],\quad \iota {>0.}$

(1)

When ${\textstyle \alpha =\eta =1}$ and ${\textstyle \gamma =0}$, the equation proceeds to the Kuramoto-Sivashinsky equation [9], which was developed by Kuramoto and Sivashinsky during their investigation of phase turbulence in the Belousov-Zhabotinsky reaction. The Kuramoto-Sivashinsky equation is a fourth-order nonlinear partial differential equation that plays a significant role in the study of fluid dynamics, combustion, and other areas of physics and mathematics.

Due to its wide range of applications, it has garnered a great deal of interest in the search for analytical and numerical solutions. Thus, the solutions of the KS equation have been accomplished through a variety of techniques, such as the finite difference method [21-22], the Exponential Cubic BSpline Collocation Method [23], the Subequation Method [24], the Adomian Decomposition Method [25-26], the Double Reduction Theory [27], the Modified Kudrayshov Method [28], the Expfunction Method [29], the q-homotopy analysis transform method [30], the homotopy analysis method [31-32], a semianalytical method [33], the Reduced Differential Transform Method [34], and numerous other techniques.

In this current research, two methods for solving the fractional Kuramoto-Sivashisky equation were implemented. The first method is a semi-analytical iterative method. Temimi and Ansari have proposed this method, namely the TAM. They have lately presented this method to solve linear and nonlinear ODEs and PDEs [35-36]. Recent applications of this iterative method have yielded exact and approximate solutions to several problems. As opposed to the VIM, the TAM doesn't require any restricted hypotheses for non-linear terms, such as the ADM, the prerequisite for the referred to as Adomian polynomial, thereby averting extensive computational work and requiring no additional parameters. In addition, it avoided homotopy construction and the solution of the corresponding equations for algebra, as in HPM.

The second method is the fractional natural decomposition method (FNDM) Rawashdeh and Maitama [37] propose this method using ADM and natural transform (NT). The method under consideration is a combination of an effective system and a natural transform, which may decrease massive computation while increasing reliability. In addition, the contemplated scheme necessitates no linearization, discretization, and transforming of partial to ordinary differential equations, or physical parameter assumptions. This allows nonlinear and complex issues to be solved with a straightforward procedure. Numerous authors have utilized it to analyze and discover solutions to numerous real-world problems.

2. Preliminaries to FC

Here, the fundamental definition of Natural transform (NT) and FC are presented [38-39].

Definition 1

The Riemann-Liouville integral of a function ${\textstyle f(\iota )\in C_{\delta }(\delta \geq {-1)}}$ having fractional order ${\textstyle (\sigma {>0)}}$ is presented as follows

$J^{\sigma }f(\iota )={\frac {1}{\Gamma (\sigma )}}\int _{0}^{\iota }(\iota {-\upsilon })^{\sigma {-1}}f(\upsilon )d\upsilon {.}$

(2)

Definition 2

The Caputo fractional order derivative of ${\textstyle f\in C_{-1}^{n}}$ is presented as

$D_{\iota }^{\sigma }={\begin{cases}\displaystyle {\frac {d^{n}f(\iota )}{d\iota ^{n}}},\left(\sigma =n\in N\right),\\\displaystyle {\frac {1}{\Gamma (n-\sigma )}}\int _{0}^{\iota }(\iota {-\upsilon })^{(n-\sigma {-1)}}f^{(n)}(\upsilon )d\upsilon ,\left((n-1)<\sigma {<}n,n\in N\right.).\end{cases}}$

(3)

Definition 3

The natural transform of ${\textstyle g(\iota )}$ is defined as [40-41]

$N^{+}[g(\iota )]=Q(s,u)={\frac {1}{u}}\int _{0}^{\infty }e^{\frac {-s\iota }{u}}g(\iota )d(\iota );s,\iota {>0},$

(4)

where ${\textstyle s}$ and ${\textstyle u}$ are the transform variables.

The inverse natural transform of a function is defined by

$N^{-}[Q(s,u)]=g(\iota )={\frac {1}{2\pi i}}\int _{p-i\infty }^{p+i\infty }e^{\frac {-s\iota }{u}}Q(s,u)d(s),$

(5)

where ${\textstyle s}$ and ${\textstyle u}$ are the natural transform variables and ${\textstyle p}$ is a real constant and the integral is taken along ${\textstyle s=p}$ in the complex plane ${\textstyle s=\vartheta {+}iy}$.

Definition 4

Natural Transform of nth derivative If ${\textstyle g^{(n)}(\iota )}$ is the nth derivative of function ${\textstyle g(\iota )}$ is given by,

$N[g^{(n)}(\iota )]=Q_{n}(s,u)={\frac {s^{n}}{u^{n}}}Q(s,u)-\sum _{k=0}^{n-1}{\frac {s^{n-(k+1)}}{u^{n-k}}}g^{(k)}(0),n\geq {1.}$

(6)

3. The fundamental ideas of two iterative approaches

An algorithm known as the iterative technique produces a series of improved approximations to a set of issues. When the appropriate sequence is converging at some specified initial approximations, the iterative approach produces an approximate solution that converges to the exact solution.

3.1 Basic Procedure for the fractional TAM

The general nonlinear fractional partial differential equation is a mathematical equation that may be used to represent the essential concepts of the suggested technique as

$\Upsilon \left(\omega (\vartheta ,\iota )\right)+\Phi \left(\omega (\vartheta ,\iota )\right)=w(\vartheta ,\iota ),\;n-1<\sigma \leq n,$

(7)

combined with the independent variable ${\textstyle \vartheta }$, dependent variable ${\textstyle \iota }$, unknown function ${\textstyle \omega (\vartheta ,\iota )}$ and boundary conditions

${\mathcal {B}}\left(\omega ,{\frac {\partial \omega }{\partial \vartheta }}\right)=0,$

where ${\textstyle \Upsilon =D_{\iota }^{\sigma }={\frac {\partial ^{\sigma }}{\partial \iota ^{\sigma }}}}$ is the Caputo fractional derivative, ${\textstyle \Phi }$ is representing the generic differential operators, the continuous functions are shown in ${\textstyle w(\vartheta ,\iota )}$ and the boundary operator is represented by ${\textstyle {\mathcal {B}}}$. The main request made here is for the differential operator ${\textstyle \Upsilon }$ , which is general. However, if necessary, we can combine a number of linear components with nonlinear terms.

The following describes how the suggested method operates. The starting condition is obtained by removing the nonlinear portion as

$D_{\iota }^{\alpha }\omega _{0}\left(\vartheta ,\iota \right)=w(\vartheta ,\iota ),\quad {\mathcal {B}}\left(\omega _{0},{\frac {\partial \omega _{0}}{\partial \vartheta }}\right)=0.$

(8)

By resolving the following issues, the next approximations of solutions are produced:

$D_{\iota }^{\alpha }\omega _{1}\left(\vartheta ,\iota \right)+\Phi \left(\omega _{0}(\vartheta ,\iota )\right)=w(\vartheta ,\iota ),\quad {\mathcal {B}}\left(\omega _{1},{\frac {\partial \omega _{1}}{\partial \vartheta }}\right)=0.$

(9)

As a result, we have a simple iterative process for solving a group of issues

$D_{\iota }^{\alpha }\omega _{n+1}\left(\vartheta ,\iota \right)+\Phi \left(\omega _{n}(\vartheta ,\iota )\right)=w(\vartheta ,\iota ),\quad {\mathcal {B}}\left(\omega _{n+1},{\frac {\partial \omega _{n+1}}{\partial \vartheta }}\right)=0.$

(10)

In this technique, it is crucial to remember that any of the ${\textstyle \omega _{n+1}\left(\vartheta ,\iota \right)}$ is individually a solution to the problem (Eq. (7)). We confirm that these iterative stages are simple to carry out and that each solution is an improvement over the previous iteration. The convergence of solutions must be confirmed by comparing successive solutions to the prior iteration. The analytical solution and the exact solution to the issue (Eq. (7)) converge as more iterations are made. This allows for the development of an adequate analytical solution with the exact solution as

$\omega (\vartheta ,\iota )={\underset {\scriptstyle {\scriptscriptstyle n\rightarrow \infty }}{\lim }}\omega _{n}(\vartheta ,\iota {)}.$

(11)

3.2 Basic Procedure for the fractional NDM

The following examples demonstrate how the recommended approach is based on the theory and method for solving fractional nonlinear partial differential equations:

$D_{\iota }^{\sigma }\omega \left(\vartheta ,\iota \right)+{\mathcal {R}}\omega (\vartheta ,\iota )+{\mathcal {F}}\omega (\vartheta ,\iota )=\hbar \left(\vartheta ,\iota \right),\;n-1<\sigma \leq n,$

(12)

with the initial condition

$\omega \left(\vartheta ,0\right)=v\left(\vartheta \right),$

(13)

where the Caputo operator of ${\textstyle \omega \left(\vartheta ,\iota \right)}$ is denoted by ${\textstyle D_{\iota }^{\sigma }={\frac {\partial ^{\sigma }}{\partial \iota ^{\sigma }}}}$, the linear function is denoted by ${\textstyle {\mathcal {R}}}$, the non-linear function is denoted by ${\textstyle {\mathcal {F}}}$ and the source term is denoted by ${\textstyle \hbar (\vartheta ,\iota )}$. Applying the NT to Eq. (12) and employing definition 5, we obtain

$\mathbb {N} ^{+}\left[\omega \left(\vartheta ,\iota \right)\right]={\frac {q^{\sigma }}{s^{\sigma }}}\sum _{i=0}^{n-1}{\frac {q^{i-\sigma }}{s^{i+1-\sigma }}}\left[D^{i}\omega \left(\vartheta ,\iota \right)\right]_{\iota =0}+$ ${\frac {q^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\hbar \left(\vartheta ,\iota \right)\right]-{\frac {q^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[{\mathcal {R}}\omega (\vartheta ,\iota )+{\mathcal {F}}\omega (\vartheta ,\iota )\right].$

(14)

Applying the inverse NT to the previous equation, we get

$\omega \left(\vartheta ,\iota \right)={\mathcal {H}}\left(\vartheta ,\iota \right)+\mathbb {N} ^{-}\left\{{\frac {q^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\hbar \left(\vartheta ,\iota \right)-{\mathcal {R}}\omega (\vartheta ,\iota )-{\mathcal {F}}\omega (\vartheta ,\iota )\right]\right\}.$

(15)

${\textstyle {\mathcal {H}}\left(\vartheta ,\iota \right)}$ exists based on the provided initial condition and nonhomogeneous term. Let's suppose that an infinite series solution has the form

$\omega \left(\vartheta ,\iota \right)=\sum _{n=0}^{\infty }\omega _{n}\left(\vartheta ,\iota \right),\qquad {\mathcal {F}}\omega (\vartheta ,\iota )=\sum _{n=0}^{\infty }A_{n},$

(16)

where ${\textstyle A_{n}}$ denotes the nonlinear term of ${\textstyle {\mathcal {F}}\omega (\vartheta ,\iota )}$, then we get

$\sum _{n=0}^{\infty }\omega _{n}\left(\vartheta ,\iota \right)={\mathcal {H}}\left(\vartheta ,\iota \right)+\mathbb {N} ^{-}\left\{{\frac {q^{\zeta }}{s^{\zeta }}}\mathbb {N} ^{+}\left[\hbar \left(\vartheta ,\iota \right)-{\mathcal {R}}\omega (\vartheta ,\iota )-{\mathcal {F}}\omega (\vartheta ,\iota )\right]\right\}.$

(17)

Ultimately, the analytical solutions are presented in the following form:

$\omega \left(\vartheta ,\iota \right)=\sum _{n=0}^{\infty }\omega _{n}\left(\vartheta ,\iota \right).$

(18)

4. Numerical examples of the KS models

This section demonstrates how the iterative methods TAM and NDM will be used to solve the fractional Kuramoto-Sivashinsky problem.

4.1 Example 1

The following form can be used to represent the fractional Kuramoto-Sivashinsky equation

$D_{\iota }^{\sigma }\omega (\vartheta ,\iota )+\omega {\frac {\partial \omega }{\partial \vartheta }}-{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}=0,$

(19)

with initial condition

$\omega (\vartheta ,0)=\zeta {+\gamma }=\zeta +{\frac {15}{19{\sqrt {19}}}}\tanh ^{3}[\kappa (\vartheta {-\eta })]-45\tanh[\kappa (\vartheta -\eta )]$

(20)

The two iterative approaches that have been suggested will be used to resolve this issue.

Solving the Example 1 by Tthe AM

By using the fractional TAM by first formulating the problem as

$\Upsilon \left(\omega (\vartheta ,\iota )\right)=D_{\iota }^{\sigma }\omega (\vartheta ,\iota )={\frac {\partial ^{\sigma }\omega (\vartheta ,\iota )}{\partial \iota ^{\sigma }}},\quad$ $\Phi \left(\omega (\vartheta ,\iota )\right)=\omega (\vartheta ,\iota ){\frac {\partial \omega (\vartheta ,\iota )}{\partial \vartheta }}-{\frac {\partial ^{2}\omega (\vartheta ,\iota )}{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega (\vartheta ,\iota )}{\partial \vartheta ^{4}}},\quad$ $w(\vartheta ,\iota )=0.$

(21)

The first problem that has to be resolved is

$\Upsilon \left(\omega _{0}(\vartheta ,\iota )\right)=0,\qquad \omega _{0}(\vartheta ,0)=\zeta {+\gamma }.$

(22)

The solution of Eq. (22) may be obtained by using a straightforward procedure, as shown below

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{0}(\vartheta ,\iota )\right)=0,\qquad \omega _{0}(\vartheta ,0)=\zeta {+\gamma }.$

(23)

As a result, using the fundamental characteristics of definition (2), we can derive the primary iteration as

$\omega _{0}(\vartheta ,\iota )=\zeta {+\gamma }=\zeta +{\frac {15}{19{\sqrt {19}}}}\tanh ^{3}[\kappa (\vartheta {-\eta })]-45\tanh[\kappa (\vartheta -\eta )]$

(24)

It is possible to compute the next iteration, and we have

$\Upsilon \left(\omega _{1}\left(\vartheta ,\iota \right)\right)+\Phi \left(\omega _{0}(\vartheta ,\iota )\right)+w(\vartheta ,\iota )=0,\qquad \omega _{1}(\vartheta ,0)=\zeta {+\gamma }.$

(25)

Then, by integrating both sides of Eq. (25) and using the fundamental characteristics of definition (2), we obtain

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{1}(\vartheta ,\iota )\right)=-I^{\sigma }\left(\omega _{0}(\vartheta ,\iota ){\frac {\partial \omega _{0}(\vartheta ,\iota )}{\partial \vartheta }}-{\frac {\partial ^{2}\omega _{0}(\vartheta ,\iota )}{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega _{0}(\vartheta ,\iota )}{\partial \vartheta ^{4}}}\right),\qquad \omega _{1}(\vartheta ,0)=\zeta {+\gamma }.$

(26)

The next iteration appears as

$\omega _{1}(\vartheta ,\iota )=\zeta +{\frac {15\tanh ^{3}(\kappa (\vartheta {-\eta }))-45\tanh(\kappa (\vartheta {-\eta }))}{19{\sqrt {19}}}}+{\frac {45\kappa \iota ^{\sigma }{\hbox{sech}}^{4}(\kappa (\vartheta {-\eta }))}{6859\Gamma (\sigma {+1)}}}$ $\times \left(19{\sqrt {19}}\zeta {+\tanh }(\kappa (\vartheta {-\eta }))\left(15\left(152{\sqrt {19}}\kappa ^{3}-1\right){\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta }))+76{\sqrt {19}}\kappa \left(1-16\kappa ^{2}\right)-30\right)\right)$

(27)

The following iteration is calculable and is provided as

$\Upsilon \left(\omega _{2}\left(\vartheta ,\iota \right)\right)+\Phi \left(\omega _{1}(\vartheta ,\iota )\right)+w(\vartheta ,\iota )=0,\qquad \omega _{2}(\vartheta ,0)=\zeta {+\gamma }.$

(28)

Then, by integrating both sides of Eq. (28) and using the fundamental characteristics of definition (2), we obtain

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{2}(\vartheta ,\iota )\right)=-I^{\sigma }\left(\omega _{1}(\vartheta ,\iota ){\frac {\partial \omega _{1}(\vartheta ,\iota )}{\partial \vartheta }}-{\frac {\partial \omega _{1}^{2}(\vartheta ,\iota )}{\partial \vartheta ^{2}}}+{\frac {\partial \omega _{1}^{4}(\vartheta ,\iota )}{\partial \vartheta ^{4}}}\right),\qquad \omega _{2}(\vartheta ,0)=\zeta {+\gamma }.$

(29)

Each repetition of the ${\textstyle \omega _{n}(\vartheta ,\iota )}$ represents a rough solution to Eq. (19) in accordance with Eq. (11), which states that. The analytical solution gets closer to the exact solution as the number of iterations rises. By continuing with this process, we are able to create the following sequence of analytical solution templates as

$\omega (\vartheta ,\iota )={\underset {\scriptscriptstyle n\rightarrow \infty }{\lim }}\omega _{n}(\vartheta ,\iota )\simeq \omega _{2}(\vartheta ,\iota {).}$

(30)

Here are some details on the exact solution to which the preceding approximate solution leads [30],

$\omega (\vartheta ,\iota )=\zeta +{\frac {15}{19{\sqrt {19}}}}\tanh ^{3}[\kappa (\vartheta {-\zeta }\iota {-\eta })]-45\tanh[\kappa (\vartheta -\zeta \iota -\eta )]$

(31)

Solving the Example 1 by the DM

Eq. (19) may be simplified by applying NT to it

$\mathbb {N} ^{+}\left[D_{\iota }^{\sigma }\omega (\vartheta ,\iota )\right]=-\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}-{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(32)

The definition of the non-linear operator is

${\frac {s^{\sigma }}{\omega ^{\sigma }}}\mathbb {N} ^{+}[\omega (\vartheta ,\iota )]-\sum _{k=0}^{n-1}{\frac {s^{\sigma {-}(k+1)}}{\varrho ^{\sigma {-}k}}}\left[D^{k}\omega \right]_{\iota =0}=-\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}-{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(33)

When Eq. (33) is made simpler, we obtain

$\mathbb {N} ^{+}[\omega (\vartheta ,\iota )]={\frac {1}{s}}\left[\omega _{0}(\vartheta ,\iota )\right]-{\frac {\varrho ^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}-{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(34)

Eq. (34) is transformed by inverse NT to give us

$\omega (\vartheta ,\iota )=\omega _{0}(\vartheta ,\iota )-\mathbb {N} ^{-1}\left[{\frac {\varrho ^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}-{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right]\right].$

(35)

We may calculate the terms of the series by using ${\textstyle \omega _{0}(\vartheta ,\iota )}$ to solve the previous equation

$\omega (\mathrm {\vartheta } ,\mathrm {\iota } )=\sum _{\mathrm {n} =0}^{\infty }\mathrm {\omega } _{\mathrm {n} }(\mathrm {\vartheta } ,\mathrm {\iota } )=\mathrm {\omega } _{0}(\mathrm {\vartheta } ,\mathrm {\iota } )+\mathrm {\omega } _{1}(\mathrm {\vartheta } ,\mathrm {\iota } )+\mathrm {\omega } _{2}(\mathrm {\vartheta } ,\mathrm {\iota } )+\ldots$

(36)

Using the NDM procedure, we get

$\omega (\vartheta ,0)=\zeta {+\gamma }=\zeta +{\frac {15}{19{\sqrt {19}}}}\tanh ^{3}[\kappa (\vartheta {-\eta })]-45\tanh[\kappa (\vartheta -\eta )],$

(37)

$\omega _{1}(\vartheta ,\iota )=-{\frac {45\kappa \iota ^{\sigma }{\hbox{sech}}^{7}(\kappa (\vartheta {-\eta }))}{27436{\sqrt {19}}\Gamma (\sigma {+1)}}}{\biggl (}\left(\left(11552\kappa ^{3}-722\kappa {+15}{\sqrt {19}}\right)\cosh(2\kappa (\vartheta {-\eta }))-31768\kappa ^{3}-722\kappa {+30}{\sqrt {19}}\right)$ $\times {4}\sinh(\kappa (\vartheta {-\eta }))-1083\zeta \cosh(\kappa (\vartheta {-\eta }))-361\zeta \cosh(3\kappa (\vartheta {-\eta })){\biggr )},$

(38)

$\omega _{2}(\vartheta ,\iota )={\frac {45\kappa ^{2}\iota ^{2\sigma }{\hbox{sech}}^{11}(\kappa (\vartheta {-\eta }))}{39617584\Gamma (2\sigma {+1)}}}{\Bigl \{}1444\zeta \left(4712{\sqrt {19}}\kappa ^{3}-152{\sqrt {19}}\kappa {+45}\right)\cosh(3\kappa (\vartheta {-\eta }))$ $-21660\zeta \left(1216{\sqrt {19}}\kappa ^{3}+38{\sqrt {19}}\kappa {-27}\right)\cosh(\kappa (\vartheta {-\eta }))-108300\zeta \cosh(5\kappa (\vartheta {-\eta }))$ $+8121056{\sqrt {19}}\zeta \kappa ^{3}\cosh(5\kappa (\vartheta {-\eta }))+109744{\sqrt {19}}\zeta \kappa \cosh(5\kappa (\vartheta {-\eta }))-21660\zeta \cosh(7\kappa (\vartheta {-\eta }))$ $-877952{\sqrt {19}}\zeta \kappa ^{3}\cosh(7\kappa (\vartheta {-\eta }))++54872{\sqrt {19}}\zeta \kappa \cosh(7\kappa (\vartheta {-\eta }))-53100{\sqrt {19}}\sinh(\kappa (\vartheta {-\eta }))$ $+469242240\kappa ^{3}\sinh(\kappa (\vartheta {-\eta }))-1097440{\sqrt {19}}\kappa ^{2}\sinh(\kappa (\vartheta {-\eta }))+1992720\kappa \sinh(\kappa (\vartheta {-\eta }))$ $-48348816640{\sqrt {19}}\kappa ^{6}\sinh(\kappa (\vartheta {-\eta }))-215098240{\sqrt {19}}\kappa ^{4}\sinh(\kappa (\vartheta {-\eta }))+34295{\sqrt {19}}\zeta ^{2}\sinh(\kappa (\vartheta {-\eta }))$ $-1481544{\sqrt {19}}\kappa ^{2}\sinh(3\kappa (\vartheta {-\eta }))+1906080\kappa \sinh(3\kappa (\vartheta {-\eta }))-13500{\sqrt {19}}\sinh(3\kappa (\vartheta {-\eta }))$ (39) $-143545152{\sqrt {19}}\kappa ^{4}\sinh(3\kappa (\vartheta {-\eta }))-85600320\kappa ^{3}\sinh(3\kappa (\vartheta {-\eta }))+16385218176{\sqrt {19}}\kappa ^{6}\sinh(3\kappa (\vartheta {-\eta }))$ $+61731{\sqrt {19}}\zeta ^{2}\sinh(3\kappa (\vartheta {-\eta }))-173280\kappa \sinh(5\kappa (\vartheta {-\eta }))+4500{\sqrt {19}}\sinh(5\kappa (\vartheta {-\eta }))$ $+68041280{\sqrt {19}}\kappa ^{4}\sinh(5\kappa (\vartheta {-\eta }))-12822720\kappa ^{3}\sinh(5\kappa (\vartheta {-\eta }))-274360{\sqrt {19}}\kappa ^{2}\sinh(5\kappa (\vartheta {-\eta }))$ $-1611041920{\sqrt {19}}\kappa ^{6}\sinh(5\kappa (\vartheta {-\eta }))+34295{\sqrt {19}}\zeta ^{2}\sinh(5\kappa (\vartheta {-\eta }))+900{\sqrt {19}}\sinh(7\kappa (\vartheta {-\eta }))$ $+1386240\kappa ^{3}\sinh(7\kappa (\vartheta {-\eta }))+109744{\sqrt {19}}\kappa ^{2}\sinh(7\kappa (\vartheta {-\eta }))-86640\kappa \sinh(7\kappa (\vartheta {-\eta }))$ $+28094464{\sqrt {19}}\kappa ^{6}\sinh(7\kappa (\vartheta {-\eta }))-3511808{\sqrt {19}}\kappa ^{4}\sinh(7\kappa (\vartheta {-\eta }))+6859{\sqrt {19}}\zeta ^{2}\sinh(7\kappa (\vartheta {-\eta })){\Bigr \}}.$

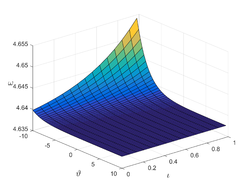
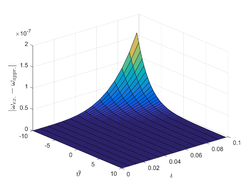
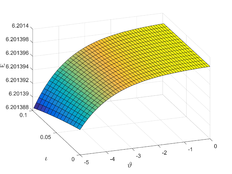
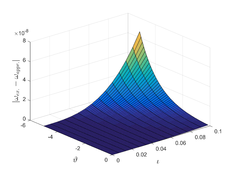
And so on. The behavior of a collection of approximate solutions obtained in Figure 1 and Table 1.

(a) Exact solution of ${\textstyle \omega (\vartheta ,\iota )}$ (b) Approximate solution of ${\textstyle \omega (\vartheta ,\iota {)}}$ (c) Absolute error at ${\textstyle \iota =1}$ (d) Representation of the approximate solution with the exact solution (e) Comparative graphical simulation in the steady state (f) The solution of the power series approaches the exact solution

Figure 1. The behavior of a collection of approximate solutions obtained for case (1) at $\sigma =1$, $\kappa ={\frac {1}{2{\sqrt {19}}}}$, $\zeta =5$ $,\eta =-25$

Table 1. Compare numerical calculations of analytical solutions $\omega \left(\vartheta ,\iota \right)$ of Eq. (19) obtained by TAM algorithm and NDM with exact,
and q-HATM solutions at $\sigma =1$, $\kappa ={\frac {1}{2{\sqrt {19}}}}$, $\zeta =5$ $,\eta =-25$

${\textstyle \vartheta }$	$\iota$	$\omega _{\scriptscriptstyle TAM}$	$\omega _{\scriptscriptstyle NDM}$	$\omega _{\scriptscriptstyle HATM}$ [30]	$\omega _{\scriptscriptstyle TAM}(\sigma =0.9)$	$\omega _{\scriptscriptstyle NDM}(\sigma =0.9)$
1	0.2	2.80424E08	2.48734E09	2.80432E08	2.14599E06	2.67151E06
	0.4	4.95147E07	8.62662E08	4.95160E07	2.08915E06	5.50393E06
	0.6	2.78302E06	7.13064E07	2.78309E06	2.7345E06	7.47041E06
	0.8	9.82780E06	3.28572E06	9.82802E06	1.67288E05	5.46055E06
	1	2.69887E05	1.10169E05	2.69893E05	4.67056E05	6.17336E06
2	0.2	1.78570E08	1.58980E09	1.78573E08	1.35933E06	1.69305E06
	0.4	3.15442E07	5.51676E08	3.15448E07	1.32002E06	3.48849E06
	0.6	1.77395E06	4.56307E07	1.77397E06	1.75053E06	4.72985E06
	0.8	6.26867E06	2.10428E06	6.26876E06	1.06596E05	3.43118E06
	1	1.72293E05	7.06240E06	1.72296E05	2.97593E05	4.02031E06
3	0.2	1.13535E08	1.01377E09	1.13536E08	8.60648E07	1.07236E06
	0.4	2.00629E07	3.51942E-08	2.00631E07	8.34089E07	2.20978E06
	0.6	1.12877E06	2.91252E07	1.12878E06	1.11763E06	2.99357E06
	0.8	3.99093E06	1.34397E06	1.99096E06	6.78091E06	2.15839E06
	1	1.09764E05	4.51409E06	1.09765E06	1.89302E05	2.60114E06
4	0.2	7.20971E09	6.45271E-10	7.20976E09	5.44714E07	6.78920E07
	0.4	1.27440E07	2.24089E08	1.27441E07	5.27063E07	1.39914E06
	0.6	7.17241E07	1.85523E07	7.17246E07	7.12053E07	1.89411E06
	0.8	2.53701E06	8.56512E07	2.53702E06	4.30781E06	1.35897E06
	1	6.98135E06	2.87858E06	6.98138E06	1.20257E05	1.67448E06
5	0.2	4.57386E09	4.10120E-10	4.57388E09	3.44656E07	4.29680E07
	0.4	8.08663E08	1.42464E08	8.08667E08	3.33064E07	8.85550E07
	0.6	4.55248E07	1.17984E07	4.55249E07	4.52901E07	1.19818E06
	0.8	1.61084E06	5.44920E07	3.61084E07	2.73379E06	8.56270E07
	1	4.43460E06	1.83226E06	4.43462E07	7.63155E06	1.07374E06

4.2 Example 2

The following form can be used to represent the fractional Kuramoto-Sivashinsky equation

$D_{\iota }^{\sigma }\omega (\vartheta ,\iota )+\omega {\frac {\partial \omega }{\partial \vartheta }}+{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}=0,$

(40)

with initial condition

$\omega (\vartheta ,0)=\zeta {+\gamma }=\zeta +{\frac {15}{19}}{\sqrt {\frac {11}{19}}}\left(11\tanh ^{3}(\kappa (\vartheta {-\eta }))-9\tanh(\kappa (\vartheta {-\eta }))\right).$

(41)

The two iterative approaches that have been suggested will be used to resolve this issue.

Solving the Example 2 by the AM:

By using the fractional TAM by first formulating the problem as

$\Upsilon \left(\omega (\vartheta ,\iota )\right)=D_{\iota }^{\sigma }\omega (\vartheta ,\iota )={\frac {\partial ^{\sigma }\omega (\vartheta ,\iota )}{\partial \iota ^{\sigma }}},\quad$$\Phi \left(\omega (\vartheta ,\iota )\right)=\omega (\vartheta ,\iota ){\frac {\partial \omega (\vartheta ,\iota )}{\partial \vartheta }}+{\frac {\partial ^{2}\omega (\vartheta ,\iota )}{\partial \vartheta ^{2}}}$$+{\frac {\partial ^{4}\omega (\vartheta ,\iota )}{\partial \vartheta ^{4}}},\quad$$w(\vartheta ,\iota )=0.$

(42)

The first problem that has to be resolved is

$\Upsilon \left(\omega _{0}(\vartheta ,\iota )\right)=0,\qquad \omega _{0}(\vartheta ,0)=\zeta {+\gamma }.$

(43)

The solution of Eq. (43) may be obtained by using a straightforward procedure, as shown below

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{0}(\vartheta ,\iota )\right)=0,\qquad \omega _{0}(\vartheta ,0)=\zeta {+\gamma }.$

(44)

As a result, using the fundamental characteristics of definition (2), we can derive the primary iteration as

$\omega _{0}(\vartheta ,\iota )=\zeta {+\gamma }=\zeta +{\frac {15}{19}}{\sqrt {\frac {11}{19}}}\left(11\tanh ^{3}(\kappa (\vartheta {-\eta }))-9\tanh(\kappa (\vartheta {-\eta }))\right).$

(45)

It is possible to compute the next iteration, and we have

$\Upsilon \left(\omega _{1}\left(\vartheta ,\iota \right)\right)+\Phi \left(\omega _{0}(\vartheta ,\iota )\right)+w(\vartheta ,\iota )=0,\qquad \omega _{1}(\vartheta ,0)=\zeta {+\gamma }.$

(46)

Then, by integrating both sides of Eq. (46) and using the fundamental characteristics of definition (2), we obtain

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{1}(\vartheta ,\iota )\right)=-I^{\sigma }\left(\omega _{0}(\vartheta ,\iota ){\frac {\partial \omega _{0}(\vartheta ,\iota )}{\partial \vartheta }}+{\frac {\partial ^{2}\omega _{0}(\vartheta ,\iota )}{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega _{0}(\vartheta ,\iota )}{\partial \vartheta ^{4}}}\right),\qquad \omega _{1}(\vartheta ,0)=\zeta {+\gamma }.$

(47)

The next iteration appears as

$\omega _{1}(\vartheta ,\iota )=\zeta {+\gamma }+{\frac {45\kappa \iota ^{\sigma }{\hbox{sech}}^{2}(\kappa (\vartheta {-\eta }))}{6859\Gamma (\sigma {+1)}}}{\biggl (}16\left(19{\sqrt {209}}\kappa \left(4\kappa ^{2}+1\right)-165\right)\tanh(\kappa (\vartheta {-\eta }))-152{\sqrt {209}}\zeta +{\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta }))$ $\times \left(209{\sqrt {209}}\zeta {+\tanh }(\kappa (\vartheta {-\eta }))\left(165\left(152{\sqrt {209}}\kappa ^{3}-121\right){\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta }))-76{\sqrt {209}}\kappa \left(224\kappa ^{2}+11\right)+18150\right)\right){\biggr )}.$

(48)

The following iteration is calculable and is provided as

$\Upsilon \left(\omega _{2}\left(\vartheta ,\iota \right)\right)+\Phi \left(\omega _{1}(\vartheta ,\iota )\right)+w(\vartheta ,\iota )=0,\qquad \omega _{2}(\vartheta ,0)=\zeta {+\gamma }.$

(49)

Then, by integrating both sides of Eq. (49) and using the fundamental characteristics of definition (2), we obtain

$I^{\sigma }\left(D_{\iota }^{\sigma }\omega _{2}(\vartheta ,\iota )\right)=-I^{\sigma }\left(\omega _{1}(\vartheta ,\iota ){\frac {\partial \omega _{1}(\vartheta ,\iota )}{\partial \vartheta }}+{\frac {\partial \omega _{1}^{2}(\vartheta ,\iota )}{\partial \vartheta ^{2}}}+{\frac {\partial \omega _{1}^{4}(\vartheta ,\iota )}{\partial \vartheta ^{4}}}\right),\qquad \omega _{2}(\vartheta ,0)=\zeta {+\gamma }.$

(50)

Each repetition of the ${\textstyle \omega _{n}(\vartheta ,\iota )}$ represents a rough solution to Eq. (40) in accordance with Eq. (11), which states that. The analytical solution gets closer to the exact solution as the number of iterations rises. By continuing with this process, we are able to create the following sequence of analytical solution templates as

$\omega (\vartheta ,\iota )={\underset {\scriptscriptstyle n\rightarrow \infty }{lim}}\omega _{n}(\vartheta ,\iota )\simeq \omega _{2}(\vartheta ,\iota {).}$

(51)

Here are some details on the exact solution to which the preceding approximate solution leads [30],

$\omega (\vartheta ,\iota )=\zeta +{\frac {15}{19}}{\sqrt {\frac {11}{19}}}\left(11\tanh ^{3}(\kappa (\vartheta {-\zeta }\iota {-\eta }))-9\tanh(\kappa (\vartheta {-\zeta }\iota {-\eta }))\right).$

(52)

Solving Example 2 by the NDM:

Eq. (40) may be simplified by applying NT to it

$\mathbb {N} ^{+}\left[D_{\iota }^{\sigma }\omega (\vartheta ,\iota )\right]=-\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}+{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(53)

The definition of the non-linear operator is

${\frac {s^{\sigma }}{\omega ^{\sigma }}}\mathbb {N} ^{+}[\omega (\vartheta ,\iota )]-\sum _{k=0}^{n-1}{\frac {s^{\sigma {-}(k+1)}}{\varrho ^{\sigma {-}k}}}\left[D^{k}\omega \right]_{\iota =0}=-\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}+{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(54)

When Eq. (54) is made simpler, we obtain

$\mathbb {N} ^{+}[\omega (\vartheta ,\iota )]={\frac {1}{s}}\left[\omega _{0}(\vartheta ,\iota )\right]-{\frac {\varrho ^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}+{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right].$

(55)

Eq. (55) is transformed by inverse NT to give us

$\omega (\vartheta ,\iota )=\omega _{0}(\vartheta ,\iota )-\mathbb {N} ^{-1}\left[{\frac {\varrho ^{\sigma }}{s^{\sigma }}}\mathbb {N} ^{+}\left[\omega {\frac {\partial \omega }{\partial \vartheta }}+{\frac {\partial ^{2}\omega }{\partial \vartheta ^{2}}}+{\frac {\partial ^{4}\omega }{\partial \vartheta ^{4}}}\right]\right].$

(56)

We may calculate the terms of the series by using ${\textstyle \omega _{0}(\vartheta ,\iota )}$ to solve the previous equation

$\omega (\mathrm {\vartheta } ,\mathrm {\iota } )=\sum _{\mathrm {n} =0}^{\infty }\mathrm {\omega } _{\mathrm {n} }(\mathrm {\vartheta } ,\mathrm {\iota } )=\mathrm {\omega } _{0}(\mathrm {\vartheta } ,\mathrm {\iota } )+\mathrm {\omega } _{1}(\mathrm {\vartheta } ,\mathrm {\iota } )+\mathrm {\omega } _{2}(\mathrm {\vartheta } ,\mathrm {\iota } )+\ldots$

(57)

Using the NDM procedure, we get

$\omega (\vartheta ,0)=\zeta {+\gamma }=\zeta +{\frac {15}{19}}{\sqrt {\frac {11}{19}}}\left(11\tanh ^{3}(\kappa (\vartheta {-\eta }))-9\tanh(\kappa (\vartheta {-\eta }))\right),$

(58)

$\omega _{1}(\vartheta ,\iota )={\frac {45\kappa \iota ^{\sigma }{\hbox{sech}}^{2}(\kappa (\vartheta {-\eta }))}{6859\Gamma (\sigma {+1)}}}{\Bigl \{}16\left(19{\sqrt {209}}\kappa \left(4\kappa ^{2}+1\right)-165\right)$$\tanh(\kappa (\vartheta {-\eta }))-152{\sqrt {209}}\zeta +{\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta }))$ $\left(209{\sqrt {209}}\zeta {+\tanh }(\kappa (\vartheta {-\eta }))\left(165\left(152{\sqrt {209}}\kappa ^{3}-121\right){\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta }))-76{\sqrt {209}}\kappa \left(224\kappa ^{2}+11\right)+18150\right)\right){\Bigr \}},$

(59)

$\omega _{2}(\vartheta ,\iota )={\frac {90\kappa ^{2}\iota ^{2\sigma }{\hbox{sech}}^{2}(\kappa (\vartheta {-\eta }))}{2476099\Gamma (2\sigma {+1)}}}{\Bigl \{}11552\zeta \left(19{\sqrt {209}}\kappa \left(4\kappa ^{2}+1\right)-165\right)-8\tanh(\kappa (\vartheta {-\eta }))$ $\times \left({\sqrt {209}}\left(6859\zeta ^{2}+9900\right)+1444\kappa \left(4\kappa ^{2}+1\right)\left(19{\sqrt {209}}\kappa \left(4\kappa ^{2}+1\right)-330\right)\right)$ $-2475\left(5776\left(1596{\sqrt {209}}\kappa ^{3}-1573\right)\kappa ^{3}+6655{\sqrt {209}}\right)\tanh(\kappa (\vartheta {-\eta })){\hbox{ sech}}^{8}(\kappa (\vartheta {-\eta }))$ $-15{\hbox{ sech}}^{6}(\kappa (\vartheta {-\eta })){\Bigl \{}-4\left(361\kappa \left(16\kappa ^{2}\left(133{\sqrt {209}}\kappa \left(662\kappa ^{2}+11\right)-92686\right)-14641\right)+459195{\sqrt {209}}\right)$ $\times \tanh(\kappa (\vartheta {-\eta }))+27797\zeta \left(152{\sqrt {209}}\kappa ^{3}-121\right){\Bigr \}}+20{\hbox{ sech}}^{4}(\kappa (\vartheta {-\eta })){\Bigl \{}\tanh(\kappa (\vartheta {-\eta }))$ (60) $-3\left(361\kappa \left(\kappa \left(8\kappa \left(19{\sqrt {209}}\kappa \left(3262\kappa ^{2}+155\right)-72897\right)+209{\sqrt {209}}\right)-16698\right)+228690{\sqrt {209}}\right)$ $+361\zeta \left(19{\sqrt {209}}\kappa \left(620\kappa ^{2}+11\right)-10527\right){\Bigr \}}+2{\hbox{ sech}}^{2}(\kappa (\vartheta {-\eta })){\Bigl \{}-1444\zeta \left(76{\sqrt {209}}\kappa \left(118\kappa ^{2}+7\right)-10065\right)$ $+11{\sqrt {209}}\left(6859\zeta ^{2}+96300\right)+5776\kappa \left(8\left(19{\sqrt {209}}\kappa \left(478\kappa ^{2}+59\right)-13695\right)\kappa ^{2}+266{\sqrt {209}}\kappa {-8085}\right)$ $\times \tanh(\kappa (\vartheta {-\eta })){\Bigr \}}{\Bigr \}}.$

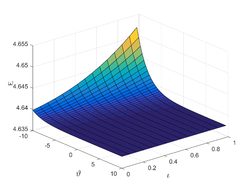
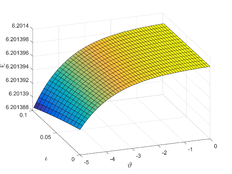
And so on. The behavior of a collection of approximate solutions obtained in Figure 2 and Table 2.

(a) Exact solution of ${\textstyle \omega (\vartheta ,\iota )}$ (b) Approximate solution of ${\textstyle \omega (\vartheta ,\iota {)}}$ (c) Absolute error at ${\textstyle \iota =1}$ (d) Representation of the approximate solution with the exact solution (e) Comparative graphical simulation in the steady state (f) The solution of the power series approaches the exact solution

Figure 2. The behavior of a collection of approximate solutions obtained for case (2) at $\sigma =1$, $\kappa =0.5{\sqrt {\frac {11}{19}}}$, $\zeta =5$ $,\eta =-25$

Table 2. Compare numerical calculations of analytical solutions $\omega \left(\vartheta ,\iota \right)$ of Eq. (40) obtained by TAM algorithm and NDM with exact,
and q-HATM solutions at $\sigma =1$, $\kappa =0.5{\sqrt {\frac {11}{19}}}$, $\zeta =5$ $,\eta =-25$

${\textstyle \vartheta }$	$\iota$	$\omega _{\scriptscriptstyle TAM}$	$\omega _{\scriptscriptstyle NDM}$	$\omega _{\scriptscriptstyle HATM}$ [30]	$\omega _{\scriptscriptstyle TAM}(\sigma =0.9)$	$\omega _{\scriptscriptstyle NDM}(\sigma =0.9)$
1	0.2	6.63085E09	6.63085E09	2.80432E08	1.96076E08	1.96076E08
	0.4	6.64967E08	6.64967E08	4.95160E07	1.38124E08	1.38124E08
	0.6	2.89030E07	2.89030E07	2.78309E06	2.11347E07	2.11347E07
	0.8	9.08435E07	9.08435E07	9.82802E06	8.09626E07	8.09626E07
	1	2.42595E06	2.42595E06	2.69893E05	2.31168E06	2.31168E06
2	0.2	3.09828E09	3.09828E09	1.78573E08	9.16171E09	9.16170E09
	0.4	3.10707E08	3.10708E08	3.15448E07	6.45387E09	6.45387E09
	0.6	1.35050E07	1.35050E07	1.77397E06	9.87523E08	9.87523E08
	0.8	4.24469E07	4.24469E07	6.26876E06	3.78300E07	3.78300E07
	1	1.13353E06	1.13353E06	1.72296E05	1.08014E06	1.08014E06
3	0.2	1.44768E09	1.44768E09	1.13536E08	4.28083E09	4.28083E09
	0.4	1.45179E08	1.45179E08	2.00631E07	3.01559E09	3.01559E09
	0.6	6.31024E08	6.31024E08	1.12878E06	4.61423E08	4.61423E08
	0.8	1.98334E07	1.98334E07	1.99096E06	1.76761E07	1.76761E07
	1	5.29645E07	5.29645E07	1.09765E06	5.04697E07	5.04697E07
4	0.2	6.76425E10	6.76430E10	7.20976E09	2.00023E09	2.00023E09
	0.4	6.78351E09	6.78351E09	1.27441E07	1.40904E09	1.40904E09
	0.6	2.94847E08	2.94848E08	7.17246E07	2.15601E08	2.15601E08
	0.8	9.26720E08	9.26720E08	2.53702E06	8.25922E08	8.25922E08
	1	2.47478E07	2.47478E07	6.98138E06	2.35821E07	2.35821E07
5	0.2	3.16056E10	3.16065E10	4.57388E09	9.34614E10	9.34609E10
	0.4	3.16960E09	3.16961E09	8.08667E08	6.58372E10	6.58377E10
	0.6	1.37768E08	1.37768E08	4.55249E07	1.00740E08	1.00740E08
	0.8	4.33012E08	4.33012E08	3.61084E07	3.85914E08	3.85914E08
	1	1.15635E07	1.15635E07	4.43462E07	1.10188E07	1.10188E07

5. Numerical results and discussion

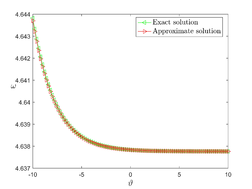
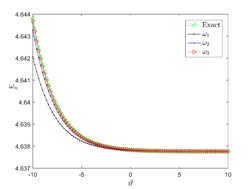
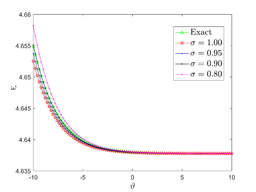
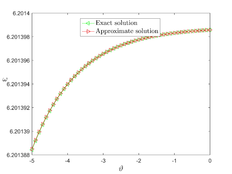
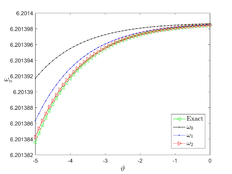
In this section, we provide the numerical solution to the Kuramoto-Sivashinsky equation for various values of ${\textstyle \vartheta }$, ${\textstyle \iota }$, ${\textstyle \omega _{n}}$ and fractional order ${\textstyle \sigma }$ using two methods: TAM and NDM. In Example 1, Figure 1 (a,b and c), we show the surfaces of the precise solution, the analytical solution derived using the TAM approach, and the absolute error for Eq. (20). Figure 1 (d) shows the ${\textstyle \omega _{n}}$-curves for the FKS equation at ${\textstyle \iota =0.1}$ and shows their convergence. In addition, in Figure 1 (e), we examined the precise solution and TAM for various values of n at ${\textstyle \iota =0.1}$, and we noticed that as n increases, the convergence of the two solutions (for negative x values) increases. As demonstrated in Figure 1 (f), values less than one increase the convergence between the exact solution and TAM. In Figure 2, we plotted the surfaces of both the exact solution and the TAM solution, as well as the absolute error between them, and compared them as in the first example, obtaining the same behaviour except in Figure 2 (f), where we discovered that values close to one provide a better approximation to the exact solution. For Examples 1 and 2, numerical results for various values of ${\textstyle \vartheta }$, ${\textstyle \iota }$, ${\textstyle \sigma =1,0.9}$ were given in Tables1 and 2 using the methods TAM and NDM, and the conclusions were reasonably similar to those in [30], but TAM method is better in convergence with the HATM method.

6. Conclusion

In this study, we successfully employed TAM and NDM to resolve the fractional Kuramoto-Sivashinsky problem. We give the numerical analysis of the FKS equation for two distinct initial conditions in the current analysis. The current techniques provide the parameter h1 which helps to control the convergence of the results obtained. The envisioned schemes manipulate and regulate the found solutions, which fast tend to the exact outcomes in a short sufficient area. According to the obtained results, TAM and NDM are capable of lowering work and evaluation time when compared to existing numerical algorithms while retaining high accuracy of results. As a result, we can infer that the used approaches are very systematic and extremely strong in analyzing fractional-order mathematical models.

Conflict of Interest: The author declare that there is no Conflict of Interest.

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R522), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

References

[1] Miller K.S., Ross B. An introduction to the fractional calculus and fractional differential equations. John Wiley & Sons, Inc., New York/Singapore, 1993.

[2] Podlubny I. Fractional differential equations, mathematics in science and engineering. Academic Press, San Diego, 1999.

[3] Almuneef A., Hagag A.E. Approximate solution of the fractional differential equation via the natural decomposition method. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 39(4), 42, 1-15, 2023.

[4] Wang Z., Huang X., Li Y.X., Song X.N. A new image encryption algorithm based on the fractional-order hyperchaotic Lorenz system. Chinese Physics B, 22(1), 010504, 2013.

[5] Almuneef A., Hagag, A.E. Analytical solution to fractional differential equation arising in thermodynamics. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 39(4), 49, 1-16, 2023.

[6] Hilfer R. (ed.). Applications of fractional calculus in physics. World scientific, Universität Mainz & Universität Stuttgart, Germany, pp. 472, 2000. . https://api.semanticscholar.org/CorpusID:117406670.

[7] Alqahtani Z., Hagag A.E. A new semi-analytical solution of compound KdV-Burgers equation of fractional order. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 39(4), 38, 1-16, 2023.

[8] Alqahtani, Z. and Hagag, A.E. A fractional numerical study on a plant disease model with replanting and preventive treatment. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 39(3), 27, 1-21, 2023.

[9] Li C., Chen G., Zhao S. Exact travelling wave solutions to the generalized Kuramoto-Sivashinsky equation. Latin American applied research, 34(1):65-68, 2004.

[10] Ellahi R., Alamri S.Z., Basit A., Majeed A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. Journal of Taibah University for Science, 12(4):476-482, 2018.

[11] Rademacher J.D., Wittenberg R.W. Viscous shocks in the destabilized Kuramoto-Sivashinsky equation. J. Comput. Nonlinear Dynam., 1(4):336-347, 2006.

[12] Zeeshan A., Hussain F., Ellahi R., Vafai K. A study of gravitational and magnetic effects on coupled stress bi-phase liquid suspended with crystal and Hafnium particles down in steep channel. Journal of Molecular Liquids, 286, 110898, 2019.

[13] Khan A.A., Bukhari S.R., Marin, M., Ellahi R. Effects of chemical reaction on third-grade MHD fluid flow under the influence of heat and mass transfer with variable reactive index. Heat Transfer Research, 50(11):1061-1080, 2019.

[14] Prakash J., Tripathi D., Tiwari A.K., Sait S.M., Ellahi R. Peristaltic pumping of nanofluids through a tapered channel in a porous environment: applications in blood flow. Symmetry, 11(7):868, 2019.

[15] Riaz A., Ellahi R., Bhatti M.M., Marin M. Study of heat and mass transfer in the EyringPowell model of fluid propagating peristaltically through a rectangular compliant channel. Heat Transfer Research, 50(16):1539-1560, 2019.

[16] Conte R. Exact solutions of nonlinear partial differential equations by singularity analysis. In Direct and Inverse Methods in Nonlinear Evolution Equations. Lecture Notes in Physics, vol 632, Springer, Berlin, Heidelberg, 2003.

[17] Kuramoto Y., Tsuzuki T. Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. Progress of theoretical physics, 55(2):356-369, 1976.

[18] Tadmor E. The well-posedness of the Kuramoto-Sivashinsky equation. SIAM Journal on Mathematical analysis, 17(4):884-893, 1986.

[19] Sivashinsky G.I. Instabilities, pattern formation, and turbulence in flames. Annual Review of Fluid Mechanics, 15(1):179-199, 1983.

[20] Hooper A.P., Grimshaw R. Nonlinear instability at the interface between two viscous fluids. The Physics of Fluids, 28(1):37-45, 1985.

[21] Akrivis G., Smyrlis Y.S. Implicit-explicit BDF methods for the Kuramoto-Sivashinsky equation. Applied Numerical Mathematics, 51(2-3):151-169, 2004.

[22] Akrivis G.D. Finite difference discretization of the KuramotoSivashinsky equation. Numerische Mathematik, 63:1-11, 1992.

[23] Ersoy O., Dag I. The exponential cubic b-Spline collocation method for the Kuramoto-Sivashinsky equation. Filomat, 30(3):853-861, 2016.

[24] Rezazadeh H., Ziabarya B.P. Sub-equation method for the conformable fractional generalized kuramoto sivashinsky equation. Computational Research Progress in Applied Science & Engineering, 2(3):106- 109, 2016.

[25] Manaa S.A., Easif F.H., Yousif M.A. Adomian decomposition method for Sslving the Kuramoto-Sivashinsky equation. IOSR Journal of Mathematics, 10:08-12, 2014.

[26] Kulkarni S., Takale K., Gaikwad S. Numerical solution of time fractional Kuramoto-Sivashinsky equation by Adomian decomposition method and applications. Malaya Journal of Matematik (MJM), 8(3):1078-1084, 2020.

[27] Okeke J.E., Okoli O.C., Obi T.A., Ujumadu R.N. New exact solution of a class of Kuramoto Sivashinsky (KS) equations using double reduction theory. International Journal of Innovative Science and Research Technology, 7(3):477-487, 2022.

[28] Kilicman A., Silambarasan R. Modified Kudryashov method to solve generalized Kuramoto-Sivashinsky equation. Symmetry, 10(10):527, 2018.

[29] Noor M.A., Mohyud-Din S.T., Waheed A. Exp-function method for solving KuramotoSivashinsky and Boussinesq equations. Journal of Applied Mathematics and Computing, 29:1-13, 2009.

[30] Veeresha P., Prakasha D.G. Solution for fractional Kuramoto-Sivashinsky equation using novel computational technique. International Journal of Applied and Computational Mathematics, 7(2):33, 2021.

[31] Abbasbandy S. Solitary wave solutions to the KuramotoSivashinsky equation by means of the homotopy analysis method. Nonlinear Dynamics, 52:35-40, 2008.

[32] Kurulay M., Secer A., Akinlar M.A. A new approximate analytical solution of Kuramoto-Sivashinsky equation using homotopy analysis method. Applied Mathematics & Information Sciences, 7(1):267-271, 2013.

[33] Shah R., Khan H., Baleanu D., Kumam P., Arif M. A semianalytical method to solve family of Kuramoto-Sivashinsky equations. Journal of Taibah University for Science, 14(1):402-411, 2020.

[34] Acan O., Keskin Y. Approximate solution of Kuramoto-Sivashinsky equation using reduced differential transform method. In AIP Conference Proceedings, 1648(1):470003, AIP Publishing LLC, 2015.

[35] Temimi H., Ansari A.R. A semi-analytical iterative technique for solving nonlinear problems. Computers & Mathematics with Applications, 61(2):203-210, 2011.

[36] Al-Hanaya A., Alotaibi M., Shqair M., Hagag A.E. MHD effects on Casson fluid flow squeezing between parallel plates. AIMS Mathematics, 8(12):29440-29452, 2023.

[37] Rawashdeh M.S. The fractional natural decomposition method: theories and applications. Mathematical Methods in the Applied Sciences, 40(7):2362-2376, 2017.

[38] Liouville J. Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions. Journal de l'École Polytechnique, 13(21):1-69, 1832.

[39] Kilbas A.A., Srivastava H.M., Trujillo J.J. (eds.). Theory and applications of fractional differential equations. Elsevier, 204:1-523, 2006.

[40] Khan Z.H., Khan W.A. N-transform properties and applications. NUST Journal of Engineering Sciences, 1(1):127-133, 2008.

[41] Belgacem F.B.M., Silambarasan R. Advances in the natural transform. In AIP Conference Proceedings, 1493(1):106-110, American Institute of Physics, 2012.